Linear Static Behavior of Damaged Laminated Composite Plates and Shells
Abstract
:1. Introduction
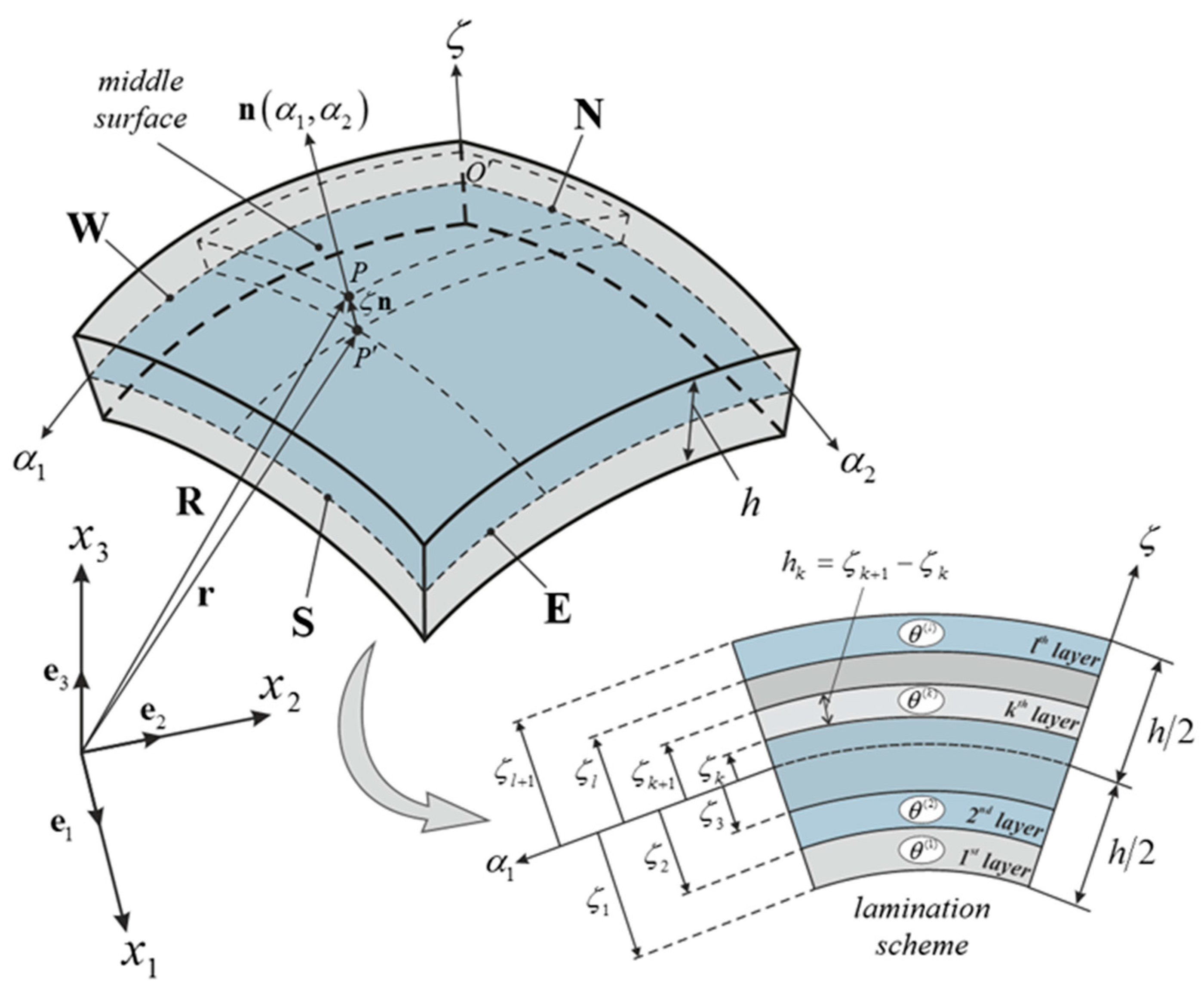
2. Shell Geometry
3. Shell Structural Model
4. Numerical Solution
5. Solution of the Static Problem
6. Strain and Stress Recovery Procedure
7. Evaluation of the Elastic Coefficients
8. Applications
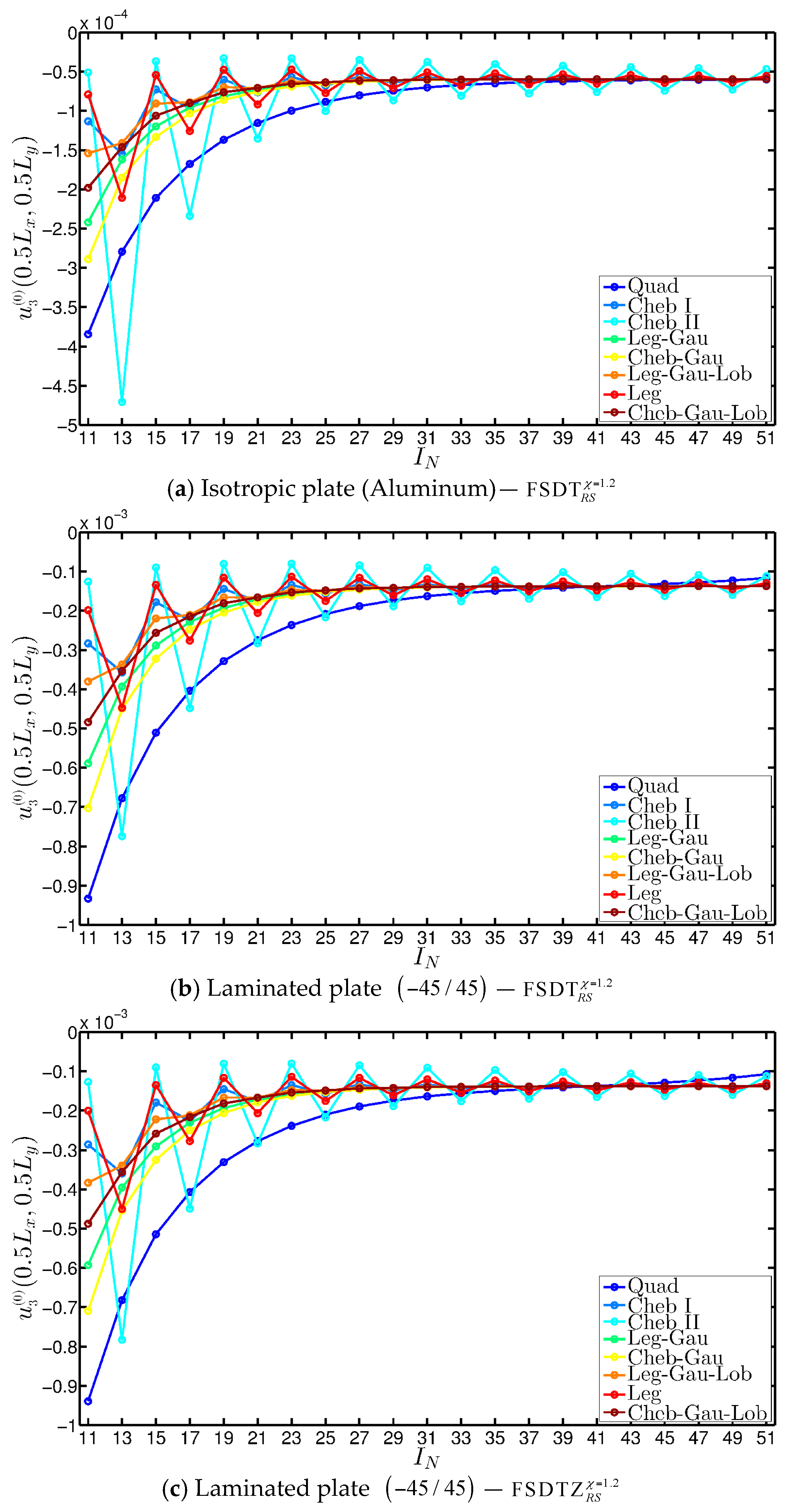
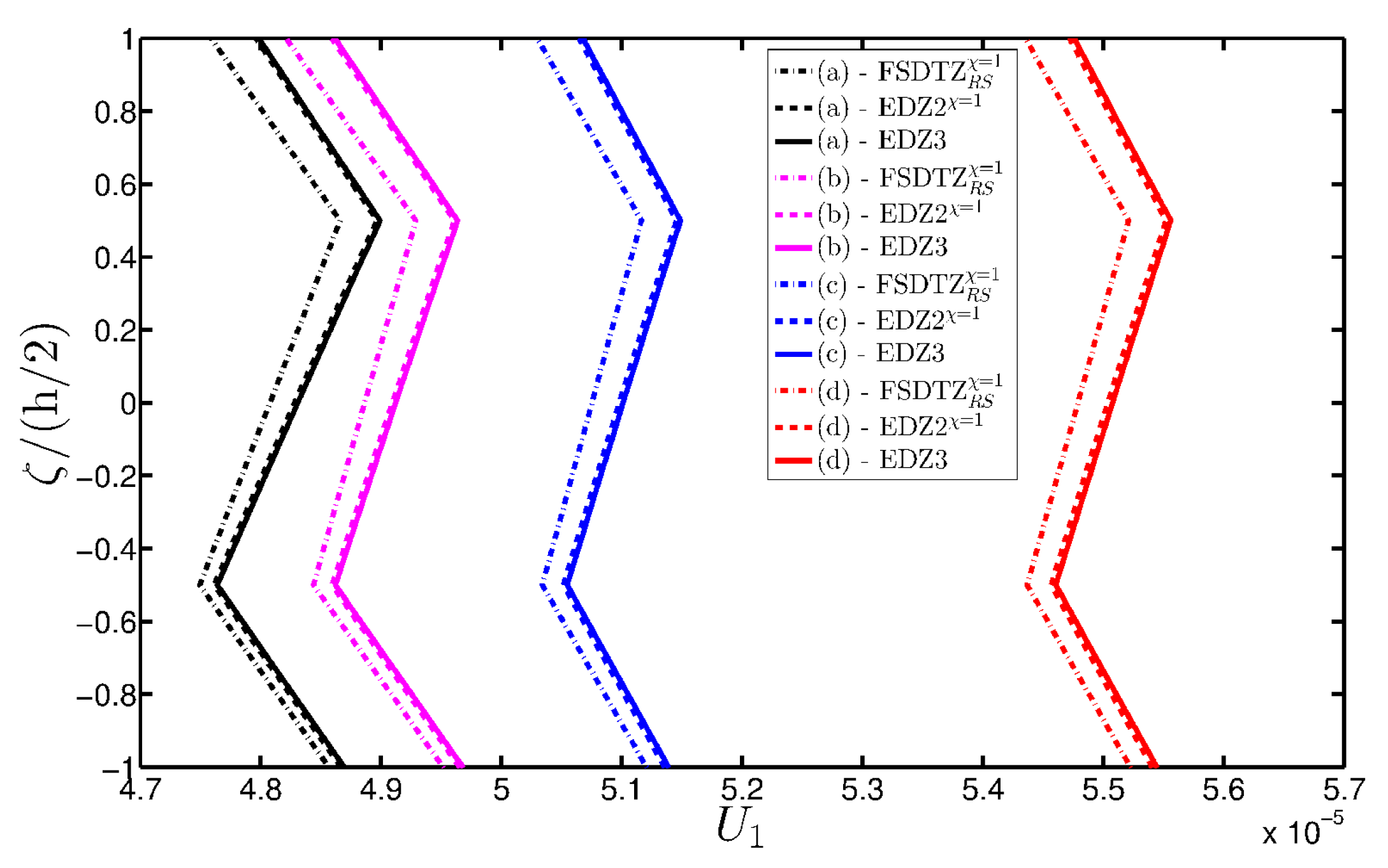
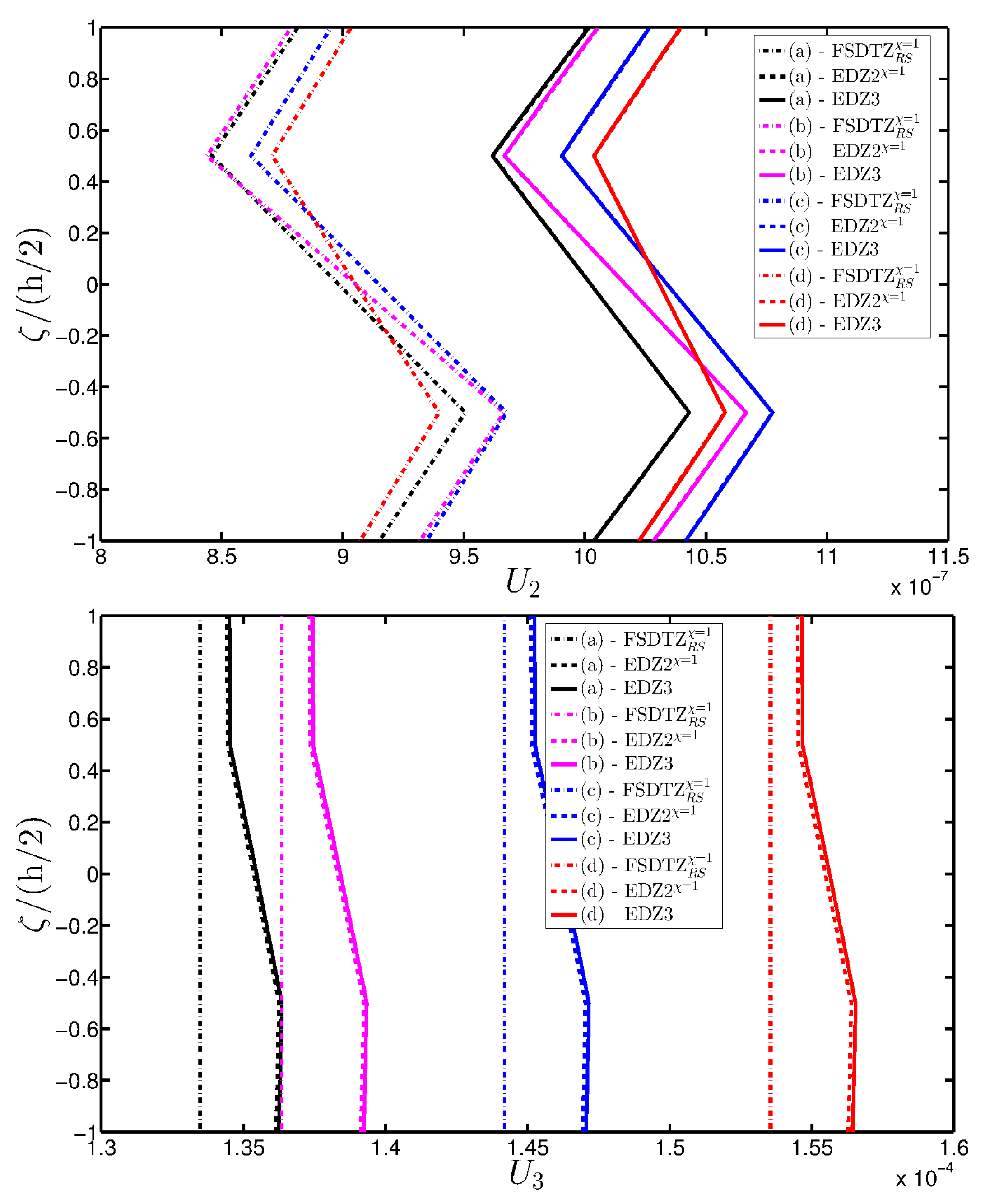
8.1. Convergence Analyses
8.2. Isotropic Square Plate
8.3. Laminated Square Plate
8.4. Cylindrical Panel
8.5. Doubly-Curved Panel of Revolution
9. Conclusions and Remarks
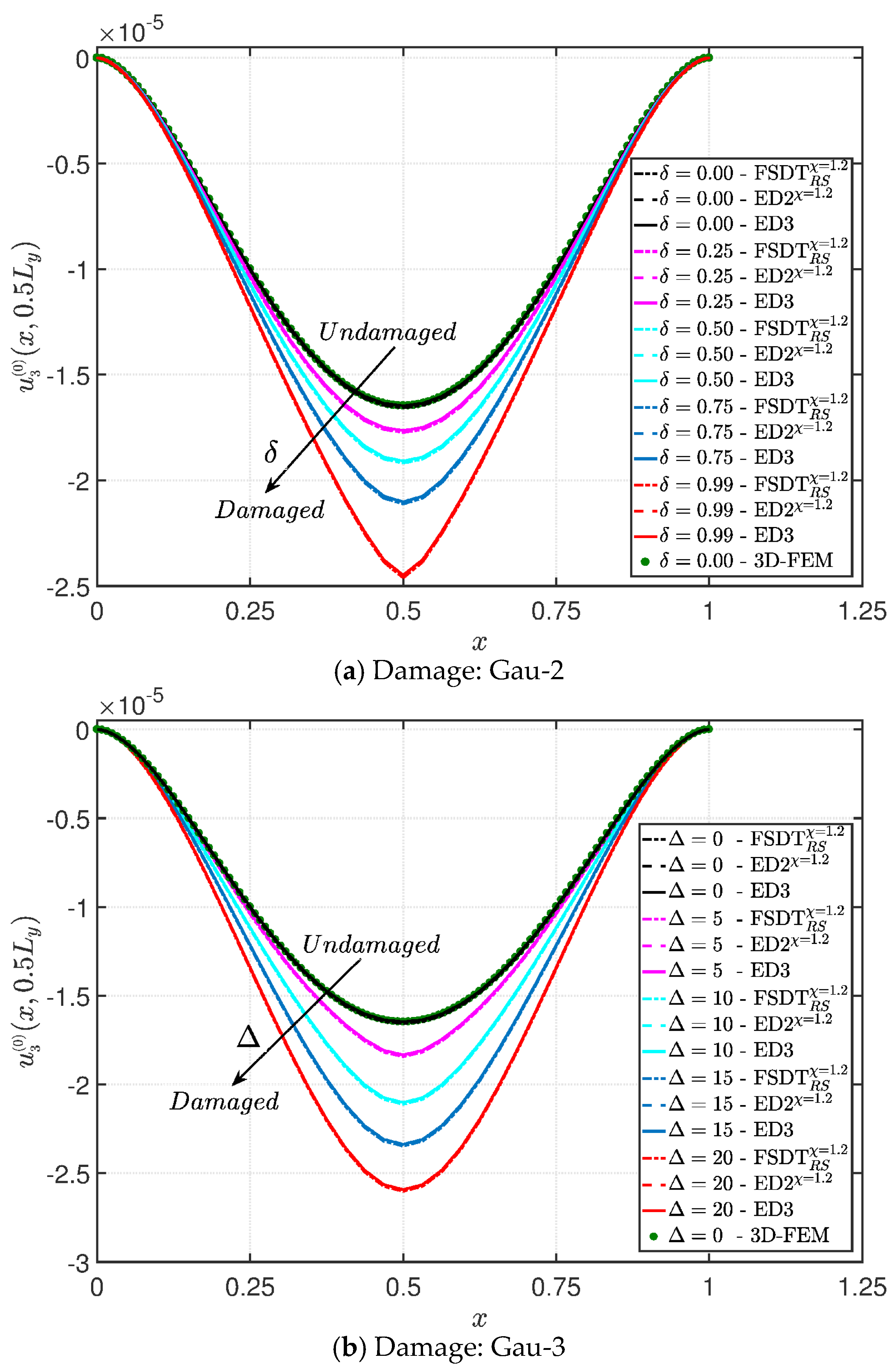
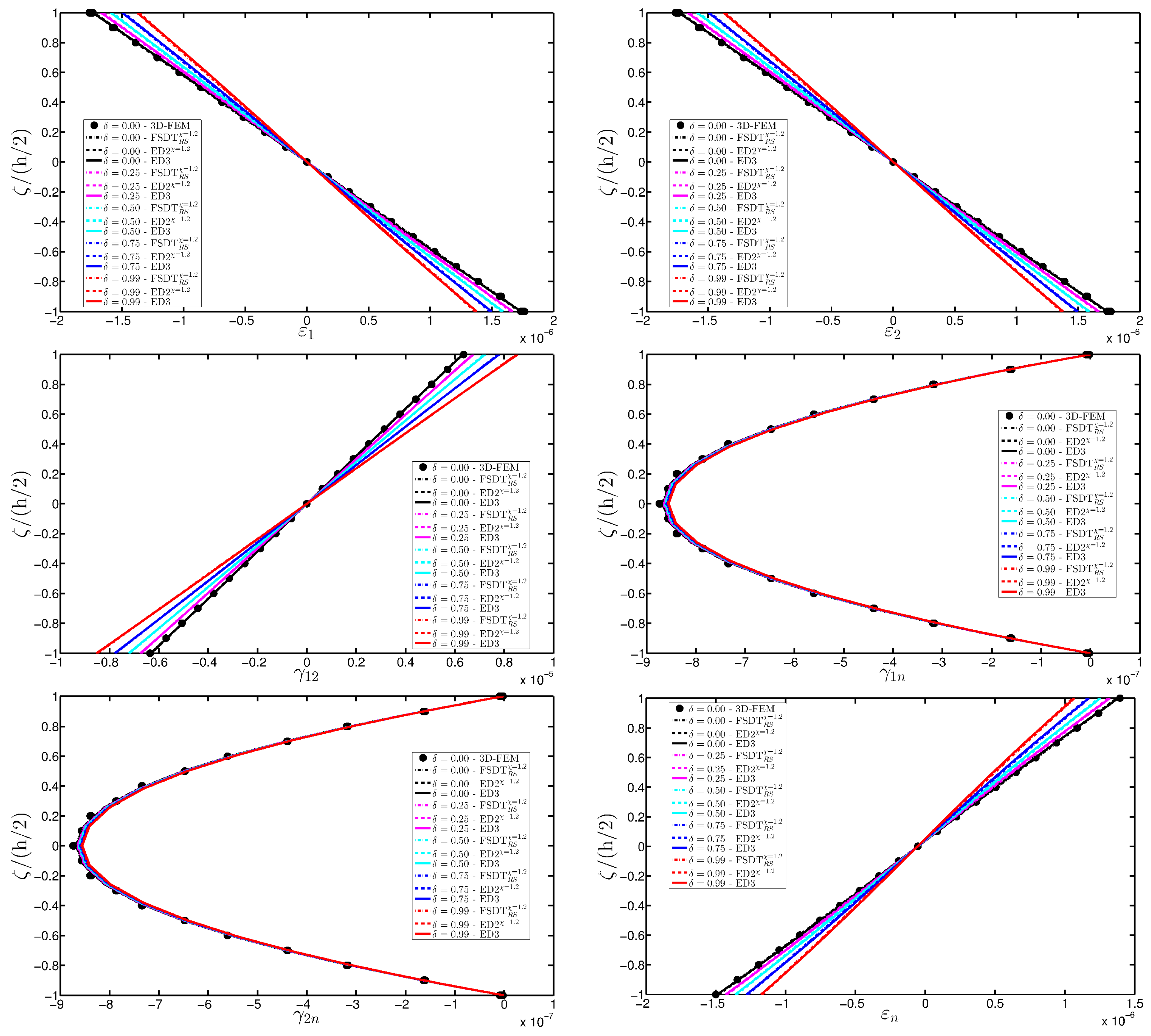
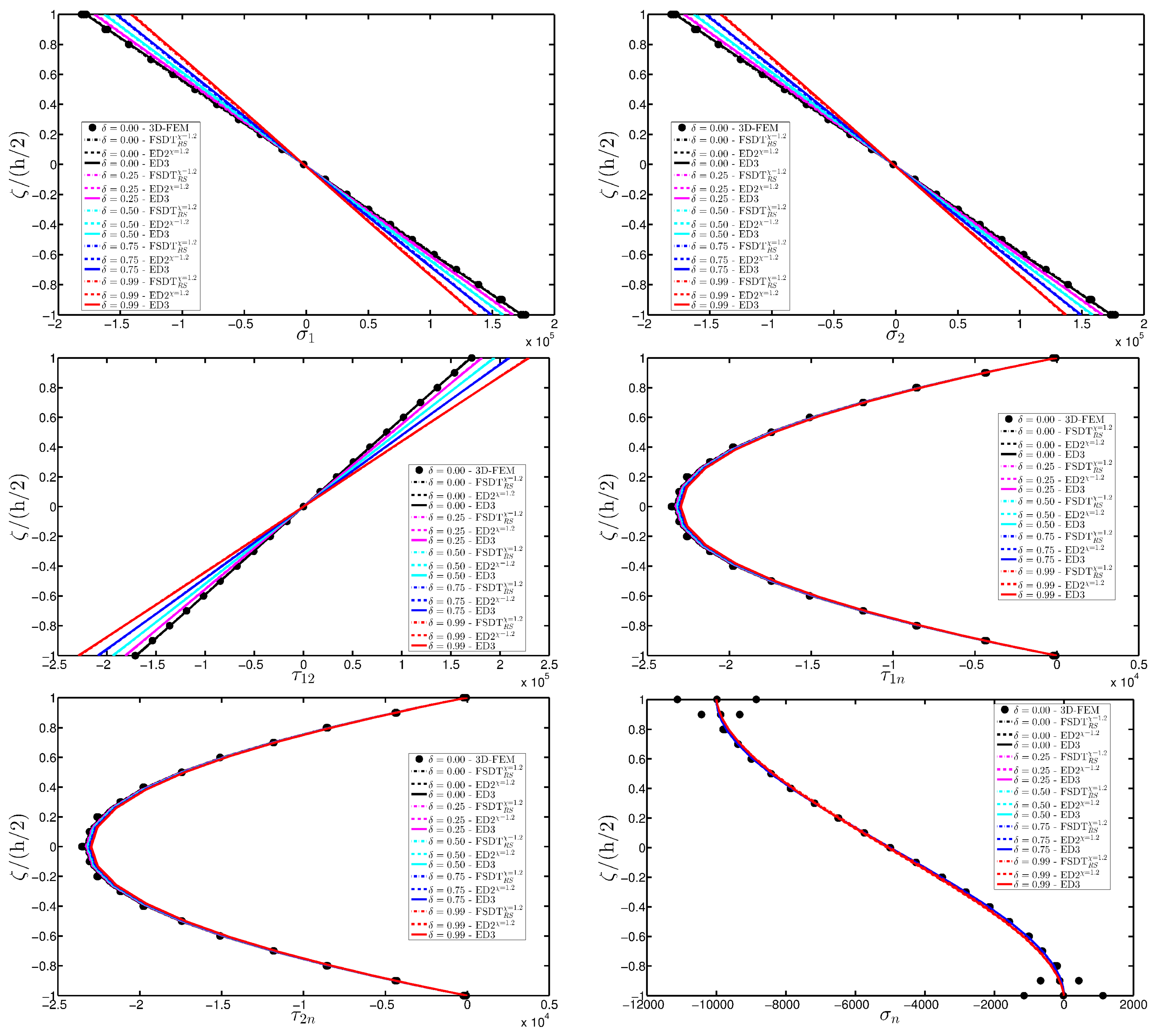
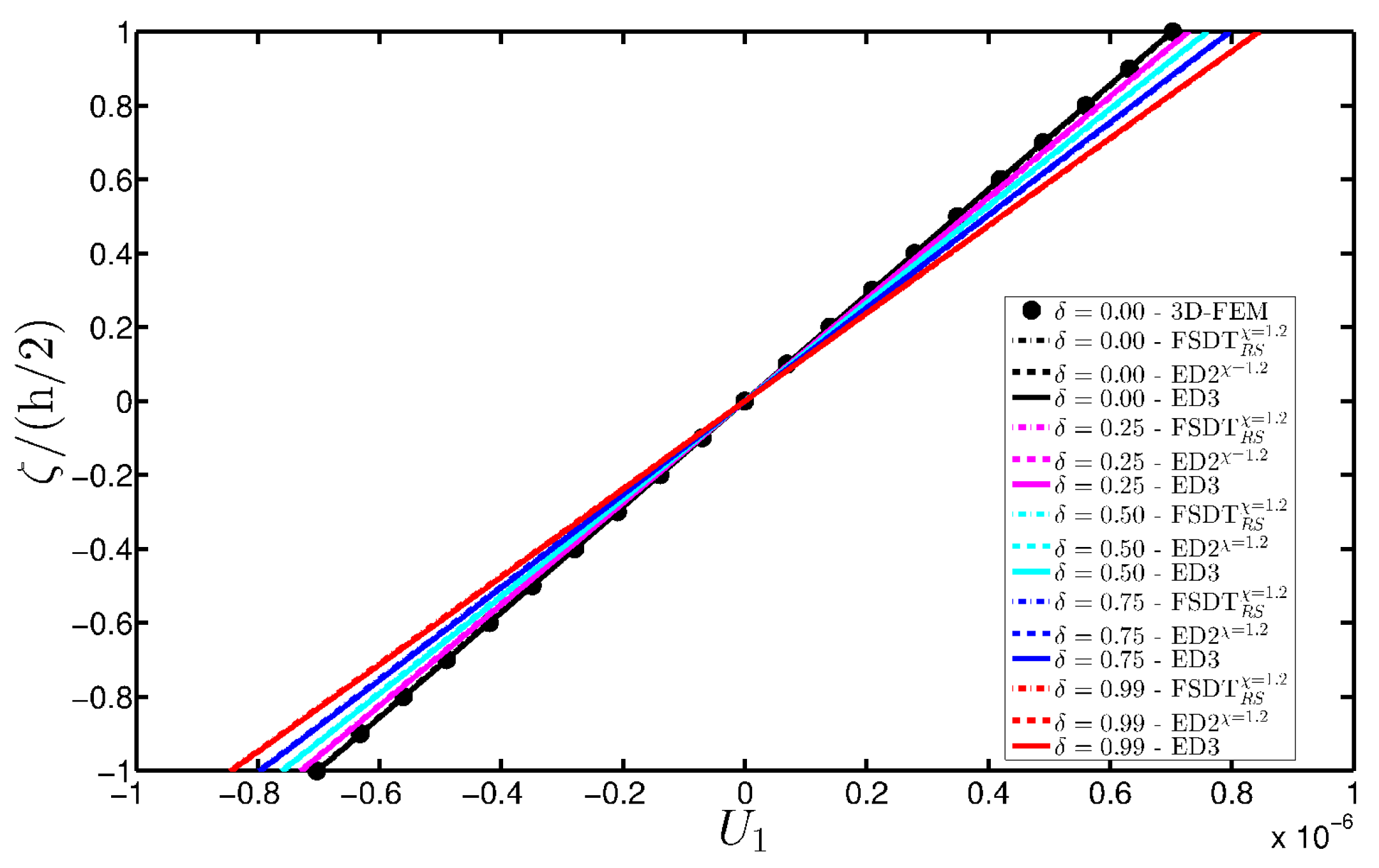
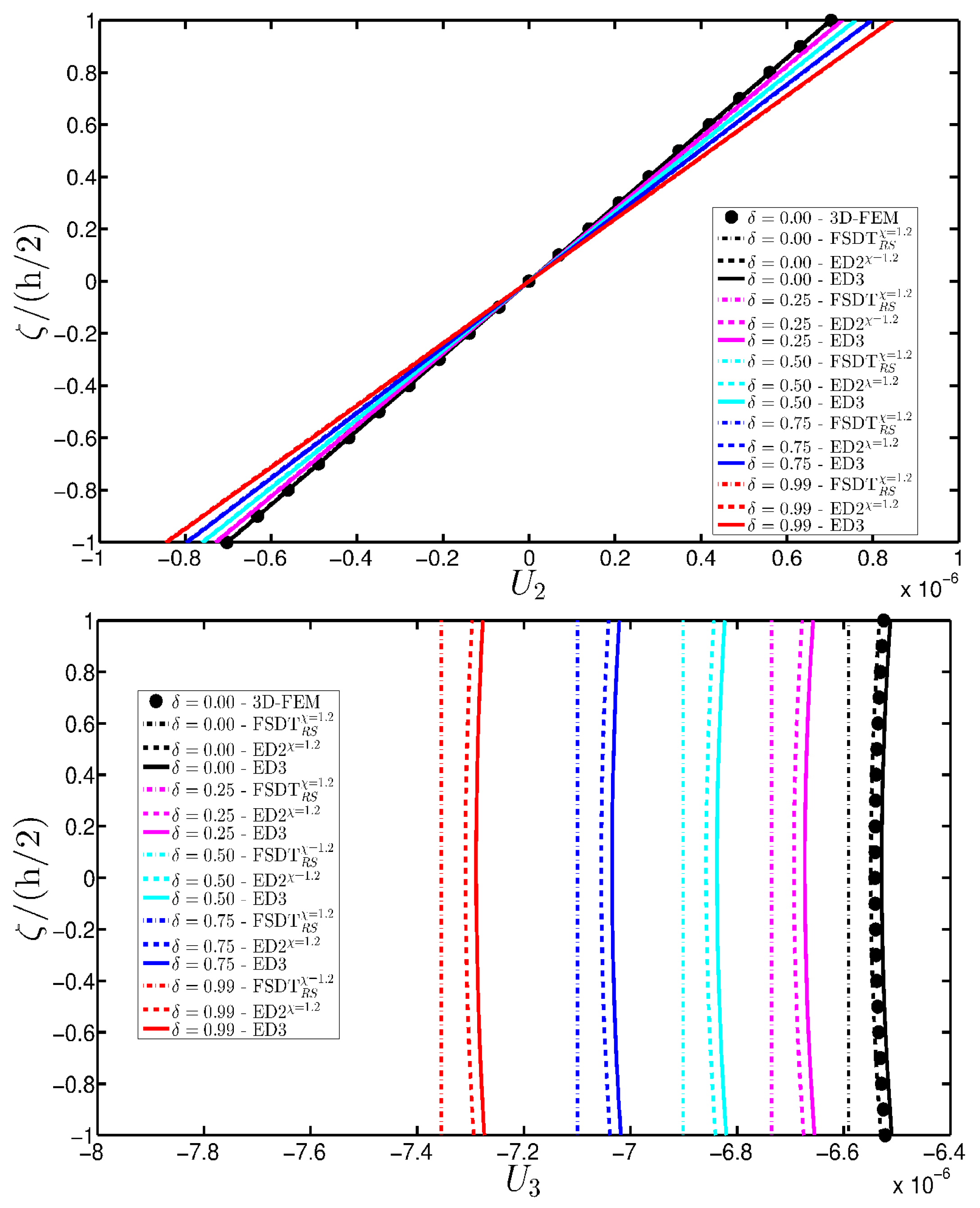
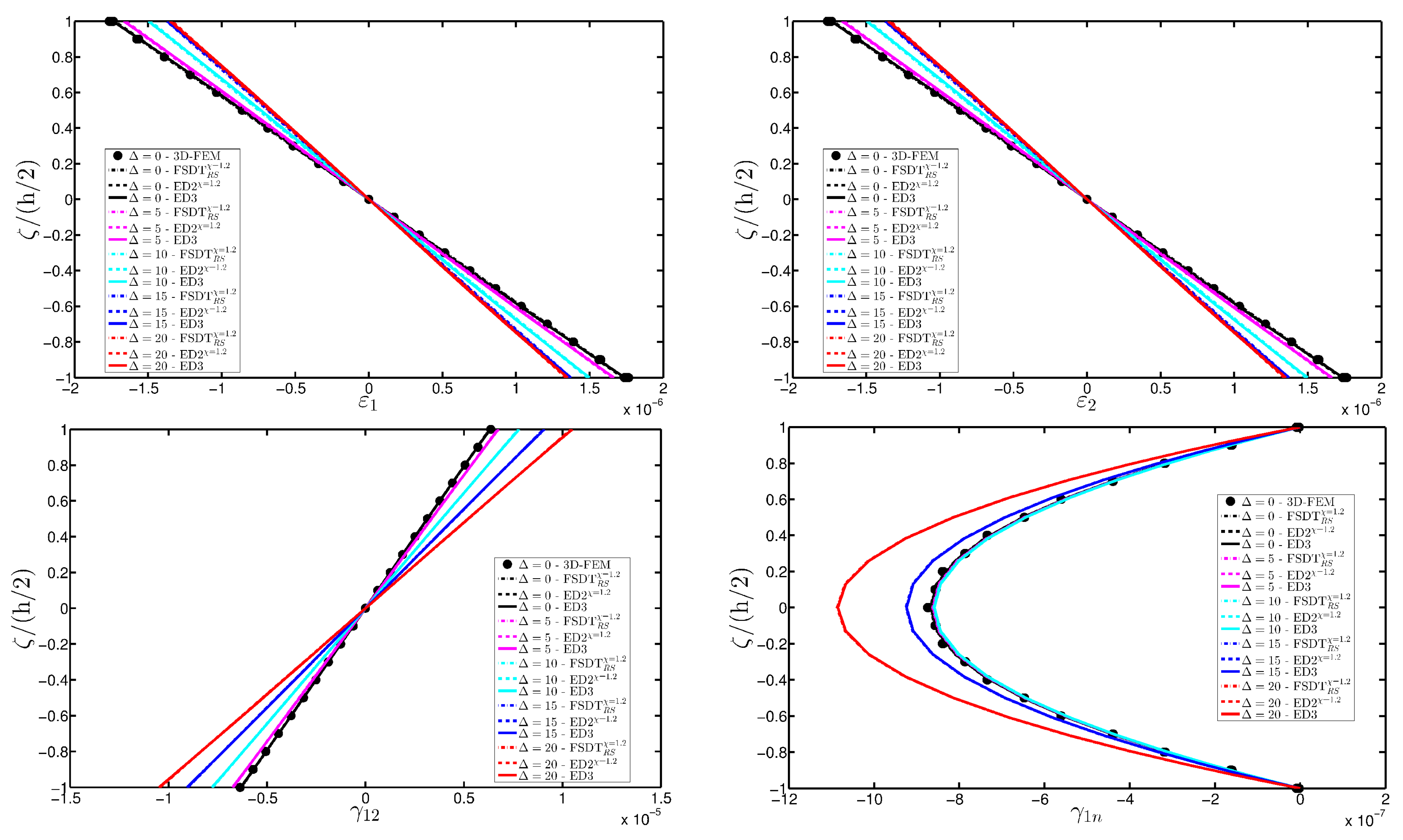
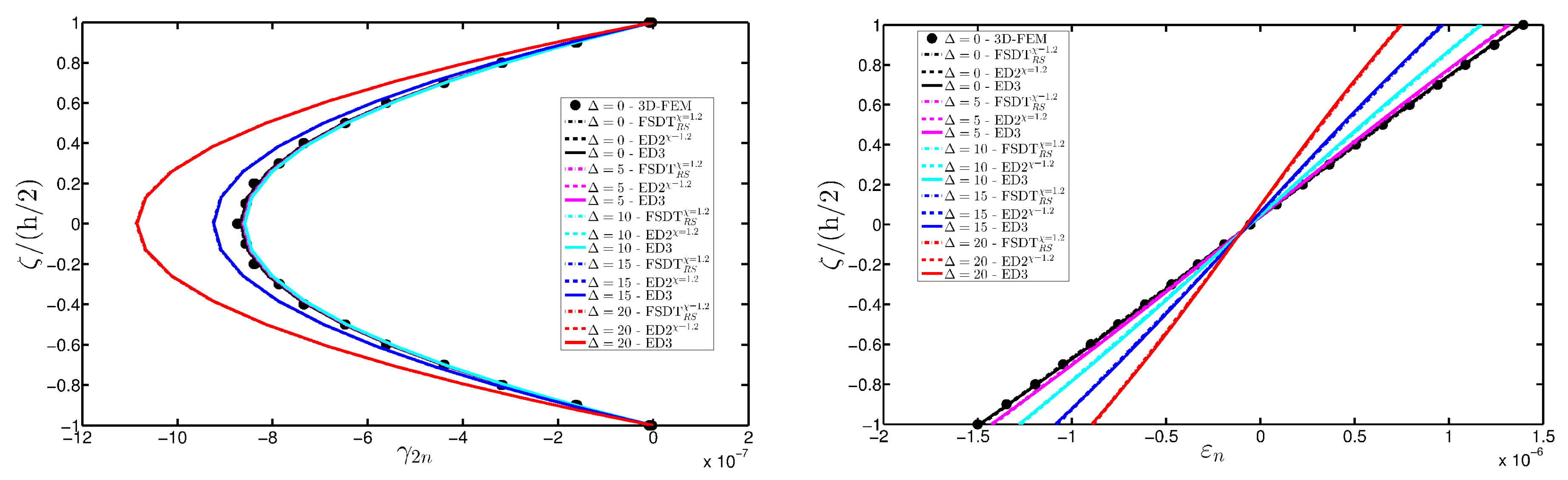
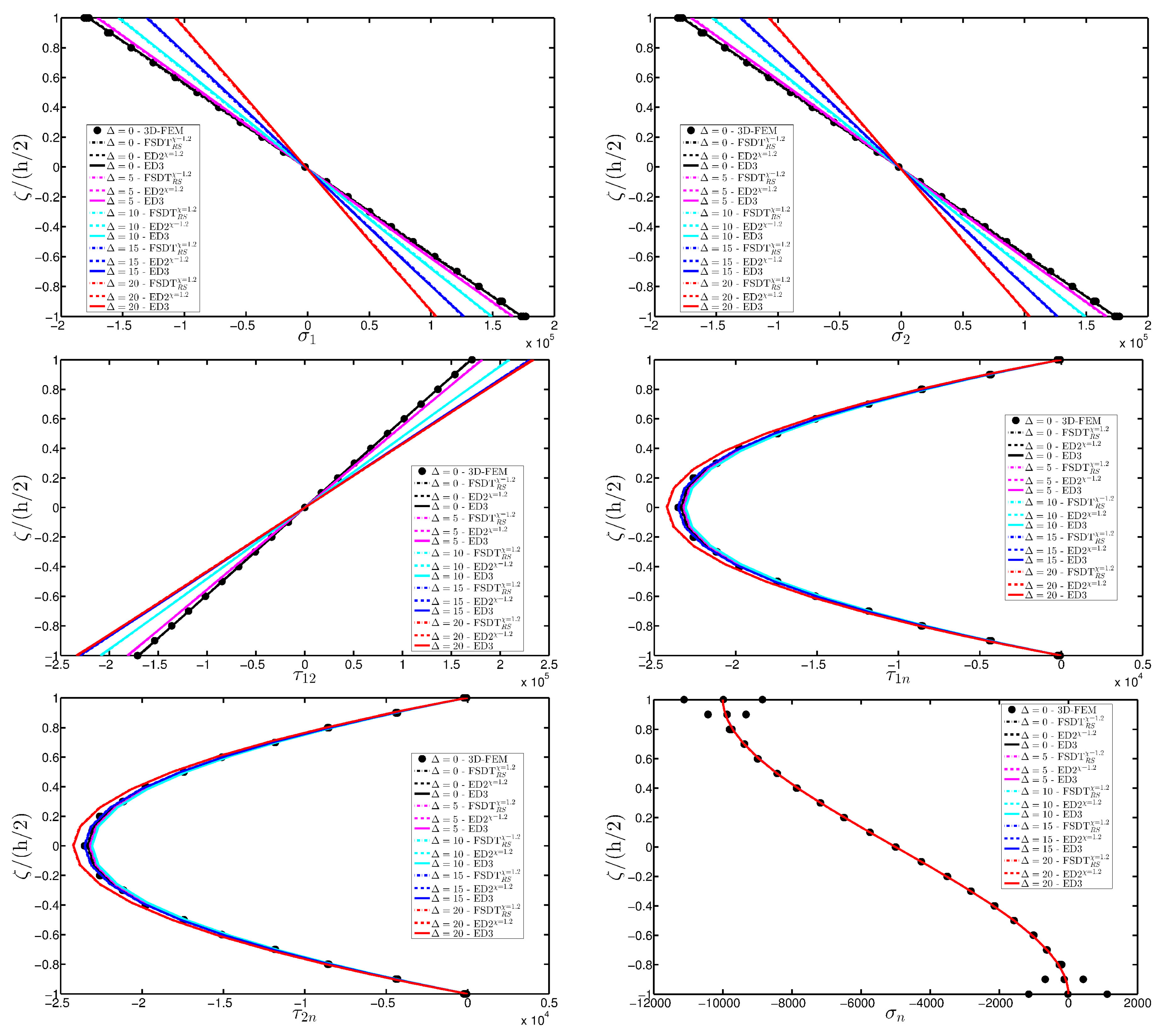
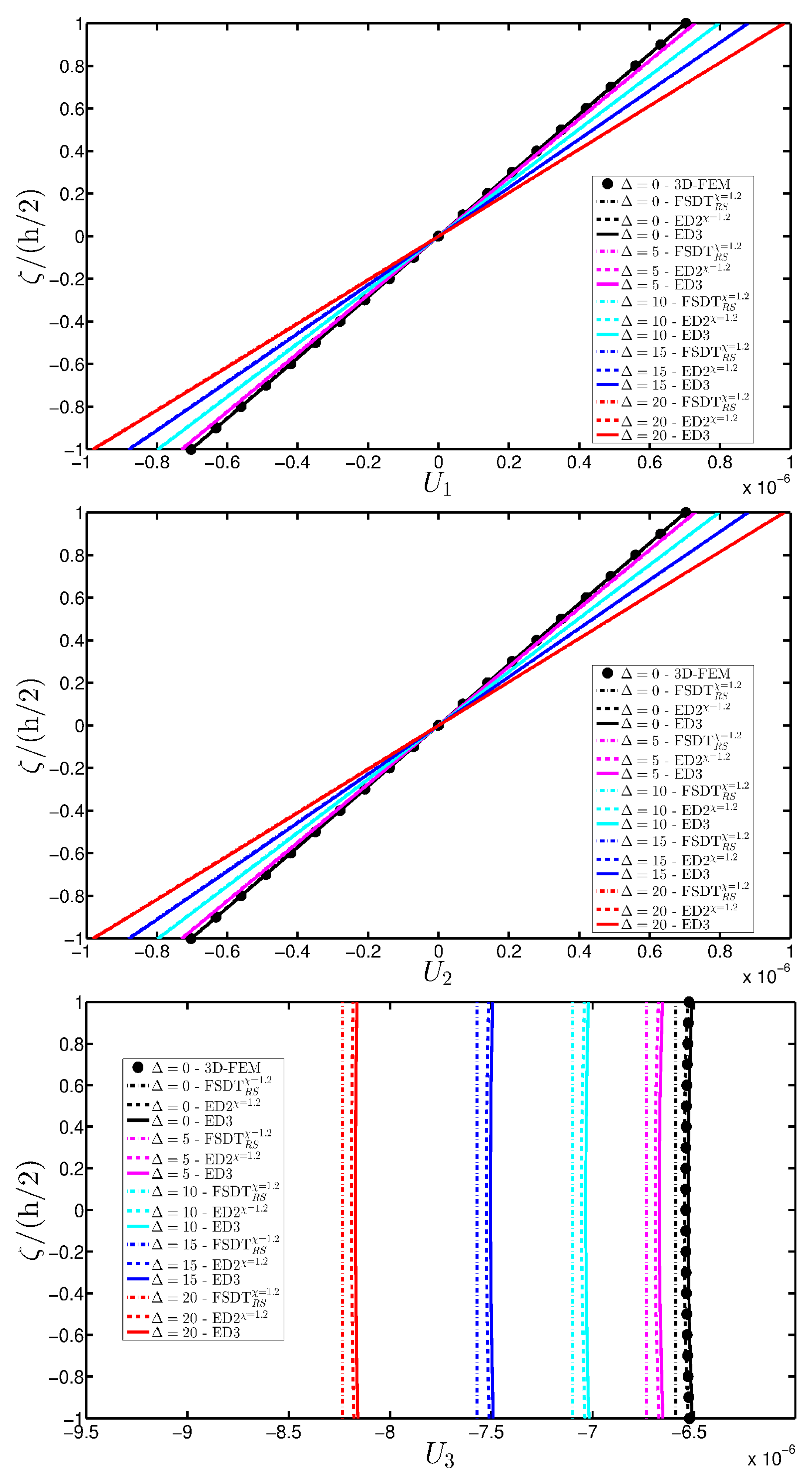
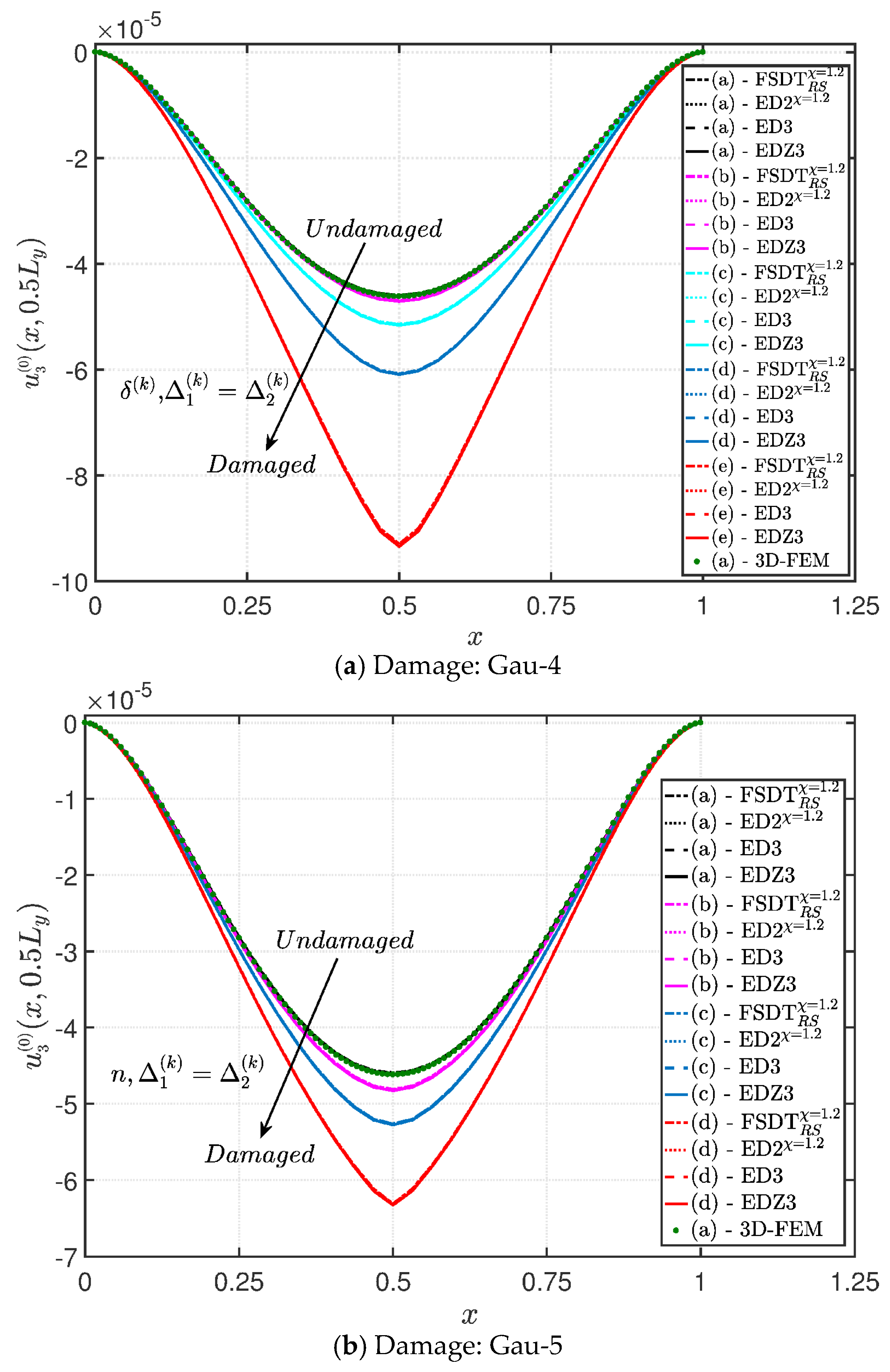
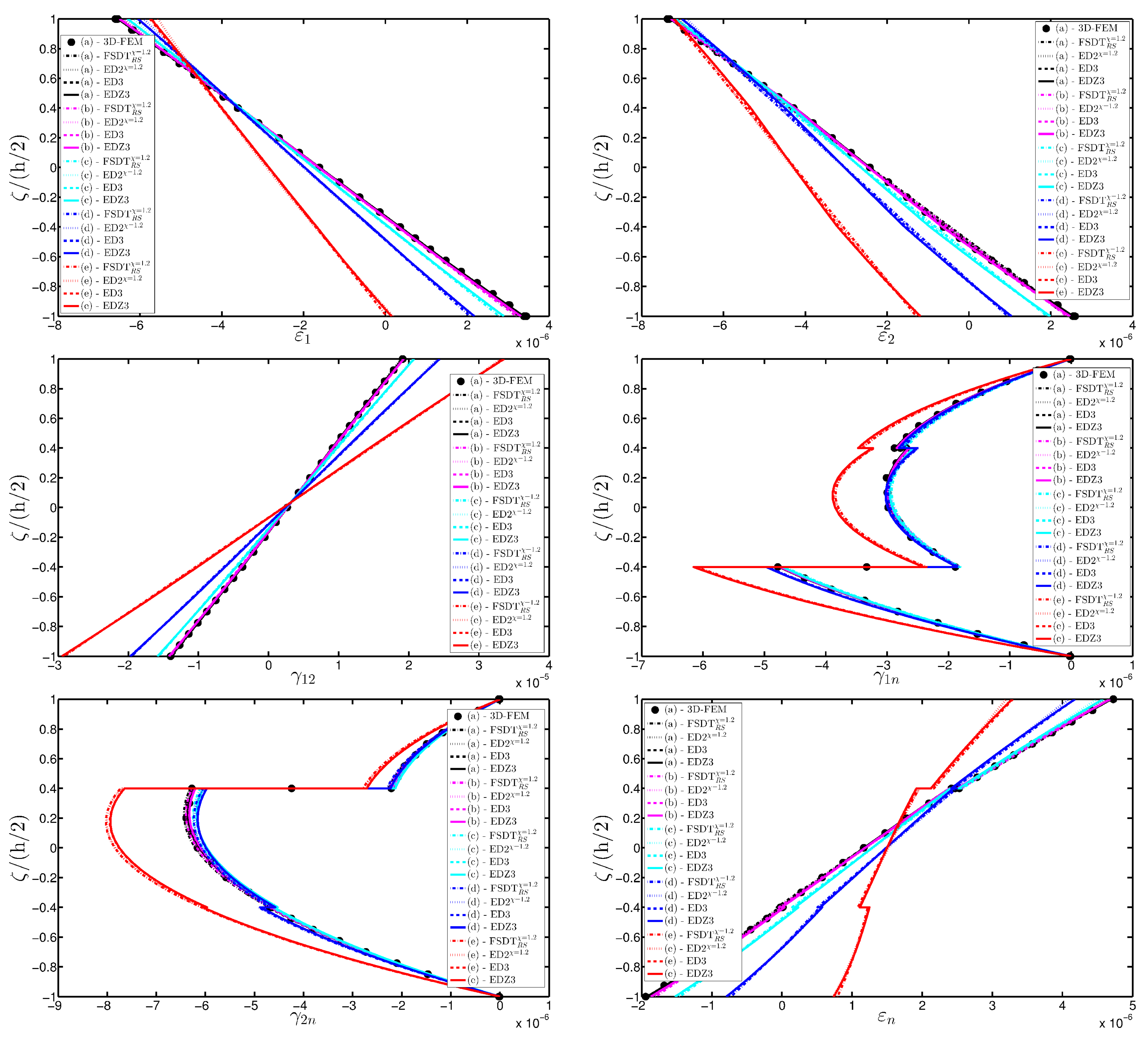
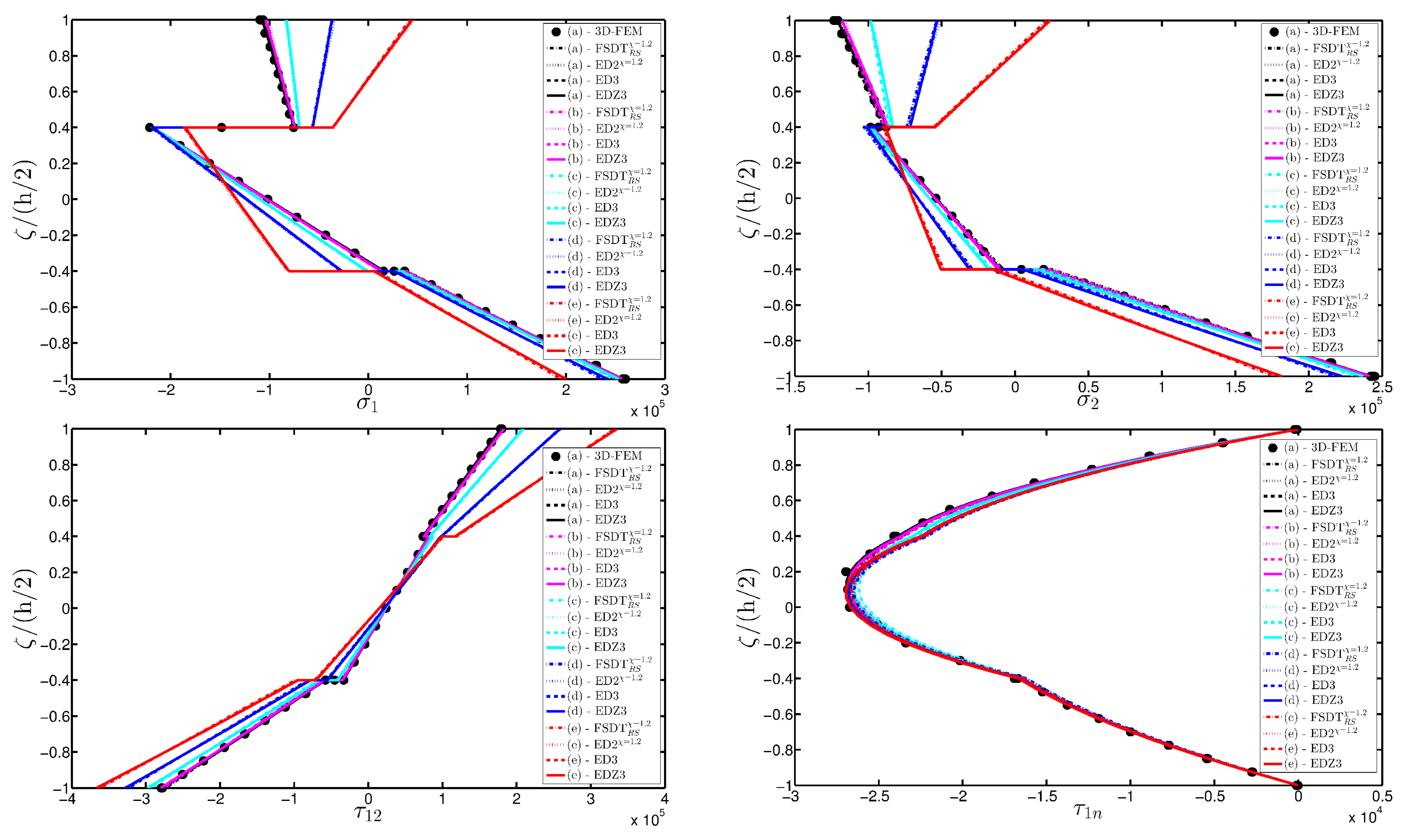
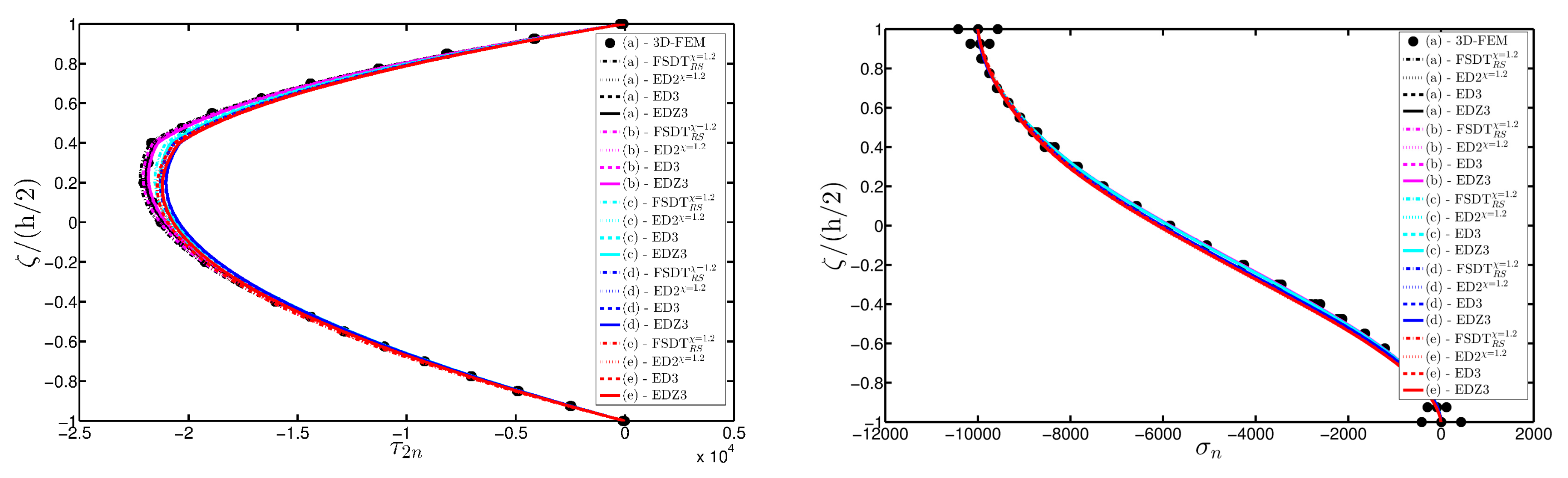
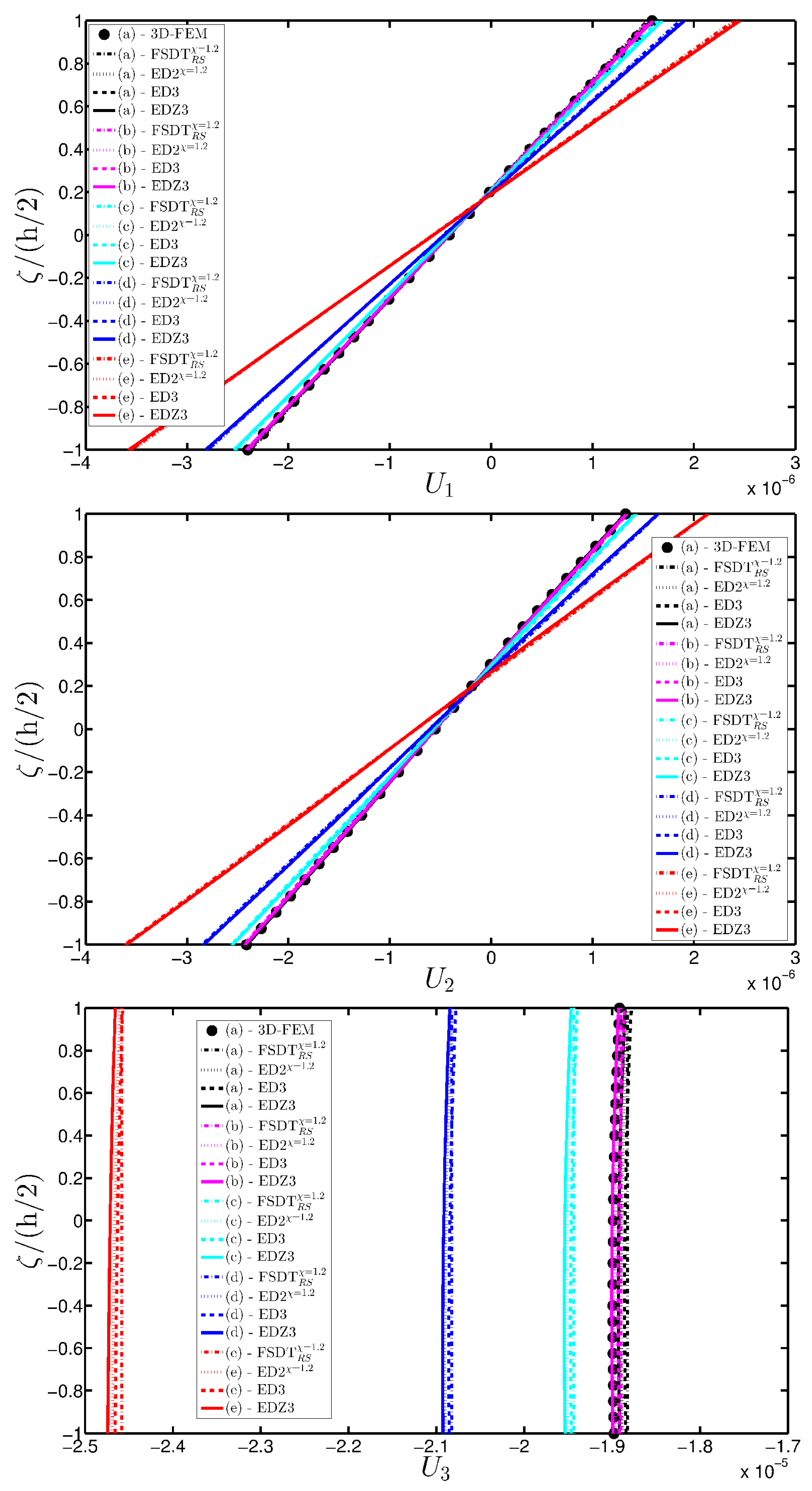
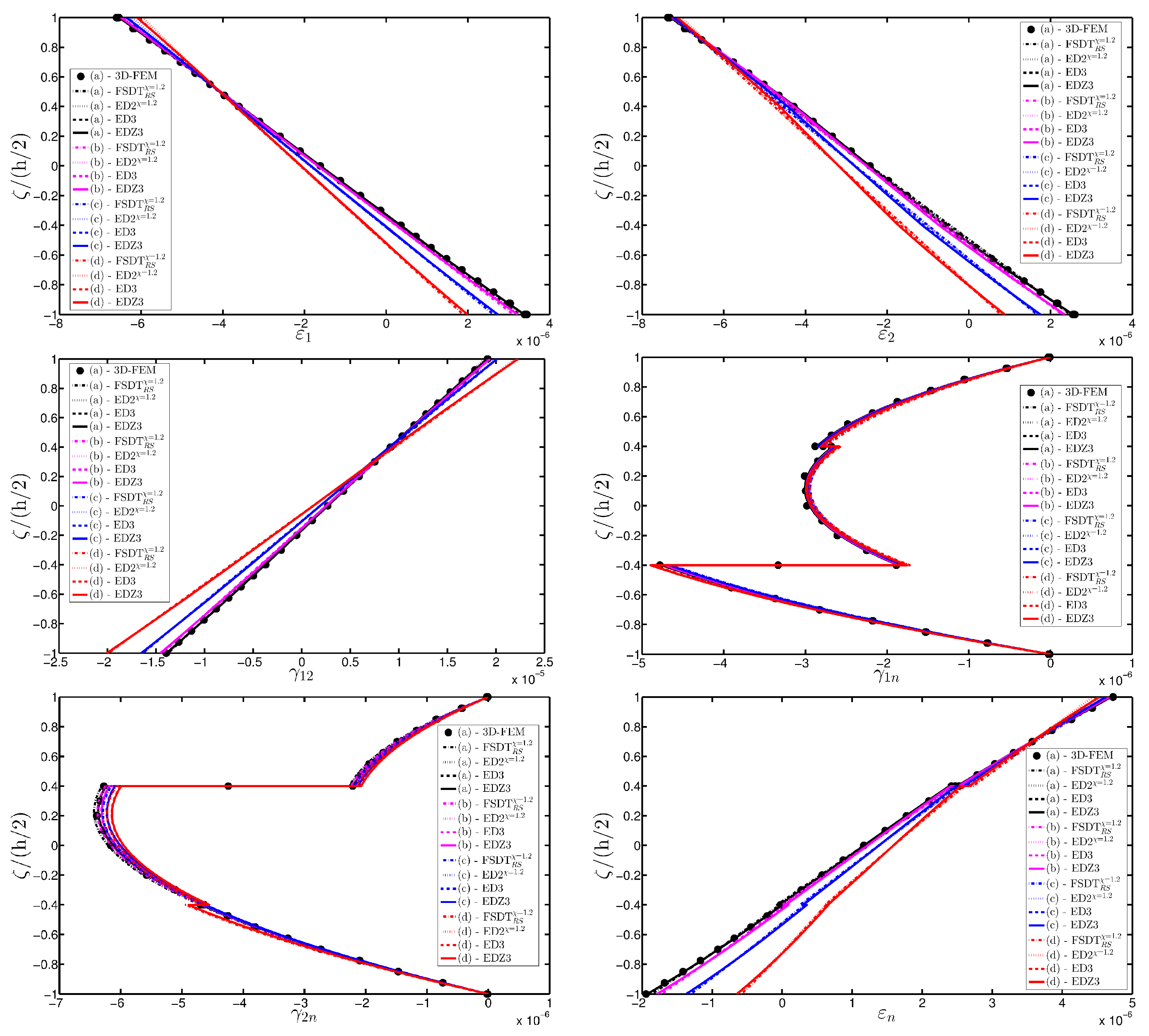
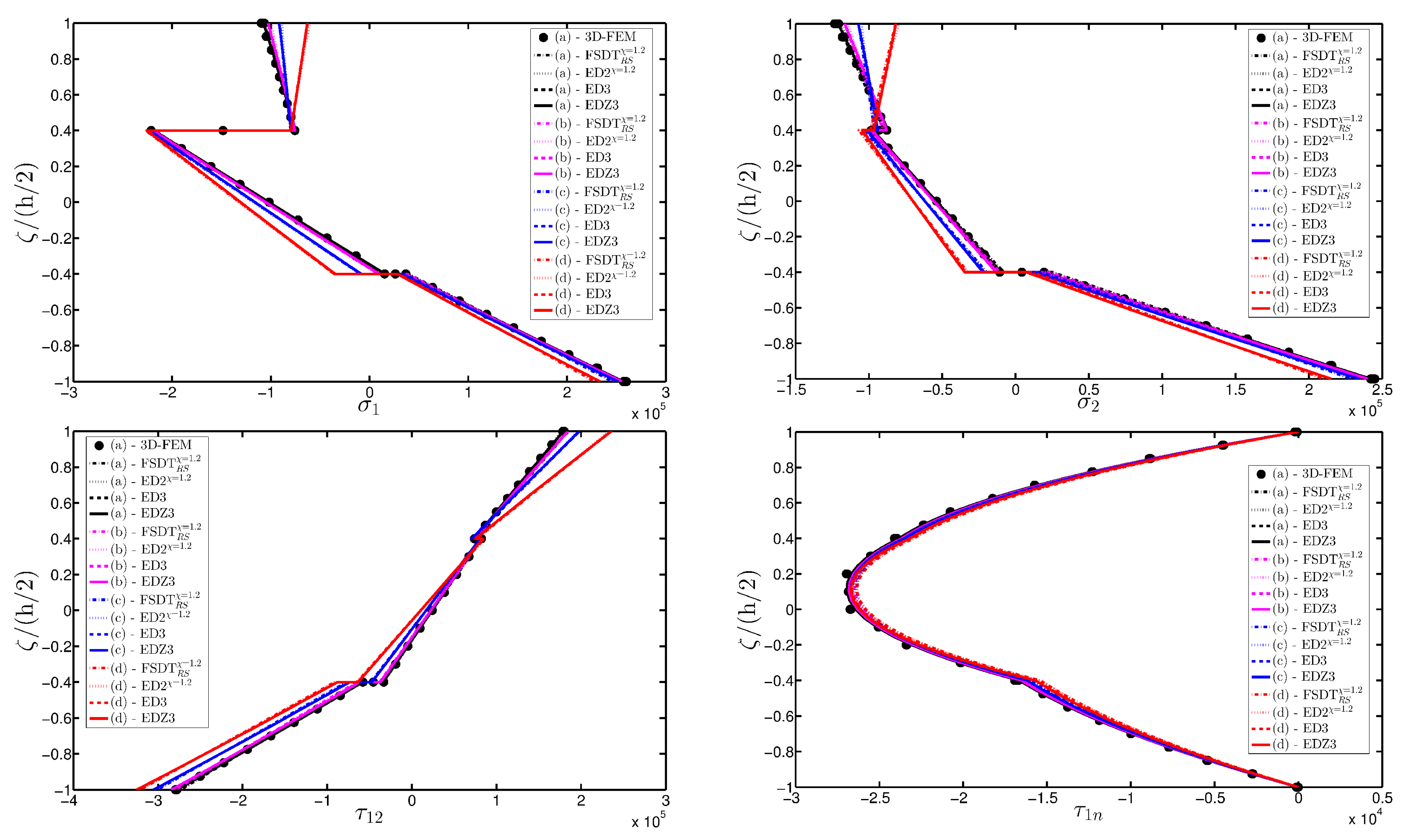
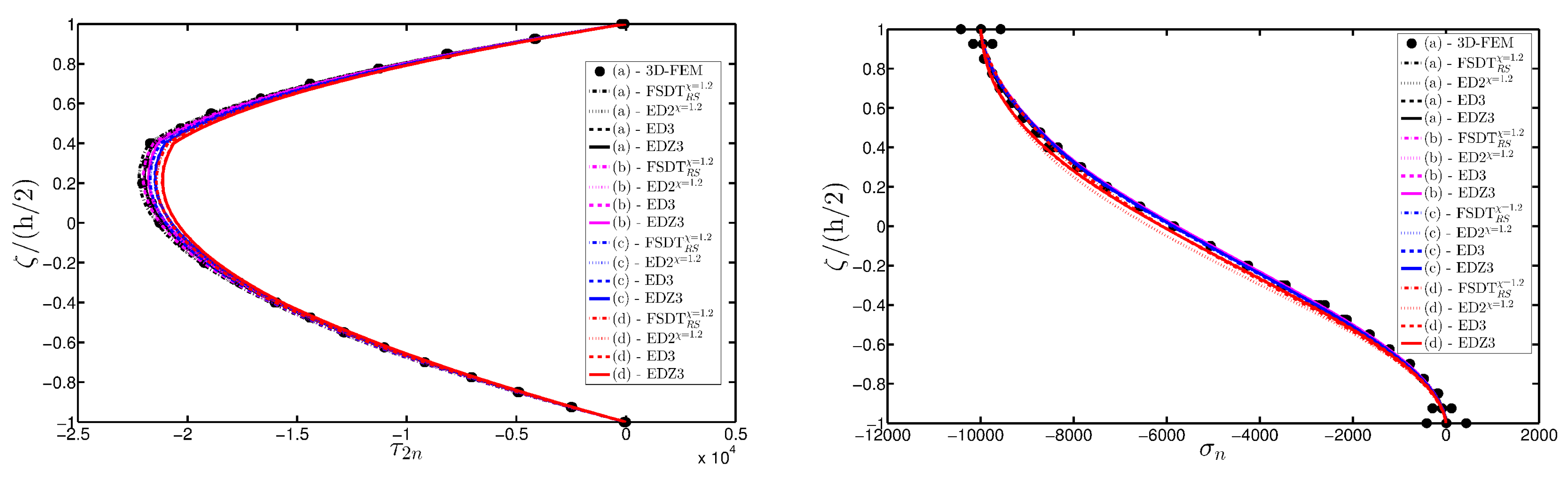
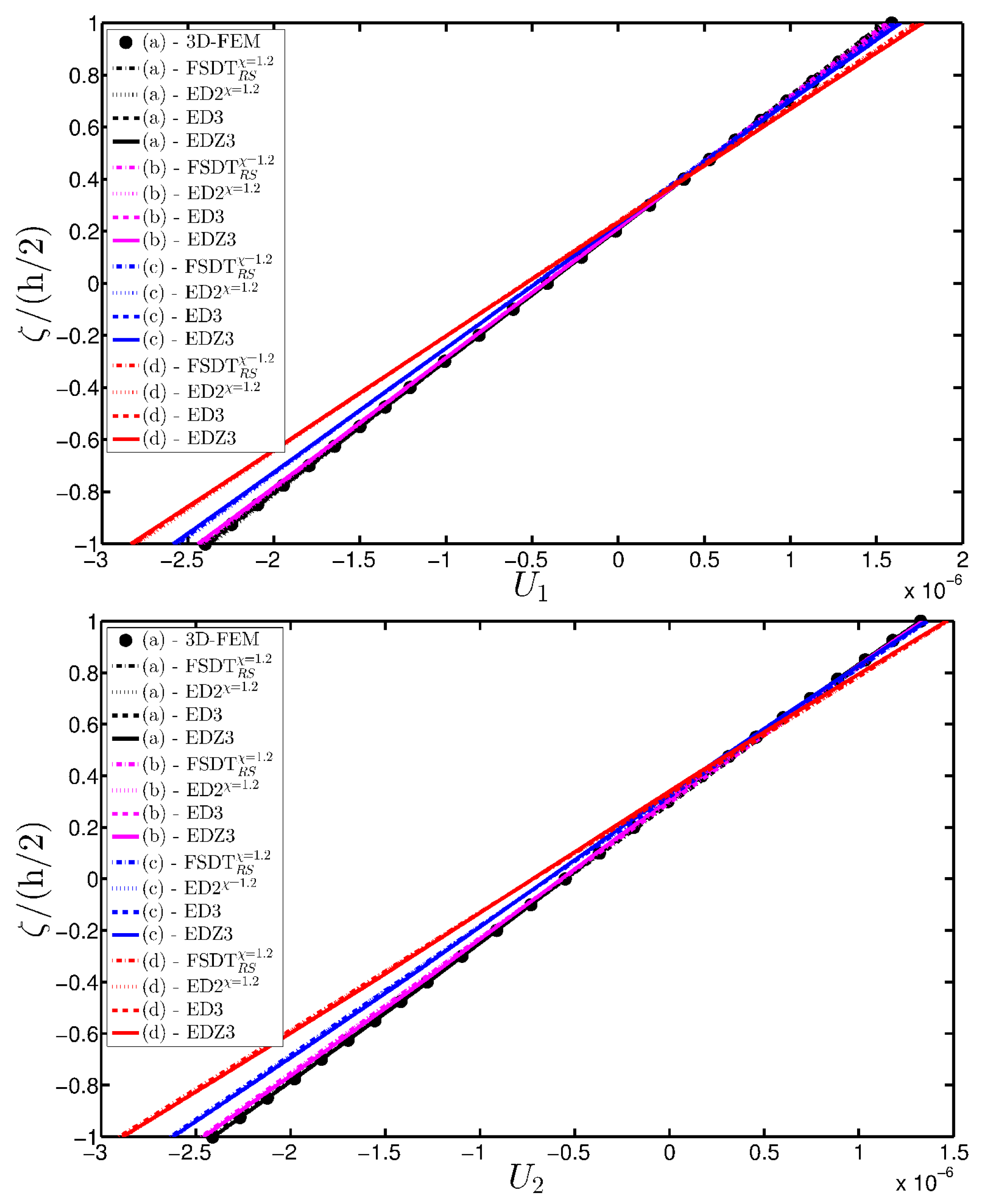
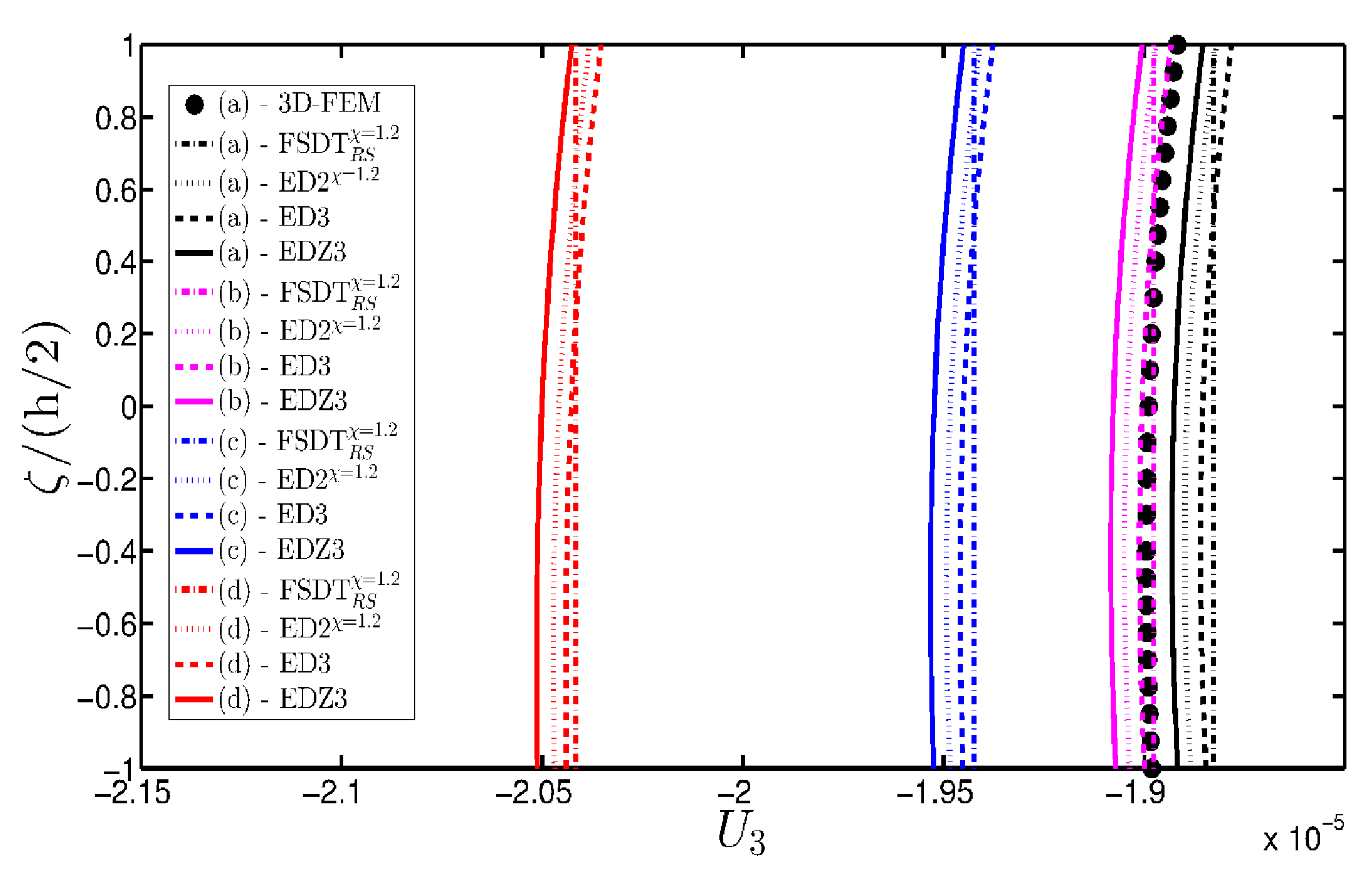
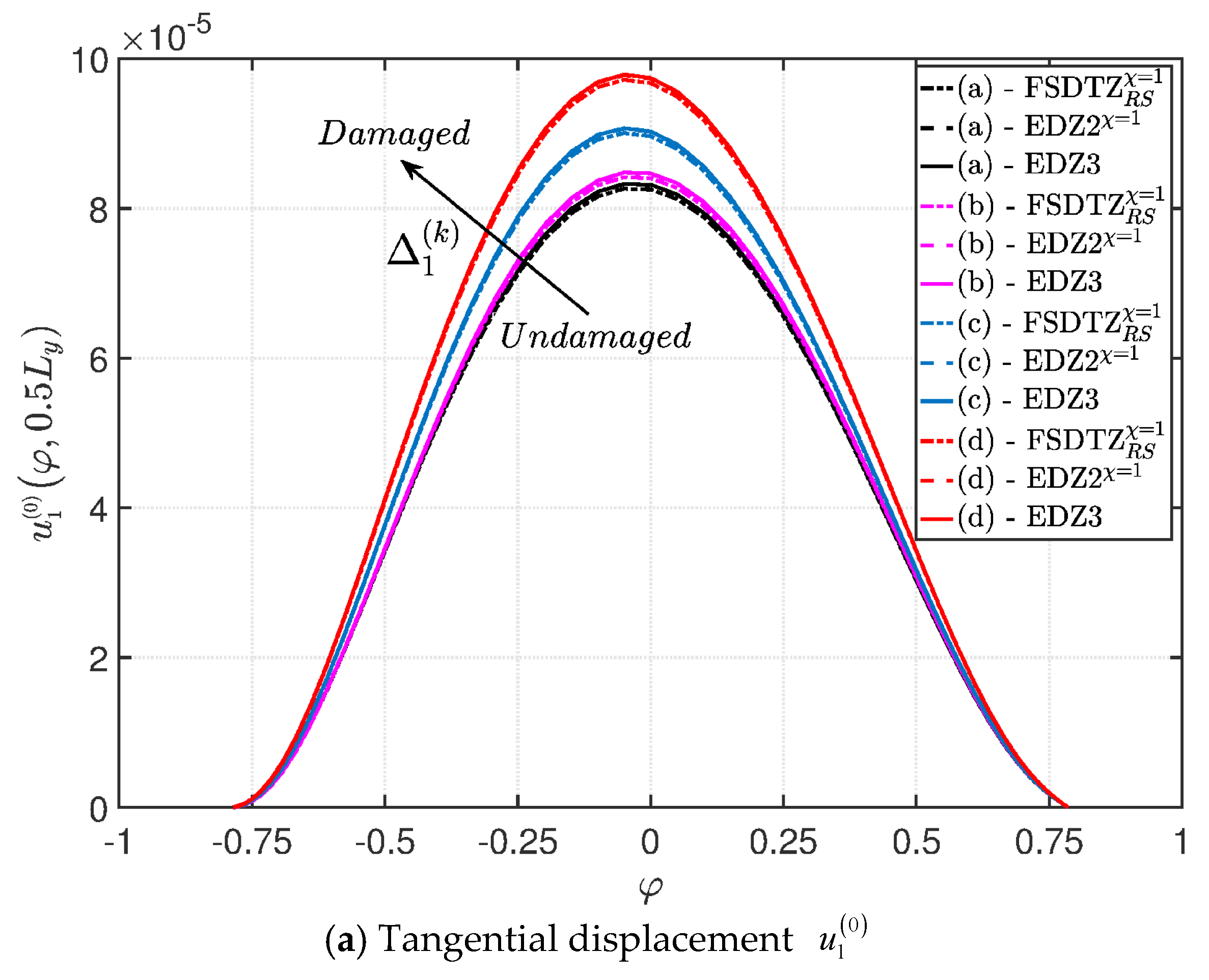
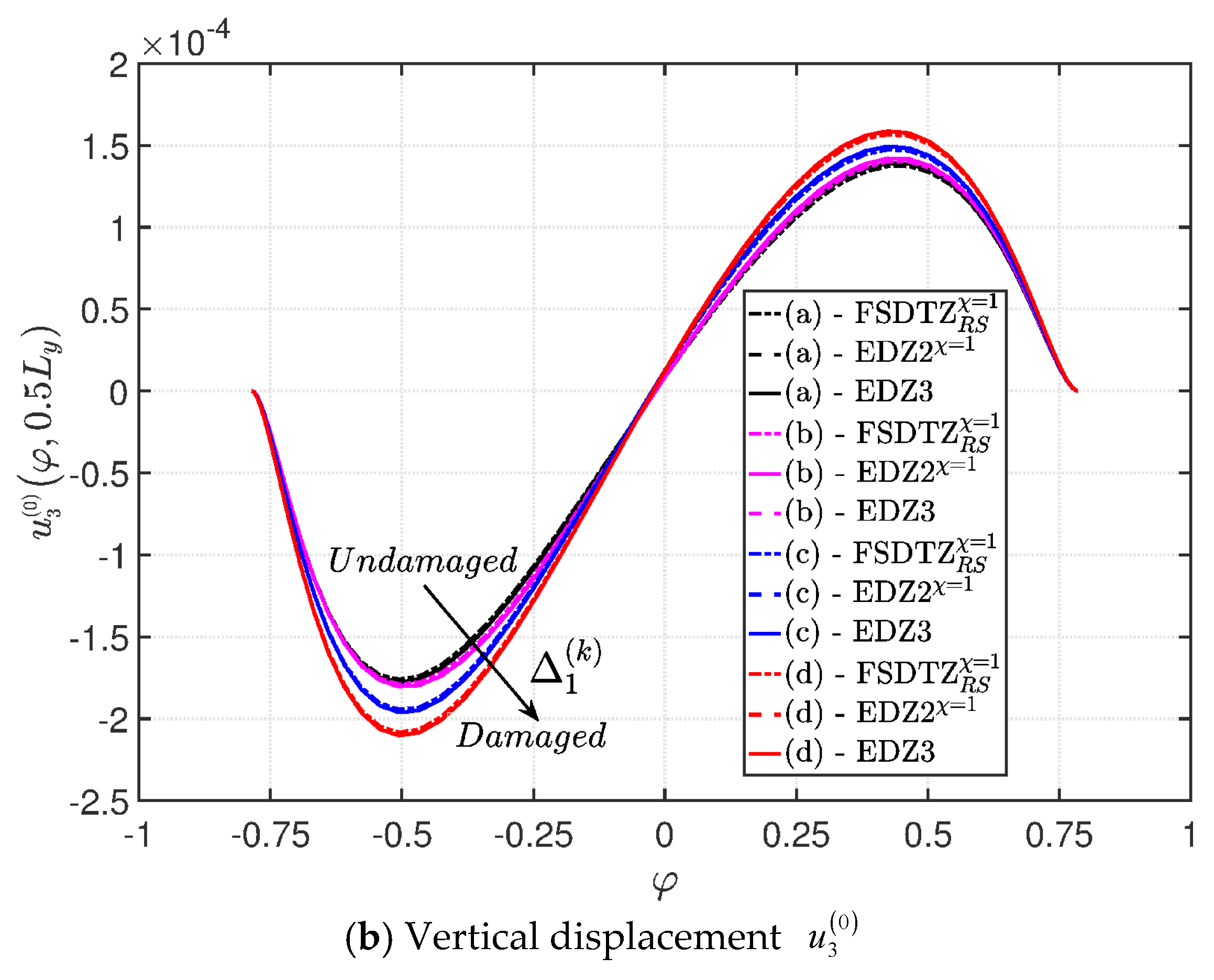
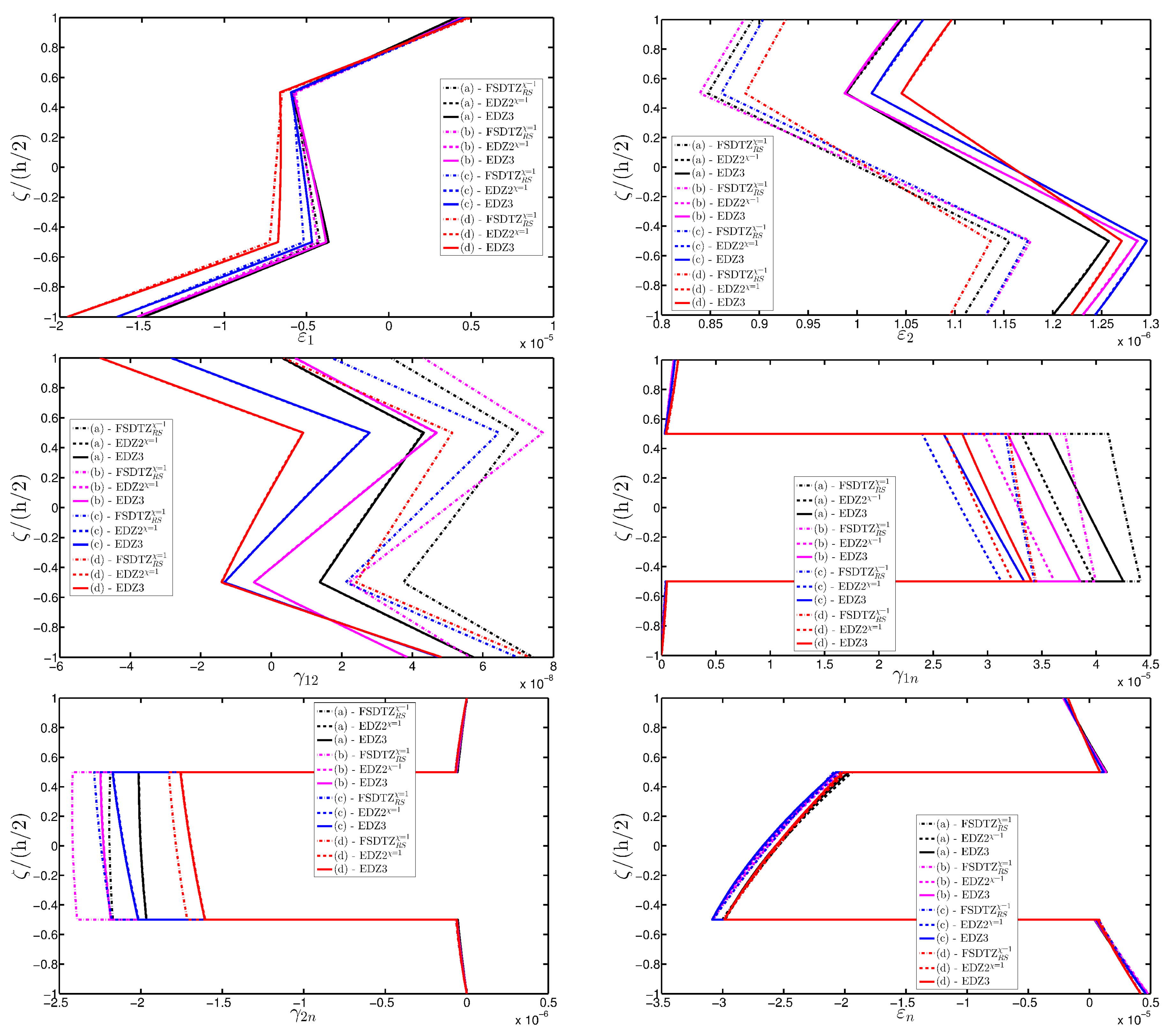
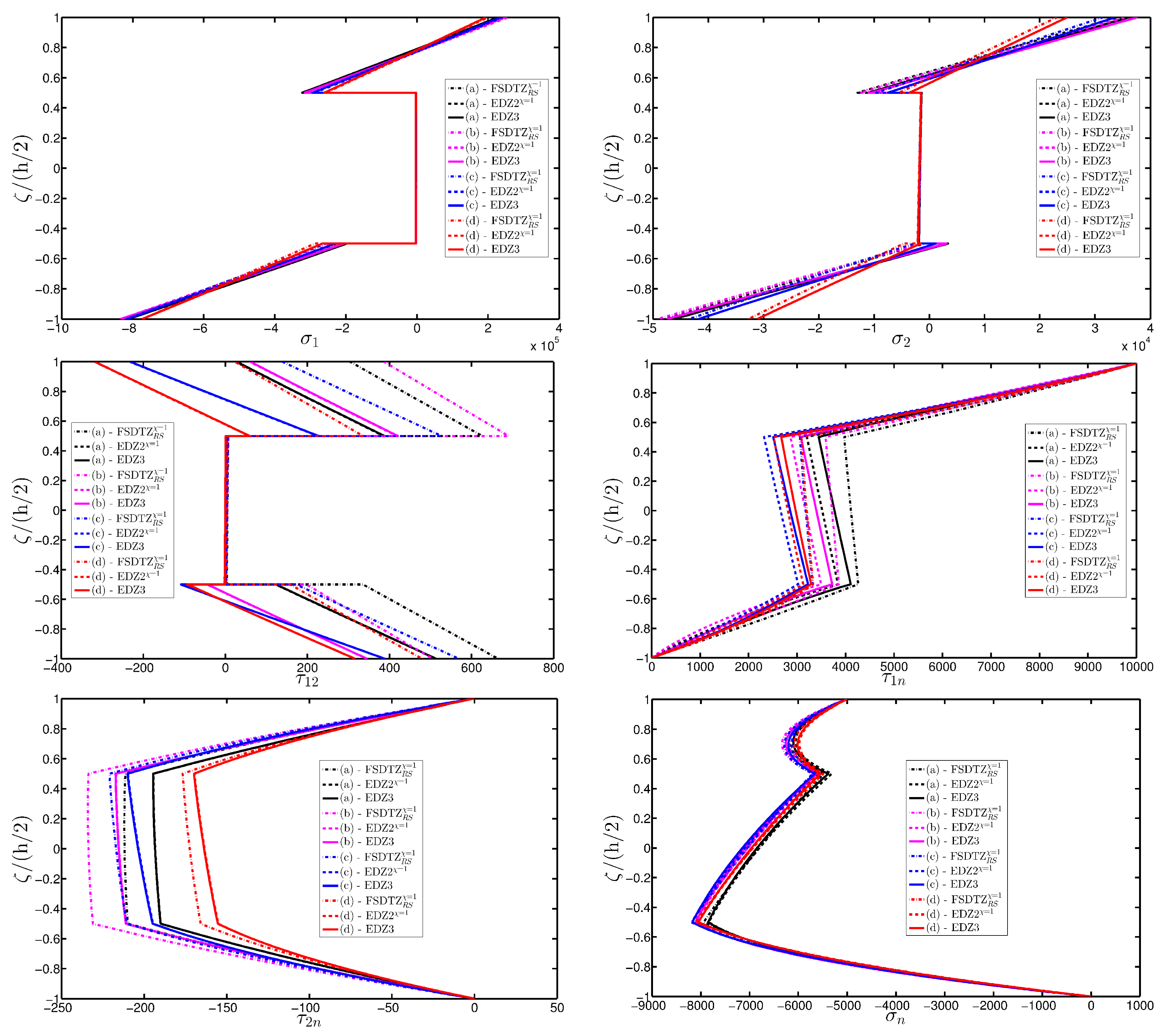
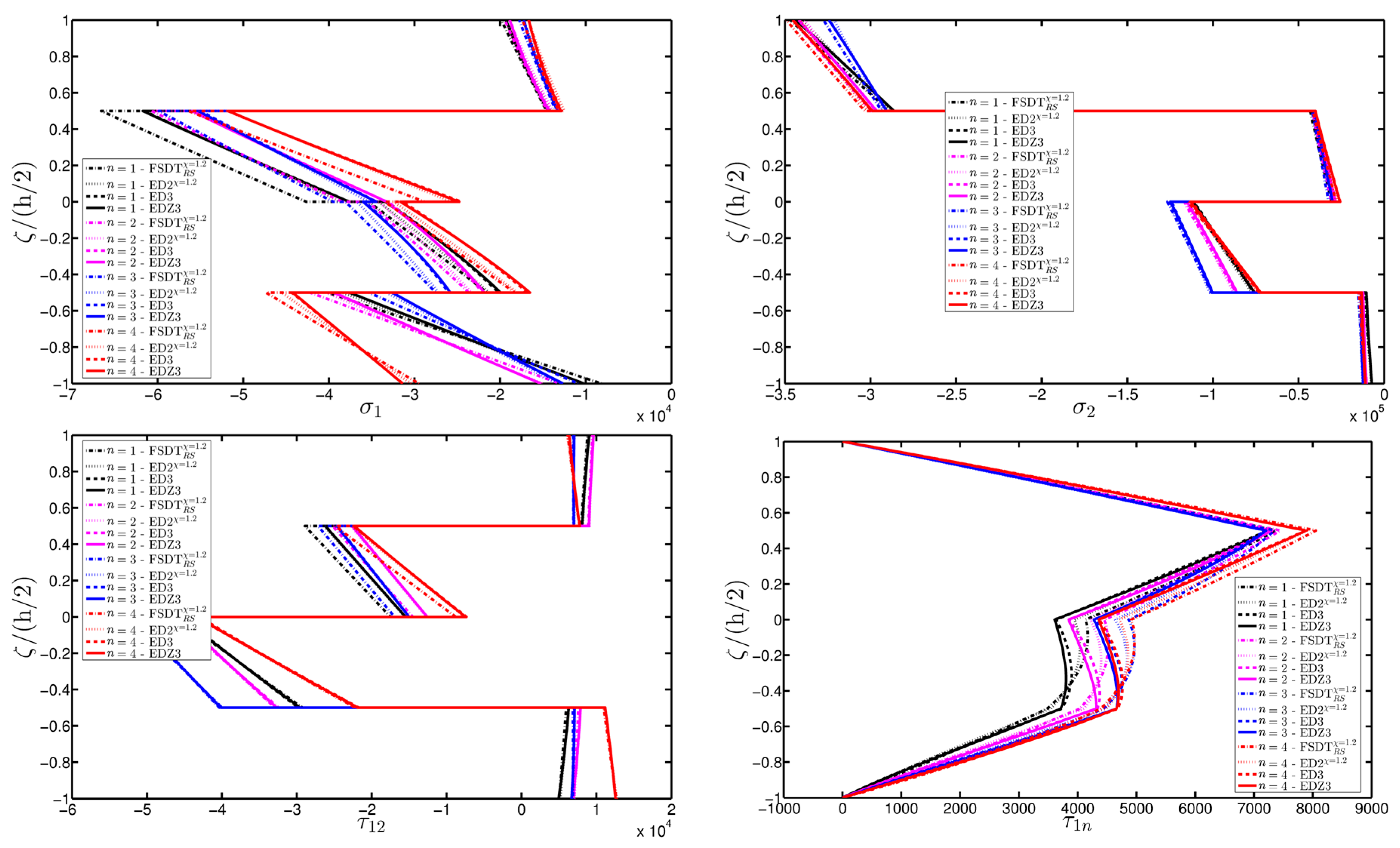
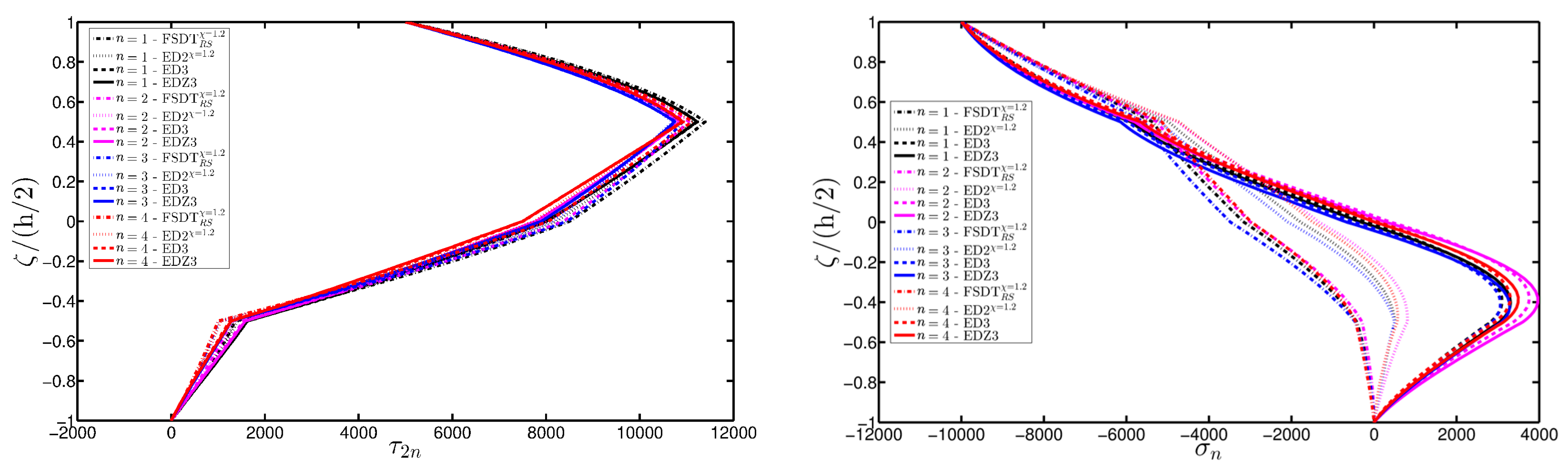
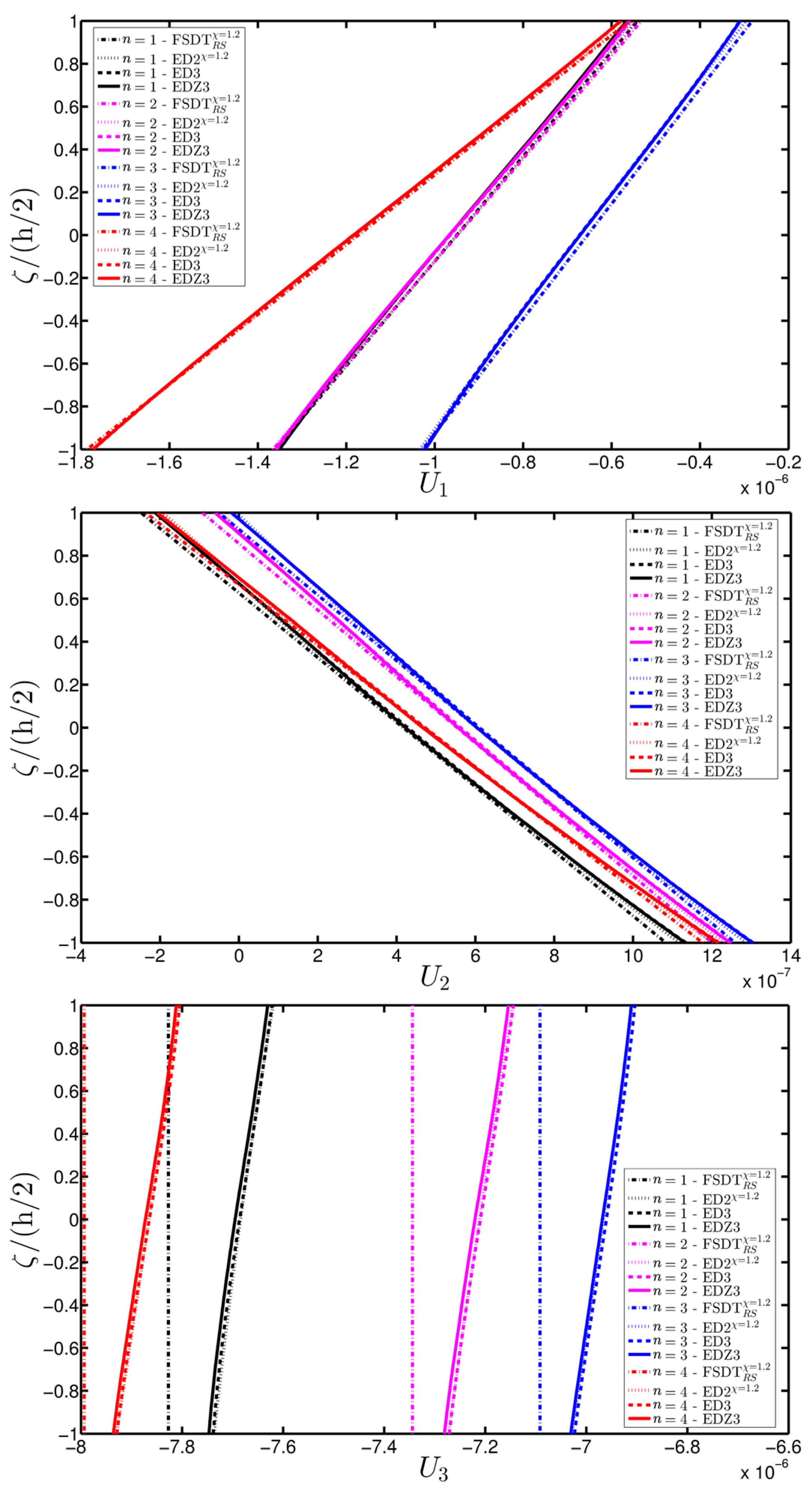
- The results were presented in terms of displacement profiles related to the shell middle surface and through-the-thickness variations of strain, stress, and displacement components at specific points of the domain. It was proven that the damage affects all these static quantities.
- The numerical approach shows a convergent behavior when applied to this kind of structural problems.
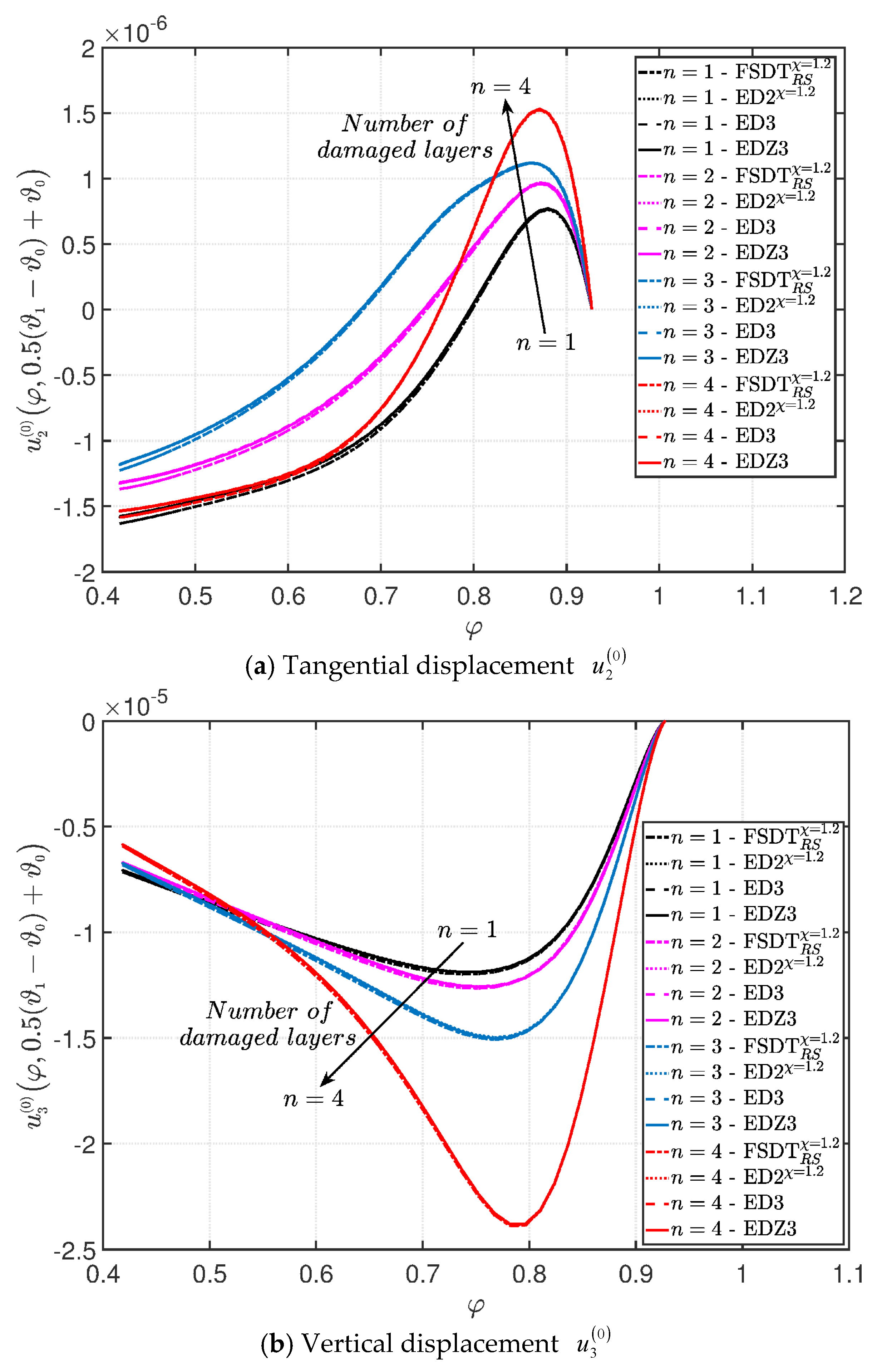
- It was proven that the damage modifies the structural response. In general, the displacement increases when the damage intensity grows or when it involves a bigger area of the domain; analogously, the overall displacement is greater when the damage spreads to the adjacent layers.
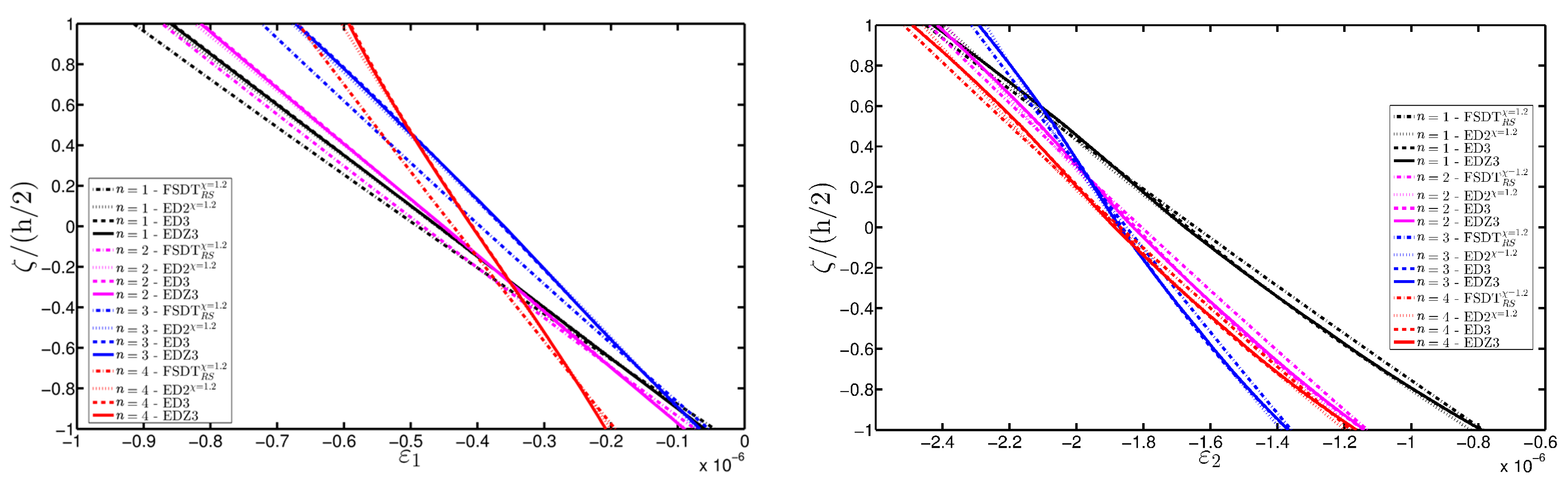
- As far as stresses and strains are concerned, the effects of the damage on their through-the-thickness profiles are lower than the effects caused on the corresponding displacements; nevertheless, it is possible to observe noticeable differences between the profiles which are related respectively to the minimum and maximum values of the parameters used in the parametric analyses to model the deterioration of the mechanical properties.
- Similar profiles in terms of strains, stresses, and displacements are obtained by means of different HSDTs. Consequently, all these enriched kinematic models are able to deal with damaged composite plates and shells.
- No significant differences are observable between a higher-order model and the corresponding one embedded with the Murakami’s function when a laminated composite is analyzed. On the other hand, the Murakami’s function is required to deal with sandwich structures with an inner soft-core.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Symbols | Definition |
| Three-dimensional position vector | |
| Local reference system of origin | |
| Shell reference surface position vector | |
| Outward unit normal vector | |
| Principal radii of curvatures | |
| Lamé parameters | |
| Principal curvilinear coordinates | |
| Shell thickness | |
| 3D displacement component vector | |
| -th order generalized displacement component vector | |
| Thickness function | |
| Murakami’s function (zig-zag effect) | |
| 3D strain component vector | |
| Kinematic differential operator | |
| Matrix containing the terms related to the shell thickness | |
| 3D stress component vector | |
| Constitutive operator | |
| Elastic constants of the stiffness matrix | |
| -th order generalized stress resultant vector | |
| Stiffness matrix | |
| Shear correction factor | |
| Equilibrium differential operator | |
| Fundamental operator | |
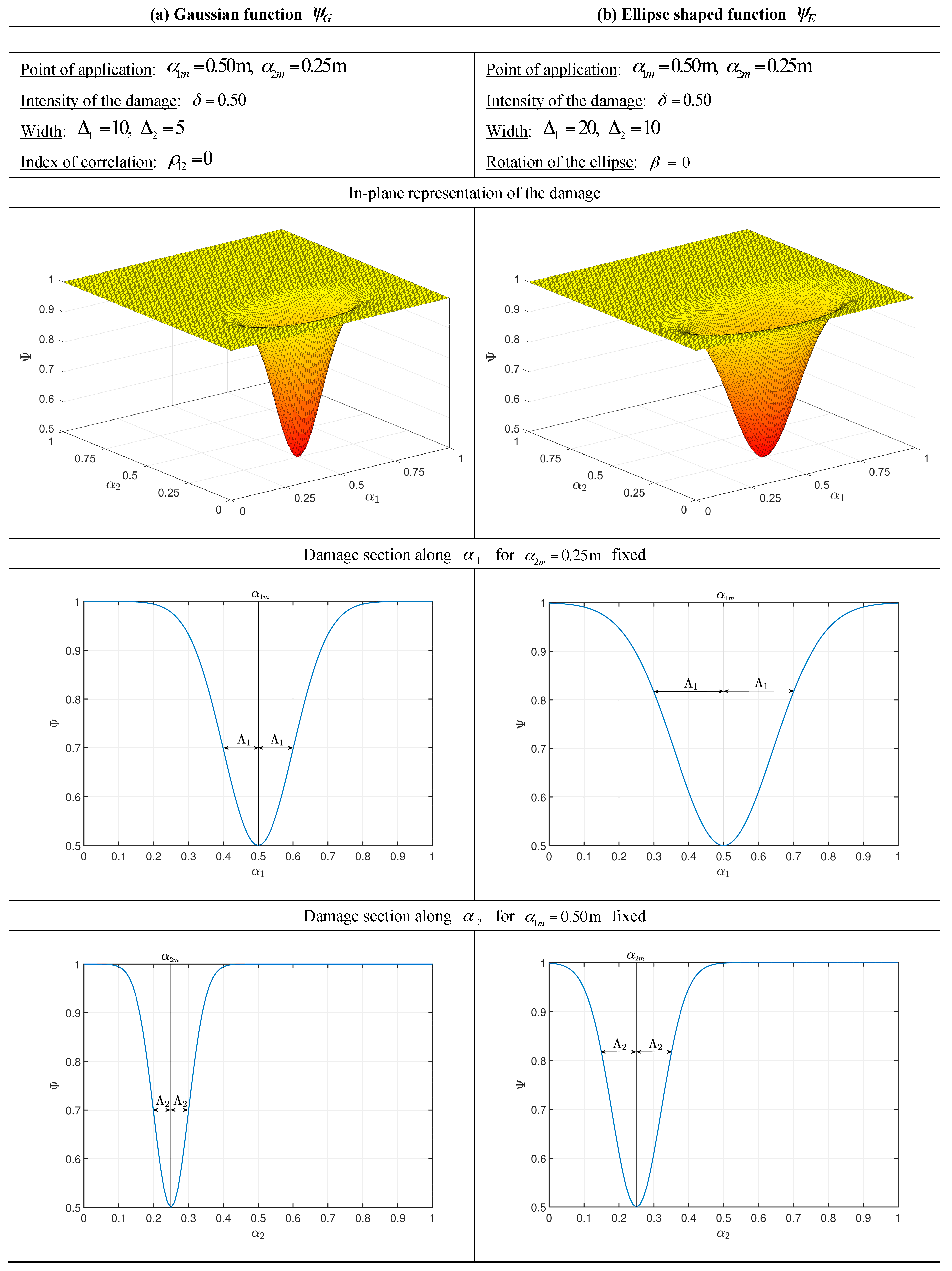
| Variation of the mechanical properties (damage) | |
| Gaussian and Elliptic variation (damage) | |
| Application point of the damage | |
| Size parameters of the damage |
References
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential Geometry. Higher-Order Structural Theories; Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential and Integral Quadrature. Strong Formulation Finite Element Method; Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Kraus, H. Thin Elastic Shells; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Viola, E.; Tornabene, F.; Fantuzzi, N. Static Analysis of Completely Doubly-Curved Laminated Shells and Panels Using General Higher-order Shear Deformation Theories. Compos. Struct. 2013, 101, 59–93. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. A Strong Formulation Finite Element Method (SFEM) Based on RBF and GDQ Techniques for the Static and Dynamic Analyses of Laminated Plates of Arbitrary Shape. Meccanica 2014, 49, 2503–2542. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate Inter-Laminar Recovery for Plates and Doubly-Curved Shells with Variable Radii of Curvature Using Layer-Wise Theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. A New Approach for Treating Concentrated Loads in Doubly-Curved Composite Deep Shells with Variable Radii of Curvature. Compos. Struct. 2015, 131, 433–452. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E. Inter-Laminar Stress Recovery Procedure for Doubly-Curved, Singly-Curved, Revolution Shells with Variable Radii of Curvature and Plates Using Generalized Higher-Order Theories and the Local GDQ Method. Mech. Adv. Mater. Struct. 2016, 23, 1019–1045. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Dimitri, R.; Tornabene, F. A SFEM-Based Evaluation of Mode-I Stress Intensity Factor in Composite Structures. Compos. Struct. 2016, 145, 162–185. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. On the Mechanics of Laminated Doubly-Curved Shells Subjected to Point and Line Loads. Int. J. Eng. Sci. 2016, 109, 115–164. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative Numerical Methods Based on SFEM and IGA for Computing Stress Concentrations in Isotropic Plates with Discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Wang, X.; Shi, G. A refined laminated plate theory accounting for the third-order shear deformation and interlaminar transverse stress continuity. Appl. Math. Model. 2015, 39, 5659–5680. [Google Scholar] [CrossRef]
- Dozio, L.; Alimonti, L. Variable kinematic finite element models of multilayered composite plates coupled with acoustic fluid. Mech. Adv. Mater. Struct. 2016, 23, 981–996. [Google Scholar] [CrossRef]
- D’Ottavio, M.; Dozio, L.; Vescovini, R.; Polit, O. Bending analysis of composite laminated and sandwich structures using sublaminate variable-kinematic Ritz models. Compos. Struct. 2016, 155, 45–62. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Z. Accurate stress analysis of sandwich panels by the differential quadrature method. Appl. Math. Model. 2017, 43, 548–565. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. General Higher-Order Shear Deformation Theories for the Free Vibration Analysis of Completely Doubly-Curved Laminated Shells and Panels. Compos. Struct. 2013, 95, 639–666. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General Higher-Order Equivalent Single Layer Theory for Free Vibrations of Doubly-Curved Laminated Composite Shells and Panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method Applied to General Higher-Order Theories of Doubly-Curved Laminated Composite Shells and Panels: The Free Vibration Analysis. Compos. Struct. 2014, 116, 637–660. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free Vibrations of Free-Form Doubly-Curved Shells Made of Functionally Graded Materials Using Higher-Order Equivalent Single Layer Theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Bacciocchi, M.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. Radial Basis Functions Based on Differential Quadrature Method for the Free Vibration of Laminated Composite Arbitrary Shaped Plates. Compos. Part B Eng. 2015, 78, 65–78. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Dynamic Analysis of Thick and Thin Elliptic Shell Structures Made of Laminated Composite Materials. Compos. Struct. 2015, 133, 278–299. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S.; Fantuzzi, N.; Viola, E. Numerical and Exact Models for Free Vibration Analysis of Cylindrical and Spherical Shell Panels. Compos. Part B Eng. 2015, 81, 231–250. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free Vibrations of Composite Oval and Elliptic Cylinders by the Generalized Differential Quadrature Method. Thin-Walled Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Tornabene, F. General Higher Order Layer-Wise Theory for Free Vibrations of Doubly-Curved Laminated Composite Shells and Panels. Mech. Adv. Mater. Struct. 2016, 23, 1046–1067. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for Laminated Composite Arbitrarily Shaped Plates. Compos. Part B Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. MLSDQ Based on RBFs for the Free Vibrations of Laminated Composite Doubly-Curved Shells. Compos. Part B Eng. 2016, 99, 30–47. [Google Scholar] [CrossRef]
- Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Viola, E. 3D Exact and 2D Generalized Differential Quadrature Models for Free Vibration Analysis of Functionally Graded Plates and Cylinders. Meccanica 2016, 51, 2059–2098. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The GDQ Method for the Free Vibration Analysis of Arbitrarily Shaped Laminated Composite Shells Using a NURBS-Based Isogeometric Approach. Compos. Struct. 2016, 154, 190–218. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Reddy, J.N. An Equivalent Layer-Wise Approach for the Free Vibration Analysis of Thick and Thin Laminated Sandwich Shells. Appl. Sci. 2017, 7, 17. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Puppa, G.D.; Tornabene, F.; Trautz, M. Strong Formulation Isogeometric Analysis for the Vibration of Thin Membranes of General Shape. Int. J. Mech. Sci. 2017, 120, 322–340. [Google Scholar] [CrossRef]
- Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Interpretation of Boundary Conditions in the Analytical and Numerical Shell Solutions for Mode Analysis of Multilayered Structures. Int. J. Mech. Sci. 2017, 122, 18–28. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. Stability and Accuracy of Three Fourier Expansion-Based Strong Form Finite Elements for the Free Vibration Analysis of Laminated Composite Plates. Int. J. Numer. Methods Eng. 2017, in press. [Google Scholar] [CrossRef]
- Alibeiglooa, A.; Shakeri, M.; Kari, M.R. Free vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third-order shear deformation theory. Ocean Eng. 2008, 35, 183–190. [Google Scholar] [CrossRef]
- Amabili, M.; Reddy, J.N. A new non-linear higher-order shear deformation theory for large-amplitude vibrations of laminated doubly curved shells. Int. J. Nonlinear Mech. 2010, 45, 409–418. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. A new trigonometric layerwise shear deformation theory for the finite element analysis of laminated composite and sandwich plates. Comput. Struct. 2012, 94–95, 45–53. [Google Scholar] [CrossRef]
- Mantari, J.L.; Soares, C.G. Generalized layerwise HSDT and finite element formulation for symmetric laminated and sandwich composite plates. Compos. Struct. 2013, 105, 319–331. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Layer-wise dynamic stiffness solution for free vibration analysis of laminated composite plates. J. Sound Vib. 2014, 333, 200–227. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Chen, X.; Xie, Y.; Miao, H. Analysis of laminated composite plates using wavelet finite element method and higher-order plate theory. Compos. Struct. 2015, 131, 248–258. [Google Scholar] [CrossRef]
- Sahoo, R.; Singh, B.N. A new trigonometric zigzag theory for buckling and free vibration analysis of laminated composite and sandwich plates. Compos. Struct. 2014, 117, 316–332. [Google Scholar] [CrossRef]
- D’Ottavio, M. A Sublaminate Generalized Unified Formulation for the analysis of composite structures. Compos. Struct. 2016, 142, 187–199. [Google Scholar] [CrossRef]
- Civalek, Ö. Discrete singular convolution method for the free vibration analysis of rotating shells with different material properties. Compos. Struct. 2017, 160, 267–279. [Google Scholar] [CrossRef]
- Reddy, J.N.; Chin, C.D. Thermomechanical Analysis of Functionally Graded Cylinders and Plates. J. Therm. Stress. 1998, 21, 593–626. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods. Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Reddy, J.N.; Kim, J. A nonlinear modified couple stress-based third-order theory of functionally graded plates. Compos. Struct. 2012, 94, 1128–1143. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. A general third-order theory of functionally graded plates with modified couple stress effect and the von Kármán nonlinearity: Theory and finite element analysis. Acta Mech. 2015, 226, 2973–2998. [Google Scholar] [CrossRef]
- Gutierrez Rivera, M.; Reddy, J.N. Stress analysis of functionally graded shells using a 7-parameter shell element. Mech. Res. Commun. 2016, 78, 60–70. [Google Scholar] [CrossRef]
- Lanc, D.; Turkalj, G.; Vo, T.; Brnic, J. Nonlinear buckling behaviours of thin-walled functionally graded open section beams. Compos. Struct. 2016, 152, 829–839. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Reissner’s Mixed Variational Theorem and Variable Kinematics in the Modelling of Laminated Composite and FGM Doubly-Curved Shells. Compos. Part B Eng. 2016, 89, 408–423. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Stability Analysis of FGM Sandwich Plates by Using Variable-kinematics Ritz Models. Mech. Adv. Mater. Struct. 2016, 23, 1104–1113. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Plotnikova, S.V.; Kulikov, M.G.; Monastyrev, P.V. Three-dimensional vibration analysis of layered and functionally graded plates through sampling surfaces formulation. Compos. Struct. 2016, 152, 349–361. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Thermoelastic stability of freely supported functionally graded conical shells within the shear deformation theory. Compos. Struct. 2016, 152, 74–84. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Zerin, Z.; Kuruoglu, N. Thermoelastic buckling of FGM conical shells under non-linear temperature rise in the framework of the shear deformation theory. Compos. Part B Eng. 2017, 108, 279–290. [Google Scholar] [CrossRef]
- Tornabene, F.; Reddy, J.N. FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: A GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 2013, 93, 635–688. [Google Scholar]
- Fantuzzi, N.; Tornabene, F.; Viola, E. Four-Parameter Functionally Graded Cracked Plates of Arbitrary Shape: A GDQFEM Solution for Free Vibrations. Mech. Adv. Mater. Struct. 2016, 23, 89–107. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Brischetto, S.; Tornabene, F.; Viola, E. 2D and 3D Shell Models for the Free Vibration Investigation of Functionally Graded Cylindrical and Spherical Panels. Compos. Struct. 2016, 154, 573–590. [Google Scholar] [CrossRef]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Generalized Stress-Strain Recovery Formulation Applied to Functionally Graded Spherical Shells and Panels Under Static Loading. Compos. Struct. 2016, 156, 145–164. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S.; Fantuzzi, N.; Bacciocchi, M. Boundary Conditions in 2D Numerical and 3D Exact Models for Cylindrical Bending Analysis of Functionally Graded Structures. Shock Vib. 2016, 2016, 2373862. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of Agglomeration on the Natural Frequencies of Functionally Graded Carbon Nanotube-Reinforced Laminated Composite Doubly-Curved Shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free Vibration Analysis of Conical Shells Reinforced with Agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear Static Response of Nanocomposite Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Compos. Part B Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free Vibration Analysis of Arbitrarily Shaped Functionally Graded Carbon Nanotube-Reinforced Plates. Compos. Part B Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Jooybar, N.; Malekzadeh, P.; Fiouz, A. Vibration of functionally graded carbon nanotubes reinforced composite truncated conical panels with elastically restrained against rotation edges in thermal environment. Compos. Part B Eng. 2016, 106, 242–261. [Google Scholar] [CrossRef]
- García-Macías, E.; Rodriguez-Tembleque, L.; Castro-Triguero, R.; Sáez, A. Buckling analysis of functionally graded carbon nanotube-reinforced curved panels under axial compression and shear. Compos. Part B Eng. 2017, 108, 243–256. [Google Scholar] [CrossRef]
- Civalek, Ö. Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Compos. Part B Eng. 2017, 111, 45–59. [Google Scholar] [CrossRef]
- Shenasa, A.G.; Malekzadehb, P.; Ziaee, S. Vibration analysis of pre-twisted functionally graded carbon nanotube reinforced composite beams in thermal environment. Compos. Struct. 2017, 162, 325–340. [Google Scholar] [CrossRef]
- Mehar, K.; Panda, S.K. Numerical investigation of nonlinear thermomechanical deflection of functionally graded CNT reinforced doubly curved composite shell panel under different mechanical loads. Compos. Struct. 2017, 161, 287–298. [Google Scholar] [CrossRef]
- Hyer, M.W.; Charette, R.F. Use of Curvilinear Fiber Format in Composite Structure Design. AIAA J. 1991, 29, 1011–1015. [Google Scholar] [CrossRef]
- Gürdal, Z.; Olmedo, R. In-Plane Response of Laminates with Spatially Varying Fiber Orientations: Variable Stiffness Concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Blom, A.W.; Tatting, B.F.; Hol, J.M.A.M.; Gürdal, Z. Fiber path definitions for elastically tailored conical shells. Compos. Part B Eng. 2009, 40, 77–84. [Google Scholar] [CrossRef]
- Blom, A.W.; Abdalla, M.M.; Gürl, Z. Optimization of Course Locations in Fiber-Placed Panels for General Fiber Angle Distributions. Compos. Sci. Technol. 2010, 70, 564–570. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Compos. Struct. 2011, 93, 3040–3047. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Weaver, P.M. Buckling analysis of variable angle tow, variable thickness panels with transverse shear effects. Compos. Struct. 2014, 107, 482–493. [Google Scholar] [CrossRef]
- Yazdani, S.; Ribeiro, P. A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 2015, 120, 531–542. [Google Scholar] [CrossRef]
- Ribeiro, P. Non-linear modes of vibration of thin cylindrical shells in composite laminates with curvilinear fibers. Compos. Struct. 2015, 122, 184–197. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Higher-Order Theories for the Free Vibration of Doubly-Curved Laminated Panels with Curvilinear Reinforcing Fibers by Means of a Local Version of the GDQ Method. Compos. Part B Eng. 2015, 81, 196–230. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Higher-Order Structural Theories for the Static Analysis of Doubly-Curved Laminated Composite Panels Reinforced by Curvilinear Fibers. Thin-Walled Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Foam Core Composite Sandwich Plates and Shells with Variable Stiffness: Effect of Curvilinear Fiber Path on the Modal Response. J. Sandw. Struct. Mater. 2017, in press. [Google Scholar] [CrossRef]
- Zucco, G.; Groh, R.M.J.; Madeo, A.; Weaver, P.M. Mixed shell element for static and buckling analysis of variable angle tow composite plates. Compos. Struct. 2016, 152, 324–338. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P. Geometrically non-linear periodic forced vibrations of imperfect laminates with curved fibres by the shooting method. Compos. Part B Eng. 2017, 109, 286–296. [Google Scholar] [CrossRef]
- Leissa, A.W.; Martin, A.F. Vibration and Buckling of Rectangular Composite Plates with Variable Fiber Spacing. Compos. Struct. 1990, 14, 339–357. [Google Scholar] [CrossRef]
- Dinardo, M.T.; Lagace, P.A. Buckling and Postbuckling of Laminated Composites with Ply Dropoffs. AIAA J. 1989, 27, 1392–1398. [Google Scholar] [CrossRef]
- Mizusawa, T. Vibration of rectangular Mindlin plates with tapered thickness by the spline strip method. Comput. Struct. 1993, 46, 451–463. [Google Scholar] [CrossRef]
- Shufrin, I.; Eisenberger, M. Vibration of shear deformable plates with variable thickness—First-order aand higher-order analyses. J. Sound Vib. 2006, 290, 465–489. [Google Scholar] [CrossRef]
- Dozio, L.; Carrera, E. A variable kinematic Ritz formulation for vibration study of quadrilateral plates with arbitrary thickness. J. Sound Vib. 2011, 330, 4611–4632. [Google Scholar] [CrossRef]
- Eisenberger, M.; Jabareen, M. Axisymmetric vibrations of circular and annular plates with variable thickness. Int. J. Struct. Stab. Dyn. 2001, 1, 195–206. [Google Scholar] [CrossRef]
- Efraim, E.; Eisenberger, M. Dynamic stiffness vibration analysis of thick spherical shell segments with variable thickness. J. Mech. Mater. Struct. 2010, 5, 821–835. [Google Scholar] [CrossRef]
- Efraim, E.; Eisenberger, M. Exact vibration analysis of variable thickness thick annular isotropic and FGM plates. J. Sound Vib. 2007, 299, 720–738. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method for the Natural Frequencies of Doubly-Curved Shells with Variable Thickness: A General Formulation. Compos. Part B Eng. 2016, 92, 265–289. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Eisenberger, M.; Fantuzzi, N.; Tornabene, F.; Viola, E. Vibration Analysis of Variable Thickness Plates and Shells by the Generalized Differential Quadrature Method. Compos. Struct. 2016, 156, 218–237. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A Numerical Investigation on the Natural Frequencies of FGM Sandwich Shells with Variable Thickness by the Local Generalized Differential Quadrature Method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Ladevèze, P.; Le Dantec, E. Damage modelling of the elementary ply for laminated composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- Daudeville, L.; Ladevèze, P. A damage mechanics tool for laminate delamination. Compos. Struct. 1993, 25, 547–555. [Google Scholar] [CrossRef]
- Reddy, J.N.; Miravete, A. Practical Analysis of Composite Laminates; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Murakami, S. Continuum Damage Mechanics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Highsmith, A.L.; Reifsnider, K.L. Stiffness-Reduction Mechanismi in Composite Laminates. In Damage in Composite Materials; ASTM STP 775; ASTM International: West Conshohocken, PA, USA, 1982; pp. 103–117. [Google Scholar]
- Luo, R.K.; Green, E.; Morrison, C.J. An approach to evaluate the impact damage initiation and propagation in composite plates. Compos. Part B Eng. 2001, 32, 513–520. [Google Scholar] [CrossRef]
- Muc, A.; Kędziora, P. A fuzzy set analysis for a fracture and fatigue damage response of composite materials. Compos. Struct. 2001, 54, 283–287. [Google Scholar] [CrossRef]
- Viola, E.; Artioli, E.; Dilena, M. Analytical and Differential Quadrature Results for Vibration Analysis of Damaged Circular Arches. J. Sound Vib. 2005, 288, 887–906. [Google Scholar] [CrossRef]
- Viola, E.; Dilena, M.; Tornabene, F. Analytical and Numerical Results for Vibration Analysis of Multi-Stepped and Multi-Damaged Circular Arches. J. Sound Vib. 2007, 299, 143–163. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zhang, H.S. Multiscale finite element modeling of failure process of composite laminates. Compos. Struct. 2010, 92, 2159–2165. [Google Scholar] [CrossRef]
- Batra, R.C.; Gopinath, G.; Zheng, J.Q. Damage and failure in low energy impact of fiber-reinforced polymeric composite laminates. Compos. Struct. 2012, 94, 540–547. [Google Scholar] [CrossRef]
- Lee, C.-S.; Kim, J.-H.; Ryu, D.-M.; Lee, J.-M. Initial and progressive failure analyses for composite laminates using Puck failure criterion and damage-coupled finite element method. Compos. Struct. 2015, 121, 406–419. [Google Scholar] [CrossRef]
- Moreno-García, P.; Lopes, H.; Araújo dos Santos, J.V. Application of higher order finite differences to damage localization in laminated composite plates. Compos. Struct. 2016, 156, 385–392. [Google Scholar] [CrossRef]
- Lambros, J.; Rosakis, A.J. Dynamic crack initiation and growth in thick unidirectional graphite/epoxy plates. Compos. Sci. Technol. 1997, 57, 55–65. [Google Scholar] [CrossRef]
- Sjögren, B.A.; Berglund, L.A. The effects of matrix and interface on damage in GRP cross-ply laminates. Compos. Sci. Technol. 2000, 60, 9–21. [Google Scholar] [CrossRef]
- Abisset, E.; Daghia, F.; Ladevèze, P. On the validation of a damage mesomodel for laminated composites by means of open-hole tensile tests on quasi-isotropic laminates. Compos. Part A Appl. Sci Manuf. 2011, 42, 1515–1524. [Google Scholar] [CrossRef]
- Fard, M.Y.; Sadat, S.M.; Raji, B.B.; Chattopadhyay, A. Damage characterization of surface and sub-surface defects in stitch-bonded biaxial carbon/epoxy composites. Compos. Part B Eng. 2014, 56, 821–829. [Google Scholar] [CrossRef]
- Biolzi, L.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Static and dynamic response of progressively damaged ionoplast laminated glass beams. Compos. Struct. 2016, 157, 337–347. [Google Scholar] [CrossRef]
- Mohagheghian, I.; Wang, Y.; Zhou, J.; Yu, L.; Guo, X.; Yan, Y.; Charalambides, M.N. Deformation and damage mechanisms of laminated glass windows subjected to high velocity soft impact. Int. J. Solids Struct. 2017, 109, 46–62. [Google Scholar] [CrossRef]
- Dumont, J.P. Damage Mechanics for 3-D Composites. Compos. Struct. 1987, 8, 119–141. [Google Scholar] [CrossRef]
- Tay, T.E.; Lim, E.H. Analysis of composite laminates with transverse cracks. Compos. Struct. 1996, 34, 419–426. [Google Scholar] [CrossRef]
- Pavan, R.C.; Creus, G.J.; Maghous, S. A simplified approach to continuous damage of composite materials and micromechanical analysis. Compos. Struct. 2009, 91, 84–94. [Google Scholar] [CrossRef]
- Kim, E.-H.; Rim, M.-S.; Lee, I.; Hwang, T.-K. Composite damage model based on continuum damage mechanics and low velocity impact analysis of composite plates. Compos. Struct. 2013, 95, 123–134. [Google Scholar] [CrossRef]
- Chen, J.-F.; Morozov, V.; Shankar, K. Simulating progressive failure of composite laminates including in-ply and delamination damage effects. Compos. Part A Appl. Sci Manuf. 2014, 61, 185–200. [Google Scholar] [CrossRef]
- Amirpour, M.; Das, R.; Bickerton, S. An elasto-plastic damage model for functionally graded plates with in-plane material properties variation: Material model and numerical implementation. Compos. Struct. 2017, 163, 331–341. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Bert, C.W. A Critical Evaluation of New Plate Theories Applied to Laminated Composites. Compos. Struct. 1984, 2, 329–347. [Google Scholar] [CrossRef]
- Reddy, J.N.; Liu, C.F. A higher-order shear deformation theory for laminated elastic shells. Int. J. Eng. Sci. 1985, 23, 319–330. [Google Scholar] [CrossRef]
- Reddy, J.N. A Generalization of the Two-Dimensional Theories of Laminated Composite Plates. Commun. Appl. Numer. M 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Librescu, L.; Reddy, J.N. A few remarks concerning several refined theories of anisotropic composite laminated plates. Int. J. Eng. Sci. 1989, 27, 515–527. [Google Scholar] [CrossRef]
- Reddy, J.N. On Refined Theories of Composite Laminates. Meccanica 1990, 25, 230–238. [Google Scholar] [CrossRef]
- Robbins, D.H.; Reddy, J.N. Modeling of Thick Composites Using a Layer-Wise Laminate Theory. Int. J. Numer. Methods Eng. 1993, 36, 655–677. [Google Scholar] [CrossRef]
- Carrera, E. Theories and Finite Elements for Multilayered, Anisotropic, Composite Plates and Shells. Arch. Comput. Methods Eng. 2002, 9, 87–140. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of zig-zag theories for multilayered plates and shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 020801. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Strong Formulation Finite Element Method: Stability and Accuracy. Fract. Struct. Integr. 2014, 29, 251–265. [Google Scholar]
- Viola, E.; Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. DiQuMASPAB Software. DICAM Department, Alma Mater Studiorum—University of Bologna, 2013. Available online: http://software.dicam.unibo.it/diqumaspab-project (accessed on 1 January 2013).

| Edge coordinates and or | Edge coordinates and or |
| Clamped (C) | |
| Free (F) | |
| Simply-supported (S) | |
| (a) Quadratic (Quad) |
| (b) Chebyshev I kind (Cheb I) |
| (c) Chebyshev II kind (Cheb II) |
| (d) Legendre-Gauss (Leg-Gau) |
| (e) Chebyshev-Gauss (Cheb-Gau) |
| (f) Legendre-Gauss-Lobatto (Leg-Gau-Lob) |
| (g) Legendre (Leg) |
| (h) Chebyshev-Gauss-Lobatto (Cheb-Gau-Lob) |
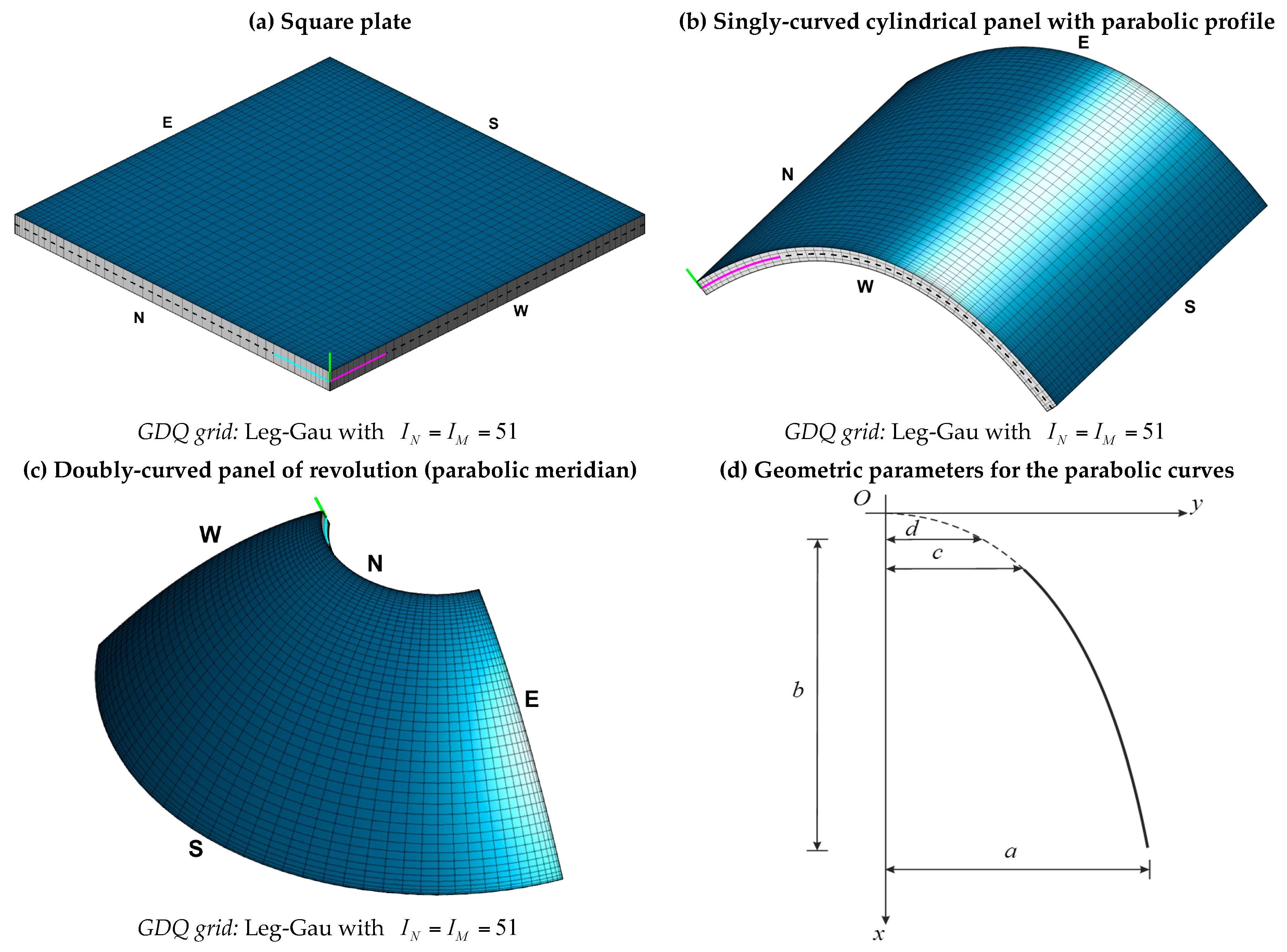
| (a) Square Plate |
| Position vector: , with , , |
| Boundary conditions: SSSS (for the convergence analyses) and CCCC (for the stress and strain recovery procedure) |
| Applied loads: |
| Thickness and lamination scheme (isotropic): (Aluminum) |
| Thickness and lamination scheme (laminated): , , with (Glass-epoxy) |
| Thickness and lamination scheme (laminated): , , with , (Glass-epoxy) |
| Evaluation point for strains, stresses and displacements: |
| (b) Singly-Curved Cylindrical Panel with Parabolic Profile |
| Position vector: , with , , , , , , , , , |
| Boundary conditions: FCFC |
| Applied loads: , |
| Thickness and lamination scheme: , , with (Glass-epoxy), (Foam) |
| Evaluation point for strains, stresses and displacements: |
| (c) Doubly-Curved Panel of Revolution with Parabolic Meridian |
| Position vector: , with , , , , , , , , , , |
| Boundary conditions: CCCF |
| Applied loads: , |
| Thickness and lamination scheme: , , with (Graphite-epoxy) |
| Evaluation point for strains, stresses and displacements: |
| Aluminum | Foam |
| Young’s modulus: Poisson’s ratio: | Young’s modulus: Poisson’s ratio: |
| Glass-Epoxy | Graphite-Epoxy |
| Young’s moduli: , Shear moduli: , Poisson’s ratios: , | Young’s moduli: , Shear moduli: , Poisson’s ratios: , |
| (a) Function 1 (Gau-1) |
| (b) Function 2 (Gau-2) |
| (c) Function 3 (Gau-3) |
| (d) Function 4 (Gau-4) |
| (e) Function 5 (Gau-5) |
| (f) Function 6 (Ell-1) |
| (g) Function 7 (Gau-6) |
| Cheb-Gau-Lob | Quad | Cheb I | Cheb II | Leg-Gau | Cheb-Gau | Leg-Gau-Lob | Leg | |
|---|---|---|---|---|---|---|---|---|
| Isotropic Plate (Aluminum)— | ||||||||
| 21 | −7.073 × 10−5 | −1.154 × 10−4 | −7.622 × 10−5 | −1.353 × 10−4 | −7.262 × 10−5 | −7.545 × 10−5 | −7.105 × 10−5 | −9.173 × 10−5 |
| 23 | −6.546 × 10−5 | −9.973 × 10−5 | −5.685 × 10−5 | −3.301 × 10−5 | −6.734 × 10−5 | −6.909 × 10−5 | −6.246 × 10−5 | −4.732 × 10−5 |
| 25 | −6.355 × 10−5 | −8.846 × 10−5 | −6.770 × 10−5 | −1.003 × 10−4 | −6.414 × 10−5 | −6.515 × 10−5 | −6.417 × 10−5 | −7.731 × 10−5 |
| 27 | −6.149 × 10−5 | −8.023 × 10−5 | −5.648 × 10−5 | −3.504 × 10−5 | −6.221 × 10−5 | −6.282 × 10−5 | −6.002 × 10−5 | −4.902 × 10−5 |
| 29 | −6.094 × 10−5 | −7.432 × 10−5 | −6.409 × 10−5 | −8.665 × 10−5 | −6.107 × 10−5 | −6.141 × 10−5 | −6.153 × 10−5 | −7.095 × 10−5 |
| 31 | −6.011 × 10−5 | −7.006 × 10−5 | −5.686 × 10−5 | −3.779 × 10−5 | −6.040 × 10−5 | −6.061 × 10−5 | −5.929 × 10−5 | −5.086 × 10−5 |
| 33 | −6.002 × 10−5 | −6.703 × 10−5 | −6.249 × 10−5 | −8.078 × 10−5 | −6.002 × 10−5 | −6.012 × 10−5 | −6.052 × 10−5 | −6.794 × 10−5 |
| 35 | −5.966 × 10−5 | −6.487 × 10−5 | −5.731 × 10−5 | −4.035 × 10−5 | −5.979 × 10−5 | −5.986 × 10−5 | −5.914 × 10−5 | −5.231 × 10−5 |
| 37 | −5.971 × 10−5 | −6.335 × 10−5 | −6.168 × 10−5 | −7.783 × 10−5 | −5.967 × 10−5 | −5.970 × 10−5 | −6.010 × 10−5 | −6.631 × 10−5 |
| 39 | −5.952 × 10−5 | −6.227 × 10−5 | −5.770 × 10−5 | −4.244 × 10−5 | −5.960 × 10−5 | −5.962 × 10−5 | −5.915 × 10−5 | −5.341 × 10−5 |
| 41 | −5.960 × 10−5 | −6.150 × 10−5 | −6.122 × 10−5 | −7.589 × 10−5 | −5.956 × 10−5 | −5.957 × 10−5 | −5.991 × 10−5 | −6.525 × 10−5 |
| 43 | −5.949 × 10−5 | −6.096 × 10−5 | −5.801 × 10−5 | −4.414 × 10−5 | −5.954 × 10−5 | −5.954 × 10−5 | −5.921 × 10−5 | −5.426 × 10−5 |
| 45 | −5.956 × 10−5 | −6.058 × 10−5 | −6.090 × 10−5 | −7.430 × 10−5 | −5.953 × 10−5 | −5.953 × 10−5 | −5.981 × 10−5 | −6.444 × 10−5 |
| 47 | −5.949 × 10−5 | −6.030 × 10−5 | −5.827 × 10−5 | −4.556 × 10−5 | −5.952 × 10−5 | −5.952 × 10−5 | −5.927 × 10−5 | −5.496 × 10−5 |
| 49 | −5.955 × 10−5 | −6.010 × 10−5 | −6.067 × 10−5 | −7.290 × 10−5 | −5.952 × 10−5 | −5.952 × 10−5 | −5.975 × 10−5 | −6.380 × 10−5 |
| 51 | −5.950 × 10−5 | −5.996 × 10−5 | −5.848 × 10−5 | −4.678 × 10−5 | −5.952 × 10−5 | −5.952 × 10−5 | −5.932 × 10−5 | −5.554 × 10−5 |
| Laminated Plate (−45/45)— | ||||||||
| 21 | −1.662 × 10−4 | −2.752 × 10−4 | −1.759 × 10−4 | −2.830 × 10−4 | −1.709 × 10−4 | −1.778 × 10−4 | −1.661 × 10−4 | −2.056 × 10−4 |
| 23 | −1.532 × 10−4 | −2.365 × 10−4 | −1.343 × 10−4 | −8.009 × 10−5 | −1.577 × 10−4 | −1.619 × 10−4 | −1.465 × 10−4 | −1.132 × 10−4 |
| 25 | −1.481 × 10−4 | −2.086 × 10−4 | −1.561 × 10−4 | −2.167 × 10−4 | −1.496 × 10−4 | −1.520 × 10−4 | −1.491 × 10−4 | −1.749 × 10−4 |
| 27 | −1.430 × 10−4 | −1.883 × 10−4 | −1.322 × 10−4 | −8.429 × 10−5 | −1.447 × 10−4 | −1.461 × 10−4 | −1.398 × 10−4 | −1.160 × 10−4 |
| 29 | −1.414 × 10−4 | −1.736 × 10−4 | −1.476 × 10−4 | −1.888 × 10−4 | −1.418 × 10−4 | −1.426 × 10−4 | −1.425 × 10−4 | −1.609 × 10−4 |
| 31 | −1.394 × 10−4 | −1.629 × 10−4 | −1.325 × 10−4 | −9.043 × 10−5 | −1.400 × 10−4 | −1.405 × 10−4 | −1.376 × 10−4 | −1.198 × 10−4 |
| 33 | −1.390 × 10−4 | −1.551 × 10−4 | −1.438 × 10−4 | −1.761 × 10−4 | −1.390 × 10−4 | −1.392 × 10−4 | −1.399 × 10−4 | −1.542 × 10−4 |
| 35 | −1.381 × 10−4 | −1.493 × 10−4 | −1.333 × 10−4 | −9.648 × 10−5 | −1.384 × 10−4 | −1.385 × 10−4 | −1.370 × 10−4 | −1.229 × 10−4 |
| 37 | −1.381 × 10−4 | −1.449 × 10−4 | −1.419 × 10−4 | −1.694 × 10−4 | −1.380 × 10−4 | −1.381 × 10−4 | −1.388 × 10−4 | −1.505 × 10−4 |
| 39 | −1.376 × 10−4 | −1.413 × 10−4 | −1.340 × 10−4 | −1.016 × 10−4 | −1.378 × 10−4 | −1.378 × 10−4 | −1.369 × 10−4 | −1.253 × 10−4 |
| 41 | −1.377 × 10−4 | −1.381 × 10−4 | −1.408 × 10−4 | −1.653 × 10−4 | −1.376 × 10−4 | −1.377 × 10−4 | −1.383 × 10−4 | −1.481 × 10−4 |
| 43 | −1.375 × 10−4 | −1.350 × 10−4 | −1.346 × 10−4 | −1.057 × 10−4 | −1.376 × 10−4 | −1.376 × 10−4 | −1.369 × 10−4 | −1.272 × 10−4 |
| 45 | −1.376 × 10−4 | −1.317 × 10−4 | −1.401 × 10−4 | −1.623 × 10−4 | −1.375 × 10−4 | −1.375 × 10−4 | −1.380 × 10−4 | −1.465 × 10−4 |
| 47 | −1.374 × 10−4 | −1.277 × 10−4 | −1.351 × 10−4 | −1.090 × 10−4 | −1.375 × 10−4 | −1.375 × 10−4 | −1.370 × 10−4 | −1.286 × 10−4 |
| 49 | −1.375 × 10−4 | −1.228 × 10−4 | −1.395 × 10−4 | −1.599 × 10−4 | −1.374 × 10−4 | −1.374 × 10−4 | −1.378 × 10−4 | −1.452 × 10−4 |
| 51 | −1.374 × 10−4 | −1.166 × 10−4 | −1.354 × 10−4 | −1.118 × 10−4 | −1.374 × 10−4 | −1.374 × 10−4 | −1.370 × 10−4 | −1.298 × 10−4 |
| Laminated Plate (−45/45)— | ||||||||
| 21 | −1.673 × 10−4 | −2.773 × 10−4 | −1.770 × 10−4 | −2.829 × 10−4 | −1.721 × 10−4 | −1.791 × 10−4 | −1.672 × 10−4 | −2.064 × 10−4 |
| 23 | −1.542 × 10−4 | −2.383 × 10−4 | −1.352 × 10−4 | −8.037 × 10−5 | −1.587 × 10−4 | −1.629 × 10−4 | −1.475 × 10−4 | −1.140 × 10−4 |
| 25 | −1.490 × 10−4 | −2.103 × 10−4 | −1.570 × 10−4 | −2.168 × 10−4 | −1.505 × 10−4 | −1.530 × 10−4 | −1.500 × 10−4 | −1.756 × 10−4 |
| 27 | −1.439 × 10−4 | −1.898 × 10−4 | −1.331 × 10−4 | −8.469 × 10−5 | −1.456 × 10−4 | −1.470 × 10−4 | −1.407 × 10−4 | −1.168 × 10−4 |
| 29 | −1.422 × 10−4 | −1.749 × 10−4 | −1.484 × 10−4 | −1.890 × 10−4 | −1.426 × 10−4 | −1.434 × 10−4 | −1.433 × 10−4 | −1.617 × 10−4 |
| 31 | −1.402 × 10−4 | −1.641 × 10−4 | −1.334 × 10−4 | −9.092 × 10−5 | −1.409 × 10−4 | −1.413 × 10−4 | −1.384 × 10−4 | −1.205 × 10−4 |
| 33 | −1.398 × 10−4 | −1.561 × 10−4 | −1.445 × 10−4 | −1.763 × 10−4 | −1.398 × 10−4 | −1.400 × 10−4 | −1.407 × 10−4 | −1.548 × 10−4 |
| 35 | −1.389 × 10−4 | −1.500 × 10−4 | −1.341 × 10−4 | −9.702 × 10−5 | −1.392 × 10−4 | −1.393 × 10−4 | −1.378 × 10−4 | −1.237 × 10−4 |
| 37 | −1.388 × 10−4 | −1.453 × 10−4 | −1.426 × 10−4 | −1.698 × 10−4 | −1.388 × 10−4 | −1.388 × 10−4 | −1.396 × 10−4 | −1.511 × 10−4 |
| 39 | −1.384 × 10−4 | −1.412 × 10−4 | −1.348 × 10−4 | −1.022 × 10−4 | −1.385 × 10−4 | −1.386 × 10−4 | −1.376 × 10−4 | −1.261 × 10−4 |
| 41 | −1.385 × 10−4 | −1.374 × 10−4 | −1.415 × 10−4 | −1.657 × 10−4 | −1.384 × 10−4 | −1.384 × 10−4 | −1.390 × 10−4 | −1.488 × 10−4 |
| 43 | −1.382 × 10−4 | −1.335 × 10−4 | −1.353 × 10−4 | −1.063 × 10−4 | −1.383 × 10−4 | −1.383 × 10−4 | −1.376 × 10−4 | −1.279 × 10−4 |
| 45 | −1.383 × 10−4 | −1.290 × 10−4 | −1.408 × 10−4 | −1.628 × 10−4 | −1.382 × 10−4 | −1.382 × 10−4 | −1.387 × 10−4 | −1.472 × 10−4 |
| 47 | −1.381 × 10−4 | −1.235 × 10−4 | −1.358 × 10−4 | −1.096 × 10−4 | −1.382 × 10−4 | −1.382 × 10−4 | −1.377 × 10−4 | −1.293 × 10−4 |
| 49 | −1.382 × 10−4 | −1.165 × 10−4 | −1.403 × 10−4 | −1.604 × 10−4 | −1.382 × 10−4 | −1.381 × 10−4 | −1.386 × 10−4 | −1.459 × 10−4 |
| 51 | −1.381 × 10−4 | −1.076 × 10−4 | −1.361 × 10−4 | −1.124 × 10−4 | −1.381 × 10−4 | −1.381 × 10−4 | −1.377 × 10−4 | −1.305 × 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear Static Behavior of Damaged Laminated Composite Plates and Shells. Materials 2017, 10, 811. https://doi.org/10.3390/ma10070811
Tornabene F, Fantuzzi N, Bacciocchi M. Linear Static Behavior of Damaged Laminated Composite Plates and Shells. Materials. 2017; 10(7):811. https://doi.org/10.3390/ma10070811
Chicago/Turabian StyleTornabene, Francesco, Nicholas Fantuzzi, and Michele Bacciocchi. 2017. "Linear Static Behavior of Damaged Laminated Composite Plates and Shells" Materials 10, no. 7: 811. https://doi.org/10.3390/ma10070811
APA StyleTornabene, F., Fantuzzi, N., & Bacciocchi, M. (2017). Linear Static Behavior of Damaged Laminated Composite Plates and Shells. Materials, 10(7), 811. https://doi.org/10.3390/ma10070811







