Comparative Study on ZnO Monolayer Doped with Al, Ga and In Atoms as Transparent Electrodes
Abstract
:1. Introduction
2. Calculation Models and Methods
3. Results and Discussion
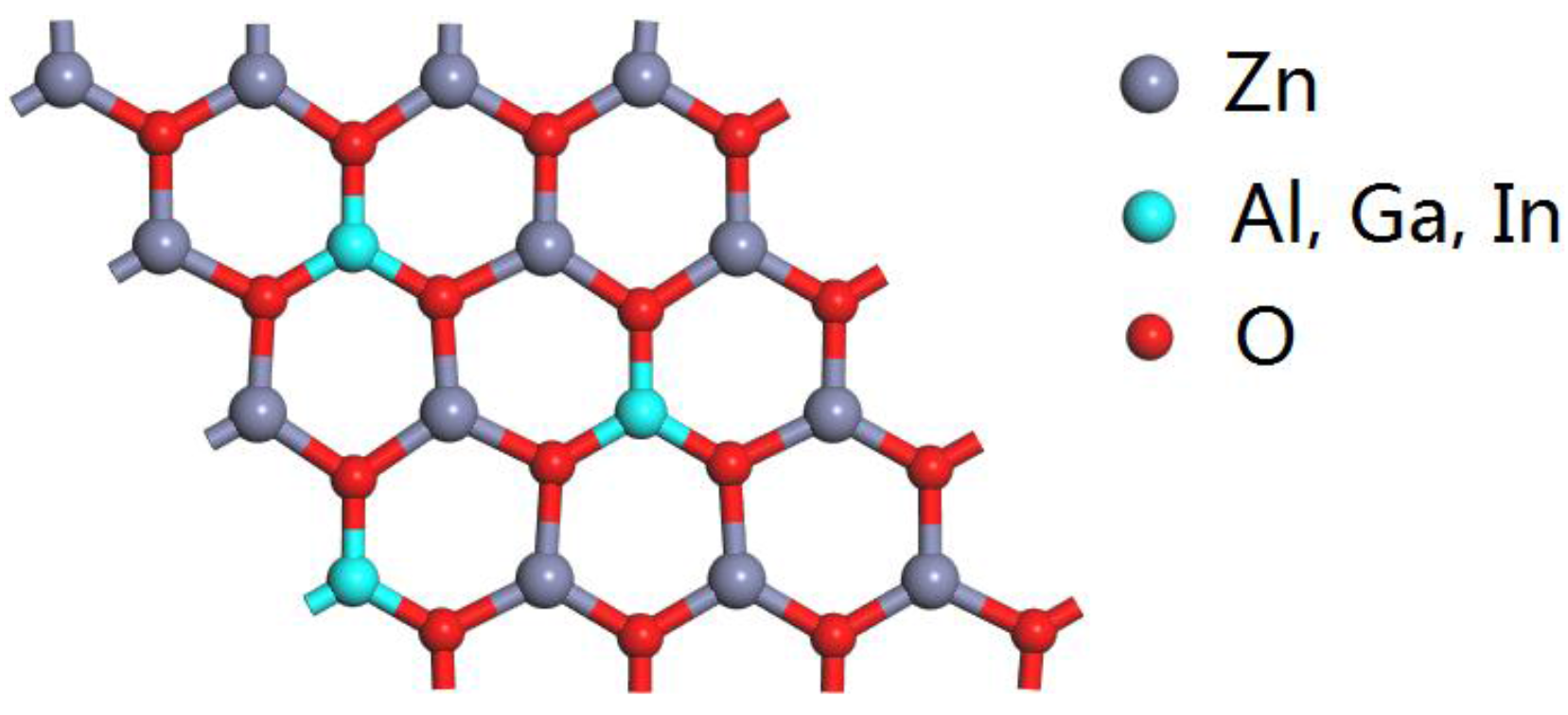
3.1. Structural Properties
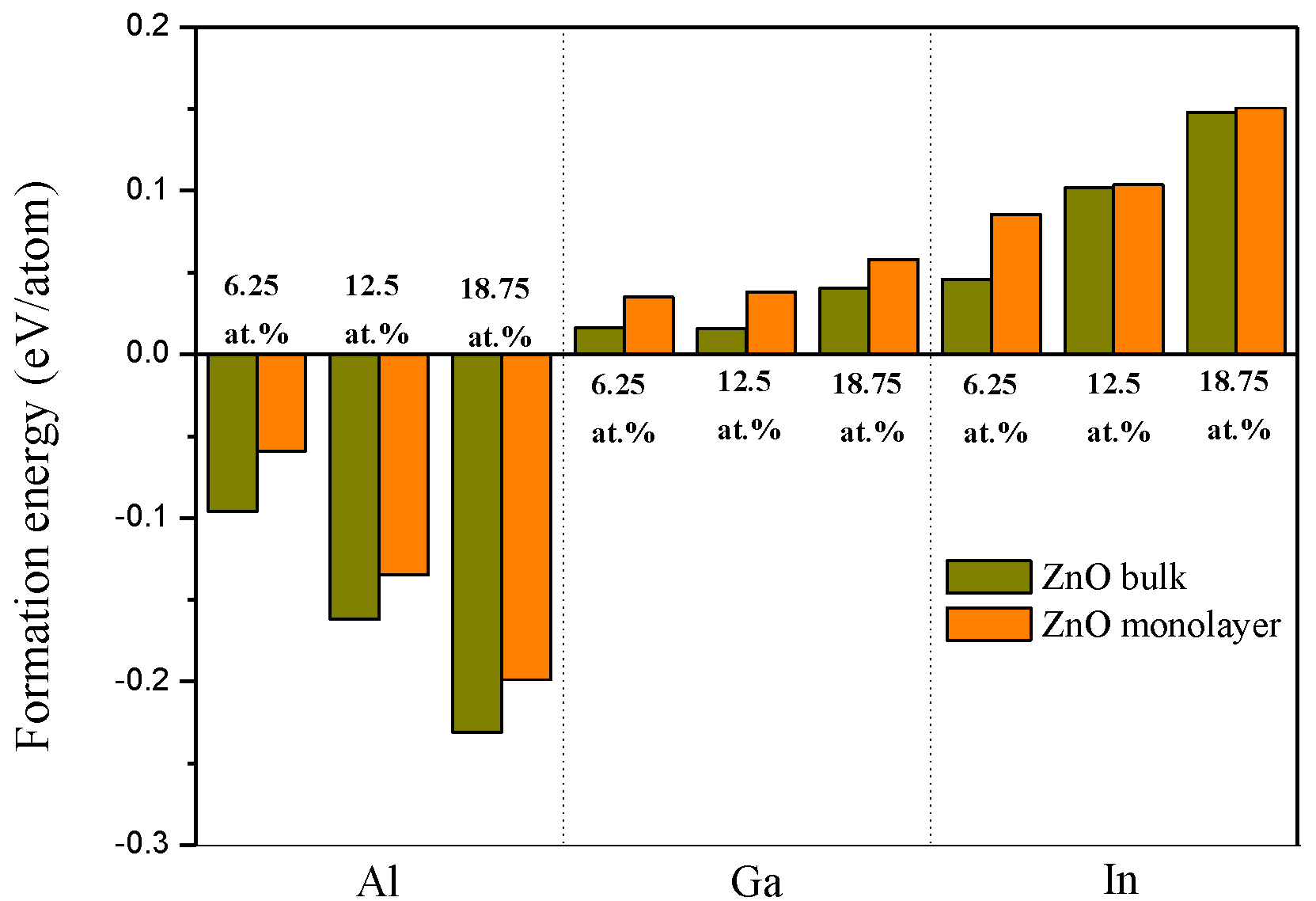
3.2. Formation Energy
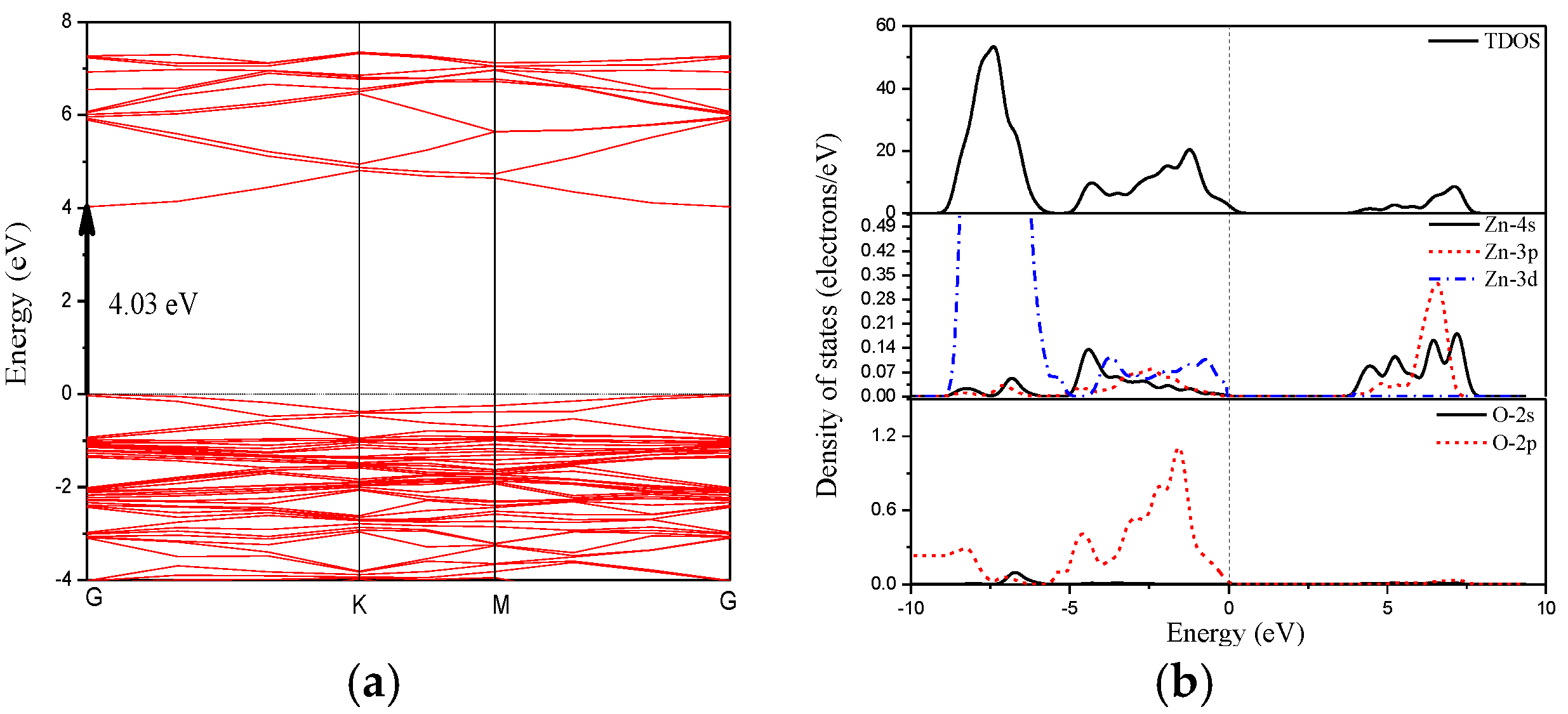
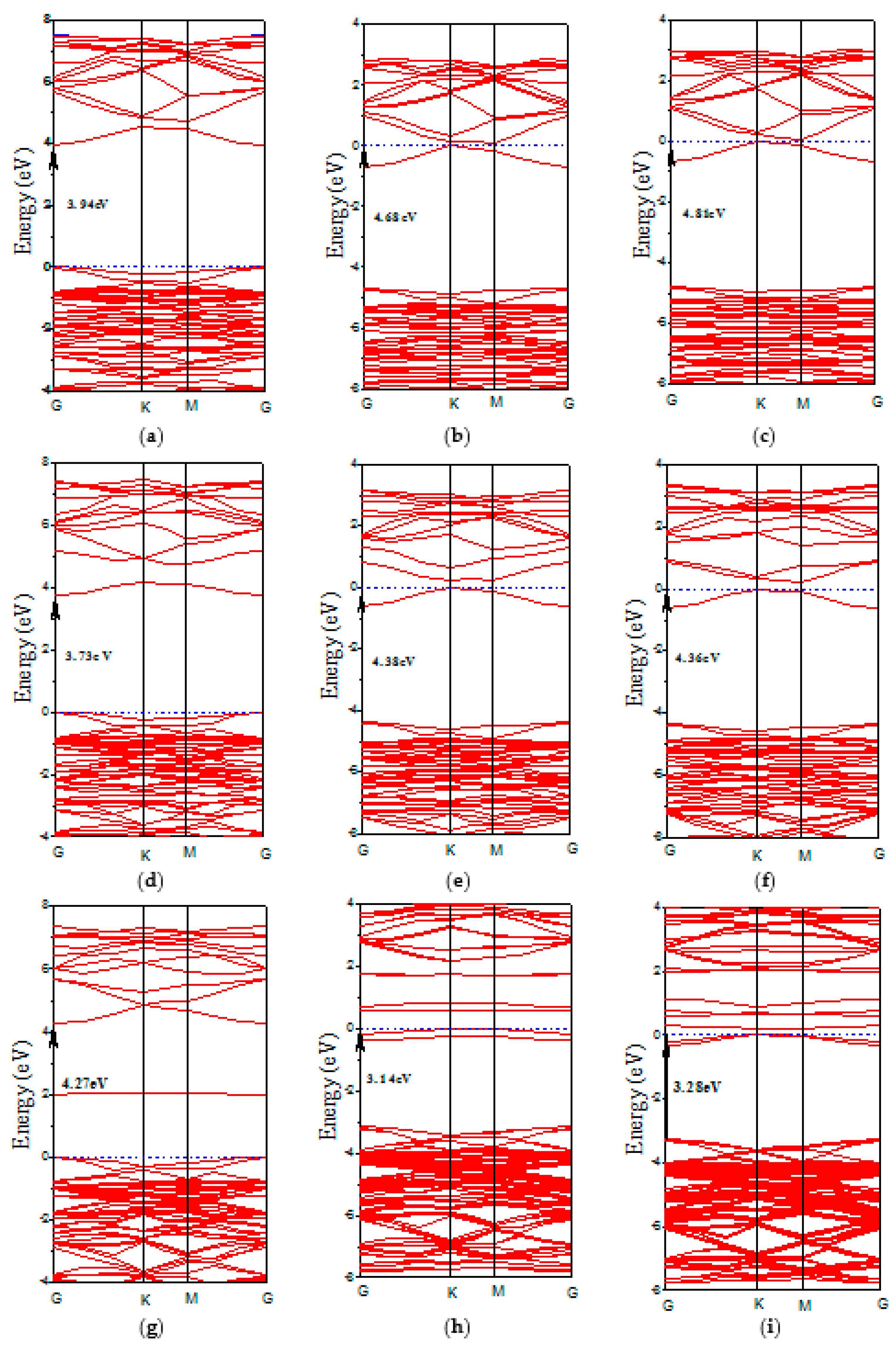
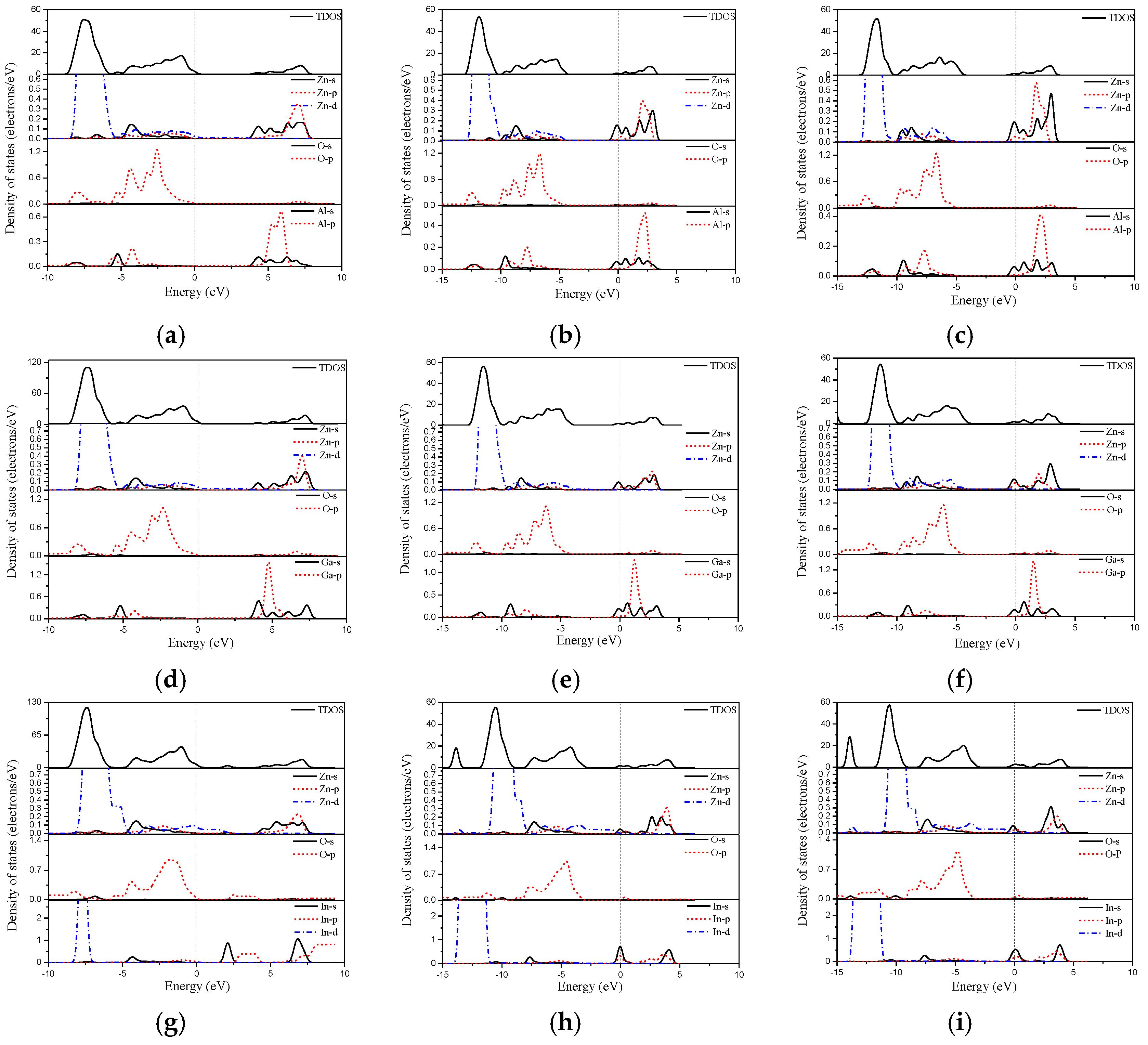
3.3. Electronic Structures
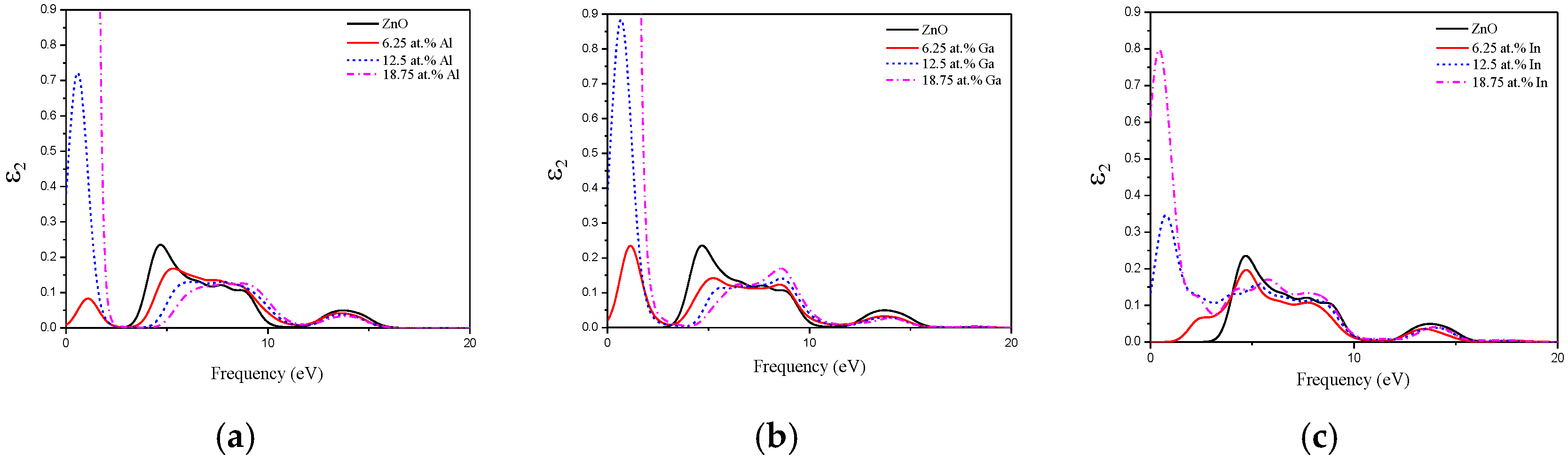
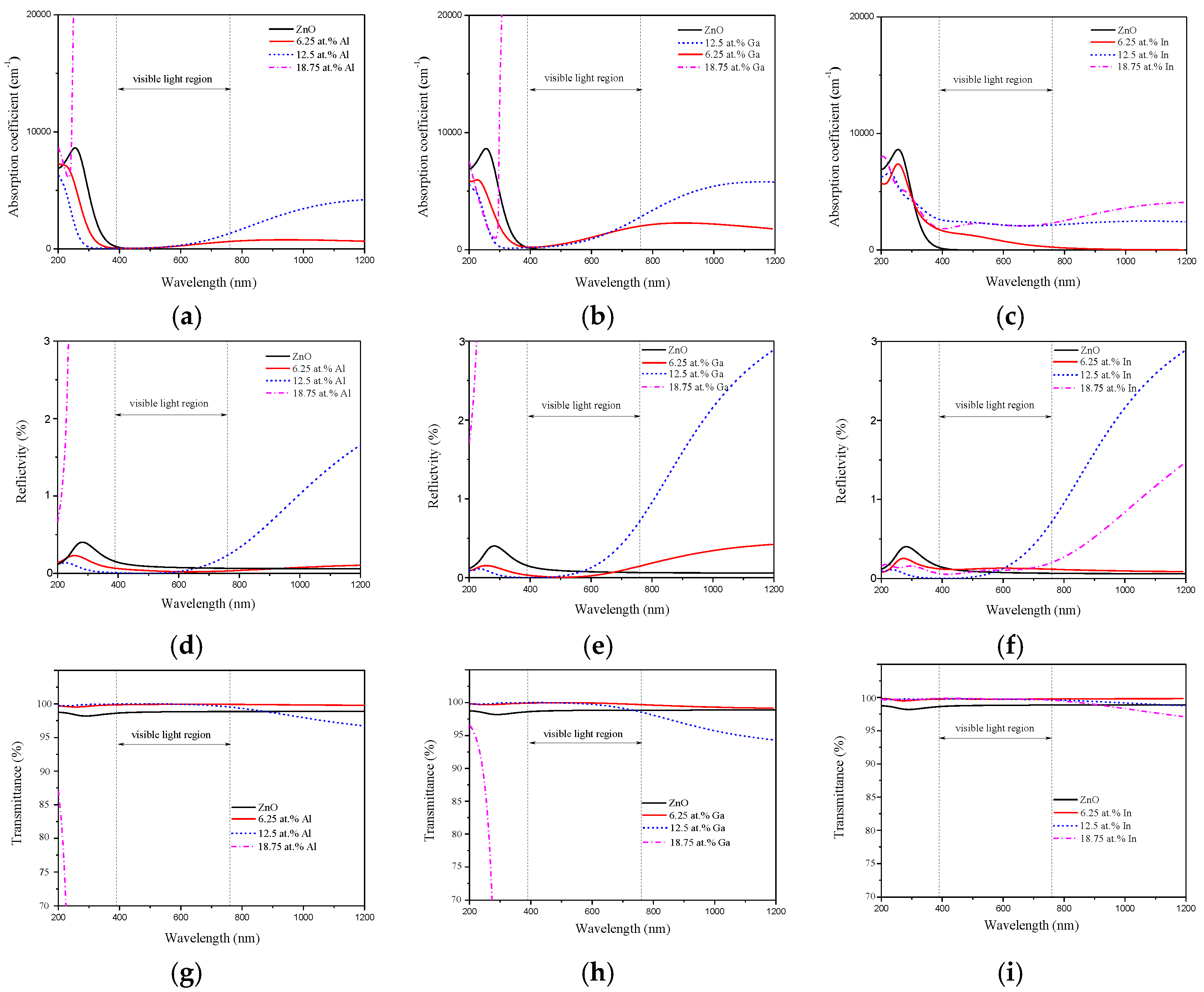
3.4. Optical Property
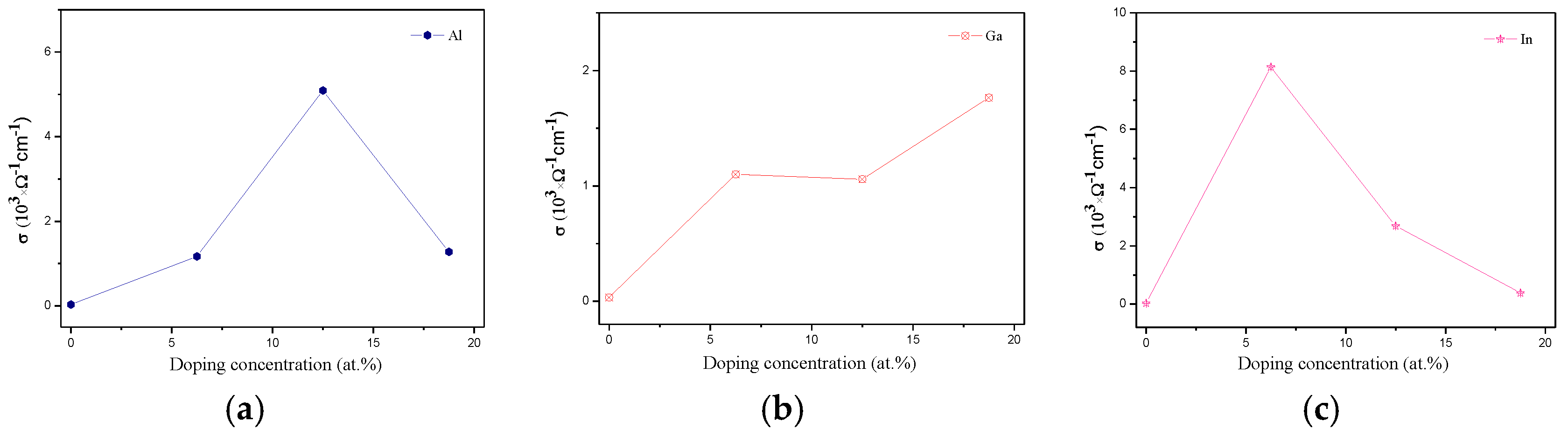
3.5. Transport Proprieties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shinde, K.P.; Pawar, R.C.; Sinha, B.B.; Kim, H.S.; Oh, S.S.; Chung, K.C. Study of effect of planetary ball milling on ZnO nanopowder synthesized by co-precipitation. J. Alloys Compd. 2014, 617, 404–407. [Google Scholar] [CrossRef]
- Tsukazaki, A.; Ohtomo, A.; Onuma, T.; Ohtani, M.; Makino, T.; Sumiya, M.; Ohtani, K.; Chichibu, S.F.; Fuke, S.; Segawa, Y.; et al. Repeated temperature modulation epitaxy for p-type doping and light-emitting diode based on ZnO. Nat. Mater. 2005, 4, 42–46. [Google Scholar] [CrossRef]
- Lu, M.P.; Lu, M.Y.; Chen, L.J. p-Type ZnO nanowires: From synthesis to nanoenergy. Nano Energy 2012, 1, 247–258. [Google Scholar] [CrossRef]
- Hoffman, R.L.; Norris, B.J.; Wager, J.F. ZnO-based transparent thin-film transistors. Appl. Phys. Lett. 2003, 82, 733–735. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.; Doğan, S.; Avrutin, V.; Cho, S.-J.; Morkoc, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 11. [Google Scholar] [CrossRef]
- Ayadi, Z.B.; Mahdhi, H.; Djessas, K.; Gauffier, J.L.; El Mir, L.; Alaya, S. Sputtered Al-doped ZnO transparent conducting thin films suitable for silicon solar cells. Thin Solid Films 2014, 553, 123–126. [Google Scholar] [CrossRef]
- Ng, Z.N.; Chan, K.Y.; Low, C.Y.; Kamaruddin, S.A.; Sahdan, M.Z. Al and Ga doped ZnO films prepared by a sol–gel spin coating technique. Ceram. Int. 2015, 41, S254–S258. [Google Scholar] [CrossRef]
- Hsu, L.-S; Yeh, C.S.; Kuo, C.C.; Huang, B.R.; Dhar, S. Optical and transport properties of undoped and Al-, Ga- and In-doped ZnO thin films. J. Optoelectron. Adv. Mater. 2005, 7, 3039. [Google Scholar]
- Kuprenaite, S.; Murauskas, T.; Abrutis, A.; Kubilius, V.; Saltyte, Z.; Plausinaitiene, V. Properties of In-, Ga- and Al-doped ZnO films grown by aerosol-assisted MOCVD: Influence of deposition temperature, doping level and annealing. Surf. Coat. Technol. 2015, 271, 156–164. [Google Scholar] [CrossRef]
- Khuili, M.; Fazouan, N.; El Makarim, H.A.; El Halani, G.; Atmani, E.H. Comparative first principles study of ZnO doped with group III elements. J. Alloys Compd. 2016, 688, 368–375. [Google Scholar] [CrossRef]
- Slassi, A.; Naji, S.; Benyoussef, A.; Hamedoun, M.; El Kenz, A. On the transparent conducting oxide Al doped ZnO: First principles and Boltzmann equations study. J. Alloys Compd. 2014, 605, 118–123. [Google Scholar] [CrossRef]
- Lee, J.H.; Chou, C.Y.; Bi, Z.; Tsai, C.F.; Wang, H. Growth-controlled surface roughness in Al-doped ZnO as transparent conducting oxide. Nanotechnology 2009, 20, 395704. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.C.; Peng, Y.C.; Chen, C.C. Effects of Ga concentration on electronic and optical properties of Ga-doped ZnO from first principles calculations. Opt. Mater. 2013, 35, 509–515. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2017, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.Y.; Sun, D.; Tan, C.L.; Tian, X.H.; Huang, Y.W. Al-doped ZnO monolayer as a promising transparent electrode material: A First-principles study. Materials 2017, 10, 359. [Google Scholar] [CrossRef]
- Xu, M.S.; Liang, T.; Shi, M.M.; Chen, H.Z. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef] [PubMed]
- Quang, H.T.; Bachmatiuk, A.; Dianat, A.; Ortmann, F.; Zhao, J.; Warner, J.H.; Eckert, J.; Cunniberti, G.; Rummeli, M.H. In situ observations of free-standing graphene-like mono- and bilayer ZnO membranes. ACS Nano 2015, 9, 11408–11413. [Google Scholar] [CrossRef] [PubMed]
- Weirum, G.; Barcaro, G.; Fortunelli, A.; Weber, F.; Schennach, R.; Surnev, S.; Netzer, F.P. Growth and surface structure of zinc oxide layers on a Pd (111) surface. J. Phys. Chem. C 2010, 114, 15432–15439. [Google Scholar] [CrossRef]
- Guo, H.Y.; Zhao, Y.; Lu, N.; Kang, E.J.; Zeng, X.C.; Wu, X.J.; Yang, J.L. Tunable magnetism in a nonmetal-substituted ZnO monolayer: A First-principles study. J. Phys. Chem. C 2012, 116, 11336–11342. [Google Scholar] [CrossRef]
- He, A.L.; Wang, X.Q.; Lu, Y.H.; Feng, Y.P. Adsorption of an Mn atom on a ZnO sheet and nanotube: A density functional theory study. J. Phys. Condens. Matter 2010, 22, 175501. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, T.M.; MiWa, R.H.; Fazzio, A. Ferromagnetic coupling in a Co-doped graphenelike ZnO sheet. Phys. Rev. B 2010, 81, 195413. [Google Scholar] [CrossRef]
- Sahoo, T.; Nayak, S.K.; Chelliah, P.; Raht, M.K.; Parida, B. Observations of two-dimensional monolayer zinc oxide. Mater. Res. Bull. 2016, 75, 134–138. [Google Scholar] [CrossRef]
- Lee, J.; Sorescu, D.C.; Deng, X.Y. Tunable lattice constant and band gap of single- and few-layer ZnO. J. Phys. Chem. Lett. 2016, 7, 1335–1340. [Google Scholar] [CrossRef] [PubMed]
- Koski, K.J.; Cui, Y. The new skinny in two-dimensional nanomaterials. ACS Nano 2013, 7, 3739–3743. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Hu, J.; Zeng, H. Two-dimensional semiconductors: Recent progress and future perspectives. J. Mater. Chem. C 2013, 1, 2952–2969. [Google Scholar] [CrossRef]
- Freeman, C.L.; Claeyssens, F.; Allan, N.L.; Harding, J.H. Graphitic nanofilms as precursors to wurtzite films: theory. Phys. Rev. Lett. 2006, 96, 066102. [Google Scholar] [CrossRef] [PubMed]
- Tusche, C.; Meyerheim, H.L.; Kirschner, J. Observation of depolarized ZnO (0001) monolayers: Formation of unreconstructed planar sheets. Phys. Rev. Lett. 2007, 99, 026102. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.L.; Sun, D.; Xu, D.S.; Tian, X.H.; Huang, Y.W. First-principles investigation of phase stability, electronic structure and optical properties of MgZnO monolayer. Materials 2016, 9, 877. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hassnip, P.J.; Clark, S.J.; Payne, M.D. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 1990, 14, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B Solid State. [CrossRef]
- Vispute, R.D.; Talyansky, V.; Choopun, S.; Sharma, R.P.; Venkatesan, T.; He, M.; Salamanca-Riba, L.G. Heteroepitaxy of ZnO on GaN and its implications for fabrication of hybrid optoelectronic devices. Appl. Phys. Lett. 1998, 73, 348–350. [Google Scholar] [CrossRef]
- Okoye, C.M.I. Theoretical study of the electronic structure, chemical bonding and optical properties of KNbO3 in the paraelectric cubic phase. J. Phys. Condens. Matter 2003, 15, 5945. [Google Scholar] [CrossRef]
- Amin, B.; Ahmad, M.I.; Maqbool, S.; Said, G.; Ahmad, R. Ab initio study of the bandgap engineering of Al1−xGaxN for optoelectronic applications. J. Appl. Phys. 2011, 109, 023109. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, J.; Yang, H.; Yang, P. Impact of high pressure on the optical and electrical properties of indium-doped n-type wurtzite zinc oxide according to first principles. Mater. Sci. Semicond. Process. 2014, 19, 66–71. [Google Scholar] [CrossRef]
- Xie, F.W.; Yang, P.; Li, P.; Zhang, L.Q. First-principle study of optical properties of (N, Ga) codoped ZnO. Opt. Commun. 2012, 285, 2660–2664. [Google Scholar] [CrossRef]
- Yang, P.; Deng, L.; Zhang, L.; Yang, H. Experimental and numerical evaluation on optical properties of Al-doped ZnO film materials. J. Am. Ceram. Soc. 2014, 97, 3549–3554. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Ziman, J.M. Electrons and Phonons; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Tan, C.L.; Sun, D.; Xu, D.S.; Tian, X.H.; Huang, Y.W. Tuning electronic structure and optical properties of ZnO monolayer by Cd doping. Ceram. Int. 2016, 42, 10997–11002. [Google Scholar] [CrossRef]
- Burstein, E. Anomalous optical absorption limit in InSb. Phys. Rev. 1954, 93, 632. [Google Scholar] [CrossRef]
- Moss, T.S. The interpretation of the properties of indium antimonide. Proc. Phys. Soc. B 1954, 67, 775. [Google Scholar] [CrossRef]
- Kumar, S.; Asokan, K.; Singh, R.K.; Chatterjee, S.; Kanjilal, D.; Ghosh, A.K. Investigations on structural and optical properties of ZnO and ZnO: Co nanoparticles under dense electronic excitations. RSC Adv. 2014, 4, 62123–62131. [Google Scholar] [CrossRef]
- Kumar, S.; Chatterjee, S.; Chattopadhyay, K.K.; Ghosh, A.K. Sol-gel-derived ZnO: Mn nanocrystals: Study of structural, Raman, and optical properties. J. Phys. Chem. C 2012, 116, 16700–16708. [Google Scholar] [CrossRef]
- Tang, G.; Liu, H.; Zhang, W. The variation of optical band gap for ZnO: In films prepared by sol-gel technique. Adv. Mater. Sci. Eng. 2013, 2013, 348601. [Google Scholar] [CrossRef]
- Ong, K.P.; Singh, D.J.; Wu, P. Analysis of the thermoelectric properties of n-type ZnO. Phys. Rev. B 2011, 83, 115110. [Google Scholar] [CrossRef]
| Compounds | Concentrations | Bond Length (Å) | Bond Angle (°) | ||
|---|---|---|---|---|---|
| dZn-O | dM-O | O-Zn-O | O-M-O | ||
| Pure | 0% | 1.910 | - | 120 | - |
| Al | 6.25% | 1.932 | 1.750 | 119.16 | 119.99 |
| 12.5% | 1.944 | 1.751 | 119.05 | 119.98 | |
| 18.75% | 1.946 | 1.753 | 119.21 | 119.88 | |
| Ga | 6.25% | 1.929 | 1.879 | 119.50 | 120 |
| 12.5% | 1.951 | 1.855 | 119.33 | 119.89 | |
| 18.75% | 1.932 | 1.881 | 119.96 | 119.73 | |
| In | 6.25% | 1.921 | 2.136 | 119.97 | 98.34 |
| 12.5% | 1.916 | 2.121 | 118.99 | 110.37 | |
| 18.75% | 1.926 | 2.116 | 119.97 | 112.96 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Tan, C.; Tian, X.; Huang, Y. Comparative Study on ZnO Monolayer Doped with Al, Ga and In Atoms as Transparent Electrodes. Materials 2017, 10, 703. https://doi.org/10.3390/ma10070703
Sun D, Tan C, Tian X, Huang Y. Comparative Study on ZnO Monolayer Doped with Al, Ga and In Atoms as Transparent Electrodes. Materials. 2017; 10(7):703. https://doi.org/10.3390/ma10070703
Chicago/Turabian StyleSun, Dan, Changlong Tan, Xiaohua Tian, and Yuewu Huang. 2017. "Comparative Study on ZnO Monolayer Doped with Al, Ga and In Atoms as Transparent Electrodes" Materials 10, no. 7: 703. https://doi.org/10.3390/ma10070703
APA StyleSun, D., Tan, C., Tian, X., & Huang, Y. (2017). Comparative Study on ZnO Monolayer Doped with Al, Ga and In Atoms as Transparent Electrodes. Materials, 10(7), 703. https://doi.org/10.3390/ma10070703






