Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density
Abstract
1. Introduction
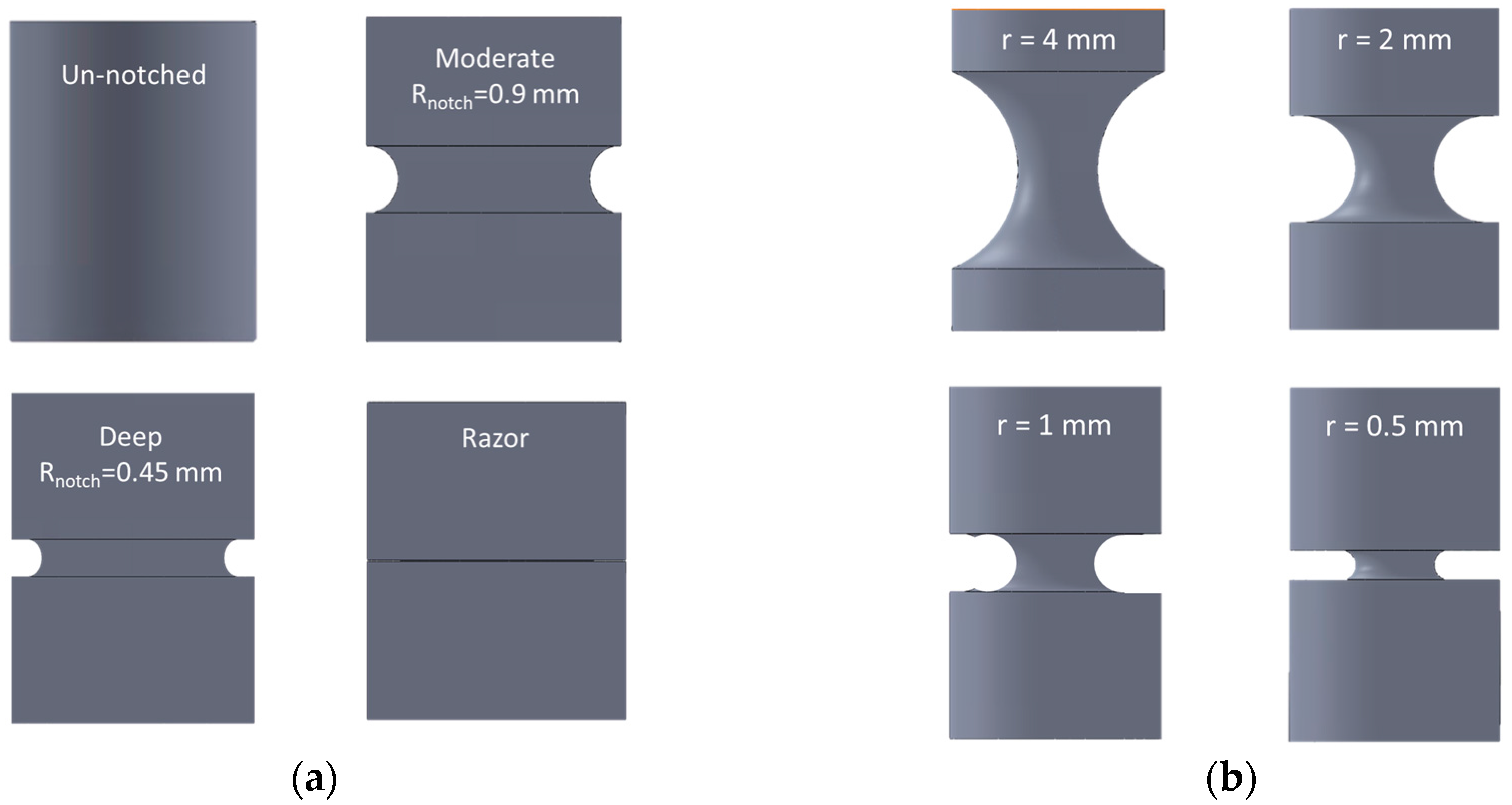
2. Experimental Reference Data
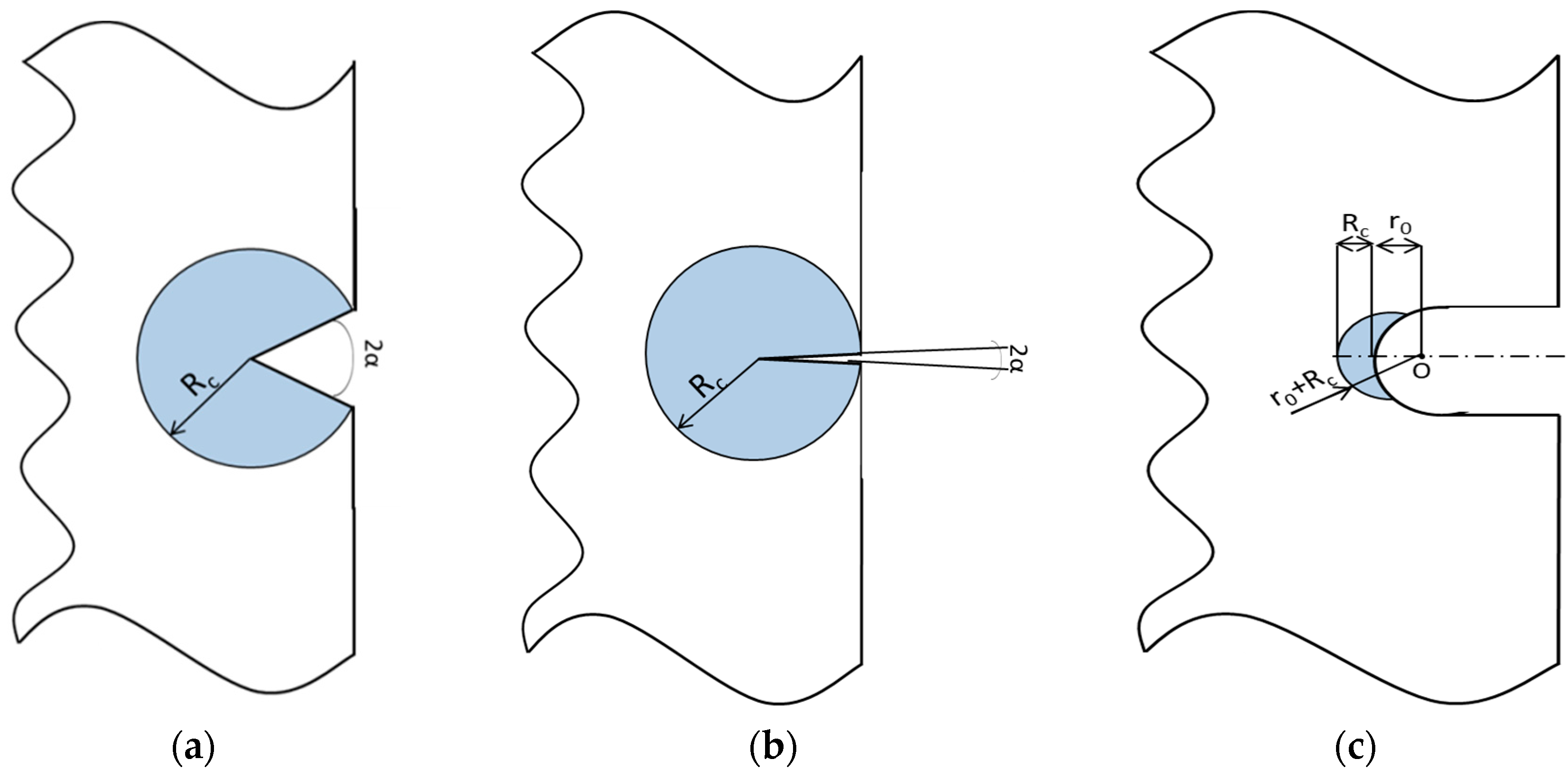
3. Brief Introduction of the SED Approach
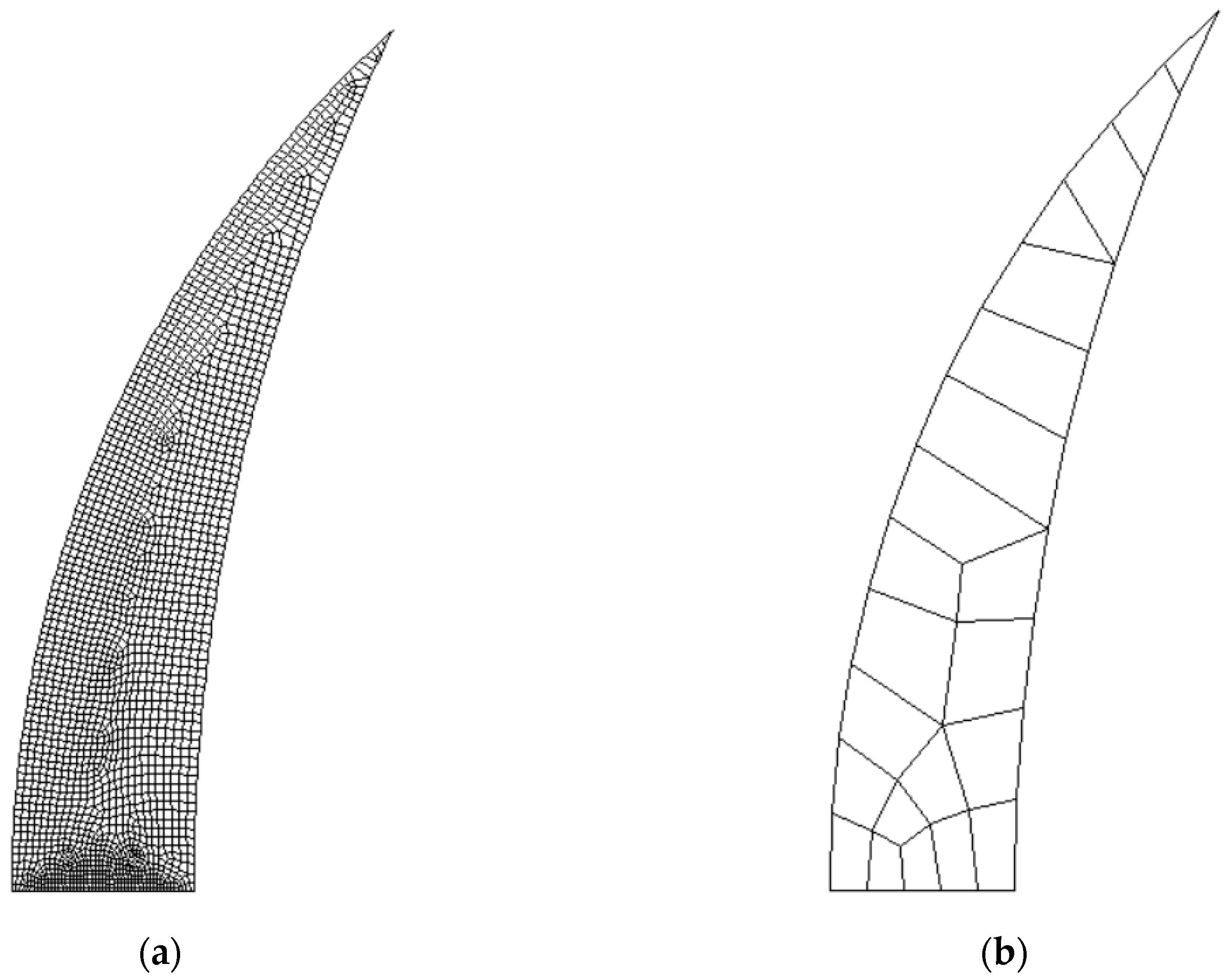
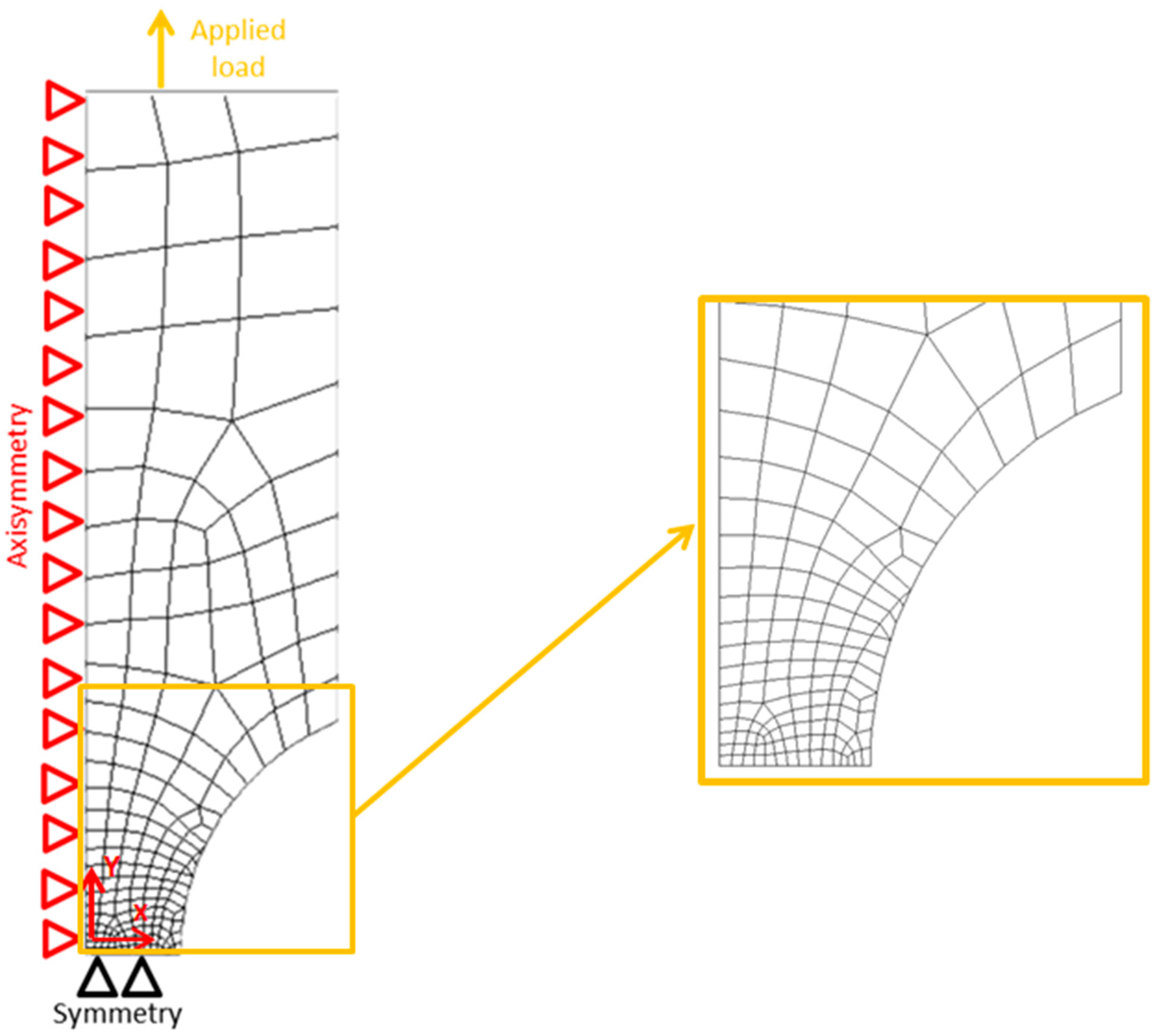
4. Finite Element Model
5. Results and Discussion
5.1. Prediction with Known Critical SED
5.2. Predictions with Known Fracture Toughness
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Seymour, R.B.; Carraher, C.E. Selection of Polymers for Special Applications; Springer: New York, NY, USA, 1984; pp. 205–216. [Google Scholar]
- Sobieraj, M.C.; Murphy, J.E.; Brinkman, J.G.; Kurtz, S.M.; Rimnac, C.M. Notched fatigue behavior of PEEK. Biomaterials 2010, 31, 9156–9162. [Google Scholar] [CrossRef] [PubMed]
- Platt, D.K. Engineering and High Performance Plastics Market Report: A Rapra Market Report; Smithers Rapra: Shawbury, UK, 2003. [Google Scholar]
- Hoskins, T.J.; Dearn, K.D.; Chen, Y.K.; Kukureka, S.N. The wear of PEEK in rolling–sliding contact—Simulation of polymer gear applications. Wear 2014, 309, 35–42. [Google Scholar] [CrossRef]
- El-Qoubaa, Z.; Othman, R. Tensile Behavior of Polyetheretherketone over a Wide Range of Strain Rates. Int. J. Polym. Sci. 2015, 2015, 275937. [Google Scholar] [CrossRef]
- Albérola, N.D.; Mélé, P.; Bas, C. Tensile mechanical properties of PEEK films over a wide range of strain rates. II. J. Appl. Polym. Sci. 1997, 64, 1053–1059. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. Recent developments in brittle and quasi-brittle failure assessment of engineering materials by means of local approaches. Mater. Sci. Eng. R 2014, 75, 1–48. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. The volume-based Strain Energy Density approach applied to static and fatigue strength assessments of notched and welded structures. Procedia Eng. 2009, 1, 155–158. [Google Scholar] [CrossRef]
- Maragoni, L.; Carraro, P.A.; Peron, M.; Quaresimin, M. Fatigue behaviour of glass/epoxy laminates in the presence of voids. Int. J. Fatigue 2017, 95, 18–28. [Google Scholar] [CrossRef]
- Sobieraj, M.C.; Kurtz, S.M.; Rimnac, C.M. Notch sensitivity of PEEK in monotonic tension. Biomaterials 2009, 30, 6485–9644. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Gatea, S.; Ou, H.; Lu, B.; Long, H. Fracture characteristics of PEEK at various stress triaxialities. J. Mech. Behav. Biomed. Mater. 2016, 64, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Gillemot, F.; Czoboly, E.; Havas, I. Fracture mechanics applications of absorbed specific fracture energy: Notch and unnotched specimens. Theor. Appl. Fract. Mech. 1985, 5, 39–45. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F.; Mutignani, F. Effect of hot dip galvanization on the fatigue strength of steel bolted connections. Fract. Int. Struct. 2017, 41, 432–439. [Google Scholar]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F.; Welo, T. 40CrMoV13.9 notched specimens under multiaxial fatigue: An overview of recent results. Fract. Int. Struct. 2017, 41, 440–446. [Google Scholar]
- Gallo, P.; Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F. Creep behavior of V-notched components. Fract. Int. Struct. 2017, 41, 456–463. [Google Scholar]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F. Static Multiaxial Fracture Behavior of Graphite Components: A Review of Recent Results. Key Eng. Mater. 2017, 754, 35–38. [Google Scholar] [CrossRef]
- Gómez, F.J.; Elices, M.; Berto, F.; Lazzarin, P. Local strain energy to assess the static failure of U-notches in plates under mixed mode loading. Int. J. Fract. 2007, 145, 29–45. [Google Scholar] [CrossRef]
- Berto, F.; Marsavina, L.; Razavi, S.M.J.; Ayatollahi, M.R. On the fracture behavior of polyurethane notched components. Procedia Struct. Integr. 2017, 3, 144–152. [Google Scholar] [CrossRef]
- Berto, F.; Cendon, D.A.; Lazzarin, P.; Elices, M. Fracture behaviour of notched round bars made of PMMA subjected to torsion at −60 °C. Eng. Fract. Mech. 2013, 102, 271–287. [Google Scholar] [CrossRef]
- Berto, F.; Elices, M.; Lazzarin, P.; Zappalorto, M. Fracture behaviour of notched round bars made of PMMA subjected to torsion at room temperature. Eng. Fract. Mech. 2012, 90, 143–160. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Torabi, A.R.; Alaei, M. Application of the equivalent material concept to ductile failure prediction of blunt V-notches encountering moderate-scale yielding. Int. J. Damage Mech. 2016, 25, 853–877. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. A review of the volume-based strain energy density approach applied to V-notches and welded structures. Theor. Appl. Fract. Mech. 2009, 52, 183–194. [Google Scholar] [CrossRef]
- Berto, F.; Campagnolo, A.; Gallo, P. Brittle Failure of Graphite Weakened by V-Notches: A Review of Some Recent Results Under Different Loading Modes. Strength Mater. 2015, 47, 488–506. [Google Scholar] [CrossRef]
- Wallin, K. Fracture Toughness of Engineering Materials: Estimation and Application; EMAS Publishing: Warrington, UK, 2011. [Google Scholar]
- Beltrami, E. Sulle condizioni di resistenza dei corpi elastici. Nuovo Cimento 1885, 18, 145–155. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ferro, P.; Berto, F.; Torgersen, J. Fatigue strength of blunt V-notched specimens produced by selective laser melting of Ti-6Al-4V. Theor. Appl. Fract. Mech. 2017, in press. [Google Scholar] [CrossRef]
- Gross, B.; Mendelson, A. Plane elastostatic analysis of V-notched plates. Int. J. Fract. Mech. 1972, 8, 267–276. [Google Scholar] [CrossRef]
- Williams, M.L. Stress singularities resulting from various boundary conditions in angular corners on plates in extension. J. Appl. Mech. 1952, 19, 526–528. [Google Scholar]
- Wu, G.-M.; Schultz, J.M. Fracture behavior of oriented poly(ether-ether-ketone) (PEEK). Polym. Eng. Sci. 1989, 29, 405–414. [Google Scholar] [CrossRef]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Marsavina, L. Local strain energy density for the fracture assessment of polyurethane specimens weakened by notches of different shape. Fract. Int. Struct. 2017, 42, 214–222. [Google Scholar]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Colussi, M. Fracture assessment of magnetostrictive materials. Fract. Int. Struct. 2017, 42, 223–230. [Google Scholar]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Mutignani, F. Local strain energy density for the fatigue assessment of hot dip galvanized welded joints: Some recent outcomes. Fract. Int. Struct. 2017, 42, 205–213. [Google Scholar]
- Gensler, R.; Béguelin, P.; Plummer, C.J.G.; Kausch, H.-H.; Miinstedt, H. Tensile behaviour and fracture toughness of poly(ether ether ketone)/poly(ether imide) blends. Polym. Bull. 1996, 37, 111–118. [Google Scholar] [CrossRef]
- Starkweather, H.W.; Moore, G.E.; Hansen, J.E.; Roder, T.M.; Brooks, R.E. Effect of crystallinity on the properties of nylons. J. Polym. Sci. 1956, 21, 189–204. [Google Scholar] [CrossRef]
- Perkins, W.G.; Capiati, N.J.; Porter, R.S. The effect of molecular weight on the physical and mechanical properties of ultra-drawn high density polyethylene. Polym. Eng. Sci. 1976, 16, 200–203. [Google Scholar] [CrossRef]
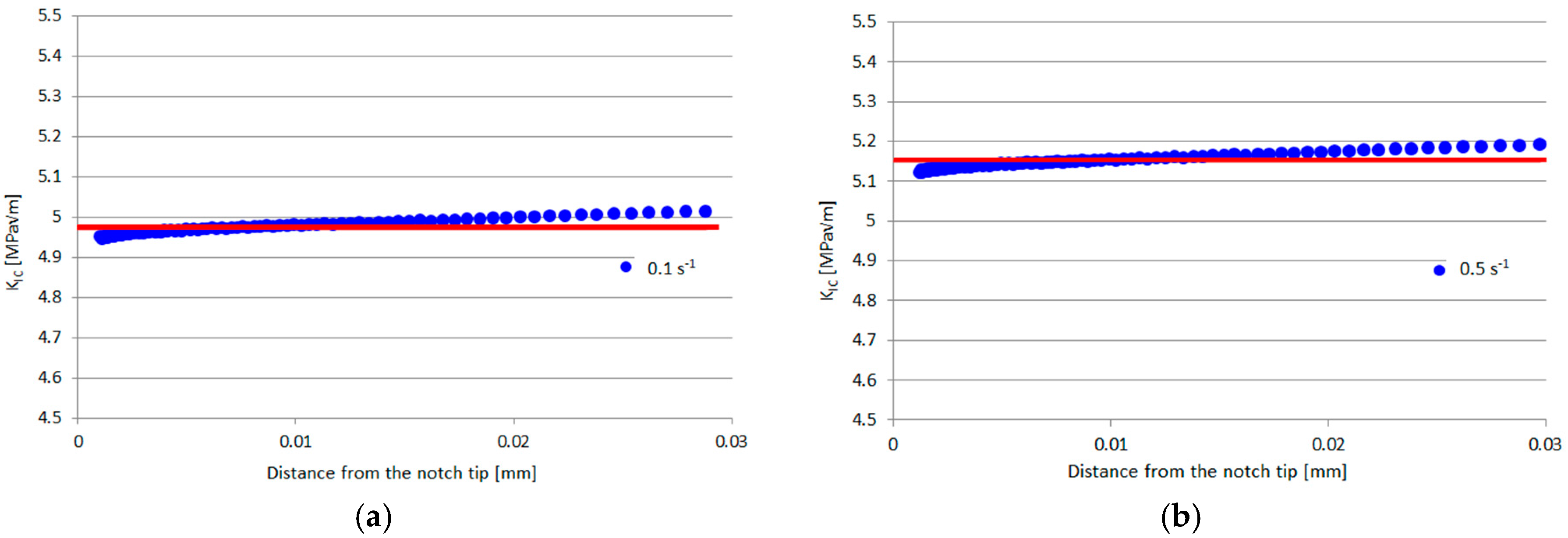
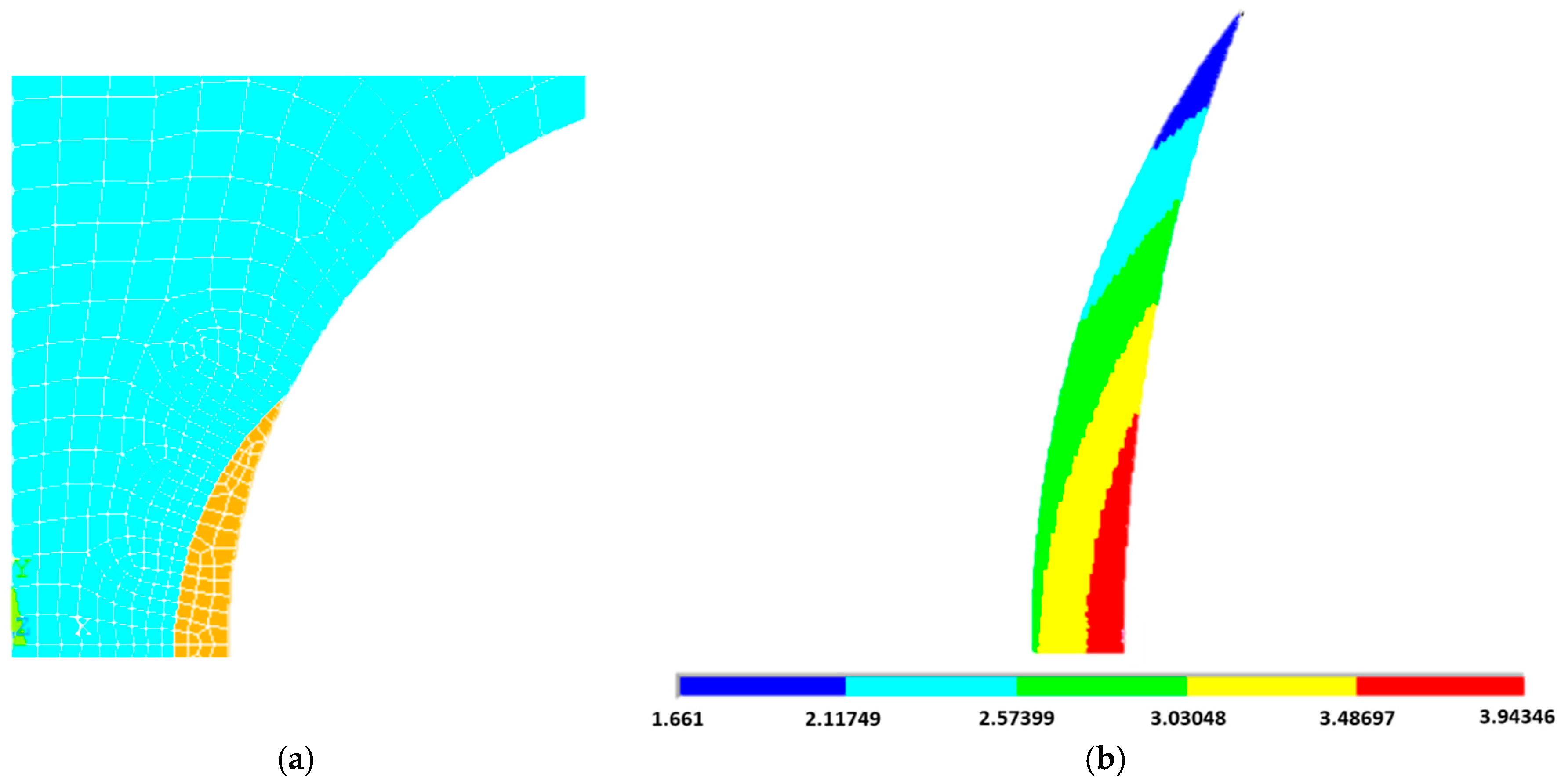
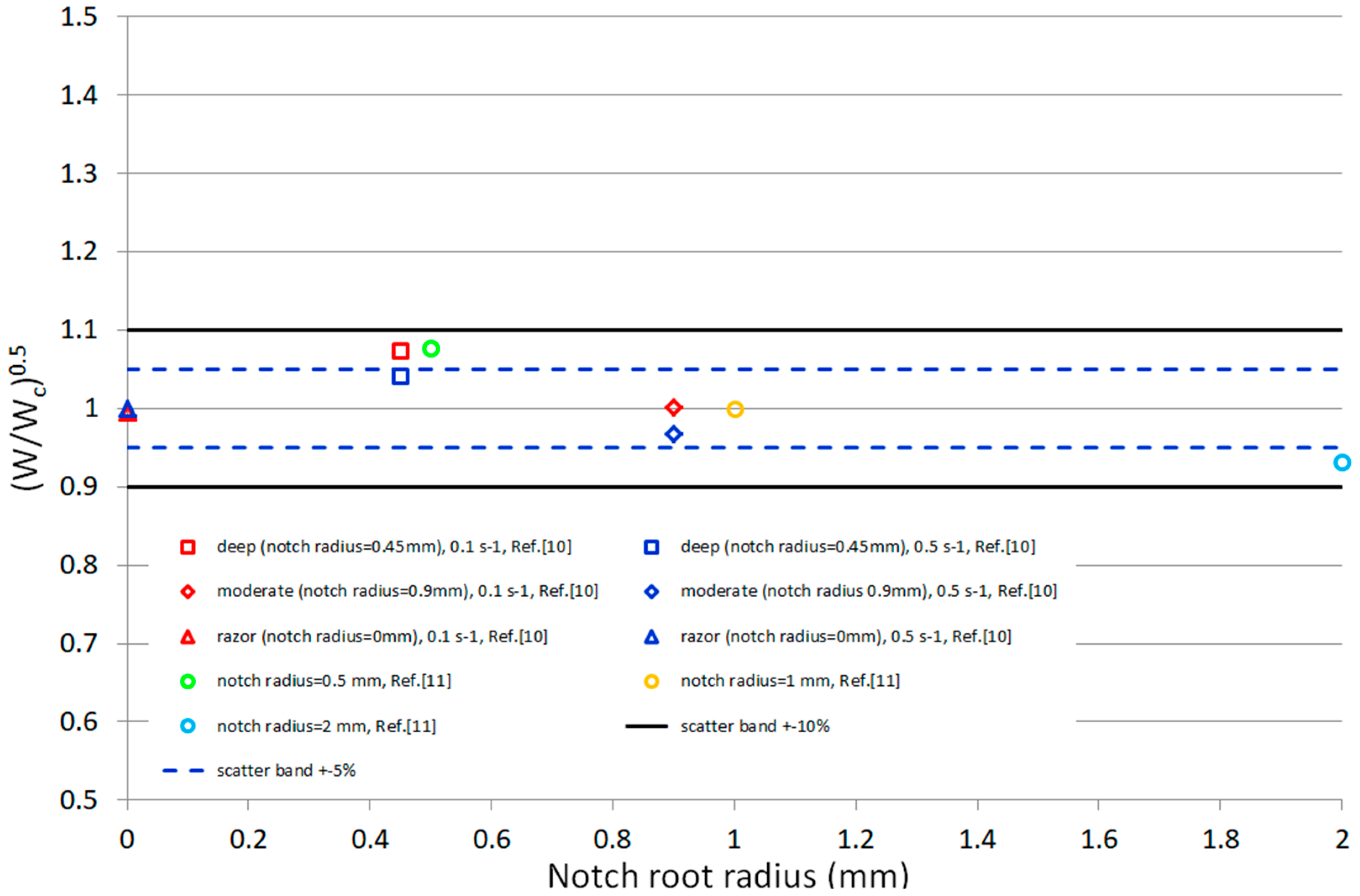
| Condition | Un-Notched | Moderate | Deep | Razor | ||||
|---|---|---|---|---|---|---|---|---|
| Strain rate (s−1) | 0.1 | 0.5 | 0.1 | 0.5 | 0.1 | 0.5 | 0.1 | 0.5 |
| Max axial true stress (MPa) | 211 ± 8.16 | 225 ± 5.35 | 132 ± 1.11 | 135 ± 0.42 | 127 ± 2.33 | 129 ± 1.36 | 119 ± 4.92 | 123 ± 4.33 |
| r(mm) | 4 | 2 | 1 | 0.5 |
| Maximum axial true stress (MPa) | 160 | 145 | 150 | 177 |
| Specimen Geometry | Strain Rate (s−1) | Experimental Data (MPa) | SED Prediction (Mpa) | Deviation |
|---|---|---|---|---|
| Deep | 0.1 | 127 | 118 | −6.8% |
| 0.5 | 129 | 124 | −4% | |
| Moderate | 0.1 | 132 | 132 | −0.1% |
| 0.5 | 135 | 139 | +3.3% | |
| Razor | 0.1 | 119 | 118 | −0.8% |
| 0.5 | 123 | 124 | +0.8% |
| Specimen Geometry | Experimental Data (MPa) | SED Prediction (MPa) | Deviation |
|---|---|---|---|
| r = 0.5 | 177 | 165 | −6.8% |
| r = 1 | 150 | 155 | +3.3% |
| r = 2 | 145 | 156 | +7.5% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peron, M.; Razavi, N.; Torgersen, J.; Berto, F. Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density. Materials 2017, 10, 1423. https://doi.org/10.3390/ma10121423
Peron M, Razavi N, Torgersen J, Berto F. Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density. Materials. 2017; 10(12):1423. https://doi.org/10.3390/ma10121423
Chicago/Turabian StylePeron, Mirco, Nima Razavi, Jan Torgersen, and Filippo Berto. 2017. "Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density" Materials 10, no. 12: 1423. https://doi.org/10.3390/ma10121423
APA StylePeron, M., Razavi, N., Torgersen, J., & Berto, F. (2017). Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density. Materials, 10(12), 1423. https://doi.org/10.3390/ma10121423








