Two B-C-O Compounds: Structural, Mechanical Anisotropy and Electronic Properties under Pressure
Abstract
1. Introduction
2. Theoretical Methods
3. Results and Discussion
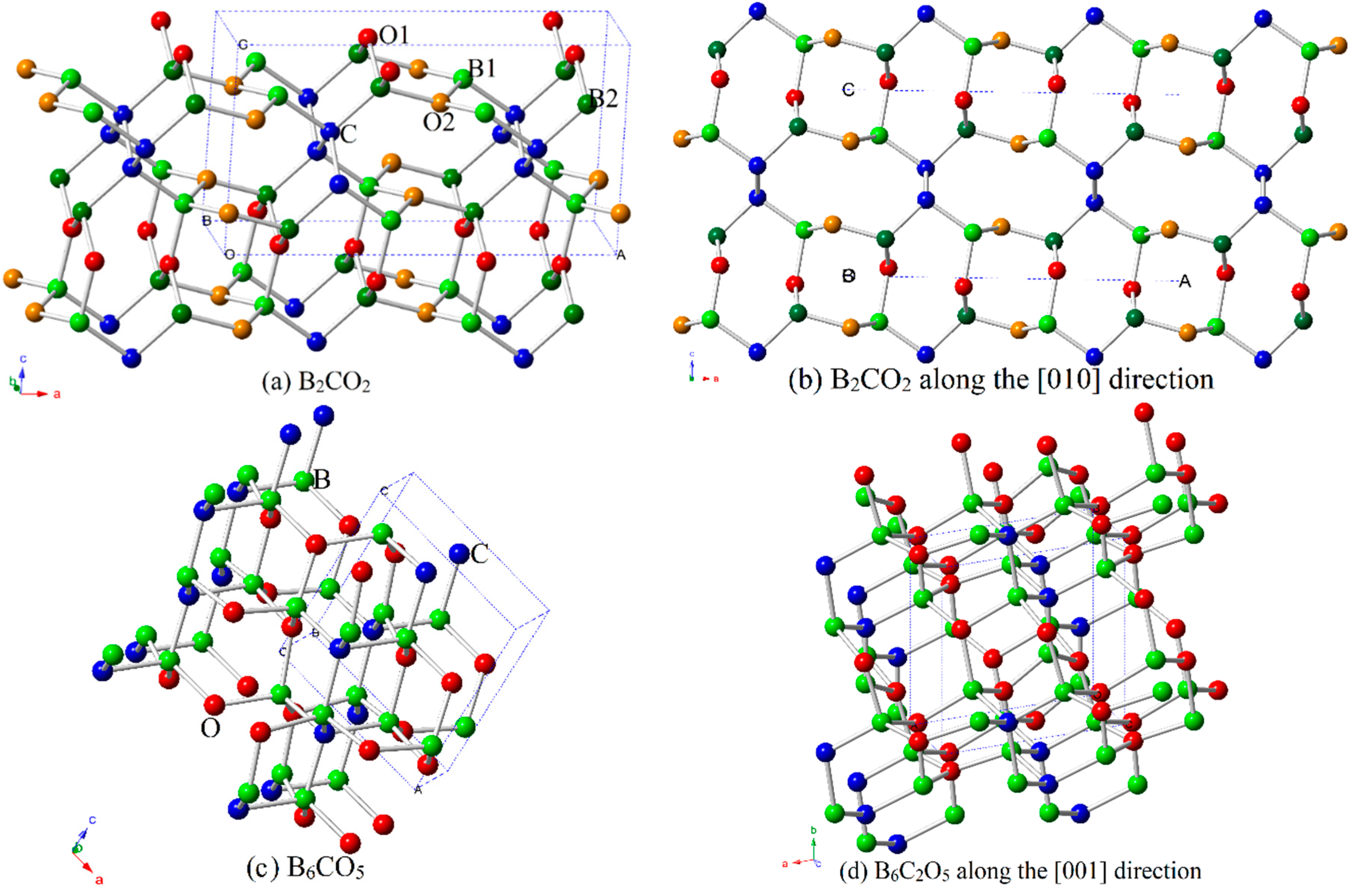
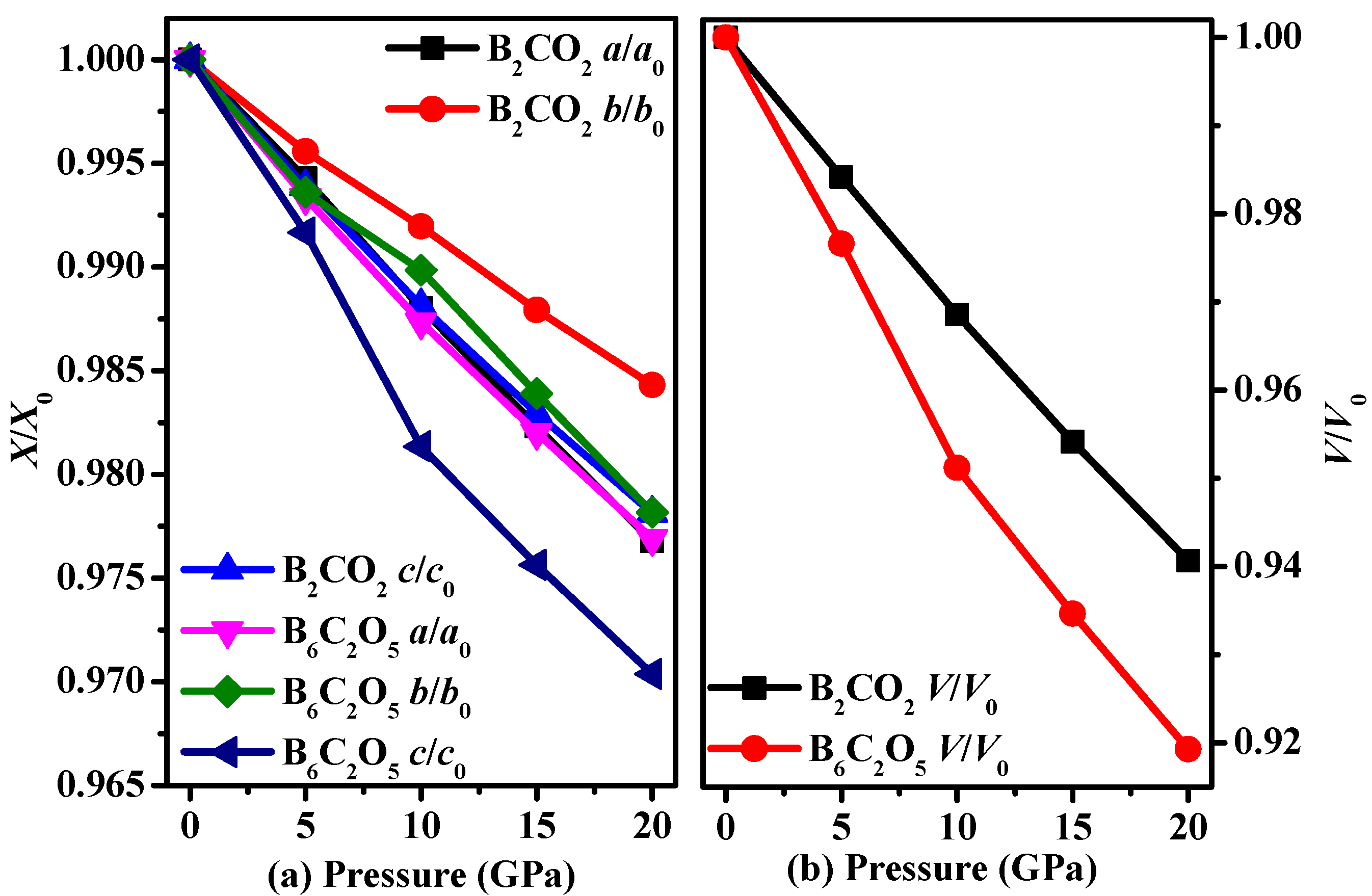
3.1. Structural Properties
3.2. Stability
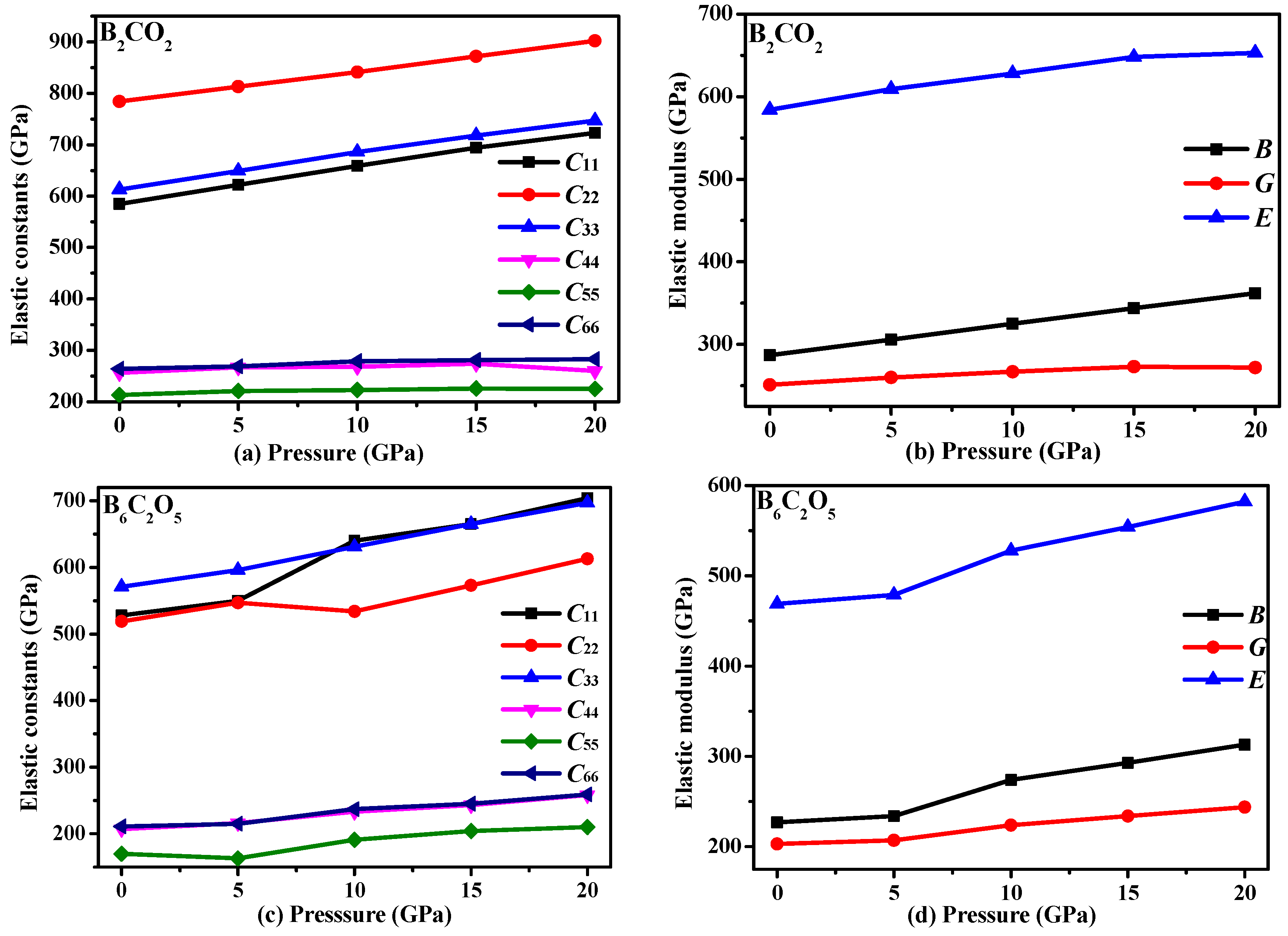
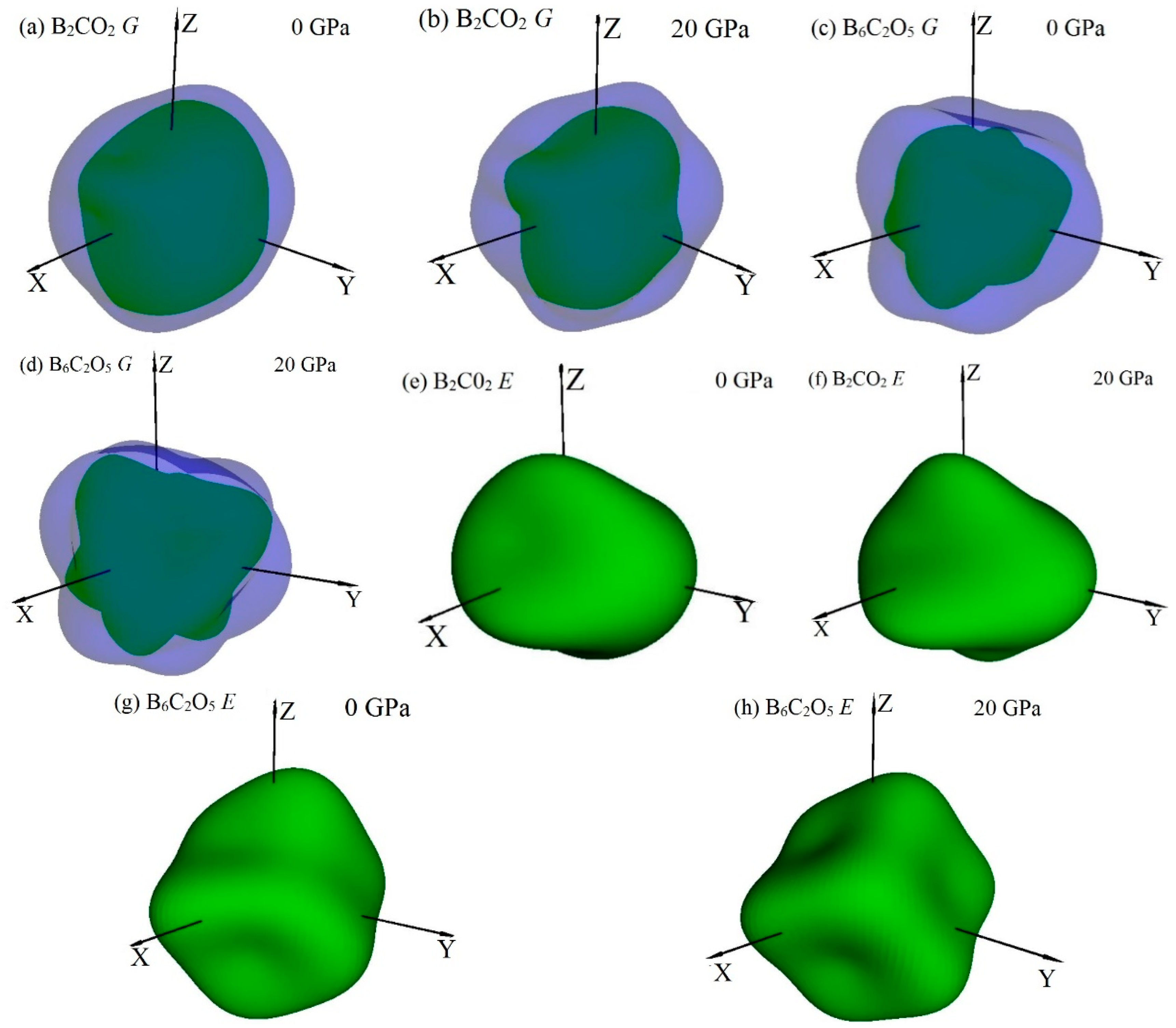
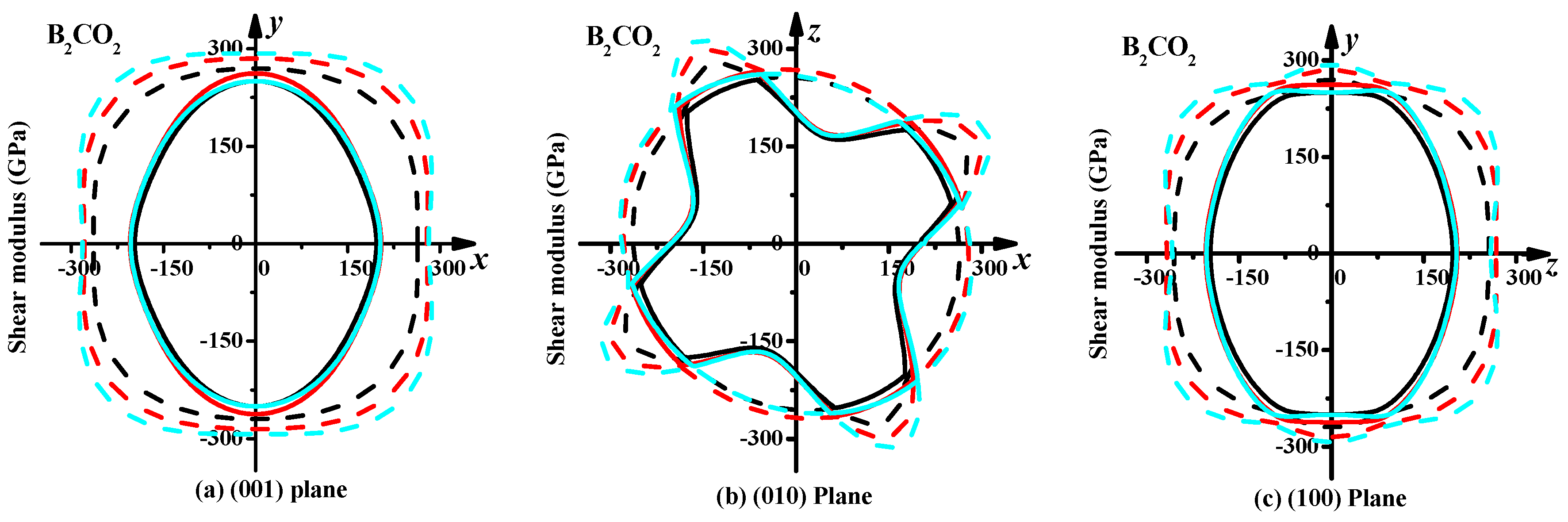
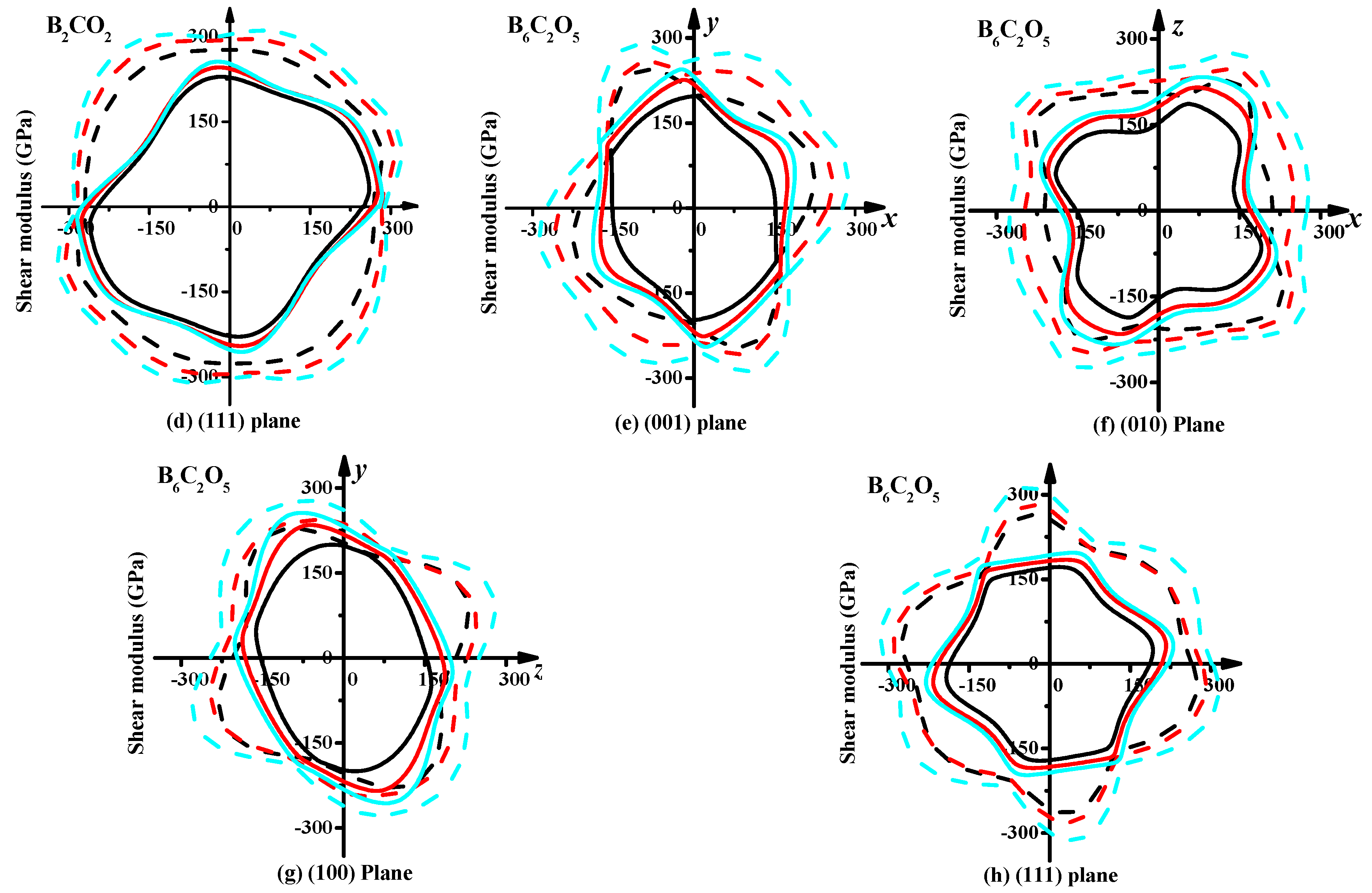
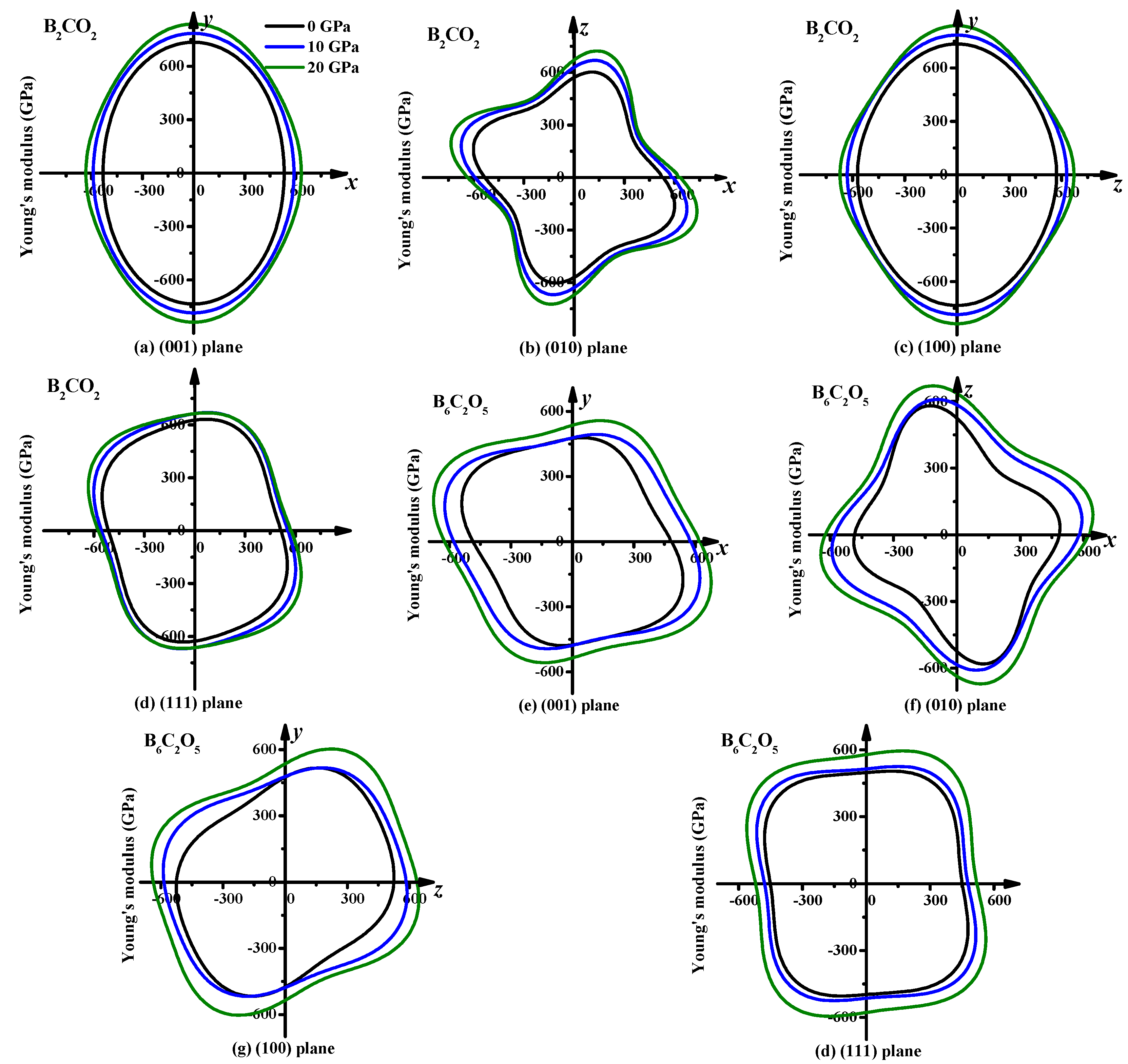
3.3. Mechanical Properties and Elastic Anisotropy
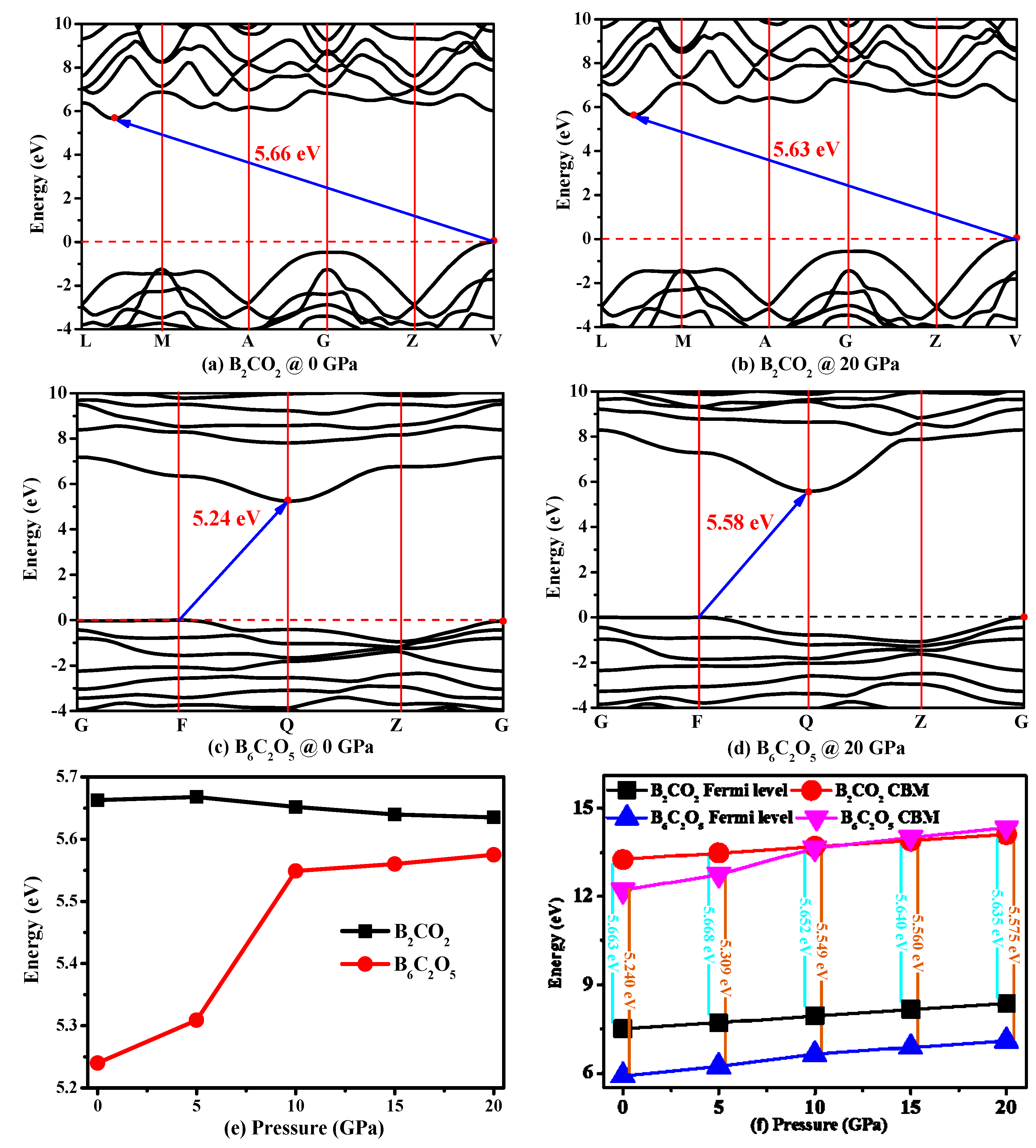
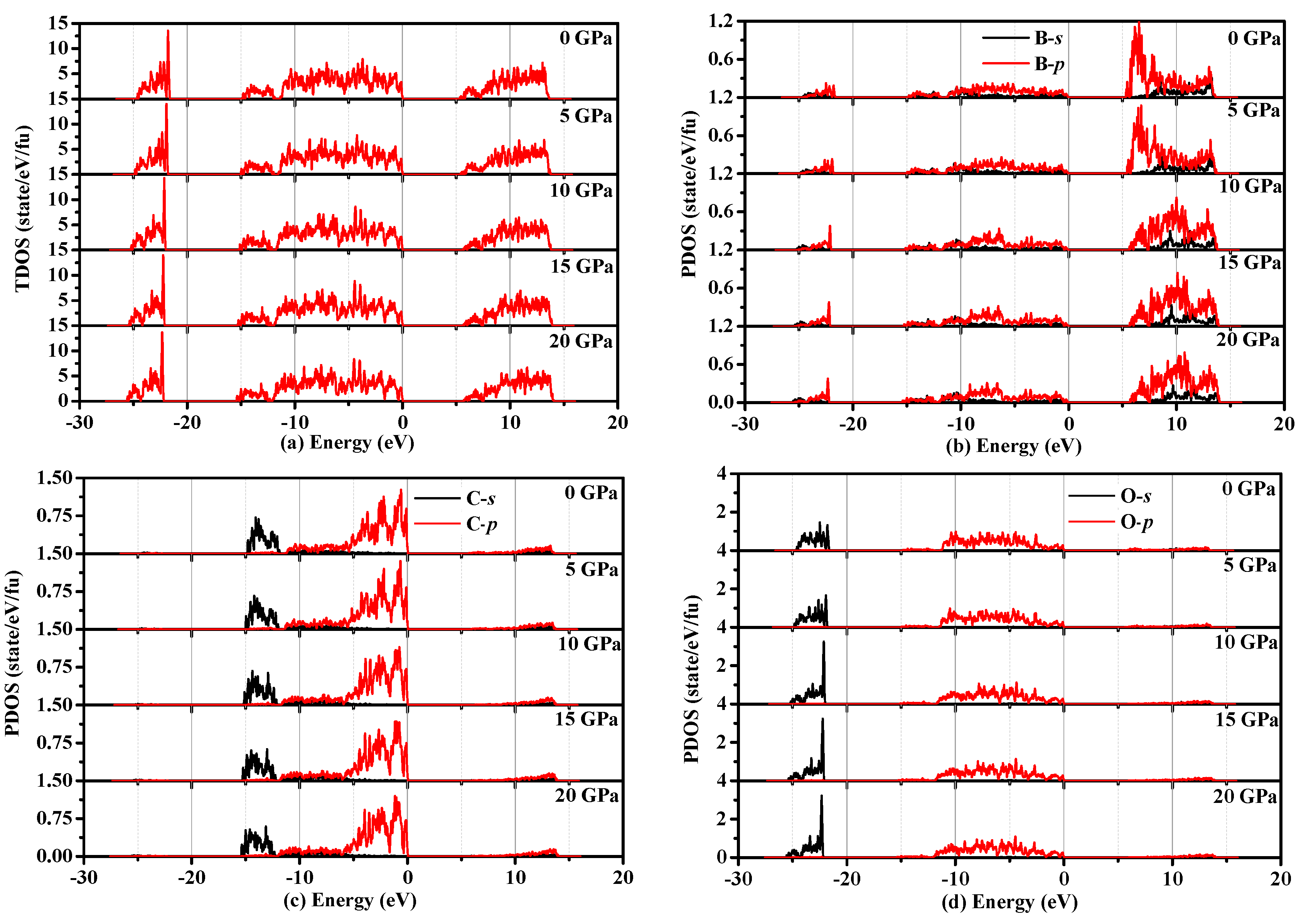
3.4. Electronic Properties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shirai, K.; Sakuma, K.; Uemura, N. Theoretical study of the structure of boron carbide B13C2. Phys. Rev. B 2014, 90, 064109. [Google Scholar] [CrossRef]
- Ektarawong, A.; Simak, S.I.; Hultman, L.; Birch, J.; Tasnádi, F.; Wang, F.; Alling, B. Effects of configurational disorder on the elastic properties of icosahedral boron-rich alloys based on B6O, B13C2, and B4C, and their mixing thermodynamics. J. Chem. Phys. 2016, 144, 134503. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; Wang, Z.Y.; Jing, Y.Y.; Wang, S.Y.; Chou, C.F.; Hu, H.; Chiou, S.H.; Tsoo, C.C.; Su, W.S. Electronic structure and optical properties of boron suboxide B6O system: First-principles investigations. Solid State Commun. 2016, 244, 12–16. [Google Scholar] [CrossRef]
- Wang, D.Y.; Yan, Q.; Wang, B.; Wang, X.Y.; Yang, J.M.; Yang, G. Predicted boron-carbide compounds: A first-principles study. J. Chem. Phys. 2014, 140, 224704. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Structural, anisotropic and thermodynamic properties of boron carbide: First principles calculations. Indian J. Pure Appl. Phys. 2016, 54, 227–235. [Google Scholar]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yu, X.Y.; Liu, Y.; Zhou, P.K.; Yan, H.T.; Zhang, D.Y. First-principles study of structural, elastic, anisotropic, and thermodynamic properties of R3-B2C. Chin. J. Phys. 2015, 53, 100601. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yang, Y.T.; Yu, X.H.; Liu, Y.; Zheng, J.P.; Zhou, P.K.; Zhang, D.Y. The elastic anisotropic and thermodynamic properties of I4mm-B3C. Acta Phys. Pol. A 2016, 129, 103–108. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, Z.S.; Luo, K.; Hu, M.; Ma, M.D.; He, J.L. Superhard orthorhombic phase of B2CO compound. Diam. Relat. Mater. 2017, 73, 7–92. [Google Scholar] [CrossRef]
- Li, Y.W.; Li, Q.; Ma, Y.M. B2CO: A potential superhard material in the B-C-O system. EPL 2011, 95, 66006. [Google Scholar] [CrossRef]
- Zhang, M.G.; Yan, H.Y.; Zheng, B.B.; Wei, Q. Influences of carbon concentration on crystal structures and idealstrengths of B2CxO compounds in the B-C-O system. Sci. Rep. 2015, 5, 15481. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.B.; Zhang, M.G.; Wang, C.J. Exploring the mechanical anisotropy and ideal strengths of tetragonal B4CO4. Materials 2017, 10, 128. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.N.; Oganov, A.R.; Qian, G.R.; Zhu, Q.; Dong, H.F.; Dong, X.; Esfahani, M.M.D. Novel superhard B-C-O phases predicted from first principles. Phys. Chem. Chem. Phys. 2016, 18, 1859–1863. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Zhao, J.J. Two-dimensional B-C-O alloys: A promising 2D material for electronic devices. Nanoscale 2016, 8, 8910–8918. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; He, D.W.; Daemen, L.L.; Shen, R.B.; Schwarz, R.B.; Zhu, Y.; Bish, D.L.; Hung, J.; Zhang, J.; Shen, G.; et al. Superhard B-C-N materials synthesized in nanostructured bulks. J. Mater. Res. 2002, 17, 3139–3145. [Google Scholar] [CrossRef]
- He, J.L.; Tian, Y.J.; Yu, D.L.; Wang, T.S.; Liu, S.M.; Guo, L.C.; Li, D.C.; Jia, X.P.; Chen, L.X.; Zou, G.T.; et al. Orthorhombic B2CN crystal synthesized by high pressure and temperature. Chem. Phys. Lett. 2001, 340, 431–436. [Google Scholar] [CrossRef]
- Nakano, S.; Akaishi, M.; Sasaki, T.; Yamaoka, S. Segregative crystallization of several diamond-like phases from the graphitic BC2N without an additive at 7.7 GPa. Chem. Mater. 1994, 6, 2246–2251. [Google Scholar] [CrossRef]
- Knittle, E.; Kaner, R.B.; Jeanloz, R.; Cohen, M.L. High-pressure synthesis, characterization, and equation of state of cubic C-BN solid solutions. Phys. Rev. B 1995, 51, 12149. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Andrault, D.; Fiquet, G.; Mezouar, M.; Rubie, D.C. Synthesis of superhard cubic BC2N. Appl. Phys. Lett. 2001, 78, 1385–1387. [Google Scholar] [CrossRef]
- Komatsu, T.; Nomura, M.; Kakudate, Y.; Fujiwara, S. Synthesis and characterization of a shock-synthesized cubic B-C-N solid solution of composition BC2.5N. J. Mater. Chem. 1996, 6, 1799–1803. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wang, Y.C.; Lv, J.; Zhu, C.Y.; Li, Q.; Zhang, M.; Li, Q.; Ma, Y.M. First-principles structural design of superhard materials. J. Chem. Phys. 2013, 138, 114101. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Zhang, M.G.; Yan, H.Y.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Imm2- and I-4m2-BCN. Comput. Mater. Sci. 2015, 97, 6–13. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yan, H.Y.; Zhang, M.G.; Lin, Z.Z.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Structural, mechanical, and electronic properties of P3m1-BCN. J. Phys. Chem. Solids 2015, 79, 89–96. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- He, D.W.; Zhao, Y.S.; Daemen, L.; Qian, J.; Shen, T.D. Boron suboxide: As hard as cubic boron nitride. Appl. Phys. Lett. 2002, 81, 643–645. [Google Scholar] [CrossRef]
- Endo, T.; Sato, T.; Shimada, M. High-pressure synthesis of B2O with diamond-like structure. J. Mater. Sci. Lett. 1987, 6, 683–685. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Turkevich, V.Z.; Turkevich, D.V. Phase diagram of the B-B2O3 system at 5 GPa: Experimental and theoretical studies. J. Phys. Chem. B 2008, 112, 6683–6687. [Google Scholar] [CrossRef] [PubMed]
- Gueorguiev, G.K.; Neidhardt, J.; Stafstrom, S.; Hultman, L. First-principles calculations on the role of CN precursors for the formation of fullerene-like carbon nitride. Chem. Phys. Lett. 2005, 401, 288–295. [Google Scholar] [CrossRef]
- Gueorguiev, G.K.; Neidhardt, J.; Stafstrom, S.; Hultman, L. First-principles calculations on the curvature evolution and cross-linkage in carbon nitride. Chem. Phys. Lett. 2005, 410, 228–234. [Google Scholar] [CrossRef]
- Liu, A.Y.; Cohen, M.L. Prediction of new low compressibility solids. Science 1989, 245, 841–842. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.Y.; Wentzcovitch, R.M. Stability of carbon nitride solids. Phys. Rev. B 1994, 50, 10362. [Google Scholar] [CrossRef]
- Teter, D.M.; Hemley, R.J. Low-compressibility carbon nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
- Manyali, G.S.; Warmbier, R.; Quandt, A.; Lowther, J.E. Ab initio study of elastic properties of super hard and graphitic structures of C3N4. Comput. Mater. Sci. 2013, 69, 299–303. [Google Scholar] [CrossRef]
- Molina, B.; Sansores, L.E. Eelectronic structure of six phases of C3N4: A theoretical approach. Mod. Phys. Lett. B 1999, 13, 193–201. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, C. First-principles study on hardness of five polymorphs of C3N4. Phys. B Condens. Matter 2008, 403, 1956–1959. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T. Two Novel C3N4 Phases: Structural, Mechanical and Electronic Properties. Materials 2016, 9, 427. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.M.; He, J.L.; Wu, E.; Liu, S.M.; Yu, D.L.; Li, D.C.; Zhang, S.Y.; Tian, Y.J. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.L.; Burke, K. Erratum: Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2009, 102, 039902. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.Y.; Han, Z.; Liu, X.H.; Yu, X.H.; Wang, D.T.; Tian, Y. Pnma-BN: Another boron nitride polymorph with interesting physical properties. Nanomaterials 2017, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Chen, X.Q.; Niu, H.Y.; Li, D.Z.; Li, Y.Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. Elam: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. First-principles study of structural and electronic properties of C14-type laves phase Al2Zr and Al2Hf. Comput. Mater. Sci. 2014, 83, 27–34. [Google Scholar] [CrossRef]

| Materials | Source | PBE | PBEsol | CA-PZ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | β (°) | a (Å) | b (Å) | c (Å) | β (°) | a (Å) | b (Å) | c (Å) | β (°) | ||
| B2CO2 | This work | 9.773 | 2.487 | 5.395 | 90.9 | 9.721 | 2.479 | 5.368 | 90.8 | 9.606 | 2.456 | 5.308 | 90.9 |
| ref. [12] | 9.776 | 2.489 | 5.395 | 90.8 | |||||||||
| B6C2O5 | This work | 4.503 | 4.536 | 4.557 | 98.1 | 4.479 | 4.526 | 4.508 | 99.3 | 4.278 | 4.474 | 4.457 | 99.3 |
| ref. [12] | 4.502 | 4.538 | 4.557 | 98.2 | |||||||||
| tP4-B2CO | This work | 2.656 | 2.656 | 3.678 | 90.0 | 2.648 | 2.648 | 3.656 | 90.0 | 2.618 | 2.618 | 3.619 | 90.0 |
| ref. [9] | 2.623 | 2.623 | 3.623 | 90.0 | |||||||||
| tI16-B2CO | This work | 3.722 | 3.722 | 7.493 | 90.0 | 3.702 | 3.702 | 7.515 | 90.0 | 3.664 | 3.664 | 7.376 | 90.0 |
| ref. [9] | 3.670 | 7.394 | 7.394 | 90.0 | |||||||||
| B2C2O | This work | 2.638 | 18.274 | 90.0 | 2.627 | 18.178 | 90.0 | 2.598 | 17.996 | 90.0 | |||
| ref. [10] | 2.647 | 18.272 | 90.0 | ||||||||||
| Materials | P | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | C15 | C25 | C35 | C46 | B | G | E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B2CO2 | 0 | 585 | 784 | 613 | 256 | 213 | 264 | 117 | 65 | 136 | −77 | 13 | 51 | −9 | 287 | 251 | 583 |
| 5 | 622 | 813 | 649 | 267 | 221 | 269 | 125 | 82 | 145 | −81 | 16 | 55 | −10 | 306 | 260 | 608 | |
| 10 | 658 | 841 | 686 | 268 | 223 | 279 | 132 | 96 | 157 | −85 | 15 | 57 | −10 | 325 | 267 | 629 | |
| 15 | 694 | 872 | 718 | 274 | 226 | 281 | 141 | 110 | 168 | −90 | 16 | 58 | −13 | 344 | 273 | 648 | |
| 20 | 723 | 902 | 747 | 260 | 225 | 283 | 150 | 126 | 180 | −95 | 13 | 64 | −18 | 362 | 272 | 653 | |
| B6C2O5 | 0 | 528 | 519 | 571 | 207 | 170 | 211 | 102 | 40 | 83 | 6 | −0.2 | −72 | −8 | 227 | 203 | 469 |
| 5 | 549 | 547 | 596 | 216 | 163 | 215 | 108 | 35 | 93 | −10 | −1 | −87 | −10 | 234 | 207 | 480 | |
| 10 | 640 | 534 | 631 | 233 | 191 | 237 | 131 | 81 | 122 | 26 | 6 | −44 | 5 | 274 | 224 | 528 | |
| 15 | 665 | 573 | 665 | 243 | 204 | 245 | 142 | 91 | 133 | 31 | 8 | −49 | 7 | 293 | 234 | 554 | |
| 20 | 704 | 613 | 697 | 258 | 210 | 259 | 155 | 104 | 142 | 35 | 11 | −53 | 9 | 312 | 244 | 581 | |
| tP4-B2CO | 0 1 | 736 | 591 | 240 | 254 | 53 | 157 | 311 | 254 | ||||||||
| tI16-B2CO | 0 1 | 600 | 646 | 304 | 283 | 182 | 144 | 310 | 265 | ||||||||
| B2C2O | 0 2 | 763 | 590 | 229 | 274 | 15 | 135 | 299 | 264 | 611 | |||||||
| c-BN | 0 3 | 779 | 446 | 165 | 370 | 384 | |||||||||||
| Pnma-BN | 0 4 | 392 | 770 | 675 | 299 | 272 | 187 | 99 | 256 | 116 | 298 | 227 | 543 | ||||
| Diamond | 0 3 | 1053 | 563 | 120 | 431 | 522 | 1116 |
| Materials | P | 0 GPa | 10 GPa | 20 GPa | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Ratio | Max | Min | Ratio | Max | Min | Ratio | ||
| B2CO2 | G | 309 | 170 | 1.82 | 333 | 177 | 1.88 | 353 | 175 | 2.02 |
| E | 734 | 414 | 1.77 | 785 | 446 | 1.76 | 837 | 460 | 1.82 | |
| B6C2O5 | G | 278 | 140 | 1.96 | 295 | 161 | 1.83 | 321 | 170 | 1.88 |
| E | 603 | 345 | 1.75 | 657 | 408 | 1.61 | 717 | 431 | 1.66 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Jin, Z. Two B-C-O Compounds: Structural, Mechanical Anisotropy and Electronic Properties under Pressure. Materials 2017, 10, 1413. https://doi.org/10.3390/ma10121413
Qiao L, Jin Z. Two B-C-O Compounds: Structural, Mechanical Anisotropy and Electronic Properties under Pressure. Materials. 2017; 10(12):1413. https://doi.org/10.3390/ma10121413
Chicago/Turabian StyleQiao, Liping, and Zhao Jin. 2017. "Two B-C-O Compounds: Structural, Mechanical Anisotropy and Electronic Properties under Pressure" Materials 10, no. 12: 1413. https://doi.org/10.3390/ma10121413
APA StyleQiao, L., & Jin, Z. (2017). Two B-C-O Compounds: Structural, Mechanical Anisotropy and Electronic Properties under Pressure. Materials, 10(12), 1413. https://doi.org/10.3390/ma10121413




