Grain Refinement Kinetics in a Low Alloyed Cu–Cr–Zr Alloy Subjected to Large Strain Deformation
Abstract
1. Introduction
2. Materials and Methods
3. Results
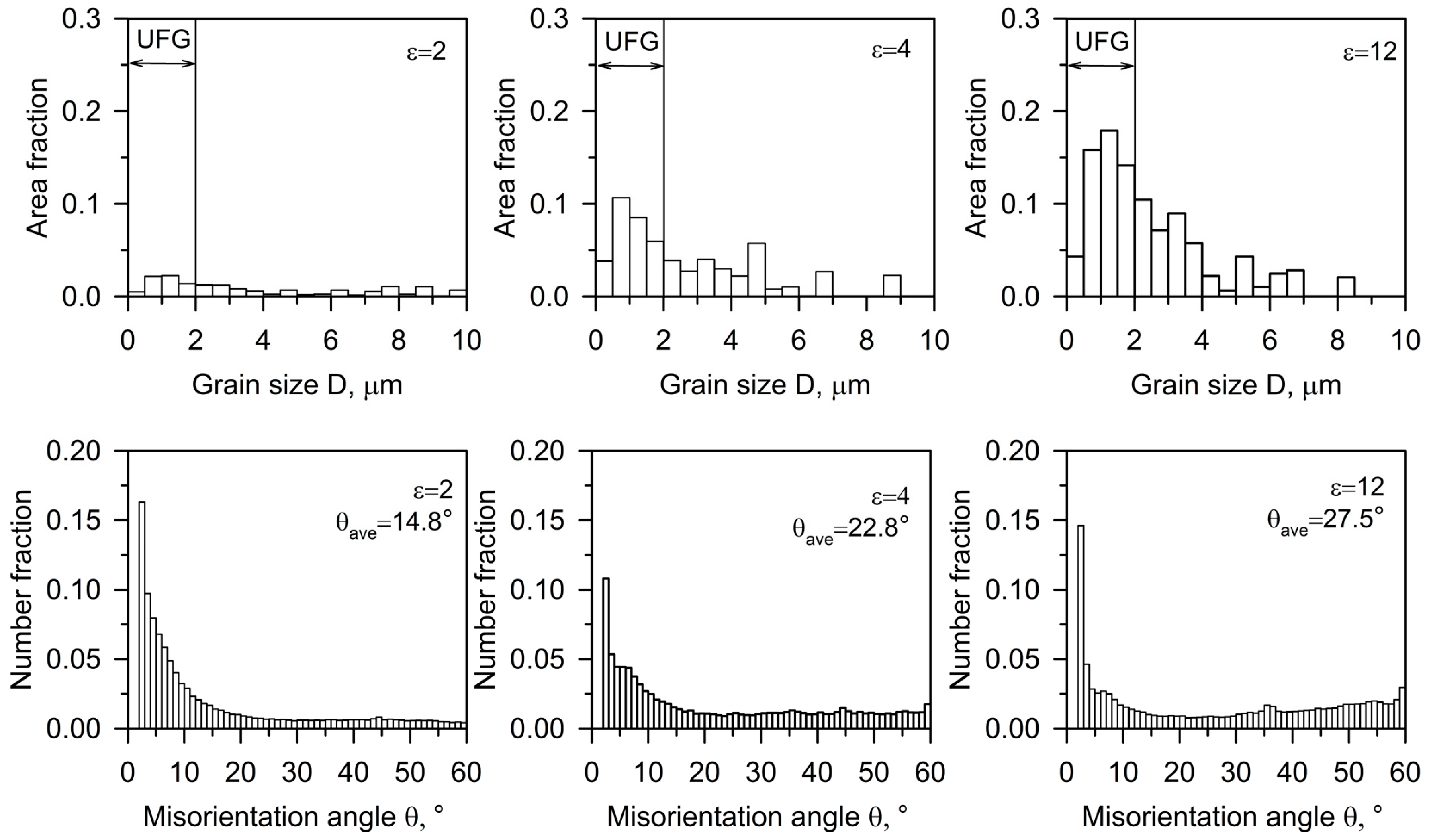
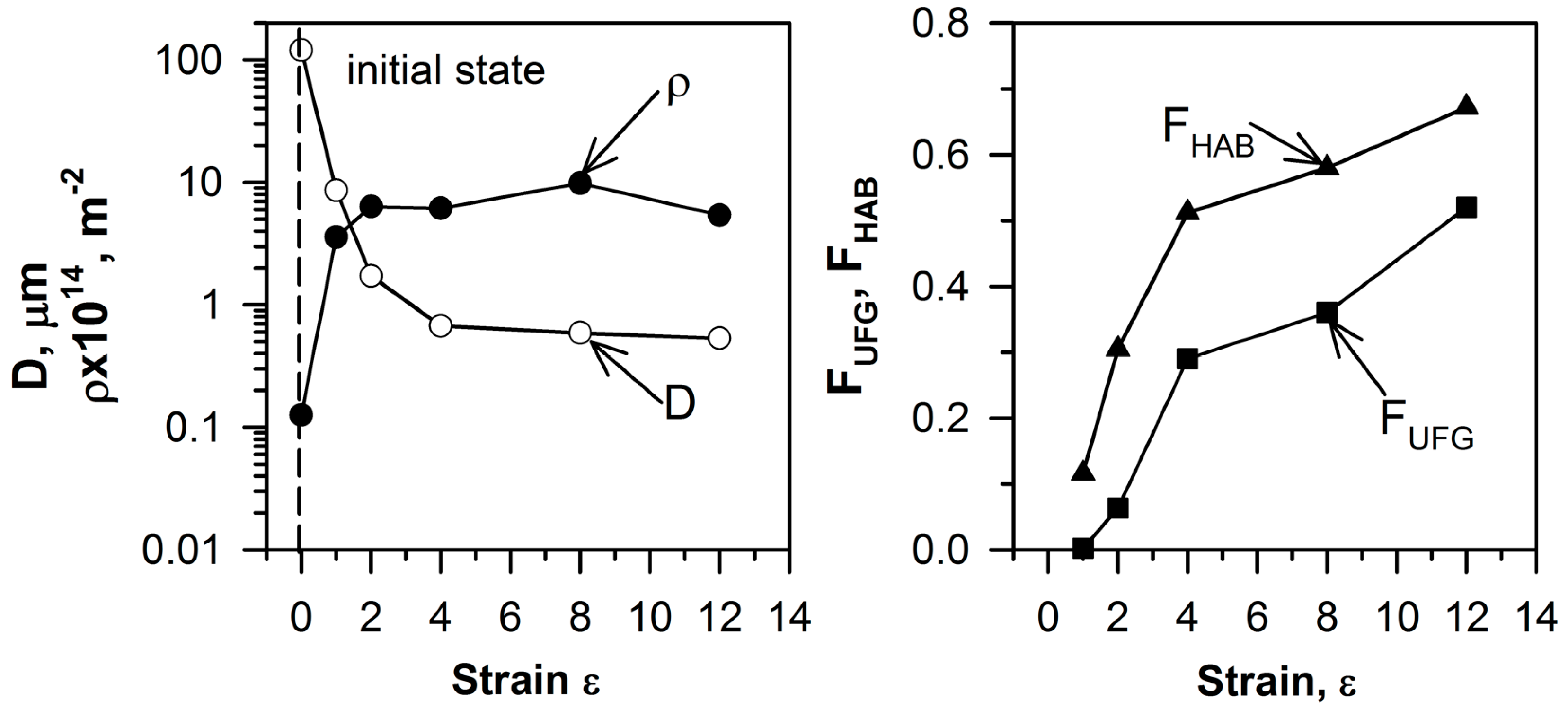
3.1. Microstructural Evolution
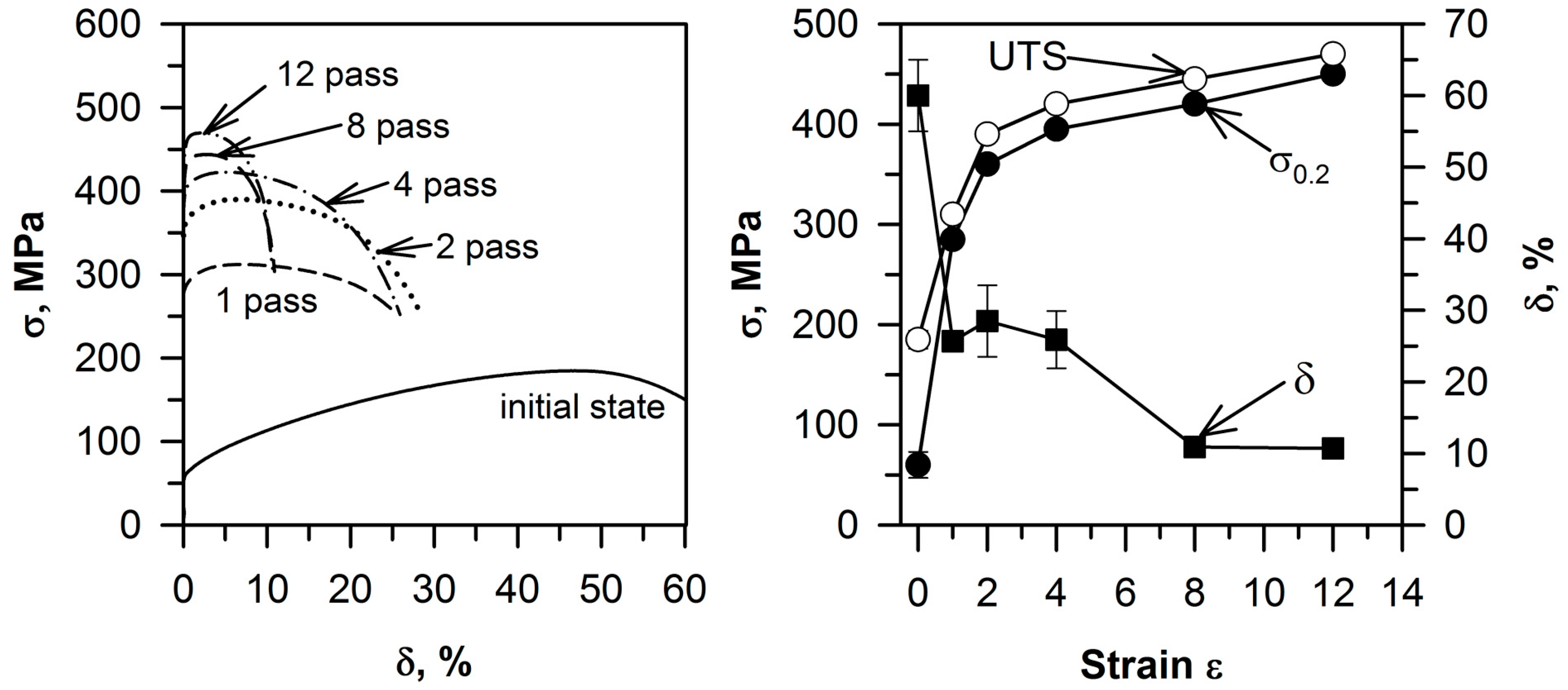
3.2. Tension Behavior
4. Discussion
5. Conclusions
- The ECAP processing was accompanied by a significant decrease in the grain size, from 120 μm in the initial condition to 0.5 μm after a total strain of 12. The grain size rapidly decreased during the first four ECAP passes, and then remained almost unchanged during further ECAP.
- The formation of the ultrafine-grained structure resulted from the deformation of band evolution and an increase in the misorienations of strain-induced subboundaries during ECAP processing. An increase in total strain led to an increase in both the high-angle boundary fraction and the ultrafine-grain fraction. The grain refinement can be discussed in the terms of continuous dynamic recrystallization.
- The ECAP deformation was accompanied by gradual strengthening. The yield strength increased from 60 MPa in the initial state to 445 MPa after 12 ECAP passes. Correspondingly, total elongation decreased from 60% to 9%.
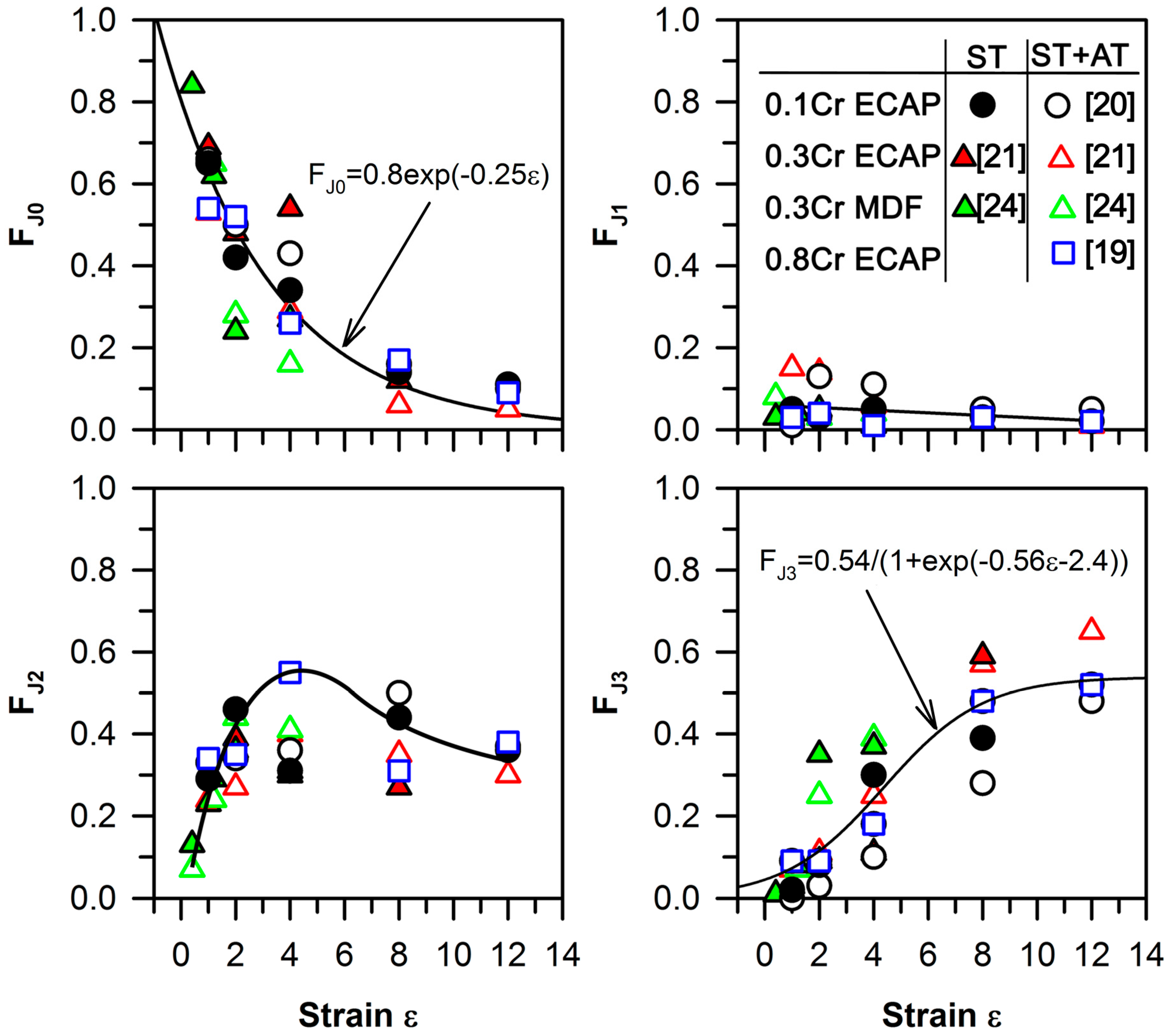
- The fraction of boundary triple junctions consisting of only low-angle boundaries gradually decreased through an exponential law function of total strain during severe plastic deformation. The fraction of boundary triple junctions, with one high-angle boundary and two low-angle boundaries was about 0.1–0.15, and did not change remarkably with straining. The fraction of boundary triple junctions with two high-angle boundaries and one low-angle boundary increased to a peak after four to six strain levels, followed by a small decrease at large strain levels. The fraction of boundary triple junctions that consisted of only high-angle boundaries increased by a sigmoid law function with deformation.
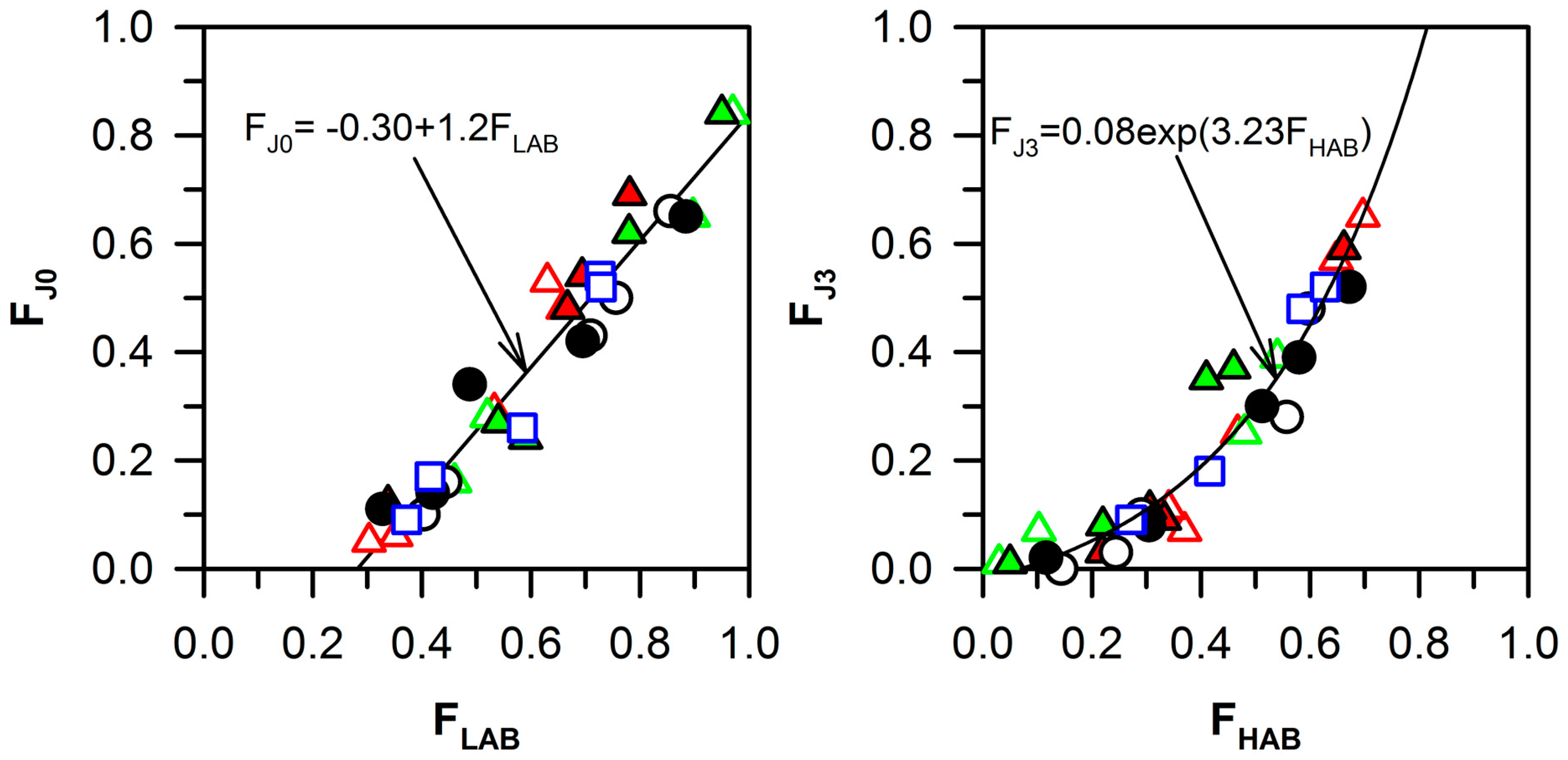
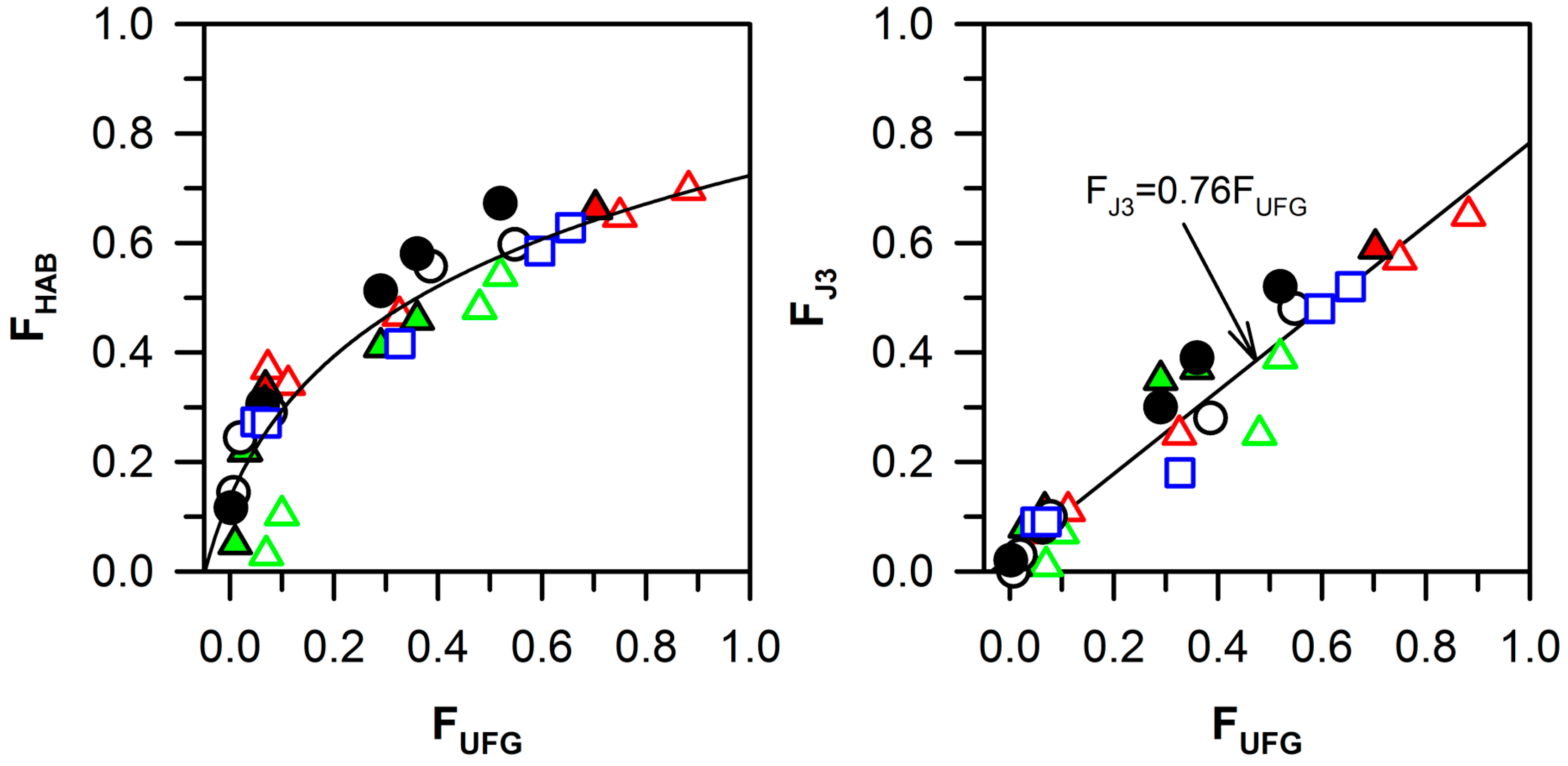
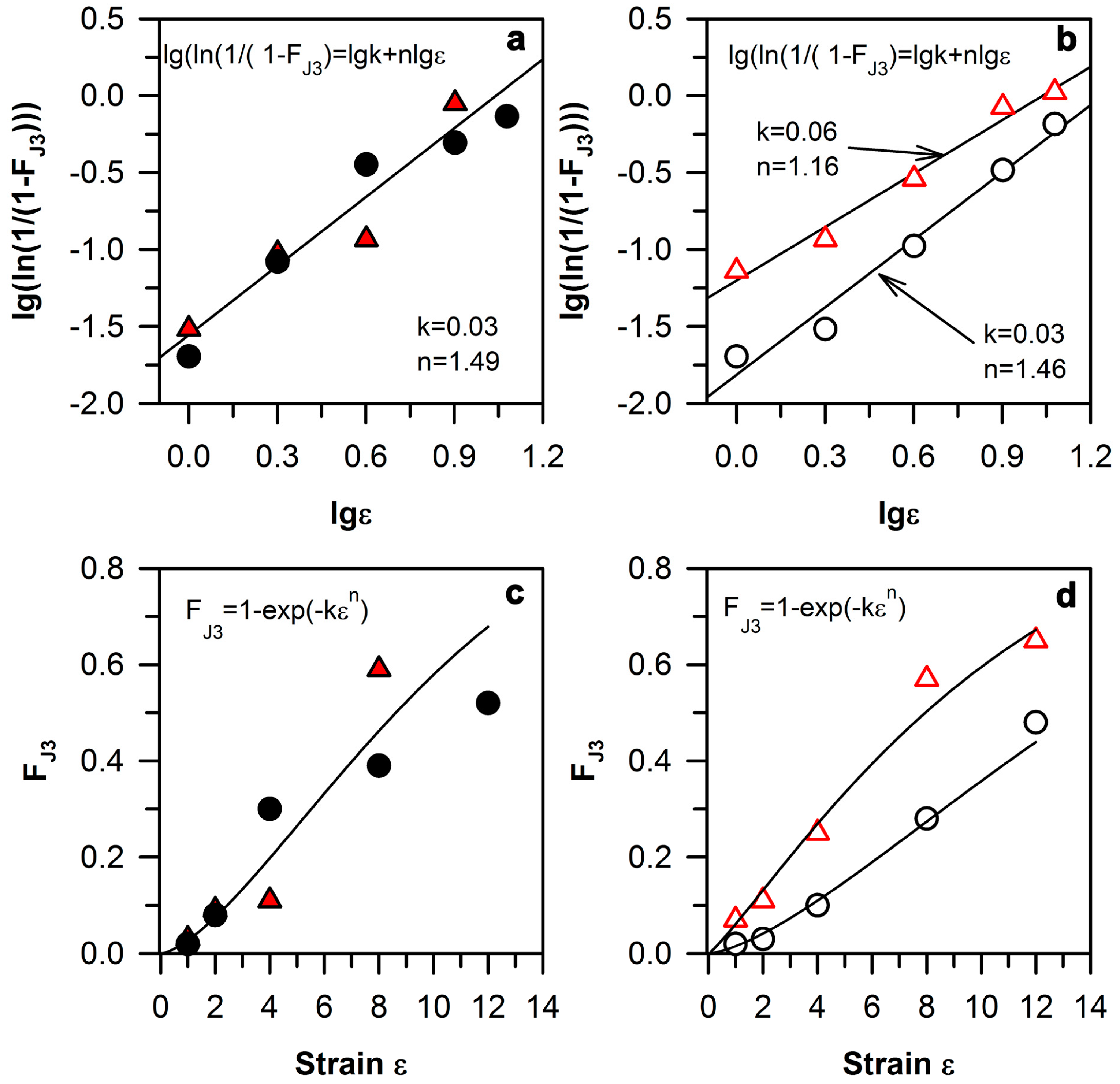
- The fractions of the low-angle boundary triple junctions and the high-angle boundary triple junctions can be related to the low-angle boundary fraction and the ultrafine-grain fraction, respectively, through linear functions. The strain dependence of the high-angle boundary triple junctions can be expressed by a modified Johnson–Mehl–Avrami–Kolmogorov equation, FJ3 = 1 − exp(−k εn), with a strain exponent of n = 1.49 and k = 0.03.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, N.Y.; Taplin, D.M.R.; Dunlop, G.L. Precipitation and aging in high-conductivity Cu–Cr alloys with additions of zirconium and magnesium. Mater. Sci. Technol. 1985, 1, 270–275. [Google Scholar] [CrossRef]
- Correia, J.B.; Davies, H.A.; Sellars, C.M. Strengthening in rapidly solidified age hardened Cu–Cr and Cu–Cr–Zr alloys. Acta Mater. 1997, 45, 177–190. [Google Scholar] [CrossRef]
- Fujii, T.; Nakazawa, H.; Kato, M.; Dahmen, U. Crystallography and morphology of nanosized Cr particles in a Cu–0.2% Cr alloy. Acta Mater. 2000, 48, 1033–1045. [Google Scholar] [CrossRef]
- Batra, I.S.; Dey, G.K.; Kulkarni, U.D.; Banerjee, S. Microstructure and properties of a Cu–Cr–Zr alloy. J. Nucl. Mater. 2001, 299, 91–100. [Google Scholar] [CrossRef]
- Chibihi, A.; Sauvage, X.; Blavette, D. Atomic scale investigation of Cr precipitation in copper. Acta Mater. 2012, 60, 4575–4585. [Google Scholar] [CrossRef]
- Shangina, D.V.; Bochvar, N.R.; Morozova, A.I.; Belyakov, A.N.; Kaibyshev, R.O.; Dobatkin, S.V. Effect of chromium and zirconium content on structure, strength and electrical conductivity of Cu–Cr–Zr alloys after high pressure torsion. Mater. Lett. 2017, 199, 46–49. [Google Scholar] [CrossRef]
- Shangina, D.; Maksimenkova, Y.; Bochvar, N.; Serebryany, V.; Raab, G.; Vinogradov, A.; Skrotzki, W.; Dobatkin, S. Influence of alloying with hafnium on the microstructure, texture, and properties of Cu–Cr alloy after equal channel angular pressing. J. Mater. Sci. 2016, 51, 5493–5501. [Google Scholar] [CrossRef]
- Murashkin, M.Y.; Sabirov, I.; Sauvage, X.; Valiev, R.Z. Nanostructured Al and Cu alloys with superior strength and electrical conductivity. J. Mater. Sci. 2016, 51, 33–49. [Google Scholar] [CrossRef]
- Zhou, H.T.; Zhong, J.W.; Zhou, X.; Zhao, Z.K.; Li, Q.B. Microstructure and properties of Cu–1.0 Cr–0.2 Zr–0.03 Fe alloy. Mater. Sci. Eng. A 2008, 498, 225–230. [Google Scholar] [CrossRef]
- Lu, L.; Shen, Y.; Chen, X.; Qian, L.; Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 2004, 304, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Xie, H.; Huang, G.; Xu, G.; Yin, X.; Feng, X.; Yang, Z. The phase transformation and strengthening of a Cu–0.71 wt% Cr alloy. J. Alloys Compd. 2017, 708, 1096–1102. [Google Scholar] [CrossRef]
- Topuz, A.I. Enabling microstructural changes of FCC/BCC alloys in 2D dislocation dynamics. Mater. Sci. Eng. A 2015, 627, 381–390. [Google Scholar] [CrossRef]
- Ghosh, G.; Miyake, J.; Fine, M.E. The systems-based design of high-strength, high-conductivity alloys. JOM 1997, 49, 56–60. [Google Scholar] [CrossRef]
- Li, J. Petch relation and grain boundary sources. Trans. Metall. Soc. AIME 1963, 277, 239–247. [Google Scholar]
- Kato, M. Hall-Petch Relationship and Dislocation Model for Deformation of Ultrafine-Grained and Nanocrystalline Metals. Mater. Trans. 2014, 55, 19–24. [Google Scholar] [CrossRef]
- Hansen, N. Boundary strengthening in undeformed and deformed polycrystals. Mater. Sci. Eng. A 2005, 409, 39–45. [Google Scholar] [CrossRef]
- Borodin, E.N.; Mayer, A.E. Influence of structure of grain boundaries and size distribution of grains on the yield strength at quasistatic and dynamical loading. Mater. Res. Express 2017, 4, 085040. [Google Scholar] [CrossRef]
- Valdés León, K.; Munoz-Morris, M.A.; Morris, D.G. Optimisation of strength and ductility of Cu–Cr–Zr by combining severe plastic deformation and precipitation. Mater. Sci. Eng. A 2012, 536, 181–189. [Google Scholar] [CrossRef]
- Mishnev, R.; Shakhova, I.; Belyakov, A.; Kaibyshev, R. Deformation microstructures, strengthening mechanisms, and electrical conductivity in a Cu–Cr–Zr alloy. Mater. Sci. Eng. A 2015, 629, 29–40. [Google Scholar] [CrossRef]
- Morozova, A.; Kaibyshev, R. Grain refinement and strengthening of a Cu–0.1 Cr–0.06 Zr alloy subjected to equal channel angular pressing. Philos. Mag. 2017, 97, 2053–2076. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Shakhova, I.; Morozova, A.; Belyakov, A.; Kaibyshev, R. Grain refinement kinetics and strengthening mechanisms in Cu–0.3 Cr–0.5 Zr alloy subjected to intense plastic deformation. Mater. Sci. Eng. A 2016, 654, 131–142. [Google Scholar] [CrossRef]
- Estrin, Y.; Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 2013, 61, 782–817. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Shakhova, I.; Yanushkevich, Z.; Fedorova, I.; Belyakov, A.; Kaibyshev, R. Grain refinement in a Cu–Cr–Zr alloy during multidirectional forging. Mater. Sci. Eng. A 2014, 606, 380–389. [Google Scholar] [CrossRef]
- Tikhonova, M.; Dolzhenko, P.; Kaibyshev, R.; Belyakov, A. Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel. Metals 2016, 6, 268. [Google Scholar] [CrossRef]
- Takata, N.; Lee, S.H.; Tsuji, N. Ultrafine grained copper alloy sheets having both high strength and high electric conductivity. Mater. Lett. 2009, 63, 1757–1760. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Segal, V.M.; Reznikov, V.I.; Drobyshevskiy, A.E.; Kopylov, V.I. 1. Under an ideal condition without the frictional effect. Russ. Metall. (Metally) 1981, 1, 99–105. [Google Scholar]
- Zhemchuzhnikova, D.; Lebyodkin, M.; Lebedkina, T.; Mogucheva, A.; Yuzbekova, D.; Kaibyshev, R. Peculiar Spatiotemporal Behavior of Unstable Plastic Flow in an AlMgMnScZr Alloy with Coarse and Ultrafine Grains. Metals 2017, 7, 325. [Google Scholar] [CrossRef]
- Abib, K.; Azzeddine, H.; Tirsatine, K.; Baudin, T.; Helbert, A.L.; Brisset, F.; Bradai, D. Thermal stability of Cu–Cr–Zr alloy processed by equal-channel angular pressing. Mater. Charact. 2016, 118, 527–534. [Google Scholar] [CrossRef]
- Dalla Torre, F.H.; Pereloma, E.V.; Davies, C.H.J. Strain hardening behaviour and deformation kinetics of Cu deformed by equal channel angular extrusion from 1 to 16 passes. Acta Mater. 2006, 54, 1135–1146. [Google Scholar] [CrossRef]
- Edalati, K.; Imamura, K.; Kiss, T.; Horita, Z. Equal-channel angular pressing and high-pressure torsion of pure copper: Evolution of electrical conductivity and hardness with strain. Mater. Trans. 2012, 53, 123–127. [Google Scholar] [CrossRef]
- Raab, G.J.; Valiev, R.Z.; Lowe, T.C.; Zhu, Y.T. Continuous processing of ultrafine grained Al by ECAP-Conform. Mater. Sci. Eng. A 2004, 382, 30–34. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Z.; Xiao, Z.; Zhao, Z. Investigations on Voids Formation in Cu–Mg Alloy during Continuous Extrusion. JOM 2017, 69, 1696–1700. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Z.; Xiao, Z.; Zhao, Z.; Yang, Z. Microstructure evolution and properties of Cu–Cr alloy during continuous extrusion process. J. Alloys Compd. 2017, 703, 454–460. [Google Scholar] [CrossRef]
- Zhu, C.; Ma, A.; Jiang, J.; Li, X.; Song, D.; Yang, D.; Chen, J. Effect of ECAP combined cold working on mechanical properties and electrical conductivity of Conform-produced Cu–Mg alloys. J. Alloys Compd. 2014, 582, 135–140. [Google Scholar] [CrossRef]
- Rollett, A.; Humphreys, F.J.; Rohrer, G.S.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Sleeman, D., Ed.; Elsevier: Kidlington, UK, 2012; p. 574. ISBN 0-08-044164-5. [Google Scholar]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Prangnell, P.B.; Bowen, J.R.; Gholinia, A.; Harris, C. Developing stable fine-grain microstructures by large strain deformation. Philos. Trans. R. Soc. Lond. A 1999, 357, 1663–1681. [Google Scholar] [CrossRef]
- Gourdet, S.; Montheillet, F. A model of continuous dynamic recrystallization. Acta Mater. 2003, 51, 2685–2699. [Google Scholar] [CrossRef]
- Bratov, V.; Borodin, E.N. Comparison of dislocation density based approaches for prediction of defect structure evolution in aluminium and copper processed by ECAP. Mater. Sci. Eng. A 2015, 631, 10–17. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y. Nanocrystalline gradient engineering: Grain evolution and grain boundary networks. Comput. Mater. Sci. 2018, 141, 282–292. [Google Scholar] [CrossRef]
- Roberts, W. Strength of Metals and Alloys (ICSMA-7); McQueen, H.J., Bailon, J.-P., Dickson, J.I., Eds.; Pergamon Press: Oxford, UK, 1986. [Google Scholar]
- Derby, B. The dependence of grain size on stress during dynamic recrystallisation. Acta Metall. 1991, 39, 955–962. [Google Scholar] [CrossRef]
- Belyakov, A.; Zherebtsov, S.; Salishchev, G. Three-stage relationship between flow stress and dynamic grain size in titanium in a wide temperature interval. Mater. Sci. Eng. A 2015, 628, 104–109. [Google Scholar] [CrossRef]
- Belyakov, A.; Zherebtsov, S.; Tikhonova, M.; Salishchev, G. Kinetics of grain refinement in metallic materials during large strain deformation. Mater. Phys. Mech. 2015, 24, 224–231. [Google Scholar]
- Shakhova, I.; Belyakov, A.; Kaibyshev, R. Kinetics of Submicrocrystalline Structure Formation in a Cu–Cr–Zr Alloy during Large Plastic Deformation. In Materials Science Forum; Trans Tech Publications: Zürich, Switzerland, 2017; Volume 879, pp. 1749–1754. [Google Scholar] [CrossRef]
- Jazaeri, H.; Humphreys, F.J. The Recrystallization of a highly deformed Al–Fe–Mn alloy. In Proceedings of the 1st International Conference on Recrystallization and Grain Growth, Aachen, Germany, 27–31 August 2001. [Google Scholar]
- Gazizov, M.; Malopheyev, S.; Kaibyshev, R. The effect of second-phase particles on grain refinement during equal-channel angular pressing in an Al–Cu–Mg–Ag alloy. J. Mater. Sci. 2015, 50, 990–1005. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozova, A.; Borodin, E.; Bratov, V.; Zherebtsov, S.; Belyakov, A.; Kaibyshev, R. Grain Refinement Kinetics in a Low Alloyed Cu–Cr–Zr Alloy Subjected to Large Strain Deformation. Materials 2017, 10, 1394. https://doi.org/10.3390/ma10121394
Morozova A, Borodin E, Bratov V, Zherebtsov S, Belyakov A, Kaibyshev R. Grain Refinement Kinetics in a Low Alloyed Cu–Cr–Zr Alloy Subjected to Large Strain Deformation. Materials. 2017; 10(12):1394. https://doi.org/10.3390/ma10121394
Chicago/Turabian StyleMorozova, Anna, Elijah Borodin, Vladimir Bratov, Sergey Zherebtsov, Andrey Belyakov, and Rustam Kaibyshev. 2017. "Grain Refinement Kinetics in a Low Alloyed Cu–Cr–Zr Alloy Subjected to Large Strain Deformation" Materials 10, no. 12: 1394. https://doi.org/10.3390/ma10121394
APA StyleMorozova, A., Borodin, E., Bratov, V., Zherebtsov, S., Belyakov, A., & Kaibyshev, R. (2017). Grain Refinement Kinetics in a Low Alloyed Cu–Cr–Zr Alloy Subjected to Large Strain Deformation. Materials, 10(12), 1394. https://doi.org/10.3390/ma10121394







