Pore Size Distribution in Granular Material Microstructure
Abstract
:1. Introduction
2. Synthetic Specimen Generation
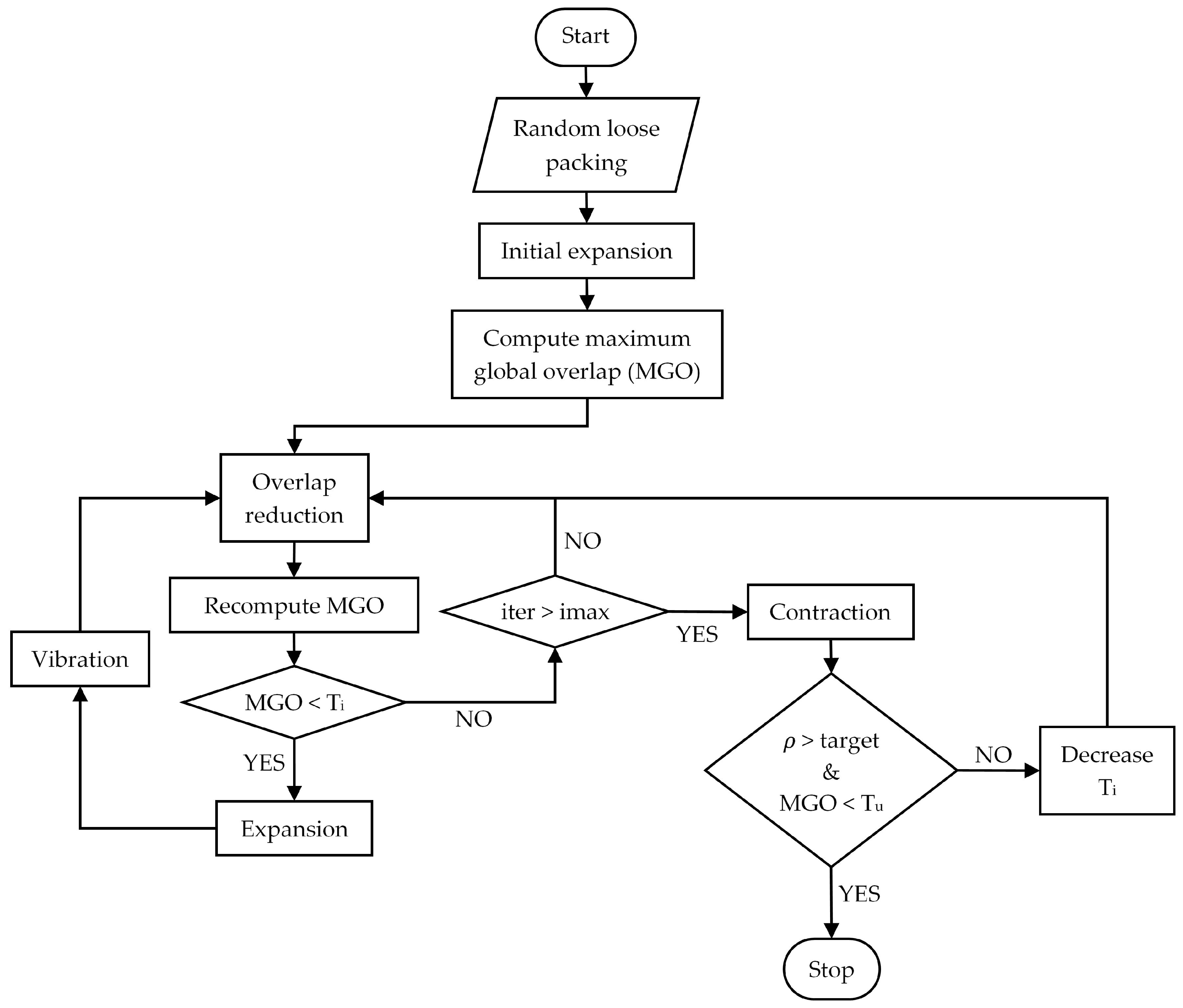
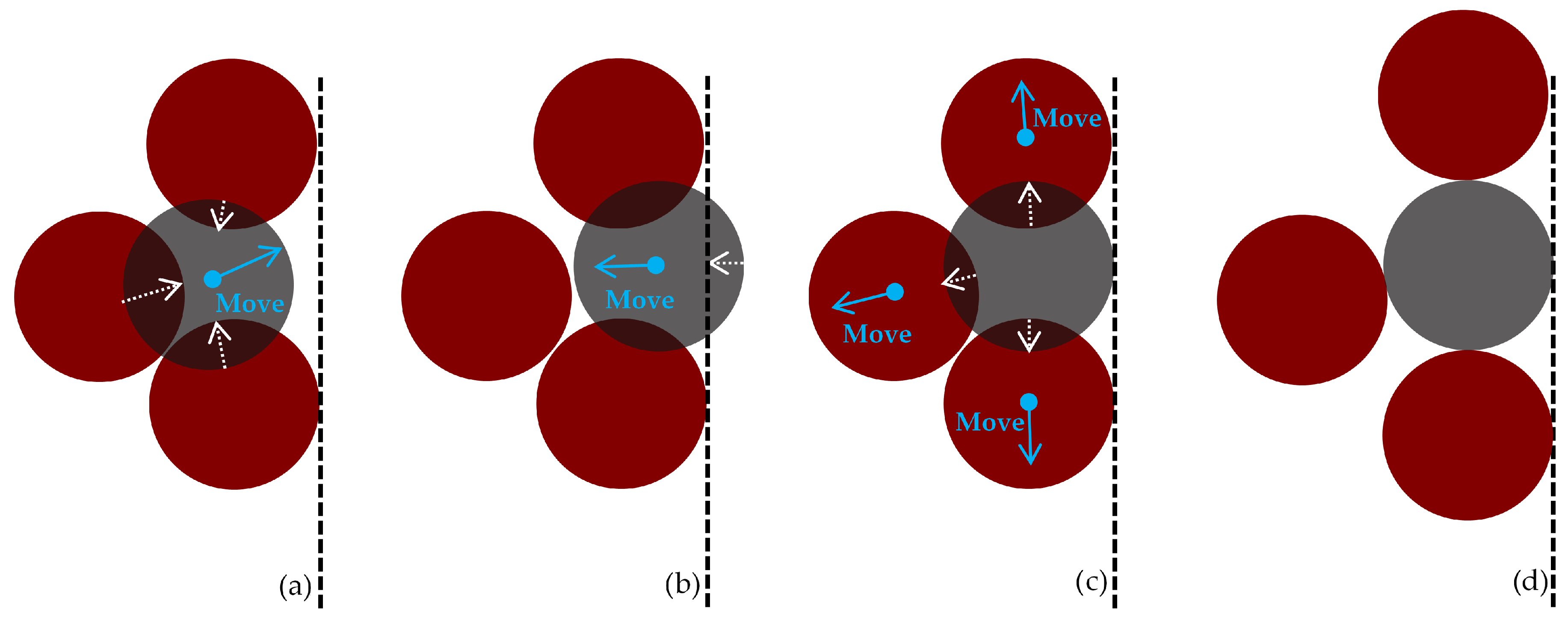
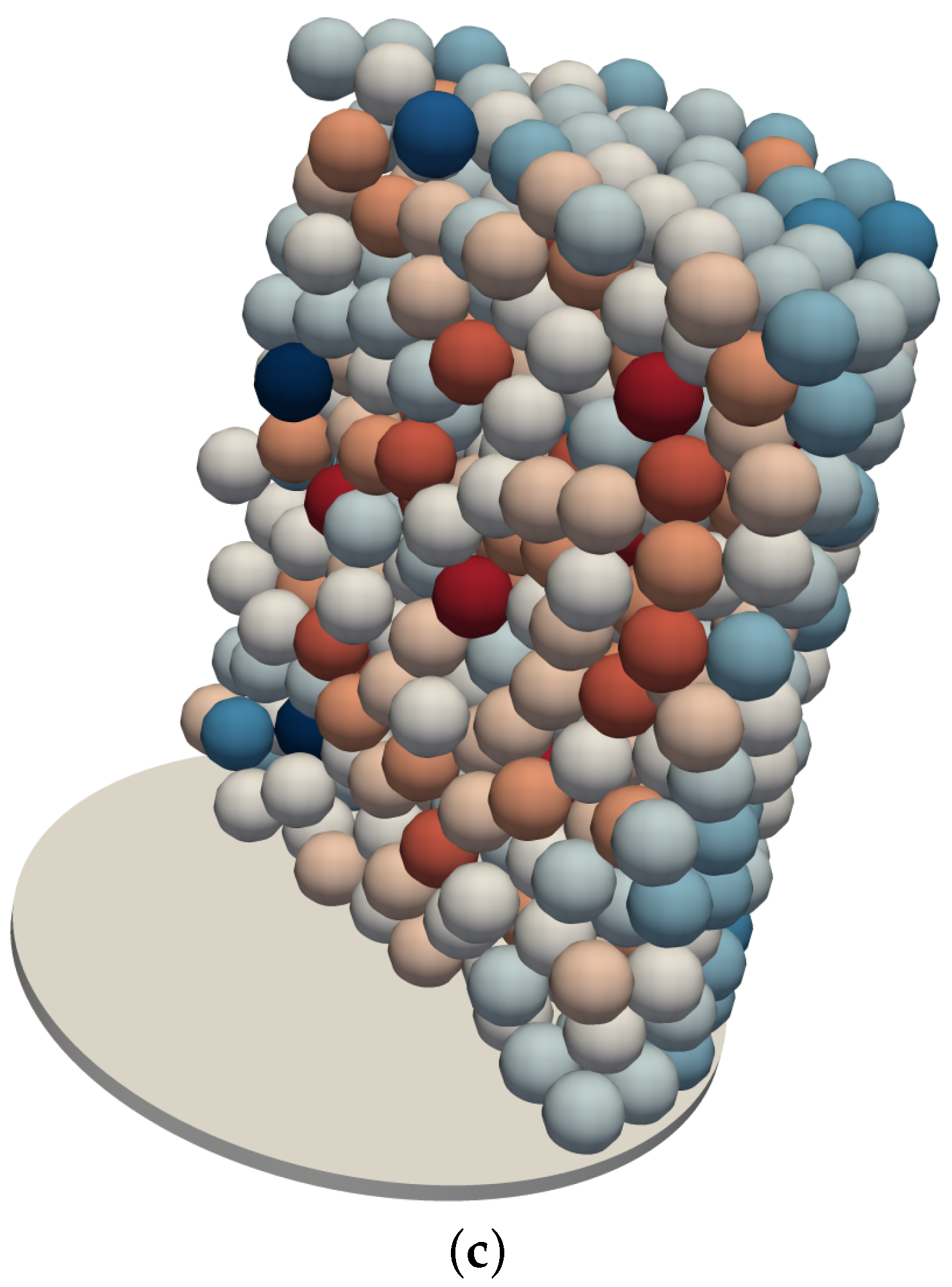
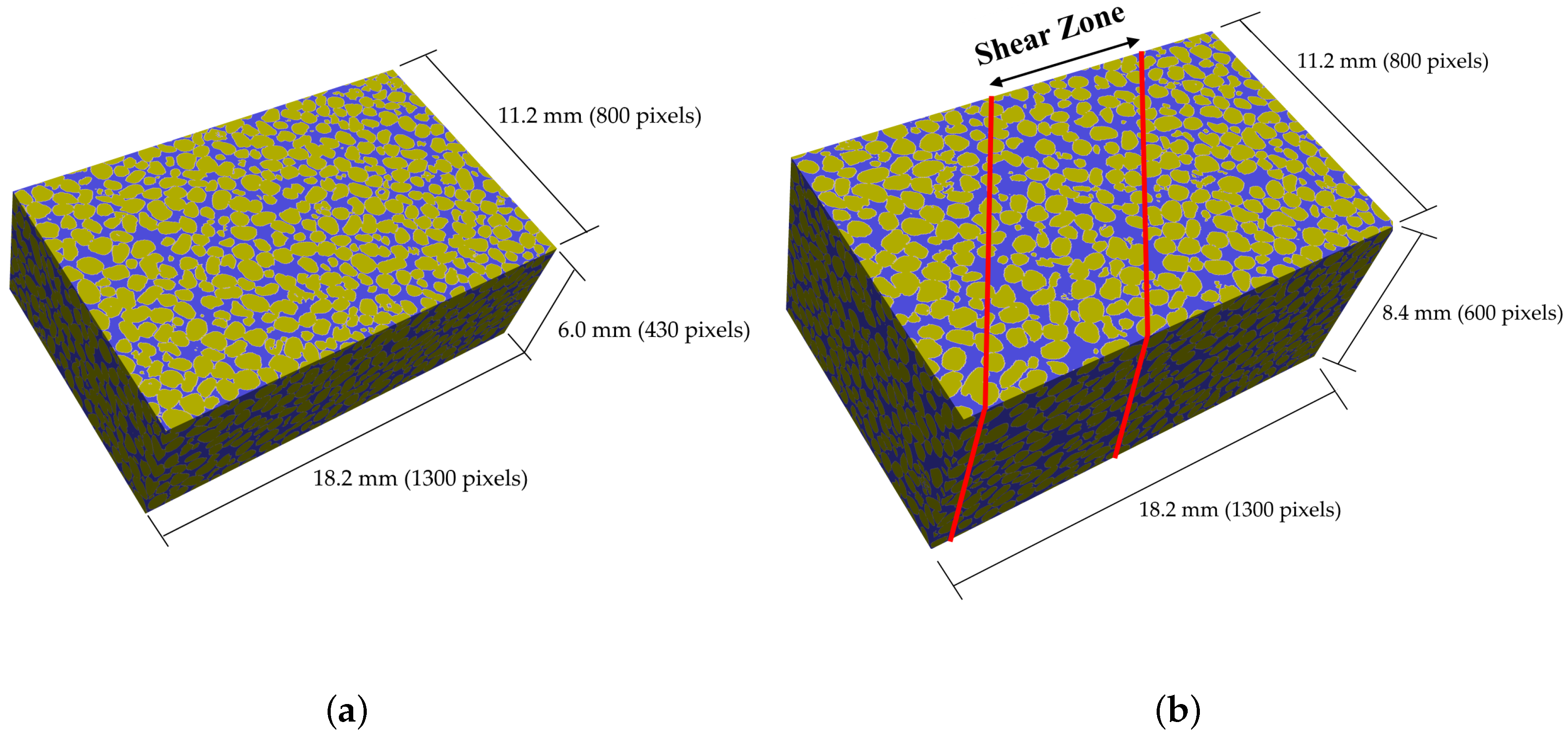
2.1. Generation Method
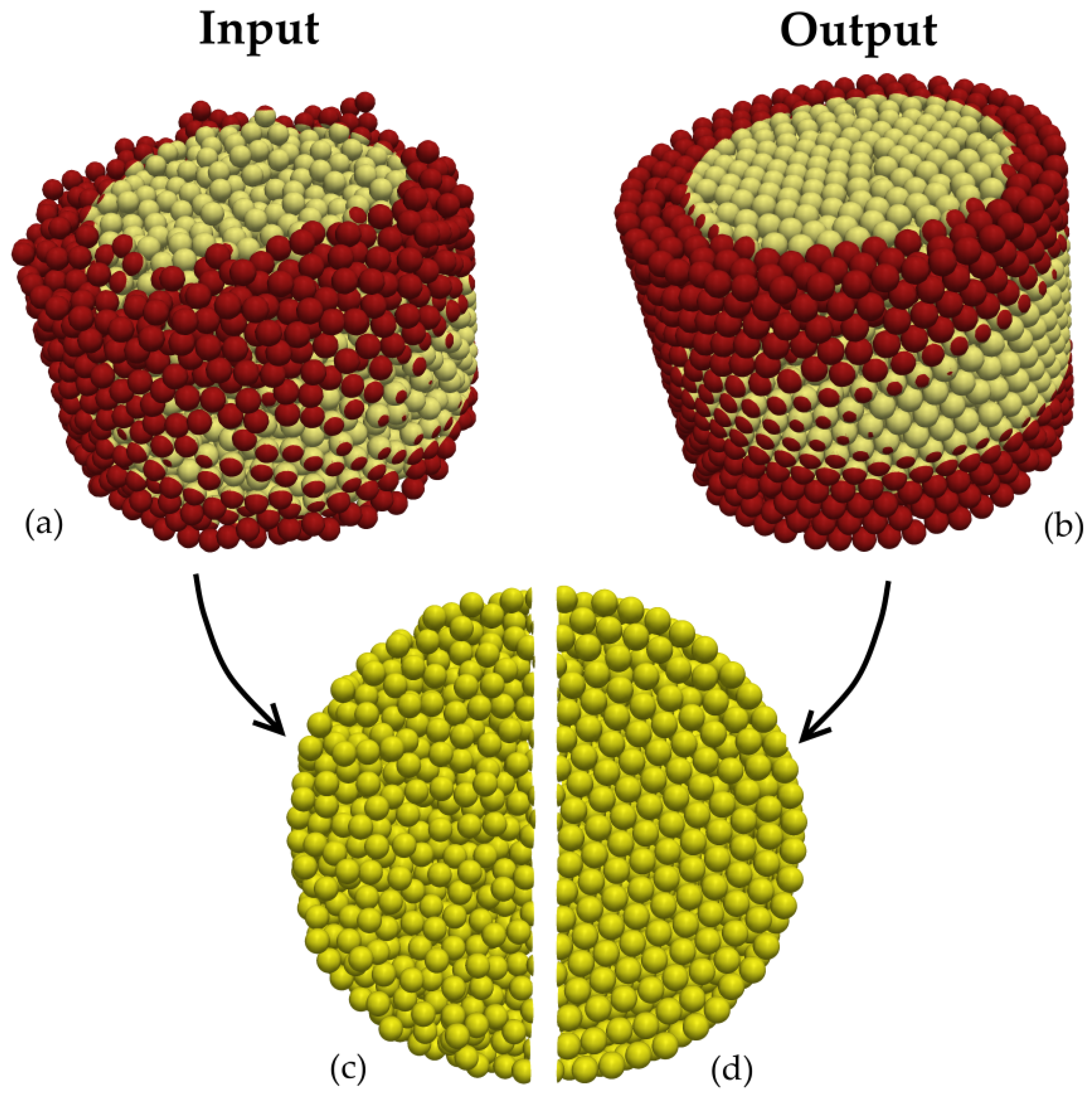
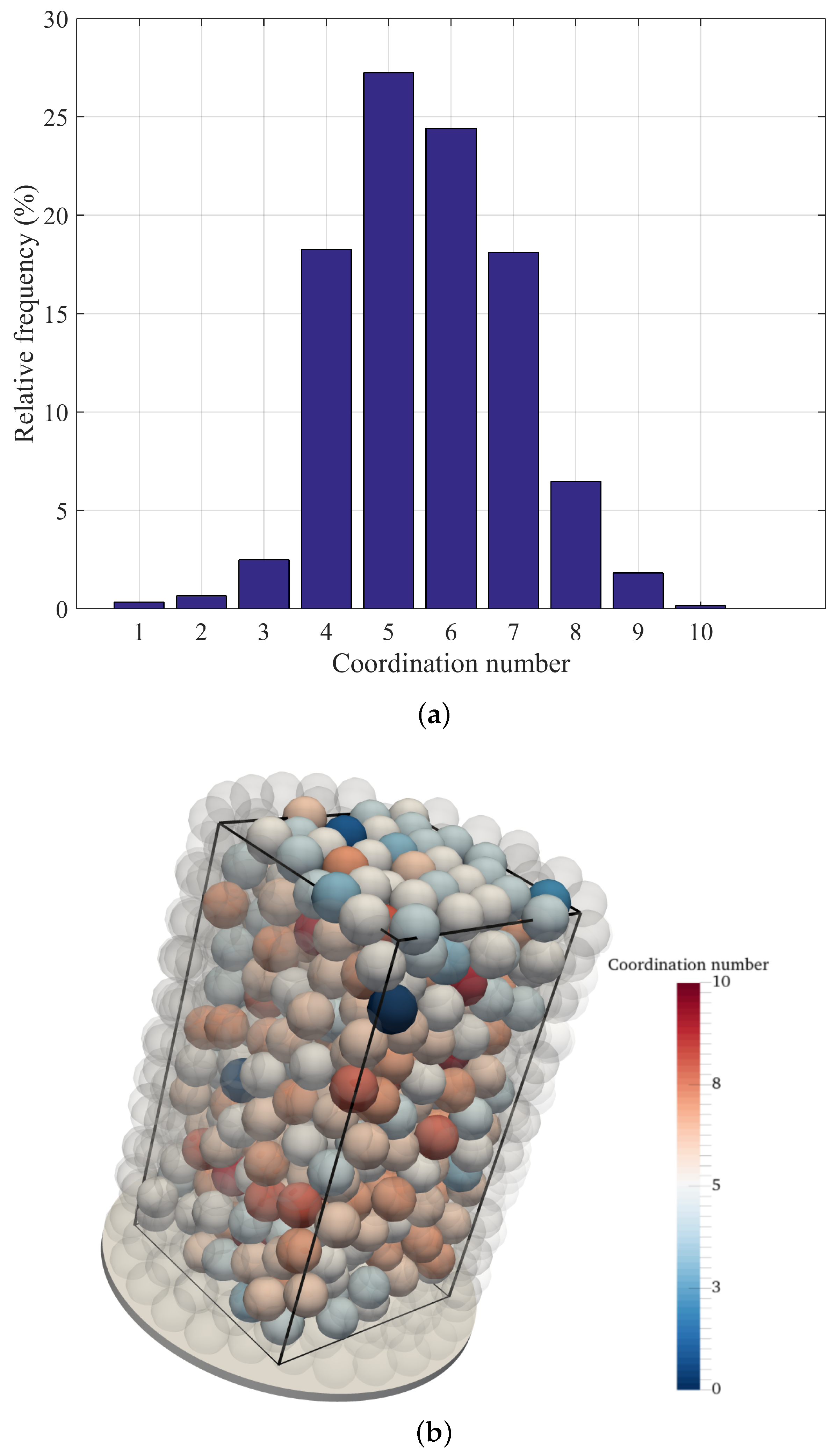
2.2. Method Validation
3. Pore Size Distribution Method
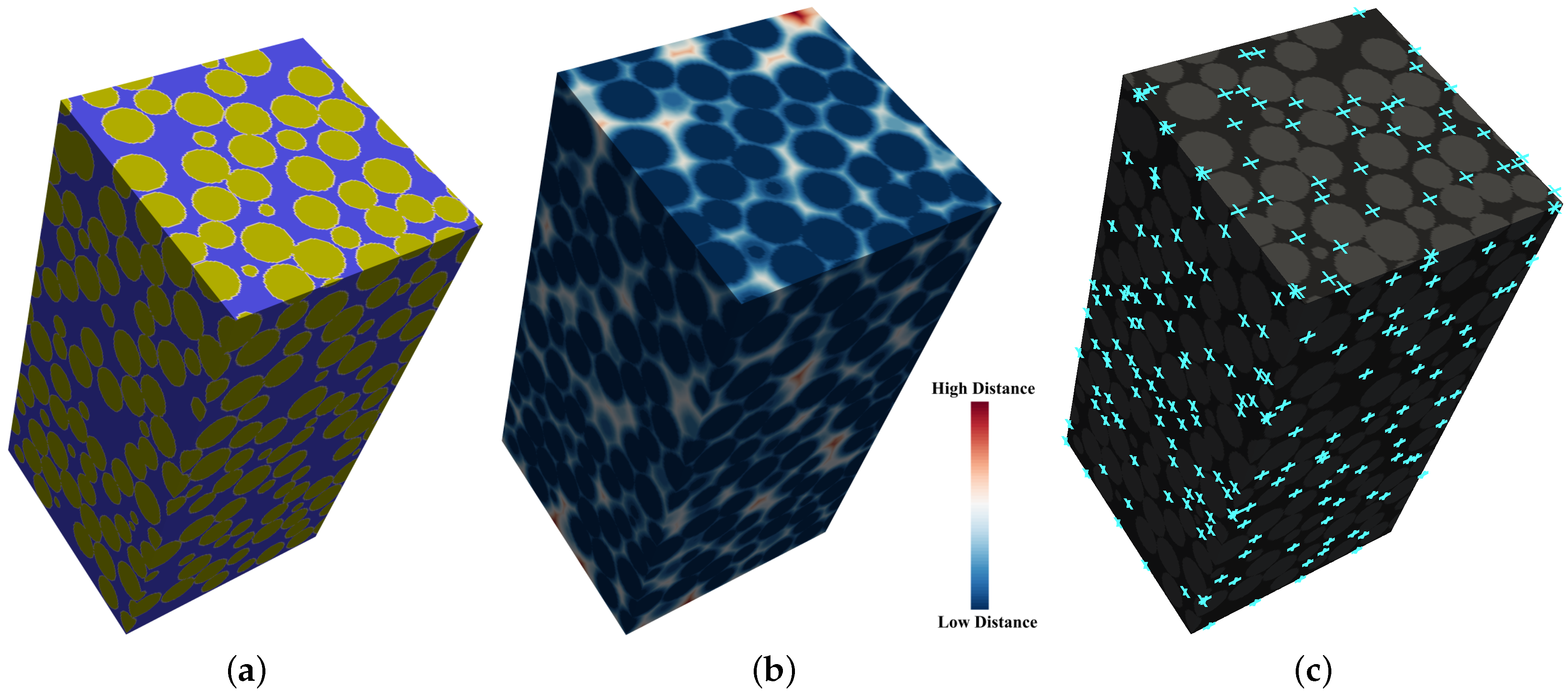
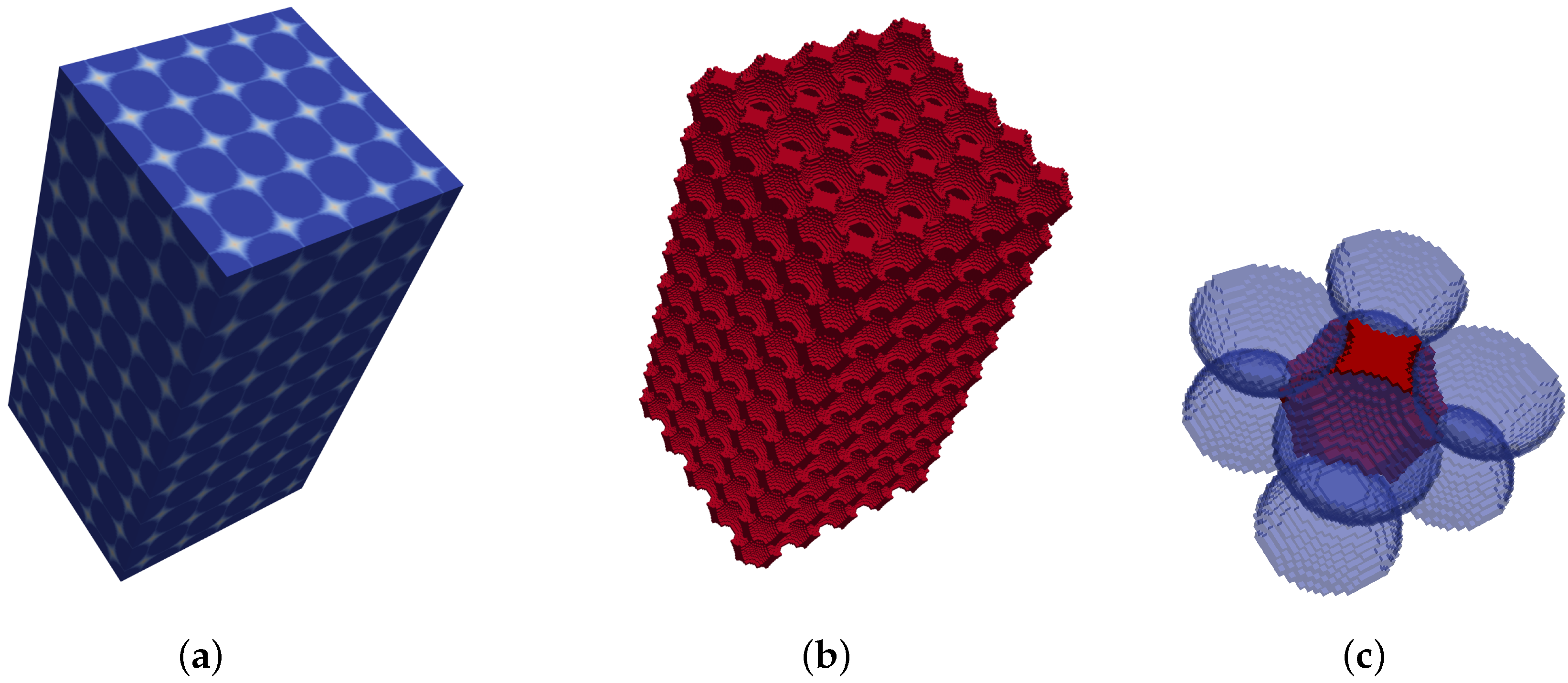
3.1. Euclidean Distance Transform (EDT)
3.2. Local Voids Center
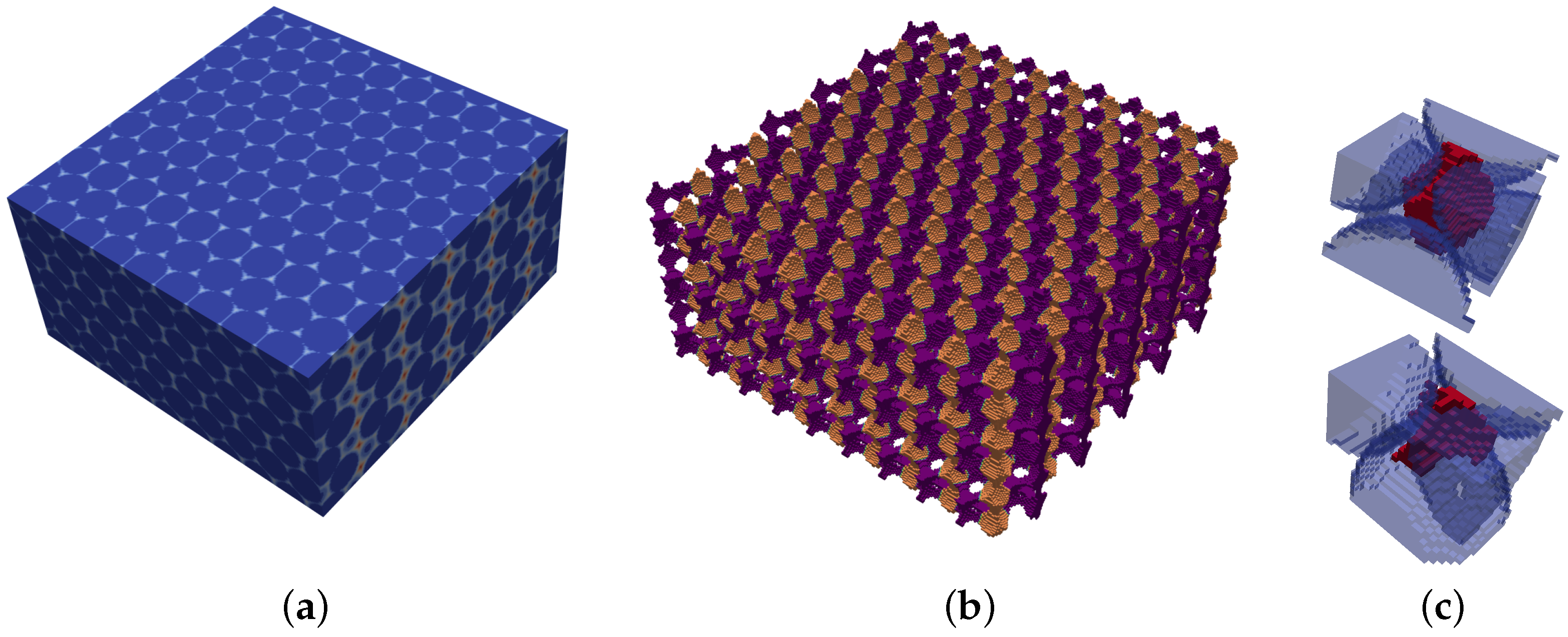
3.3. Segmentation
3.4. Validation
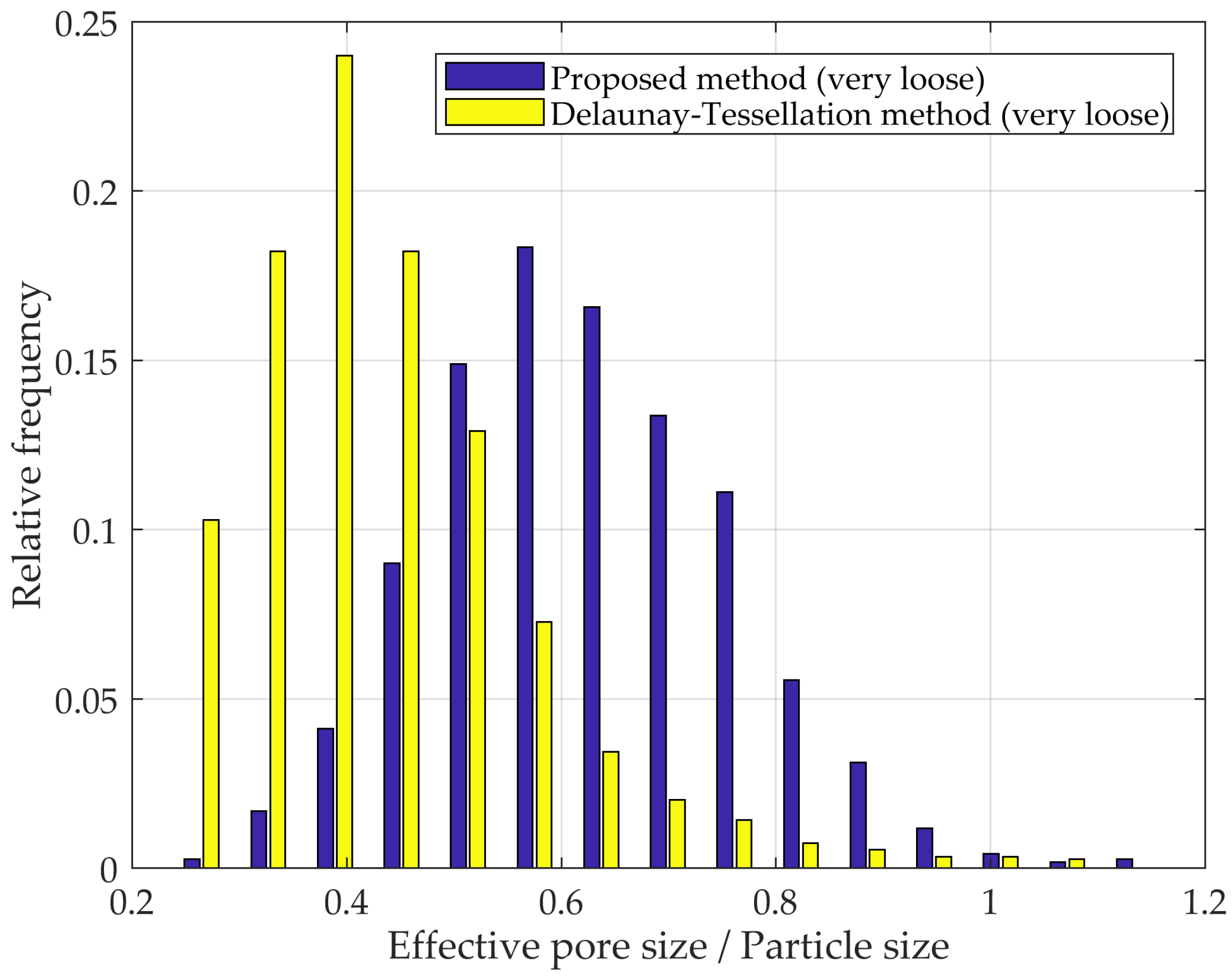
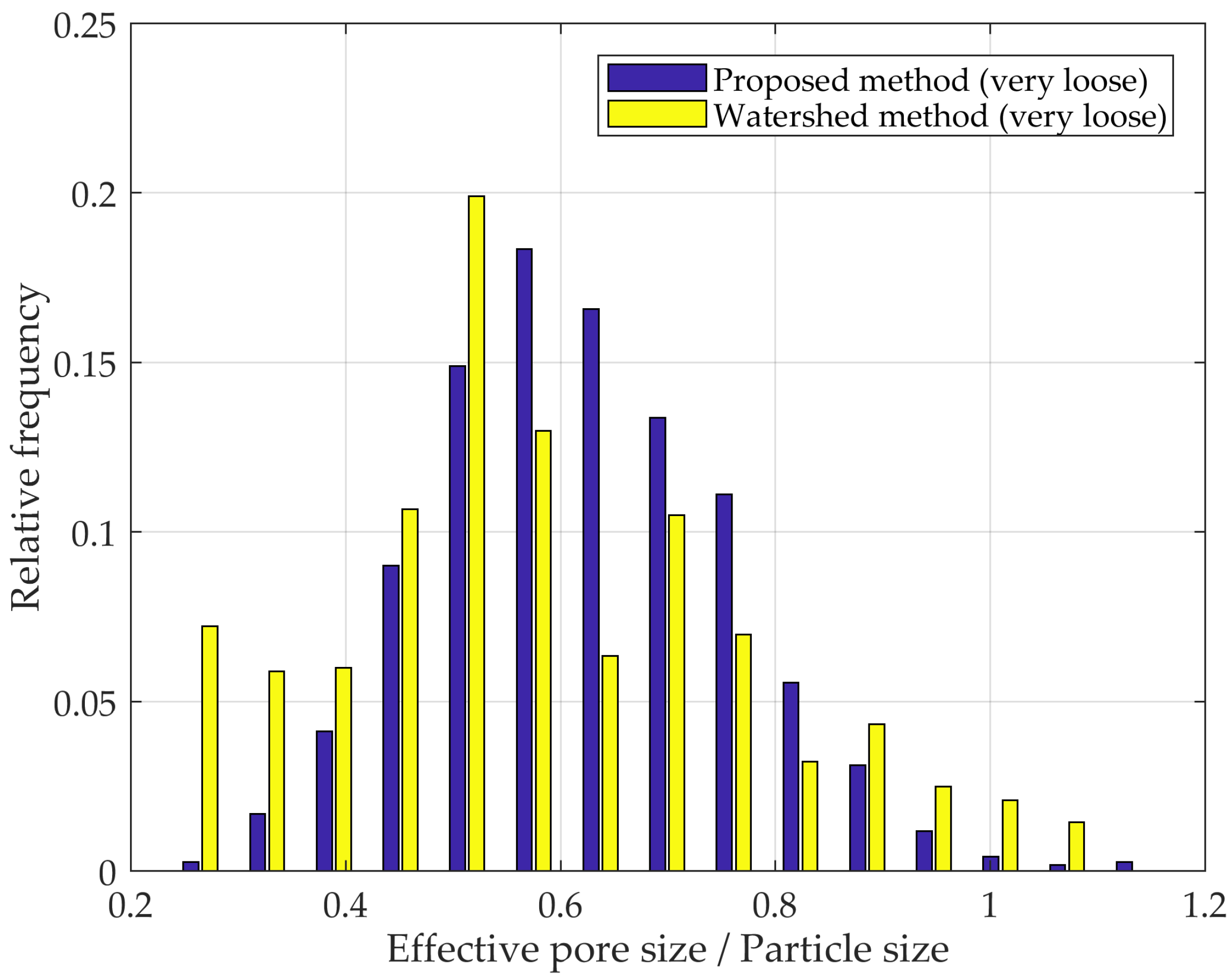
3.5. Comparison with Other Methods
4. PSD in Synthetic Microstructure
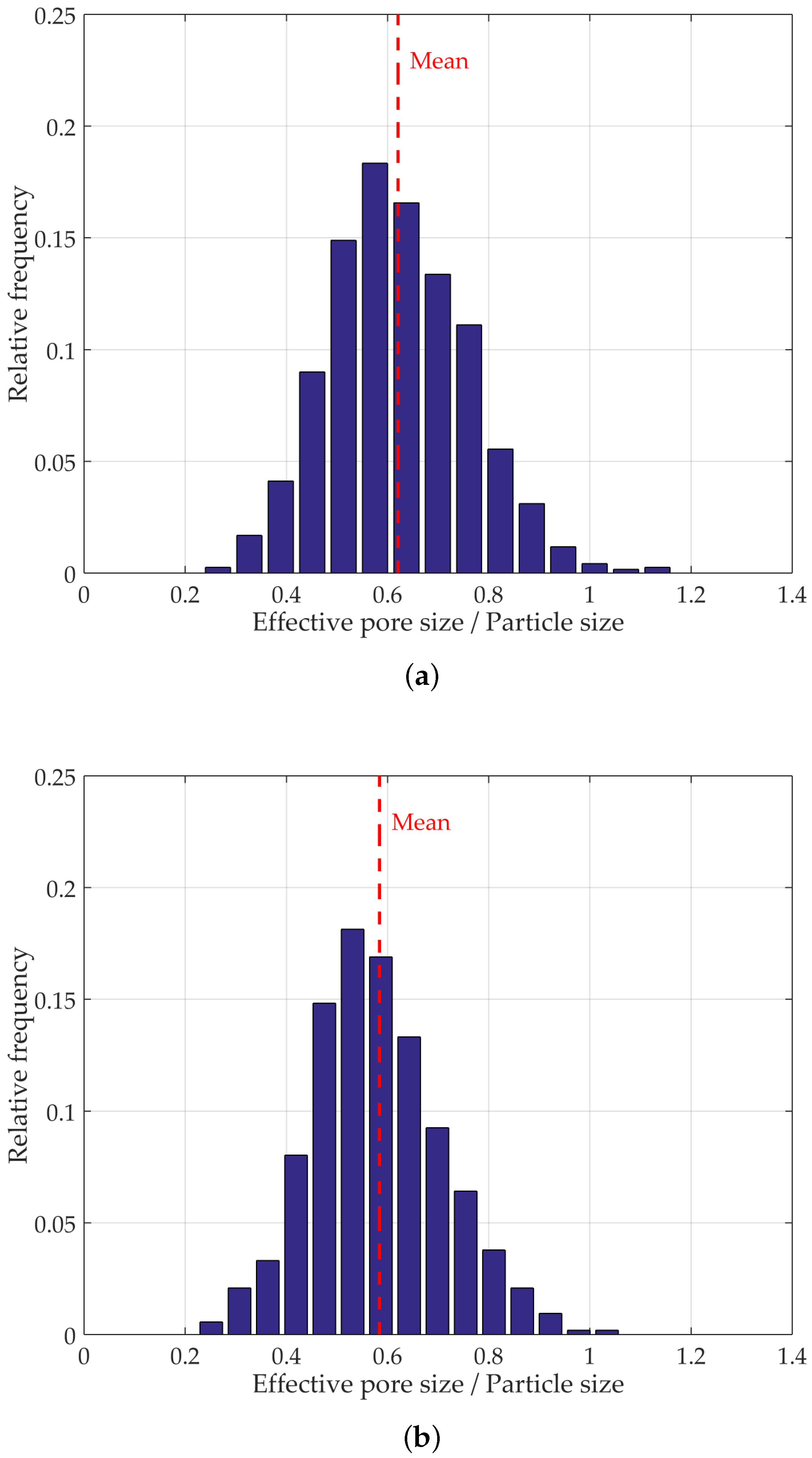
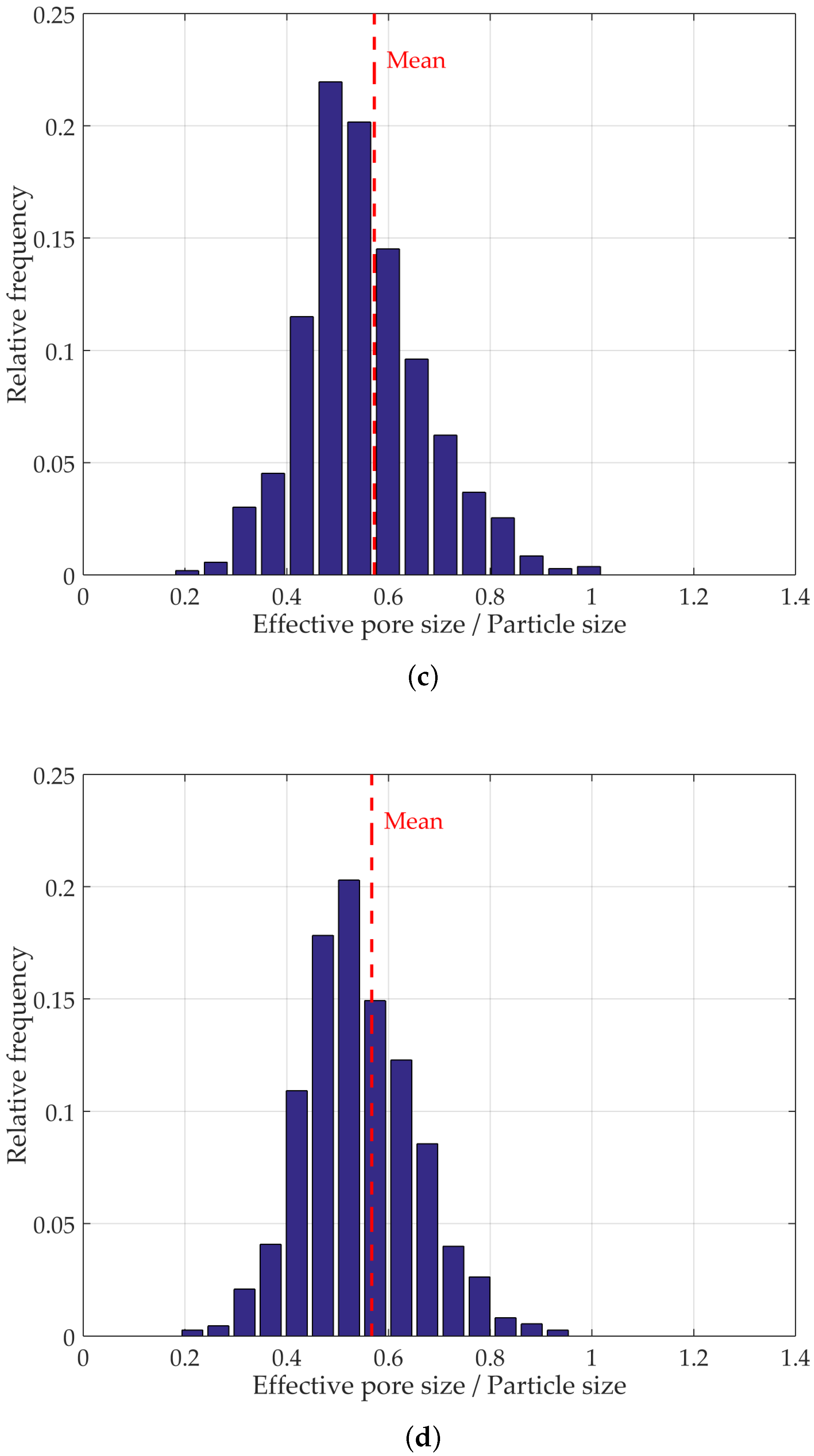
4.1. PSD of Packings at Different Densities
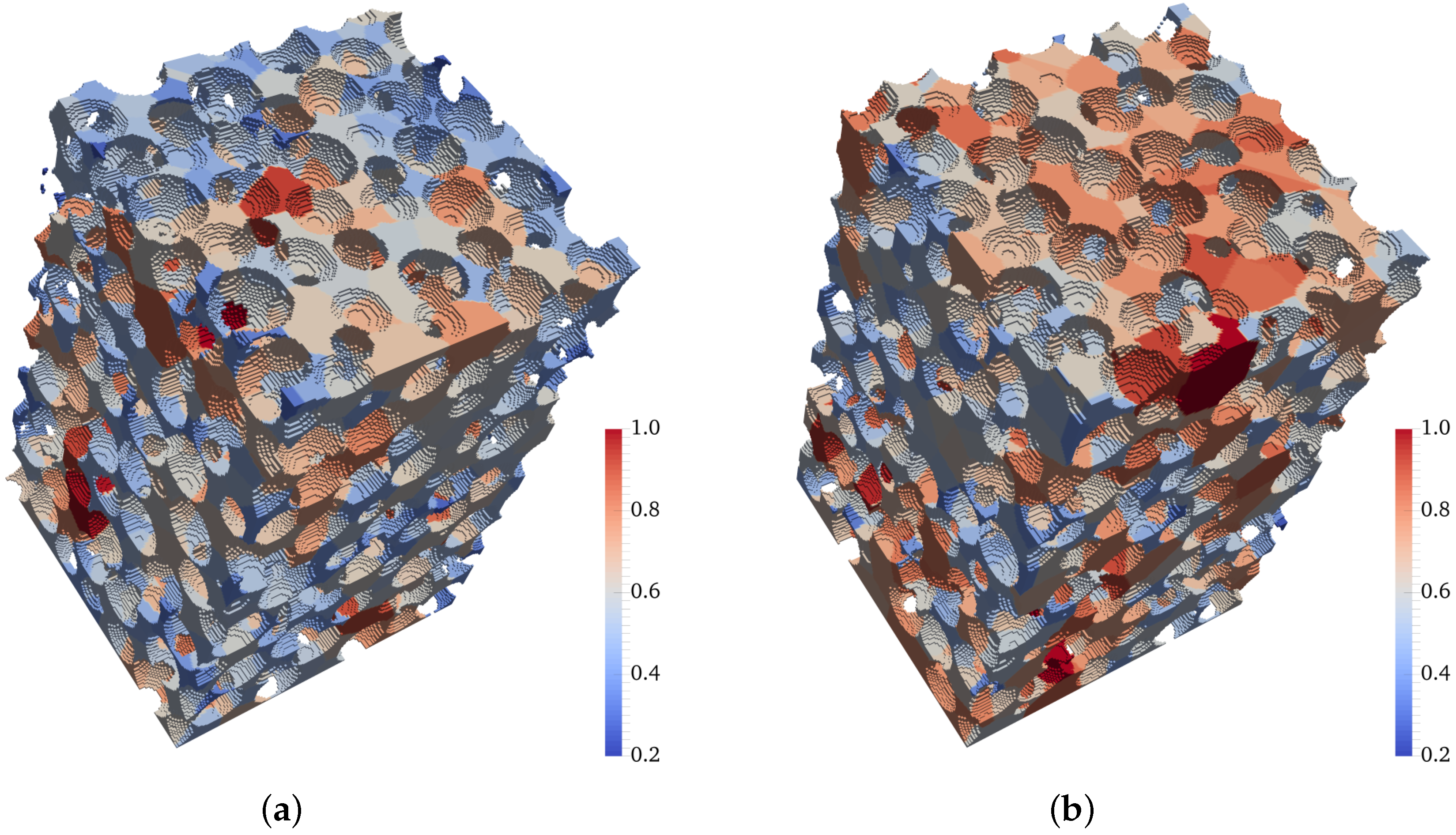
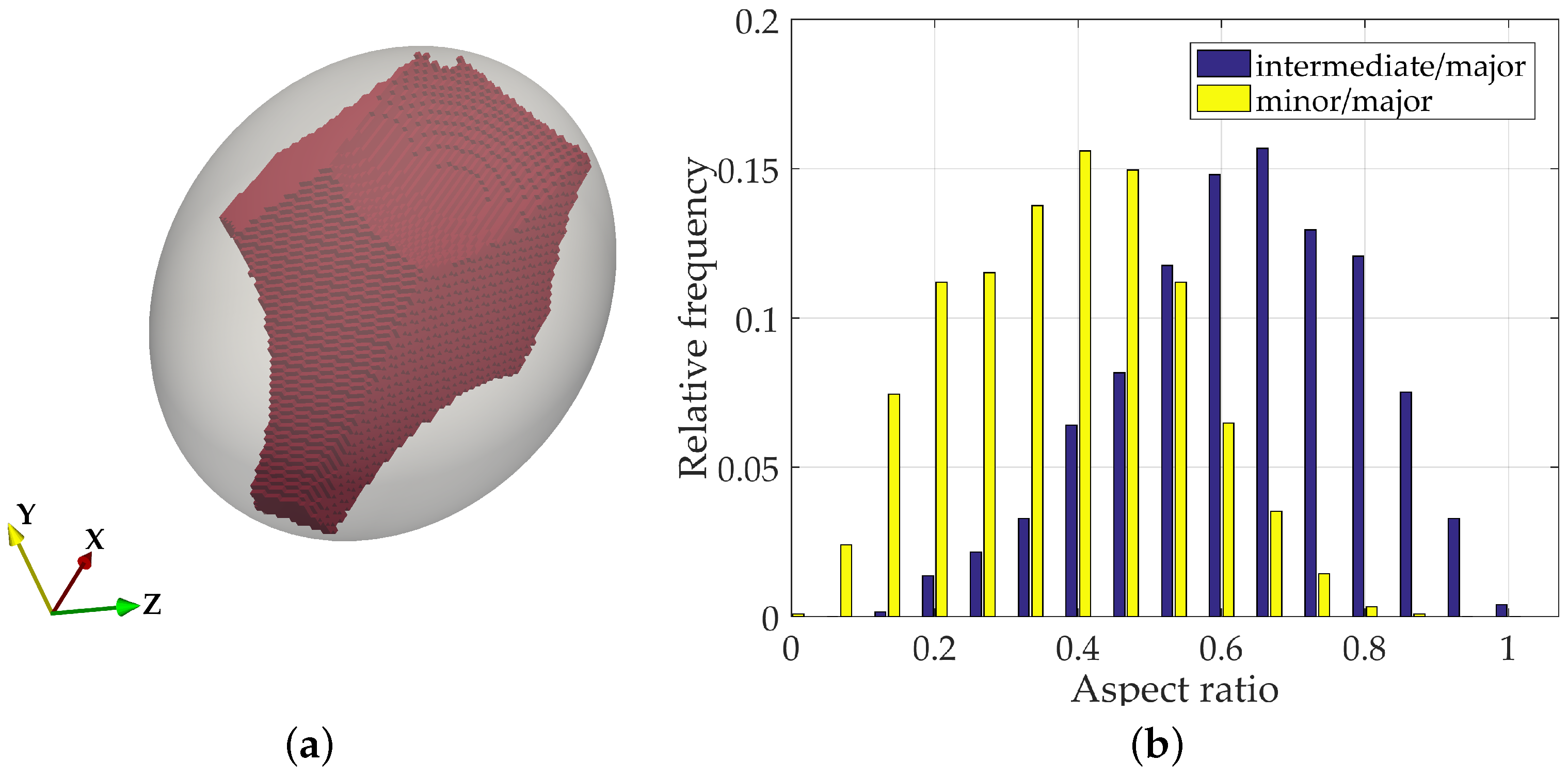
4.2. Pore Shape
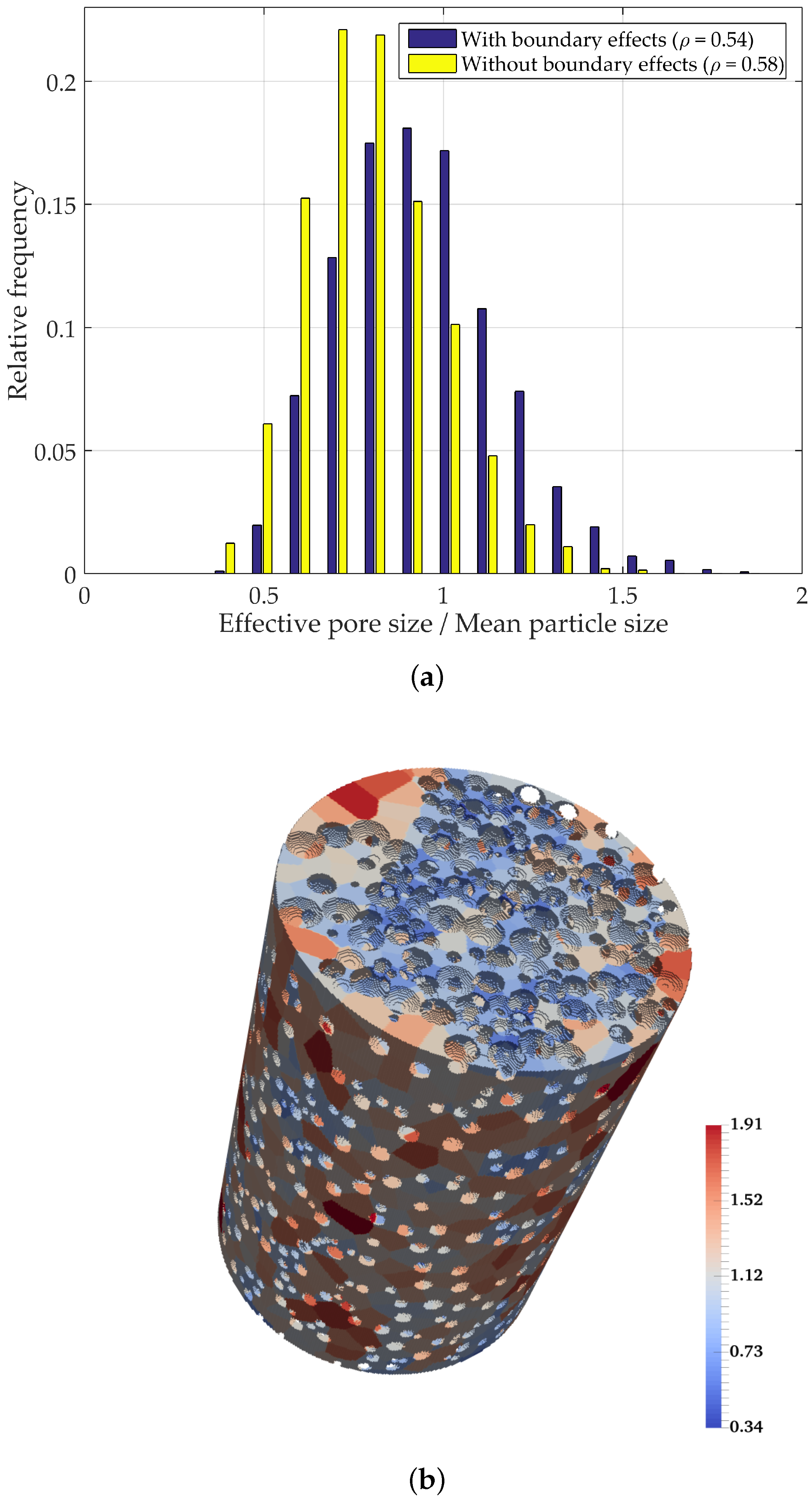
4.3. Boundary Effects on PSD Analysis of Multi-Sized Packed Spheres
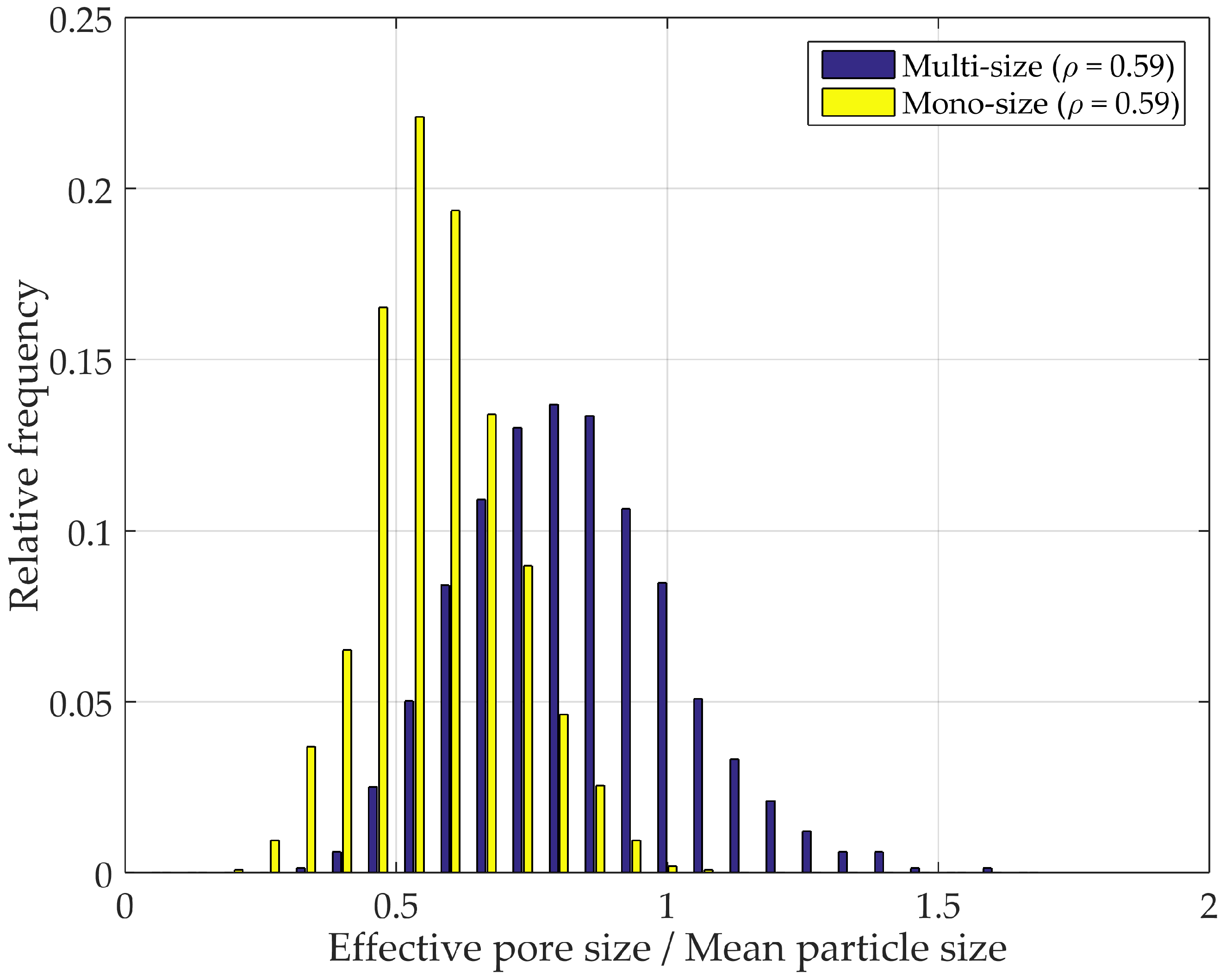
4.4. PSD Mono-Sized and Multi-Sized Spheres Packing
4.5. PSD in Ottawa 20–30 Sand Specimens
5. Conclusions
- No user defined parameters are required;
- It can be applied in any type of microstructure generated synthetically or experimentally;
- Particle shape is not a constraint in this method;
- Pore centers and polyhedral shapes of pores are calculated;
- It can capture the PSD variations for even small changes in a microstructure.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Braun, C.; Helmig, R.; Manthey, S. Macro-scale effective constitutive relationships for two-phase flow processes in heterogeneous porous media with emphasis on the relative permeability-saturation relationship. J. Contam. Hydrol. 2005, 76, 47–85. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Hilpert, M.; Miller, C. Pore-scale modeling of saturated permeabilities in random sphere packings. Phys. Rev. E 2001, 64, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Held, R.J.; Celia, M.A. Pore-scale modeling extension of constitutive relationships in the range of residual saturations. Water Resour. Res. 2001, 37, 165–170. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny-Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- McDowell-Boyer, L.M.; Hunt, J.R.; Sitar, N. Particle transport through porous media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- Campos, L.C. Modelling and Simulation of the Biological and Physical Processes of Slow Sand Filtration. Ph.D. Thesis, Imperial College of Science, London, UK, 2002. [Google Scholar]
- Tufenkji, N.; Miller, G.F.; Ryan, J.N.; Harvey, R.W. Transport of Cryptosporidium Oocysts in Porous Media: Role of Straining and Physicochemical. Environ. Sci. Technol. 2004, 38, 5932–5938. [Google Scholar] [CrossRef] [PubMed]
- Al-raoush, R.; Thompson, K.; Willson, C.S. Comparison of Network Generation Techniques for Unconsolidated Porous Media. Soil Sci. Soc. Am. J. 2003, 1700, 1687–1700. [Google Scholar] [CrossRef]
- Chan, S.; Ng, K. Geometrical characteristics of the pore space in a random packing of equal spheres. Powder Technol. 1988, 54, 147–155. [Google Scholar] [CrossRef]
- Reboul, N.; Vincens, E.; Cambou, B. A statistical analysis of void size distribution in a simulated narrowly graded packing of spheres. Granul. Matter 2008, 10, 457–468. [Google Scholar] [CrossRef]
- Mason, G. A model of the pore space in a random packing of equal spheres. J. Colloid Interface Sci. 1971, 35, 279–287. [Google Scholar] [CrossRef]
- Gao, S.; Meegoda, J.N.; Hu, L. Two methods for pore network of porous media. Int. J. Numer. Anal. Methods Geomech. 2012. [Google Scholar] [CrossRef]
- Sjah, J.; Vincens, E. Determination of the constriction size distribution of granular filters by filtration tests. Int. J. Numer. Anal. Methods Geomech. 2012. [Google Scholar] [CrossRef]
- Lindquist, W.B.; Lee, S.M.; Coker, D.A.; Jones, K.W.; Spanne, P. Medial axis analysis of void structure in three-dimensional tomographic images of porous media. J. Geophys. Res. 1996, 101, 8297–8310. [Google Scholar] [CrossRef]
- Koval, I.; Roozbahani, M.; Frost, D. Comparison between geometrical and dynamic particle packing. In Geomechanics from Micro to Macro; Soga, K., Kumar, K., Biscontin, G., Kuo, M., Eds.; CRC Press: Boca Raton, FL, USA, 2014; p. 109. [Google Scholar]
- Rabbani, A.; Ayatollahi, S.; Kharrat, R.; Dashti, N. Estimation of 3D pore network coordination number of rocks from watershed segmentation of a single 2-D image. Adv. Water Resour. 2016, 94, 264–277. [Google Scholar] [CrossRef]
- Schmitt, M.; Halisch, M.; Muller, C.; Fernandes, C.P. Classification and quantification of pore shapes in sandstone reservoir rocks with 3D X-ray micro-computed tomography. Solid Earth 2016, 7, 285–300. [Google Scholar] [CrossRef]
- Roozbahani, M.M.; Graham-Brady, L.; Frost, J.D. Mechanical trapping of fine particles in a medium of mono-sized randomly packed spheres. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1776–1791. [Google Scholar] [CrossRef]
- Frisken, S.; Perry, R. Adaptively sampled distance fields: A general representation of shape for computer graphics. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 249–254. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications, 1st ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Baldacci, F. An unbiased and intervoxel watershed algorithm for 3D image segmentation. In Proceedings of the 9th International Conference on Image Analysis and Recognition, Aveiro, Portugal, 25–27 June 2012; Springer: Berlin, Germany, 2012; pp. 330–337. [Google Scholar]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; pp. 0–5. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2007; p. 738. [Google Scholar]
- Wijewickrema, S.N.R.; Paplinski, A.P. Principal component analysis for the approximation of a fruit as an ellipse. In Full Papers / WSCG 2005, the 13th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision 2005; University of West Bohemia: Plzen, Czech Republic, 2005; pp. 1–6. [Google Scholar]
- Fuggle, A.R.; Roozbahani, M.M.; Frost, J.D. Size Effects on the Void Ratio of Loosely Packed Binary Particle Mixtures; Geo-Congress 2014 Technical Papers; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 129–138. [Google Scholar]
- Roozbahani, M.M.; Huat, B.B.; Asadi, A. The effect of different random number distributions on the porosity of spherical particles. Adv. Powder Technol. 2013, 24, 26–35. [Google Scholar] [CrossRef]
- Jodrey, W.S.; Tory, E.M. Simulation of random packing of spheres. Simulation 1979, 32, 1–12. [Google Scholar] [CrossRef]
- He, D.; Ekere, N.; Cai, L. Computer simulation of random packing of unequal particles. Phys. Rev. E 1999, 60, 7098–7104. [Google Scholar] [CrossRef]
- Frost, R.; Schon, J.C.; Salamon, P. Simulation of random close packed discs and spheres. Comput. Mater. Sci. 1993, 1, 343–350. [Google Scholar] [CrossRef]
- Clarke, A.S.; Wiley, J.D. Numerical simulation of the dense random packing of a binary mixture of hard spheres: Amorphous metals. Phys. Rev. B 1987, 35, 7350–7356. [Google Scholar] [CrossRef]
- American Society for Testing and Materials. ASTM C778-13—Standard Specification for Sand; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Lu, Y. Reconstruction, Characterization, Modeling and Visualization of Inherent and Induced Digital Sand Microstructures. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2010. [Google Scholar]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Holtz, R.D.; Kovacs, W. An Introduction to Geotechnical Engineering; Prentice-Hall Civil Engineering and Engineering Mechanics Series; Prentice-Hall: Upper Saddle Rive, NJ, USA, 1981. [Google Scholar]
- Mitchell, J.K. Fundamentals of Soil Behavior, 2nd ed.; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Hu, G.; Orkoulas, G.; Christofides, P.D. Regulation of film thickness, surface roughness and porosity in thin film growth using deposition rate. Chem. Eng. Sci. 2009, 64, 3903–3913. [Google Scholar] [CrossRef]
- Zeebroeck, M.V. The Discrete Element Method (DEM) to Simulate Fruit Impact Damage during Transport and Handling. Ph.D. Thesis, Katholieke Universiteit Leuven Faculteit Bio-ingenieurswetenschappen Dissertationes, Leuven, Belgium, 2005. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Malone, K.F.; Xu, B.H. Determination of contact parameters for discrete element method simulations of granular systems. Particuology 2008, 6, 521–528. [Google Scholar] [CrossRef]
- Jerier, J.F.; Imbault, D.; Donze, F.V.; Doremus, P. A geometric algorithm based on tetrahedral meshes to generate a dense polydisperse sphere packing. Granul. Matter 2009, 11, 43–52. [Google Scholar] [CrossRef]
- Jerier, J.F.; Richefeu, V.; Imbault, D.; Donzé, F.V. Packing spherical discrete elements for large scale simulations. Comput. Methods Appl. Mech. Eng. 2010, 199, 1668–1676. [Google Scholar] [CrossRef]
- Dullien, F.A. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Smilauer, V.; Catalano, E.; Chareyre, B.; Dorofeenko, S.; Duriez, J.; Dyck, N.; Eliáš, J.; Er, B.; Eulitz, A.; Gladky, A.; et al. Yade Documentation. Available online: https://yade-dem.org/doc/Yade.pdf (accessed on 27 October 2017).
- Kamien, R.D.; Liu, A.J. Why is random close packing reproducible? Phys. Rev. Lett. 2007, 99, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Radin, C. Random close packing of granular matter. J. Stat. Phys. 2008, 131, 567–573. [Google Scholar] [CrossRef]
- Mueller, G. Numerically packing spheres in cylinders. Powder Technol. 2005, 159, 105–110. [Google Scholar] [CrossRef]
- Mueller, G.E. Radial porosity in packed beds of spheres. Powder Technol. 2010, 203, 626–633. [Google Scholar] [CrossRef]
- Song, C.; Wang, P.; Makse, H.A. A phase diagram for jammed matter. Nature 2008, 453, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Puckett, J.G. State Variables in Granular Materials: An Investigation of Volume and Stress Fluctuations. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2012. [Google Scholar]
- Zamponi, F. Mathematical physics: Packings close and loose. Nature 2008, 453, 606–607. [Google Scholar] [CrossRef] [PubMed]



| Model | Description | Packing Density |
|---|---|---|
| Very loose random packing | Spheres slowly settled | 0.56 |
| Loose random packing | Dropped into bed or packed by hand | 0.59 to 0.60 |
| Poured random packing | Spheres poured into bed | 0.609 to 0.625 |
| Dense random packing | The bed vibrated | 0.625 to 0.641 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roozbahani, M.M.; Borela, R.; Frost, J.D. Pore Size Distribution in Granular Material Microstructure. Materials 2017, 10, 1237. https://doi.org/10.3390/ma10111237
Roozbahani MM, Borela R, Frost JD. Pore Size Distribution in Granular Material Microstructure. Materials. 2017; 10(11):1237. https://doi.org/10.3390/ma10111237
Chicago/Turabian StyleRoozbahani, M. Mahdi, Rodrigo Borela, and J. David Frost. 2017. "Pore Size Distribution in Granular Material Microstructure" Materials 10, no. 11: 1237. https://doi.org/10.3390/ma10111237
APA StyleRoozbahani, M. M., Borela, R., & Frost, J. D. (2017). Pore Size Distribution in Granular Material Microstructure. Materials, 10(11), 1237. https://doi.org/10.3390/ma10111237





