Dispersions of Goethite Nanorods in Aprotic Polar Solvents
Abstract
:1. Introduction
2. Results and Discussion
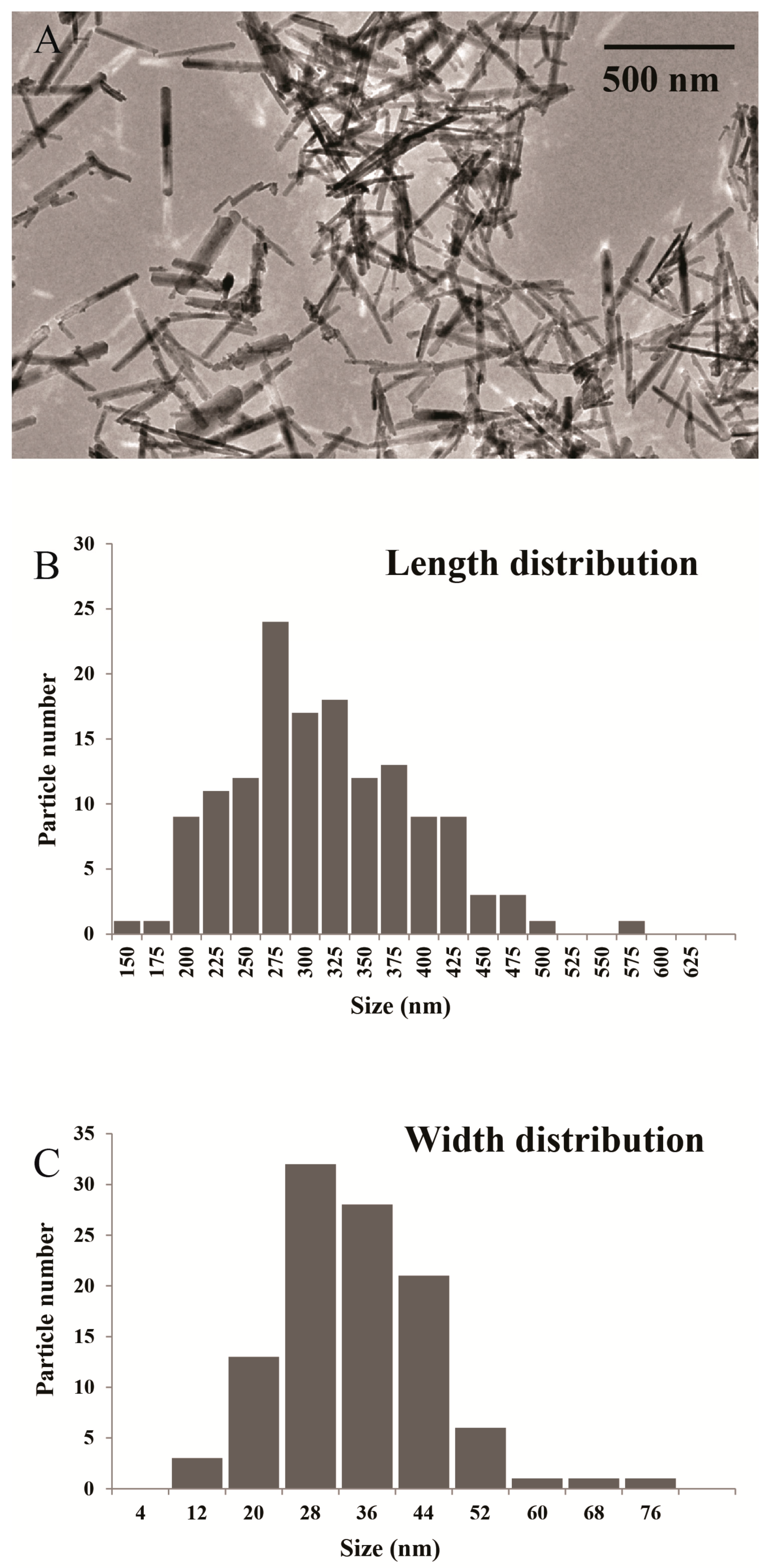
2.1. Colloidal Stability of Goethite Nanorod Suspensions
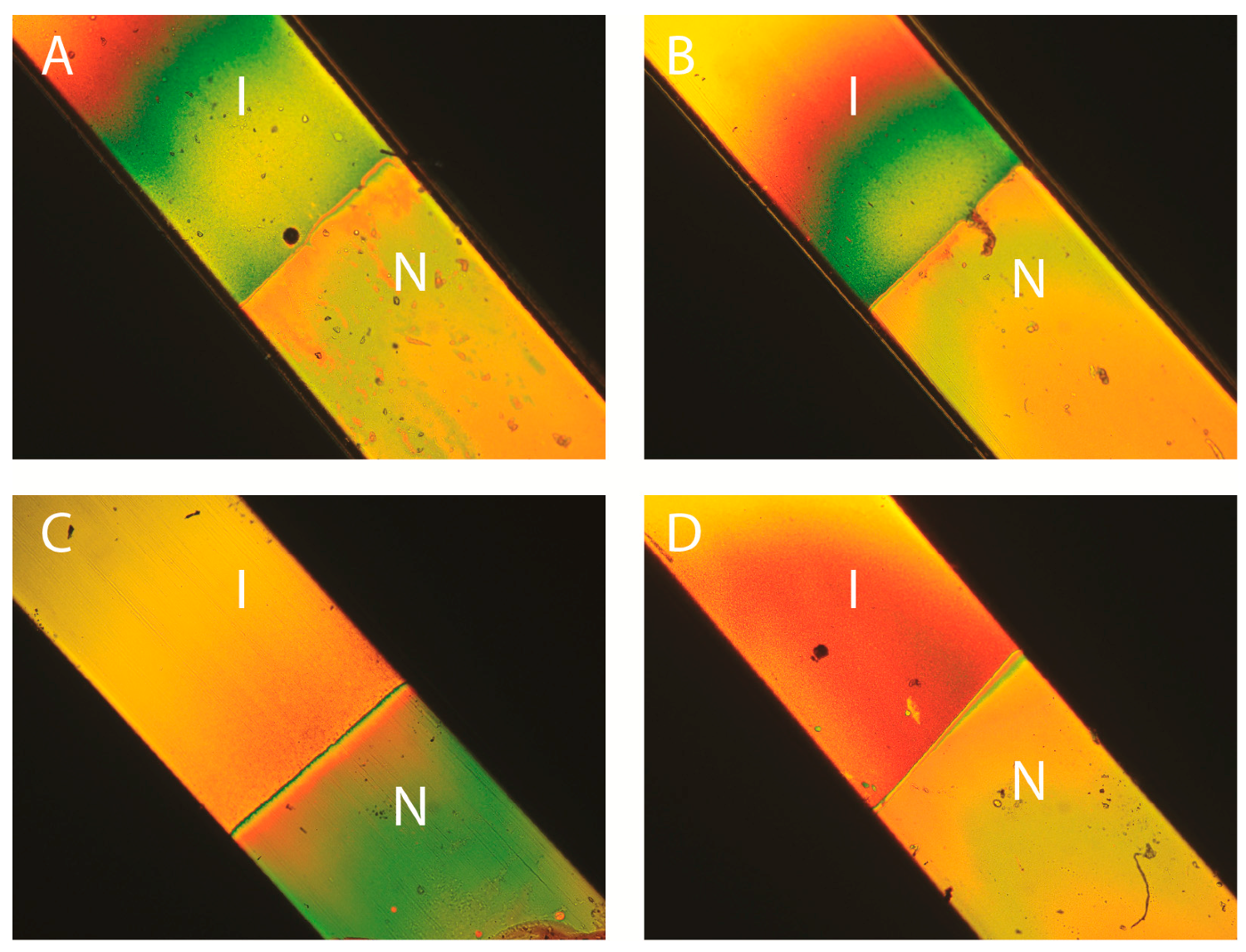
2.2. Existence of a Nematic Phase
2.3. Magneto-Optic Response of the Goethite Suspensions
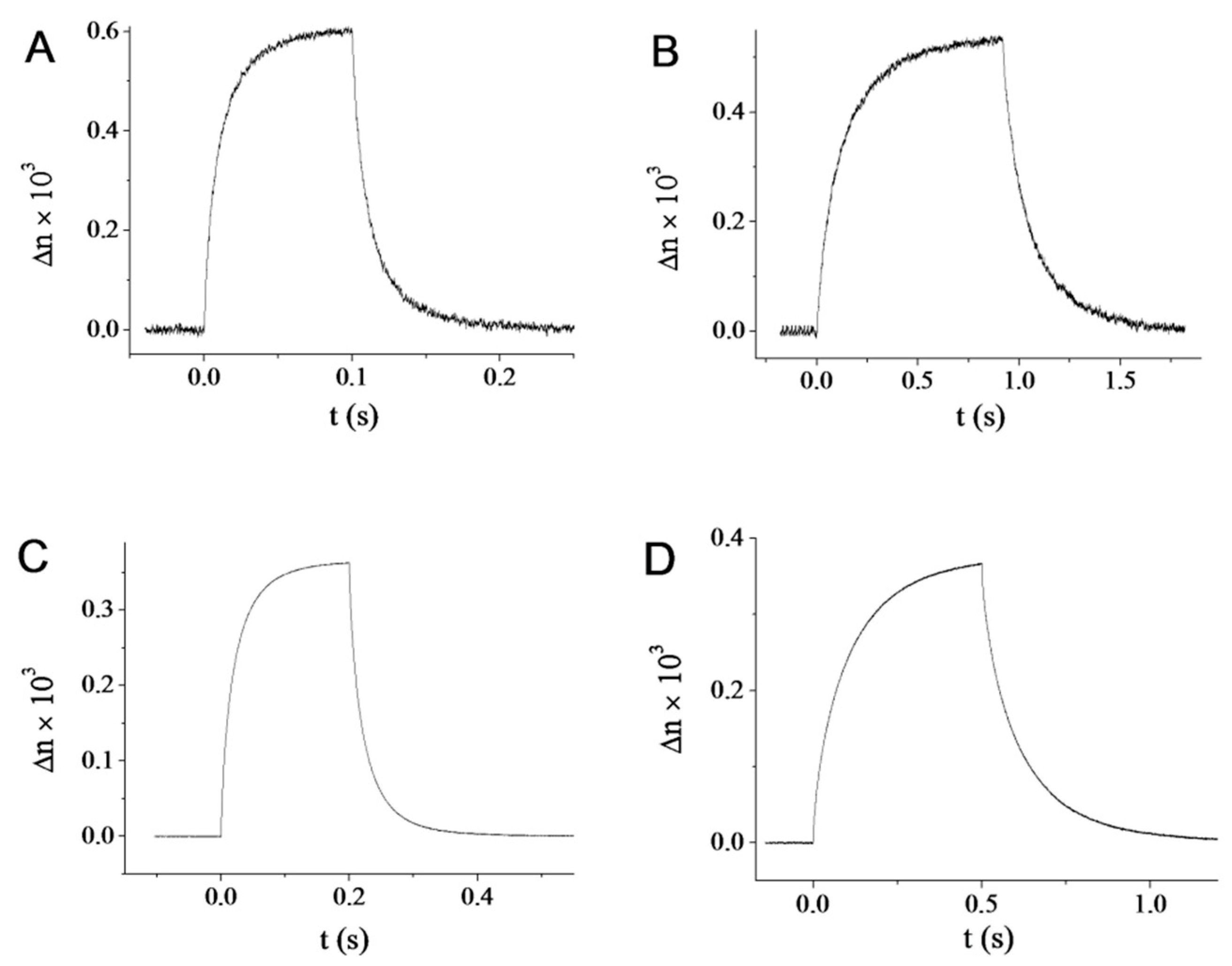
2.4. Electro-Optic Response of the Goethite Suspensions
3. Materials and Methods
3.1. Goethite Synthesis
3.2. Electron Microscopy
3.3. Goethite Solvent Exchange
3.4. Optical Microscopy
3.5. Electro-Optics
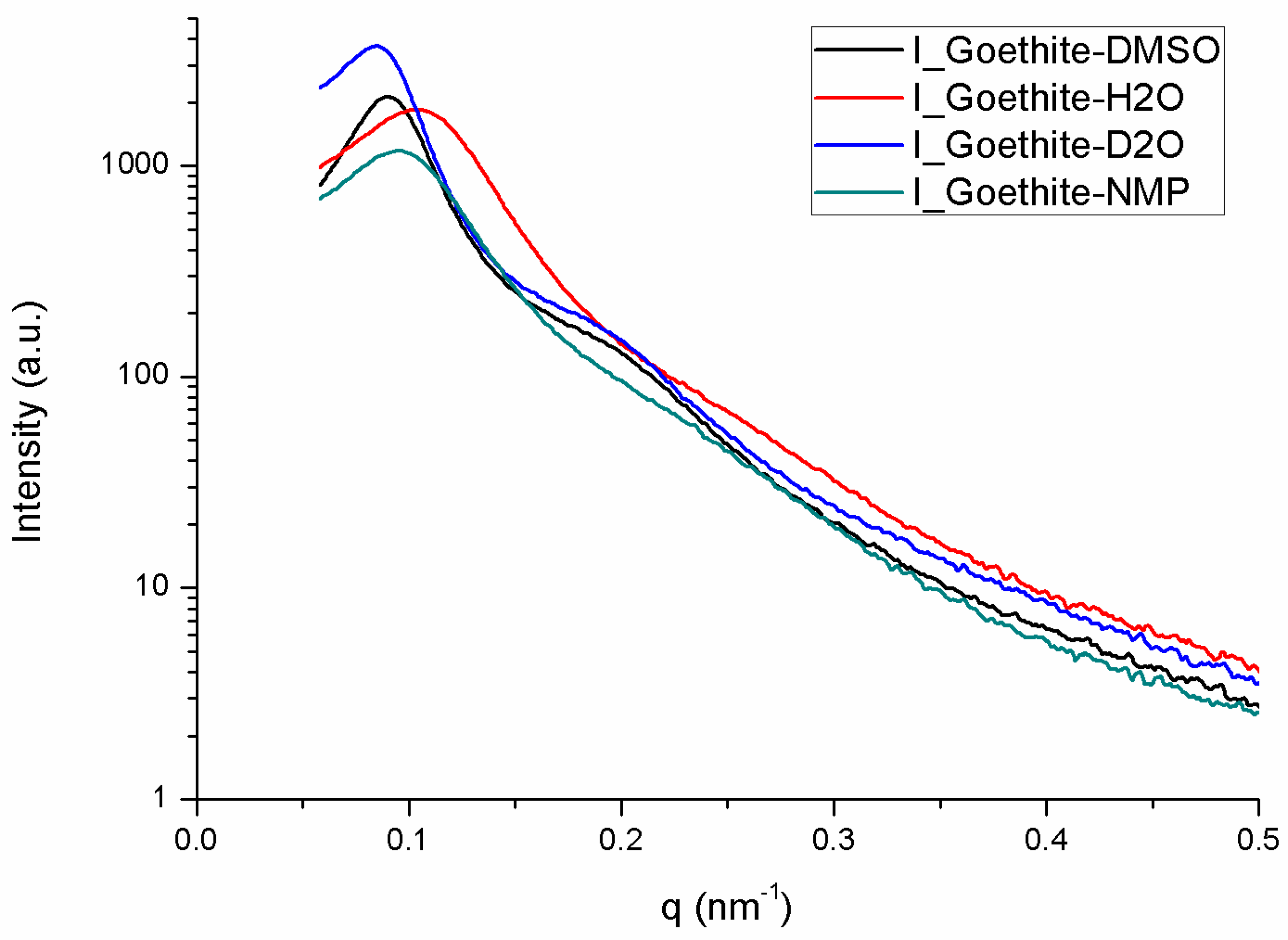
3.6. Synchrotron Small-Angle X-Ray Scattering
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lekkerkerker, H.N.W.; Vroege, G.J. Liquid crystal phase transitions in suspensions of mineral colloids: New life from old roots. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2013, 371, 20120263. [Google Scholar] [CrossRef] [PubMed]
- Dogic, Z.; Fraden, S. Ordered phases of filamentous viruses. Curr. Opin. Colloid Interface Sci. 2006, 11, 47–55. [Google Scholar] [CrossRef]
- Kwoleck, S. Wholly Aromatic Carbocyclic Polycarbonamide Fiber Having Orientation Angle of Less Than about 45°. U.S. Patent US3819587 A, 25 June 1974. [Google Scholar]
- Davidson, P. Mineral liquid crystals: Liquid-crystalline suspensions of mineral nanoparticles. In Handbook of Liquid Crystals; Collings, P.J., Goodby, J.W., Kato, T., Tschierske, C., Gleeson, H., Raynes, P., Eds.; Wiley-VCH: Weinheim, Germany, 2014; Volume 6, pp. 77–98. [Google Scholar]
- Davidson, P.; Gabriel, J.C.P. Mineral liquid crystals. Curr. Opin. Colloid Interface Sci. 2005, 9, 377–383. [Google Scholar] [CrossRef]
- Gabriel, J.C.P.; Davidson, P. New trends in colloidal liquid crystals based on mineral moieties. Adv. Mater. 2000, 12, 9–20. [Google Scholar] [CrossRef]
- Lemaire, B.J.; Davidson, P.; Ferre, J.; Jamet, J.P.; Panine, P.; Dozov, I.; Jolivet, J.P. Outstanding magnetic properties of nematic suspensions of goethite (alpha-FeOOH) nanorods. Phys. Rev. Lett. 2002, 88, 125507. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, B.J.; Davidson, P.; Petermann, D.; Panine, P.; Dozov, I.; Stoenescu, D.; Jolivet, J.P. Physical properties of aqueous suspensions of goethite (α-FeOOH) nanorods-Part II: In the nematic phase. Eur. Phys. J. E 2004, 13, 309–319. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, B.J.; Davidson, P.; Ferre, J.; Jamet, J.P.; Petermann, D.; Panine, P.; Dozov, I.; Jolivet, J.P. Physical properties of aqueous suspensions of goethite (α-FeOOH) nanorods-Part I: In the isotropic phase. Eur. Phys. J. E 2004, 13, 291–308. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, B.J.; Davidson, P.; Panine, P.; Jolivet, J.P. Magnetic-field-induced nematic-columnar phase transition in aqueous suspensions of goethite (α-FeOOH) nanorods. Phys. Rev. Lett. 2004, 93, 267801. [Google Scholar] [CrossRef] [PubMed]
- Vroege, G.J.; Thies-Weesie, D.M.E.; Petukhov, A.V.; Lemaire, B.J.; Davidson, P. Smectic liquid-crystalline order in suspensions of highly polydisperse goethite nanorods. Adv. Mater. 2006, 18, 2565–2568. [Google Scholar] [CrossRef]
- Van den Pol, E.; Petukhov, A.V.; Thies-Weesie, D.M.E.; Byelov, D.V.; Vroege, G.J. Experimental Realization of Biaxial Liquid Crystal Phases in Colloidal Dispersions of Boardlike Particles. Phys. Rev. Lett. 2009, 103, 258301. [Google Scholar] [CrossRef] [PubMed]
- Vroege, G.J. Biaxial phases in mineral liquid crystals. Liq. Cryst. 2014, 41, 342–352. [Google Scholar] [CrossRef]
- Cotton, A.; Mouton, H. Regarding the phenomenon of Majorana. C. R. Hebd. Seances Acad. Sci. 1905, 141, 317–319. [Google Scholar]
- Kerr, J. XL. A new relation between electricity and light: Dielectrified media birefringent. Philos. Mag. 1875, 50, 337–348. [Google Scholar] [CrossRef]
- Coursault, D.; Blanc, C.; Nobili, M.; Dupont, L.; Davidson, P.; Chanéac, C.; Dozov, I.; Abbas, S. Electric Birefringence and Electric Dichroism of Goethite Colloidal Suspensions. In Proceedings of the 25th International Liquid Crystal Conference, Dublin, Ireland, 29 June–4 July 2014. [Google Scholar]
- Abbas, S.; Dupont, L.; Davidson, P.; Dozov, I.; Chanéac, C. Filtre optique Fabry-Perot avec pour matériau électrooptique une suspension de nanoparticules de Goethite. In Proceedings of the CMOI 2015: 14ème colloque international francophone sur les Méthodes et Techniques Optiques pour l’Industrie, Plomeur-Bodou, France, 16–20 November 2015. [Google Scholar]
- Jolivet, J.P.; Chaneac, C.; Tronc, E. Iron oxide chemistry. From molecular clusters to extended solid networks. Chem. Commun. 2004, 481–487. [Google Scholar] [CrossRef]
- Atkinson, R.J.; Posner, A.M.; Quirk, J.P. Adsorption of potential-determining ions at ferric oxide–aqueous electrolute interface. J. Phys. Chem. 1967, 71, 550–558. [Google Scholar] [CrossRef]
- Poniewierski, A. Ordering of Hard Needles at a Hard-Wall. Phys. Rev. E 1993, 47, 3396–3403. [Google Scholar] [CrossRef]
- Davidson, P.; Petermann, D.; Levelut, A.M. The Measurement of the Nematic Order-Parameter by X-Ray-Scattering Reconsidered. J. Phys. II 1995, 5, 113–131. [Google Scholar] [CrossRef]
- Frka-Petesic, B.; Radavidson, H.; Jean, B.; Heux, L. Dynamically Controlled Iridescence of Cholesteric Cellulose Nanocrystal Suspensions Using Electric Fields. Adv. Mater. 2017, 29, 1606208. [Google Scholar] [CrossRef] [PubMed]
- Bruckner, J.R.; Kuhnhold, A.; Honorato-Rios, C.; Schilling, T.; Lagerwall, J.P.F. Enhancing Self-Assembly in Cellulose Nanocrystal Suspensions Using High-Permittivity Solvents. Langmuir 2016, 32, 9854–9862. [Google Scholar] [CrossRef] [PubMed]
- Nicolosi, V.; Chhowalla, M.; Kanatzidis, M.G.; Strano, M.S.; Coleman, J.N. Liquid Exfoliation of Layered Materials. Science 2013, 340, 1226419. [Google Scholar] [CrossRef]
- O’Konski, C.T.; Zimm, B.H. New method for studying electrical orientation and relaxation effects in aqueous colloids-preliminary results with tobacco mosaic virus. Science 1950, 111, 113–116. [Google Scholar] [CrossRef] [PubMed]
- O’Konski, C.T.; Haltner, A.J. Characterization of the monomer and dimer of tobacco mosaic virus by transient electric birefringence. J. Am. Chem. Soc. 1956, 78, 3604–3610. [Google Scholar] [CrossRef]
- Dozov, I.; Paineau, E.; Davidson, P.; Antonova, K.; Baravian, C.; Bihannic, I.; Michot, L.J. Electric-Field-Induced Perfect Anti-Nematic Order in Isotropic Aqueous Suspensions of a Natural Beidellite Clay. J. Phys. Chem. B 2011, 115, 7751–7765. [Google Scholar] [CrossRef] [PubMed]
- Paineau, E.; Antonova, K.; Baravian, C.; Bihannic, I.; Davidson, P.; Dozov, I.; Imperor-Clerc, M.; Levitz, P.; Madsen, A.; Meneau, F.; et al. Liquid-Crystalline Nematic Phase in Aqueous Suspensions of a Disk-Shaped Natural Beidellite Clay. J. Phys. Chem. B 2009, 113, 15858–15869. [Google Scholar] [CrossRef] [PubMed]
- Antonova, K.; Dozov, I.; Davidson, P.; Paineau, E.; Baravian, C.; Bihannic, I.; Michot, L. Electric-Field Effects in Aqueous Suspensions of Beidellite Clay Detected by Electro-Optical and SAXS Experiments. Bulg. J. Phys. 2012, 39, 72–91. [Google Scholar]



| Solvents | Abb. | n | εr | Tm (°C) | Tb (°C) | Viscosity (mPa·s) | Surface Tension (dynes/cm) |
|---|---|---|---|---|---|---|---|
| Dimethylsulfoxide | DMSO | 1.479 | 48 | 19 | 189 | 2.0 | 42.9 |
| N-methyl-2-pyrrolidone | NMP | 1.470 | 32 | −24 | 204 | 1.67 | 44.6 |
| Dimethylformamide | DMF | 1.430 | 37 | −60 | 152 | 0.79 | 34.4 |
| Propylene Carbonate | PC | 1.421 | 64 | −49 | 242 | 2.50 | 40.9 |
| Acetonitrile | AN | 1.344 | 37.5 | −44 | 82 | 0.37 | 28.7 |
| Solvent | φ (%) | ∆nsat | ∆nsp | Esat (V/mm) | CK (m2/V2) | fc (kHz) | τon (ms) | τoff (ms) |
|---|---|---|---|---|---|---|---|---|
| H2O | 3.2 | 0.031 | 0.97 | 88 | 4.0 × 10−12 | 140 | 13.6 | 13.1 |
| D2O | 5.5 | 0.032 | 0.58 | 60 | 7.3 × 10−12 | 260 | 130 | 130 |
| DMSO | 2.7 | 0.023 | 0.99 | 118 | 1.2 × 10−12 | 20 | 26 | 27 |
| NMP | 4.8 | 0.0154 | 0.32 | 186 | 3.1 × 10−13 | 20 | 102 | 101 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coursault, D.; Dozov, I.; Blanc, C.; Nobili, M.; Dupont, L.; Chanéac, C.; Davidson, P. Dispersions of Goethite Nanorods in Aprotic Polar Solvents. Materials 2017, 10, 1191. https://doi.org/10.3390/ma10101191
Coursault D, Dozov I, Blanc C, Nobili M, Dupont L, Chanéac C, Davidson P. Dispersions of Goethite Nanorods in Aprotic Polar Solvents. Materials. 2017; 10(10):1191. https://doi.org/10.3390/ma10101191
Chicago/Turabian StyleCoursault, Delphine, Ivan Dozov, Christophe Blanc, Maurizio Nobili, Laurent Dupont, Corinne Chanéac, and Patrick Davidson. 2017. "Dispersions of Goethite Nanorods in Aprotic Polar Solvents" Materials 10, no. 10: 1191. https://doi.org/10.3390/ma10101191
APA StyleCoursault, D., Dozov, I., Blanc, C., Nobili, M., Dupont, L., Chanéac, C., & Davidson, P. (2017). Dispersions of Goethite Nanorods in Aprotic Polar Solvents. Materials, 10(10), 1191. https://doi.org/10.3390/ma10101191






