Cellulose Nanocrystals (CNCs) from Corn Stalk: Activation Energy Analysis
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Preparation of CNCs
3. Characterization
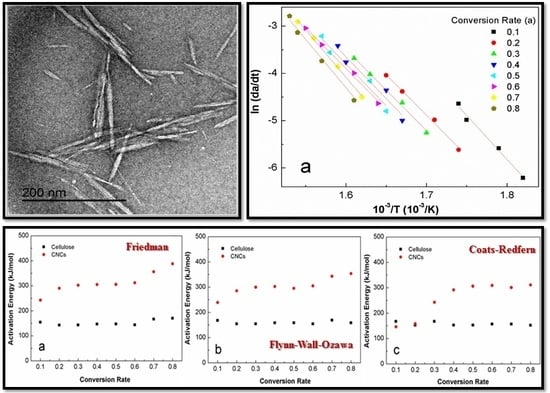
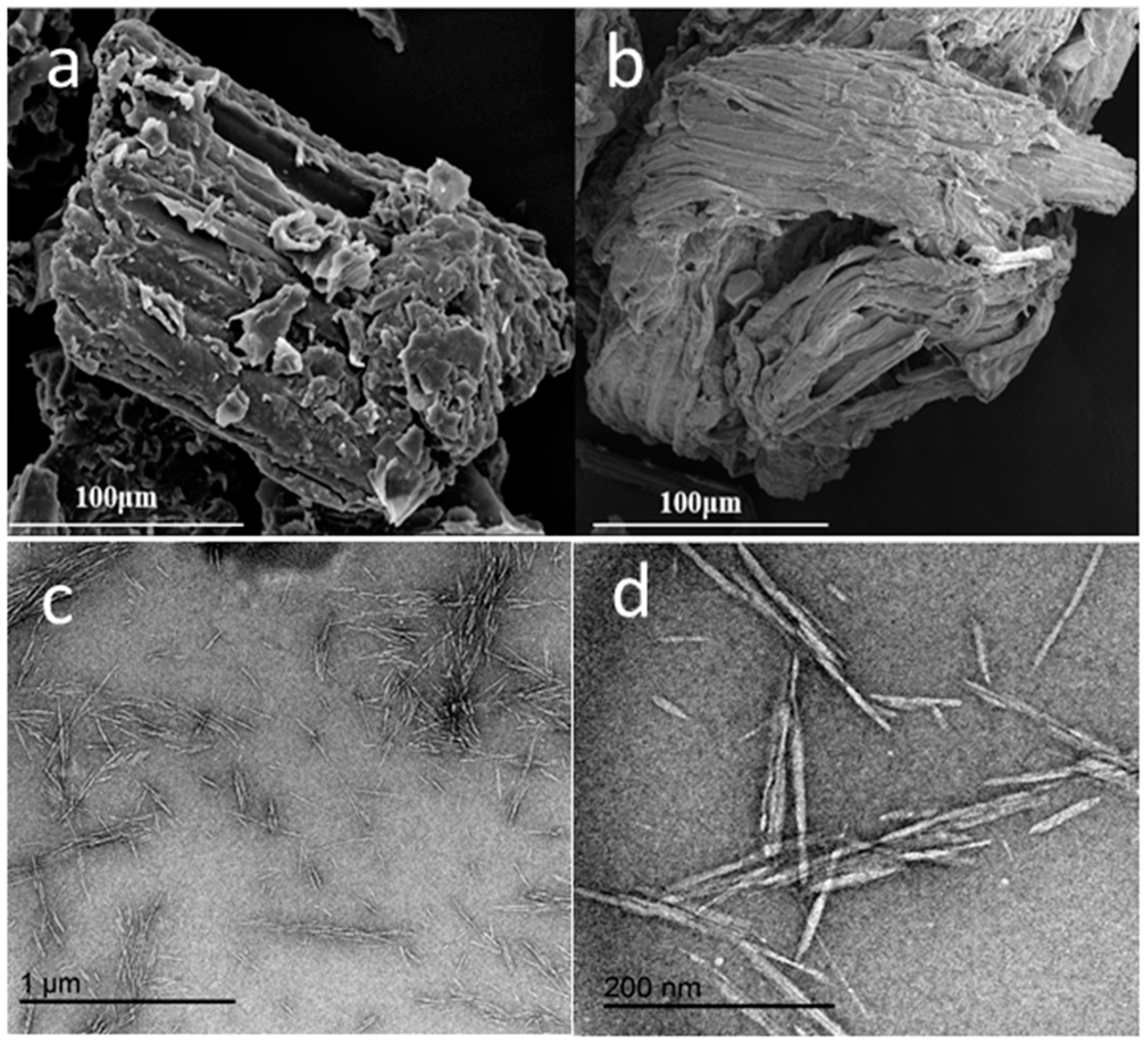
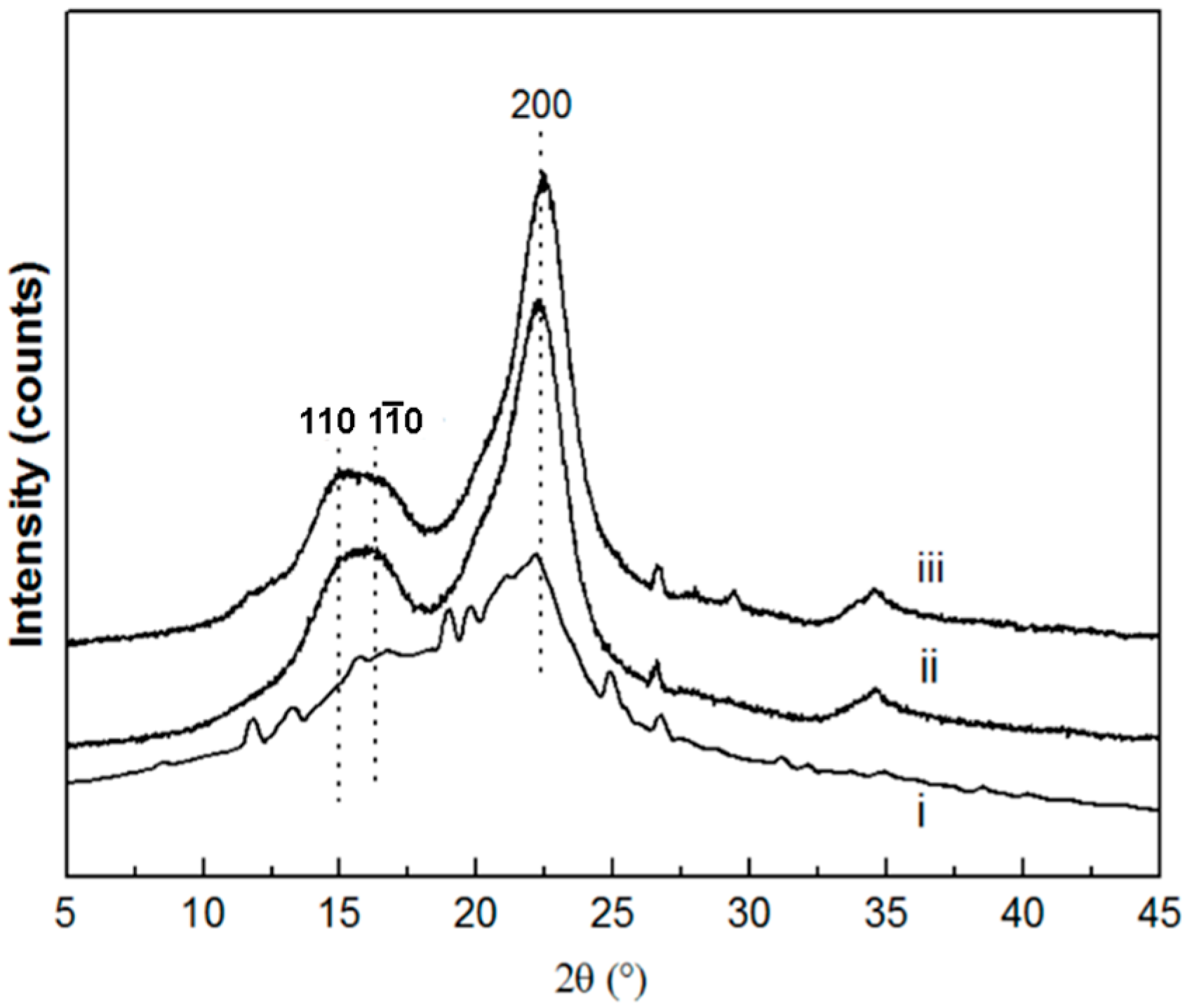
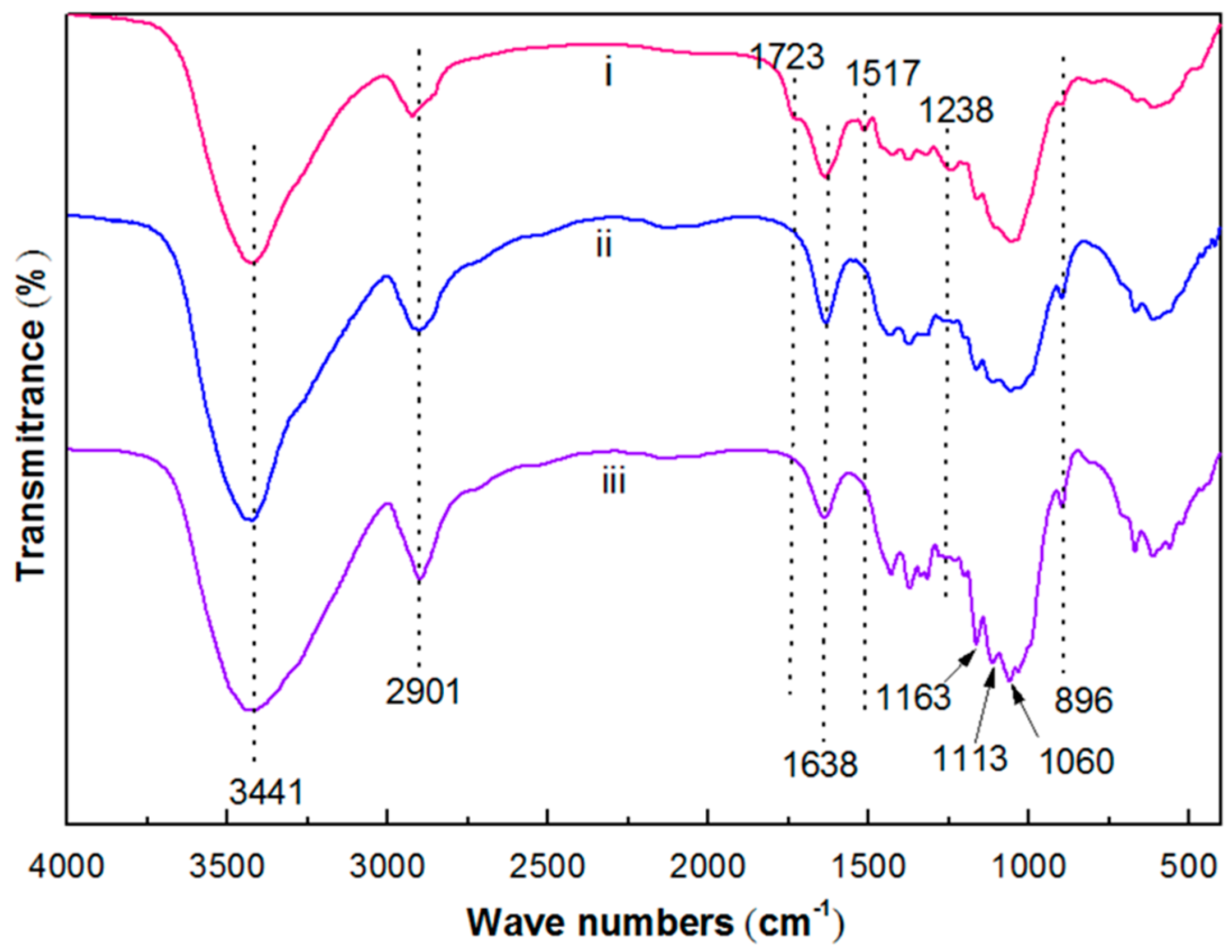
3.1. Basic Morphology and Crystalline Structure
3.2. Thermal Characterization
3.3. Activation Energy Modeling
4. Results and Discussion
4.1. Morphology and Crystalline Structure
4.2. Thermal Properties
4.3. Apparent Activation Energy
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fortunati, E.; Luzi, F.; Puglia, D.; Dominici, F.; Santulli, C.; Kenny, J.M.; Torre, L. Investigation of thermo-mechanical, chemical and degradative properties of PLA-limonene films reinforced with cellulose nanocrystals extracted from Phormium tenax leaves. Eur. Polym. J. 2014, 56, 77–91. [Google Scholar] [CrossRef]
- Cho, M.-J.; Park, B.-D. Tensile and thermal properties of nanocellulose-reinforced poly(vinyl alcohol) nanocomposites. J. Ind. Eng. Chem. 2011, 17, 36–40. [Google Scholar] [CrossRef]
- Ljungberg, N.; Cavaillé, J.Y.; Heux, L. Nanocomposites of isotactic polypropylene reinforced with rod-like cellulose whiskers. Polymer 2006, 47, 6285–6292. [Google Scholar] [CrossRef]
- Wang, D.; Yu, J.; Zhang, J.; He, J.; Zhang, J. Transparent bionanocomposites with improved properties from poly(propylene carbonate) (PPC) and cellulose nanowhiskers (CNWs). Compos. Sci. Technol. 2013, 85, 83–89. [Google Scholar] [CrossRef]
- Goffin, A.L.; Raquez, J.M.; Duquesne, E.; Siqueira, G.; Habibi, Y.; Dufresne, A.; Dubois, P. Poly(ε-caprolactone) based nanocomposites reinforced by surface-grafted cellulose nanowhiskers via extrusion processing: Morphology, rheology, and thermo-mechanical properties. Polymer 2011, 52, 1532–1538. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, X.; Pei, C. Effect of sisal fiber surface treatment on properties of sisal fiber reinforced polylactide composites. Int. J. Polym. Sci. 2011, 2011, 803428. [Google Scholar] [CrossRef]
- Abou-Zeid, R.E.; Hassan, E.A.; Bettaieb, F.; Khiari, R.; Hassan, M.L. Use of cellulose and oxidized cellulose nanocrystals from olive stones in chitosan bionanocomposites. J. Nanomater. 2015, 2015, 687490. [Google Scholar] [CrossRef]
- Abraham, E.; Elbi, P.A.; Deepa, B.; Jyotishkumar, P.; Pothen, L.A.; Narine, S.S.; Thomas, S. X-ray diffraction and biodegradation analysis of green composites of natural rubber/nanocellulose. Polym. Degrad. Stab. 2012, 97, 2378–2387. [Google Scholar] [CrossRef]
- Khan, A.; Khan, R.A.; Salmieri, S.; Le Tien, C.; Riedl, B.; Bouchard, J.; Chauve, G.; Tan, V.; Kamal, M.R.; Lacroix, M. Mechanical and barrier properties of nanocrystalline cellulose reinforced chitosan based nanocomposite films. Carbohydr. Polym. 2012, 90, 1601–1608. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Lawton, D.; Thompson, M.R.; Liu, Q. Biocomposites reinforced with cellulose nanocrystals derived from potato peel waste. Carbohydr. Polym. 2012, 90, 709–716. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Dan, Y.; Peng, J.; Turng, L.-S.; Sabo, R.; Clemons, C. Thermal and mechanical properties of natural rubber composites reinforced with cellulose nanocrystals from southern pine. Adv. Polym. Tech. 2014, 33. [Google Scholar] [CrossRef]
- Henrique, M.A.; Flauzino Neto, W.P.; Silvério, H.A.; Martins, D.F.; Gurgel, L.V.A.; Barud, H.D.S.; Morais, L.C.D.; Pasquini, D. Kinetic study of the thermal decomposition of cellulose nanocrystals with different polymorphs, cellulose I and II, extracted from different sources and using different types of acids. Ind. Crops Prod. 2015, 76, 128–140. [Google Scholar] [CrossRef]
- Deepa, B.; Abraham, E.; Cherian, B.M.; Bismarck, A.; Blaker, J.J.; Pothan, L.A.; Leao, A.L.; de Souza, S.F.; Kottaisamy, M. Structure, morphology and thermal characteristics of banana nano fibers obtained by steam explosion. Bioresour. Technol. 2011, 102, 1988–1997. [Google Scholar] [CrossRef] [PubMed]
- Roman, M.; Winter, W.T. Effect of sulfate groups from sulfuric acid hydrolysis on the thermal degradation behavior of bacterial cellulose. Biomacromolecules 2004, 5, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Shi, Q.; Guo, W.; Terrell, L.; Qureshi, A.T.; Hayes, D.J.; Wu, Q. Electrospun bio-nanocomposite scaffolds for bone tissue engineering by cellulose nanocrystals reinforcing maleic anhydride grafted PLA. ACS Appl. Mater. Interfaces 2013, 5, 3847–3854. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Wu, Q.; Lei, Y.; Guo, W.; Xu, Y. Thermal decomposition kinetics of natural fibers: Activation energy with dynamic thermogravimetric analysis. Polym. Degrad. Stab. 2008, 93, 90–98. [Google Scholar] [CrossRef]
- Bui, H.H.; Tran, K.Q.; Chen, W.H. Pyrolysis of microalgae residues—A kinetic study. Bioresour. Technol. 2016, 199, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Hu, M.; Zhu, X.; Guo, D.; Liu, S.; Hu, Z.; Xiao, B.; Wang, J.; Laghari, M. Characteristics and kinetic study on pyrolysis of five lignocellulosic biomass via thermogravimetric analysis. Bioresour. Technol. 2015, 192, 441–450. [Google Scholar] [CrossRef] [PubMed]
- Bach, Q.-V.; Tran, K.-Q.; Skreiberg, Ø.; Trinh, T.T. Effects of wet torrefaction on pyrolysis of woody biomass fuels. Energy 2015, 88, 443–456. [Google Scholar] [CrossRef]
- Miranda, M.I.G.; Bica, C.I.D.; Nachtigall, S.M.B.; Rehman, N.; Rosa, S.M.L. Kinetical thermal degradation study of maize straw and soybean hull celluloses by simultaneous DSC–TGA and MDSC techniques. Thermochim. Acta 2013, 565, 65–71. [Google Scholar] [CrossRef]
- Tonoli, G.H.; Teixeira, E.M.; Correa, A.C.; Marconcini, J.M.; Caixeta, L.A.; Pereira-da-Silva, M.A.; Mattoso, L.H. Cellulose micro/nanofibres from Eucalyptus kraft pulp: Preparation and properties. Carbohydr. Polym. 2012, 89, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Bettaieb, F.; Khiari, R.; Dufresne, A.; Mhenni, M.F.; Putaux, J.L.; Boufi, S. Nanofibrillar cellulose from Posidonia oceanica: Properties and morphological features. Ind. Crops Prod. 2015, 72, 97–106. [Google Scholar] [CrossRef]
- Chen, W.; Abe, K.; Uetani, K.; Yu, H.; Liu, Y.; Yano, H. Individual cotton cellulose nanofibers: Pretreatment and fibrillation technique. Cellulose 2014, 21, 1517–1528. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Q.; Zhou, D.; Huang, R. Thermal decomposition properties of materials from different parts of corn stalk. BioResources 2015, 10, 2020–2031. [Google Scholar] [CrossRef]
- Kim, S.S.; Agblevor, F.A. Pyrolysis characteristics and kinetics of chicken litter. Waste Manag. 2007, 27, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Granada, E.; Míguez, J.L.; Febrero, L.; Collazo, J.; Eguía, P. Development of an experimental technique for oil recovery during biomass pyrolysis. Renew. Energy 2013, 60, 179–184. [Google Scholar] [CrossRef]
- Li, G.; Chen, H. Synergistic mechanism of steam explosion combined with fungal treatment by Phellinus baumii for the pretreatment of corn stalk. Biomass Bioenergy 2014, 67, 1–7. [Google Scholar] [CrossRef]
- Kim, U.-J.; Eom, S.H.; Wada, M. Thermal decomposition of native cellulose: Influence on crystallite size. Polym. Degrad. Stab. 2010, 95, 778–781. [Google Scholar] [CrossRef]
- Segal, L.; Creely, J.; Martin, A.; Conrad, C. An empirical method for estimating the degree of crystallinity of native cellulose using the X-ray diffractometer. Text. Res. J. 1959, 29, 786–794. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Mishra, G.; Bhaskar, T. Non isothermal model free kinetics for pyrolysis of rice straw. Bioresour. Technol. 2014, 169, 614–621. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Gao, R.; Lu, Y.; Li, J.; Sun, Q. Fabrication and characterization of nanofibrillated cellulose and its aerogels from natural pine needles. Carbohydr. Polym. 2015, 119, 202–209. [Google Scholar] [CrossRef] [PubMed]
- Mohamad Haafiz, M.K.; Eichhorn, S.J.; Hassan, A.; Jawaid, M. Isolation and characterization of microcrystalline cellulose from oil palm biomass residue. Carbohydr. Polym. 2013, 93, 628–634. [Google Scholar] [CrossRef] [PubMed]
- Azeredo, H.M.; Mattoso, L.H.; Wood, D.; Williams, T.G.; Avena-Bustillos, R.J.; McHugh, T.H. Nanocomposite edible films from mango puree reinforced with cellulose nanofibers. J. Food Sci. 2009, 74, N31–N35. [Google Scholar] [CrossRef] [PubMed]
- Besbes, I.; Alila, S.; Boufi, S. Nanofibrillated cellulose from TEMPO-oxidized eucalyptus fibres: Effect of the carboxyl content. Carbohydr. Polym. 2011, 84, 975–983. [Google Scholar] [CrossRef]
- Alemdar, A.; Sain, M. Isolation and characterization of nanofibers from agricultural residues: Wheat straw and soy hulls. Bioresour. Technol. 2008, 99, 1664–1671. [Google Scholar] [CrossRef] [PubMed]
- Pereira, A.L.; do Nascimento, D.M.; Souza Filho Mde, S.; Morais, J.P.; Vasconcelos, N.F.; Feitosa, J.P.; Brigida, A.I.; Rosa Mde, F. Improvement of polyvinyl alcohol properties by adding nanocrystalline cellulose isolated from banana pseudostems. Carbohydr. Polym. 2014, 112, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Sain, M.; Panthapulakkal, S. Bioprocess preparation of wheat straw fibers and their characterization. Ind. Crops Prod. 2006, 23, 1–8. [Google Scholar] [CrossRef]
- Kalita, E.; Nath, B.K.; Agan, F.; More, V.; Deb, P. Isolation and characterization of crystalline, autofluorescent, cellulose nanocrystals from saw dust wastes. Ind. Crops Prod. 2015, 65, 550–555. [Google Scholar] [CrossRef]
- Jiang, F.; Hsieh, Y.L. Chemically and mechanically isolated nanocellulose and their self-assembled structures. Carbohydr. Polym. 2013, 95, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Reddy, J.P.; Rhim, J.W. Characterization of bionanocomposite films prepared with agar and paper-mulberry pulp nanocellulose. Carbohydr. Polym. 2014, 110, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Fahma, F.; Iwamoto, S.; Hori, N.; Iwata, T.; Takemura, A. Isolation, preparation, and characterization of nanofibers from oil palm empty-fruit-bunch (OPEFB). Cellulose 2010, 17, 977–985. [Google Scholar] [CrossRef]
- Xiao, B.; Sun, X.; Sun, R. Chemical, structural, and thermal characterizations of alkali-soluble lignins and hemicelluloses, and cellulose from maize stems, rye straw, and rice straw. Polym. Degrad. Stab. 2001, 74, 307–319. [Google Scholar] [CrossRef]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lv, G.; Wu, S.; Yang, G.; Chen, J.; Liu, Y.; Kong, F. Comparative study of pyrolysis behaviors of corn stalk and its three components. J. Anal. Appl. Pyrolysis 2013, 104, 185–193. [Google Scholar] [CrossRef]
- Mondragon, G.; Fernandes, S.; Retegi, A.; Peña, C.; Algar, I.; Eceiza, A.; Arbelaiz, A. A common strategy to extracting cellulose nanoentities from different plants. Ind. Crops Prod. 2014, 55, 140–148. [Google Scholar] [CrossRef]
- Kargarzadeh, H.; Ahmad, I.; Abdullah, I.; Dufresne, A.; Zainudin, S.Y.; Sheltami, R.M. Effects of hydrolysis conditions on the morphology, crystallinity, and thermal stability of cellulose nanocrystals extracted from kenaf bast fibers. Cellulose 2012, 19, 855–866. [Google Scholar] [CrossRef]
- Lu, H.; Gui, Y.; Zheng, L.; Liu, X. Morphological, crystalline, thermal and physicochemical properties of cellulose nanocrystals obtained from sweet potato residue. Food Res. Int. 2013, 50, 121–128. [Google Scholar] [CrossRef]
- Rosa, M.F.; Medeiros, E.S.; Malmonge, J.A.; Gregorski, K.S.; Wood, D.F.; Mattoso, L.H.C.; Glenn, G.; Orts, W.J.; Imam, S.H. Cellulose nanowhiskers from coconut husk fibers: Effect of preparation conditions on their thermal and morphological behavior. Carbohydr. Polym. 2010, 81, 83–92. [Google Scholar] [CrossRef]
- Morgado, D.L.; Frollini, E. Thermal decomposition of mercerized linter cellulose and its acetates obtained from a homogeneous reaction. Polímeros 2011, 21, 111–117. [Google Scholar] [CrossRef]
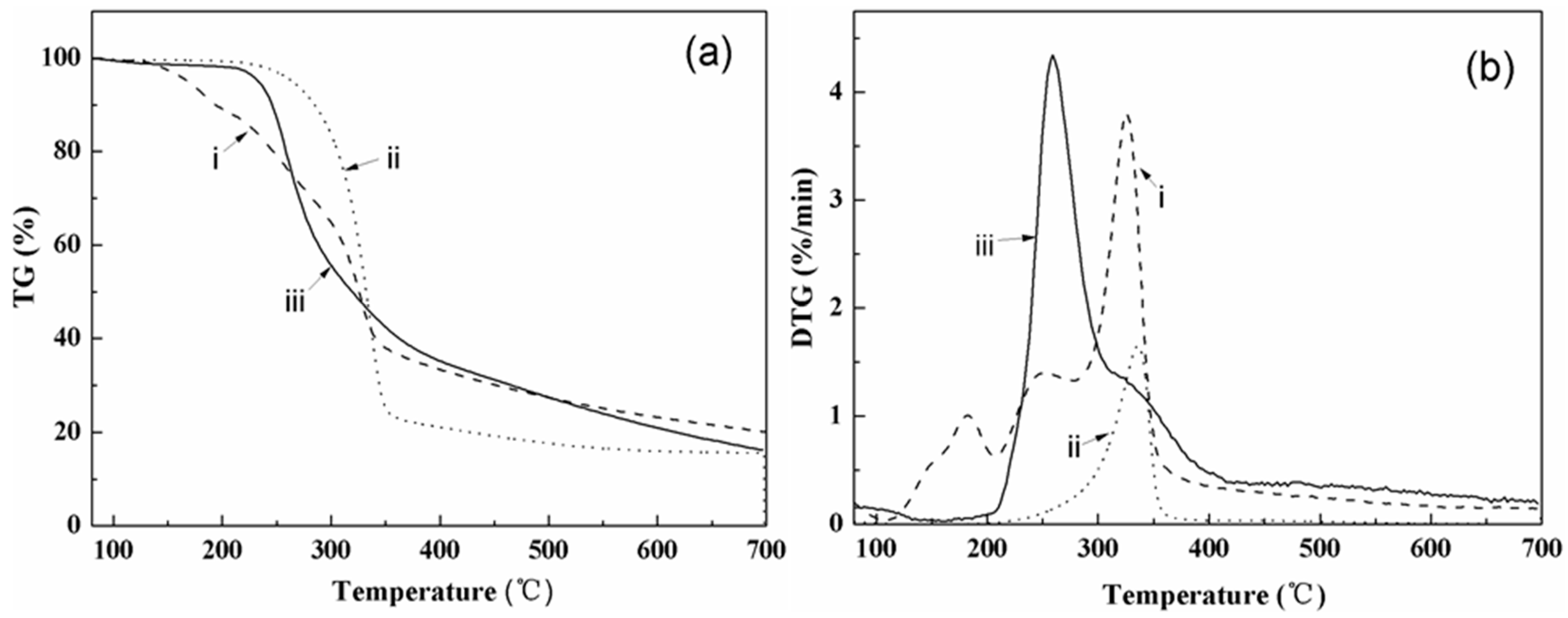
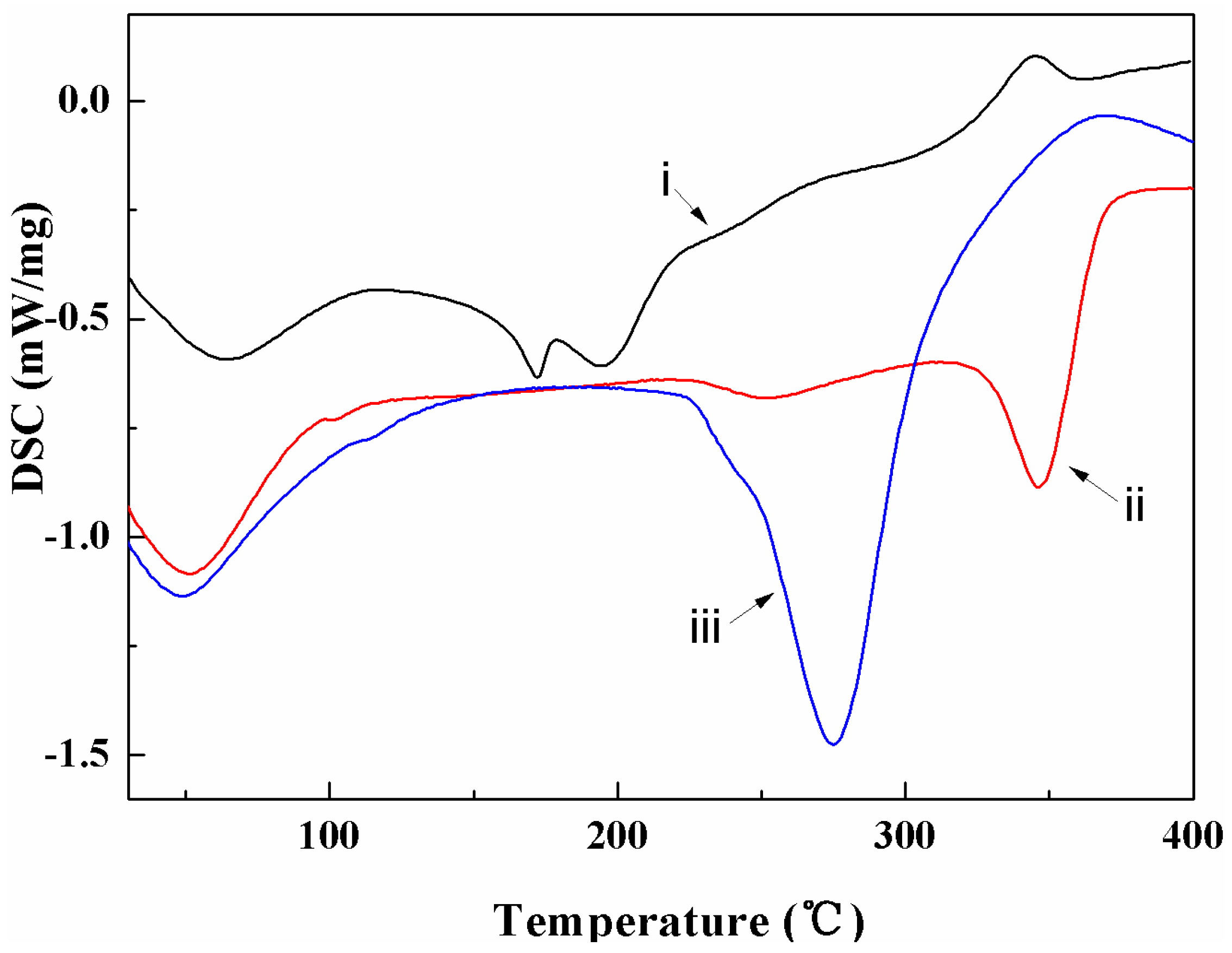
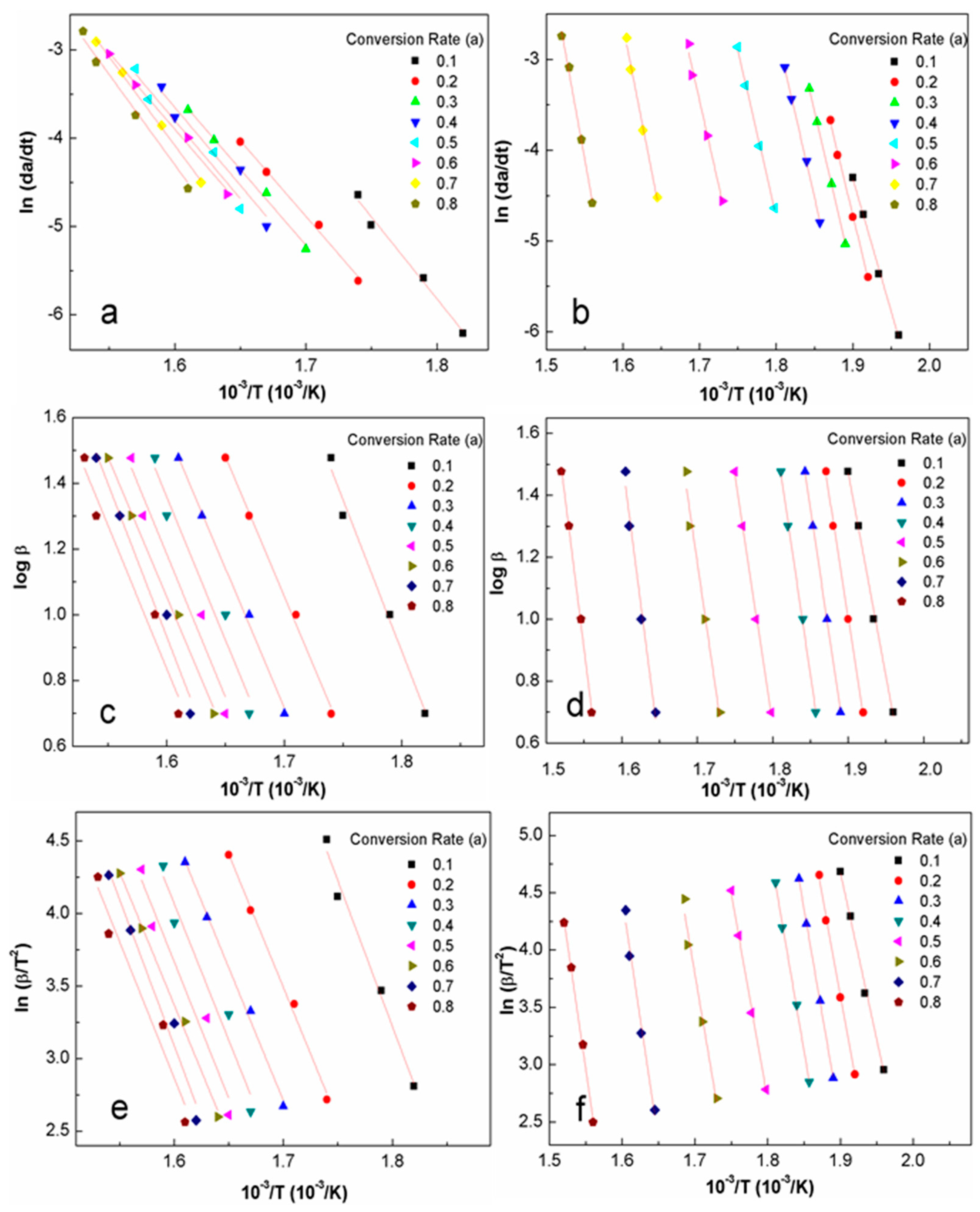

| Heating Rate (°C/min) | Sample | To (°C) | Wo (%) | Tp (°C) | Wp (%) | Ts (°C) | Ws (%) | Residue (%) | (Ws-Wo) (%) | (Ts-To) (°C) |
|---|---|---|---|---|---|---|---|---|---|---|
| i | 169.24 | 7.58 | 326.20 | 51.71 | 339.19 | 59.04 | 19.53 | 51.46 | 169.95 | |
| 5 | ii | 305.55 | 37.98 | 321.31 | 52.38 | 332.56 | 63.20 | 22.14 | 25.22 | 27.01 |
| iii | 241.38 | 10.09 | 258.92 | 20.86 | 279.10 | 30.43 | 16.12 | 20.34 | 37.72 | |
| i | 175.91 | 5.00 | 332.20 | 45.34 | 353.45 | 54.45 | 30.98 | 49.45 | 177.54 | |
| 10 | ii | 314.24 | 37.13 | 330.57 | 53.17 | 341.25 | 64.21 | 21.41 | 27.08 | 27.01 |
| iii | 248.47 | 9.17 | 269.16 | 24.30 | 286.79 | 34.36 | 20.67 | 25.19 | 38.32 | |
| i | 177.00 | 5.77 | 344.84 | 51.13 | 365.71 | 63.40 | 17.90 | 57.63 | 188.71 | |
| 20 | ii | 320.42 | 32.43 | 340.19 | 50.80 | 350.55 | 62.40 | 22.55 | 29.79 | 30.13 |
| iii | 239.63 | 5.07 | 259.49 | 17.18 | 280.24 | 30.95 | 21.96 | 25.88 | 40.61 | |
| i | 177.03 | 7.61 | 345.49 | 47.75 | 368.65 | 65.54 | 23.16 | 57.93 | 191.62 | |
| 30 | ii | 317.94 | 41.34 | 340.27 | 44.01 | 368.52 | 68.43 | 21.88 | 27.09 | 50.58 |
| iii | 230.15 | 5.56 | 259.79 | 19.00 | 291.06 | 36.21 | 21.39 | 30.65 | 60.91 |
| Conversion Rate | Friedman | F-W-O | Coats-Redfern | |||
|---|---|---|---|---|---|---|
| E (KJ/mol) a | R2 | E (KJ/mol) a | R2 | E (KJ/mol) a | R2 | |
| 0.1 | 154.3 (±0.2) | 0.9834 | 167.7 (±0.2) | 0.9829 | 167.0 (±0.2) | 0.9810 |
| 0.2 | 142.5 (±0.2) | 0.9917 | 154.4 (±0.2) | 0.9947 | 152.6 (±0.1) | 0.9939 |
| 0.3 | 142.9 (±0.2) | 0.9915 | 154.4 (±0.2) | 0.9947 | 152.3 (±0.1) | 0.9939 |
| 0.4 | 146.8 (±0.2) | 0.9395 | 158.5 (±0.2) | 0.9458 | 156.5 (±0.2) | 0.9388 |
| 0.5 | 147.1 (±0.2) | 0.9394 | 158.5 (±0.2) | 0.9458 | 156.4 (±0.2) | 0.9387 |
| 0.6 | 143.7 (±0.2) | 0.9913 | 154.4 (±0.2) | 0.9947 | 152.0 (±0.2) | 0.9939 |
| 0.7 | 166.4 (±0.3) | 0.9976 | 169.1 (±0.2) | 0.9702 | 167.3 (±0.2) | 0.9662 |
| 0.8 | 169.9 (±0.3) | 0.9867 | 158.5 (±0.2) | 0.9458 | 156.1 (±0.1) | 0.9385 |
| Mean | 151.7 (±0.2) | 0.9776 | 175.4 (±0.2) | 0.9718 | 157.5 (±0.2) | 0.9681 |
| Conversion Rate | Friedman | F-W-O | Coats-Redfern | |||
|---|---|---|---|---|---|---|
| E (KJ/mol) a | R2 | E (KJ/mol) a | R2 | E (KJ/mol) a | R2 | |
| 0.1 | 242.6 (±0.2) | 0.9959 | 239.0 (±0.2) | 0.9955 | 242.7 (±0.2) | 0.9952 |
| 0.2 | 289.9 (±0.1) | 0.9972 | 285.2 (±0.2) | 0.9971 | 291.2 (±0.2) | 0.9968 |
| 0.3 | 302.2 (±0.3) | 0.9999 | 299.4 (±0.2) | 0.9996 | 305.9 (±0.2) | 0.9995 |
| 0.4 | 304.9 (±0.3) | 0.9984 | 302.3 (±0.1) | 0.9974 | 308.9 (±0.1) | 0.9972 |
| 0.5 | 305.3 (±0.3) | 0.9976 | 295.0 (±0.2) | 0.9984 | 300.8 (±0.2) | 0.9982 |
| 0.6 | 311.7 (±0.3) | 0.9836 | 304.8 (±0.1) | 0.9721 | 310.8 (±0.1) | 0.9704 |
| 0.7 | 356.1 (±0.3) | 0.9899 | 343.0 (±0.1) | 0.9721 | 350.5 (±0.2) | 0.9769 |
| 0.8 | 387.9 (±0.3) | 0.9933 | 353.5 (±0.1) | 0.9782 | 360.9 (±0.1) | 0.9973 |
| Mean | 312.6 (±0.3) | 0.9945 | 302.8 (±0.2) | 0.9888 | 309.0 (±0.2) | 0.9914 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Zhou, L.; Li, M.-C.; Wu, Q.; Zhou, D. Cellulose Nanocrystals (CNCs) from Corn Stalk: Activation Energy Analysis. Materials 2017, 10, 80. https://doi.org/10.3390/ma10010080
Huang S, Zhou L, Li M-C, Wu Q, Zhou D. Cellulose Nanocrystals (CNCs) from Corn Stalk: Activation Energy Analysis. Materials. 2017; 10(1):80. https://doi.org/10.3390/ma10010080
Chicago/Turabian StyleHuang, Siwei, Ling Zhou, Mei-Chun Li, Qinglin Wu, and Dingguo Zhou. 2017. "Cellulose Nanocrystals (CNCs) from Corn Stalk: Activation Energy Analysis" Materials 10, no. 1: 80. https://doi.org/10.3390/ma10010080
APA StyleHuang, S., Zhou, L., Li, M.-C., Wu, Q., & Zhou, D. (2017). Cellulose Nanocrystals (CNCs) from Corn Stalk: Activation Energy Analysis. Materials, 10(1), 80. https://doi.org/10.3390/ma10010080