Ultrasonic Monitoring of the Interaction between Cement Matrix and Alkaline Silicate Solution in Self-Healing Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimens
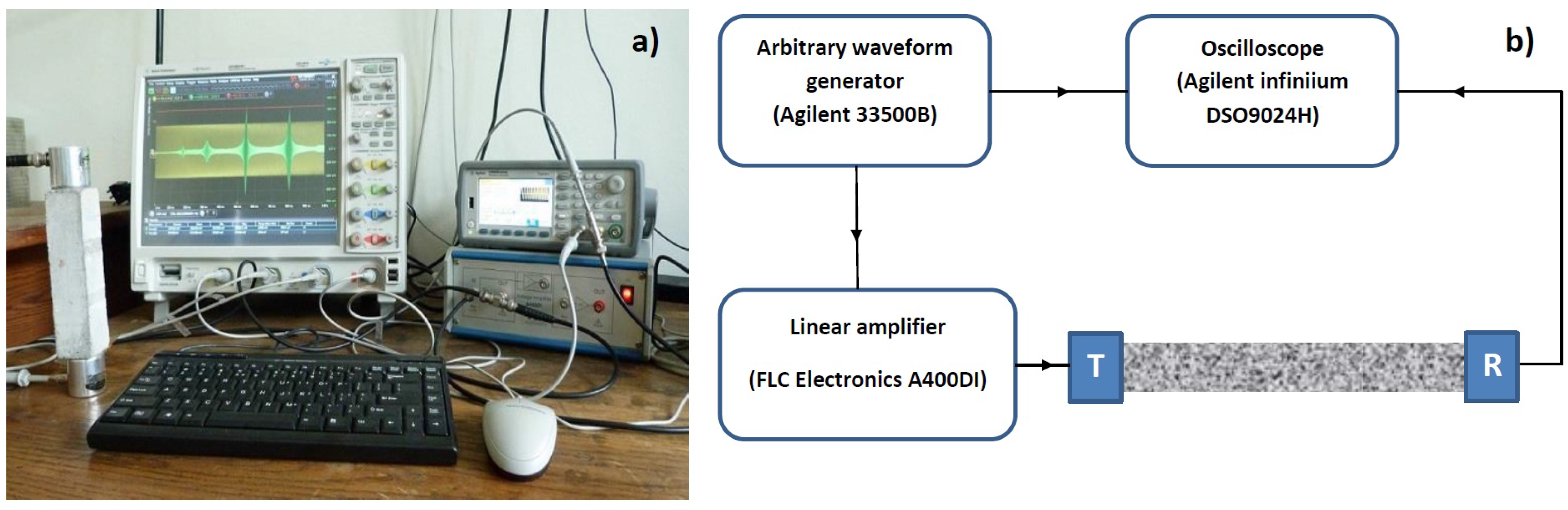
2.2. Ultrasonic Testing Configurations
- in the initial state, referred to as “0” (i.e., when the prisms were still intact, before the creation of the transversal crack at mid-span via the initial three-point-bending test);
- in the damaged state, referred to as “1” (i.e., immediately after the generation of the mechanical disconnection at mid-span and before the application of the healing agent on the fracture surface);
- at regular time intervals denoted as “2” to “n”, during the healing process. The first set of measures during healing was taken a few minutes after the healing process has started, and the monitoring procedure continued up to three weeks; though major changes in the acoustic behavior turned out to be established in the first few days, as will be detailed in the following.
- Resonant modes analysis under frequency sweep excitation;
- Linear and nonlinear analysis (transmission coefficients and harmonics generation) under continuous wave excitation;
- Nonlinear analysis according to the Scaling Subtraction Method (SSM) under pulse excitation.
2.3. Ultrasonic Testing Experimental Setup
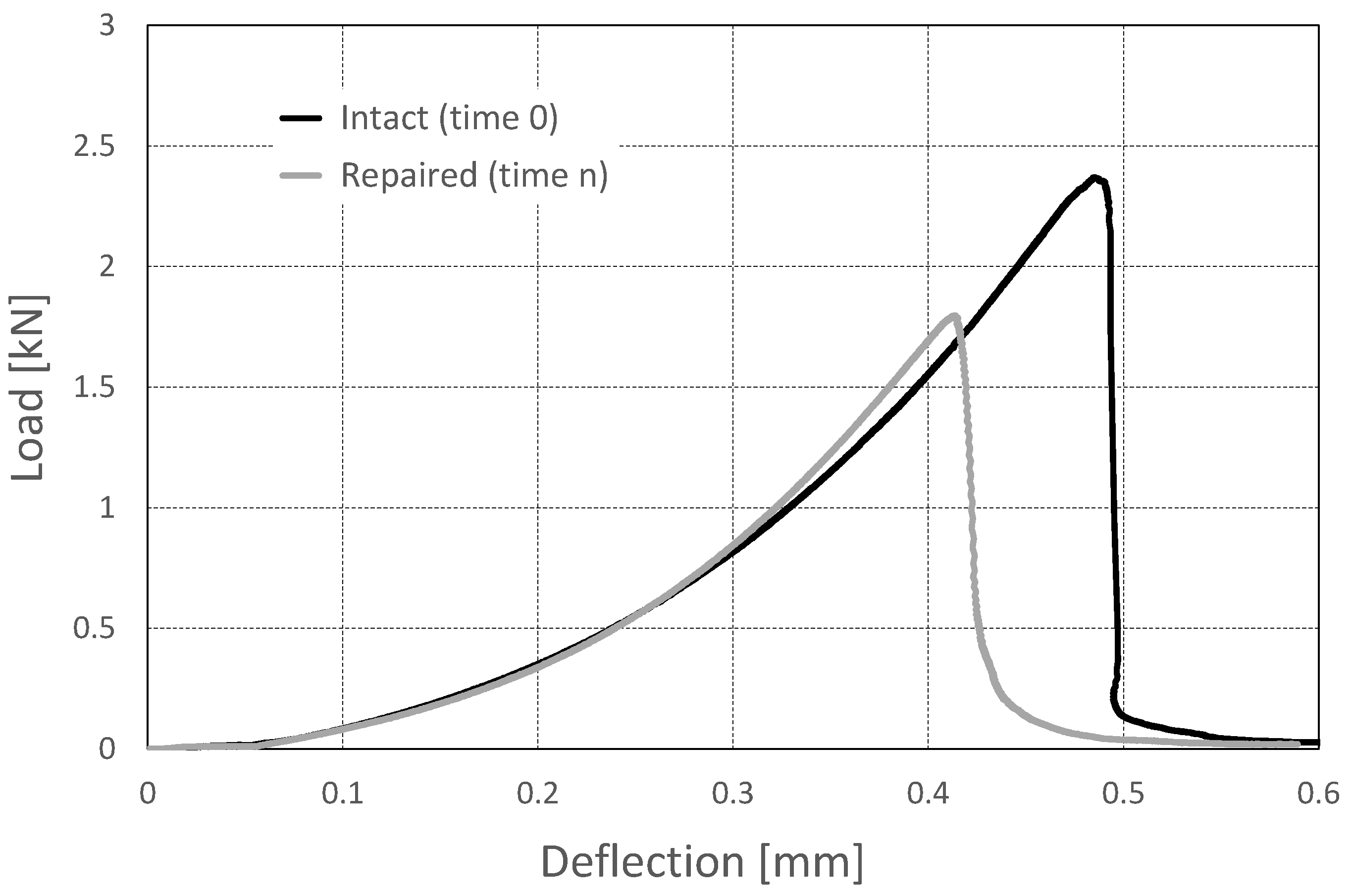
2.4. Mechanical Testing
3. Ultrasonic Tests: Results and Discussion
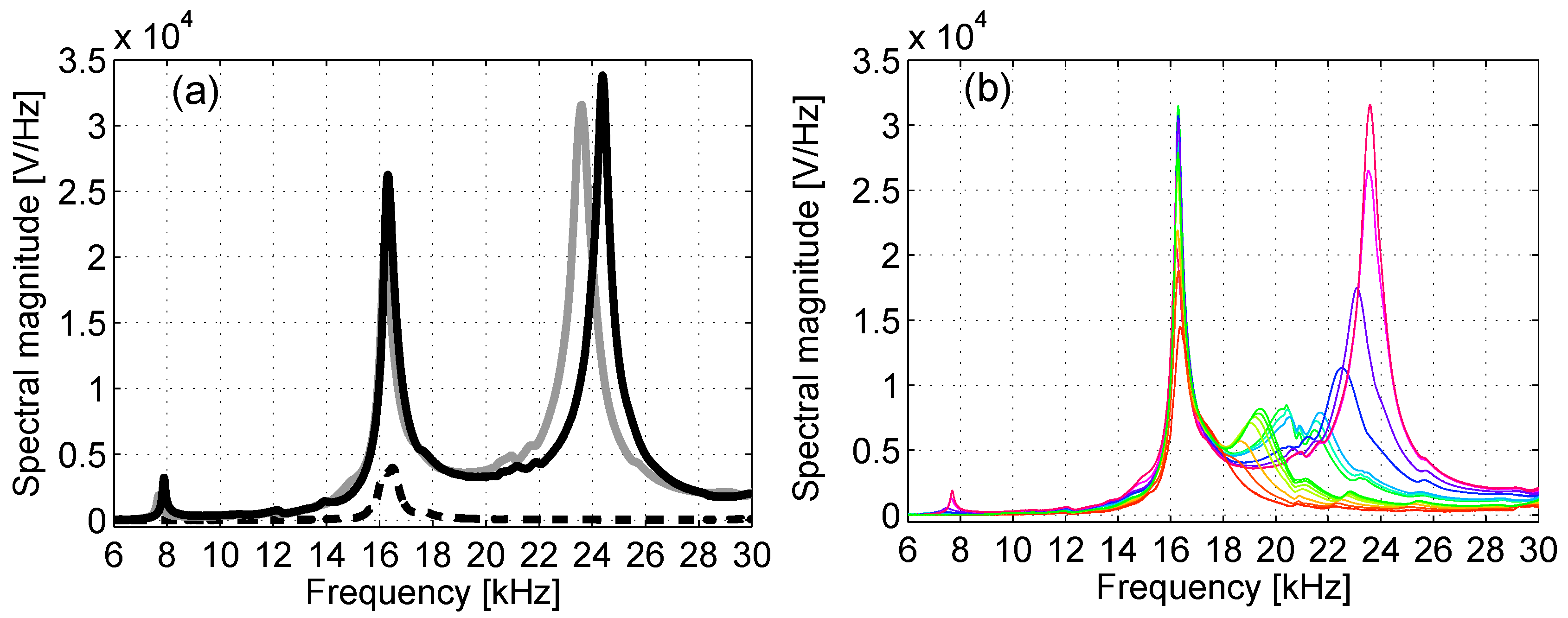
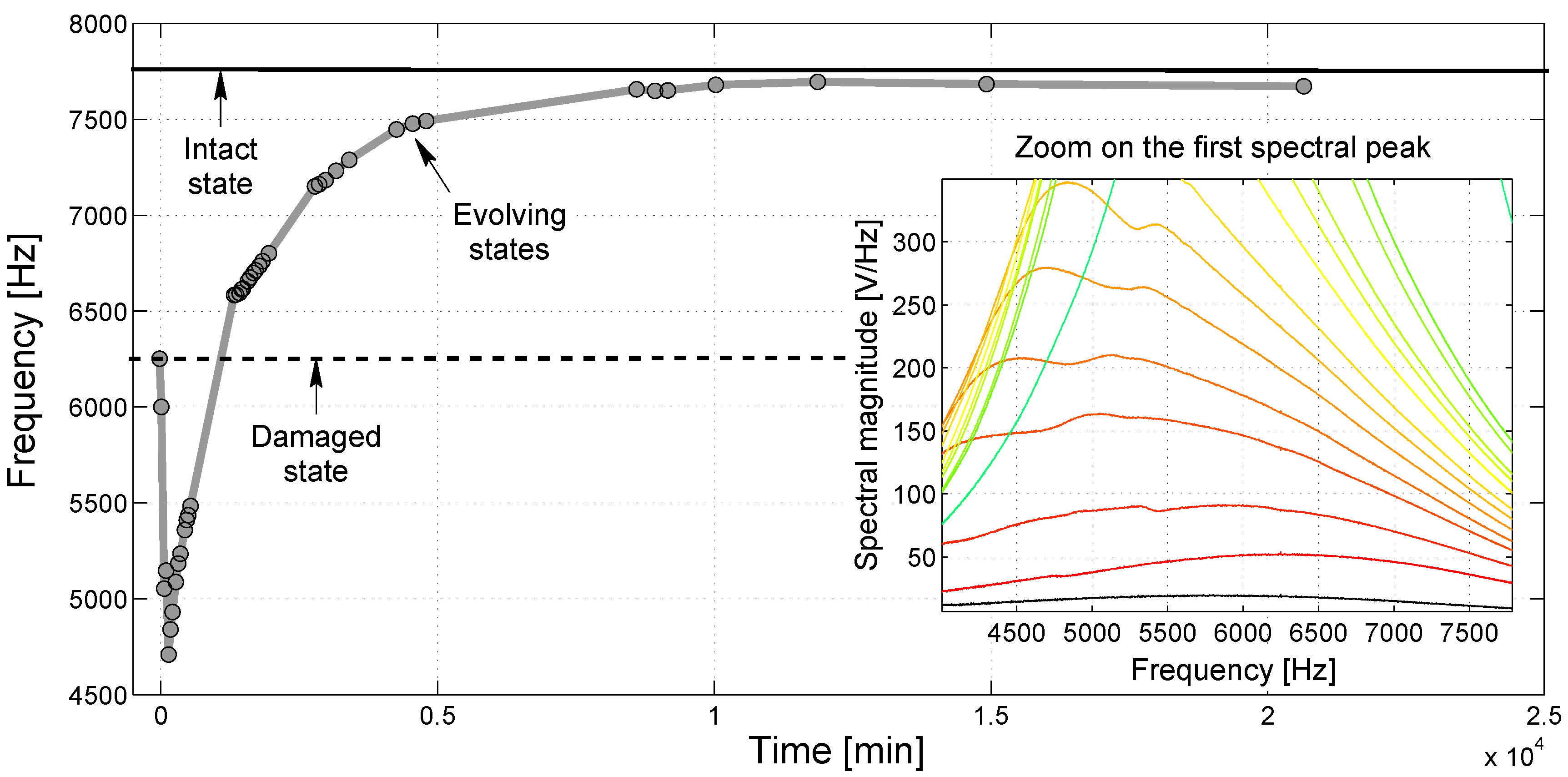
3.1. Resonant Modes Analysis under Frequency Sweep Excitation
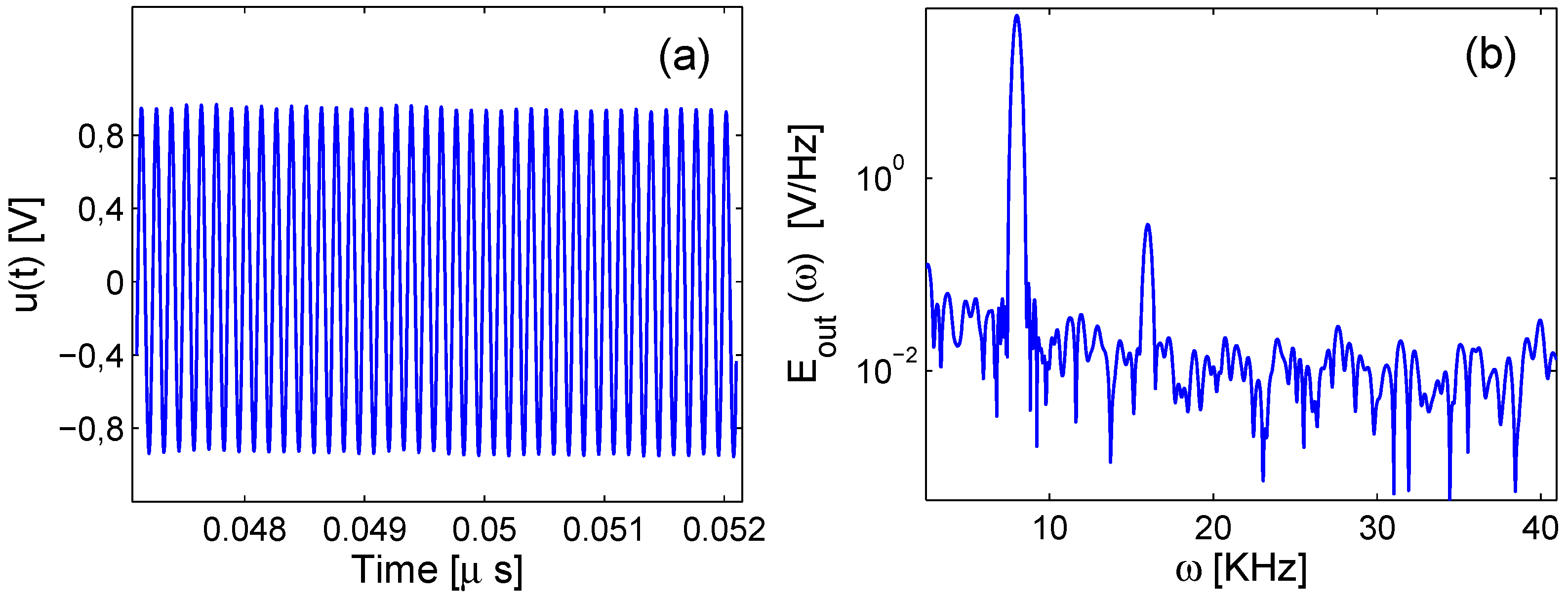
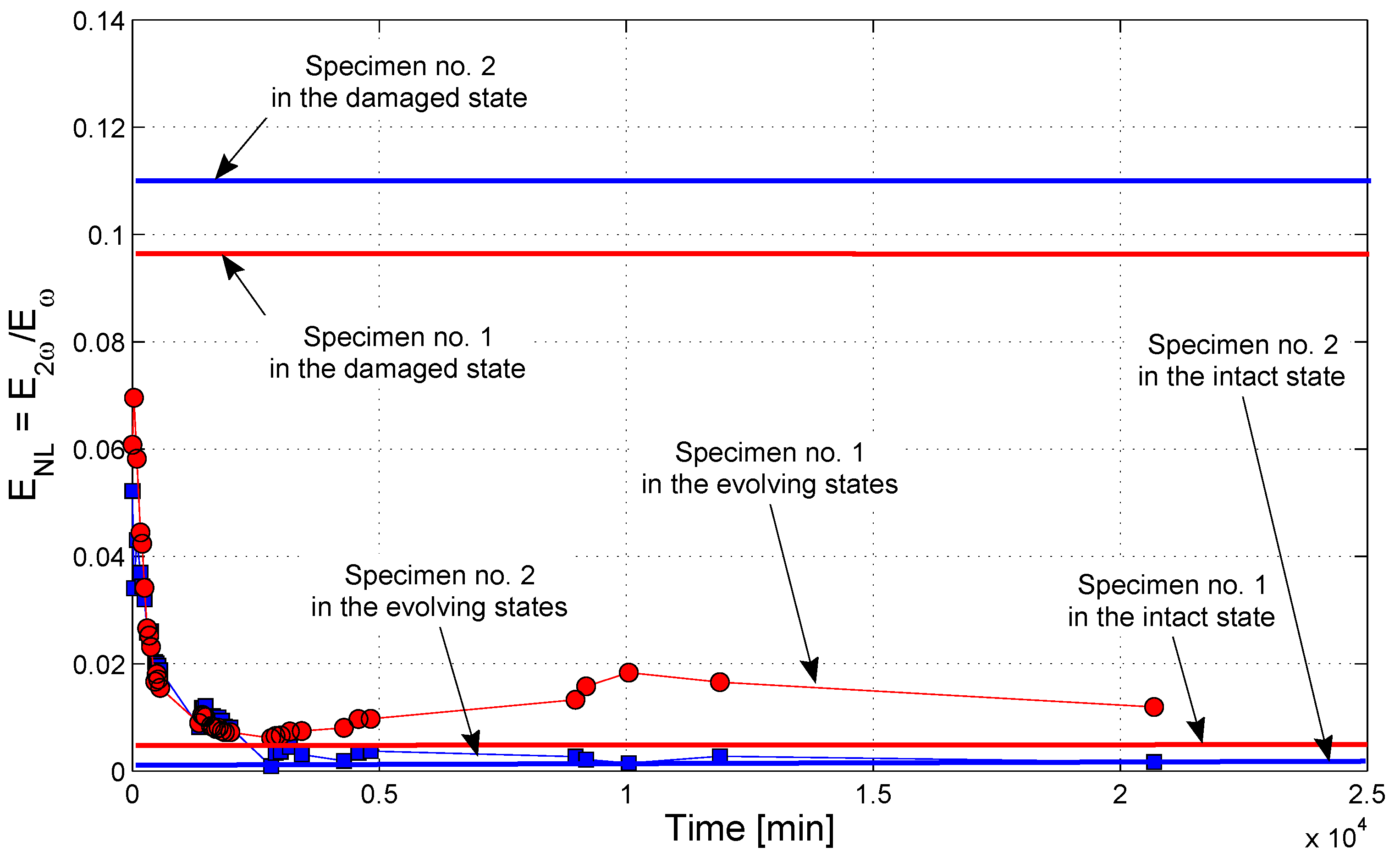
3.2. Linear and Nonlinear Analysis under Continuous Wave Excitation
3.3. Nonlinear Analysis According to the Scaling Subtraction Method under Pulse Excitation
- exciting the specimens using a sequence of pulses at various amplitudes in the range 50 mV–15 V (by means of the same equipment described in Section 2.3). More specifically, a rectangular pulse of width s was used;
- at each time from “2” to “n”, recording the output response of the specimen to such a variable-amplitude excitation (in a time window of 10 ms, with a sampling rate of 10 MSa/s);
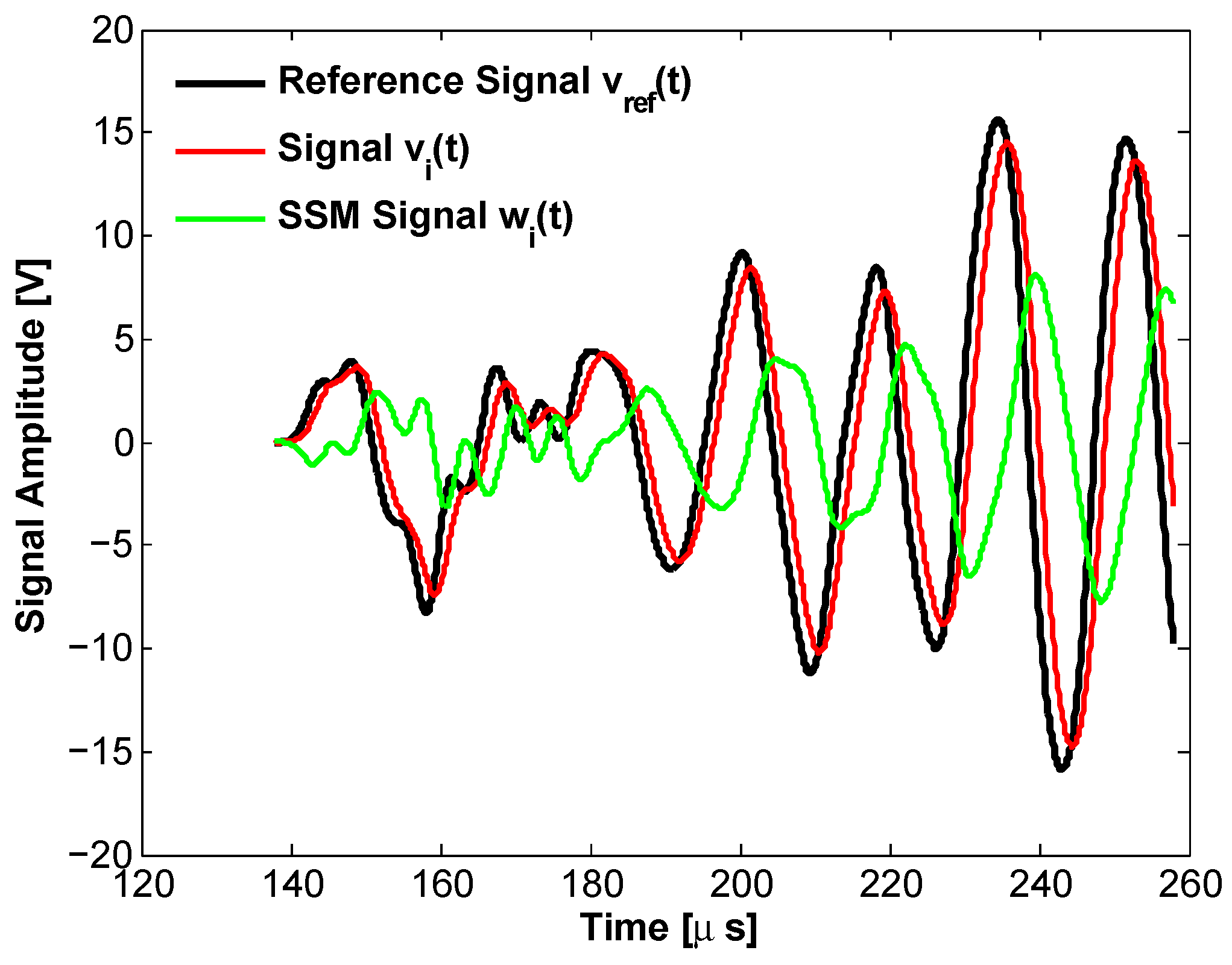
- calculating the so-called “reference signals” at injection amplitude , defined as where is the signal detected at the lowest excitation amplitude ;
- computing the “scaled-subtracted signals” obtained as the difference in time between the actual output signals at the various excitation amplitudes and the reference signals at the same amplitudes: ; examples are reported in Figure 8;
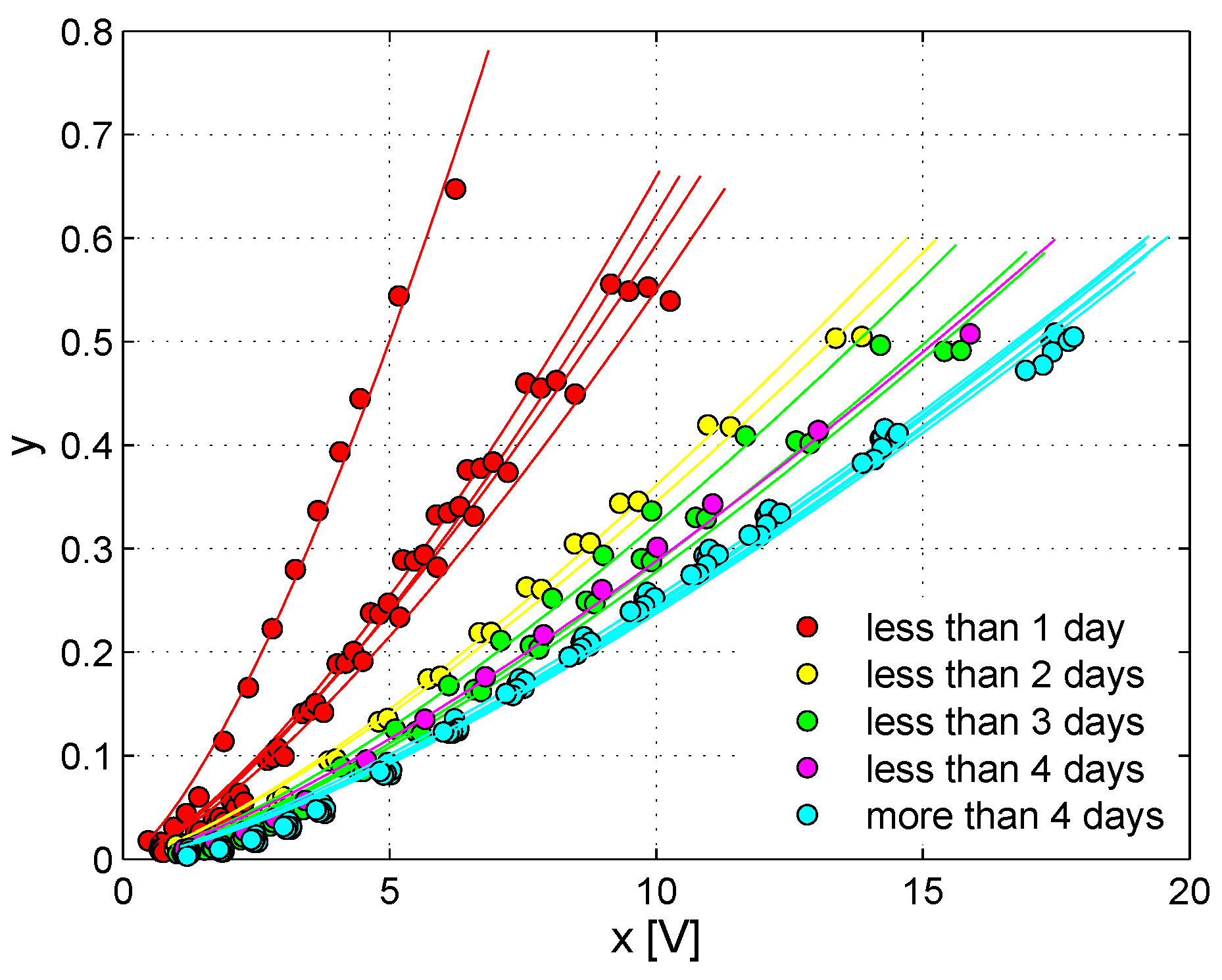
- summarizing the information contained in the whole temporal signals using compact indicators: in this case, in continuity with [33], the root mean square (RMS) of the signals ( and ) over a prescribed time interval including only the first arrivals was used. It represents the average power of the signals over the assigned time interval and was denoted as x (RMS of the output signal ) or η (RMS of the scaled-subtracted signal ), while the ratio was referred to as y;
- analyzing the relation between y and x and its evolution in time, thus providing information on the type and extent of nonlinearity in the system as a function of the progression of the healing process.
3.4. Discussion
- Immediately after applying the sodium silicate solution, the value of all of the indicators is very close to that of the broken sample;
- After a few days, the healing agent is supposedly almost completely solidified, and the ultrasonic parameters are very close to those measured on the sample in its initial intact state.
4. Mechanical Tests: Results and Discussion
5. Conclusions
- define a measure of the expected final recovery without the need for a destructive testing;
- speed-up the optimization of the healing agents by sensibly reducing the time needed to assess the recovery in different conditions and for different healing agents;
- define a protocol to ultrasonically monitor the healing process when the healing agent is released from broken capsules, as in real conditions.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Tittelboom, K.; De Belie, N. Self-healing in cementitious materials—A review. Materials 2013, 6, 2182–2217. [Google Scholar] [CrossRef]
- Huang, H.; Ye, G. Simulation of self healing by further hydration in cementitious materials. Cem. Concr. Compos. 2012, 34, 460–467. [Google Scholar] [CrossRef]
- Sisomphon, K.; Copuroglu, O.; Koenders, E.A.B. Self-healing of surface cracks in mortars with expansive additive and crystalline additive. Cem. Concr. Res. 2012, 34, 566–574. [Google Scholar] [CrossRef]
- Jonkers, H.M.; Thijssen, A.; Muyzer, G.; Copuroglu, O.; Schlangen, E. Application of bacteria as self-healing agent for the development of sustainable concrete. Ecol. Eng. 2010, 36, 230–235. [Google Scholar] [CrossRef]
- Mihashi, H.; Kaneko, Y.; Nishiwaki, T.; Otsuka, K. Fundamental study on development of intelligent concrete characterized by self-healing capability for strength. Trans. Jpn. Concr. Inst. 2000, 22, 441–450. [Google Scholar] [CrossRef]
- Hillouin, B.; Van Tittelboom, K.; Gruyaert, E.; De Belie, N.; Loukili, A. Design of polymeric capsules for self-healing concrete. Cem. Concr. Compos. 2015, 55, 298–307. [Google Scholar] [CrossRef]
- Maes, M.; Van Tittelboom, K.; De Belie, N. The efficiency of self healing cementitious materials by means of encapsulated polyurethane in chloride containing environments. Constr. Build. Mater. 2014, 71, 528–537. [Google Scholar] [CrossRef]
- Formia, A.; Terranova, S.; Antonaci, P.; Pugno, N.M.; Tulliani, J.M. Setup of extruded cementitious hollow tubes as containing/releasing devices in self-healing systems. Materials 2015, 8, 1897–1923. [Google Scholar] [CrossRef]
- Antonaci, P.; Pugno, N.M.; Tulliani, J.M. Production and mechanical behavior of micro-encapsulated self-healing cement: A case study. In Proceedings of the 5th World Tribology Congress, Torino, Italy, 8–10 September 2013; pp. 1399–1402.
- LaRosa Thompson, J.; Silsbee, M.R.; Gill, P.M.; Scheetz, B.E. Characterization of silicate sealers on concrete. Cem. Concr. Res. 1997, 7, 1561–1567. [Google Scholar] [CrossRef]
- Kouassi, S.S.; Tognonvi, M.T.; Soro, J.; Rossignol, S. Consolidation mechanism of materials obtained from sodium silicate solution and silica-based aggregates. J. Non-Cryst. Solids 2011, 357, 3013–3021. [Google Scholar] [CrossRef]
- Palmero, P.; Formia, A.; Antonaci, P.; Brini, S.; Tulliani, J.M. Geopolymer technology for application-oriented dense and lightened materials. Elaboration and characterization. Ceram. Int. 2015, 41, 12967–12979. [Google Scholar] [CrossRef]
- Latifi, N.; Eisazadeh, A.; Marto, A. Strength behavior and microstructural characteristics of tropical laterite soil treated with sodium silicate-based liquid stabilizer. Environ. Earth Sci. 2014, 72, 91–98. [Google Scholar] [CrossRef]
- Pakir, F.; Marto, A.; Yunus, N.Z.M.; Tajudin, S.A.A.; Tan, C.S. Effect of sodium silicate as liquid based stabilizer on shear strenght of marine clay. J. Teknol. 2015, 76, 45–50. [Google Scholar]
- McGettigan, E. Silicon-based weatherproofing materials. Concr. Int. 1992, 14, 52–56. [Google Scholar]
- Song, Z.; Xue, X.; Li, Y.; Yang, J.; He, Z.; Shen, S.; Jiang, L.; Zhang, W.; Xu, L.; Zhang, H.; et al. Experimental exploration of the waterproofing mechanism of inorganic sodium silicate-based concrete sealers. Constr. Build. Mater. 2016, 104, 276–283. [Google Scholar] [CrossRef]
- Jiang, L.; Xue, X.; Zhang, W.; Yang, J.; Zhang, H.; Li, Y.; Zhang, R.; Zhang, Z.; Xu, L.; Qu, J.; et al. The investigation of factors affecting the water impermeability of inorganic sodium silicate-based concrete sealers. Constr. Build. Mater. 2015, 93, 729–736. [Google Scholar] [CrossRef]
- Prasetia, I. The ineffectiveness of sodium based surface treatment on the mitigation of alkali silica reaction. Int. J. Adv. Eng. Technol. 2015, 8, 466–474. [Google Scholar]
- Huang, H.; Ye, G. Application of sodium silicate solution as self-healing agent in cementitious materials. In Proceedings of the International RILEM Conference on Advances in Construction Materials Through Science and Engineering, Hong Kong, China, 5–7 September 2011; pp. 530–536.
- Pelletier, M.M.; Brown, R.; Shukla, A.; Bose, A. Self Healing Concrete with a Microencapsulated Healing Agent. Cem. Concr. Res. 2011. [Google Scholar]
- Aggelis, D.G.; Barkoula, N.M.; Matikas, T.E.; Paipetis, A.S. Acoustic structural health monitoring of composite materials: Damage identification and evaluation in cross ply laminates using acoustic emission and ultrasonics. Compos. Sci. Technol. 2012, 72, 1127–1133. [Google Scholar] [CrossRef]
- Van den Abeele, K.; Desadeleer, W.; De Schutter, G.; Wevers, M. Active and passive monitoring of the early hydration process in concrete using linear and nonlinear acoustics. Cem. Concr. Res. 2009, 739, 426–432. [Google Scholar] [CrossRef]
- Li, Z.J. Microcrack characterization in concrete under uniaxial tension. Mag. Concr. Res. 1996, 48, 219–228. [Google Scholar] [CrossRef]
- Musyoka, N.M.; Petrik, L.F.; Hums, E.; Baser, H.; Schwieger, W. In situ ultrasonic monitoring of zeolite a crystallization from coal fly ash. Catal. Today 2012, 190, 38–46. [Google Scholar] [CrossRef]
- Vlad, M.; González, L.; Gómez, S.; López, J.; Carlson, J.E.; Fernández, E. Ultrasound monitoring of the setting of calcium-based bone cements. J. Mater. Sci. Mater. Med. 2012, 23, 1563–1568. [Google Scholar] [CrossRef] [PubMed]
- Bui, D.; Kodjo, S.A.; Rivard, P.; Fournier, B. Evaluation of concrete distributed cracks by ultrasonic travel time shift under an external mechanical perturbation: Study of indirect and semi-direct transmission configurations. J. Nondestruct. Eval. 2013, 32, 25–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Abraham, O.; Grondin, F.; Loukili, A.; Tournat, V.; Duff, A.L.; Lascoup, B.; Durand, O. Study of stress-induced velocity variation in concrete under direct tensile force and monitoring of the damage level by using thermally-compensated coda wave interferometry. Ultrasonics 2012, 52, 1038–1045. [Google Scholar] [CrossRef] [PubMed]
- Lesage, J.C.; Sinclair, A.N. Characterization of prestressed concrete cylinder pipe by resonance acoustic spectroscopy. J. Pipeline Syst. Eng. Pract. 2015, 6, 04014011. [Google Scholar] [CrossRef]
- Payan, C.; Ulrich, T.J.; Le Bas, P.Y.; Saleh, T.; Guimaraes, M. Quantitative linear and nonlinear resonance inspection techniques and analysis for material characterization: Application to concrete thermal damage. J. Acoust. Soc. Am. 2014, 136, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Antonaci, P.; Bruno, C.L.E.; Scalerandi, M.; Tondolo, F. Effects of corrosion on linear and nonlinear elastic properties of reinforced concrete. Cem. Concr. Res. 2013, 51, 96–103. [Google Scholar] [CrossRef]
- Hilloulin, B.; Legland, J.B.; Lys, E.; Abraham, O.; Loukili, A.; Grondin, F.; Durand, O.; Tournat, V. Monitoring of autogenous crack healing in cementitious materials by the nonlinear modulation of ultrasonic coda waves, 3D microscopy and X-ray microtomography. Constr. Build. Mater. 2016, 123, 143–152. [Google Scholar] [CrossRef]
- Baccouche, Y.; Bentahar, M.; Mechri, C.; El Guerjouma, R.; Hédi Ben Ghozlen, M. Hysteretic nonlinearity analysis in damaged composite plates using guided waves. J. Acoust. Soc. Am. 2013, 133, EL256–EL261. [Google Scholar] [CrossRef] [PubMed]
- Antonaci, P.; Bruno, C.L.E.; Gliozzi, A.S.; Scalerandi, M. Monitoring evolution of compressive damage in concrete with linear and nonlinear ultrasonic methods. Cem. Concr. Res. 2010, 40, 1106–1113. [Google Scholar] [CrossRef]
- Bouchaala, F.; Payan, C.; Garnier, V.; Balayssac, J.P. Carbonation assessment in concrete by nonlinear ultrasound. Ceme. Concr. Res. 2011, 41, 557–559. [Google Scholar] [CrossRef]
- Shah, A.A.; Ribakov, Y. Non-destructive evaluation of concrete in damaged and undamaged states. Mater. Des. 2009, 30, 3504–3511. [Google Scholar] [CrossRef]
- Kim, G.; Kim, J.Y.; Kurtis, K.E.; Jacobs, L.J.; Le Pape, Y.; Guimaraes, M. Quantitative evaluation of carbonation in concrete using nonlinear ultrasound. Mater. Struct. 2016, 49, 399–409. [Google Scholar] [CrossRef]
- Bentahar, M.; El Aqra, H.; El Guerjouma, R.; Griffa, M.; Scalerandi, M. Hysteretic elasticity in damaged concrete: Quantitative analysis of slow and fast dynamics. Phys. Rev. B 2006, 73, 014116. [Google Scholar] [CrossRef]
- Chen, J.; Kim, J.Y.; Kurtis, K.E.; Jacobs, L.J. Theoretical and experimental study of the nonlinear resonance vibration of cementitious materials with an application to damage characterization. J. Acoust. Soc. Am. 2011, 130, 2728–2734. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, L. Experimental study of effects of water-cement ratio and curing time on nonlinear resonance of concrete. Mater. Struct. 2015, 148, 423–433. [Google Scholar] [CrossRef]
- Scalerandi, M.; Gliozzi, A.S.; Ait Ouarabi, M.; Boubenider, F. Continuous waves probing in dynamic acoustoelastic testing. Appl. Phys. Lett. 2016, 108, 214103. [Google Scholar] [CrossRef]
- Hilloulin, B.; Zhang, Y.; Abraham, O.; Loukili, A.; Grondin, F.; Durand, O.; Tournat, V. Small crack detection in cementitious materials using nonlinear coda wave modulation. NDT E Int. 2014, 68, 98–104. [Google Scholar] [CrossRef]
- Zhang, Y.; Abraham, O.; Tournat, V.; Le Duff, A.; Lascoup, B.; Loukili, A.; Grondin, F.; Durand, O. Validation of a thermal bias control technique for Coda Wave Interferometry (CWI). Ultrasonics 2013, 53, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Bruno, C.L.E.; Gliozzi, A.S.; Scalerandi, M.; Antonaci, P. Analysis of elastic nonlinearity using the scaling subtraction method. Phys. Rev. B 2009, 79, 064108. [Google Scholar] [CrossRef]
- Antonaci, P.; Bruno, C.L.E.; Gliozzi, A.S.; Scalerandi, M. Evolution of damage-induced nonlinearity in proximity of discontinuities in concrete. Int. J. Solids Struct. 2010, 47, 1603–1610. [Google Scholar] [CrossRef]
- Scalerandi, M.; Griffa, M.; Antonaci, P.; Wyrzykowski, M.; Lura, P. Nonlinear elastic response of thermally damaged consolidated granular media. J. Appl. Phys. 2013, 113, 154902. [Google Scholar] [CrossRef]
- Antonaci, P.; Formia, A.; Gliozzi, A.S.; Scalerandi, M.; Tulliani, J.M. Diagnostic application of nonlinear ultrasonics to characterize degradation by expansive salts in masonry systems. NDT E Int. 2013, 55, 57–63. [Google Scholar] [CrossRef]
- Formia, A.; Irico, S.; Bertola, F.; Canonico, F.; Antonaci, P.; Pugno, N.M.; Tulliani, J.M. Experimental analysis of self-healing cement-based materials incorporating extruded cementitious hollow tubes. J. Int. Mater. Syst. Struct. 2016, 27, 2633–2652. [Google Scholar] [CrossRef]
- Van den Abeele, K.; Sutin, A.; Carmeliet, J.; Johnson, P.A. Micro-damage diagnostics using nonlinear elastic wave spectroscopy (NEWS). NDT E Int. 2001, 34, 239–248. [Google Scholar] [CrossRef]
- Van den Abeele, K.; De Visscher, J. Damage assessment in reinforced concrete using spectral and temporal nonlinear vibration techniques. Cem. Concr. Res. 2000, 30, 1453–1464. [Google Scholar] [CrossRef]
- Scalerandi, M.; Idjimarene, S.; Bentahar, M.; El Guerjouma, R. Evidence of evolution of microstructure in solid elastic media based on a power law analysis. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 334–347. [Google Scholar] [CrossRef]
- Tournat, V.; Gusev, V.E.; Zaitsev, V.Yu.; Castagnède, B. Acoustic second-harmonic generation with shear to longitudinal mode conversion in granular media. Europhys. Lett. 2004, 66, 798–804. [Google Scholar] [CrossRef]
- Tournat, V.; Zaitsev, V.; Gusev, V.; Nazarov, V.; Béquin, P.; Castagnède, B. Probing weak forces in granular media through nonlinear dynamic dilatancy: Clapping contacts and polarization anisotropy. Phys. Rev. Lett. 2004, 92, 085502. [Google Scholar] [CrossRef] [PubMed]
- Ait Ouarabi, M.; Boubenider, F.; Gliozzi, A.S.; Scalerandi, M. Nonlinear coda wave analysis of hysteretic elastic behavior in strongly scattering elastic media. Phys. Rev. B 2016, 94, 134103. [Google Scholar] [CrossRef]
- Bentahar, M.; El Guerjouma, R.; Idijmarene, S.; Scalerandi, M. Influence of noise on the threshold for detection of elastic nonlinearity. J. Appl. Phys. 2013, 113, 043516. [Google Scholar] [CrossRef]
- Scalerandi, M.; Gliozzi, A.S.; Olivero, D. Discrimination between cracks and recrystallization in steel using nonlinear techniques. J. Nondestruct. Eval. 2014, 33, 269–278. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Gusev, V.E.; Tournat, V.; Richard, P. Slow relaxation and aging phenomena at the nanoscale in granular materials. Phys. Rev. Lett. 2014, 112, 108302. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ait Ouarabi, M.; Antonaci, P.; Boubenider, F.; Gliozzi, A.S.; Scalerandi, M. Ultrasonic Monitoring of the Interaction between Cement Matrix and Alkaline Silicate Solution in Self-Healing Systems. Materials 2017, 10, 46. https://doi.org/10.3390/ma10010046
Ait Ouarabi M, Antonaci P, Boubenider F, Gliozzi AS, Scalerandi M. Ultrasonic Monitoring of the Interaction between Cement Matrix and Alkaline Silicate Solution in Self-Healing Systems. Materials. 2017; 10(1):46. https://doi.org/10.3390/ma10010046
Chicago/Turabian StyleAit Ouarabi, Mohand, Paola Antonaci, Fouad Boubenider, Antonio S. Gliozzi, and Marco Scalerandi. 2017. "Ultrasonic Monitoring of the Interaction between Cement Matrix and Alkaline Silicate Solution in Self-Healing Systems" Materials 10, no. 1: 46. https://doi.org/10.3390/ma10010046
APA StyleAit Ouarabi, M., Antonaci, P., Boubenider, F., Gliozzi, A. S., & Scalerandi, M. (2017). Ultrasonic Monitoring of the Interaction between Cement Matrix and Alkaline Silicate Solution in Self-Healing Systems. Materials, 10(1), 46. https://doi.org/10.3390/ma10010046





