Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy
Abstract
:1. Introduction
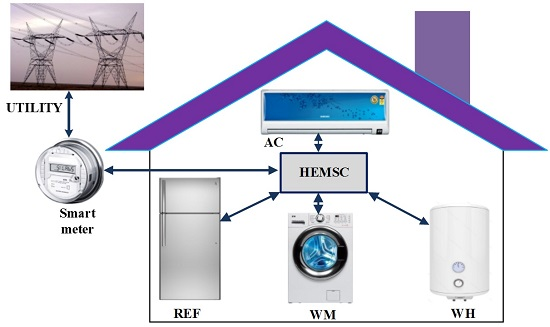
2. Load Model of Home Appliances
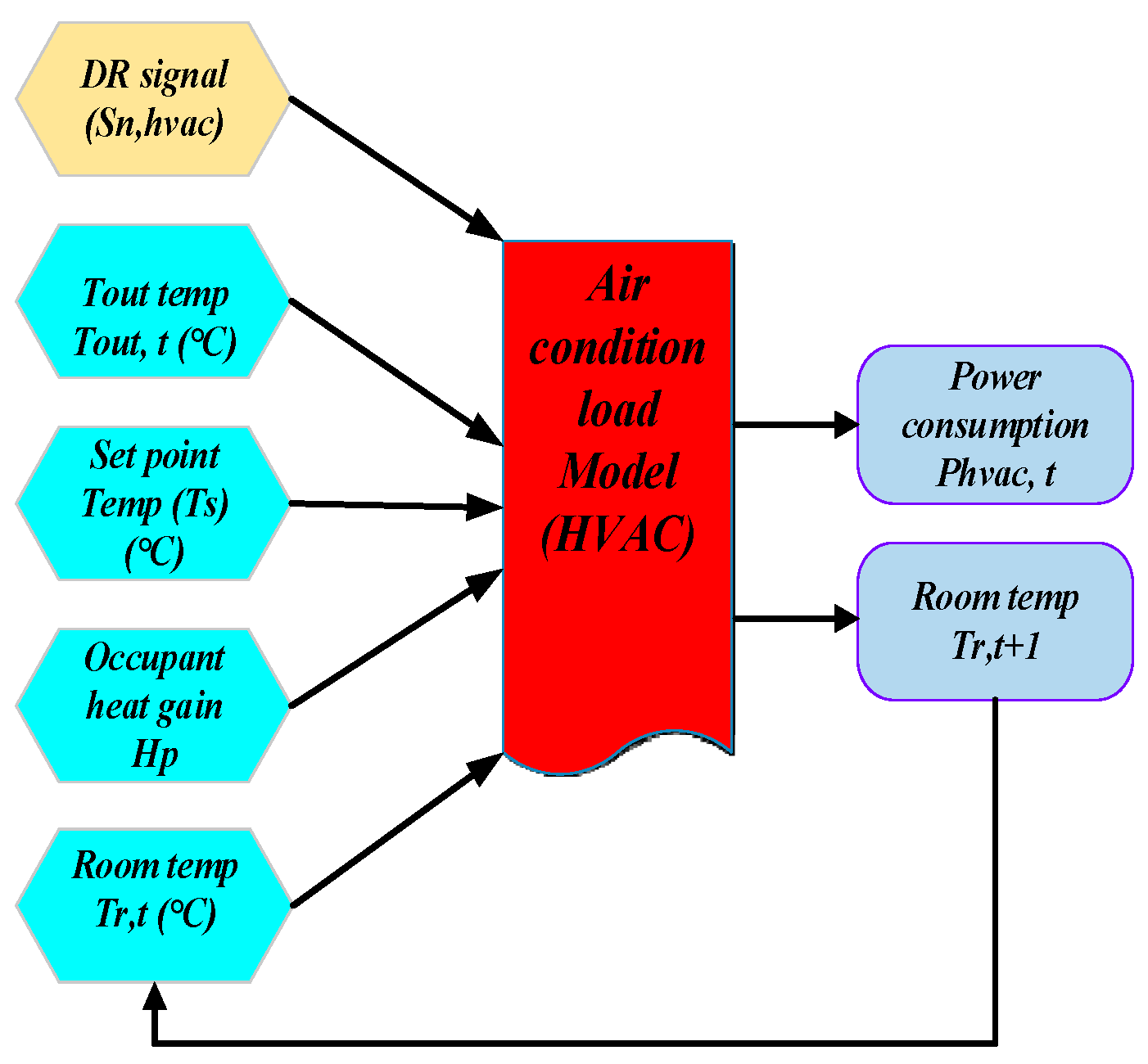
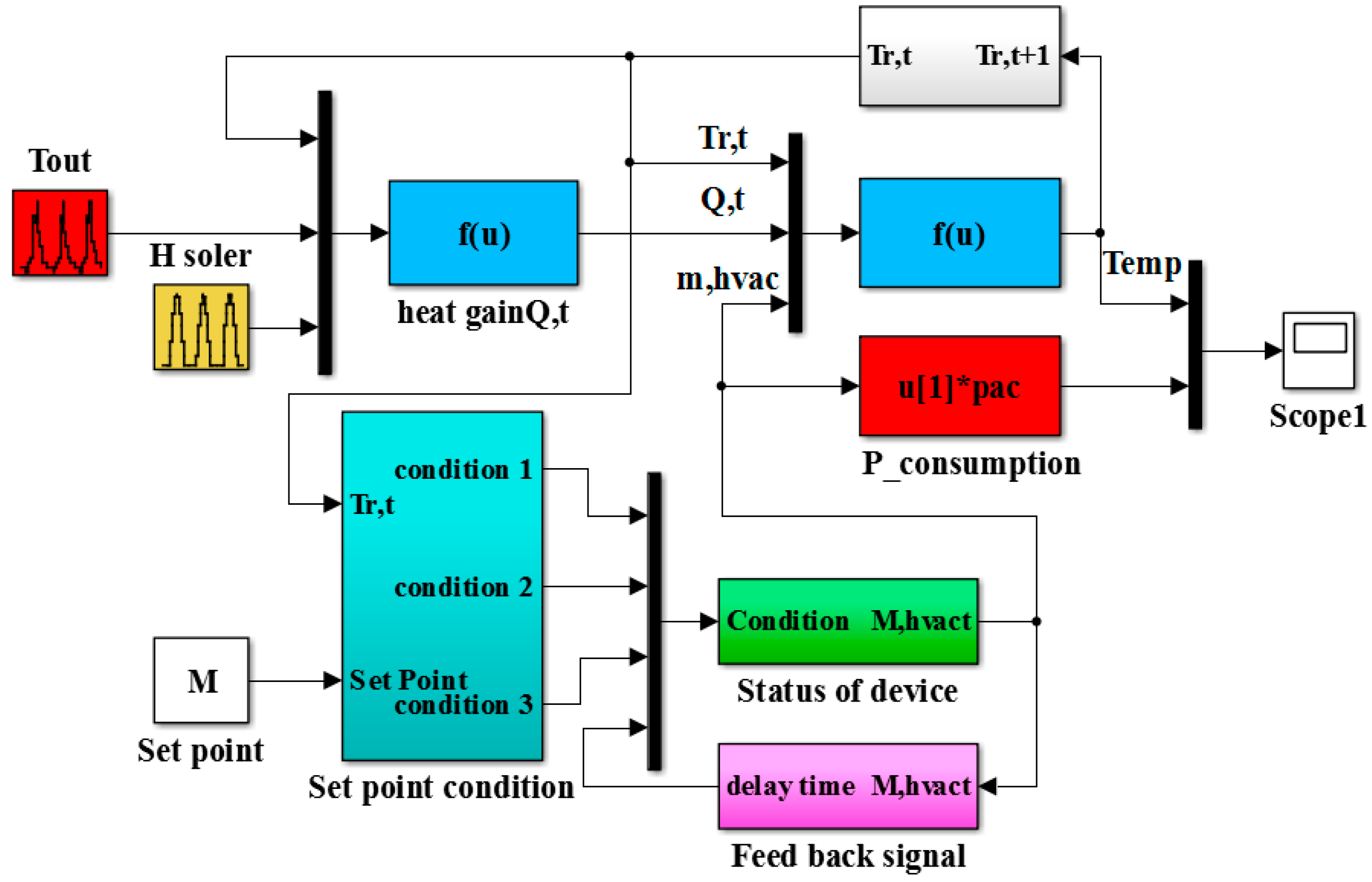
2.1. Air Conditioner Modeling
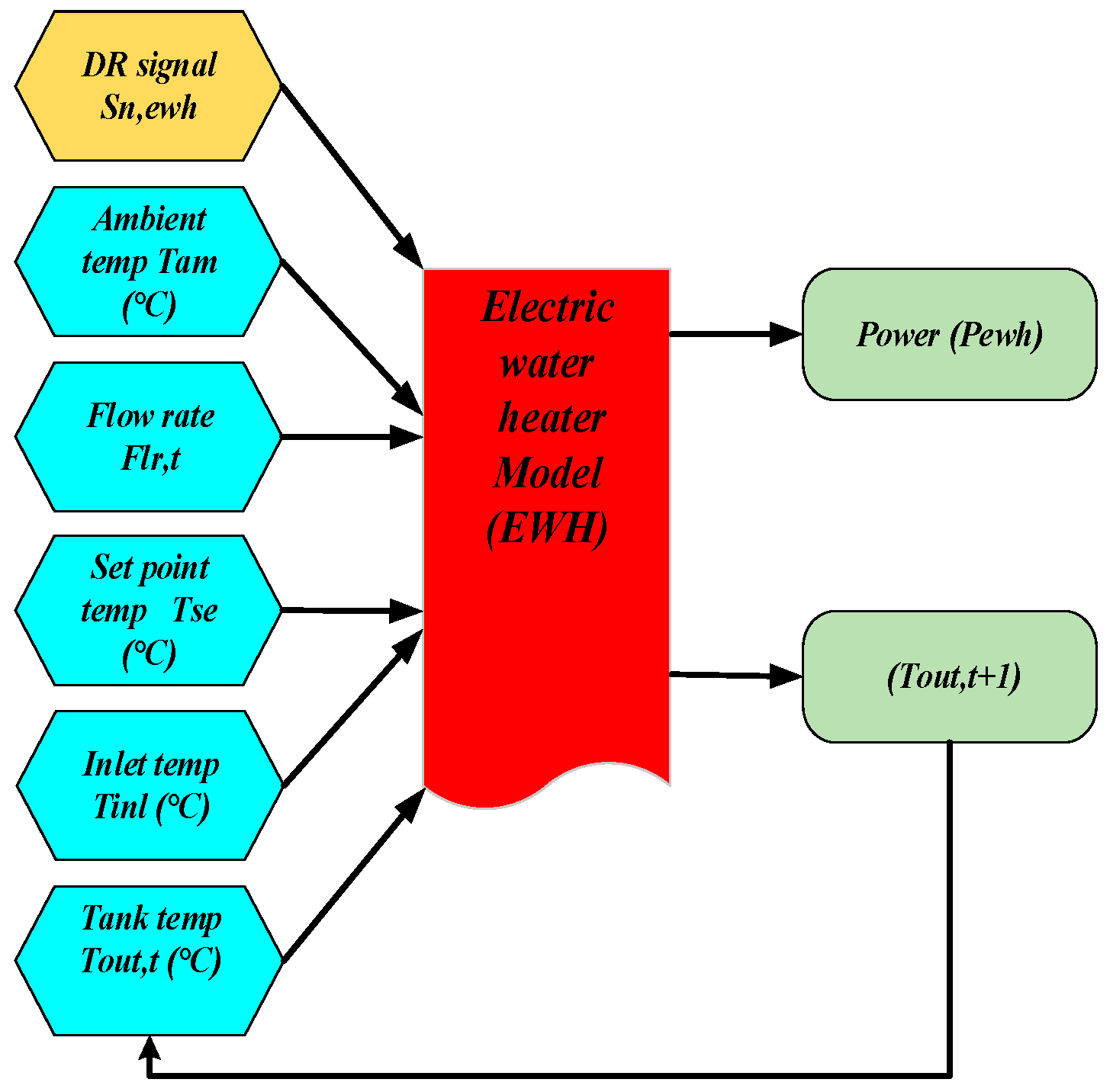
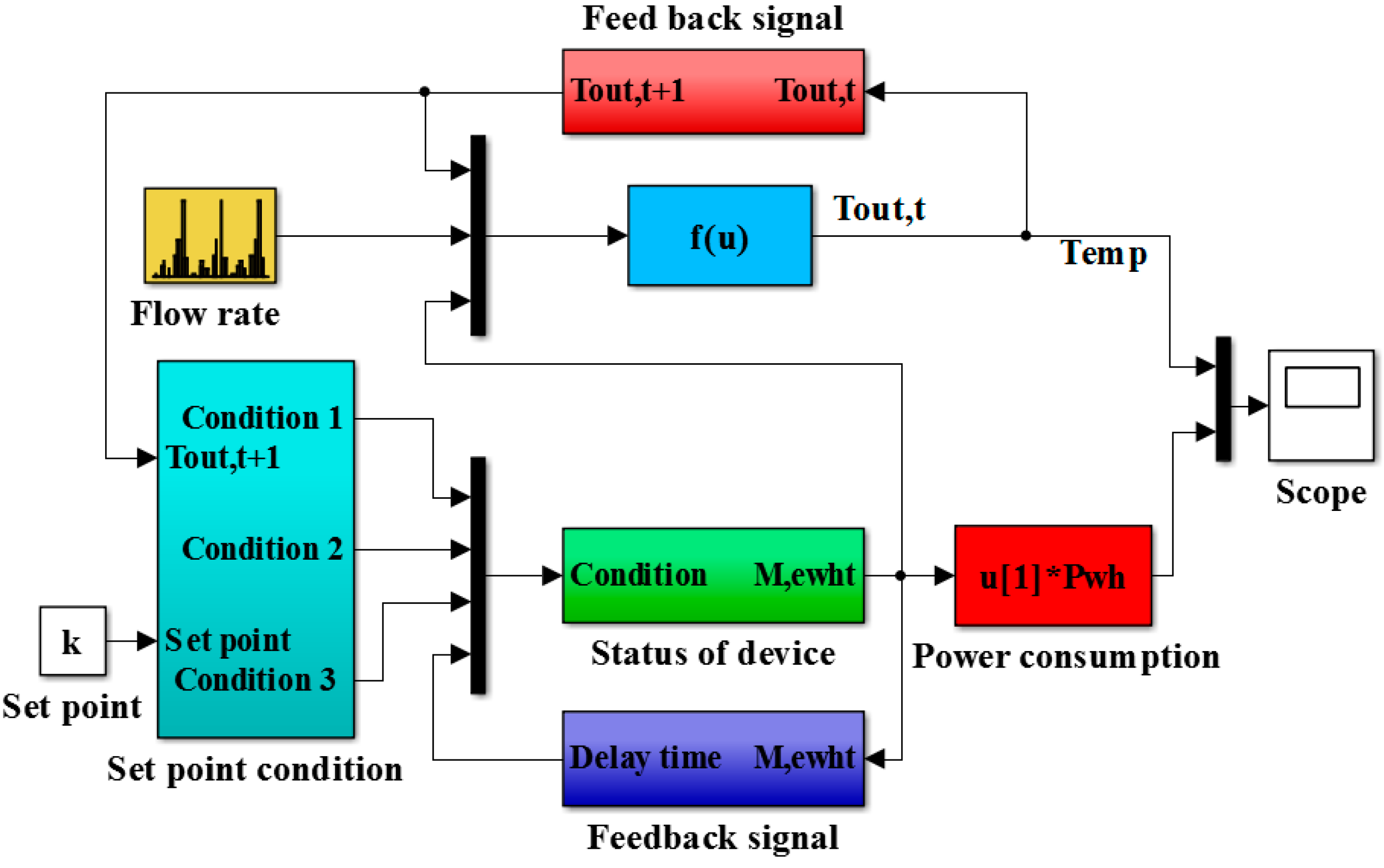
2.2. Electric Water Heater Modeling
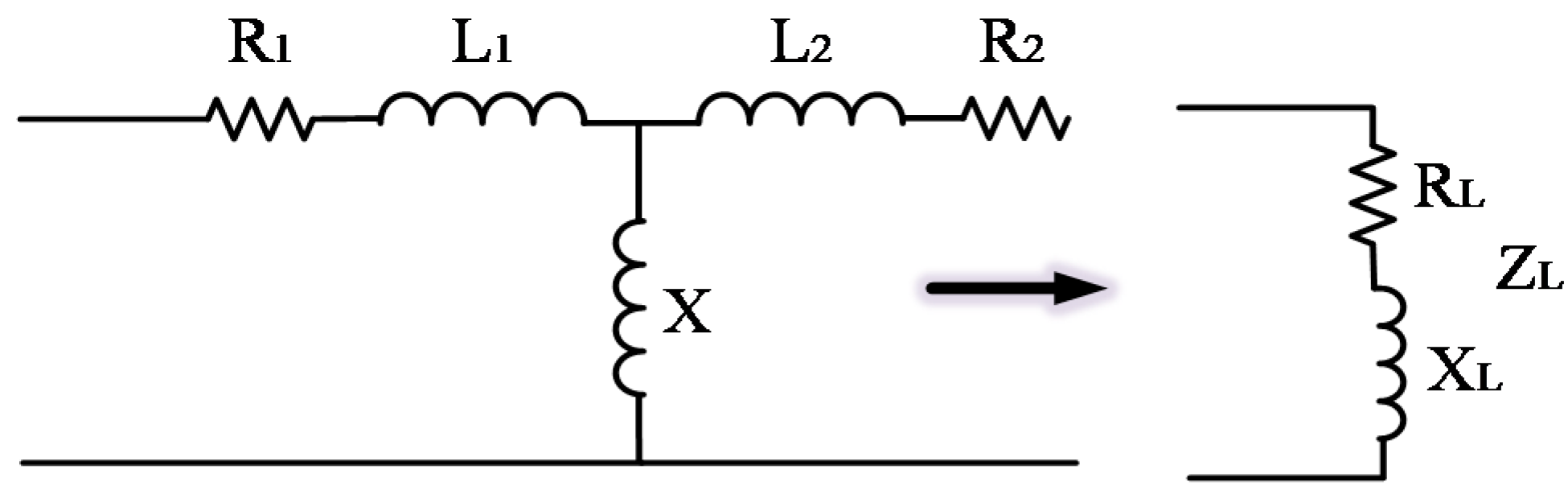
2.3. Water Heater and Refrigerator Modeling
3. Gathering Data for Household Appliance Models
4. Artificial Intelligent Techniques Used for Home Energy Management Scheduling Controller
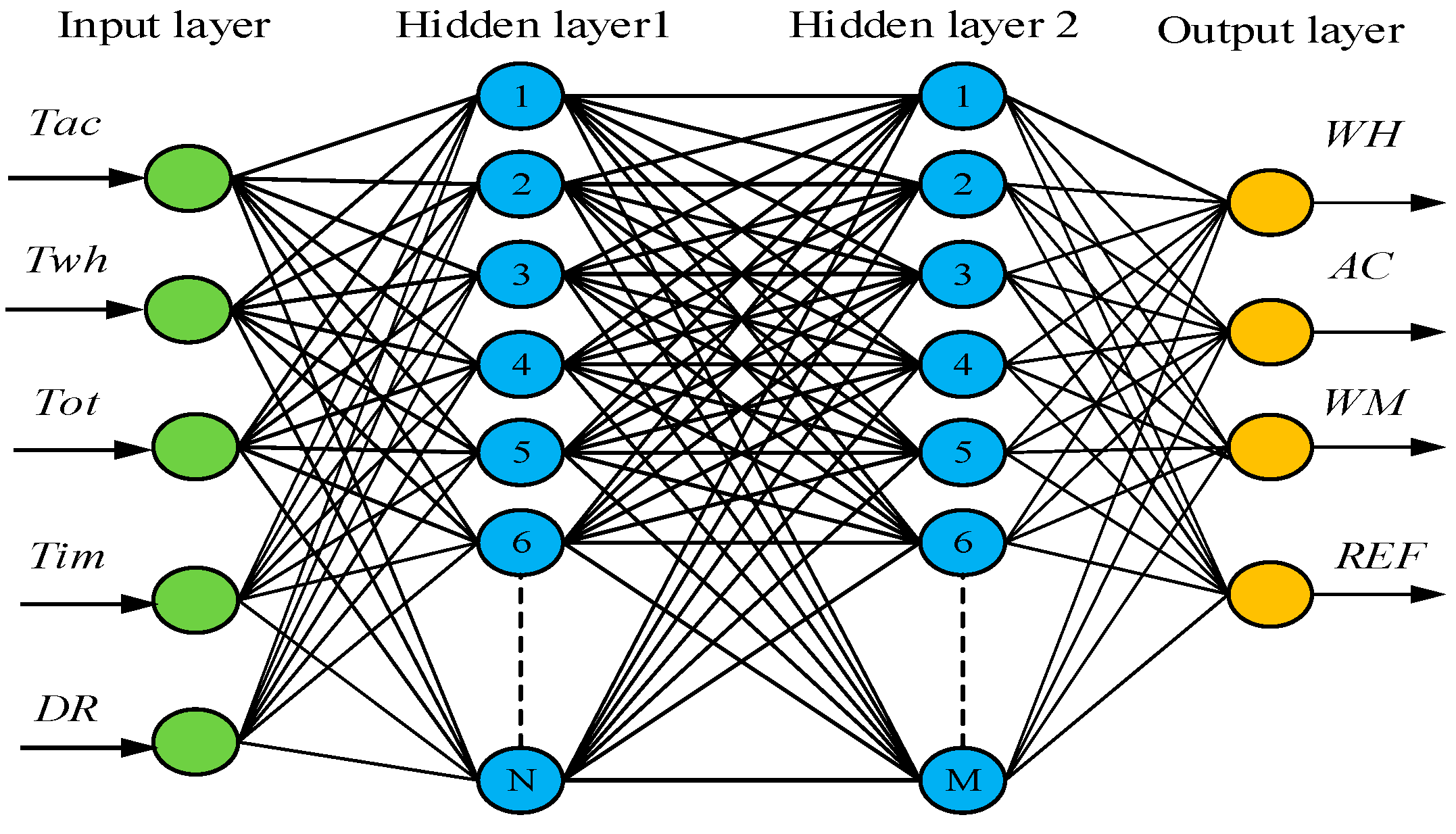
4.1. Artificial Neural Network Technique
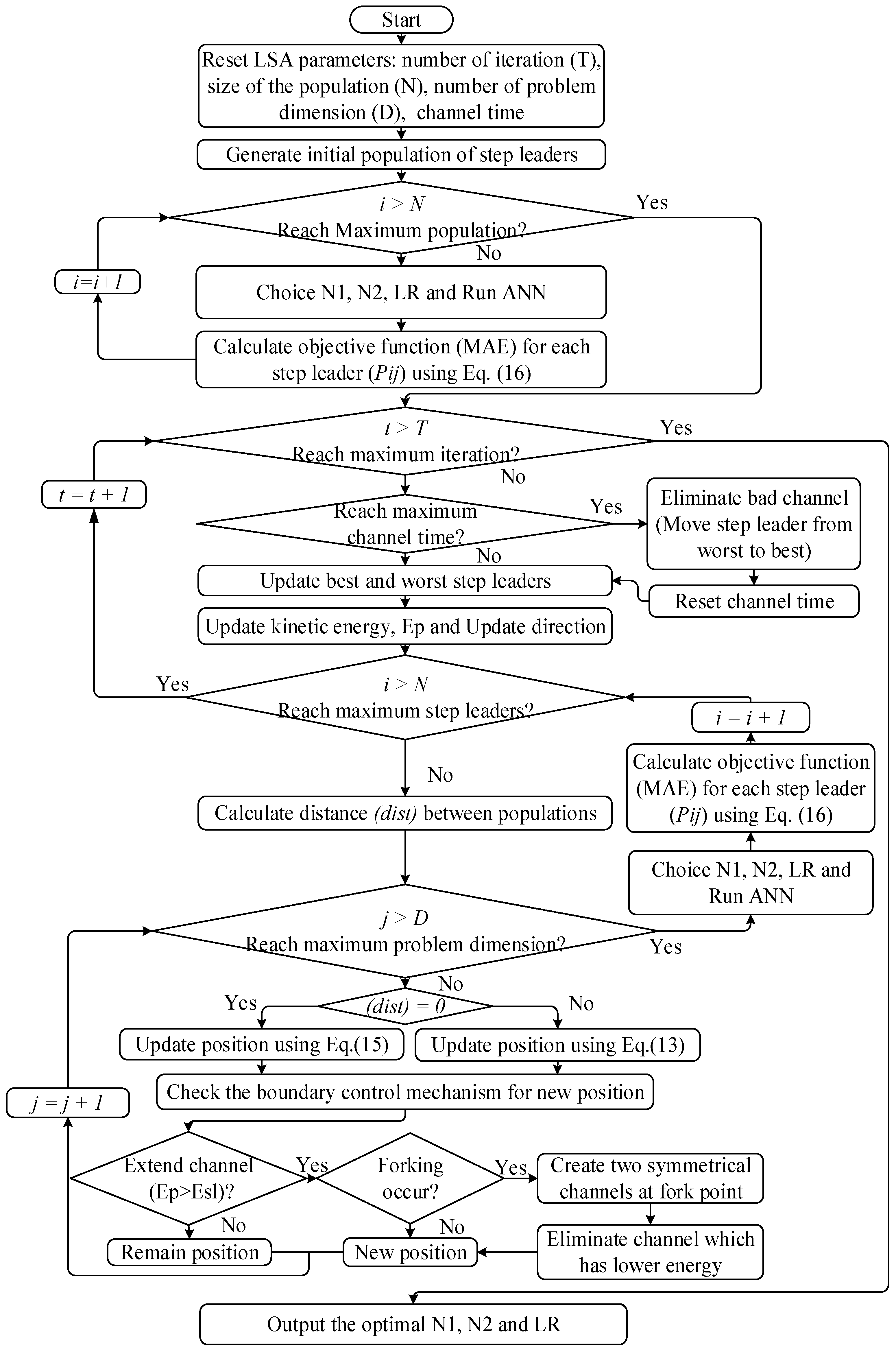
4.2. Overview of Lightning Search Algorithm
4.3. Proposed Hybrid Lightning Search Algorithm-Based Artificial Neural Network
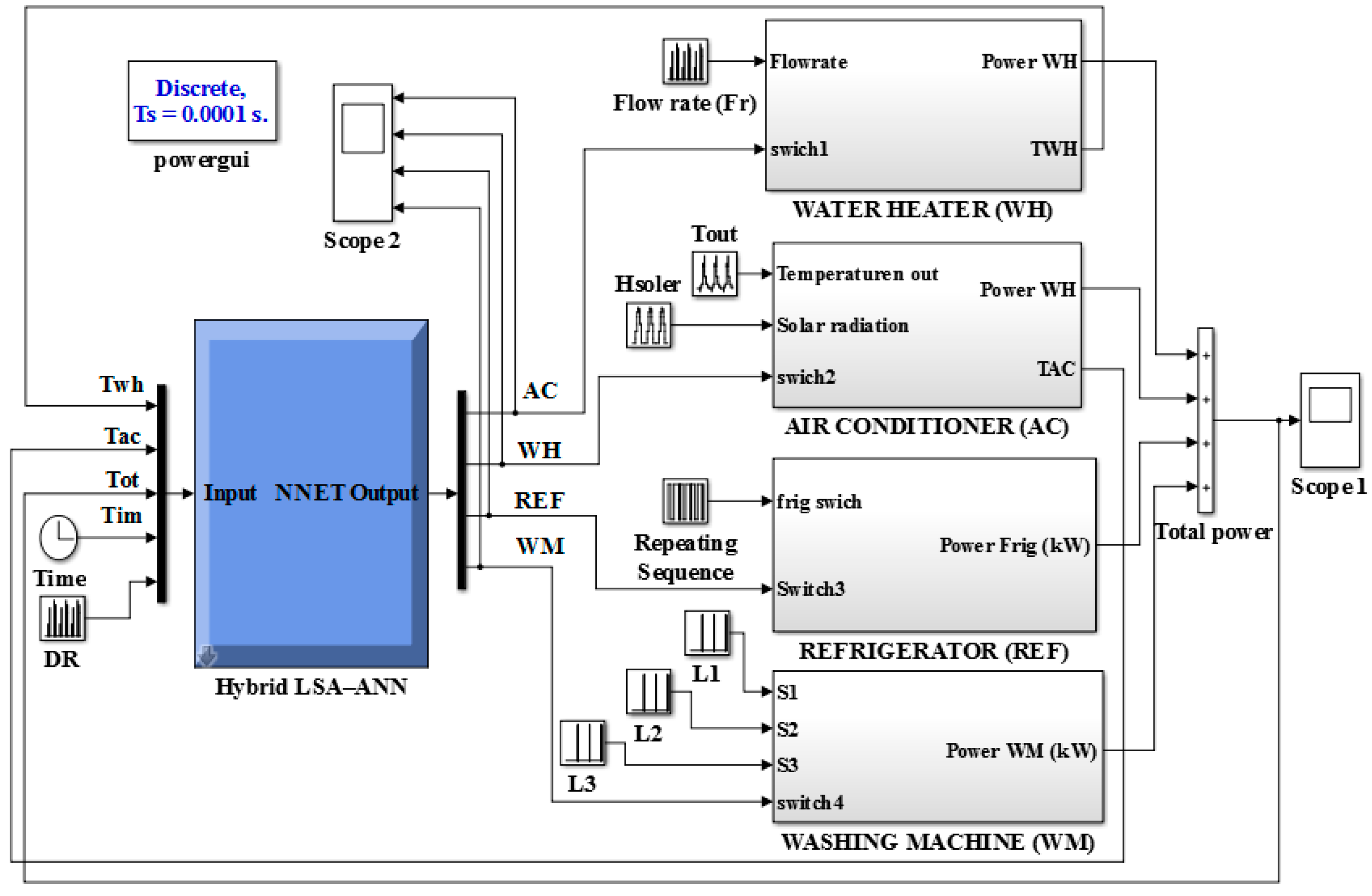
5. Overall Proposed Home Energy Management Scheduling Controller System
6. Results and Discussion
6.1. Home Appliance Simulation Result
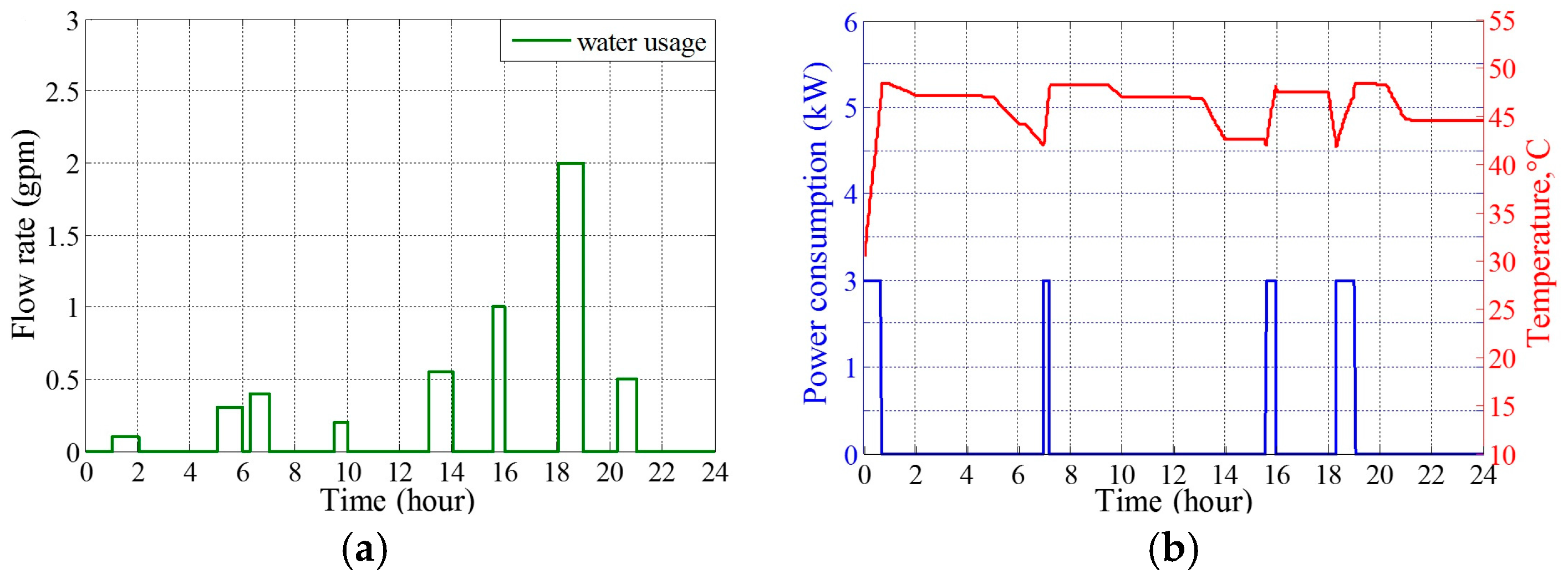
6.1.1. Water Heater Simulation Result
6.1.2. Air Conditioner Simulation Results
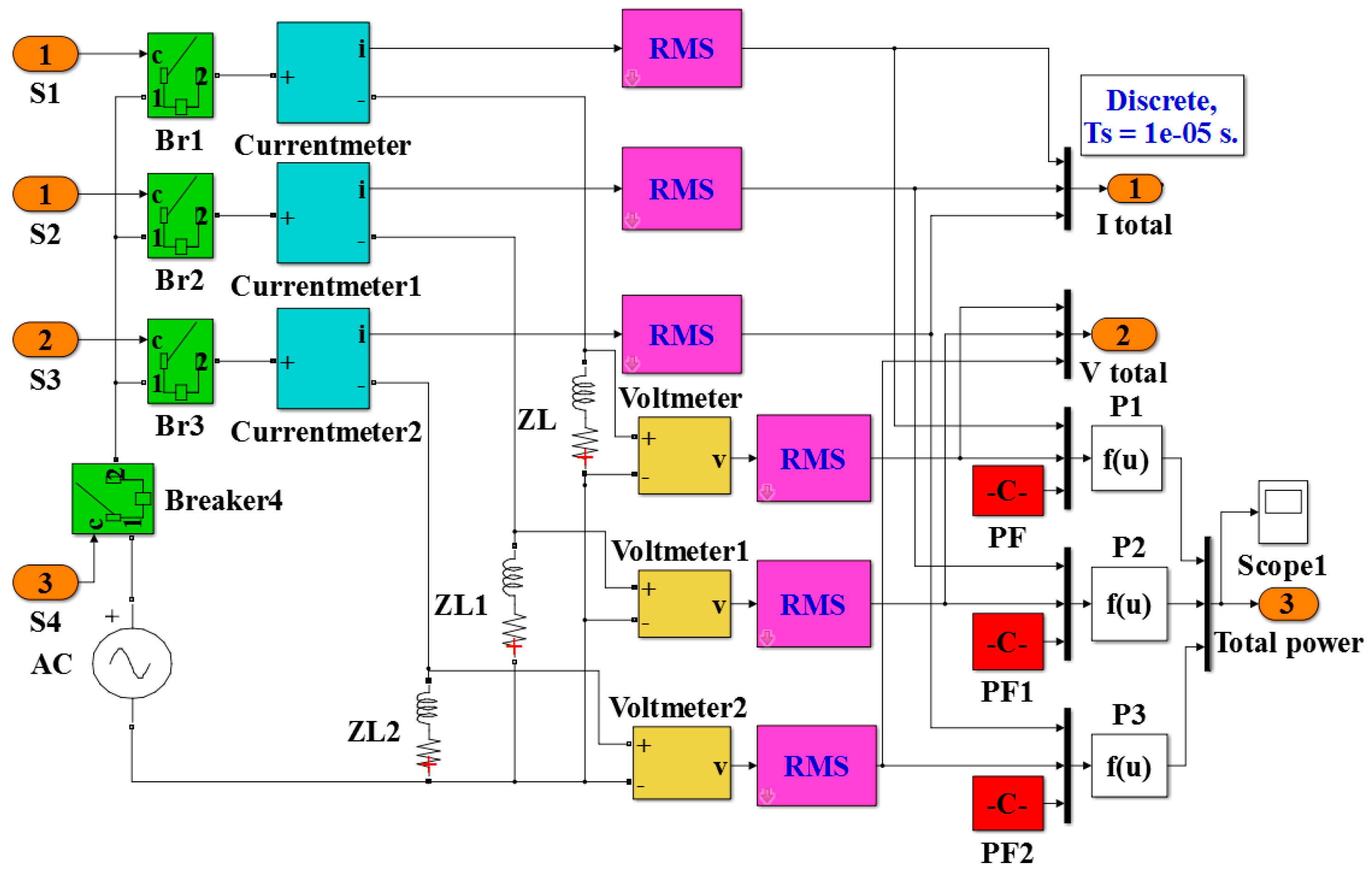
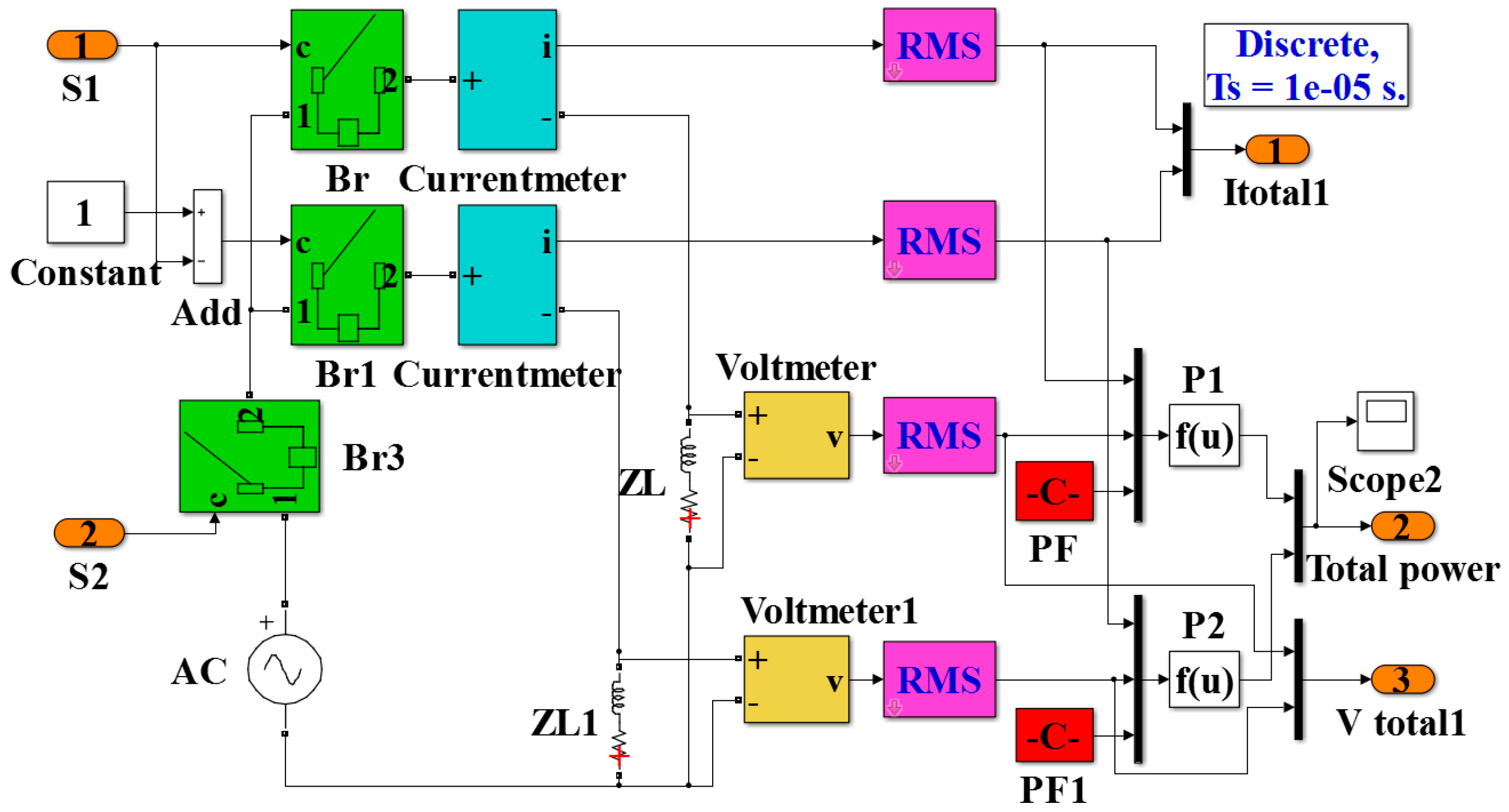
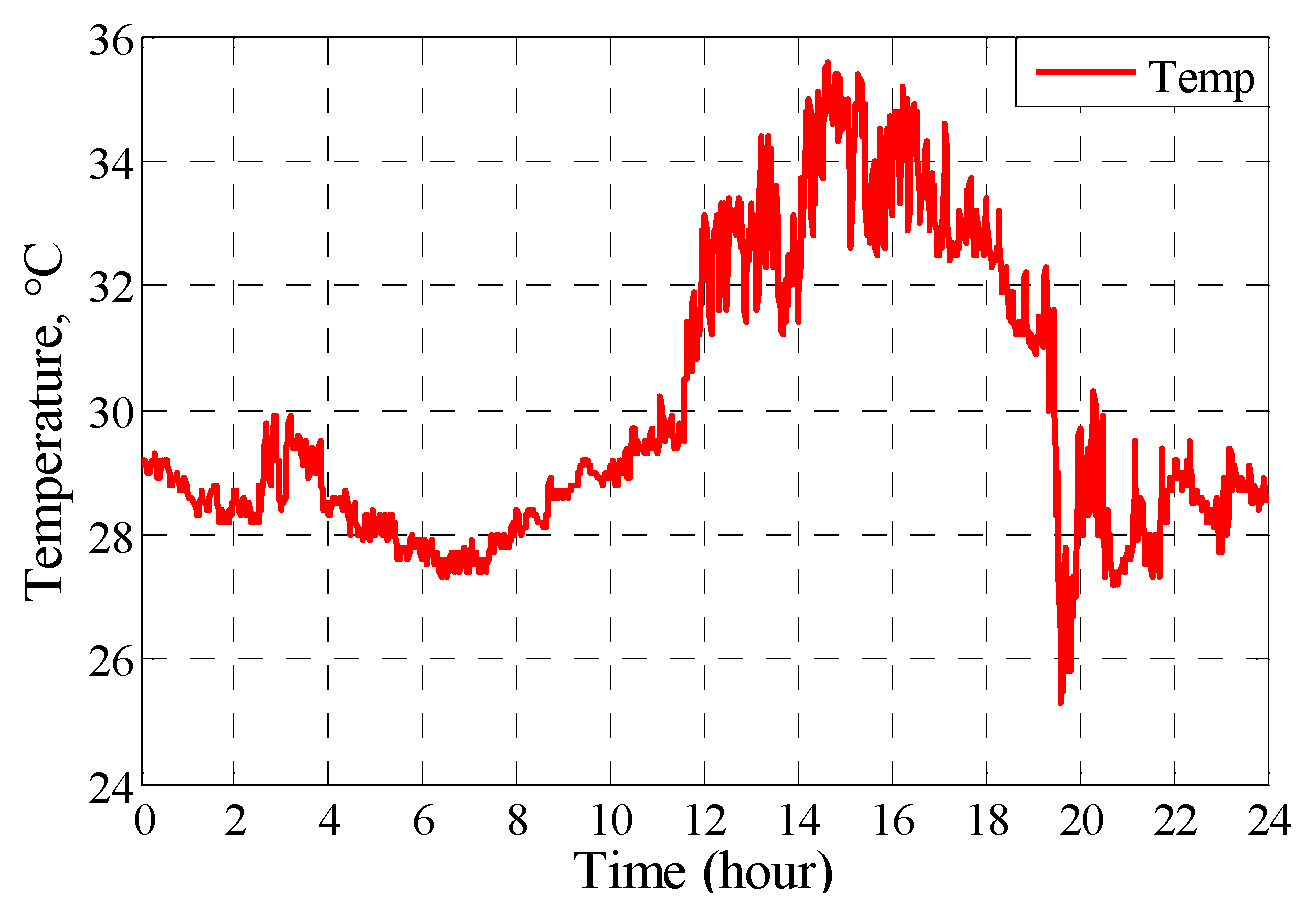
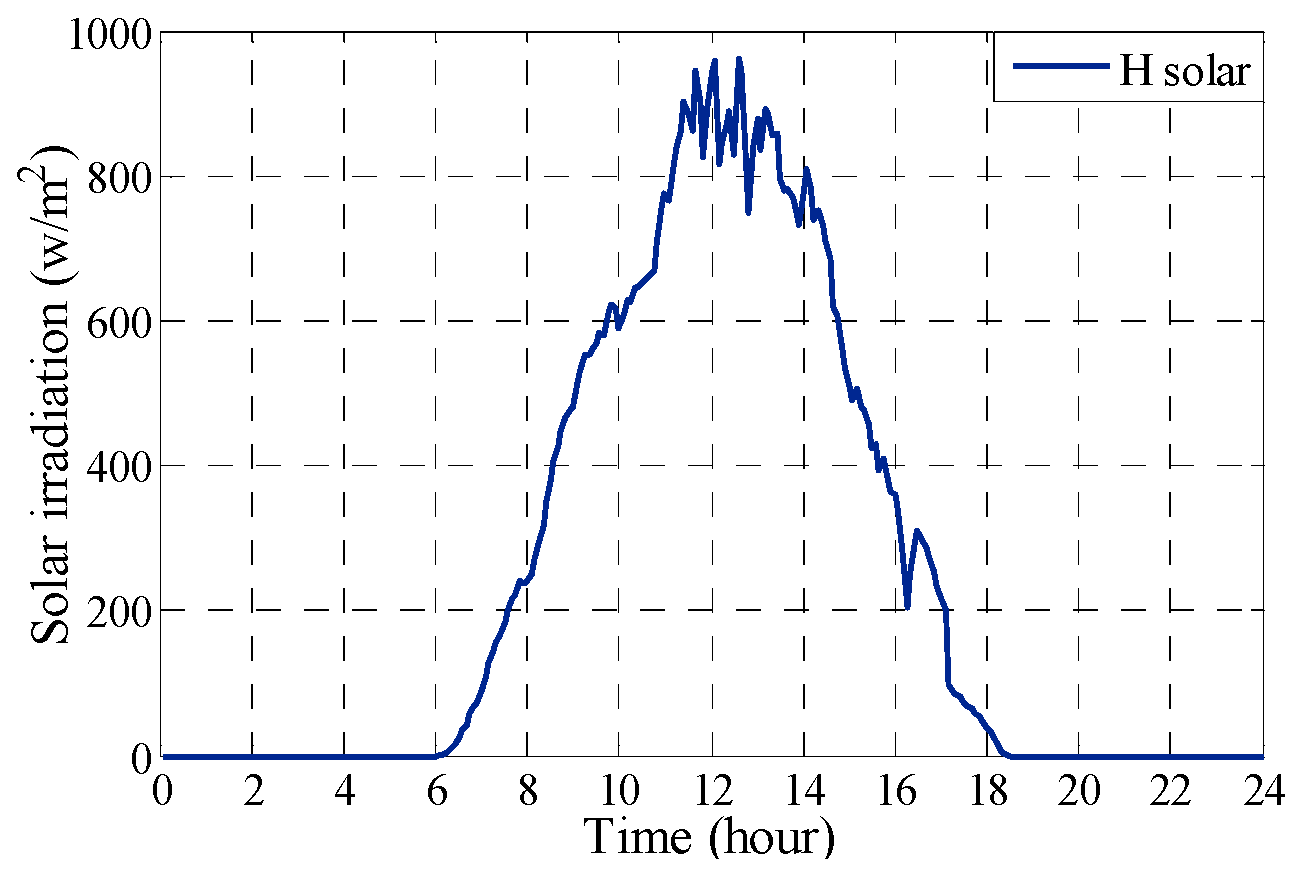
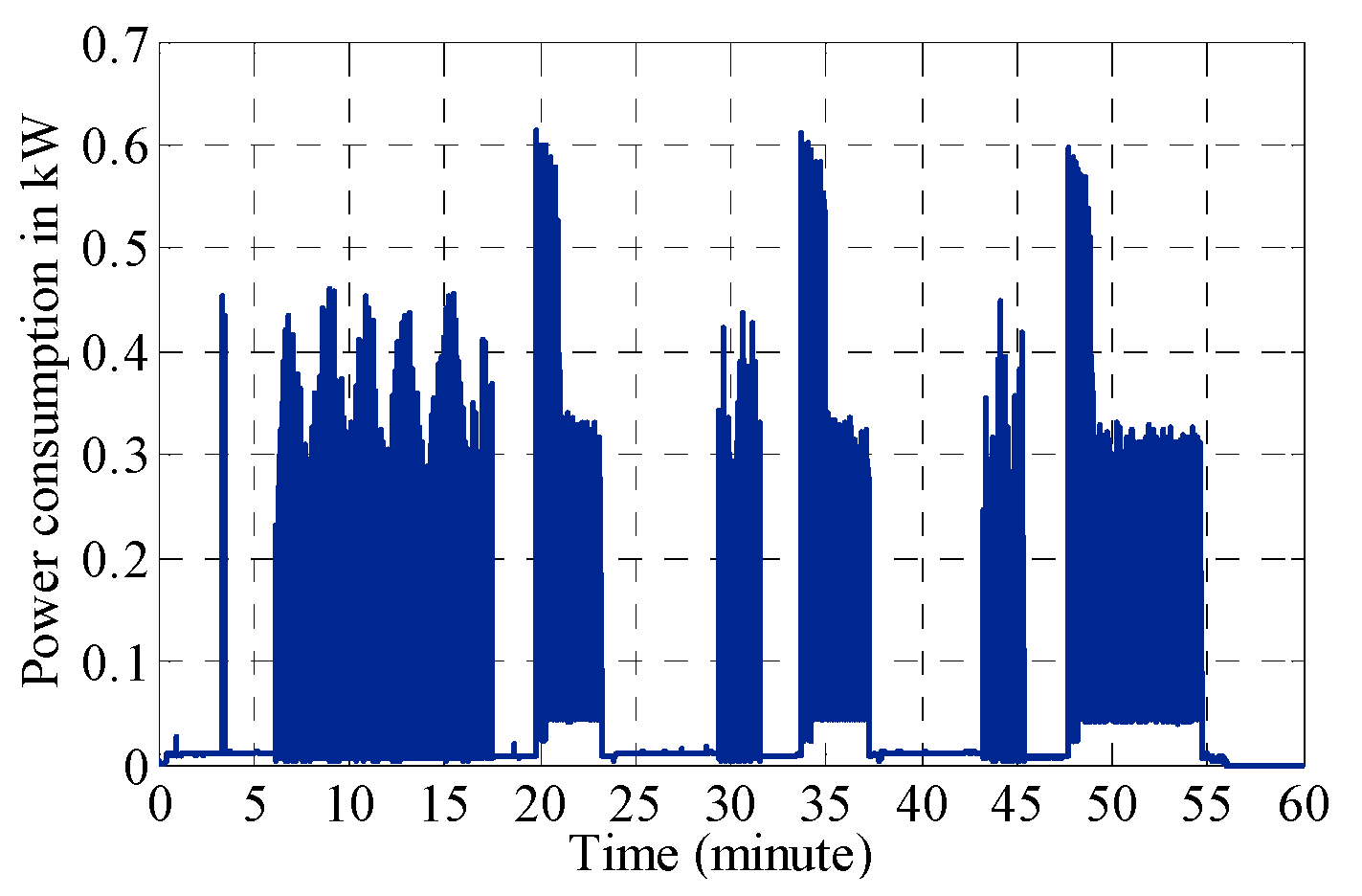
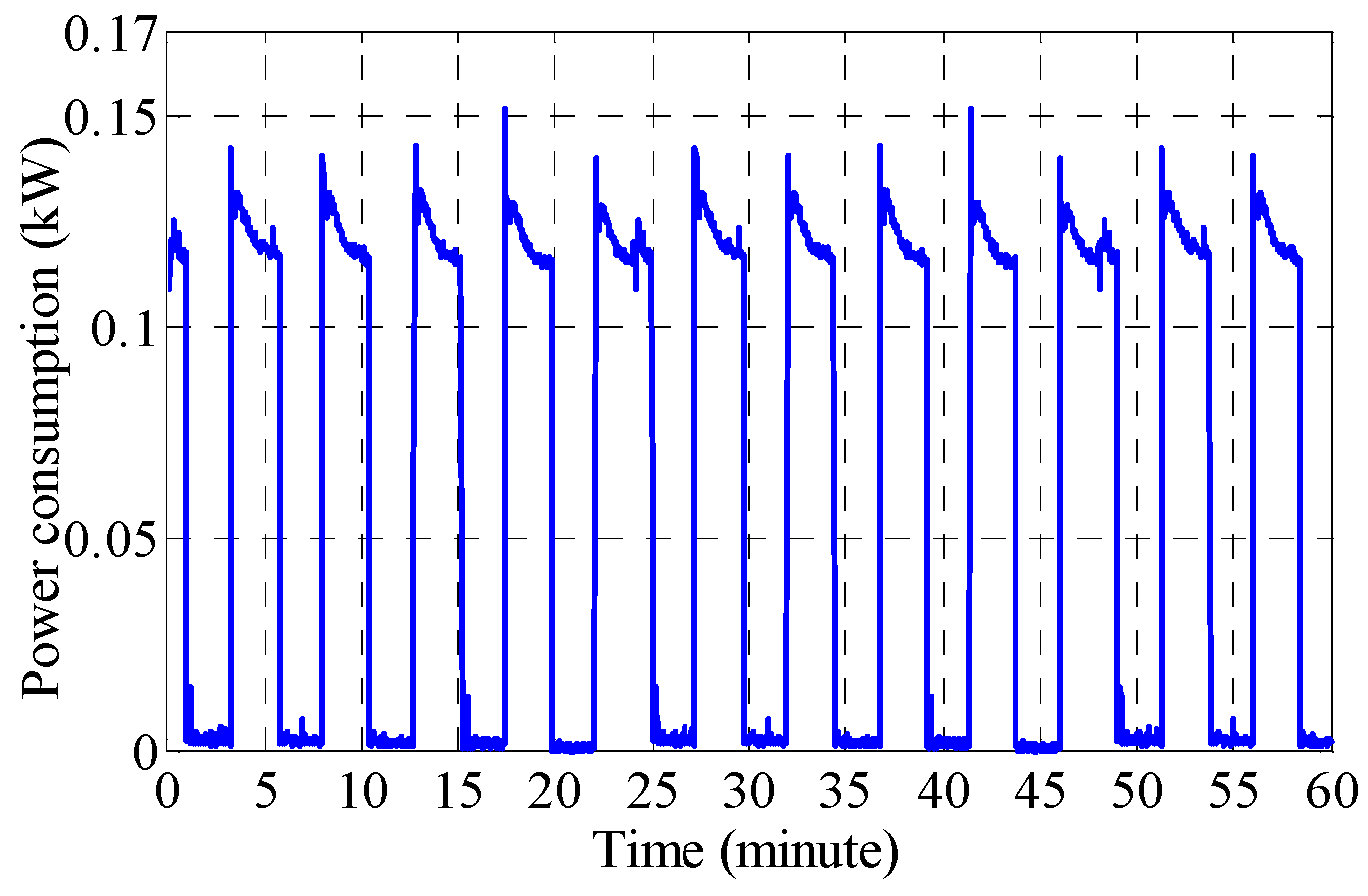
6.2. Experimental Measurement Data
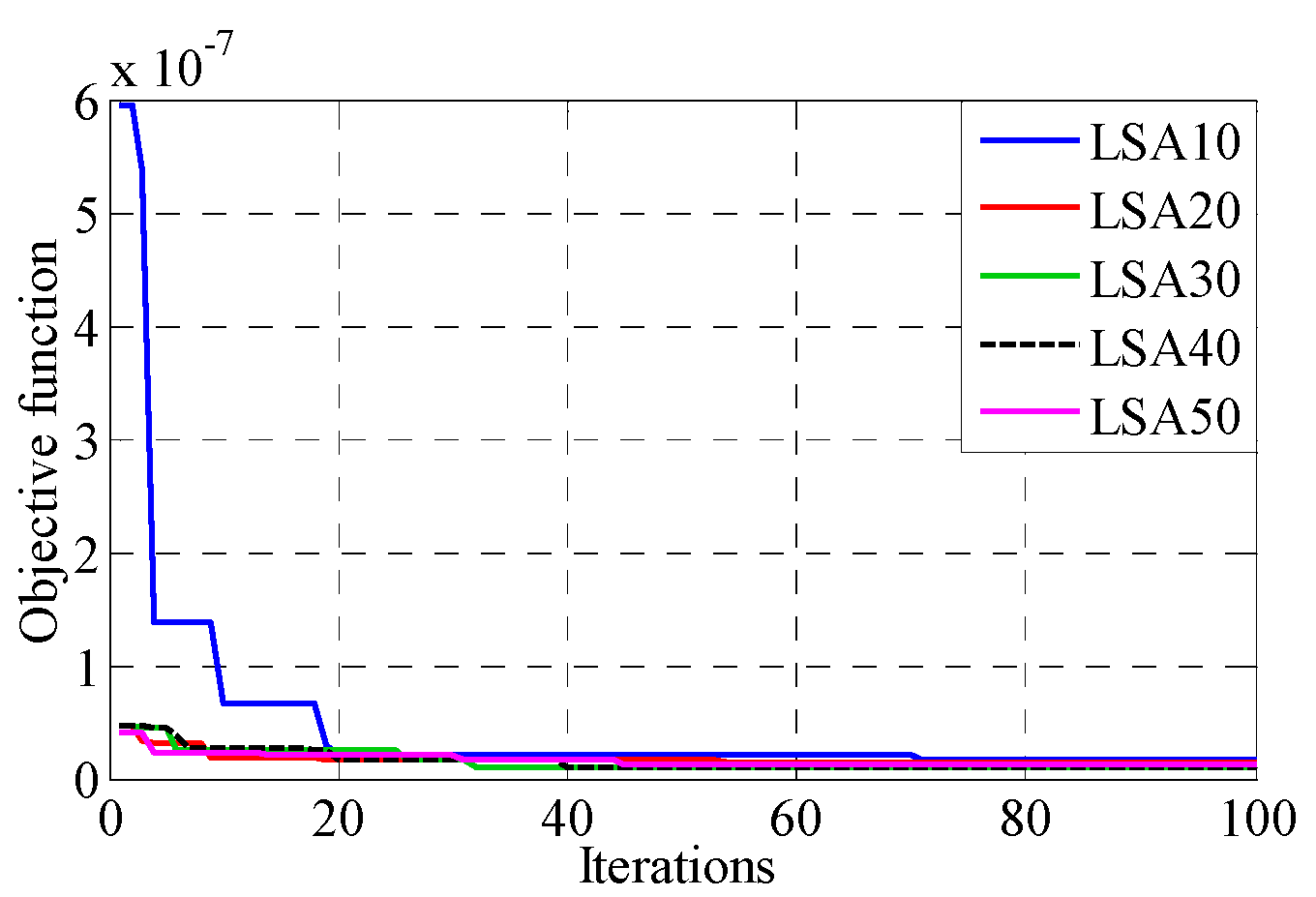
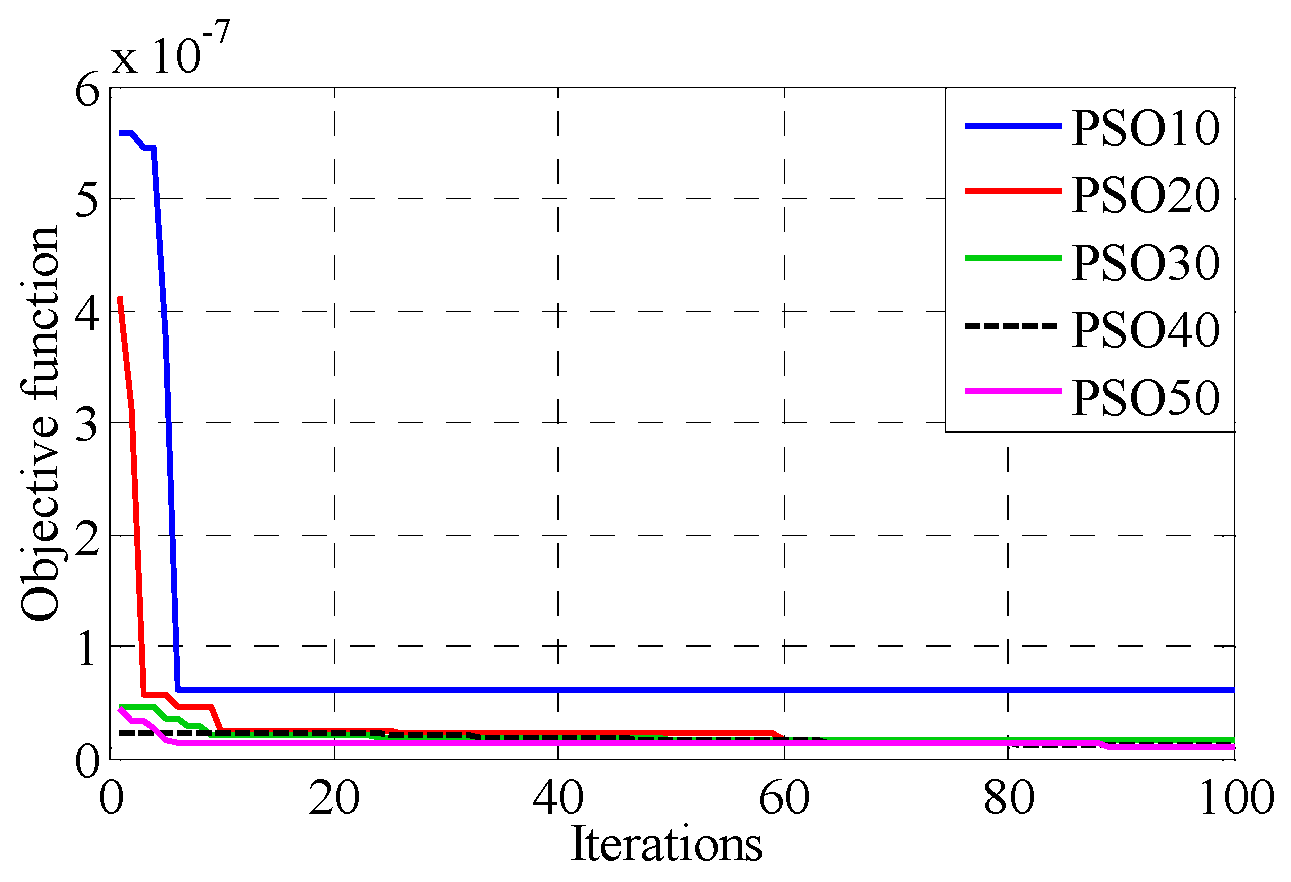
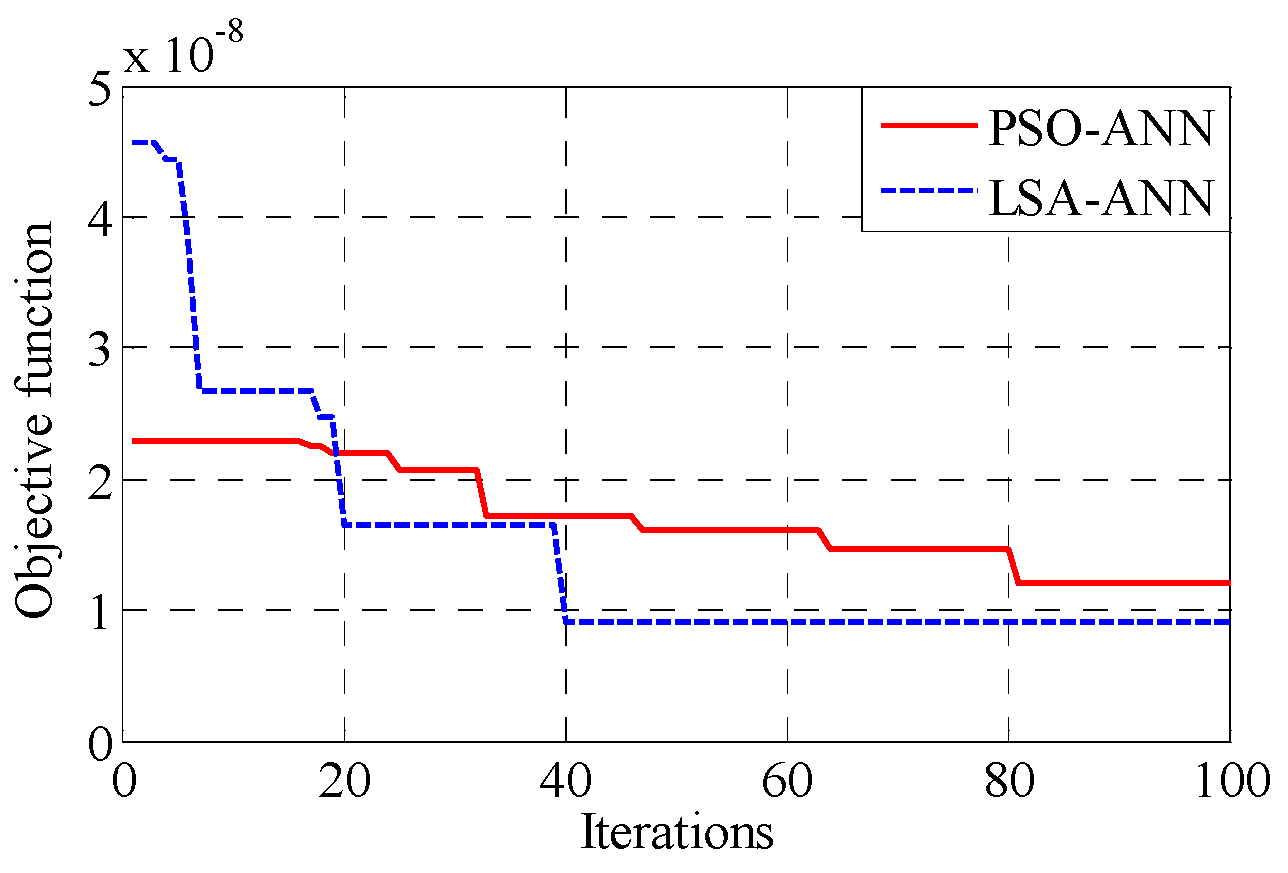
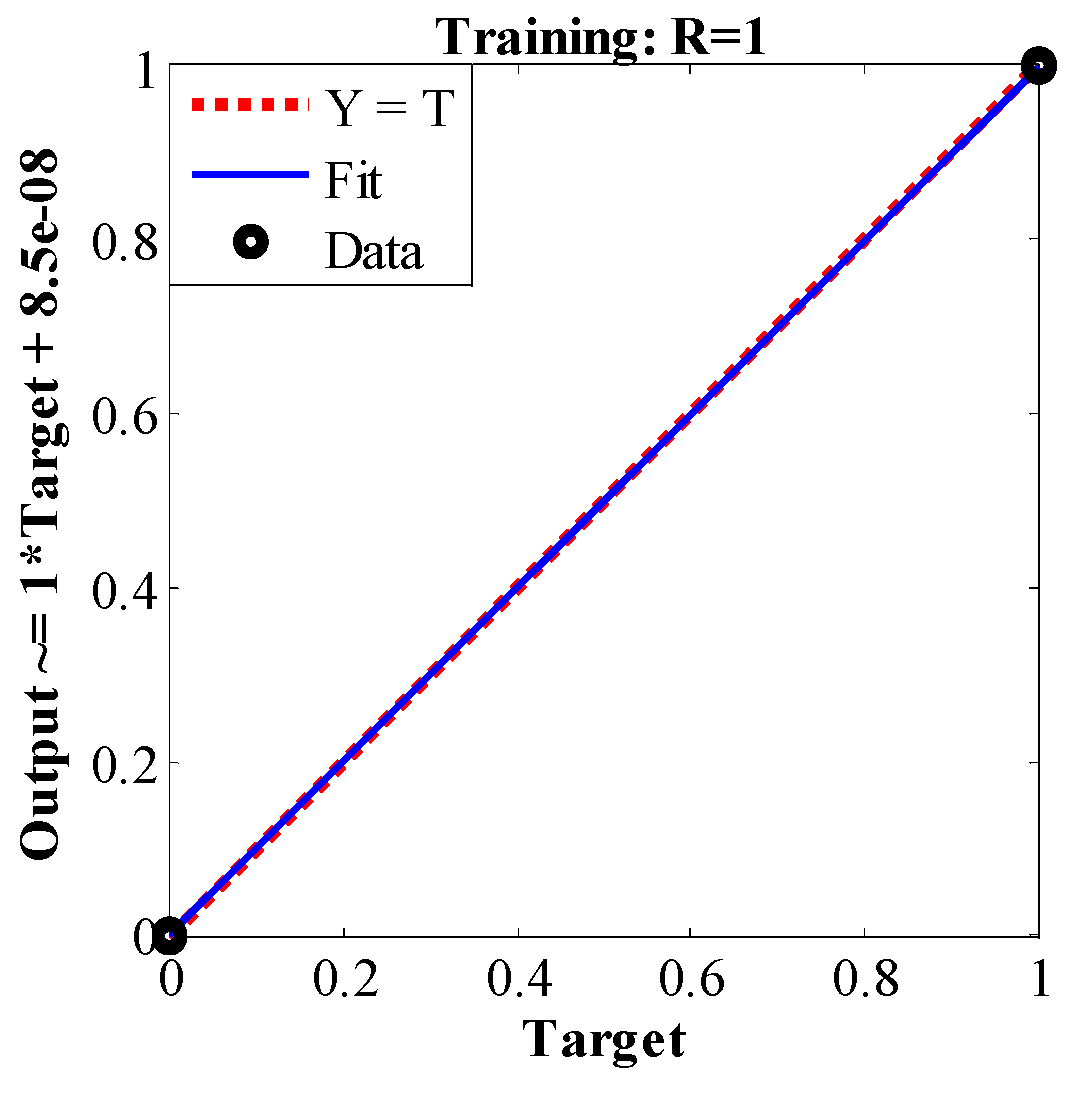
6.3. Results of the Hybrid Lightning Search Algorithm-Based Artificial Neural Network
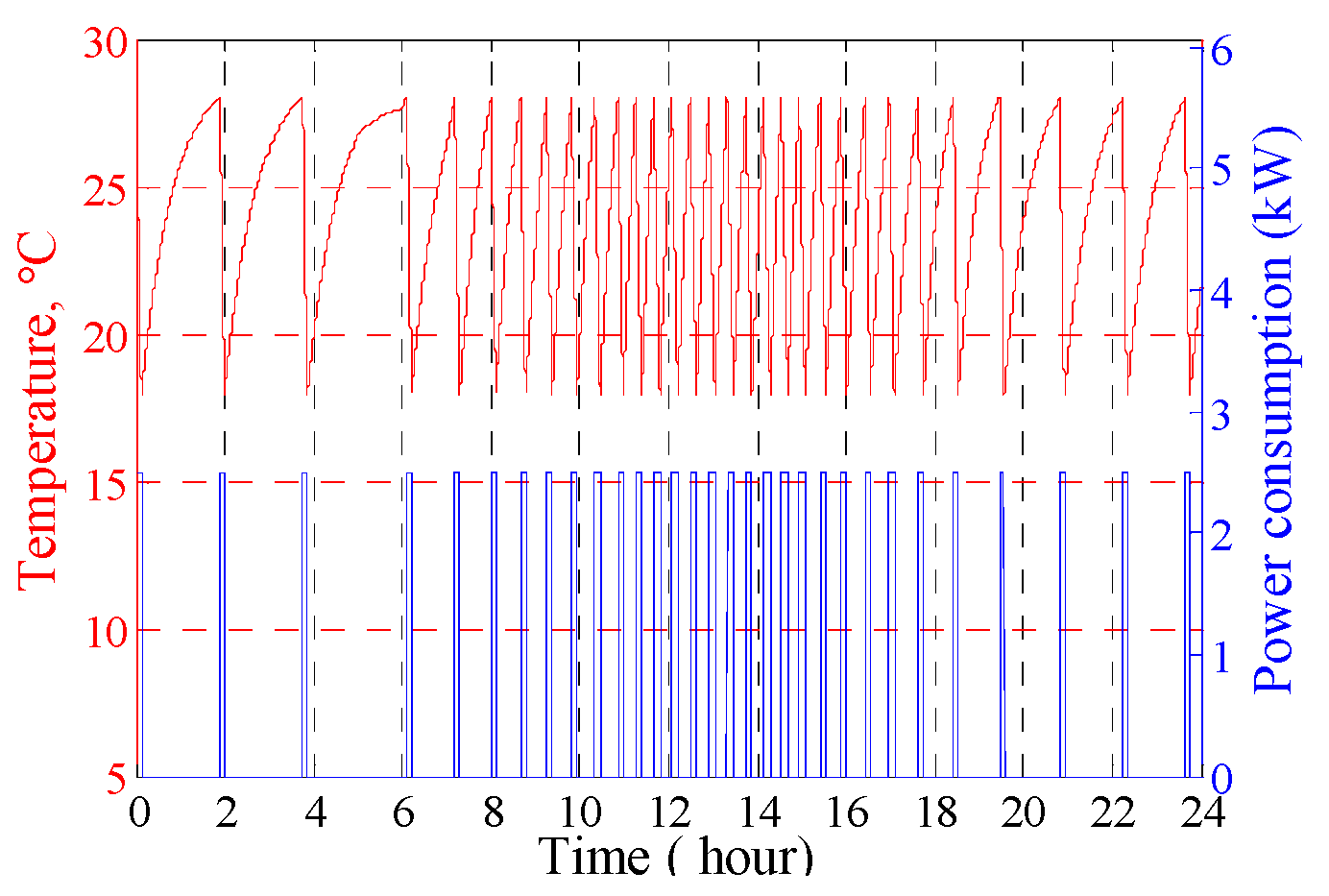
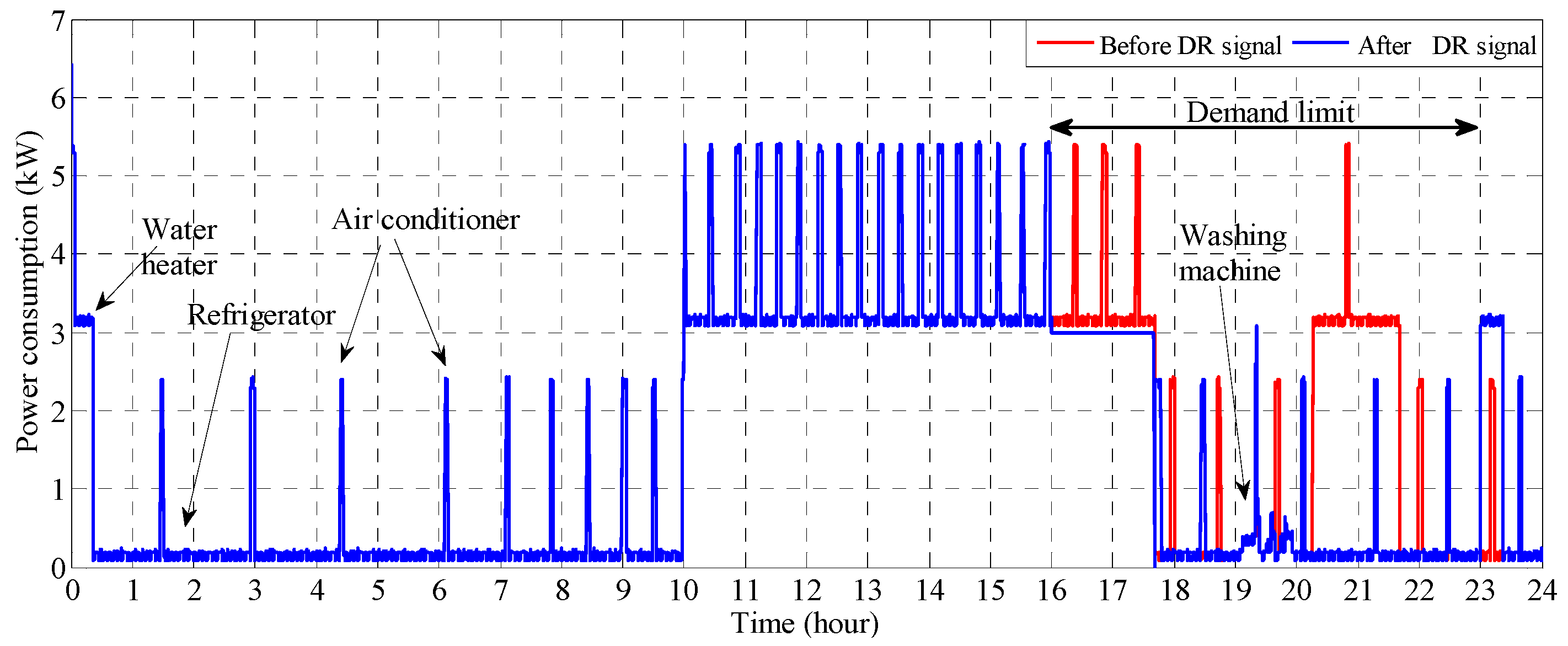
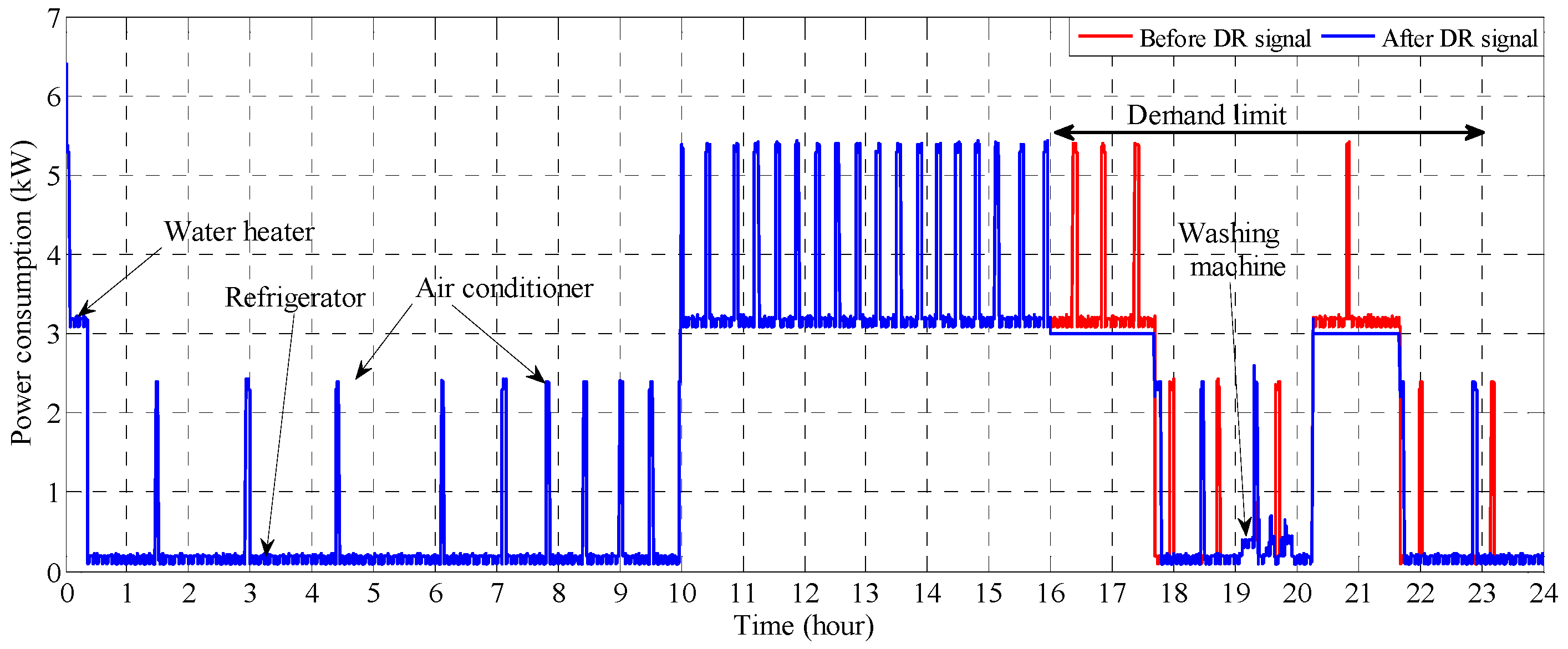
6.4. Results of the Proposed Hybrid LSA-ANN Based Home Energy Management Scheduling Controller
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deploying a Smarter Grid through Cable Solutions and Services, 2010. Available online: http://www.nexans.com/Corporate/2010/WHITE_PAPER_SMART_GRIDS_2010.pdf (accessed on 9 August 2016).
- Hammond, G.P.; Pearson, P.J. Challenges of the transition to a low carbon, more electric future: From here to 2050. Energy Policy 2013, 52, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Barton, J.; Huang, S.; Infield, D.; Leach, M.; Ogunkunle, D.; Torriti, J.; Thomson, M. The evolution of electricity demand and the role for demand side participation, in buildings and transport. Energy Policy 2013, 52, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Huaman, R.N.E.; Tian, X.J. Energy related CO2 emissions and the progress on ccs projects: A review. Renew. Sustain. Energy Rev. 2014, 31, 368–385. [Google Scholar] [CrossRef]
- Yun, G.Y.; Kim, H.; Kim, J.T. Effects of occupancy and lighting use patterns on lighting energy consumption. Energy Build. 2012, 46, 152–158. [Google Scholar] [CrossRef]
- Richardson, I.; Thomson, M.; Infield, D.; Clifford, C. Domestic electricity use: A high-resolution energy demand model. Energy Build. 2010, 42, 1878–1887. [Google Scholar] [CrossRef] [Green Version]
- Horst, G.R.; Zhang, J.; Syvokozov, A.D. Total home Energy Management System. U.S. Patent 7561977 B2, 14 July 2009. [Google Scholar]
- Arif, M.T.; Oo, A.M.T.; Stojcevski, A. An investigation for improved home energy management. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014.
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A survey on demand response programs in smart grids: Pricing methods and optimization algorithms. IEEE Commun. Surv. Tutor. 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Patel, K.; Khosla, A. Home energy management systems in future smart grid networks: A systematic review. In Proceedings of the 2015 1st International Conference on Next Generation Computing Technologies (NGCT), Dehradun, India, 4–5 September 2015; pp. 479–483.
- Farzamkia, S.; Ranjbar, H.; Hatami, A.; Iman-Eini, H. A novel PSO (particle swarm optimization)-based approach for optimal schedule of refrigerators using experimental models. Energy 2016, 107, 707–715. [Google Scholar] [CrossRef]
- Abd Ali, J.; Hannan, M.A.; Mohamed, A. A novel quantum-behaved lightning search algorithm approach to improve the fuzzy logic speed controller for an induction motor drive. Energies 2015, 8, 13112–13136. [Google Scholar] [CrossRef]
- Ali, J.A.; Hannan, M.; Mohamed, A.; Abdolrasol, M.G. Fuzzy logic speed controller optimization approach for induction motor drive using backtracking search algorithm. Measurement 2016, 78, 49–62. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Mohamed, A.; Shareef, H. Optimal power quality monitor placement in power systems using an adaptive quantum-inspired binary gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2014, 57, 404–413. [Google Scholar] [CrossRef]
- Kang, S.J.; Park, J.; Oh, K.-Y.; Noh, J.G.; Park, H. Scheduling-based real time energy flow control strategy for building energy management system. Energy Build. 2014, 75, 239–248. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Leon-Garcia, A. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. Dynamic residential load scheduling based on adaptive consumption level pricing scheme. Electr. Power Syst. Res. 2016, 133, 27–35. [Google Scholar] [CrossRef]
- Hernandez, C.A.; Romero, R.; Giral, D. Optimization of the use of residential lighting with neural network. In Proceedings of the 2010 International Conference on Computational Intelligence and Software Engineering (CiSE), Wuhan, China, 10–12 December 2010.
- Pedrasa, M.A.; Spooner, E.D.; MacGill, I.F. Robust scheduling of residential distributed energy resources using a novel energy service decision-support tool. In Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies (ISGT), Anaheim, CA, USA, 17–19 January 2011.
- Setlhaolo, D.; Xia, X.; Zhang, J. Optimal scheduling of household appliances for demand response. Electr. Power Syst. Res. 2014, 116, 24–28. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, R.; Wang, L. Multi-agent control system with intelligent optimization for smart and energy-efficient buildings. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1144–1149.
- Yuce, B.; Rezgui, Y.; Mourshed, M. ANN–GA smart appliance scheduling for optimised energy management in the domestic sector. Energy Build. 2016, 111, 311–325. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M.; Ali, J.A. Accurate wireless sensor localization technique based on hybrid PSO–ANN algorithm for indoor and outdoor track cycling. IEEE Sens. J. 2016, 16, 529–541. [Google Scholar] [CrossRef]
- Homod, R.Z.; Sahari, K.S.M.; Almurib, H.A.; Nagi, F.H. RLF and TS fuzzy model identification of indoor thermal comfort based on PMV/PPD. Build. Environ. 2012, 49, 141–153. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Development of physical-based demand response-enabled residential load models. IEEE Trans. Power Syst. 2013, 28, 607–614. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Building Energy Codes Progeam. Available online: http://www.Energycodes.Gov/support/shgc_faq.Stm (accessed on 15 May 2016).
- Kandar, M.; Nikpour, M.; Ghasemi, M.; Fallah, H. Study of the effectiveness of solar heat gain and day light factors on minimizing electricity use in high rise buildings. World Acad. Sci. Eng. Technol. 2011, 73, 73–77. [Google Scholar]
- Ahmed, M.S.; Shareef, H.; Mohamed, A.; Ali, J.A.; Mutlag, A.H. Rule base home energy management system considering residential demand response application. Appl. Mech. Mater. 2015, 785, 526–531. [Google Scholar] [CrossRef]
- Bertoldi, P.; Hirl, B.; Labanca, N. Energy Efficiency Status Report 2012; Joint Research Centre, European Commission: Ispra, Italy, 2012. [Google Scholar]
- Mutlag, A.H.; Mohamed, A.; Shareef, H. A nature-inspired optimization-based optimum fuzzy logic photovoltaic inverter controller utilizing an eZdsp F28335 board. Energies 2016, 9, 120. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]




| Parameter | Value | Type |
|---|---|---|
| Number of inputs | 5 | ANN inputs |
| Number of outputs | 4 | ANN outputs |
| Number of hidden layers | 2 | ANN hidden layer |
| Number of neurons in hidden layer N1 | 6 | Obtained from LSA |
| Number of neurons in hidden layer N2 | 4 | Obtained from LSA |
| Number of iterations | 1000 | ANN iterations |
| Learning rate | 0.6175 | Obtained from LSA |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.S.; Mohamed, A.; Homod, R.Z.; Shareef, H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies 2016, 9, 716. https://doi.org/10.3390/en9090716
Ahmed MS, Mohamed A, Homod RZ, Shareef H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies. 2016; 9(9):716. https://doi.org/10.3390/en9090716
Chicago/Turabian StyleAhmed, Maytham S., Azah Mohamed, Raad Z. Homod, and Hussain Shareef. 2016. "Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy" Energies 9, no. 9: 716. https://doi.org/10.3390/en9090716
APA StyleAhmed, M. S., Mohamed, A., Homod, R. Z., & Shareef, H. (2016). Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies, 9(9), 716. https://doi.org/10.3390/en9090716