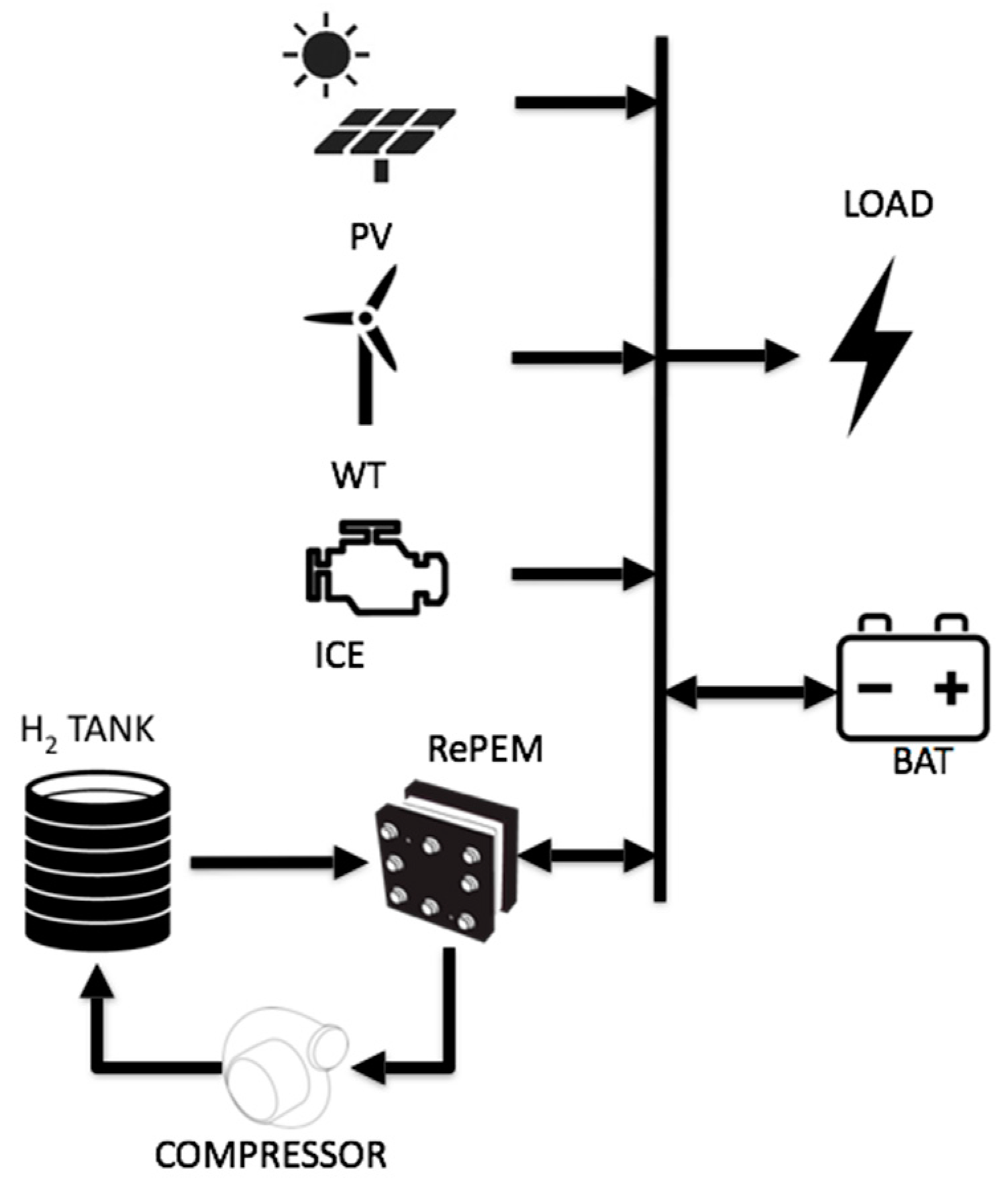
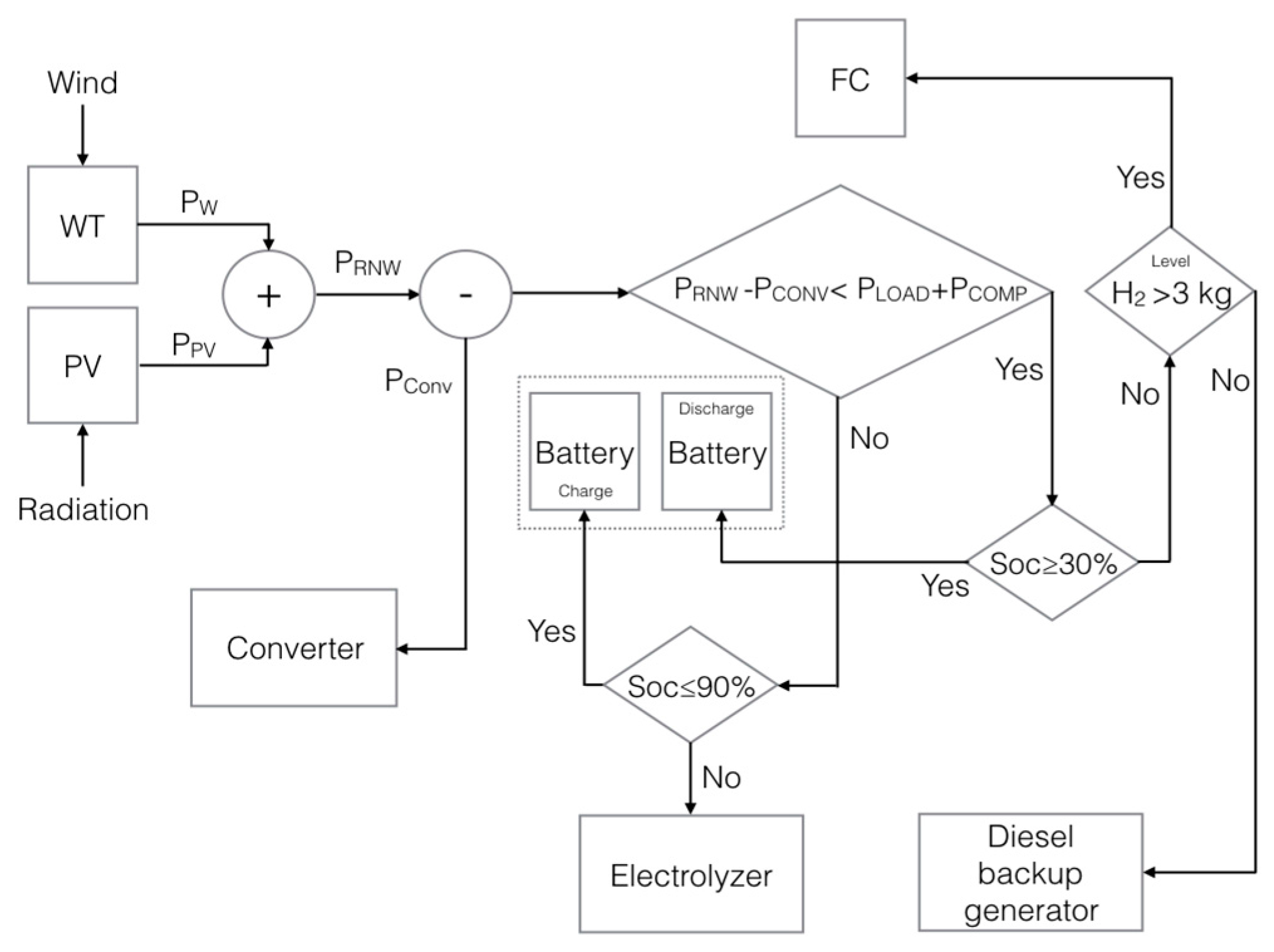
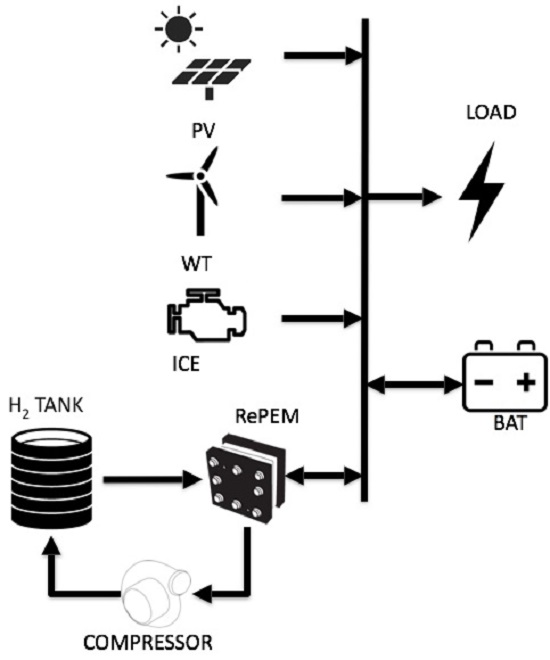
2.1. Component Sizing
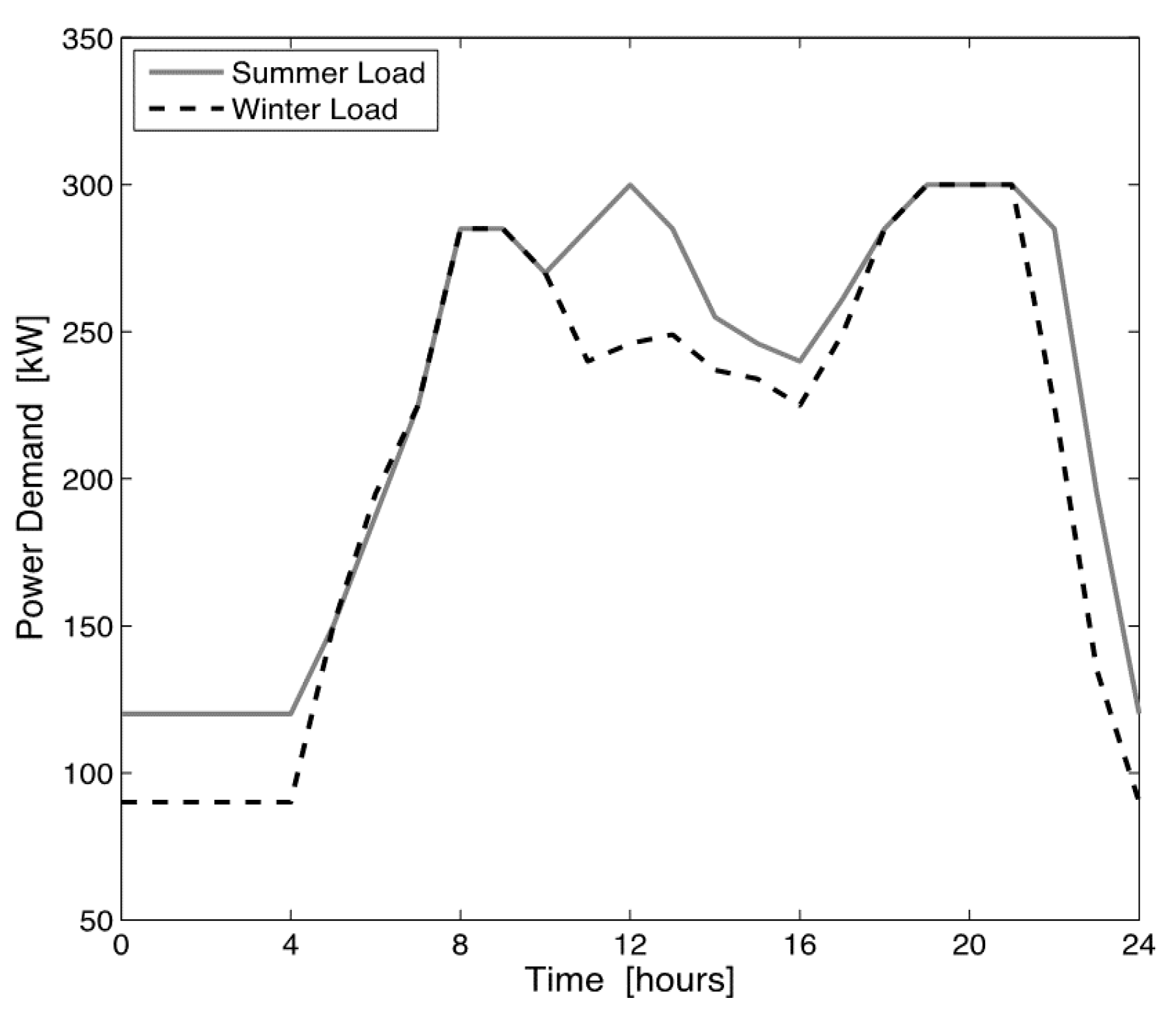
An electrical power demand profile has been assumed in order to reproduce the possible power demand of one of these artificial islands. The project is still on-going, therefore there is no availability of measured data to reproduce real power load profiles. Nonetheless, since these islands will be likely equipped with facilities for tourists, the employed load curves were derived from a past study, realized within a National Operative Program [
11], where the power demand of a mid-size hospitality structure, comparable to the one that could be built on the island, was carefully evaluated by in-situ measurements. The resulting profiles are shown in
Figure 2, and have been used to represent typical summer and winter daily loads, characterized by a peak power demand of 300 kW and a minimum power of 90 kW during winter and 120 kW during summer.
Number of WT, PV panels and the size of the BAT have been optimized by means of HOMER Pro
®, which allows for modeling and sizing each component and for power plant operation analysis. HOMER is one of the most widely used tools for power plant components sizing, having the possibility of combining a great number of renewable energy systems and being able to perform optimizations and sensitivity analyses, which make easier and faster the evaluation of the best system configurations among the many possible [
10].
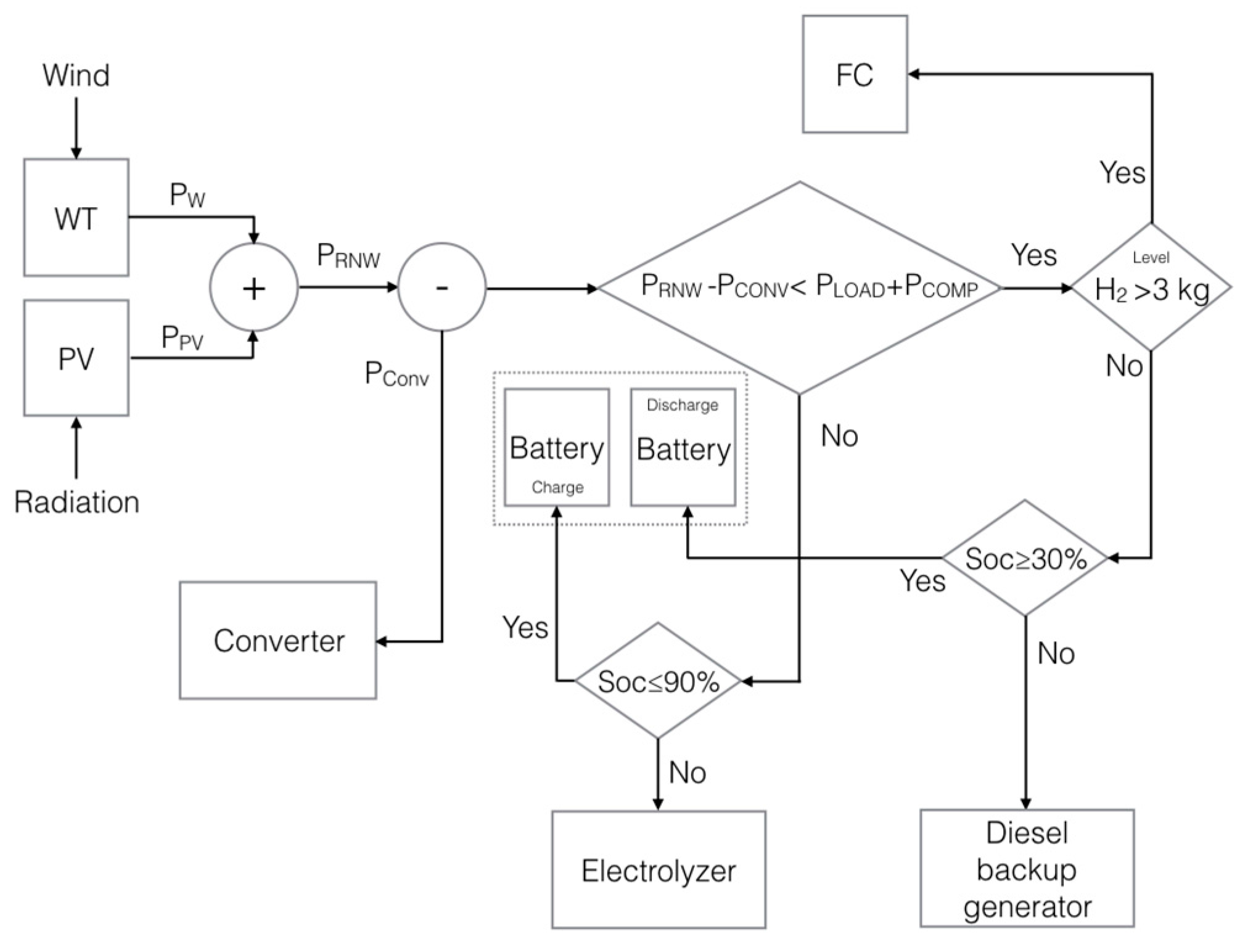
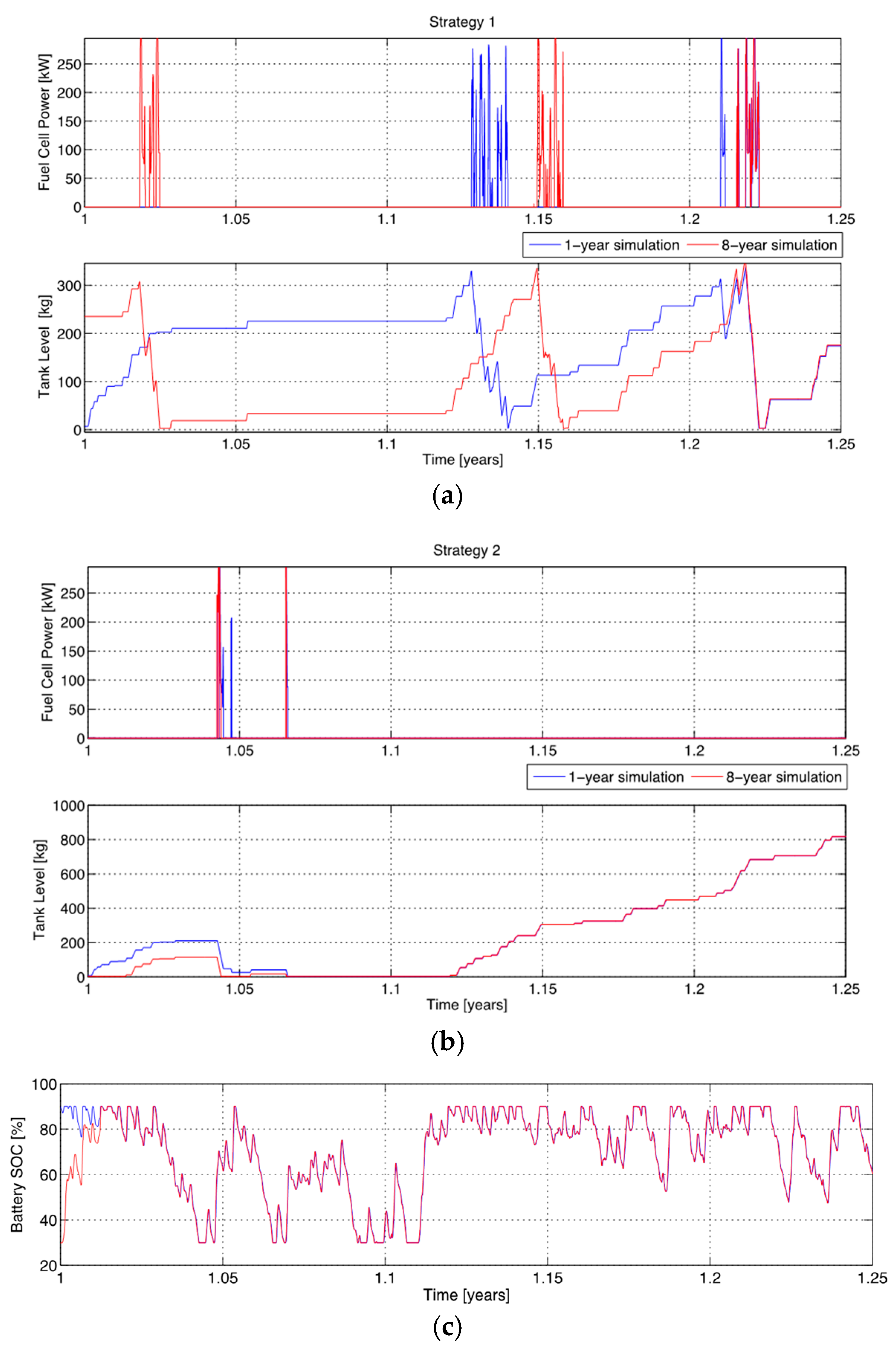
The reversible fuel cell has been sized, a-posteriori, on the basis of a sensitivity analysis, as a trade-off between fossil fuel consumption and initial investment costs, once the plant setup was configured by HOMER. The choice of an a-posteriori sizing of the RePEM has been made to cope with the lack of such a template in HOMER and to use it as a tuning parameter for the power management control strategies, in order to find a trade-off between battery degradation rate and fossil fuel consumption.
HOMER optimizes the plant configuration by applying a full factorial design of experiments and choosing the configuration with the minimum cost of energy, which estimates the installing and operating costs of the system over its lifespan, as already explained in [
12].
In the full factorial array definition, the wind turbine rated power has been set equal to 1 MW, and the number of turbines is the result of the optimization. Such a high value for the rated power is a consequence of a mean annual load factor of only 10.2%, i.e., the turbine utilization factor, function of the specific wind speed profile, considered equal to the one available from a weather station located in Mazara del Vallo, Sicily.
The PV array size has been varied between 800 kW and 1.1 MW, by a fixed step of 100 kW. Similar to the wind turbine, these high values of the rated power are dictated by a mean annual load factor of 15.9%, as a function of the solar radiation profile that HOMER itself extracts from given latitude and longitude values, i.e., N 37°33′ latitude and E 12°0′ longitude [
13,
14,
15].
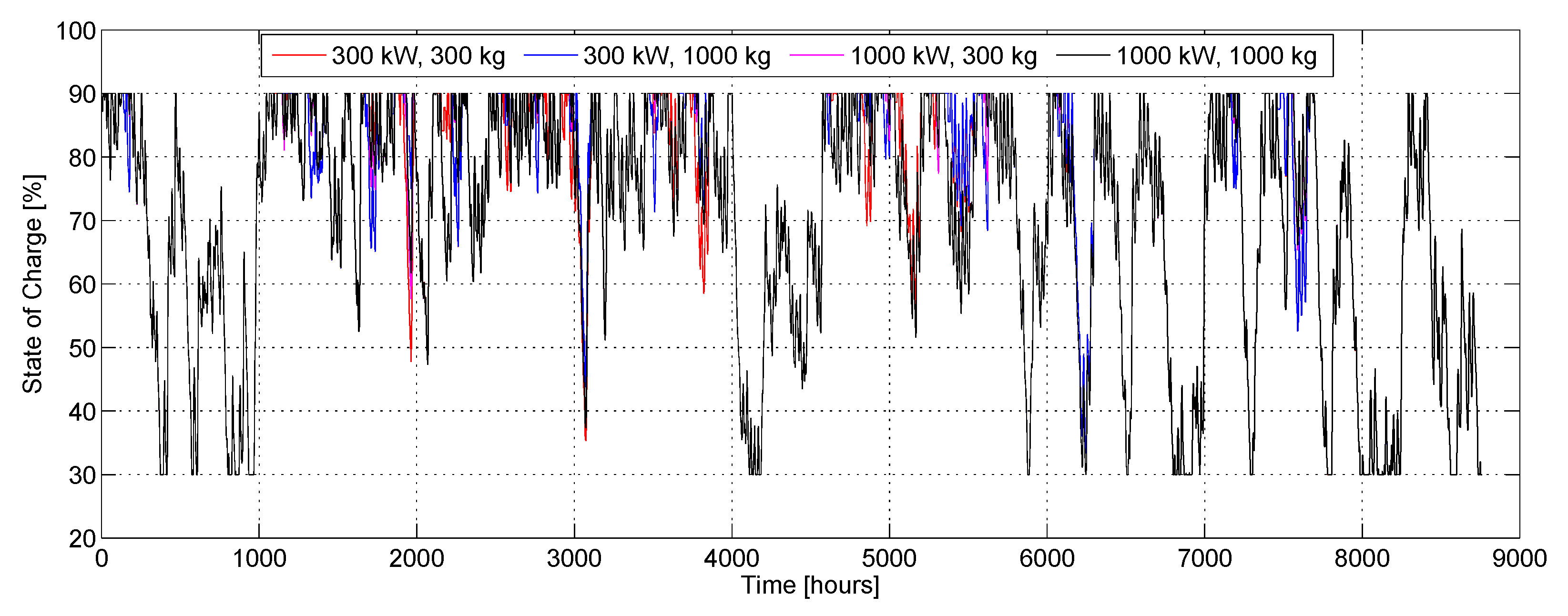
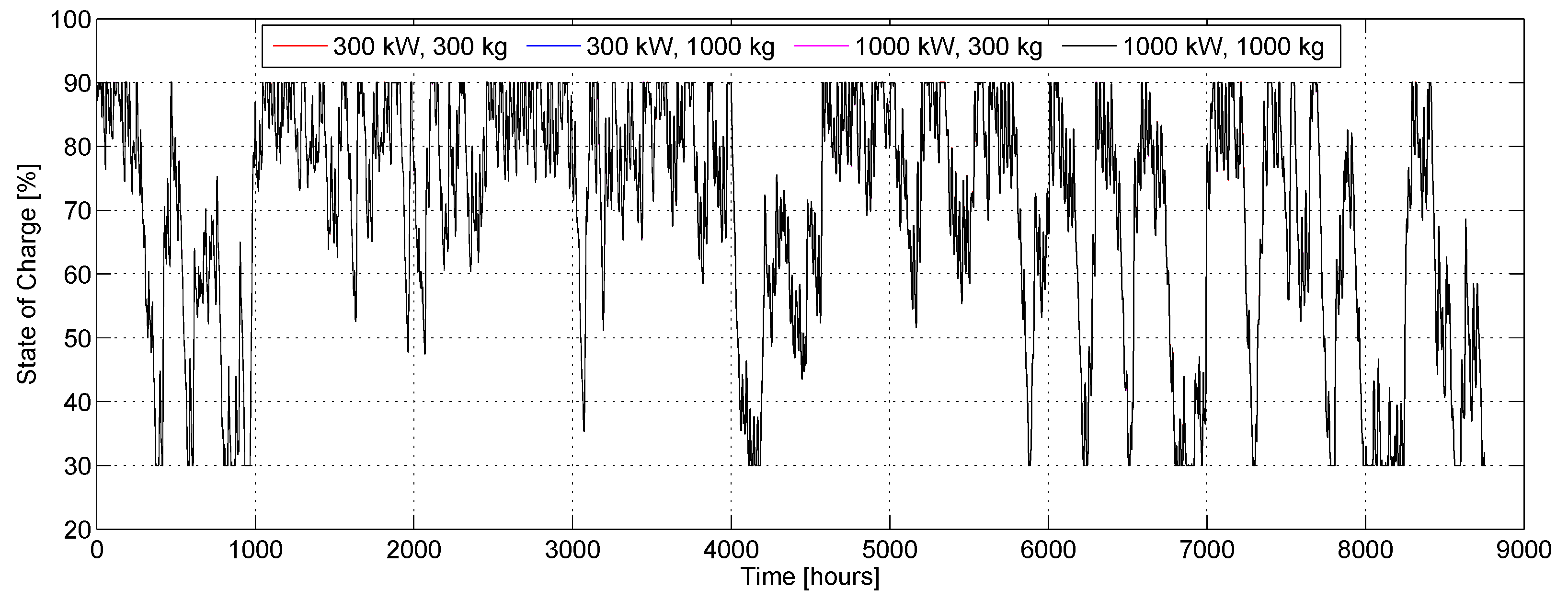
For the BAT, a number of strings in parallel varying in the range of 100–700 has been considered, with a step of 100. A single battery string is composed of 12 cells, set in series, with nominal cell voltage of 2 V, nominal capacity of 3000 Ah and SOC range 30%–90% [
16].
The final configuration obtained in the optimization performed with HOMER consists of: 1 wind turbine, 1.1 MW rated power for the PV array and 200 battery strings.
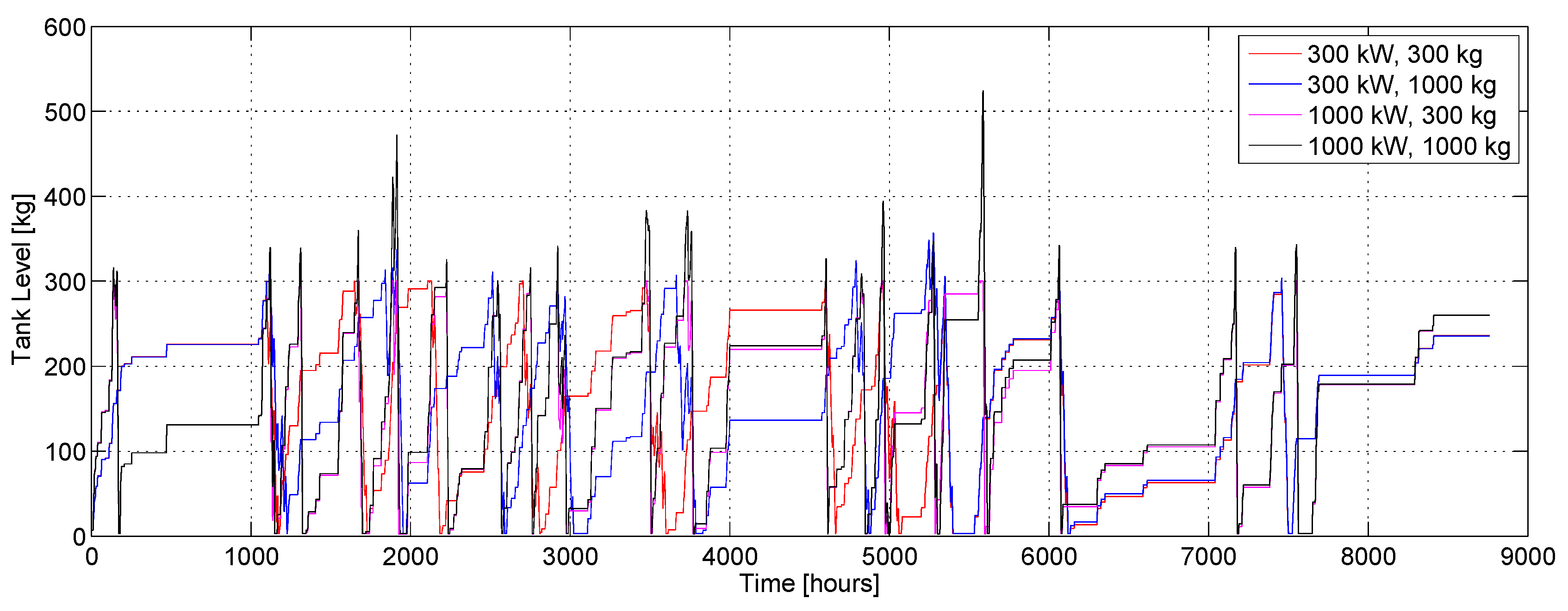
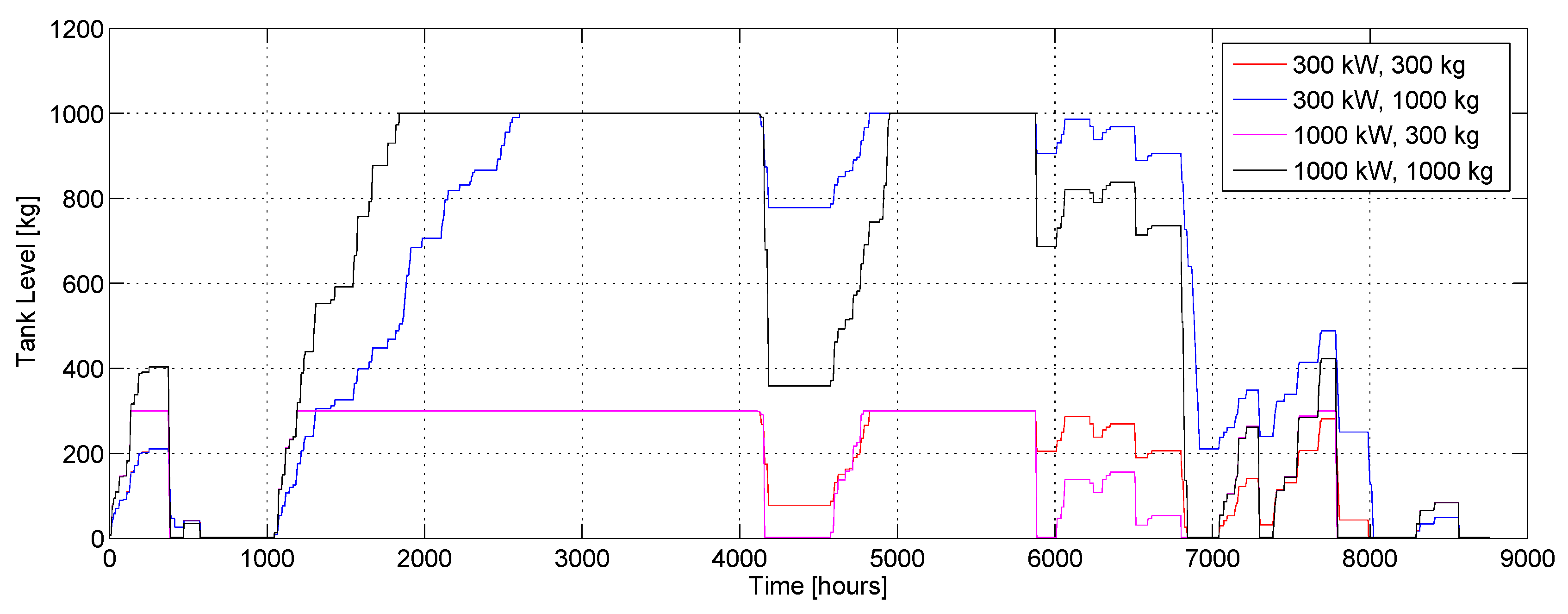
For the reversible fuel cell offline sizing, five scenarios, shown in
Table 1, have been considered, varying the maximum stack power and the tank capacity. A fixed volume has been considered in the different scenarios for the tank, therefore different energy consumptions can be ascribed to the compressor in the five cases, affecting the overall efficiency of the power plant.
Finally, for the ICE, being a backup system, it has been sized as to be able to satisfy the peak power demand, i.e., 300 kW. In fact, its usage must cope with failures or it should be used to fulfill power demands higher than the maximum considered.
2.2. Component Modeling
Once the power plant was sized, its operation has been simulated by means of an energy-based quasi-static simulator developed in Matlab/Simulink
® environment [
17], which includes an equivalent circuit model for the battery operation and battery state of charge dynamics, and a semi-empirical model for the RePEM.
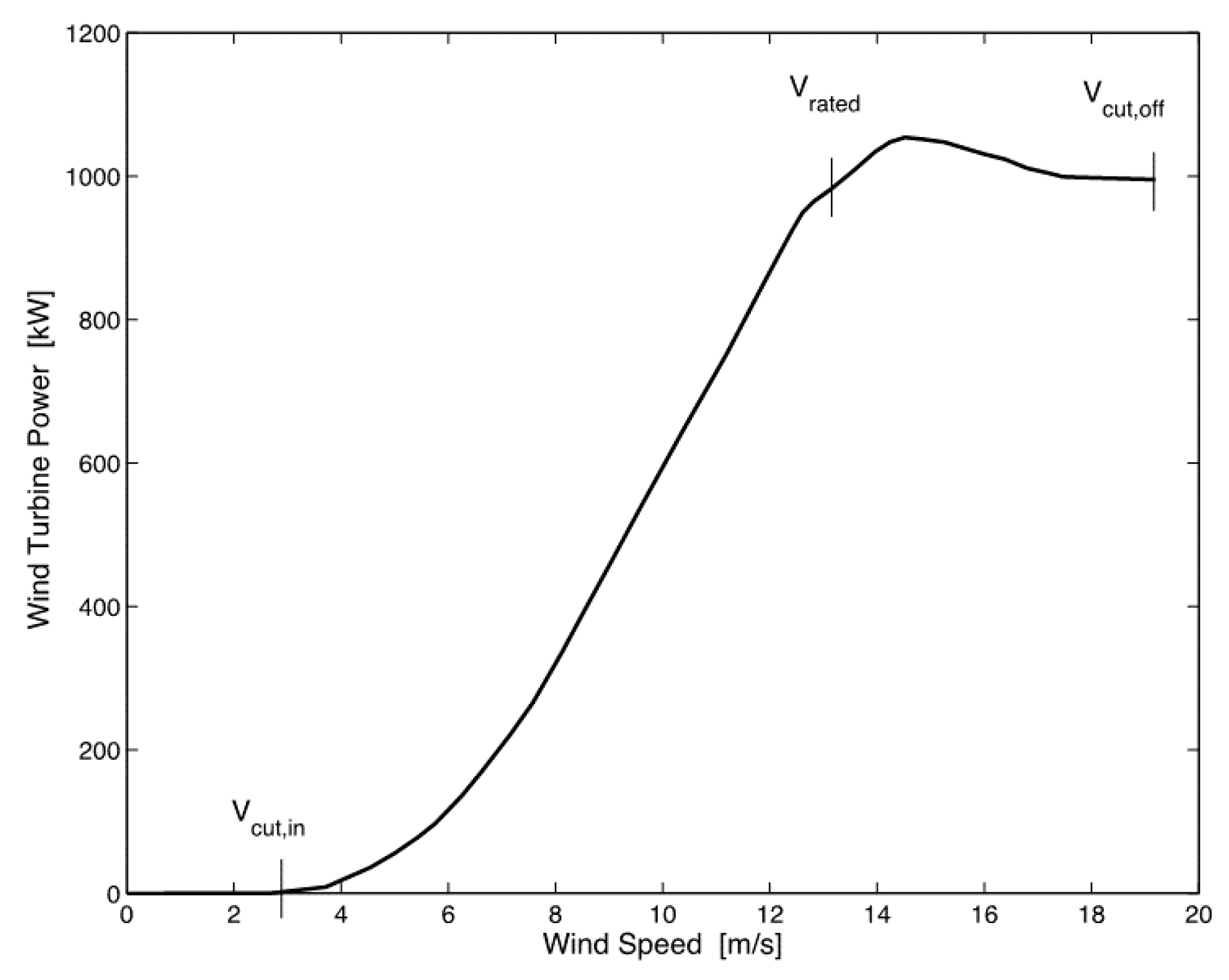
(1) Wind turbine: this component has been modeled as a device which converts wind kinetic power into mechanical power (
PW), by means of a user defined wind turbine power curve, shown in
Figure 3, for the considered turbine.
The turbine power is obviously a function of wind speed as per Equation (1):
where
Vcut,in is the cut-in wind speed, i.e., the wind speed at which the turbine starts generating output power;
Vcut,off is the maximum allowable wind speed, above which blades damage could occur;
V is the wind speed, whose values—collected at a certain anemometer height—are corrected to the turbine hub height; ρ is the air density;
AT is the area swept by the blades; and
Cp is turbine power coefficient, or rotor efficiency, which also depends on the wind speed. Nevertheless, WT with a rated capacity of about 1 MW or larger are usually equipped with an active stall control mechanism. In such systems, the controller makes the turbine run at maximum efficiency, i.e., maximum power coefficient—until the rated power is reached. Once the wind speed has reached the so-called rated wind speed value, pitch angle is adjusted so that to stall the turbine and limit the output power.
(2) Photovoltaic panels: for the PV array, dependency on temperature has been included as suggested by [
19]. The power output from the PV system has been evaluated as:
where
Apv is the PV system area, while η
PV is the panel efficiency, given by:
where η
pv,ref is the module electrical efficiency at reference cell temperature
Tref and at solar radiation flux of 1 kW/m
2, while β is the temperature coefficient, which is mainly a material property. The quantities η
pv,ref and β are normally given by the panel manufacturer and, in this work, considering a mono-crystalline silicon module and a reference temperature of 25 °C, the reference efficiency has been set equal to 0.15, while β to 0.004 K
−1 [
19].
The cell operating temperature
Tc has been evaluated by using the following relation:
where
Tamb is the ambient temperature, whose profile is available in HOMER from latitude and longitude data, i.e., N 37°33′ latitude and E 12°0′ longitude. Unfortunately, these data are available only as monthly average, which is considered sufficiently appropriate for this analysis, although future studies will be addressed to consider the effect of at least hourly variation.
The term
TNOCT represents the nominal cell operating temperature, which is defined as the cell temperature operating in standard reference temperature
TS of 20 °C, irradiance
INOCT of 0.8 kW/m², wind speed of 1 m/s and considering the module tilted at 45°. In this study
TNOCT is set to 47 °C [
20], but the previous relation was corrected by means of a derating factor,
fPV becoming:
The parameter fPV is a constant scaling dimensionless factor, which takes into account effects of everything which would cause the output of the PV array deviate from what expected under ideal conditions—such as dust on panel, wire losses, elevated temperature, etc.
(3) Reversible fuel cell: the RePEM model is based on the approach suggested by [
21] and integrated with some empirical relations and coefficients retrieved from [
22,
23,
24]. Considering ohmic and activation losses, η
ohm and η
act, the load voltage can be calculated as:
with:
where EL stands for electrolyzer and FC stands for fuel cell. Since for the sake of simplicity, influence of pressure and temperature has been neglected in the model,
VOC,RePEM coincides to the Nernst potential. The ohmic losses are given by:
where
IRePEM is the current across the device and
Rohm represents the ohmic resistance, evaluated with the following empirical relation, as proposed by [
22]:
where
lm is the membrane thickness in cm,
Am is the cell active area in cm
2, λ
m is a parameter related to the membrane hydration (7 if dry enough; 14 for good hydration; 22 for bathed),
Tcell is the cell temperature, here fixed equal to 338 K.
The activation losses expression is retrieved from [
22,
23], leading to:
where R is the universal gas constant, and α is the charge transfer coefficient, which expresses how the change in the voltage across the reaction interface changes the rate of the reaction. It has been fixed equal to 0.452 [
22], which is the value usually considered for hydrogen and oxygen reacting on a platinum catalyst;
n is the number of electrons transferred per mole, which equals 2 for hydrogen;
F is the Faraday constant equal to 96.485 C/kmol;
iRePEM is the cell current density, given by the ratio between the current and the active area; and
i0 represents the exchange current density at equilibrium potential, i.e., when the net current is equal to zero, and has been fixed equal to 0.13 mA, as suggested by [
22].
Given the voltage from Equation (6) and by using information about the required output or available input power, one can evaluate the current flowing through the cell and, thus, the hydrogen consumption or production
(kg/s), by means of the following relation:
where
ns is the number of cells,
MH2 is the hydrogen molecular weight (kg/kmol) and η
F is the Faraday efficiency, given by [
24]:
Finally, the RePEM performance curves obtained with the above exposed model, i.e., polarization curve, power and efficiency, are shown in
Figure 4 as a function of the current density. In this plot, current is negative in FC mode and positive in EL mode. One can immediately note that the device performs better when it operates in EL mode than in FC mode, the latter one supplying a maximum power nearly 26% lower than the former one. Nonetheless, in the proposed power plant the excess power to be absorbed in EL mode is always significantly higher than the maximum power to be supplied in FC mode and, therefore, the performance curves are well suited for the application.
(4) Hydrogen tank: the hydrogen tank stores hydrogen produced by the RePEM in EL mode for later use by the RePEM itself in FC mode. The hydrogen tank is defined as the maximum amount of hydrogen it should contain in kilograms as shown in
Table 1; the process of adding hydrogen to the tank is assumed to consume the electricity required by the compressor and the tank experiences no leakage. In this work, the initial tank level is set to the 5% of the maximum tank level and no constraints hold on the final tank level at the end of the year.
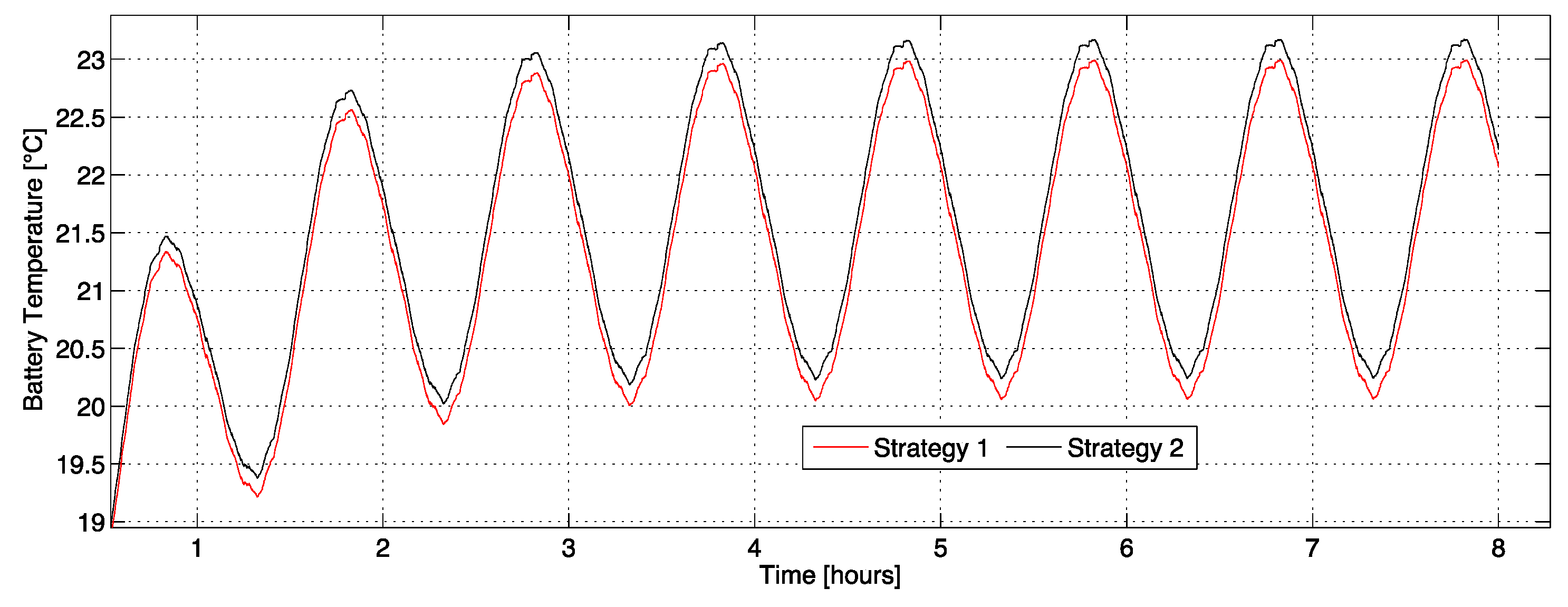
(5) Battery pack: the BAT has been modeled by means of a zero order equivalent circuit model. In this model, VOC,BAT is the open-circuit voltage, RBAT is the equivalent internal resistance and VBAT is the load voltage across the cell terminals. In this analysis, VOC,BAT and Qnom, which is the nominal charge capacity, are approximated as a function of SOC, while RBAT is mapped as function of both SOC and battery operating temperature, TBAT.
The battery operating temperature has been evaluated as the ambient temperature summed by a temperature variation related to internal thermal losses, which can be calculated from the current
IBAT and the internal resistance as proposed by [
25], according to:
which represents a first order differential equation, with parameters for thermal resistance
Rth and thermal capacity
Cth—a function of the specific BAT geometry, mass and materials. The term
RBATIBAT2 represents the power loss in the battery and τ is the integration time variable.
Knowing the battery temperature and state of charge,
VOC,BAT(SOC) and
RBAT(SOC,
TBAT) can be estimated and, for a flowing current, the battery voltage output can be derived from the well-known Kirchhoff voltage law:
By multiplying both sides by the current
IBAT (positive during discharge), the battery power is expressed as:
The variation of the battery SOC is proportional to the current at the battery terminal by means of the following:
Hence, the SOC variation can be evaluated by solving Equation (14) for the current and expressing the state of charge derivative in Equation (15) as a function of battery power.
For the battery lifetime estimation, the semi-empirical algorithm proposed by [
26] for OPzS (flooded lead acid type) batteries, which considers both the dependence on depth of discharge (DOD) and operating temperature, is employed. The applied algorithm estimates the maximum number of cycles
NC, and thus the aging rate, as shown in the following:
In the present study, the depth of discharge to be used in Equation (16) is evaluated as the moving average of the instantaneous DOD, calculated with a sample time of 1 h. The aging rate is the reciprocal of the number of cycles obtained with Equation (16), but an index of the battery lifetime is the cumulate of the aging rate of each cycle, which gives the aging rate corresponding to the total number of cycles experienced by the battery. When this index reaches the value of 1, the number of cycles equals the maximum number of cycles the battery can undergo and the battery is at the end of its life. Therefore, the reciprocal of the cumulated aging rate represents the battery lifetime, measured in years.
(6) Converter: the power converter is simply modeled as a device crossed by electrical power, affected by losses,
PCONV,L, so that:
For sake of simplicity, these losses have been considered to count for the 5% of the total net power flow across the converter.