Structure Optimization of Stand-Alone Renewable Power Systems Based on Multi Object Function
Abstract
:1. Introduction
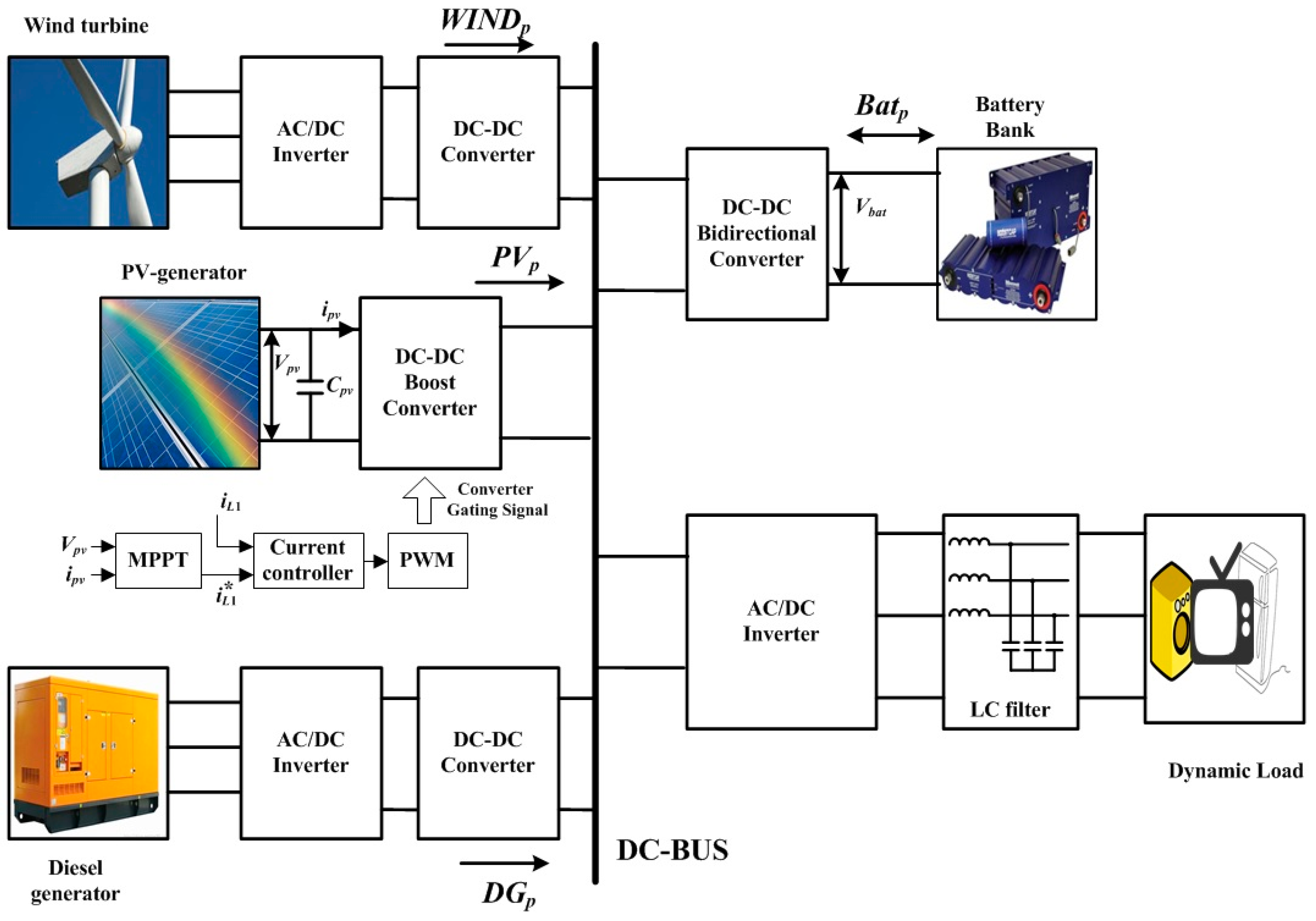
2. Stand-Alone Hybrid PV/Wind/Diesel/Battery System
2.1. System Configuration
2.2. Operation Strategies
3. Modelling of Hybrid Power System Components
3.1. Wind Turbine System
3.2. Photovoltaic System
3.3. Diesel Power System
3.4. Battery Model
4. Cost Modelling of Hybrid Power System
4.1. Annualized Capital Cost (ACS)
4.2. Replacement Capital Cost
4.3. Loss of Power Supply Probability (LPSP)
5. Population-Based Optimization Algorithm
5.1. Genetic Algorithm
| Begin |
| t: = 0 |
| P(t): = InitPopulation(); |
| Evaluate(P(t)) |
| While (stop criteria unsatisfied) |
| P’(t) = Select(P(t)); |
| P’(t) = Crossover(P’(t)); |
| P’(t) = Mutate(P’(t)) |
| Evaluate(P’(t)); |
| P(t + 1) = UpdateNewPop(P(t),P’(t)); |
| t = t + 1; |
| end |
5.2. Particle Swarm Optimization
| For each particle |
| Initialize particle |
| END |
| Do For each particle |
| Calculate fitness value |
| If the fitness value is better than the best fitness value (pBest) in history, set current value as the new pBest |
| End |
| Choose the particle with the best fitness value of all the particles as the gBest |
| For each particle |
| Calculate particle velocity according Equation (a)
V(t + 1) = w * v(t) + c1 * rand() * (pbest(t) – present(t)) + c2 * rand() * (gbest(t) − present(t))
|
| Update particle position according Equation (b)
present(t + 1)= present(t) + v(t + 1)
|
| End |
| While maximum iterations or minimum error criteria is not attained |
| w is inertia weight; c1, c2 is the learning factor, or accelerated variable; rand () is a random number between (0,1). |
5.3. Teaching Learning-Based Optimization
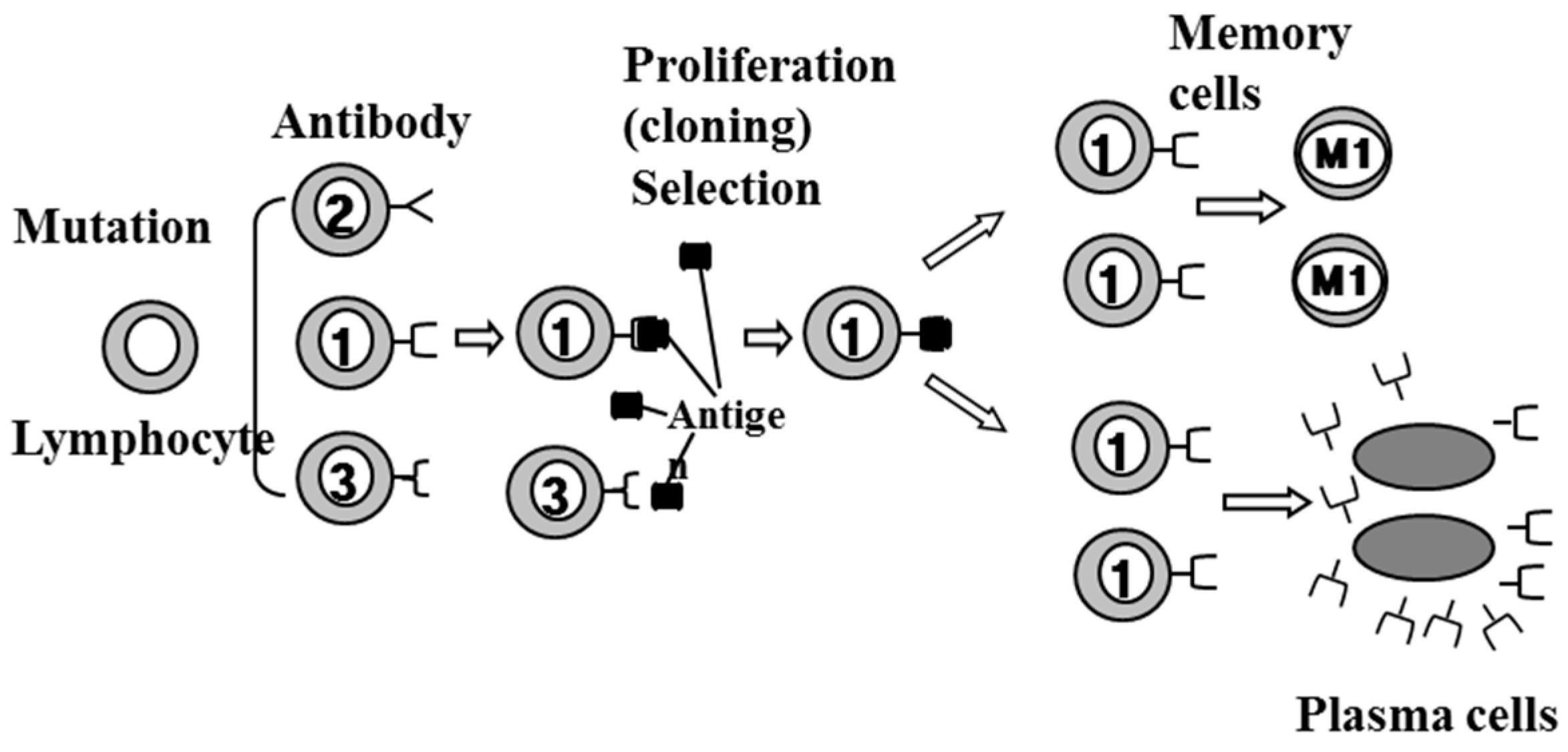
5.4. Clonal Selection Algorithm
- 1)
- Initialization of antibodies;
- 2)
- Cloning and selection (proliferation and differentiation on the encounter of cells with antigens);
- 3)
- Maturation and diversification of antibody types by performing affinity maturation process through random genetic changes;
- 4)
- Removal of differentiated immune cells that possess low affinity.
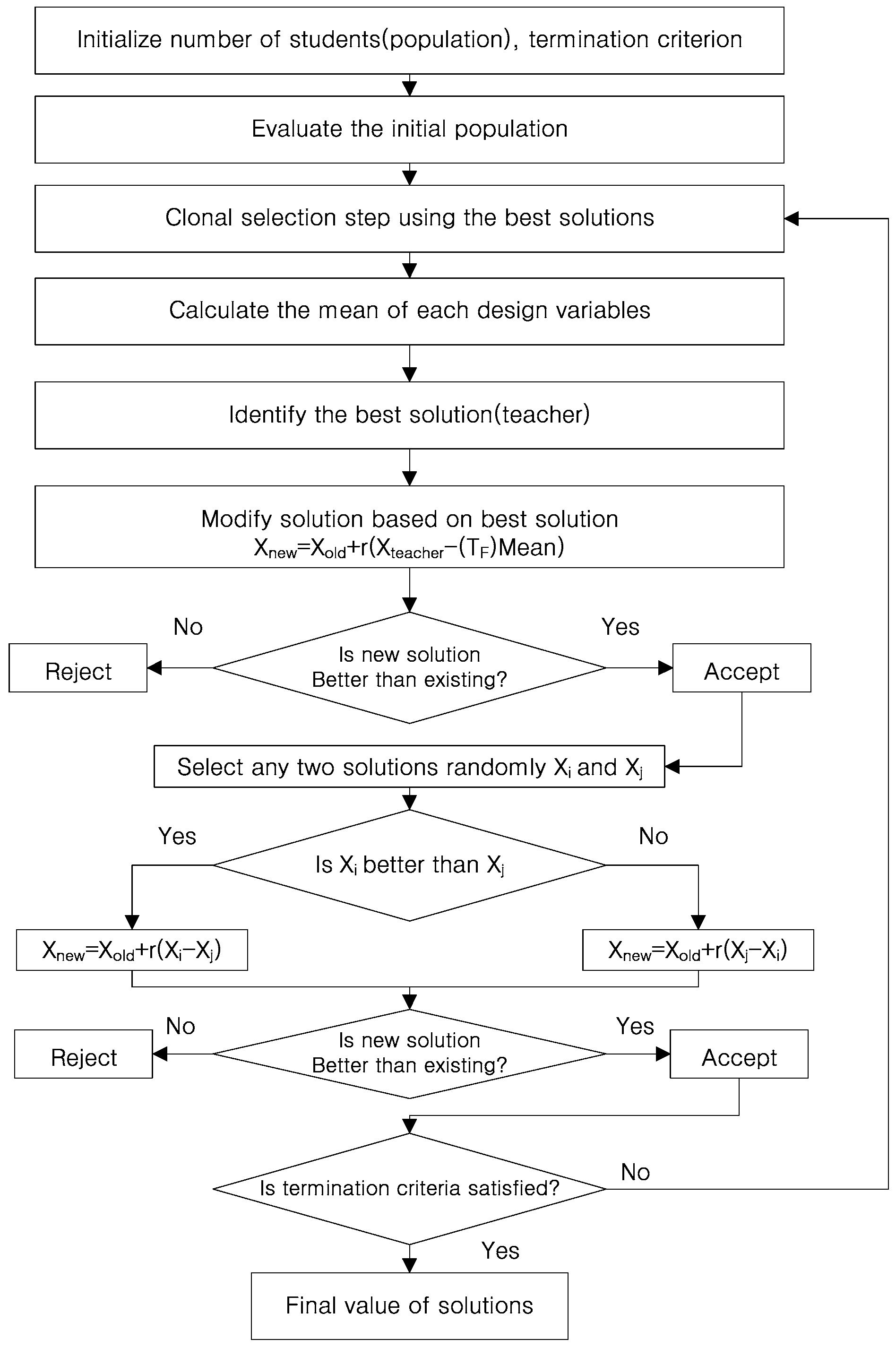
5.5. The Proposed Hybrid Optimization
- Step 1:
- Initialize the learners (i.e., the population) and design variables of the optimization problem (i.e., the number of subject) by random generation.
- Step 2:
- Evaluate the initial learner and select the best learner (i.e., the best solution) as a teacher and assign learners in descending order.
- Step 3:
- Clonal selection (CS) step
- CS-step 3-1:
- Select clones from the assigned learners for clonal selection optimization;
- CS-step 3-2:
- Differentiation step (i.e., duplicate the best learners);
- CS-step 3-3:
- Mutation step (reproduce the clones by mutation);
- CS-step 3-4:
- Evaluate the clones and compare the performance of the teacher (the best learner) with the clones. If the best clone is better than the teacher, assign it as the teacher, otherwise the teacher in Step 2 is retained.
- Step 4:
- Teacher Phase: Update each learner’s knowledge with the help of the teacher’s knowledge using Equation (15).
- Step 5:
- Learner Phase: Update the learners’ knowledge by utilizing the knowledge of some other learner of the same class using Equation (16) or (17).
- Step 6:
- Repeat the procedure from Step 3 to 5 until the termination criterion is met.
5.6. The Object Function of Proposed Hybrid Optimization Algorithm
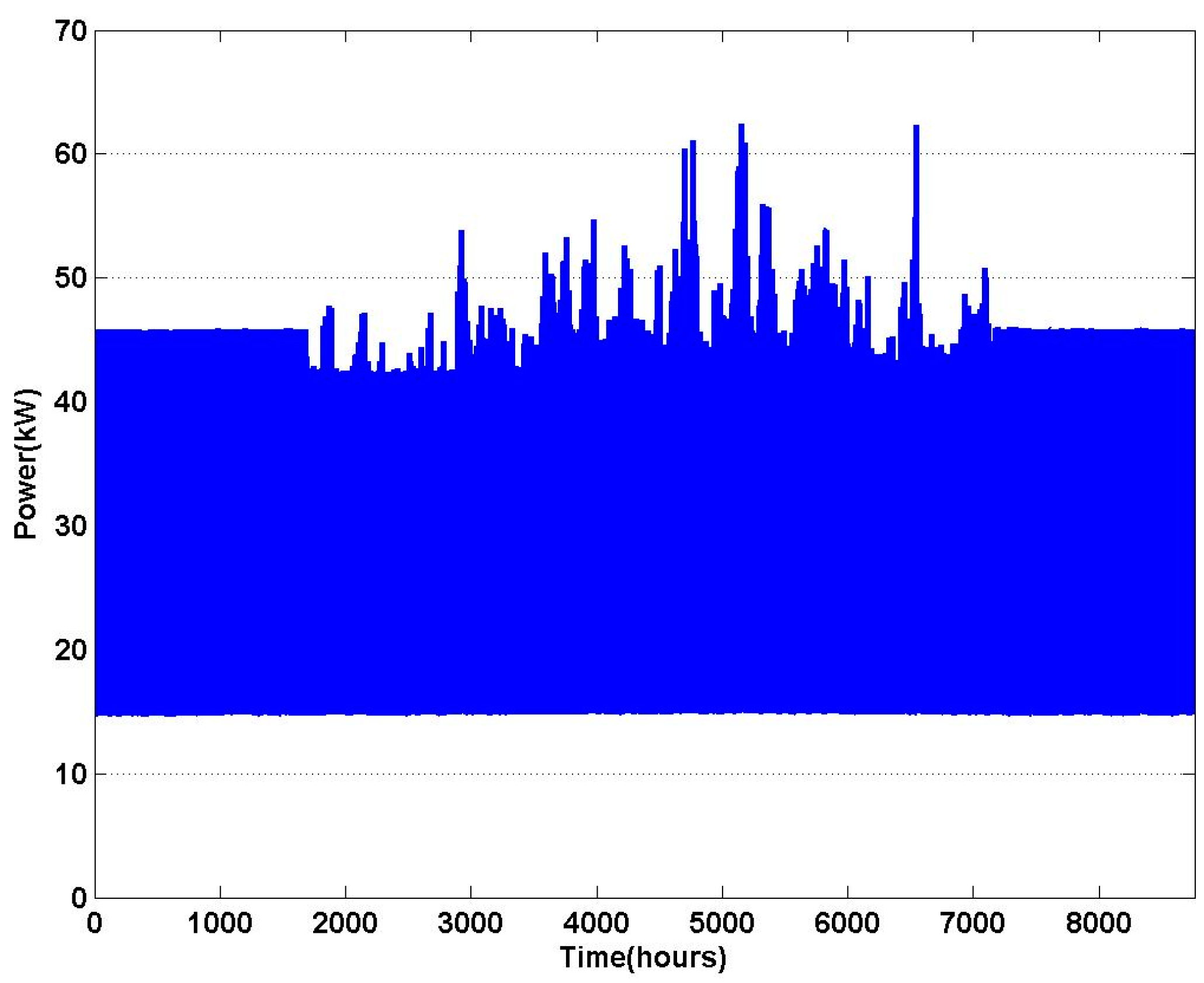
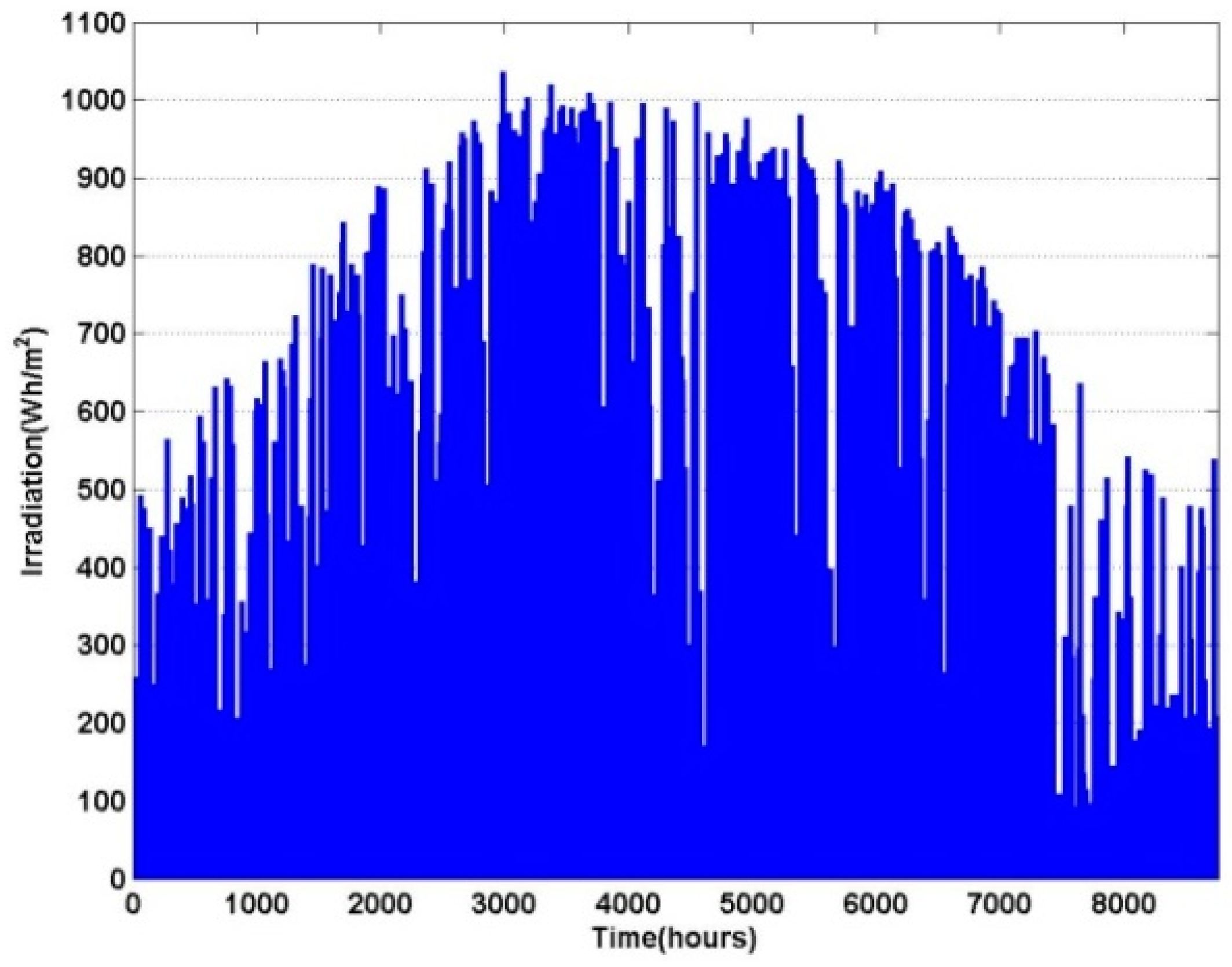
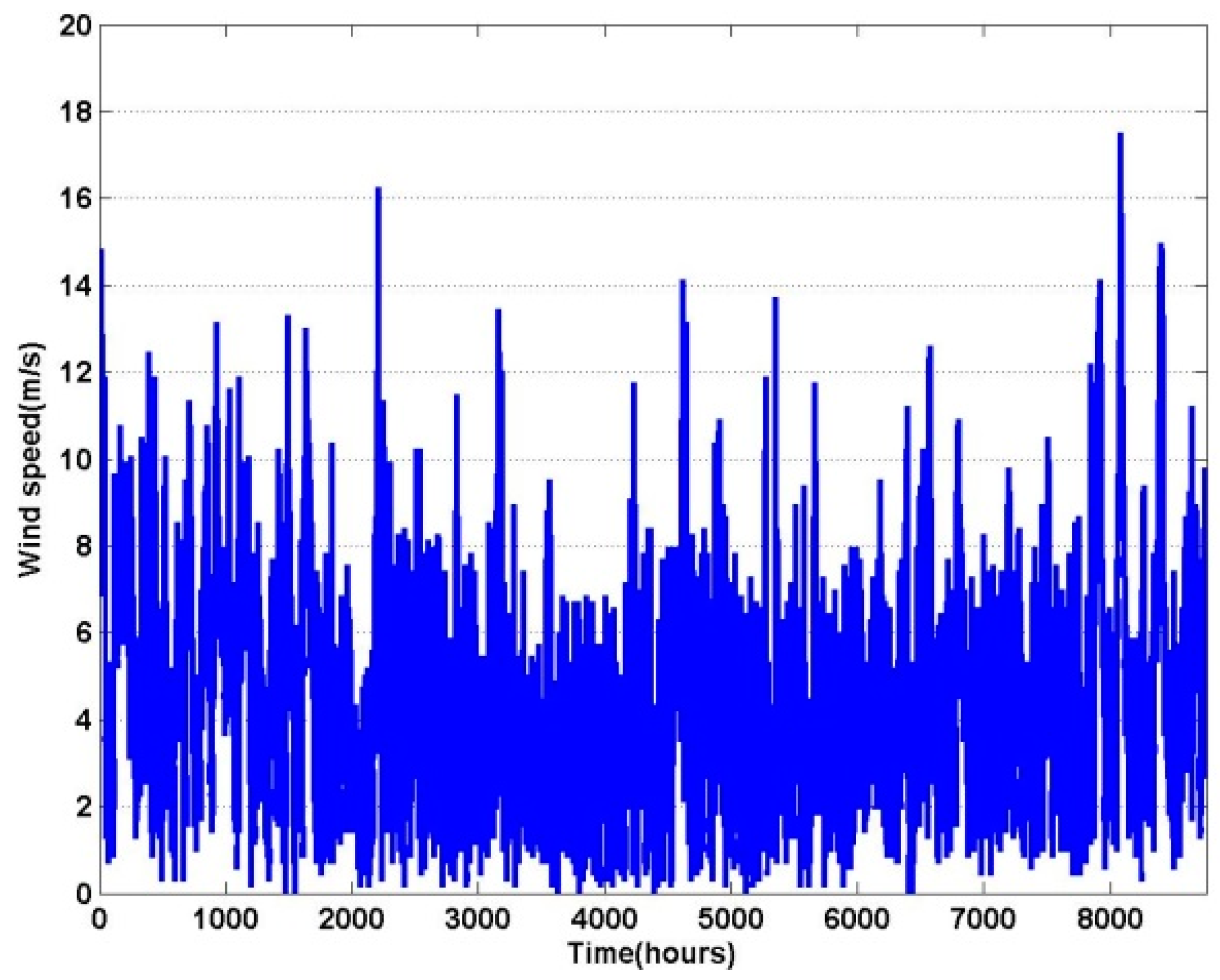
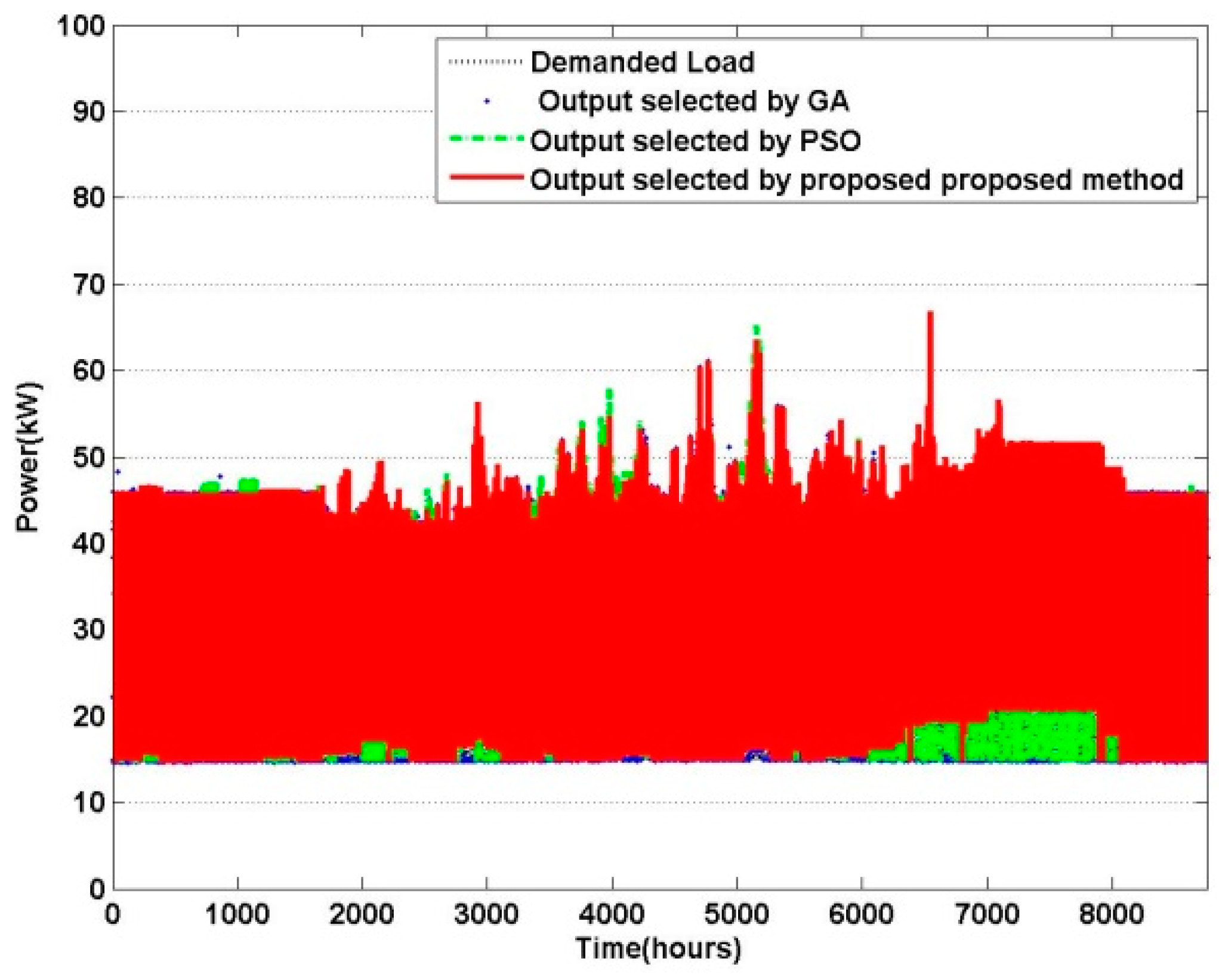
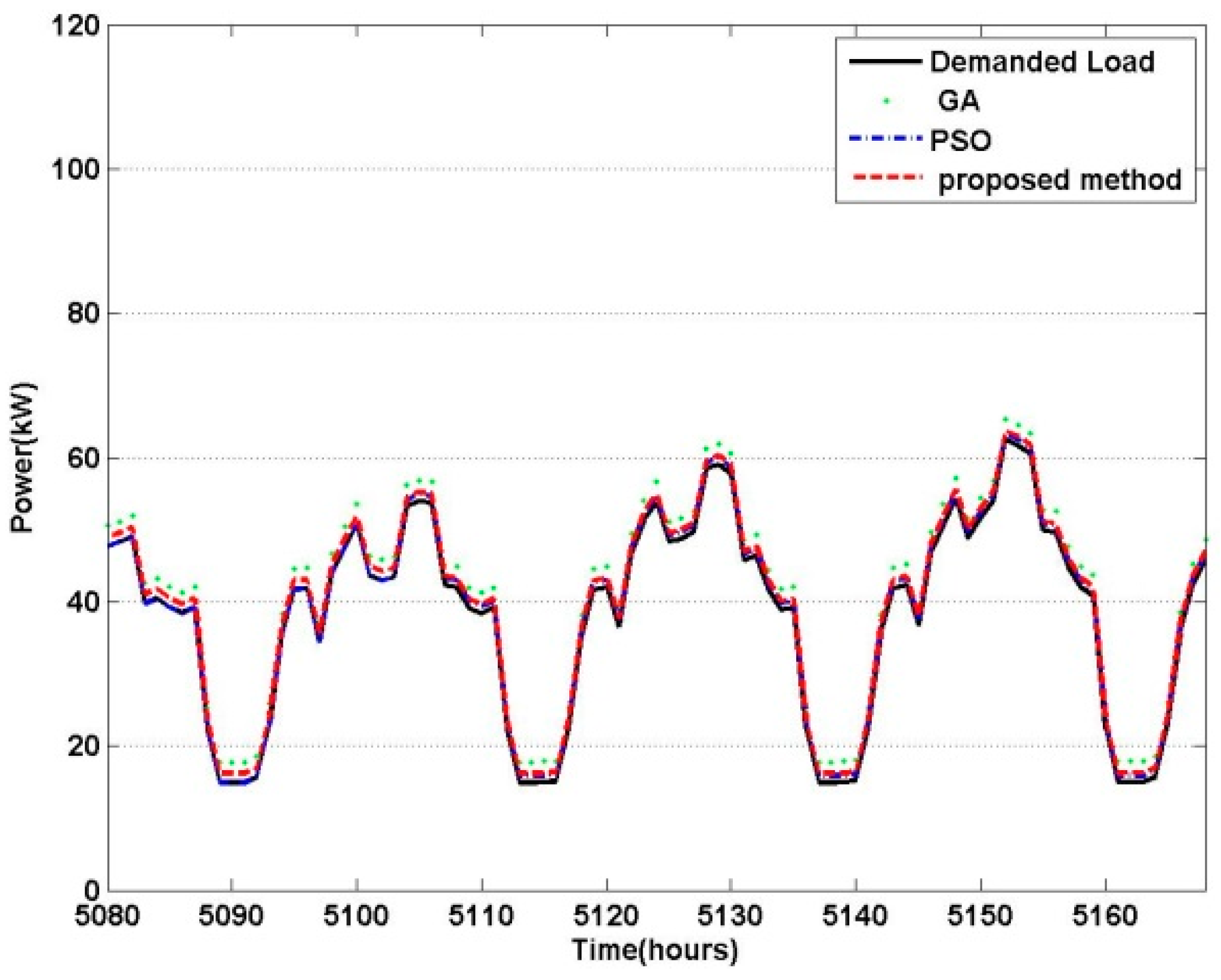
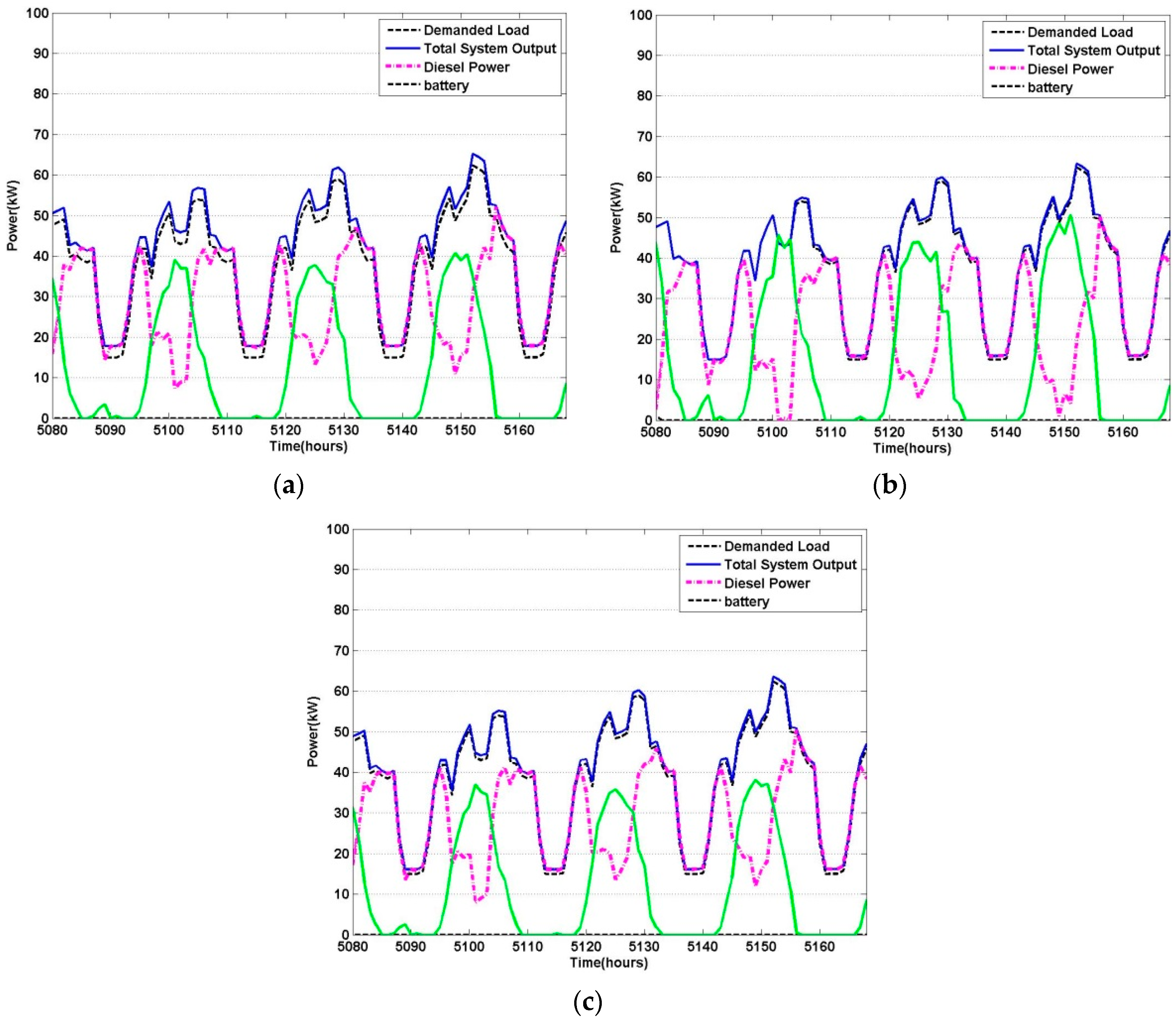
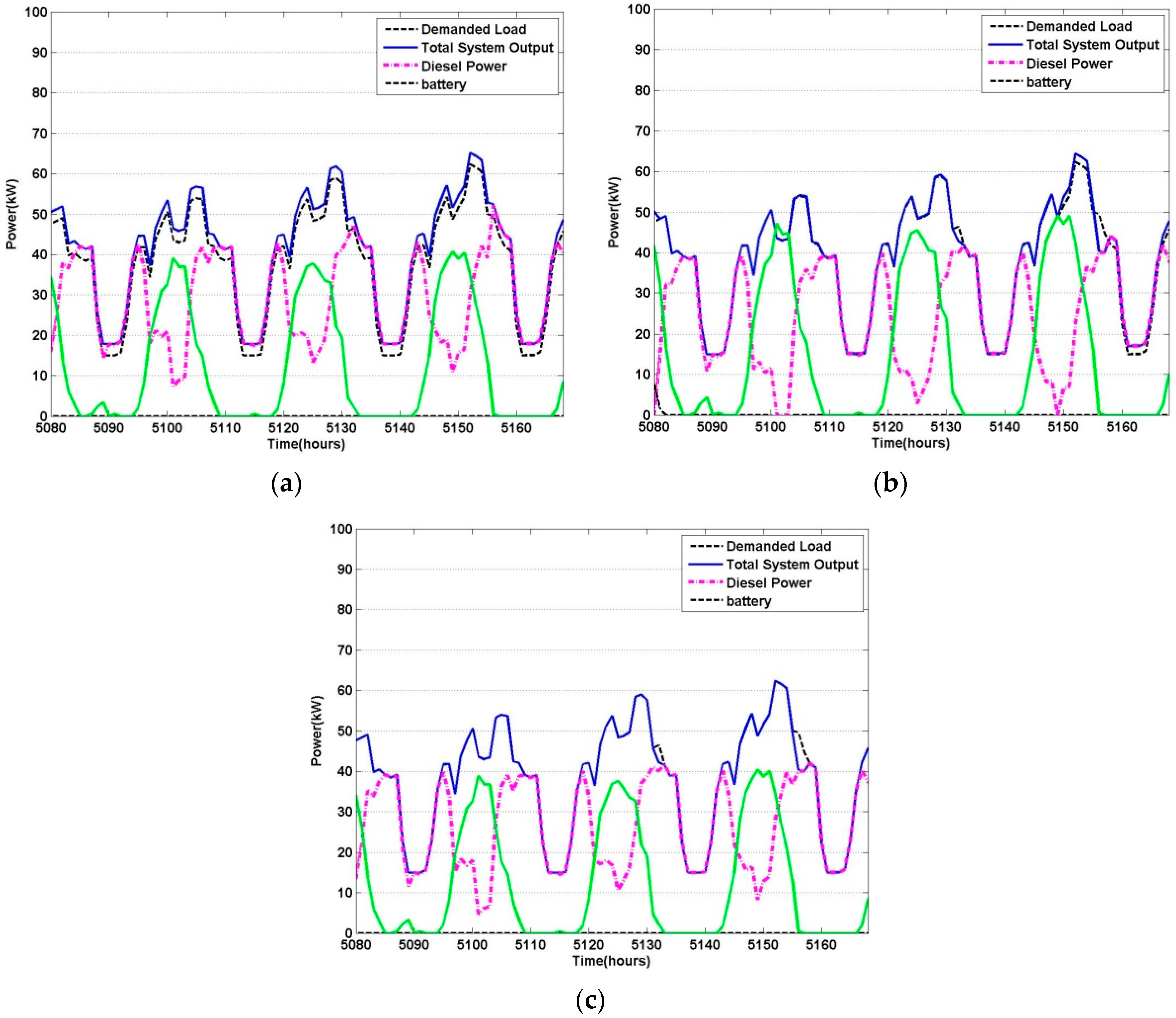
6. Simulation and Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maleki, A.; Askarzadeh, A. Comparative study of artificial intelligence techniques for sizing of a hydrogen-based stand-alone photovoltaic/wind hybrid system. Int. J. Hydrog. Energy 2014, 39, 9973–9984. [Google Scholar] [CrossRef]
- Hosseinalizadeh, R.; Shakouri, H.; Amalnick, M.S.; Taghipour, P. Economic sizing of a hybrid (PV-WT-FC) renewable energy system (HRES) for stand-alone usages by an optimization-simulation model: Case study of Iran. Renew. Sustain. Energy Rev. 2016, 54, 139–150. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Yang, H.; Wei, Z.; Lou, C. Optimal design and techno-economic analysis of a hybrid solar-wind power generation system. Appl. Energy 2009, 86, 163–169. [Google Scholar] [CrossRef]
- Yang, H.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Diaf, S.; Diaf, D.; Belhamel, M.; Haddadi, M.; Louche, A. A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 2007, 35, 5708–5718. [Google Scholar] [CrossRef]
- Borowy, B.S.; Salameh, Z.M. Methodology for optimally sizing the combination of a battery bank and PV array in a wind/PV hybrid system. IEEE Trans. Energy Convers. 1996, 11, 367–375. [Google Scholar] [CrossRef]
- Belfkira, R.; Zhang, L.; Barakat, G. Optimal sizing study of hybrid wind/PV/diesel power generation unit. Sol. Energy 2011, 85, 100–110. [Google Scholar] [CrossRef]
- Koutroulis, E.; Kolokotsa, D.; Potirakis, A.; Kalaitzakis, K. Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms. Sol. Energy 2006, 80, 1072–1088. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Y.; Gan, L. Dynamic Control of Wind/Photovoltaic Hybrid Power Systems Based on an Advanced Particle Swarm Optimization. In Proceedings of the 2008 IEEE International Conference on Industrial Technology (ICIT), Chengdu, China, 21–24 April 2008; pp. 1–6.
- Hakimi, S.; Moghaddas-Tafreshi, S. Optimal sizing of a stand-alone hybrid power system via particle swarm optimization for Kahnouj area in south-east of Iran. Renew. Energy 2009, 34, 1855–1862. [Google Scholar] [CrossRef]
- Askarzadeh, A. A discrete chaotic harmony search-based simulated annealing algorithm for optimum design of PV/wind hybrid system. Sol. Energy 2013, 97, 93–101. [Google Scholar] [CrossRef]
- Askarzadeh, A. Developing a discrete harmony search algorithm for size optimization of wind-photovoltaic hybrid energy system. Sol. Energy 2013, 98, 190–195. [Google Scholar] [CrossRef]
- Tan, W.S.; Hassan, M.Y.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Multi-distributed generation planning using hybrid particle swarm optimisation-gravitational search algorithm including voltage rise issue. IET Gener. Transm. Distrib. 2013, 7, 929–942. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Multi-objective design of PV-wind-diesel-hydrogen-battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Abbes, D.; Martinez, A.; Champenois, G. Life cycle cost, embodied energy and loss of power supply probability for the optimal design of hybrid power systems. Math. Comput. Simul. 2014, 98, 46–62. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Narimani, M.R. A new multi objective optimization approach based on TLBO for location of automatic voltage regulators in distribution systems. Eng. Appl. Artif. Intell. 2012, 25, 1577–1588. [Google Scholar] [CrossRef]
- Sahu, B.K.; Pati, T.K.; Nayak, J.R.; Panda, S.; Kar, S.K. A novel hybrid LUS-TLBO optimized fuzzy-PID controller for load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2016, 74, 58–69. [Google Scholar] [CrossRef]
- Burnet, F.M. A modification of Jerne’s theory of antibody production using the concept of clonal selection. Aust. J. Sci. 1976, 26, 119–121. [Google Scholar] [CrossRef]
- De Castro, L.N.; Von Zuben, F.J. Learning and optimization using the clonal selection principle. IEEE Trans. Evol. Comput. 2002, 6, 239–251. [Google Scholar] [CrossRef]
- Masoum, M.A.; Dehbonei, H.; Fuchs, E.F. Theoretical and experimental analyses of photovoltaic systems with voltage and current-based maximum power-point tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef]
- Skarstein, O.; Uhlen, K. Design considerations with respect to long-term diesel saving in wind/diesel plants. Wind Eng. 1989, 13, 72–87. [Google Scholar]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 1 August 2015).
- Commercial and Residential Hourly Load Profiles for All TMY3 Locations in the United States. Available online: http://en.openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states (accessed on 15 August 2015).

| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 5% | - | - | |
| 20 years | - | - | |
| Wind turbine | |||
| 1 kW | 3200$ | ||
| 2.5 m/s | 100$ | ||
| 13 m/s | 0$ | ||
| 11 m/s | Life Span | 20 years | |
| PV panel | |||
| 120 W | A | 1.07 m2 | |
| 614$ | Efficiency | 12% | |
| 0$ | Life Span | 20 years | |
| 0$ | - | - | |
| Diesel generator | |||
| 1.9 kW | 0$ | ||
| 1713.15$ | Life Span | 8,760 h | |
| 0.2 $/h | 1.24 $/L | ||
| Power converter/inverter | |||
| Rated power | 3 kW | Life Span | 10 years |
| 95% | 2000$ | ||
| Battery | |||
| Voltage | 12 V | 130$ | |
| 1.35 kWh | Life Span | 5 years | |
| 85% | 0.0002 | ||
| 130$ | - | - |
| Method | Parameter | Values |
|---|---|---|
| GA | Population size | 100 |
| Probability of crossover | 0.65 | |
| Probability of mutation | 0.05 | |
| Iteration | 100 | |
| PSO | Particle size | 100 |
| Inertia weight | 1 | |
| c1, c2 | 2, 2 | |
| Iteration | 100 | |
| Proposed method | Class size | 100 |
| The No. of clones | 5 | |
| Probability of Mutation for clonal selection | 0.25 | |
| SV1 and SV2 | 1 × 106 |
| GA | PSO | TLBO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Constraints | Best Structure [Nwind, Npv, Nbatt, NDG] | Total Cost | LPSP (%) | Best Structure [Nwind, Npv, Nbatt, NDG] | Total Cost | LPSP (%) | Best Structure [Nwind, Npv, Nbatt, NDG] | Total Cost | LPSP (%) | |
| LPSP = 0 | Mean | [37.4, 253, 7.2, 13] | 8.94 × 104 | 0.00% | [14.8, 237.6, 8, 10.4] | 9.03 × 104 | 0.00% | [18, 225, 1.6, 9.2] | 8.91 × 104 | 0.00% |
| Best | [41, 215, 1, 11] | 8.86 × 104 | 0.00% | [23, 214, 10, 11] | 8.88 × 104 | 0.00% | [17, 214, 1, 21] | 8.85 × 104 | 0.00% | |
| LPSP < 1% | Mean | [36.5, 257, 7.1, 11.8] | 8.92 × 104 | 0.98% | [12.40, 256.4, 1.6, 9] | 8.94 × 104 | 0.98% | [17.8, 228, 1.8, 9.2] | 8.89 × 104 | 0.92% |
| Best | [38, 240, 7, 9] | 8.86 × 104 | 0.90% | [17, 217, 1, 9] | 8.86 × 104 | 0.78% | [8, 218, 1, 1] | 8.85 × 104 | 0.67% | |
| LPSP < 2% | Mean | [37.1, 252, 77.6, 11.3] | 8.91 × 104 | 1.92% | [21.4, 280, 14.4, 7.4] | 9.00 × 104 | 1.95% | [18, 225, 1.8, 6.4] | 8.88 × 104 | 1.82% |
| Best | [29, 255, 4, 8] | 8.83 × 104 | 1.86% | [19, 273, 12, 8] | 8.96 × 104 | 1.79% | [8, 218, 1, 1] | 8.83 × 104 | 1.79% | |
| LPSP < 3% | Mean | [37.8, 246, 7.5, 12] | 8.92 × 104 | 2.86% | [25.8, 280, 29.2, 6.4] | 9.18 × 104 | 2.61% | [20.6, 225.8, 1.8, 6.5] | 8.856 × 104 | 2.77% |
| Best | [29, 255, 4, 8] | 8.83 × 104 | 1.86% | [18, 242, 1, 8] | 8.83 × 104 | 2.37% | [22, 215, 1, 8] | 8.82 × 104 | 2.24% | |
| LPSP < 4% | Mean | [37.8, 246, 7.5, 12] | 8.92 × 104 | 2.85% | [15.6, 302.4, 19, 8.2] | 9.12 × 104 | 2.47% | [21.6, 218, 1.6, 6.2] | 8.851 × 104 | 2.89% |
| Best | [29, 255, 4, 8] | 8.83 × 104 | 1.86% | [13, 263, 1, 8] | 8.87 × 104 | 2.57% | [22, 215, 1, 8] | 8.82 × 104 | 2.24% | |
| LPSP < 5% | Mean | [37.8, 246, 7.5, 12] | 8.92 × 104 | 2.85% | [19.2, 256.6, 6.6, 8.2] | 8.93 × 104 | 2.42% | [21.6, 218, 1.6, 6.2] | 8.851 × 104 | 2.89% |
| Best | [29, 255, 4, 8] | 8.83 × 104 | 1.86% | [26, 207, 1, 8] | 8.82 × 104 | 2.10% | [22, 215, 1, 8] | 8.82 × 104 | 2.24% | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.-H.; Chun, M.-G.; Hong, W.-P. Structure Optimization of Stand-Alone Renewable Power Systems Based on Multi Object Function. Energies 2016, 9, 649. https://doi.org/10.3390/en9080649
Cho J-H, Chun M-G, Hong W-P. Structure Optimization of Stand-Alone Renewable Power Systems Based on Multi Object Function. Energies. 2016; 9(8):649. https://doi.org/10.3390/en9080649
Chicago/Turabian StyleCho, Jae-Hoon, Myung-Geun Chun, and Won-Pyo Hong. 2016. "Structure Optimization of Stand-Alone Renewable Power Systems Based on Multi Object Function" Energies 9, no. 8: 649. https://doi.org/10.3390/en9080649
APA StyleCho, J.-H., Chun, M.-G., & Hong, W.-P. (2016). Structure Optimization of Stand-Alone Renewable Power Systems Based on Multi Object Function. Energies, 9(8), 649. https://doi.org/10.3390/en9080649






