Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System †
Abstract
:1. Introduction
2. Models and Methodology
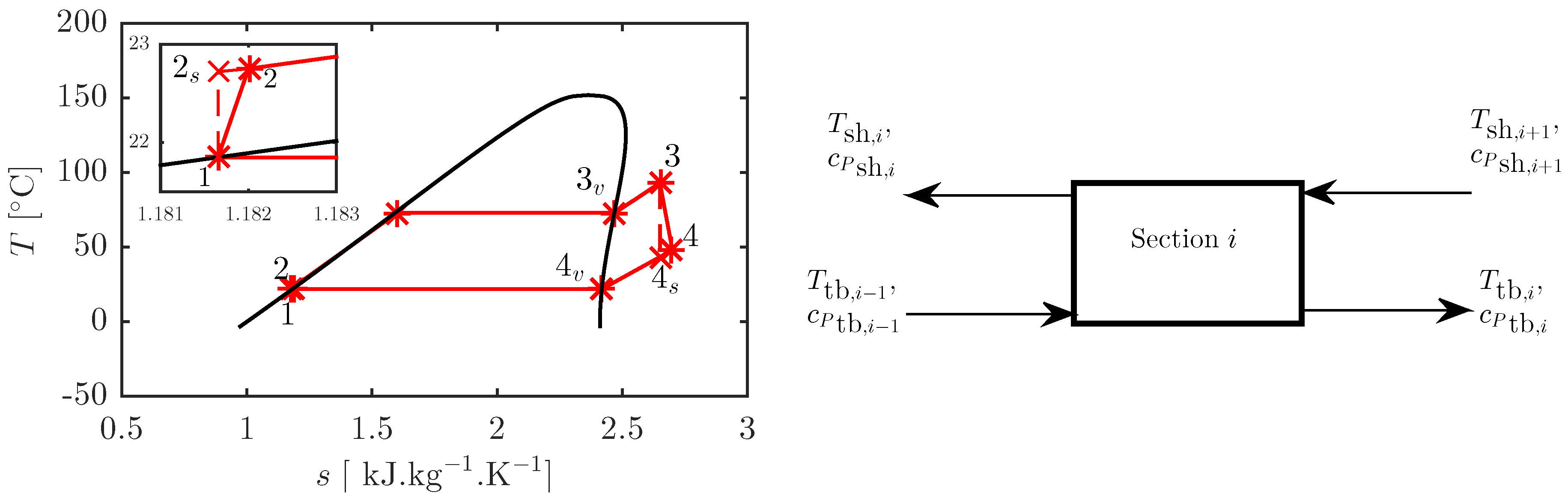
2.1. ORC Thermodynamic Model
2.2. Heat Exchanger Sizing
2.3. Component Cost Estimation
2.4. Application and Problem Definition
3. Results and Discussion
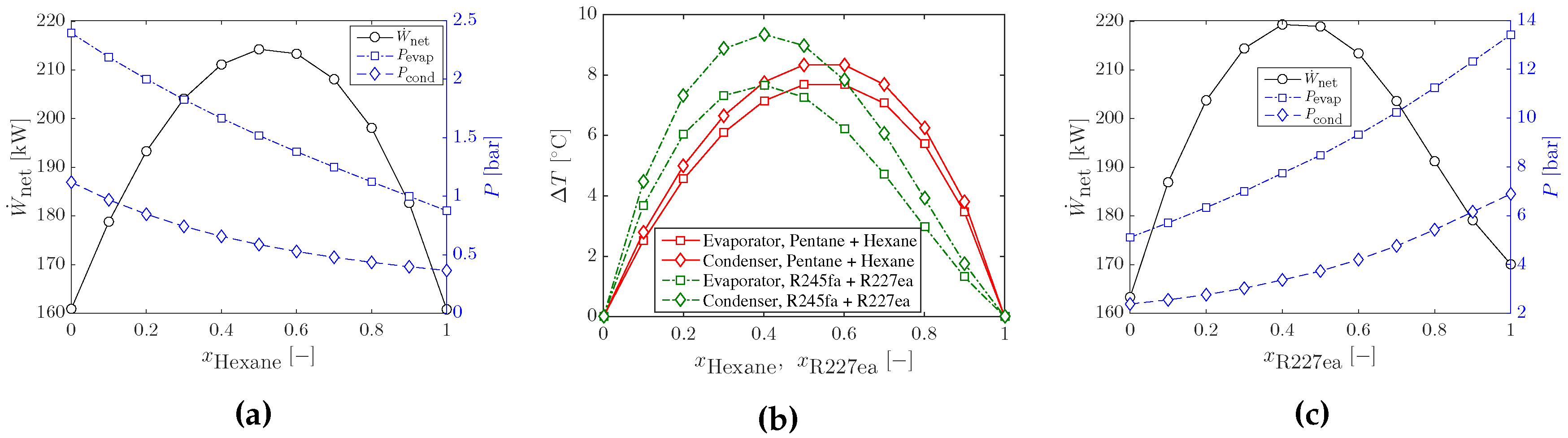
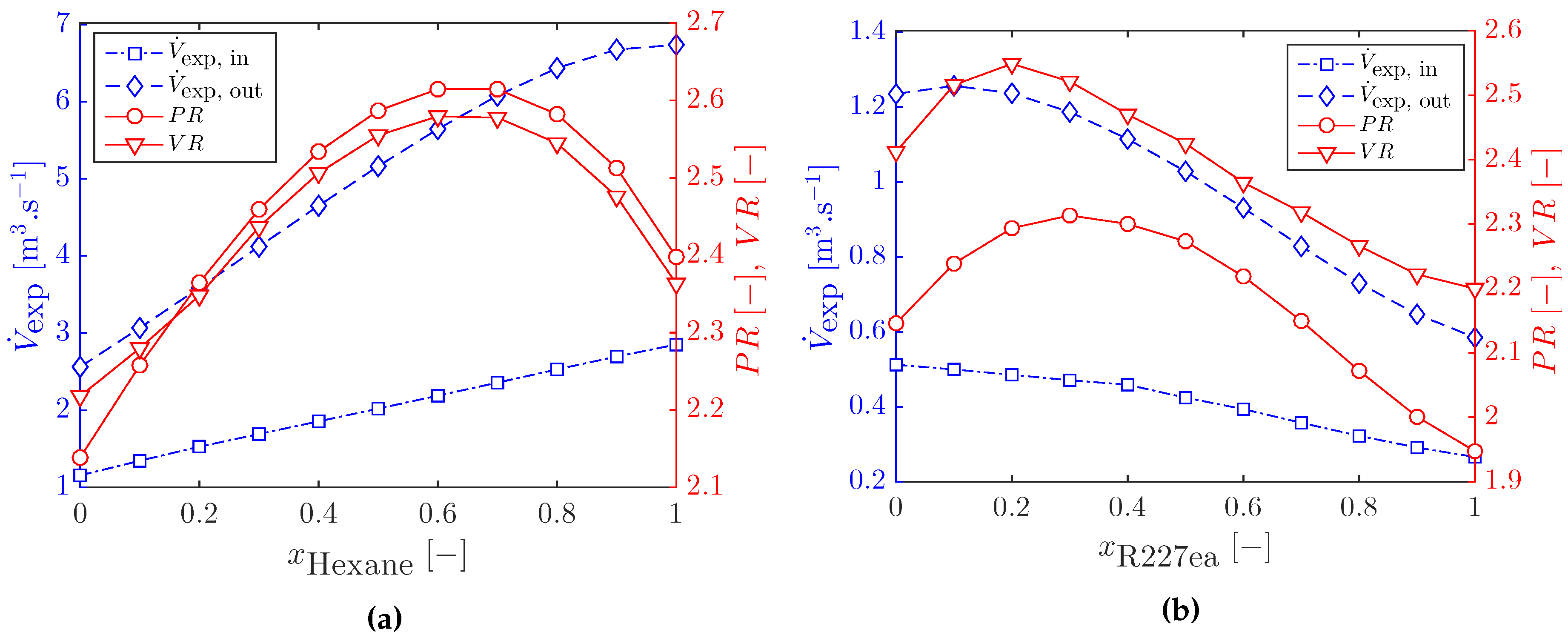
3.1. Optimal Cycles with Working-Fluid Mixtures
3.2. Sizing and Costing of Optimal ORC Systems
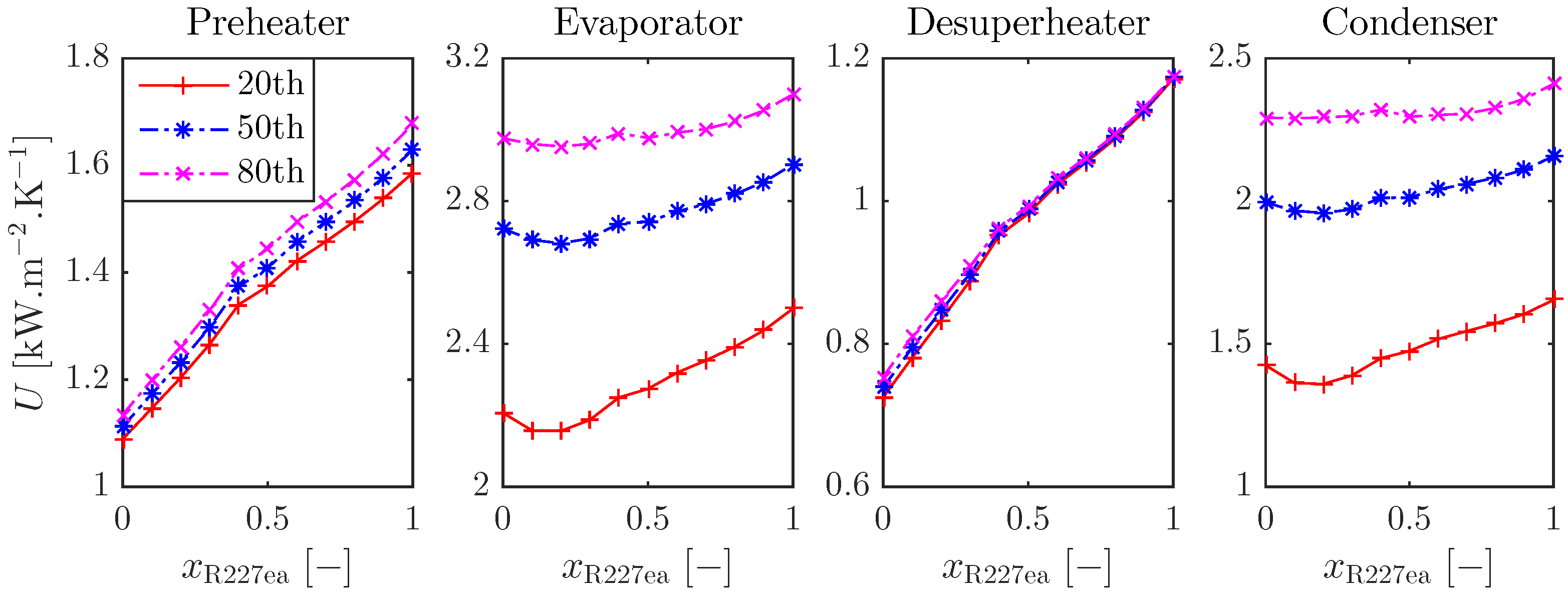
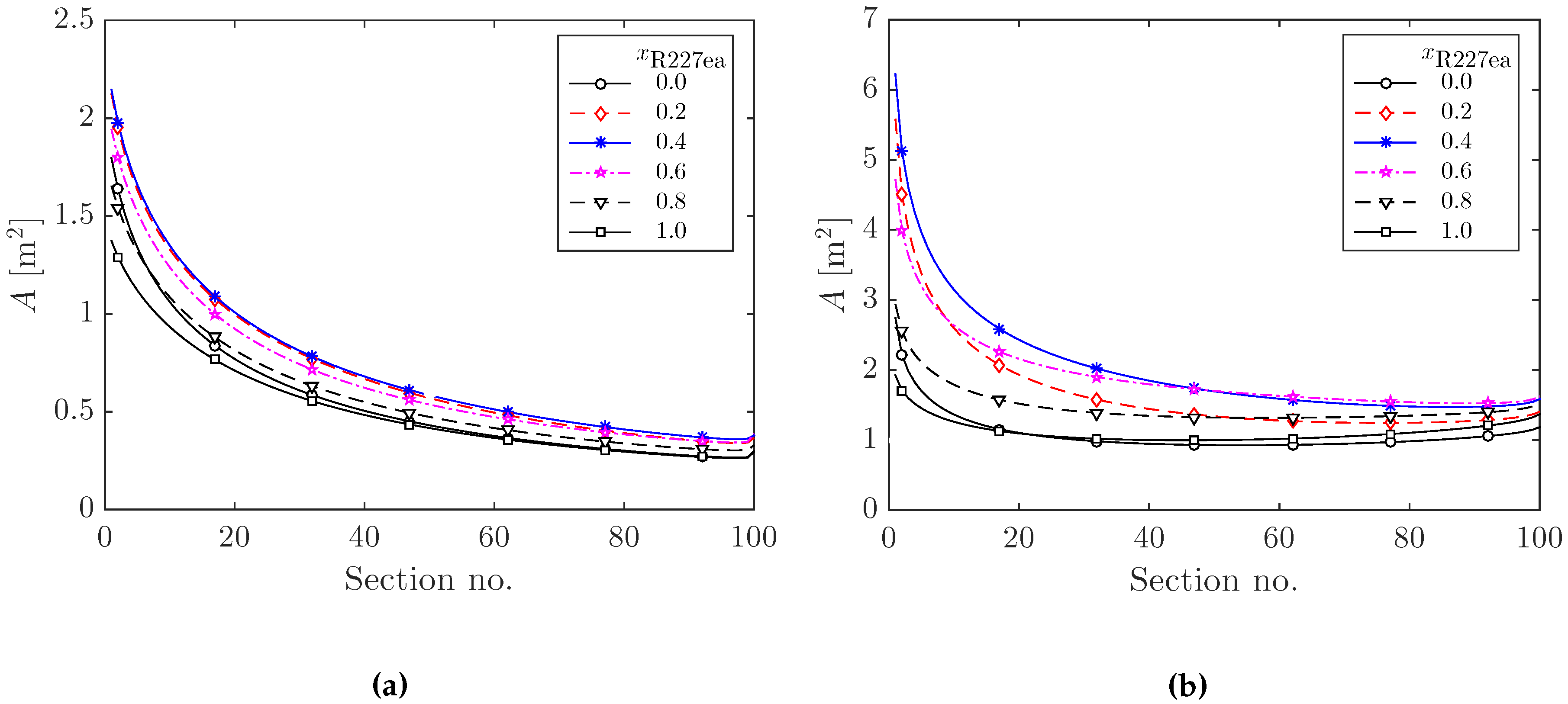
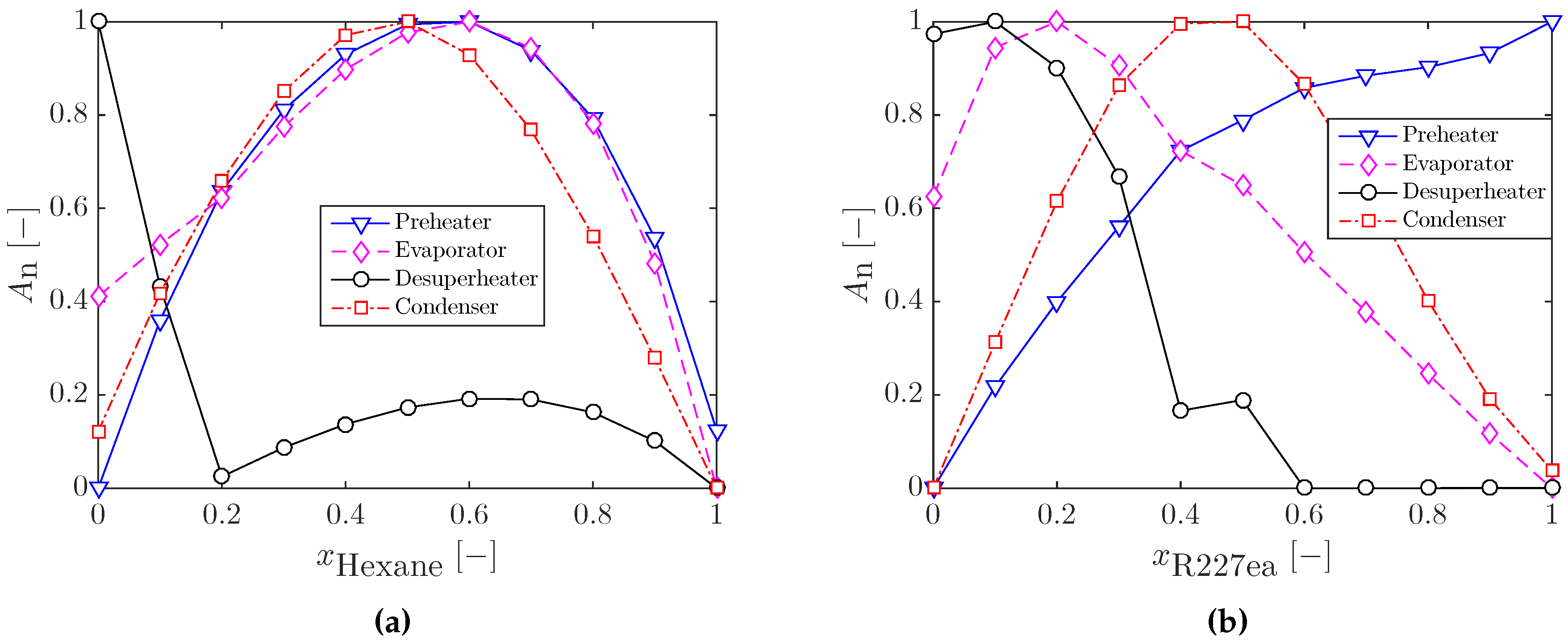
3.2.1. Heat Exchanger Sizing for Optimal ORC Systems
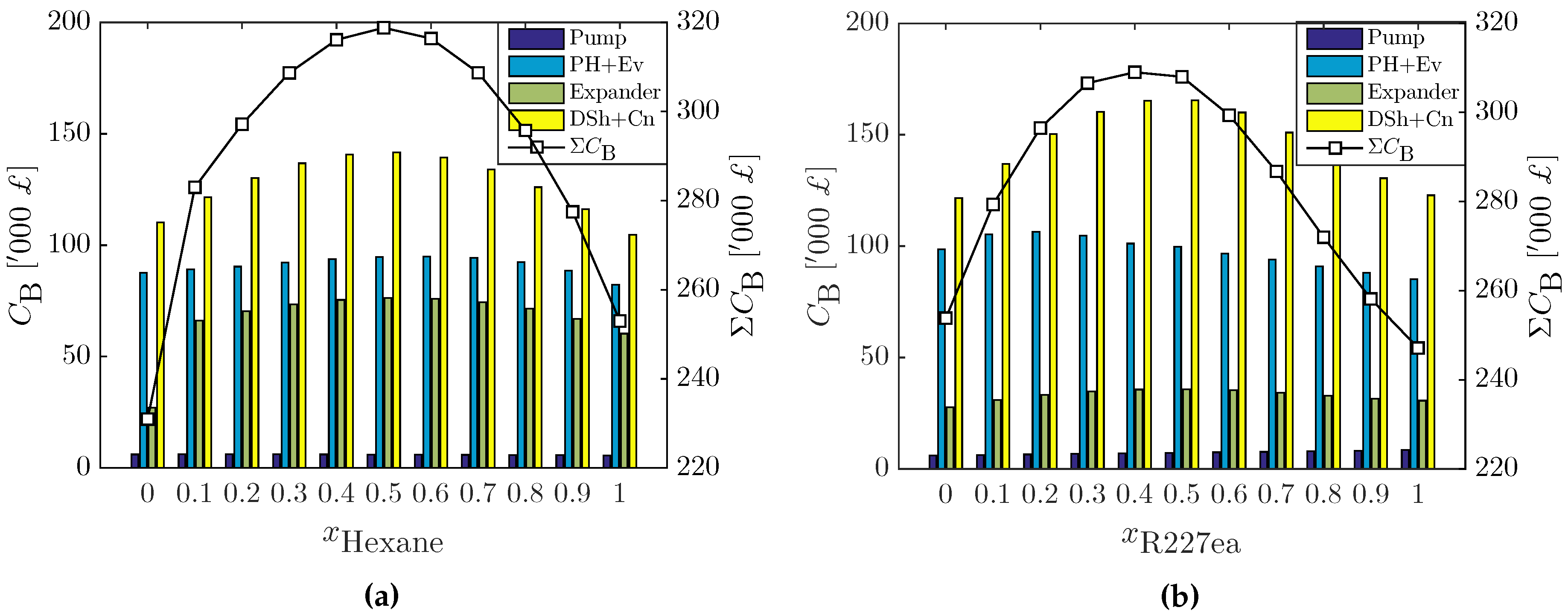
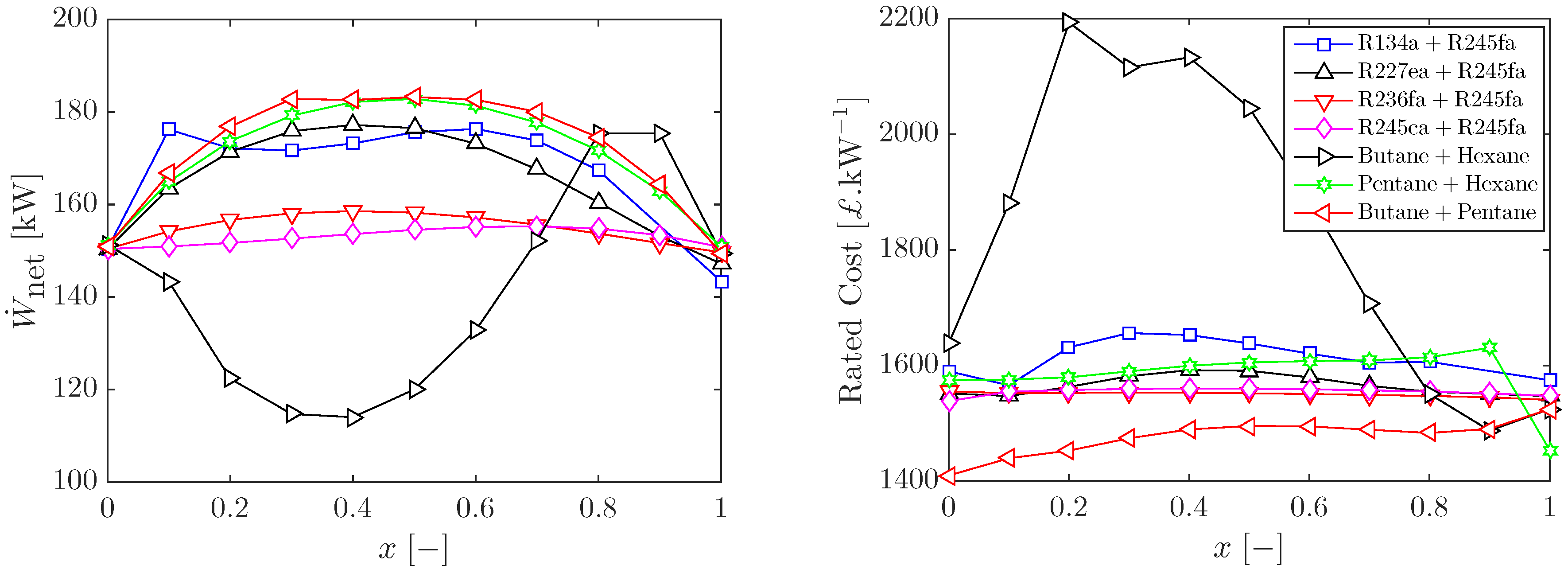
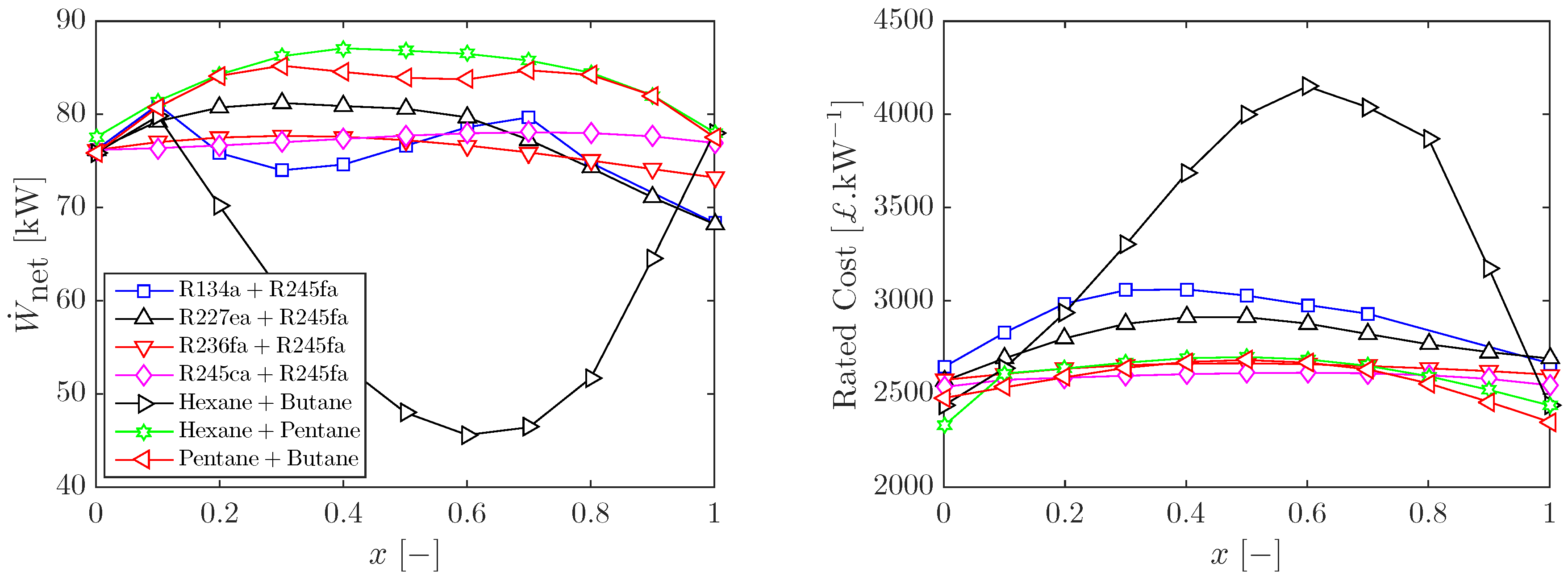
3.2.2. Cost Estimation of Optimal ORC Systems
3.3. Heat Input Limitations and Other Working-Fluid Mixtures
- is allowed to attain a maximum possible value; this is the case in Section 3.1 where the optimal cycle heat input () for different working fluids is seen to vary between 3.2 MW and 4.0 MW.
- MW.
- MW.
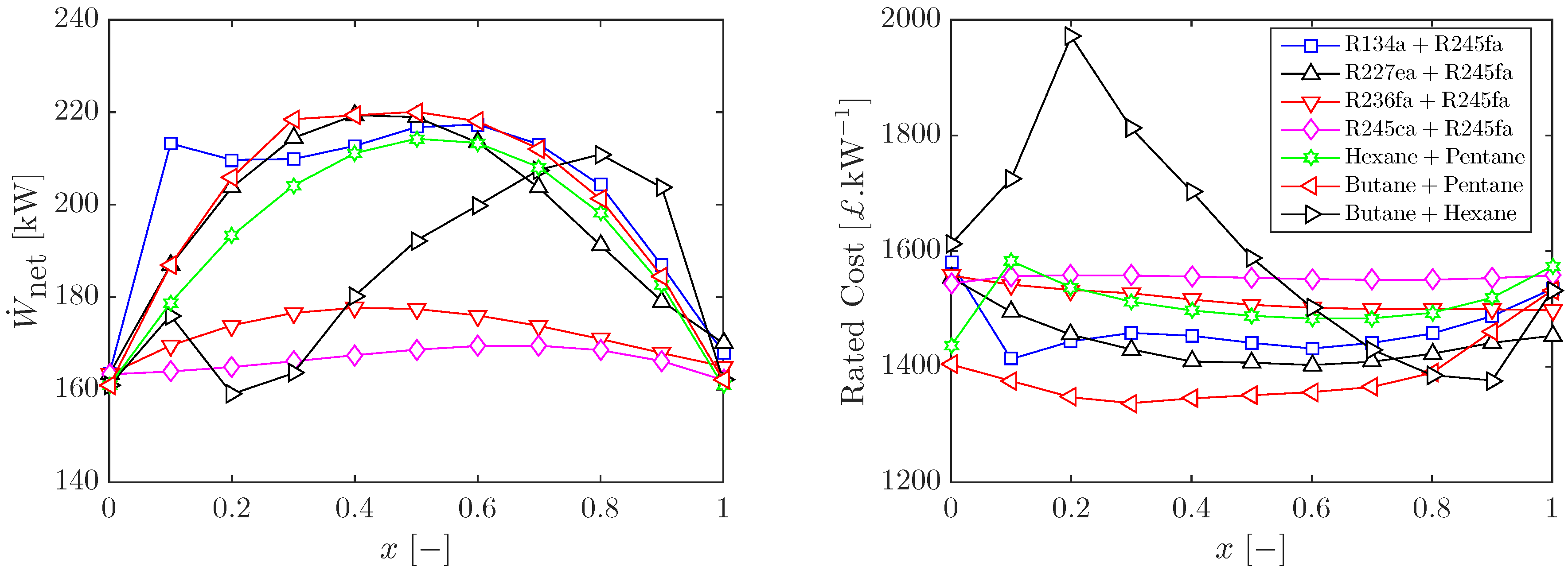
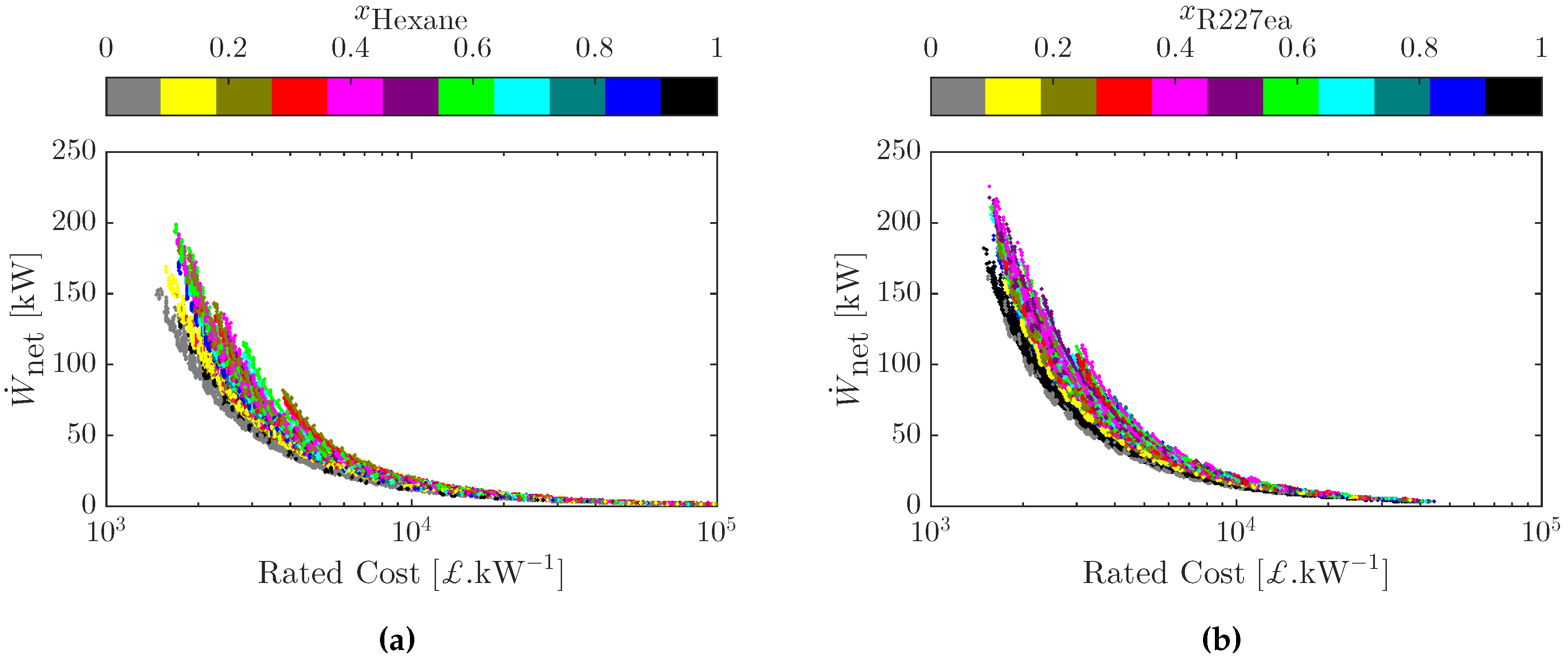
3.4. Multi-Objective Cost-Power Optimization
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Heat transfer area [] | Ev | Evaporator |
| Component-base cost [£] | HTA | Heat-transfer area | |
| Isobaric specific heat-capacity [kJ·kg·K] | HTC | Heat-transfer coefficient | |
| Degree of superheat [-] | HX | Heat exchanger | |
| Tube thickness [m] | LHS | Left-hand side | |
| h | Specific enthalpy [kJ·kg] | ORC | Organic Rankine cycle |
| h | Heat-transfer coefficient [kW·m·K] | PH | Preheater |
| H | Pump head [m] | RHS | Right-hand side |
| k | Thermal conductivity [kW·m·K] | SH | Superheater |
| Mass flow-rate [kg·s] | |||
| P | Pressure [bar] | Subscripts | |
| Expander pressure ratio [-] | ‘1’, ‘2’, ‘3’, ‘4’ | Working-fluid state points | |
| q | Vapour quality on mass basis [-] | ‘cond’ | Condensation |
| Heat flow-rate [kW] | ‘crit’ | Critical | |
| s | Specific entropy [kJ·kg·K] | ‘cs’ | Heat sink |
| T | Temperature [°C] | ‘evap’ | Evaporation |
| U | Overall HTC [kW·m·K] | ‘exp’ | Expander |
| Volumetric flow-rate [m·s] | ‘hs’ | Heat source | |
| Expander volume ratio [-] | ‘i’ | Segment number | |
| w | Specific work-output [kJ·kg] | ‘in’ | Input |
| Power [kW] | ‘is’ | Isentropic | |
| x | Mass fraction [-] | ‘lim’ | Limit |
| ‘lm’ | Logarithm mean | ||
| Greek symbols | ‘max’ | Maximum | |
| η | Efficiency [%] | ‘min’ | Minimum |
| μ | Dynamic viscosity [Pa·s] | ‘n’ | Normalized |
| ρ | Density [kg·m] | ‘out’ | Output/Outlet |
| ‘s’ | Isentropic | ||
| Abbreviations | ‘sh’ | Shell-side | |
| CAMD | Computer-aided molecular design | ‘tb’ | Tube-side |
| CHP | Combined heat and power | ‘th’ | Thermal |
| Cn | Condenser | ‘v’ | Vapour volume |
| DSh | Desuperheater | ‘wf’ | Working fluid |
References
- Markides, C.N. Low-concentration solar-power systems based on organic Rankine cycles for distributed-scale applications: Overview and further developments. Front. Energy Res. 2015, 3:47, 1–16. [Google Scholar] [CrossRef]
- Angelino, G.; di Paliano, P.C. Multicomponent working fluids for ORCs. Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Garg, P.; Kumar, P.; Srinivasan, K.; Dutta, P. Evaluation of isopentane, R-245fa and their mixtures as working fluids for organic Rankine cycles. Appl. Ther. Eng. 2013, 51, 292–300. [Google Scholar] [CrossRef]
- Wang, J.L.; Zhao, L.; Wang, X.D. A comparative study of pure and zeotropic mixtures in low-temperature solar Rankine cycle. Appl. Energy 2010, 87, 3366–3373. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C.N. On the use of SAFT-VR Mie for assessing large-glide fluorocarbon working-fluid mixtures in organic Rankine cycles. Appl. Energy 2016, 163, 263–282. [Google Scholar] [CrossRef]
- Lecompte, S.; Lemmens, S.; Huisseune, H.; van den Broek, M.; De Paepe, M. Multi-objective thermo-economic optimization strategy for ORCs applied to subcritical and transcritical cycles for waste heat recovery. Energies 2015, 8, 2714–2741. [Google Scholar] [CrossRef]
- Sami, S.M. Energy and exergy analysis of new refrigerant mixtures in an organic Rankine cycle for low temperature power generation. Int. J. Ambient Energy 2010, 31, 23–32. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. A supercritical Rankine cycle using zeotropic mixture working fluids for the conversion of low-grade heat into power. Energy 2011, 36, 549–555. [Google Scholar] [CrossRef]
- Aghahosseini, S.; Dincer, I. Comparative performance analysis of low-temperature organic Rankine cycle (ORC) using pure and zeotropic working fluids. Appl. Ther. Eng. 2013, 54, 35–42. [Google Scholar] [CrossRef]
- Gao, H.; Liu, C.; He, C.; Xu, X.; Wu, S.; Li, Y. Performance analysis and working fluid selection of a supercritical organic Rankine cycle for low grade waste heat recovery. Energies 2012, 5, 3233–3247. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in organic Rankine cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Shu, G.; Gao, Y.; Tian, H.; Wei, H.; Liang, X. Study of mixtures based on hydrocarbons used in ORC (organic Rankine cycle) for engine waste heat recovery. Energy 2014, 74, 428–438. [Google Scholar] [CrossRef]
- Dong, B.; Xu, G.; Cai, Y.; Li, H. Analysis of zeotropic mixtures used in high-temperature organic Rankine cycle. Energy Convers. Manag. 2014, 84, 253–260. [Google Scholar] [CrossRef]
- Preißinger, M.; Brüggemann, D. Thermal stability of hexamethyldisiloxane (MM) for high-temperature organic Rankine cycle (ORC). Energies 2016, 9, 183. [Google Scholar] [CrossRef]
- Lecompte, S.; Ameel, B.; Ziviani, D.; van den Broek, M.; De Paepe, M. Exergy analysis of zeotropic mixtures as working fluids in organic Rankine cycles. Energy Convers. Manag. 2014, 85, 727–739. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Linke, P.; Papadopoulos, A.I.; Grujic, A.S. On the role of working fluid properties in organic Rankine cycle performance. Appl. Ther. Eng. 2012, 36, 406–413. [Google Scholar] [CrossRef]
- Mathkor, R.Z.; Agnew, B.; Al-Weshahi, M.A.; Latrsh, F. Exergetic analysis of an integrated tri-generation organic Rankine cycle. Energies 2015, 8, 8835–8856. [Google Scholar] [CrossRef]
- Li, Y.R.; Du, M.T.; Wu, C.M.; Wu, S.Y.; Liu, C. Potential of organic Rankine cycle using zeotropic mixtures as working fluids for waste heat recovery. Energy 2014, 77, 509–519. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P. On the systematic design and selection of optimal working fluids for organic Rankine cycles. Appl. Ther. Eng. 2010, 30, 760–769. [Google Scholar] [CrossRef]
- Lampe, M.; Kirmse, C.; Sauer, E.; Stavrou, M.; Gross, J.; Bardow, A. Computer-aided molecular design of ORC working fluids using PC-SAFT. Comput. Aided Chem. Eng. 2014, 34, 357–362. [Google Scholar]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P.; Seferlis, P.; Voutetakis, S. Toward optimum working fluid mixtures for organic Rankine cycles using molecular design and sensitivity analysis. Ind. Eng. Chem. Res. 2013, 52, 12116–12133. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Haslam, A.J.; Markides, C.N. Towards the computer-aided molecular design of organic Rankine cycle systems with advanced fluid theories. In Proceedings of the 2015 Sustainable Thermal Energy Management Network Conference, Newcastle, UK, 7–8 July 2015.
- Jung, D.S.; McLinden, M.; Radermacher, R.; Didion, D. Horizontal flow boiling heat transfer experiments with a mixture of R22/R114. Int. J. Heat Mass Transf. 1989, 32, 131–145. [Google Scholar] [CrossRef]
- Celata, G.; Cumo, M.; Setaro, T. A review of pool and forced convective boiling of binary mixtures. Exp. Ther. Fluid Sci. 1994, 9, 367–381. [Google Scholar] [CrossRef]
- Gungor, K.; Winterton, R. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
- Gungor, K.; Winterton, R. Simplified general correlation for saturated flow boiling and comparisons of correlations with data. Chem. Eng. Res. Design 1987, 65, 148–156. [Google Scholar]
- Thome, J.R. Prediction of binary mixture boiling heat transfer coefficients using only phase equilibrium data. Int. J. Heat Mass Transf. 1983, 26, 965–974. [Google Scholar] [CrossRef]
- Ünal, H. Prediction of nucleate pool boiling heat transfer coefficients for binary mixtures. Int. J. Heat Mass Transf. 1986, 29, 637–640. [Google Scholar] [CrossRef]
- Jung, D.; McLinden, M.; Radermacher, R.; Didion, D. A study of flow boiling heat transfer with refrigerant mixtures. Int. J. Heat Mass Transf. 1989, 32, 1751–1764. [Google Scholar] [CrossRef]
- Kondou, C.; Baba, D.; Mishima, F.; Koyama, S. Flow boiling of non-azeotropic mixture R32/R1234ze(E) in horizontal microfin tubes. Int. J. Refrig. 2013, 36, 2366–2378. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Dhasan, M.; Rajagopal, S. Flow boiling heat transfer coefficient of R-134a/R-290/R-600a mixture in a smooth horizontal tube. Ther. Sci. 2008, 12, 33–44. [Google Scholar] [CrossRef]
- Lim, T.; Kim, J. An experimental investigation of heat transfer in forced convective boiling of R134a, R123 and R134a/R123 in a horizontal tube. KSME Int. J. 2004, 18, 513–525. [Google Scholar]
- Chiou, C.; Lu, D.; Liao, C.; Su, Y. Experimental study of forced convective boiling for non-azeotropic refrigerant mixtures R-22/R-124 in horizontal smooth tube. Appl. Ther. Eng. 2009, 29, 1864–1871. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C.N. An assessment of working-fluid mixtures using SAFT-VR Mie for use in organic Rankine cycle systems for waste-heat recovery. Comput. Ther. Sci. Int. J. 2014, 6, 301–316. [Google Scholar] [CrossRef]
- Kunz, O.; Wagner, W. The GERG-2008 wide-range equation of state for natural gases and other mixtures: An expansion of GERG-2004. J. Chem. Eng. Data 2012, 57, 3032–3091. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP; NIST: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Shin, J.Y.; Kim, M.S.; Ro, S.T. Correlation of evaporative heat transfer coefficients for refrigerant mixtures. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 23–26 July 1996; p. 316.
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis and Design of Chemical Processes; Pearson Education: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Seider, W.D.; Seader, J.D.; Lewin, D.R. Product & Process Design Principles: Synthesis, Analysis and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hewitt, G.F.; Pugh, S.J. Approximate design and costing methods for heat exchangers. Heat Transf. Eng. 2007, 28, 76–86. [Google Scholar] [CrossRef]
- Beardsmore, G.; Budd, A.; Huddlestone-Holmes, C.; Davidson, C. Country update—Australia. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 9–25 April 2015; pp. 19–24.
- Markides, C.N. The role of pumped and waste heat technologies in a high-efficiency sustainable energy future for the UK. Appl. Therm. Eng. 2013, 53, 197–209. [Google Scholar]
- Chys, M.; van den Broek, M.; Vanslambrouck, B.; De Paepe, M. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Braimakis, K.; Leontaritis, A.D.; Preißinger, M.; Karellas, S.; Brüggeman, D.; Panopoulos, K. Waste heat recovery with innovative low-temperature ORC based on natural refrigerants. In Proceedings of the 27th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Turku, Finland, 15–19 June 2014.
- Braimakis, K.; Preißinger, M.; Brüggeman, D.; Karellas, S.; Panopoulos, K. Low grade waste heat recovery with subcritical and supercritical organic Rankine cycle based on natural refrigerants and their binary mixtures. Energy 2015, 88, 80–92. [Google Scholar] [CrossRef]
- Byrd, R.; Hribar, M.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Opt. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Andreasen, J.G.; Kærn, M.R.; Pierobon, L.; Larsen, U.; Haglind, F. Multi-objective optimization of organic Rankine cycle power plants using pure and mixed working fluids. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015.
- Andreasen, J.G.; Kærn, M.R.; Pierobon, L.; Larsen, U.; Haglind, F. Multi-objective optimization of organic Rankine cycle power plants using pure and mixed working fluids. Energies 2016, 9, 322. [Google Scholar] [CrossRef]
- Heberle, F.; Brüggemann, D. Thermo-economic evaluation of organic Rankine cycles for geothermal power generation using zeotropic mixtures. Energies 2015, 8, 2097–2124. [Google Scholar] [CrossRef]
- Heberle, F.; Brüggemann, D. Thermo-economic analysis of zeotropic mixtures and pure working fluids in organic Rankine cycles for waste heat recovery. Energies 2016, 9, 226. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Markides, C.N. Effect of working-fluid mixtures on organic Rankine cycle systems: Heat transfer and cost analysis. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015.
| Component | S | F | |||
|---|---|---|---|---|---|
| Pump | (m3·s−1·m1/2) | 2.7 | 9.0073 | 0.4636 | 0.0519 |
| Expander | (kW) | 1.0 | 6.5106 | 0.8100 | 0.0000 |
| Expander * | (kW) | 1.0 | 7.3194 | 0.8100 | 0.0000 |
| Heaters/Coolers | HTA (m2) | 1.0 | 10.106 | −0.4429 | 0.0901 |
| Evaporator/Condenser | HTA (m2) | 1.0 | 9.5638 | 0.5320 | −0.0002 |
| kW | % | kW | - | MW | MW | MW | MW | kW | % | kW | - | MW | MW | MW | MW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 161 | 5.00 | 21.1 | 2.17 | 7.74 | 0.45 | 73.1 | 0.47 | 2.75 | 0.30 | 2.75 | 0.0 | 163 | 4.97 | 11.5 | 4.05 | 14.5 | 1.00 | 74.7 | 0.50 | 2.78 | 0.48 | 2.64 |
| 0.1 | 179 | 5.25 | 21.8 | 2.20 | 8.29 | 0.18 | 77.2 | 0.53 | 2.88 | 0.23 | 3.00 | 0.1 | 187 | 5.17 | 11.8 | 5.18 | 16.2 | 1.00 | 82.1 | 0.60 | 3.01 | 0.52 | 2.92 |
| 0.2 | 193 | 5.43 | 22.5 | 2.16 | 8.68 | 0.00 | 80.5 | 0.57 | 2.99 | 0.18 | 3.19 | 0.2 | 204 | 5.30 | 11.7 | 6.44 | 18.0 | 0.84 | 87.1 | 0.70 | 3.15 | 0.49 | 3.15 |
| 0.3 | 204 | 5.55 | 23.3 | 2.05 | 8.86 | 0.00 | 83.2 | 0.59 | 3.09 | 0.19 | 3.29 | 0.3 | 214 | 5.39 | 11.1 | 7.88 | 19.9 | 0.54 | 90.1 | 0.78 | 3.20 | 0.41 | 3.36 |
| 0.4 | 211 | 5.61 | 23.7 | 1.92 | 8.98 | 0.00 | 84.9 | 0.61 | 3.15 | 0.20 | 3.35 | 0.4 | 219 | 5.42 | 10.3 | 9.66 | 22.3 | 0.11 | 91.6 | 0.87 | 3.17 | 0.25 | 3.58 |
| 0.5 | 214 | 5.64 | 23.9 | 1.78 | 9.03 | 0.00 | 85.8 | 0.62 | 3.18 | 0.20 | 3.38 | 0.5 | 219 | 5.40 | 9.79 | 11.0 | 23.5 | 0.12 | 91.7 | 0.91 | 3.14 | 0.26 | 3.57 |
| 0.6 | 213 | 5.61 | 23.8 | 1.62 | 9.02 | 0.00 | 85.8 | 0.62 | 3.18 | 0.21 | 3.38 | 0.6 | 213 | 5.33 | 9.02 | 12.7 | 25.1 | 0.00 | 90.6 | 0.95 | 3.05 | 0.21 | 3.57 |
| 0.7 | 208 | 5.55 | 23.4 | 1.44 | 8.94 | 0.00 | 84.7 | 0.60 | 3.15 | 0.20 | 3.34 | 0.7 | 204 | 5.21 | 8.29 | 14.3 | 26.3 | 0.00 | 88.6 | 0.97 | 2.94 | 0.22 | 3.48 |
| 0.8 | 198 | 5.44 | 22.7 | 1.26 | 8.77 | 0.00 | 82.4 | 0.58 | 3.06 | 0.20 | 3.24 | 0.8 | 191 | 5.06 | 7.52 | 15.9 | 27.5 | 0.00 | 85.9 | 0.98 | 2.81 | 0.22 | 3.37 |
| 0.9 | 183 | 5.28 | 21.7 | 1.06 | 8.48 | 0.00 | 78.4 | 0.53 | 2.93 | 0.19 | 3.09 | 0.9 | 179 | 4.89 | 6.80 | 17.9 | 29.0 | 0.00 | 83.3 | 0.99 | 2.67 | 0.23 | 3.25 |
| 1.0 | 161 | 5.05 | 20.2 | 0.85 | 8.02 | 0.00 | 72.3 | 0.47 | 2.71 | 0.17 | 2.85 | 1.0 | 170 | 4.76 | 6.19 | 20.2 | 30.7 | 0.00 | 81.4 | 1.02 | 2.55 | 0.24 | 3.17 |
| Pentane + Hexane | PH | Ev | DSh | Cn | R-245fa + R227ea | PH | Ev | DSh | Cn |
|---|---|---|---|---|---|---|---|---|---|
| (m) | 21.8 | 48.5 | 15.8 | 80.8 | (m) | 24.5 | 51.1 | 15.2 | 109 |
| (m) | 25.8 | 65.3 | 23.4 | 150 | (m) | 37.2 | 82.6 | 29.9 | 204 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyewunmi, O.A.; Markides, C.N. Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System. Energies 2016, 9, 448. https://doi.org/10.3390/en9060448
Oyewunmi OA, Markides CN. Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System. Energies. 2016; 9(6):448. https://doi.org/10.3390/en9060448
Chicago/Turabian StyleOyewunmi, Oyeniyi A., and Christos N. Markides. 2016. "Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System" Energies 9, no. 6: 448. https://doi.org/10.3390/en9060448
APA StyleOyewunmi, O. A., & Markides, C. N. (2016). Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System. Energies, 9(6), 448. https://doi.org/10.3390/en9060448







