Energy Conversion: A Comparison of Fix- and Self-Referenced Wave Energy Converters

Abstract

The paper presents an investigation of fix-referenced and self-referenced wave energy converters and a comparison of their corresponding wave energy conversion capacities from real seas. For conducting the comparisons, two popular wave energy converters, point absorber and oscillating water column, and their power conversion capacities in the fixed-referenced and self-referenced forms have been numerically studied and compared. In the numerical models, the device’s power extractions from seas are maximized using the correspondingly optimized power take-offs in different sea states, thus their power conversion capacities can be calculated and compared. From the comparisons and analyses, it is shown that the energy conversion capacities of the self-referenced devices can be significantly increased if the motions of the device itself can be utilized for wave energy conversion; and the self-referenced devices can be possibly designed to be compliant in long waves, which could be a very beneficial factor for device survivability in the extreme wave conditions (normally long waves). In this regards, the self-referenced WECs (wave energy converters) may be better options in terms of wave energy conversion from the targeted waves in seas (frequently the most occurred), and in terms of the device survivability, especially in the extreme waves when compared to the fix-referenced counterparts.

1. Introduction

Wave energy has been widely regarded to have potential to significantly contribute to the energy mix and blue economy if the technology were to mature. This is especially evident in Europe and USA where huge efforts are being made to bring the technologies to the level of generating power to the grid from waves [1,2,3,4]. Historically, some practical and commercial developments have progressed, while some others are still at different development stages and technology readiness levels (TRLs). The former includes the Ocean Energy (OE) buoy [5] and West Wave project [6], and the latter includes the technologies found nowadays mainly in labs [7,8,9,10]. It is reported that there are more than 1000 filed patents for wave energy technologies [11], and a well-received classification of the wave energy technologies is given in [12]. Now international collaborations and efforts have been in place to build the standards and the baseline devices to standardize wave energy technologies [13,14].

Despite the great advances in developing wave energy technologies since the 1970s, researchers and developers of wave energy are still faced with some fundamental challenges, and significant improvements and advancements are urgently needed for both the device performance in converting wave energy and the reliability and survivability of the device and of the subsystems in long-term energy production and under extreme wave conditions. All these factors are directly related to the cost of wave energy [15] and current technology developments have been specially targeting to reduce the cost of wave energy and to improve the power performance and reliability so to make wave energy comparable to other renewable resources and ultimately to the conventional energy production. In Europe, the costs of tidal and wave energy are proposed to be reduced to €0.10/kW by 2030 and 2035, respectively (Ocean Energy Europe [16]) from €0.50–0.65/kW of current technologies (SI Ocean [15]).

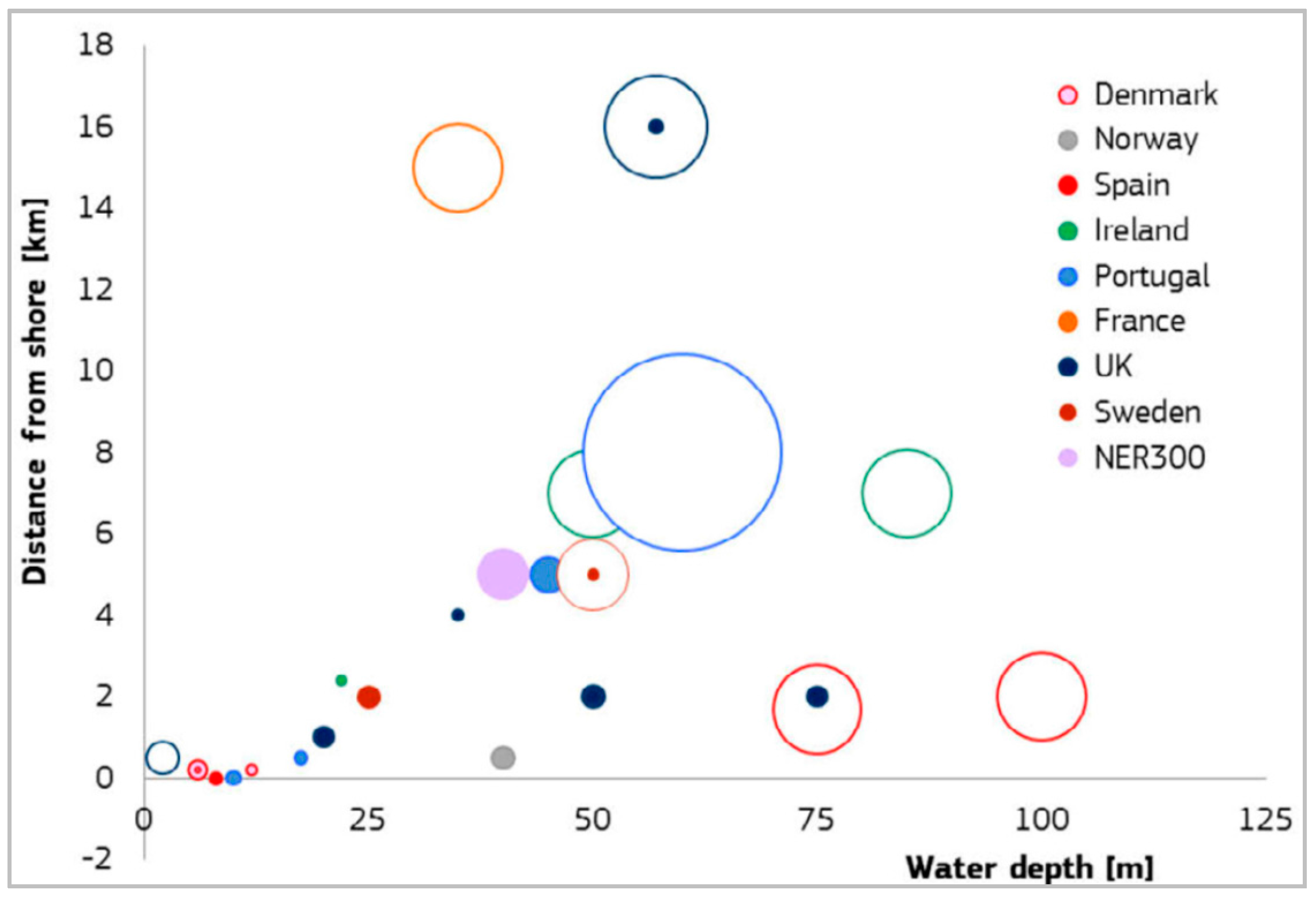
In the development of wave energy, nearshore or shallow water regions are frequently considered for developing wave energy converters/farms due to the closeness to the shore and the easy infrastructure, for instance, the cable connection and the availability for the operation and maintenance. One important aspect of these developments is the availability of wave energy resources in shallow water regions. Folley et al. [17] have shown that the wave resources reduce by less than 10% when traveling from a water depth of 50 m to 10 m. Hence the development of wave energy in shallow water regions has been preferred. Magagna et al. [18] collected information on current and proposed wave energy deployments (see Figure 1). It can be seen that so far most of the installed wave energy converters are deployed in the water depths of less than 50 m, and most of the proposed wave farms are deployed in the water depths of less than 100 m. Similarly, Johanning et al. [19] concluded that wave energy converters (WECs) would be very likely installed in the shallow to intermediate depths, typically at around 50 m contour in the open areas for wave energy production. For wave energy converters, such water depths may be in the transitional regions between self-referenced and fix-referenced deployments. Thus, a basic question would be which one is more efficient in terms of wave energy conversion: fix-referenced or self-referenced? To answer this question, the comparisons have been made for both point absorber (PA) [20] and oscillating water column (OWC) [21]. In reality, they are two popular wave energy conversion technologies and both of them can be deployed in either fix-referenced form [22,23,24,25] or self-referenced form [20,21,26,27,28].

Fix-referenced point absorbers may be the simplest wave energy converters, and the main motion mode for power conversion is heave [29,30,31], though other motion modes may contribute to a small part of the power conversion. In the simplification in the analysis, these minor factors are ignored so that we can concentrate on the optimisation of the PTO for maximising wave energy conversion ([32,33]). For floating or self-referenced point absorbers, technology developments have been seen, for instance, the famous devices, Power Buoy [26], Wave bob [34] and the US reference model (RM3, [20]). Again, the main motions are the relative heave motions between two floating bodies in the floating PA. Though the PTO optimization for a floating PA would be more complicated, it is still quite straightforward for the cases with only the relative heave motions (Falnes [35] and Sheng et al. [36]). The similar PTO optimization methods may be possible for individual multi-motion modes ([37,38]), the multiple relative motions for power conversion are very different and difficult. Though great advances have been seen in the PA wave energy converters of both fixed and floating types, the comparison of these two different deployments in terms of wave energy conversions has not been directly made. This research will use the recent developed PTO optimization technologies (Sheng et al. [36]) for a generic PA (RM3, [20]). RM3 is essentially a floating (self-referenced) point absorber, but for a comparison, it can also be considered as a fix-referenced PA when the spar is fixed (no motion is allowed for it). It will be seen that for a floating PA with its relative motions between the moving components being used, it could be beneficial for improving its wave energy conversion efficiency, as well as its compliance thus its survivability in the extreme waves (with long wave periods).

Fixed OWCs are those shoreline devices seen in some practical wave energy plants, and they may represent the most advanced developments in wave energy technologies. Heath [24] reports that the LIMPET OWC plant has generated power from waves to grid for more than 60,000 h in a period of more than 10 years, and there are some other shoreline OWC plants, such as PICO [39] and Mutriku [40], both still operational. Relatively, the technologies of floating OWCs are in different development stages. Though the backward bent duct buoys (BBDBs) are frequently referred, for instance, the OE buoy, developed by Ocean Energy Ltd. ([41]), and the US reference model (RM6, [27]), different types of OWC devices are also in development. The structurally simple spar-type floating OWC devices are being studied and developed in Portugal [21,42] and Spain (Oceantec [43]). Again, there is no direct comparison between the floating and fixed OWC wave energy converters in terms of wave energy conversion. For this purpose, the spar-type OWC wave energy converter [42] will be studied and compared for both fixed and floating deployments. The PTO optimization method can be analogous to that of PA as shown by Sheng et al. [44]. This method may be different from the OWC PTO optimization made by Bull [27], however, it must be pointed out that the results of these two methods would be same if the dynamic system is fully linear.

The different powers for different deployments of wave energy converters have suggested that the floating devices can be designed to be more efficient if the device motions can be used effectively, and to be more compliant in extreme waves (for the waves with long periods), so it may be beneficial for improving the device survivability in seas.

2. Generic Wave Energy Converters

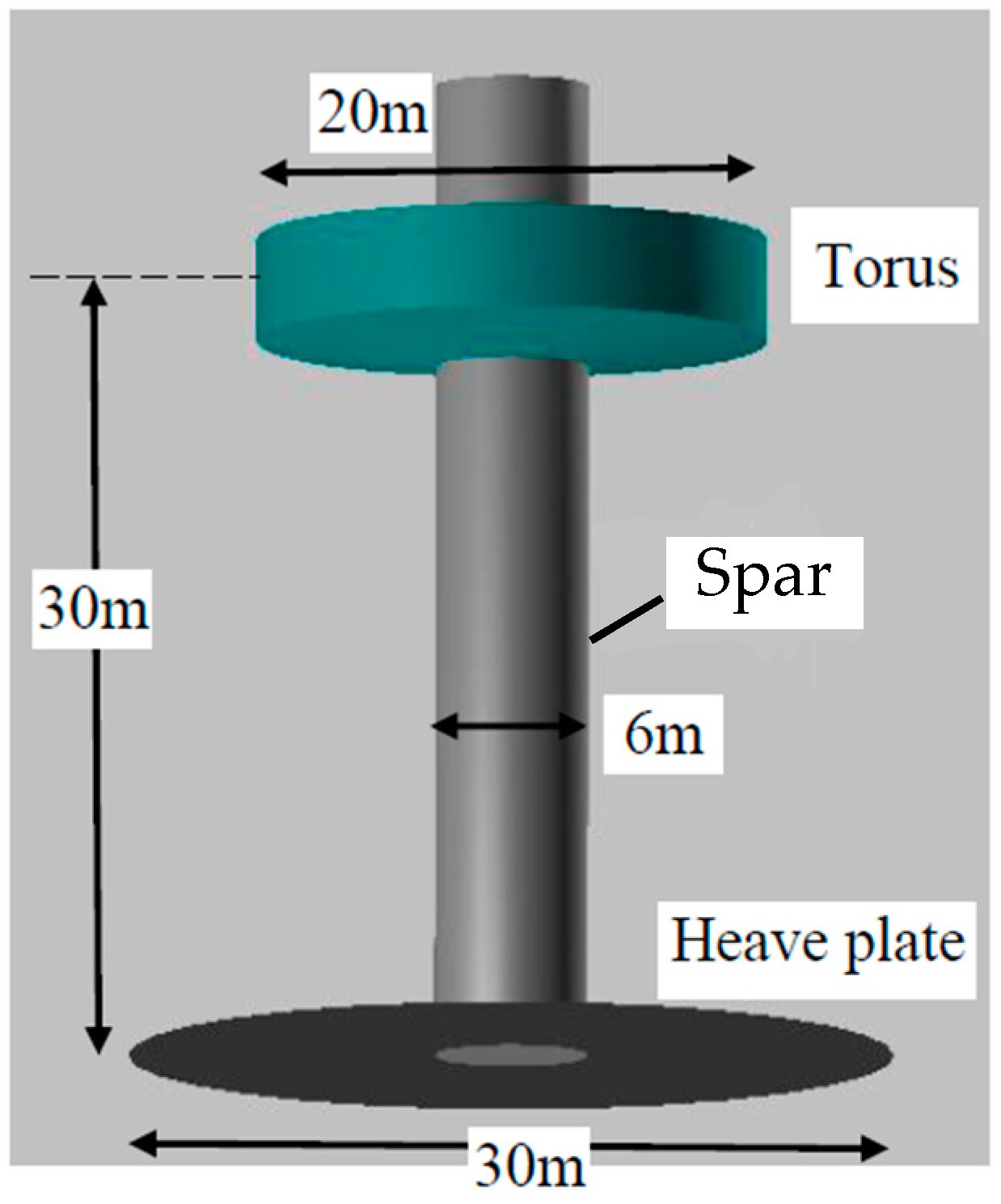
The first generic wave energy converter is a point absorber, the US reference model No.3 (RM3) wave energy converter [20]. The original design of the wave energy converter is a self-referenced (floating) point absorber (see Figure 2). This point absorber consists of two main moving bodies: the torus of diameter 20 m with a small draft, and the spar which is connected to a large heave plate (30 m in diameter). Overall, the point absorber has a draft of 30 m, and the displacements 848.2 m³ and 680.8 m³ for the spar (the cylinder, the heave plate has been simplified as zero thickness) and for the torus, respectively. In converting wave energy, the torus will very much move in-phase, whilst the spar moves out-of-phase with the passing waves. These in-phase and out-of-phase motions could generate a large relative motion between these two bodies, thus providing good motions for converting wave energy. In the case of a fix-referenced RM3, the spar can be taken as a fixed structure.

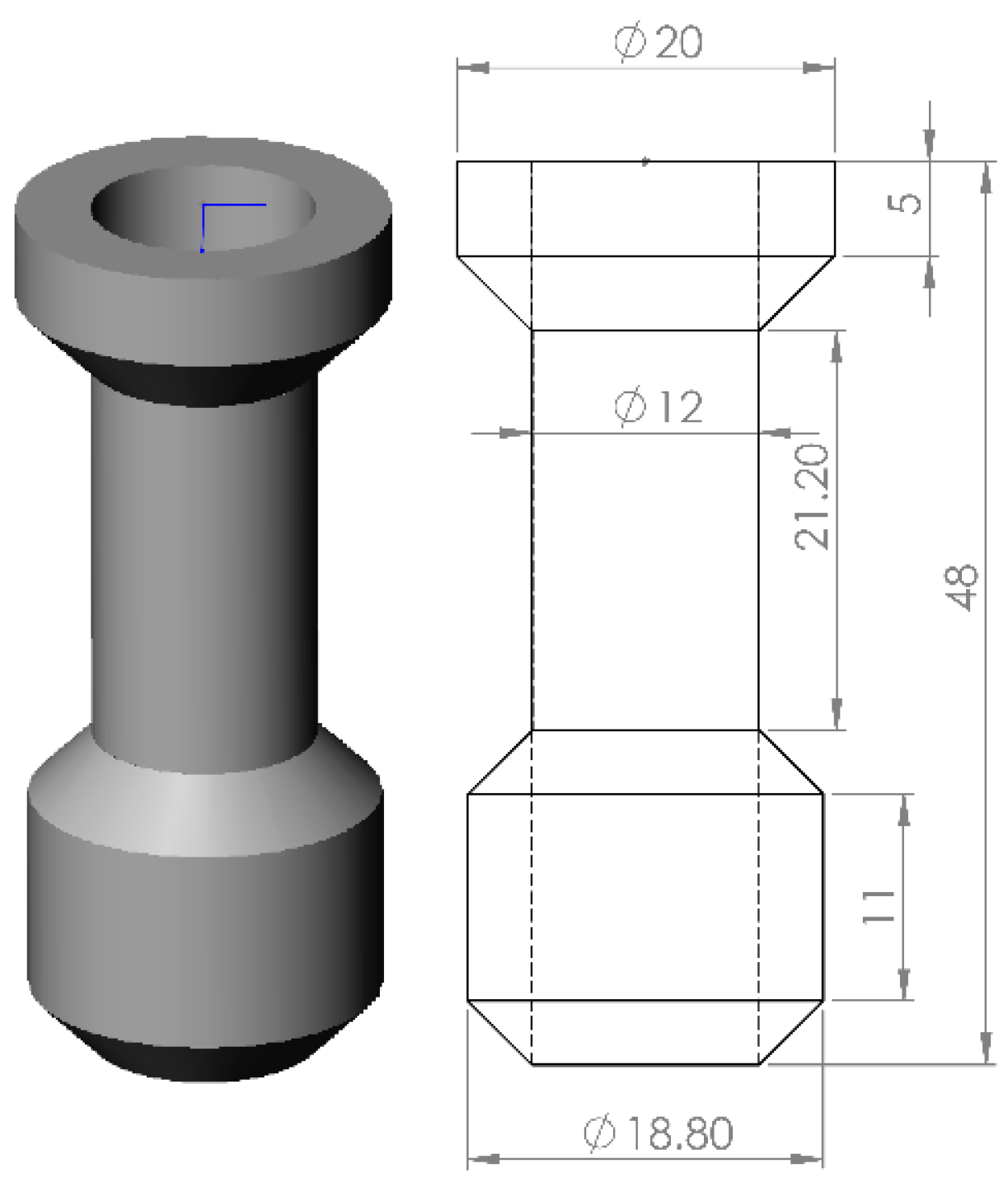
The second generic wave energy converter is a spar-OWC, which has been widely studied in Portugal [42] (see Figure 3). The selected generic OWC has a water column of 12 m in diameter, a float of an overall diameter 20 m and of a draft 48 m (the middle section is thin structure, and in hydrodynamic analysis, it is taken as zero thickness). The device has a displacement of 3609.3 m³. In converting wave energy from the target waves, the structure will move in-phase, whilst the water body in the water column (taken as an “imaginary piston” [21,45]) moves out-of-phase with the passing waves. These in-phase and out-of-phase motions could generate a large relative motion so to generate alternatively pressurized and depressurized air in the air chamber for energy conversion if an air turbine power take-off is applied.

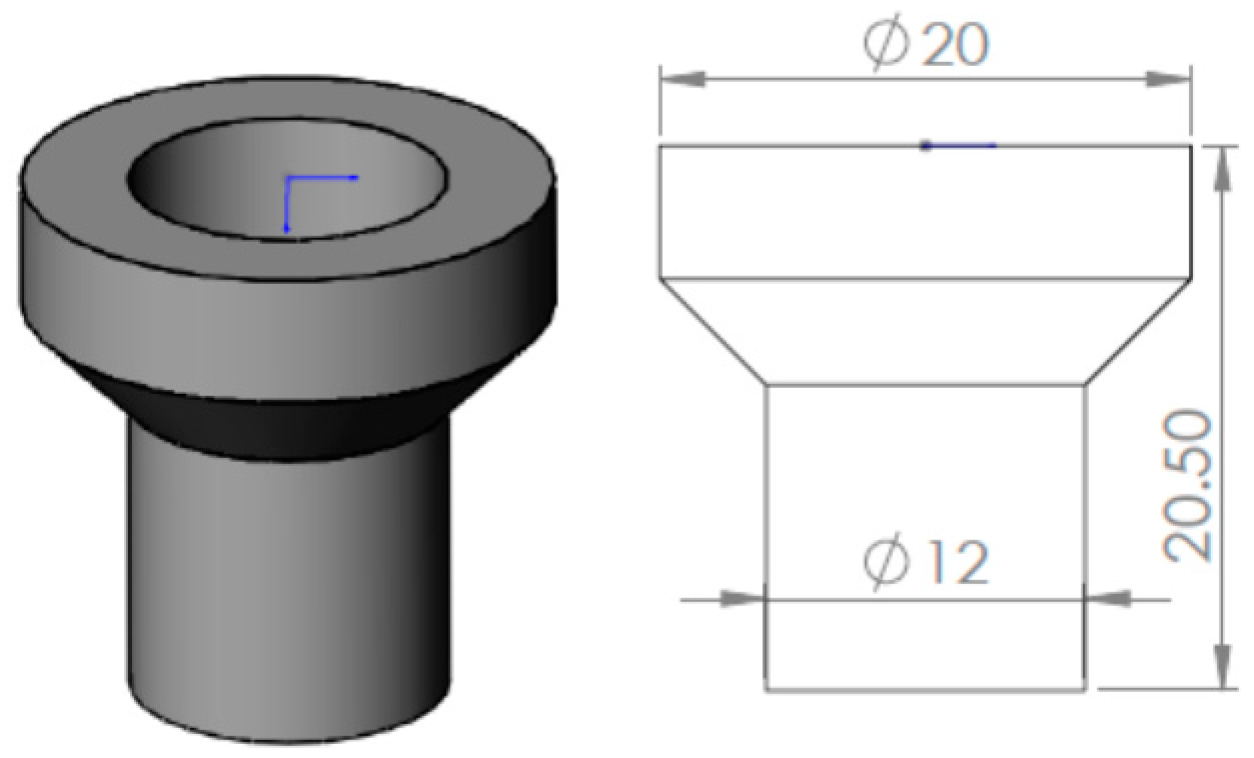
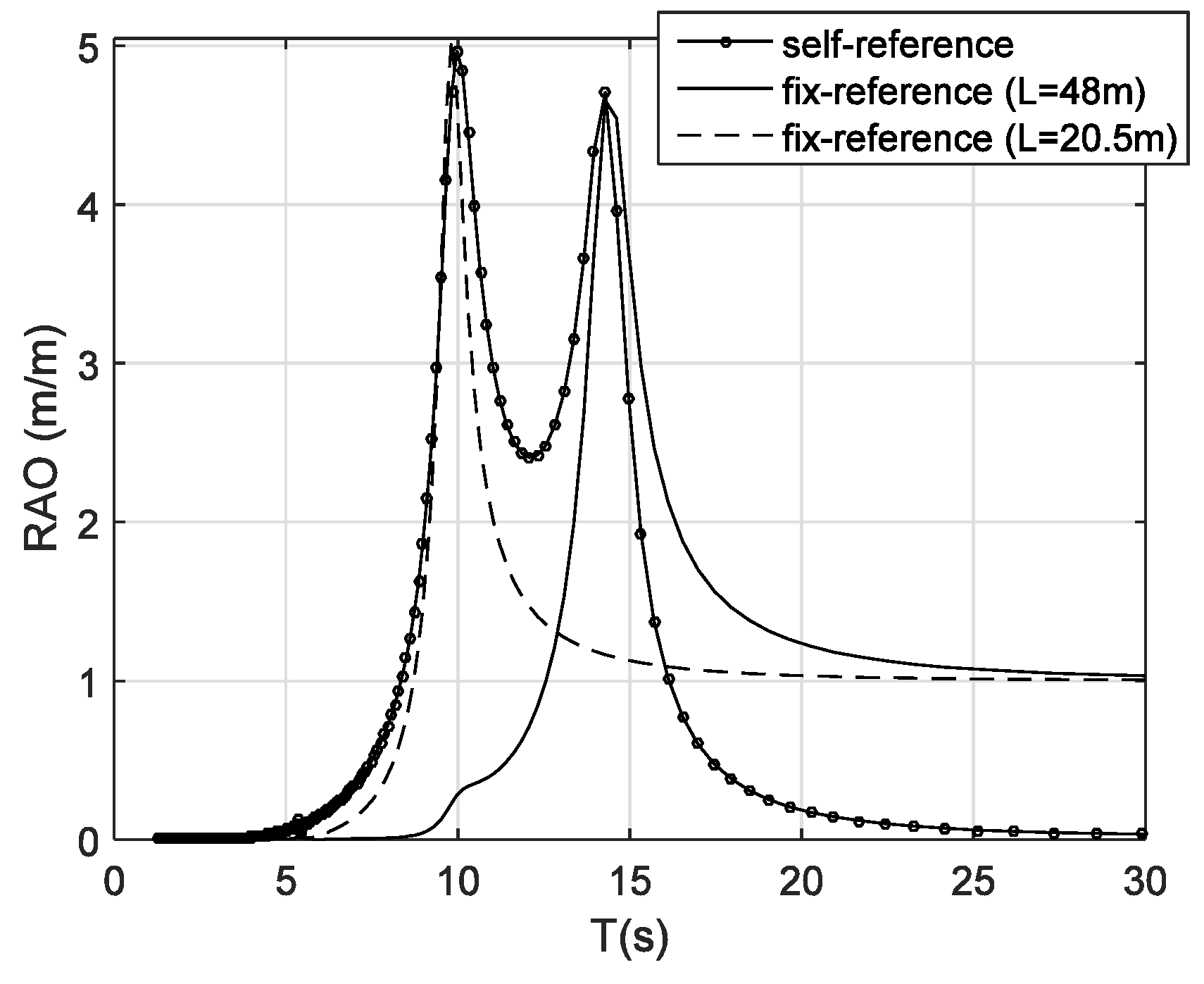
For representing a fixed OWC, the OWC structure can be simply specified as a fixed structure for analysis and comparison. It is noted that, however, this simple fixed spar OWC (with a large draft) may not be good converting energy from short waves, because of its relatively long resonance period (T₀ = 14.3 s), meaning the fixed OWC with a draft L = 48 m may not extract wave energy effectively from the waves of a period shorter than 14.3 s.

Comparatively, the floating OWC has its first resonance period of 10 s and second resonance period of 14.3 s. This means the floating OWC can extract energy efficiently from the waves of periods from 10 s to 14.3 s. Therefore, for a fairer comparison, the fixed OWC draft is adjusted to L = 20.5 m (Figure 4) (its internal water surface motion has a heave resonance period close to 10 s).

3. Analysis Method

In hydrodynamic analysis, the boundary element method (BEM) is based on the potential flow theory. In this case, it is the commercial BEM code WAMIT [46]. In the BEM code, multiple rigid bodies can be easily considered, with each body being given six degrees of freedom (DOFs). For a two-body system, the motions of the first body are identified by motion modes 1, 2,…, 6 and the second body by 7, 8,…, 12 for their surge, sway, heave, roll, pitch and yaw motions, respectively. In the following analysis this convention will be followed.

For the abovementioned floating wave energy converters, the most important motion for power conversion is the relative heave motion between two bodies. In the hydrodynamic analysis of the motions of the floating point absorber, the first body is the spar, with x₃ (v₃) representing its heave motion (velocity). The second body is the torus, with x₉ (v₉) being its heave motion (velocity). Similarly, for the OWC, the first body is the OWC structure itself, with x₃ (v₃) representing the heave motion (velocity) of the first body. The second body is an ‘imaginary piston’ representing the water body in the water column, with x₉ (v₉) being its heave motion (velocity).

Following [36], for such floating/self-referenced WECs (PA and OWC), the heave motions of the two-body systems are normally independent of the other motion modes, especially when the motions are small. For power conversion the relative heave motions of the two bodies are taken, and the corresponding dynamic equation can be expressed as:

$$\{\begin{array}{c}\left[i\omega Q_{33}+b_{33}+B_{33}\right]v_3+\left[i\omega Q_{39}+b_{39}\right]v_9=f_3-B_{pto}(v_3-v_9)\\ \left[i\omega Q_{93}+b_{93}\right]v_3+\left[i\omega Q_{99}+b_{99}+B_{99}\right]v_9=f_9+B_{pto}(v_3-v_9)\end{array}$$

(1)

with:

$$\{\begin{array}{l}{Q}_{33}=\left(m_{33}+a_{33}\right)-\frac{c_{33}}{{\omega }^2}\\ Q_{39}=a_{39}-\frac{c_{39}}{{\omega }^2}\\ Q_{93}=a_{93}-\frac{c_{93}}{{\omega }^2}\\ Q_{99}=\left(m_{99}+a_{99}\right)-\frac{c_{99}}{{\omega }^2}\end{array}$$

(2)

where m₃₃ and m₉₉ are the mass of the bodies, a₃₃, a₃₉, a₉₃, a₉₉ the added mass; b₃₃, b₃₉, b₉₃, b₉₉ the damping coefficients; B₃₃ and B₉₉ the additional damping coefficients for the heave motions of the structure and the piston; c₃₃, c₃₉, c₉₃, c₉₉ the restoring force coefficients; f₃, f₉ the complex excitations of the heave motions of two bodies; v₃, v₉ the complex heave motion velocity amplitudes of the two bodies; B_pto is the damping coefficient (for PA) or the equivalent damping coefficient (for OWC) for the linear PTOs, with the equivalent damping coefficient being defined [44] as:

$$B_{pto}=k_1{A}_0^2$$

(3)

where k₁ is the linear air turbine damping coefficient, and A₀ the sectional area of water column.

Rewriting of Equation (1) yields:

$$\{\begin{array}{c}\left[i\omega Q_{33}+\left(b_{33}+B_{33}+B_{pto}\right)\right]v_3+\left[i\omega Q_{39}+\left(b_{39}-B_{pto}\right)\right]v_9=f_3\\ \left[i\omega Q_{93}+\left(b_{93}-B_{pto}\right)\right]v_3+\left[i\omega Q_{99}+\left(b_{99}+B_{99}+B_{pto}\right)\right]v_9=f_9\end{array}$$

(4)

The average power conversion is given by:

$${\overline{P}}_{PA}=\frac{1}{2}{B}_{pto}{\left|v_9-v_3\right|}^2$$

(5)

The solution of the dynamic Equation (4) is:

$$v_3-v_9=\frac{Z_1+i{Z}_2}{Y_1+Y_2{B}_{pto}+i\omega \left(Y_3+Y_4{B}_{pto}\right)}$$

(6)

with:

$$\{\begin{array}{l}{Z}_1=f_{3R}\left(b_{99}+B_{99}+b_{93}\right)-f_{9R}\left(b_{33}+B_{33}+b_{39}\right)\hfill \\ -\omega f_{3I}\left(Q_{99}+Q_{93}\right)+\omega f_{9I}\left(Q_{33}+Q_{39}\right)\hfill \\ Z_2=f_{3I}\left(b_{99}+B_{99}+b_{93}\right)-f_{9I}\left(b_{33}+B_{33}+b_{39}\right)\hfill \\ +\omega f_{3R}\left(Q_{99}+Q_{93}\right)-\omega f_{9R}\left(Q_{33}+Q_{39}\right)\hfill \\ Y_1=\left(b_{33}+B_{33}\right)\left(b_{99}+B_{99}\right)-b_{93}{b}_{39}-{\omega }^2\left(Q_{33}{Q}_{99}-Q_{93}{Q}_{39}\right)\hfill \\ Y_2=b_{33}+B_{33}+b_{99}+B_{99}+b_{39}+b_{93}\hfill \\ Y_3=\left(b_{33}+B_{33}\right)Q_{99}+\left(b_{99}+B_{99}\right)Q_{39}-b_{93}{Q}_{39}-b_{39}{Q}_{93}\hfill \\ Y_4=Q_{33}+Q_{99}+Q_{39}+Q_{93}\hfill \end{array}$$

(7)

where f_3R and f_9R are the real parts of the excitations f₃ and f₉, and f_3I and f_9I are the imaginary parts of the excitations f₃ and f₉.

The average power is given by

$$\overline{P}=\frac{1}{2}{B}_{pto}\frac{Z_1^2+Z_2^2}{{\left(Y_1+Y_2{B}_{pto}\right)}^2+{\omega }^2{\left(Y_3+Y_4{B}_{pto}\right)}^2}$$

(8)

The optimised linear PTO damping coefficient is calculated as

$$B_{pto}=\sqrt{\frac{Y_1^2+{\omega }^2{Y}_3^2}{Y_2^2+{\omega }^2{Y}_4^2}}$$

(9)

The corresponding capture power in regular waves is calculated as

$${\overline{P}}_{\max }=\frac{1}{4}\frac{Z_1^2+Z_2^2}{Y_1{Y}_2+{\omega }^2{Y}_3{Y}_4+\sqrt{\left(Y_1^2+{\omega }^2{Y}_3^2\right)\left(Y_2^2+{\omega }^2{Y}_4^2\right)}}$$

(10)

3.1. Power Conversion in Irregular Waves

Real ocean waves are significantly different from regular waves of unique wave height and period, hence when the real ocean waves are referred to, they are normally characterised by a significant wave height (H_s), a characteristic period (T_c), a corresponding spectrum shape and a wave spreading function. For a single point in sea, the measured waves can be simply represented by a conventional long-crested wave as

$$S_w(\omega )=\frac{5}{16}\frac{{\omega }_p^4}{{\omega }^5}\exp \left(-\frac{5}{4}\frac{{\omega }_p^4}{{\omega }^4}\right)$$

(11)

or the standard JONSWAP spectrum as

$$S_w(\omega )=0.2049\frac{{\omega }_p^4}{{\omega }^5}\exp \left(-\frac{5}{4}\frac{{\omega }_p^4}{{\omega }^4}\right)\times {3.3}^{\gamma }$$

(12)

with ${\omega }_p=\frac{2\pi }{T_p}$ and $\gamma =\exp \left[-\frac{{\left(\omega -{\omega }_p\right)}^2}{2{\omega }_p^2{\sigma }^2}\right]$ for $\sigma =\{\begin{array}{c}0.07,if\omega \le {\omega }_p\\ 0.09,if\omega >{\omega }_p\end{array}$.

A real sea state consists of a number of components of different amplitudes and frequencies, and each wave cycle varies in both amplitude and period. The optimisation of the PTO damping means a constant damping for the sea state, rather than the individual waves in the sea state. For the optimised PTO damping coefficient, B_pto, the corresponding wave energy conversion curve $\overline{P}$ is defined using Equation (8) (the capture power per unit wave amplitude), and from which the captured power in irregular waves for a constant PTO damping coefficient can be calculated, see [47], as:

$$P_{irr}=2{\displaystyle {\int }_0^{\infty }\overline{P}{S}_w(\omega )}d\omega$$

(13)

It has been proposed by [36] that the corresponding period for the optimised damping very likely falls between T_p (the longest period) and T_z (the shortest period). To more accurately acquire the optimised damping coefficients, the number of the periods between T_p and T_z can be divided into 20 or more even periods, and we can easily choose the period and damping coefficient corresponding to the most energy conversion as the optimization conditions.

3.2. Wave Scatter Diagram

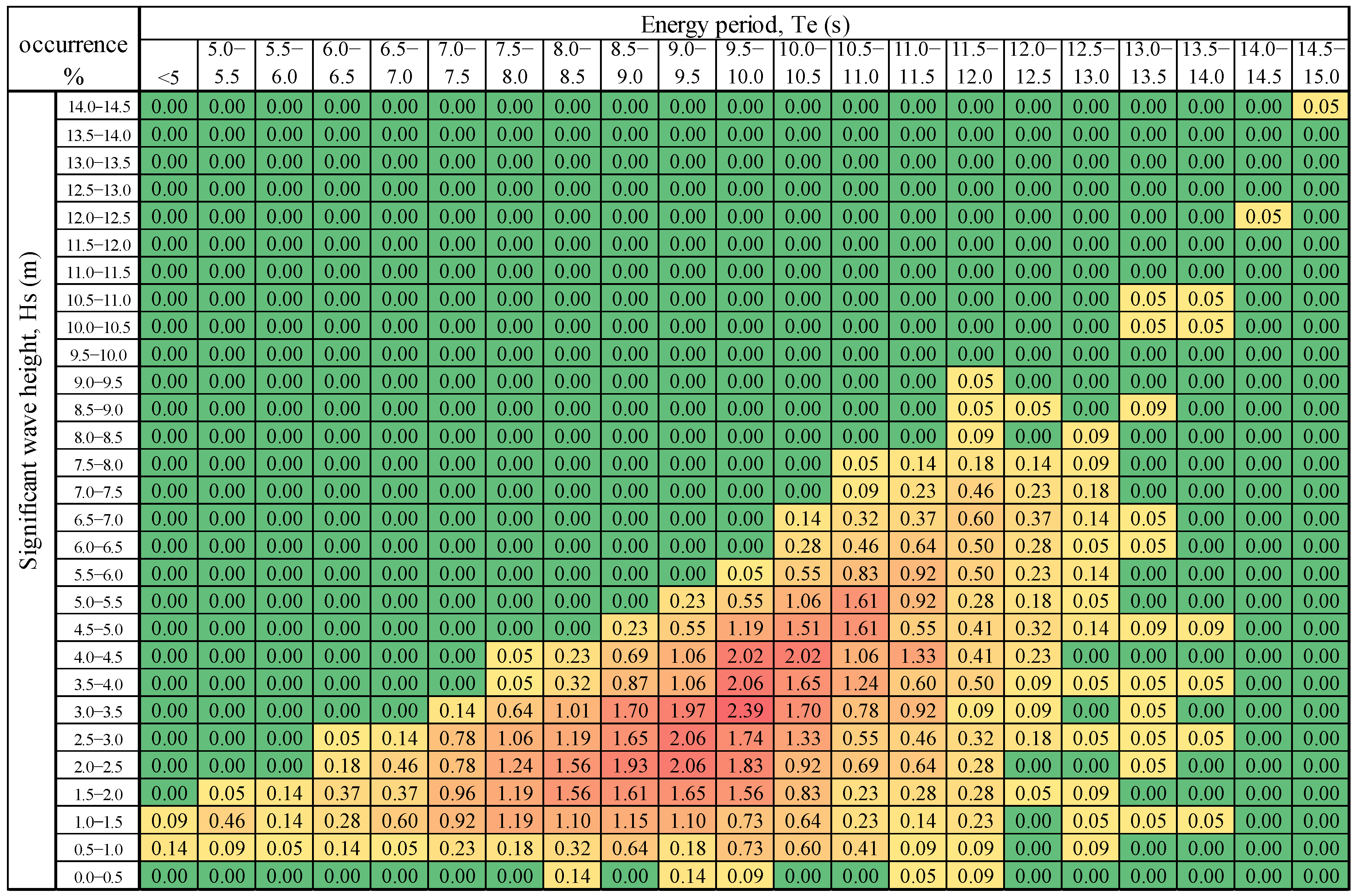
Figure 5 shows a scatter diagram for the wave measured in Belmullet (Ireland; water depth = 50 m, 2008), in which the wave scatter diagram has been given in a format of IEC 62600-101 standard [48]. The average annual power is 69.86 kW/m, which is based on the middle wave height and period in each bin, rather than the high points with largest wave height and largest period for each bin, which give the average annual energy of 80.12 kW/m). It can be seen that the waves frequently happen for a certain wave periods and weight heights. For instance, the waves with wave periods (T_e = 7.0 s–12.5 s, corresponding to the frequency range 0.5–0.9 rad/s as suggested by Falcao [49]) happen at a probability of 0.94, meaning 94% of the waves fall to the range. Out of this period range, different waves may happen, but very occasionally.

4. Examples and Analysis

4.1. Point Absorber

For the point absorber, the additional damping coefficients are only applied to the spar with B₃₃ = 40 kN/(m/s), while for the torus structure, the dish-like structure provides a dominant radiation damping for the structure motion, hence an additional damping is not necessary. As such, it will be seen from the examples in this section that the responses of the heave motions of the two bodies of the point absorber is reasonable and believed to be practical. For the original RM3 design (i.e., the heave plate diameter is D = 30 m), the float has a heave resonance period of 5.37 s, but the spar has a heave resonance of 36.96 s, meaning that the float moves in-phase with the wave when its period is larger than 5.37 s, while the spar moves out-of-phase with the wave when the wave period is less than 36.96 s (the dashed line in Figure 6). Apparently, these two heave resonance periods cover a large range of the waves. For a comparison, for the case of heave plate D = 25 m, the 2nd resonance period is 28.56 s (the solid line in Figure 6). It is interesting to note that from Figure 6, the larger difference between the two resonance periods, the smaller of the relative motion (RAO) (dashed lines in the figures) may have. It should be noted that the small relative motion (RAO) is generally not good for energy conversion.

4.1.1. Maximal Power Conversions in Regular Waves

The maximal capture power based on the optimised damping coefficient is calculated from Equation (10). Figure 7 shows the comparison of the maximal capture powers for the fix-referenced and self-referenced PAs (‘fix-referenced’ and ‘self-referenced’ in the legend) and the self-referenced devices are with two different heave plates (D = 25 m and D = 30 m). There is a gain for the self-referenced PA over a range of wave periods. For the case of D = 30 m, the gain is for the periods from 7 to 13 s, which just falls on the wave periods of interest based on common wave energy resource assessment, while for the case of D = 25 m, the gain for the periods of 6–11.5 s. For the self-referenced PAs, there are large but narrow peaks at T = 10 s for D = 25 m and T = 12.1 s for D = 30 m, which may be responsible for the capture power increase for the self-referenced PAs. It will be seen the gains for certain wave periods are very beneficial for increase the power conversion by the self-referenced PAs.

4.1.2. Power Conversion in Irregular Waves

When the point absorber is placed in seas, the linear optimised damping coefficient for the PTO will be only dependent on the wave period/frequency, and independent of the wave height. For a given sea state, the optimised damping can obtained using the method mentioned in Section 3.1. For a comparison, the maximal capture powers from irregular waves (H_s = 2 m for all the cases) for the different heave plates can be seen in Figure 8 (in which D20 means the heave plate diameter of 20 m and so on). From the curves, it can be seen that the cases of D = 25 m and D = 27.5 m give the highest energy conversion (~130 kW). In particular, for the case of D = 25 m, the self-referenced PA can extract more energy than the fix-referenced PA for the periods of 6 s to 12.5 s (slightly different from the gain for 6–11.5 s in regular waves). The wave periods from 6 to 12.5 s are normally the waves of most interest for wave energy conversion [49]. For a larger heave plate (D = 30 m), there will be a smaller increase in the capture power when compared to the fix-referenced PA, but it extends the wave period to 14.5 s for producing more energy than the fix-referenced PA.

Figure 9 shows the gains for the self-referenced PAs with different heave plates (D = 25 m and D = 30 m) (compared to fix-referenced PA). It can be seen that for the case for D = 25 m, big gains have been obtained from 6 to 12 s, and a largest gain occurs is an increase 35% of capture power at T_p = 10 s.

4.2. Oscillating Water Column

4.2.1. Heave Responses of the Floating and Fixed OWC

Figure 10 gives a comparison of the internal water surface responses of the floating and the fixed OWCs with a draft of 48 m (additional damping coefficients B₃₃ = B₉₉ = 200 kN/(m/s) have been added to the heave motions of the structure and the water body). It can be seen that with a draft of 48 m, the fixed OWC has one resonance period of 14.3 s, same as the second resonance period in the floating OWC.

For a fairer comparison, the draft of the fixed OWC is shortened so to have a resonance period of T₁ = 10.1 s, same as the first resonance period of the floating OWC. To get the required draft of the fixed OWC, the following equation is used for calculating the internal water motion resonance period T₀ [50]:

$$T_0=2\pi \sqrt{\frac{L+0.41\times S^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{g}}$$

(14)

where L is the draft, S the sectional area of the water column, and g the acceleration of gravity.

For a target period T = 10.1 s, the draft of the fixed OWC is calculated as L = 20.5 m (see Figure 4). Figure 10 shows the closeness of the water body heave response for the fixed shortened OWC. To get similar response at the resonance, for the fixed OWC, the additional damping coefficient is B₉₉ = 100 kN/(m/s). As such the comparison of the responses are plotted in Figure 10.

4.2.2. Power Conversion in Irregular Waves

The maximal capture power in regular waves is given in Figure 11 for a wave weight of H = 2 m). It can be seen that the floating OWC can be very efficient in converting wave energy for the wave periods from 9 s to 14 s, while for the longer fixed OWC, the maximal capture power is relatively small and narrowly banded, though it can take more energy from the very long waves of periods longer than 15 s (Figure 11). However, in reality, such long waves happen rarely, which may be excluded for energy conversion. For the fixed OWC (shorter version), its peak happens at T = 10 s, but its peak value is much smaller than that of the floating OWC (Figure 11). Again, this fixed OWC can only generate more energy when the wave period is larger than 15 s.

4.2.3. Power Conversion in Irregular Waves

When considering the power extraction from irregular waves (H_s = 2 m for all the cases), Figure 12 shows the fixed and floating OWC with same draft (L = 48 m). It can be seen that the floating OWC can take much more energy out from waves for the waves of T_e = 5 s to 20 s, and the floating device generally converts 3–5 times more energy from the waves of periods of T_e = 9–14 s. For the second case (Figure 12), the fixed OWC with a shorter draft can take more energy, but still very limit when compared to the floating OWC. Figure 13 shows the gains of the floating OWC comparted to the fixed OWC. For the most happened waves (periods from 7 to 13 s), the floating OWC can take more than 200% of the wave energy when compared to the fixed OWC.

5. Annual Wave Energy Conversions from Seas

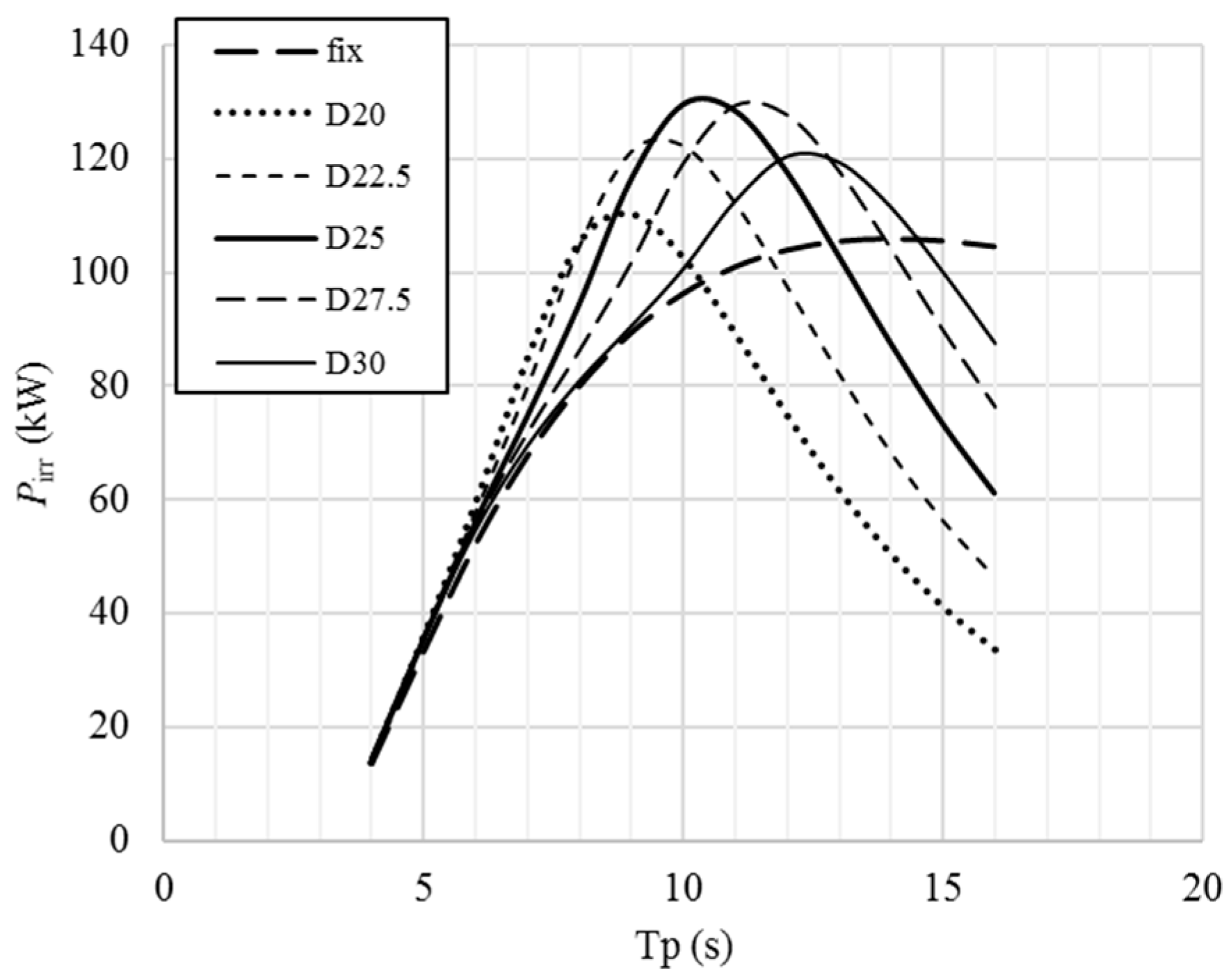
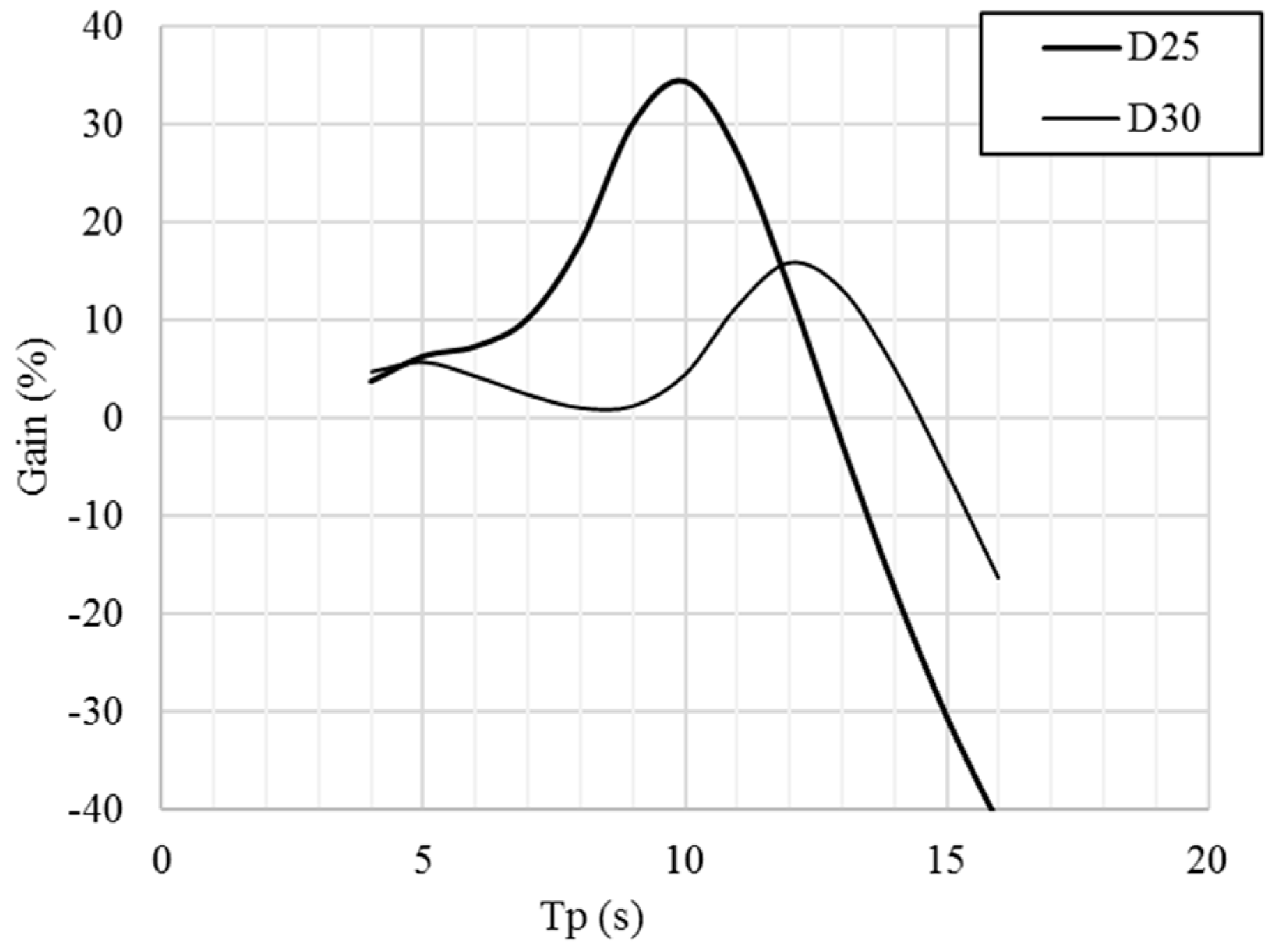
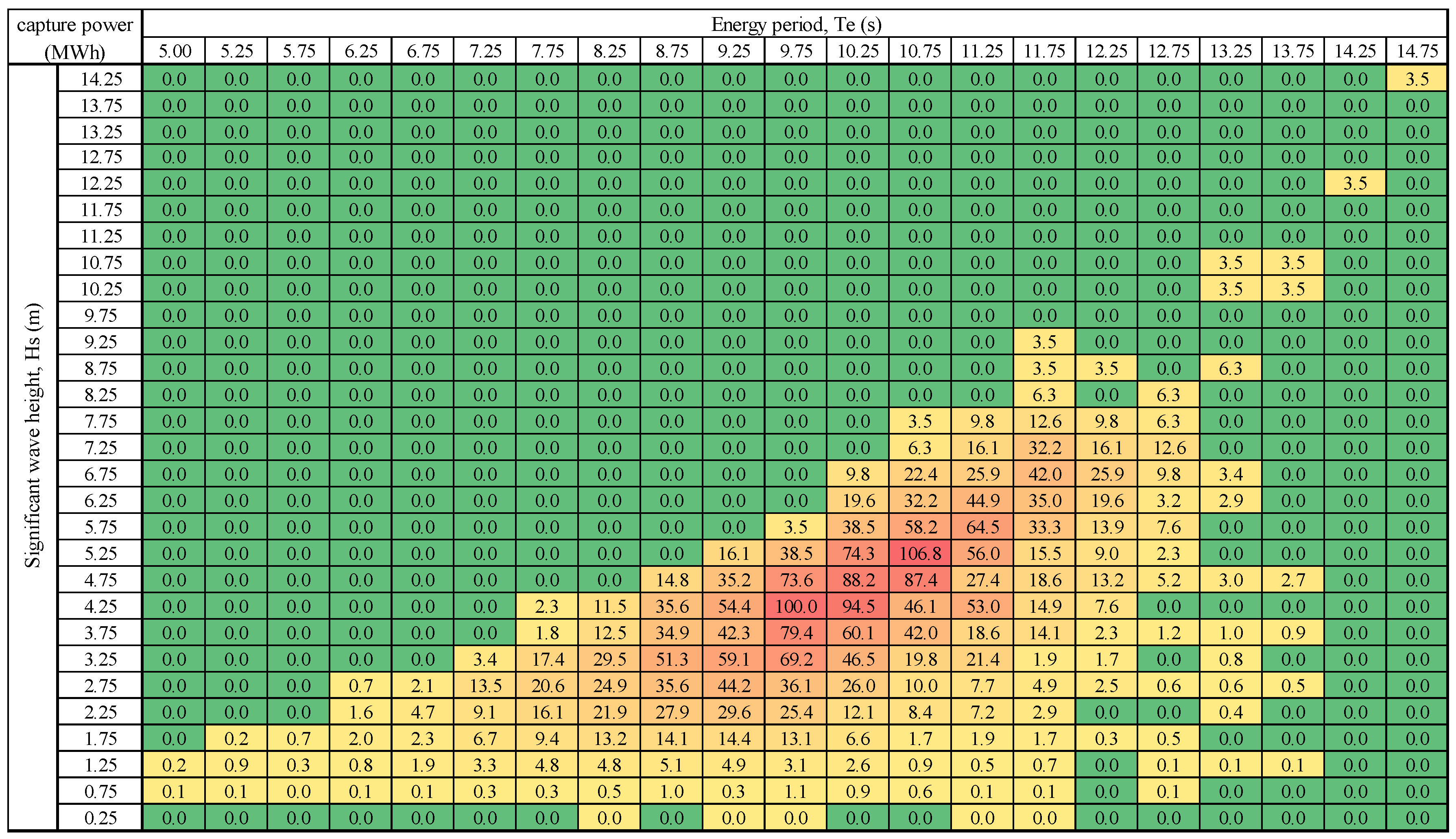
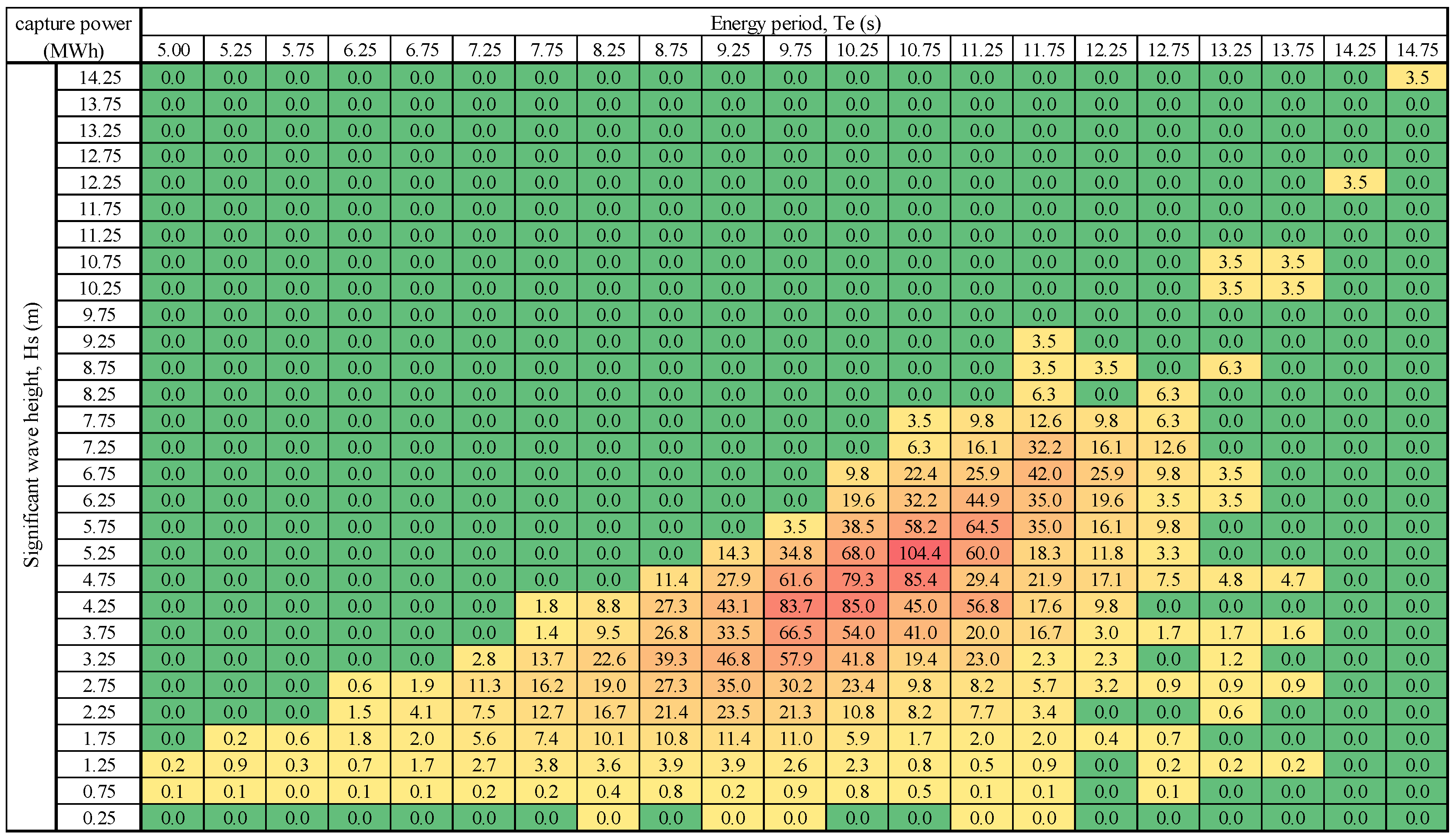
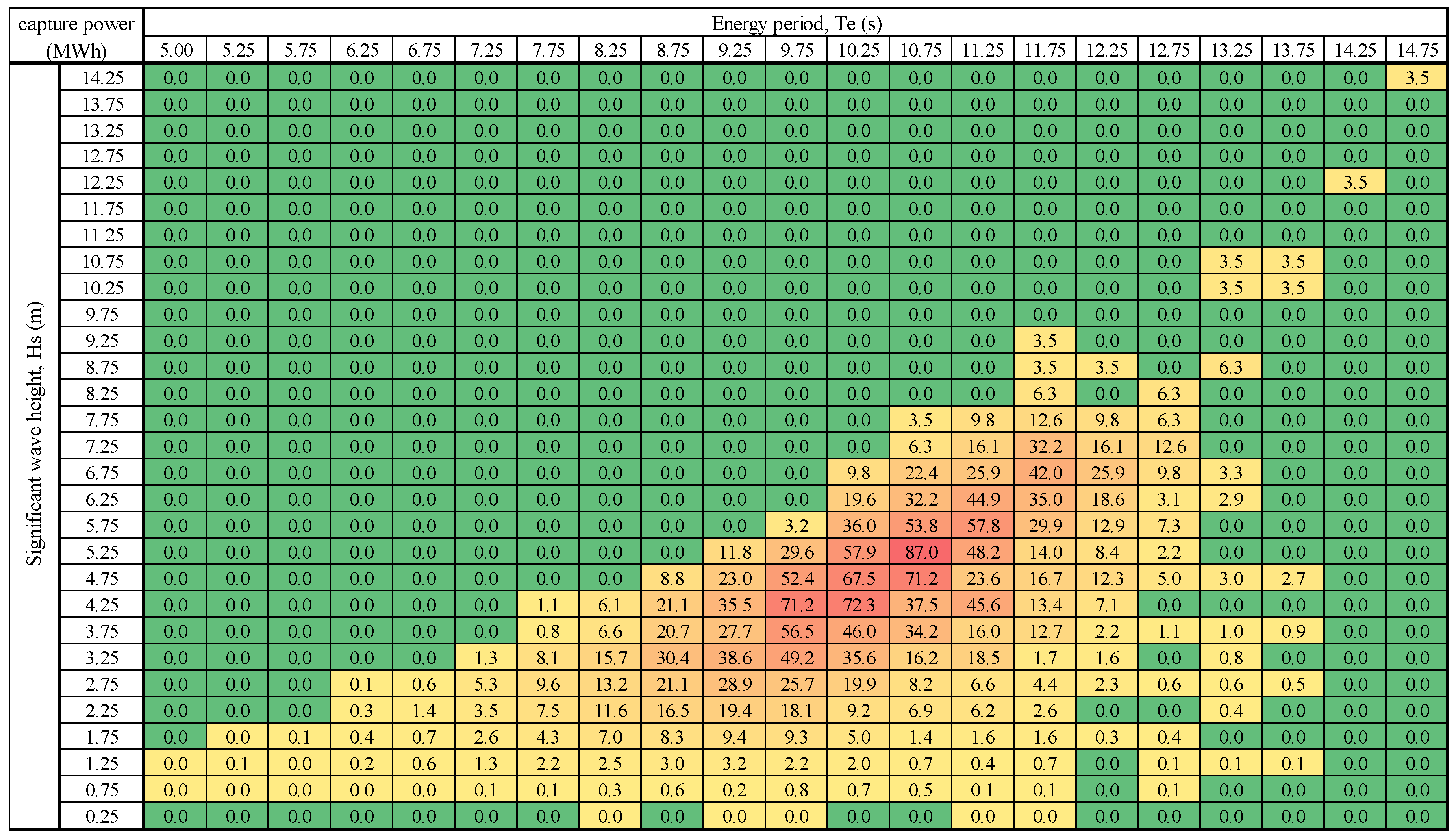
As it is already shown above that the self-referenced/floating devices can extract more energy from certain given waves, in this section, the study will be on the annual energy conversions from seas for both the PAs and OWCs. Also, the PA with a heave plate of a diameter 25 m gives better wave energy conversion for the targeted waves. Hence in the following analysis, the PA with a heave plate of 25 m will be used.

Based on the power conversion curves in Figure 8 and the scatter diagram in Figure 5, the initial power matrix is proposed to be simply calculated using the following formula:

$$P_{ij}=\{\begin{array}{ll}{P}_{irr}(T_{e,i})\times H_{s,j}^2/4,\hfill & if{P}_{irr}(T_{e,i})\times H_{s,j}^2/4<800\hfill \\ 800,\hfill & if{P}_{irr}(T_{e,i})\times H_{s,j}^2/4\ge 800\hfill \end{array}$$

(15)

where T_e,i is the ith horizontal bin in the following figure (note: the factor ¼ is used because the optimised capture power P_irr has been calculated using a significant wave height of 2 m), H_s,j the jth vertical bin.

The power output has been capped by a simplified initial rated power of 800 kW, which is chosen for a general comparison. However, it must be noted that the recommended rated powers of the devices may not be good for the purpose of the comparisons, because the different deployments may lead to different rated power.

Based on the initial power matrix, the capture power in each bin can be easily calculated by:

$$E_{ij}=P_{ij}\times q_{ij}\times 8760/100$$

(16)

where q_ij is the occurrence (in percentage) in the ith horizontal and jth vertical bin given in Figure 5, and in the formula, the constant 8760 is the number of hours in a year, 100 for the modification factor due to the fact in the scatter diagram, the percentage is used.

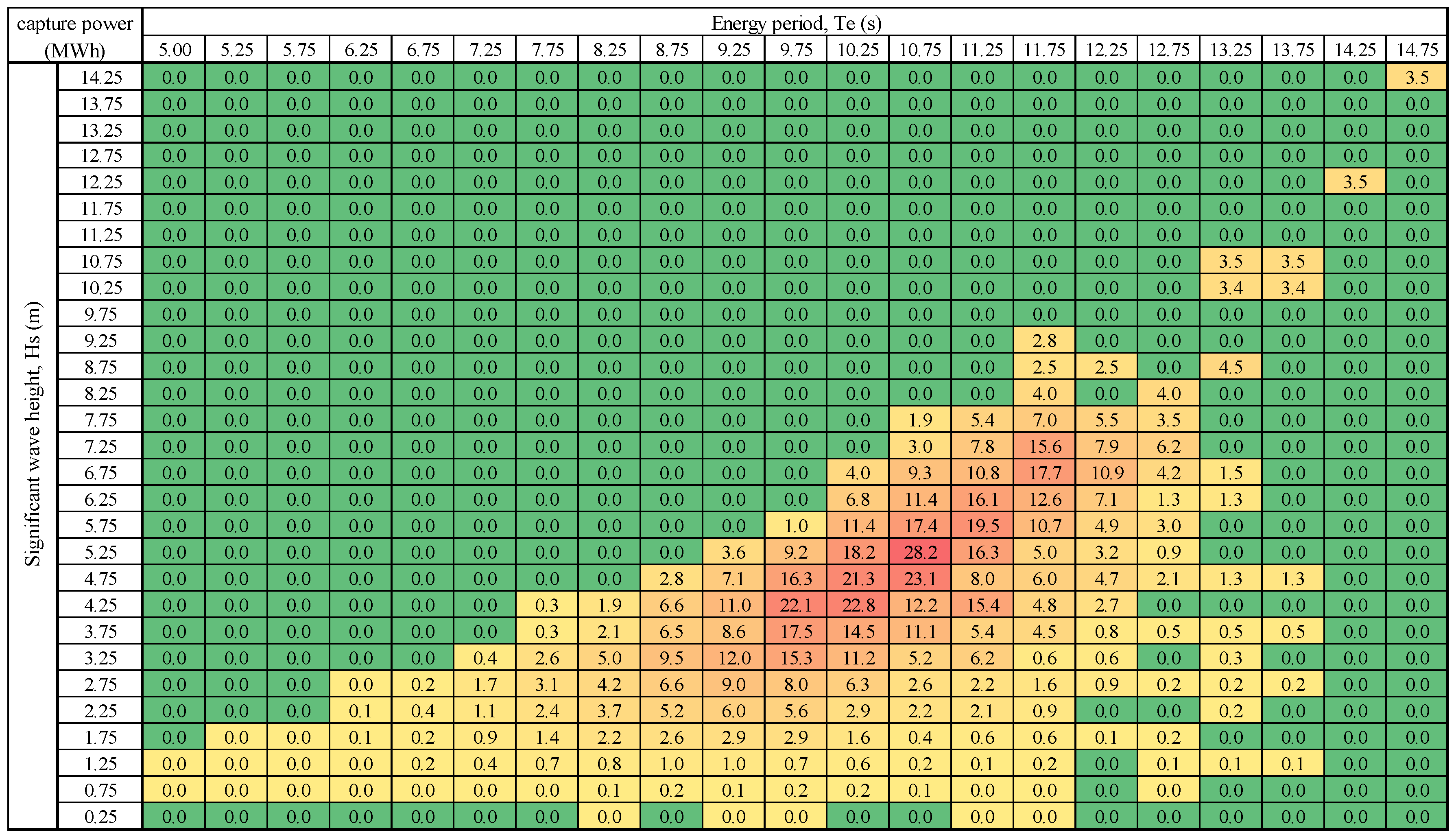
Figure 14 and Figure 15 are the capture powers for the self-referenced PA and the fix-referenced PA. From the figures, it can be seen that the self-referenced PA can slightly capture more energy than the fix-referenced PA in most wave conditions (bins). The maximal capture powers for the self- and fix-referenced PAs happen at the same wave condition (the bin of wave height of 5.25 m and period of 10.75 s), with the maximal capture powers being 106.8 MWh and 104.4 MWh, respectively, a difference of 2.3%. For the smaller wave periods, the self-referenced PA can capture more energy than the fix-referenced PA. The annual capture powers are 2960 MWh and 2730 MWh, respectively. Overall, the self-referenced PA can capture 8.4% more energy than the fix-referenced PA annually.

Figure 16 and Figure 17 are the capture powers for the floating OWC and the fixed OWC. From the figures, it can be seen that the floating OWC can significantly capture much more energy than the fixed OWC in almost all wave conditions (bins). The maximal capture powers for the floating and fixed OWCs happen at the slightly diffeent wave conditions (the bin of wave height of 5.75 m and period of 10.75 s and the bin of wave height of 5.25 m and period of 10.75 s). The maximal capture powers are 87.0MWh and 28.2 MWh, respectively, a difference of 209%. The annual capture powers are 2300 MWh and 812 MWh respectively, meaning the floating OWC can capture 180% more energy than the fixed OWC annually.

6. Discussion

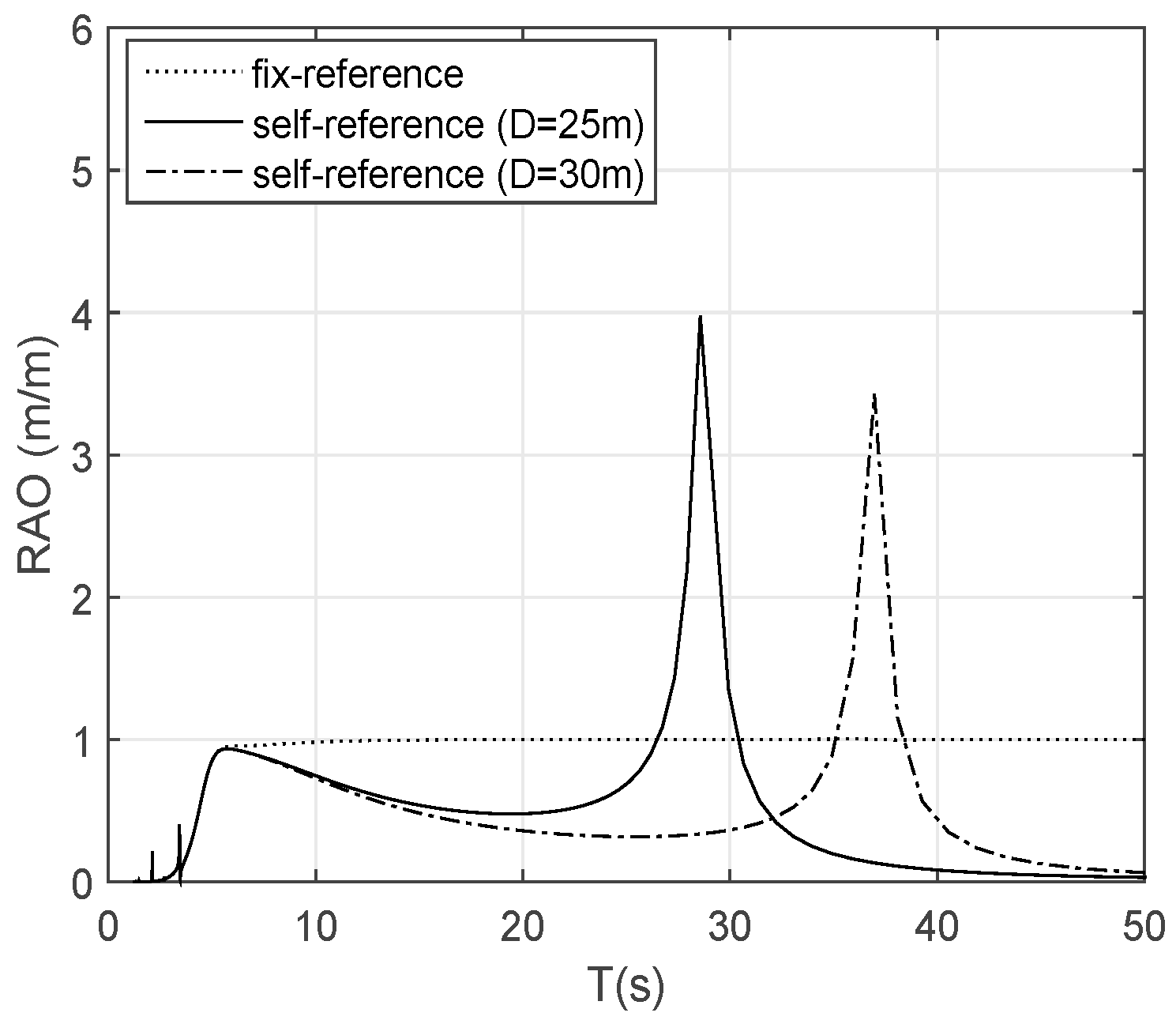
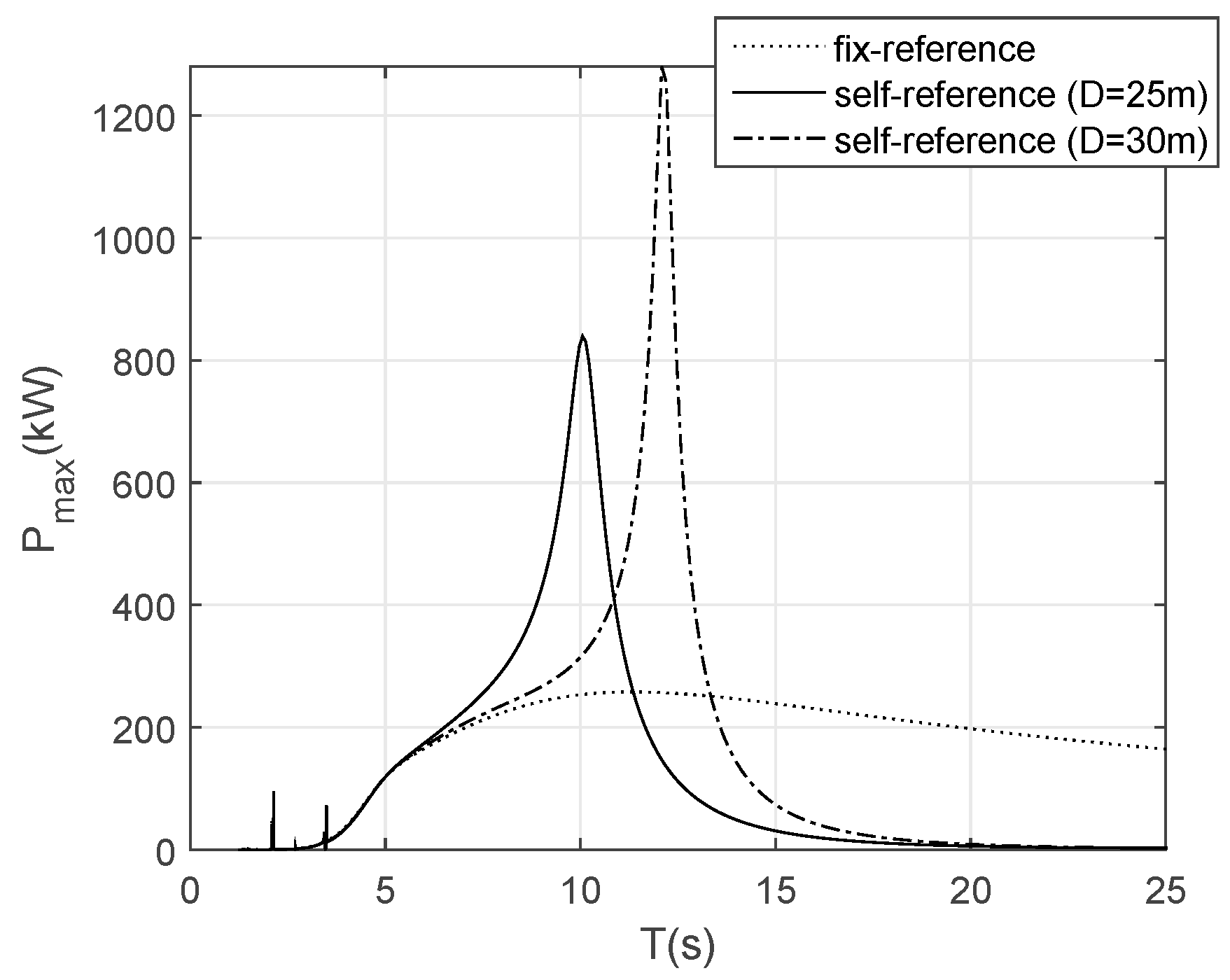
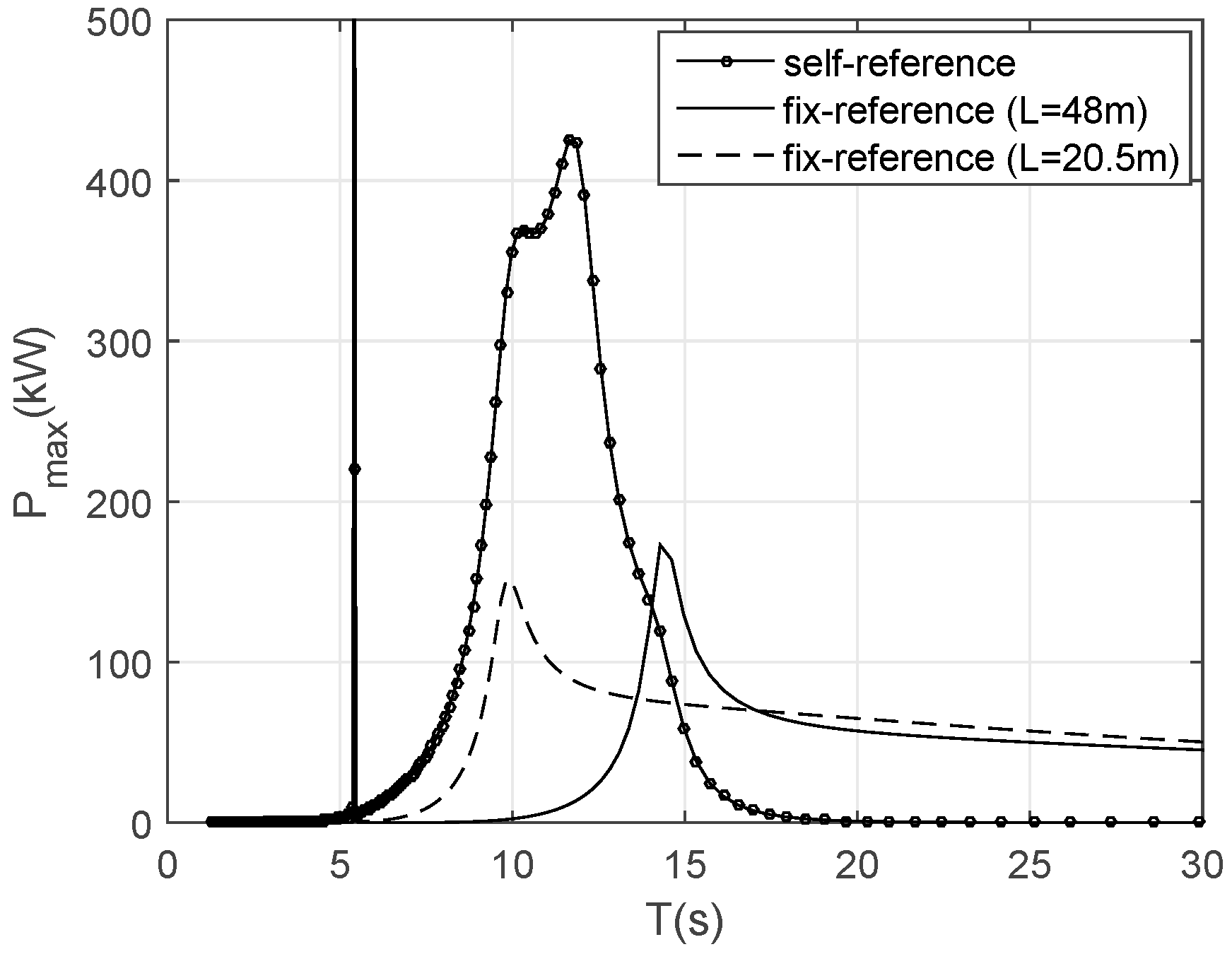
From the examples above, it can be seen the floating/self-referenced wave energy converters can capture more energy from sea than their fixed or fixed-referenced device counterparts. The main reason for this is that the floating or self-referenced wave energy converters can utilize the structure motion or relative motion for improving energy conversion. This is especially true for the floating OWC. When compared to the fixed OWC, the structure heave motion is very important for improving wave energy conversion capacity, in particular for those target waves. The difference between the two responses of their heave motions can largely improve the response and power performance in a wider bandwidth (see Figure 10), and as such, the relative motion can be enlarged so for significant improvement of the wave energy capture capacity for the waves of interest (Figure 11). This improvement can benefit both the power performance and the device survivability, since the floating device can be much more efficient in the most occurred waves but less efficient for the long waves (Figure 12). The latter is important for the device survivability for being more compliant in the extreme waves and for the avoidance of over-powering problems in the very large and long waves.

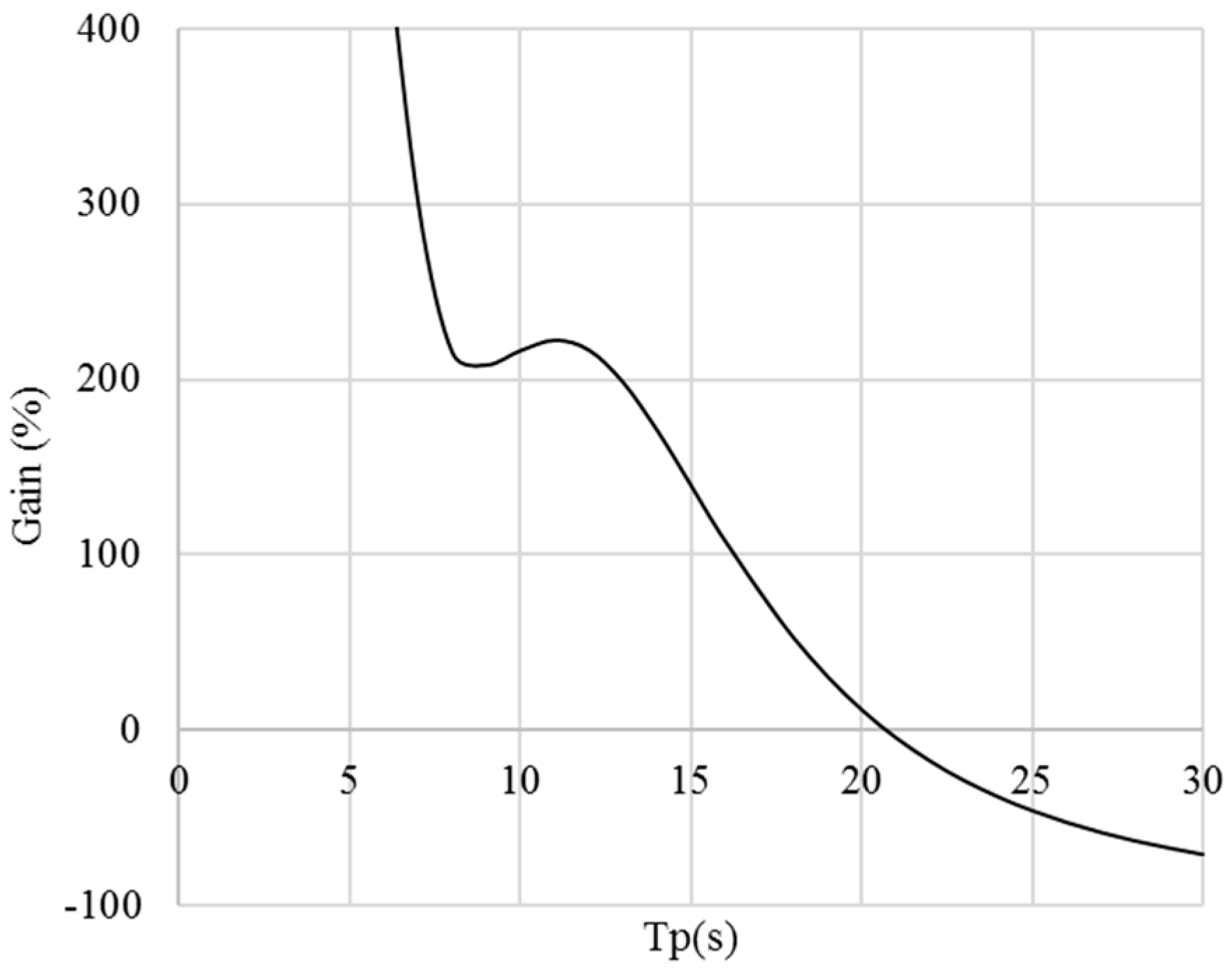
The case for the self- and fix-referenced PAs are slightly different. Though the self-referenced PA can capture more energy than the fix-referenced counterpart, the increase of the capture power is not as significant as that in OWCs. The reason for this is that the spar in the self-referenced PA has a very long resonance period, which means the motion of the spar may not make a significant contribution for power conversion. The heave plate performs more like a reference structure, rather than a part which can significantly contribute to increase wave power production. Learning from the case of the OWC, it can be envisaged that the PA can be further optimized so that the two resonance periods can be closer to make the device more efficient.

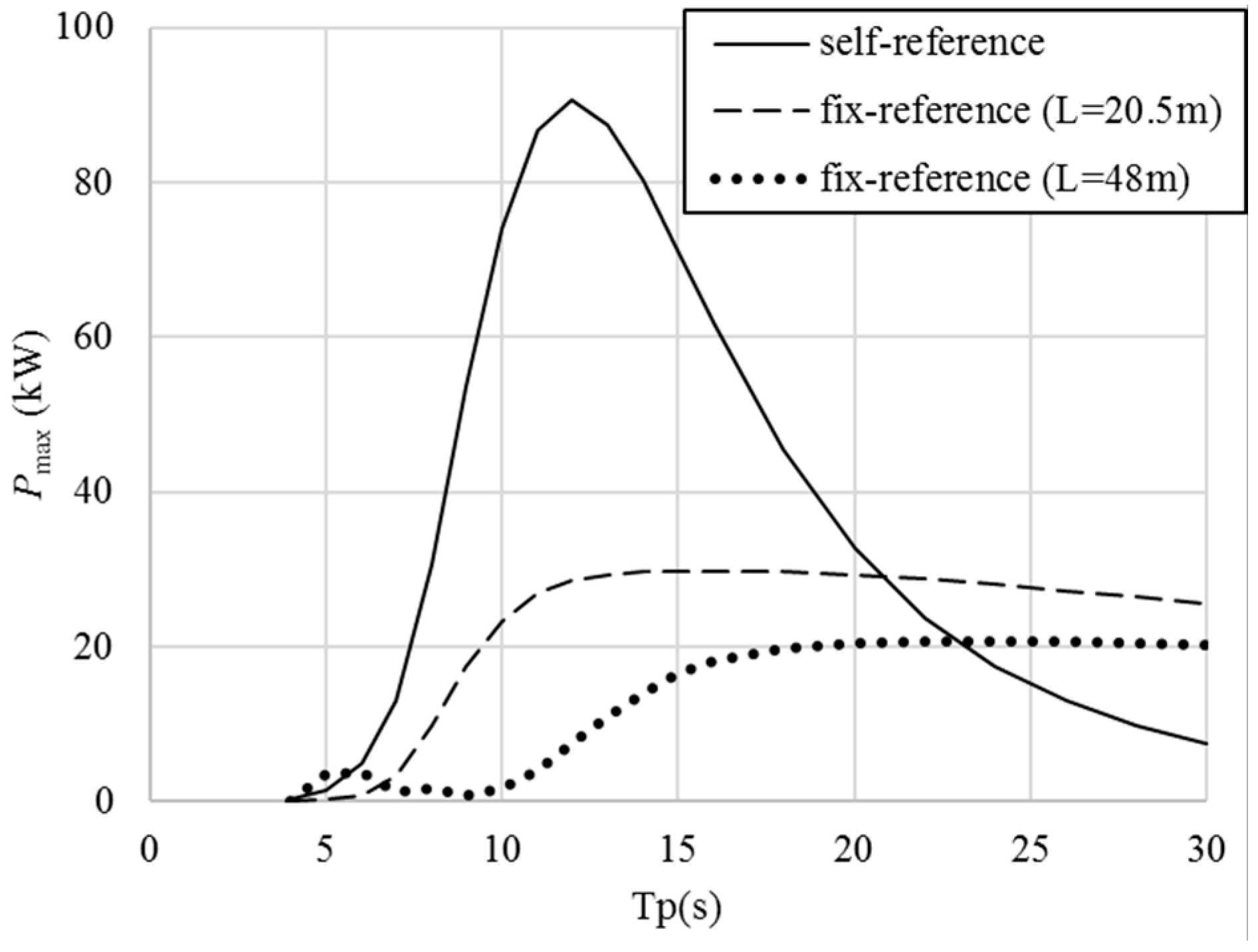
It must be emphasized that the choice of the device deployment may not be only decided for energy conversion, while some other practical considerations and limits must be taken into account, such as the device survivability, the PTO and generator capacity and efficiency, the electronics and control systems, mooring design if the device is floating or self-referencing and so on. In practice, device survivability may be the most important factor we need to consider. For wave energy converters, they have to be designed to efficiently produce power from the operational sea waves, but they must survive from much energetic seas. Another practical issue is that the device cannot produce too much energy for which the device’s mechanism, PTO, generator and electronics may not be able to handle: structural overloading in mechanics may cause structure failures, while the power overloading can cause the failures of the PTO, generator and electronics. As it has been suggested, for wave energy converters, their capacity of PTO and generator will be limited for both the cost of the components and the energy conversion efficiency. Babarit et al. [51] proposed that the maximal PTO power (PTO rated power) can be set to 20 times the mean annual absorbed power, and Henriques et al. [52] indicated that to reduce the losses of the PTO system at partial load, the recommended generator with a rated power is twice the maximal expected average power conversion. All these have suggested that limited maximal PTO power and generator must be applied for practical purposes.

It must be noted that for improving wave energy conversion, different control strategies have been proposed and studied, especially for those small fix-referenced wave energy converters which experience narrow energy conversion bandwidths [53,54,55,56,57,58], and accordingly these control technologies can extend the bandwidth of the device in converting wave energy. Also, control technologies are generally more effective for fix-referenced devices than those self-referenced devices. The research has shown that the control systems could increase the power conversion by a few times [59] for fix-referenced devices whilst they can be relatively low for the self-referenced devices [60]. Hence the conclusions in the research may be very different if the control technologies are considered.

Another issue is for the distinction between floating or self-referenced devices. As the water depths for wave energy converter may be roughly around 50 m–100 m, this type of water depth should be regarded as shallow water in terms of mooring design and deployment. For such water depths, conventional mooring systems developed for the oil and gas industry may not be very practical, and also the special requirements of the wave energy converters are very different, in which there may be two contradictory requirements: limiting the device’s drifting while providing enough compliancy to the device power conversion ([61]). Consequently, special mooring configurations and components have been considered. A recent effort to encompass the problem is to incorporate some special elastic components on the mooring lines so to reduce the stiffness of the mooring lines and thus the maximal loads on mooring lines. It has been shown that this development may benefit both for reducing the maximal loads on the mooring lines while maintaining the required minimal breaking load (MBL) to provide enough room for mooring safety. Casaubieilh et al. [62] have shown that a 70% reduction of the maximal mooring loads on mooring lines can been attained by implementing the elastic mooring components in the mooring line. Similar results have been independently reported by Thies et al. [63].

7. Conclusions

In some open shallow water regions, developing wave energy can be very attractive, due to the fact that enough wave resources may be available for massive wave energy production, while these regions are generally very close to the shore facilitating easy cable connections and access to the needed infrastructure. Generally, these regions may fall to the transition water depths for fix- or self-referenced WECs, implying both deployments are possible, and both may have significant challenges. For a fix-referenced/fixed WEC, the cable connection and the access to the device can be easy, but the device, the power take-off system and other components may suffer from survivability problems under the severest sea conditions. For a self-referenced/floating WEC, the device can be designed to be more efficient in converting energy from the waves of interest and more compliant for the severe sea conditions (with long wave periods). However, the shallow water mooring design may be a challenge.

This paper examines and compares the power performance of the fix- or self-referenced PA and OWC wave energy converters in terms of extracting wave energy from seas. Generally, from the study the following conclusions can be drawn:

For a floating/self-referenced wave energy converter, it is possible to use the motion of the device (or part of the device) to enhance the power performance of the device while to design the device to be compliant to the waves with long periods.

Separating the resonance periods between the motions for power conversion is important to increase the device response in a wider range and thus for better power performance. However, it is also important to keep an appropriate difference between these resonance periods. Too large difference between the resonance periods may not be good to improve the device’s power performance, as seen in the floating point absorber.

Floating wave energy converters of both PA and OWC type can generally extract more energy for the target waves (that is, the most frequently happening waves). Both floating WECs can take more energy from waves of periods 6–11 s. For the case of the OWCs, the floating OWC can annually take 180% more energy than that of fixed OWC.

It is also shown that for the self-referenced PA, the heave plate is better modified to a diameter of D = 25 m in terms of the sea conditions at Belmullet, thus a better power performance can be attained for the target waves. It may also be expected that the self-referenced PA can be further optimized by increasing the diameter of the spar at the water plane, thus narrowing the gap of the two resonance periods as seen in the case of the floating OWC, for which the two resonance periods are not significantly different, which means a good compliance of the OWC device in long waves. It must be noted that the original RM3 was designed for the sea conditions on the west coast of the US [13]. By comparison, it can be seen that the wave periods in the west coast of the US are longer than those waves in the Atlantic Arc of Europe.

Future work may be needed to examine the power performance for both fix- and self-referenced PA and OWC in terms of design optimizations of these two WECs. In addition, the quality of the capture power may be needed to be examined, because the self-referenced PA has a large but narrow peak which may cause some problems of too much power production for the power take-off and generator system for certain waves.