Ensemble Learning Approach for Probabilistic Forecasting of Solar Power Generation
Abstract
:1. Introduction
Our Contributions
2. Related Work
2.1. Point Forecasting
2.1.1. Statistical Methods
2.1.2. Machine Learning Methods
2.2. Probabilistic Forecasting
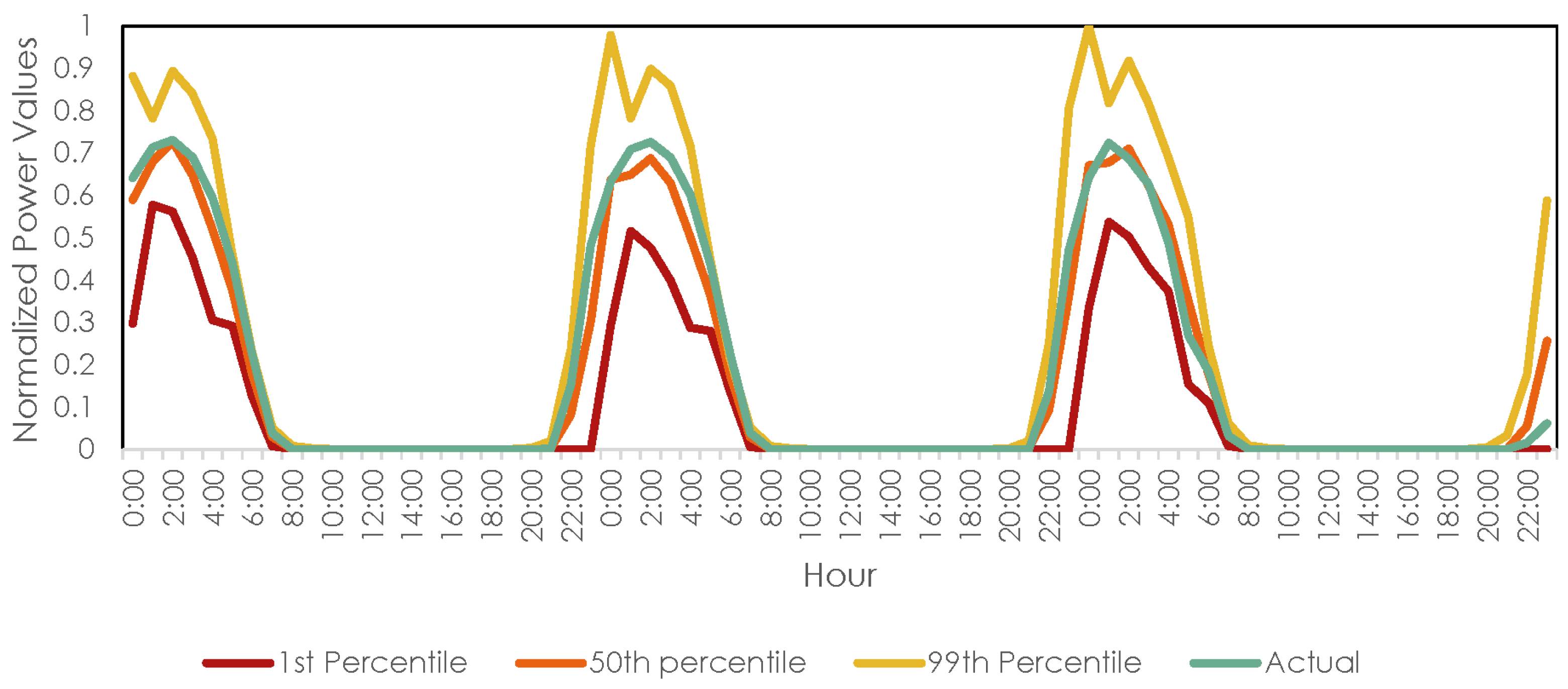
3. Dataset and Problem Formulation
- Zone 1: altitude = 595 m; panel type = Solarfun SF160-24-1M195; No. of panels = 8; nominal power = 1560 W; panel orientation = 38°clockwise from north; panel tilt = 36°.
- Zone 2: altitude = 602 m; panel type = Suntech STP190S-24/Ad+; No. of panels = 26; nominal power = 4940 W; panel orientation = 327°clockwise from north; panel tilt = 35°.
- Zone 3: altitude = 951 m; panel type = Suntech STP200-18/ud; No. of panels = 20; nominal power = 4000 W; panel orientation = 31°clockwise from north; panel tilt = 21°.
- tclw: Total column liquid water, vertical integral of cloud liquid water content. Unit of measurement: kg/m2.
- tciw: Total column ice water, vertical integral of cloud ice water content. Unit: kg/m2.
- SP: Surface pressure. Unit: Pa.
- r: Relative humidity at 1000 mbar, defined with respect to saturation over ice below −23 °C and over water above 0 °C. For the period in between, a quadratic interpolation is applied. Unit: %.
- TCC: Total cloud cover. Unit: zero to one.
- 10u: 10-meter Uwind component. Unit: m/s.
- 10v: 10-meter Vwind component. Unit: m/s.
- 2T: two-meter temperature. Unit: K.
- SSRD: Surface solar radiation down. Unit: J/m2.
- STRD: Surface thermal radiation down. Unit: J/m2.
- TSR: Top net solar radiation, net solar radiation at the top of the atmosphere. Unit: J/m2.
- TP: Sum of convective precipitation and stratiform precipitation. Unit: m.
4. Proposed Method
4.1. Grouping of Data
4.2. Generating Point Forecasts
- Decision tree regressor: A model is fitted using each of the input variables. For each of the individual variables, the mean squared error is used to determine the best split. The maximum number of features to be considered at each split is set to the total number of features [28].
- Gradient boosting: An ensemble model that uses decision trees as weak learners and builds the model in a stage-wise manner by optimizing the loss function [29].
- KNN regressor (uniform): The output is predicted using the values from the k-nearest neighbors (KNNs) [30]. In the uniform model, all of the neighbors are given an equal weight. Five nearest neighbors are used in this model, i.e., . The “Minkowski” distance metric is used in finding the neighbors.
- KNN regressor (distance): In this variant of KNN, the neighbors closer to the target are given higher weights. The choice of k and the distance metric are the same as above.
- Lasso regression: A variation of linear regression that uses the shrinkage and selection method. The sum of squares error is minimized, but with a constraint on the absolute value of the coefficients [31].
- Random forest regressor: An ensemble approach that works on the principle that a group of weak learners when combined would give a strong learner. The weak learners used in random forest are decision trees. Breiman’s bagger, in which at each split all of the variables are taken into consideration, is used [32].
- Ridge regression: It penalizes the use of a large number of dimensions in the dataset using linear least squares to minimize the error [33].
4.3. Generating Probabilistic Forecasts
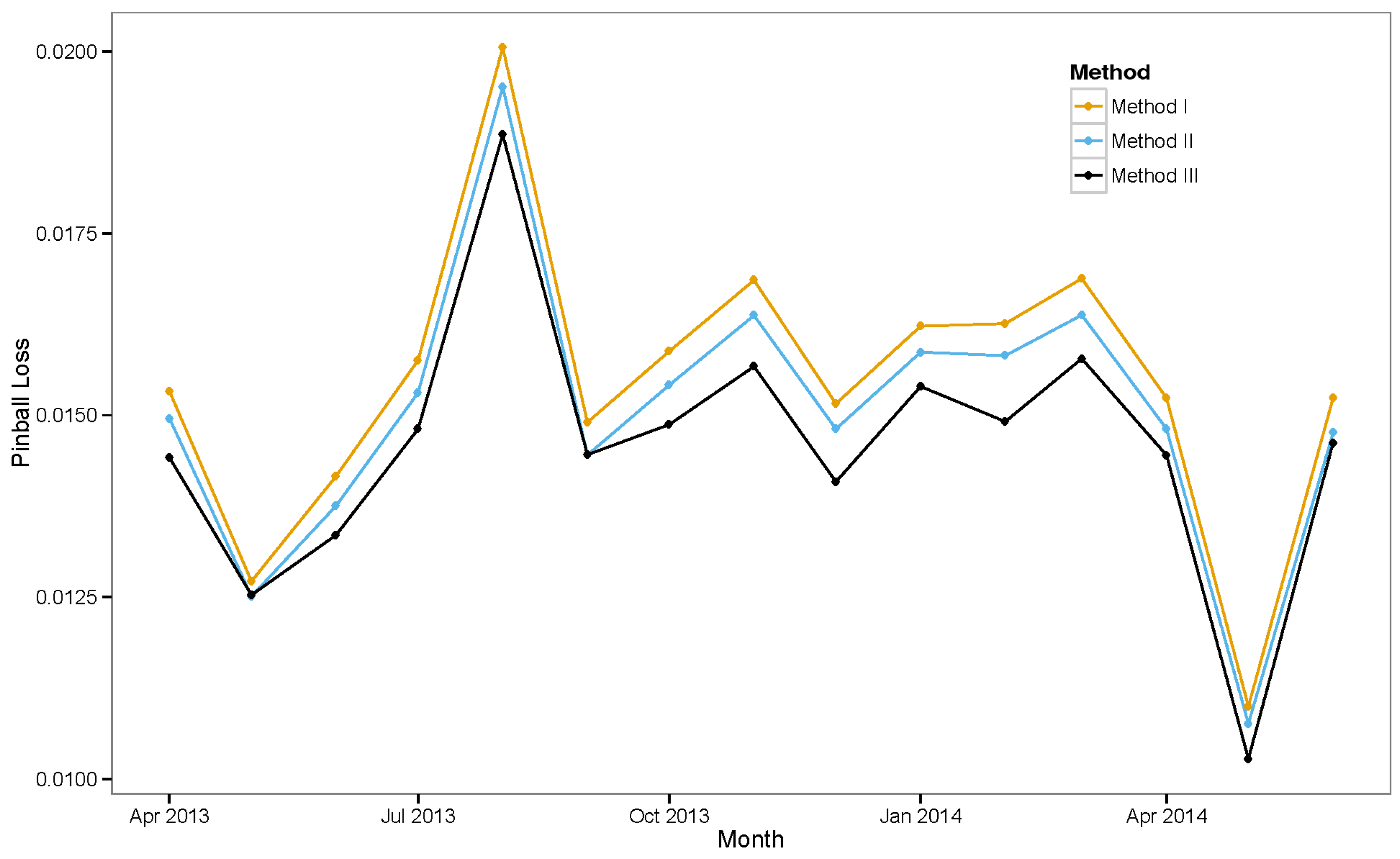
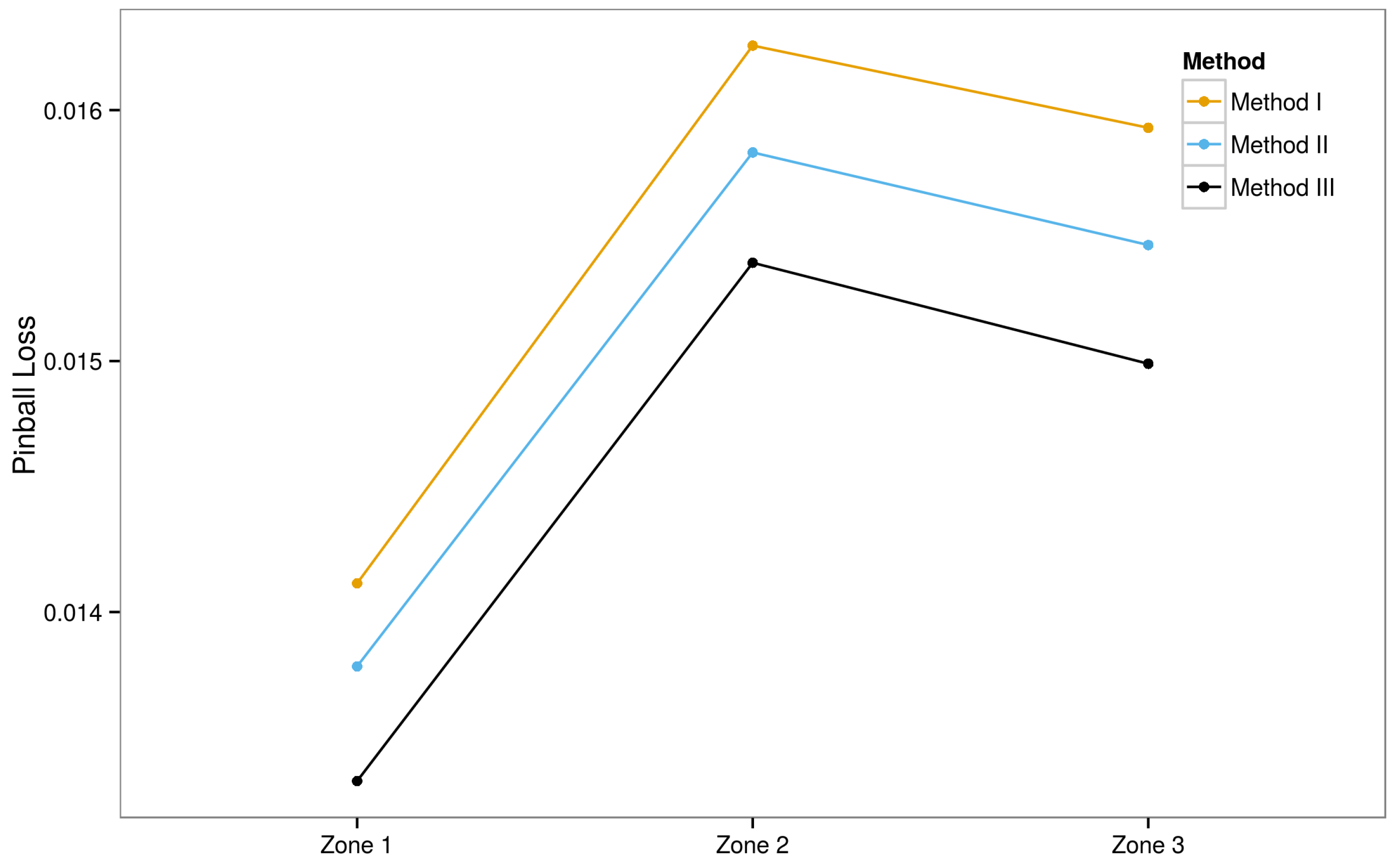
4.3.1. Method I: Linear Method
4.3.2. Method II: Normal Distribution Method
4.3.3. Method III: Normal Distribution Method with Additional Features
5. Experimental Setup
5.1. Training and Testing Datasets
5.2. Evaluation Metrics
5.3. Benchmark Models
- ARIMA: The autoregressive integrated moving average (ARIMA) model is one of the most widely-used techniques in time series forecasting. The function auto.arima() from the forecast package [37] in R is used. It automatically detects the best parameters to fit the data.
- Naive: In this method, all of the forecasts are set to the last observed value. Surprisingly enough, this model works well for many economic and financial time series problems [39].
- Seasonal naive: This method is similar to the naive method, but the forecasts are set to the last observed value from the same season [39].
6. Experimental Results
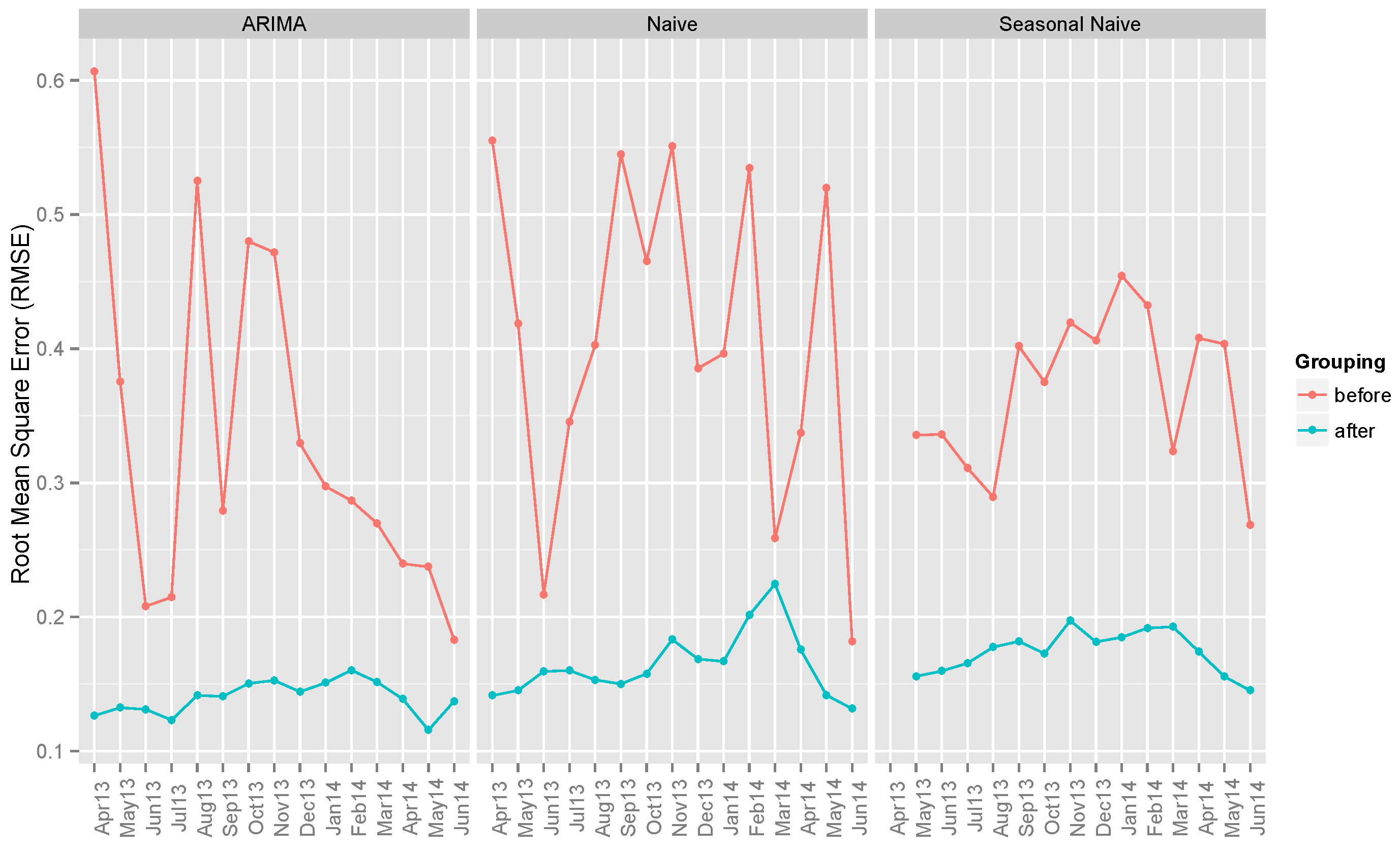
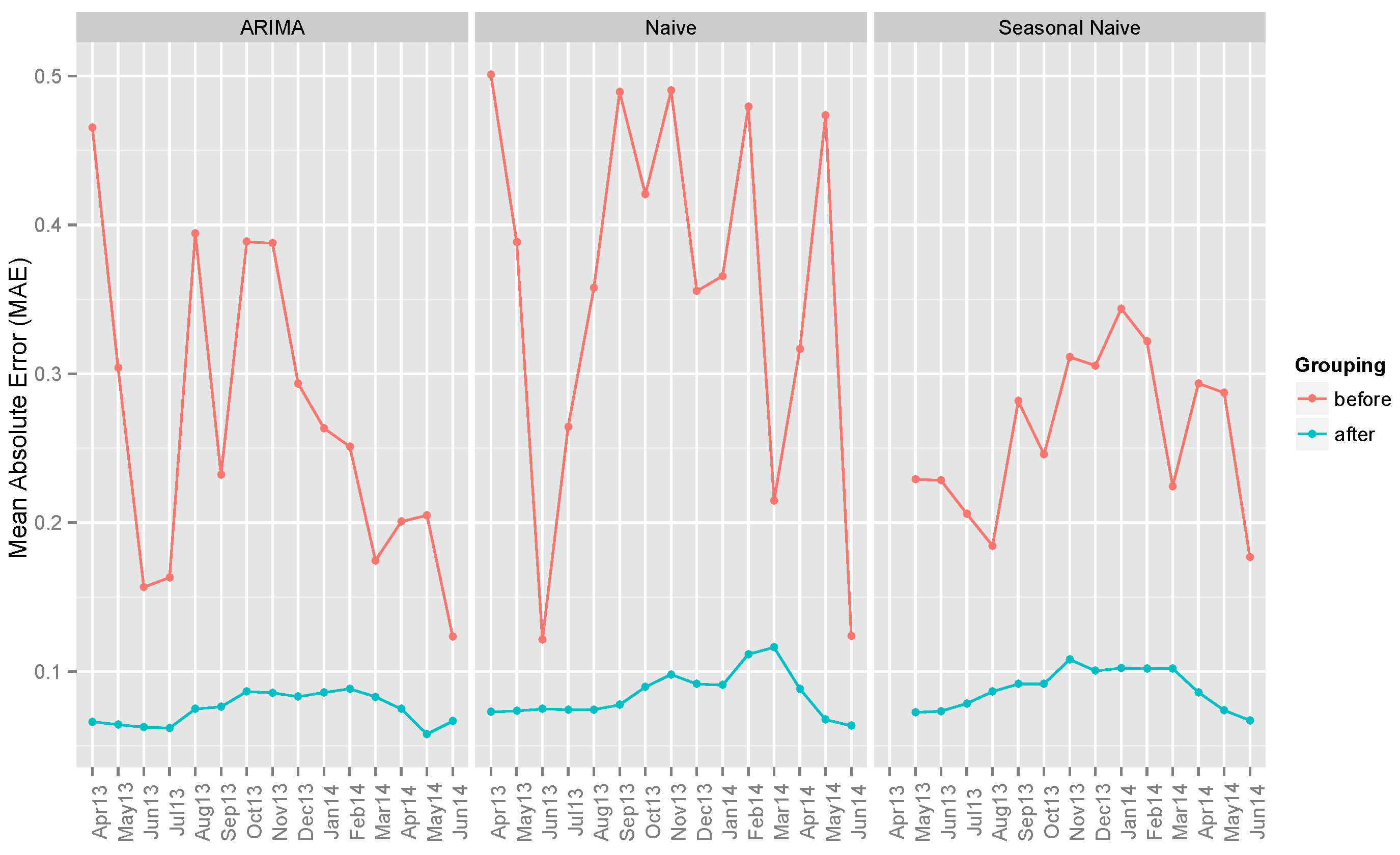
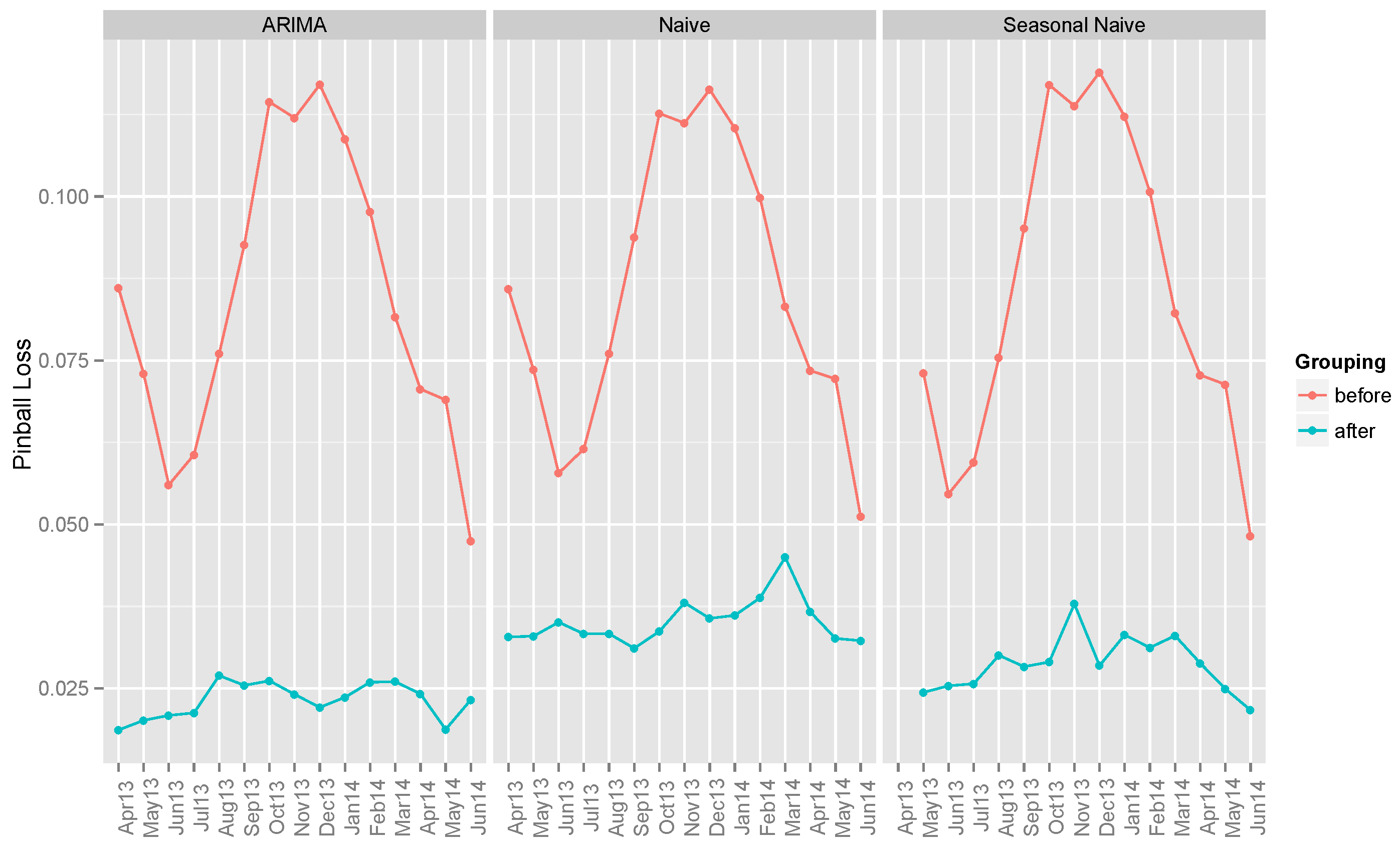
6.1. Benchmark Models
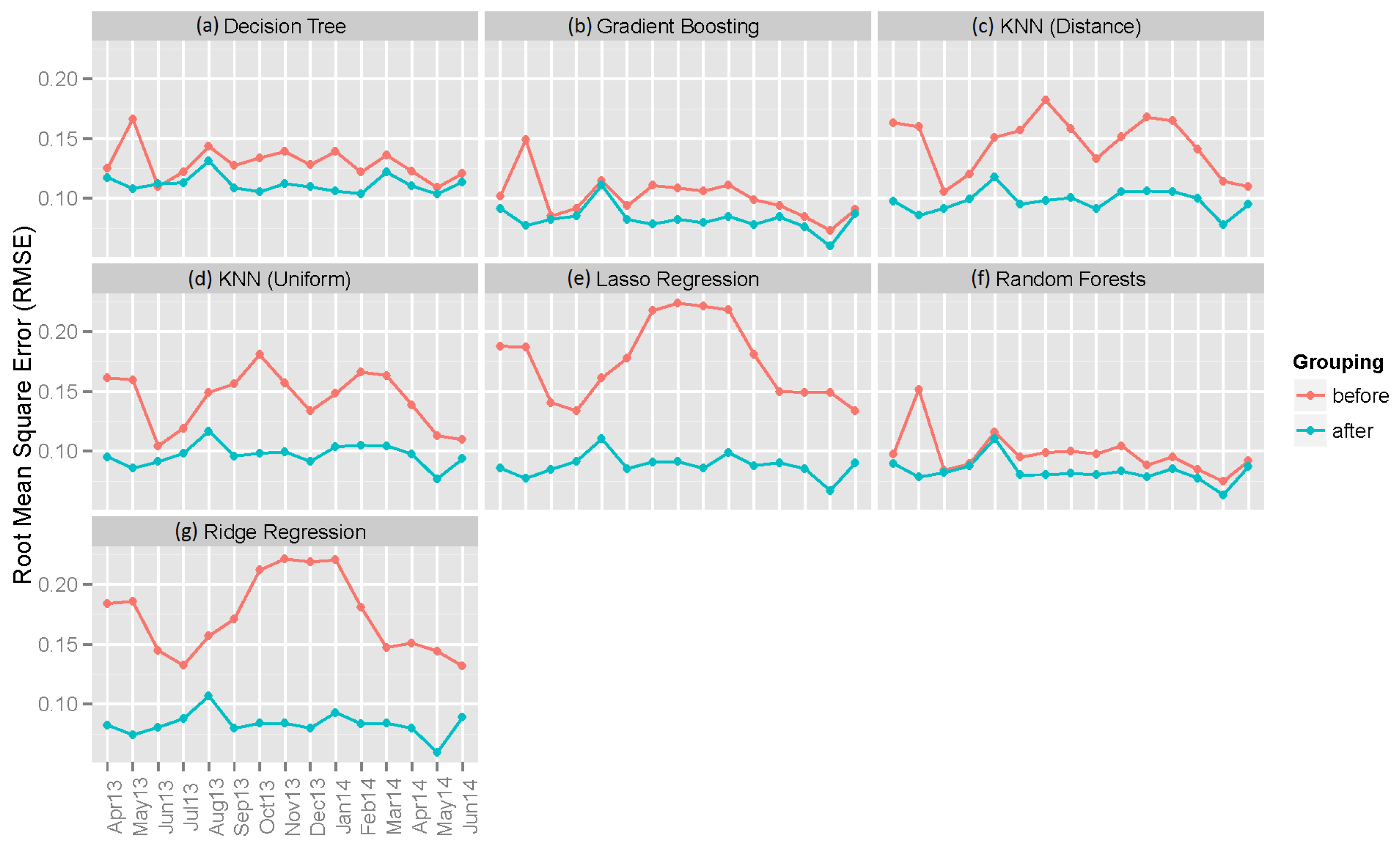
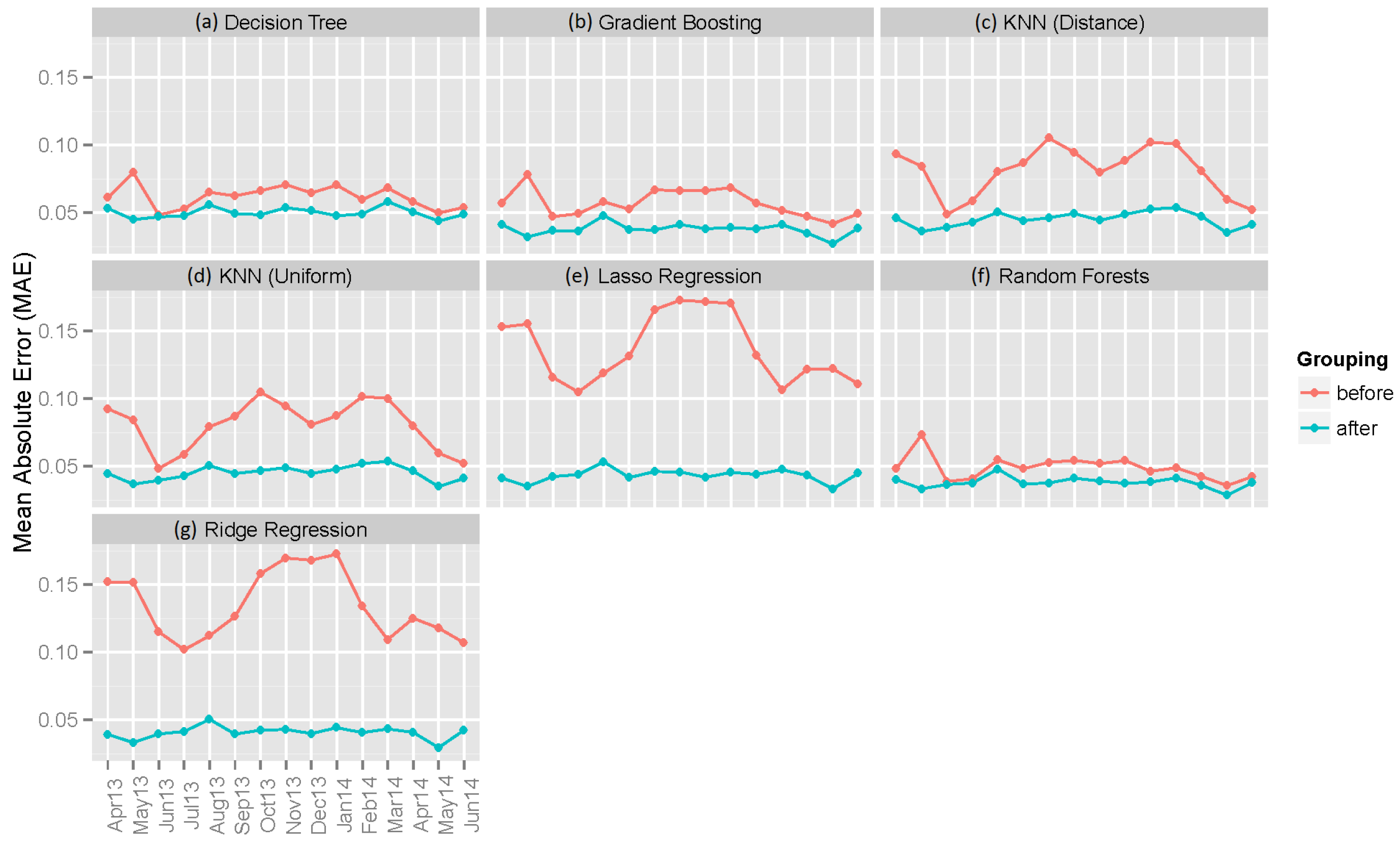
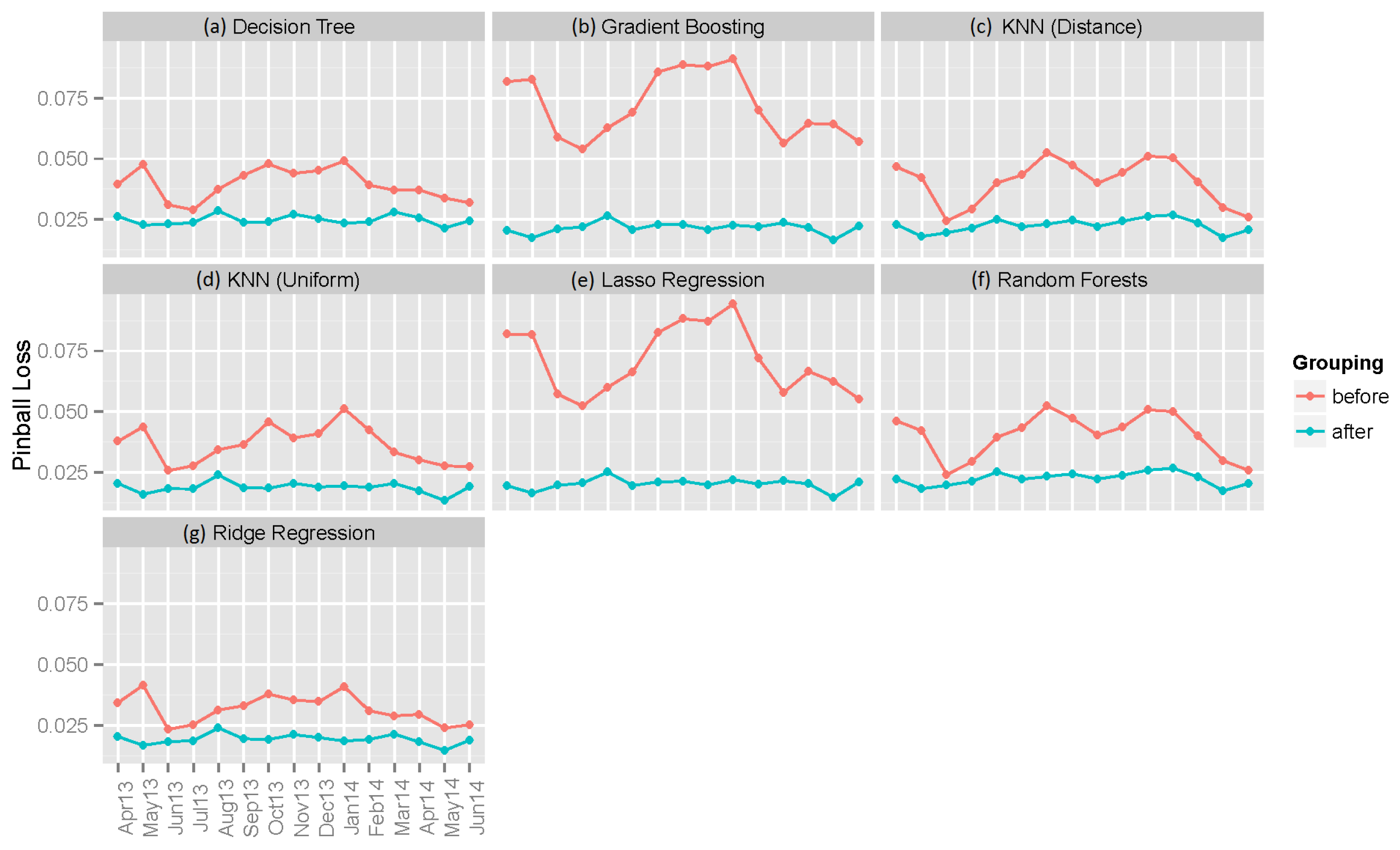
6.2. Individual Machine Learning Models
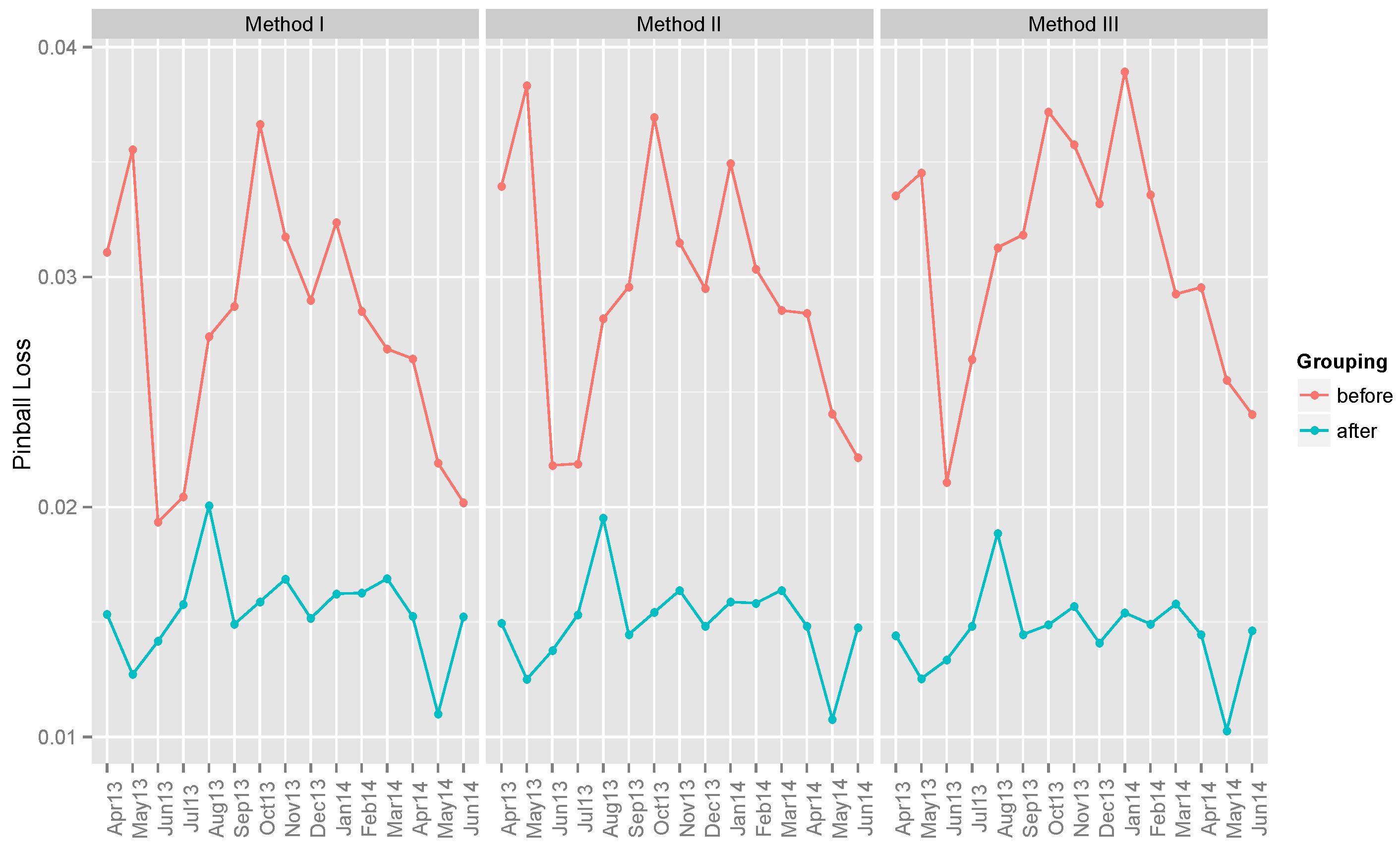
6.3. Ensemble Models
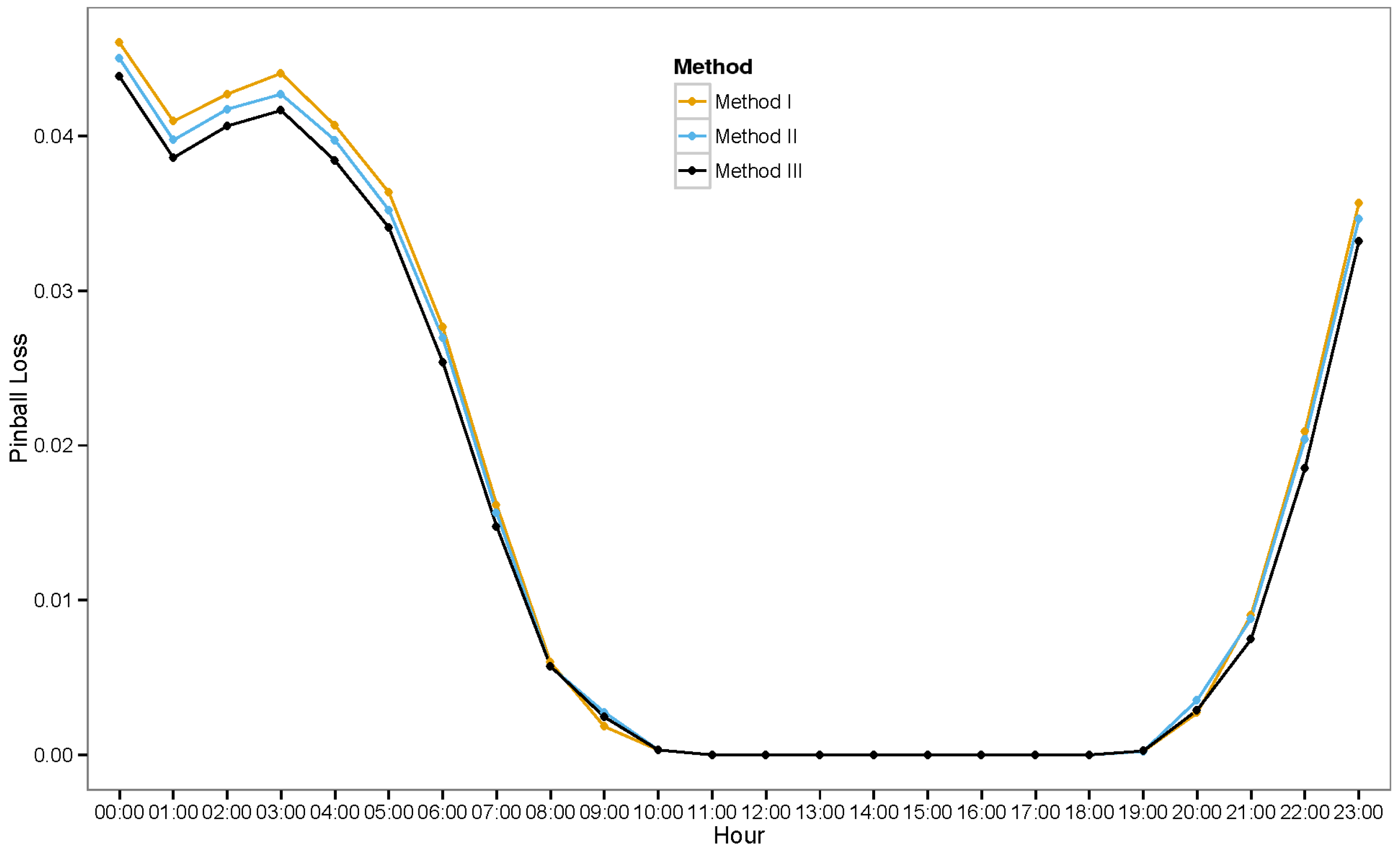
6.3.1. Ensemble Method III
7. Conclusions
- Does combining the results from different models improve the performance?
- Does grouping the data from each hour and running separate models on them give a better performance?
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davidson, D.J.; Andrews, J. Not all about consumption. Science 2013, 339, 1286–1287. [Google Scholar] [CrossRef] [PubMed]
- International Energy Agency. International Energy Outlook 2013. Available online: http://www.eia.gov/forecasts/archive/ieo13 (accessed on 1 November 2016).
- Goldemberg, J.; Johansson, T.B.; Anderson, D. World Energy Assessment Overview: 2004 Update; United Nations Development Programme, Bureau for Development Policy: New York, NY, USA, 2004. [Google Scholar]
- International Energy Agency. Technology Roadmap: Solar Photovoltaic Energy. 2014. Available online: http://www.iea.org/publications/freepublications/publication/technology-roadmap-solar-photovoltaic-energy---2014-edition.html (accessed on 1 November 2016).
- Runyon, J. Transparency and Better Forecasting Tools Needed for the Solar Industry. 2012. Available online: http://www.renewableenergyworld.com/rea/news/article/2012/12/transparency-and-better-forecasting-tools-needed-for-the-solar-industry (accessed on 1 November 2016).
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Madsen, H. Probabilistic forecasts of solar irradiance using stochastic differential equations. Environmetrics 2014, 25, 152–164. [Google Scholar] [CrossRef]
- Grantham, A.; Gel, Y.R.; Boland, J. Nonparametric short-term probabilistic forecasting for solar radiation. Sol. Energy 2016, 133, 465–475. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Yaqub, W.; Aung, Z. Probabilistic forecasting of solar power: An ensemble learning approach. In Proceedings of the 7th International KES Conference on Intelligent Decision Technologies (KES-IDT), Sorrento, Italy, 17–19 June 2015; Volume 39, pp. 449–458.
- Mohammed, A.A. Probabilistic Forecasting of Solar Power: An Ensemble Learning Approach. Master’s Thesis, Masdar Institute of Science and Technology, Abu Dhabi, UAE, 2015. [Google Scholar]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-term solar power forecasting. Sol. Energy 2009, 83, 1772–1783. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, J.; Liu, C.; Xu, X.; Wang, W.; Zhou, X. Comparative study of power forecasting methods for PV stations. In Proceedings of the 2010 IEEE International Conference on Power System Technology (POWERCON), Hangzhou, China, 24–28 October 2010; IEEE: New York, NY, USA, 2010; pp. 1–6. [Google Scholar]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System (CARDS) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Forecasting of global and direct solar irradiance using stochastic learning methods, ground experiments and the NWS database. Sol. Energy 2011, 85, 746–756. [Google Scholar] [CrossRef]
- Hossain, M.R.; Oo, A.M.T.; Shawkat Ali, A.B.M. Hybrid prediction method for solar power using different computational intelligence algorithms. Smart Grid Renew. Energy 2013, 4, 76–87. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A power prediction method for photovoltaic power plant based on wavelet decomposition and artificial neural networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- Li, Z.; Rahman, S.M.; Vega, R.; Dong, B. A hierarchical approach using machine learning methods in solar photovoltaic energy production forecasting. Energies 2016, 9, 55. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutza, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; de Pison, F.J.M.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic forecasting. Annu. Rev. Stat. Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Hong, T. Energy forecasting: Past, present, and future. Foresight 2014, 32, 43–48. [Google Scholar]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- GEFCOM. Global Energy Forecasting Competition 2014 Probabilistic Solar Power Forecasting. 2014. Available online: https://crowdanalytix.com/contests/global-energy-forecasting-competition-2014-probabilistic-solar-power-forecasting (accessed on 1 November 2016).
- European Centre for Medium-Range Weather Forecasts. 2016. Available online: http://www.ecmwf.int/ (accessed on 1 November 2016).
- Coiffier, J. Fundamentals of Numerical Weather Prediction; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bell, R.M.; Koren, Y. Lessons from the Netflix prize challenge. ACM SIGKDD Explor. Newsl. 2007, 9, 75–79. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Supervised machine learning: A review of classification techniques. Informatica 2007, 31, 249–268. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Langford, E. Quartiles in elementary statistics. J. Stat. Educ. 2006, 14, n3. [Google Scholar]
- Larson, R.; Farber, E. Elementary Statistics: Picturing the World; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G.; Razbash, S.; Schmidt, D.; Zhou, Z.; Khan, Y.; Bergmeir, C.; Wang, E. Forecast: Forecasting Functions for Time Series and Linear Models. R Package Version 5.6. 2014. Available online: http://CRAN.R-project.org/package=forecast (accessed on 1 November 2016).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.R-project.org/ (accessed on 1 November 2016).
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Toronto, ON, Canada, 2013. [Google Scholar]

| Model | Before Grouping | After Grouping | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Pinball Loss | RMSE | MAE | Pinball Loss | |
| Benchmark | ||||||
| ARIMA | 0.33363 | 0.26691 | 0.08418 | 0.13988 | 0.07454 | 0.02318 |
| Naive | 0.40756 | 0.35748 | 0.08526 | 0.16410 | 0.08433 | 0.03518 |
| Seasonal Naive | 0.36894 | 0.25997 | 0.08535 | 0.17405 | 0.08829 | 0.02873 |
| Machine Learning | ||||||
| Decision Tree | 0.12973 | 0.06211 | 0.03954 | 0.11190 | 0.04999 | 0.02483 |
| Gradient Boosting | 0.10105 | 0.05719 | 0.07159 | 0.08284 | 0.03784 | 0.02164 |
| KNN (Distance) | 0.14537 | 0.08109 | 0.04055 | 0.09790 | 0.04519 | 0.02259 |
| KNN (Uniform) | 0.14406 | 0.08072 | 0.03633 | 0.09696 | 0.04501 | 0.01891 |
| Lasso Regression | 0.17546 | 0.13690 | 0.07108 | 0.08826 | 0.04329 | 0.02028 |
| Random Forest | 0.09801 | 0.04886 | 0.04036 | 0.08312 | 0.03798 | 0.02251 |
| Ridge Regression | 0.17349 | 0.13471 | 0.03185 | 0.08320 | 0.04056 | 0.01936 |
| Ensemble | ||||||
| Method I | 0.02775 | 0.01544 | ||||
| Method II | 0.02934 | 0.01503 | ||||
| Method III | 0.03105 | 0.01457 | ||||
| Contributor | Pinball Loss |
|---|---|
| original set only (i.e., Method II) | 0.01503 |
| 1st additional set only | 0.01516 |
| 2nd additional set only | 0.01794 |
| original set + 1st additional set | 0.01510 |
| original set + 2nd additional set | 0.01498 |
| 1st additional set + 2nd additional set | 0.01483 |
| original set + 1st additional set + 2nd additional set (i.e., Method III) | 0.01457 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed Mohammed, A.; Aung, Z. Ensemble Learning Approach for Probabilistic Forecasting of Solar Power Generation. Energies 2016, 9, 1017. https://doi.org/10.3390/en9121017
Ahmed Mohammed A, Aung Z. Ensemble Learning Approach for Probabilistic Forecasting of Solar Power Generation. Energies. 2016; 9(12):1017. https://doi.org/10.3390/en9121017
Chicago/Turabian StyleAhmed Mohammed, Azhar, and Zeyar Aung. 2016. "Ensemble Learning Approach for Probabilistic Forecasting of Solar Power Generation" Energies 9, no. 12: 1017. https://doi.org/10.3390/en9121017
APA StyleAhmed Mohammed, A., & Aung, Z. (2016). Ensemble Learning Approach for Probabilistic Forecasting of Solar Power Generation. Energies, 9(12), 1017. https://doi.org/10.3390/en9121017







