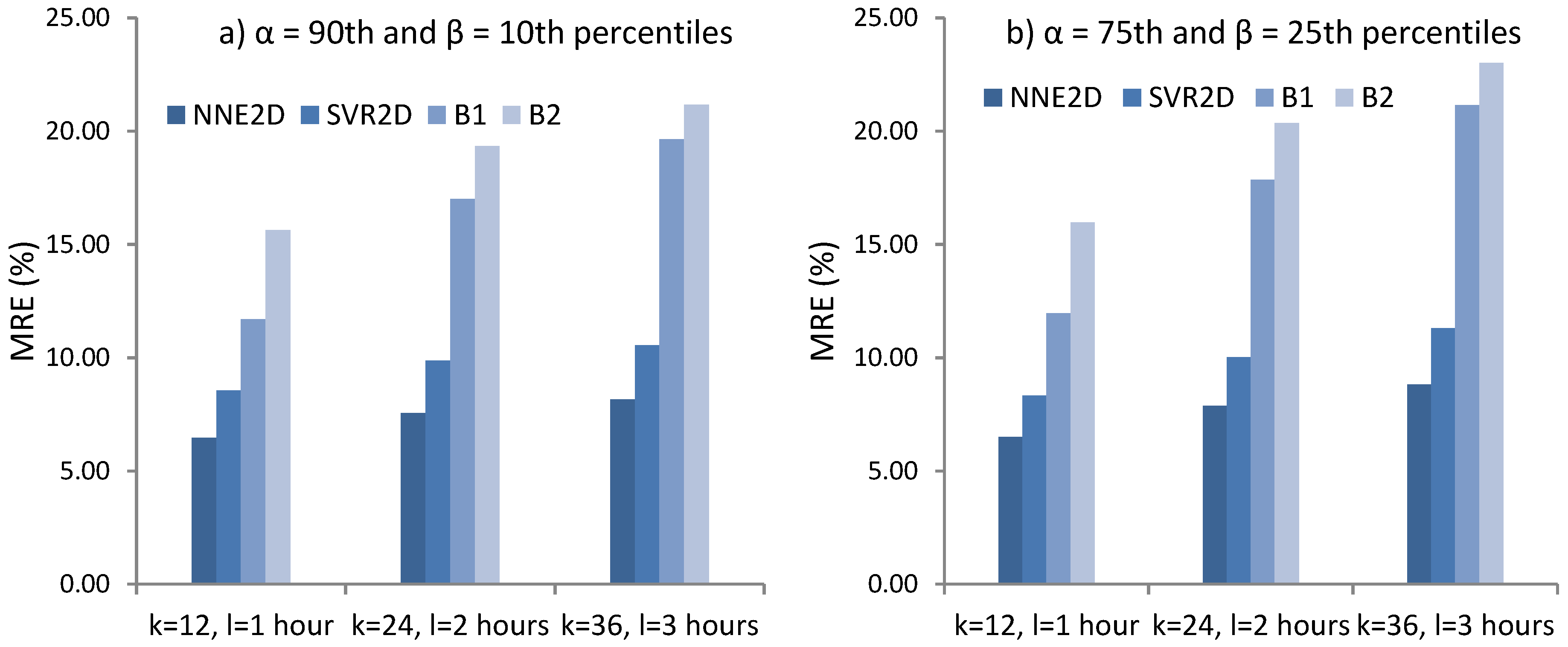1. Introduction
Generating electricity from renewable sources is a key factor in the transition to a clean and sustainable energy future, to address environmental concerns and limit the global warming. Solar energy generated from PV systems is one of the most promising and fastest growing types of renewable energy [
1]. This growth is driven by government incentives that encourage the use of solar energy and by the decreasing cost of PV panels, making them more affordable. Since 2000, the installation of PV systems worldwide has increased 100 times, reaching 178 GW in 2014, and this capacity is expected to triple by 2019 [
2]. It is also expected that by 2050 PV systems will provide 29% of the electricity in Australia [
3] and 25% of the electricity in Europe [
4].
In comparison to the traditional fossil and nuclear energy sources, solar energy is freely available, can be easily harnessed and is environmentally free. However, unlike the traditional energy sources, it is highly variable as it depends on the solar irradiance, cloud cover and other meteorological factors. This creates challenges for its mass integration in the electricity grid. The European Photovoltaic Industry Association has identified forecasting as one of the key factors enabling large-scale integration of solar power in the electricity grid [
4]. Accurate forecasting ensures reliable supply, reduces the costs by allowing more efficient and secure management of electricity grids and also supports solar energy trading at electricity markets [
4].
Solar power forecasting has been an active area of research. A comprehensive review of the state-of-the-art methods for PV power forecasting is presented in [
5]. There are two groups of forecasting approaches: indirect and direct. The indirect approaches firstly forecast the solar irradiance or use forecasts of solar irradiance produced by meteorological centers, and then convert them to PV power forecasts by considering the characteristics of the PV plant. The second group directly forecasts the PV power output. Notable examples of the first group are [
6,
7,
8,
9,
10]. For example, Lorenz et al. [
6] predicted the hourly PV power output for up to 2 days ahead based on the weather forecasts of solar irradiance. They also derived regional power forecasts by up-scaling the forecasts of representative PV systems. Urraca et al. [
10] predicted the solar irradiance 1 h ahead based on recorded meteorological data and computed solar variables. They developed two types of models: fixed and moving, and applied a number of prediction algorithms—Support Vector Regression (SVR), random forests, linear regression and nearest neighbor.
Recent examples of the second group, direct forecasting approaches, include [
11,
12,
13,
14,
15,
16,
17]. For example, Chen et al. [
12] predicted the PV power output for the 24 h of the next day using the PV power from the previous day and the weather forecast for the next day. They classified the days into sunny, cloudy and rainy, and built a separate prediction model, a Radial-Basis Function Neural Network (RBFNN), for each category. A Self-Organising Map (SOM) was used to learn the characteristics of the three types of days based on the weather predictions of solar irradiance and cloudiness. To forecast the PV output for a new day, SOM was firstly used to output the type of the day, and then the RBFNN model for this type of day was used to generate the prediction. Pedro and Coimbra [
11] predicting the PV power 1 and 2 h ahead from previous PV power data by using Autoregressive Integrated Moving Average (ARIMA), nearest neighbors and Neural Networks (NNs) methods.
While the focus in previous work has been on point forecasting, in this paper we consider interval forecasting, and in particular 2D-interval forecasting, which was recently introduced by Torgo and Ohashi [
18]. The differences between the three types of forecasting tasks–point, interval and 2D-interval can be summarized as follows: (1) Point forecasts predict a single value—at time
t the task is to predict the value of the time series for time
t +
h, where
h is the forecasting horizon (
h = 1 for 1-step ahead prediction); (2) Interval forecasts predict an interval of plausible values. A standard interval forecast consists of an upper and lower bound, between which a single future value is expected to lie with high probability [
19], i.e., at time
t the task is to predict an interval of plausible values of the time series for time
t +
h; (3) A 2D-interval forecast [
18] is an interval forecast for a range (or an interval) of future values not a single value, i.e., at time
t the task is to predict the upper and lower bound for the range of future values [
t +
h,
t +
k].
Although point forecasts are the most common types of forecasts, interval forecasts are more useful than point forecasts for applications requiring risk management and balancing of demand and supply, such as electricity production, electricity and financial markets, water distribution and manufacturing [
18,
19]. Predicting an interval of plausible values instead of only predicting a single value gives more information about the variability of the target variable, which in turn can help to assess the uncertainty of the future values and be used to make more accurate decisions. 2D-interval forecasts are particularly relevant for applications where the predicted variable has a high inherent variability, such as solar and wind power prediction.
Torgo and Ohashi [
18] showed an application of 2D-interval forecasting for two water prediction tasks: predicting the values of water quality parameters (e.g., pH, iron, etc.) in a distribution network for a metropolitan area in Portugal and predicting the water consumption in a residential area network in Spain. In our previous work [
20] we presented an application of 2D-interval forecasting for solar power prediction from previous PV power and weather data. We predicted the maximum and minimum values of the interval, using a SVR based method. In this paper we extend our previous work by predicting summary statistics (10–90th and 25–75th percentiles) instead of the maximum and minimum values, applying feature selection using Mutual Information (MI) and using an ensemble of NNs as a classification algorithm. In this work we also use only previous PV power data instead of both PV power and weather data, and show that it is sufficient for good prediction.
The contribution of our work is the following:
- (1)
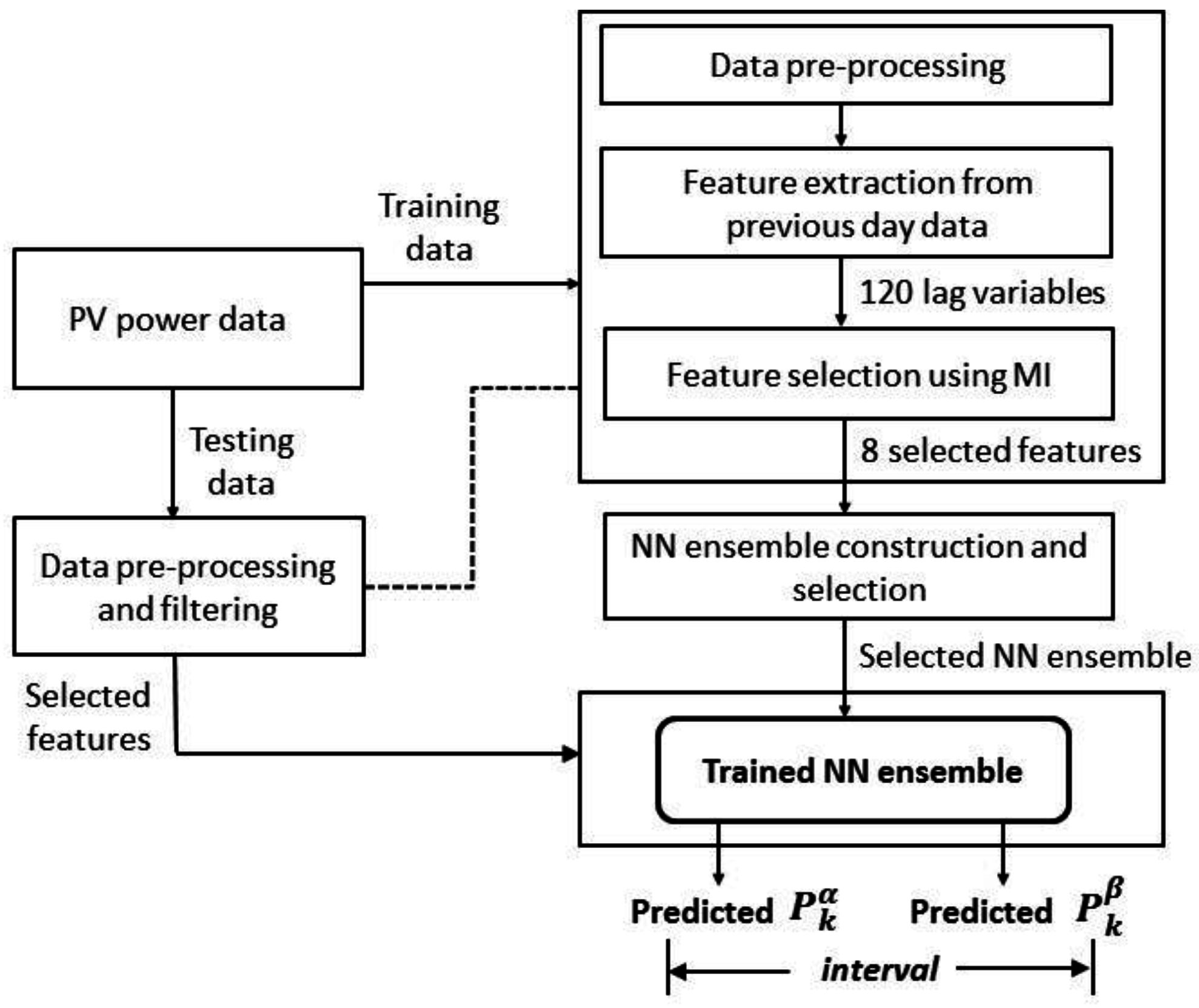
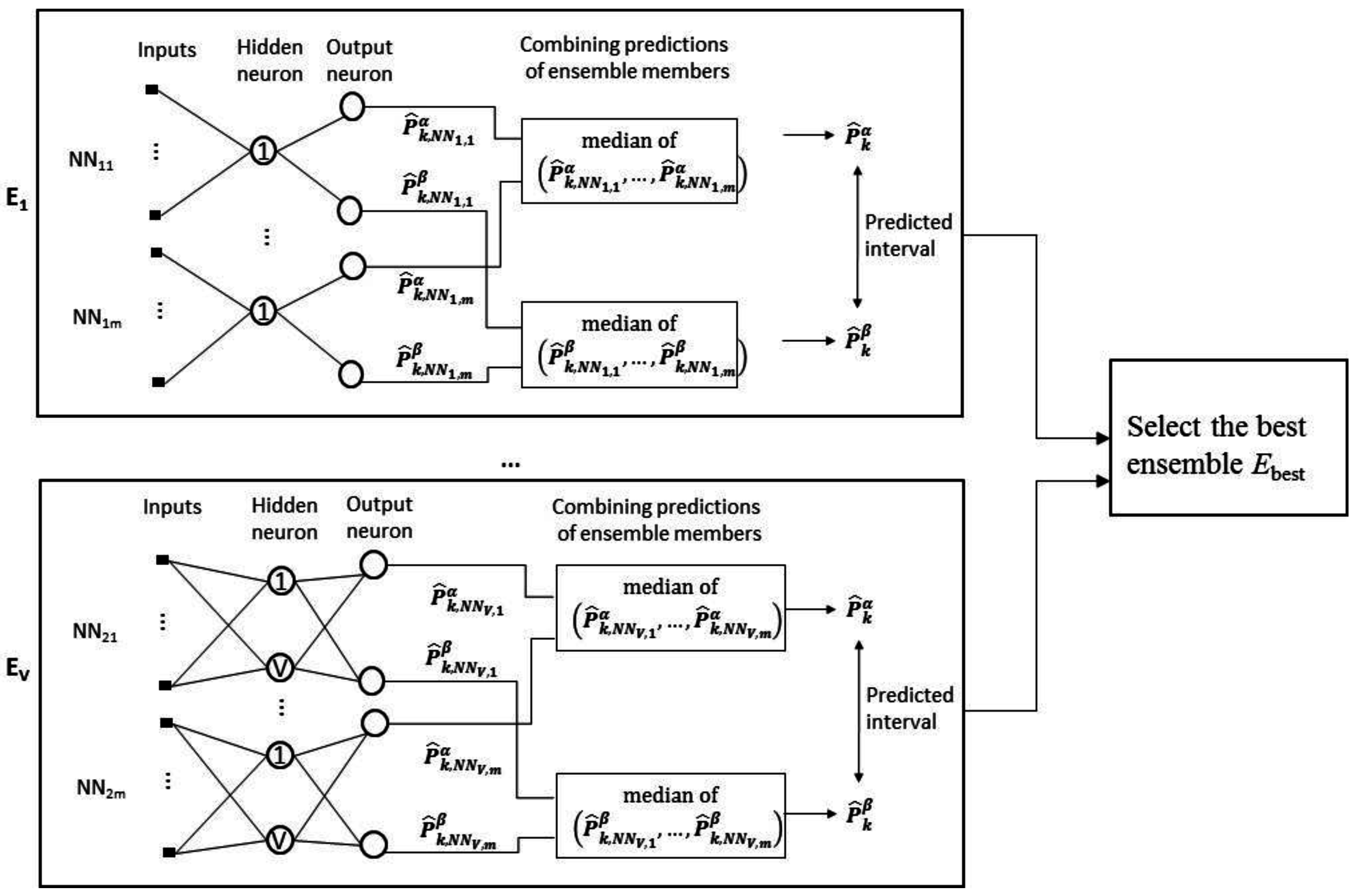
We consider the task of interval forecasting for solar power generated by PV systems. Specifically, we consider 2D-interval forecasting where we predict two summary statistics for a future interval of PV power values—10–90th and 25–75th percentiles. Our proposed approach called Neural Network Ensemble for 2D-interval forecasting (NNE2D) uses MI to select a small set of informative variables and an ensemble of NNs for prediction. It doesn’t require any previous weather data or future weather predictions; it only uses previous PV power data.
- (2)
We evaluate the performance of NNE2D using Australian data for two years, sampled at 5-min intervals, for three different interval lengths (from 1 h to 3 h). We compare the results with two persistence methods used as baselines, a model based on SVR and also with our two multivariate approaches from [
20]. The results show that NNE2D is a promising approach, outperforming the other methods in terms of accuracy and coverage probability, and hence is a viable method for practical applications.
This paper is organized as follows.
Section 2 describes the data used in this study and
Section 3 provides a problem statement.
Section 4 describes our proposed approach NNE2D for computing 2D-interval forecasts and
Section 5 presents the methods used for comparison.
Section 6 describes the experimental setup.
Section 7 presents and discusses the results, and
Section 8 concludes the paper.
2. Data
We use solar power data from the largest flat-panel, grid-connected, PV system in Australia. It is located at the St Lucia campus of the University of Queensland in Brisbane and has about 5000 solar panels distributed at the roof-top of four buildings, generating up to 1.22 MW of electricity.
The data is measured at 1-min intervals for 24 h. We collected data for 10 h during the day, from 7:00 am to 5:00 pm, for two complete years—from 1 January 2013 to 31 December 2014. Outside these 10 h the solar power is either zero or very low due to the absence of solar irradiation. The data is publicly available at [
21].
The original data set consists of 2 × 365 × 600 = 438,000 measurements in 1-min resolution. There were only 1518 missing values which is about 0.35%. Each missing value was replaced by the average of the values from the previous 5 min, i.e., with the 5 most recent observations of the PV power output. The 1-min data was aggregated into 5-min intervals by averaging every 5 consecutive measurements, resulting in 2 × 365 × 120 = 87,600 measurements in total. The data was normalized to the range (0,1).
The generated PV power depends on the weather conditions, especially the solar irradiance.
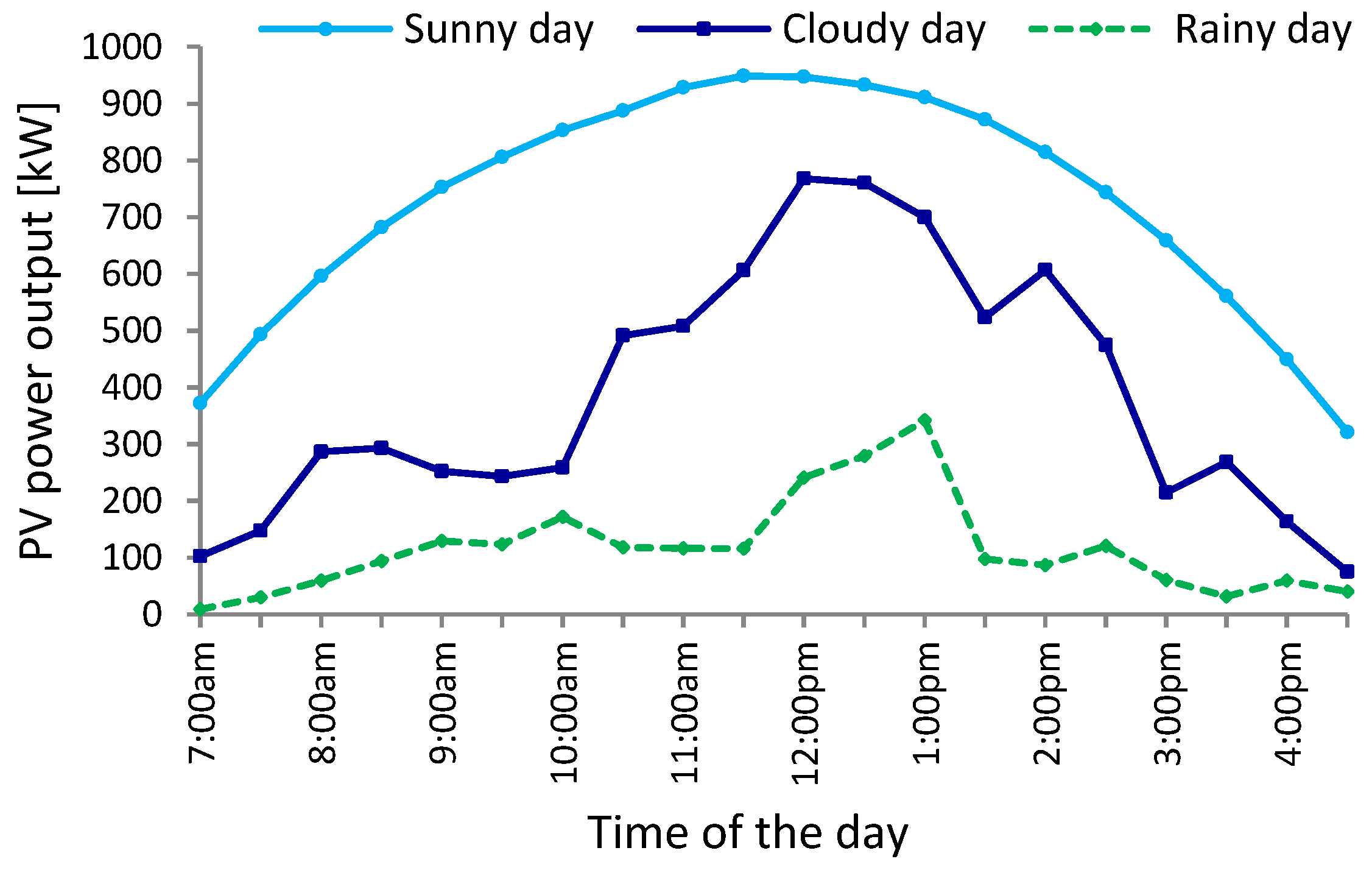
Figure 1 plots the solar power profiles at half-hourly intervals, for three different types of days: sunny (13 April 2013), cloudy (15 April 2013) and rainy (20 April 2013). The three graphs differ considerably—for sunny days, the power output from a PV system is the highest and typically follows a bell shaped curve; for cloudy and rainy days, the generated PV power is lower and it varies during the day due to the changes in the weather conditions.
3. Problem Definition
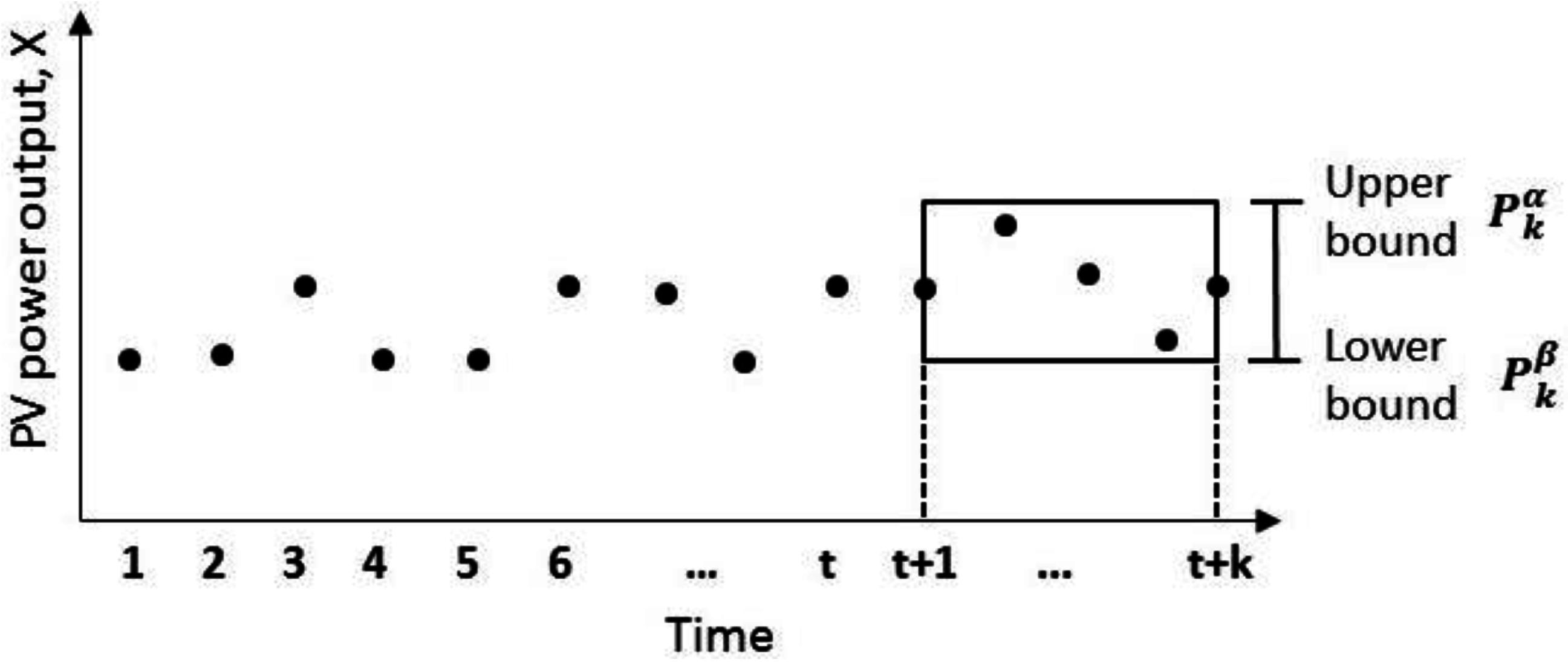
Let
be a discrete time series of PV power outputs up to time
. Our goal is to compute the 2D-interval forecast for the next interval with length
k, i.e., for the values
. Specifically, at time
t we predict the upper and lower bounds for the values of
in the interval
(see
Figure 2).
There are different ways to construct the upper and lower bounds of the
-length interval using descriptive statistics—e.g., using the 75th and 25th percentiles as in [
18] or using the maximum and minimum values as in [
20]. In this study, we follow the first method as percentiles are more robust to noise and outliers than minimum and maximum values. Let
and
are the
and
percentiles (
) for the PV power time series
for the
-length future time interval
. The interval formed by them corresponds to the interval where
of the values of
are expected to lie [
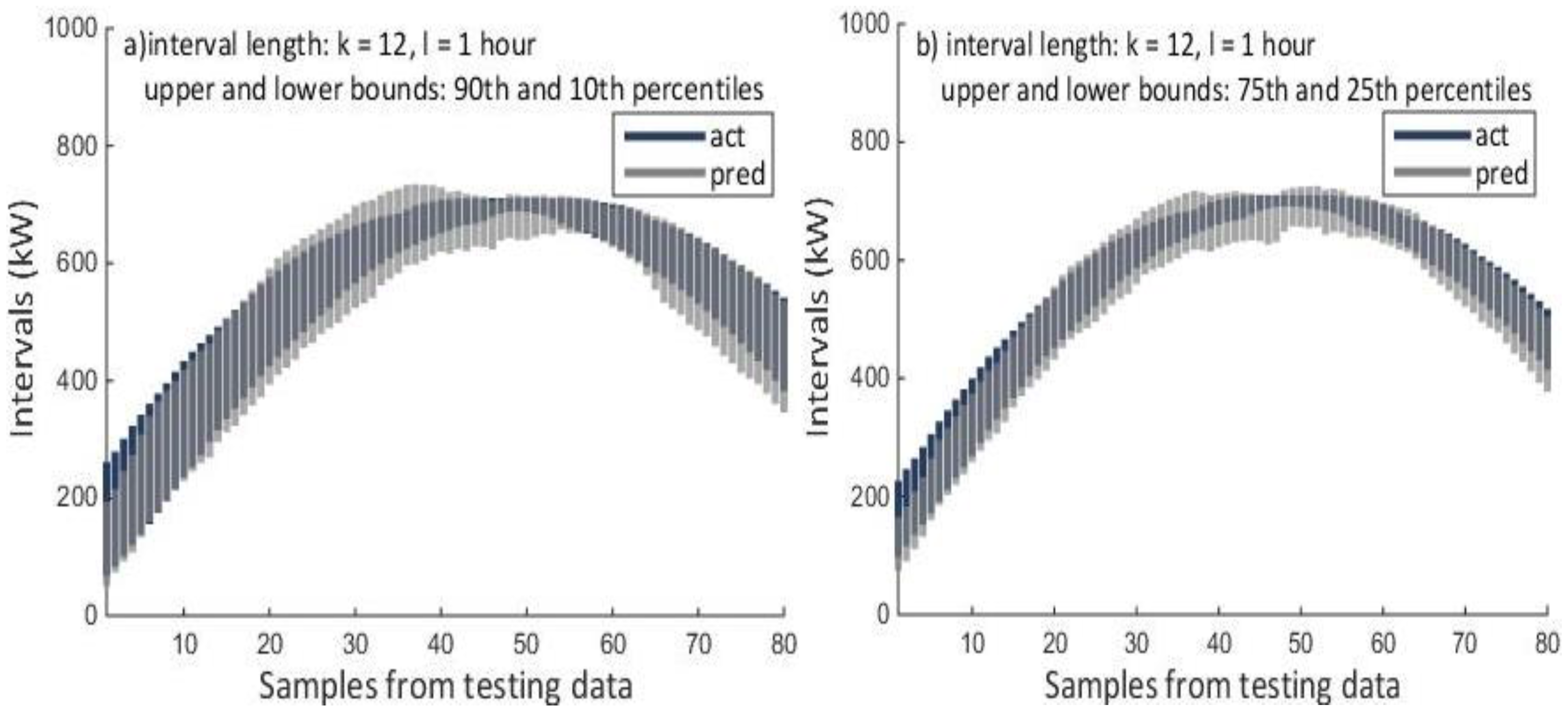
6]. In this work, we construct two types of 2D-interval forecasts: by using the 90th and 10th percentiles, as well as 75th and 25th percentiles. However, our method is general and can be used for intervals with different bounds and lengths, depending on the specific application and scenario.
5. Methods Used for Comparison
To provide a comprehensive evaluation of NNE2D, we compare its performance with two persistence models and a method similar to NNE2D but using SVR instead of an NN ensemble.
5.1. Persistence Models
We use two persistence models as baselines for comparison. Persistence models consider the recently observed values of time series data as predicted values and are used as baselines. We implemented two persistence models: B1 and B2.
The first baseline () uses the previous -length interval. The 2D-interval forecast at time t for the interval [t + 1, t + k] is given by the percentiles of the previous interval [t − k − 1, t], i.e.,: α percentile of and β percentile of .
The second baseline (
) uses the
k-interval from the previous day, at the same time. The 2D-interval forecast at time
t for the interval [
t + 1,
t +
k] is given by using the percentiles of the time series for the interval [
t −
k −
d + 1,
t −
d], where
d is the total number of observations in a day, i.e.,
α percentile of
and
β percentile of
. Zhang et al. [
33] showed that for point forecasting a persistence model similar to
was more accurate compared to ARIMA, NNs and SVR when the consecutives days have similar PV power characteristics.
5.2. SVR Based Method
We also evaluate the performance of SVR as a prediction algorithm instead of an NN ensemble, under the same experimental conditions. We call this method SVR2D.
SVR is an advanced prediction algorithm [
34] that has shown excellent performance in several domains [
35,
36,
37], including solar power forecasting, e.g., [
9,
13,
38].
The key idea of SVR is to map the input data into a higher dimensional feature space using a non-linear transformation and then apply linear regression in the new space. The linear regression in the new space corresponds to nonlinear regression in the original space. The task is formulated as an optimisation problem. The main goal is to minimize the error on the training data, but the flatness of the line and the trade-off between training error and model complexity are also considered to prevent overfitting. The solution is defined by a small subset of training examples, called support vectors.
Solving the optimization problem requires computing dot products of input vector in the new space which is computationally expensive in high dimensional spaces. To help with this, kernel functions satisfying the Mercer’s theorem are used—they allow the dot products to be computed in the original lower dimensional space and then mapped to the new space.
Since SVR can have only one output, SVR2D divides the 2D-interval prediction task into two subtasks: predicting the upper bound
and predicting the lower bound
, and builds a separate SVR prediction model for each of them:
We used Radial Basis Function (RBF) kernel, which was selected after empirical evaluation and comparison of different kernel functions.
8. Conclusions
We considered the task of 2D-interval forecasting and its application for predicting the electricity power generated by solar PV systems. Specifically, at time
t we predict summary statistics for the distribution of the PV power time series in the future time interval [
t + 1,
t +
k] such as the 90th and 10th percentiles, and also the 75th and 25th percentiles. This type of forecasting task was recently introduced by Torgo and Ohashi in [
18] and is useful to quantify uncertainty in applications which require balancing of demand and supply, especially when the predicted variable has a high variability such as in solar power forecasting.
Our proposed method NNE2D uses a variable selection based on MI and an ensemble of NNs to compute the lower and upper bounds (expressed as percentiles) of the 2D-interval forecasts. It was evaluated for predicting the solar PV power output using Australian PV power data for two years, sampled at 5-min intervals, for future intervals with length from 1 to 3 h. The prediction was done using only previous PV power data, without any weather data.
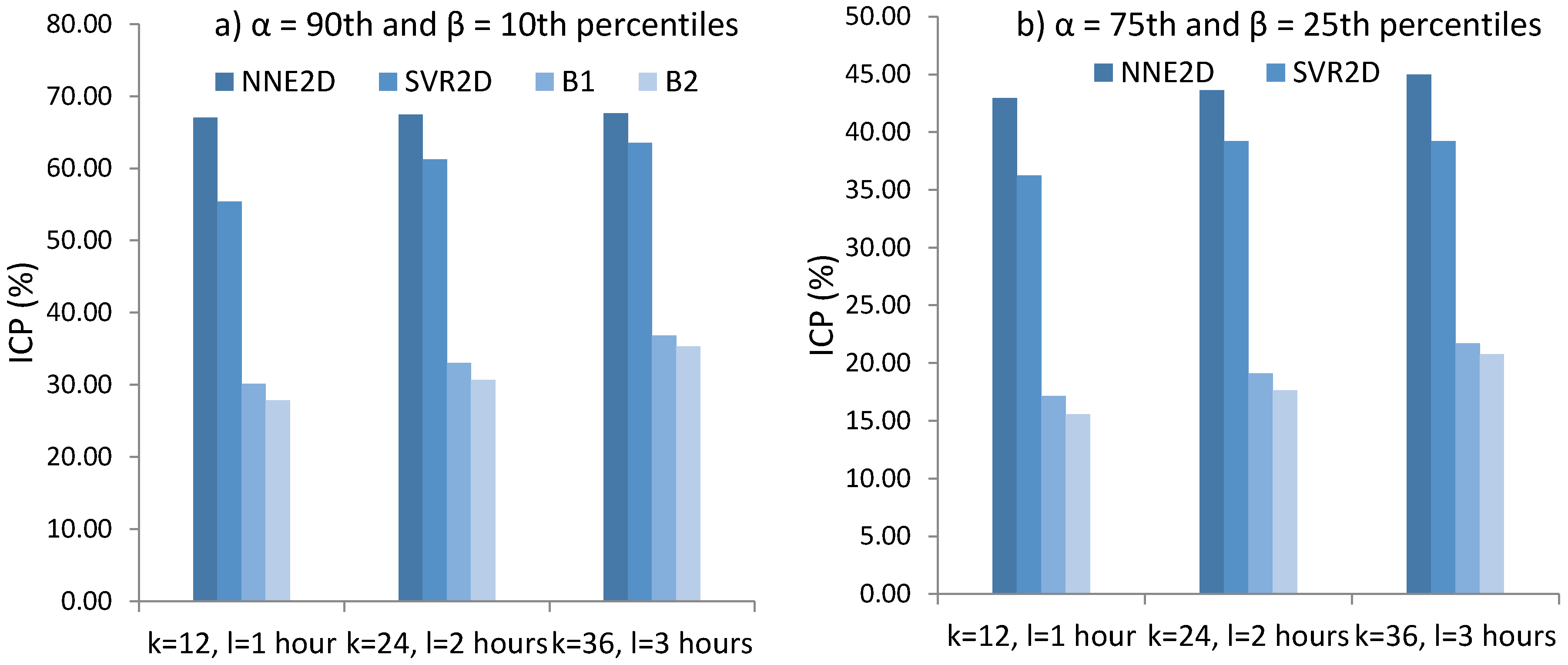
NNE2D was compared with two persistence models used as baselines and a method based on SVR. It achieved MRE of 6.47%–8.16% and coverage probability ICP of 67.04–67.66 for the 10–90th percentiles and MRE of 6.50–8.83 and ICP of 42.96%–45% for the 25–75th percentiles, considerably outperforming the methods used for comparison. NNE2D also showed superior performance when compared to similar but multivariate methods that use both PV power and weather data. This shows that for very-short term forecasting up to 3 h, there is no need to use weather data. In addition, NNE2D was fast to train which makes it suitable for both online and offline training.
Considering both prediction accuracy and the computational requirements, we conclude that NNE2D is a promising approach for 2D-interval forecasts and is viable for practical applications. It can be used to predict other summary statistics for future intervals, not only percentiles, depending on the specific task and forecasting scenarios.
There are several avenues for future work that we will explore. Firstly, we plan to conduct a detailed sensitivity analysis investigating the impact of the relative size of the training, validation and testing sets and the effect of resampling of these sets when evaluating the performance. Secondly, we will examine if the daily periodical component of the PV power (more pronounced for some types of days, e.g., sunny) can be used to improve the results. Thirdly, we will explore alternative data normalization methods, e.g., based on the daily cycle, that consider the sunrise and sunset times and the solar height. Furthermore, we plan to apply our method to other energy time series, in particular wind energy, electricity demand and electricity price.