Estimate of Hot Dry Rock Geothermal Resource in Daqing Oilfield, Northeast China
Abstract
:1. Introduction
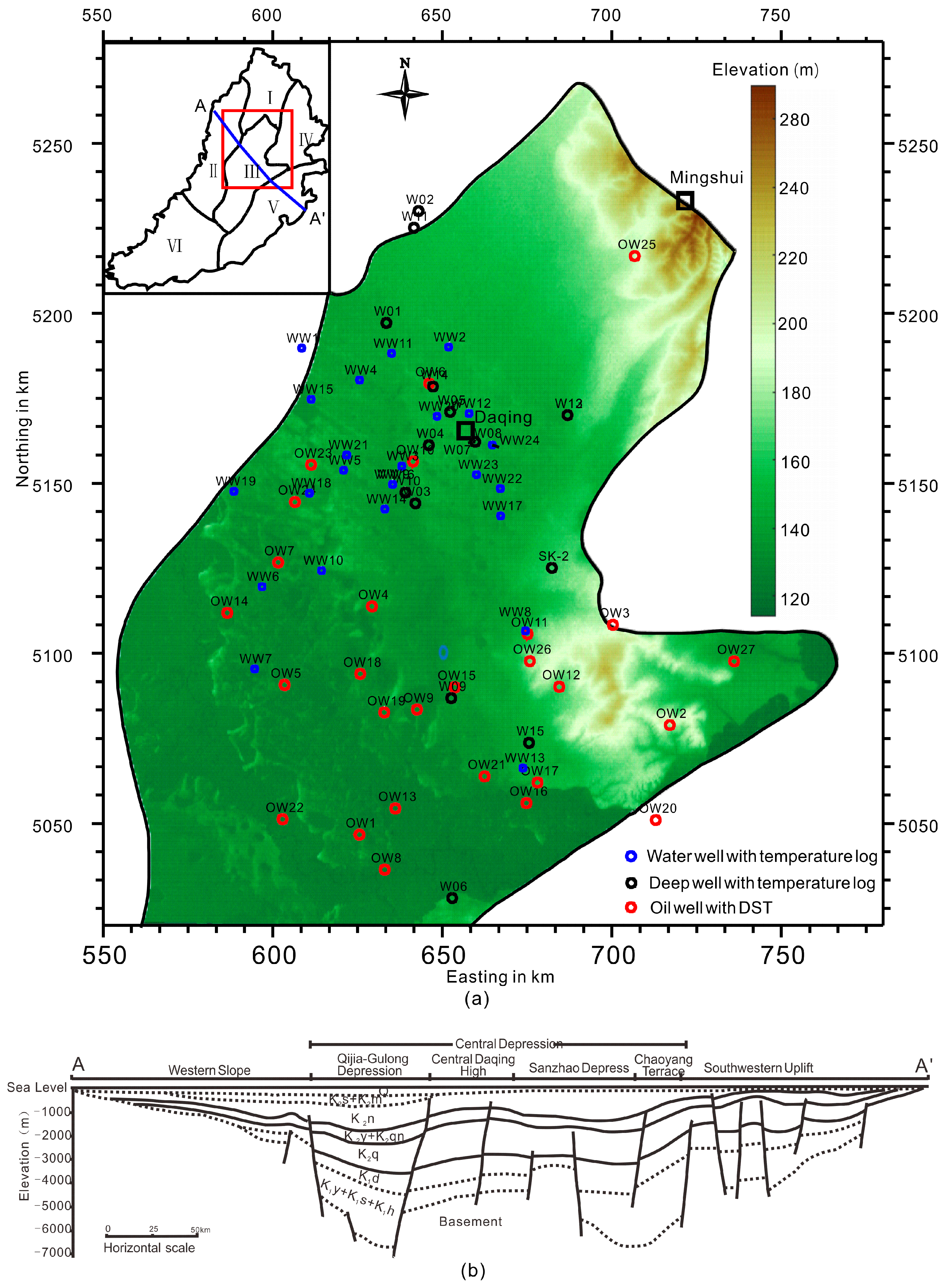
2. Data Source
3. Methodology
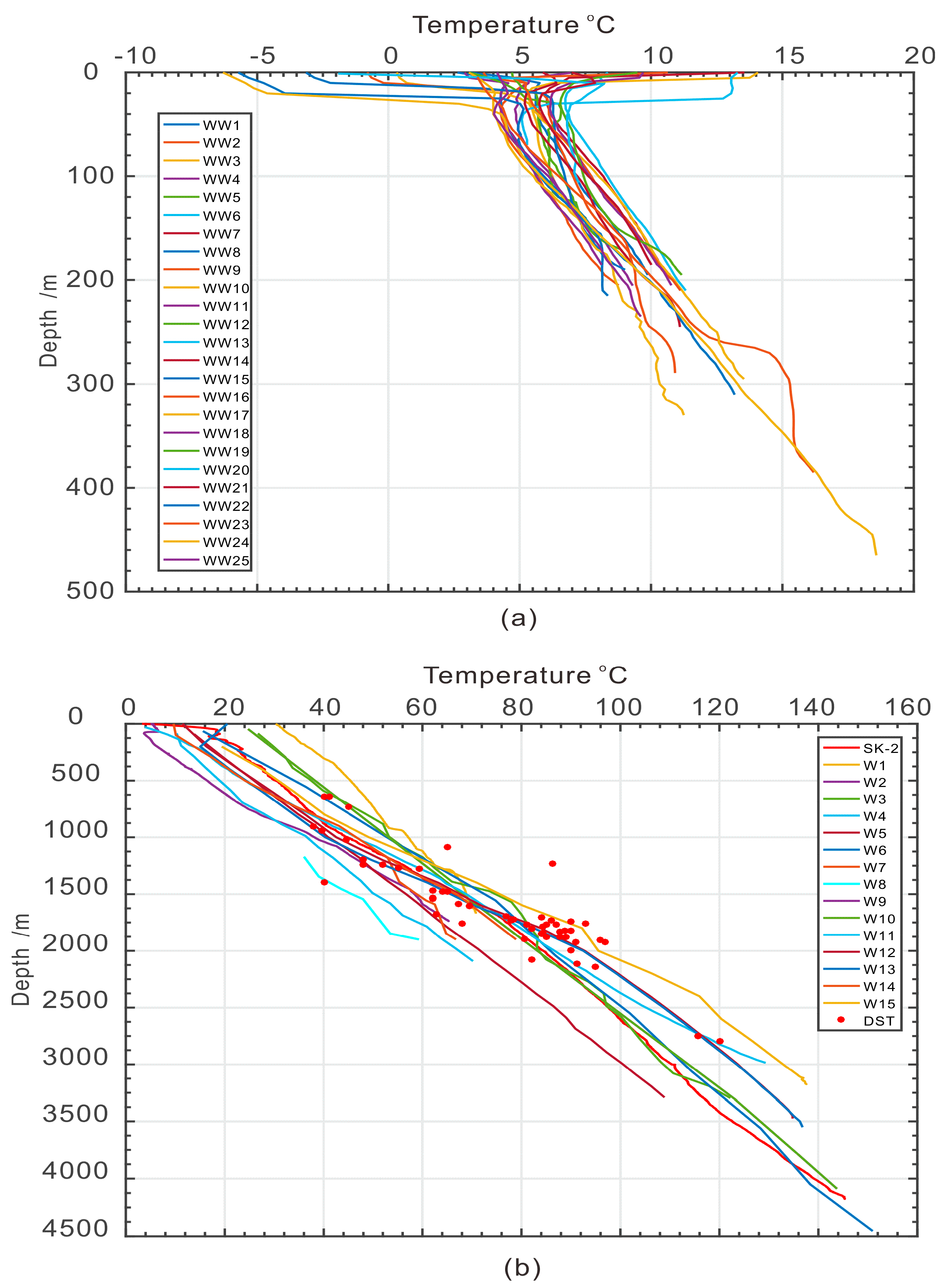
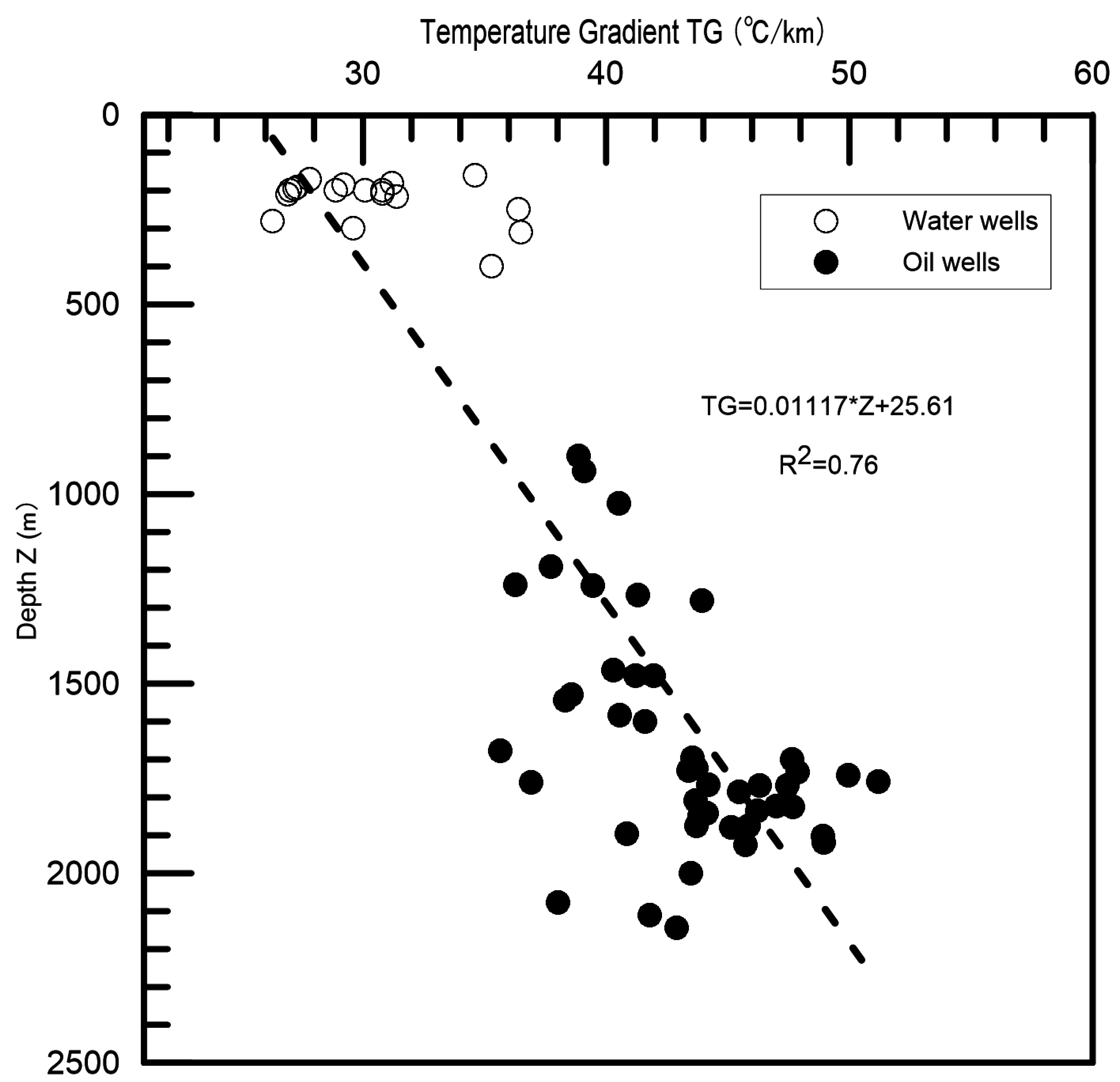
3.1. Temperature Extrapolation
3.2. Volumetric Method
4. Results
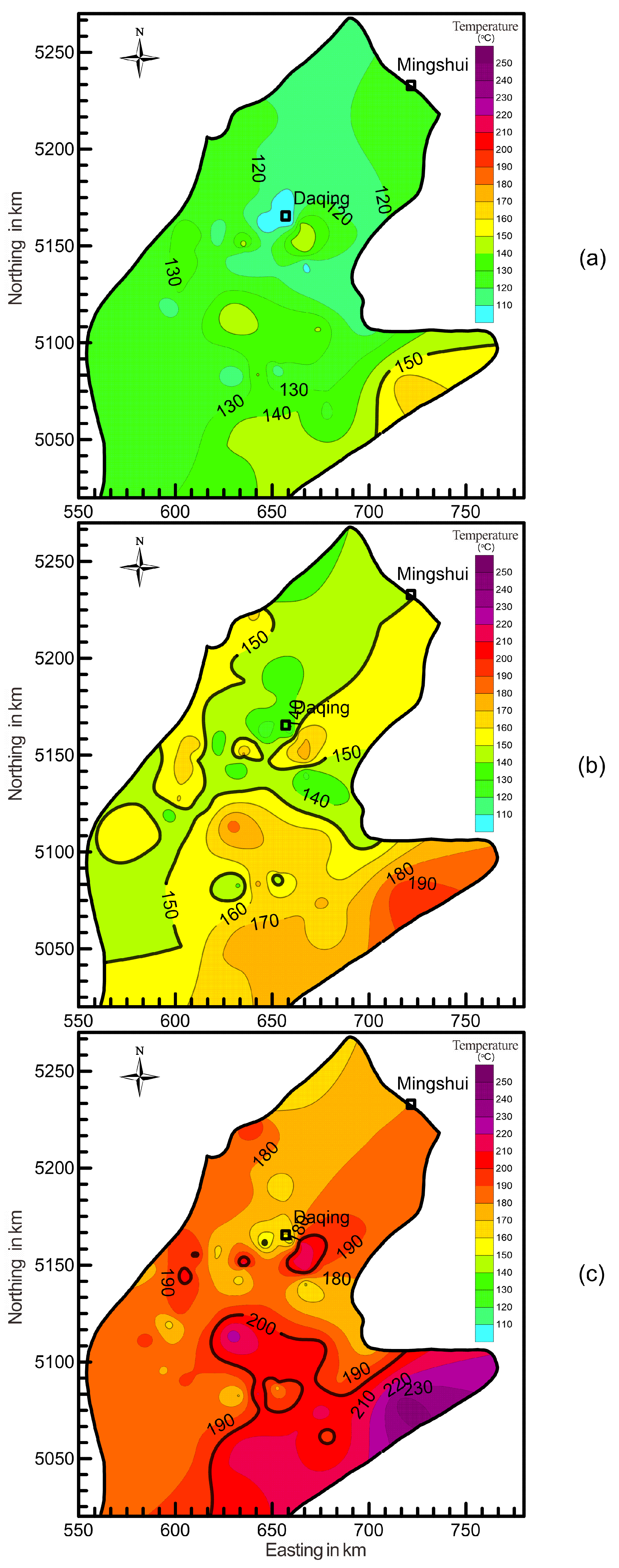
4.1. The Temperature Field
- (1)
- At the depth of 3 km, temperature ranges from 100 to 165 °C, showing the overall trend of being higher in the southeast and lower to the north and northwest (Figure 4a). The regions with temperatures higher than 150 °C are limited within Chaoyang Terrace, with area approximately 40 km2. Temperature is low at the northern part of study area, especially in the Central Daqing High.
- (2)
- At the depth of 4 km, temperatures are 121–199 °C, with the overall trend of being higher in the south and lower to the north (Figure 4b). The temperature at Chaoyang Terrace is as high as 190 °C. The total area with temperature exceeding 150 °C is about 850 km2, which means approximate a half of the areas met the conditions. Low temperature area lies within the north of study area.
- (3)
- At the depth of 5 km, temperatures are 147–245 °C, with the overall trend being same to the depth of 4 km (Figure 4c). Total area of the region with temperature higher than 200 °C reached 250 km2, and mainly underlies Chaoyang Terrace, Sanzhao Depression, and Central Daqing High. Low temperature is exhibited at Qijia-Gulong Depression.
4.2. The Heat Content from 3 to 5 km
5. Discussion and Conclusions
- (1)
- A total of 28 temperature logs were measured, and temperature data from 30 wells were collected, indicating that Daqing Oilfield was located in a geothermal anomalous area, with an average temperature gradient of 34 °C·km−1.
- (2)
- The median deep temperature field (3–5 km) was characterized according to the constraint of multiple-source temperature data.
- (3)
- The heat content from 3 to 5 km is evaluated to be 24.28 × 1021 J. The limit of recoverable HDR resource at the depth interval is 0.33 × 1021 J, equivalent to 1.330 × 1013 t standard coal.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, L.; Yuan, J.; Liang, H.; Li, K. Energy from Abandoned oil and gas reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 20–22 October 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. [Google Scholar]
- Xin, S.; Liang, H.; Hu, B.; Li, K. Electrical power generation from low temperature co-produced geothermal resources at Huabei oilfield. In Proceedings of the thirty-seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. SGP-TR-194.
- Wang, S.J.; Yan, J.H.; Li, M.; Li, K.W.; Hu, S.B. New advances in the study of oilfield geothermal resources evaluation. Chin. J. Geol. 2014, 49, 771–780, (In Chinese with English abstract). [Google Scholar]
- Li, Q.; Yu, H.X. Geothermal power generation experiment engineering in buried-hill oilfield and its application prospect. Chin. J. Geol. 2012, 32, 20–23, (In Chinese with English abstract). [Google Scholar]
- Li, K.W.; Wang, L.; Mao, X.P.; Liu, C.W.; Lu, J.H. Evaluation and efficient development of geothermal resource associated with oilfield. Sci. Technol. Rev. 2012, 30, 32–41, (In Chinese with English abstract). [Google Scholar]
- Petty, S.; Bour, D.L.; Livesay, B.J.; Baria, R.; Adair, R. Synergies and opportunities between EGS development and oilfield drilling operations and producers. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 24–26 March 2009; Society of Petroleum Engineers: Richardson, TX, USA, 2009. [Google Scholar]
- Conser, A. Double Dipping: Utilizing Oil Wells for Geothermal Energy. William Mary Environ. Law Policy Rev. 2013, 37, 813–843. [Google Scholar]
- Zhang, Y.; Li, Z.; Guo, L.; Gao, P.; Jin, X.; Xu, T. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Guo, L.; Gao, P.; Jin, X.; Xu, T. Feasibility Evaluation of EGS Project in the Xujiaweizi Area: Potential Site in Songliao Basin, Northeastern China. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015; pp. 1–14.
- Höök, M.; Tang, X.; Pang, X.; Aleklett, K. Development journey and outlook of Chinese giant oilfields. Pet. Explor. Dev. 2010, 37, 237–249. [Google Scholar] [CrossRef]
- Zhai, Z.W.; Shi, S.M.; Zhu, H.L. Discussion on utilization of oilfield production water type geothermal resource-take Daqing Oilfield as an example. J. Nat. Resour. 2011, 26, 382–387. [Google Scholar]
- He, C.; Dong, S.; Chen, X.; Santosh, M.; Niu, S. Seismic evidence for plume-induced rifting in the Songliao Basin of Northeast China. Tectonophysics 2014, 627, 171–181. [Google Scholar] [CrossRef]
- Chen, L.; Tao, W.; Zhao, L.; Zheng, T. Distinct lateral variation of lithospheric thickness in the Northeastern North China Craton. Earth Planet. Sci. Lett. 2008, 267, 56–68. [Google Scholar] [CrossRef]
- Tan, S.Y.; Shi, Y.Q.; Zhao, Y.J. The formation and prospective evaluation of geothermal resources in the Songliao Basin. World Geol. 2001, 20, 155–160, (In Chinese with English abstract). [Google Scholar]
- Wu, Q.F.; Xie, Y.Z. Geothermal heat flow in the Songhuajiang-Liaoning Basin. Seismol. Geol. 1985, 7, 59–64, (In Chinese with English abstract). [Google Scholar]
- Wang, J.; Huang, S.Y.; Huang, G.S.; Wang, J.Y. Basic Characteristics of the Earth’s Temperature Distribution in China; Seismological Press: Beijing, China, 1990. [Google Scholar]
- Zhu, H.L. Research on the Sedimentary Geothermal Resources in North Songliao Basin. Ph.D. Thesis, Northeast Petroleum University, Daqing, China, 2011. [Google Scholar]
- Liu, C.; Li, K.; Chen, Y.; Chen, J. Geothermal Gradient in the Oilfields in China. In Proceedings of the 41st Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016.
- Beardsmore, G.R.; Cull, J.P. Crustal Heat Flow: A guide to Measurement and Modelling; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Jiang, G.; Tang, X.; Rao, S.; Gao, P.; Zhang, L.; Zhao, P.; Hu, S. High-quality heat flow determination from the crystalline basement of the south-east margin of North China Craton. J. Asian Earth Sci. 2016, 118, 1–10. [Google Scholar] [CrossRef]
- Zhao, C.Q. Distribution Characteristics and the Resource Assessment of Geothermal Resources in Longfeng District. Ph.D. Thesis, Northeast Petroleum University, Daqing, China, 2012. [Google Scholar]
- Ryder, R.T.; Jin, Q.; McCabe, P.J.; Nuccio, V.F.; Persits, F. Qingshankou-Putaohua/Shaertu and Jurassic Coal-Denglouku/Nongan Total Petroleum Systems in the Songliao Basin, China; US Geological Survey Bulletin 2203-A; US Geological Survey: Reston, VA, USA, 2003. [Google Scholar]
- Wang, P.; Mattern, F.; Didenko, N.A.; Zhu, D.; Singer, B.; Sun, X. Tectonics and cycle system of the Cretaceous Songliao Basin: An inverted active continental margin basin. Earth-Sci. Rev. 2016, 159, 82–102. [Google Scholar] [CrossRef]
- Sui, W.X. How to realize the geothermal resources: Exploration prospecting breakthrough and geothermal resource research in northern Songliao basin, Heilongjiang province. Tectonophysics 2013, 606, 1–13, (In Chinese with English abstract). [Google Scholar]
- Feng, Z.Q.; Jia, C.Z.; Xie, X.N.; Zhang, S.; Feng, Z.H.; Cross, T.A. Tectonostratigraphic units and stratigraphic sequences of the nonmarine Songliao basin, northeast China. Basin Res. 2010, 22, 79–95. [Google Scholar]
- Zhao, Z.; Xu, S.; Jiang, X.; Lin, C.; Cheng, H.; Cui, J.; Jia, L. Deep strata geologic structure and tight sandy conglomerate gas exploration in Songliao Basin, East China. Pet. Explor. Dev. 2016, 43, 13–25. [Google Scholar] [CrossRef]
- Hurtig, E. Temperature and heat-flow density along European transcontinental profiles. Tectonophysics 1995, 244, 75–83. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; p. 372. [Google Scholar]
- Haenel, R.; Stegena, L.; Rybach, L. Handbook of Terrestrial Heat-Flow Density Determination: With Guidelines and Recommendations of the International Heat Flow Commission; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Spichak, V.; Geiermann, J.; Zakharova, O.; Calcagno, P.; Genter, A.; Schill, E. Deep temperature extrapolation in the Soultz-sous-Forêts geothermal area using magnetotelluric data. In Proceedings of the 35th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 1–3 February 2010.
- Nansheng, Q. Geothermal regime in the Qaidam basin, northeast Qinghai–Tibet Plateau. Geol. Mag. 2003, 140, 707–719. [Google Scholar] [CrossRef]
- Rao, S.; Hu, S.B.; Zhu, C.Q.; Tang, X.Y.; Li, W.W.; Wang, J.Y. The characteristics of heat flow and lithospheric thermal structure in Junggar Basin, northwest China. Chin. J. Geophys. 2013, 56, 2760–2770, (In Chinese with English abstract). [Google Scholar]
- Wu, X.X. Research of Geothermal Resources on Hot Dry Rock in North Songliao Basin. Ph.D. Thesis, Northeast Petroleum University, Daqing, China, 2014. [Google Scholar]
- Chopra, P.; Holgate, F. A GIS analysis of temperature in the Australian crust. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005.
- Blackwell, D.D.; Negraru, P.T.; Richards, M.C. Assessment of the enhanced geothermal system resource base of the United States. Nat. Resour. Res. 2006, 15, 283–308. [Google Scholar] [CrossRef]
- Wang, J.Y.; Hu, S.B.; Pang, Z.H.; He, L.J.; Zhao, P.; Rao, S.; Tang, X.Y.; Kong, Y.L.; Luo, L.; Li, W.W. Estimate of Geothermal Resources Potential for Hot Dry Rock in the Continental Area of China. Sci. Technol. Rev. 2012, 30, 25–31, (In Chinese with English abstract). [Google Scholar]
- Hu, S.B.; Xiong, L.P. Correction for disturbance of vertical groundwater movement to heat flow measurement. Chin. J. Geol. 1994, 29, 85–92, (In Chinese with English abstract). [Google Scholar]
- Xiong, L.P.; Gao, W.A. The characteristics of geo-temperature field in uplift and depression zone. Chin. J. Geophys. 1982, 5, 448–456, (In Chinese with English abstract). [Google Scholar]
- Zhang, L.; Liu, M.; Li, K. Estimation of geothermal reserves in oil and gas reservoirs. In SPE Western Regional Meeting, San Jose, CA, USA, 24–26 March 2009; Society of Petroleum Engineers: Richardson, TX, USA, 2009. [Google Scholar]
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Muffler, L.J.P. Assessment of Geothermal Resources of the United States, 1978; Geological Survey: Reston, VA, USA, 1979. [Google Scholar]
- Li, K.; Sun, W. Modified Method for Estimating Geothermal Resources in Oil and Gas Reservoirs. Math. Geosci. 2015, 47, 105–117. [Google Scholar] [CrossRef]
- Olasolo, P.; Juárez, M.C.; Morales, M.P.; D’Amico, S.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sustain. Energy Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Rybach, L.; Bodmer, P.; Pavoni, N.; Mueller, S. Siting Criteria for Heat Extraction from Hot Dry Rock—Application to Switzerland. Pure Appl. Geophys. 1978, 116, 1211–1224. [Google Scholar] [CrossRef]
- Sanyal, S.K. Sustainability and renewability of geothermal power capacity. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005.
- Williams, C.F.; Reed, M.J.; Mariner, R.H. A Review of Methods Applied by the US Geological Survey in the Assessment Of Identified Geothermal Resources; US Geological Survey Open-File Report; US Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
| Depth Z (km) | Lithology | Thermal Conductivity K (W/K/m) | Density ρ (g/cm3) | Specific Heat Cp (J/kg/k) |
|---|---|---|---|---|
| 2–3 | Mudstone and Sandstone | 2.31 | - | - |
| 3–4 | Mudstone and Sandstone | 2.51 | 2.47–2.61 | 940 |
| 4–5 | Rhyolite and Tuffaceous breccia lava | 2.87 | 2.70–2.80 | 1070 |
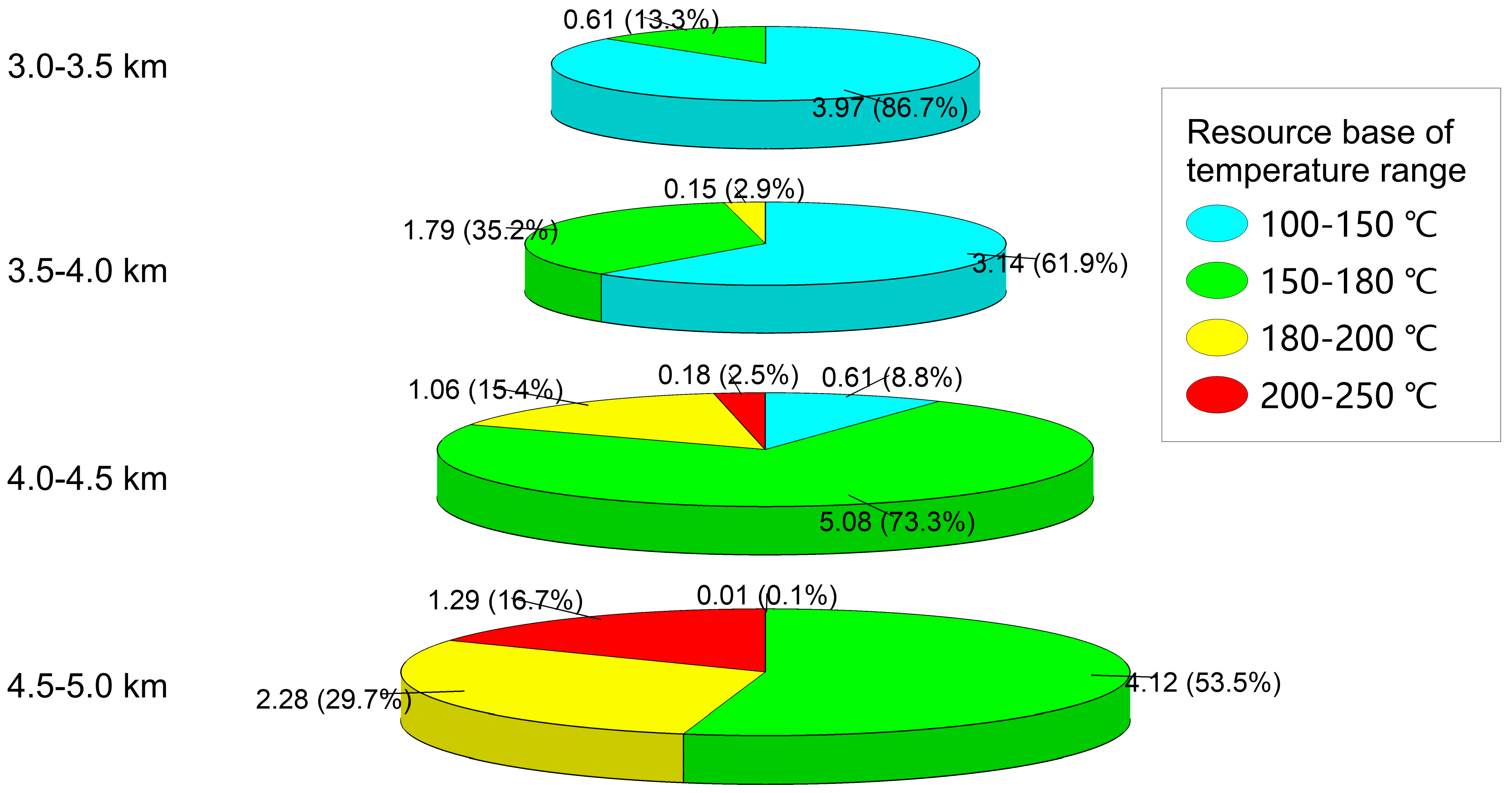
| Depth Range (km) | Q × 1021 (J) | ||||
|---|---|---|---|---|---|
| –150 °C | 150–180 °C | 180–200 °C | 200– °C | Total | |
| 3.0–3.5 | 3.97 | 0.61 | 0.00 | 0.00 | 4.58 |
| 3.5–4.0 | 3.14 | 1.79 | 0.15 | 0.00 | 5.07 |
| 4.0–4.5 | 0.61 | 5.08 | 1.06 | 0.18 | 6.93 |
| 4.5–5.0 | 0.01 | 4.12 | 2.28 | 1.29 | 7.70 |
| Total | 7.72 | 11.60 | 3.50 | 1.46 | 24.28 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Wang, Y.; Shi, Y.; Zhang, C.; Tang, X.; Hu, S. Estimate of Hot Dry Rock Geothermal Resource in Daqing Oilfield, Northeast China. Energies 2016, 9, 731. https://doi.org/10.3390/en9100731
Jiang G, Wang Y, Shi Y, Zhang C, Tang X, Hu S. Estimate of Hot Dry Rock Geothermal Resource in Daqing Oilfield, Northeast China. Energies. 2016; 9(10):731. https://doi.org/10.3390/en9100731
Chicago/Turabian StyleJiang, Guangzheng, Yi Wang, Yizuo Shi, Chao Zhang, Xiaoyin Tang, and Shengbiao Hu. 2016. "Estimate of Hot Dry Rock Geothermal Resource in Daqing Oilfield, Northeast China" Energies 9, no. 10: 731. https://doi.org/10.3390/en9100731
APA StyleJiang, G., Wang, Y., Shi, Y., Zhang, C., Tang, X., & Hu, S. (2016). Estimate of Hot Dry Rock Geothermal Resource in Daqing Oilfield, Northeast China. Energies, 9(10), 731. https://doi.org/10.3390/en9100731





