Low Voltage Ride-Through Capability Solutions for Permanent Magnet Synchronous Wind Generators
Abstract
:1. Introduction
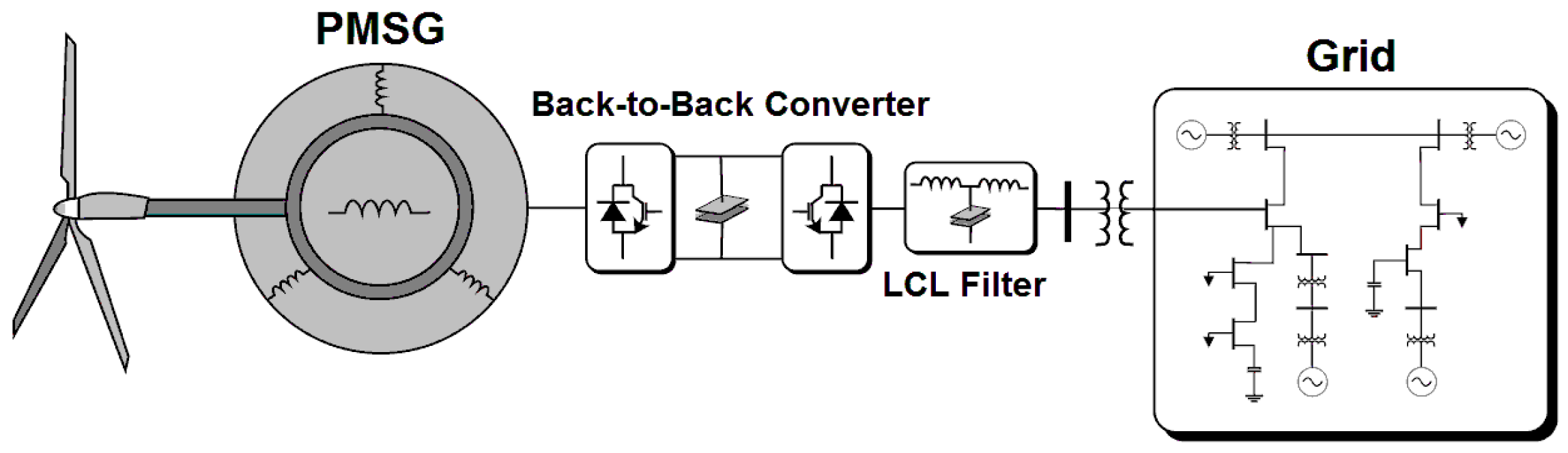
2. Full Converter Permanent Magnet Synchronous Generator Wind Energy Conversion System
2.1. Permanent Magnet Synchronous Generator
2.2. Grid Side
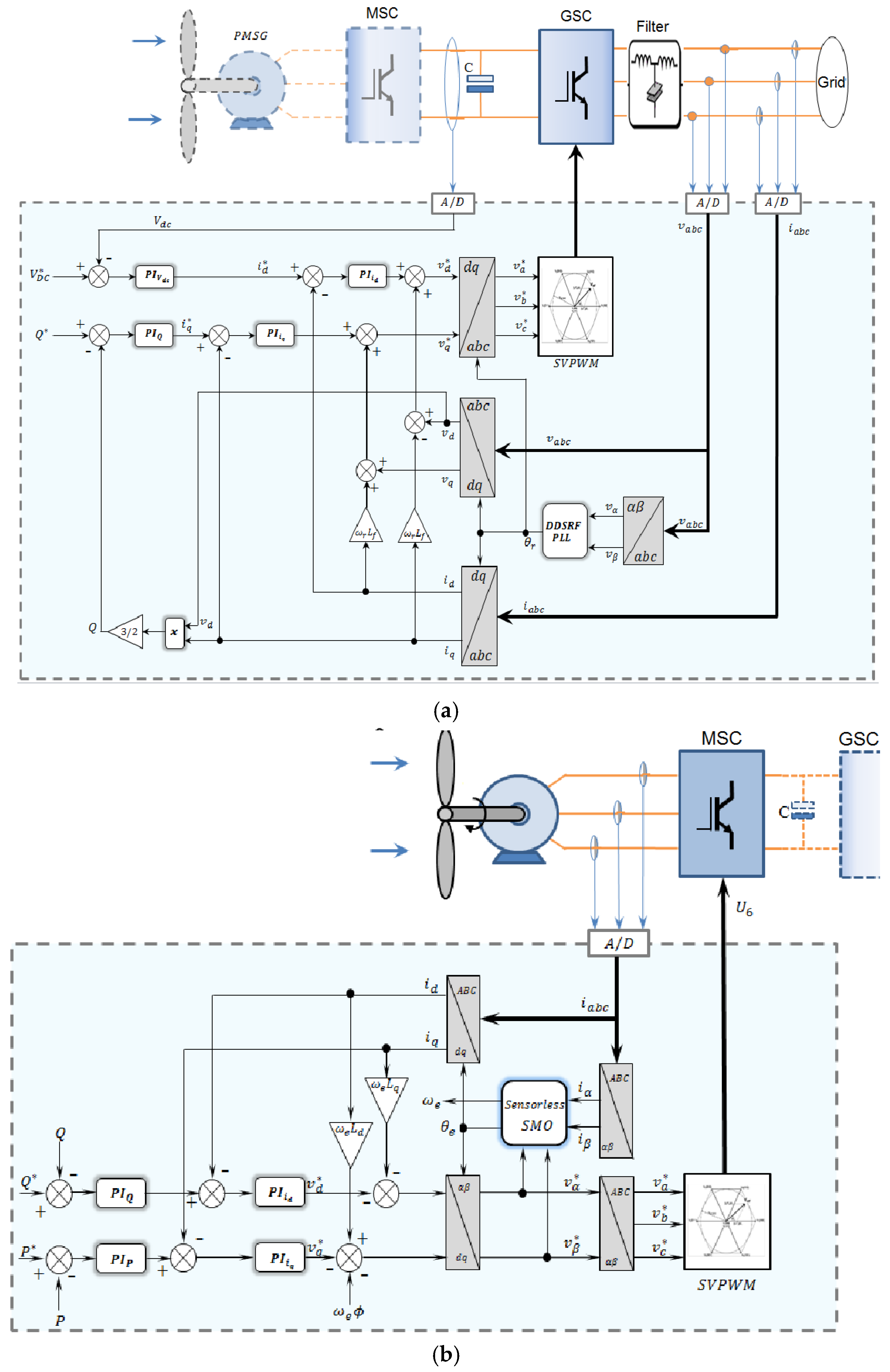
2.3. The Classic Control Structure
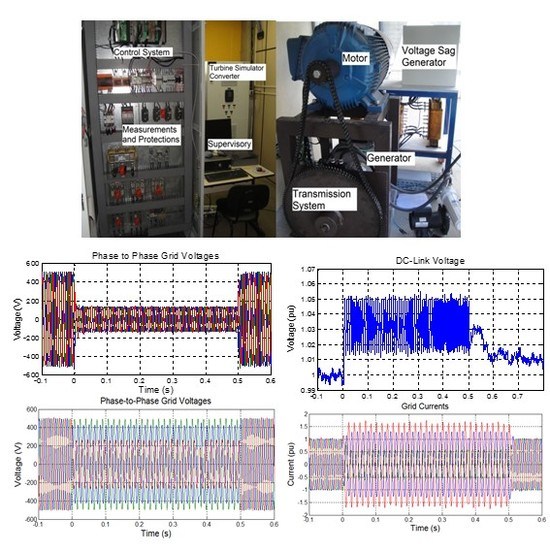
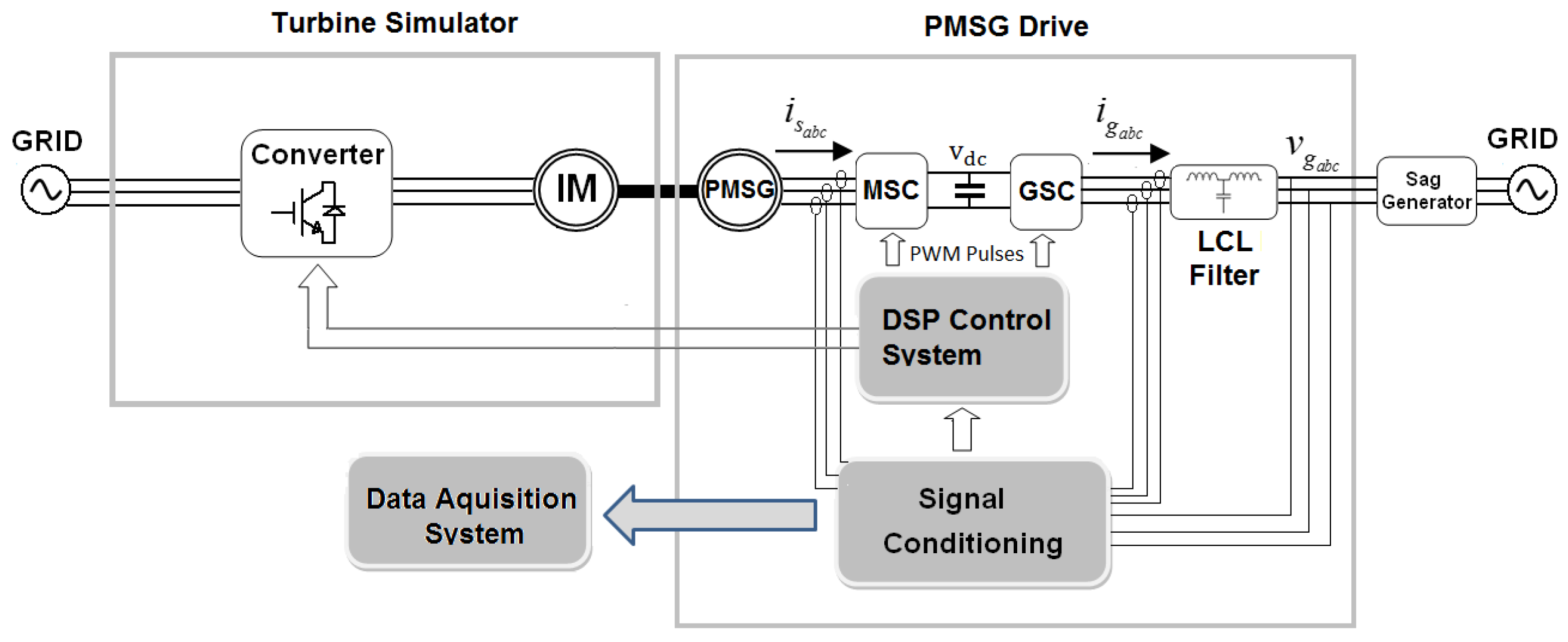
2.4. Test Bench

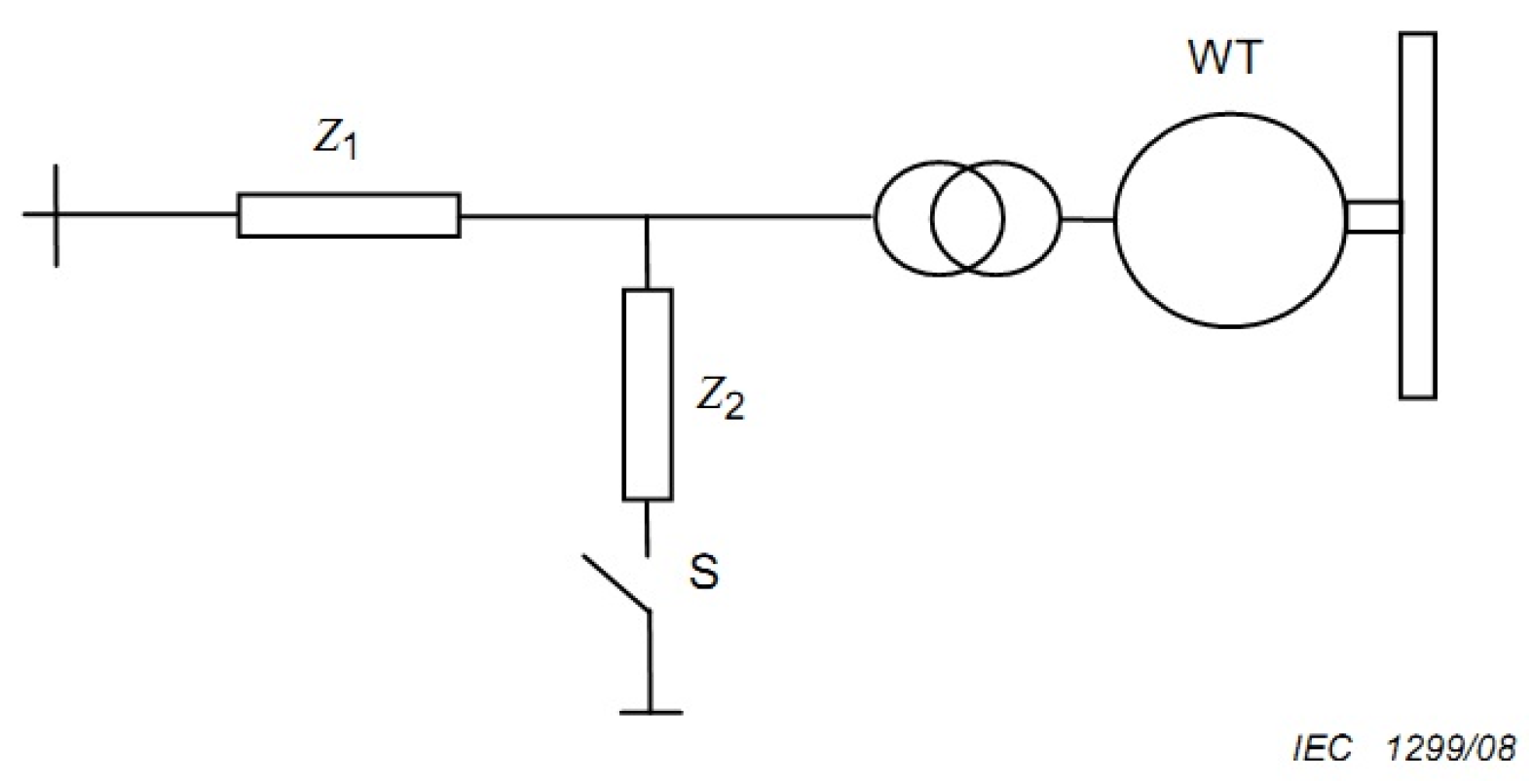
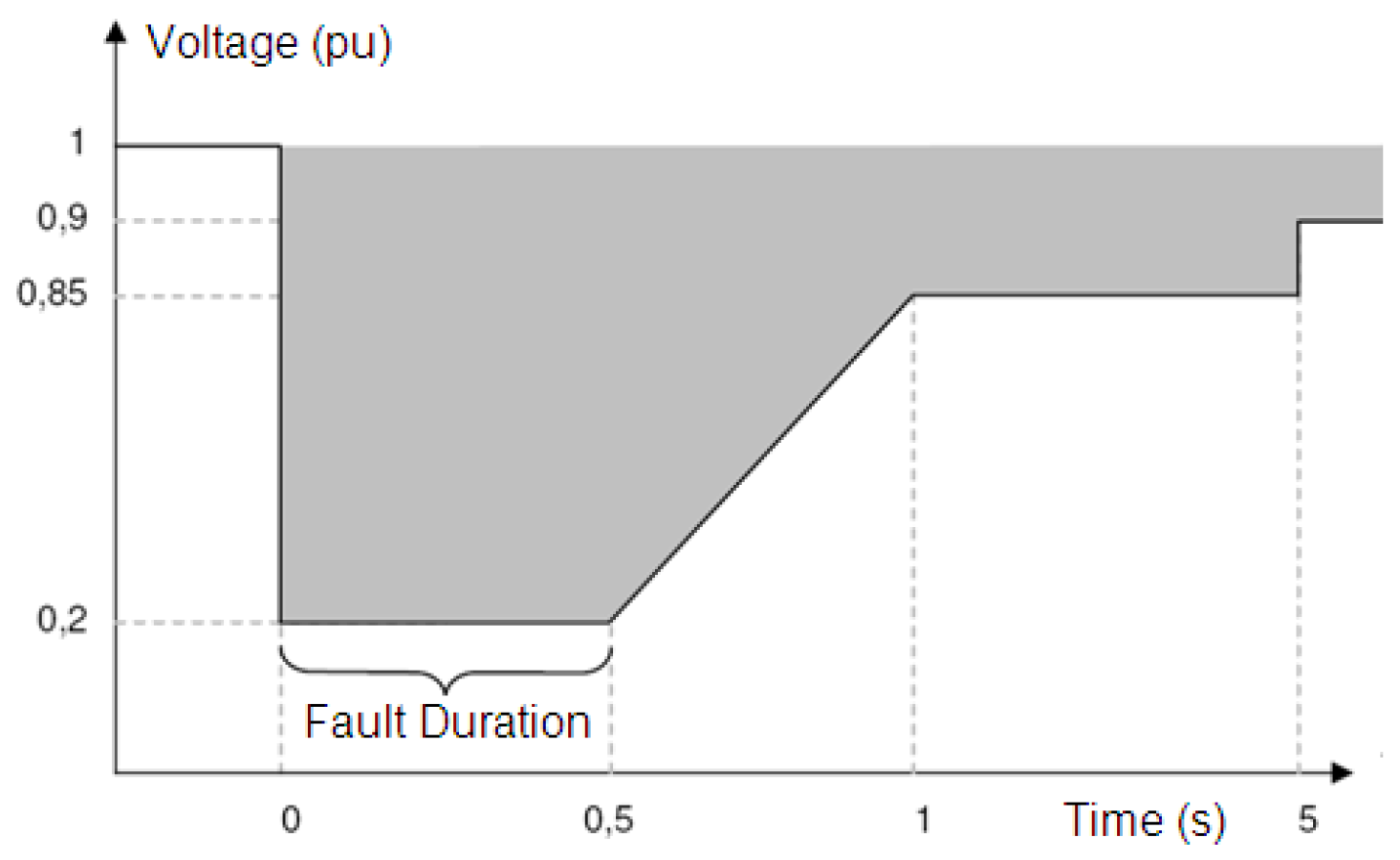
| Case | Voltage Magnitude | Positive Sequence Magnitude | Duration (s) | Shape |
|---|---|---|---|---|
| Three-phase | 90% ± 5% | 90% | 0.5 ± 0.05 |  |
| Three-phase | 50% ± 5% | 50% | 0.5 ± 0.05 |  |
| Three-phase | 20% ± 5% | 20% | 0.2 ± 0.05 | 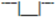 |
| Two-phase | 90% ± 5% | 95% | 0.5 ± 0.05 | 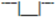 |
| Two-phase | 50% ± 5% | 75% | 0.5 ± 0.05 | 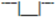 |
| Two-phase | 20% ± 5% | 60% | 0.2 ± 0.05 | 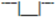 |
3. Symmetrical Voltage Sags
3.1. Experimental Results
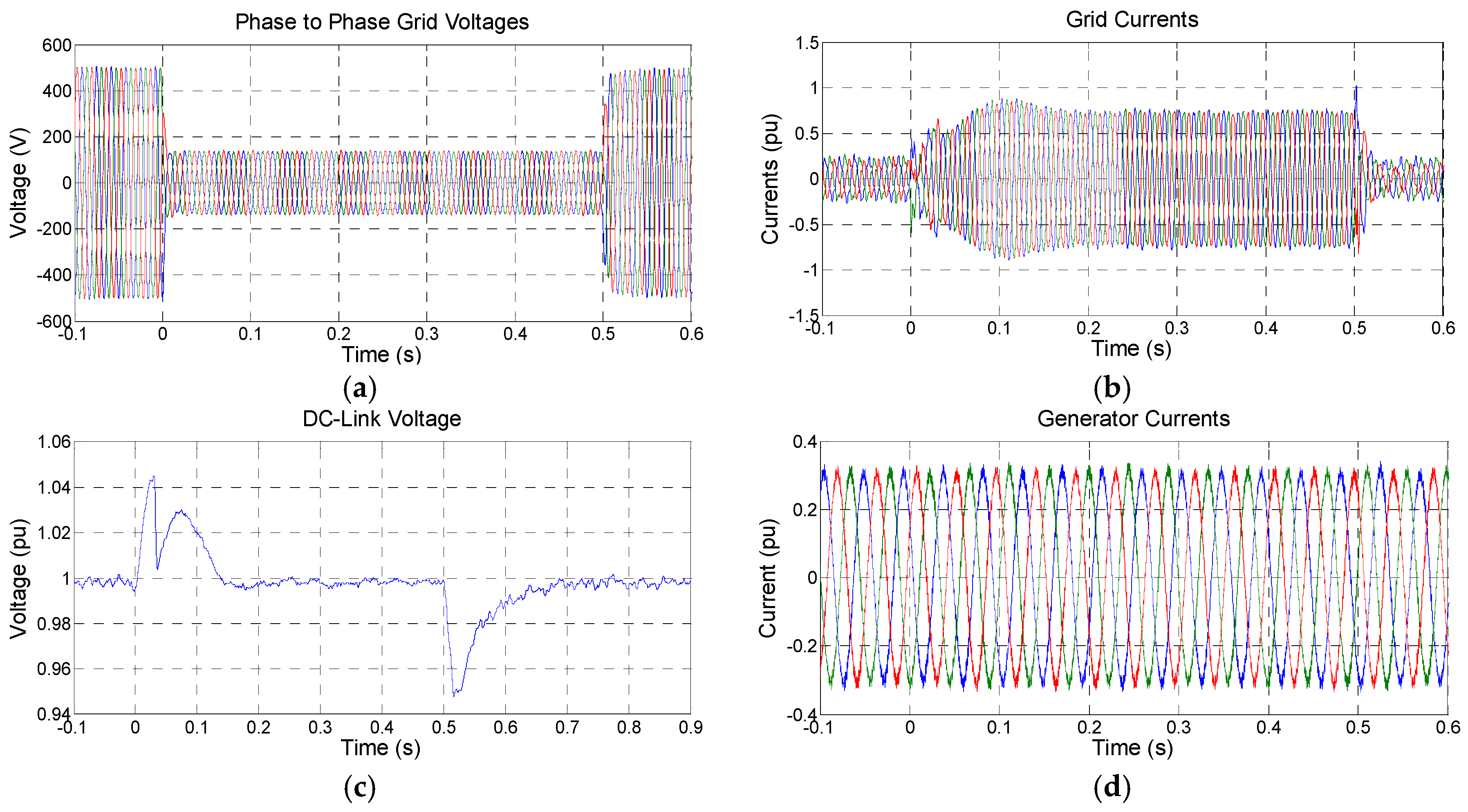
3.2. Results Discussion
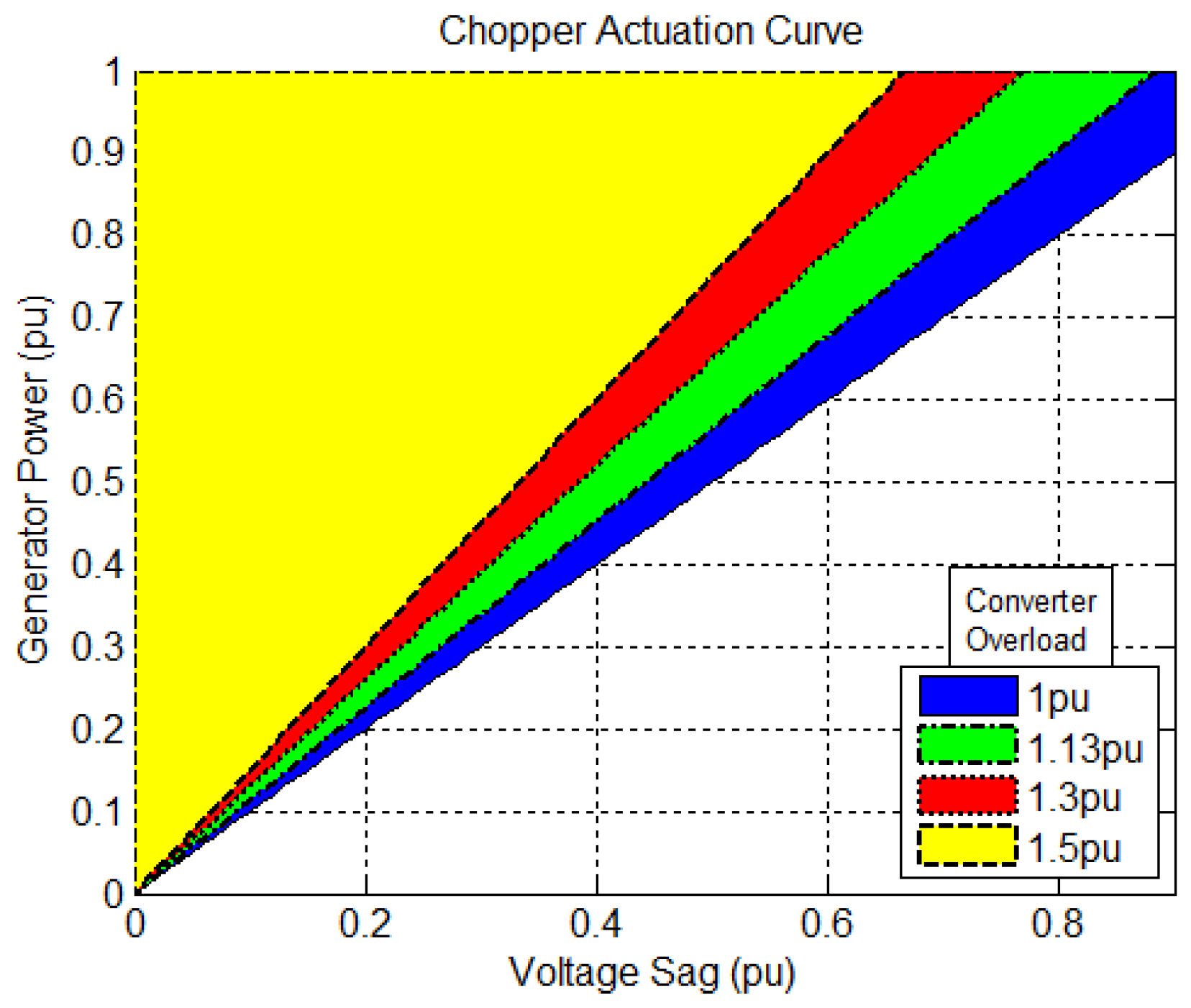
3.3. Analysis of the Low Voltage Ride-Through Capability Control Strategies Proposed in the Literature
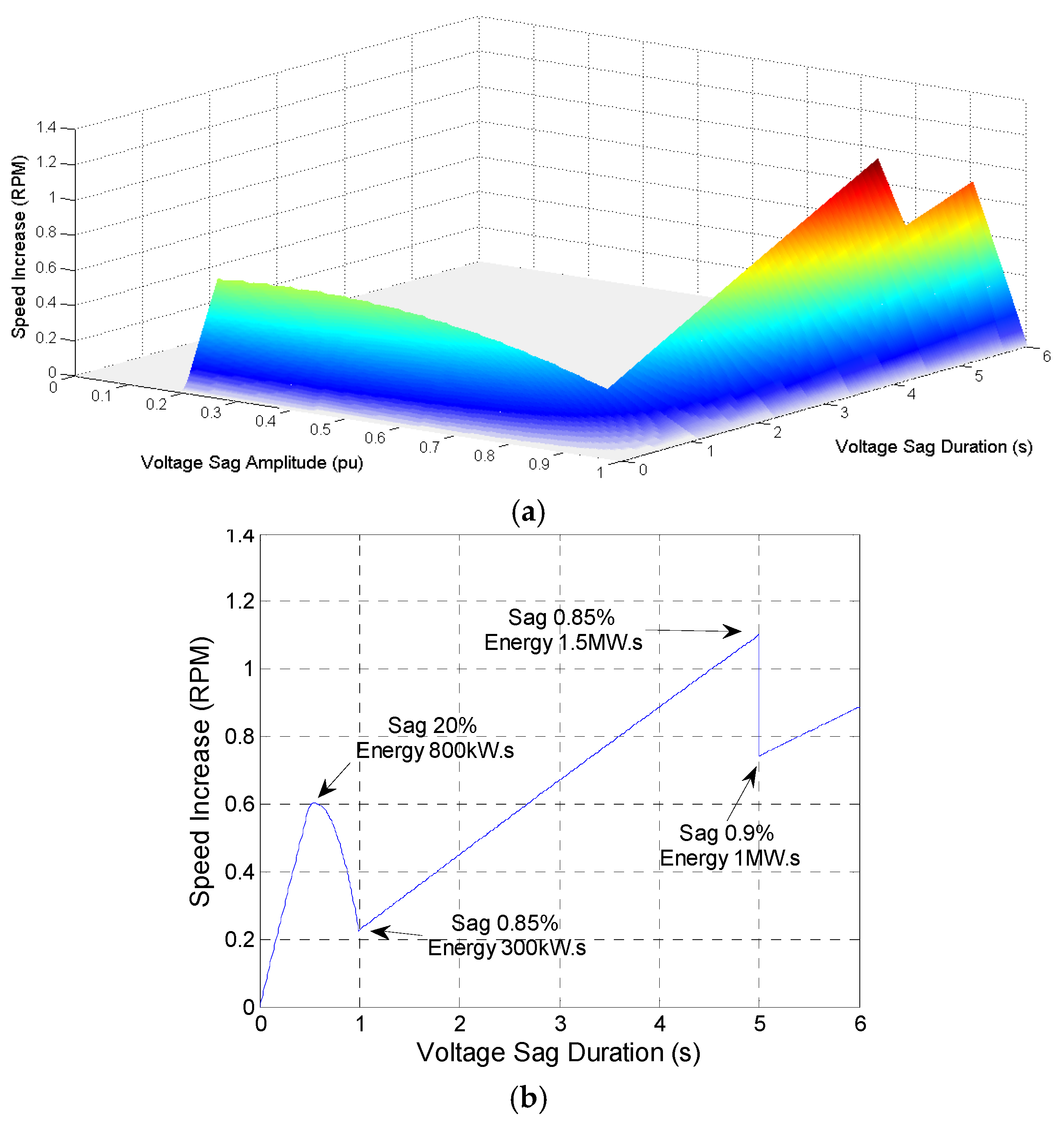
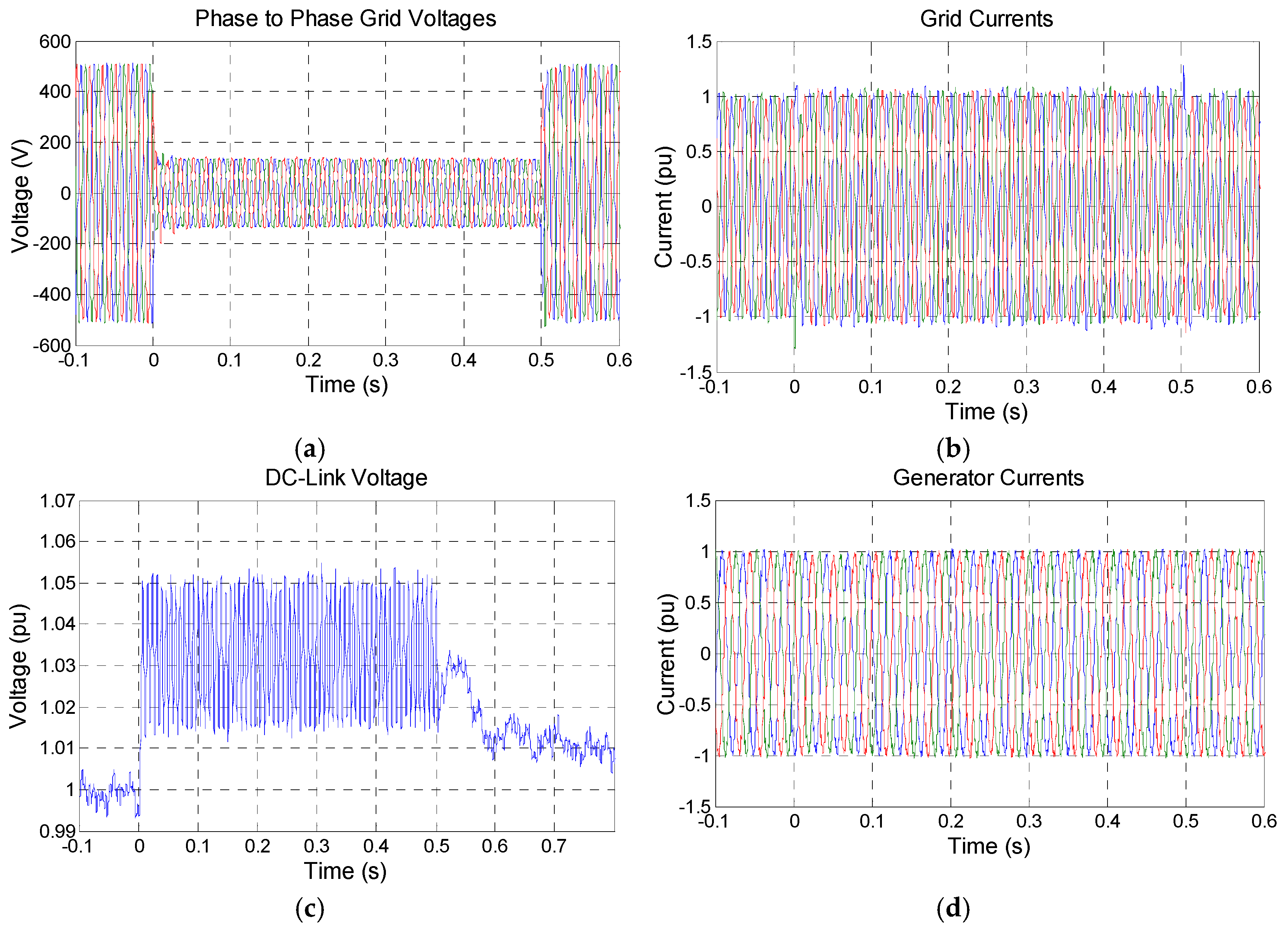
4. Asymmetric Voltage Sags
4.1. Experimental Results
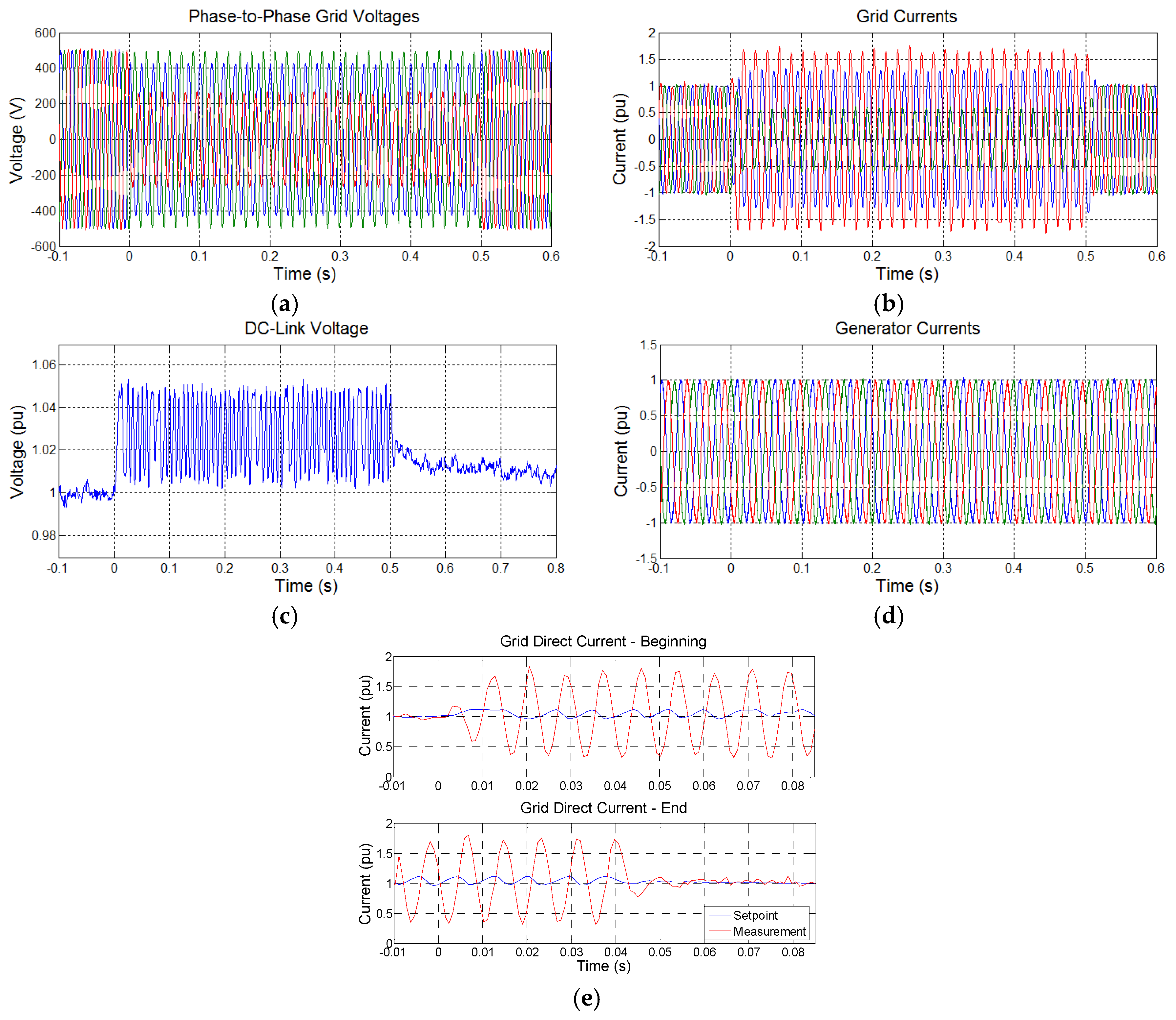
4.2. Results Discussion and Low Voltage Ride-through Capability Control Strategies Proposed in the Literature
5. Resonant Control
5.1. The Control Strategy
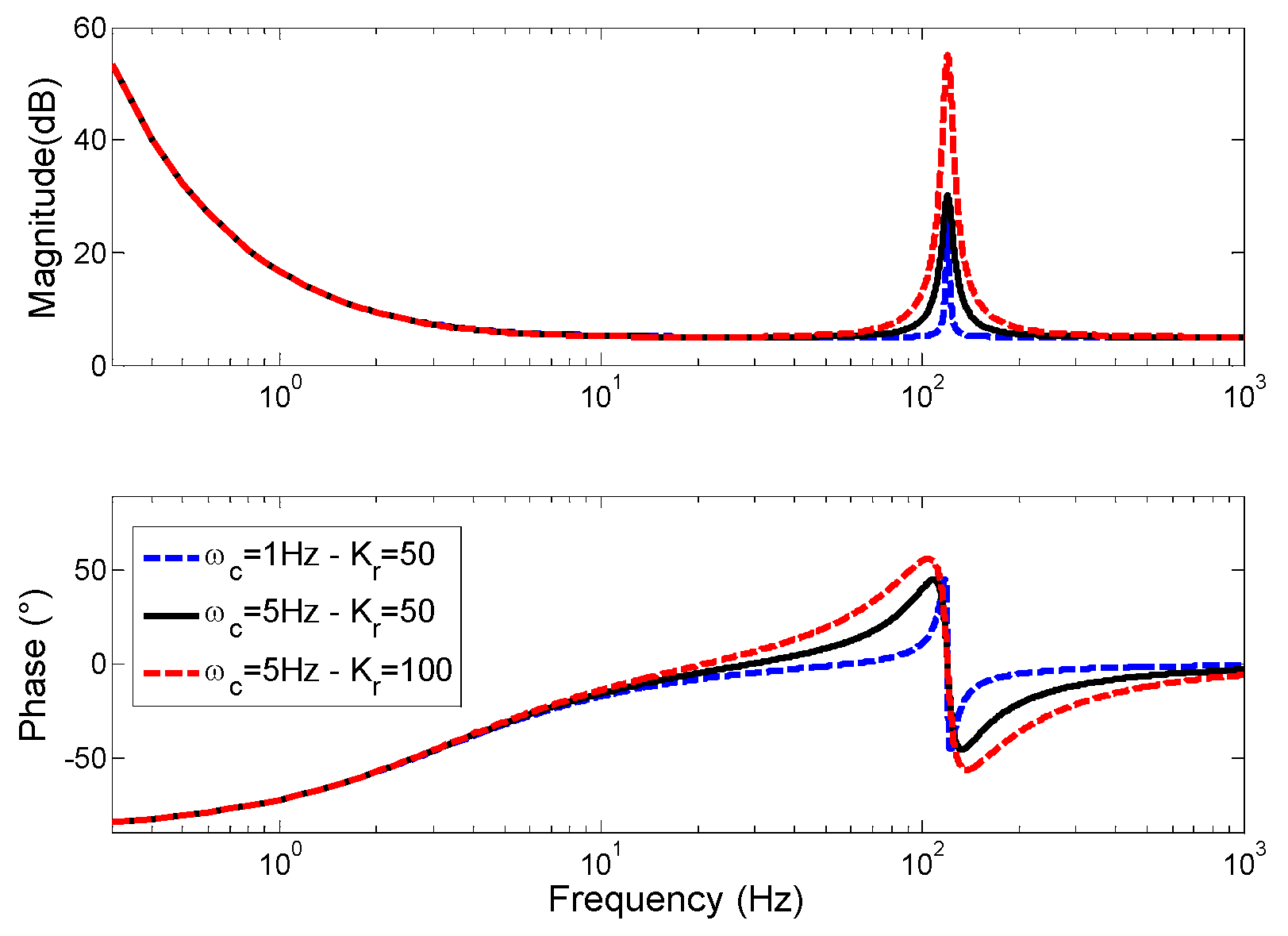
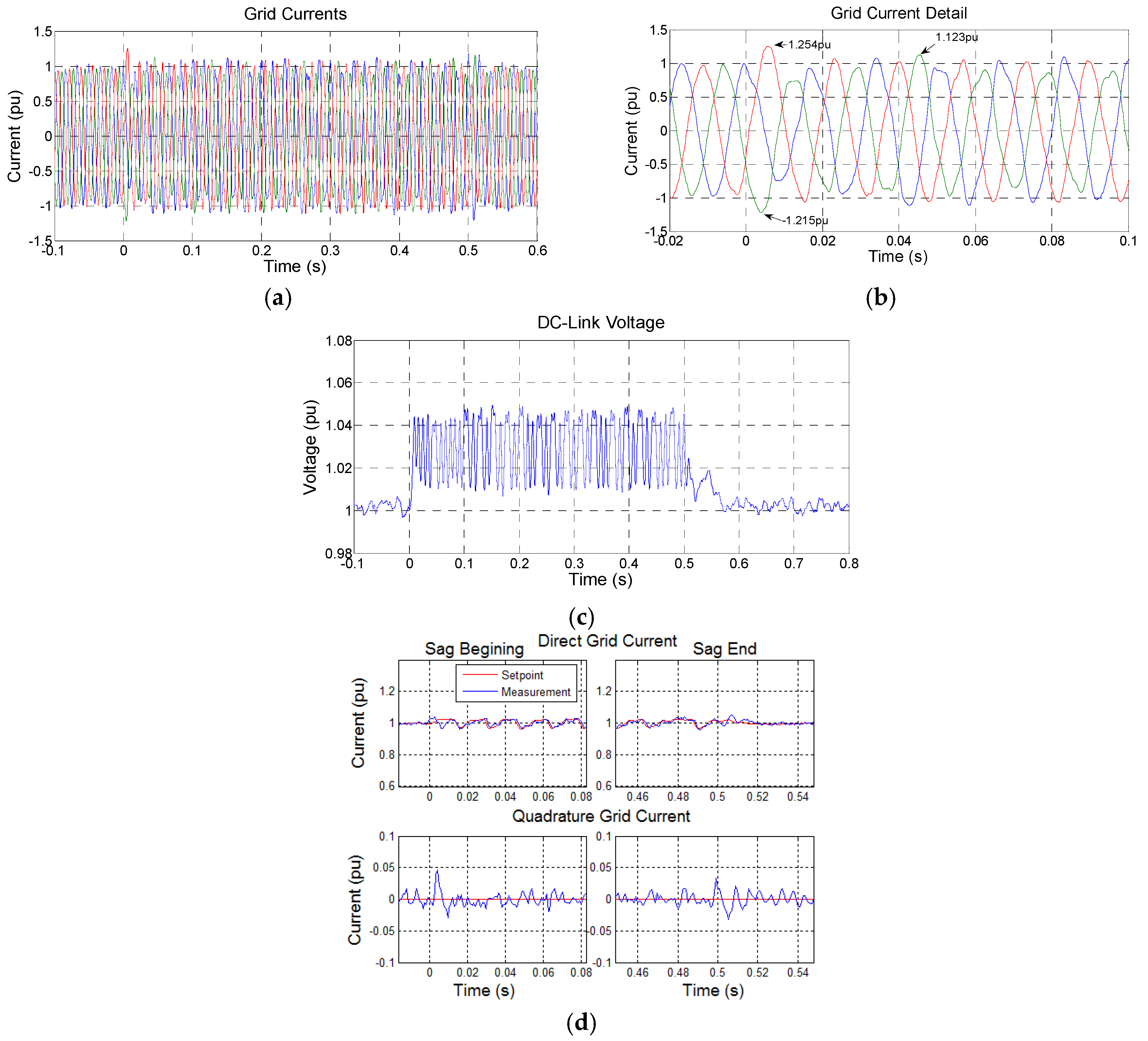
5.2. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Machine Side Converter | ||||
| Control | Proportional (Kp) | Integral (Ki) | ||
| Current control loop | 2 | 20 | ||
| Power loop | 0.05 | 1 | ||
| Grid Side Converter | ||||
| Control | Proportional (Kp) | Integral (Ki) | Resonant (Kr) | |
| Current control loop | 2 | 100 | 50 | |
| DC-Link control loop | 0.6 | 10 | - | |
| Generator | |
| Rated power | 34 kW |
| Frequency | 60 Hz |
| Pole pair number | 24 |
| Rated speed | 150 rpm |
| Rated current | 76 A |
| Rated voltage | 365 V |
| Motor (turbine simulator) | |
| Rated power | 37 kW |
| Frequency | 60 Hz |
| Number of poles | 8 |
| Rated current | 83 A |
| Rated voltage | 380 V |
| Converter | |
| Rated power | 42 kVA |
| Grid voltage | 380 V |
| Switching frequency | 6 kHz |
| DC-link voltage | 640 V |
References
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Grid Code High and Extra High Voltage; E.ON Netz GmbH: Bayreuth, Germany, 2006.
- Grid Codes Sub-module 3.6: Minimal Technical Requirements for the Grid Connection; National System Operator (ONS): Rio de Janeiro, Brazil, 2009. (In Portuguese)
- Zhu, Z.Q.; Hu, J. Electrical machines and power-electronic systems for high-power wind energy generation applications: Part I—market penetration, current technology and advanced machine systems. Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32, 7–33. [Google Scholar]
- López, J.; Sanchis, P.; Roboam, X.; Marroyo, L. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips. IEEE Trans. Energy Convers. 2007, 22, 709–717. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, M.; Song, Z.-F.; Xia, C.-L. Proportional-Resonant Control of Doubly-Fed Induction Generator Wind Turbines for Low-Voltage Ride-Through Enhancement. Energies 2012, 5, 4758–4778. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, C.; Hu, M. Improved Control Strategy for DFIG Wind Turbines for Low Voltage Ride Through. Energies 2013, 6, 1181–1197. [Google Scholar] [CrossRef]
- Mendes, V.F.; Sousa, C.V.; Silva, S.R.; Rabelo, B.; Hofmann, W. Modeling and Ride-Through Control of Doubly Fed Induction Generators During Symmetrical Voltage Sags. IEEE Trans. Energy Convers. 2011, 26, 1161–1171. [Google Scholar] [CrossRef]
- Lima, F.K.A.; Luna, A.; Rodriguez, P.; Watanabe, E.H.; Blaabjerg, F. Rotor Voltage Dynamics in the Doubly Fed Induction Generator during Grid Faults. IEEE Trans. Power Electron. 2010, 25, 118–130. [Google Scholar] [CrossRef]
- Arribas, J.R.; Rodríguez, A.F.; Muñoz, Á.H.; Nicolás, C.V. Low Voltage Ride-through in DFIG Wind Generators by Controlling the Rotor Current without Crowbars. Energies 2014, 7, 498–519. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Hamad, M.S.; Dessouky, Y.G.; Williams, B.W. A review on recent low voltage ride-through solutions for PMSG wind turbine. In Proceedings of the 2012 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 20–22 June 2012.
- Conroy, J.F.; Watson, R. Low-voltage ride-through of a full converter wind turbine with permanent magnet generator. IET Renew. Power Gener. 2007, 1, 182–189. [Google Scholar] [CrossRef]
- Wang, W.; Ge, B.; Bi, D.; Qin, M.; Liu, W. Energy storage based LVRT and stabilizing power control for direct-drive wind power system. In Proceedings of the International Conference on Power System Technology (POWERCON), Hangzhou, China, 24–28 October 2010.
- Huang, H.; Mao, C.; Lu, J.; Wang, D. Electronic Power Transformer Control Strategy in Wind Energy Conversion Systems for Low Voltage Ride-through Capability Enhancement of Directly Driven Wind Turbines with Permanent Magnet Synchronous Generators (D-PMSGs). Energies 2014, 7, 7330–7347. [Google Scholar] [CrossRef]
- Yang, X.; Duan, X.; Feng, F.; Tian, L. Low Voltage Ride-Through of Directly Driven Wind Turbine with Permanent Magnet Synchronous Generator. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Wuhan, China, 27–31 March 2009.
- Geng, H.; Yang, G.; Xu, D.; Wu, B. Unified Power Control for PMSG-Based WECS Operating Under Different Grid Conditions. IEEE Trans. Energy Convers. 2011, 26, 822–830. [Google Scholar] [CrossRef]
- Hansen, A.-D.; Michalke, G. Multi-pole permanent magnet synchronous generator wind turbines’ grid support capability in uninterrupted operation during grid faults. IET Renew. Power Gener. 2009, 3, 333–348. [Google Scholar] [CrossRef]
- Deng, F.; Chen, Z. Low-voltage ride-through of variable speed wind turbines with permanent magnet synchronous generator. In Proceedings of the 5th Annual Conference of IEEE Industrial Electronics (IECON’09), Porto, Portugal, 3–5 November 2009.
- Kim, K.H.; Jeung, Y.-C.; Lee, D.-C.; Kim, H-G. LVRT Scheme of PMSG Wind Power Systems Based on Feedback Linearization. IEEE Trans. Power Electron. 2012, 27, 2376–2384. [Google Scholar] [CrossRef]
- Alepuz, S.; Calle, A.; Busquets-Monge, S.; Kouro, S.; Wu, B. Use of Stored Energy in PMSG Rotor Inertia for Low-Voltage Ride-Through in Back-to-Back NPC Converter-Based Wind Power Systems. IEEE Trans. Ind. Electron. 2013, 60, 1787–1796. [Google Scholar] [CrossRef]
- Wu, Z.; Dou, X.; Chu, J.; Hu, M. Operation and Control of a Direct-Driven PMSG-Based Wind Turbine System with an Auxiliary Parallel Grid-Side Converter. Energies 2013, 6, 3405–3421. [Google Scholar] [CrossRef]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Analysis of Electric Machinery and Drive Systems, 3rd ed.; IEEE Press, Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-fillter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Xu, L.; Andersen, B.R.; Cartwright, P. VSC transmission operating under unbalanced AC conditions—analysis and control design. IEEE Trans. Power Deliv. 2005, 20, 427–434. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled double synchronous reference frame PLL for power converters control. IEEE Trans. Ind. Appl. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; CRC Press: Blacksburg, VA, USA, 2010. [Google Scholar]
- Huang, K.; Zheng, L.; Huang, S.; Xiao, L.; Li, W. Sensorless control for direct-drive PMSG wind turbines based on sliding mode observer. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011.
- Suul, J.A.; Molinas, M.; Norum, L.; Undeland, T. Tuning of control loops for grid connected voltage source converters. In Proceedings of the IEEE 2nd International Power and Energy Conference (PECon), Johor Bahru, Malaysia, 1–3 December 2008.
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical methods for carrier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]
- Wind Turbine: Measurement and Assessment of Power Quality Characteristics of Grid Connected Wind Turbines, 2nd ed.; IEC61400-21; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2008.
- Electromagnetic Compatibility (EMC)—Part 4-34: Testing and Measurement Techniques—Voltage Dips, Short Interruptions and Voltage Variations Immunity Tests for Equipment with Mains Current More than 16A per Phase; IEC61000; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2009.
- Melicio, R.; Mendes, V.M.F.; Catalao, J.P.S. A pitch control malfunction analysis for wind turbines with permanent magnet synchronous generator and full-power converters: Proportional integral versus fractional-order controllers. Electr. Power Compon. Syst. 2010, 38, 387–406. [Google Scholar] [CrossRef]
- Yin, B.; Oruganti, R.; Panda, S.K.; Bhat, A.K.S. An Output-Power-Control Strategy for a Three-Phase PWM Rectifier under Unbalanced Supply Conditions. IEEE Trans. Ind. Electron. 2008, 55, 2140–2151. [Google Scholar] [CrossRef]
- Song, H.S.; Nam, K. Dual current control scheme for PWM converter under unbalanced input voltage conditions. IEEE Trans. Ind. Electron. 1999, 46, 953–959. [Google Scholar] [CrossRef]
- Hu, J.; He, Y.; Xu, L.; Williams, B.W. Improved control of DFIG systems during network unbalance using PI—R current regulators. IEEE Tran. Ind. Electron. 2009, 56, 439–451. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Luna, A.; Lima, K.; Corcoles, F.; Watanabe, E.; Rodriguez, P.; Teodorescu, R. Control of DFIG-WT under unbalanced grid voltage conditions. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009.
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady state error. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 27 June–1 July 1999.
- Yepes, A.G.; Freijedo, F.D.; Lopez, O.; Doval-Gandoy, J. High-Performance Digital Resonant Controllers Implemented With Two Integrators. IEEE Trans. Power Electron. 2011, 26, 563–576. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; López, O.; Malvar, J.; Fernandez-Comesaña, P. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendes, V.F.; Matos, F.F.; Liu, S.Y.; Cupertino, A.F.; Pereira, H.A.; De Sousa, C.V. Low Voltage Ride-Through Capability Solutions for Permanent Magnet Synchronous Wind Generators. Energies 2016, 9, 59. https://doi.org/10.3390/en9010059
Mendes VF, Matos FF, Liu SY, Cupertino AF, Pereira HA, De Sousa CV. Low Voltage Ride-Through Capability Solutions for Permanent Magnet Synchronous Wind Generators. Energies. 2016; 9(1):59. https://doi.org/10.3390/en9010059
Chicago/Turabian StyleMendes, Victor F., Frederico F. Matos, Silas Y. Liu, Allan F. Cupertino, Heverton A. Pereira, and Clodualdo V. De Sousa. 2016. "Low Voltage Ride-Through Capability Solutions for Permanent Magnet Synchronous Wind Generators" Energies 9, no. 1: 59. https://doi.org/10.3390/en9010059
APA StyleMendes, V. F., Matos, F. F., Liu, S. Y., Cupertino, A. F., Pereira, H. A., & De Sousa, C. V. (2016). Low Voltage Ride-Through Capability Solutions for Permanent Magnet Synchronous Wind Generators. Energies, 9(1), 59. https://doi.org/10.3390/en9010059