Optimal Maintenance Management of Offshore Wind Farms
Abstract
:1. Introduction
- -
- The wind power captured by wind turbines (WTs) is more than onshore.
- -
- The size of offshore wind farms can be larger than onshore.
- -
- The environmental impact for offshore is less than in onshore.
- -
- It is more complex to evaluate the wind characteristics.
- -
- Larger investment costs. The offshore installation cost is 1.44 million €/MW, where the onshore is 0.78 million €/MW [3].
- -
- Operation and maintenance (O & M) tasks are more complex and expensive than onshore. The offshore O & M costs tasks are from 18% to 23% of the total system costs, being 12% for onshore wind farms [4].
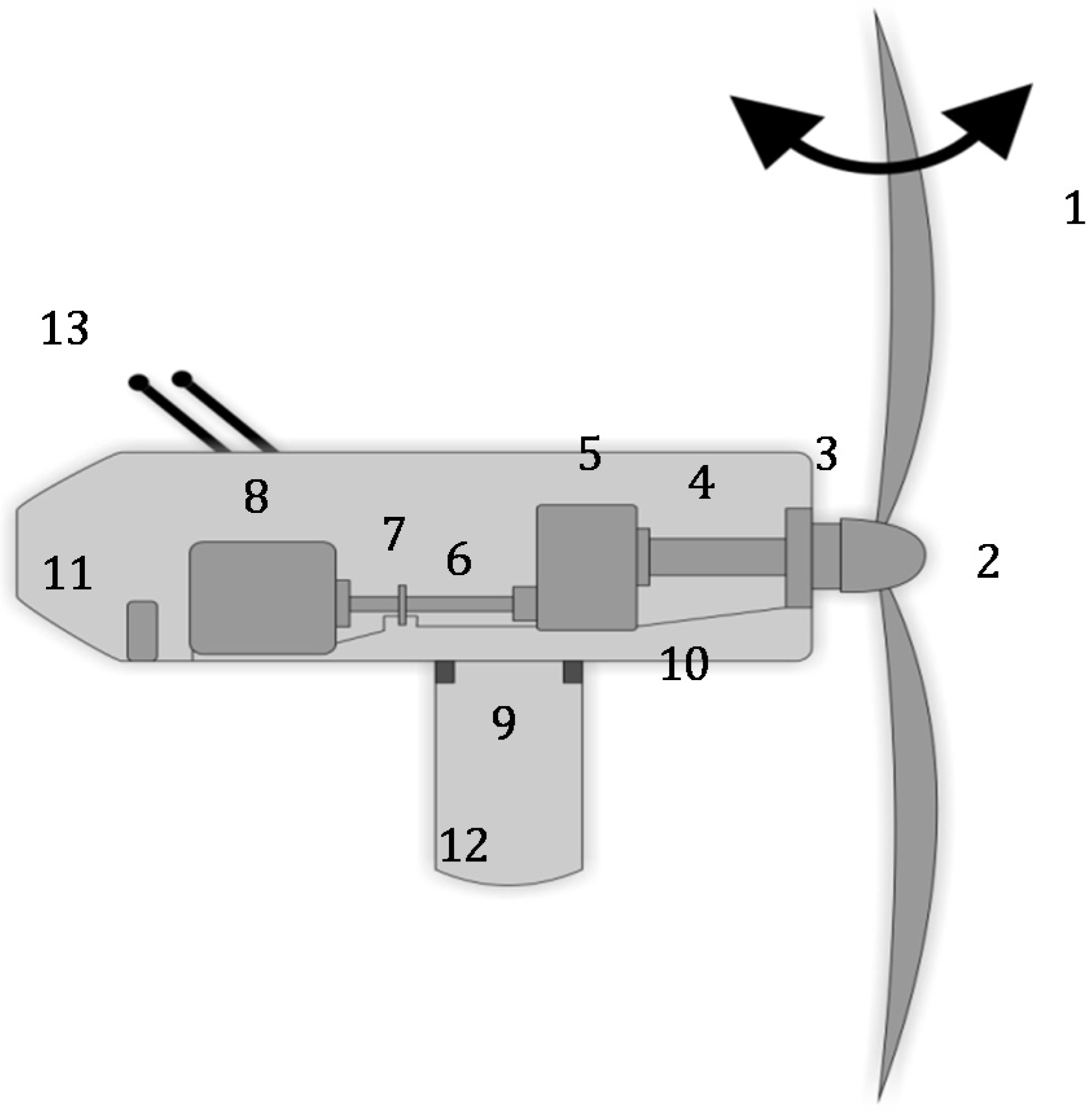
2. CM Applied to WT
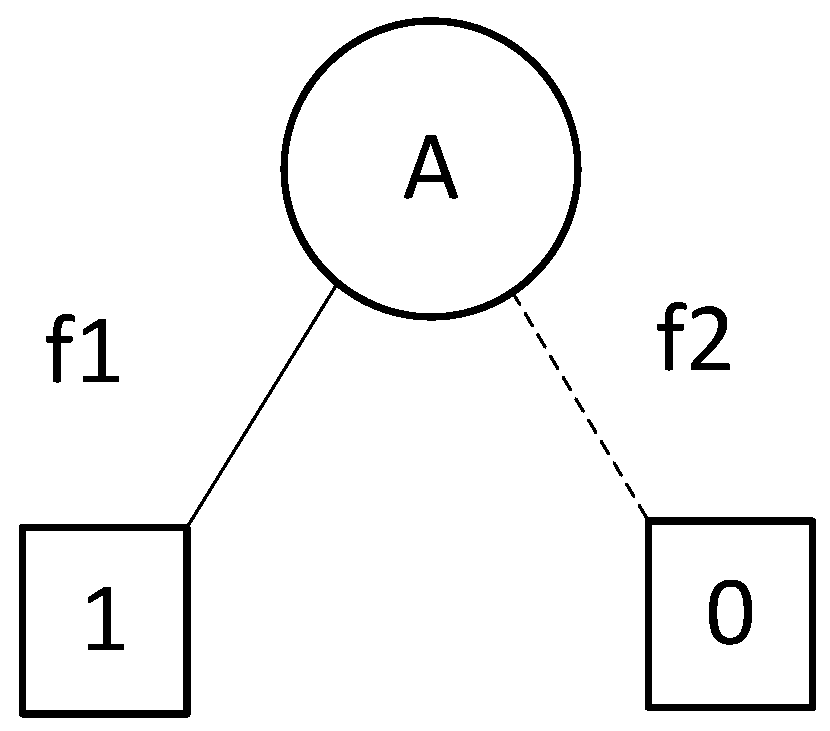
3. FTA and BDD
4. FTA for WTs
| Foundation and Tower Failure | Structural fault [17,38,42,43,44,45] | |
| Yaw system failure [46] | ||
| Critical Rotor Failure | Blade failure | Structural failure [17,34,47,48,49,50,51,52,53] |
| Pitch system failure [54,55] | ||
| Hydraulic system fault [50,56] | ||
| Meteorological unit failure [50,57] | ||
| Rotor system failure | Rotor hub [42,46] | |
| Bearings [45,46,47] | ||
| Power Train Failure | Low speed train failure [17,46,48] | |
| Critical gearbox failure [7,46,53,58,59,60,61,62] | ||
| High speed train failure | Shaft [6,46,58] | |
| Critical brake failure [6,56] | ||
| Electrical Components Failure | Critical generator failure [6,46,58,60,63,64,65] | |
| Power electronics and electric controls failure [17,56,58,60] | ||
- -
- g001 corresponds to a “Foundation and Tower Failure” described in Section 4.1.
- -
- g002 corresponds to a “Critical Rotor Failure” depicted in Section 4.2.
- -
- g003 corresponds to a “Power Train Failure” showed in Section 4.4.
- -
- g004 corresponds to a “Electrical Components Failure” presented in Section 4.3.
4.1. Foundation and Tower
4.2. Blade System
4.3. Generator, Electrical and Electronic Components
4.4. Power Train
5. Maintenance Management Approach
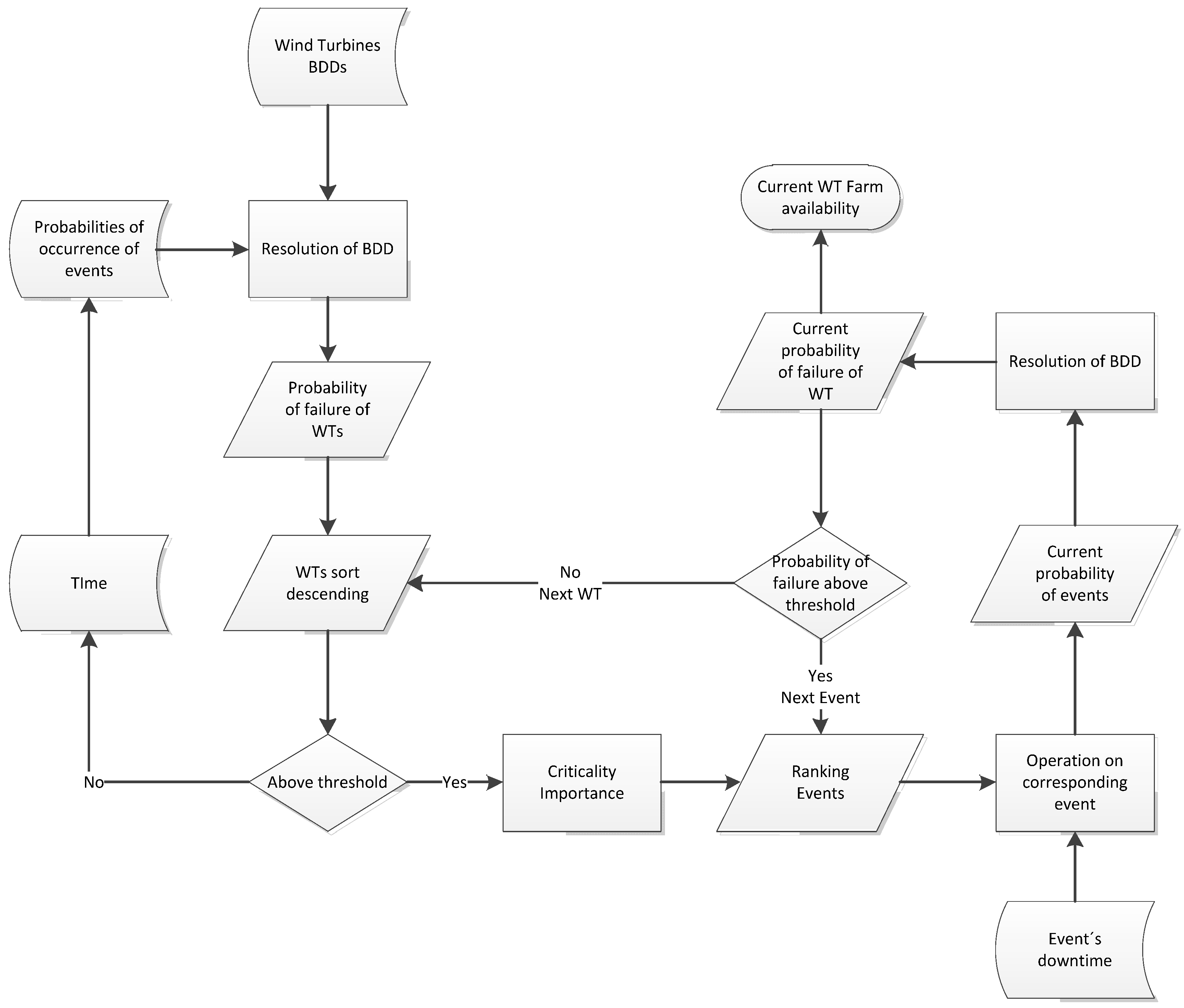
6. Case Study
- Constant probabilityIn this model the probability of the event is constant over the time:
- Exponential increasing probabilityIn this model, the probability function assigned is:where determines the rising velocity of the probability.
- Linear increasing probabilityIn this model, the probability function is:where m determines the rising velocity of the probability.
- Periodic probabilityThis model represents those components that need to be replaced, repaired, and zeroed in a periodical way. In this model, the events have a periodic behavior following the next expression:where is a positive parameter and determines the rising velocity of the probability, and is a parameter that defines the size of the time period.
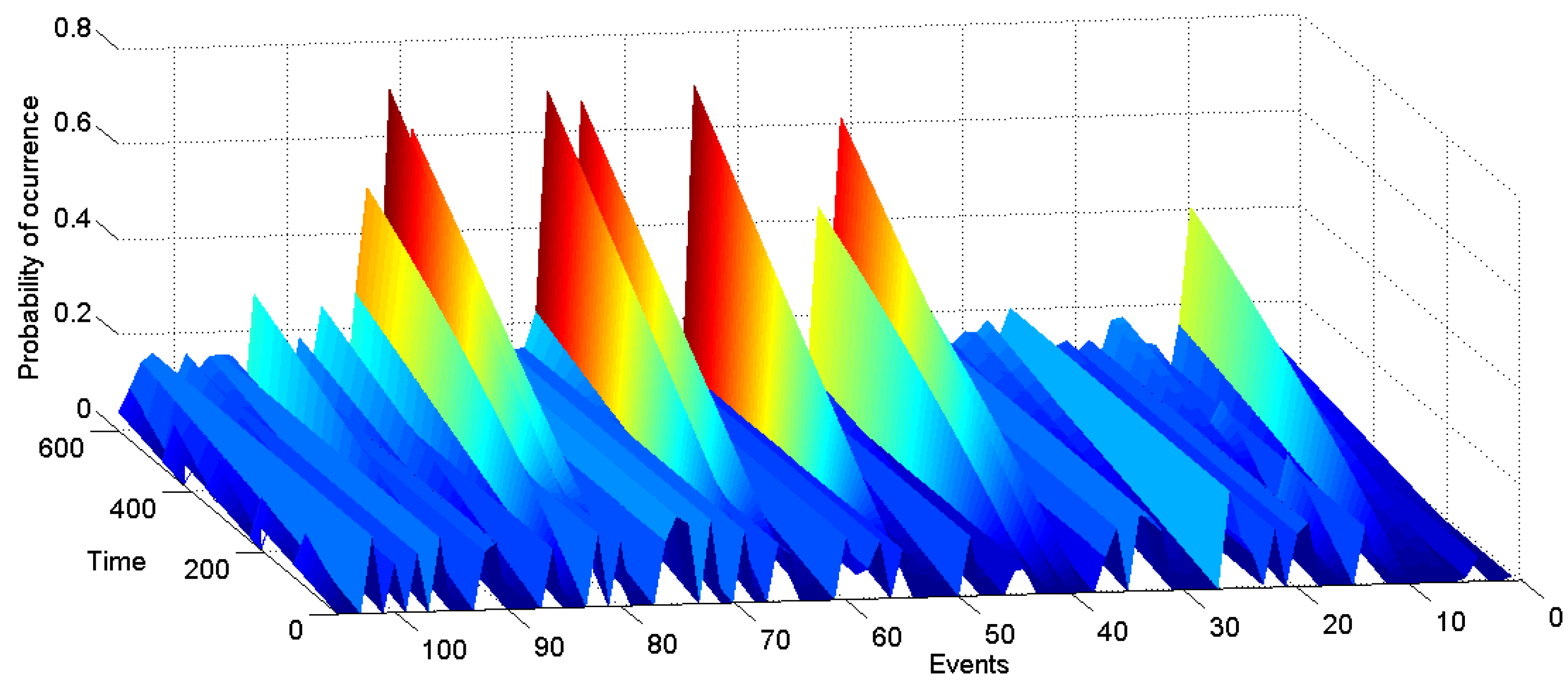
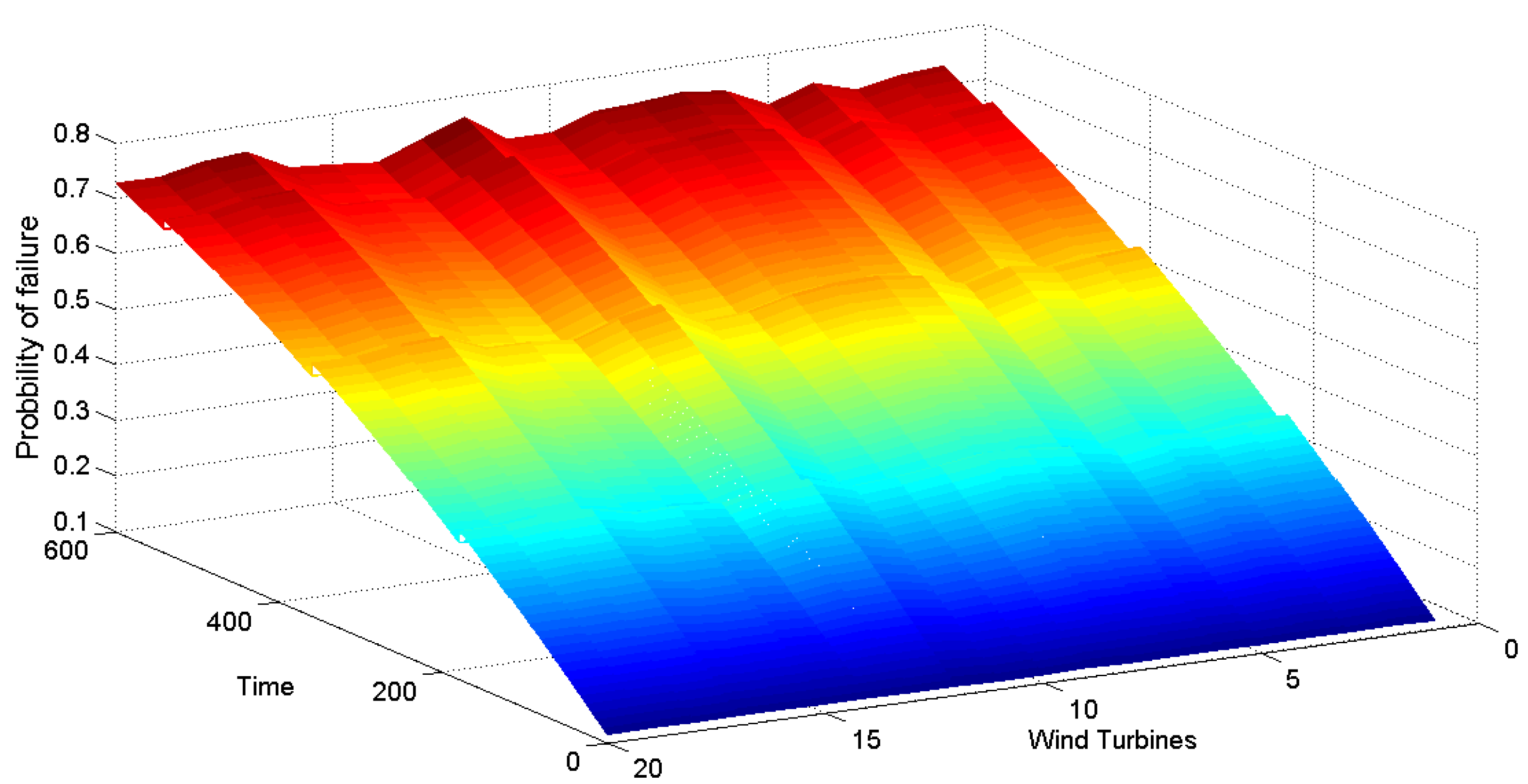
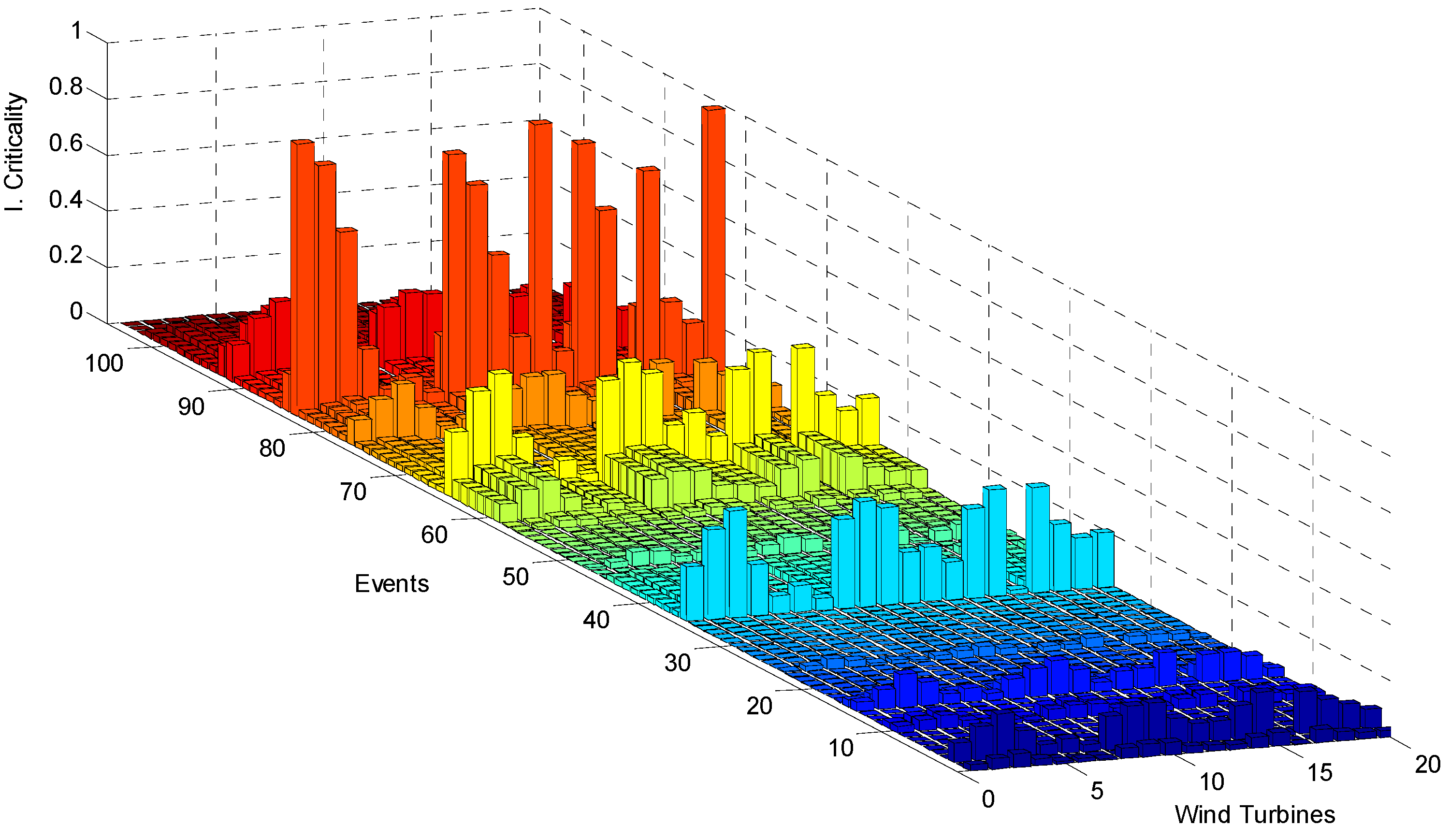
7. Results
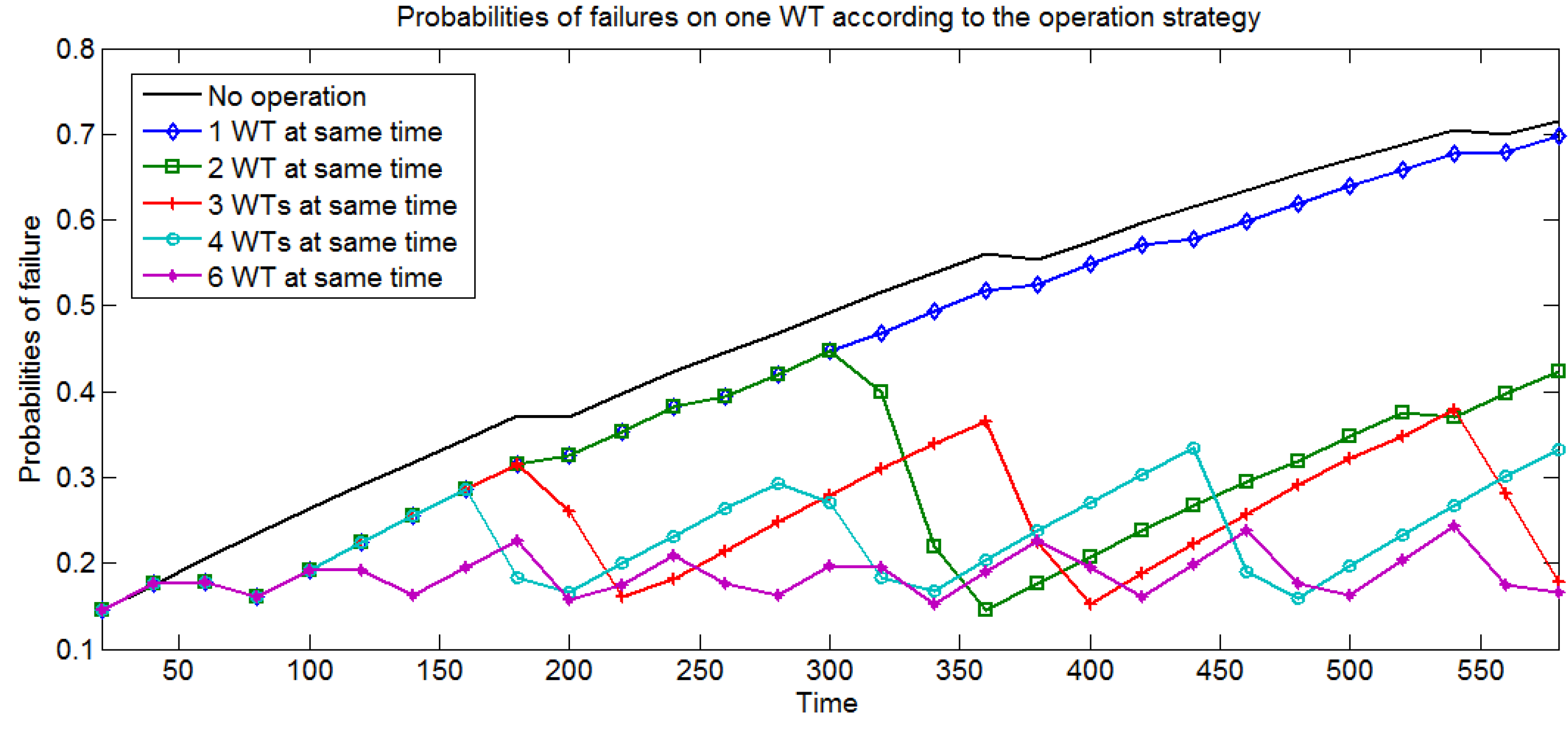
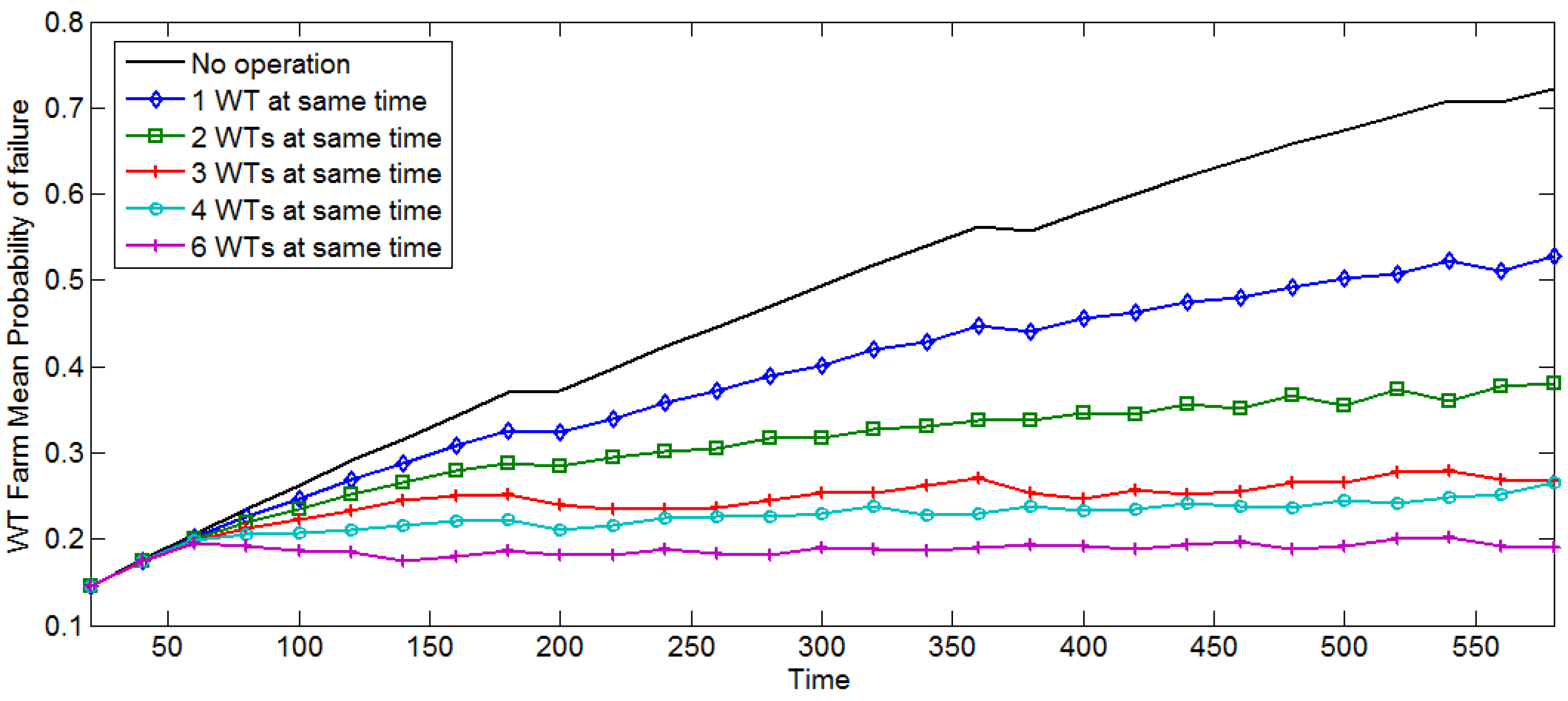
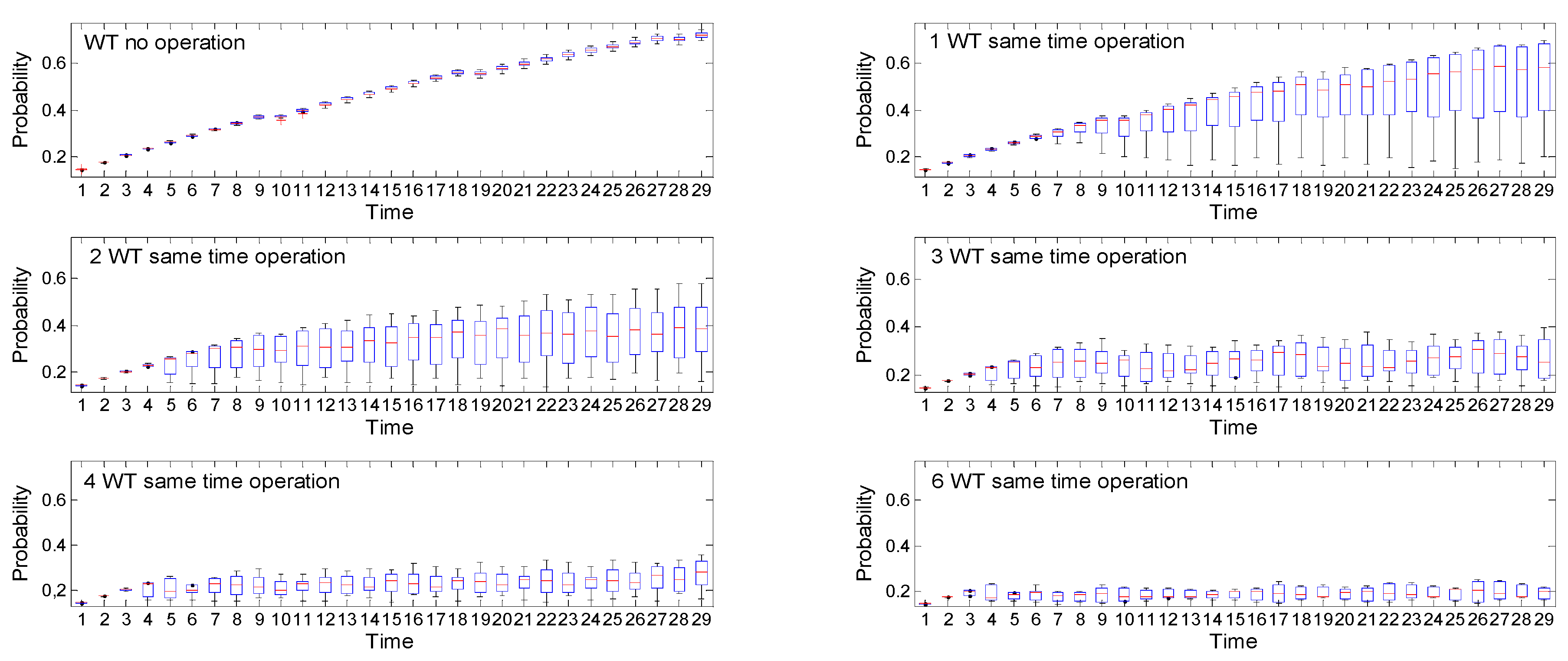
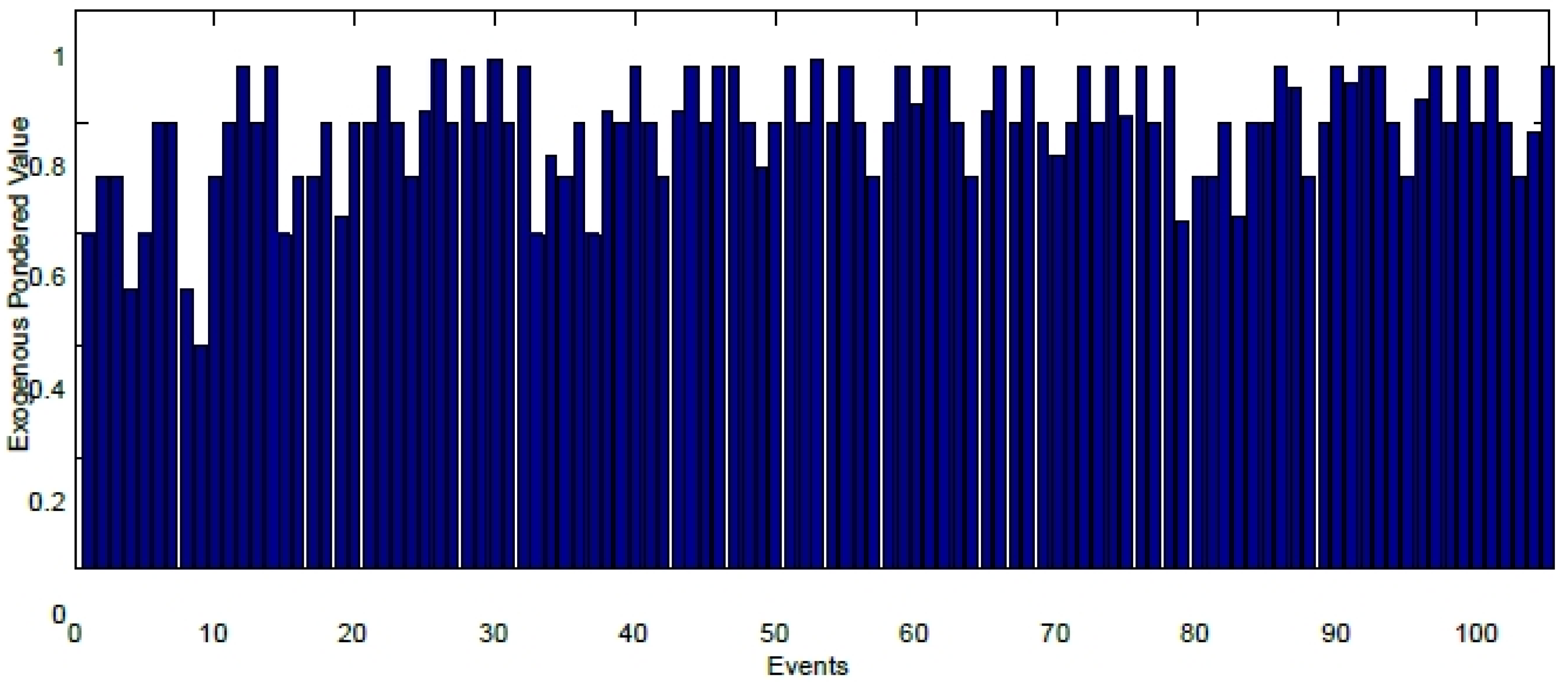
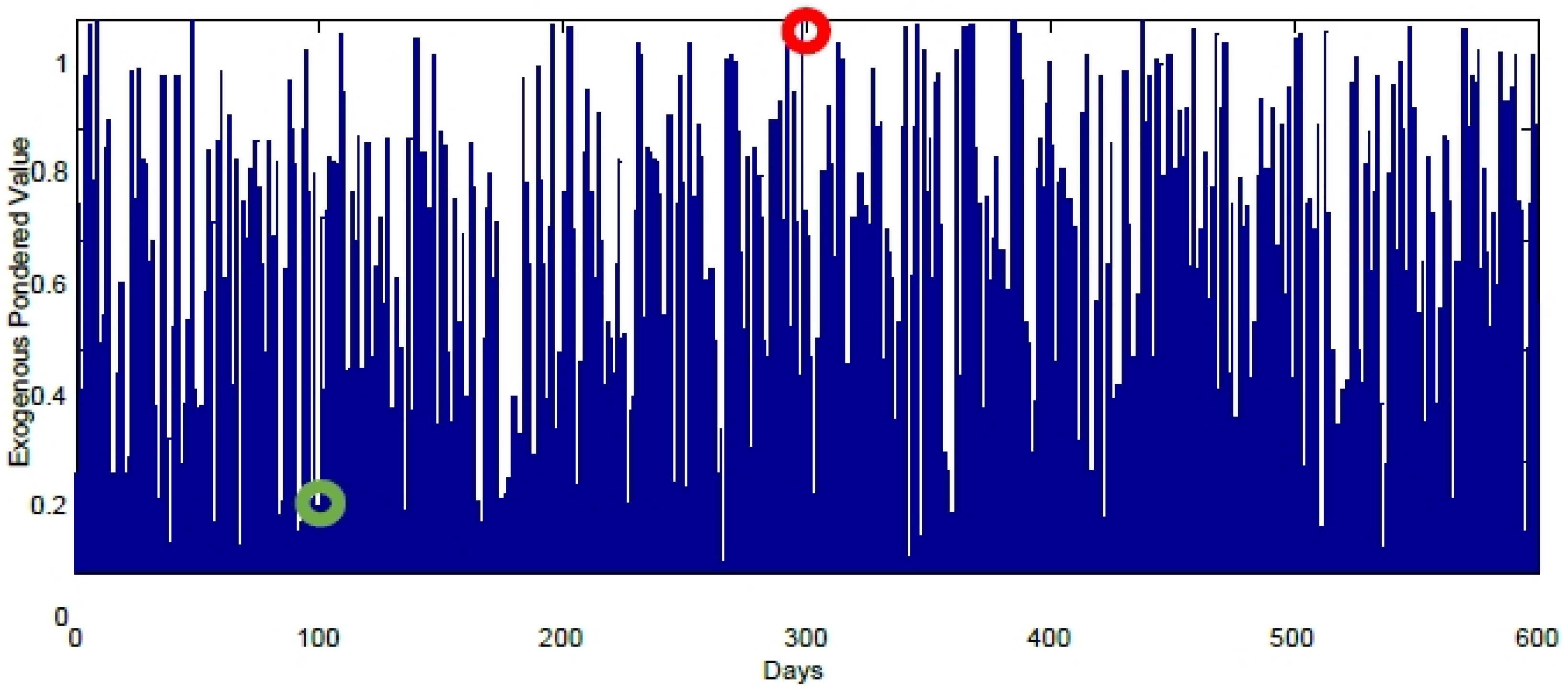

8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix 1. FT for a Wind Turbine
Appendix 2. Events and Probabilistic Models
| Fault Tree 1 Foundation and Tower Failure | Probabilistic Model Assignment | |||
| Intermediate Event | Code | Final Event | Code | |
| Yaw System Failure | g005 | Yaw motor fault | e001 | Constant |
| Critical Structural Failure | g006 | Abnormal Vibration I | e002 | Linear Increasing |
| yaw motor failure | g007 | Abnormal Vibration H | e003 | Linear Increasing |
| Wrong Yaw Angle | g008 | Cracks in concrete base | e004 | Constant |
| Structural Failure (Foundation and tower) | g009 | Welding damage | e005 | Constant |
| No electric power for yaw motor | g010 | Corrosion | e006 | Linear Increasing |
| Metereologhical Unit Failure | g011 | Loosen studs in joining foundation and first section | e007 | Linear Increasing |
| Structural Fault (Foundation and tower) | g012 | Loosen bolts in joining different sections | e008 | Linear Increasing |
| Gaps in the foundation section | e009 | Exponential Increasing | ||
| Vane damage | e010 | Exponential Increasing | ||
| Anemometer damage | e011 | Exponential Increasing | ||
| High wind speed | e012 | Periodic | ||
| No power supply from generator | e013 | Constant | ||
| No power supply from grid | e014 | Constant | ||
| Fault Tree 2 Critical Rotor Failure | Probabilistic Model Assignment | |||
| Intermediate Event | Code | Final Event | Code | |
| Critical blade failure | g013 | High wind speed | e015 | Periodic |
| Blade Failure | g014 | Blade Angle asymmetry | e016 | Exponential Increasing |
| Pitch System Failure | g015 | Abnormal Vibration A | e017 | Exponential Increasing |
| Critical structural Failure (Blades) | g016 | Motor failure | e018 | Exponential Increasing |
| Hydraulic system Failure | g017 | Leakages | e019 | Constant |
| Wrong Blade Angle | g018 | Over pressure | e020 | Constant |
| Hydraulic system Fault | g019 | Corrosion | e021 | Exponential Increasing |
| Metereologhical Unit Failure | g020 | Vane damage | e022 | Constant |
| Structural Failure (Blades) | g021 | Anemometer damage | e023 | Constant |
| Leading and traililling edges | g022 | Abnormal Vibration B | e024 | Constant |
| Shell | g023 | Root Cracks | e025 | Constant |
| Tip | g024 | Cracks | e026 | Constant |
| Rotor System Failure | g025 | Erosion | e027 | Exponential Increasing |
| Rotor System Fault | g026 | Delamination in leading edges of blades | e028 | Exponential Increasing |
| Bearings (Rotor) | g027 | Delamination in trailing edges of blades | e029 | Exponential Increasing |
| Rotor Hub | g028 | Debonding in edges of blades | e030 | Exponential Increasing |
| Wear | g029 | Delamination in shell | e031 | Exponential Increasing |
| Imbalance | g030 | Crack with structural damage | e032 | Constant |
| Crack on the beam-shell joint | e033 | Constant | ||
| Open tip | e034 | Constant | ||
| Lightning strike | e035 | Periodic | ||
| Abnormal Vibration C | e036 | Constant | ||
| Cracks | e037 | Constant | ||
| Corrosion of Pins | e038 | Exponential Increasing | ||
| Abrasive Wear | e039 | Exponential Increasing | ||
| Pitting | e040 | Linear Increasing | ||
| Deformation of face & rolling element | e041 | Linear Increasing | ||
| Lubrication Fault | e042 | Linear Increasing | ||
| Clearance loosening at root | e043 | Exponential Increasing | ||
| Cracks | e044 | Constant | ||
| Surface Roughness | e045 | Constant | ||
| Mass Imbalance | e046 | Exponential Increasing | ||
| Fault in Pitch adjustment | e047 | Exponential Increasing | ||
| Fault Tree 3 Electrical Components Failure | Probabilistic Model Assignment | |||
| Intermediate Event | Code | Final Event | Code | |
| Critical Generator Failure | g031 | Abnormal Vibration G | e048 | Exponential Increasing |
| Power Electronics and Electric Controls Failure | g032 | Cracks | e049 | Constant |
| Mechanical Failure (Generator) | g033 | Imbalance | e050 | Exponential Increasing |
| Electrical Failure (Generator) | g034 | Asymmetry | e051 | Exponential Increasing |
| Bearing Generator Failure | g035 | Air-Gap eccentricities | e052 | Linear Increasing |
| Rotor and Stator Failure | g036 | Broken bars | e053 | Linear Increasing |
| Bearing Generator Fault | g037 | Dynamic eccentricity | e054 | Linear Increasing |
| Rotor and Stator Fault | g038 | Sensor T error | e055 | constant |
| Abnormal Signals A | g039 | T above limit | e056 | Periodic |
| Overwarming generator | g040 | Short Circuit (Gen) | e057 | Constant |
| Electrical Fault (PE) | g041 | Open Circuit (Gen) | e058 | Constant |
| Mechanical Fault (PE) | g042 | Short Circuit | e059 | Constant |
| Open Circuit | e060 | Constant | ||
| Gate drive circuit | e061 | linear increasing | ||
| Corrosion | e062 | Periodic | ||
| Dirt | e063 | Periodic | ||
| Terminals damage | e064 | linear increasing | ||
| Fault Tree 4 Power Train Failure | Probabilistic Model Assignment | |||
| Intermediate Event | Code | Final Event | Code | |
| Low speed train Failure | g043 | Abnormal Vibration D | e065 | Constant |
| Critical Gearbox Failure | g044 | Cracks in main bearing | e066 | Constant |
| High speed train Failure | g045 | Spalling | e067 | Linear Increasing |
| Main Bearing failure | g046 | Corrosion of Pins | e068 | Linear Increasing |
| Low speed shaft failure | g047 | Abrasive Wear | e069 | Constant |
| Main Bearing fault | g048 | Deformation of face & rolling element | e070 | Linear Increasing |
| Wear main bearing | g049 | Pitting | e071 | exponential increasing |
| Low speed shaft fault | g050 | Imbalance | e072 | Constant |
| Wear low shaft | g051 | Cracks in l.s. shaft | e073 | Linear Increasing |
| Gearbox Fault | g052 | Spalling | e074 | Constant |
| Bearings failure(Gearbox) | g053 | Abrasive Wear | e075 | Constant |
| Lubrication fault | g054 | Pitting | e076 | Constant |
| Gear Failure | g055 | Abnormal Vibration F | e077 | Linear Increasing |
| Wear bearing gearbox | g056 | Corrosion of Pins | e078 | Exponential Increasing |
| Gear Fault | g057 | Abrasive Wear | e079 | Linear Increasing |
| Tooth Wear | g058 | Pitting | e080 | Constant |
| Offset | g059 | Deformation of face & rolling element | e081 | Linear Increasing |
| High speed shaft Failure | g060 | Oil Filtration | e082 | Constant |
| Critical Brake Failure | g061 | Particle Contamination | e083 | Exponential Increasing |
| High speed structural damage | g062 | Overwarming gearbox | e084 | Linear Increasing |
| Wear high shaft | g063 | Abnormal Vibration E | e085 | Periodic |
| Brake Fault | g064 | Eccentricity | e086 | Constant |
| Abnormal Signals B | g065 | Pitting | e087 | Linear Increasing |
| Hydraulic brake system Fault | g066 | Cracks in gears | e088 | Exponential Increasing |
| Abnormal Signals C | g067 | Gear tooth deterioration | e089 | Exponential Increasing |
| Overwarming brake | g068 | Poor design | e090 | Periodic |
| Tooth surface defects | e091 | Constant | ||
| Abnormal Vibration J | e092 | Constant | ||
| Cracks in h.s. shaft | e093 | Linear Increasing | ||
| Imbalance | e094 | Periodic | ||
| Overwarming | e095 | Exponential Increasing | ||
| Spalling | e096 | Constant | ||
| Abrasive Wear | e097 | Linear Increasing | ||
| Pitting | e098 | Constant | ||
| Cracks in brake disk | e099 | Exponential Increasing | ||
| Motor brake fault | e100 | Constant | ||
| Oil Leakage | e101 | Linear Increasing | ||
| Over pressure | e102 | Constant | ||
| Abnormal speed | e103 | Linear Increasing | ||
| T sensor error | e104 | Periodic | ||
| T above limit | e105 | Periodic | ||
References
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Esteban, M.D.; Diez, J.J.; López, J.S.; Negro, V. Why offshore wind energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Guidelines for the Certification of Condition Monitoring Systems for Wind Turbines; Germanisher LLoyd: Hamburg, Germany, 2007.
- Tavner, P. Offshore Wind Turbines Reliability, Availability and Maintenance; The Institution of Engineering and Technology: London, UK, 2012. [Google Scholar]
- Novaes Pires, G.; Alencar, E.; Kraj, A. Remote Conditioning Monitoring System for a Hybrid Wind Diesel System-Application at Fernando de Naronha Island. Brasil. Available online: http://www.globalislands.net/userfiles/_brazil_FdNpdf2.pdf (accessed on 10 July 2015).
- Tsai, C.-S.; Hsieh, C.-T.; Huang, S.-J. Enhancement of damage-detection of wind turbine blades via CWT-based approaches. IEEE Trans. Energy Convers. 2006, 21, 776–781. [Google Scholar] [CrossRef]
- Guo, P.; Bai, N. Wind turbine gearbox condition monitoring with AAKR and moving window statistic methods. Energies 2011, 4, 2077–2093. [Google Scholar] [CrossRef]
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electronics 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Jiang, W.; Fan, Q.; Gong, J. Optimization of welding joint between tower and bottom flange based on residual stress considerations in a wind turbine. Energy 2010, 35, 461–467. [Google Scholar] [CrossRef]
- Pérez, J.M.P.; Márquez, F.P.G.; Tobias, A.; Papaelias, M. Wind turbine reliability analysis. Renew. Sustain. Energy Rev. 2013, 23, 463–472. [Google Scholar] [CrossRef]
- Soua, S.; van Lieshout, P.; Perera, A.; Gan, T.-H.; Bridge, B. Determination of the combined vibrational and acoustic emission signature of a wind turbine gearbox and generator shaft in service as a pre-requisite for effective condition monitoring. Renew. Energy 2013, 51, 175–181. [Google Scholar] [CrossRef]
- Chacon, J.L.F.; Andicoberry, E.A.; Kappatos, V.; Asfis, G.; Gan, T.-H.; Balachandran, W. Shaft angular misalignment detection using acoustic emission. Appl. Acoust. 2014, 85, 12–22. [Google Scholar] [CrossRef]
- Park, S.; Inman, D.J.; Yun, C.-B. An outlier analysis of MFC-based impedance sensing data for wireless structural health monitoring of railroad tracks. Eng. Struct. 2008, 30, 2792–2799. [Google Scholar] [CrossRef]
- De la Hermosa González, R.R.; Márquez, F.P.G.; Dimlaye, V.; Ruiz-Hernández, D. Pattern recognition by wavelet transforms using macro fibre composites transducers. Mech. Syst. Signal Proc. 2014, 48, 339–350. [Google Scholar] [CrossRef]
- Nie, M.; Wang, L. Review of condition monitoring and fault diagnosis technologies for wind turbine gearbox. Procedia CIRP 2013, 11, 287–290. [Google Scholar] [CrossRef]
- Zeng, Z.; Tao, N.; Feng, L.; Li, Y.; Ma, Y.; Zhang, C. Breakpoint detection of heating wire in wind blade moulds using infrared thermography. Infrared Phys. Technol. 2014, 64, 73–78. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Pinar Pérez, J.M.; Pliego Marugán, A.; Papaelias, M. Identification of critical components of wind turbines using FTA over the time. Renew. Energy 2016, 87, 869–883. [Google Scholar] [CrossRef]
- Lambert, H.E. Measures of Importance of Events and Cut Sets. Reliability and Fault Tree Analysis; SIAM: Philadelphia, PA, USA, 1975; pp. 77–100. [Google Scholar]
- Pliego Marugán, A.; García, F.P. A novel approach to diagnostic and prognostic evaluations applied to railways: A real case study. J. Rail Rapid Transit 2015. [Google Scholar] [CrossRef]
- Sinnamon, R.M.; Andrews, J.D. Fault tree analysis and binary decision diagrams. In Proceedings of the Reliability and Maintainability Symposium, Las Vegas, NV, USA, 22–25 January 1996; pp. 215–222.
- Jinglun, Z.; Quan, S. Reliability analysis based on binary decision diagrams. J. Qual. Maint. Eng. 1998, 4, 150–161. [Google Scholar] [CrossRef]
- Bryant, R.E. Graph-based algorithms for Boolean function manipulation. IEEE Trans. Comput. 1986, 100, 677–691. [Google Scholar] [CrossRef]
- Remenyte, R.; Andrews, J.D. Qualitative analysis of complex modularized fault trees using binary decision diagrams. Proc. Inst. Mech. Eng. O 2006, 220, 45–53. [Google Scholar] [CrossRef]
- Prescott, D.R.; Remenyte-Prescott, R.; Reed, S.; Andrews, J.; Downes, C. A reliability analysis method using binary decision diagrams in phased mission planning. Proc. Inst. Mech. Eng. Part O 2009, 223, 133–143. [Google Scholar] [CrossRef]
- Moret, B.M. Decision trees and diagrams. ACM Comput. Surv. 1982, 14, 593–623. [Google Scholar] [CrossRef]
- Lee, C.-Y. Representation of switching circuits by binary-decision programs. Bell Syst. Technol. J. 1959, 38, 985–999. [Google Scholar] [CrossRef]
- Akers, S.B. Binary decision diagrams. IEEE Trans. Comput. 1978, 100, 509–516. [Google Scholar] [CrossRef]
- Pliego Marugán, A.; García Márquez, F.P.; Lorente, J. Decision making process via binary decision diagram. Int. J. Manag. Sci. Eng. Manag. 2015, 10, 3–8. [Google Scholar] [CrossRef]
- Fujita, M.; Fujisawa, H.; Kawato, N. Evaluation and improvements of Boolean comparison method based on binary decision diagrams. In Proceedings of the Computer-Aided Design IEEE International Conference (ICCAD-88), Santa Clara, CA, USA, 7–10 November 1988; pp. 2–5.
- Márquez, F.P.G.; Mangurán, A.P.; Zaman, N. For information systems design. Softw. Dev. Technol. Constr. Inf. Syst. Des. 2013, 1, 308–318. [Google Scholar]
- Brace, K.S.; Rudell, R.L.; Bryant, R.E. Efficient implementation of a BDD package. In Proceedings of the 27th ACM/IEEE Design Automation Conference, Orlando, FL, USA, 24–28 June 1991; pp. 40–45.
- Liu, Q.; Homma, T. A new computational method of a moment-independent uncertainty importance measure. Reliab. Eng. Syst. Saf. 2009, 94, 1205–1211. [Google Scholar] [CrossRef]
- Cheok, M.C.; Parry, G.W.; Sherry, R.R. Use of importance measures in risk-informed regulatory applications. Reliab. Eng. Syst. Saf. 1998, 60, 213–226. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. On the Importance of Different Components in a Multicomponent System; Washington University Seattle Lab of Statistical Research: Washington, DC, USA, 1968. [Google Scholar]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P. Failure modes and effects analysis (FMEA) for wind turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- RELIAWIND Project. European Union’s Seventh Framework Programme for RTD (FP7). Available online: http://www.reliawind.eu/ (accessed on 22 January 2014).
- Lotsberg, I. Structural mechanics for design of grouted connections in monopile wind turbine structures. Mar. Struct. 2013, 32, 113–135. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tu, W.-T. Failure analysis and risk management of a collapsed large wind turbine tower. Eng. Fail. Anal. 2011, 18, 295–313. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Turbine—Part 1: Design Requirements, IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Development and Demonstration of a Novel Integrated Condition Monitoring System for Wind Turbines, NIMO Project. (NIMO, Ref.:FP7-ENERGY-2008-TREN-1: 239462). Available online: http://www.nimoproject.eu (accessed on 30 January 2012).
- Demonstration of Methods and Tools for the Optimisation of Operational Reliability of Large-Scale Industrial Wind Turbines, OPTIMUS Project. (OPTIMUS, Ref.: FP-7-Energy-2012-TREN-1: 322430). Available online: http://www.optimusproject.eu (accessed on 25 February 2014).
- Ciang, C.C.; Lee, J.-R.; Bang, H.-J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19. [Google Scholar] [CrossRef]
- Stol, K.A. Disturbance tracking control and blade load mitigation for variable-speed wind turbines. J. Sol. Energy Eng. 2003, 125, 396–401. [Google Scholar] [CrossRef]
- Caithness Windfarm Information Forum. Available online: http://www.caithnesswindfarms.co.uk/ (accessed on 30 January 2012).
- Cotton, I.; Jenkins, N.; Pandiaraj, K. Lightning protection for wind turbine blades and bearings. Wind Energy 2001, 4, 23–37. [Google Scholar] [CrossRef]
- Hameed, Z.; Hong, Y.; Cho, Y.; Ahn, S.; Song, C. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Padgett, W. A multiplicative damage model for strength of fibrous composite materials. IEEE Trans. Reliab. 1998, 47, 46–52. [Google Scholar] [CrossRef]
- Jørgensen, E.R.; Borum, K.K.; McGugan, M.; Thomsen, C.; Jensen, F.M.; Debel, C.; Sørensen, B.F. Full Scale Testing of Wind Turbine Blade to Failure-Flapwise Loading; RISØ National Laboratory: Copenhagen, Denmark, 2004. [Google Scholar]
- Jensen, F.M.; Falzon, B.; Ankersen, J.; Stang, H. Structural testing and numerical simulation of a 34m composite wind turbine blade. Compos. Struct. 2006, 76, 52–61. [Google Scholar] [CrossRef]
- Borum, K.K.; McGugan, M.; Brondsted, P. Condition monitoring of wind turbine blades. In Proceedings of the 27th Riso International Symposium on Materials Science: Polymer Composite Materials for Wind Power Turbines, Denmark, 4–7 September 2006; pp. 139–145.
- Van Leeuwen, H.; van Delft, D.; Heijdra, J.; Braam, H.; Jo̸rgensen, E.; Lekou, D.; Vionis, P. Comparing Fatigue Strength from Full Scale Blade Tests with Coupon-Based Predictions; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 1–9. [Google Scholar]
- Griffin, D.A.; Zuteck, M.D. Scaling of composite wind turbine blades for rotors of 80 to 120 meter diameter. J. Sol. Energy Eng. 2001, 123, 310–318. [Google Scholar] [CrossRef]
- Herbert, G.J.; Iniyan, S.; Sreevalsan, E.; Rajapandian, S. A review of wind energy technologies. Renew. Sustain. Energy Rev. 2007, 11, 1117–1145. [Google Scholar] [CrossRef]
- Gray, C.S.; Watson, S.J. Physics of failure approach to wind turbine condition based maintenance. Wind Energy 2010, 13, 395. [Google Scholar] [CrossRef]
- Maughan, J.R. Technology and reliability improvements in GE’s 1.5 MW WT fleet. In Proceedings of the 2nd WT Reliability Workshop, Albuquerque, NM, USA, 17–18 September 2007.
- Liu, W.; Tang, B.; Jiang, Y. Status and problems of wind turbine structural health monitoring techniques in china. Renew. Energy 2010, 35, 1414–1418. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Wu, X.; Yang, Z. A review of recent advances in wind turbine condition monitoring and fault diagnosis. In Proceedings of the Power Electronics and Machines in Wind Applications (PEMWA), Lincoln, NM, USA, 24–26 June 2009; pp. 1–7.
- Ribrant, J. Reliability Performance and Maintenance—A Survey of Failures in Wind Power Systems. Ph.D. Thesis, KTH School of Electrical Engineering, Stockholm, Sweden, 2006. [Google Scholar]
- Fischer, K.; Besnard, F.; Bertling, L. A limited-scope reliability-centred maintenance analysis of wind turbines. In Proceedings of the European Wind Energy Conference and Exhibition EWEA 2011, Brussels, Belgium, 14–17 March 2011; pp. 89–93.
- Feng, Y.; Qiu, Y.; Crabtree, C.J.; Long, H.; Tavner, P.J. Use of SCADA and CMS signals for failure detection and diagnosis of a wind turbine gearbox. In Proceedings of the European Wind Energy Conference and Exhibition 2011, Sheffield, UK, 2011; pp. 17–19.
- Entezami, M.; Hillmansen, S.; Weston, P.; Papaelias, M. Fault detection and diagnosis within a WT mechanical braking system. In Proceedings of the International Conference on Condition Monitoring and Machinery Failure Prevention Technologies (CM 2012 and MFPT 2011), Cardiff, UK, 20–22 June 2011.
- Popa, L.M.; Jensen, B.-B.; Ritchie, E.; Boldea, I. Condition monitoring of wind generators. In Proceedings of the Industry Applications Conference (38th IAS Annual Meeting), Salt Lake City, UT, USA, 12–16 October 2003; pp. 1839–1846.
- Douglas, H.; Pillay, P.; Ziarani, A. Broken rotor bar detection in induction machines with transient operating speeds. IEEE Trans. Energy Convers. 2005, 20, 135–141. [Google Scholar] [CrossRef]
- Hansen, A.D.; Michalke, G. Fault ride-through capability of DFIG wind turbines. Renew. Energy 2007, 32, 1594–1610. [Google Scholar] [CrossRef]
- Bazeos, N.; Hatzigeorgiou, G.; Hondros, I.; Karamaneas, H.; Karabalis, D.; Beskos, D. Static, seismic and stability analyses of a prototype wind turbine steel tower. Eng. Struct. 2002, 24, 1015–1025. [Google Scholar] [CrossRef]
- Scottishpower SP Transmission Ltd. Black Law Wind Farm Extension Grid Connection Environmental Statement. Available online: http://www.spenergynetworks.co.uk/userfiles/file/Black_Law_Environmental_Statement_Windfarm_Extension_Grid_Connection.pdf (accessed on 20 July 2015).
- Van Bussel, G.; Zaaijer, M. Estimation of Turbine Reliability Figures within the DOWEC Project; DOWEC Report Nr. 10048; The Netherlands; Issue 4, October 2003. [Google Scholar]
- García, F.P.; Pedregal, D.J.; Roberts, C. Time series methods applied to failure prediction and detection. Reliab. Eng. Syst. Saf. 2010, 95, 698–703. [Google Scholar] [CrossRef]
- Márquez, F.P.; Chacón Muñoz, J.M.; Tobias, A.M. B-spline approach for failure detection and diagnosis on railway point mechanisms case study. Qual. Eng. 2015, 27, 177–185. [Google Scholar] [CrossRef]
- Tavner, P.; Qiu, Y.; Korogiannos, A.; Feng, Y. The Correlation between Wind Turbine Turbulence and Pitch Failure. In Proceedings of European Wind Energy Conference & Exhibition, Brussels, Belgium, 14–17 March 2011.
- Wu, A.P.; Chapman, P.L. Simple expressions for optimal current waveforms for permanent-magnet synchronous machine drives. IEEE Trans. Energy Conver. 2005, 20, 151–157. [Google Scholar] [CrossRef]
- Spinato, F.; Tavner, P.J.; van Bussel, G.J.W.; Koutoulakos, E. IET Reliability of WT subassemblies. Renew. Power Gener. 2009, 3, 387–401. [Google Scholar] [CrossRef]
- De la Hermosa González, R.R.; Márquez, F.P.G.; Dimlaye, V. Maintenance management of wind turbines structures via mfcs and wavelet transforms. Renew. Sustain. Energy Rev. 2015, 48, 472–482. [Google Scholar] [CrossRef]
- Marquez, F.P.G. An approach to remote condition monitoring systems management. In Proceedings of the Institution of Engineering and Technology International Conference on Railway Condition Monitoring, Birmingham, UK, 29–30 November 2006; pp. 156–160.
- Márquez, F.P.G.; Pedregal, D.J.; Roberts, C. New methods for the condition monitoring of level crossings. Int. J. Syst. Sci. 2015, 46, 878–884. [Google Scholar] [CrossRef]
- Vasquez, T. Weather Forecasting Handbook; Weather Graphics Technologies: Garland, TX, USA, 2002; ISBN 0970684029. [Google Scholar]
- Sørensen, J.D. Framework for risk-based planning of operation and maintenance for offshore wind turbines. Wind Energy 2009, 12, 493–506. [Google Scholar] [CrossRef]
- Rothkopf, M.H.; McCarron, J.K.; Fromovitz, S. A weather model for simulating offshore construction alternatives. Manag. Sci. 1974, 20, 1345–1349. [Google Scholar] [CrossRef]
- Yasseri, S.; Bahai, H.; Bazargan, H.; Aminzadeh, A. Prediction of safe sea-state using finite element method and artificial neural networks. Ocean Eng. 2010, 37, 200–207. [Google Scholar] [CrossRef]
- Härdle, W.; Horowitz, J.; Kreiss, J.P. Bootstrap methods for time series. Int. Stat. Rev. 2003, 71, 435–459. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pliego Marugán, A.; García Márquez, F.P.; Pinar Pérez, J.M. Optimal Maintenance Management of Offshore Wind Farms. Energies 2016, 9, 46. https://doi.org/10.3390/en9010046
Pliego Marugán A, García Márquez FP, Pinar Pérez JM. Optimal Maintenance Management of Offshore Wind Farms. Energies. 2016; 9(1):46. https://doi.org/10.3390/en9010046
Chicago/Turabian StylePliego Marugán, Alberto, Fausto Pedro García Márquez, and Jesús María Pinar Pérez. 2016. "Optimal Maintenance Management of Offshore Wind Farms" Energies 9, no. 1: 46. https://doi.org/10.3390/en9010046
APA StylePliego Marugán, A., García Márquez, F. P., & Pinar Pérez, J. M. (2016). Optimal Maintenance Management of Offshore Wind Farms. Energies, 9(1), 46. https://doi.org/10.3390/en9010046








