Wind Turbine Fault Detection through Principal Component Analysis and Statistical Hypothesis Testing
Abstract
:1. Introduction
2. Wind Turbine Benchmark Model
2.1. Reference Wind Turbine
| Reference Wind Turbine | Magnitude |
|---|---|
| Rated power | 5 MW |
| Number of blades | 3 |
| Rotor/Hub diameter | 126 m, 3 m |
| Hub Height | 90 m |
| Cut-In, Rated, Cut-Out Wind Speed | 3 m/s, m/s, 25 m/s |
| Rated generator speed () | rpm |
| Gearbox ratio | 97 |

2.2. Generator-Converter Model
2.3. Pitch Actuator Model
2.4. Fault Scenarios
| Number | Fault | Type |
|---|---|---|
| F1 | Pitch actuator | Change in dynamics: air content in oil |
| F2 | Pitch actuator | Change in dynamics: pump wear |
| F3 | Pitch actuator | Change in dynamics: hydraulic leakage |
| F4 | Torque actuator | Offset |
| F5 | Generator speed sensor | Scaling |
| F6 | Pitch angle sensor | Stuck |
| F7 | Pitch angle sensor | Scaling |
2.4.1. Actuator Faults
| Faults | (rad/s) | ζ |
|---|---|---|
| Fault Free(FF) | 11.11 | 0.6 |
| High air content in oil (F1) | 5.73 | 0.45 |
| Pump wear (F2) | 7.27 | 0.75 |
| Hydraulic leakage (F3) | 3.42 | 0.9 |
2.4.2. Sensor Faults
| Number | Sensor Type | Symbol | Units |
|---|---|---|---|
| 1 | Generated electrical power | kW | |
| 2 | Rotor speed | rad/s | |
| 3 | Generator speed | rad/s | |
| 4 | Generator torque | Nm | |
| 5 | first pitch angle | deg | |
| 6 | second pitch angle | deg | |
| 7 | third pitch angle | deg | |
| 8 | fore-aft acceleration at tower bottom | m/s | |
| 9 | side-to-side acceleration at tower bottom | m/s | |
| 10 | fore-aft acceleration at mid-tower | m/s | |
| 11 | side-to-side acceleration at mid-tower | m/s | |
| 12 | fore-aft acceleration at tower top | m/s | |
| 13 | side-to-side acceleration at tower top | m/s |
3. Fault Detection Strategy
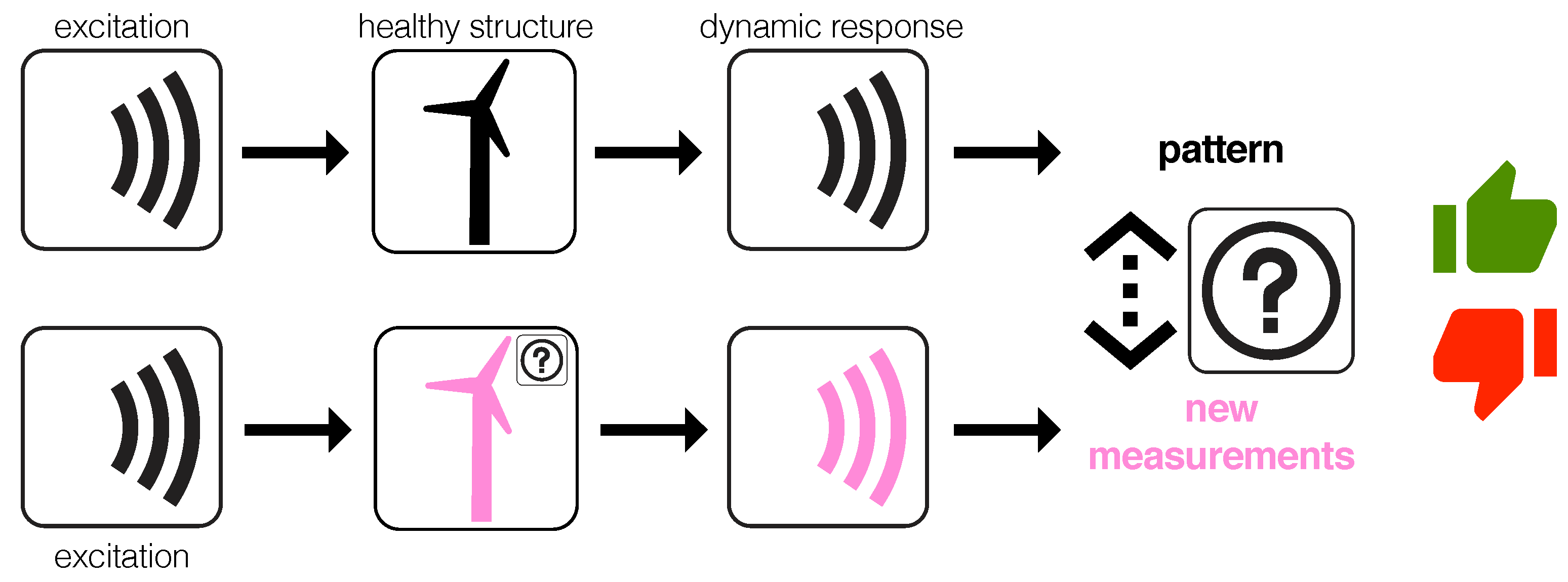
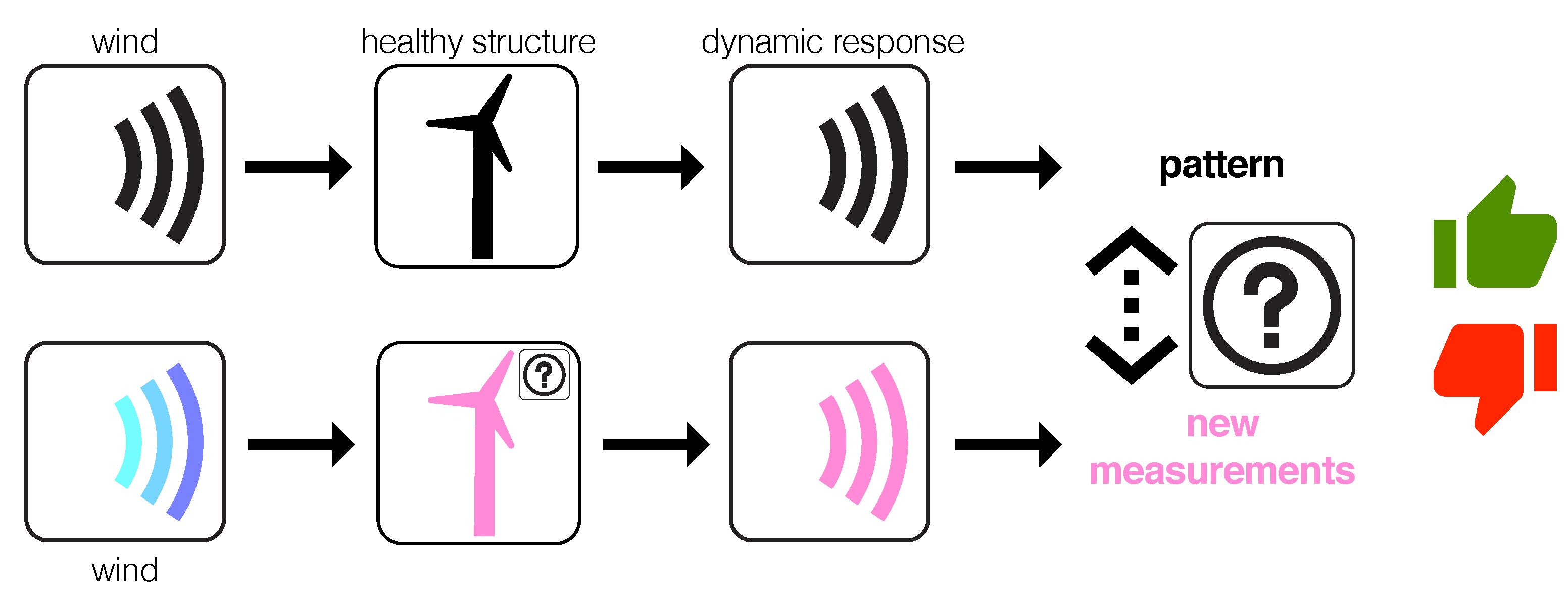
3.1. Data Driven Baseline Modeling Based on PCA
Group Scaling
3.2. Fault Detection Based on Hypothesis Testing
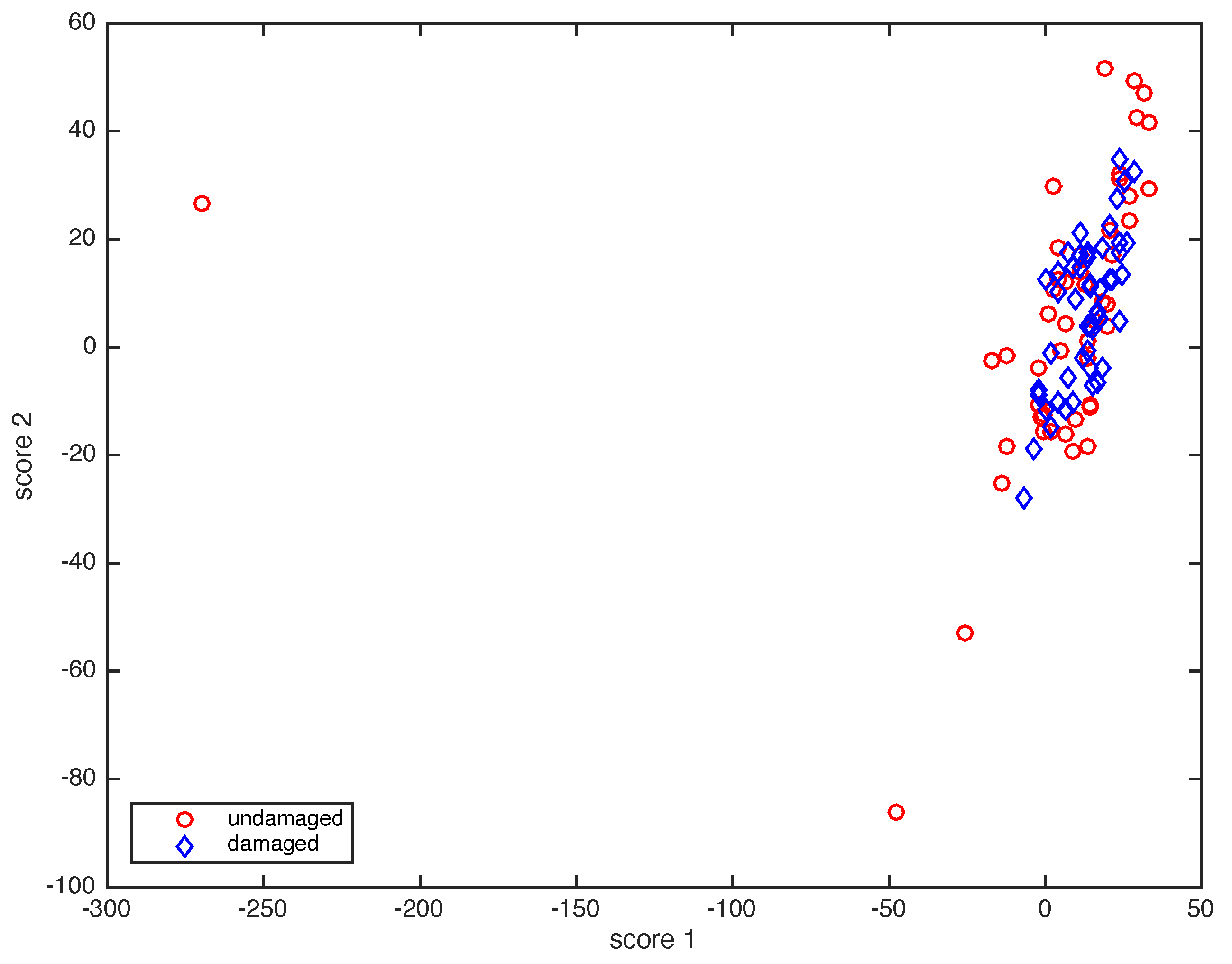
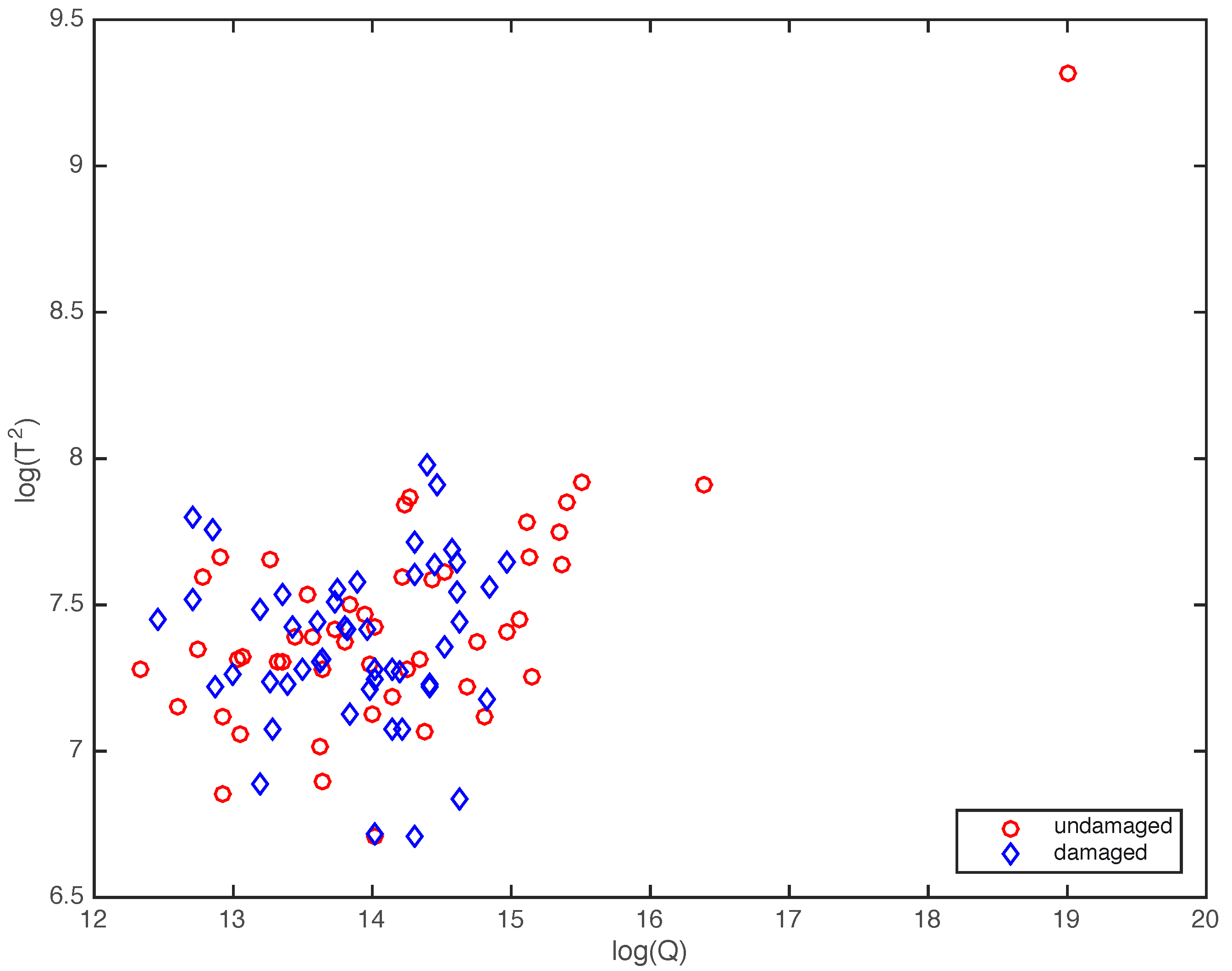
3.2.1. The Random Nature of the Scores
3.2.2. Test for the Equality of Means
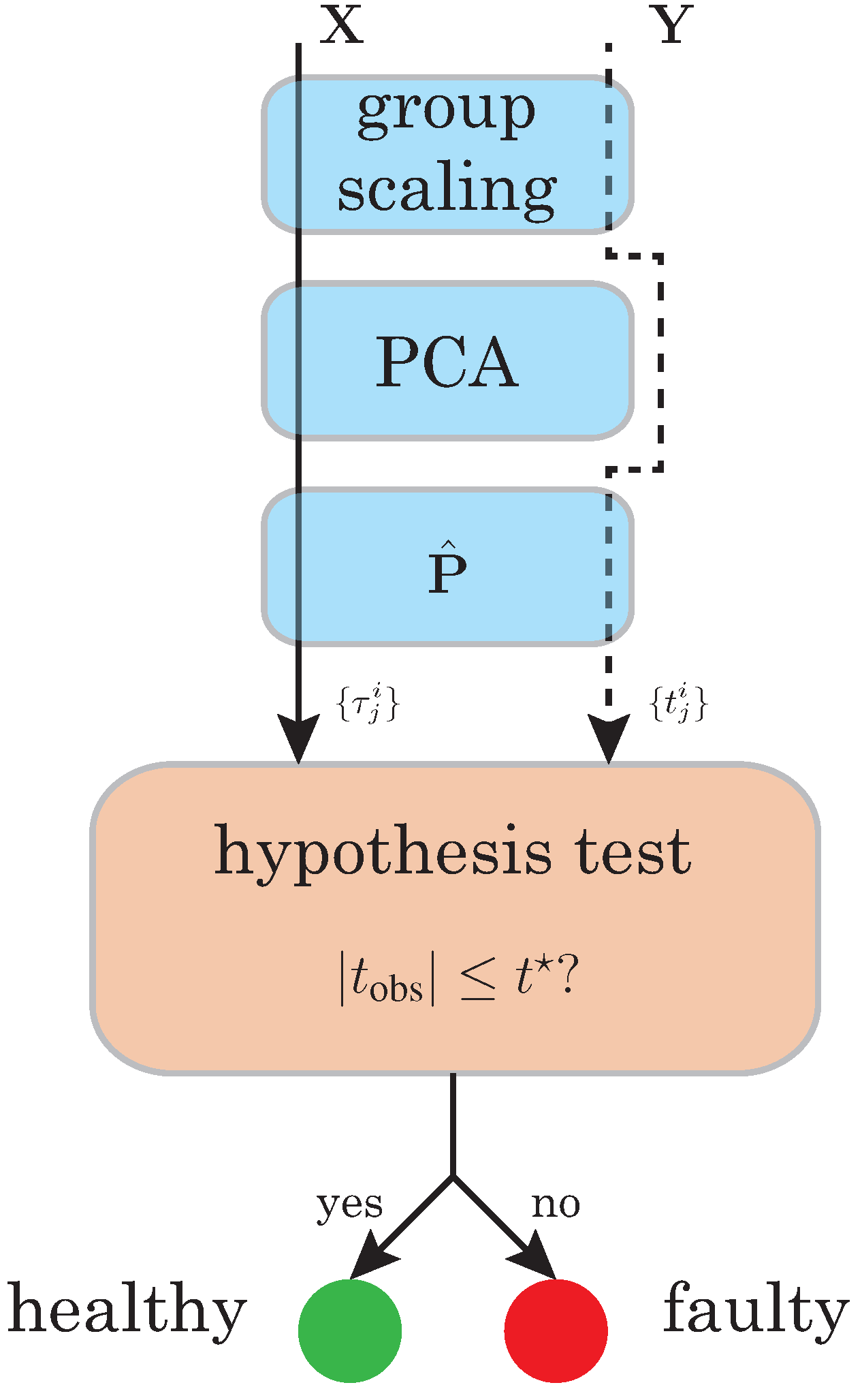
4. Simulation Results
4.1. Type I and Type II errors
- 16 samples of a healthy wind turbine; and
- 8 samples of a faulty wind turbine with respect to each of the eight different fault scenarios described in Table 2.
| Undamaged Sample () | Damaged Sample () | |
|---|---|---|
| Fail to reject | Correct decision | Type II error (missing fault) |
| Reject | Type I error (false alarm) | Correct decision |
| score 1 | score 2 | score 3 | score 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fail to reject | 16 | 0 | 12 | 1 | 11 | 5 | 9 | 1 | |||
| Reject | 0 | 8 | 4 | 7 | 5 | 3 | 7 | 7 | |||
- Type I error (false positive or false alarm), when the wind turbine is healthy but the null hypothesis is rejected and therefore classified as faulty. The probability of committing a type I error is α, the level of significance.
- Type II error (false negative or missing fault), when the structure is faulty but the null hypothesis is not rejected and therefore classified as healthy. The probability of committing a type II error is called γ.
4.2. Sensitivity and Specificity
| Undamaged Sample () | Damaged Sample () | |
|---|---|---|
| Fail to reject | Specificity () | False negative rate (γ) |
| Reject | False positive rate (α) | Sensitivity () |
| score 1 | score 2 | score 3 | score 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fail to reject | 1.00 | 0.00 | 0.75 | 0.13 | 0.69 | 0.62 | 0.56 | 0.13 | |||
| Reject | 0.00 | 1.00 | 0.25 | 0.87 | 0.31 | 0.38 | 0.44 | 0.87 | |||
4.3. Reliability of the Results
| Undamaged Sample () | Damaged Sample () | |
|---|---|---|
| Fail to reject | P() | |
| Reject | P() |
| score 1 | score 2 | score 3 | score 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fail to reject | 1.00 | 0.00 | 0.92 | 0.08 | 0.69 | 0.31 | 0.90 | 0.10 | |||
| Reject | 0.00 | 1.00 | 0.36 | 0.64 | 0.62 | 0.38 | 0.50 | 0.50 | |||
4.4. The Receiver Operating Curves (ROC)
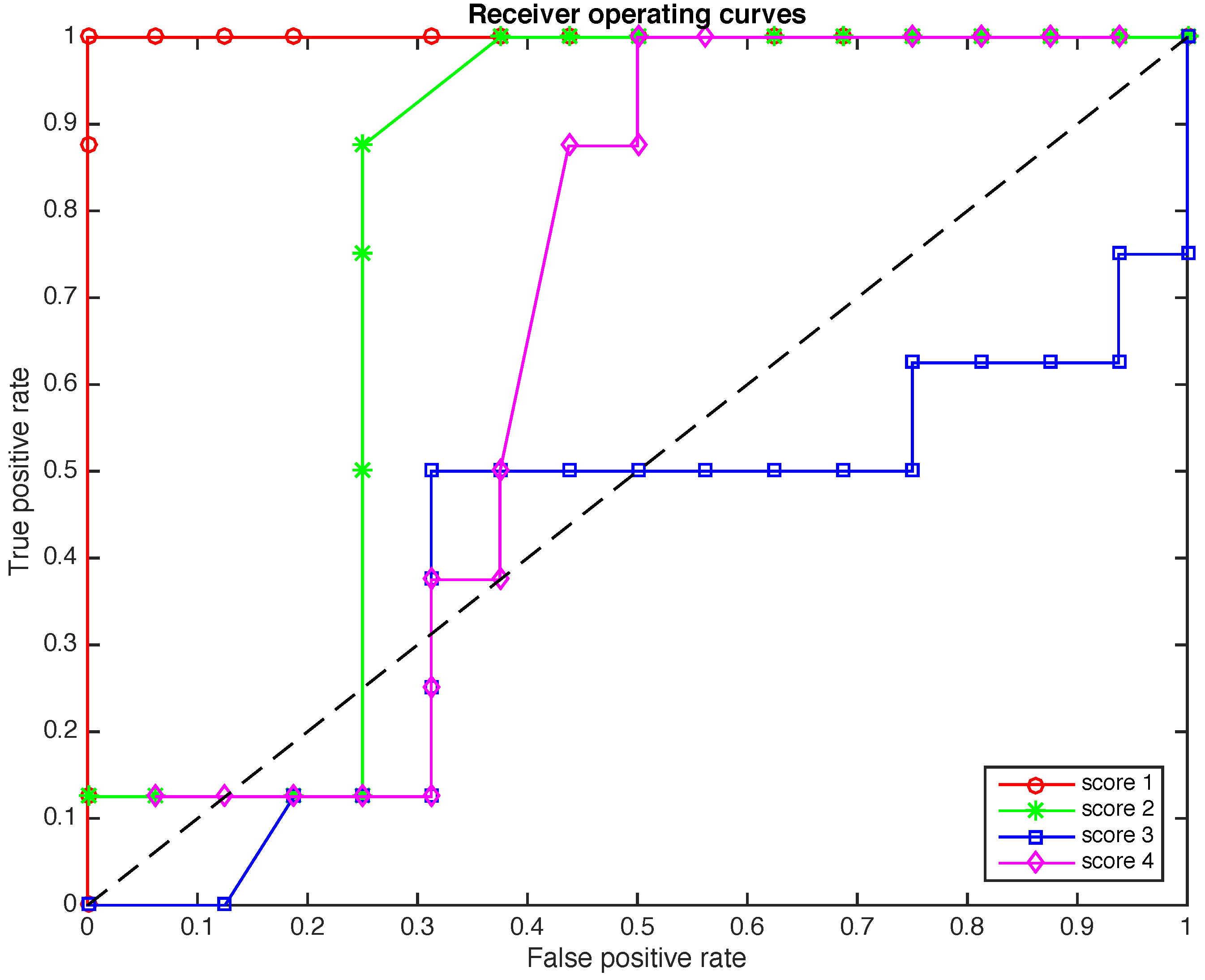
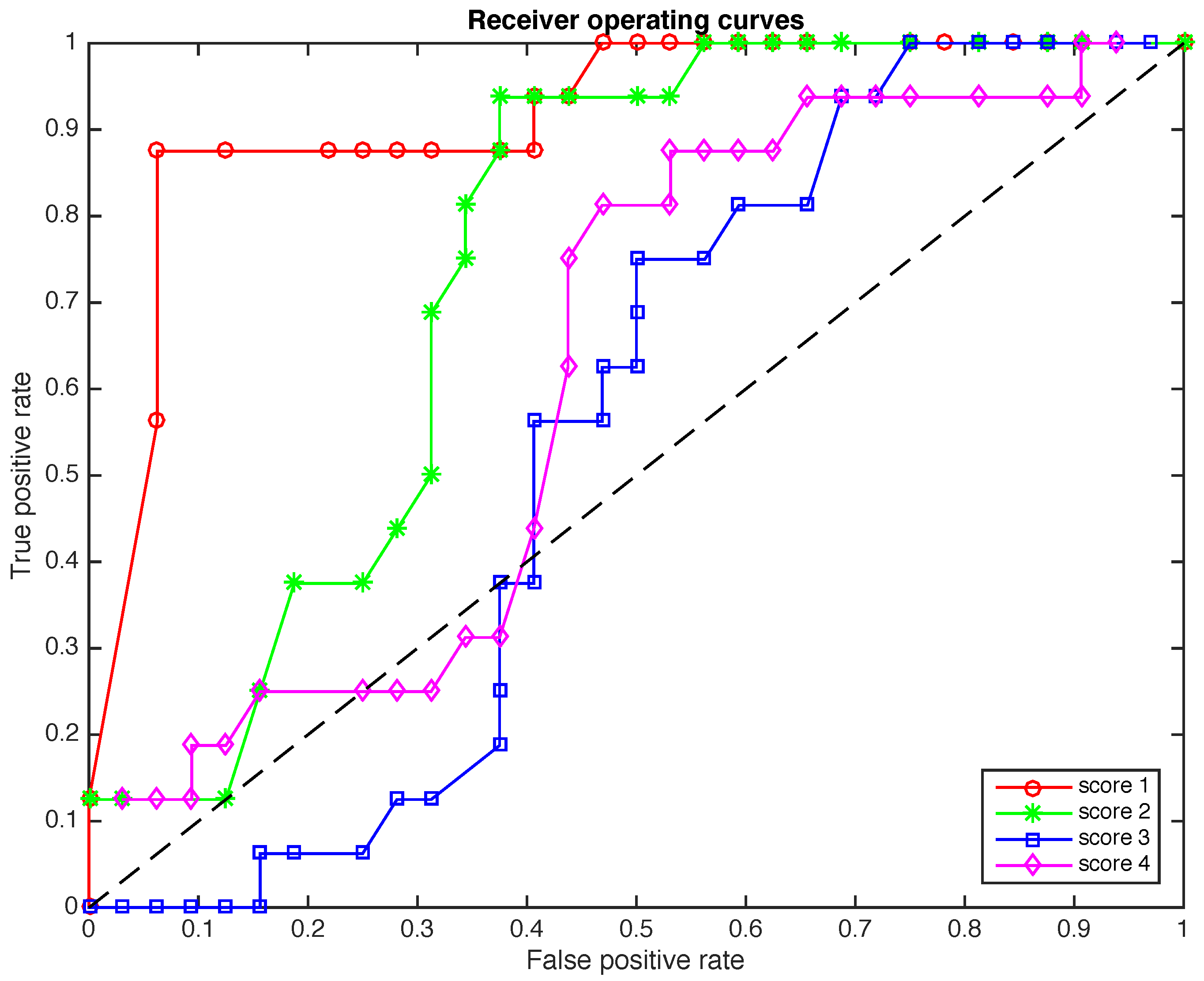
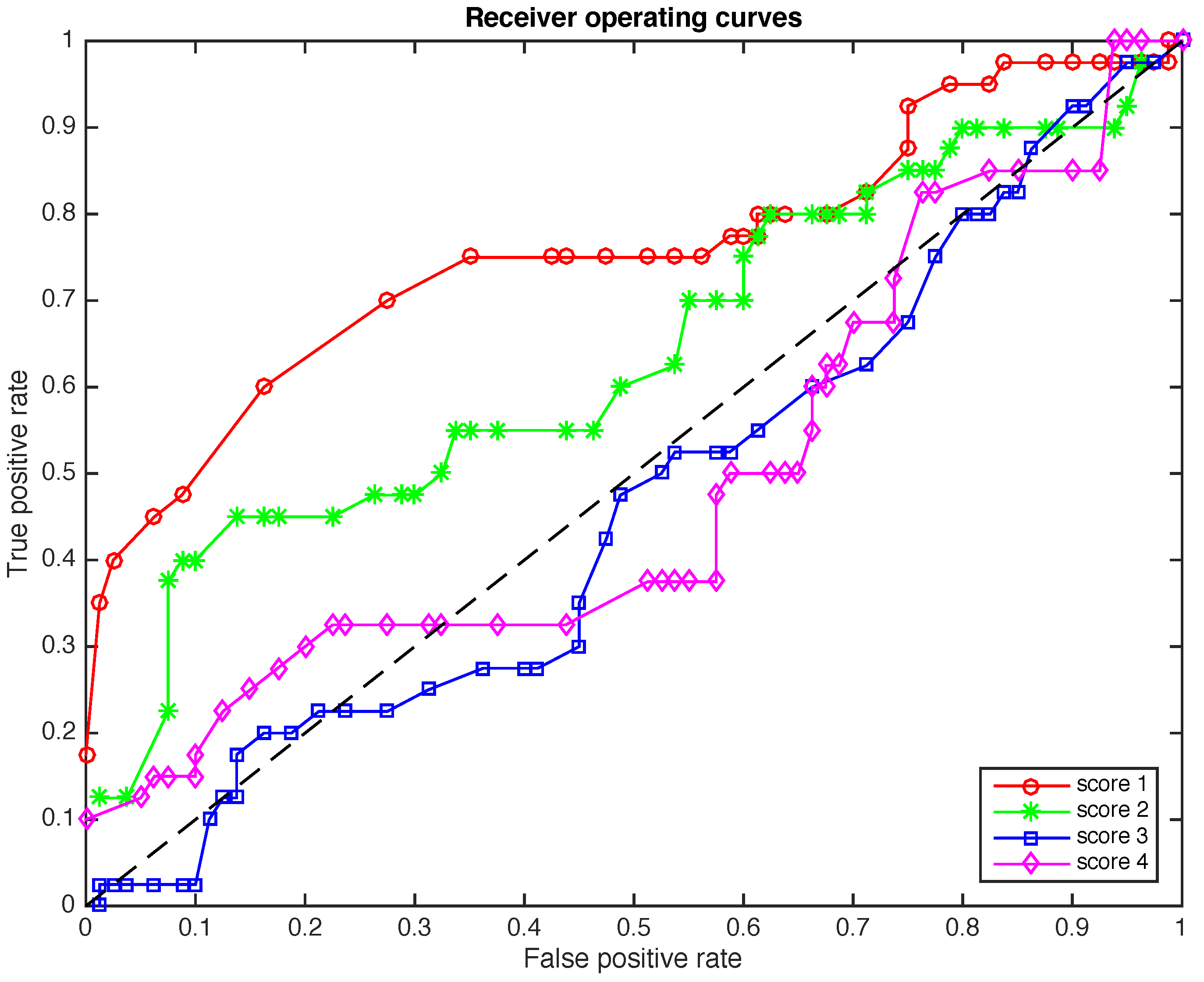
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| β | Pitch angle |
| Pitch angle reference | |
| Generator efficiency | |
| Generator speed | |
| Electrical Power | |
| Reference generator torque | |
| Real generator torque | |
| α | Significance level for the test (probability of committing a type I error) |
| γ | Probability of committing a type II error |
| L | Number of time instants per row per sensor |
| N | Number of sensors |
| ν | Size of the samples to diagnose |
| Principal components of the data set (loading matrix) | |
| Transformed (or projected) matrix to the principal component space (score matrix) | |
| Residual error matrix | |
| Data matrix (original) | |
| Data matrix to diagnose | |
| Baseline sample | |
| Sample to diagnose |
References
- Sinha, Y.; Steel, J. A progressive study into offshore wind farm maintenance optimisation using risk based failure analysis. Renew. Sustain. Energy Rev. 2015, 42, 735–742. [Google Scholar] [CrossRef]
- Odgaard, P.; Johnson, K. Wind turbine fault diagnosis and fault tolerant control—An enhanced benchmark challenge. In Proceedings of the 2013 American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 1–6.
- Soman, R.N.; Malinowski, P.H.; Ostachowicz, W.M. Bi-axial neutral axis tracking for damage detection in wind-turbine towers. Wind Energy 2015. [Google Scholar] [CrossRef]
- Adams, D.; White, J.; Rumsey, M.; Farrar, C. Structural health monitoring of wind turbines: Method and application to a HAWT. Wind Energy 2011, 14, 603–623. [Google Scholar] [CrossRef]
- Griffith, D.T.; Yoder, N.C.; Resor, B.; White, J.; Paquette, J. Structural health and prognostics management for the enhancement of offshore wind turbine operations and maintenance strategies. Wind Energy 2014, 17, 1737–1751. [Google Scholar] [CrossRef]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer Science & Business Media: London, UK, 2008. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J.; Nielsen, R.; Damgaard, C. Observer based detection of sensor faults in wind turbines. In Proceedings of the European Wind Energy Conference, Marseille, France, 16–19 March 2009; pp. 4421–4430.
- Zhang, X.; Zhang, Q.; Zhao, S.; Ferrari, R.M.; Polycarpou, M.M.; Parisini, T. Fault detection and isolation of the wind turbine benchmark: An estimation-based approach. In Proceedings of the International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; Volume 2, pp. 8295–8300.
- Shaker, M.S.; Patton, R.J. Active sensor fault tolerant output feedback tracking control for wind turbine systems via T-S model. Eng. Appl. Artif. Intell. 2014, 34, 1–12. [Google Scholar] [CrossRef]
- Shi, F.; Patton, R. An active fault tolerant control approach to an offshore wind turbine model. Renew. Energy 2015, 75, 788–798. [Google Scholar] [CrossRef]
- Vidal, Y.; Tutiven, C.; Rodellar, J.; Acho, L. Fault diagnosis and fault-tolerant control of wind turbines via a discrete time controller with a disturbance compensator. Energies 2015, 8, 4300–4316. [Google Scholar] [CrossRef]
- Dong, J.; Verhaegen, M. Data driven fault detection and isolation of a wind turbine benchmark. In Proceedings of the International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; Volume 2, pp. 7086–7091.
- Simani, S.; Castaldi, P.; Tilli, A. Data-driven approach for wind turbine actuator and sensor fault detection and isolation. In Proceedings of the International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; pp. 8301–8306.
- Laouti, N.; Sheibat-Othman, N.; Othman, S. Support vector machines for fault detection in wind turbines. In Proceedings of International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; Volume 2, pp. 7067–7072.
- Stoican, F.; Raduinea, C.F.; Olaru, S. Adaptation of set theoretic methods to the fault detection of wind turbine benchmark. In Proceedings of the International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; pp. 8322–8327.
- Odgaard, P.F.; Stoustrup, J. Gear-box fault detection using time-frequency based methods. Annu. Rev. Control 2015, 40, 50–58. [Google Scholar] [CrossRef]
- Pang-Ning, T.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Pearson Addison Wesley: Boston, MA, USA, 2005. [Google Scholar]
- Zaher, A.; McArthur, S.; Infield, D.; Patel, Y. Online wind turbine fault detection through automated SCADA data analysis. Wind Energy 2009, 12, 574. [Google Scholar] [CrossRef]
- Kusiak, A.; Li, W.; Song, Z. Dynamic control of wind turbines. Renew. Energy 2010, 35, 456–463. [Google Scholar] [CrossRef]
- Jonkman, J. NWTC Information Portal (FAST). Available online: https://nwtc.nrel.gov/FAST (accessed on 18 December 2015).
- Jonkman, J.M.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Kelley, N.; Jonkman, B. NWTC Information Portal (Turbsim). Available online: https://nwtc.nrel.gov/TurbSim (accessed on 18 December 2015).
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2012. [Google Scholar]
- Anaya, M.; Tibaduiza, D.; Pozo, F. A bioinspired methodology based on an artificial immune system for damage detection in structural health monitoring. Shock Vibration 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Anaya, M.; Tibaduiza, D.; Pozo, F. Detection and classification of structural changes using artificial immune systems and fuzzy clustering. Int. J. Bio-Inspired Comput. in press.
- Mujica, L.E.; Ruiz, M.; Pozo, F.; Rodellar, J.; Güemes, A. A structural damage detection indicator based on principal component analysis and statistical hypothesis testing. Smart Mater. Struct. 2014, 23, 1–12. [Google Scholar] [CrossRef]
- Mujica, L.E.; Rodellar, J.; Fernández, A.; Güemes, A. Q-statistic and T2-statistic PCA-based measures for damage assessment in structures. Struct. Health Monit. 2011, 10, 539–553. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Lin, B.; Jorgensen, S.B. Observer and data-driven-model-based fault detection in power plant coal mills. IEEE Trans. Energy Convers. 2008, 23, 659–668. [Google Scholar] [CrossRef]
- Ugarte, M.D.; Militino, A.F.; Arnholt, A. Probability and Statistics with R; Chemical Rubber Company (CRC) Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- De Groot, M.H.; Schervish, M.J. Probability and Statistics; Pearson: Boston, MA, USA, 2012. [Google Scholar]
- Yinghui, L.; Michaels, J.E. Feature extraction and sensor fusion for ultrasonic structural health monitoring under changing environmental conditions. IEEE Sens. J. 2009, 9, 1462–1471. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozo, F.; Vidal, Y. Wind Turbine Fault Detection through Principal Component Analysis and Statistical Hypothesis Testing. Energies 2016, 9, 3. https://doi.org/10.3390/en9010003
Pozo F, Vidal Y. Wind Turbine Fault Detection through Principal Component Analysis and Statistical Hypothesis Testing. Energies. 2016; 9(1):3. https://doi.org/10.3390/en9010003
Chicago/Turabian StylePozo, Francesc, and Yolanda Vidal. 2016. "Wind Turbine Fault Detection through Principal Component Analysis and Statistical Hypothesis Testing" Energies 9, no. 1: 3. https://doi.org/10.3390/en9010003
APA StylePozo, F., & Vidal, Y. (2016). Wind Turbine Fault Detection through Principal Component Analysis and Statistical Hypothesis Testing. Energies, 9(1), 3. https://doi.org/10.3390/en9010003







