Data-Driven Baseline Estimation of Residential Buildings for Demand Response †
Abstract
:1. Introduction
2. Data Mining Model
2.1. Data Preprocessing
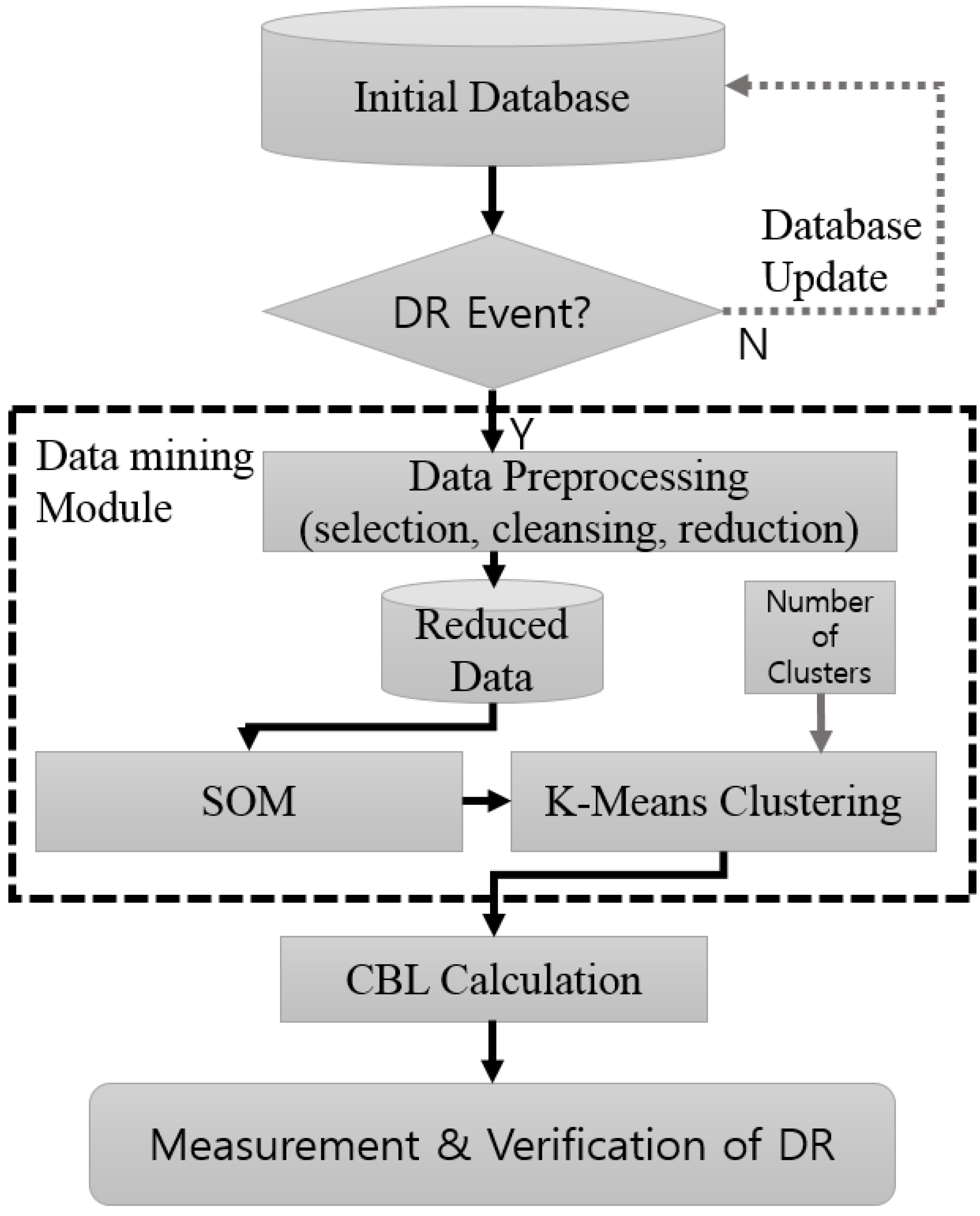
2.2. Self-Organizing Map (SOM)
2.3. K-Means Clustering
2.4. Proposed Algorithm for Baseline Load Estimation
| Algorithm 1 Baseline Load Estimation Algorithm |
|
| Vector | Description |
|---|---|
| 12 h consumption before DR activation | |
| Average temperature | |
| Gradient of the load consumption (optional) | |
| Working day indicator (optional) |
3. Residential Demand Response (DR): Case Study
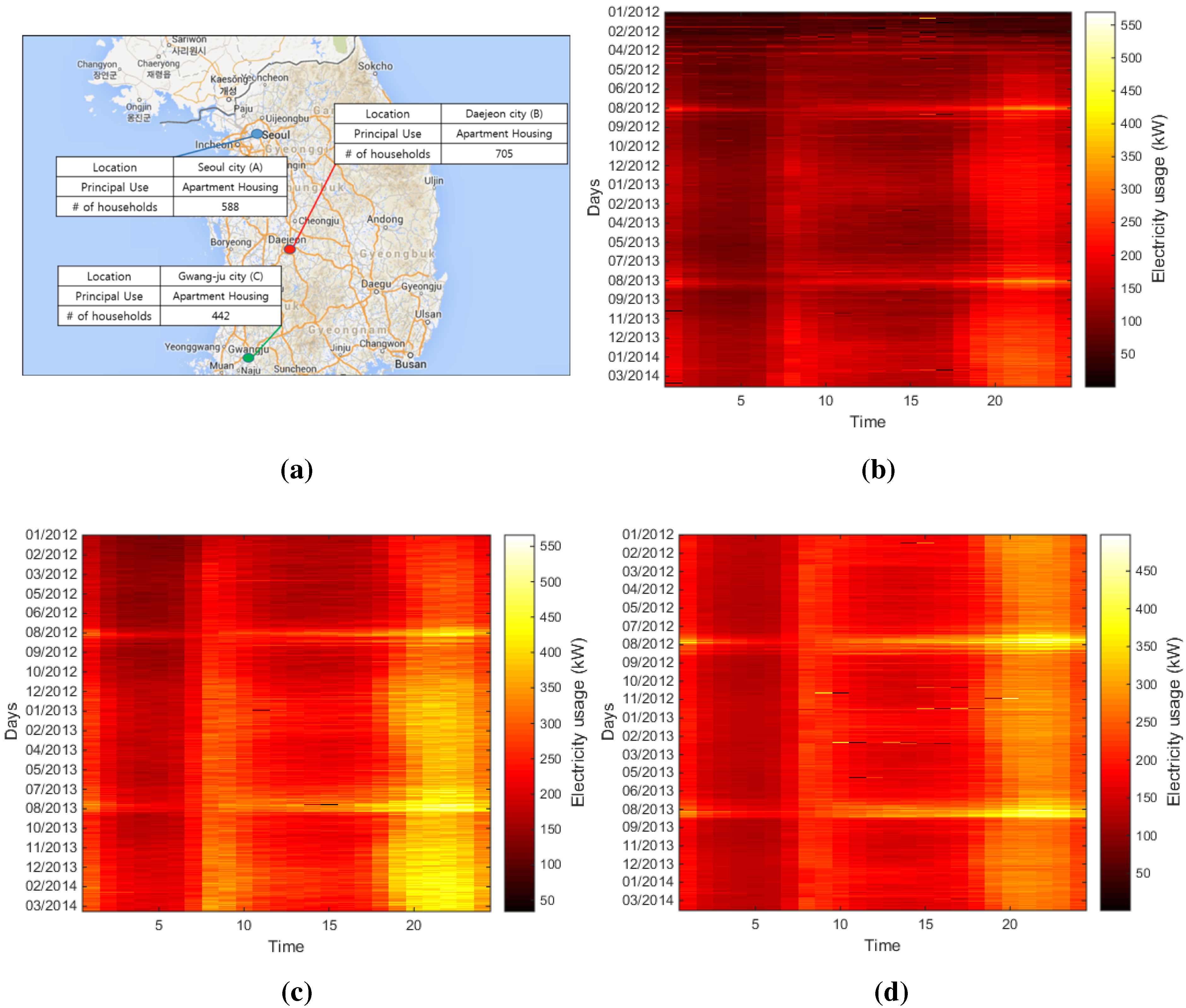
3.1. Load Characteristic

3.2. Data Processing

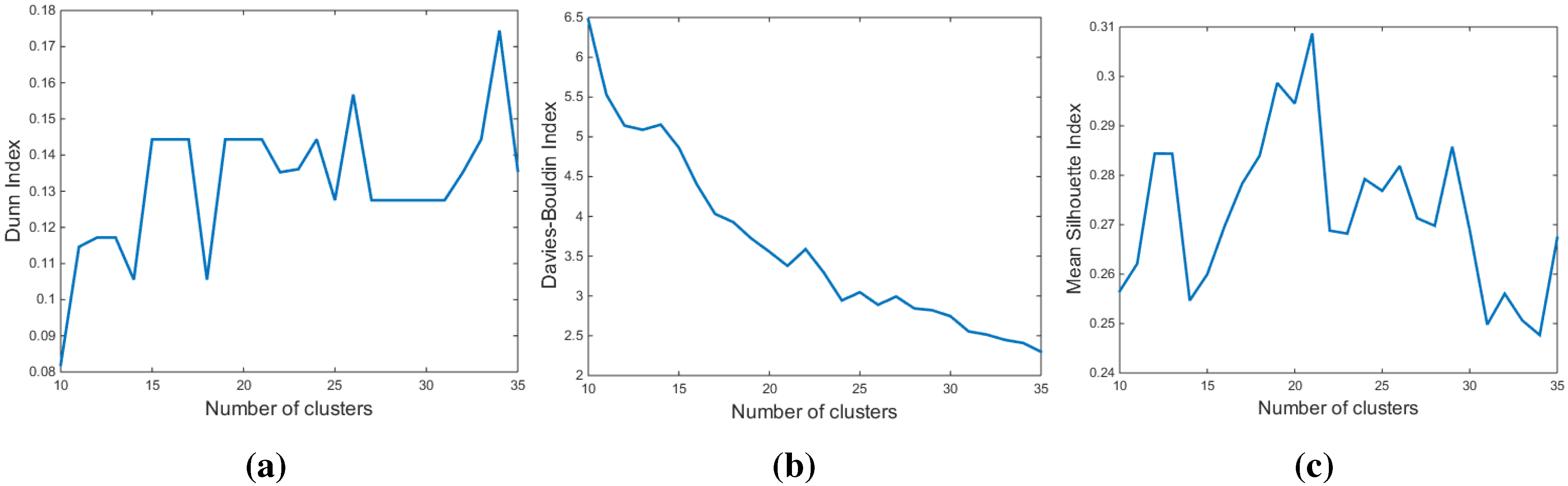
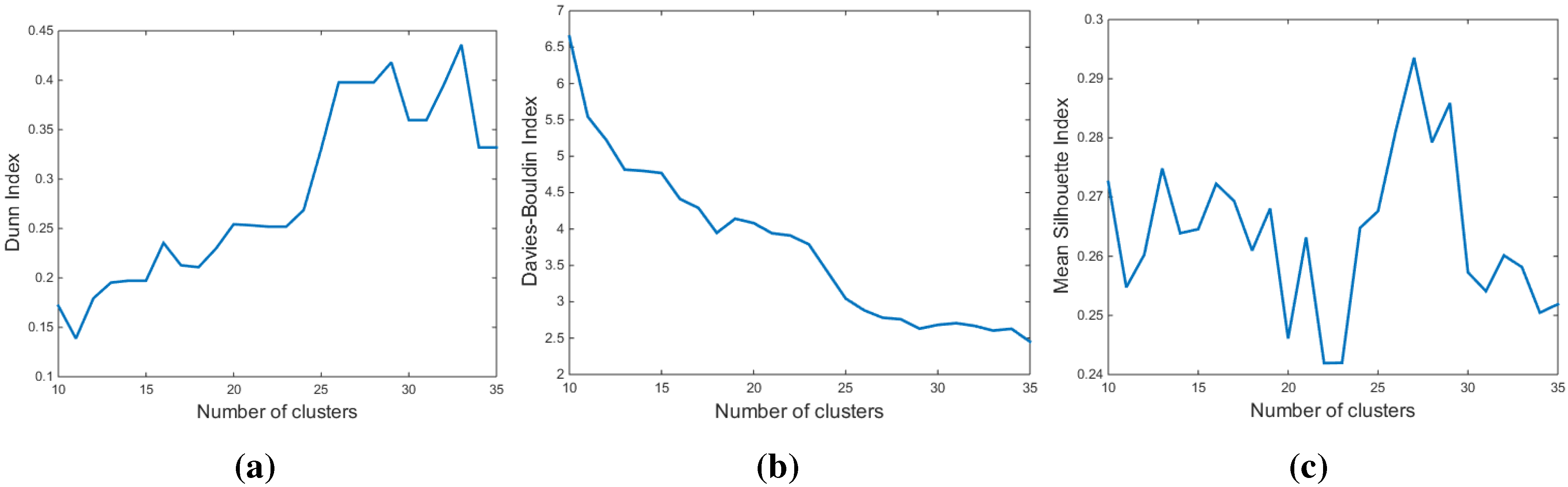
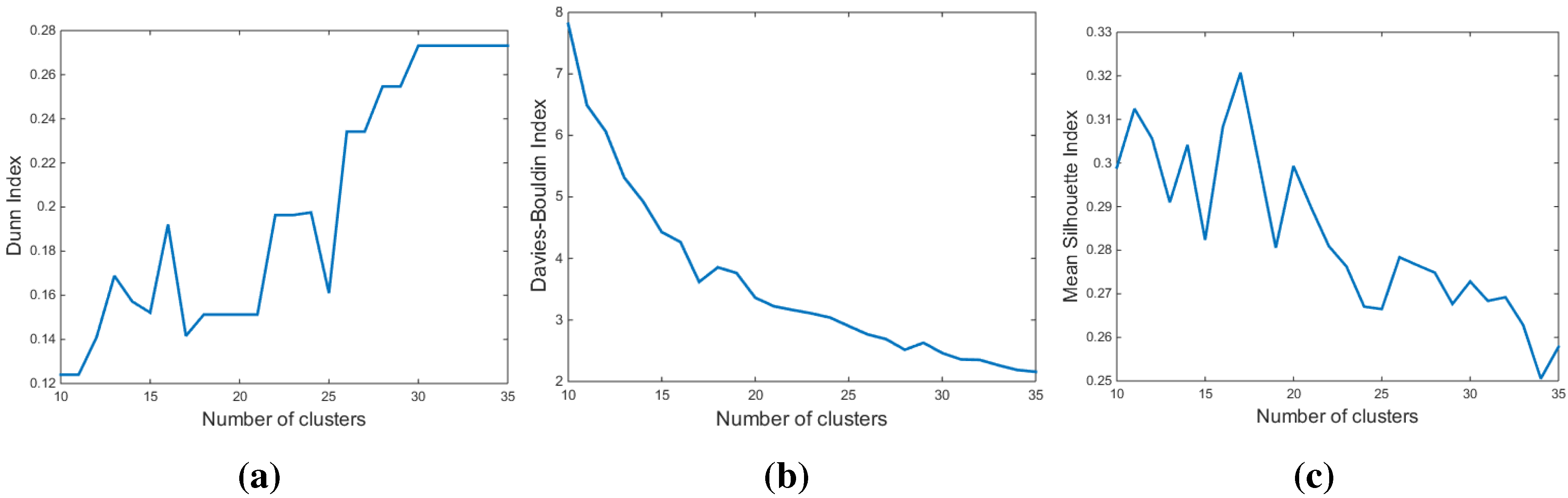
3.3. Determination of the Number of Clusters
3.3.1. The Dunn Index (DI)
3.3.2. The Davies-Bouldin Index (DBI)
3.3.3. The Silhouette Index (SI)
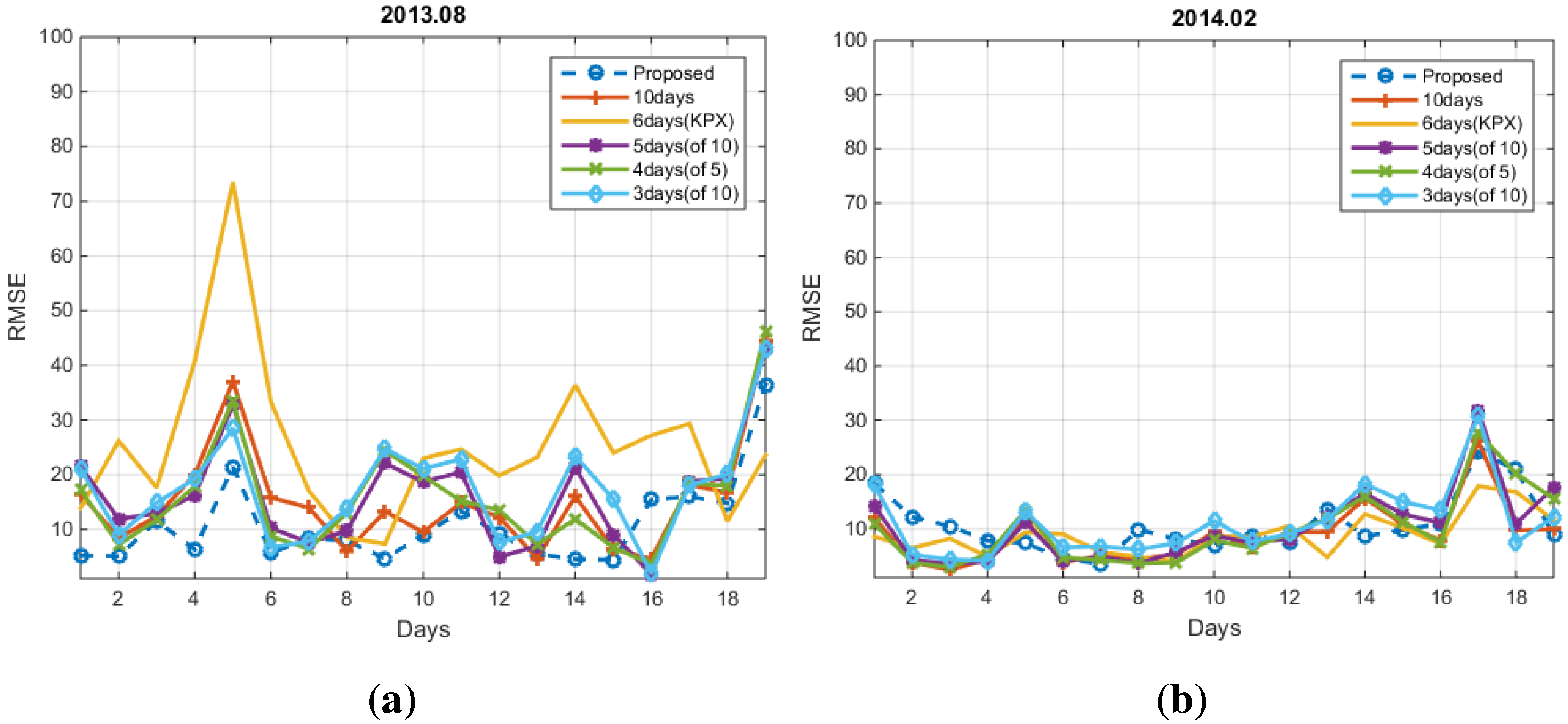
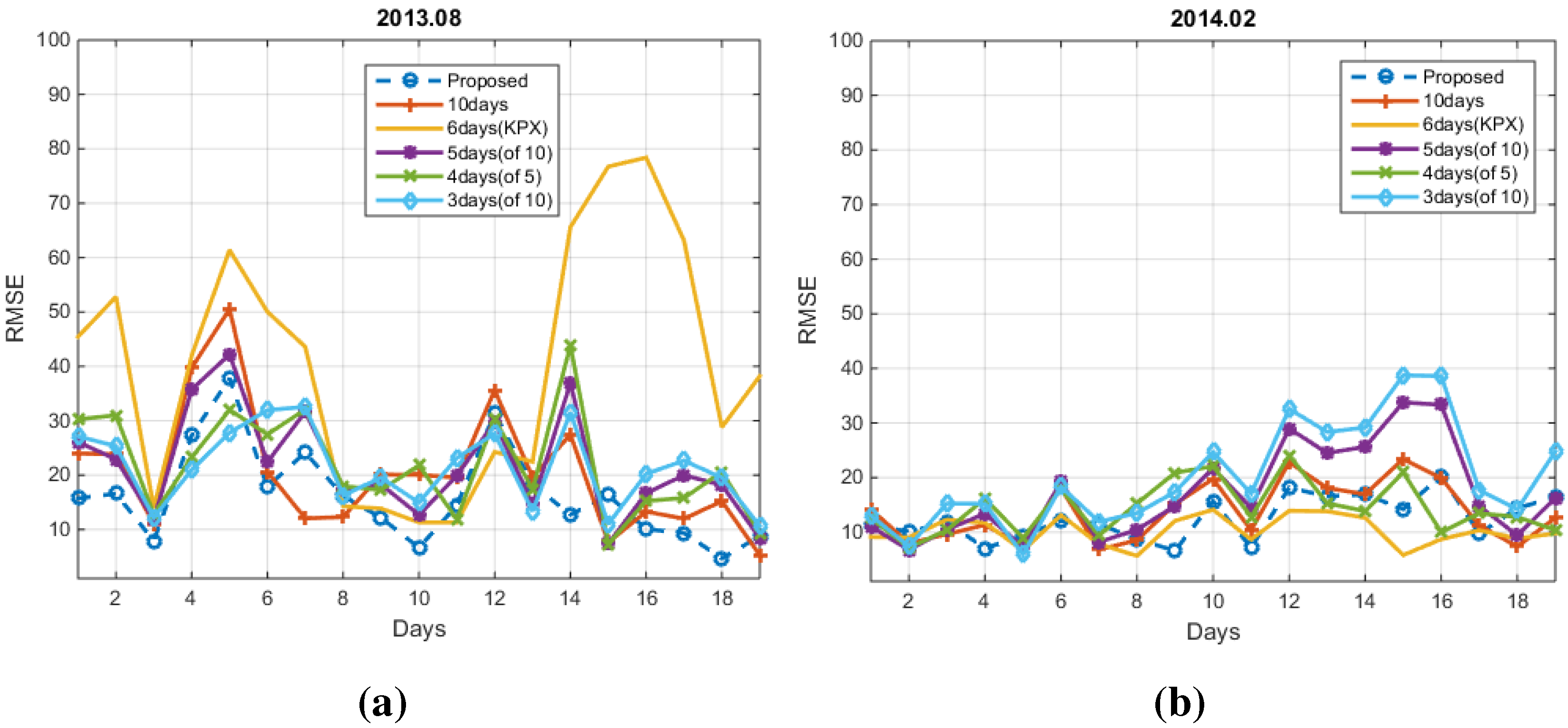
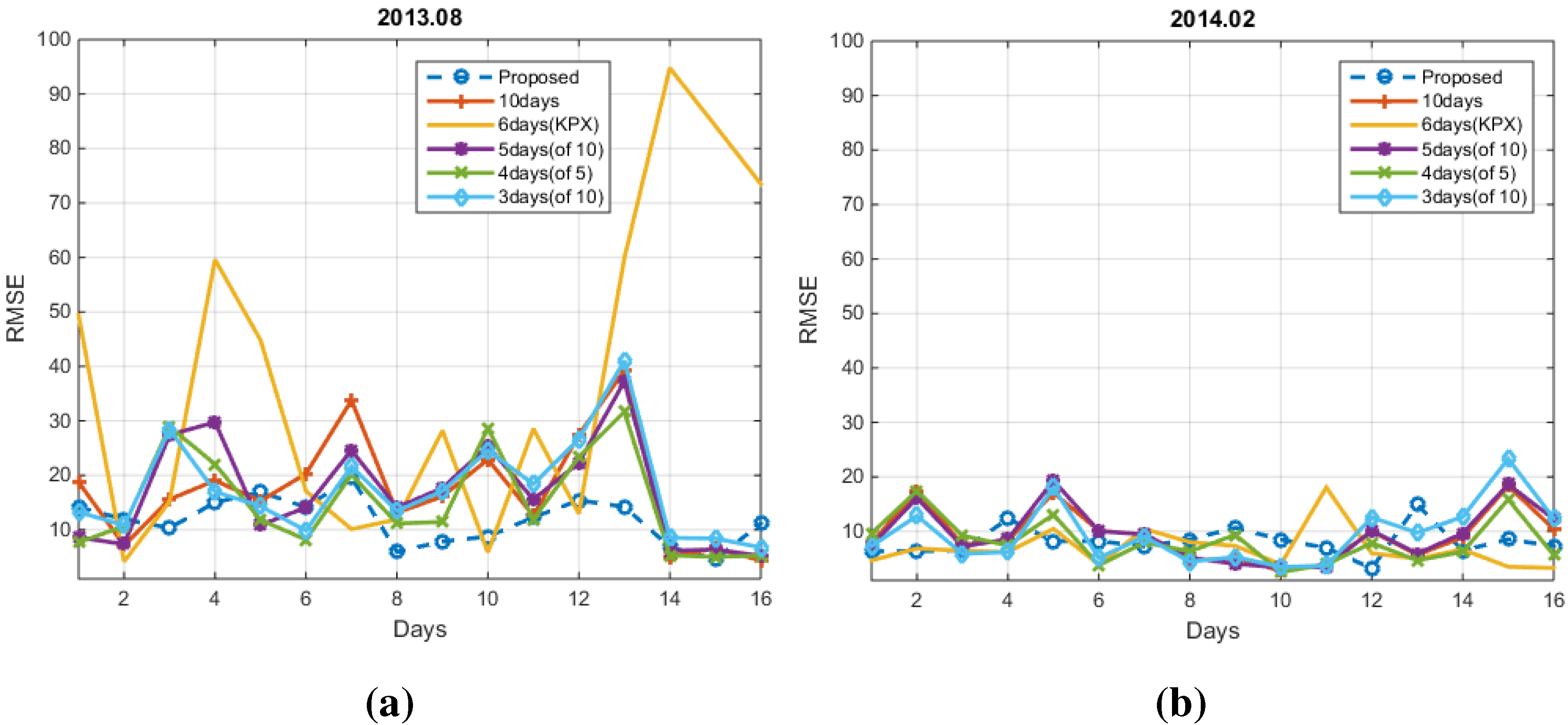
4. Experimental Results
4.1. Conventional Methods
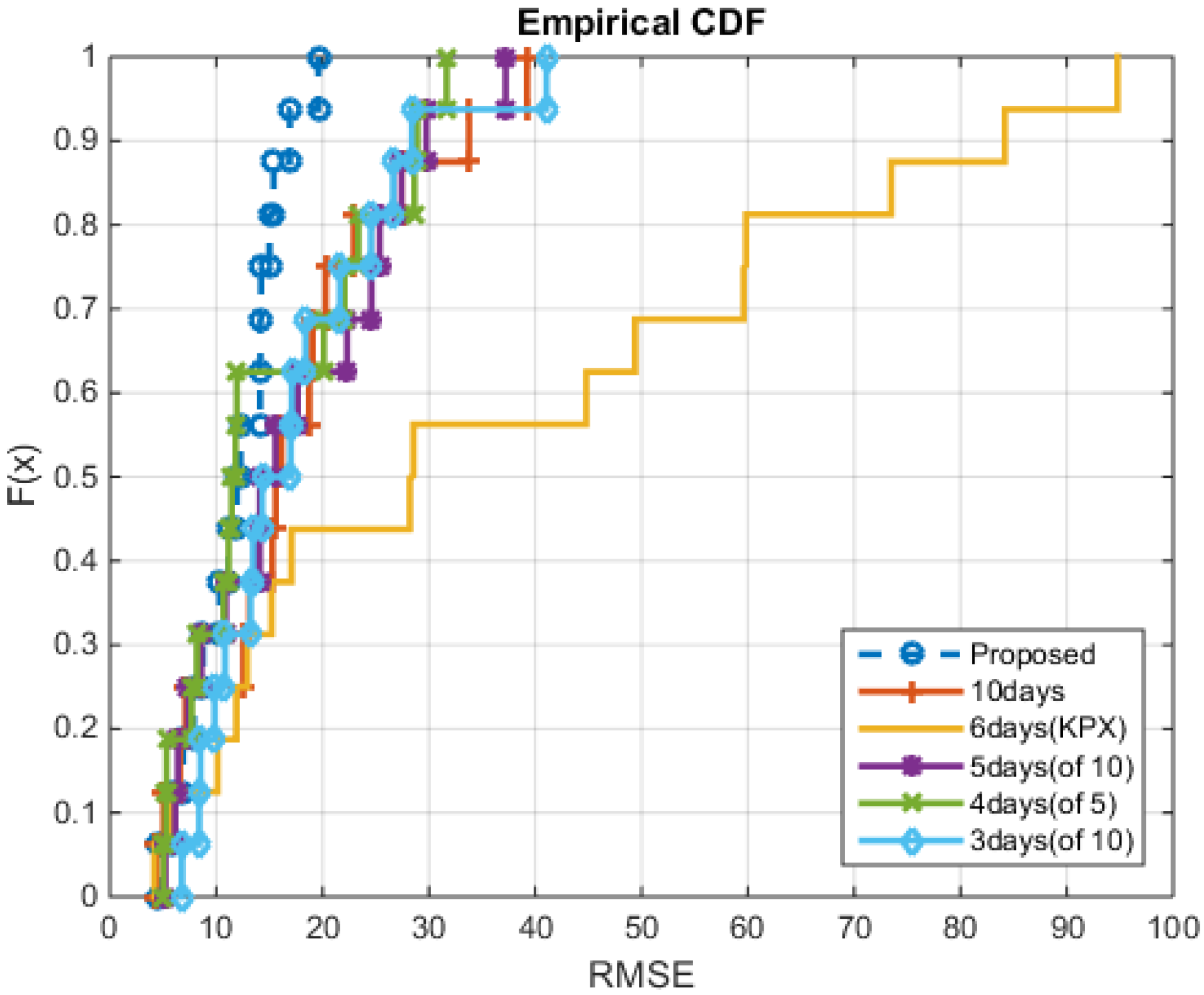
4.2. Numerical Results
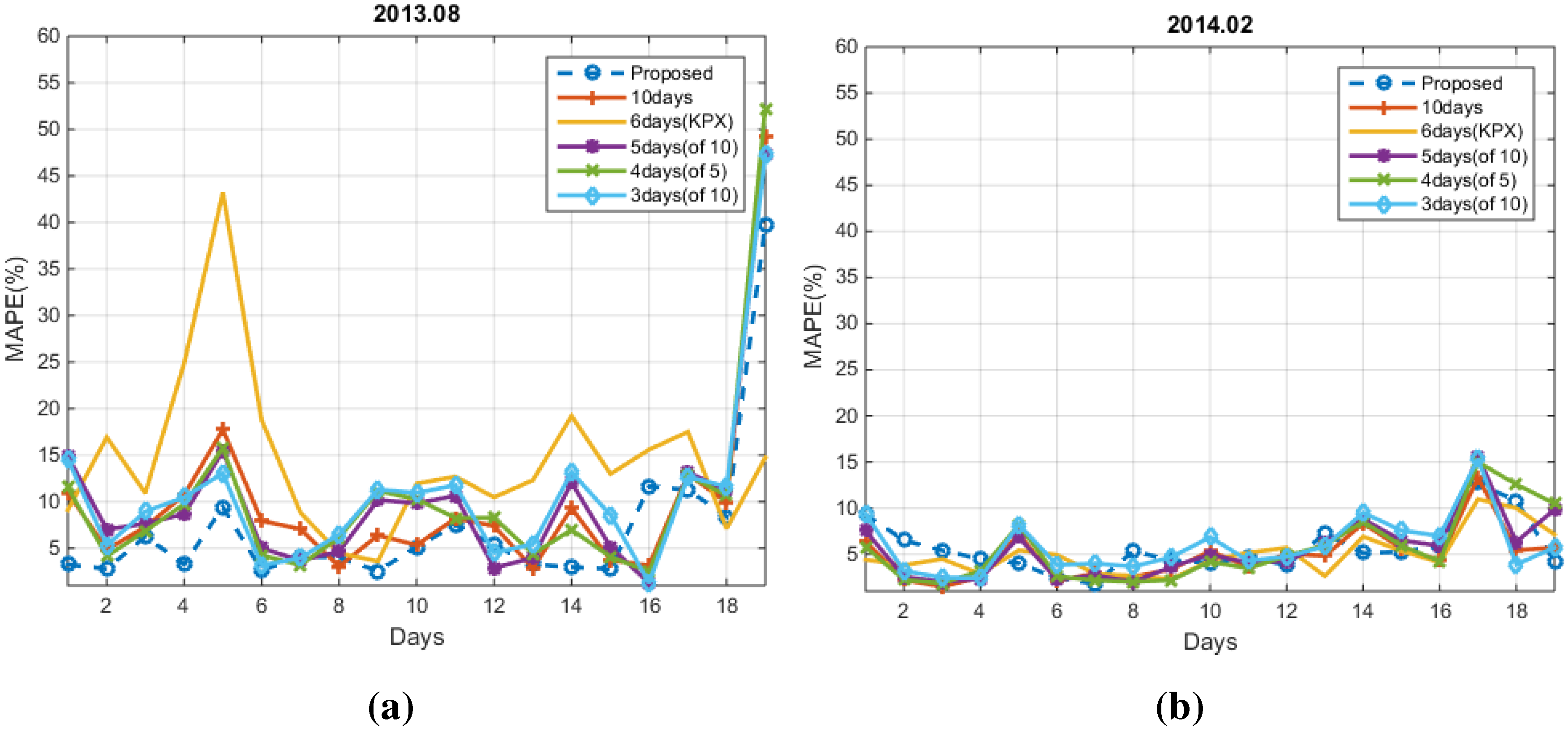
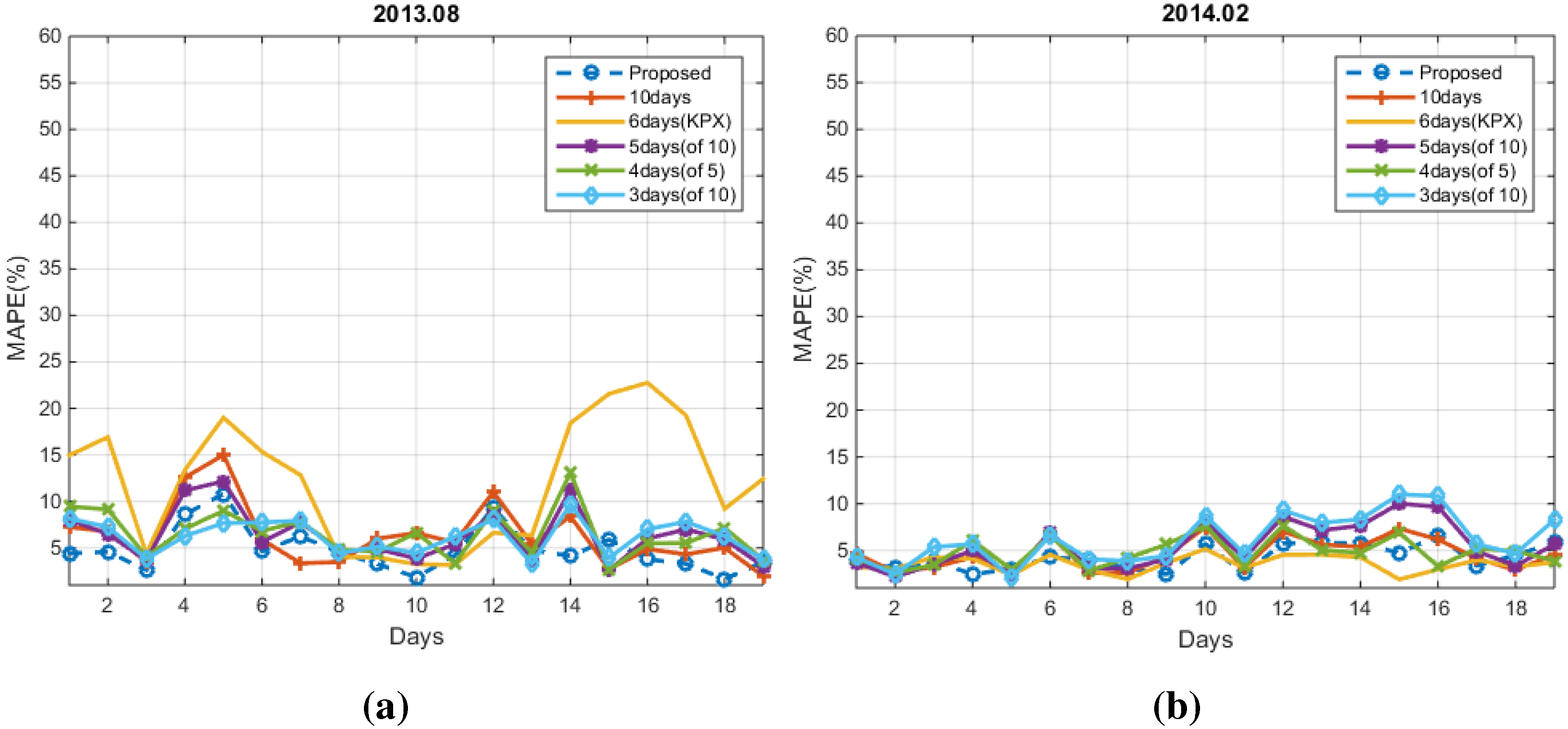
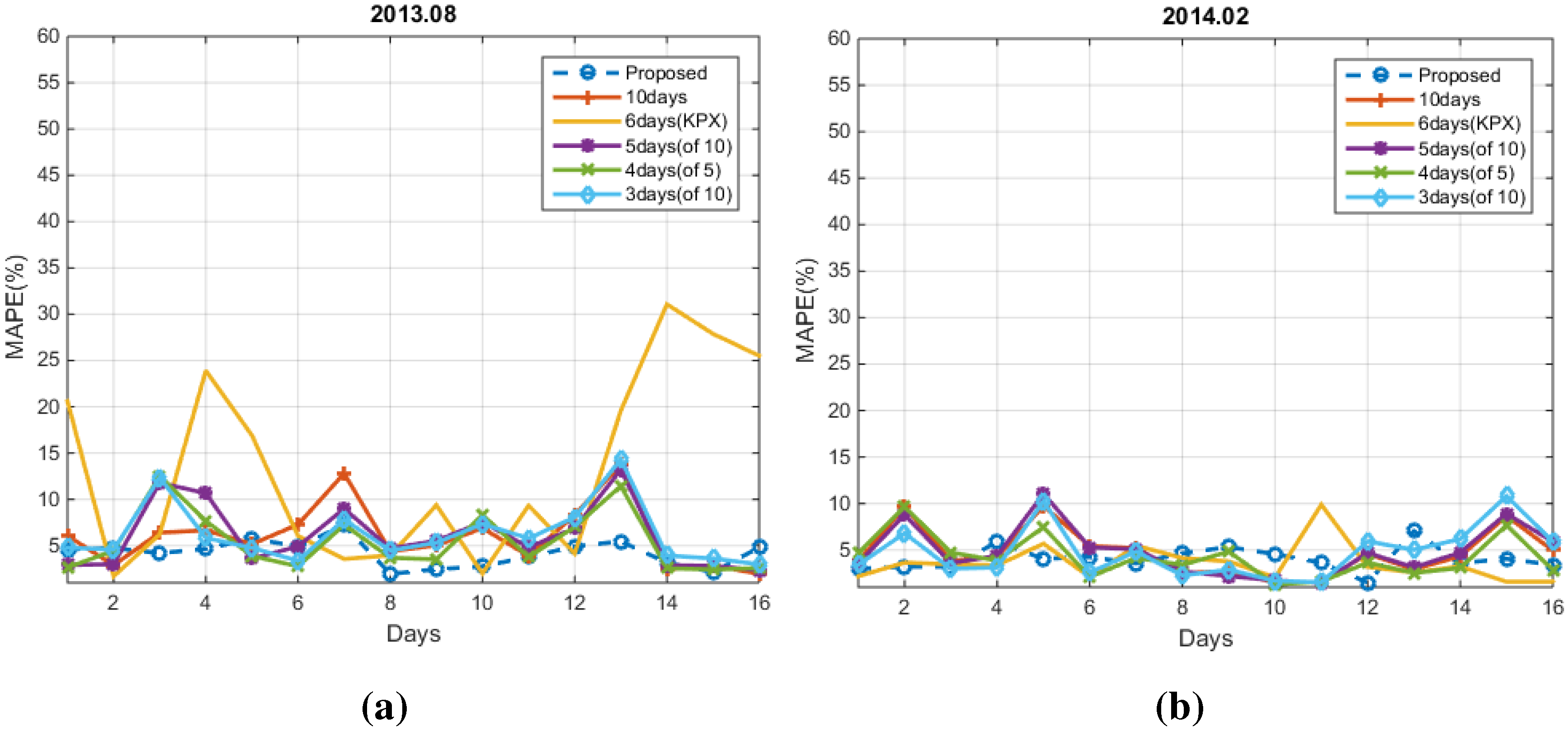

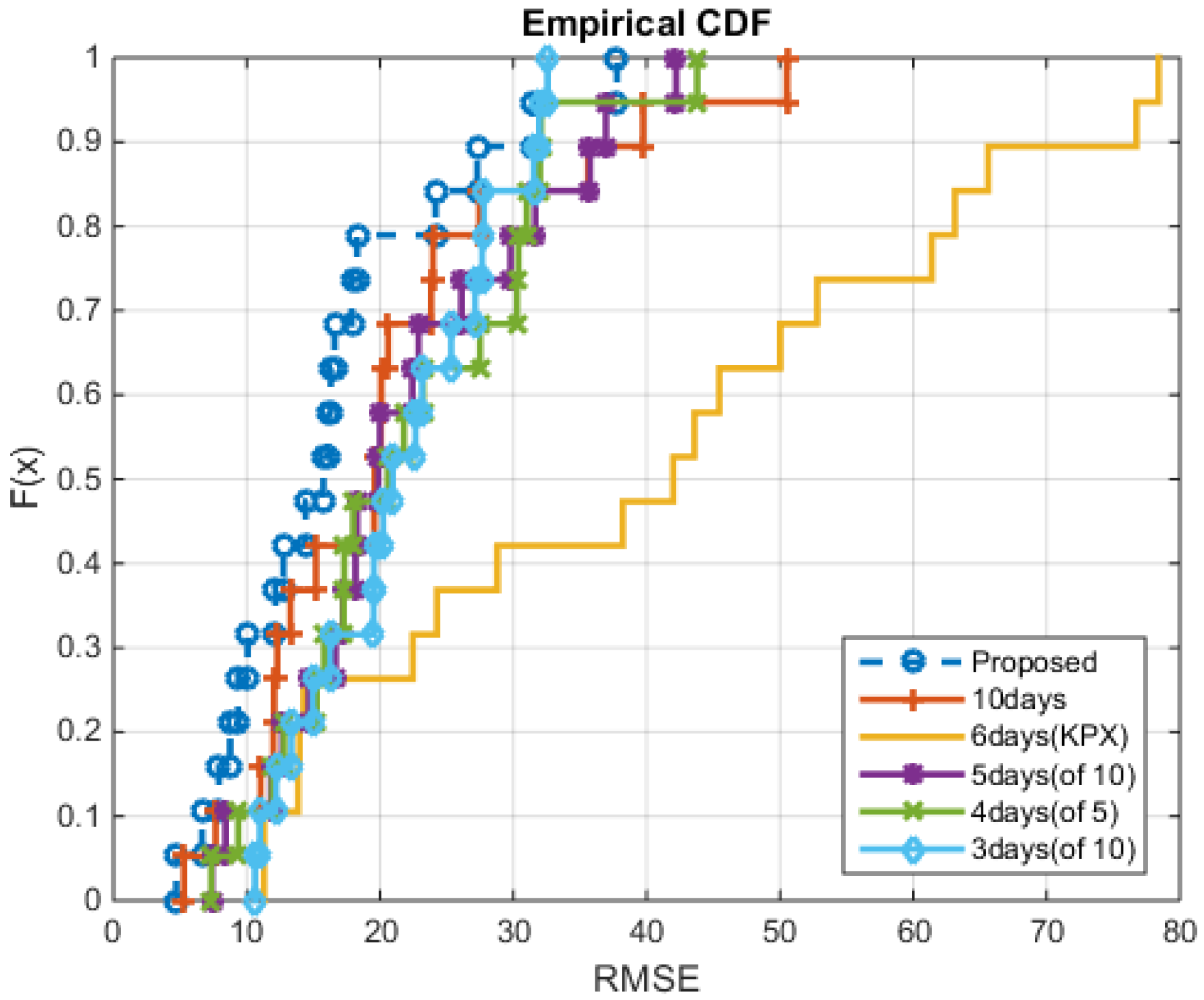
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Ruiz, N.; Cobelo, I.; Oyarzabal, J. A direct load control model for virtual power plant management. IEEE Trans. Power Syst. 2009, 24, 959–966. [Google Scholar] [CrossRef]
- Goldberg, M.L.; Agnew, G.K. Measurement and Verification for Demand Response; U.S. Department of Energy: Washington, DC, USA, 2013. [Google Scholar]
- Committee, A.L.R. Demand Response Measurement & Verification; Association of Edison Illuminating Companies: Birmingham, AL, USA, 2009. [Google Scholar]
- Faria, P.; Vale, Z.; Antunes, P. Determining the adjustment baseline parameters to define an accurate customer baseline load. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5.
- The Demand Response Baseline; EnerNOC: Boston, MA, USA, 2011.
- PJM Empirical Analysis of Demand Response Baseline Methods; KEMA, Inc.: Arnhem, The Netherlands, 2011.
- Kim, J.; Nam, Y.; Hahn, T.; Hong, H. Demand Response Program Implementation Practices in Korea. In Proceedings of the 18th International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; pp. 3704–3707.
- Braithwait, S.; Hansen, D.; Armstrong, D. 2009 Load Impact Evaluation of California Statewide Critical-Peak Pricing Rates for Non-Residential Customers: Ex Post and Ex Ante Report; Christensen Associates Energy Consulting, LLC: Madison, WI, USA, 2010. [Google Scholar]
- Iglesias, F.; Kastner, W. Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies 2013, 6, 579–597. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 498–505. [Google Scholar] [CrossRef]
- Chaouch, M. Clustering-based improvement of nonparametric functional time series forecasting: Application to intra-day household-level load curves. IEEE Trans. Smart Grid 2014, 5, 411–419. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Pardo, A.; Meneu, V.; Valor, E. Temperature and seasonality influences on Spanish electricity load. Energy Econ. 2002, 24, 55–70. [Google Scholar] [CrossRef]
- Bessec, M.; Fouquau, J. The non-linear link between electricity consumption and temperature in Europe: A threshold panel approach. Energy Econ. 2008, 30, 2705–2721. [Google Scholar] [CrossRef]
- Tasdighi, M.; Ghasemi, H.; Rahimi-Kian, A. Residential microgrid scheduling based on smart meters data and temperature dependent thermal load modeling. IEEE Trans. Smart Grid 2014, 5, 349–357. [Google Scholar] [CrossRef]
- Addy, N.; Mathieu, J.L.; Kiliccote, S.; Callaway, D.S. Understanding the effect of baseline modeling implementation choices on analysis of demand response performance. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 133–141. [Google Scholar]
- Coughlin, K.; Piette, M.A.; Goldman, C.; Kiliccote, S. Statistical analysis of baseline load models for non-residential buildings. Energy Build. 2009, 41, 374–381. [Google Scholar] [CrossRef]
- Fayyad, U.M.; Piatetsky-Shapiro, G.; Smyth, P. From Data Mining to Knowledge Discovery: An Overview. In Advances in Knowledge Discovery and Data Mining; American Association for Artificial Intelligence: Menlo Park, CA, USA, 1996; pp. 1–34. [Google Scholar]
- Figueiredo, V.; Rodrigues, F.; Vale, Z.; Gouveia, J.B. An electric energy consumer characterization framework based on data mining techniques. IEEE Trans. Power Syst. 2005, 20, 596–602. [Google Scholar] [CrossRef]
- Ramos, S.; Duarte, J.M.; Duarte, F.J.; Vale, Z. A data-mining-based methodology to support MV electricity customers’ characterization. Energy Build. 2015, 91, 16–25. [Google Scholar] [CrossRef]
- Valor, E.; Meneu, V.; Caselles, V. Daily air temperature and electricity load in Spain. J. Appl. Meteorol. 2001, 40, 1413–1421. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: New York, NY, USA, 2001; Volume 30. [Google Scholar]
- Rokach, L. A survey of clustering algorithms. In Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2010; pp. 269–298. [Google Scholar]
- Huang, Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning from Data; AMLBook: Berlin, Germany, 2012. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Annual Energy Outlook; Energy Information Administration: Washington, DC, USA, 2015.
- Woo, C.; Herter, K. Residential Demand Response Evaluation: A Scoping Study; Technical Report for Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2006. [Google Scholar]
- Park, S.; Ryu, S.; Choi, Y.; Kim, H. A framework for baseline load estimation in demand response: Data mining approach. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 638–643.
- Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. Self-organizing map in Matlab: The SOM Toolbox. In Proceedings of the MATLAB Digital Signal Processing Conference, Espoo, Finland, 16–17 November 1999; Volume 99, pp. 16–17.
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Martinez Alvarez, F.; Troncoso, A.; Riquelme, J.C.; Aguilar Ruiz, J.S. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. Cybern. Syst. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Dunn, J.C. Well-separated clusters and optimal fuzzy partitions. J. Cybern. 1974, 4, 95–104. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Demand Response: A Multi-Purpose Resource For Utilities and Grid Operators; EnerNOC: Boston, MA, USA, 2009.
- Coughlin, K.; Piette, M.A.; Goldman, C.; Kiliccote, S. Estimating Demand Response Load Impacts: Evaluation of Baseline Load Models for Non-Residential Buildings in California; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2008. [Google Scholar]
- Hurley, D.; Peterson, P.; Whited, M. Demand Response as a Power System Resource; Regulatory Assistance Project: Montpelier, VT, USA, 2013. [Google Scholar]
- Li, G.; Liu, C.C.; Mattson, C.; Lawarree, J. Day-ahead electricity price forecasting in a grid environment. IEEE Trans. Power Syst. 2007, 22, 266–274. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Ryu, S.; Choi, Y.; Kim, J.; Kim, H. Data-Driven Baseline Estimation of Residential Buildings for Demand Response. Energies 2015, 8, 10239-10259. https://doi.org/10.3390/en80910239
Park S, Ryu S, Choi Y, Kim J, Kim H. Data-Driven Baseline Estimation of Residential Buildings for Demand Response. Energies. 2015; 8(9):10239-10259. https://doi.org/10.3390/en80910239
Chicago/Turabian StylePark, Saehong, Seunghyoung Ryu, Yohwan Choi, Jihyo Kim, and Hongseok Kim. 2015. "Data-Driven Baseline Estimation of Residential Buildings for Demand Response" Energies 8, no. 9: 10239-10259. https://doi.org/10.3390/en80910239
APA StylePark, S., Ryu, S., Choi, Y., Kim, J., & Kim, H. (2015). Data-Driven Baseline Estimation of Residential Buildings for Demand Response. Energies, 8(9), 10239-10259. https://doi.org/10.3390/en80910239







