Data Mining Techniques for Detecting Household Characteristics Based on Smart Meter Data
Abstract
:1. Introduction
- (1)
- To deliver additional information in smart metering solutions as a part of intelligent home infrastructure that enables energy usage visualizations, increases awareness and understanding of home energy consumption which ultimately may lead to an overall energy consumption decrease;
- (2)
- To utilize a set of household behavioral data (patterns of home appliances usage) that can significantly improve the accuracy of the forecasts generated at the household level;
- (3)
- To provide the input needed in demand response systems where the individual customers can directly participate in demand management with timely recommendations aimed at energy savings.
2. Literature Review on Related Works
3. Smart Meter Data
| Time ID | Observed Real Power (in Watts) | Reference Home Appliance Data (“1”—ON State, “0”—OFF State) | ||||
|---|---|---|---|---|---|---|
| WM | DW | TD | KE | MO | ||
| 120910 | 301 | 0 | 0 | 0 | 0 | 0 |
| 120911 | 312 | 0 | 0 | 0 | 0 | 0 |
| 120912 | 300 | 0 | 0 | 0 | 0 | 0 |
| 120913 | 314 | 0 | 0 | 0 | 0 | 0 |
| 120914 | 306 | 0 | 0 | 0 | 0 | 0 |
| 120915 | 314 | 0 | 0 | 0 | 0 | 0 |
| 120916 | 378 | 0 | 0 | 0 | 0 | 0 |
| 120917 | 1478 | 0 | 0 | 0 | 1 | 0 |
| 120918 | 1524 | 0 | 0 | 0 | 1 | 0 |
| 120919 | 1598 | 0 | 0 | 0 | 1 | 0 |
| 120920 | 1605 | 0 | 0 | 0 | 1 | 0 |
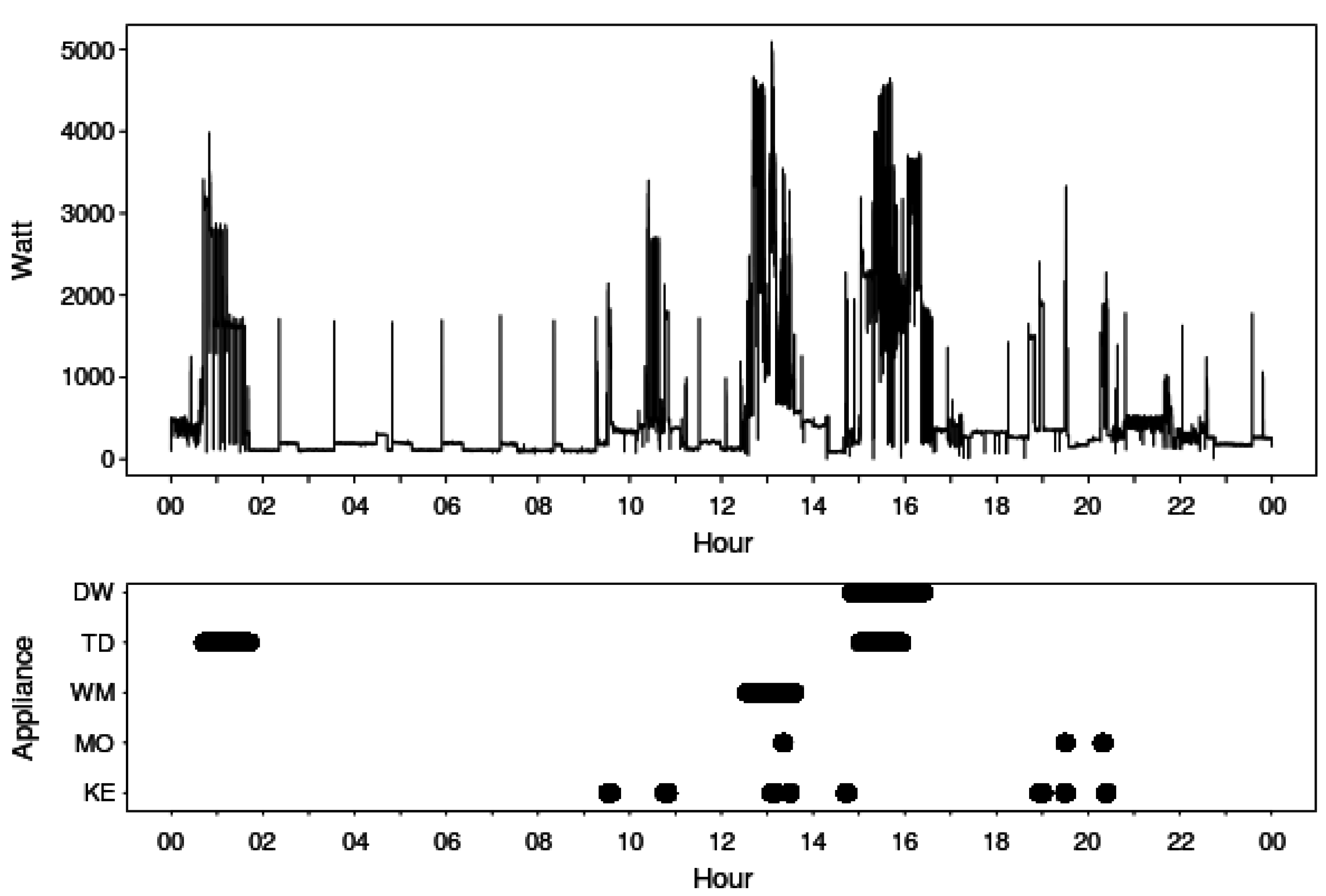
4. Revealing Usage Pattern Characteristics with Data Mining Techniques
4.1. The Rationale behind the Choice of the Methods
4.2. Data Preparation
| Hour | KE | MO | WM | TD | DW |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.02 | 0.06 | 0 |
| 1 | 0 | 0 | 0 | 0.04 | 0 |
| 2 | 0 | 0 | 0 | 0.02 | 0 |
| 3 | 0 | 0 | 0.02 | 0 | 0 |
| 4 | 0 | 0.01 | 0 | 0.02 | 0 |
| 5 | 0 | 0.01 | 0 | 0.02 | 0 |
| 6 | 0.03 | 0.03 | 0.02 | 0 | 0 |
| 7 | 0.12 | 0.16 | 0.02 | 0 | 0.08 |
| 8 | 0.08 | 0.08 | 0.06 | 0.02 | 0.06 |
| 9 | 0.09 | 0.08 | 0.05 | 0.02 | 0.09 |
| 10 | 0.07 | 0.06 | 0.05 | 0.07 | 0.08 |
| 11 | 0.06 | 0.04 | 0.08 | 0.06 | 0.11 |
| 12 | 0.05 | 0.01 | 0.08 | 0.04 | 0.05 |
| 13 | 0.05 | 0.02 | 0.05 | 0.06 | 0.08 |
| 14 | 0.05 | 0.03 | 0.05 | 0.04 | 0.06 |
| 15 | 0.03 | 0.02 | 0.06 | 0.04 | 0.09 |
| 16 | 0.04 | 0.03 | 0.08 | 0.11 | 0.06 |
| 17 | 0.03 | 0.02 | 0.03 | 0.06 | 0.03 |
| 18 | 0.06 | 0.1 | 0.05 | 0.04 | 0.05 |
| 19 | 0.08 | 0.03 | 0.06 | 0.02 | 0.03 |
| 20 | 0.09 | 0.12 | 0.08 | 0.07 | 0.03 |
| 21 | 0.05 | 0.09 | 0.08 | 0.07 | 0.06 |
| 22 | 0.02 | 0.06 | 0.06 | 0.09 | 0.05 |
| 23 | 0.01 | 0 | 0.06 | 0.06 | 0.02 |
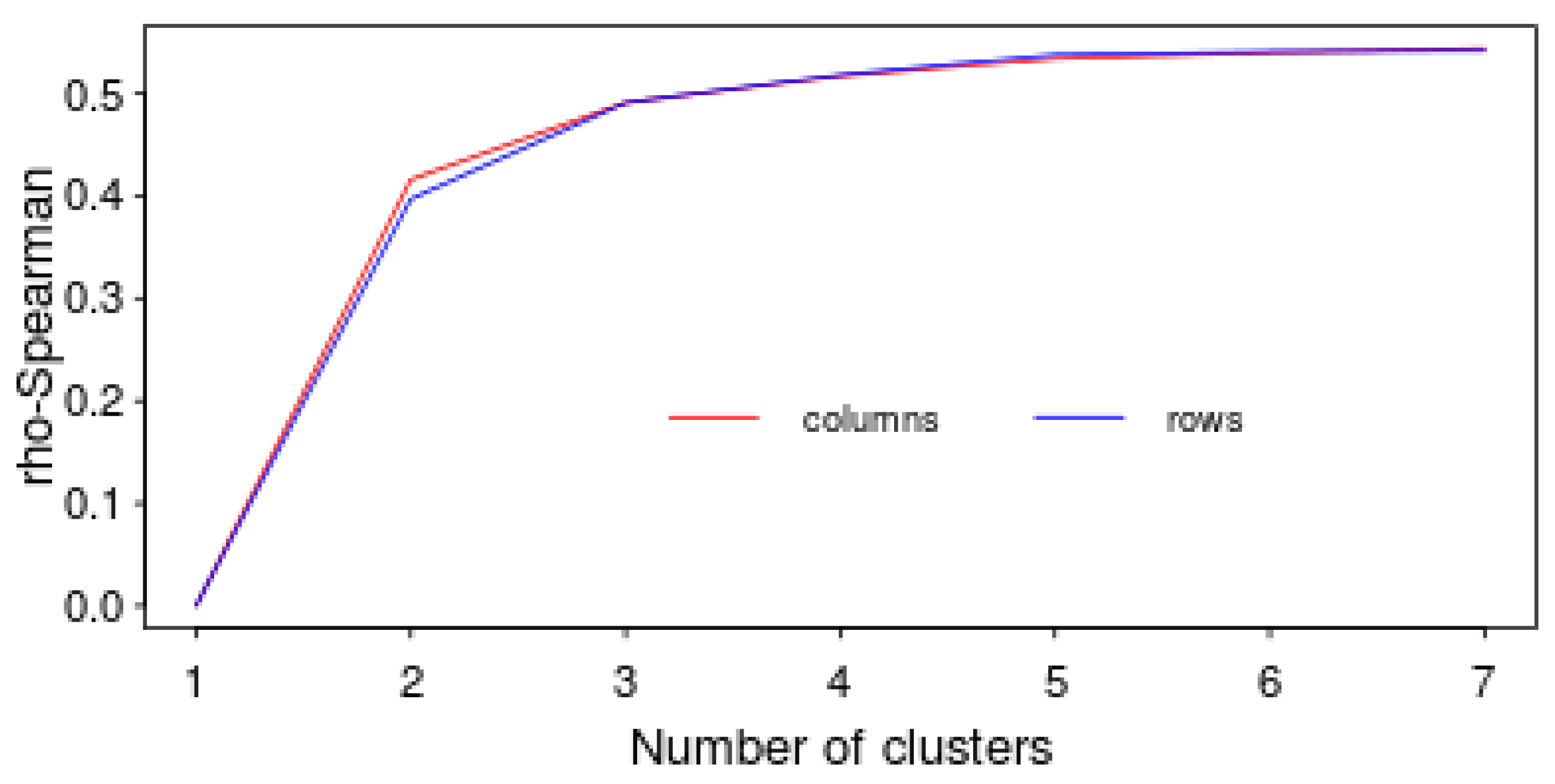
4.3. Detecting Patterns Using Hierarchical Clustering
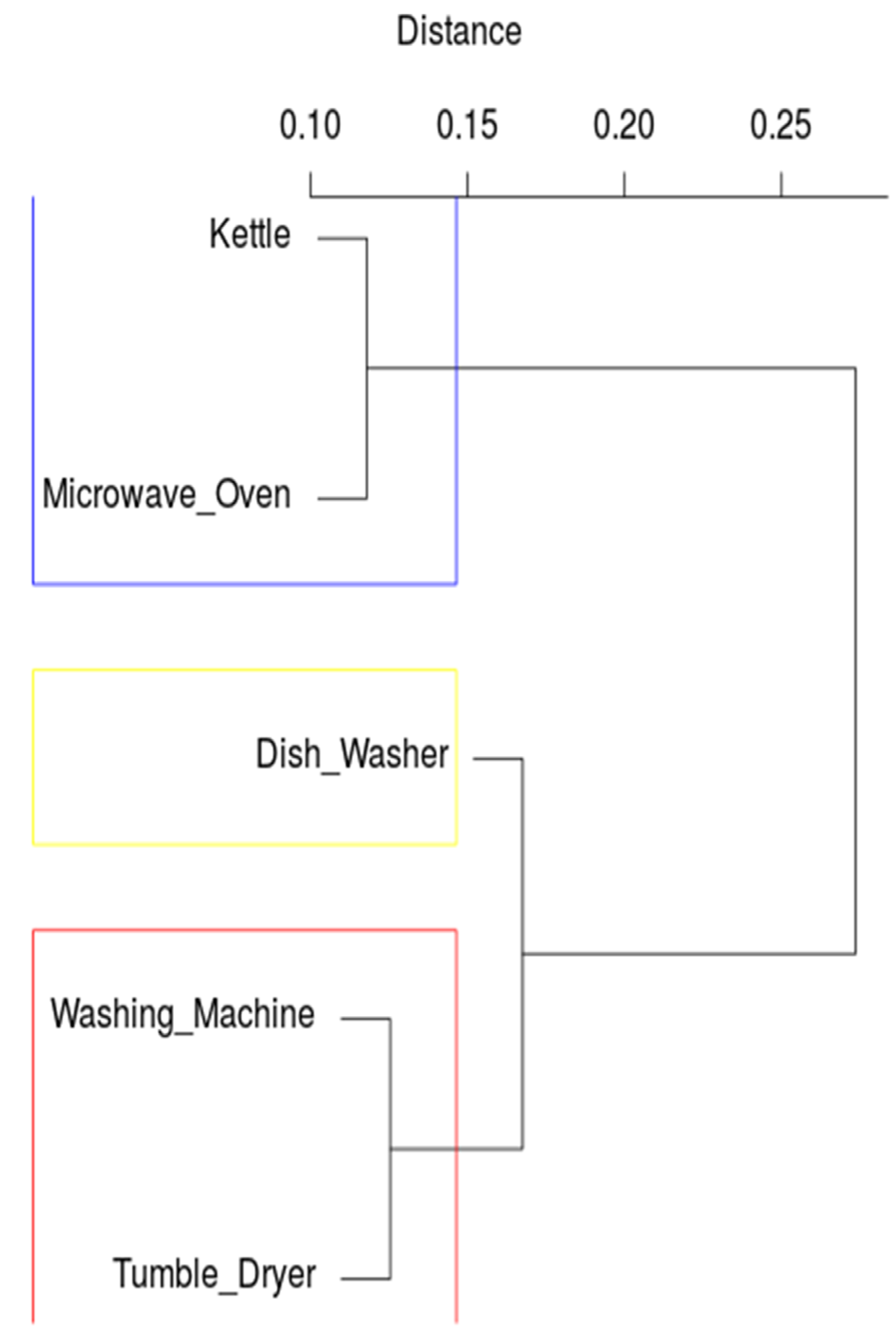
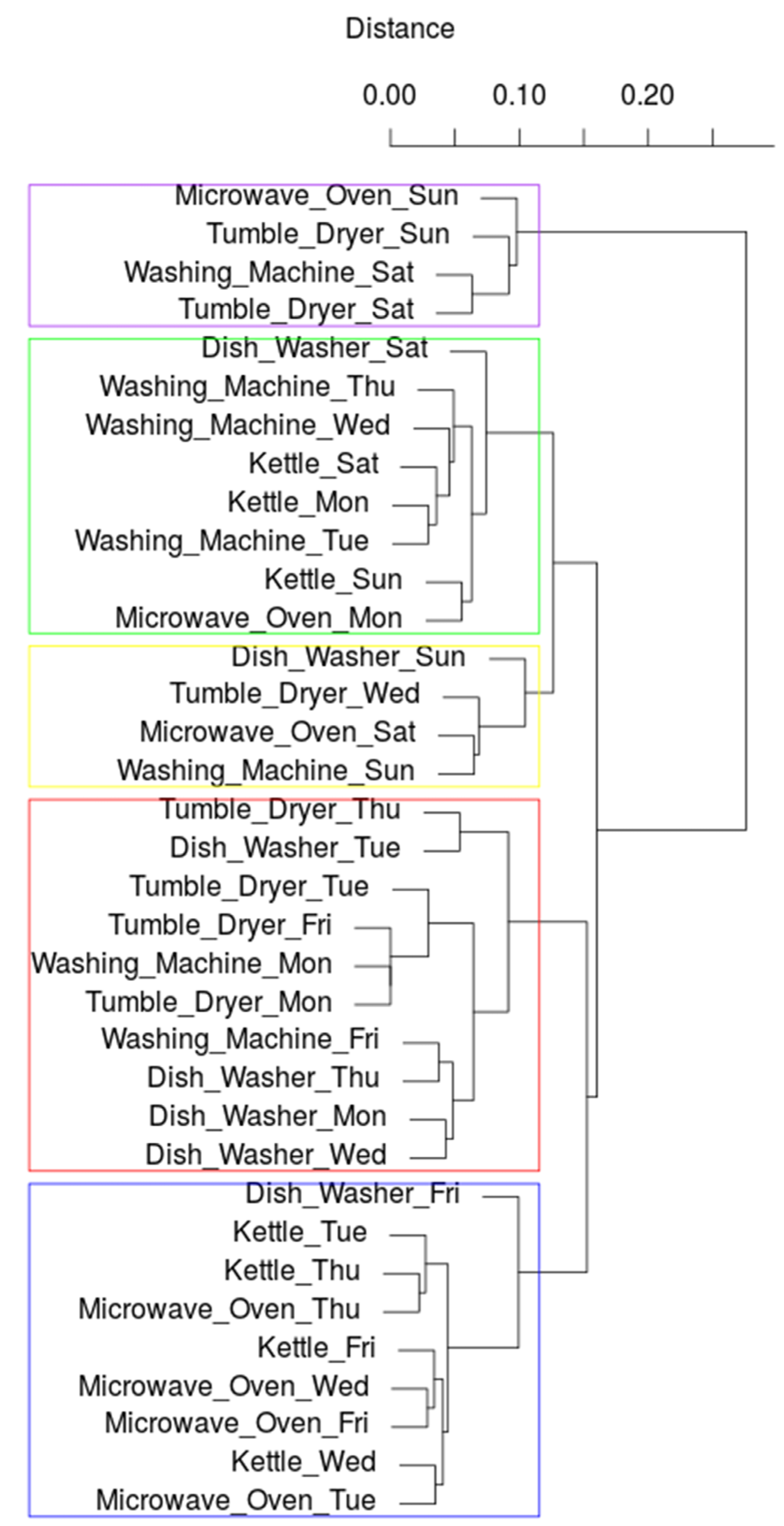
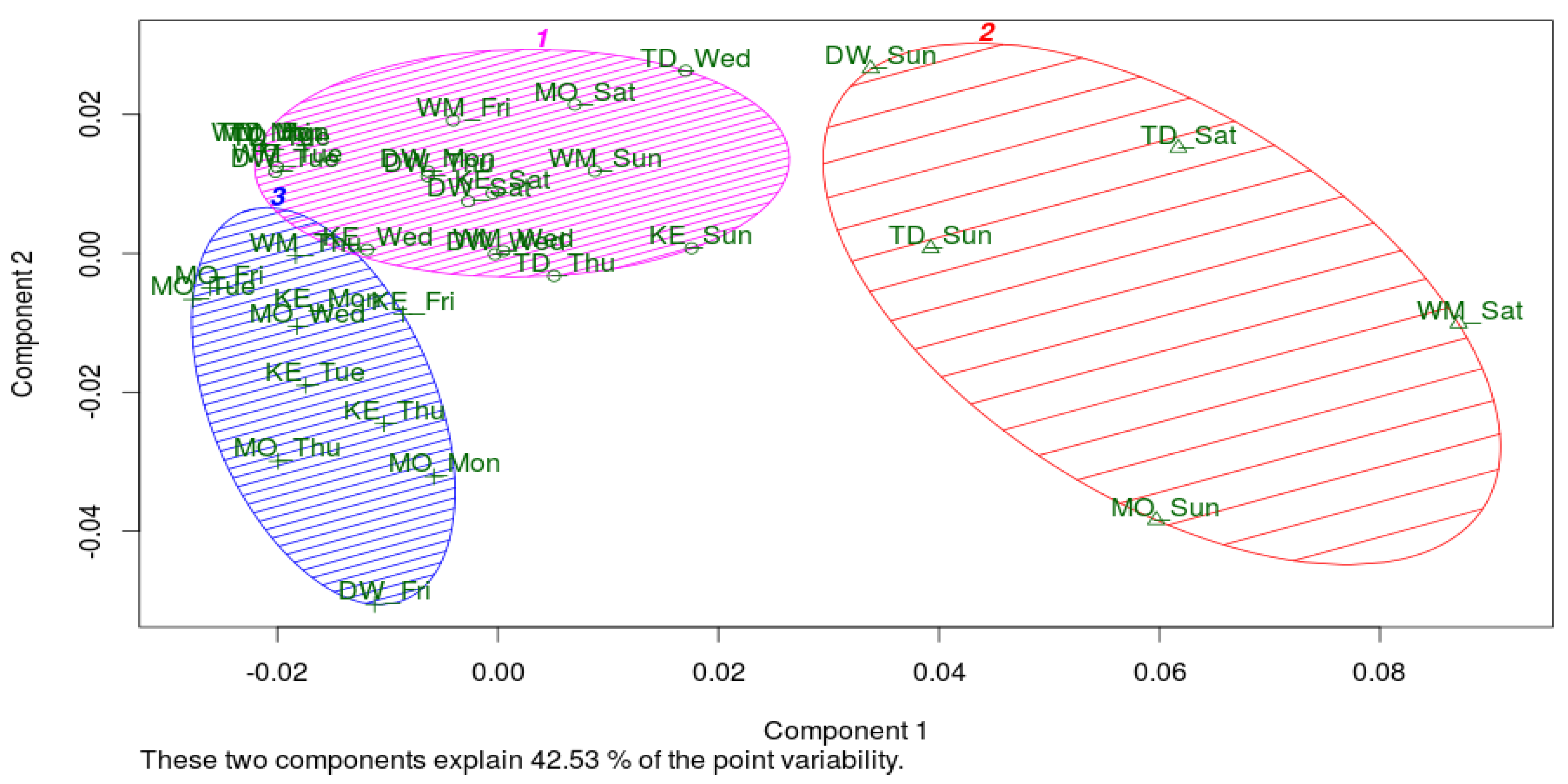
4.4. Detecting patterns Using C-Means Clustering and Multidimensional Scaling
4.5. Detecting Patterns Using Grade Data Analysis
- Gray—the measure for the element is neutral (ranging between 0.99 and 1.01) what means that the real value of the measure is equal to its expected value;
- black or dark gray—the measure for the element is over-represented (between 1.01 and 1.5 for weak over-representation and more than 1.5 for strong) what means that the real value of the measure is greater than the expected one;
- light gray or white the measure for the element is under-represented (between 0.66 and 0.99 for weak under-representation and less than 0.66 for strong under-representation) what means that the real value of measure is less than the expected one.
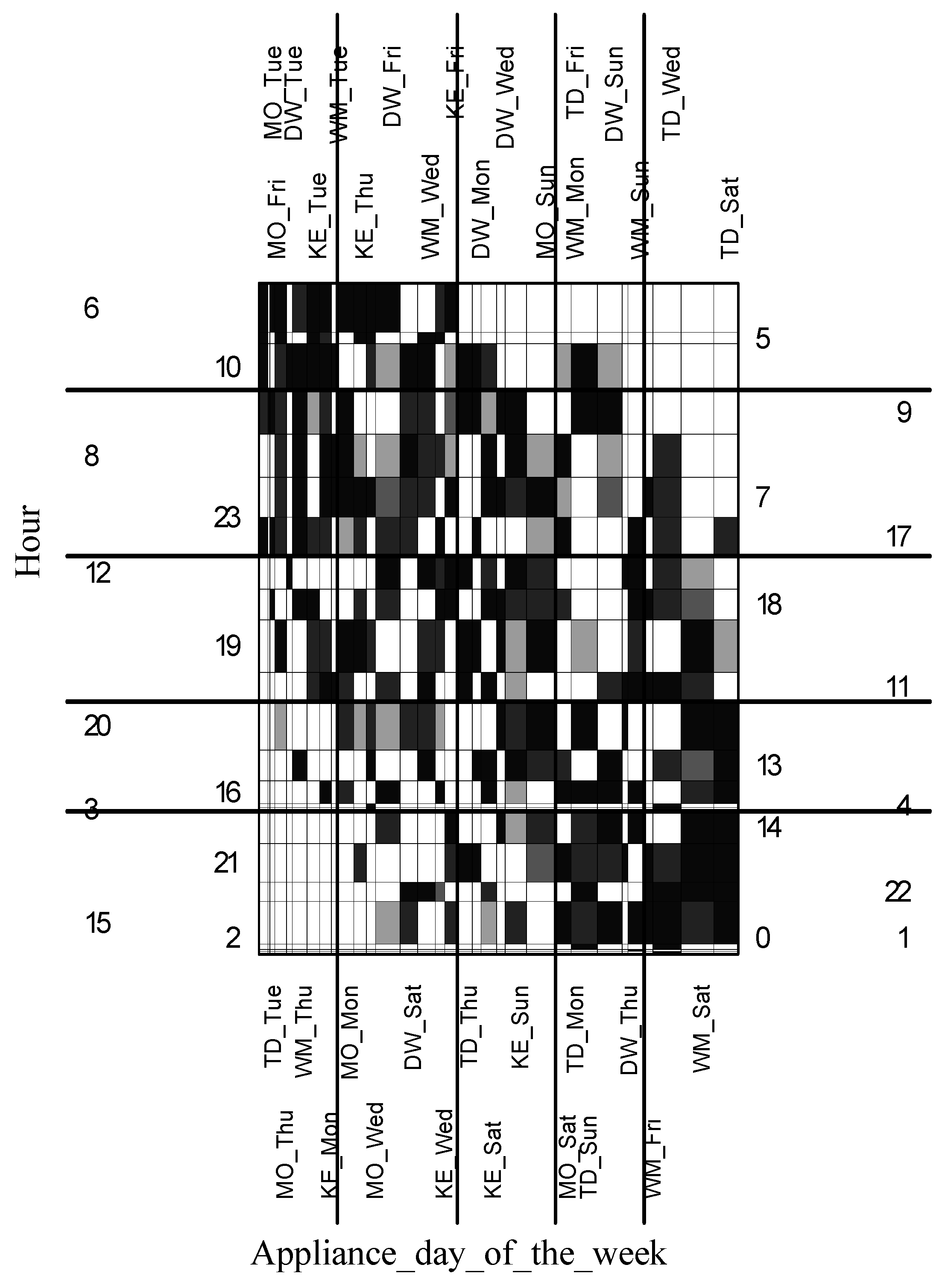
4.6. Detecting Patterns Using Sequential Association Rules
- with the support equal to 0.1 and with the confidence of 100%, if in a certain hour the washing machine operated, in the next hour the tumble dryer and kettle operated;
- with the support equal to 0.1 and with the confidence of 100%, if in a certain hour the washing machine operated, in the next hour the washing machine and kettle operated, and in the next hour the washing machine also operated, so did the tumble dryer and kettle;
- rule No. 4 with the support equal to 0.15, and with the confidence of 75% shows that the occurrence in a sequence of such devices as kettle, dish washer and washing machine influences the occurrence in a sequence of such appliances as tumble dryer and kettle.
- with the support equal to 0.1 and with the confidence of 66%, if in a certain hour the kettle operated, in the next hour the washing machine was turned ON, then in the next hour the washing machine and microwave were in operation.
| Sequence Stamp | Time Stamp | Elements |
|---|---|---|
| 20120910 | 8 | kettle |
| 20120910 | 9 | kettle, microwave |
| 20120910 | 10 | kettle, dish washer |
| 20120910 | 11 | kettle, dish washer |
| 20120910 | 18 | microwave |
| 20120910 | 19 | kettle |
| 20120910 | 20 | washing machine |
| 20120910 | 21 | washing machine, tumble dryer |
| 20120910 | 22 | microwave, washing machine, tumble dryer |
| 20120911 | 10 | kettle, microwave, dish washer, tumble dryer |
| 20120911 | 11 | tumble dryer, dish washer |
| 20120911 | 12 | kettle |
| 20120911 | 13 | microwave |
| 20120911 | 19 | washing machine |
| 20120911 | 20 | microwave, washing machine |
| 20120911 | 21 | kettle, microwave, tumble dryer |
| Sequence | Support | Confidence | Lift |
|---|---|---|---|
| {washing machine} => {kettle, tumble dryer} | 0.10 | 1.00 | 4.44 |
| {kettle} => {kettle, tumble dryer} | 0.10 | 1.00 | 4.44 |
| {washing machine},{kettle, washing machine},{washing machine} => {kettle, tumble dryer} | 0.10 | 1.00 | 4.44 |
| {kettle},{dish washer},{kettle},{washing machine},{washing machine} => {kettle, tumble dryer} | 0.15 | 0.75 | 3.33 |
| {washing machine},{kettle},{washing machine} => {washing machine, tumble dryer} | 0.10 | 0.66 | 2.96 |
| {kettle},{washing machine} => {microwave, washing machine} | 0.10 | 0.66 | 2.96 |
5. Conclusions
- (1)
- big appliances consuming greater amounts of electricity were predominantly used during weekend days or late afternoons during working days;
- (2)
- the kettle and microwave oven were frequently used in the morning during working days;
- (3)
- the use of the washing machine implied the kettle and tumble dryer would be switched on soon;
- (4)
- time-based associations can be easily observed using segmentation algorithms while associations between devices can be revealed using sequential rules;
- (5)
- working periods of the washing machine and the tumble dryer are very similar and depend on each other;
- (6)
- in general, appliances were operated in a way that they formed stable patterns as to the time of the use and day of the week.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beckel, C.; Sadamoria, L.; Staake, T.; Santini, S. Revealing Household Characteristics from Smart Meter Data. Energy 2014, 78, 397–410. [Google Scholar] [CrossRef]
- Costanza, E.; Ramchurn, S.D.; Jennings, N.R. Understanding domestic energy consumption through interactive visualisation: A field study. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, UbiComp ’12, New York, NY, USA, 5–8 September 2012; pp. 216–225.
- Abrahamse, W.; Steg, L.; Vlek, C.; Rothengatter, T. A review of intervention studies aimed at household energy conservation. J. Environ. Psychol. 2005, 25, 273–291. [Google Scholar] [CrossRef]
- Chetty, M.; Tran, D.; Grinter, R. Getting to Green: Understanding Resource Consumption in the Home. In Proceedings of the Ubicomp ’08, Seoul, Korea, 21–24 September 2008; pp. 242–251.
- Froehlich, J.; Findlater, L.; Landay, J. The design of eco-feedback technology. In Proceedings of the CHI ’10, Atlanta, GA, USA, 10–15 April 2010; pp. 1999–2008.
- Fischer, C. Feedback on household electricity consumption: A tool for saving energy? Energy Effic. 2008, 1, 79–104. [Google Scholar] [CrossRef]
- Fitzpatrick, G.; Smith, G. Technology-enabled feedback on domestic energy consumption: articulating a set of design concerns. IEEE Pervasive Comput. 2009, 8, 37–44. [Google Scholar] [CrossRef]
- Rollins, S.; Banerjee, N.; Choudhury, L.; Lachut, D. A system for collecting activity annotations for home energy management. Pervasive Mob. Comput. 2014, 15, 153–165. [Google Scholar] [CrossRef]
- Gustafsson, A.; Gyllensward, M. The power-aware cord: energy awareness through ambient information display. In Proceedings of the CHI EA ’05, Portland, OR, USA, 2–7 April 2005; pp. 1423–1426.
- Rodgers, J.; Bartram, L. Exploring ambient and artistic visualization for residential energy use feedback. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2489–2497. [Google Scholar] [CrossRef] [PubMed]
- Firth, S.; Lomas, K.; Wright, A.; Wall, R. Identifying trends in the use of domestic appliances from household electricity consumption measurements. Energy Build. 2008, 40, 926–936. [Google Scholar] [CrossRef]
- Chang, H.H. Non-intrusive demand monitoring and load identification for energy management systems based on transient feature analyses. Energies 2012, 5, 4569–4589. [Google Scholar] [CrossRef]
- Tina, G.M.; Amenta, V.A. Consumption awareness for energy savings: NIALM algorithm efficiency evaluation. In Proceedings of the 5th International Renewable Energy Congress (IREC), Hhammamet, Tunisia, 25–27 March 2014.
- Dent, I. Deriving Knowledge of Household Behaviour from Domestic Electricity Usage Metering. Ph.D. Thesis, University of Nottingham, Nottingham, England, UK, 1 July 2015. [Google Scholar]
- Zeifman, M.; Roth, K. Nonintrusive appliance load monitoring: Review and outlook. Consumer Electronics. IEEE Trans. Consum. Electron. 2011, 57, 76–84. [Google Scholar] [CrossRef]
- Ghofrani, M.; Hassanzadeh, M.; Etezadi-Amoli, M.; Fadali, M.F. Smart meter based short-term load forecasting for residential customers. In Proceedings of the North American Power Symposium (NAPS), Northeastern University, Boston, MA, USA, 4–6 August 2011; pp. 1–5.
- Aung, Z.; Williams, J.; Sanchez, A.; Toukhy, M.; Herrero, S. Towards Accurate Electricity Load Forecasting in Smart Grids. In Proceedings of the 4th International Conference on Advances in Databases, Knowledge and Data Applications, DBKDA 2012, Saint Gilles, Reunion Island, 29 February–5 March 2012; pp. 51–57.
- Javed, F.; Arshad, N.; Wallin, F.; Vassileva, I.; Dahlquist, E. Forecasting for demand response in smart grids: an analysis on use of anthropologic and structural data and short term multiple loads forecasting. Appl. Energy 2012, 69, 151–160. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Ząbkowski, T. Short term electricity forecasting using individual smart meter data. Procedia Comput. Sci. 2014, 35, 589–597. [Google Scholar] [CrossRef]
- Ząbkowski, T.; Gajowniczek, K. Forecasting of individual electricity usage using smart meter data. Quantitative Methods in Economics 2013, 14, 289–297. [Google Scholar]
- Ghaemi, S.; Brauner, G. User behavior and patterns of electricity use for energy saving. In Proceedings of the Internationale Energiewirtschaftstagung an der TU Wien, IEWT, Vienna, Austria, 11–13 February 2009.
- Yohanis, Y.G.; Mondol, J.D.; Wright, A.; Norton, B. Real-life energy use in the UK: How occupancy and dwelling characteristics affect domestic energy use. Energy Build. 2008, 40, 1053–1059. [Google Scholar] [CrossRef]
- Hargreaves, T.; Nye, M.; Burgess, J. Making energy visible: A qualitative field study of how householders interact with feedback from smart energy monitors. Energy Policy 2010, 38, 6111–6119. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar]
- Lance, G.N.; Williams, W.T. A general theory of classificatory sorting strategies 1. Hierarchical systems. Comput. J. 1967, 9, 373–380. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Gower, J.C. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika 1966, 53, 325–328. [Google Scholar] [CrossRef]
- Mardia, K.V. Some properties of classical multidimensional scaling. Commun. Stat. Theory Methods 1978, A7, 1233–1241. [Google Scholar] [CrossRef]
- Siedlecki, W.; Siedlecka, K.; Sklanski, J. An overview of mapping for exploratory pattern analysis. Pattern Recognit. 1988, 21, 411–430. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Pison, G.; Struyf, A.; Rousseeuw, P.J. Displaying a clustering with CLUSPLOT. Comput. Stat. Data Anal. 1999, 30, 381–392. [Google Scholar] [CrossRef]
- Szczesny, W. On the performance of a discriminant function. J. Classif. 1991, 8, 201–215. [Google Scholar]
- Ciok, A.; Kowalczyk, T.; Pleszczyńska, E. How a New Statistical Infrastructure Induced a New Computing Trend in Data Analysis. In Rough Sets and Current Trends in Computing; Polkowski, L., Skowron, A., Eds.; Lecture Notes in Artificial Intelligence; Springer Verlag: Berlin, Germany, 1998; Volume 1424, pp. 75–82. [Google Scholar]
- Szczesny, W. Grade correspondence analysis applied to contingency tables and questionnaire data. Intell. Data Anal. 2002, 6, 17–51. [Google Scholar]
- Kowalczyk, T.; Pleszczyńska, E.; Ruland, F. Grade Models and Methods of Data Analysis. With applications for the Analysis of Data Population, 1st ed.; Studies in Fuzziness and Soft Computing; Springer Verlag: Berlin, Germany; Heidelberg, Germany; New York, NY, USA, 2004; Volume 151. [Google Scholar]
- GradeStat—Program for Grade Data Analysis. Available online: http://www.gradestat.ipipan.waw.pl (accessed on 10 January 2015).
- Agrawal, R.; Srikant, R. Mining sequential patterns. In Proceedings of the 11th International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1995.
- Bębel, B.; Morzy, M.; Morzy, T.; Królikowski, Z.; Wrembel, R. OLAP-Like analysis of time point-based sequential data. In Advances in Conceptual Modeling; Springer Verlag: Berlin, Germany, 2012; pp. 153–161. [Google Scholar]
- Zaki, M.J. Spade: An efficient algorithm for mining frequent sequences. Mach. Learn. 2001, 42, 31–60. [Google Scholar] [CrossRef]
- Radziszewska, W.; Nahorski, Z.; Parol, M.; Pałka, P. Intelligent computations in an agent-based prosumer-type electric microgrid control system. In Issues and Challenges of Intelligent Systems and Computational Intelligence; Springer Verlag: Berlin, Germany, 2014; pp. 293–312. [Google Scholar]
- Radziszewska, W.; Kowalczyk, R.; Nahorski, Z. El Farol Bar problem, Potluck problem and electric energy balancing–on the importance of communication. In Proceedings of the 2014 Federated Conference on Computer Science and Information Systems, Warsaw, Poland, 7–10 September 2014; pp. 1515–1523.
- Pałka, P.; Radziszewska, W.; Nahorski, Z. Balancing electric power in a microgrid via programmable agents auctions. Control Cybern. 2012, 41, 777–797. [Google Scholar]
- Radziszewska, W.; Nahorski, Z. Modeling of power consumption in a small microgrid. In Proceedings of the 28th EnviroInfo 2014 Conference, Oldeburg, Germany, 10–12 September 2014; pp. 381–388.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajowniczek, K.; Ząbkowski, T. Data Mining Techniques for Detecting Household Characteristics Based on Smart Meter Data. Energies 2015, 8, 7407-7427. https://doi.org/10.3390/en8077407
Gajowniczek K, Ząbkowski T. Data Mining Techniques for Detecting Household Characteristics Based on Smart Meter Data. Energies. 2015; 8(7):7407-7427. https://doi.org/10.3390/en8077407
Chicago/Turabian StyleGajowniczek, Krzysztof, and Tomasz Ząbkowski. 2015. "Data Mining Techniques for Detecting Household Characteristics Based on Smart Meter Data" Energies 8, no. 7: 7407-7427. https://doi.org/10.3390/en8077407
APA StyleGajowniczek, K., & Ząbkowski, T. (2015). Data Mining Techniques for Detecting Household Characteristics Based on Smart Meter Data. Energies, 8(7), 7407-7427. https://doi.org/10.3390/en8077407







