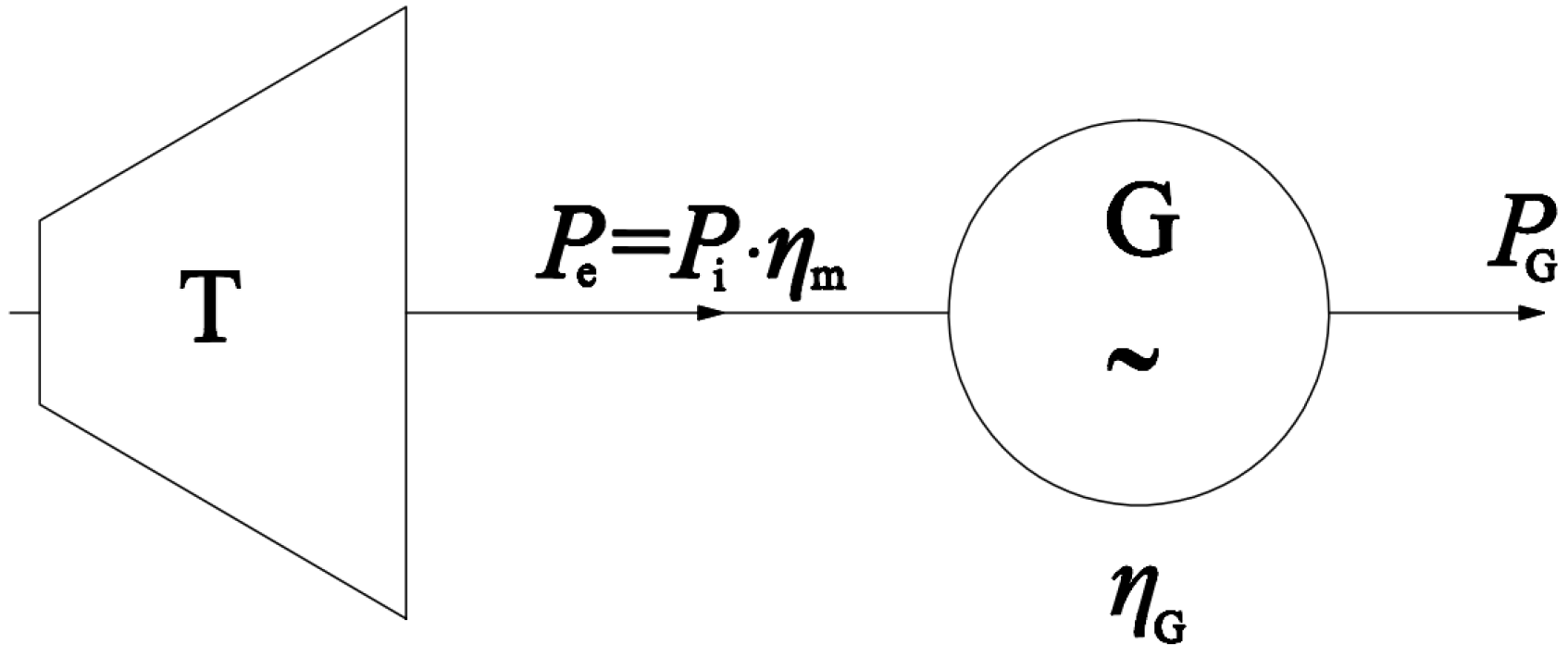1. Introduction
Low speed two-stroke turbocharged diesel engines are the most commonly used marine propulsion engines today. These engines are the most efficient, exhibiting 50% efficiency, with the remaining 50% of the energy released from fuel combustion being dispelled to the atmosphere as waste heat.
The potential uses of waste heat and other forms of low temperature energy have been investigated for decades, but its use to generate power by means of ORC systems is a relatively recent notion. Such systems are similar to conventional steam power plants in their configuration. By the use of organic working fluids instead of steam, it is possible to increase the plant efficiency and reduce its cost when recovering power from heat sources at temperatures below 500 °C.
When cooling water is available, Aly [
1] estimated that the heat recovered from diesel engine exhaust gases can be used to obtain an additional 15% to 16% increase in the total power output. The uses for exhaust gas heat, taken into account by Shu
et al. [
2], are turbocharger/power, fresh water obtained by using multiple effect distillation or multi-stage flash desalination technology, electric/power obtained from a Rankine cycle system and air conditioning and ice-making obtained by means of sorption refrigeration. They estimated that 2150 kW can be generated using the exhaust gas from a turbocharged diesel engine of 69,900 kW power output to raise the steam in a dual pressure system with a multi stage turbine. Heat is also recovered from the jacket cooling water and scavenging air cooler to preheat feed water before it enters the boiler. This could be raised to 4000 kW if part of the exhaust gases bypasses the turbocharger. The best result was achieved with an additional power turbine using bypass exhaust gases to generate a total of 5610 kWe. This increased the overall plant thermal efficiency by 8.03%. Butcher and Reddy [
3] carried out a second law analysis of the influence of the gas composition, specific heat and pinch point temperature on the performance of a Heat Recovery Steam Generator (HRSG). They found that the performance of the power generation system is very sensitive to the gas composition. The pinch point (PP) is a dominant parameter and should be selected carefully. Wang
et al. [
4] revealed that R11, R141b, R113 and R123 exhibit slightly better thermodynamic performance than other fluids, while R245fa and R245ca are the most suitable ones (R11 and R113 have been completely banned since 2005). In this work, which is a continuation of work presented in [
5], a new method for waste heat recovery (WHR) was investigated to decrease the fuel consumption and emissions of ship propulsion systems.
2. WHR System Modeling
A study was made to determine whether a CHP system could be developed to obtain the entire auxiliary power and heating requirements for the ship, during navigation, from its waste heat. This was based on the use of an ORC WHR system, using R245fa and the R123 as working fluids. The analysis was based on the use of steady flow thermodynamic equations. These are applicable for all operating conditions, other than those encountered during extremely heavy seas, bad weather conditions or when maneuvering. The thermodynamic properties of air, exhaust gases, fuel, water and the working fluids were all obtained using version 9 of the National Institute of Standards and Technology (NIST) Refprop program [
6]. The cogeneration system was analyzed as a thermodynamic flow process, and presented schematically with
h-s and
T-s diagrams.
Suezmax-sized oil tankers were considered for this study, with 18,660 kW@91rpm at SMCR, which equals 100% Nominal Maximum Continuous Rating (NMCR). In such a tanker, the auxiliary power is normally obtained from a 912 kWe diesel genset.
The heavy fuel oil (HFO) and lube oil (LO) have to be heated before separation. This is done for the HFO in a feeder/booster module, the HFO tanks (service tanks, settling tanks, storage tanks), and the low grade sulfur (LGS) HFO tank. In addition, seasonal heating must be provided for the crew. The steam required for these and any other ship heating requirements is generated in a boiler. A common design is for a composite boiler consisting of an oil-fired section and an exhaust gas section, both placed in a common shell. During navigation, the exhaust gas heat from the main engine is utilized as the heat source for these functions. In port, when the main engine is shut down, the oil fired section takes over to produce steam. The following assumptions were made in these calculations:
Table 1.
Heat consumption during navigation for fuel, lube oil and hot water heating.
Table 1.
Heat consumption during navigation for fuel, lube oil and hot water heating.
| Steam heat consumers | Consumed energy (kW) | Max. temperature (°C) |
|---|
| ME/AE FO module | 196 | from 110 °C to 145 °C |
| HFO storage tanks | 160 | 45 °C |
| Others | 320 | max 98 °C |
The steam heat consumer classified as others includes heating of the HFO, DO, LO and hot water for crew requirements, up to a maximum temperature of 98 °C. In this work, the heating of the crew living space was neglected for ISO Standard Conditions. Hence, as shown in
Table 1, the total heat requirement during navigation is 676 kW.
Although previous calculations [
5] showed that it was not necessary to use heat from the jacket cooling water, in this study, the heat from the main engine jacket cooling water was included as well as that from the scavenged air and the exhaust gases. The initial data refer to the standard ambient reference conditions according to ISO 3046 [
7]. The engine data; specific fuel consumption, temperature and mass flow rate of the exhaust gases, jacket cooling water and scavenged air were acquired from the MAN engine room dimensioning software [
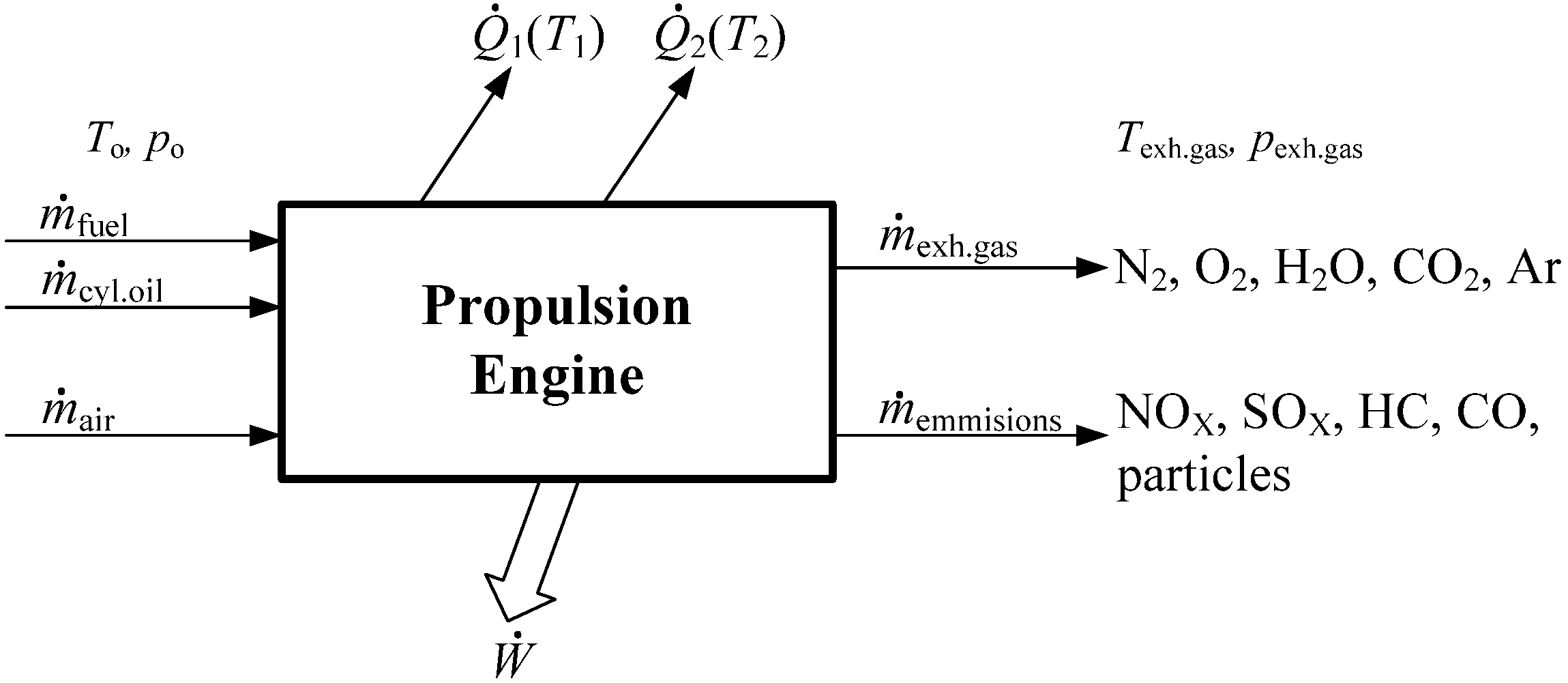
8] for the 6S70MC-C7-T1 engine. These values are not constant. The only constant value used is the information on exhaust emissions obtained from the MAN data for a similar engine. The composition of the exhaust gas was calculated using an in house zero-dimensional model. The propulsion engine model depicting the main input and output variables is shown in
Figure 1.
Figure 1.
The propulsion engine model depicting main input and output substances and energy flows.
Figure 1.
The propulsion engine model depicting main input and output substances and energy flows.
It was assumed that the fluid flow through the propulsion engine is steady. The observer position is stationary with respect to the control volume surrounding the drive motor, which, in this case, is the ship’s propulsion engine.
The first law of thermodynamics can be expressed as the conservation of energy in the control volume. Disregarding changes in potential and kinetic energy, the following can be expressed as:
where
is the total heat inflow;
the shaft work outflow and
and
are the mass flow rates and specific enthalpies of the individual flow substances.
Although the scavenged air consumption was taken from MAN B&W CEAS_ERD at ISO standard conditions, the composition of the air was calculated by NIST using our initial values. The fuel composition for MDO and cylinder oil composition were also taken into account. The heat input from the fuel is expressed in terms of its Lower Calorific Value while the fuel and air mass flow rates must meet the following relation:
2.1. Working Fluid and Cycle Selection
The exhaust gas temperatures for the assumed diesel engine vary from 230 °C to 250 °C [
8], while Larsen
et al. [
9] suggested that for heat sources of more than 240 °C the most efficient is the supercritical ORC cycle. A similar conclusion was reached by Gao
et al. [
10]. In addition to the temperature and mass flow rate of exhaust gases [
8] for the main engine load from 25% to 100%
SMCR, other data are provided including mass flow rate and pressure of turbocharged air, temperature before and after the air cooler, the scavenge air cooler heat, jacket water cooler heat and main lubrication oil heat. Accordingly, a supercritical cycle was assumed for this study, with the R245fa as the working fluid with an optimal maximum pressure of 4.5 MPa. This is in very good correlation with the work of Gao
et al. [
10].
Table 2.
Properties of R123, R245fa and R245ca [
6].
Table 2.
Properties of R123, R245fa and R245ca [6].
| Property | R123 | R245fa | R245ca |
|---|
| Chemical/structural formula | C2HCl2F3 | CHF2CH2CF3 | CHF2 CF2CH2F |
| Molecular mass kg/kmol | 152.93 | 134.05 | 134.05 |
| Boiling point at 1.0133 bar | 27.82 °C | 15.140 °C | 25.133 °C |
| Density kg/m3 at 1.0133 bar | (L) 1,456.6 (V) 6.4717 | (L) 1,364.9 (V) 5.9619 | (L) 1,386.0 (V) 5.7371 |
| Enthalpy kJ/kg at 1.0133 bar | (L) 228.03 (V) 398.22 | (L) 219.51 (V) 415.55 | (L) 232.82 (V) 433.78 |
| Critical point °C/bar | 183.68 / 36.618 | 154.01/36.51 | 174.42/39.25 |
| Atmospheric Life Time (ALT) | 1.3 y | 7.6 y | 6.2y |
| Ozone Depletion Potential (ODP) | 0.02 | 0 | 0 |
| GWP | 77 | 1030 | 693 |
| ASHRAE safety group | B1 | B1 | n.a. |
As an alternative to the R245fa, R123 was also considered and some of its properties are shown in
Table 3, together with the properties of the R245ca. A
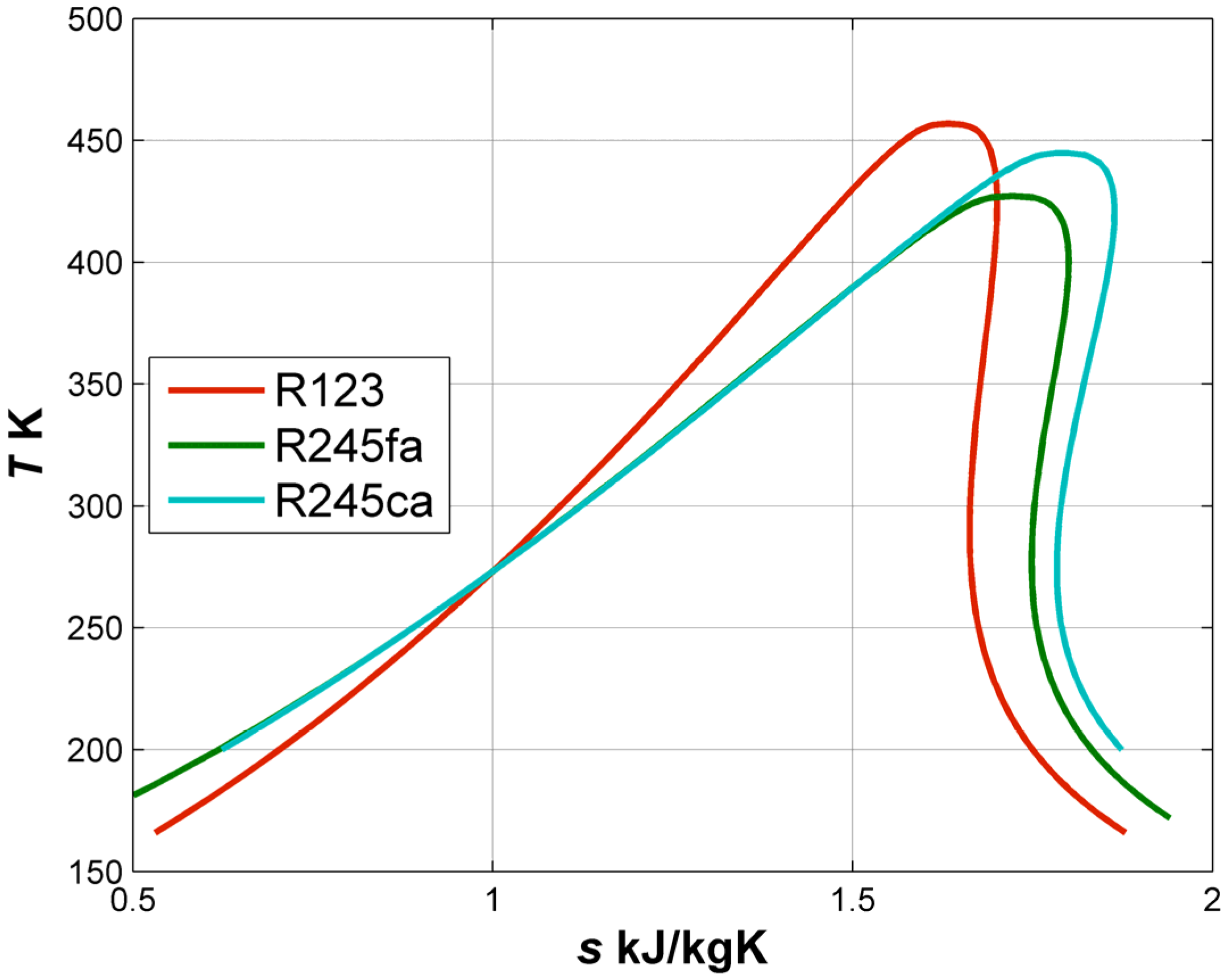
T-s diagram of the most commonly used or considered fluids for the power recovery systems from low grade heat is shown in
Figure 2.
Figure 2.
T-s diagram of the selected working fluids based on [
6].
Figure 2.
T-s diagram of the selected working fluids based on [
6].
Organic fluids such as R245fa, R245ca and R123 are recognized as very convenient fluids for the use in organic Rankine cycles. Fluids R245fa and R245ca are dry fluids, and R123 can be considered as an isentropic fluid, even though it is a dry fluid.
The main advantage of operating at a supercritical pressure is that the continuously increasing temperature during heat input results in a better match with the heat source and hence produces a higher thermal efficiency. Currently, turbines with power outputs ranging from a few kW up to 3 MW are used as expanders in ORC processes and these achieve adiabatic efficiencies of approximately 85% in turbines of over 0.5 MW output [
11,
12].
According to [
13,
14], the advantages of organic fluid turbines are their high adiabatic efficiencies, the low mechanical stress on the turbine due to the low blade speed, no blade erosion due to the absence of moisture during expansion, while the low turbine rotational speed enables direct coupling to the generator, and a longer service life compared to steam turbines. Additionally, organic working fluids enable higher cycle efficiencies to be obtained compared to steam, due to a better temperature matching in the heating process.
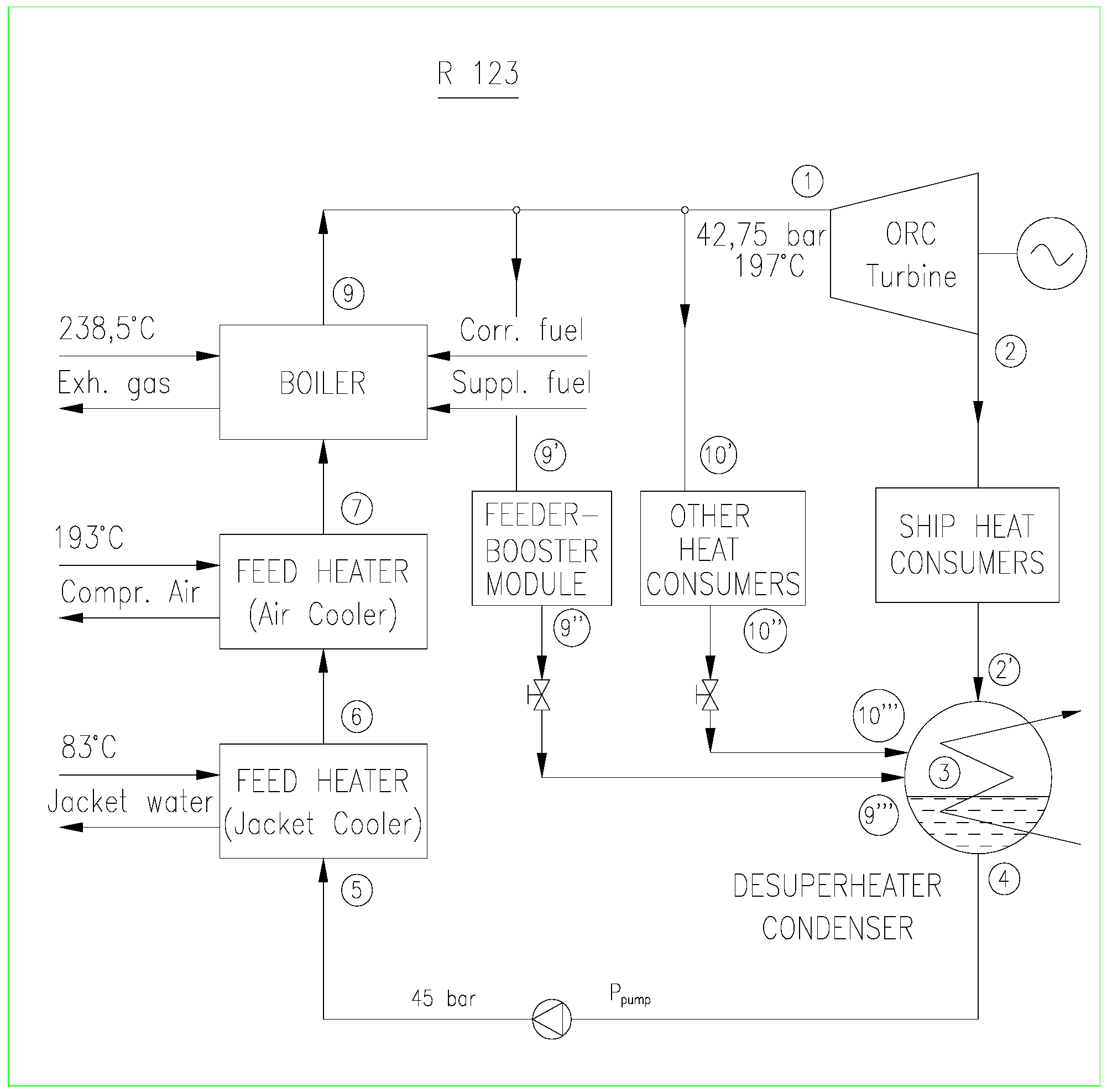
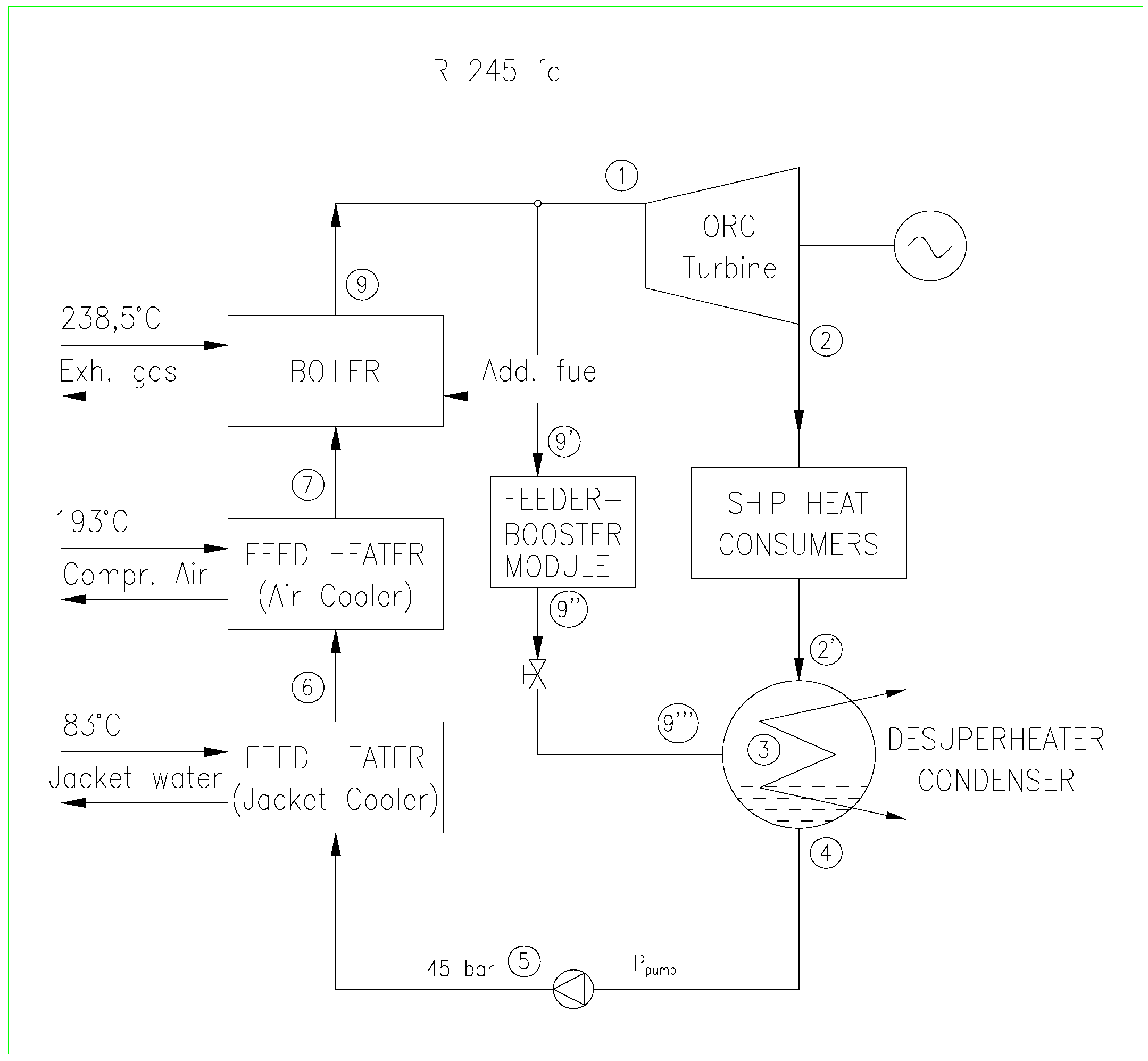
In this case it was assumed that the boiler functions through direct heating of the working fluid by the exhaust gases from the main ship engine without an intermediate thermal loop. The CHP plant with R245fa as the working fluid is shown in
Figure 3, and with R123 as the working fluid in
Figure 4.
Figure 3.
Schematic diagram of the CHP plant with R245fa fluid [
5,
15].
Figure 3.
Schematic diagram of the CHP plant with R245fa fluid [
5,
15].
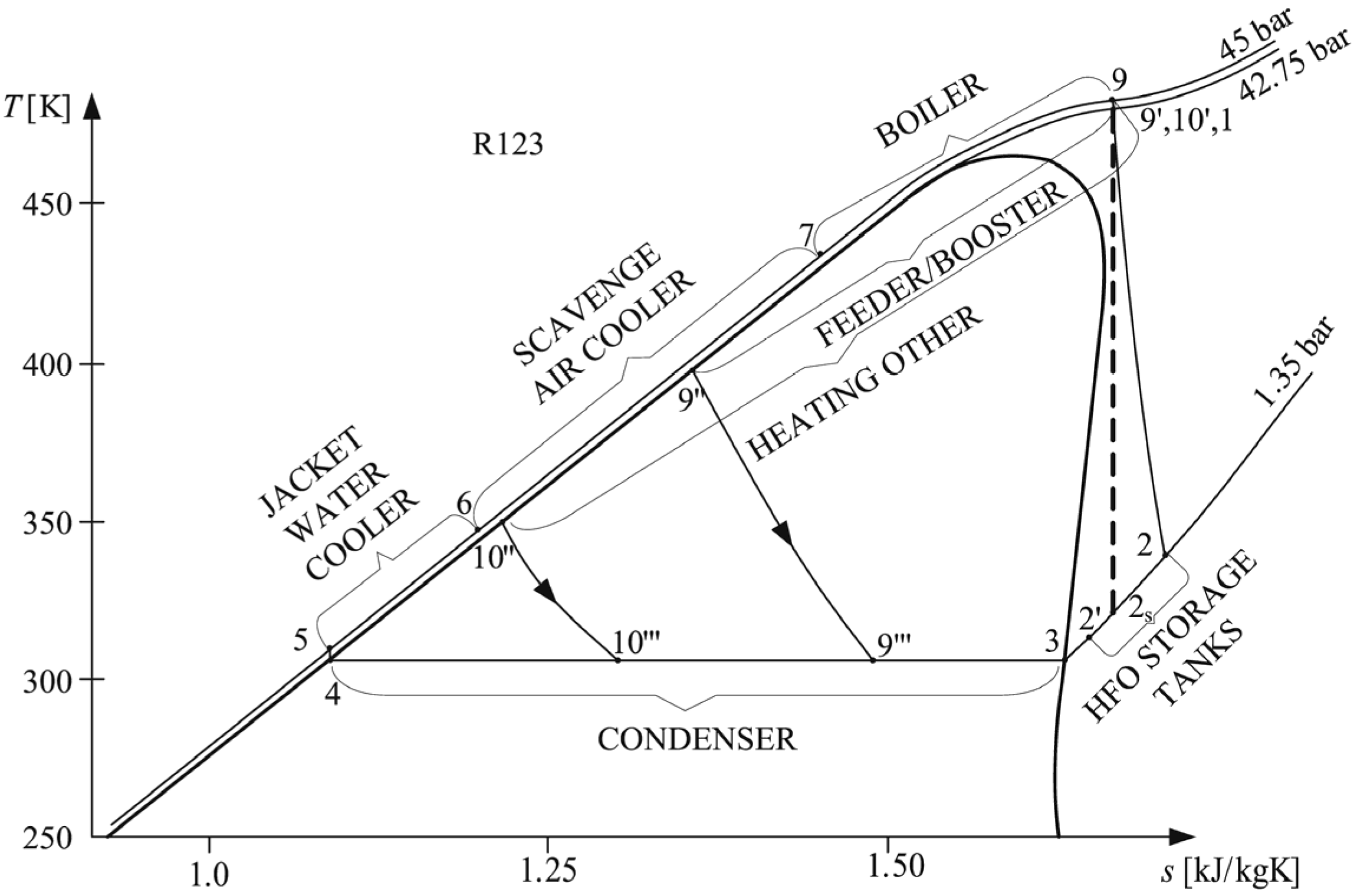
Figure 4.
Schematic diagram of CHP plant with R123 fluid PP15 [
15].
Figure 4.
Schematic diagram of CHP plant with R123 fluid PP15 [
15].
2.2. Thermodynamic Analysis of the WHR Plant and the Calculation for a Vapor Turbine using R245fa and R123 as Working Fluids for Full Electrical Power
All the displayed computations were performed, assuming the ISO standard conditions. The losses in fluid pressure were not considered except those between the boiler and the turbine. The computations for the auxiliary engine were made using HFO. In the Emission Control Area (ECA), the standard HFO is not acceptable; LGS HFO, marine DO or natural gas is used. In the ECA, a 0.10% sulfur limit came into effect on 1
st January 2015. This means that low grade sulfur marine gas oil (LGSMGO) or natural gas must be used as a ship’s fuel. As these fuels are more expensive (especially LGSMGO) than the HFO, the potential financial savings, from waste heat recovery, are thereby increased [
16]. When using fuel with LGS, the exhaust gas temperature can fall below 145 °C. As already explained, direct coupling of the turbine to the generator was assumed and therefore, as shown in
Figure 5, no gearbox was considered in the calculations.
Figure 5.
Turbine genset for electricity production during ship sails.
Figure 5.
Turbine genset for electricity production during ship sails.
The
T-s diagram of the CHP plant with a turbine and the R245fa as the working fluid is shown in
Figure 6 and R123 as the working fluid is shown in
Figure 7.
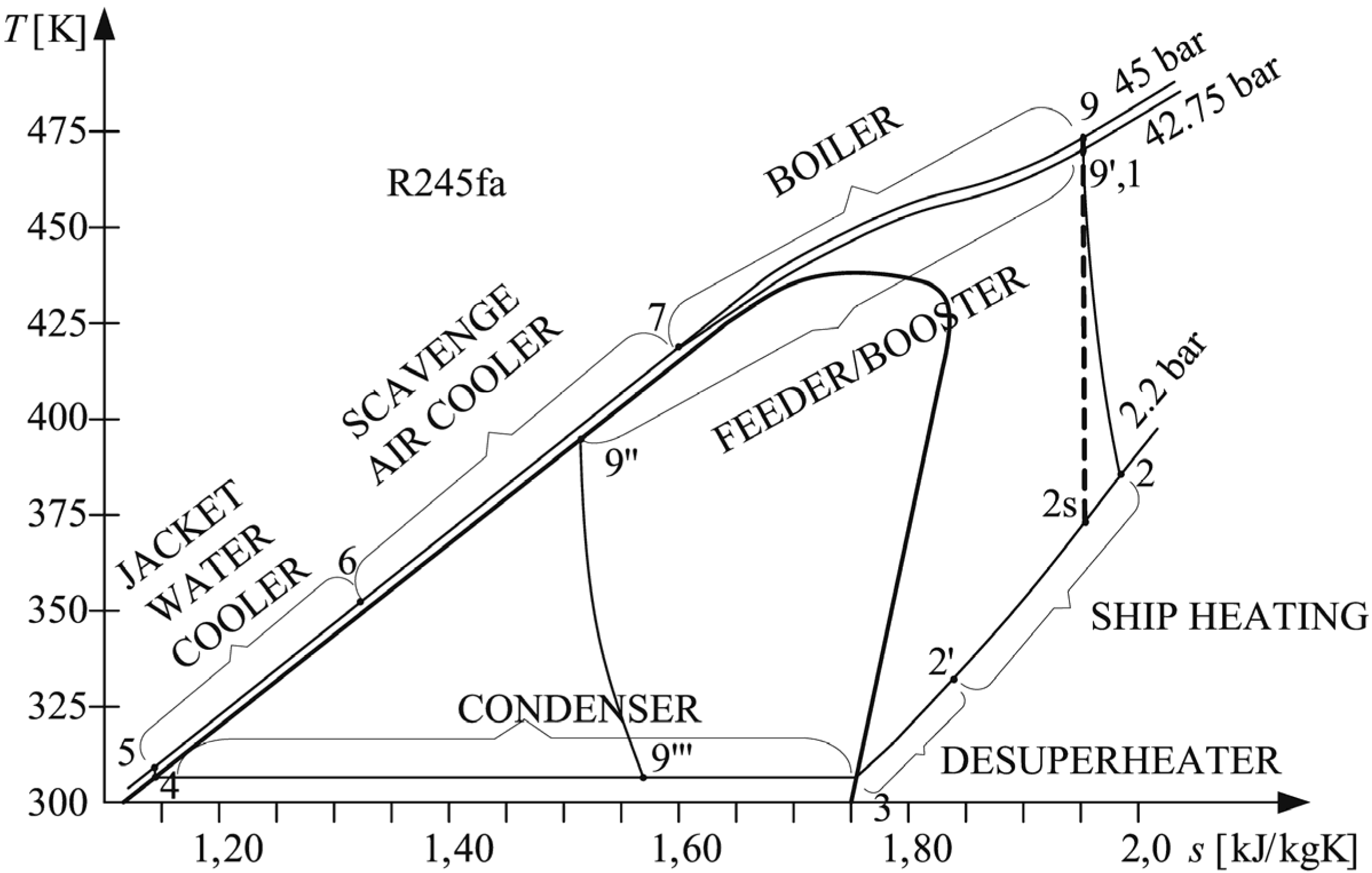
Figure 6.
T-s diagram for the ORC CHP Plant with R245fa fluid [
5,
15].
Figure 6.
T-s diagram for the ORC CHP Plant with R245fa fluid [
5,
15].
Figure 7.
T-s diagram for ORC CHP Plant with R123 fluid [
15].
Figure 7.
T-s diagram for ORC CHP Plant with R123 fluid [
15].
Before starting with the calculations it was necessary to assume values for some parameters, as shown in
Table 3.
In accordance with the similar designs/power, η
m and η
G were selected. The internal turbine power and the internal efficiency are as follows:
Table 3.
Major assumptions for the thermodynamic analysis.
Table 3.
Major assumptions for the thermodynamic analysis.
| Parameter | Unit | Value |
|---|
| Turbine Isentropic Efficiency, ηi = ηTS | – | 0.85 |
| Turbine mechanical efficiency, ηm | – | 0.96 |
| Gearbox efficiency, ηGB | – | 1.00 |
| Generator efficiency, ηG | – | 0.95 |
| Pump isentropic efficiency, ηp | – | 0.85 |
| Pump mechanical efficiency, ηpm | – | 0.8 |
| Heat lost in the heat exchanger, hl | % | 1 |
| Heat lost in the HRSG, hl | % | 2 |
| Combustion efficiency of supplement fuel, ηb | – | 0.99 |
| HFO Lower heating value, QLHVp | kJ/kg | 40,210 |
| Minimum exhaust gas temperature at HRSG outlet, T | °C | 145 |
| Pinch Point (PP) | °C | 15 |
| Working fluid pressure loss from HRGS to turbine, ploss | % | 5 |
| Working fluid temperature loss from HRGS to turbine, Tloss | °C | 3 |
| Power factor, cosφ | – | 0.8 |
| Full electric power during navigation for Diesel genset, PG | kW | 912 |
| Standard electric power during navigation for Diesel genset, PG | kW | 620 |
| Power plant working hours per year, th/y | h/y | 5,796.2 |
The small difference in enthalpies and the power target justify the considerable amount of fluid in this cycle. However, the fluid outlet state (
T2,
p2) has still a large specific volume. Therefore, fluid outlet speeds of
c2 = 40 to 60 m/s should be used. The outlet diameter of the pipeline towards the condenser can be estimated using the continuity equation:
In macroscopic form and control volume (
Vc):
For steady state one dimensional flow:
Furthermore, the following are applicable:
Because the temperature of the R245fa working fluid is 108.02 °C, after expansion in the turbine, the heat rejected from the working fluid, prior to condensation, can be used for all heating needs on the ship except for heating the HFO in the feeder/booster module before injection. To heat the HFO in the feeder/booster module, it is necessary to heat an additional amount of the working fluid in the HRSG. This additional working fluid is extracted before the turbine and transferred to the HFO heaters. For the R245fa fluid, the procedure is explained in ref [
5]. When using the R123 working fluid, the situation is different. The R123 working fluid after expansion in the turbine has a low temperature, 54.3 °C, and thus it is possible to heat HFO storage tanks only. All other heatings require heating an additional amount of the R123 fluid in the HRSG. Therefore, it is not only necessary to heat an additional amount of R123 for heating the HFO in the feeder-booster module (196 kW), it is also necessary to heat all other heat consumers (320 kW) with an additional amount of the R123 in the HRSG. The HFO storage tanks (160 kW) are heated with working fluid after exiting the turbine.
The required heat power for the booster module is the same for both working fluids:
where
hl is the percentage of heat lost in the heat exchanger. Hence,
The working fluid (
Figure 4 and
Figure 5) enters the fuel module at 197 °C and leaves it at 120 °C (
Table 5), which is 10 °C higher than the initial temperature of the heated HFO. For the given temperatures and for
, the enthalpies
h9' and
h9'' can be obtained. Because the working fluid is throttled after heating the HFO inside the fuel module,
p2''' =
p2 and
h9'' =
h9'''.
For the R123 working fluid, other heat consumers require 320 kW, and another amount of working fluid is heated at 45 bar up to 200 °C. This fluid heats HFO/DO and LO before separators, service and settling tanks, and water for the crew demands. The maximum heating temperature is 98 °C. After heating other consumers, R123 fluid is at state 10’’. After throttling to 10’’’, the fluid flows to the condenser. The feed ORC fluid from the condenser at the state point 4 is pumped up to 45 bar, reaching the state point 5.
The feed-pump power is as follows:
Compared to the water-based process, the ORC requires a much larger feed pump due to the considerably larger mass flow rate of the organic fluid. The computation is repeated to calculate the power required for the generator and turbine:
The computation was repeated to check the pump power and mass flow rate of the working fluid. The total mass flow rate of the working fluid is as follows:
The computation was repeated with the new generator and the turbine power using Equations (13) and (20).
After the condenser, the working fluid is pumped to 45 bar and the first heating is in the jacket water cooler. It is assumed that TORC,6 = 75 °C. At the iteration start, it is assumed that the jacket water outlet temperature is Tjacket,2 = 59.0 °C.
After being heated with the hot water from the cylinder jacket, the working fluid flows to the two-stage scavenged air heat exchanger. If the fluids do not change phase, the following is true:
The heat lost in the heat exchanger air/organic fluid depends on cooling through insulation only, totaling approximately 1% with normal insulation design:
In the boiler, the working fluid should be heated from 150 °C to 200 °C at 45 bar (assuming that no working fluid pressure is lost through the boiler):
According to [
3], the heat lost in the HRSG is typically 2%–3%. The pinch point is assumed to be 15 °C while the minimal temperature at the boiler outlet is 145 °C because at temperatures below 145 °C, sulfuric acid may form/by condensation. Therefore:
Since the working fluid at high main engine loads can heat easily with scavenged air to 150 °C, it is necessary to keep the exhaust gases temperature at the HRSG outlet at least 15 °C higher, in that range the exhaust gas temperature should be 165 °C. The exhaust gas energy disposal can be calculated by Equation (27):
The surplus/shortage of energy in the exhaust gases totals the following:
In order to produce 912 kW/1012.5 kW/1038.9 kW of electrical energy, supplemental fuel is required for the exhaust gas boiler at some engine loads:
When using R123 as a working fluid it is also necessary to burn the corrected supplemental fuel at full electrical power to keep the pinch point 15 °C at certain main engine loads. Therefore:
One of the tasks of this work is the calculation of the fuel consumption during an auxiliary Diesel genset acceptance test:
According to the manufacturer’s instructions, 5% higher fuel consumption in the auxiliary engine is allowed during service:
The fuel saving at 100%
SMCR is as follows:
The pinch point of 15 °C is selected. The temperature difference, through the exhaust gas boiler at the main engine loads is varying from 50% to 100% and the working fluid parameters from state 7 to state 9 have to be calculated:
2.3. Calculation for a Vapor Turbine Using the Organic Fluids for Standard Electrical Power
The computation for organic fluid was repeated for the standard electrical power (620 kWe). The same equations and assumptions were used, the regenerative ORC and the heat production for ship demands remain unchanged, and the turbine genset running on organic working fluid is identical to that previously used. Therefore, the turbo genset was used, as shown in the
T-s diagrams and in
Figure 6 and
Figure 7. The mechanical efficiency of the turbine and the generator will be the same as in the previous computation.
The internal turbine power is:
The utilization boiler parameters are the same as at full electrical power. Pressure and heat losses are identical to the previous ones.
The internal turbine efficiency using the R245fa or the R123 working fluid is 85% and the expansion finishes at the superheated region for the R245fa, and for the R123 at superheated region .
The ship heating requirements are the same as at full electrical power. For the heating of working fluid the heat from jacket water, scavenged air and exhaust gases are used.
The calculation shows that at these conditions the exhaust gas energy is sufficient from 60% to 100% of SMCR. Only below 60% SMCR of the main engine load, it is necessary to burn a small amount of the supplemental fuel in the utilization boiler to cover all ship power and heat demands.
2.4. Definitions of Efficiencies
The thermal efficiency of the organic CHP cycle is defined as follows:
The efficiency of the heat-exchange system, which transfers the heat from the heat source, in this case waste heat to the organic fluid, is defined as follows:
The efficiency of the cogeneration system or waste heat cogeneration efficiency can be defined as follows:
In the analyzed ship power system, the waste heat is not always sufficient for the production of the necessary work and the heat demanded. In some ranges of main engine loads it is necessary to burn supplemental fuel (sometimes adding corrected fuel) to keep necessary PP in the HRSG, and the above equation becomes:
In the case when heating on board is not considered, (even though it is performed), the above equation becomes the efficiency in electrical power production from the waste heat:
At this point it is necessary to emphasize that the calculation was done in such a way that the main engine waste heat was used only in the amount which is needed for ship electrical (and heat) consumption during navigation. The surplus of waste heat energy, especially at high main engine loads, is not used in this calculation; therefore this surplus energy is lost in a chimney.
At some main engine loads it is necessary to burn supplemental fuel in the HRSG. Therefore, the defined efficiency is not “clear” waste heat efficiency. As an alternative, it is possible to move from denominator to numerator but with the negative sign.
The total efficiency of the analyzed ship thermal power plant is as follows:
It is important to notice that this efficiency could be higher if the total waste heat energy would be used for the production of electrical power. This surplus electrical power could be used to gain propulsion power through the propeller shaft generator.
The gain in the total efficiency of the analyzed ship thermal CHP plant compared to the efficiency of the conventional main engine is:
3. Results
The fuel consumption of the auxiliary diesel genset during navigation depends on the ship demand. This research accounts for two possible network loads: full electrical power and standard electrical power. Therefore, it is assumed that the ship heat consumption is always the same at ISO standard conditions, while electrical power consumption could be full electrical power consumption or standard electrical power consumption. The calculated electrical power using organic RC instead of Diesel genset is shown in
Table 4.
Table 4.
Calculated ship electrical power using ORC.
Table 4.
Calculated ship electrical power using ORC.
| Parameter | Unit | Value |
|---|
| Full electric power during navigation for the R245fa, PG1 | kW | 1012.5 |
| Standard electric power during navigation for the R245fa, PG1 | kW | 690.1 |
| Full electric power during navigation for the R123, PG1 | kW | 1038.9 |
| Standard electric power during navigation for the R123, PG1 | kW | 711.5 |
Although the ORC technology has been developed and introduced in shore-based industrial plants for a few decades (geothermal energy, solar energy, biomass, waste heat,
etc.), the available literature and results useful for comparison are scarce. The results related to full electrical power consumption during navigation are presented in
Table 5,
Table 6,
Table 7,
Table 8 and
Table 9.
Table 5 shows the working fluid states before and after the feeder/booster module.
Table 5.
State points of working fluid R123; HFO feeder/booster heating and other heating.
Table 5.
State points of working fluid R123; HFO feeder/booster heating and other heating.
| State Point in the Diagram | 9 | 9’ | 9’’ | 9’’’ | 10’ | 10’’ | 10’’’ |
|---|
| Pressure, p (bar) | 45 | 42.75 | 42.75 | 1.3507 | 42.75 | 42.75 | 1.3507 |
| Temperature, T (°C) | 200 | 197 | 120 | 36.00 | 197 | 80.0 | 36.00 |
| Density, ρ (kg/m3) | 475.03 | 434.49 | 1,206.5 | 15.291 | 434.49 | 1,331.6 | 29.341 |
| Specific enthalpy, h (kJ/kg) | 461.73 | 462.96 | 328.48 | 328.48 | 462.96 | 283.93 | 283.93 |
| Specific entropy, s (kJ/kg K) | 1.6813 | 1.6850 | 1.3790 | 1.4227 | 1.6850 | 1.2596 | 1.2786 |
| Vapour mass flow, (kg/s) | 28.409 | 1.4721 | 1.4721 | 1.4721 | 1.8054 | 1.8054 | 1.8054 |
The working fluid calculation results before and after the turbine are shown in
Table 6. The data for the working fluid after the turbine and before heating are presented in
Table 7.
Table 6.
R123 vapor state points before and after turbine; repeated calculation.
Table 6.
R123 vapor state points before and after turbine; repeated calculation.
| State Point in the diagram | 9 | 01 | 02s | 02 | 2s | 2 |
|---|
| Pressure, p (bar) | 45 | 42.75 | 1.4531 | 1.4531 | 1.3507 | 1.3507 |
| Temperature, T (°C) | 200 | 197 | 47.08 | 56.32 | 45.03 | 54.3 |
| Density, ρ (kg/m3) | 475.03 | 434.49 | 8.7833 | 8.4918 | 8.1947 | 7.9220 |
| Saturation temperature, Tsat (°C) | – | – | 38.16 | 38.16 | 36.00 | 36.00 |
| Specific enthalpy vapor, h (kJ/kg) | 461.73 | 462.96 | 410.89 | 417.64 | 409.64 | 416.39 |
| Specific entropy, s (kJ/kg K) | 1.6813 | 1.6850 | 1.6851 | 1.7059 | 1.6850 | 1.7059 |
| Vapor quality, x (kg/kg) | – | – | Superh. * | Superh. | Superh. | Superh. |
| Vapor mass flow from turbine, kg/s) | – | 25.132 | 25.132 | 25.132 | 25.132 | 25.132 |
| Total condensate mass flow, kg/s) | 28.409 | – | – | – | – | – |
Table 7.
R123 state points after the turbine and before heating; repeated calculation.
Table 7.
R123 state points after the turbine and before heating; repeated calculation.
| State point in the diagram | 2 | 2s | 3 | 4 | 5 |
|---|
| Pressure, p bar | 1.3507 | 1.3507 | 1.3507 | 1.3507 | 45 |
| Temperature, T °C | 54.3 | 45.03 | 36.00 | 36.00 | 37.63 |
| Specific enthalpy vapor/liquid, h kJ/kg | 416.39 | 409.64 | 403.14 | 236.44 | 239.47 |
| Specific entropy, s kJ/kg K | 1.7059 | 1.6850 | 1.6642 | 1.1250 | 1.1250 |
| Density ρ kg/m3 | 7.9220 | 8.1947 | 8.4829 | 1,435.4 | 1,445.0 |
| R123 mass flow, kg/s | 25.132 | 25.132 | 25.132 | 28.409 | 28.409 |
The data for the working fluid after the feed pump and after heating with jacket water, scavenged air and exhaust gases are presented in
Table 8.
Table 8.
R123 state points at heating; repeated calculation.
Table 8.
R123 state points at heating; repeated calculation.
| State point in the diagram | 6 | 7 | 9 |
|---|
| Pressure, p (bar) | 45 | 45 | 45 |
| Temperature, T (°C) | 75 | 150 | 200 |
| Specific enthalpy vapor/liquid, h (kJ/kg) | 278.60 | 364.48 | 461.73 |
| Specific entropy, s (kJ/kg K) | 1.2439 | 1.4667 | 1.6813 |
| Density ρ (kg/m3) | 1,346.7 | 1.089.9 | 475.03 |
| R123 mass flow, (kg/s) | 28.409 | 28.409 | 28.409 |
The converged jacket water, scavenged air and exhaust gases data (state points) before and after cooling of the working fluid, and after iterations are displayed in
Table 9.
Table 9.
Jacket water, scavenged air and exhaust gases state points after iteration.
Table 9.
Jacket water, scavenged air and exhaust gases state points after iteration.
| Parameter | Jacket water | Scavenged air | Exhaust gases |
|---|
| State point | in | out | in | out | in | out |
| Pressure, p (bar) | 2.5 | 2.5 | 3.79 | 3.79 | 1.03 | 1.015 |
| Temperature, T (°C) | 83.535 | 58.818 | 193.0 | 142.09 | 238.5 | 183.08 |
| Specific enthalpy, h (kJ/kg) | 350.01 | 246.43 | 483.55 | 431.23 | 599.75 | 541.01 |
| Density ρ (kg/m3) | 969.62 | 983.86 | 2.8178 | 3.1642 | 0.6996 | 0.7732 |
| Mass flow rate (kg/s) | 10.8395 | 10.8395 | 47.111 | 47.111 | 48.0 | 48.0 |
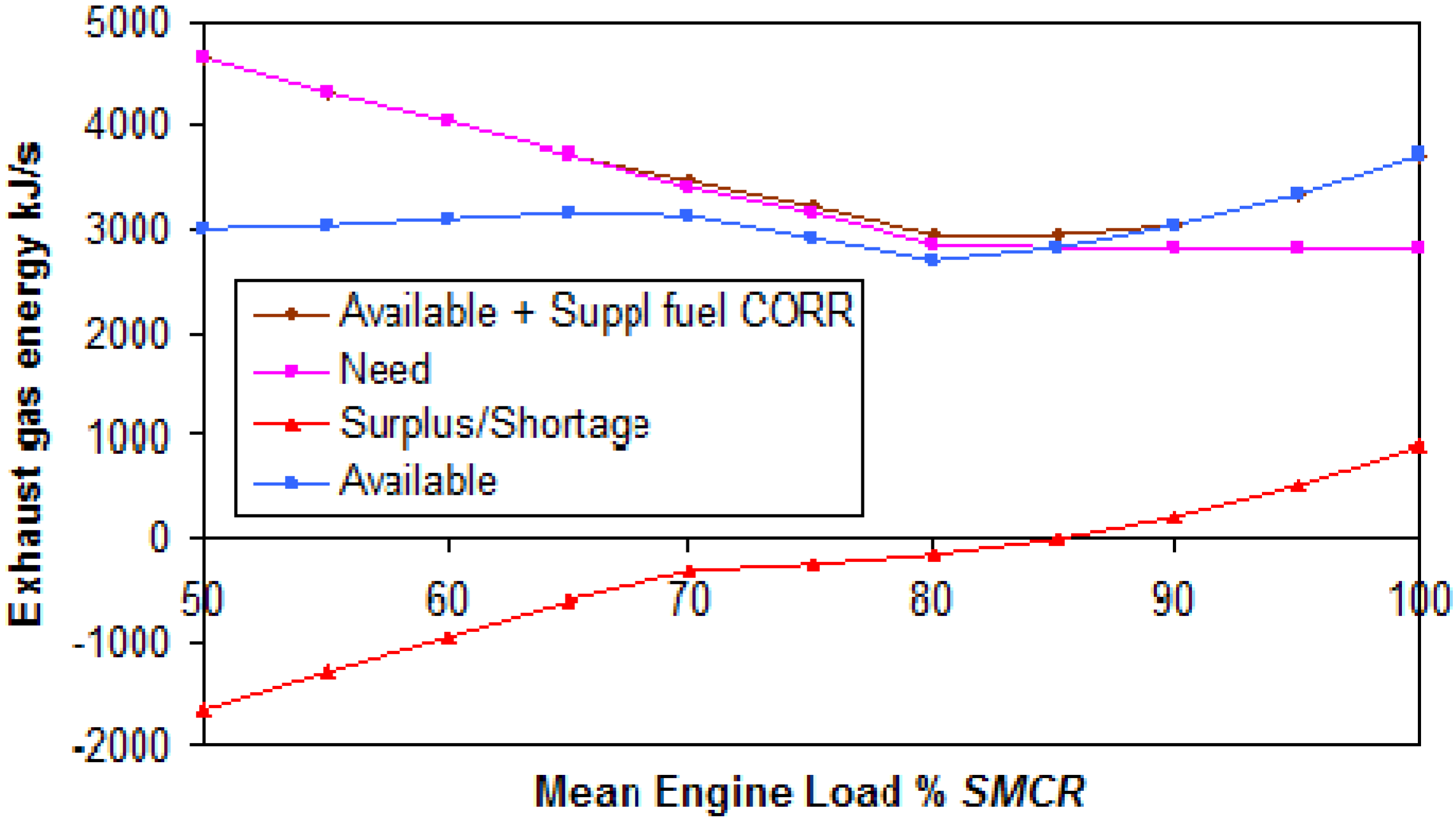
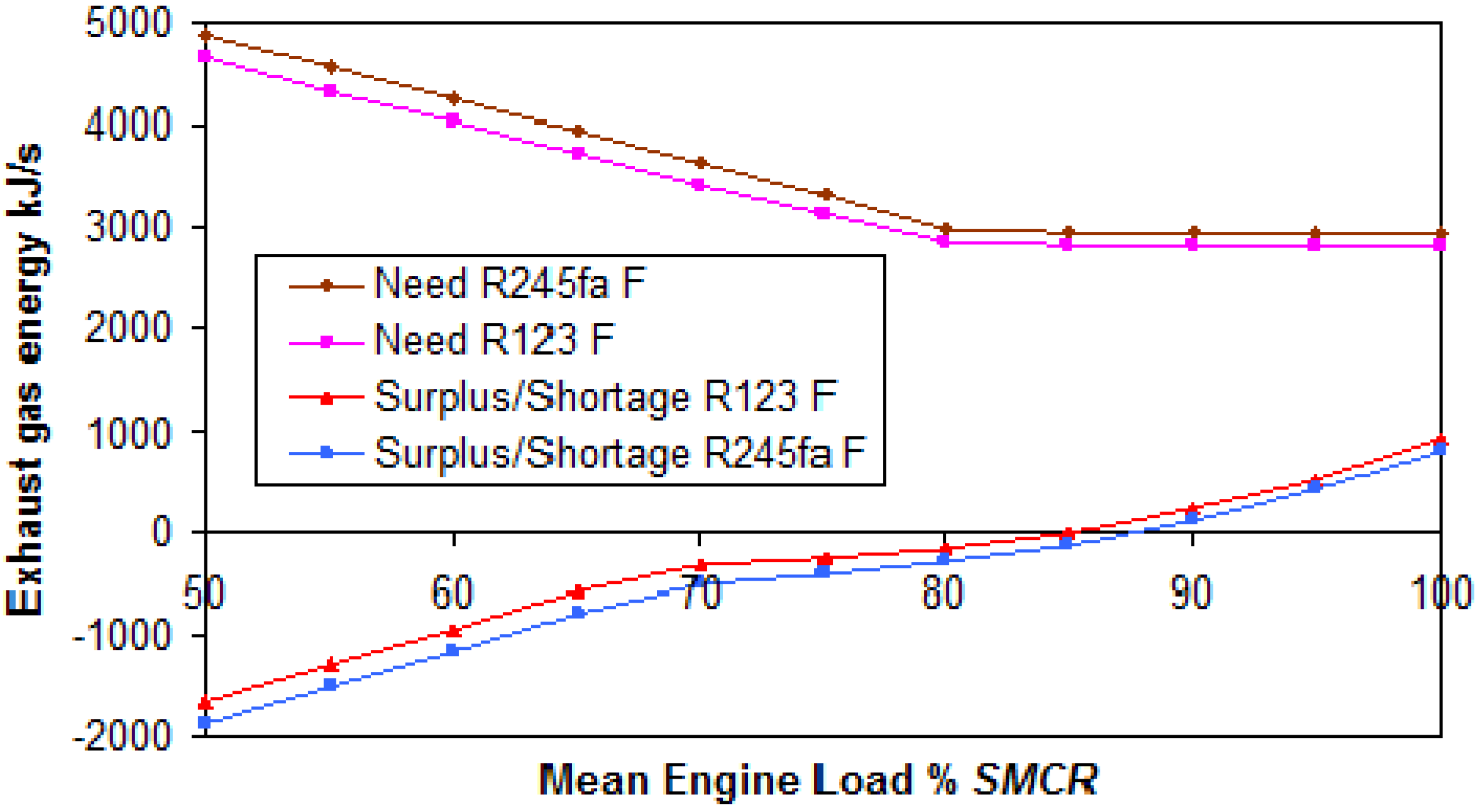
The surplus or shortage of exhaust gas energy, and necessary supplemental HFO at full electrical power are shown in
Figure 8 and
Figure 9.
Figure 8.
Exhaust gas energy and supplemental HFO at full electrical power for the R123 fluid.
Figure 8.
Exhaust gas energy and supplemental HFO at full electrical power for the R123 fluid.
Figure 9.
Exhaust gas energy and supplemental HFO at full electrical power for the R245fa fluid.
Figure 9.
Exhaust gas energy and supplemental HFO at full electrical power for the R245fa fluid.
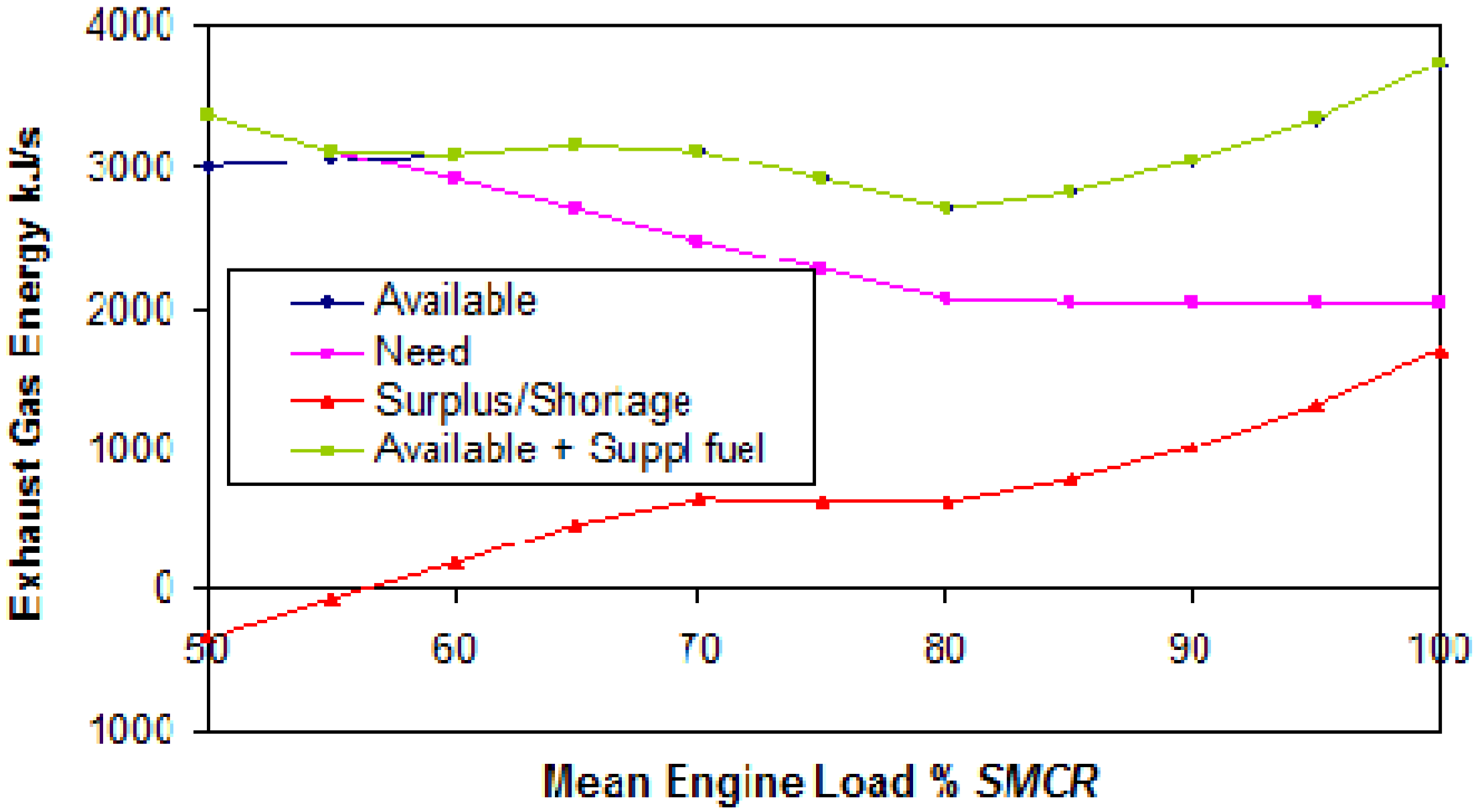
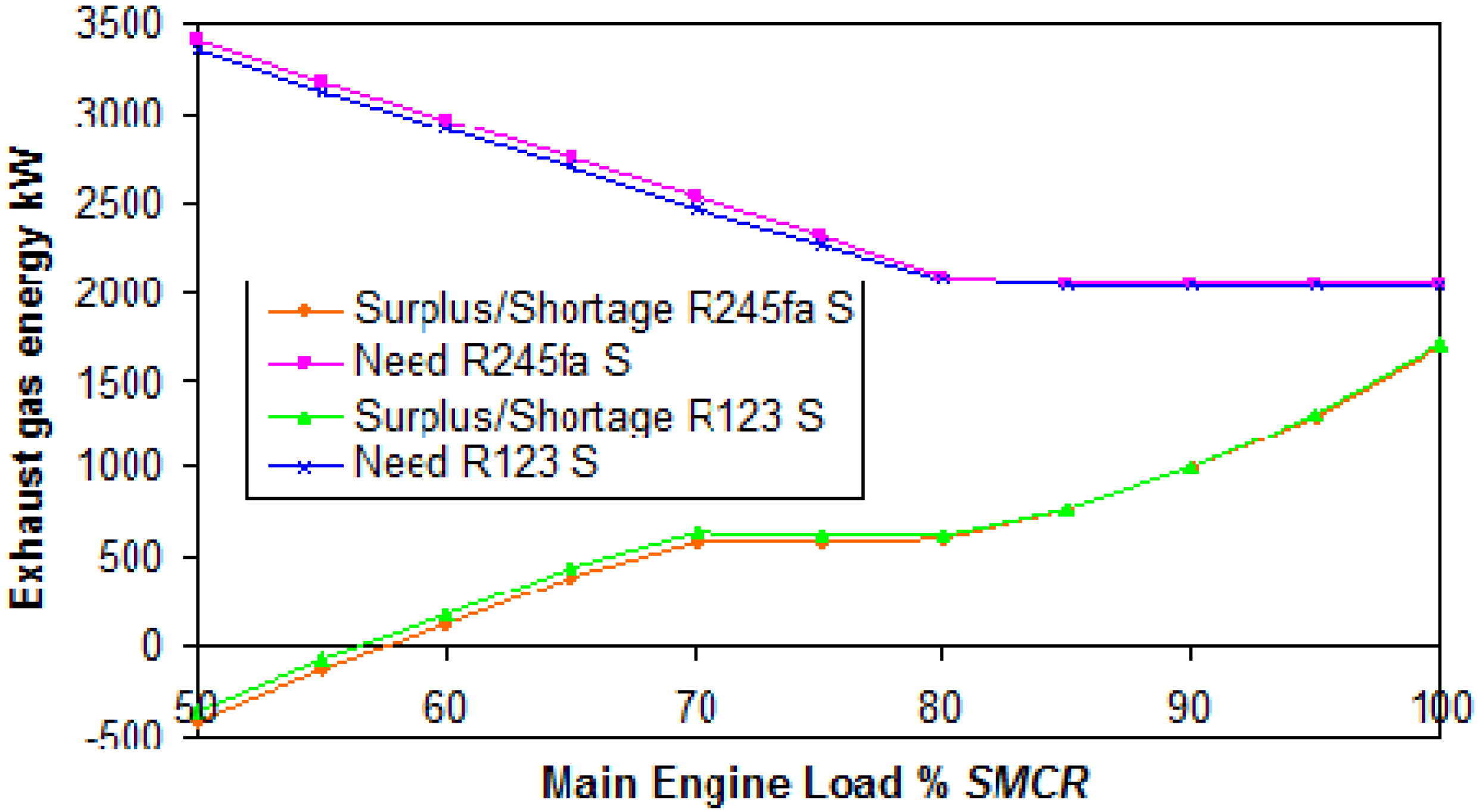
The surplus or shortage of exhaust gas energy, and necessary supplemental HFO energy at standard electrical power are shown in
Figure 10 and
Figure 11.
Figure 10.
Exhaust gas energy and supplemental HFO energy at standard electrical power and heat for the R123 fluid.
Figure 10.
Exhaust gas energy and supplemental HFO energy at standard electrical power and heat for the R123 fluid.
Figure 11.
Exhaust gas energy and supplemental HFO energy at standard electrical power and heat for the R245fa fluid.
Figure 11.
Exhaust gas energy and supplemental HFO energy at standard electrical power and heat for the R245fa fluid.
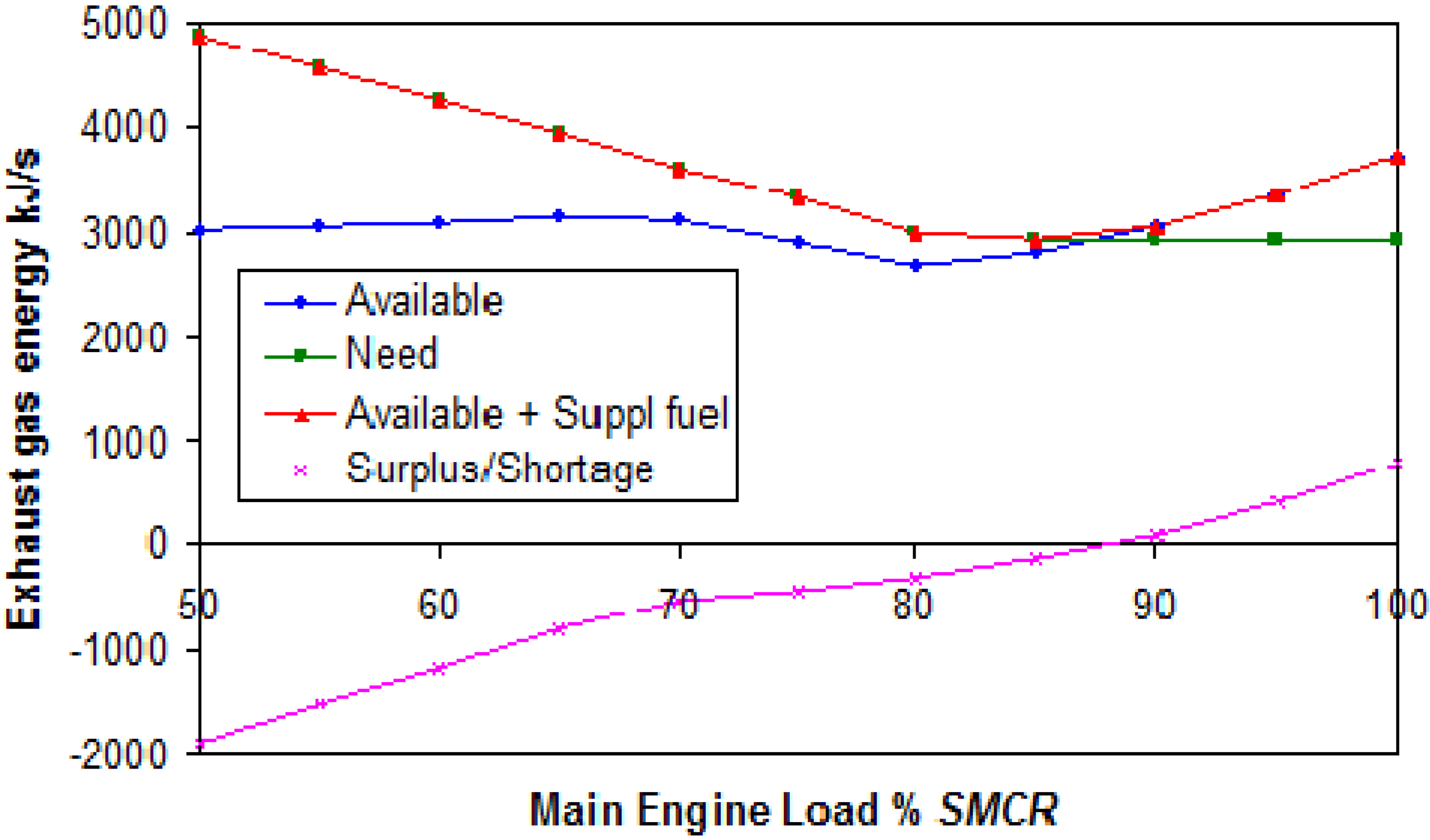
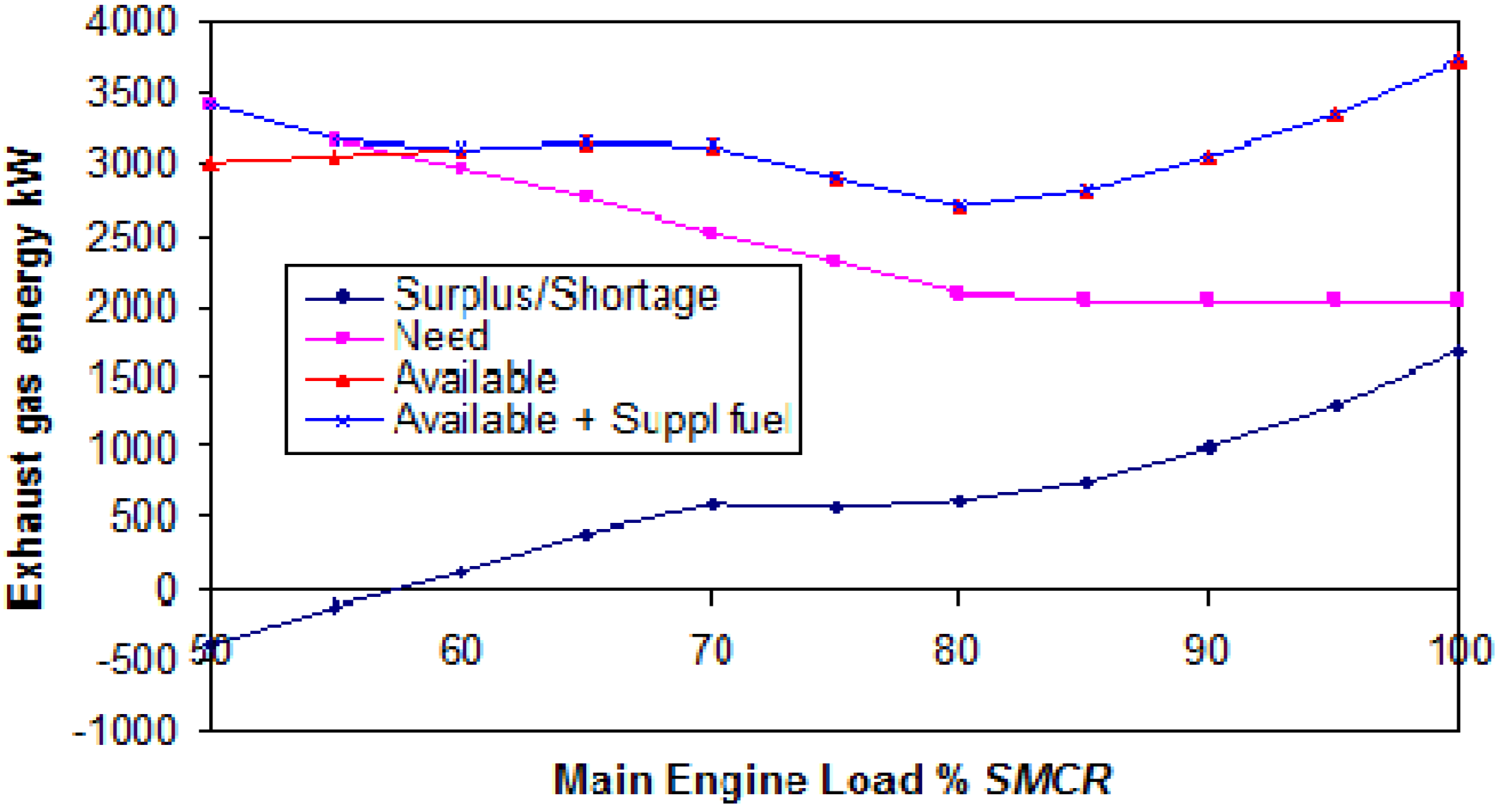
Exhaust gas energy need for full and standard electrical power and heat are shown in
Figure 12 and
Figure 13.
Figure 12.
Exhaust gas energy need and surplus/shortage of energy at full electrical power and heat.
Figure 12.
Exhaust gas energy need and surplus/shortage of energy at full electrical power and heat.
Figure 13.
Exhaust gas energy need and surplus/shortage of energy at standard electrical power and heat.
Figure 13.
Exhaust gas energy need and surplus/shortage of energy at standard electrical power and heat.
The supercritical single pressure vapor system utilizes the exhaust gas heat; see the process diagrams in
Figure 3 and
Figure 4,
T-s diagrams in
Figure 6 and
Figure 7, and the corresponding temperature/heat transmission diagrams in
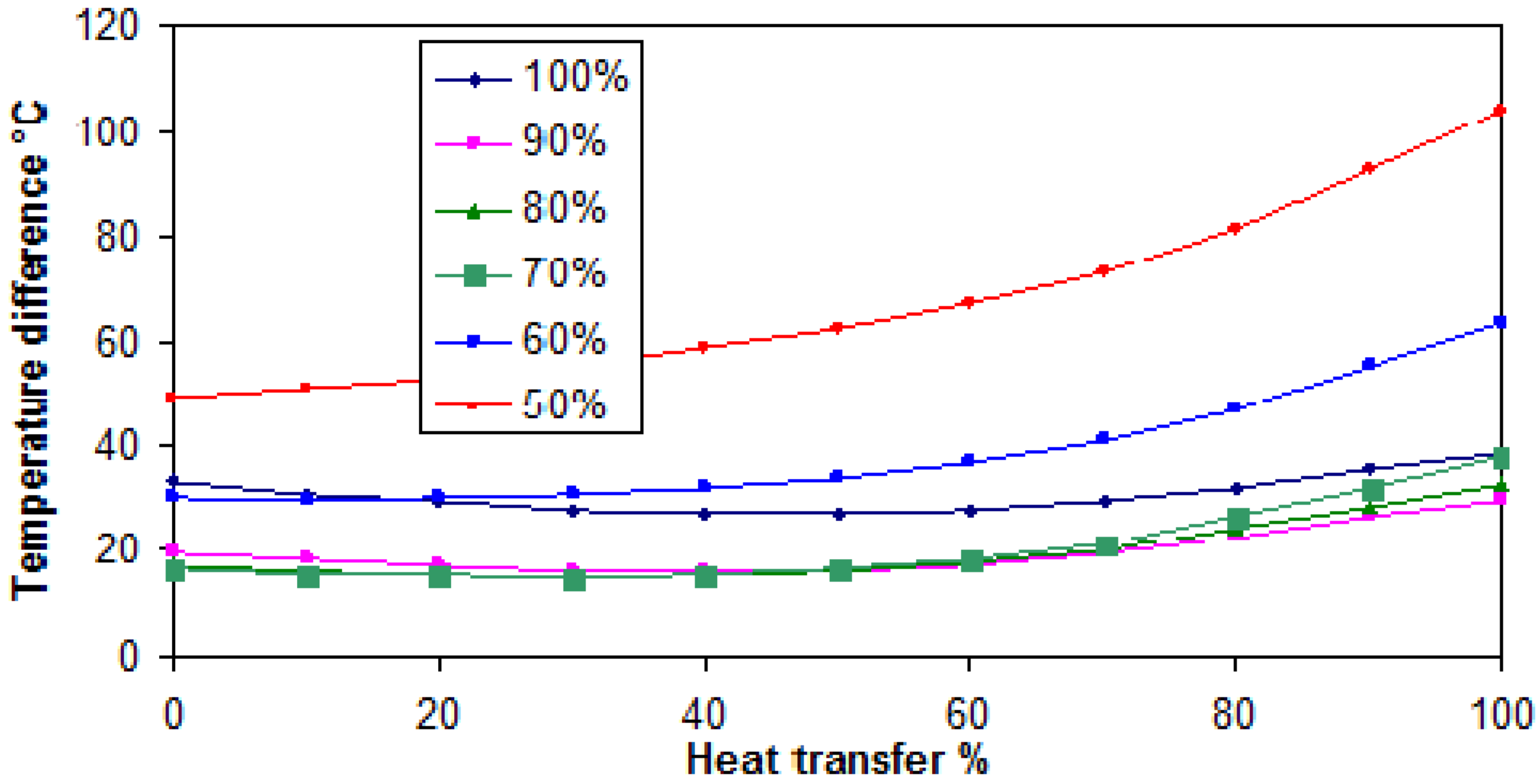
Figure 14 and
Figure 15. The check of the temperature difference between the exhaust gases and the working fluids was performed carefully taking into account that the PP should be at 15 ºC. In [
17] in
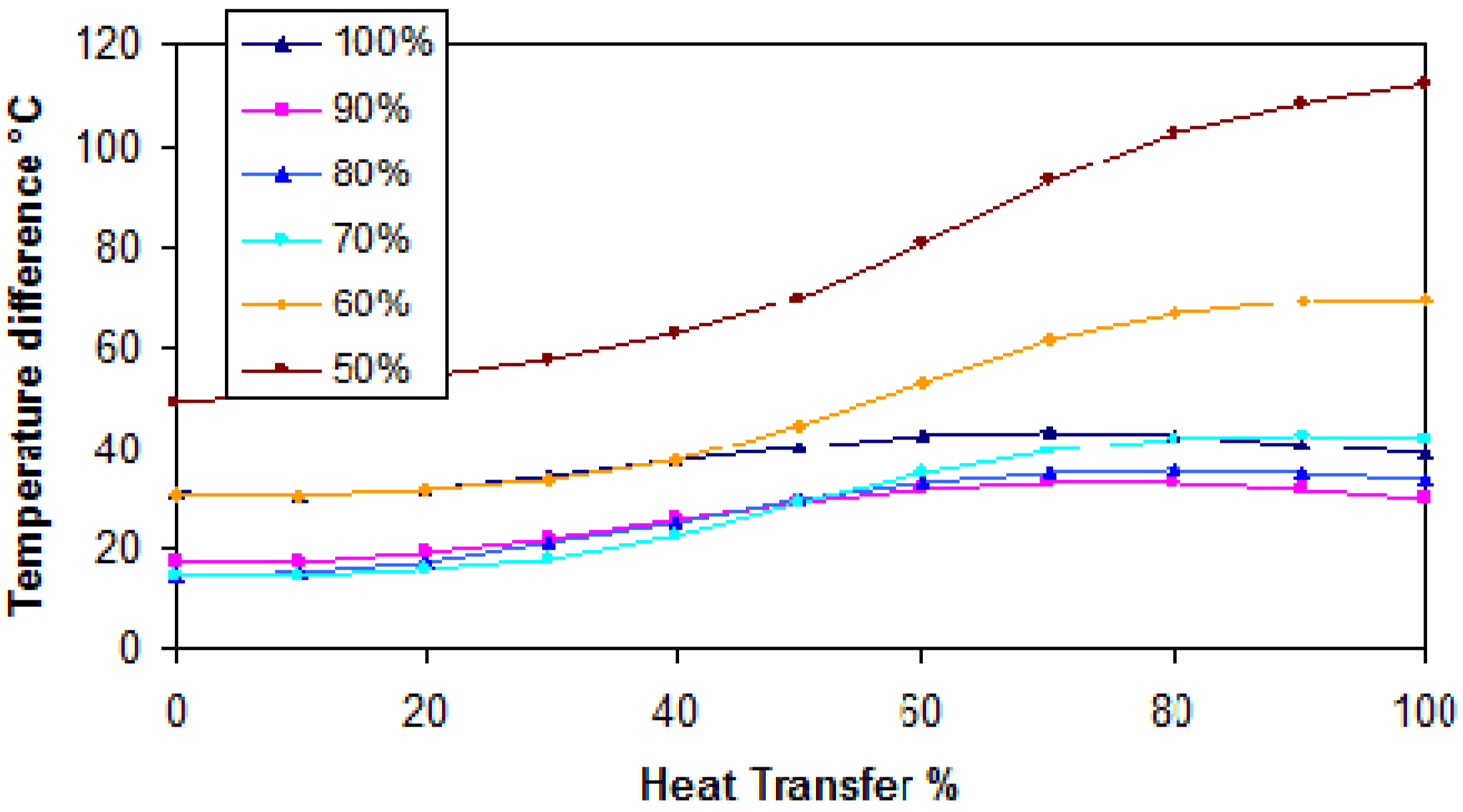
Figure 10 the graphs show the influence of the PP on the boiler heat transfer surface and steam production. The lower the PP, the larger is the heat transfer surface, the more efficient is the exhaust gas boiler, and the higher is the gas pressure loss across the boiler. The verification of the temperature difference through the exhaust gas boiler at main engine loads from 50% to 100%
SMCR is shown in
Figure 14 for R123 working fluid. For the R245fa the temperature difference is shown in
Figure 15.
Figure 14.
Temperature difference in the exhaust gas boiler with the organic working fluid R123 at full electrical power and the main engine loads from 50% to 100% SMCR.
Figure 14.
Temperature difference in the exhaust gas boiler with the organic working fluid R123 at full electrical power and the main engine loads from 50% to 100% SMCR.
Figure 15.
Temperature difference in the exhaust gas boiler with the organic working fluid R245fa at full electrical power and the main engine loads from 50% to 100% SMCR.
Figure 15.
Temperature difference in the exhaust gas boiler with the organic working fluid R245fa at full electrical power and the main engine loads from 50% to 100% SMCR.
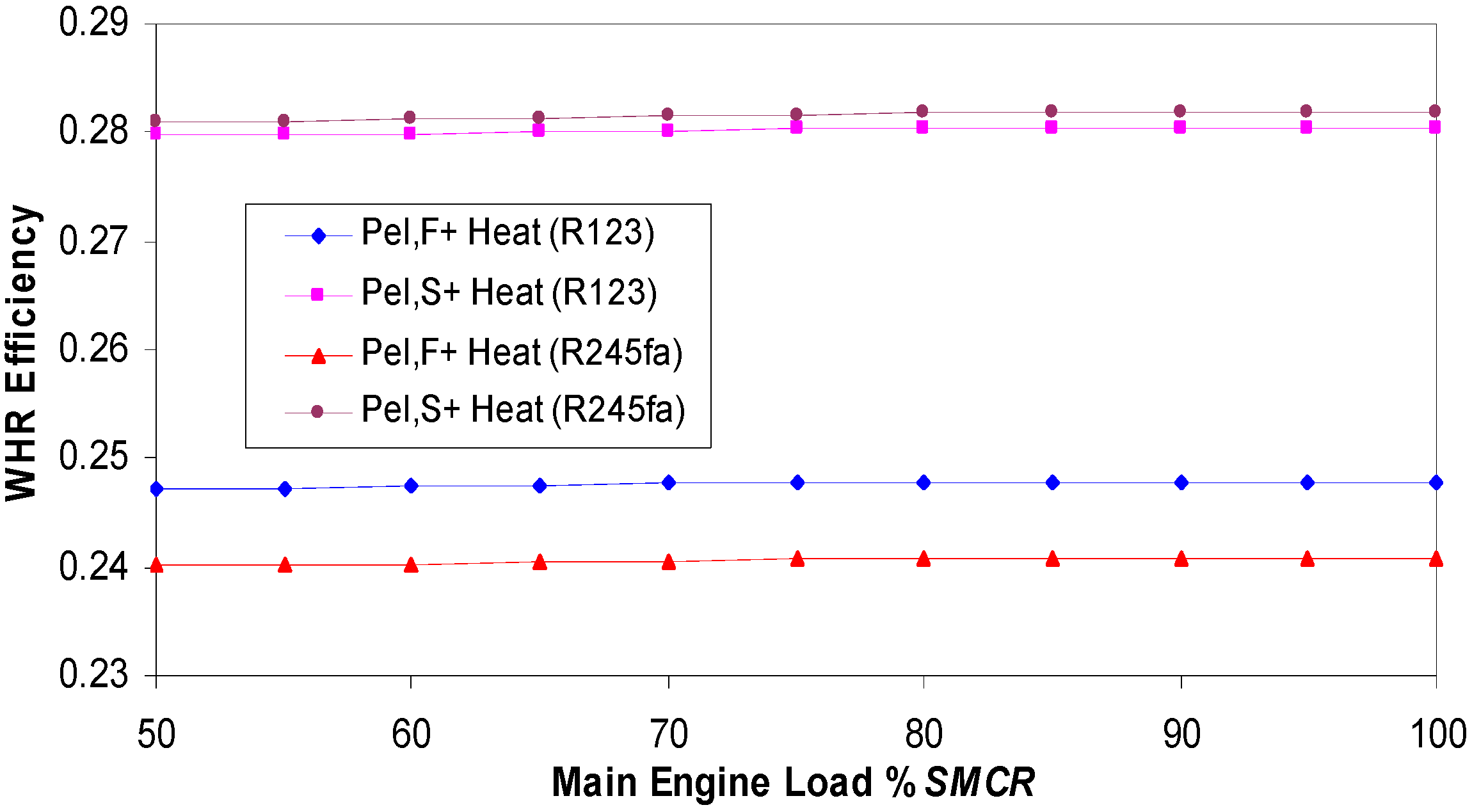
The efficiencies of main engine waste heat recovery are shown in
Figure 16 and
Figure 17.
Figure 16 shows the η
CHP,system i.e., the efficiency in the conversion of main engine waste heat to ship electricity and heat.
Figure 17 displays η
P,el i.e., the efficiency in conversion of main engine waste heat to ship electricity.
Figure 16.
WHR Efficiency with organic fluids—ηCHP,system (electrical power and heat).
Figure 16.
WHR Efficiency with organic fluids—ηCHP,system (electrical power and heat).
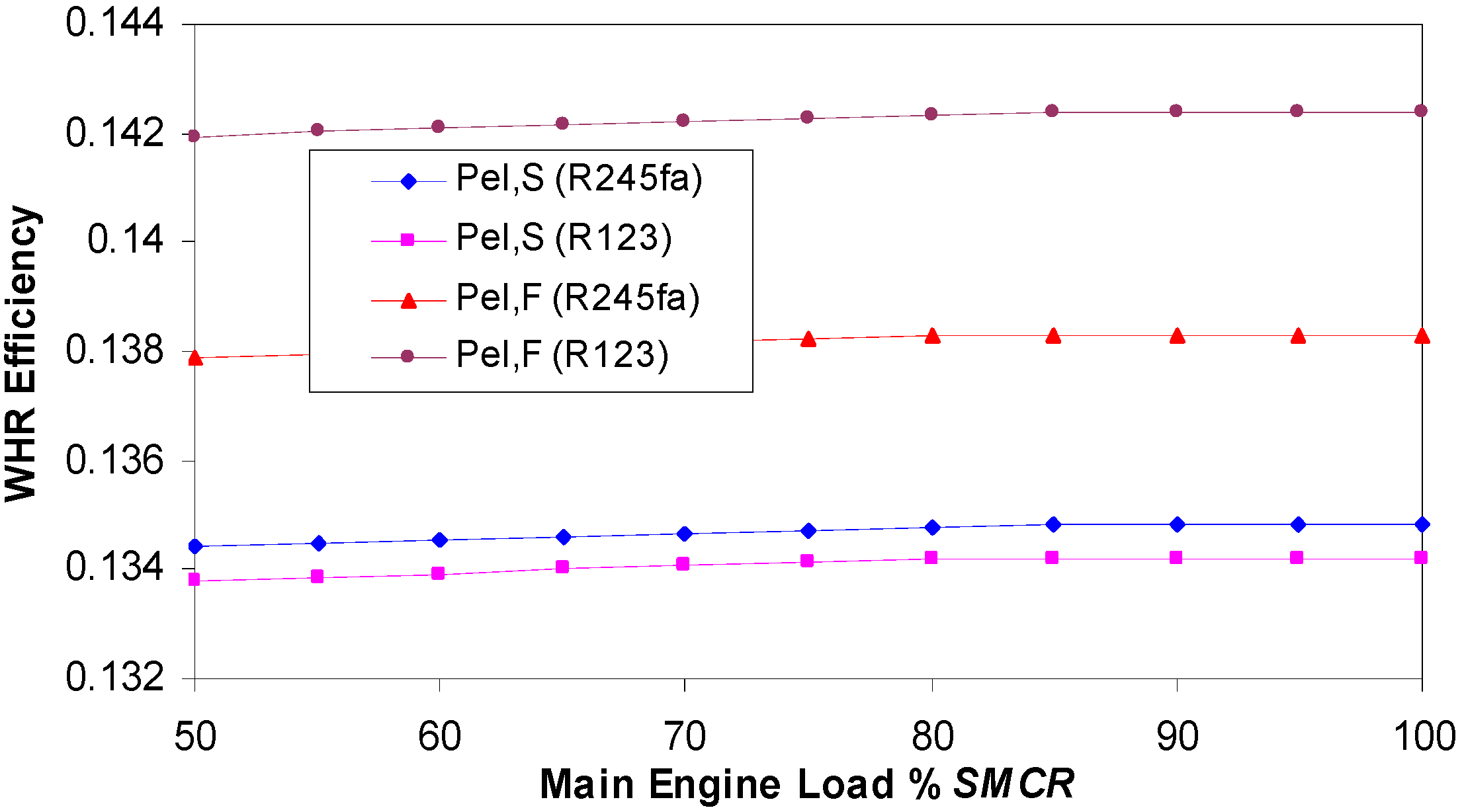
Figure 17.
WHR Efficiency with organic fluids—ηP,el (electrical power only).
Figure 17.
WHR Efficiency with organic fluids—ηP,el (electrical power only).
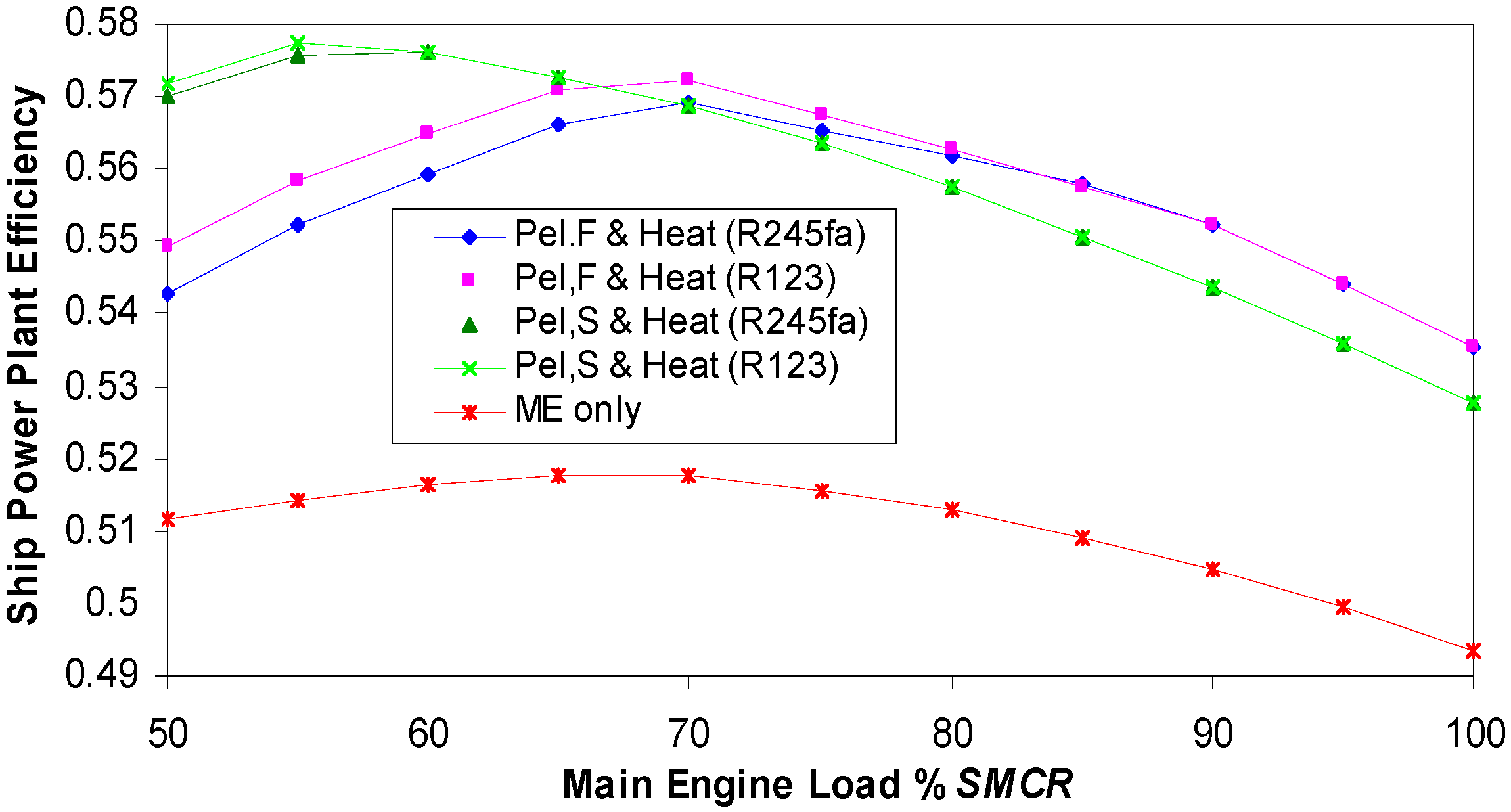
Figure 18.
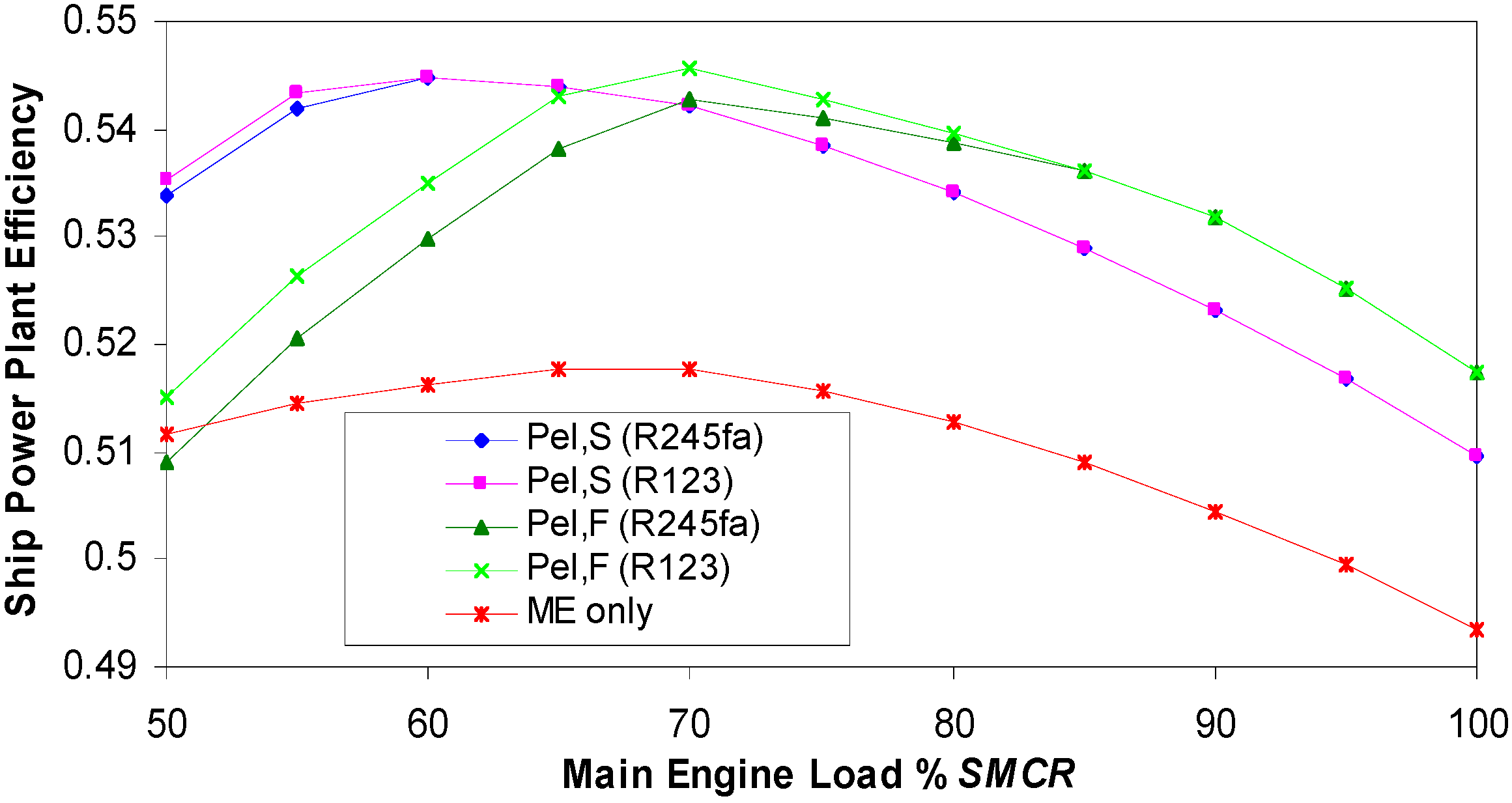
Ship Power Plant Efficiency with organic fluids—ηCHP,ship total (power and heat).
Figure 18.
Ship Power Plant Efficiency with organic fluids—ηCHP,ship total (power and heat).
Figure 19 presents a similar situation as
Figure 18 but neglecting heat used for onboard heating. The results are similar, however, the values are lower.
Figure 19.
Ship Power Plant Efficiency with organic fluids—ηP,ship (power only).
Figure 19.
Ship Power Plant Efficiency with organic fluids—ηP,ship (power only).
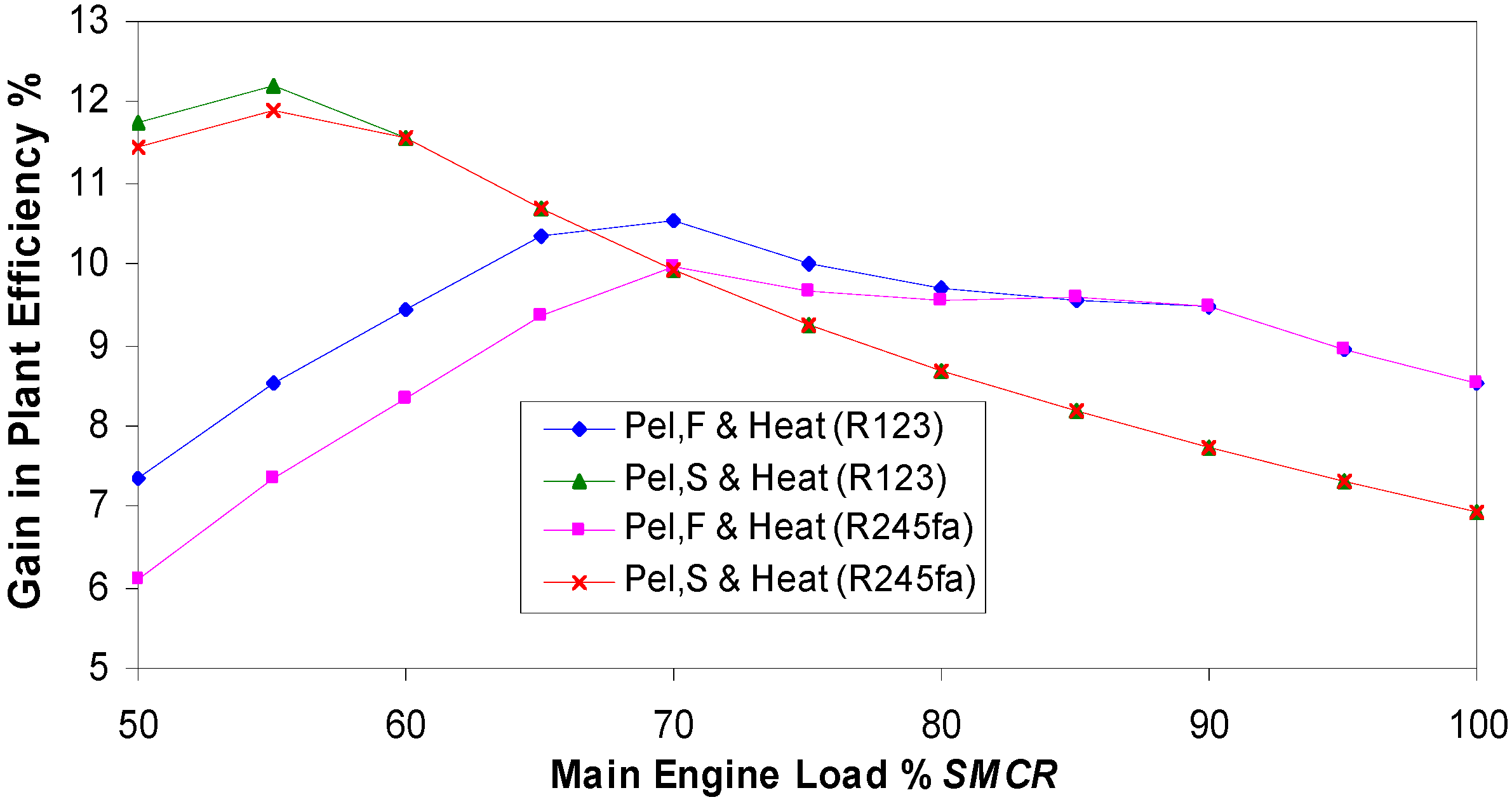
Figure 20 shows the gain in the ship power efficiencies when heat and power (main engine and electrical power) efficiencies are compared to the conventional main engine efficiency.
Figure 20.
Gain in Ship Power Plant Efficiency with organic fluids—heat and electrical power.
Figure 20.
Gain in Ship Power Plant Efficiency with organic fluids—heat and electrical power.
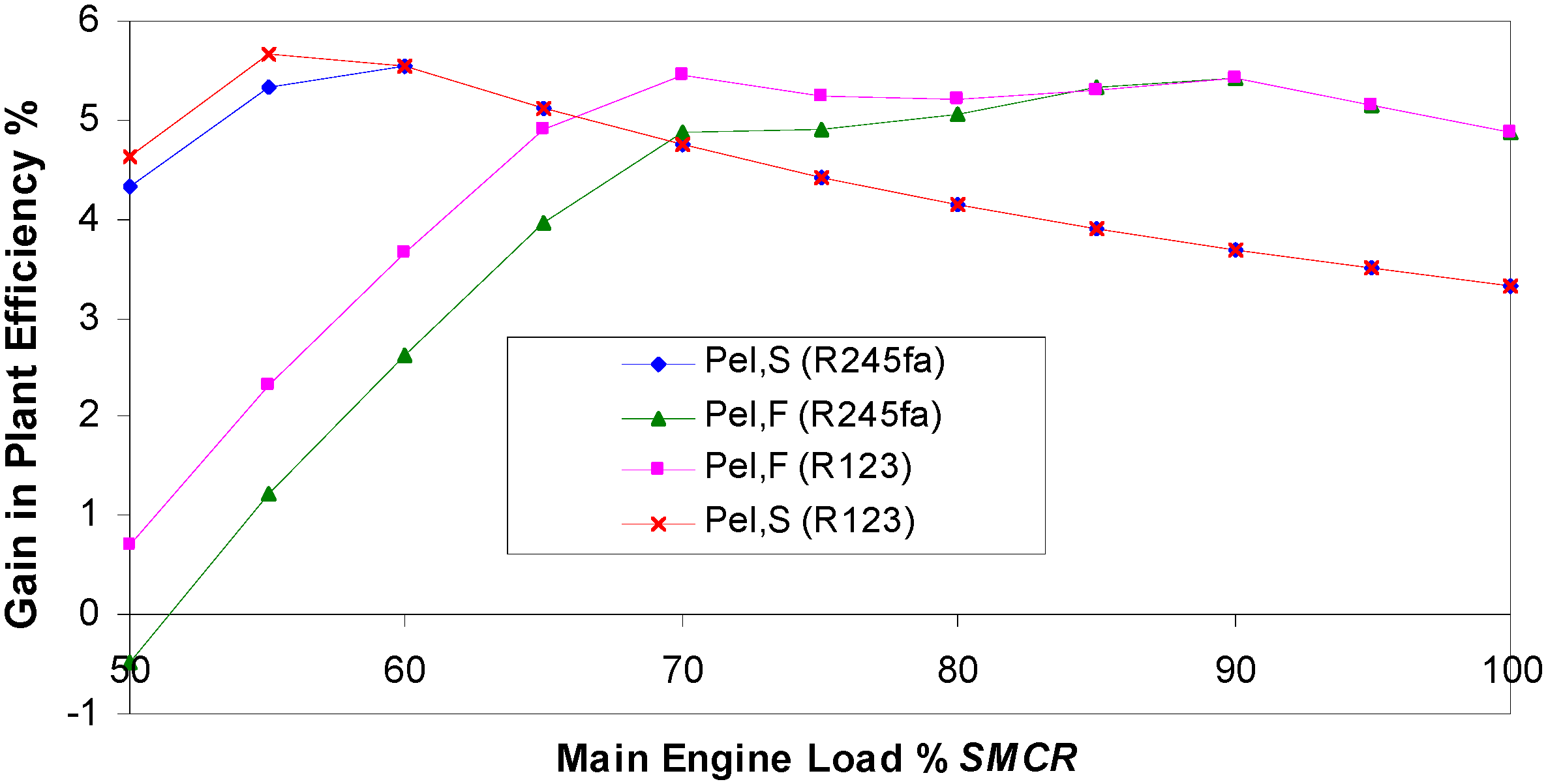
Figure 21 shows the gain in the ship power efficiencies when power (main engine and electrical power) efficiencies, are compared to the conventional main engine efficiency.
Figure 21.
Gain in Ship Power Plant Efficiency with organic fluids—electrical power only.
Figure 21.
Gain in Ship Power Plant Efficiency with organic fluids—electrical power only.
4. Discussion
Because the process containing organic fluids R245fa or R123 has a much larger mass flow rate, the required feed pump power is considerably higher compared to a steam cycle. Therefore, the full electrical power necessary for the R245fa cycle is 1,012.5 kWe instead of 912 kWe, and 690.1 kWe instead of 620 kWe for standard electrical power. For the R123 cycle, the necessary full electrical power is 1,038.9 kWe instead of 912 kWe, and 711.5 kWe instead of 620 kWe for standard electrical power.
The surplus of exhaust gas energy at full electrical load using R245fa organic fluid appears to be over 88% SMCR, and over 85% SMCR with R123 organic fluid. It is necessary to burn supplemental fuel when R123 fluid is used, in case when the exhaust gas energy is too low. In the region of 65% to 90% SMCR it is also necessary to burn a small amount of corrective fuel to keep the PP at 15 °C.
The surplus exhaust gas energy for the R123 and R245fa fluids at standard electrical power starts over 56% SMCR. A considerable exhaust gas energy surplus is from 65% to 80%, and significant from 85% to 100% SMCR.
At full electrical power demand (
Figure 12), the need for exhaust gas energy is lower for the R123 than for the R245fa fluid. The same is at standard electrical power demand (
Figure 13), but the difference is smaller.
Figure 13 shows that the surplus of the exhaust gas energy is high for both working fluids if the ship electrical demand is standard. The expansion in the turbine with the R123 fluid takes place until 1.35 bar and 54.3 °C, which is more favorable compared to the R245fa fluid. At the same inlet parameters to the turbine and lower output parameters from the turbine, the R123 fluid has a more efficient Rankine cycle. Additionally, the maximum inlet temperature for the R245fa fluid is 200 °C (by Gao
et al. [
10] the max inlet temperature is 227 °C), while the R123 due to the thermal stability allows a higher inlet temperature. The advantage of the organic Rankine cycle with the R123 fluid is even higher.
The WHR efficiency for production of heat and electricity η
CHP,system is higher for standard electrical power than for full electrical power (see
Figure 16). The highest WHR efficiency for the R245fa fluid is 28.18% and it is lower for the R123 fluid amounting to 28.05%. At full electrical power and heat, η
CHP,system is higher for the R123 working fluid and equals 24.79% compared to 24.1% for the R245fa fluid. At standard electrical power the exhaust gas energy is high enough over nearly a complete working range of the main engine, and there is no need to burn supplemental fuel. At full electrical power, below 90%
SMCR it is necessary to burn supplemental fuel, but η
CHP,system is also high.
Figure 17 presents the same situation as
Figure 16, but in this case the heat consumed on board is not taken into consideration.
Figure 17 presents only the produced electrical power from the main engine waste heat. In this case the highest η
P,el has full electricity production by the R123 working fluid and amounts over 14.23%. η
P,el at full electrical power with the R245fa working fluid achieves 13.83%. These results could be partially compared to the results of Larsen
et al. [
9] in
Table 5 for SI process and R245fa fluid. Their η
th = 17%, but in our calculation the surplus of the exhaust gas energy is lost in the chimney. The values of η
P,el at standard electrical load amount to 13.48% for the R245fa fluid, and 13.42% for the R123 fluid. The reason for such a low efficiency is a high amount of the exhaust gas energy exiting unused the atmosphere (see
Figure 13). Karellas and Schuster [
18] presented the system with internal combustion engine and ORC with R245fa working fluid. The heat source (thermal oil) reached the temperature of about 240 °C. For the supercritical ORC process η
system = 12.72% was achieved, which is close to our results ranging from 13.4% to 13.8%. Vescovo [
19] states: “Customized ORC systems are employed to recover heat from lower temperature heat sources (below 250 °C) and refrigerant-based working fluids (non-flammable, non-corrosive, with low toxicity) are used in these systems. These plants are typically used for low temperature liquid flow heat recovery, and electrical efficiencies vary widely, depending upon the heat source temperatures and other specific conditions, ranging from 8% to 18%.”
Figure 18 shows the ship power plant efficiency, η
CHP,ship total, in production of propulsion power, heat and electricity on board. For conventional ship design, the main engine efficiency η
ME is over 51% from 50% to 80%
SMCR. With additional heat and power production from waste heat, the highest η
CHP,ship total efficiency is at 70%
SMCR and reaches 57.2% for the R123 fluid, and 56.9 % for the R245fa fluid. In the complete service range (from 60 to 85% SMCR) η
CHP,ship total is high. When producing standard electrical power, η
CHP,ship total is even higher and equals 57.72% at low main engine loads up to 70%
SMCR. Due to the waste heat lost through the chimney, η
CHP,ship total decreases at higher main engine loads.
Figure 19 shows the efficiency of the ship's power plant using the waste heat of the main engine. For full electrical load maximum efficiency η
P,ship is achieved at 70%
SMCR and amounts to 54.58% for R123 fluid, and 54.28% for R245fa fluid. In a standard electrical load η
P,ship is slightly smaller and identical for both fluids. The reason of this is that over 60%
SMCR there is a considerable excess heat in the exhaust gases that are lost in the chimney.
The company MAN B&W Diesel A/S in [
20] for 12K98ME/MC engine in Thermo Efficiency System (TES) version operating at ISO ambient reference conditions and at 100%
SMCR (68,640 kW@94 rpm) obtained total power output efficiency of 54.2%. The waste heat energy was recovered in the steam turbine. Schmid of Wärtsilä [
21] showed similar results for 12RT-flex96C engine where the overall efficiency of 54.9% was obtained using the WHR by steam turbine and power turbine. In our work with organic fluids, such efficiency was obtained at 70%
SMCR (Fig 19) where the lost exhaust gas energy is not taken into account. In this work a large amount of exhaust gas energy is lost, especially at higher main engine loads.
The gain in the plant efficiencies are shown in
Figure 20 and
Figure 21. In
Figure 20 the gain ranges from 9.44% at 60%
SMCR up to 10.55% at 70%
SMCR for the R123 fluid. This gain is high up to 90%
SMCR and equals 9.46%. The gain with R245fa fluid is lower. In the case of standard electrical power the gain is high at low main engine loads and exceeds over 12%, but decreases at higher main engine loads due to the loss of exhaust gas energy.
When the gain is considered not taking into account the ship heat consumption (
Figure 21), the R123 has again better values in full and standard electricity production. During full electrical load, this gain equals approximately 5% in the range from 65 to 100%
SMCR. Ahnger [
22] states that the organic Rankine cycle products of today give 8%–10% additional power—even for small engines. Those are much higher values than shown in
Figure 21. But, at full electrical load and especially at standard electrical load, a great amount of exhaust gas energy is lost through the chimney, instead to be used in the ORC ship power plant. Such calculations have not been performed in this paper.
A partial model validation can be performed by comparing the results obtained by Larsen
et al. [
9] and the ones obtained in the real-life WHR systems built by Dresser Rand, Mitsubishi Heavy Industries Ltd, Shinko Ind. Ltd and Siemens. MAN B&W [
23] recommends an ORC plant for a propulsion engine power below 15,000 kW, whereas for 15,000 kW to 25,000 kW the power gas turbine or superheated steam turbine cycle is recommended.
5. Conclusions
The application of the supercritical ORC during the production of electrical energy and heat, using waste heat energy from the main engine jacket water, scavenged air and exhaust gases has been explored in this work. A CHP plant with R245fa or R123 fluid using supercritical ORC meets all the demands for electrical energy and heat while burning only a small amount of supplemental fuel in the HRSG.
This paper deals with the savings in fuel consumption for the WHR CHP plant using organic fluids. The comparison was made: (i) with conventional low speed two stroke propulsion engines, (ii) with TES developed by MAN B&W and WHR Plant developed by Wärtsilä, and, (iii) with similar organic Rankine plants.
Using the ORC for electricity production, the ship power plant efficiency rises significantly compared to the conventional main engine. During the standard electrical load a great amount of surplus exhaust gas energy is lost through the chimney. This lost gas energy can be converted to electrical energy and transferred to the propeller shaft. That would additionally increase the ship power plant efficiency.
The comparison with MAN and Wärtsilä waste heat recovery systems showed similar results. However, the MAN and Wärtsilä systems are not applicable for such small engines as shown in this work. The comparison with similar organic RC plants provided results which are in good correlation, but the work which should take into account the exhaust gas energy lost in a chimney would give the right answer.
To enhance the cogeneration efficiency, the maximum temperature of the applied organic fluid should be increased in order to increase the turbine outlet temperature and improve the quality of the heat consumed on board. The R123 fluid provides better results compared to R245fa, therefore, its usage should be taken into consideration after 2020/2030.
This analysis has revealed the possible savings in fuel consumption when using the supercritical ORC CHP for low temperature WHR in ship propulsion plants. Concurrently, the lower fuel consumption reduces greenhouse gas emissions and their environmental impact.