Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review
Abstract
:1. Introduction
2. Overview
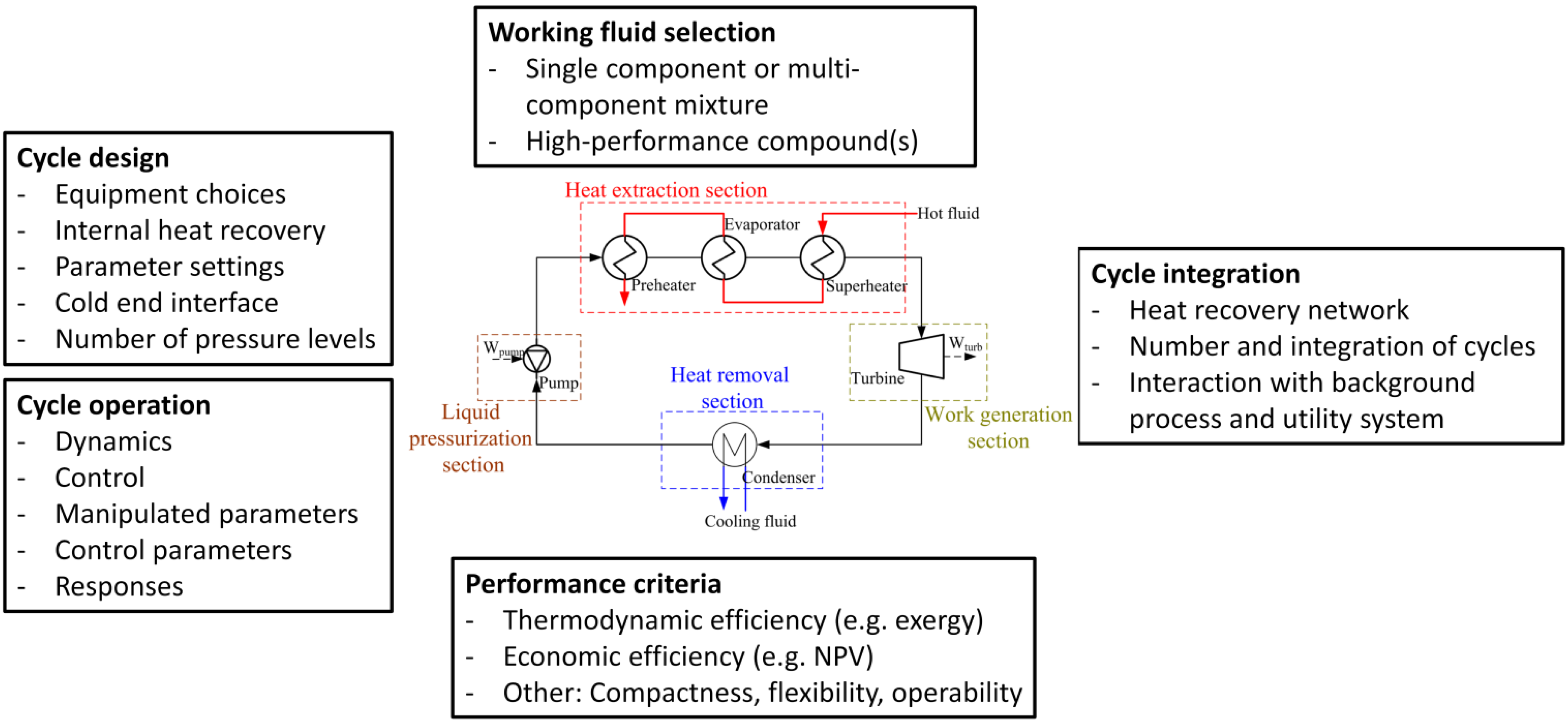
3. Design and Selection of ORC Working Fluids
3.1. Working Fluid Selection Applications
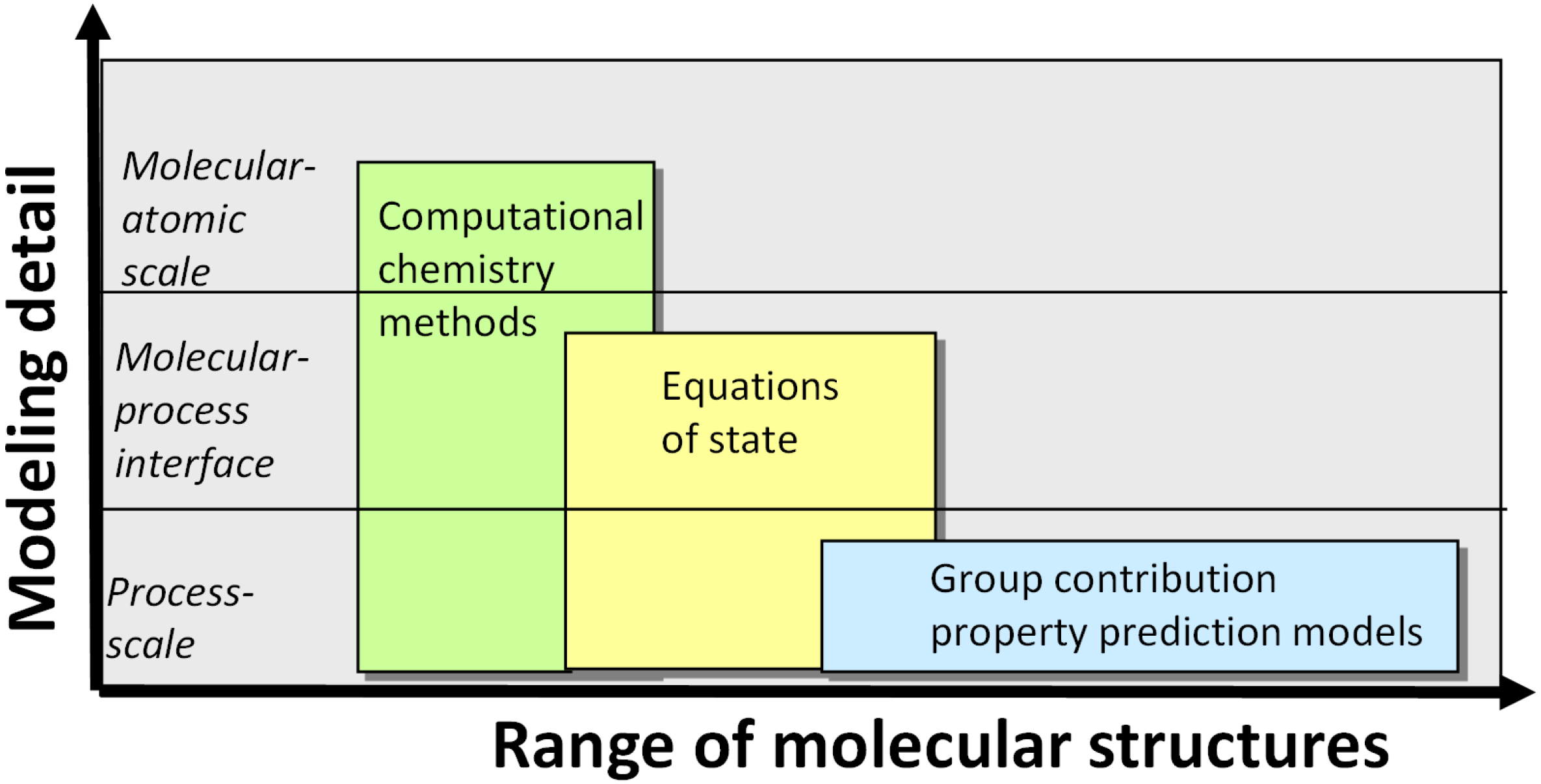
3.2. Computer-aided Tools: Main Concepts and Challenges
- a)
- The exhaustive generation and evaluation of a very wide range of molecular structures prior to the selection of the working fluid which exhibits a truly optimum performance.
- b)
- The utilization of predictive models which are sufficiently accurate to ensure that the performance of the selected working fluid is both optimum and rigorously validated prior to its practical utilization in an ORC plant.
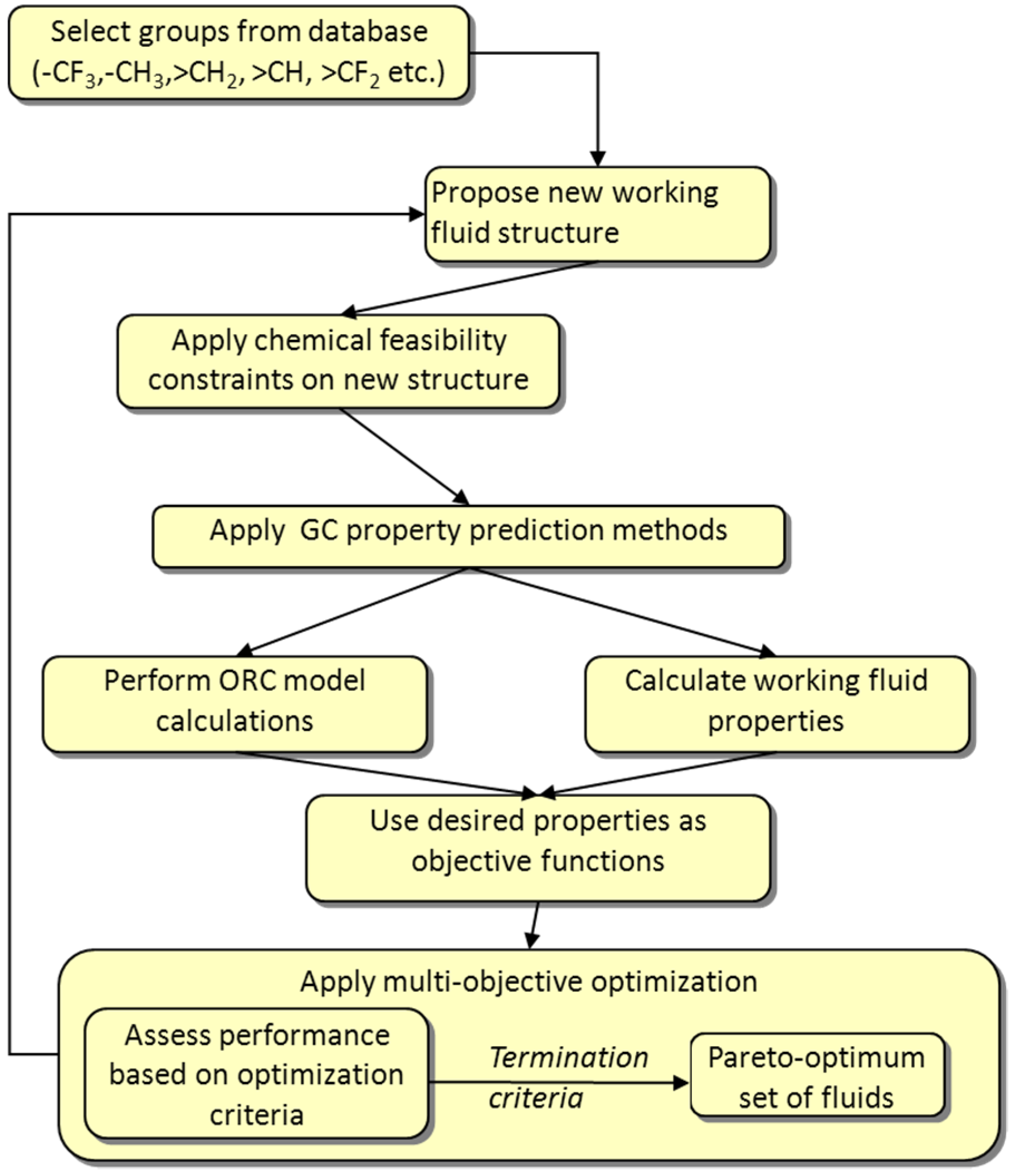
3.3. Optimization-Based CAMD of Pure Fluids
- The selection of several functional groups from a database enables the generation of a molecule that is tested in terms of chemical feasibility.
- The desired properties of any feasible molecule are subsequently calculated based on the contribution of each functional group in the molecule.
- Several of these properties are used as a measure of molecular performance, i.e., as objective functions in the employed optimization algorithm. The employed properties may directly reflect molecular characteristics or ORC process features.
- The optimization is then used to assess the performance based on specific algorithmic criteria and to inflict alterations in the molecular structure using functional groups available in the database, in order to generate a new molecule.
- This iterative procedure continues until a molecule with the optimum performance is identified, based on algorithmic termination criteria that ensure optimality.
- Several designed fluids are known chemicals, documented in the online NIST (www.nist.gov) or other databases, indicating the ability of CAMD to identify fluids which are readily available for utilization.
- Despite their public or commercial availability, many of the fluids obtained from CAMD have not been previously considered for ORC applications, indicating the ability of the method to point towards new design directions, overlooked by trial-and-error methods.
- The fluid 3,3,3-trifluoropropene only differs by a single fluorine atom from 2,3,3,3-tetrafluoropropene which has been commercialized in recent years by an international company [39] as an ORC working fluid, highlighting opportunities to quickly investigate other options which are very similar to the proposed designs.
- Several unconventional and possibly novel working fluid structures were also identified combining ether and amine functional groups in fluorinated carbon chains. These groups were later shown to result in high ORC thermal efficiency in a study based on molecular thermodynamics [42] which accounted for the results of Papadopoulos et al. [4], among other fluids.
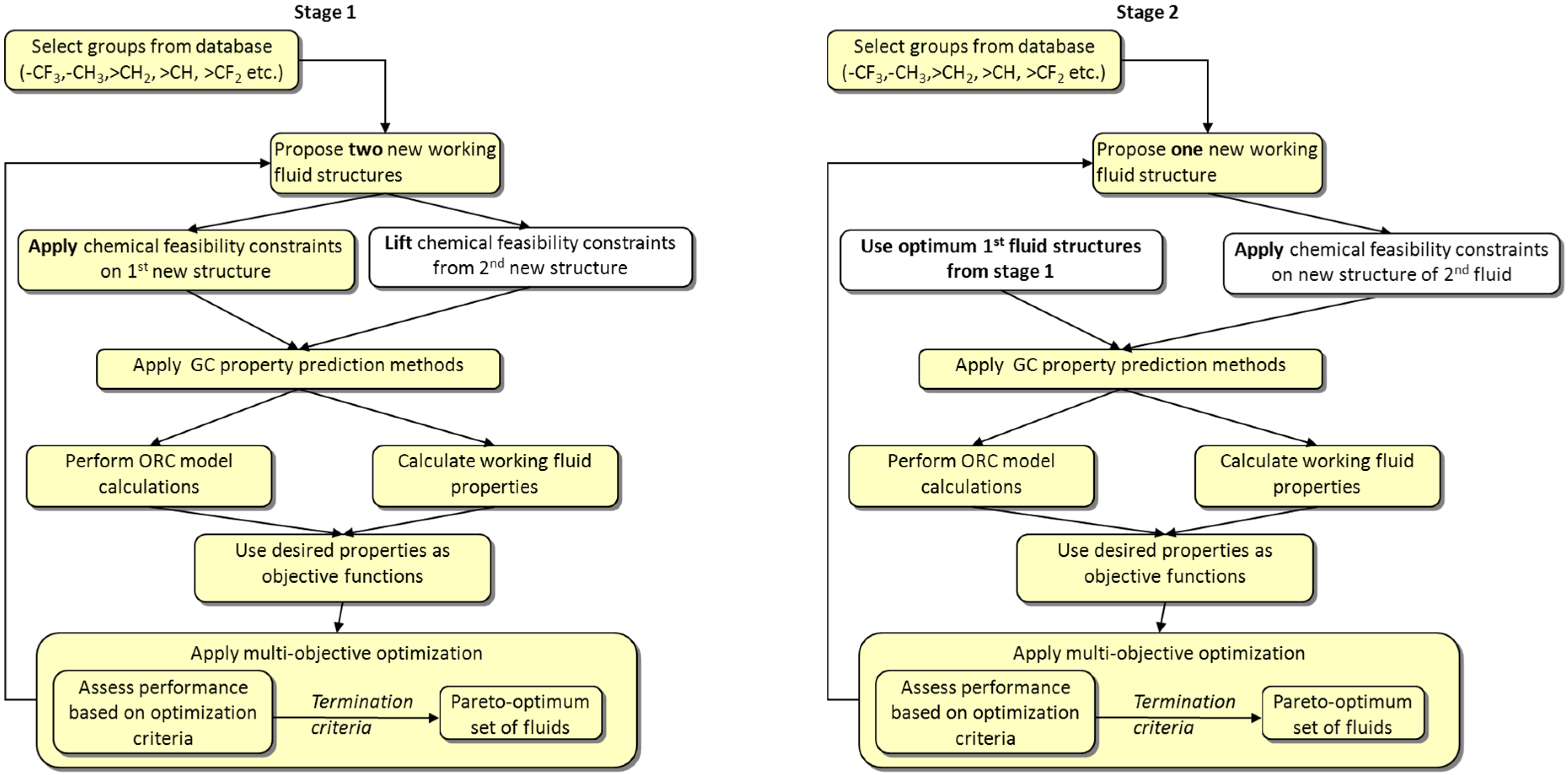
| Main Points | Papadopoulos et al. [4,5,37] a | Palma-Flores et al. [43] c | Lampe et al. [44,45] b |
|---|---|---|---|
| Implemented stages | Stage 1: CAMD optimizing molecular structure. Stage 2: Evaluation of optimum molecules in ORC process optimization. | Stage 1: CAMD optimizing molecular structure. Stage 2: Evaluation of optimum molecules in ORC process simulation. | Stage 1: CoMT-CAMD optimizing molecular parameters and ORC process. Stage 2: Mapping of optimum molecular parameter values in molecular structures of existing molecules. |
| Property prediction method | GC + EoS; (e.g., standard cubic) | GC + EoS; (e.g., standard cubic) | PC-SAFT + QSPR (for ideal heat capacity) |
| Working fluid optimization parameters (Stage 1) | Functional groups (discrete, result in optimum structure) | Functional groups (discrete, result in optimum structure) | Segment number, diameter and van der Waals interactions (continuous, result in optimum values) |
| Optimization approach (Stage 1) | Multi-objective optimization, Simulated Annealing | Single objective optimization, MINLP solver | Single objective optimization, NLP solver |
| Working fluid optimization criteria (Stage 1) | Density, Enthalpy of vaporization, Liquid heat capacity, Viscosity, Thermal conductivity, Toxicity, Flammability, Melting point temperature, Critical temperature, Ozone depletion potential (qualitative), Global warming potential (qualitative). | Enthalpy of vaporization, Liquid heat capacity, ratio of the two, weighted sum of the two and the standard Gibbs energy of formation of an ideal gas. | ORC net power output. |
| Optimization criteria (Stage 2) | Unified index considering maximization of power output revenues and minimization of capital costs (vaporizer and condenser areas). | ORC thermal efficiency. | Expected loss in process performance of optimum (theoretical fluid) compared to real fluids in a database. |
| Identified fluids a |
|
|
|
3.4. Optimization-based CAMD of Mixtures
| Main Points | Papadopoulos et al. [18,19] d | Molina-Thierry and Flores-Tlacuahuac, [51] e |
|---|---|---|
| Implemented stages | Stage 1: CAMD optimizing 1st and theoretical 2nd structure, concentration and ORC process. Stage 2: CAMD optimizing 1st and 2nd structure, concentration and ORC process. | Optimizing number and type of working fluids in mixture (generated from a pre-specified set of pure fluids), mixture concentration and ORC process. |
| Property prediction method | GC + EoS (e.g., standard cubic) | GC + EoS (e.g., standard cubic) |
| Working fluid optimization parameters (Stage 1) | Functional groups (discrete, result in optimum structure), concentration (continuous) | Preselected set of pure fluids used to form mixture combinations (discrete), concentration (continuous) |
| Optimization approach (Stage 1) | Multi-objective optimization, Simulated Annealing | Single objective optimization, testing of several objectives, MINLP solver |
| Working fluid and process optimization criteria (Stage 1) | Exergetic efficiency, thermal efficiency, flammability of each fluid, mixture maximum and minimum flash points (constraint), mixture azetropic concentration (constraint). | Change of the enthalpy of vaporization at the cycle high pressure level, specific net work output, first and second law efficiency, area in between profiles (temperature-enthalpy) of the working fluid and heat source or sink on the heat exchanger |
| Optimization criteria (Stage 2) | Same as Stage 1 | Not applicable |
| Uncertainty in mixture selection | Considered through a systematic non-linear sensitivity analysis approach | - |
| Identified fluids |
|
|
3.5. Uncertainty in Predictions
3.6. Simultaneous vs. Integrated Design Approaches
- The meaning of simultaneous is that decisions regarding the working fluid structure, composition or concentration (in case of mixtures) are taken within the same optimization algorithm that identifies the optimum ORC operating and/or sizing characteristics. The advantage of a simultaneous approach is that the working fluid and ORC interactions are accounted for together and drive the optimization search to identify an optimum solution. This is reasonable because a working fluid is an inherent component of the ORC system in which it is utilized. However, simultaneous approaches may suffer from combinatorial complexity if the design options in both the working fluid and ORC sides are extensive. The relevant reviewed works incorporate a basic ORC structure into working fluid design in order to identify fluids directly based on their impact in the ORC process. It would be ideal to also consider the structural characteristics of the ORC (e.g., recuperation, pressure levels etc.) simultaneously with working fluid design but this would lead to an intractable optimization problem due to the vast number of potential options and the non-linearities of the employed models. For example, Palma-Flores et al. [43] consider more complex ORC structures in simulations performed after the optimum working fluids were identified.
- The meaning of an integrated design approach is that working fluids are first designed using fluid properties as objective functions and the obtained fluid(s) are then introduced in a full ORC model simulation or optimization, as in the case of pure fluid design presented in Papadopoulos et al. [4,5]. Integrated design approaches evolved from the need to decompose the CAMD and process design problems so that an extensive search space (e.g., working fluid and process structures, operating parameters etc.) may be considered within reasonable computational efficiency. The key to the efficient integration of a CAMD and a process design stage is to identify the working fluid(s) that will subsequently facilitate high performance in ORC optimization, while avoiding the premature exclusion of useful fluid options. In a broader sense simultaneous approaches could become part of the problem decomposition rationale employed in integrated approaches. This is because at some point optimum working fluids and process characteristics obtained from the simultaneous design stage will have to be transferred to a subsequent, independent design stage to perform optimizations either using more detailed and realistic models or exploring a much wider design space. Integrated approaches address the problem of obtaining and transferring useful and inclusive design information in the subsequent stage.
| Merits | Shortcomings | |
|---|---|---|
| Fluid selection from a pre-specified list | Few options to investigate in an optimum selection problem of reduced size, ORC model may be used, selection may also be based only on molecular properties, commercially available fluids may be used directly | The consideration of few options limits the search, arbitrarily excluded working fluids may be the ones that maximize ORC performance, novel working fluids may not be identified |
| Simultaneous design methods | Directly link molecular characteristics with ORC process performance, novel working fluids may be identified | Require an ORC model, which may however reduce computational efficiency if modeling rigor is increased |
| Integrated design methods | Enable the consideration of a more extensive design space and/or more detailed models in each design stage, maintain manageable computational effort, novel working fluids may be identified | Require efficient integration between stages to avoid excluding important designs early on in the search |
| Molecular properties as objectives | Easy to calculate and implement through GC methods, no need for an ORC model, appropriate for CAMD and multi-objective formulations | Indirectly reflect on ORC process performance characteristics, not appropriate for use in single-objective formulations |
| ORC process performance indices as objectives | Directly link CAMD with ORC performance, provide associations with cost/profit characteristics (e.g., net generated work) or direct use of them, support more realistic solutions when more detailed models are used | Detailed ORC models may impact on computational efficiency, associations to cost/profit through less detailed models may be limited to specific ORC characteristics, overlooking other important costs, depending on the model detail |
| Single-objective formulations | Easy to implement, result in a single optimum solution | The use of different properties as the objective function is likely to result in different optimum working fluids |
| Multi-objective formulations | Handle multiple and often conflicting objectives simultaneously, result in a rich set of working fluids, appropriate for molecular properties | More difficult to implement than single-objective formulation |
3.7. Single- vs. Multi-objective Optimization and Types of Objective Functions
- There is no need to select one of the properties as an objective function in order to guide CAMD into the identification of a single optimum molecule, while there is no need to set upper and lower bounds (which are often not known a priori) in the remaining properties which are used as constraints. This is very important because there are many working fluid properties that may be considered as objective functions and a multi-objective formulation does not have limitations on how many may be included.
- Such an approach results in a Pareto front which consists of many working fluids, instead of one obtained in a single-objective case. The Pareto fluids represent multi-fold and rich trade-offs in the entire ORC performance spectrum. They can be incorporated as discrete options in a subsequent comprehensive ORC design stage (see next section) where the optimization and computational efficiency remain manageable (Papadopoulos and Linke [16]).
- Stijepovic et al. [17] investigated the impact of different working fluid properties in the cycle thermal, exergetic efficiency and economics as a function of heat transfer areas and net generated work. It was found that high values of fluid compressibility factor and low values of saturated liquid molar volumes favor all three criteria. Fluids of high molecular weights favor thermal efficiency and of high isobaric heat capacities favor exergetic efficiency and economic performance, whereas low enthalpy of vaporization also favors the same criteria. Low critical pressure, high saturated liquid thermal conductivity and saturated gas volume favor economic performance.
- Palma-Flores et al. [43] report that the molecules resulting from minimization of liquid heat capacity and of a complex objective that combines a weighted sum of enthalpy of vaporization, liquid heat capacity and standard Gibbs energy of formation of an ideal gas result in higher thermal efficiency and work output.
- Papadopoulos et al. [18] finds that exergetic efficiency increases at a higher rate than thermal efficiency decreases, as the concentration moves from pure component to approximately equal amounts of components in the mixture. The use of a multi-objective approach appears helpful.
- Molina-Thierry and Flores-Tlacuahuac [51] find that the first law efficiency is the most appropriate objective to use in a single objective formulation.
4. Optimization Approaches for Organic Rankine Cycles
4.1. Main Concepts and Computational Challenges
- (a)
- Computational fluid dynamic (CFD) models for detailed equipment design [55].
- (b)
- Process level models that incorporate thermodynamic calculations with equipment details for equipment sizing within the flowsheet.
- (c)
- Thermodynamic cycle models which account for energy balances and phase change operations.
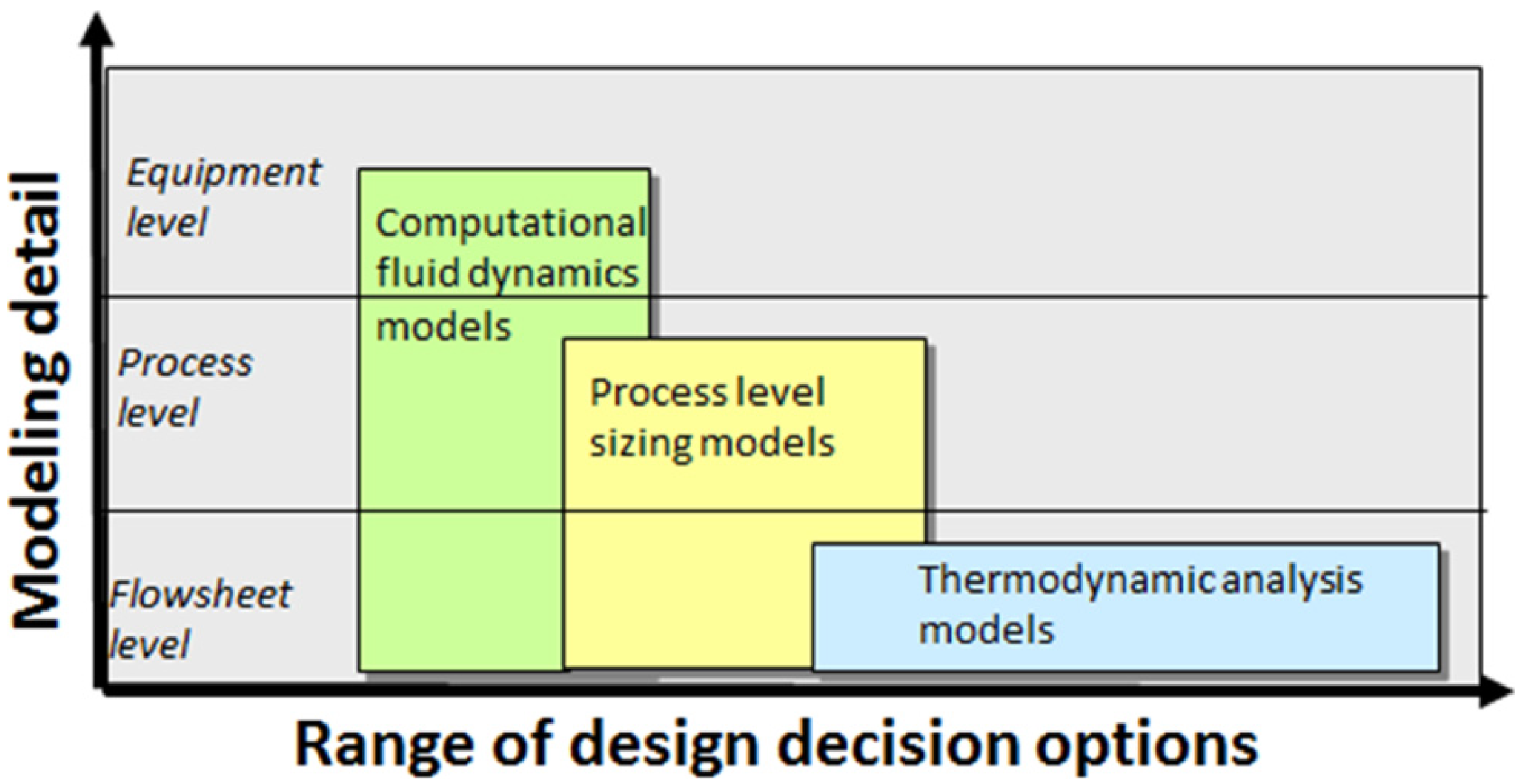
4.2. Reviewed Approaches
| Authors | Optimization Approach | Decision Parameters | Objective Functions |
|---|---|---|---|
| Franco and Villani [57] | Iterative hierarchical identification of optimum ORC size and operating parameters for each combination | Six pure working fluids, sizes of cooling systems and recovery heat exchanger, three cycle structures (supercritical, dual pressure level, ORC with superheater) | First, second law efficiency, brine consumption |
| Salcedo et al. [58] | MINLP problem, deterministic nonlinear algorithm | Equipment sizes, operating conditions, one cycle structure | Cost of water produced in desalination plant, global warming potential |
| Wang et al. [59,60,61] | Genetic algorithm [59,62], multi-objective genetic algorithm [60,61] | Turbine inlet pressure and temperature, temperatures against heat sources and sinks [59,60], geometry of ORC heat exchanger [61], one cycle structure | Net power output to total heat transfer area [59], exergetic efficiency and capital cost [60], pressure drop, heat transfer area [61] |
| Xi et al. [62] | Genetic Algorithm | Three regenerative cycle structures, six pure working fluids, operating parameters | Exergetic efficiency |
| Walraven et al. [63,64] | Deterministic NLP | Eight pure working fluids, tube diameters, baffle spacing in heat exchangers, two different cycle structures | Levelized cost of electricity [63], net present value [64] |
| Victor et al. [30] | Simulated Annealing | Composition of working fluid mixture, ORC, Kalina cycle | Thermal efficiency |
| Authors | Optimization Approach | Decision Parameters | Objective Functions |
|---|---|---|---|
| Gerber and Marechal [65] | Multi-period, multi-objective, evolutionary algorithm across multiple periods, MILP in single periods (cycle structure and operation) | Two cycle structures (single-loop, intermediate draw-off), evaporation and saturation temperature (both structures), draw-off split fraction and condensation temperature (2nd structure) | Investment and operating cost, exergetic and energetic efficiency |
| Pierobon et al. [67] | Genetic algorithm (cycle operation and working fluid) | Five pure working fluids, size of heat exchangers, turbine inlet pressure and temperature, the condensing temperature, pinch points, superheating temperature difference, target velocities in heat exchangers | Thermal efficiency, total system volume, net present value |
| Larsen et al. [68] | Genetic algorithm (cycle structure, operation and working fluid) | Set of working fluids, structures with recuperation and/or superheating | Thermal efficiency |
| Clarke and McLeskey [69] | Multi-objective particle swarm (cycle operation and working fluid) | Seventeen working fluids, evaporation temperature, minimum approach temperature, effectiveness of superheater and recuperator, temperature difference in condenser | Specific work output, specific heat exchanger area |
| Authors | Optimization Approach | Decision Parameters | Objective Functions |
|---|---|---|---|
| Stijepovic et al. [70] | Iterative addition of pressure loops to optimize an evolving structure, deterministic NLP inside each loop to optimize the operating parameters | Number of pressure loops, working fluid flowrates, saturation temperatures, evaporator outlet temperatures per loop, two expandable multi-pressure ORC configurations, type of turbine (induction, expansion) | Exergy loss, work output |
| Toffolo [72] | Genetic algorithm to synthesize structure, sequential quadratic programming to optimize objective function | Number and configuration of pressure loops, expansion and heat exchange stages | Net generated electrical power |
4.3. ORC Process Structure Classes and Types
- Fixed flowsheet approaches: Those that focus on parameter optimization as well as on addressing equipment design decisions for a pre-specified ORC flowsheet.
- Flowsheet selection approaches: Those that consider cycle operating and equipment design for different pre-specified flowsheets. In such cases the pre-specified flowsheet structures may be decision parameters in the optimization or each structure may be optimized separately, one-by-one in terms of operating and equipment characteristics.
- Flowsheet design approaches: Those that have broadened the scope towards the inclusion of structural design decisions within the cycle. In such cases the flowsheet structure is not entirely pre-specified but a flexible structure gradually evolves into different configurations and the optimum flowsheet results from the optimization, together with operating and equipment characteristics.
- Structures that intend to decrease irreversibility and match the temperature profiles between heat source and the working fluid involve transcritical cycles, trilateral cycles, cycles with zeotropic mixtures as working fluids, cycles with multiple evaporation pressures, organic flash cycles and cascade cycles.
- Structures that intend to increase thermal efficiency by maximizing the mean temperature difference between heat addition and heat rejection involve cycles with the addition of a recuperator, Regenerative cycles with turbine bleeding, cycles with reheaters and cycles with vapor injector.
4.4. Stochastic vs. Deterministic Optimization Methods
- Deterministic optimization methods exploit analytical properties (e.g., convexity and monotonicity) of the problem to generate a deterministic sequence of points converging to an (local or global) optimal solution [74]. They are often represented through variations of NLP (continuous variables) and MINLP (integer and continuous variables) problem formulations, although there are also several other problem classes [75]. They provide insights regarding the local [74] or global optimality of a solution through analytical mathematical conditions [75]. From a practical perspective they require a lower number of objective function evaluations to reach an optimum solution than stochastic methods and enable the identification of locally [53] or globally [75] optimum solutions in non-convex problems. Limitations of these methods involve the computationally intensive use of derivative transformations and difficulties in the initialization of simulations when complex models are considered. A fundamental issue of deterministic methods is to transcend local optimality [74] hence the development of mechanisms to prevent the convergence in local optima in highly non-convex problems is also a very active research field [76].
- Stochastic optimization methods, i.e., methods for which the outcome is random, are particularly suited for problems that possess no known structure that can be exploited. These methods generally require little or no additional assumptions on the optimization problem [74]. The three main classes of stochastic methods are: Two-phase methods, random search methods, and random function methods [74]. The most well-known representatives of stochastic methods are Genetic Algorithms and Simulated Annealing [52,53] which are also called metaheuristics. Simulated Annealing is a typical representative of random search methods which is easily implementable, robust and applicable to a very general class of global optimization problems [74]. Metaheuristics usually emulate physical systems in order to explore the solution space of a given problem and identify the optimum solution through a series of probabilistic transformations. These methods do not suffer from the same limitations as the deterministic methods because their inherent mathematical operations are simple, their algorithmic mechanisms provide venues to target the globally optimal domain and discrete design parameters are handled easier. They can even be applied to ill-structured problems for which no efficient local search procedures exist [74]. However, the lack of these limitations is traded-off for convergence to a distribution of nearly optimal solutions and sometimes for long computational times required for the implementation of the stochastic runs. These characteristics are not necessarily shortcomings as the distribution of nearly optimal scenarios provides statistical guarantees for the quality of the solutions. These methods are very useful at early design stages when there is a vast number of discrete or continuous decision options to be investigated. The existence of multiple close-to-target optimum solutions provides valuable design insights into the problem which can be reviewed and analyzed by users prior to transferring meaningful conclusions onto a subsequent stage where the design problem can be defined with considerably less uncertainty.
| Merits | Shortcomings | |
|---|---|---|
| Deterministic methods | Fewer function evaluations than stochastic methods to reach an optimum, analytical mathematical determination of local or global optimum | Intensive computations, difficult simulation initialization in non-convex models, mechanisms to avoid local optima is an active research field, require knowledge of analytical problem properties (e.g., convexity, monotonicity) |
| Stochastic methods | Suitable for early stage design with extensive and discretized design spaces, easier to implement than deterministic methods, no knowledge of optimization problem structure is required, rich design insights from close but different optimum solutions | Larger number of function evaluations to identify optimum solution, statistical assessment of solution optimality |
| Single-objective formulations | Easy to implement, result in a single optimum solution | Need for well-defined problems, use of different objective functions results in different designs, an appropriate objective function needs to be selected |
| Multi-objective formulations | Handle multiple and often conflicting objectives simultaneously, results in a rich set of finite designs representing important trade-offs | More difficult to implement than single-objective formulation |
| Thermodynamic objectives | Useful for early design stages using less rigorous process models | Appropriate objectives need to be selected and combined, indirect and approximate association with costs |
| Economic objectives | Support detailed and realistic designs when used with sufficiently detailed process models | More complex objectives than cost or profit may be needed, appropriate objectives should be selected based on optimization formulations and goals |
4.5. Single- vs. Multi-Objective Optimization and Types of Objective Functions
- In single-objective optimization, they find that the Compromise criteria (NPV) are the most suitable because the obtained designs enable a fair compromise between profitability, operational efficiency, and environmental performance. The other criteria either favor solutions with small capital investment and cash flow but fast payback time and high profitability (Qualitative criteria) or vice versa (Quantitative criteria).
- In multi-objective optimization the NPV results in Pareto optimum designs that are close to the environmentally friendliest designs obtained by Quantitative criteria (e.g., Profit or TAC). On the other hand, the Qualitative criteria unveil environmental trade-offs in a much wider range.
5. Operation and Control of ORC Systems
5.1. Main Concepts and Computational Challenges
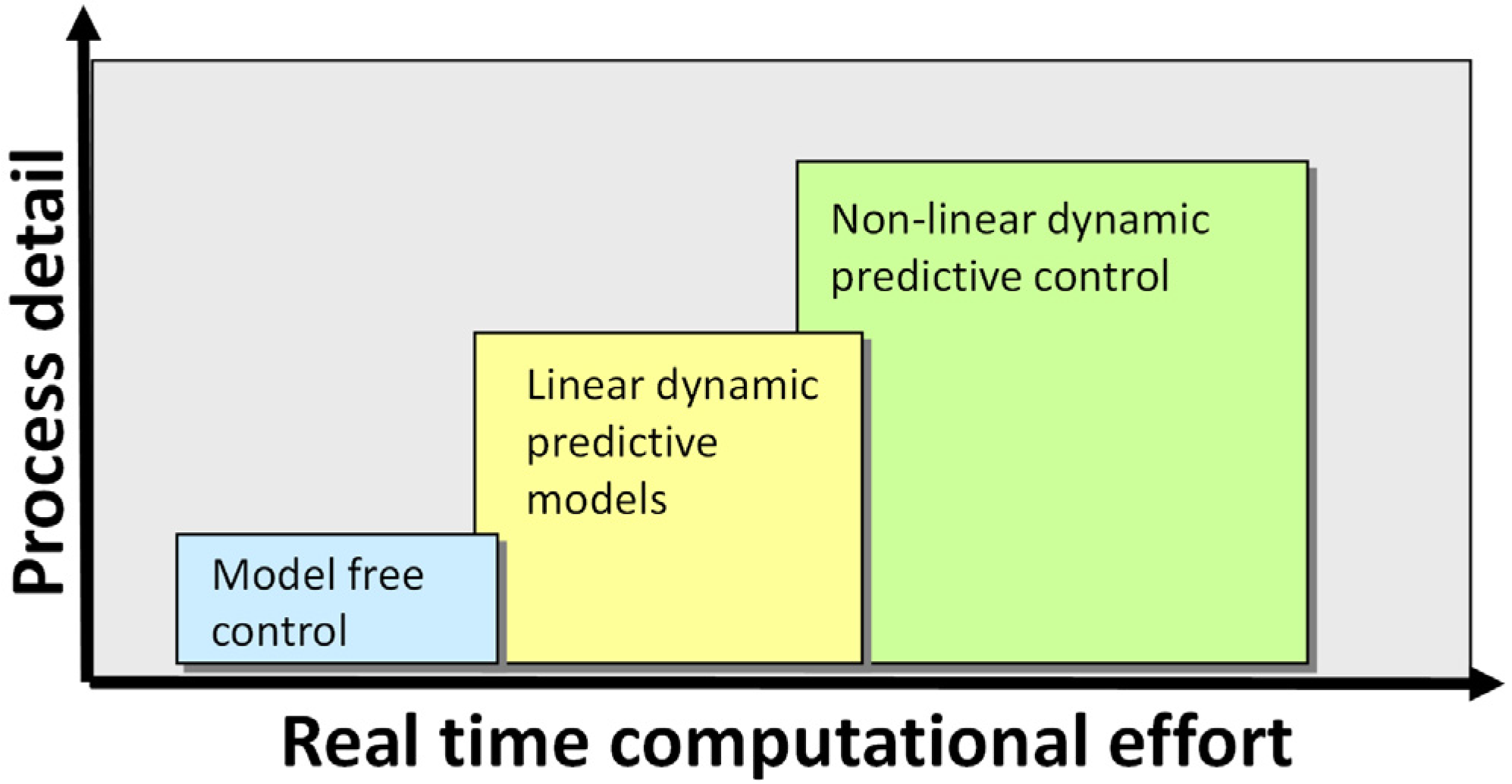
5.2. Dynamic Models
| Authors | Modeling Method | Equipment | Purpose |
|---|---|---|---|
| Quoilin et al. [85] | Empirical (regression) | Entire ORC system | Control system design |
| Zhang et al. [88,89,90] | Empirical (regression) | Entire ORC system | Control system design |
| Wei et al. [92] | First principles | Entire ORC system | Start-up and shut-down simulations |
| Bamgbopa and Uzgoren [93] | First principles | Heat exchangers (dynamic), pump expander (static) | Power output computation |
| Bamgbopa and Uzgoren [94] | First principles | Solar ORC | Steady state efficiency |
5.3. Control Approaches
| Authors | System Type | Control Approach | Manipulated/Controlled Parameters |
|---|---|---|---|
| Quoilin et al. [95] | Low grade ORC waste heat recovery | PID (multi-loop) | Pump speed, expander speed/evaporating temperature, superheating |
| Peralez et al. [96] | ORC waste heat recovery | Nonlinear model inversion | Exhaust gas by-pass valve, expander by-pass valve, pump speed, expander speed/Superheating temperature |
| Hou et al. [101] | ORC waste heat recovery | Minimum variance controller (multi-variable) | Throttle valve position, mass flow rate of working fluid, mass flow rate of exhaust gas, air flow rate/power, throttle pressure, evaporator outlet temperature, condenser outlet temperature |
| Zhang et al. [88,99] | ORC waste heat recovery | Linear Quadratic Regulator with extended observer (multi-variable) | Throttle valve position, working fluid pump speed, exhaust gas velocity, air velocity/power, throttle pressure, evaporator outlet temperature, condenser outlet temperature |
| Zhang et al. [89] | ORC waste heat recovery | Model predictive control (multi-variable) | Throttle valve position, working fluid pump speed, exhaust gas velocity, air velocity/power, throttle pressure, evaporator outlet temperature, condenser outlet temperature |
| Zhang et al. [90] | ORC waste heat recovery | Constrained generalized predictive controller (multi-variable) | Throttle valve position, working fluid pump speed, exhaust gas velocity, air velocity/power, throttle pressure, evaporator outlet temperature, condenser outlet temperature, Constraints on system variables. |
5.4. Remarks on Employed Methods
- Multi-loop control systems are relatively simple to implement but require careful tuning to enable stable and acceptable dynamic performance. Highly interactive systems hinder the achievable control performance and therefore the introduction of model based control techniques becomes a viable option. System interaction is further increased whith more complex ORC configurations (e.g., multi-pressure or multi-temperature systems, multiple expansion units and so forth).
- Model based control systems require the development of accurate dynamic models for the individual subsystems. Usually, linear models with suitable disturbance models and integral action can meet the control objectives. The model development effort is accompanied by the execution of well-designed experiments in order to estimate model parameters and validate the model structure and predictions. In addition, an online parameter estimation procedure is attached to the feedback loop so that the control models can adapt to plant drifts. Model based control usually results in improved dynamic performance as process interaction is taken into consideration explicitly but model accuracy is an essential factor for acceptable set-point tracking and disturbance rejection.
6. ORC Integration with Multiple Heat Source Streams
6.1. Main Concepts
6.2. Reviewed Approaches
| Authors | Integration Approach | Evaluated Options | Integration/Design Criteria |
|---|---|---|---|
| Kwak et al. [119] | Total site analysis, optimization of ORC operation | Sixteen working fluids, turbine inlet temperature condenser outlet temperature | Total annualized cost |
| Chen et al. [120] | Superstructure-based optimization of HEN integrated with ORC, MINLP solver | Number and connections of HEN, operating parameters of HEN and ORC | Generated ORC work |
| Marechal and Kalitventzeff [121] | Mathematical model of exergy composite curves (MILP solver), ORC operation optimization and fluid selection (MILP solver) | List of few pre-selected fluids, utility flowrates, several ORC operating characteristics | Costs, exergy losses |
| Soffiato et al. [108] | SQP solver (deterministic) for ORC optimization in an iterative procedure, pinch composite curves for ORC-heat source matching, evaluation of each ORC structure and working fluid combination | Six working fluids, three pre-selected structures (simple cycle, regenerative cycle, and two-stage cycle), the evaporation pressures and the degrees of superheating in one or two stages, the ratio between the mass flow rates in the two stages | Net ORC power output |
| Lira-Barragán et al. [117] | Multi-objective MINLP, results reported for all working fluids | Three working fluids, structure and operating characteristics of heat exchanger network, existence of ORC and/or absorption refrigeration system | Economic (annual profit), environmental (greenhouse gas emissions), social (number of jobs generated) |
| Gutiérrez-Arriaga et al. [118] | Pinch grand composite curves, Genetic Algorithms to optimize operation of a basic ORC, results reported for 3 different working fluids | Three working fluids, operating ORC parameters | Gross annual profit |
| Kapil et al. [114] | Total site analysis (NLP optimization), ORC process simulation | Pressure of different steam levels | Enthalpy difference of shifted heat sink and source, thermal efficiency, purchase cost |
| Hipólito-Valencia [115,116] | Heat exchanger network superstructure, MINLP solver | Total heat transfer area, network configuration, operating parameters, two working fluids | Total annualized cost |
| Authors | Integration Approach | Evaluated Options | Integration/Design Criteria |
|---|---|---|---|
| Yu et al. [124] | Pinch-based energy recovery targeting, iterative enumeration | Eleven working fluids, cycle operating parameters | Power output |
| Safarian and Aramoun [125] | Exergy- and energy-based analysis to identify best ORC structure, evaluation of each structure separately | Basic ORC, ORC incorporating turbine bleeding, regenerative ORC, ORC incorporating both turbine bleeding and regeneration | Degree of thermodynamic perfection, exergetic efficiency, thermal efficiency, influence coefficient, exergy loss |
| Luo et al. [126] | Pinch-based energy targeting, simulation-based objective function evaluation | Terminal temperature and heat load of the process-heated boiler feed water | Fuel consumption of steam power plant |
| Tchanche et al. [123] | Energy and exergy flow analysis, evaluation of each working fluid and ORC structure combination separately through simulations | Four working fluids, four structures (basic ORC, ORC with regenerative heat exchanger, with open or closed feed liquid heater) | Exergy losses, degree of thermodynamic perfection, exergetic efficiency, energetic efficiency |
| Romeo et al. [107] | Pinch-based energy integration, different temperature levels, evaluation of ORC structure for each working fluid | Pre-selected two-stage (dual pressure) ORC, temperature of waste heat source, six pre-selected working fluids | Energetic efficiency |
| DiGenova et al. [2] | Pinch composite curves for ORC-heat source matching options, evaluation of each structure separately | Five ORC structures (basic ORC, with reheat stages, with multiple pressure levels, recuperator and balanced recuperator) | Thermal efficiency |
| Hackl and Harvey [112] | Total site analysis, ORC simulations with different working fluids | Five pure fluids, one mixture, ORC operating parameters | Net excess heat, cost of electricity, payback period of investment, CO2 emissions reduction |
| Desai and Bandyopadhyay [113] | Pinch-based graphical integration, ORC simulations with different fluids | Sixteen fluids, basic ORC, ORC with turbine bleeding and regeneration, heat exchanger network configuration and conditions | Net work output, thermal efficiency |
| Song et al. [122] | Matching of heat sources at different temperatures with different ORC configurations and fluids, simulations | Eight pure and six mixed working fluids, Dual integrated or independent ORC, single ORC | Net power output, heat transfer area and their ratio |
6.3. Remarks on Integration
- Enriched representations of ORC configurations and multiple heat steams in the form of superstructures to provide a representation of all possible alternative configurations, including multi-pressure and multi-cycle systems.
- Multi-scale approaches to bridge the gap between higher-level ORC integration and detailed design decisions impacting on performance such as heat exchanger design optimization.
- Multi-scale approaches to support integrated decision making across the working fluid selection, ORC design and ORC integration problem levels, and
- Global search schemes for ORC integration with multiple heat sources similar to the approaches that emerge for ORC design optimization.
7. Concluding Remarks
Author Contributions
Nomenclature
| CAMD | Computer-Aided Molecular Design |
| CARMA | Controlled auto-regressive moving average |
| CFD | Computational fluid dynamic |
| CoMT | Continuous molecular targeting |
| COSMO-RS | Conductor-like screening model for real solvents |
| DFT | Density functional theory |
| EAC | Equivalent annual cost |
| EoS | Equation of state |
| GC | Group contribution |
| GWP | Global warming potential |
| HEN | Heat exchanger network |
| IRR | Internal rate of return |
| MILP | Mixed integer linear programming |
| MNLP | Mixed integer non-linear programming |
| NLP | Non-linear programming |
| NPV | Net present value |
| ODP | Ozone depletion potential |
| ORC | Organic Rankine cycle |
| PBT | Profit before taxes |
| PC-SAFT | Perturbed chain statistical associating fluid theory |
| PI | Proportional-integral |
| PID | Proportional-integral-derivative |
| PT | Payback time |
| QSPR | Quantitative structure-property relationships |
| ROI | Return on investment |
| SQP | Sequential quadratic programming |
| TAC | Total annual cost |
Conflicts of Interest
References
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles—A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- DiGenova, K.J.; Botros, B.B.; Brisson, J.G. Method for customizing an organic Rankine cycle to a complex heat source for efficient energy conversion, demonstrated on a Fischer Tropsch plant. Appl. Energy 2013, 102, 746–754. [Google Scholar] [CrossRef]
- Hung, T.C. Waste heat recovery of organic Rankine cycle using dry fluids. Energy Convers. Manag. 2001, 42, 539–553. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P. On the systematic design and selection of optimal working fluids for organic Rankine cycles. Appl. Therm. Eng. 2010, 30, 760–769. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P.; Seferlis, P.; Voutetakis, S. Power generation from low enthalpy geothermal fields by design and selection of efficient working fluids for organic Rankine cycles. Chem. Eng. Trans. 2010, 21, 61–66. [Google Scholar]
- Preißinger, M.; Heberle, F.; Brüggemann, D. Advanced organic Rankine cycle for geothermal application. Int. J. Low Carbon Technol. 2013. [Google Scholar] [CrossRef]
- Mavrou, P.; Papadopoulos, A.I.; Stijepovic, M.; Seferlis, P.; Linke, P.; Voutetakis, S. Novel and conventional working fluid mixtures for solar Rankine cycles: Performance assessment and multi-criteria selection. Appl. Therm. Eng. 2015, 75, 384–396. [Google Scholar] [CrossRef]
- Schuster, A.; Karellas, S.; Kakaras, E.; Spliethoff, E. Energetic and economic investigation of innovative organic Rankine cycle applications. Appl. Therm. Eng. 2008, 29, 1809–1817. [Google Scholar] [CrossRef]
- Tsoka, C.; Johns, W.R.; Linke, P.; Kokossis, A. Towards sustainability and green chemical engineering: Tools and technology requirements. Green Chem. 2004, 8, 401–406. [Google Scholar] [CrossRef]
- Biegler, L.T.; Grossmann, I.E.; Westerberg, A.W. Systematic Methods of Chemical Process Design; Prentice Hall International Series in the Physical and Chemical Engineering Sciences; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Klemeš, J.J. Process Integration Handbook; Woodhead Publishing: Cambridge, UK, 2013. [Google Scholar]
- Seferlis, P.; Georgiadis, M.C. The Integration of Process Design and Control; Computer Aided Chemical Engineering, 17; Elsevier Science B.V.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Adjiman, C.S. Optimal solvent design approaches. In Encyclopedia of Optimization, 2nd ed.; Floudas, C.A., Pardalos, P.M., Eds.; Springer: New York, NY, USA, 2009; pp. 2750–2757. [Google Scholar]
- Adjiman, C.S.; Galindo, A. Molecular systems engineering. In Process Systems Engineering; Pistikopoulos, E.N., Georgiadis, M.C., Dua, V., Eds.; Wiley: Weinheim, Germany, 2010; Volume 6. [Google Scholar]
- Ng, L.Y.; Chong, F.K.; Chemmangattuvalappil, N.G. Challenges and opportunities in computer-aided molecular design. Comput. Chem. Eng. 2015. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Linke, P. Integrated solvent and process selection for separation and reactive separation systems. Chem. Eng. Process. Process Intensif. 2009, 48, 1047–1060. [Google Scholar] [CrossRef]
- Stijepovic, M.; Linke, P.; Papadopoulos, A.I.; Grujic, A. On the role of working fluid properties in organic Rankine cycle performance. Appl. Therm. Eng. 2012, 36, 406–413. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P.; Seferlis, P.; Voutetakis, S. Toward optimum working fluid mixtures for organic Rankine cycles using molecular design and sensitivity analysis. Ind. Eng. Chem. Res. 2013, 52, 12116–12133. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P.; Seferlis, P.; Voutetakis, S. Molecular design of working fluid mixtures for organic Rankine cycles. Comput. Aided Chem. Eng. 2013, 32, 289–294. [Google Scholar]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Angelino, G.; di Paliano, P.C. Multicomponent working fluids for organic Rankine cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Demuth, O.J.; Kochan, R.J. Analyses of Mixed Hydrocarbon Binary Thermodynamic Cycles for Moderate Temperature Geothermal Resources Using Regeneration Techniques; Technical Report; Idaho National Engineering Lab.: Idaho Falls, ID, USA, 1981. Available online: http://www.osti.gov/geothermal/servlets/purl/5281969-D6H9jj/native/5281969.pdf (accessed on 7 April 2015).
- Gawlik, K.; Hassani, V. Advanced binary cycles: Optimum working fluids. In Proceedings of the 32nd Intersociety Energy Conversion Engineering Conference, Honolulu, HI, USA, 27 July–1 August 1997; Volume 3, pp. 1809–1814.
- Borsukiewicz-Gozdur, A.; Nowak, W. Comparative analysis of natural and synthetic refrigerants in application to low temperature Clausius-Rankine cycle. Energy 2007, 32, 344–352. [Google Scholar] [CrossRef]
- Angelino, G.; di Paliano, P.C. Air cooled siloxane bottoming cycle for molten carbonate fuel cells. In Proceedings of the Fuel Cell Seminar, Portland, OR, USA, 30 October–2 November 2010.
- Bliem, C. Zeotropic mixtures of halocarbons as working fluids in binary geothermal power generation cycles. In Proceedings of the 22nd Intersociety Energy Conversion Engineering Conference; Portland, OR, USA, 10–14 August 1987. Available online: http://www.osti.gov/bridge/servlets/purl/5914218-ULxh0x/5914218.pdf (accessed on 7 April 2015).
- Wang, X.D.; Zhao, L. Analysis of zeotropic mixtures used in low-temperature solar Rankine cycles for power generation. Sol. Energy 2009, 83, 605–613. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in organic Rankine cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Chys, M.; van den Broek, M.; Vanslambrouck, B.; de Paepe, M. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Victor, R.A.; Kim, J.-K.; Smith, R. Composition optimisation of working fluids for organic Rankine cycles and Kalina cycles. Energy 2013, 55, 114–126. [Google Scholar] [CrossRef]
- Woodland, B.J.; Krishna, A.; Groll, E.A.; Braun, J.E.; Travis Horton, W.; Garimella, S.V. Thermodynamic comparison of organic Rankine cycles employing liquid-flooded expansion or a solution circuit. Appl. Therm. Eng. 2013, 61, 859–865. [Google Scholar] [CrossRef]
- Elsayed, A.; Embaye, M.; Al-Dadah, R.; Mahmoud, S.; Rezk, A. Thermodynamic performance of Kalina cycle system 11 (KCS11): Feasibility of using alternative zeotropic mixtures. Int. J. Low Carbon Technol. 2013, 8 (Suppl. S1), i69–i78. [Google Scholar]
- Micheli, D.; Pinamonti, P.; Reini, M.; Taccani, R. Performance analysis and working fluid optimization of a cogenerative organic rankine cycle plant. J. Energy Resour. Technol. 2013, 135, 021601. [Google Scholar] [CrossRef]
- Ramachandran, K.I.; Deepa, G.; Namboori, K. Computational Chemistry and Molecular Modeling Principles and Applications; Springer-Verlag GmbH: New Delhi, India, 2008. [Google Scholar]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. A 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Hukkerikar, A.S.; Sarup, B.; Ten Kate, A.; Abildskov, J.; Sin, G.; Gani, R. Group-contribution+ (GC+) based estimation of properties of pure components: Improved property estimation and uncertainty analysis. Fluid Phase Equilibr. 2012, 321, 25–43. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P.; Seferlis, P.; Voutetakis, S. Multi-level design and selection of optimum working fluids and ORC systems for power and heat cogeneration from low enthalpy renewable sources. Comput. Aided Chem. Eng. 2012, 30, 66–70. [Google Scholar]
- Papadopoulos, A.I.; Linke, P. Multiobjective molecular design for integrated process-solvent systems synthesis. AIChE J. 2006, 52, 1057–1069. [Google Scholar] [CrossRef]
- Zyhowski, G.; Brown, A. Low global warming fluids for replacement of HFC-245fa and HFC-134a in ORC applications. In Proceedings of First International Seminar on ORC systems, Delft, The Netherlands, 22–23 September 2011.
- Schwiegel, M.; Flohr, F.; Meurer, C. Working Fluid for an Organic Rankine Cycle Process, ORC Process and ORC Apparatus. Patent No. US 20110162366, 7 July 2011. [Google Scholar]
- Wang, H.; Zhang, S.; Guo, T.; Chen, C. HFO-1234yf-Containing Mixed Working Fluid for Organic Rankine Cycle. Patent No. CN101747867, 23 June 2010. [Google Scholar]
- Wang, J.; Zhang, J.; Chen, Z. Molecular entropy, thermal efficiency, and designing of working fluids for organic Rankine cycles. Int. J. Thermophys. 2012, 33, 970–985. [Google Scholar] [CrossRef]
- Palma-Flores, O.; Flores-Tlacuahuac, A.; Canseco-Melchor, G. Optimal molecular design of working fluids for sustainable low-temperature energy recovery. Comput. Chem. Eng. 2014, 72, 334–339. [Google Scholar] [CrossRef]
- Lampe, M.; Groß, J.; Bardow, A. Simultaneous process and working fluid optimization for organic Rankine cycles (ORC) using PC-SAFT. Comput. Aided Chem. Eng. 2012, 30, 572–576. [Google Scholar]
- Lampe, M.; Stavrou, M.; Bücker, M.; Gross, J.; Bardow, A. Simultaneous optimization of working fluid and process for organic Rankine cycles (ORCs) using PC-SAFT. Ind. Eng. Chem. Res. 2014, 53, 8821–8830. [Google Scholar] [CrossRef]
- Roskosch, D.; Atakan, B. Reverse engineering of fluid selection for thermodynamic cycles with cubic equations of state, using a compression heat pump as example. Energy 2015, 81, 202–212. [Google Scholar] [CrossRef]
- Samudra, A.P.; Sahinidis, N.V. Optimization-based framework for computer-aided molecular design. AIChE J. 2013, 59, 3686–3701. [Google Scholar] [CrossRef]
- Sahinidis, N.V.; Tawarmalani, M.; Yu, M. Design of alternative refrigerants via global optimization. AIChE J. 2003, 49, 1761–1775. [Google Scholar] [CrossRef]
- Duvedi, A.P.; Achenie, L.E.K. Designing environmentally safe refrigerants using mathematical programming. Chem. Eng. Sci. 1996, 51, 3727–3739. [Google Scholar] [CrossRef]
- Marcoulaki, E.C.; Kokossis, A.C. On the development of novel chemicals using a systematic synthesis approach. Part I. Optimisation framework. Chem. Eng. Sci. 2000, 55, 2529–2546. [Google Scholar] [CrossRef]
- Molina-Thierry, D.P.; Flores-Tlacuahuac, A. Simultaneous optimal design of organic mixtures and Rankine cycles for low-temperature energy recovery. Ind. Eng. Chem. Res. 2015, 54, 3367–3383. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Linke, P. On the synthesis and optimization of liquid-liquid extraction processes using stochastic search methods. Comput. Chem. Eng. 2004, 28, 2391–2406. [Google Scholar] [CrossRef]
- Cavazzuti, M. Optimization Methods: From Theory to Design; Springer-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Kasaš, M.; Kravanja, Z.; Novak Pintarič, Z. Suitable modeling for process flow sheet optimization using the correct economic criterion. Ind. Eng. Chem. Res. 2011, 50, 3356–3370. [Google Scholar] [CrossRef]
- Harinck, J.; Pasquale, D.; Pecnik, R.; van Buijtenen, J.; Colonna, P. Performance improvement of a radial organic Rankine cycle turbine by means of automated computational fluid dynamic design. J. Power Energy 2013, 227, 637–645. [Google Scholar] [CrossRef]
- Weith, T.; Heberle, F.; Preißinger, M.; Brüggemann, D. Performance of siloxane mixtures in a high-temperature organic Rankine cycle considering the heat transfer characteristics during evaporation. Energies 2014, 7, 5548–5565. [Google Scholar] [CrossRef]
- Franco, A; Villani, M. Optimal design of binary cycle power plants for water-dominated, medium-temperature geothermal fields. Geothermics 2009, 38, 379–391. [Google Scholar] [CrossRef]
- Salcedo, R.; Antipova, E.; Boer, D.; Jimenez, L.; Guillen-Gosalbez, G. Multi-objective optimization of solar Rankine cycles coupled with reverse osmosis desalination considering economic and life cycle environmental impacts. Desalination 2012, 286, 358–371. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Ma, S.; Dai, Y. Thermodynamic analysis and optimization of an (organic rankine cycle) ORC using low grade heat source. Energy 2013, 49, 356–365. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Li, M.; Dai, Y. Multi-objective optimization of an organic Rankine cycle (ORC) for low grade waste heat recovery using evolutionary algorithm. Energy Convers. Manag. 2013, 71, 146–158. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, M.; Xia, J.; Dai, Y. Multi-objective optimization design of a condenser in an organic Rankine cycle for low grade waste heat recovery using evolutionary algorithm. Int. Commun. Heat Mass 2013, 45, 47–54. [Google Scholar] [CrossRef]
- Xi, H.; Li, N.J.; Xu, C.; He, Y.L. Parametric optimization of regenerative organic Rankine cycle (ORC) for low grade waste heat recovery using genetic algorithm. Energy 2013, 58, 473–482. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Economic system optimization of air cooled organic Rankine cycles powered by low temperature geothermal heat sources. Energy 2015, 80, 104–113. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Minimizing the levelized cost of electricity production from low temperature geothermal heat sources with ORCs: Water or air cooled? Appl. Energy 2015, 142, 144–153. [Google Scholar] [CrossRef]
- Gerber, L.; Marechal, F. Defining optimal configurations for geothermal systems using process design and process integration techniques. Appl. Therm. Eng. 2012, 43, 29–41. [Google Scholar] [CrossRef]
- Halemane, K.P.; Grossmann, I.E. Optimal process design under uncertainty. AIChE J. 1983, 29, 425–433. [Google Scholar] [CrossRef]
- Pierobon, L.; Nguyen, T.V.; Larsen, U.; Haglind, F.; Elmegaard, B. Multi-objective optimization of organic Rankine cycles in an offshore platform. Energy 2013, 58, 538–549. [Google Scholar] [CrossRef]
- Larsen, U.; Pierobon, L.; Haglind, F.; Gabrieli, C. Design and optimisation of organic Rankine cycles for waste heat recovery on marine applications using principles of natural selection. Energy 2014, 55, 803–812. [Google Scholar] [CrossRef]
- Clarke, J.; McLeskey, J.T. Multi-objective particle swarm optimization of binary geothermal power plants. Appl. Energy 2015, 138, 302–314. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Papadopoulos, A.I.; Linke, P.; Grujic, A.S.; Seferlis, P. An exergy Composite curves approach for the design of optimum multi-pressure organic Rankine cycle processes. Energy 2014, 69, 285–298. [Google Scholar] [CrossRef]
- Linnhoff, D.; Dhole, V.R. Shaftwork targets for low-temperature process design. Chem. Eng. Sci. 1992, 47, 2081–2091. [Google Scholar] [CrossRef]
- Toffolo, A. A synthesis/design optimization algorithm for Rankine cycle based energy systems. Energy 2014, 66, 115–127. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; Vanslambrouck, B.; de Paepe, M. Review of organic Rankine cycle (ORC) architectures for waste heat recovery. Renew. Sustain. Energy Rev. 2015, 47, 448–461. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Romeijn, H.E.; Tuy, H. Recent developments and trends in global optimization. J. Comput. Appl. Math. 2000, 124, 209–228. [Google Scholar] [CrossRef]
- Floudas, C.A.; Akrotirianakis, I.G.; Caratzoulas, S.; Meyer, C.A.; Kallrath, J. Global optimization in the 21st century: Advances and challenges. Comput. Chem. Eng. 2005, 29, 1185–1202. [Google Scholar] [CrossRef]
- Floudas, C.A.; Gounaris, C.E. A review of recent advances in global optimization. J. Glob. Optim. 2009, 45, 3–38. [Google Scholar] [CrossRef]
- Novak Pintarič, Z.; Kravanja, Z. Selection of the economic objective function for the optimization of process flow sheets. Ind. Eng. Chem. Res. 2006, 45, 4222–4232. [Google Scholar] [CrossRef]
- Novak Pintarič, Z.; Kravanja, Z. The importance of proper economic criteria and process modeling for single- and multi-objective optimizations. Comput. Chem. Eng. 2015. [Google Scholar] [CrossRef]
- Marlin, T.E. Process Control: Designing Processes and Control Systems for Dynamic Performance; McGraw-Hill: Singapore, 1995. [Google Scholar]
- Goodwin, G.C.; Graebe, S.E.; Salgado, M.E. Control System Design; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Rossiter, J.A. Model Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Kouvaritakis, B.; Cannon, M. Nonlinear Predictive Control: Theory and Practice; The Institution of Engineering and Technology: London, UK, 2001. [Google Scholar]
- Zavala, V.M.; Biegler, L.T. The advanced-step NMPC controller: Optimality, stability and robustness. Automatica 2009, 45, 86–93. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an organic Rankine cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Smith, C.A.; Corripio, A. Principles and Practice of Automatic Process Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zhang, J.; Zhang, W.; Hou, G.; Fang, F. Dynamic modeling and multivariable control of organic Rankine cycles in waste heat utilizing processes. Comput. Math. Appl. 2012, 64, 908–921. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Y.; Li, Y.; Hou, G.; Fang, F. Generalized predictive control applied in waste heat recovery power plants. Appl. Energy 2013, 102, 320–326. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Y.; Wang, R.; Xu, J.; Fang, F. Modeling and constrained multivariable predictive control for ORC (Organic Rankine Cycle) based waste heat energy conversion systems. Energy 2014, 66, 128–138. [Google Scholar] [CrossRef]
- Twomey, B.; Jacobs, P.A.; Gurgenci, H. Dynamic performance estimation of small-scale solar cogeneration with an organic Rankine cycle using a scroll expander. Appl. Therm. Eng. 2013, 51, 1307–1316. [Google Scholar] [CrossRef]
- Wei, D.; Lu, X.; Lu, Z.; Gu, J. Dynamic modeling and simulation of an organic Rankine cycle (ORC) system for waste heat recovery. Appl. Therm. Eng. 2008, 28, 1216–1224. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Uzgoren, E. Quasi-dynamic model for an organic Rankine cycle. Energy Convers. Manag. 2013, 72, 117–124. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Uzgoren, E. Numerical analysis of an organic Rankine cycle under steady and variable heat input. Appl. Energy 2013, 107, 219–228. [Google Scholar] [CrossRef]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery organic Rankine cycles. Appl. Energy 2013, 88, 2183–2190. [Google Scholar] [CrossRef]
- Peralez, J.; Tona, P.; Lepreux, O.; Sciarretta, A.; Voise, L.; Dufour, P.; Nadri, M. Improving the control performance of an organic Rankine cycle system for waste heat recovery from a heavy-duty diesel engine using a model-based approach. In Proceedings of the 2013 IEEE Conference on Decision and Control (CDC), Florence, Italy, 10–13 December 2013.
- Kosmadakis, G.; Manolakos, D.; Papadakis, G. An investigation of design concepts and control strategies of a double-stage expansion solar organic Rankine cycle. Int. J. Sustain. Energy 2015, 34, 446–467. [Google Scholar] [CrossRef]
- Luong, D.; Tsao, T.-C. Linear quadratic integral control of an organic Rankine cycle for waste heat recovery in heavy-duty diesel powertrain. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 3147–3152.
- Zhang, J.; Feng, J.; Zhou, Y.; Fang, F.; Yue, H. Linear active disturbance rejection control of waste heat recovery systems with organic Rankine cycles. Energies 2012, 5, 5111–5125. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer-Verlag: London, UK, 2004. [Google Scholar]
- Hou, G.; Bi, S.; Lin, M.; Zhang, J.; Xu, J. Minimum variance control of organic Rankine cycle based waste heat recovery. Energy Convers. Manag. 2014, 86, 576–586. [Google Scholar] [CrossRef]
- Ibarra, M.; Rovira, A.; Alarcón-Padilla, D.C.; Blanco, J. Performance of a 5kWe organic Rankine cycle at part-load operation. Appl. Energy 2014, 120, 147–158. [Google Scholar] [CrossRef]
- Manente, G.; Toffolo, A.; Lazzaretto, A.; Paci, M. An organic Rankine cycle off-design model for the search of the optimal control strategy. Energy 2013, 58, 97–106. [Google Scholar] [CrossRef]
- De Escalona, J.M.; Sánchez, D.; Chacartegui, R.; Sánchez, T. Part-load analysis of gas turbine & ORC combined cycles. Appl. Therm. Eng. 2012, 36, 63–72. [Google Scholar] [CrossRef]
- Pierobon, L.; Nguyen, T.V.; Mazzucco, A.; Larsen, U.; Haglind, F. Part load performance of a wet indirectly fired gas turbine integrated with an ORC turbogenerator. Energies 2014, 7, 8294–8316. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Linke, P. Optimal waste heat recovery and reuse in industrial zones. Energy 2011, 36, 4019–4031. [Google Scholar]
- Romeo, L.M.; Lara, Y.; Gonzalez, A. Reducing energy penalties in carbon capture with organic Rankine cycles. Appl. Therm. Eng. 2011, 31, 2928–2935. [Google Scholar] [CrossRef]
- Soffiato, M.; Frangopoulos, C.A.; Manente, G.; Rech, S.; Lazzaretto, A. Design optimization of ORC systems for waste heat recovery on board a LNG carrier. Energy Convers. Manag. 2015, 92, 523–534. [Google Scholar] [CrossRef]
- Linhoff, B.; Flower, J.R. Synthesis of heat exchanger networks: I. Systematic generation of energy optimal networks. AIChE J. 1978, 24, 633–642. [Google Scholar] [CrossRef]
- Smith, R. Chemical Process: Design and Integration; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Varbanov, P.S.; Fodor, Z.; Klemeš, J.J. Total Site targeting with process specific minimum temperature difference (ΔTmin). Energy 2012, 44, 20–28. [Google Scholar] [CrossRef]
- Hackl, R.; Harvey, S. Applying process integration methods to target for electricity production from industrial waste heat using Organic Rankine Cycle (ORC) technology. In Proceedings of the World Renewable Energy Congress, Linköping, Sweden, 8–11 May 2011.
- Desai, B.D.; Bandyopadhyay, S. Process integration of organic Rankine cycle. Energy 2009, 34, 1674–1686. [Google Scholar] [CrossRef]
- Kapil, A.; Bulatov, I.; Smith, R.; Kim, J.K. Site-wide low-grade heat recovery with a new cogeneration targeting method. Chem. Eng. Res. Des. 2012, 90, 677–689. [Google Scholar] [CrossRef]
- Hipólito-Valencia, B.J.; Rubio-Castro, E.; Ponce-Ortega, J.M.; Serna-González, M.; Nápoles-Rivera, F.; El-Halwagi, M.M. Optimal integration of organic Rankine cycles with industrial processes. Energy Convers. Manag. 2013, 73, 285–302. [Google Scholar] [CrossRef]
- Hipólito-Valencia, B.J.; Rubio-Castro, E.; Ponce-Ortega, J.M.; Serna-González, M.; Nápoles-Rivera, F.; El-Halwagi, M.M. Optimal design of inter-plant waste energy integration. Appl. Therm. Eng. 2014, 62, 633–652. [Google Scholar] [CrossRef]
- Lira-Barragán, L.F.; Ponce-Ortega, J.M.; Serna-González, M.; El-Halwagi, M.M. Sustainable integration of trigeneration systems with heat exchanger networks. Ind. Eng. Chem. Res. 2014, 53, 2732–2750. [Google Scholar] [CrossRef]
- Gutiérrez-Arriaga, C.G.; Abdelhady, F.; Bamufleh, H.S.; Serna-González, M.; El-Halwagi, M.M.; Ponce-Ortega, J.M. Industrial waste heat recovery and cogeneration involving organic Rankine cycles. Clean Technol. Environ. Policy 2015, 17, 767–779. [Google Scholar] [CrossRef]
- Kwak, D.-H.; Binns, M.; Kim, J.-K. Integrated design and optimization of technologies for utilizing low grade heat in process industries. Appl. Energy 2014, 131, 307–322. [Google Scholar] [CrossRef]
- Chen, C.-L.; Chang, F.-Y.; Chao, T.-H.; Chen, H.-C.; Lee, J.-Y. Heat-Exchanger network synthesis involving organic Rankine cycle for waste heat recovery. Ind. Eng. Chem. Res. 2014, 53, 16924–16936. [Google Scholar] [CrossRef]
- Marechal, F.; Kalitventzeff, B. A methodology for the optimal insertion of organic Rankine cycles in industrial processes. In 2nd International Symposium of Process Integration, Dalhousie University, Halifax, Canada, 2004.
- Song, J.; Li, Y.; Gu, C.W.; Zhang, L. Thermodynamic analysis and performance optimization of an ORC (Organic Rankine Cycle) system for multi-strand waste heat sources in petroleum refining industry. Energy 2014, 71, 673–680. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Exergy analysis of micro-organic Rankine power cycles for a small scale solar driven reverse osmosis desalination system. Appl. Energy 2010, 87, 1295–1306. [Google Scholar] [CrossRef]
- Yu, H.; Feng, X.; Wang, Y. A new pinch based method for simultaneous selection of working fluid and operating conditions in an ORC (Organic Rankine Cycle) recovering waste heat. Energy 2015. [Google Scholar] [CrossRef]
- Safarian, S.; Aramoun, F. Energy and exergy assessments of modified Organic Rankine Cycles (ORCs). Energy Rep. 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, B.; Chen, Y.; Mo, S. Heat integration of regenerative Rankine cycle and process surplus heat through graphical targeting and mathematical modeling technique. Energy 2012, 45, 556–569. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linke, P.; Papadopoulos, A.I.; Seferlis, P. Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review. Energies 2015, 8, 4755-4801. https://doi.org/10.3390/en8064755
Linke P, Papadopoulos AI, Seferlis P. Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review. Energies. 2015; 8(6):4755-4801. https://doi.org/10.3390/en8064755
Chicago/Turabian StyleLinke, Patrick, Athanasios I. Papadopoulos, and Panos Seferlis. 2015. "Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review" Energies 8, no. 6: 4755-4801. https://doi.org/10.3390/en8064755
APA StyleLinke, P., Papadopoulos, A. I., & Seferlis, P. (2015). Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review. Energies, 8(6), 4755-4801. https://doi.org/10.3390/en8064755







