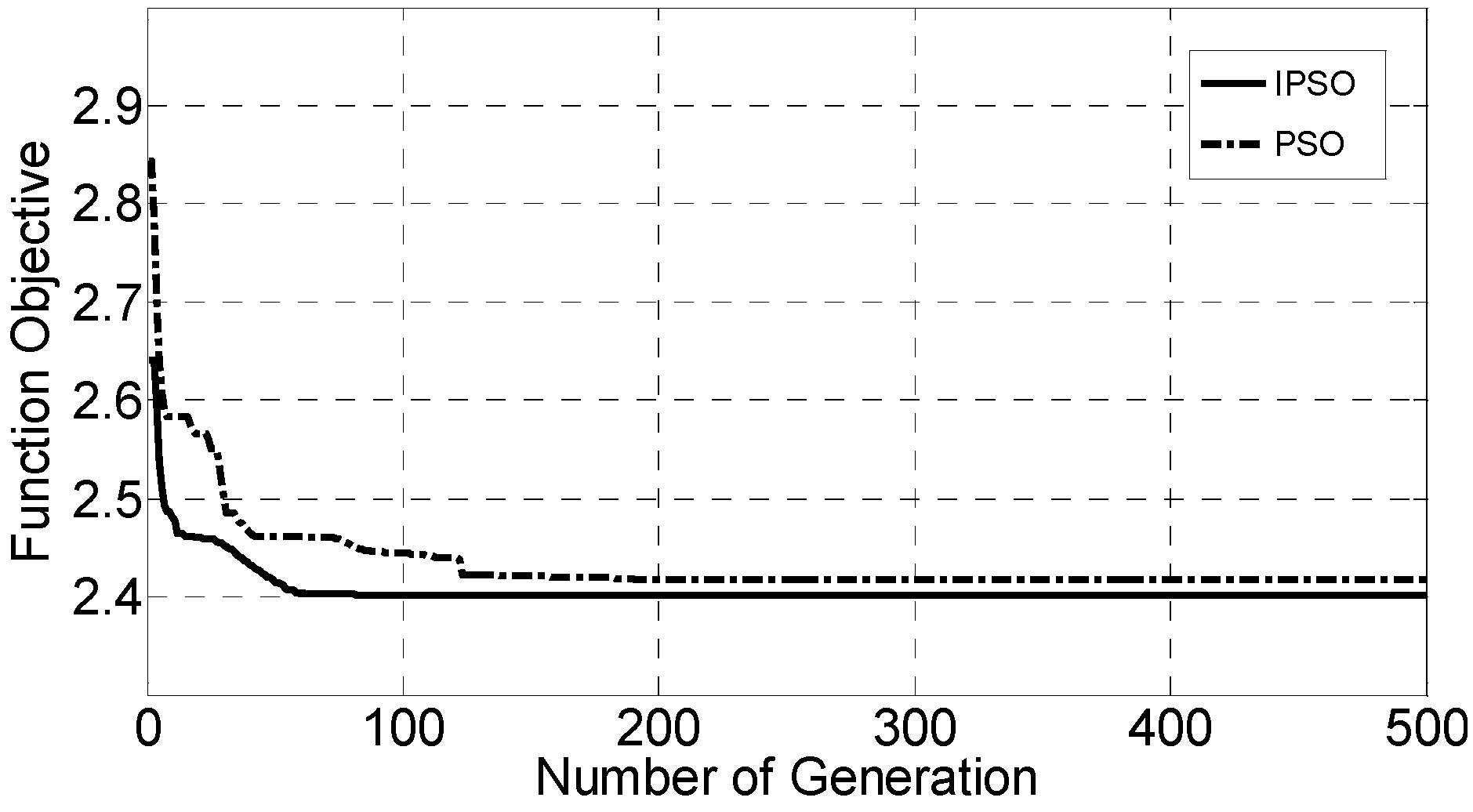1. Introduction
In order to increase the reliability of the electricity supply to the sensitive load, microgrid concept was proposed and developed in recent years [
1,
2]. Microgrid normally consists of distributed energy resources (DER), energy storage devices and loads. Most of the time, microgrid can be regarded as a self-controlled system that separates and isolates itself from the utility when a severe disturbance nearby occurs, and reconnects itself to the grid automatically when the disturbance is cleared. Obviously, the operational characteristics of the microgrid are quite different from those of the traditional electrical equivalent. Hence, the increasing penetration of the microgrid will have significant impact on the dynamic performances of the distribution network.
To investigate the interactive effect between microgrid and distribution network, a suitable microgrid model is needed. The detailed model of the microgrid comprises dozens of differential equations of all dynamic and static components [
2,
3,
4]. In a simple distribution network with a small number of microgrids, the detailed model of the microgrid is suitable for the dynamic simulation of the distribution network when the microgrid under connected operation mode [
5]. However, with increasing penetration of the microgrid into the distribution network, the simulation of a large-scale distribution network becomes very difficult. Under this condition, if an equivalent model of the microgrid is employed, the simulation of the distribution network can be simplified.
Microgrid should operate under connected mode most time to take full advantages of distributed generator. Compared with the distribution network, microgrid can be seen as a controlled load or a controlled electric source under this operation mode. In connected mode, the interactions between loads and distributed generations can be ignored, and the microgrid synthesized dynamic characteristics will be considered in the simulation of distribution network.
Distributed generation is the basis of microgrid; if the equivalent model of the distributed generation is utilized, dynamic simulation of the microgrid can be simplified. An equivalent model compared with the detailed model of the photovoltaic was discussed in [
6], and the equivalent model could well describe the dynamic characteristics of the photovoltaic under different faults in power grid. The authors of [
7,
8] proposed a photovoltaic source dynamic model, the parameters of which were identified based on a least-squares regression-based data processing algorithm. The singular perturbations theory was applied to reduce the model order of the wind farm in [
9], and the dynamics of the reduced-order model matched well with those of the detailed model under different operational conditions. Aggregate modeling and detailed modeling for the transient interaction between a large wind farm and a power system were discussed in [
10], and the aggregate modeling decreased the simulation time without significantly compromising the accuracy in different conditions. In [
11,
12], an equivalent method was proposed for integrating wind power generation system in power flow and transient simulation, the unit plants equivalent method and the multiply equivalent method were used for the power flow calculation and transient dynamics simulation, respectively. A probabilistic clustering concept for aggregate modeling of wind farms was proposed in [
13], the support vector clustering technique was used to cluster wind turbines based on wind farm layout and incoming wind. Due to the short distances of the electric circuits in the microgrid, there is a strong electromagnetic coupling between the electrical components. These characteristics increase the difficulty in the microgrid analysis. A generalized homology equivalence theory based on differential geometry was used for the microgrid equivalent modeling in [
14], and the mathematical analysis of its reduced-order nature was discussed.
Parameter estimation method is a very difficult and challenging task in system modeling. Recently, global optimization techniques such as genetic algorithm [
15], evolutionary algorithm [
16] and differential evolution [
17] have been proposed to solve the parameter estimation problems. Though the genetic algorithm (GA) was employed successfully to solve complex non-linear optimization problems, some deficiencies of GA have been identified in recent research [
18]. This degradation in efficiency is apparent when the parameters being optimized are highly correlated and the premature convergence of the GA degrades its performance in terms of reducing the search capability.
Particle swarm optimization (PSO) is an evolutionary computation technique in nature motivated by the simulation of social behaviors. In searching the optimal solution of a problem, information of the best position of each individual particle and the best position among the whole swarm are used to direct the searching. Due to the simple concept, easy implementation and quick convergence, nowadays PSO has gained much attention and wide applications in different fields. Authors of papers [
19,
20,
21,
22,
23,
24] showed that PSO is a feasible approach to parameter estimation of nonlinear systems. In [
19], PSO was applied in harmonic estimation. A modified PSO was utilized in the maximum power point tracking for the photovoltaic system in [
20]. In the field of parameter estimation, PSO-based parameter estimation technique of proton exchange membrane fuel cell models was proposed in [
21], and PSO with quantum was introduced successfully in synchronous generator offline and online parameters estimation problem. Parameter estimation of an induction machine using PSO was shown in [
22], and the dynamic PSO and chaos PSO were better than the standard PSO. PSO was used for jointly estimating both the parameters and states of the lateral flow immunoassay model in [
23]. Diffusion particle swarm optimization was proposed to optimize the maximum likelihood function in [
24], and the PSO technique has been shown to provide a good solution to bearing estimation as it alleviates the effects of multi-modality.
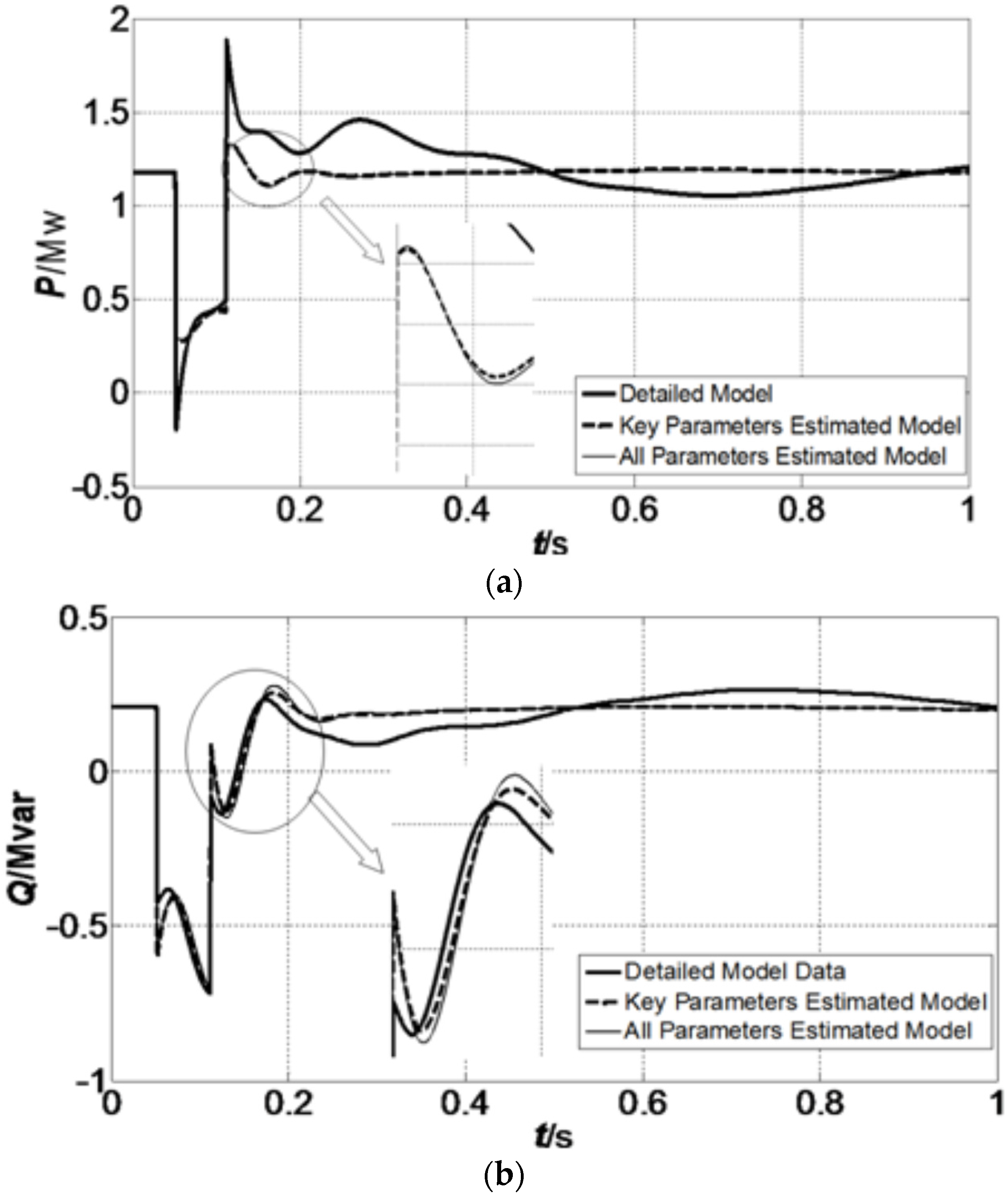
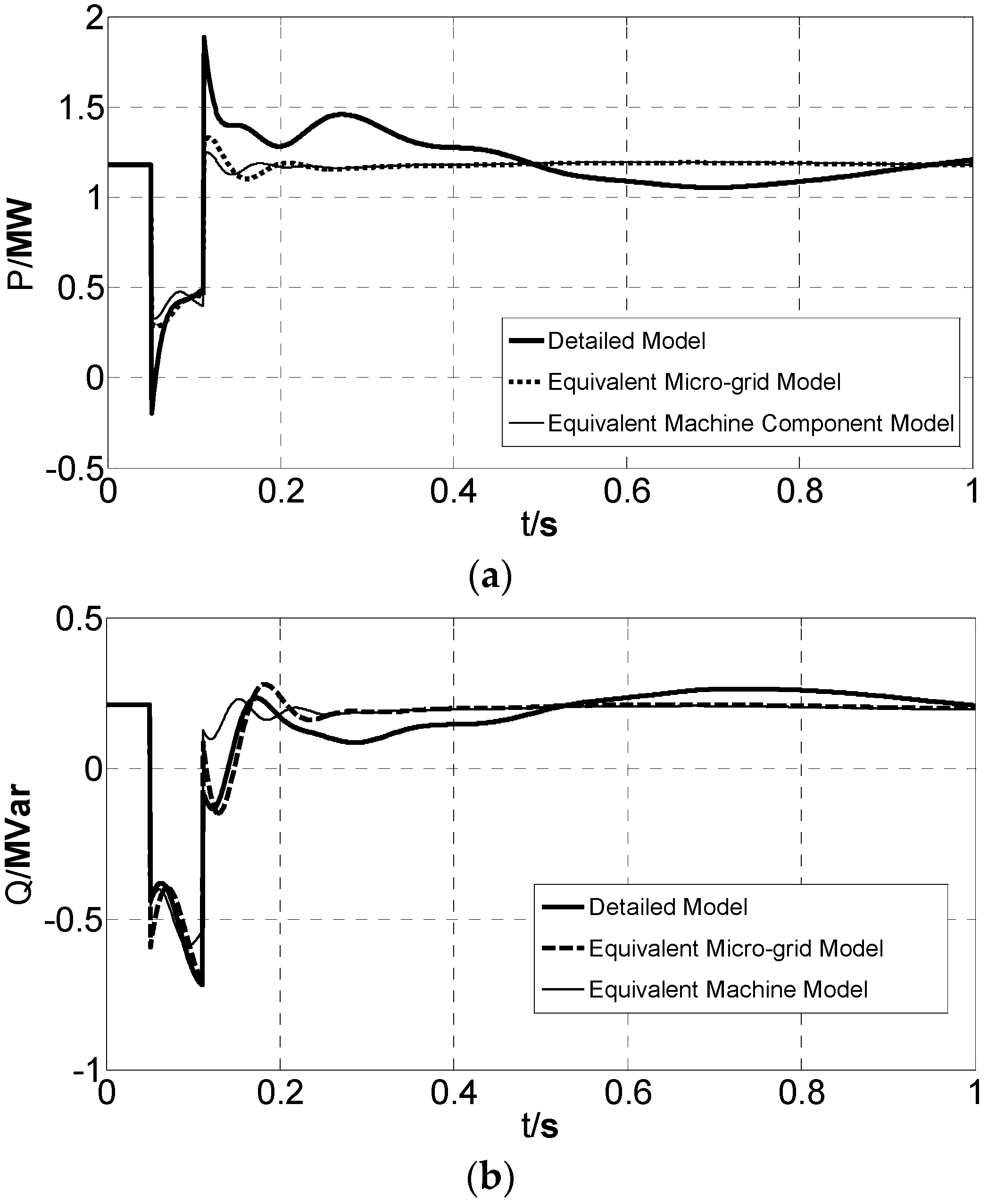
Research has been carried out in the fields of detailed modeling of microgrid and equivalent modeling of the distributed generation. With the increasing penetration of microgrids, the interaction between the microgrid and the distribution network should not be ignored in the power system real-time simulation. However, this will increase the complexity of the simulation with the detailed model of the microgrid components. Hence, a simplified equivalent model of the microgrid is extremely urgent for the simulation analysis of the distribution network. Based on the component detailed models and synthetically dynamic characteristics of the microgrid, an equivalent model of microgrid is proposed in this paper. The proposed equivalent model contains two parts: equivalent static component and equivalent machine component. In order to increase the accuracy of the parameters estimation, trajectory sensitivity is used to identify the key parameters for the further steps of parameter estimation. Particle Swarm Optimization (PSO) is improved and employed to estimate the parameters of the equivalent model. The presented equivalent model and modeling method are shown to be effective by the simulation study on a microgrid connected into distribution network.
2. Microgrid Equivalent Model
A microgrid is made up of a large number of distribution generations, electrical loads and storage devices. Typically, there are two types of components: static components and rotating machines [
1]. Static components contain photovoltaic (PV) and static loads. It is common that PV connects to the microgrid through power electronics equipment. Maximum Point Power Tracking (MPPT) and constant power control strategy are applied to the power electronics equipment when the microgrid is connected in the grid-connected operation mode [
25]. The output power of these distribution generations is controllable and the dynamic characteristics of them are similar with the static load. In principle, the static load is represented by an exponential of the voltage and frequency [
26]. Hence, the output power of the static components can be described by an exponential of the voltage and frequency.
Rotating machine components contain induction motor load, asynchronous induction wind generator and synchronous generator. The structure and the mathematical equations of the asynchronous induction wind generator are similar with those of the induction motor load [
27]. The synchronous machine generator and the asynchronous wind generator have similar dynamic characteristics during faults, and the only difference between them is the modeling reference frames. The synchronous machine rotor angular velocity is constant and the velocity voltage is zero in steady-state conditions [
28]. However, the rotor angular velocity of synchronous will deviate slightly from the synchronous velocity during a fault since the synchronous machine capability is small in most microgrids. The rotor angular velocity is not equal to the system synchronous velocity and its electrical structure is similar with that of the asynchronous induction wind generator, so the synchronous machine generator can be regarded as an asynchronous machine generator during a fault. Furthermore, the synchronous machine generator, the asynchronous induction wind generator and the induction motor load can be described with a unified mathematical model in the transient dynamic analysis.
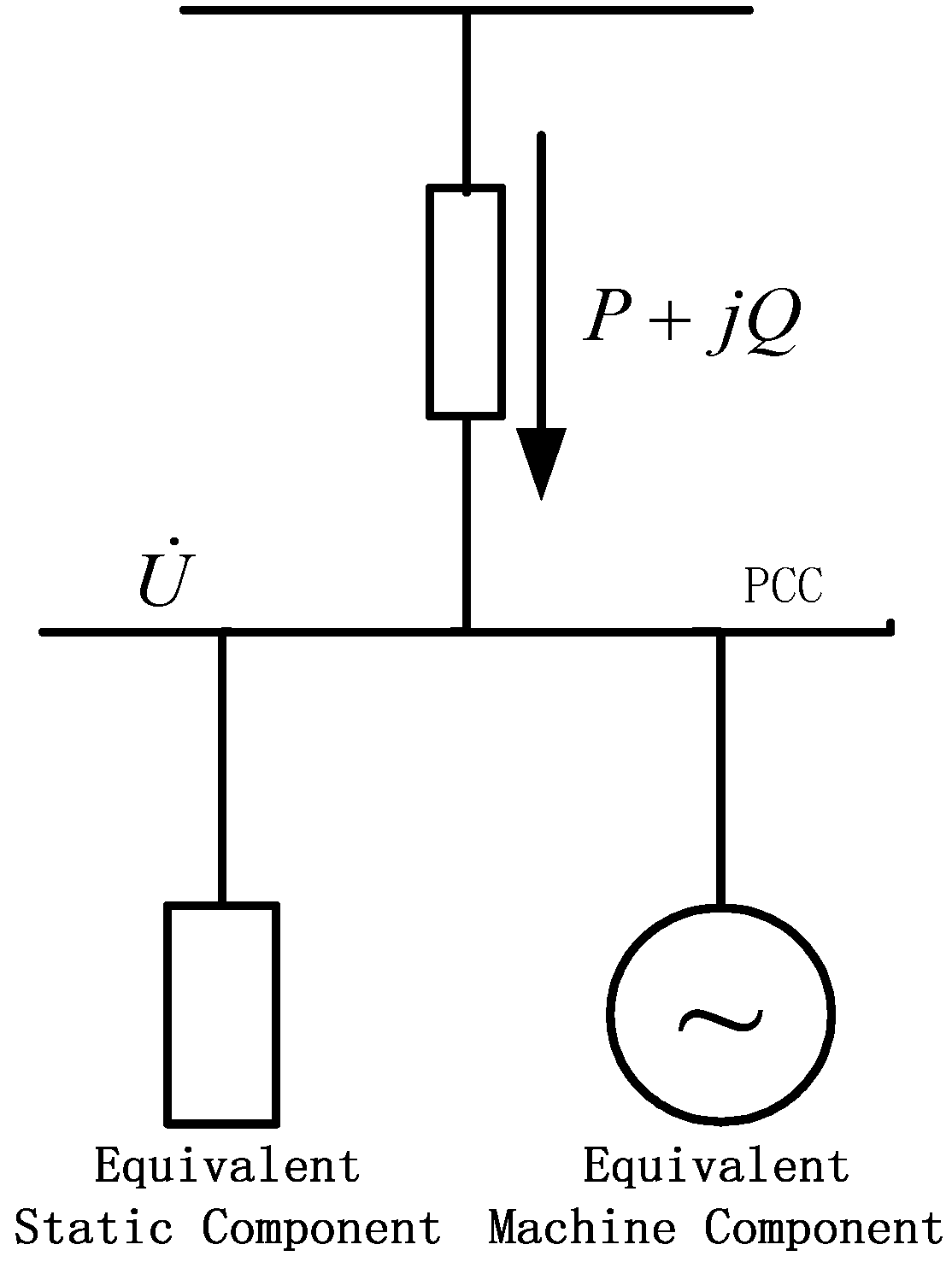
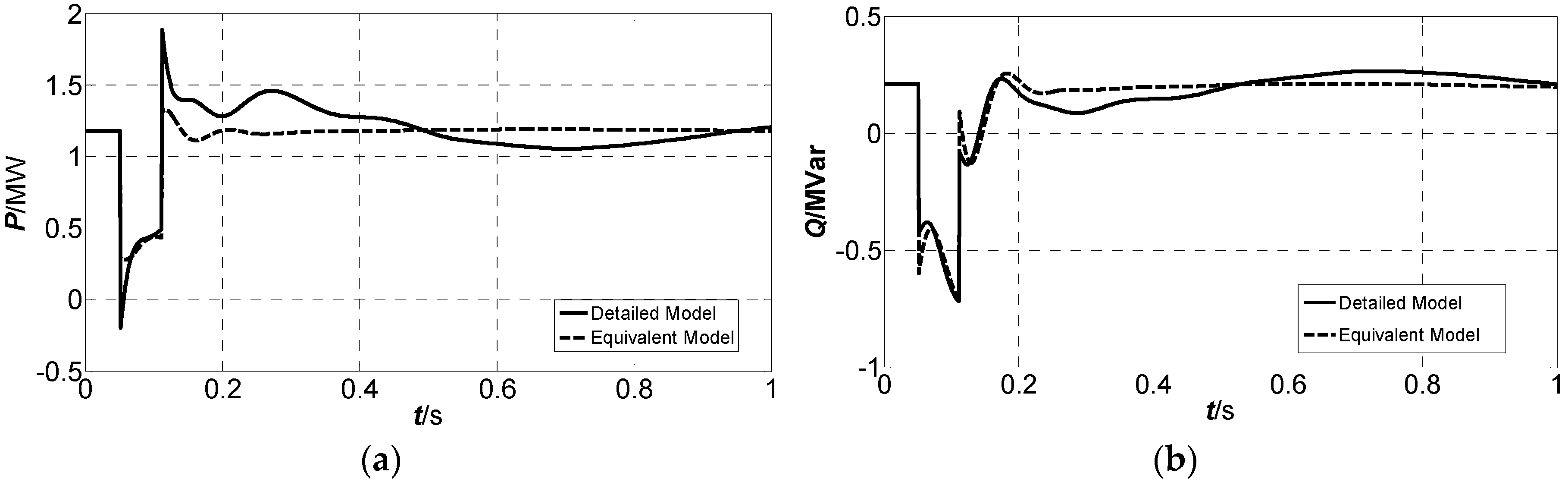
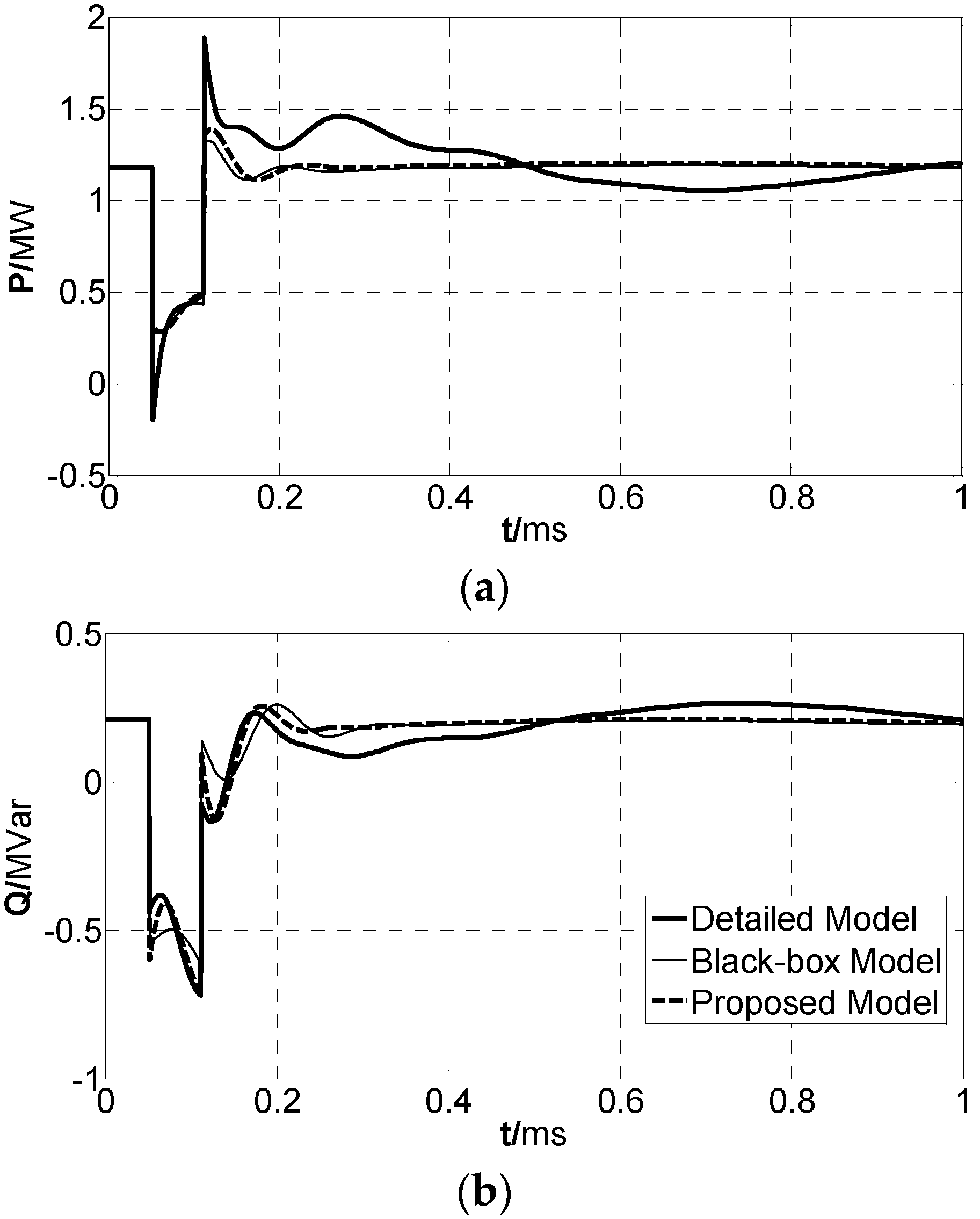
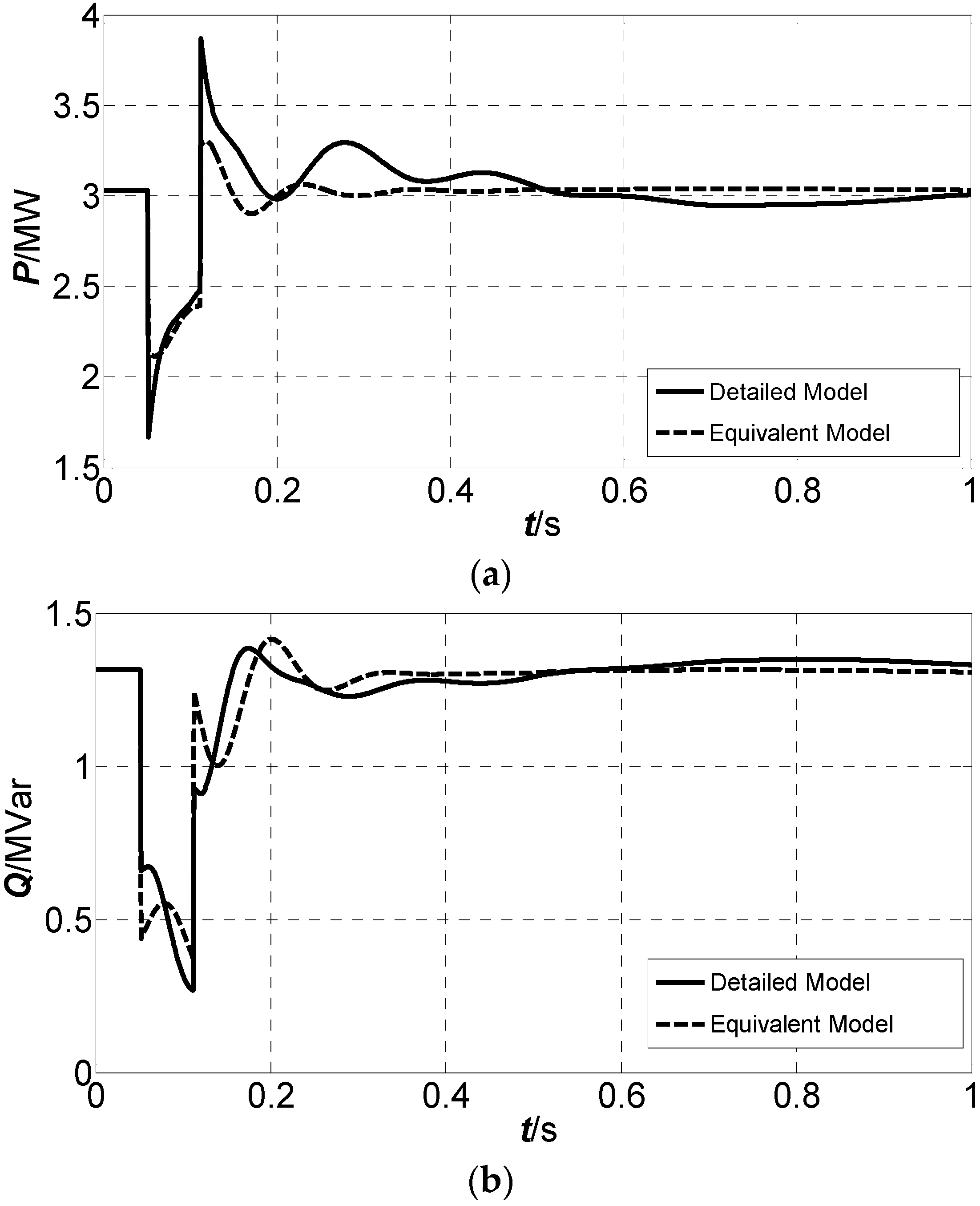
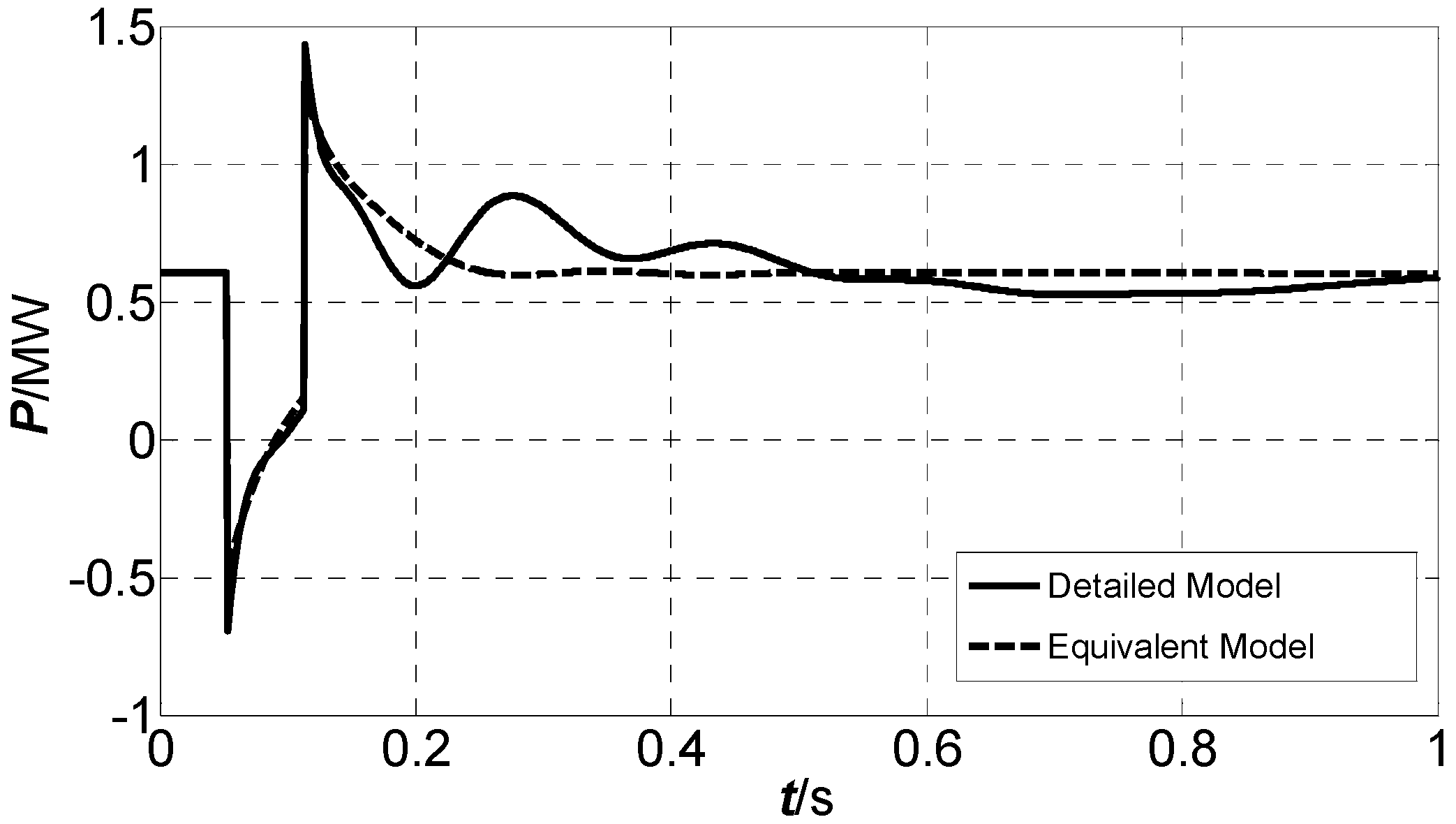
As shown in
Figure 1, the equivalent model of the microgrid is comprised of an equivalent static component and an equivalent machine component. The equivalent static component is parallel to the equivalent machine component, and they are connected to the distribution network through the Point of Coupling Common (PCC).
2.1. Equivalent Machine Component
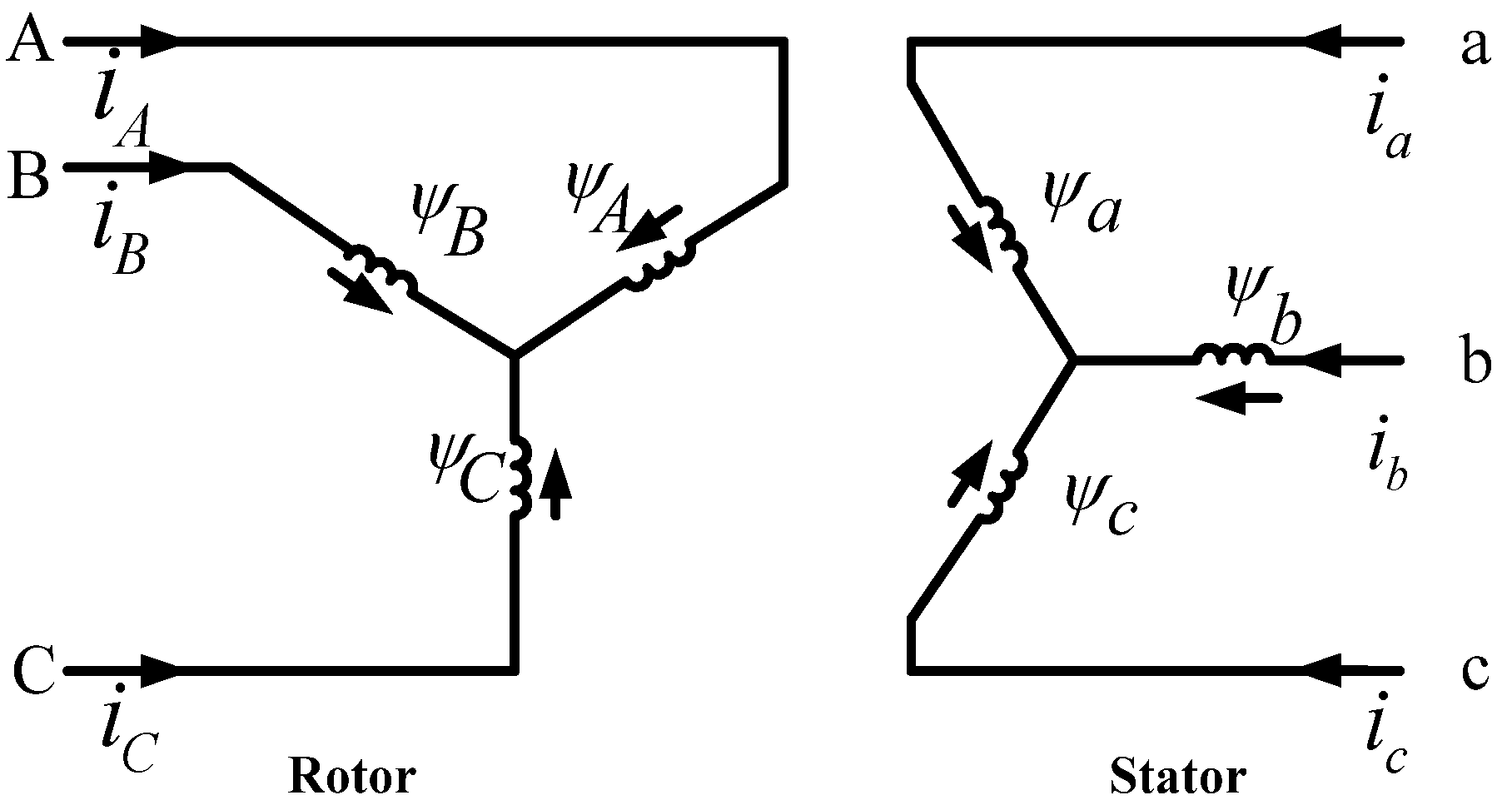
The stator and rotor circuits of the equivalent machine component are shown in
Figure 2.
Rotor angular velocity
is different from the stator angular velocity
. Applying
transformation [
29], stator voltage equations can be written as
Figure 1.
The equivalent model of microgrid.
Figure 1.
The equivalent model of microgrid.
Figure 2.
Equivalent circuit of the equivalent machine component.
Figure 2.
Equivalent circuit of the equivalent machine component.
Rotor voltage equations can be written as
where
and
are the stator voltages;
and
are the stator flux linkages;
is stator resistance;
and
are stator currents;
and
are rotor voltages;
and
are rotor flux linkages;
and
are rotor resistance;
and
are rotor currents;
is the rotor slip; and
is the per time derivative.
The stator flux linkage is
The rotor flux linkage is
where
and
are the stator inductances;
and
are the rotor inductances; and
and
are mutual inductances.
Using the definitions below:
rotor voltage equations may be rewritten as follows:
When representing power system stability studies,
and
are neglected in the stator voltage relations. Their neglect corresponds to ignoring the dc component in the stator transient currents, permitting representation of only fundamental frequency components [
28]. With the stator transients neglected, stator voltage equations may be rewritten as:
From Equations (5) and (7), we have
The rotor acceleration equation, with time expressed in seconds, is
where
is the electromagnetic torque,
is the mechanical torque, and
is the inertia constant of the rotor. Eliminating the rotor currents by expressing them in terms of the stator currents and rotor flux linkages, we find that the per unit electromagnetic torque is
The system frequency of the microgrid is constant when the microgrid operation in connected mode. Thus, rotor acceleration equation with
pu can be written as:
The output active power and reactive power of the equivalent machine component may be written as:
2.2. Equivalent Static Component
Static load model represents the load characteristics as an algebraic function of the bus voltage magnitude and frequency [
26]. Equivalent static component, including static load and distribution generation such as PV in microgrid, is described using algebraic equations. The active and reactive power of the equivalent static component model are related to the system voltage and frequency in the following form:
where
and
are the active and reactive power of the equivalent static component when the voltage magnitude is
and frequency is
, respectively. The subscript
identifies the values of the respective variables at the initial operating condition of PCC. The parameters of this model are the exponents
,
,
and
, where
is the coefficient of the active power and voltage,
is the coefficient of active power and frequency,
is the coefficient of reactive power and voltage, and
is the coefficient of reactive power and frequency.
The system frequency of the microgrid is constant when the microgrid operates in grid-connected mode. Thus, with
pu, the model of the equivalent static component can be written as:
2.3. Parameters of the Equivalent Model
From model Equations (6), (8), (11), (12) and (14), it can be seen that the equivalent model parameters include , , , , , , , , , , , , , and . In order to describe the physical characteristics of the equivalent model, the equivalent model parameters are initialized with corresponding fundamental parameters and will be further estimated in the microgrid modeling. Based on the definitions of the parameters in Equation (5), the fundamental parameters of the equivalent machine component are , , , , , , , , , , and , where is the stator leakage inductance; and are mutual inductances of and axis; and are rotor resistances of and axis; and and are rotor leakage inductances of and axis.
There are other two important parameters, namely and . Where is the initial slip of the equivalent machine component, and presents the type of equivalent machine. If , the equivalent machine component absorbs power from the distribution network, and has the characteristics of induction motor load. Oppositely, means that the equivalent machine component injects power into the distribution network, and has the characteristics of asynchronous generator. is the fraction of the equivalent machine component active power with respect to the total initial active power . The active power flow between the microgrid and the distribution network is bidirectional. Thus, indicates that the microgrid absorbs power from the distribution network, and indicates that the microgrid injects power into the distribution network. The similar definition is also applied to reactive power Q.
As a result, the 13 parameters, namely , , , , , , , , , , , , and , in the equivalent microgrid model need to be estimated in the microgrid equivalent dynamic modeling.
3. Equivalent Model Parameter Sensitivity Analysis
The number of the parameters to be estimated has significant impact on the accuracy of the parameters estimation. Parameter sensitivity analysis is an efficient method to determine the key parameters of the equivalent model. Parameter trajectory sensitivity is defined as:
where
is the time domain trajectory of the output variable,
is the vector of the parameters of the equivalent model,
is the
jth parameter of the equivalent model,
is the number of the parameters, and
is the sampling sequence.
In order to improve the accuracy of parameter trajectory sensitivity, median method is used to calculate the trajectory sensitivity when
is small enough, which is shown as:
where
is the initial value of the parameter
,
is the variation of
, and
is the initial value of the output variable in steady-state.
3.1. Trajectory Sensitivity
Time domain parameter trajectory sensitivity curve can describe the behaviors of the output variable. For convenience of comparison, the average sensitivity can be calculated as
where
is the average of the
j-th parameter with respect to the trajectory of the output variable
is the number of sample points,
is the initial value of the output variable.
Trajectory sensitivity demonstrates the impact of the variation of the parameter on that of the output variable’s trajectory. If the trajectory sensitivity of a parameter is larger than that of the other parameters, the parameter plays a more important role on the dynamics of the output variable; in other words, the parameter can be estimated easily by using the dynamics of the output variable. In contrast, if the trajectory sensitivity of a parameter is very small, e.g., even close to zero, it is difficult to estimate the parameter using the dynamics of the output variable.
3.2. Trajectory Sensitivity Phase
If a couple of parameters have an unknown relationship between each other, they are dependent on each other and unidentifiable as well. However, these unidentifiable parameters can be identified using trajectory sensitivity analysis [
29].
Assuming that the parameters
and
are coupling with each other, the output of the power system can be written as
The sensitivities of the parameters
and
can be analyzed as [
27]
It should be pointed out that
and
vary with time, while
and
are constant [
29,
30]. Hence,
and
reach zero at the same time. In other words, the trajectory sensitivities of these two couple unidentifiable parameters are either in phase or in reverse with each other. The trajectory sensitivity of these two parameters will pass zero at the same time. Oppositely, if the output variable curves of the two parameters do not pass zero at the same time approximately, they are independent and can be identified using the dynamics of output variables of the system [
31].