Abstract
We translate between biophysical and economic metrics that characterize the role of energy in the economy. Specifically, using data from the International Energy Agency, we estimate the energy intensity ratio (EIR), a price-based proxy for a power return ratio (PRR ). The EIR is a useful metric, because for most countries and energy commodities, it can indicate the biophysical trends of net energy when data are too scarce to perform an original net energy analysis. We calculate EIR for natural gas, coal, petroleum and electricity for forty-four countries from 1978 to 2010. Global EIR values generally rise from 1978 to 1998, decline from 1998 to 2008 and then slightly rebound. These trends indicate one interpretation of the net energy of the world economy. To add perspective to our recent, but short, time series, we perform the same calculations for historical England and United Kingdom energy prices to demonstrate that a given energy price translates to different PRRs (EIR in this case) depending on the structure of the economy and technology. We review the formulation of PRRs and energy return ratios (ERR ) to indicate why PRRs translate to (the inverse of) energy prices and ERRs translate to (the inverse of) energy costs. We show why for any given value of an ERR or PRR, there is not a single corresponding energy cost or price, and vice versa. These principles in turn provide the basis to perform better modeling of future energy scenarios (e.g., low-carbon transition) by considering the relationship between economic metrics (cost and price) and biophysical metrics (energy and power return ratios) based on energy, material and power flows.
1. Introduction
This manuscript is Part 1 of 3 papers comparing net energy and economic metrics. Each manuscript has similar background and motivation sections. Part 1 includes a fuller background and motivation before analyzing how net energy and power metrics translate to individual energy commodity (and technology) costs and prices, respectively. Part 2 analyzes how net energy metrics translate to total expenditures on energy [1]. Part 3 places the calculations of expenditures on energy in historical, current and future contexts [2].
1.1. Background
Considerable debate exists surrounding the role of energy in society and the economy, and much of the disagreement stems from different methodological approaches and the time span under consideration. Conclusions range from the possible unimportance of all natural resources [3], to energy price spikes being a chief determinant of recessions [4], to energy and prime-movers as being equally important to labor and capital in driving economic growth [5], to energy and prime-movers as the critical elements, more important than labor or capital, in driving economies during industrialization [6] and possibly over the long-term [7,8]. Countries with high per capita gross domestic product (GDP) tend to consume more primary energy per capita [9], even more so when considering energy embodied in imported products [10].
Access to a sufficient quantity of affordable energy and energy services is one of several important factors (e.g., also proper governance [11]) for modern living standards in an industrial or post-industrial economy. As we deplete fossil stocks and extract renewable flows from the highest quality resource areas, technological improvements enable access to lower quality energy resources, while converting those resources to services more efficiently. Yet, the end of extraction of a particular energy resource is not marked by its full depletion, but rather by its cost of production becoming greater than what consumers can afford to pay, are willing to pay or can pay for less expensive alternatives (including energy efficiency). For example, due to various reasons, including high extraction costs and less expensive imports, one regional energy resource that has undergone an almost complete rise and fall in production is United Kingdom coal [12].
A lack of inexpensive energy options is reflected economically in higher energy prices and cost shares. Biophysically, this higher cost is reflected in energy life cycles with lower net energy and lower energy return ratios (ERRs), such as energy return on energy invested (EROI) [13]. Net energy is defined as energy delivered as output (or extracted, depending on the life cycle boundary) minus the energy invested in delivering that output. ERRs use the same data to express net energy as a ratio of the energy delivered (or extracted) divided by the energy invested to deliver that output. From this point forward, we use the terms energy return ratio and power return ratio (PRR) as catchall terms for more specific net energy and power metrics defined in this paper.
Energy costs and ERRs are two ways of expressing the same concept because they are fundamentally inversely related (as discussed in detail in this paper in Section 4.1) [14,15,16,17]. To an economist, the costs, prices and energy cost share are important metrics; to an ecologist and biophysical systems modeler, the ERR and PRR are important metrics for models and perspectives not purely based on monetary flows. It is important to translate between economic and biophysical descriptions of technologies and economies. However, exactly how can we relate economic and biophysical perspectives? How can we measure if affordability of energy were either acting as or indicating a constraint on economic production or growth? In this Part 1, as well as in Parts 2 and 3 [1,2], we contribute data and concepts that are important to answer these two questions at the energy commodity and global scales.
1.2. Missing Perspective
Answering global questions requires global data, but data and perspective on global net energy metrics are severely lacking. Thus, most macroeconomic or macrobiophysical analyses focus on a single country, technology, commodity and/or industry that has sufficient data. This single-country focus often limits these analyses to developed countries that have sufficient datasets: the United States, Western Europe and Japan.
While much research effort is spent calculating ERRs of individual energy technologies and fuels for comparative analysis [14,18,19,20,21,22,23,24,25,26], there is a dearth of work linking individual ERRs to microeconomic or macroeconomic metrics. Despite four decades since the development of the mathematical foundations in net energy analysis that relate economic accounts to country-level energy consumption [27,28], existing research has not effectively placed technology-specific net energy into the context of the broader macroeconomic modeling, economic projections and energy-economic decision-making. This disconnect and missing perspective serves as a motivation for this paper series [1,2] and other research of the corresponding author [14,15,16,29].
1.3. Part 1 Goal and Content
The question answered by net energy analysis is intuitive and attractive to many: How much energy does it take to produce and/or deliver energy? Aside from knowing that we want systems that produce more output with fewer inputs (energy or otherwise), we do not know how much more matters. Therefore, why do researchers calculate net energy metrics if we cannot translate them to other indicators or apply them for decision-making? We seek to determine how we can practically interpret net energy metrics for decision-making and to describe the (possible) structure of the economy. Thus, the main goals of Part 1 of this manuscript series are two-fold: (1) to provide the most comprehensive global view of the net energy (or specifically power) of world energy commodities; and (2) to place net energy metrics into the context of the economic metrics with which people are most familiar: cost and price.
People generally want lower (energy) prices. Because most of us are more familiar with energy prices and costs than we are with net energy metrics, it behooves us to explore how net energy metrics relate to prices and costs. If we can understand these relations, then we can start to make more practical use of net energy metrics for decision-making and planning, such as in the context of a transition to a low-carbon and/or renewable economy. Instead of projecting future costs, we might do better by projecting future net energy metrics.
Perhaps the most prominent net energy term is “energy return on energy invested”, or EROI. However, we do not blindly adopt this term in this manuscript. Unfortunately, the term EROI is sometimes used too broadly in that it refers to different mathematical definitions. For example, EROI sometimes refers to ratios of energy and sometimes to ratios of power. Thus, we find it important to distinguish among specific mathematical definitions of ratios of power (e.g., PRR) and ratios of energy (e.g., ERR), and we use a unique name for each equation rather than a single term, such as EROI. A single term should not refer to different mathematical definitions, and that is why this manuscript begins with these ERR and PRR definitions.
The new calculations and results described in this paper are of energy intensity ratios (EIRs, Section 2.2) for the major energy commodities across the world. The EIR represents how much energy one can obtain by spending one dollar (or other monetary unit) relative to how much energy it takes to generate an average dollar of output from the economy. As we discuss, EIRs are proxies for power return ratios (PRRs) that derive from energy analysis and/or life cycle assessment. However, in order to understand how to interpret the EIRs over time, we must describe the formulations of PRRs and their integral over time, energy return ratios (ERRs). The ERRs equate quantitatively to energy output divided by energy inputs (or energy invested), hence the popular acronym EROI.
This rest of this manuscript is organized as follows. Section 1.4 continues with additional background to provide perspective on the different viewpoints of the role of energy in society. Section 2 describes the EIR calculations of this paper, as well as providing a background to net energy metrics calculated in the literature. Section 2.1 provides the background for calculating energy return ratios (ERRs) and power return ratios (PRRs). We use the terms ERR and PRR as generic descriptors of the more specific terms described in this section. We provide significant detail on distinguishing ERRs from PRRs, so that the reader understands that the EIRs, which use annual energy flows, are proxies for PRRs and not ERRs. Section 2.2 explains the EIR calculation itself. Section 3.1 shows the EIR calculations for the world (1978–2010), and Section 3.2 does the same for England and United Kingdom (1300–2008). Section 4.1 discusses how we can relate ERRs and PRRs to costs and price, respectively, while using the insights from the EIR calculations. Section 4.2 provides the long-term perspective that is needed to properly consider the proposition discussed in Section 4.1. We interpret these long-term EIRs in the context of power return ratios (PRRs) and the transition to the modern fossil-fueled and industrial economic era. Section 5 concludes the paper.
1.4. Summary of Multidisciplinary Perspectives and Motivation
All models are wrong, but some are useful. This statement is certainly poignant for energy, society and the economy. Researchers consider the role of energy in society from multiple perspectives: anthropological [30,31,32,33], economic [4,6,7,34,35,36,37,38], ecological and biophysical [8,9,13,39], and others. With these different perspectives come a multitude of quantitative and qualitative methods of analysis. These analyses try to answer questions related to how energy and natural resources influence and enable societal growth, structure and organization.
Biophysical and ecological perspectives on the economy and energy note similarities between our natural ecology and our “industrial ecology”. Brown et al. [40] note that many global materials have peaked in terms of global production rate per capita. Brown and colleagues also note that since 1980, the per capita energy consumption of a country scales with the power of its per capita GDP just as a mammal’s metabolism scales with the power of its mass [9]. This comparison, while not directly comparable (i.e., GDP per capita measures a flow of money, but animal mass measures a stock), makes sense if one considers that both scaling relationships describe the energy cost of maintaining the structure and/or functions of a complex adaptive system [40].
From an anthropological perspective, Tainter describes the possible economic contraction, loss of complexity or collapse that may occur if a society consumes too much of its gross energy or resources on acquiring, transporting and upgrading energy [30,31,32]. The Roman Empire is perhaps the most classic example of collapse from diminishing returns. Its continued growth eventually became infeasible as the resource cost to sustain the empire outpaced any resources gained from territorial expansion [30]. Since most of the empire’s energy resources were derived from the land (e.g., food and wood), diminished returns on expanding borders directly translated to less energy returned to Rome. Other analyses of agrarian societies note how cycles of population growth and decline typically take 300–500 years [33]. These cycles seem to follow a common pattern across cultures and regions: expansion of resources or food from technology and/or conquest; population increases because of the increased bounty; eventually there are diminishing returns on productivity (e.g., food/farmer or food/land); and finally, the governing authority loses power, and population decreases (due to deaths or migration), because the tax base and resource can no longer support the now larger population. According to Turchin and Nefedov [33], the United Kingdom is perhaps 200–250 years into its latest “modern” cycle. One motivation of this paper (as well as Parts 2 and 3 [1,2]) is to contribute to the discussion of how we can, and cannot, compare our modern industrial economy to pre-industrial economies.
The econometric literature shows that it is valuable for econometric studies to have time series of energy cost shares or expenditures on energy as a fraction of income, GDP or personal consumption expenditures [6,36,37,41]. The reason is that the energy cost share serves to illuminate how low-cost energy relates, usually positively, to economic growth. Energy cost shares for pre-industrial economies were much higher than for industrial and post-industrial economies. Some econometric analyses adjust the quantity of energy consumed by some quality factor to more accurately input the concept of energy into econometric analyses. This quality factor is often one based on the relative prices of resources (e.g., the price per MJ is higher for oil than coal) [41], thermodynamic characterizations, such as fuel exergy, technology conversion efficiency and useful work delivered [34,35] or emergy [42,43]. Thus, the calculations of this paper have value in that they will inform future energy-economic analyses.
2. Methods
We undertake the calculations in this paper by utilizing the International Energy Agency (IEA)’s rich data database of energy prices. The IEA data span dozens of countries and years. Further, we also take this opportunity to use the rich historical data on England’s and the U.K.’s energy prices. To our knowledge, no one has interpreted these energy and economic data in the context of net energy.
2.1. Review of Net Energy Metrics Calculated Using Full Life Cycle Energy versus Annual Energy (or Power) Flows
In performing energy and economic analyses, there are often limited data. Thus, it is not always possible to directly compare a net energy metric to its most relevant monetary metric. Our purpose for this section is to outline the power flows and energy accumulations (energy = power × time) associated with net energy analyses. By doing this, we highlight the difference between energy return ratios (ERRs) calculated at the device/project level (i.e., over the entire life cycle) and power return ratios (PRRs) that are often calculated at the industry/economy level using annual power flows. Just as energy is the integral of power over time, ERRs are the integral of PRRs over time. Our descriptions further allow us to focus on the power flows that most directly compare to the annual monetary flow data that are available as prices, input-output tables or other data.
The reason we present a somewhat lengthy discussion of the definitions of ERRs and PRRs is three-fold:
- ERRs and PRRs are mathematically distinct, yet not always treated as such in the net energy literature,
- distinguishing between “gross” and “net” ratios allows one to specify the difference between extraction of primary energy (gross extraction) and delivery of energy carriers to consumers (net delivered energy) without using the same term and acronym (e.g., each term has a distinct mathematical definition [29,44]) and,
- to compare ERRs and PRRs to economic metrics (e.g., to costs and prices, respectively), it is important that we understand which metrics to use for comparison (discussed in Section 4.1).
Our discussion follows a step-by-step process that builds information from a single life cycle to several life cycles occurring simultaneously. Figure 1 describes a single life cycle, discusses the life cycle power flows, shows how these power flows are integrated over time and, finally, demonstrates how the integrated power flows end up at the final ERRs at the end of the life cycle. Then, Figure 2 concatenates three of the life cycles from Figure 1, such that they overlap in time. By looking at three life cycles, we can more easily imagine a real-world scenario with multiple energy technologies operating simultaneously. Finally, Figure 3 and Figure 4 present additional visualizations of PRRs and ERRs of multiple life cycles concatenated upon each other, just as is the case in the real world.
In Figure 1, we use (not completely) the nomenclature of Murphy et al. [45] to demonstrate the relations among various ERRs, as well as to indicate the PRRs for a hypothetical single energy technology life cycle. The values of the power flows and power plant efficiency are based on the life cycle assessment of a coal-fired power plant in Spath et al. [46] (the Lower Emission Boiler System model). In Figure 1, P (or ) represents power, E represents energy and η is a power conversion efficiency of primary energy (feedstock) to an energy carrier as an output from the energy technology. The subscripts on the power flows and energy accumulations refer to five different inputs and outputs of the life cycle: cap = embodied energy invested over time for initial capital (e.g., manufacturing, construction); op = power inputs invested during operation of the technology; feed = feedstock primary power inputs for conversion (e.g., coal into a power plant); heat = heat dissipated from burning feedstock that is converted to an energy carrier (; d = embodied energy invested over time for decommissioning at the end of life; and ext = power extracted from the Earth (e.g., primary energy).
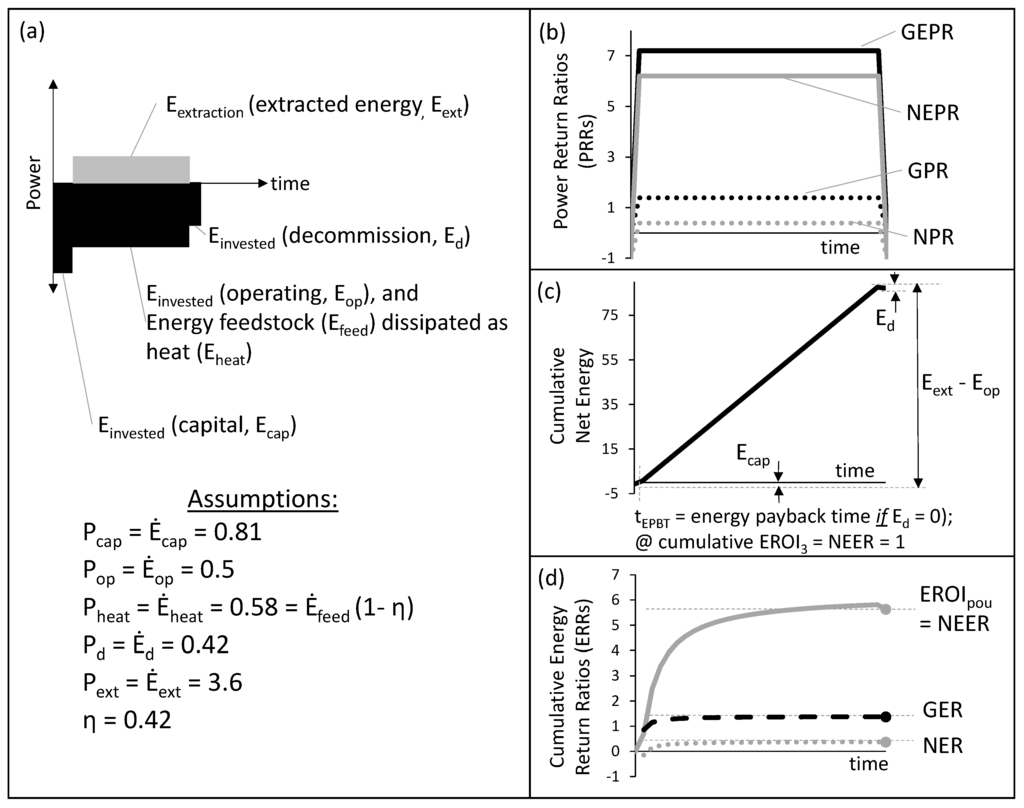
Figure 1.
The power flows and energy relations among various factors that are used to calculate energy and power return ratios for single energy technology life cycle (largely following [45] for nomenclature and [46] for input values). (a) Pictogram depicting the assumptions and the five types of power flows for this example; (b) the instantaneous power return ratios (PRRs) are defined similarly to energy return ratios (ERRs), except using only instantaneous power flow data rather than power integrated over time; (c) the cumulative net energy over time is the integral of the instantaneous net power (net power = P P); (d) the cumulative ERR for three common ERRs. EROI = EROI (EROI, energy return on energy invested) from [45] equal to the net external energy ratio (NEER) from [29,44,47]. Gross energy ratio (GER) and net energy ratio (NER) from [29]. E, energy.
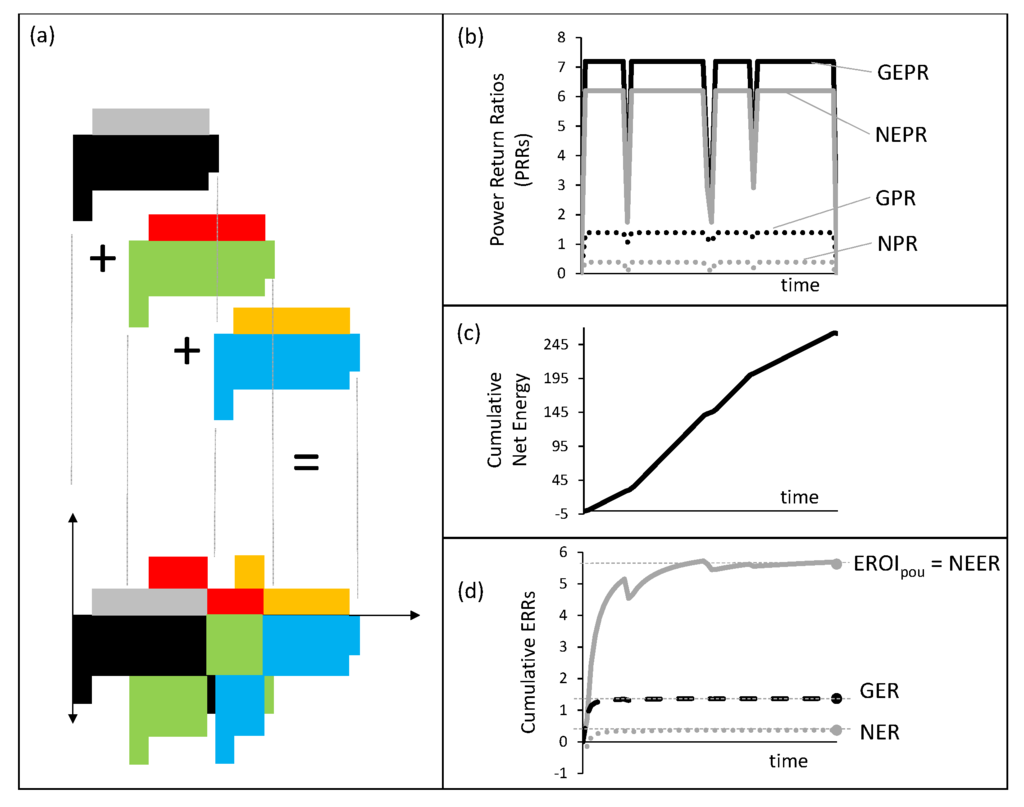
Figure 2.
The power flows and energy relations among various factors that are used to calculate energy return ratios (ERRs) for three of the same single energy technologies’ life cycle installed at different times. (a) Pictogram depicting the technology being installed at three different times. The bottom image shows the power inputs and outputs for the sum of all three installations; (b) The instantaneous power return ratios (PRRs) are defined the same as ERRs, except using only instantaneous power flow data rather than power integrated over time; (c) The cumulative net energy over time that is the integral of the instantaneous net power (net power = P P); (d) The cumulative energy return ratio (ERR) for three common ERRs. EROI = EROI from [45] equal to the net external energy ratio (NEER) from [29,44,47]. Gross energy ratio (GER) and net energy ratio (NER) from [29].

Figure 3.
This figure shows that when multiple technologies are installed over time, the instantaneous power return ratios (PRRs) and the cumulative energy return ratios (ERRs) can end up greater than or less than each other (but GER > NER and GPR > NPR). (a) Individual gross power ratio (GPR), net power ratio (NPR), cumulative gross energy ratio (GER) and cumulative net energy ratio (NER) for each of the three technology installations based upon the time of installation; (b) The summed GPR, NPR, GER, and NER from all three technology installations.

Figure 4.
This figure shows that when multiple technologies are installed over time, the instantaneous power return ratios (PRRs) and the cumulative energy return ratios (ERRs) can end up greater than or less than each other (but gross external energy ratio (GEER) > NEER and gross external power ratio (GEPR) > net external power ratio (NEPR)). (a) Individual gross external power ratio (GEPR), net external power ratio (NEPR), cumulative gross external energy ratio (GEER) and cumulative net external energy ratio (NEER) for each of the three technology installations based on the time of installation; (b) the summed GEPR, NEPR, GEER and NEER from all three technology installations.
Here, we show summary in Table 1, to which the reader can refer during the course of reading this paper to see the distinctions among the various energy and power return ratio acronyms.

Table 1.
A summary of the categorization of the several energy return ratios (ERRs) and power return ratios (PRRs). For reference, EROI = energy return on (energy) invested; EROI subscripts are: ext = extraction (or Boundary 1), pou = point of use (or Boundary 3) [45].
| Gross output | Net output | |||
|---|---|---|---|---|
| Feedstock included as input? | No | Yes | No | Yes |
| Power Return Ratio | GEPR | GPR | NEPR | NPR |
| Energy Return Ratio | GEER | GER | NEER | NER |
| (= EROI EROI) | (= EROI EROI) | |||
2.1.1. Power Return Ratios
Equations (1)–(4) show the four PRRs that we discuss in this paper. These PRRs are the instantaneous equivalents of life cycle ERRs (Equations (5)–(8)) that life cycle researchers often calculate. We discuss two types of PRRs (and ERRs in Section 2.1.2). The “external” ratios (e.g., GEPR = gross external power ratio and NEPR = net external power ratio) do not consider the portion of feedstock fuel consumed and dissipated as heat as part of P during a conversion process with efficiency, η. The other “non-external” ratios (GPR = gross power ratio and NPR = net power ratio) do consider the heat dissipation () from consuming the feedstock fuel as part of P. If efficiency is 100% (), then the corresponding external and non-external ratios are equivalent (e.g., NEPR = NPR, GEPR = GPR, as well as NEER = NER and GEER = GER, per the ERRs in Section 2.1.2).
Figure 1a depicts the five power flow types that represent generic stages of the life cycle. Net power flow (net power = P P) and net power ratio (NPR, Figure 1b) are negative during the capital (E_cap) and decommission (E_d) phases and positive during the extraction (E_ext) phase. This is because the model of Figure 1 assumes the following holds during capital and decommission phases: P, P, and thus, P P.
The difference between GEPR and NEPR, as well as between GPR and NPR, is that the denominator of the equation is subtracted from in the numerator of NEPR and NPR, but not GEPR and GPR. This distinction is why the G stands for “gross” and the N stands for “net”. Hence “net power” (or “net energy” per Section 2.1.2) is equal to gross output minus intermediate energy consumption and investment. Thus, for a consistently-modeled system with no assumed exogenous information, GPR = NPR + 1 and GEPR = NEPR + 1 (see [29] for a fuller explanation).
The denominator of Equations (3) and (4) is not equal power invested, because it includes the continuous flow of feedstock into the technology. We defer further discussion of the inclusion of feedstock until the next section on ERRs, such that we can relate to existing literature that calculates the net energy ratio (NER) and the gross energy ratio (GER). We show equations for NPR and GPR for completeness, yet do not propose how to compare them with economic metrics.
2.1.2. Energy Return Ratios
We now review four energy return ratios (ERRs) definitions in Equations (5)–(8). These four equations refer to energy output and energy invested over the full life cycle of a technology or system. Thus, they are the integral of the PRRs over the entire life cycle from initial time to final lifetime . The units represented by E in the equations are those of energy (e.g., J), not power (e.g., J/s = W). Note that compared to Murphy et al. [45] (for example), we choose not to give the same name (e.g., EROI) to two equations that have different definitions. In Murphy et al. [45], their Equation (1) defines EROI (energy return on energy invested) as a function of a quantity of energy divided by another quantity of energy, and their Equation (2) again uses the acronym EROI, but defined as an instantaneous power flow divided by another instantaneous power flow. Here, we treat ratios of energy as mathematically and conceptually distinct from ratios of power.
Net external energy ratio (NEER, as in King [29] and Brandt et al. [44]) is a calculation at the same boundary condition as energy return on energy invested (EROI) at Boundary 3, EROI, of Murphy et al. [45]. Here, we make a distinction from Murphy et al. [45] in that to discuss energy delivered (as an energy carrier, such as gasoline) to the “point of use”, we must subtract the denominator (invested energy) from the numerator. The calculation of Equation (5) has also been phrased as EROI at the point of use (EROI), the energy payback ratio [48] and the external energy ratio [46]. By omitting the invested life cycle energy from the numerator, we are left with the gross primary energy extracted only. Equation (6) shows that this change provides the gross external energy ratio (GEER) as in King [29] and Brandt et al. [44], also equal to EROI, or EROI at the point of extraction, of: Murphy et al. [45].
Equations (7) and (8) are the same as Equations (5) and (6), respectively, except that they include as part of energy input the energy that is dissipated as waste heat (E) when consuming the feedstock fuel. This quantity is not the same as “cumulative energy demand” as calculated in many life cycle assessments that include the full energy content of feedstocks (as discussed in [49]). As discussed in King [29], Equations (7) and (8) count feedstock energy input only as that energy that is dissipated as heat by the technology being modeled (e.g., energy leaving a power plant originated in the feedstock, but was not dissipated within the plant boundary) [29].
One goal of this manuscript is to show which ERRs can be compared to monetary flows to gain insight into relations between energy and the economy. Thus, it is important to consider the NEER vs. NER and GEER vs. GER distinction if we want to compare energy flows to monetary, or cash, flows. We describe in Section 4 that NEER and GEER are metrics to be compared to costs (inversely related [16]) and not NER nor GER. However, the inverse relationship is difficult to precisely describe in practice (see Section 4.1).
Now that we have reviewed ERRs, we can refer to the ERR calculations in the example of Figure 1. Figure 1c shows the integral of the net power, or the cumulative net energy, at each point in time in the life cycle. The cumulative net energy first decreases at the beginning during the capital phase before increasing once energy extraction begins. Once the E E = EE, this time is called the energy payback time (t). The energy payback time is the instant when cumulative net energy output is equal to all embodied energy invested over the life cycle. For visualization purposes, in Figure 1c, we label t assuming that E. The t is longer than labeled if E.
Figure 1d shows that the final cumulative ERR values are the same as the ERRs calculated in Equations (5)–(8). The cumulative ERRs are defined as the integral of the PRRs up until some intermediate time, t. Equation (9) shows cumulative NEER, and the other ERRs follow the same formulation using their respective numerators and denominators. It takes the full lifetime of the technology or system to reach the final ERR. Note that if there is an investment of energy for decommissioning, then just before the decommissioning phase, the cumulative ERR is greater than the final ERR. The differences between cumulative ERRs and full life cycle ERRs are important as we consider comparing ratios of power and energy (power integrated over time) to monetary flows. Those differences are also relevant in the context of the practical reality of modeling impacts from retiring energy infrastructure.
Figure 1 considers modeling a single technology life cycle, but in the real world, there are many energy technologies and systems being installed (practically) simultaneously. Figure 2 takes the information from the single technology in Figure 1 and assumes that technology is installed at three different times with the life cycles overlapping in time (see Figure 2a). Because each life cycle is the same, the PRRs of the three combined life cycles never exceed their respective maximum values of the PRRs of the individual life cycle (see Figure 2b). The PRRs of the combined system do, however, fluctuate depending on when each individual life cycle begins and ends.
In Figure 2c, we show that the cumulative net energy at the final time is three times the cumulative net energy at the end of a single life cycle. Furthermore, the ERRs at the final time of the three life cycle scenario (see Figure 2d) are equivalent to the ERRs at the final time of the single life cycle. The cumulative NEER in Figure 2d most clearly shows how the cumulative ERRs can fluctuate over time depending on when energy technologies are installed and decommissioned.
Figure 3 compares “non-external” PRRs and ERRs on the same figure, and Figure 4 compares the “external” PRRs and ERRs. The interpretation of the power and energy return ratios, however, is the same in both cases. We focus our discussion on Figure 3, and we notice some important features. It is not intuitive or easy to envision the power flows of several life cycles added together. Figure 3b and Figure 4b show that the instantaneous summed PRRs are sometimes less and sometimes more than the respective instantaneous cumulative and final ERRs. That is to say, GPR is greater than cumulative and final GER most of the time, but when the life cycles begin and end (e.g., in the middle of the time series), GPR < GER during the capital construction and decommission phases (i.e., during times of high investment). Similarly, NEPR is greater than cumulative and final NEER most of the time, but when the life cycles begin and end (e.g., in the middle of the time series), NEPR < NEER during the capital construction and decommission phases.
2.2. Energy Intensity Ratios
Previously, the corresponding author introduced a proxy metric for a power return ratio (PRR) called the energy intensity ratio (EIR) [14,50] in which he calculated the EIR of coal, oil, natural gas and electricity for the United States. EIR is a ratio of two energy intensities: the energy intensity of an energy commodity (the energy content purchased by a dollar, e.g., MJ/$ of oil) divided by the energy intensity per unit of GDP of the country in which that commodity price exists (see Equation (10)).
EIR is a PRR “proxy” because, unlike most PRRs that strive to convert input and output information into units of power (often energy/year), including embodied energy translated from mass or monetary data, EIR is price based. Our EIR uses annual data (e.g., energy/year, GDP/year) and annual average prices, which are affected by short-term supply and demand. Thus, EIR is an analog to PRRs, and not ERRs.
Equation (10) defines the price-based EIR of energy commodity n in a country for a given time period. In this paper, we use annual data, where p is the price in units of money per energy content, ϵ is the energy intensity of the country, TPES is total primary energy supply (energy/year; see Section 4 of the Supplemental Information for the IEA definition) and GDP is the gross domestic product based on market exchange rates. We believe it is important to use GDP at market exchange rates, because oil is priced in U.S. dollars, and expenditures for oil are larger than for each other energy commodity.
Effectively, EIR scales prices (p) for an energy commodity (n) into a dimensionless ratio. King [14] showed that the time series of EIR correlates well to those of PRRs based on running average investments and energy production data of the United States. The major reason for this high correlation is as follows. The EIR represents how much power one can obtain by spending one dollar relative to how much power it takes to generate an average dollar of output from the economy. The numerator represents the price of an energy commodity output from an industry or sector; thus, it is akin to a system energy or power output. The EIR denominator represents the power input needed to produce GDP (money/year); thus, it is akin to a system energy or power input (see Equation (11)).
There is another reason that EIR correlates well with existing PRR calculations, such as in Guilford et al. [21] and Cleveland [51], and it has to do with the inclusion of indirect energy or power inputs. These two references calculate the invested power (or energy/year) as both direct and indirect. The direct power is from energy carriers, such as diesel and electricity. The indirect power is that power embodied in monetary investments. For example, Guilford et al. [21] assume a nominal energy intensity of the U.S. oil and gas industry as 14 MJ/$2005. That is to say, for every dollar produced by oil and gas extraction, 14 MJ of primary energy were assumed to be extracted to support all subsequent activities. The indirect investments can be a substantial fraction of the total. Figure 2 of King and Hall [15] indicates that since 1980 for the U.S. oil and gas industry, annual indirect energy investments are roughly equal to annual direct energy investments.
Therefore, a full PRR (or ERR) calculation cannot neglect indirect power (or energy) investments. These indirect estimates can be estimated as monetary investment multiplied by the energy intensity (MJ/$) of the sector from which the purchase is made. The weighted average of the energy intensities of all economic sectors is the energy intensity of the overall economy, ϵ = TPES/GDP. Thus, one could make a broad simplification that all investments, in energy or non-energy sectors, occur at the average energy intensity of the overall economy, ϵ, and Henshaw et al. [16] demonstrated this simplified approach. In effect, the EIR calculation makes this same simplifying assumption that all monetary investments to produce energy occur at the overall economy energy intensity rather than at some industry-specific energy intensity.
The EIR represents how much energy one can obtain by spending one dollar (or other monetary unit) relative to how much energy it takes to generate an average dollar of output from the economy. One benefit of using EIR as a PRR proxy is that energy commodity price data are more readily available for individual countries than data for energy production inputs (e.g., diesel, steel, etc.). Thus, one can gain insight into the net energy of commodities in countries with few data or low domestic energy production. In some sense, the EIR might be the only option for a calculation to estimate the net energy of commodities in countries with few data.
2.2.1. IEA Data
We obtain the energy intensity of each country, the ratio TPES/GDP, directly from the IEA data in tonnes of oil equivalent (toe) per thousand $2005 USD and convert to MJ assuming the conversion factor 41,868 MJ = 1 toe. For each of nine commodity prices, we calculate country-specific and a “worldwide” average energy intensity ratio (EIR). We calculate the world average EIR by weighting each of 44 country-specific EIR by the fraction of GDP that country contributes to the summed GDP of the countries (see Figure 5) (the 44 countries with data in the IEA database are: the United States, the United Kingdom, Spain, Russia, the Netherlands, Japan, Italy, Germany, Canada, France, Austria, Denmark, Finland, Norway, Sweden, Argentina, Australia, Belgium, Brazil, China, Chinese Taipei, Colombia, Czech Republic, Greece, Hungary, India, Indonesia, Iran, Iraq, South Korea, Kuwait, Libya, Malaysia, Mexico, New Zealand, Nigeria, Poland, Portugal, Qatar, Saudi Arabia, South Africa, Switzerland, Turkey and Venezuela) [52]. If the IEA data do not list a price for a given commodity in a given country, no value is plotted in Figure 5.

Figure 5.
The individual price-based energy intensity ratios, EIR, for all energy commodities considered in this paper show a general trend of increasing from the early 1980s through approximately 1998 followed by a decade-long decline through 2008 until the onset of the Great Recession. Thin gray lines represent individual country calculations, and the single thick red line is the GDP-weighted average of all EIR each year. NG = natural gas, Elec = electricity, Ind = industrial, and Res = residential, such that, for example, EIR is the “EIR of the price of natural gas purchased by the residential sector.”
We use annual average prices that represent the energy commodity sales at a particular point in the supply chain. It is important to compare only EIRs and PRRs at similar boundary conditions, or points in the supply chain. Gasoline and ethanol prices, EIR and PRRs can be compared, as they are both energy carriers refined for final consumption, but neither should be compared to oil, because it is a primary energy feedstock for various refined products. As such, EIR EIR, just as the price of oil is less than the price of gasoline.
2.2.2. Aggregation of EIR
There are several energy commodities, and thus, there are several EIR. Equations (12) and (13) show that by aggregating all EIR by the proportion of expenditures on that commodity n, one arrives at a value that equates to the inverse of total expenditures on energy for that country, (see Part 2 of this series for a full discussion and calculation of [1]).
Because the sum of all energy consumption is the definition of TPES (i.e., ),
The utility of the framework of Equations (12) and (13) is not so much that one could use system-wide EIR projections to project future expenditures on energy for energy scenarios. EIR is a retrospective metric based on historical price and macroeconomic data. The real utility would be to substitute for EIR a time series of an appropriate ratio of biophysical energy output and input flows. The power flows in turn come from the life cycle processes modeled to calculate PRRs and ERRs of individual technologies. Thus, a sequence of historical, or future (e.g., scenario), investments in multiple energy systems can translate to a time series of power input and output flows for the entire system or economy.
That is to say, as we contemplate scenarios of increasing use of energy production technologies that do not have individually-listed commodity prices (e.g., no commodity electricity price for wind and photovoltaic power), PRRs and ERRs calculated from net energy analyses can inform estimates of future total expenditures on energy and, thus, the economic implications of a time series of energy investments. For future scenarios, instead of projecting future prices without a biophysical basis, net energy analysts could project future PRRs, ERRs, materials and labor needs and then back out cost shares and cost supply curves (not necessarily prices).
2.2.3. England and United Kingdom Data
We use Roger Fouquet’s collection of historical data on England’s and the United Kingdom’s energy prices, gross domestic product and total primary energy supply [53,54,55]. As noted in Fouquet [54], average heating fuel prices are weighted by consumer expenditures (i.e., price multiplied by consumption) on the fuels. Fouquet’s data are largely estimates of annual average prices.
3. Results
The major results from calculating country-specific and worldwide aggregate energy intensity ratios (EIR) are as follows, with more detail in the rest of this section:
- All world average EIR follow a similar trend over the studied time periods, as they increase from 1978 to the late 1990s and early 2000s, before they decline through 2008 with a slight rebound to 2010 after the Great Recession in 2008.
- The time series for England and the U.K. indicates that high EIR are not unprecedented before World War II, but that EIR of coal generally declined from 1300 to 1850.
3.1. Energy Intensity Ratios: World
In a previous paper that introduced the EIR, King [14] showed that there was a high correlation of U.S. EIRs with existing calculations of EROI (using input data on annual flows, as energy/year and money/year, not power integrated over time) for two of the U.S. energy sectors: coal, as well as oil and gas. We interpret the trends of EIR in this paper in the same manner. There are very few ERR or PRR calculations of energy commodities or sectors by country or the world. Table 2 in Section 4.1 compares our EIR calculations to a couple of relevant calculations in the literature.
The following EIR patterns generally hold: EIR EIR EIR and EIR EIR EIR; Elec = for electric sector, Ind = for industrial sector and Res = for residential sector. This pattern is due to the fact that higher costs and prices, hence lower EIR, are associated with the increased distribution infrastructure and investment (e.g., p p p, where p is the price of commodity n for purchase by consumer i). More infrastructure and investment is required to deliver energy to many residential consumers than fewer industrial consumers and to even fewer electricity generating plants. In other words, EIR, or energy return ratios (ERRs) and power return ratios (PRRs) more generally, are higher (e.g., costs and prices are lower) when analyzing smaller boundaries or shorter subsets of supply chains. For the same reasons, EIR EIR and EIR EIR.
The anomalously high average values for EIR of residential NG (EIR) in 1993 and 1994 are due to significantly lower reported prices for Russia during those two years. The only other years with Russia residential NG prices are 2000–2004. The single anomalous high value for EIR of coal for electricity (EIR) in 1980 is for Poland. The high outlier time series for EIR of coal for residential consumption (EIR) is for South Africa.
Our calculations show that the overall global EIR trend for each energy commodity increases from 1978 to the late 1990s and early 2000s before it declines through 2008 with a slight rebound to 2010 after the Great Recession in 2008. The trend for the two decades leading up to 2000 implies that power return ratios of energy commodities were increasing following the Western governments’ supply and efficiency responses to the practically simultaneous 1973 Arab oil embargo and OPEC rise in posted oil price [56]. For the decade leading up to 2008, the global EIR decline indicates that energy commodities were becoming more expensive to the economy, which implies a broad decreasing trend in net energy output relative to energy inputs to produce the energy. This decline in EIR from 1998 to 2008, or steady increase in prices, has also been attributed to increased globalization and demand for resources. For example, Kilian describes the global oil price rise from 2003 to 2008 primarily as a function of unexpected increasing demand (relative to supply) in emerging Asian economies (e.g., China) [57]. One future research goal is to explain when changes in EIR are simply driven by supply and demand versus when they indicate a change in the underlying biophysical cost of production (i.e., net energy, ERR, PRR).
3.2. Energy Intensity Ratios: Historical England and U.K.
We present the long-term EIR of various energy commodities for England and the United Kingdom (U.K.) in Figure 6. The plot on the right of each (a)–(c) subset of Figure 6 is to enable easier comparison of the calculations using Fouquet and IEA data for the last 30 years. These EIR are perhaps the only biophysical-like metrics over such a long time period. Because EIR are highly correlated for U.S. time series, as investigated by King [14], we hypothesize that the same holds for other countries that produce the particular energy commodities under study. For most of the history of England and the U.K., we can assume they produced the vast majority of their energy from wood, coal (perhaps up to 1950, as U.K. coal production peaked in 1913 [12]) and gas. U.K. oil production (e.g., in the North Sea) occurs after 1970, and thus, the pre-1970 EIR is simply a measure of the relative economic effectiveness of U.K. consumption of oil imports. The U.K. produced practically all of its natural gas (and town gas per Fouquet data) until approximately 2005. To make compatible comparisons of the two data sources used for Figure 6, we have used the data collected by Fouquet to calculate energy intensity to then scale both his and the IEA energy prices into EIR [53,54,55]. Here, we calculate the England/U.K. energy intensity as the total energy consumption from Fouquet [53] (energy consumed for domestic heat, industrial heat, power (industry), passenger transport, freight transport and light) divided by GDP estimates. The historical (1270–1870) GDP estimates are those from Broadberry et al. [58].


Figure 6.
Energy intensity ratios for England and the United Kingdom for the following commodities: (a) wood and coal; (b) oil and natural gas; and (c) electricity. Calculations use three data sources for comparison: all nine energy commodity prices from the International Energy Agency (IEA) data (1978–2010), historical oil price from the BPStatistical Review (1861–2010) and historic firewood, coal, gas and electricity prices from Fouquet [54] (1300–2008). NG = natural gas, Elec = electricity, Ind = industrial and Res = residential. EIR is the “EIR of the price of natural gas purchased by the residential sector”.
4. Discussion
Individual energy technology life cycles are characterized by the series of processes, or investments, that are required to build the technology. Each investment in turn requires a certain amount of primary energy as an input (e.g., part of TPES) and produces a certain amount of net economic output (e.g., part of GDP) (see [27,28,59] for the methods that calculate the energy intensity of each economic sector). The former divided by the latter is an energy intensity (primary energy inputs divided by net economic output) that describes the structure of the technology life cycle. Some energy technology life cycles have investments with low overall energy intensity (e.g., those with a high ratio of services as investment) and some with high overall energy intensity (e.g., those with a high ratio of energy carriers as investment).
Like individual life cycles, economies can also have different structures that are partially characterized by the energy intensity of the economy. When we mention the energy intensity of an economy (e.g., TPES/GDP), this single number is really an average of all of the energy intensities of all individual industries and products in the economy: energy industries and non-energy industries. Thus, it is impossible to discuss the energy intensity of an overall economy without understanding the energy intensities of the underlying industries and processes that reside within the economy.
Hence, in net energy analysis, it is important to understand the linkages between the energy intensity of individual energy technology life cycles and the energy intensity, and hence structure, of the overall economy. Our discussion focuses on how we can use this understanding to translate between economic and biophysical descriptions of the economy.
4.1. Energy and Power Return Ratios in Relation to Cost and Prices (for Future Energy Scenarios)
The purpose of this section is to present the case that energy return ratios (ERRs) can provide insights into monetary costs of energy, as well as power return ratios (PRRs) can infer energy prices and/or operational costs. We believe one goal of using ERRs and PRRs is to relate to costs and prices, respectively, and thus help project the economic ramifications of future energy scenarios. Let us be clear, we are not the first to propose to use net energy as an indicator for technology assessment or projections. The Federal Nonnuclear Energy Research and Development Act of 1974 specified the calculation of net energy to evaluate energy technologies for research, development and deployment: “Section 5904 (a)(5): The potential for production of net energy by the proposed technology at the stage of commercial application shall be analyzed and considered in evaluating proposals”. [60].
The energy intensity ratio (EIR) is by definition inversely related to the price, , of an energy commodity. EIR also follows the same trend as PRRs in that the numerator represents an energy flow output (the commodity) and the denominator represents the average primary energy input per dollar of output, or energy intensity ( TPES/GDP), of the economy that purchased the energy output (see Equation (11)). Proper interpretation of data is needed to understand how much the domestic price actually relates to domestic production. The net energy analyses of the 1970s, such as [27,61], used economic I-O tables to break the assumption that every dollar invested from different industries and sectors was associated with the same amount of primary energy. Thus, some sectors are more energy intensive than other. Costanza [28] and Costanza and Herendeen [59] demonstrate that the differences in the calculated energy intensities among industries depends on two modeling assumptions: how one assumes energy “enters” the economy and the boundary between intermediate consumption (e.g., the input-output transactions of the producing part of the economy) and output. For modeling energy inputs, those authors demonstrate energy entering the economy at the point of physical entry into sectors (e.g., oil and gas energy enters into the oil and gas extraction sector) and energy entering as the relevant quantities at the points of consumption by each economic sector (not only energy sectors). In addition, Costanza and Herendeen [59] discuss implications of including labor costs and personal consumption within the input-output transactions matrix instead of considering them, as usual, as external to the input-output transactions matrix.
Most net energy analyses of energy industries (e.g., oil and gas) over time are actually formulations of PRRs, rather than ERRs, since they use data in units of power, or energy flows per year. Hall’s and Cleveland’s analyses of the U.S. oil and gas sector are good examples [21,51]. They term their calculation EROI, what we term GEPR in this present paper. King and Hall [15] plotted U.S. oil prices versus the EROI results of Guilford et al. [21] and hypothesized inverse curves governing the underlying trend between the two. Heun and de Wit [17] also explored the inverse relationship between GEPR (using the term EROI) and oil price. Here, we make Figure 7, similar to that in King and Hall [15], that also includes EIR. We use Figure 7 only to enhance the interpretation of Figure 8, which uses the calculations of the present paper.
In interpreting Figure 7, it is important to note that today, oil prices are dictated by global supply and demand pressures. However, this was not always the case. Before 1970, the U.S. was the marginal oil producer, and during the few decades leading up to 1970, the Texas Railroad Commission (RRC) was able to maintain price stability by throttling Texas oil production to prevent a price collapse due to overproduction [62]. Until the late 1970s, EIR and GEPR = EROI were quite similar, and King [14] (Figure 3) shows that U.S. EIR was less than GEPR = EROI when considering only the direct energy inputs, but greater than GEPR = EROI when considering both indirect and direct energy inputs. In effect, it seems the Texas RRC was effective at incentivizing some, but not too much, annual investment for oil production in order to minimize price volatility. The RRC set the oil price higher than needed to cover operational costs, but not too much higher, to induce new capital investment and allow profits.
It is not a surprise that this U.S. example shows that EIR is similar to EROI = GEPR from Guilford et al. [21] and Cleveland [51]. Both metrics utilize information about how the economy uses energy to produce GDP (e.g., U.S. energy intensity informs both of the calculations, but in different ways). Thus, this feedback exists, perhaps driving them to similar results. We do not have many calculations of the GEPR (= EROI) of production in various countries or the world overall to which to compare our present EIR calculations. Hence, the EIR calculations have value in that they use prices to provide some feel for the underlying GEPRs (= EROIs) of global production. They are not a PRR or an ERR calculation, but they are more than nothing. Table 2 shows our EIR calculations compared to two calculations of oil and gas EROI (Norway and a global estimate). The EIRs follow generally the same pattern over time and are close in estimation, particularly after 2000, when global commodity prices were generally increasing until 2008.

Figure 7.
U.S. oil first purchase price versus both EIR and EROI EROI as calculated by [21,51] for the U.S. oil and gas sector. Both figures show the same data: (a) uses linearly-scaled axes; and (b) uses logarithmically-scaled axes. See King and Hall [15] for a full explanation. Oil prices are annual U.S. crude oil first purchase prices from the Energy Information Administration’s Annual Energy Review and Monthly Energy Review. MROI = monetary return on investment relating to annual profit (MROI = 1 is breakeven).

Table 2.
Comparisons of EIR to EROI (= GEPR) calculations in the literature (selected years cited in references): Grandell et al. [63] for Norway oil and petroleum and Gagnon et al. [64] for the world oil and gas.
| EIR | EROI | EROI | EIR | EIR | EROI | |
|---|---|---|---|---|---|---|
| Year | Norway | Norway | Norway | World | World | World |
| This Paper | [63] | [63] | This Paper | This Paper | [64] | |
| 1991 | 50 | 35 | 44 | 34 | 31 | – |
| 1992 | 54 | 35 | 44 | 37 | 32 | 26 |
| 1996 | 59 | 46 | 59 | 36 | 34 | 34 |
| 1999 | 73 | 40 | 56 | 46 | 40 | 35 |
| 2006 | 29 | 26 | 47 | 16 | 23 | 18 |
| 2008 | 21 | 20 | 40 | 11 | 22 | – |
Figure 8 plots average prices ($2005/MJ) for the 44-country aggregate (weighted by GDP of each country) versus the EIR using that price and the 44-country energy intensity (= TPES/GDP). As mentioned earlier in the paper, we expect an ERR or a PRR analysis of a commodity or a technology to calculate smaller metrics for larger life cycle boundaries or longer supply chains. Figure 8b shows that residential NG has a higher price, and lower EIR, than NG for industrial purchase. Further, Figure 8c shows that electricity has a higher price, and lower EIR, than the NG and coal that fuel thermal power plants. We do not need EIR (nor ERRs, nor PRRs) to understand these points, but plots as in Figure 8 help us imagine how we can use ERR and PRR calculations to inform future energy scenarios (e.g., prices or other metrics). For example, net energy calculations can inform if distributed generation and storage technologies that can employ different supply chains and business models and infrastructure can supply residential electricity at higher ERR and PRR than the existing or future electric grid.
The two inverse curves in Figure 8a–c represent the 44-country world energy intensity in 1978 (13.9 MJ/$2005) and 2010 (10.5 MJ/$2005). We show these curves to help envision that as the economy becomes more efficient, the curves move up and to the right of the figure. Similarly, a single technology life cycle, or its annual embodied power inputs, can have a range from a low to a high overall energy intensity for the investment. This concept is shown in Figure 7. The postulated solid curve (lower-leftmost) relates GEPR and oil price via relatively high energy-intensive (33 MJ/$2005) investments for oil and gas development. The postulated dotted curve (upper-rightmost) represents investments at higher profit and lower energy intensity (13.5 MJ/$2005). Increased wages and use of services are one reason for a time period of lower energy intensity for investing in oil and gas development.
We use Figure 8d to think more conceptually about how the energy intensity of the investment for energy production can relate economic and net energy metrics. The y-axis can represent a marginal price that might relate well to a PRR. Furthermore, the y-axis might represent a levelized cost of energy, that would better relate to an ERR of a full life cycle. For example, previously, the lead author simultaneously calculated (using a wind farm installation cash flow model) the energy return ratio of NEER (= EROI) and (inversely related) levelized cost of energy (LCOE) [16].
Assume that we have calculated the ERR of an energy technology, as in Figure 8d. If the technology investments leading to ERR were mostly for up-front capital (e.g., manufacturing, construction) and services (e.g., engineering consulting), then the overall lifetime investments would be of low energy intensity because capital and services have relatively low energy intensity. That technology might have cost c. However, if an energy technology with ERR had high operating costs and direct energy inputs, then its overall investment would be of relatively higher energy intensity, and it might have cost c. This insight follows from the fact that energy carriers (e.g., direct energy inputs) are characterized by higher MJ/$ than the average product from the overall economy. The same rationale holds if we estimate a price (or a cost), p, for an energy technology instead of an ERR or PRR. This single price or cost might correspond to a range of low to high PRRs or ERRs, respectively. Thus, just as one could project monetary metrics to back calculate ERRs and PRRs, one could project ERRs and PRRs to project monetary metrics. Perhaps some hybrid combination is also possible.

Figure 8.
Price vs. EIR for the 44-country “world” aggregate prices, weighting each country price by the country GDP, for: (a) oil; (b) natural gas; and (c) electricity, along with the price of coal and NG purchased by electric generators; (d) the subfigure shows that depending on the characteristics of the required inputs (money and/or energy) for the energy supply chain or life cycle, a calculated ERR or PRR can relate to a range of prices, or vice versa.
4.2. Historical England and U.K. EIR
In considering the historical EIR time series of England and the U.K. (Figure 6), one of the main trends that stands out is that EIR of coal (at the pit and average) has a secular decline from 1300 to 1860. Fouquet [54] notes that over this time, his average coal price becomes dominated by the price in London, which includes taxes as nearly one-third of the price. Further, Fouquet’s (domestic) firewood price reflects considerable transport costs to non-local areas. Thus, our EIR translates best to a net external power ratio, or energy return on investment at the point of use. Coal at the pithead is also the only commodity with EIR before the 1940s. Thus, the post-World War II era is unique in having high EIR energy that is not coal.
In comparing the long-term EIR (left of Figure 6) to the more recent one (right of Figure 6), we can more clearly distinguish meaningful differences in the prices of the IEA and Fouquet. Fouquet’s energy prices are largely those for the end-consumer. Thus, the EIR for average coal is similar to the EIR using IEA residential prices. The same holds true for the EIR using Fouquet’s average gas (town and natural gas) and electricity prices, as they match best with EIR and EIR using IEA data. The one meaningful difference in the time series is that for all commodities (coal, gas and electricity), EIRs using Fouquet’s prices are lower in the 1980s–mid-1990s than those using IEA’s residential prices. After around 1995, all EIRs (e.g., prices) seem to agree relatively well.
Everyone alive today has lived in a time of generally decreasing economic energy intensity (for developed countries), but this has not always been the case, as Figure 9a shows for England and the U.K. While describing the full history of energy and technology in the U.K. is beyond the scope of this paper (see [53,54,55] for more details), we make a few general statements. For our purposes, the broad trends are most important rather than debating the annual variations in data (which Fouquet also notes imply greater accuracy than exist). Suffice it to say that energy, combined with prime movers and other technologies providing energy services, is key to a modern economy and defines the structure of the economy to a large degree. Over the course of 700 years, the energy intensity of England and the United Kingdom has varied by nearly relative to the pre-industrial average. U.K. industrialization in the 1800s coincided with increasing energy intensity as an increasing rate of energy consumption outpaced economic output, which also increased rapidly. Ever since the 1870s, the U.K.’s economy has restructured to produce more value from less (domestic) energy consumption.
It is only since the 1870s that the effective power return ratio of coal, using EIR as a proxy, began to rise again. Thus, over the history of the U.K., real energy prices (and hence, PRRs and ERRs) have fluctuated in the context of available energy, technology and labor. As such, the EIR of energy commodities fluctuated, as well. While we do not perform a causal analysis relating high energy and power return resources, we can map the structure of the economy to EIR and prices to provide a conceptual understanding.

Figure 9.
(a) England’s/the U.K.’s economy energy intensity; (b) price vs. EIR for coal (average) and firewood for England and the United Kingdom from 1300 to 2008. Three example inverse curves show the constant energy intensity of England’s/the U.K.’s economy at 390,1000 and 150 Mtoe/£2000 in the years 1560, 1870 and 2008, respectively. Data from Fouquet [54].
Figure 9b plots coal (average) and wood prices versus EIR of each. If it were not for a changing structure in the economy, here characterized by the country energy intensity (ϵ = TPES/GDP), then all points in Figure 9b would lie on a single inverse curve. By presenting the EIR, price and energy intensity data as shown, we gain a historical perspective on how energy return ratios (ERRs) and power return ratios (PRRs) might have related to prices, as discussed in Section 4.1.
For example, population pressure in pre-industrial England was relatively high during the time periods of high energy intensity in Figure 9a (see [33]). This population pressure affected farm wages that were low from 1250 to 1350, high from 1400 to 1500 and again lower from 1550 to 1650 [65]. Since farming was a large part of the pre-industrial economy, as a part of the energy sector in providing fodder and food for animate (animal and human) power, there is a relationship between farm wages (e.g., costs) for the energy sector and the energy intensity of the economy overall that needs exploration. That is to say, when farm (e.g., energy) wages were high, the pre-industrial English energy intensity was low, and vice versa. Since farm wages were the major input to the pre-industrial energy sector (e.g., agriculture), they translated to more expensive energy (e.g., food and fodder) that incentivized more efficient consumption. It is precisely this type of relationship that we need to understand for modeling future energy scenarios from both economic and biophysical perspectives. We cannot separate the combination of high ERR fuels and new conversion technologies (e.g., steam engines) from the feedbacks within the overall economy. As Figure 9b shows, over time, a given EIR was not associated with a single price. It is left to future work to understand this relationship of prices to ERRs and PRRs based on the information of the actual wood and coal life cycle processes.
5. Conclusions
We believe that to make net energy analysis relevant to decision-making, one approach is to translate between economic and biophysical descriptions of energy systems and technologies. In taking this approach, it is important to make sure one is linking the proper metrics. Thus, the metrics must be clearly defined as described in this paper. The energy intensity ratio calculated (EIR) in this paper is one metric to translate between economic (e.g., prices of energy commodities) and biophysical (e.g., power and energy return ratios) descriptions of the value of energy commodities. The EIR is based on annual energy price data, but scaled via the energy intensity (total primary energy supply/GDP) to translate to the power return ratios of a biophysical or net energy modeler. EIR is a proxy for the gross external power ratio (for primary energy commodities) and the net external power ratio (for delivered energy commodities). Levelized costs of energy best translate to energy return ratios (ERR), such as the net external energy ratio (NEER) calculated using information over the entire life cycle of the energy system. We find it important to distinguish among the mathematical definitions of these terms, and we use a unique terminology for each equation so as not to confuse a single term (e.g., energy return on energy invested, EROI) with more than one definition.
For any calculated value for an ERR, there is not a single cost of energy. Likewise, for any given calculated power return ratio (PRR), there is not a single price of energy. In order to more fully translate between prices and power return ratios, or levelized costs and energy return ratios, it is necessary to consider the structure of the investments for an energy technology or system. This structure can be measured by the energy intensity of the life cycle inputs. We expect energy systems and technologies with a high proportion of capital and services inputs to have lower energy intensity of investment (e.g., lower MJ/$ for inputs), which translates to a higher cost or price at a constant ERR or PRR, respectively. Examples of these kinds of technologies are wind and photovoltaic power, which have no fuel costs and low operating costs. Conversely, we expect energy systems and technologies with a high proportion of direct energy inputs (e.g., fuels) to have higher energy intensity of investment (e.g., higher MJ/$ for inputs), which translates to a lower cost or price at a constant ERR or PRR, respectively.
Just as the structure of investments for an energy technology can help link its ERR to its cost, the structure of the economy overall affects the underlying assumptions for the calculations. We showed that the calculated EIR for global oil, coal, natural gas and electricity prices all show a similar trend: increasing from 1978 to around the year 2000, then decreasing to 2008 before rebounding up slightly to 2010. During this short time span, many economies changed their structure significantly by becoming more efficient in the use of energy. However, the changes pale in comparison to the structure changes that morphed the pre-industrial England economy to that of the United Kingdom today. For over five centuries (1300–1800), the EIR of English coal was always higher than the EIR of wood, even though the EIR of coal slowly declined over that time.
If an overall economy has high energy intensity, then this might be linked to its ability to produce high ERR energy, as we show occurred during industrialization in the United Kingdom in the 1800s. Conversely, a country that cannot produce high ERR energy (e.g., due to lack of quality resources) is more incentivized to reduce energy intensity to make the most economic use of produced and imported energy. Future research should strive for better models to link ERRs to costs and PRRs to marginal prices.
Supplementary Files
Supplementary File 1Supplementary File 2Acknowledgments
This work was partially supported by, and the authors thank, the Jackson School of Geosciences Energy Theme at The University of Texas at Austin.
Author Contributions
Carey W. King designed and structured the research. Alyssa Donovan, John P. Maxwell, Carey W. King obtained and organized the data from the various sources while performing calculations for the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- King, C.W.; Maxwell, J.P.; Donovan, A. Comparing world economic and net energy metrics, Part 2: Expenditures Perspective. Energies 2015, 8, 12975–12996. [Google Scholar] [CrossRef]
- King, C.W. Comparing world economic and net energy metrics, Part 3: Macroeconomic Historical and Future Perspectives. Energies 2015, 8, 12997–13020. [Google Scholar] [CrossRef]
- Solow, R. A Contribution to the Theory of Economic-Growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Hamilton, J. Historical Oil Shocks. In Routledge Handbook of Major Events in Economic History; Parker, R.E., Whaples, R.M., Eds.; Routledge: New York, NY, USA, 2013; p. 239265. [Google Scholar]
- Ayres, R.; Voudouris, V. The economic growth enigma: Capital, labour and useful energy? Energy Policy 2014, 64, 16–28. [Google Scholar] [CrossRef]
- Kander, A.; Stern, D.I. Economic growth and the transition from traditional to modern energy in Sweden. Energy Econ. 2014, 46, 56–65. [Google Scholar] [CrossRef]
- Kümmel, R. The Second Law of Economics: Energy, Entropy, and the Origins of Wealth; Springer: Berlin, Germany, 2011. [Google Scholar]
- Hall, C.A.S.; Klitgaard, K.A. Energy and the Wealth of Nations: Understanding the Biophysical Economy, 1st ed.; Springer: Berlin, Germany, 2012. [Google Scholar]
- Brown, J.H.; Burnside, W.R.; Davidson, A.D.; Delong, J.R.; Dunn, W.C.; Hamilton, M.J.; Mercado-Silva, N.; Nekola, J.C.; Okie, J.G.; Woodruff, W.H.; et al. Energetic Limits to Economic Growth. BioScience 2011, 61, 19–26. [Google Scholar] [CrossRef]
- Peters, G.P.; Hertwich, E.G. CO2 embodied in international trade with implications for global climate policy. Environ. Sci. Technol. 2008, 42, 1401–1407. [Google Scholar] [CrossRef] [PubMed]
- Acemoglu, D.; Robinson, J.A. Why Nations Fail: The Origins of Power, Prosperity, and Poverty; Crown Business: New York, NY, USA, 2012. [Google Scholar]
- Rutledge, D. Estimating long-term world coal production with logit and probit transforms. Int. J. Coal Geol. 2011, 85, 23–33. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Cleveland, C.J.; Kaufmann, R.K. Energy and Resource Quality: The Ecology of the Economic Process; Wiley: New York, NY, USA, 1986. [Google Scholar]
- King, C.W. Energy intensity ratios as net energy measures of United States energy production and expenditures. Environ. Res. Lett. 2010, 5, 044006. [Google Scholar] [CrossRef]
- King, C.W.; Hall, C.A.S. Relating Financial and Energy Return on Investment. Sustainability 2011, 3, 1810–1832. [Google Scholar] [CrossRef]
- Henshaw, P.F.; King, C.; Zarnikau, J. System Energy Assessment (SEA), Defining a Standard Measure of EROI for Energy Businesses as Whole Systems. Sustainability 2011, 3, 1908–1943. [Google Scholar] [CrossRef]
- Heun, M.K.; de Wit, M. Energy return on (energy) invested (EROI), oil prices, and energy transitions. Energy Policy 2011, 40, 147–158. [Google Scholar] [CrossRef]
- Brandt, A.R. Converting oil shale to liquid fuels: Energy inputs and greenhouse gas emissions of the Shell in situ conversion process. Environ. Sci. Technol. 2008, 42, 7489–7495. [Google Scholar] [CrossRef] [PubMed]
- Brandt, A.R. Converting Oil Shale to Liquid Fuels with the Alberta Taciuk Processor: Energy Inputs and Greenhouse Gas Emissions. Energy Fuels 2009, 23, 6253–6258. [Google Scholar] [CrossRef]
- Brandt, A.R.; Englander, J.; Bharadwaj, S. The energy efficiency of oil sands extraction: Energy return ratios from 1970 to 2010. Energy 2013, 55, 693–702. [Google Scholar] [CrossRef]
- Guilford, M.C.; Hall, C.A.S.; O’Connor, P.; Cleveland, C.J. A New Long Term Assessment of Energy Return on Investment (EROI) for U.S. Oil and Gas Discovery and Production. Sustainability 2011, 3, 1866–1887. [Google Scholar] [CrossRef]
- Farrell, A.E.; Plevin, R.J.; Turner, B.T.; Jones, A.D.; O’Hare, M.; Kammen, D.M. Ethanol can contribute to energy and environmental goals. Science 2006, 311, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Raugei, M.; Fullana-i-Palmer, P.; Fthenakis, V. The energy return on energy investment (EROI) of photovoltaics: Methodology and comparisons with fossil fuel life cycles. Energy Policy 2012, 45, 576–582. [Google Scholar] [CrossRef]
- Dale, M.; Benson, S.M. Energy Balance of the Global Photovoltaic (PV) Industry—Is the PV Industry a Net Electricity Producer? Environ. Sci. Technol. 2013, 47, 3482–3489. [Google Scholar] [CrossRef] [PubMed]
- Fthenakis, V.M.; Kim, H.C. Photovoltaics: Life-cycle analyses. Sol. Energy 2011, 85, 1609–1628. [Google Scholar] [CrossRef]
- Zhang, Y.; Colosi, L.M. Practical ambiguities during calculation of energy ratios and their impacts on life cycle assessment calculations. Energy Policy 2013, 57, 630–633. [Google Scholar] [CrossRef]
- Bullard, C.W., III; Herendeen, R.A. The energy cost of goods and services. Energy Policy 1975, 3, 268–278. [Google Scholar] [CrossRef]
- Costanza, R. Embodied Energy and Economic Valuation. Science 1980, 210, 1219–1224. [Google Scholar] [CrossRef] [PubMed]
- King, C.W. Matrix method for comparing system and individual energy return ratios when considering an energy transition. Energy 2014, 72, 254–265. [Google Scholar] [CrossRef]
- Tainter, J. The Collapse of Complex Societies; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Tainter, J.A. Energy, complexity, and sustainability: A historical perspective. Environ. Innov. Soc. Transit. 2011, 1, 89–95. [Google Scholar] [CrossRef]
- Tainter, J.A. Energy and Existential Sustainability: The Role of Reserve Capacity. J. Environ. Account. Manag. 2013, 1, 213–228. [Google Scholar] [CrossRef]
- Turchin, P.; Nefedov, S.A. Secular Cycles; Princeston University Press: Princeston, NJ, USA, 2009. [Google Scholar]
- Ayres, R.U.; Warr, B. Accounting for growth: The role of physical work. Struct. Chang. Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Ayres, R.U. Sustainability economics: Where do we stand? Ecol. Econ. 2008, 67, 281–310. [Google Scholar] [CrossRef]
- Stern, D.; Kander, A. The Role of Energy in the Industrial Revolution and Modern Economic Growth; Technical Report for The Australian National University: Canberra, Australia, 2011. [Google Scholar]
- Stern, D.I.; Kander, A. The Role of Energy in the Industrial Revolution and Modern Economic Growth. Energy J. 2012, 33. [Google Scholar] [CrossRef]
- Hamilton, J. Causes and Consequences of the Oil Shock of 2007–2008. In Brookings Papers on Economic Activity; Romer, D., Wolfers, J., Eds.; Brookings Institution Press: Washington, DC, USA, 2009; p. 69. [Google Scholar]
- Hall, C.A.S.; Balogh, S.; Murphy, D.J.R. What is the Minimum EROI that a Sustainable Society Must Have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Brown, J.H.; Burger, J.R.; Burnside, W.R.; Chang, M.; Davidson, A.D.; Fristoe, T.S.; Hamilton, M.J.; Hammond, S.T.; Kodric-Brown, A.; Mercado-Silva, N.; et al. Macroecology meets macroeconomics: Resource scarcity and global sustainability. Ecol. Eng. 2014, 65, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, C.J.; Kaufmann, R.K.; Stern, D.I. Aggregation and the role of energy in the economy. Ecol. Econ. 2000, 32, 301–317. [Google Scholar] [CrossRef]
- Odum, H.T. Environmental Accounting: Energy and Environmental Decision Making; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Campbell, D.E.; Lu, H.; Walker, H.A. Relationships among the Energy, Emergy and Money Flows of the United States from 1900 to 2011. Front. Energy Res. 2014, 2. [Google Scholar] [CrossRef]
- Brandt, A.R.; Dale, M.; Barnhart, C.J. Calculating systems-scale energy efficiency and net energy returns: A bottom-up matrix-based approach. Energy 2013, 62, 235–247. [Google Scholar] [CrossRef]
- Murphy, D.J.R.; Hall, C.A.S.; Dale, M.; Cleveland, C.J. Order from Chaos: A Preliminary Protocol for Determining EROI for fuels. Sustainability 2011, 3, 1888–1907. [Google Scholar] [CrossRef]
- Spath, P.L.; Mann, M.K.; Kerr, D.R. Life Cycle Assessment of Coal-fired Power Production, NREL/TP-570-25119; Technical Report NREL/TP-570-25119; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1999.
- Brandt, A.R.; Dale, M. A General Mathematical Framework for Calculating Systems-Scale Efficiency of Energy Extraction and Conversion: Energy Return on Investment (EROI) and Other Energy Return Ratios. Energies 2011, 4, 1211–1245. [Google Scholar] [CrossRef]
- Modahl, I.S.; Raadal, H.L.; Gagnon, L.; Bakken, T.H. How methodological issues affect the energy indicator results for different electricity generation technologies. Energy Policy 2013, 63, 283–299. [Google Scholar] [CrossRef]
- Arvesen, A.; Hertwich, E.G. More caution is needed when using life cycle assessment to determine energy return on investment (EROI). Energy Policy 2015, 76, 1–6. [Google Scholar] [CrossRef]
- Hall, C.A.S. Congratulations to Carey King. Environ. Res. Lett. 2012, 7, 011006. [Google Scholar] [CrossRef]
- Cleveland, C.J. Net energy from the extraction of oil and gas in the United States. Energy 2005, 30, 769–782. [Google Scholar] [CrossRef]
- Maxwell, J.P. Energy Intensity Ratios as Net Energy Measures for Selected Countries 1978–2010. Master’s Thesis, The Unversity of Texas at Austin, Austin, TX, USA, 2013. [Google Scholar]
- Fouquet, R. Heat, Power, and Light: Revolutions in Energy Services; Edward Elgar Publishing Limited: Northampton, MA, USA, 2008. [Google Scholar]
- Fouquet, R. Divergences in Long-Run Trends in the Prices of Energy and Energy Services. Rev. Environ. Econ. Policy 2011, 5, 196–218. [Google Scholar] [CrossRef]
- Fouquet, R. Long run demand for energy services: Income and price elasticities over 200 years. Rev. Environ. Econ. Policy 2014, 8. [Google Scholar] [CrossRef]
- Mitchell, T. Carbon Democracy: Political Power in the Age of Oil; Verso: London, UK; New York, NY, USA, 2013; p. 292. [Google Scholar]
- Kilian, L. Oil Price Shocks, Monetary Policy and Stagflation. CEPR Discussion Papers 7324. Available online: http://www.rba.gov.au/publications/confs/2009/kilian.html (accessed on 3 March 2015).
- Broadberry, S.; Campbell, B.; Klein, A.; Overton, M.; van Leeuwen, B. British Economic Growth, 1270–1870: An Output-Based Approach; Studies in Economics, School of Economics, University of Kent: Canterbury, Kent, UK, 2012. [Google Scholar]
- Costanza, R.; Herendeen, R.A. Embodied energy and economic value in the United States economy: 1963, 1967, and 1972. Resour. Energy 1984, 6, 129–163. [Google Scholar] [CrossRef]
- Congress of USA. Federal Nonnuclear Energy Research and Development Act, (PL 93-577); Congress of USA: Washington, DC, USA, 1974.
- Bullard, C.W.; Penner, P.S.; Pilati, D.A. Net energy analysis: Handbook for combining process and input-output analysis. Resour. Energy 1978, 1, 267–313. [Google Scholar] [CrossRef]
- Yergin, D. The Prize: The Epic Quest for Oil, Money, & Power; Free Press: New York, NY, USA, 1991; p. 928. [Google Scholar]
- Grandell, L.; Hall, C.A.; Höök, M. Energy Return on Investment for Norwegian Oil and Gas from 1991 to 2008. Sustainability 2011, 3, 2050–2070. [Google Scholar] [CrossRef]
- Gagnon, N.; Hall, C.A.S.; Brinker, L. A preliminary investigation of energy return on energy investment for global oil and gas production. Energies 2009, 2, 490–530. [Google Scholar] [CrossRef]
- Clark, G. The Long March of History: Farm Laborers Wages in England 1208–1850. NA Econ. 2001, 1, 1–35. Available online: http://www.najecon.org/naj/cache/625018000000000238.pdf (accessed on 3 March 2015). [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).