Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon
Abstract
:1. Introduction
2. Backgrounds
2.1. Price Responsiveness Model
2.2. Designing a Critical Peak Pricing (CPP) Scheme without Payback
3. Characterization of the Payback Phenomenon
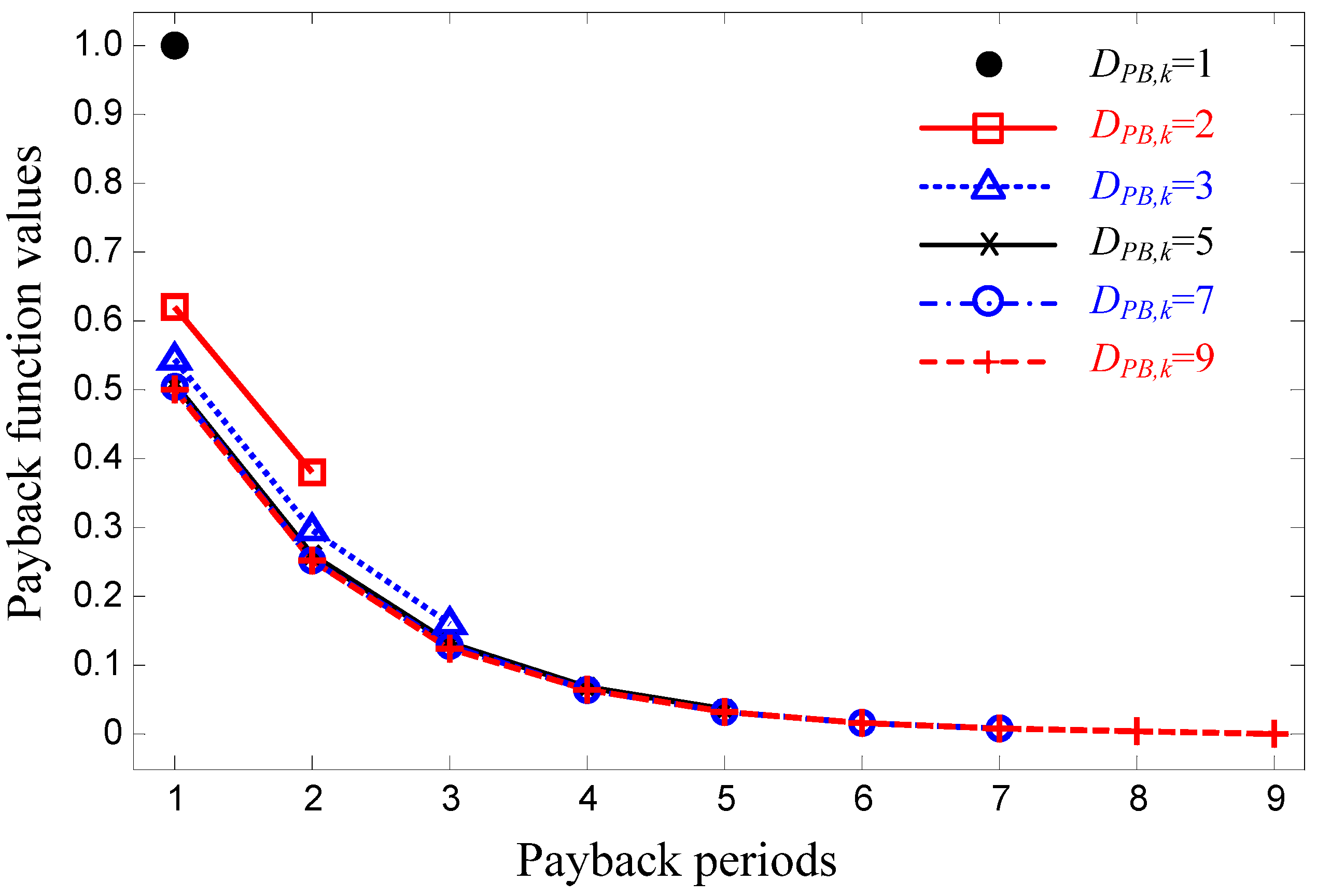
4. Payback Effects on CPP Design
4.1. Payback Effects on the Event Scheduling Problem
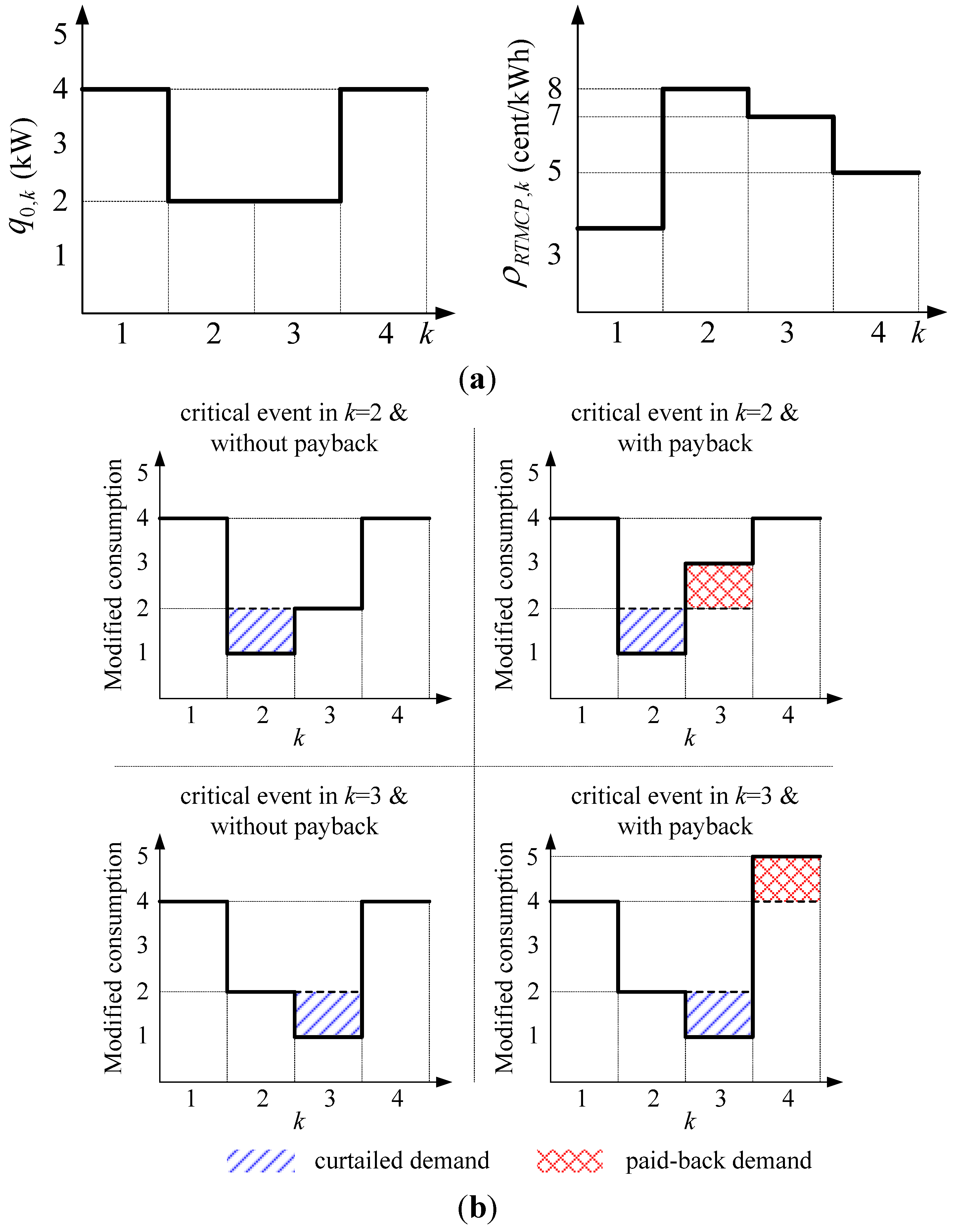
| Critical Event Period | Without Payback ($) | With Payback ($) | |
|---|---|---|---|
| revenue | 84 | 88 | |
| cost | 54 | 61 | |
| profit | 30 | 27 | |
| revenue | 84 | 88 | |
| cost | 55 | 60 | |
| profit | 29 | 28 | |
4.2. Payback Effects on the Optimal Peak Rate
5. Simulations and Verification
5.1. Simulation Methods
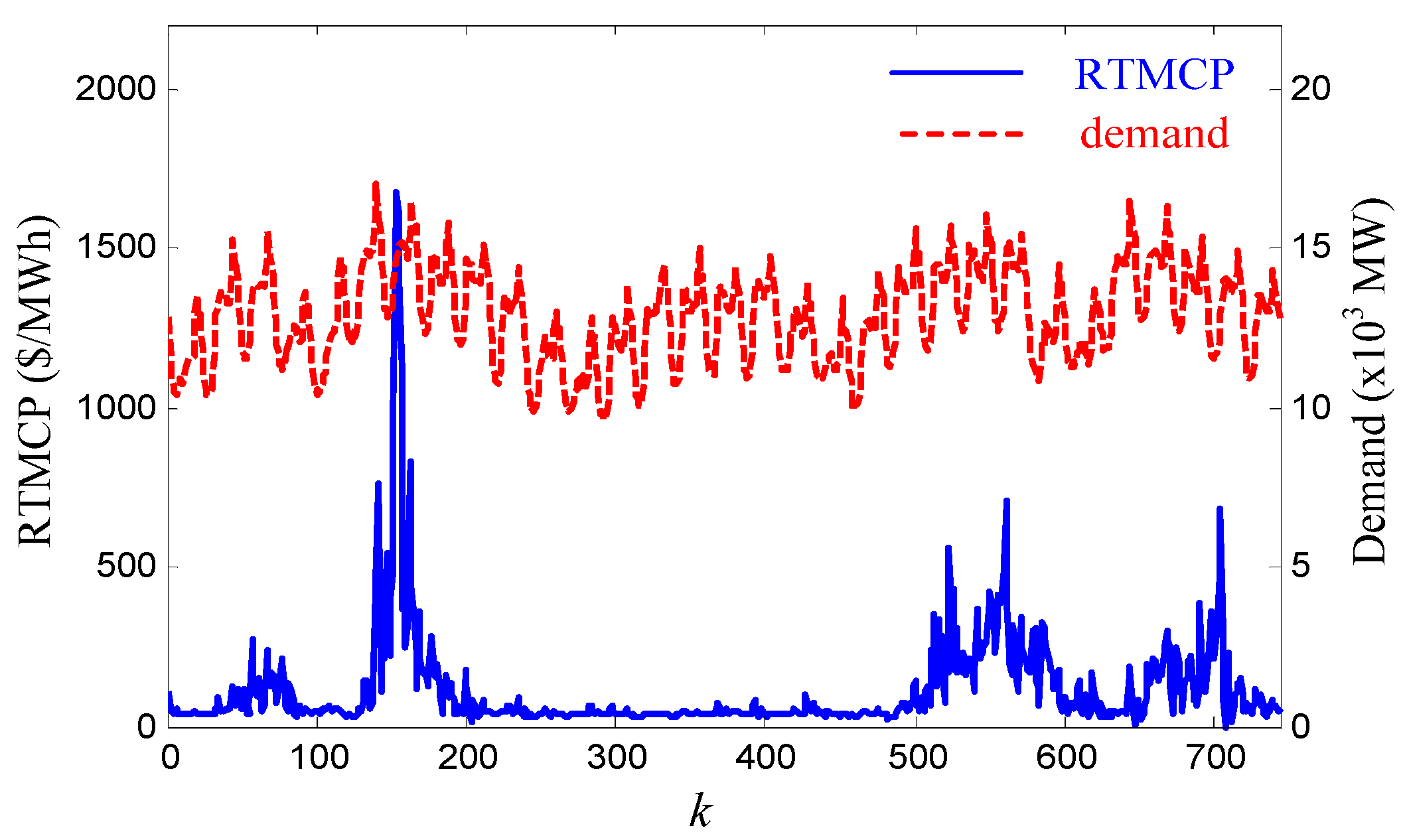
5.2. Results: Payback Effects on the Optimal Event Schedule
| Optimal Schedule of Critical Events | Profit (Million Dollars) | |
|---|---|---|
| Without payback | {154, 561, 668} | 46.476 |
| Exponentially decreasing payback {0.54, 0.30, 0.16} | {157, 561, 644} | 40.265 |
| Uniformly distributed payback {1/3, 1/3, 1/3} | {157, 561, 704} | 40.843 |
5.3. Result: Payback Effects on the Optimal Peak Rate
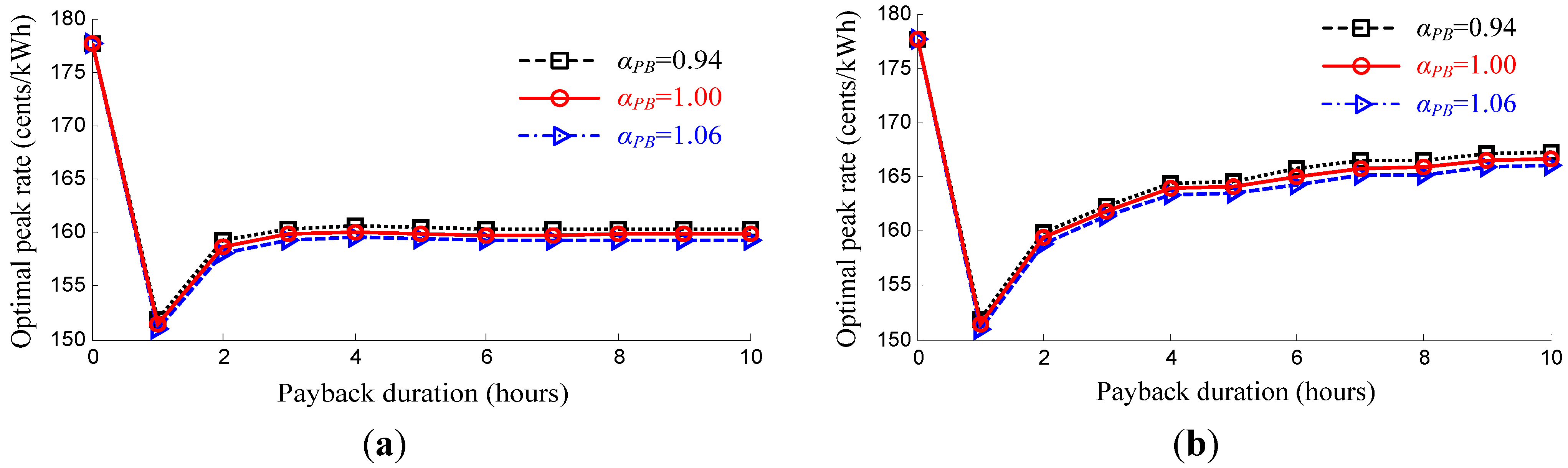
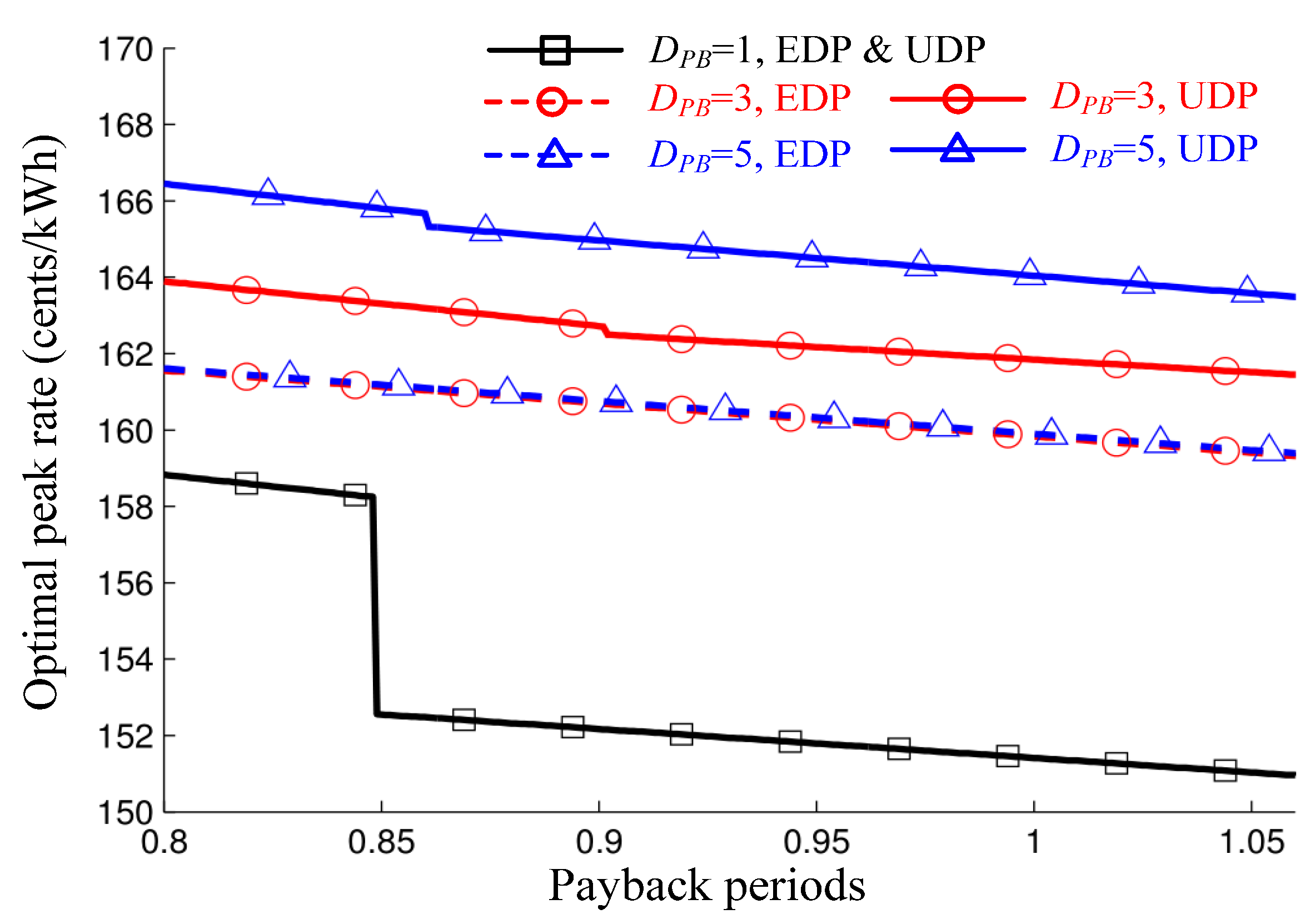
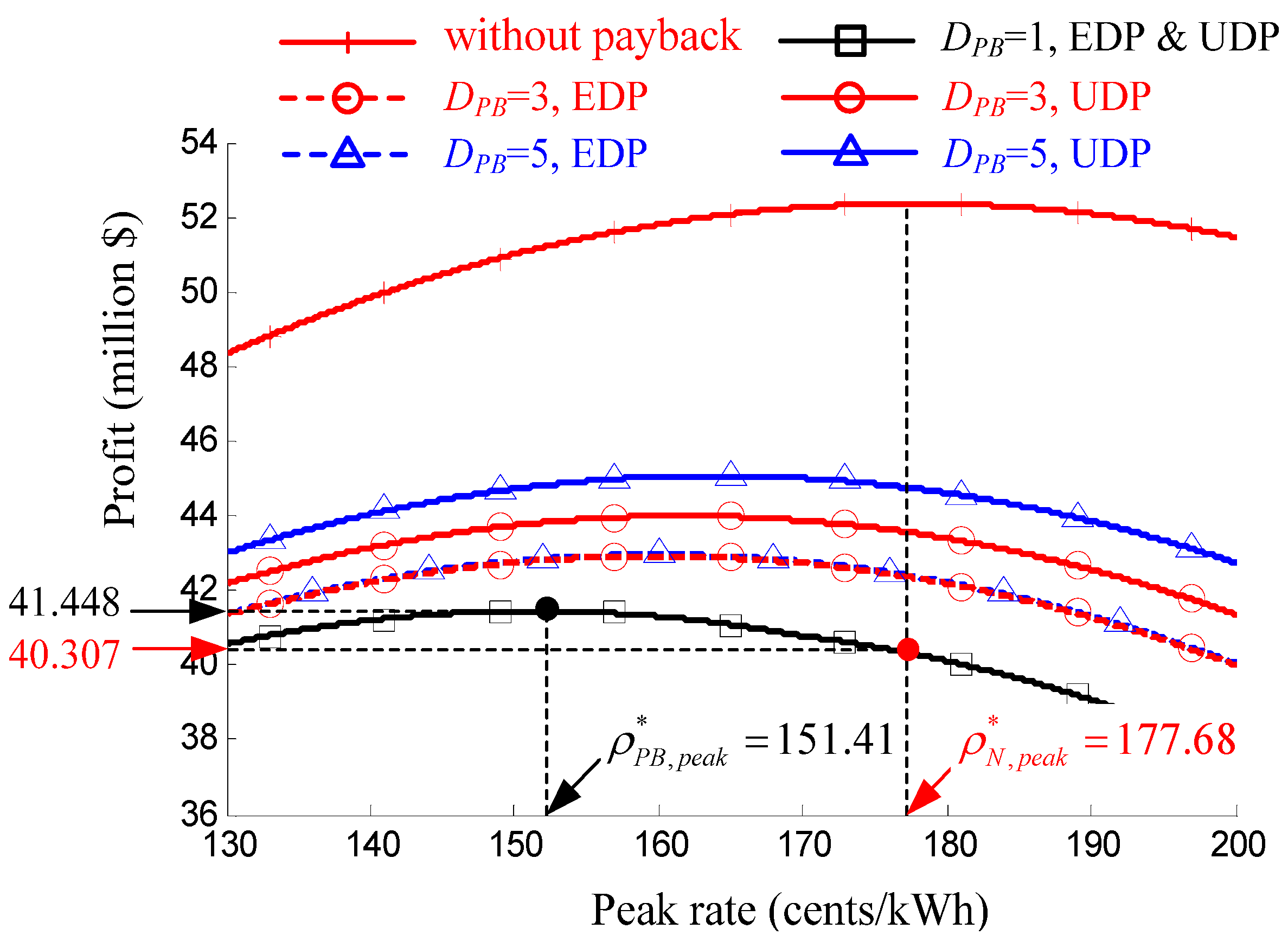
6. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| off-peak rate of a critical peak pricing scheme | |
| peak rate of a critical peak pricing scheme | |
| real-time market clearing price in period | |
| optimal peak rate for a normal situation without payback | |
| optimal peak rate considering payback effects | |
| difference of from | |
| nominal consumption of customers in period | |
| consumption of customers in period when a critical event is triggered | |
| recovered demand due to payback in period | |
| cumulative consumption during the critical event periods starting from the period | |
| cumulative curtailed demand for a critical event starting in period | |
| paid-back demand for the critical event in period | |
| revenue of a load serving entity in period | |
| cost of a load serving entity in period | |
| profit index in period | |
| profit index in a normal situation without payback in period | |
| profit index considering payback effects in period | |
| binary event decision variable in period | |
| maximum number of critical events | |
| duration of the critical event | |
| payback duration | |
| payback function | |
| normalized payback function | |
| payback ratio | |
| price elasticity of customers | |
| scheduling time horizon of the event scheduling problem | |
| minimum interval between successive events | |
| constant for the exponentially decreasing payback function | |
| constant for the uniformly distributed payback function | |
| solution of the events scheduling problem for a given peak rate | |
| solution of the events scheduling problem for the optimal peak rate |
Abbreviations
| ARMA | autoregressive moving average |
| CPP | critical peak pricing |
| DR | demand response |
| EDP | exponentially decreasing payback |
| LSE | load serving entity |
| RTMCP | real-time market clearing price |
| RTP | real-time pricing |
| TOU | time-of-use |
| UDP | uniformly distributed payback |
References
- U.S. Department of Energy. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them: A Report to the United States Congress; U.S. Department of Energy: Washington, DC, USA, 2006.
- Kirschen, D.S. Demand-side view of electricity markets. IEEE Trans. Power Syst. 2003, 18, 520–527. [Google Scholar] [CrossRef]
- Doostizadeh, M.; Ghasemi, H. A day-ahead electricity pricing model based on smart metering and demand-side management. Energy 2012, 46, 221–230. [Google Scholar] [CrossRef]
- Ferrero, R.W.; Rivera, J.F.; Shahidehpour, S.M. Application of games with incomplete information for pricing electricity in deregulated power pools. IEEE Trans. Power Syst. 1998, 13, 184–189. [Google Scholar] [CrossRef]
- Kirschen, D.S.; Strbac, G. Fundamentals of Power System Economics; John Wiley & Sons: Chichester, UK, 2004; pp. 75–79. [Google Scholar]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Elect. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Herter, K. Residential implementation of critical peak pricing of electricity. Energy Policy 2007, 35, 2121–2130. [Google Scholar] [CrossRef]
- Joo, J.-Y.; Ahn, S.H.; Yoon, Y.T.; Choi, J.W. Option valuation applied to implementing demand response via critical peak pricing. In Proceedings of the IEEE PES General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7.
- Chen, W.; Wang, X.; Petersen, J.; Tyagi, R.; Black, J. Optimal scheduling of demand response events for electric utilities. IEEE Trans. Smart Grid 2013, 4, 2309–2319. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.; Fu, M. Optimal implementation strategies for critical peak pricing. In Proceedings of the 6th International Conference on the European Energy Market (EEM), Leuven, Belgium, 27–29 May 2009; pp. 1–6.
- Park, S.C.; Jin, Y.G.; Song, H.Y.; Yoon, Y.T. Designing a critical peak pricing scheme for the profit maximization objective considering price responsiveness of customers. Energy 2015, 83, 521–531. [Google Scholar] [CrossRef]
- Zhang, X. Optimal scheduling of critical peak pricing considering wind commitment. IEEE Trans. Sustain. Energy 2014, 5, 637–645. [Google Scholar] [CrossRef]
- Wei, D.; Chen, N. Air conditioner direct load control by multi-pass dynamic programming. IEEE Trans. Power Syst. 1995, 10, 307–313. [Google Scholar]
- Ericson, T. Direct load control of residential water heaters. Energy Policy 2009, 37, 3502–3512. [Google Scholar] [CrossRef]
- Cohen, A.I.; Patmore, J.W.; Oglevee, D.H.; Berman, R.W.; Ayers, L.H.; Howard, J.F. An integrated system for residential load control. IEEE Trans. Power App. Syst. 1987, 2, 645–651. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Negnevitsky, M.; de Groot, M. Modeling load recovery impact for demand response applications. IEEE Trans. Power Syst. 2013, 28, 1216–1225. [Google Scholar] [CrossRef]
- Karangelos, E.; Bouffard, F. Towards full integration of demand-side resources in joint forward energy/reserve electricity markets. IEEE Trans. Power Syst. 2012, 27, 280–289. [Google Scholar] [CrossRef]
- Kirschen, D.S.; Strbac, G.; Cumperayot, P.; de Paiva Mendes, D. Factoring the elasticity of demand in electricity. IEEE Trans. Power Syst. 2000, 15, 612–617. [Google Scholar] [CrossRef]
- Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Shaw, R.; Attree, M.; Jackson, T.; Kay, M. The value of reducing distribution losses by domestic load-shifting: A network perspective. Energy Policy 2009, 37, 3159–3167. [Google Scholar] [CrossRef]
- Strbac, G.; Kirschen, D.S. Assessing the competitiveness of demand-side bidding. IEEE Trans. Power Syst. 1999, 14, 120–125. [Google Scholar] [CrossRef]
- Piette, M.A.; Watson, D.; Motegi, N.; Kiliccote, S. Automated Critical Peak Pricing Field Tests: 2006 Pilot Program Description and Results; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2007. [Google Scholar]
- Schweppe, F.C.; Caramanis, M.C.; Tabors, R.D.; Bohn, R.E. Spot Pricing of Electricity; Springer: New York, NY, USA, 1988; pp. 327–333. [Google Scholar]
- Weron, R. Modeling and Forecasting Electricity Loads and Prices: A Statistical Approach; John Wiley & Sons: Chichester, UK, 2007; pp. 84–85; 109–110. [Google Scholar]
- PJM Market & Operations: Real-time Energy Market Data. Available online: http://www.pjm.com/markets-and-operations/energy/real-time.aspx (accessed on 14 February 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.C.; Jin, Y.G.; Yoon, Y.T. Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon. Energies 2015, 8, 11363-11379. https://doi.org/10.3390/en81011363
Park SC, Jin YG, Yoon YT. Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon. Energies. 2015; 8(10):11363-11379. https://doi.org/10.3390/en81011363
Chicago/Turabian StylePark, Sung Chan, Young Gyu Jin, and Yong Tae Yoon. 2015. "Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon" Energies 8, no. 10: 11363-11379. https://doi.org/10.3390/en81011363
APA StylePark, S. C., Jin, Y. G., & Yoon, Y. T. (2015). Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon. Energies, 8(10), 11363-11379. https://doi.org/10.3390/en81011363





