Active Participation of Air Conditioners in Power System Frequency Control Considering Users’ Thermal Comfort
Abstract
:1. Introduction
2. Fuzzy Rule Based Decentralized Control for Frequency Regulation
2.1. Fuzzy Evaluation of Human Thermal Comfort
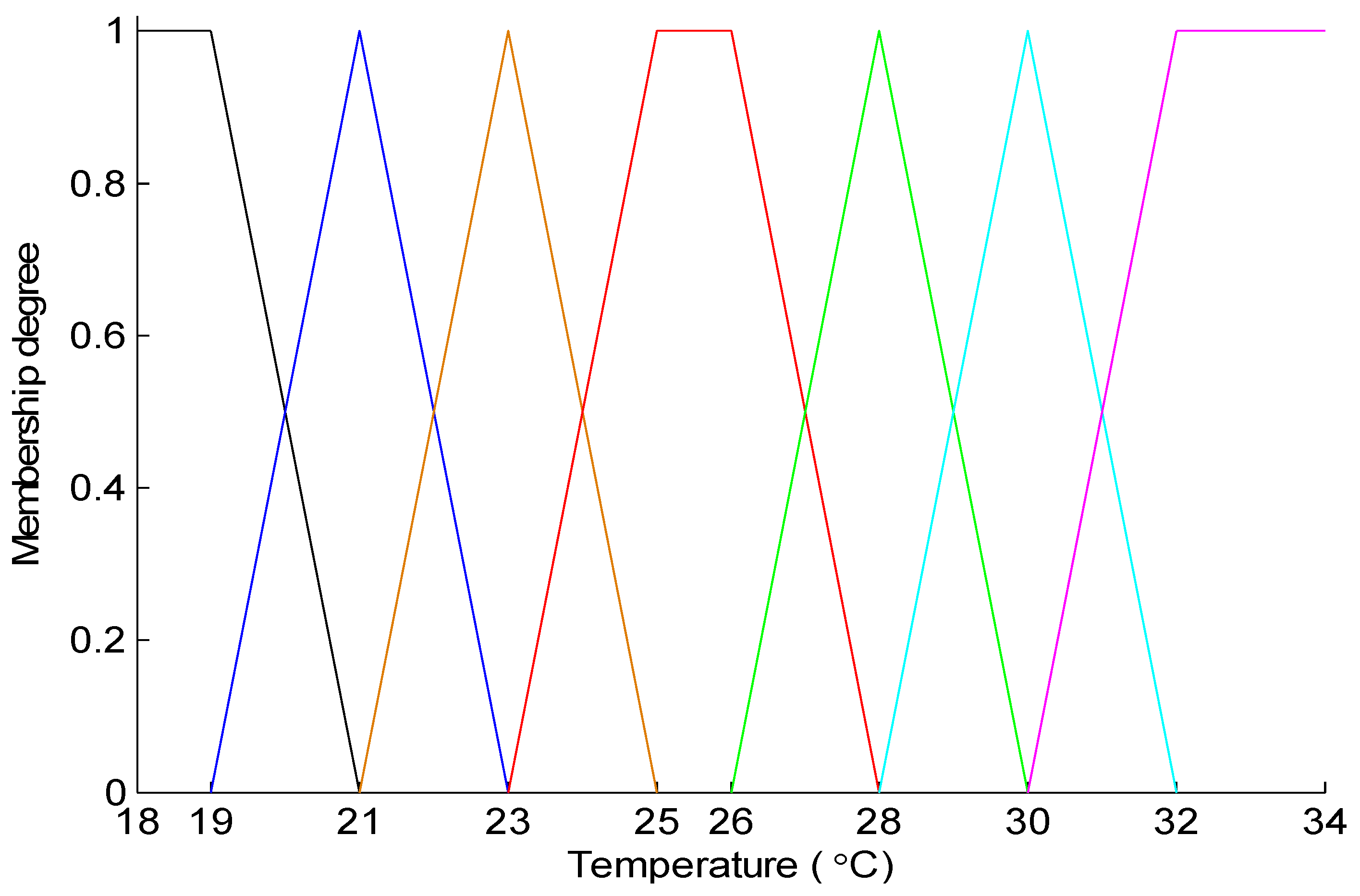
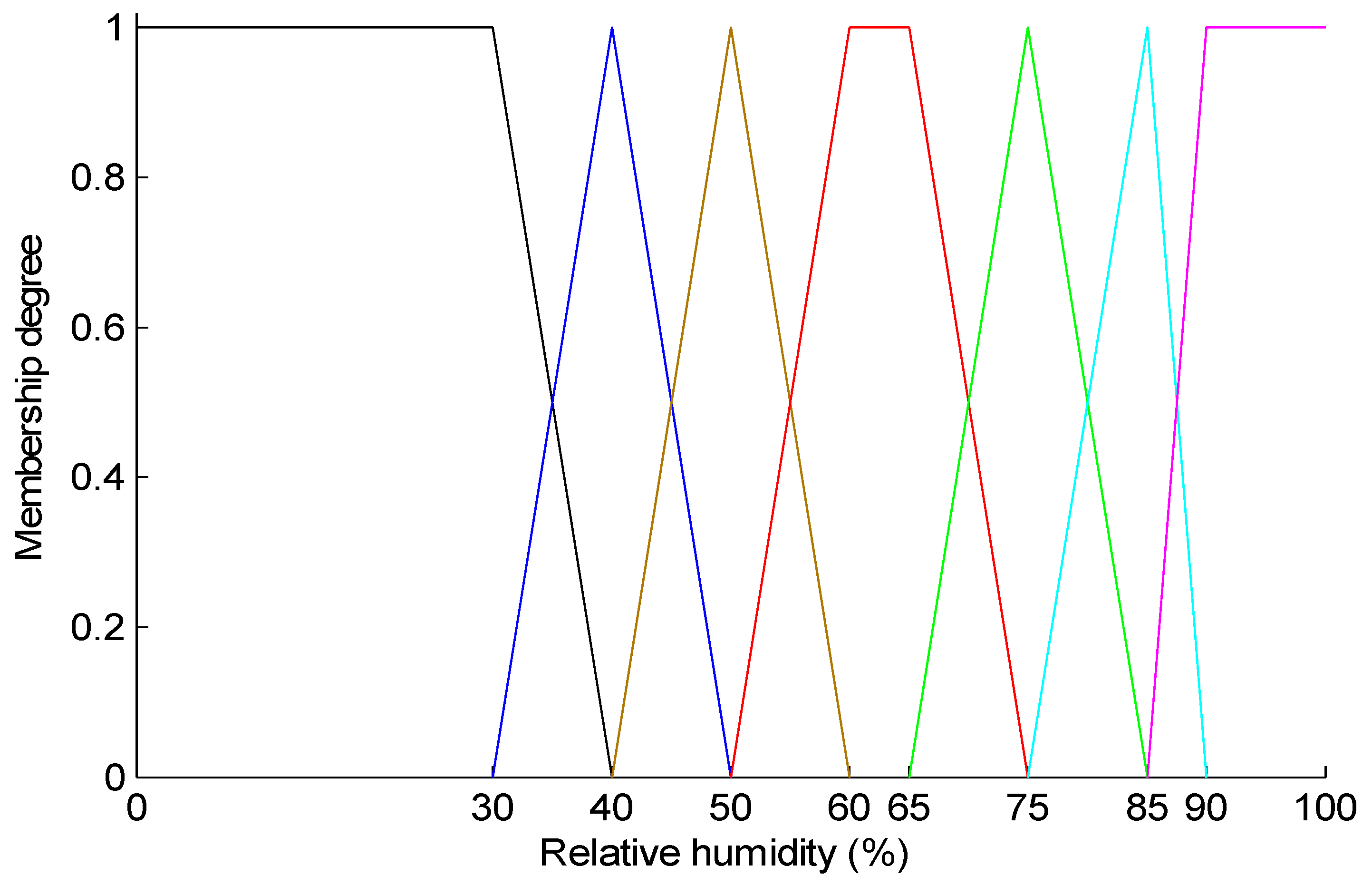
2.2. Decentralized Control Design for Frequency Regulation
2.3. Aggregation of Air Conditioners’ Response
- (1)
- (2)
- To attract more electricity users to participate in active load control, a power grid can design various incentive tools. Incentive-based demand response programs have been carried out in recent years [44,45,46]. Users can contract with the power grid on the compensation and award packages for their comfort loss and contributions for the power grid.
- (3)
- Conventionally, generating units supply spinning reserves and non-spinning reserves for the power system. At demand peak periods, the cost of maintaining high reserve level is very large. Air conditioners are capable of providing reserves with much lower cost than generating units. The economic saving through the proposed strategy can be quantified by the value of reduced reserve capacity procured from the generation side.
3. Power System Dynamics Model
3.1. Dynamical Model of Generating Units
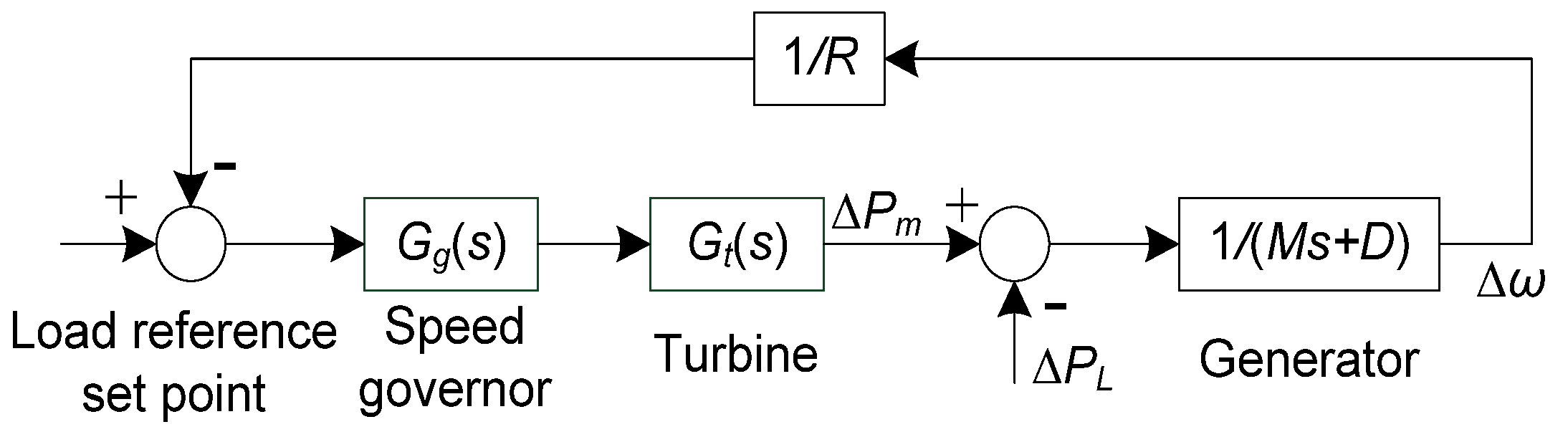
3.2. Network Model
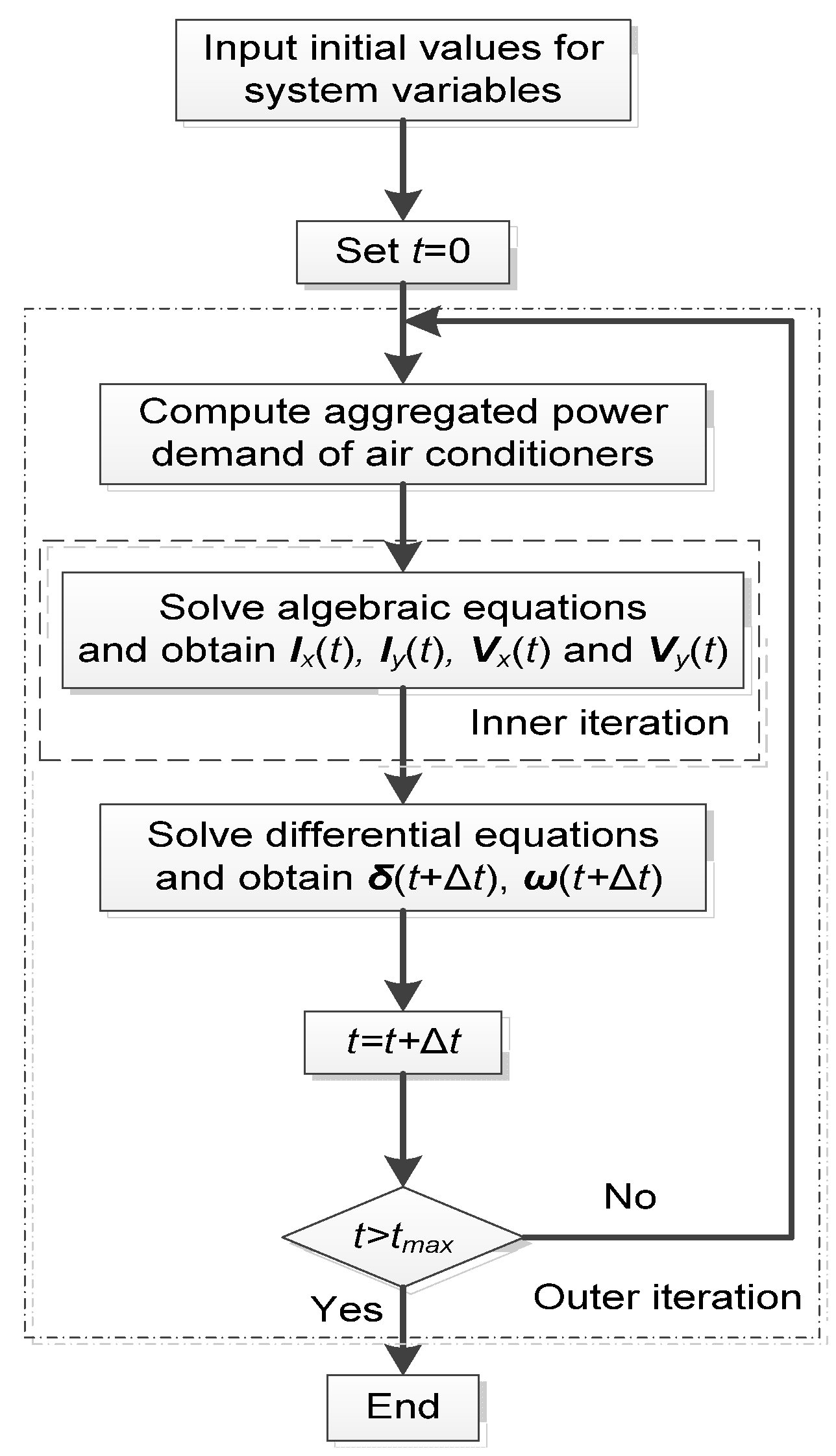
3.3. Solving Dynamics
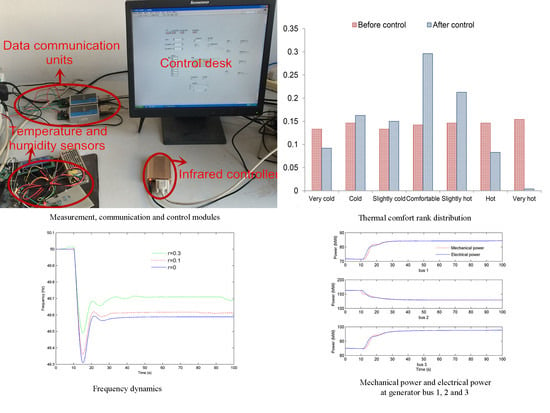
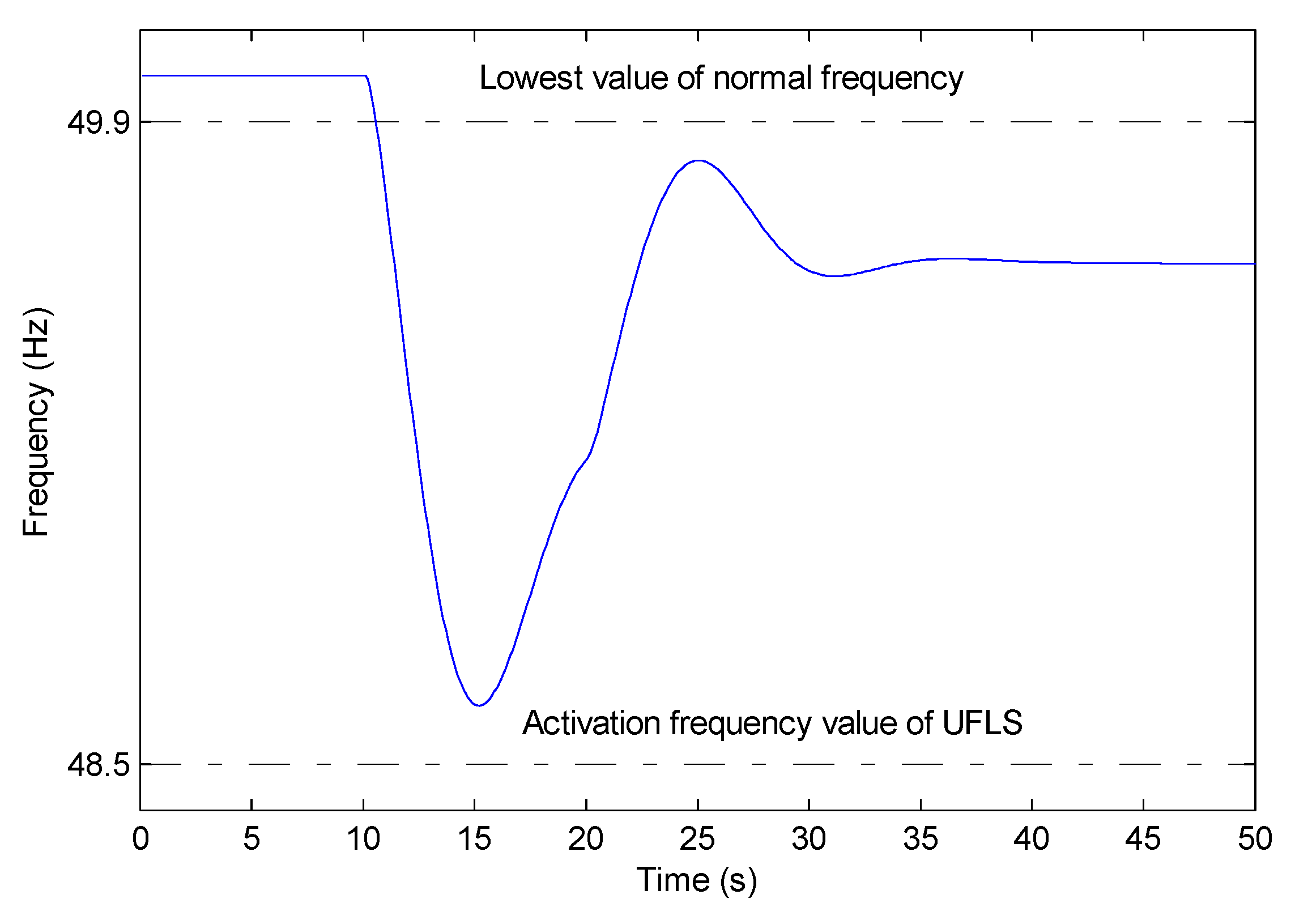
4. Case Studies
4.1. Experimental Results of Decentralized Control Design
| Weights | Relative humidity influence ranks | ||
|---|---|---|---|
| Small | Medium | Large | |
| λ1 | 0.9 | 0.8 | 0.6 |
| λ2 | 0.1 | 0.2 | 0.4 |


| Thermal comfort ranks | Very cold | Cold | Slightly cold | Comfortable | Slightly hot | Hot | Very hot |
|---|---|---|---|---|---|---|---|
| Before control | 0.133 | 0.146 | 0.133 | 0.142 | 0.146 | 0.146 | 0.154 |
| After control | 0.092 | 0.1625 | 0.150 | 0.296 | 0.2125 | 0.083 | 0.004 |
4.2. Simulation Results of Test Power System

| Parameters | Values (s) | Parameters | Values(p. u.) |
|---|---|---|---|
| TG | 0.2 | D | 1 |
| TRH | 7 | R | 0.05 |
| TCH | 0.3 | FHP | 0.3 |
| M | 10 |
| Frequency (Hz) | Ratio of air conditioning demand in load at bus 8 | |||||
|---|---|---|---|---|---|---|
| r = 0 | r = 0.1 | r = 0.2 | r = 0.3 | r = 0.4 | r = 0.5 | |
| Lowest point | 49.31 | 49.36 | 49.45 | 49.49 | 49.56 | 49.64 |
| Steady state | 49.59 | 49.62 | 49.68 | 49.71 | 49.73 | 49.81 |

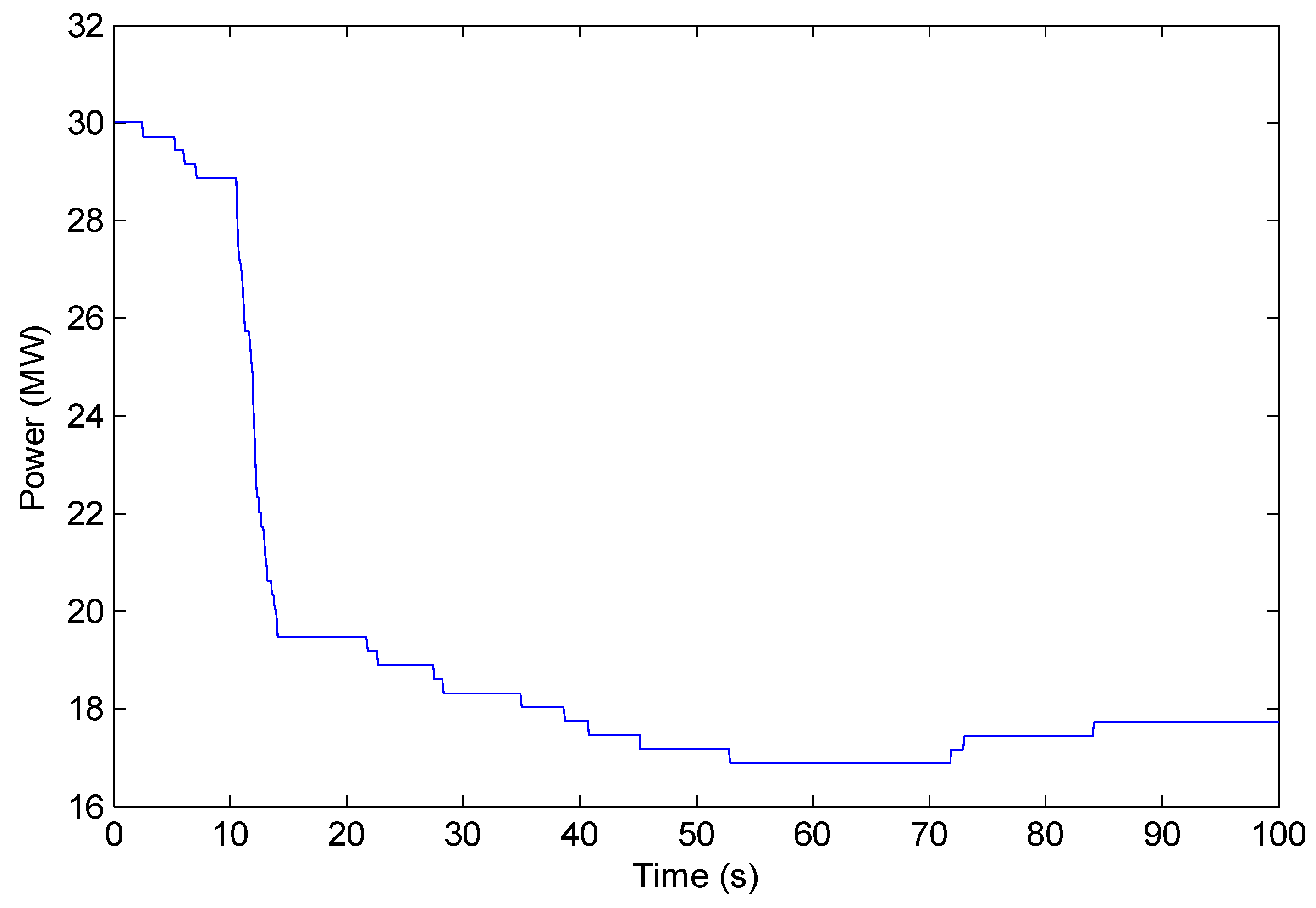
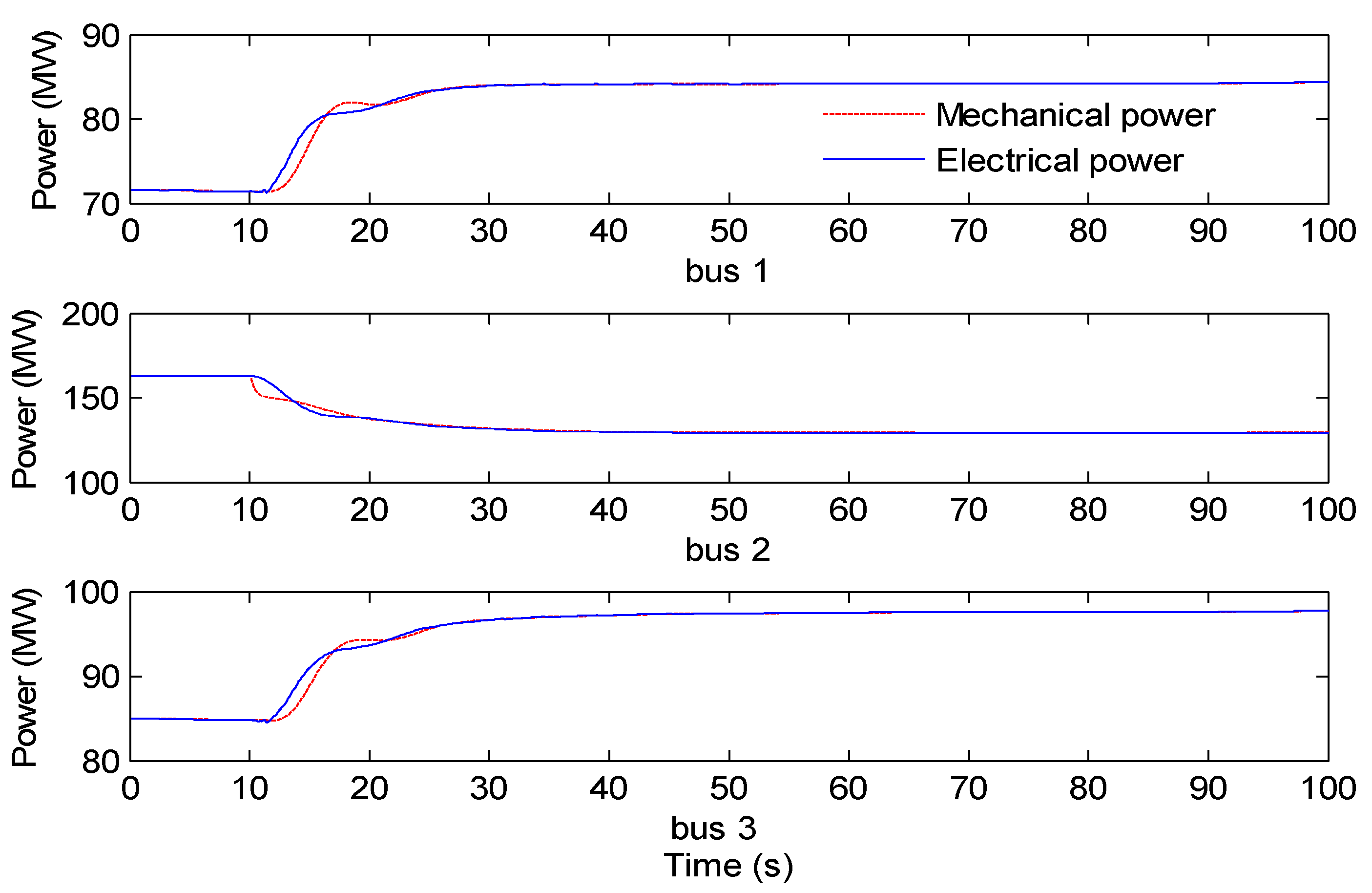
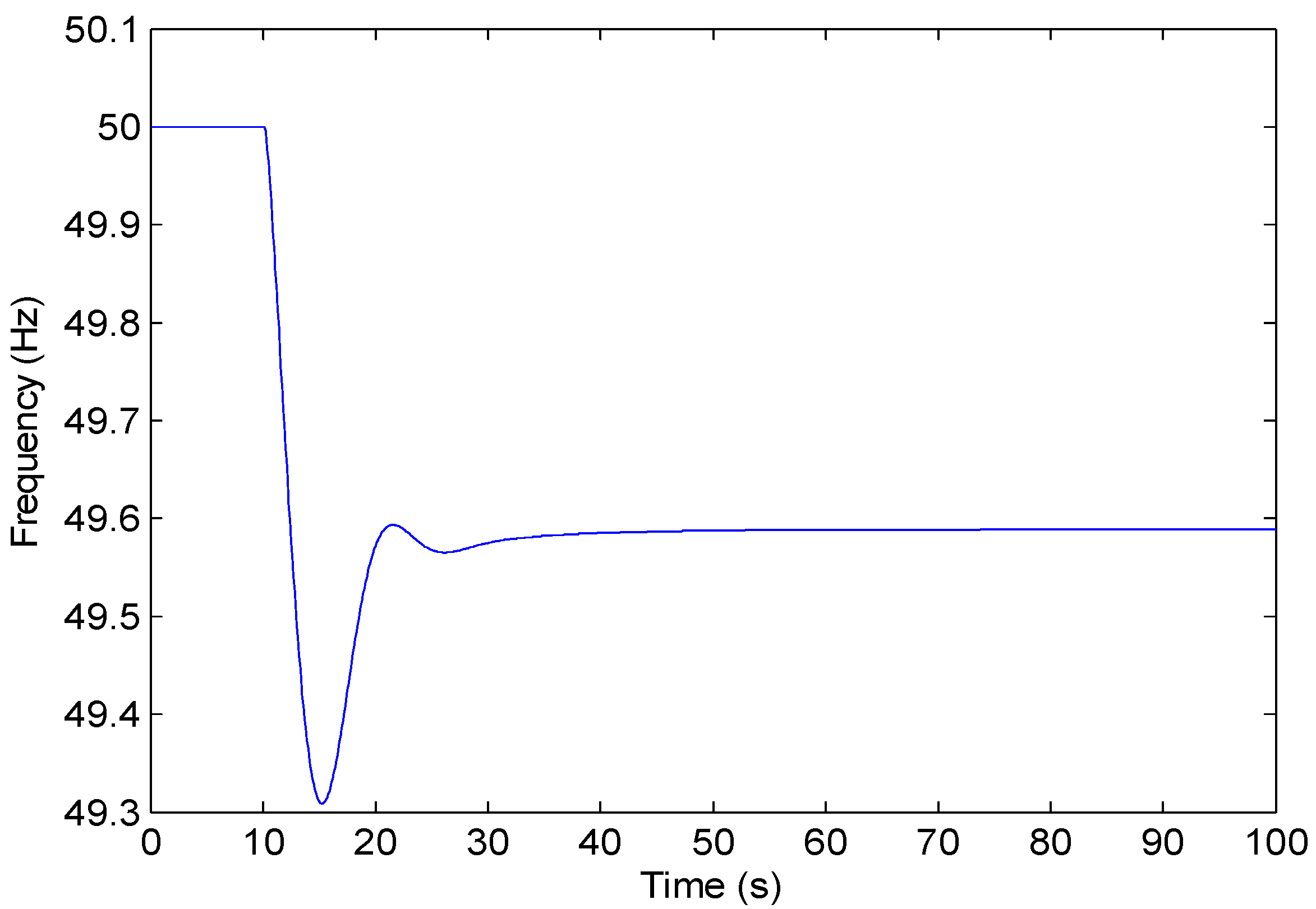
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Thermodynamics Model for Air-Conditioned Space
| Parameters | Expectation | Variance |
|---|---|---|
| Cew | 1.875 MJ/°C | 0.03 MJ/°C |
| Cin | 1.2 MJ/°C | 0.03 MJ/°C |
| Ciw | 3.1 MJ/°C | 0.05 MJ/°C |
| Rgs | 0.08 °C/W | 0.0002 °C/W |
| Riw | 0.01 °C/W | 0.00002 °C/W |
| Rew | 0.028 °C/W | 0.00002 °C/W |
| Rcew | 0.005 °C/W | 0.00002 °C/W |
| Parameters | Range (°C) | Parameters | Range (W) |
|---|---|---|---|
| Xext | [25,28] | Peq | [490,510] |
| Xin | [18,33] | Pe-w | [190,210] |
| Xiw | [20,30] | PHVAC | [2500,3000] |
| Xew | [24,27] | ||
| Xadj-r | [20,30] |
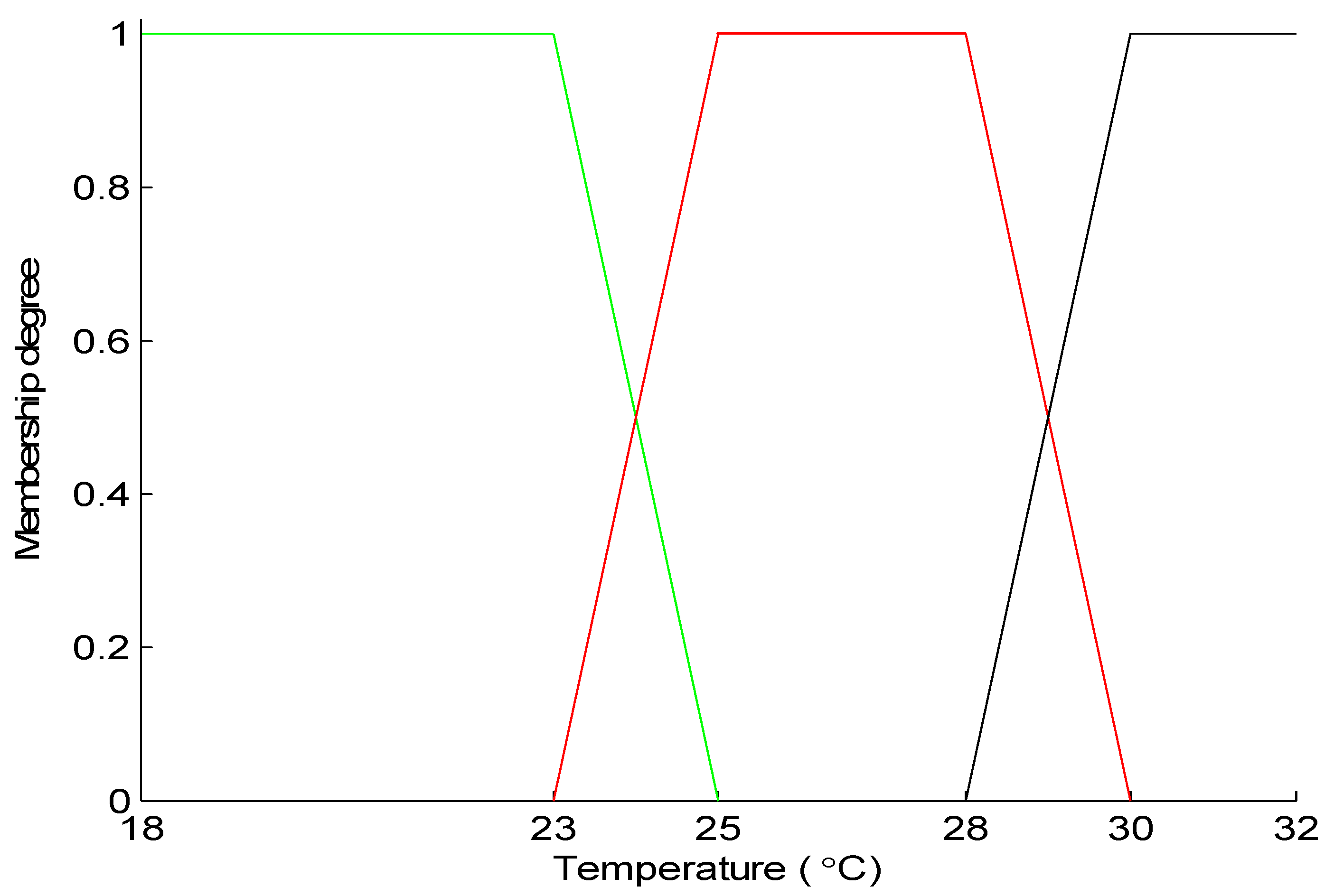
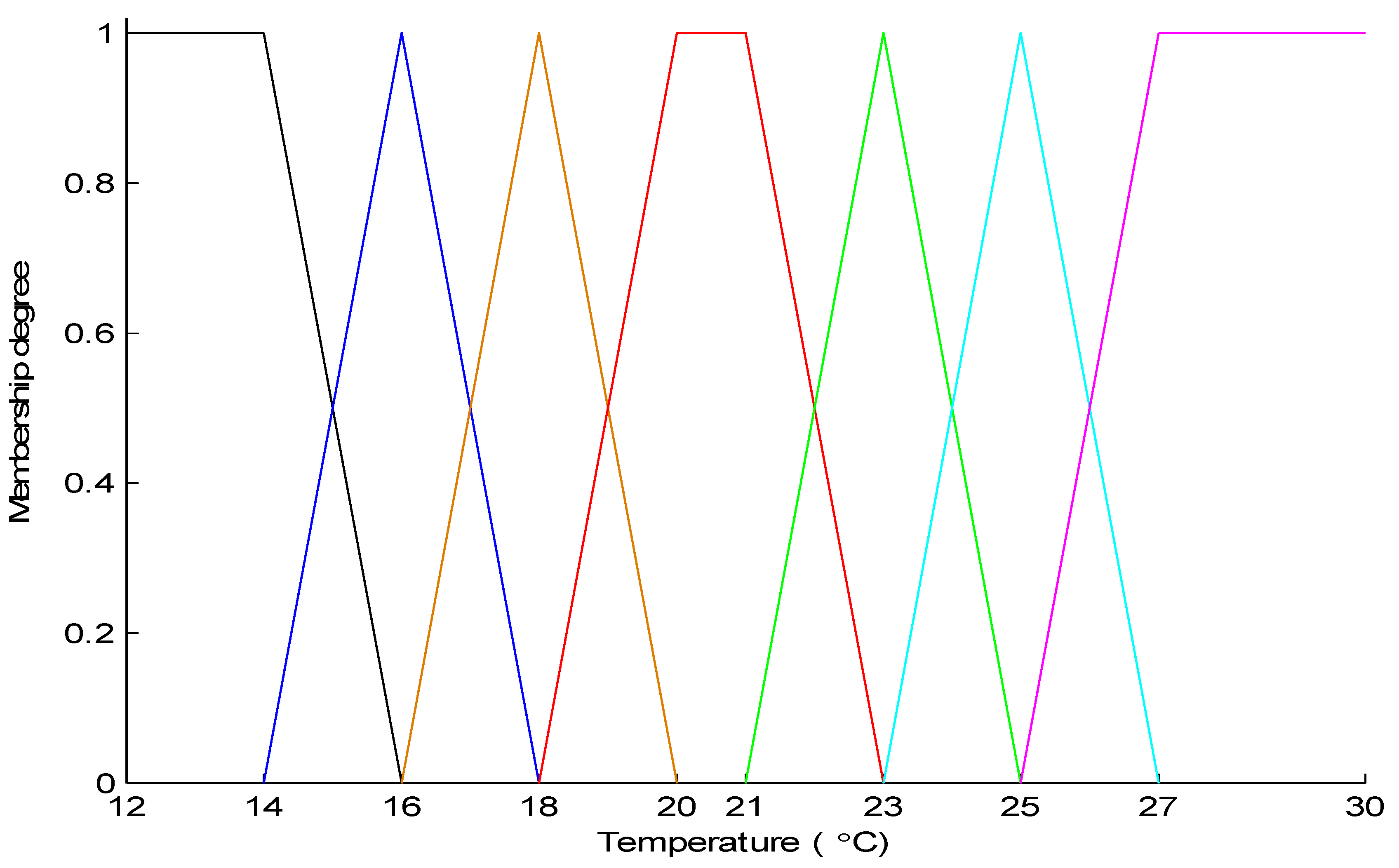
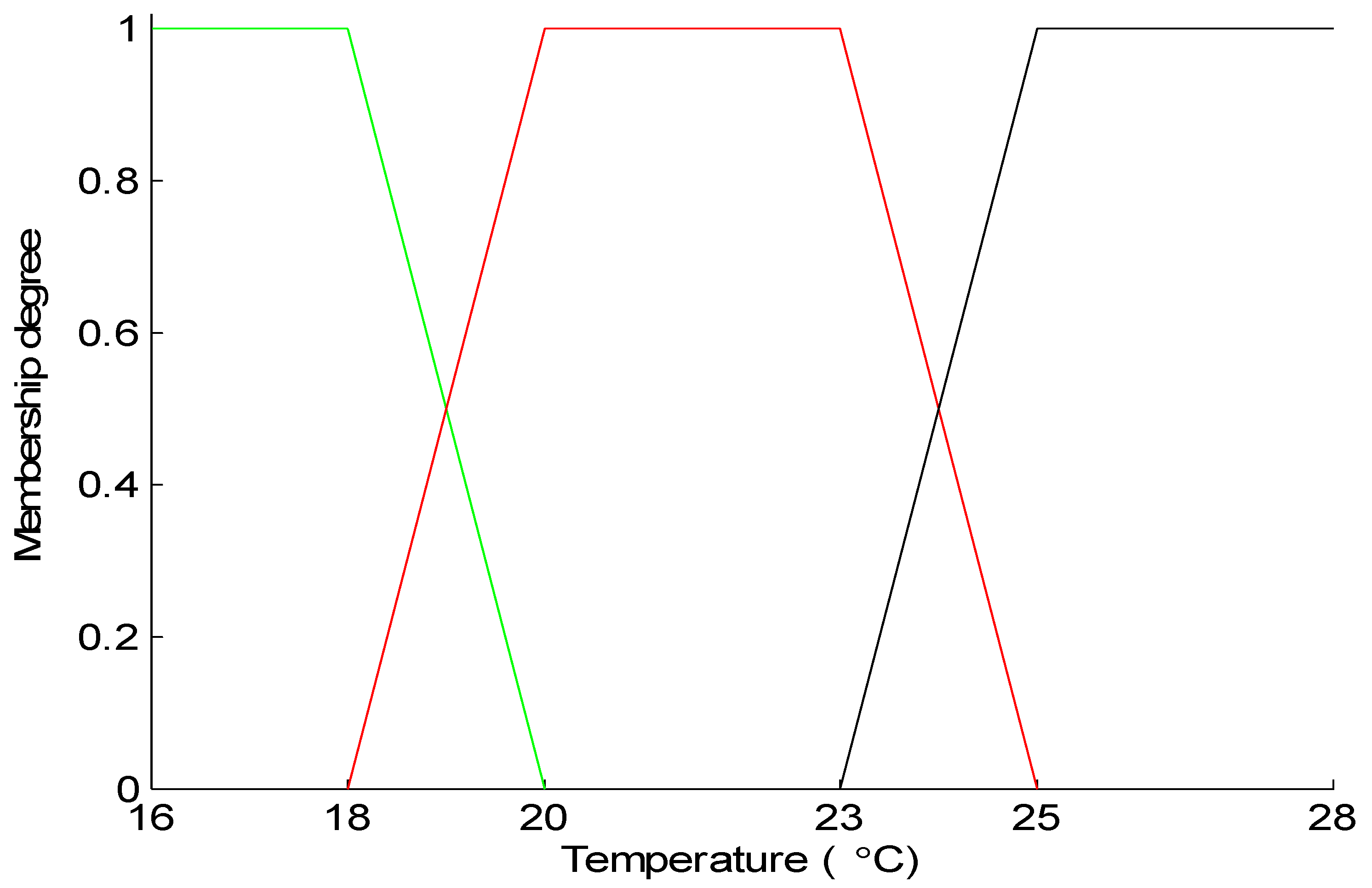
Appendix B. Thermal Membership Functions in Winter
References
- Wang, X.; Song, Y.; Irving, M. Modern Power System Analysis, 1st ed.; Springer U.S.: New York, NY, USA, 2008. [Google Scholar]
- Wood, A.J.; Wollenberg, B.F. Power Generation, Operation and Control, 2nd ed.; Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Zhao, C.; Ufuk, T.; Low, S. Swing dynamics as primary-dual algorithm for optimal load control. In Proceedings of the IEEE 3rd International Conference on Smart Grid Communications, Tainan, Taiwan, 5–8 November 2012; pp. 570–575.
- Zhao, C.; Ufuk, T.; Low, S. Optimal load control via frequency measurement and neighborhood area communication. IEEE Trans. Power Syst. 2013, 28, 3576–3587. [Google Scholar]
- Ummels, B.C.; Gibescu, M.; Pelgrum, E.; Kling, W.L.; Brand, A.J. Impacts of wind power on thermal generation unit commitment and dispatch. IEEE Trans. Energy Convers. 2007, 22, 44–51. [Google Scholar] [CrossRef]
- Doherty, R.; Mullane, A.; Nolan, G.; Burke, D.J.; Bryson, A.; O’Malley, M. An assessment of the impact of wind generation on system frequency control. IEEE Trans. Power Syst. 2010, 25, 452–460. [Google Scholar] [CrossRef]
- Kayikci, M.; Milanovic, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Kaspirek, M.; Mezera, D.; Jiricka, J. Problems of voltage stabilization in MV and LV distribution grids due to the operation of renewable energy sources. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4.
- Lalor, G.; Mullane, A.; O’Malley, M. Frequency control and wind turbine technologies. IEEE Trans. Power Syst. 2005, 20, 1905–1913. [Google Scholar] [CrossRef]
- Lee, D.J.; Wang, L. Small-signal stability analysis of an autonomous hybrid renewable energy power generation/energy storage system part I: Time-domain simulations. IEEE Trans. Energy Convers. 2008, 23, 311–320. [Google Scholar] [CrossRef]
- Faria, P.; Vale, Z.; Baptista, J. Demand response programs design and use considering intensive penetration of distributed generation. Energies 2015, 8, 6230–6246. [Google Scholar] [CrossRef]
- Douglass, P.J.; Garcia-Valle, R.; Nyeng, P.; Ostergaard, J.; Togeby, M. Smart demand for frequency regulation: Experimental results. IEEE Trans. Smart Grid 2013, 4, 1713–1720. [Google Scholar] [CrossRef]
- Tan, Z.; Li, H.; Ju, L.; Song, Y. An optimization model for large-scale wind power grid connection considering demand response and energy storage systems. Energies 2014, 7, 7282–7304. [Google Scholar] [CrossRef]
- Biegel, B.; Hansen, L.H.; Andersen, P.; Stoustrup, J. Primary control by ON/OFF demand-side devices. IEEE Trans. Smart Grid 2013, 4, 2061–2071. [Google Scholar] [CrossRef]
- Chu, C.M.; Jong, T.L. A novel direct air-conditioning load control method. IEEE Trans. Power Syst. 2008, 23, 1356–1363. [Google Scholar]
- Pedrasa, M.A.A.; Oro, M.M.; Reyes, N.C.R.; Pedrasa, J.R.I. Demonstration of direct load control of air conditioners in high density residential buildings. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 400–405.
- Salehfar, H.; Patton, A.D. Modeling and evaluation of the system reliability effects of direct load control. IEEE Trans. Power Syst. 1989, 4, 1024–1030. [Google Scholar] [CrossRef]
- Xu, Z.; Ostergaard, J.; Togeby, M.; Marcus-Moller, C. Design and modeling of thermostatically controlled loads as frequency controlled reserve. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6.
- Xu, Z.; Ostergaard, J.; Togeby, M. Demand as frequency controlled reserve. IEEE Trans. Power Syst. 2011, 26, 1062–1071. [Google Scholar] [CrossRef]
- Short, J.A.; Infield, D.G.; Freris, L.L. Stabilization of grid frequency through dynamic demand control. IEEE Trans. Power Syst. 2007, 22, 1284–1293. [Google Scholar] [CrossRef]
- Yang, H.; Tang, S.; Zeng, Z.; He, X.; Zhao, R.; Kuroda, M. Demand response of inverter air conditioners and applications in distribution system voltage stability enhancement. In Proceedings of the 2013 International Conference on Electrical Machines and Systems, Busan, Korea, 26–29 October 2013; pp. 954–959.
- Zhang, Y.; Lu, N. Demand-side management of air conditioning cooling loads for intra-hour load balancing. In Proceedings of the 2013 Power & Energy Society on Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6.
- Son, J.Y.; Park, J.H.; Moon, K.D.; Lee, Y.H. Resource-aware smart home management system by constructing resource relation graph. IEEE Trans. Consum. Electron. 2011, 57, 1112–1119. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Afsharnia, S. Electrical demand side contribution to frequency control in power systems: A review on technical aspects. Renew. Sust. Energ. Rev. 2015, 41, 1267–1276. [Google Scholar] [CrossRef]
- Molina-Garcia, A.; Munoz-Benavente, I.; Hansen, A.D.; Gomez-Lazaro, E. Demand-side contribution to primary frequency control with wind farm auxiliary control. IEEE Trans. Power Syst. 2014, 29, 2391–2399. [Google Scholar] [CrossRef]
- Sullivan, M.; Bode, J.; Kellow, B.; Woehleke, S.; Eto, J. Using residential AC load control in grid operations: PG&E’s ancillary service pilot. IEEE Trans. Smart Grid 2013, 4, 1162–1170. [Google Scholar]
- Albert, A.; Rajagopal, R. Thermal profiling of residential energy use. IEEE Trans. Power Syst. 2015, 30, 602–611. [Google Scholar] [CrossRef]
- Southern California Edison (SCE). Program Impact Evaluation of 2004 SCE Energy Smart Thermostat Program Final Report; SCE: Rosemead, CA, USA, 2005. [Google Scholar]
- Keuring Van Elektrotechnische Materialen (KEMA). 2005 Smart Thermostat Program Impact Evaluation; KEMA: San Diego, CA, USA, 2006. [Google Scholar]
- Zhao, C.; Ufuk, T.; Li, N.; Low, S. Design and stability of load-side primary frequency control in power systems. IEEE Trans. Autom. Control 2014, 59, 1177–1189. [Google Scholar] [CrossRef]
- Alajmi, A.F.; Baddar, F.A.; Bourisli, R.I. Thermal comfort assessment of an office building served by under-floor air distribution (UFAD) system-a case study. Build. Environ. 2015, 85, 153–159. [Google Scholar] [CrossRef]
- Nikolaou, T.G.; Kolokotsa, D.S.; Stavrakakis, G.S.; Skias, I.D. On the application of clustering techniques for office buildings’ energy and thermal comfort classification. IEEE Trans. Smart Grid 2012, 3, 2196–2210. [Google Scholar] [CrossRef]
- Hamdi, M.; Lachiver, G. A fuzzy control system based on the human sensation of thermal comfort. In Proceedings of the 1998 IEEE International Conference on IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 487–492.
- Bermejo, P.; Redondo, L.; de la Ossa, L.; Rodriguez, D.; Flores, J.; Urea, C.; Gamez, J.A.; Puerta, J.M. Design and simulation of a thermal comfort adaptive system based on fuzzy logic and on-line learning. Energy Build. 2012, 49, 367–379. [Google Scholar] [CrossRef]
- Ku, K.L.; Liaw, J.S.; Tsai, M.Y.; Liu, T. Automatic control system for thermal comfort based on predicted mean vote and energy saving. IEEE Trans. Autom. Sci. Eng. 2015, 12, 378–383. [Google Scholar] [CrossRef]
- Yan, F.; Li, H.; Wang, L.; Zhou, H. Simulation of indoor dynamic thermal comfort based on CFD. In Proceedings of the 2011 4th International Conference on Intelligent Computation Technology and Automation, Shenzhen, Guangdong, China, 28–29 March 2011; pp. 860–865.
- Malhame, R.; Chong, C.Y. Electric load model synthesis by diffusion approximation of a high-order hybrid-state stochastic system. IEEE Trans. Autom. Control 1985, 30, 854–860. [Google Scholar] [CrossRef]
- Balan, R.; Cooper, J.; Chao, K.M.; Stan, S.; Donca, R. Parameter identification and model based predictive control of temperature inside a house. Energy Build. 2011, 43, 748–758. [Google Scholar] [CrossRef]
- Molina, A.; Gabaldon, A.; Fuentes, J.A.; Alvarez, C. Implementation and assessment of physically based electrical load models: Application to direct load control residential programmes. IET Gener. Transm. Distrib. 2003, 150, 61–66. [Google Scholar] [CrossRef]
- Turner, A.; Chan, T.N.; Gibbs, A.N. A fast reacting power system load shedding management system. In Proceedings of the 9th Conference on the Electric Supply Industry (CEPSI), Hong Kong, China; 1992. [Google Scholar]
- Tang, J.; Liu, J.; Ponci, F.; Monti, A. Adaptive load shedding based on combined frequency and voltage stability assessment using synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 2035–2047. [Google Scholar] [CrossRef]
- Molina-Garcia, A.; Bouffard, F.; Kirschen, D.S. Decentralized demand side contribution to primary frequency control. IEEE Trans. Power Syst. 2011, 26, 411–419. [Google Scholar] [CrossRef]
- Angeli, D.; Kountouriotis, P. A stochastic approach to dynamic demand refrigerator control. IEEE Trans. Control Syst. Technol. 2012, 20, 581–592. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Zhong, H.; Xie, L.; Xia, Q.; Kang, C.; Rahman, S. Multi-stage coupon incentive-based demand response in two-settlement electricity markets. In Proceedings of the 2015 IEEE Power & Energy Society on Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015; pp. 1–5.
- Zhong, H.; Xie, L.; Xia, Q. Coupon incentive-based demand response: Theory and case study. IEEE Trans. Power Syst. 2013, 28, 1266–1276. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Chu, X.; Zhang, W.; Liu, Y. Active Participation of Air Conditioners in Power System Frequency Control Considering Users’ Thermal Comfort. Energies 2015, 8, 10818-10841. https://doi.org/10.3390/en81010818
Zhang R, Chu X, Zhang W, Liu Y. Active Participation of Air Conditioners in Power System Frequency Control Considering Users’ Thermal Comfort. Energies. 2015; 8(10):10818-10841. https://doi.org/10.3390/en81010818
Chicago/Turabian StyleZhang, Rongxiang, Xiaodong Chu, Wen Zhang, and Yutian Liu. 2015. "Active Participation of Air Conditioners in Power System Frequency Control Considering Users’ Thermal Comfort" Energies 8, no. 10: 10818-10841. https://doi.org/10.3390/en81010818
APA StyleZhang, R., Chu, X., Zhang, W., & Liu, Y. (2015). Active Participation of Air Conditioners in Power System Frequency Control Considering Users’ Thermal Comfort. Energies, 8(10), 10818-10841. https://doi.org/10.3390/en81010818