1. Introduction
Modern power systems operate closer to their operation and stability limits. This is because of load demand growth, the open access of transmission network, and economic operation [
1]. Therefore, dynamic security assessment has become increasingly important. Power system transient stability analysis is a fundamental tool for this dynamic security assessment. It determines whether a contingency a power system will reach a new operating point after, and it examines how system values change during transient deviations from an equilibrium following a contingency [
2,
3]. Based on the simulation results from potentially many contingency cases, system operators can take corrective and preventive actions to maintain stable operation of power systems.
A transient stability simulator solves a set of nonlinear differential and algebraic equations (DAEs) representing machines and controllers placed in the power systems, and the power system network, respectively. It utilizes numerical integration methods to estimate dynamic states at the next time step and uses iterative techniques to solve the nonlinear algebraic equations. Numerical integration methods are divided into two main categories: implicit and explicit methods [
4]. Each method has its own advantages and disadvantages in regards to stability and reliability calculations [
5]. Due in part from their ease of implementation, explicit numerical integration methods are widely used in commercial transient stability packages [
6,
7,
8]. However, for a stiff power system in which a wide variety of different time frames exist, explicit numerical integration methods might require very small time steps to avoid numerical instability. Entire simulation with very small time steps would require substantial computation.
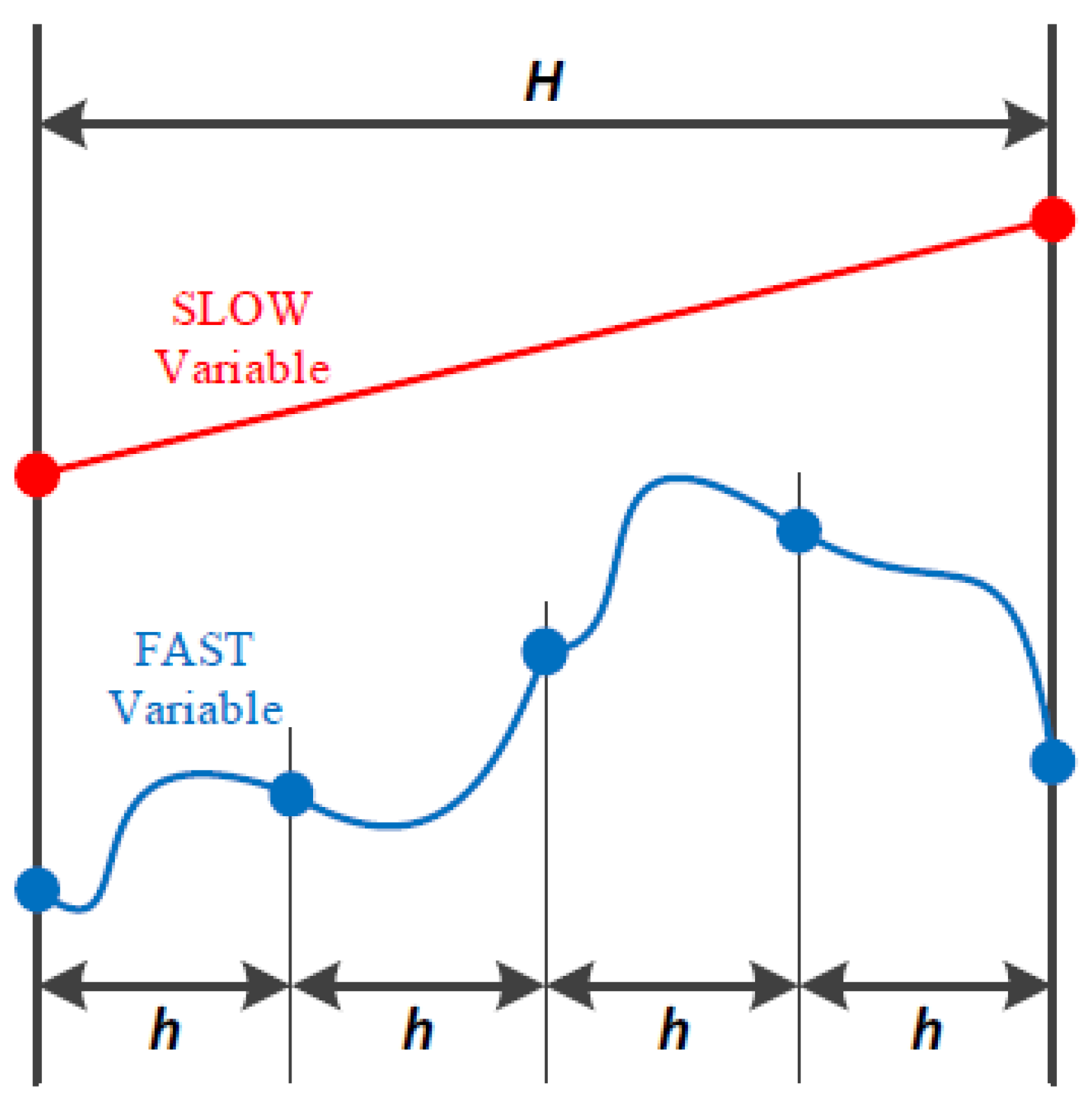
The multi-rate method provides an efficient integration technique for systems exhibiting a wide variety of time responses. The multi-rate method integrates different variables with different time steps [
9]. It uses small time steps, called subintervals, for fast varying variables and larger time steps for more slowly varying ones. The subinterval integration approach, coupled with a longer main time step, allows for the network algebraic equations and slow dynamic equations to be evaluated much less frequently and thus computational benefits can be achieved, in particular for a large power system with very few fast variables. The method was applied to power system transient stability problem for the first time in [
10] and advanced in [
11,
12]. Some widely used transient stability packages employ the multi-rate method [
6,
7,
8].
As modern systems have become increasingly complex such as with the introduction of load dynamics, other power electronic models, and renewable energy sources, the system has become potentially more susceptible to numerical instability issues. Appropriate time steps should be carefully determined to prevent the numerical instability. However, commercial transient stability packages that utilize the multi-rate method often do not provide guidelines or a built-in function to select an appropriate subinterval time step. Instead, they use either a fixed value for all models of a type, or in the case of PowerWorld Simulator, heuristics based on model parameters. The tradeoff is between excessive computation if the interval is too short, and potential numeric instability if it is too long.
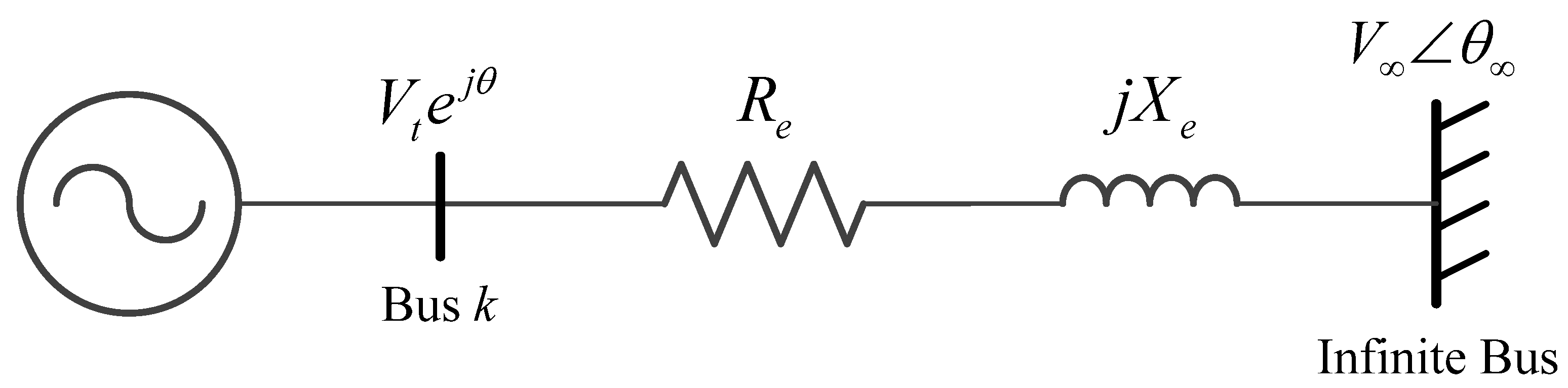
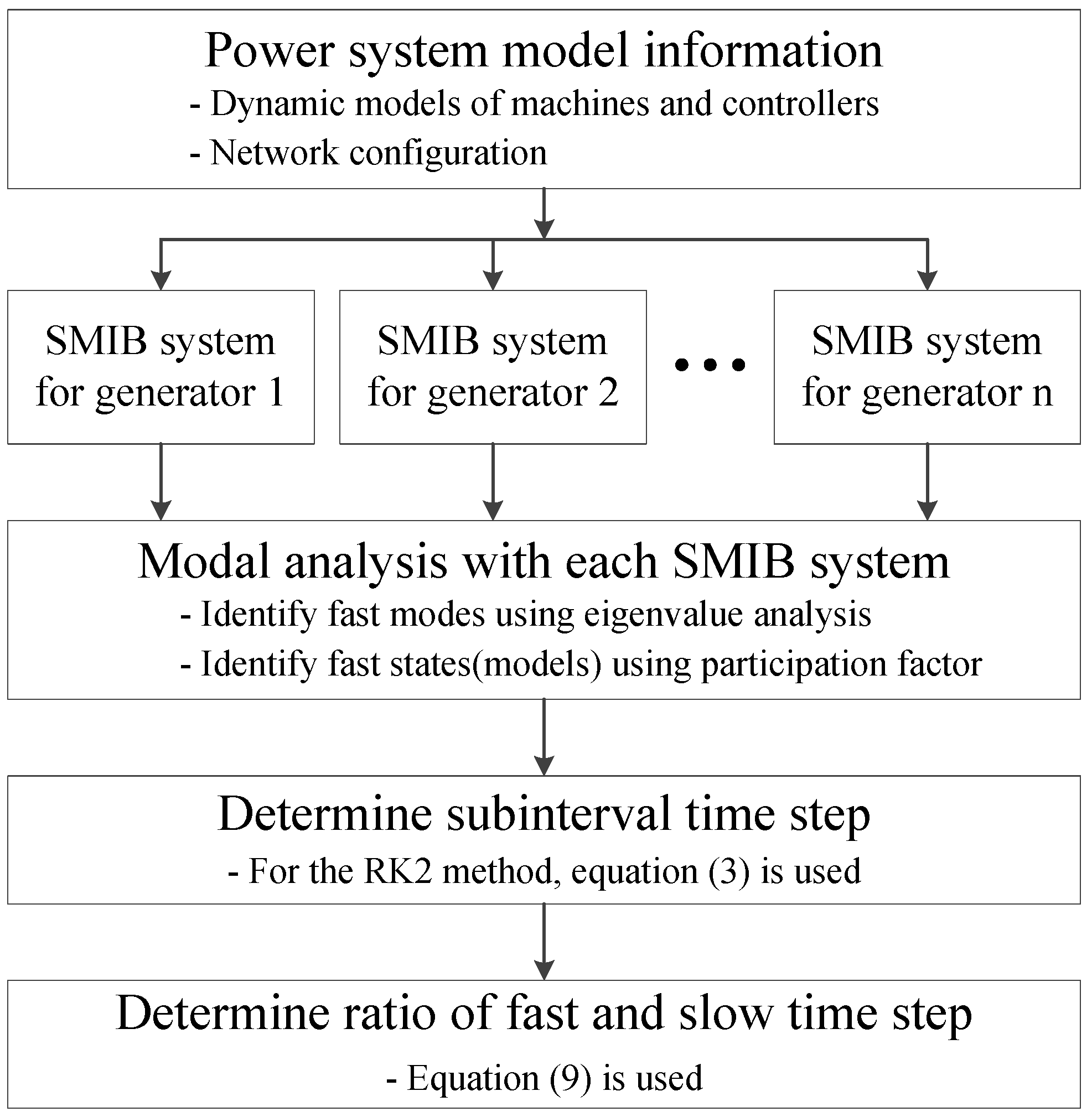
In this paper, a new subinterval selection approach is presented to determine the optimal numerical integration time step for the use with the multi-rate method. An appropriate subinterval can be determined by identifying how fast dynamic states are varying in the considered power system. The proposed approach uses modal analysis for single machine infinite bus (SMIB) models [
3]. It analyzes the SMIB model eigenvalues, and thus fast dynamic states can be recognized. A primary source of fast dynamics in power systems are generators and their controllers. Instead of considering the whole system, the SMIB approach focuses on each generator with its controllers to identify the fast dynamics. Thus, the required computation for modal analysis with the SMIB approach can be quite modest, even for large systems. Depending on the SMIB approach eigenvalues, appropriate subinterval values can be determined to avoid numerical instability issues and to minimize the required computations.
This paper is organized as follows:
Section 2 presents background information including the explicit numerical integration method, the multi-rate method and eigenvalue analysis with a SMIB system. In
Section 3, a problem is defined and a new optimal time step selection method is then proposed.
Section 4 illustrates simulation results with the GSO 37-bus case. The conclusion is made in
Section 5.
4. Case Study
The proposed approach was tested with the PowerWorld Simulator, which provides SMIB eigenvalue analysis and uses a multi-rate numerical integration method [
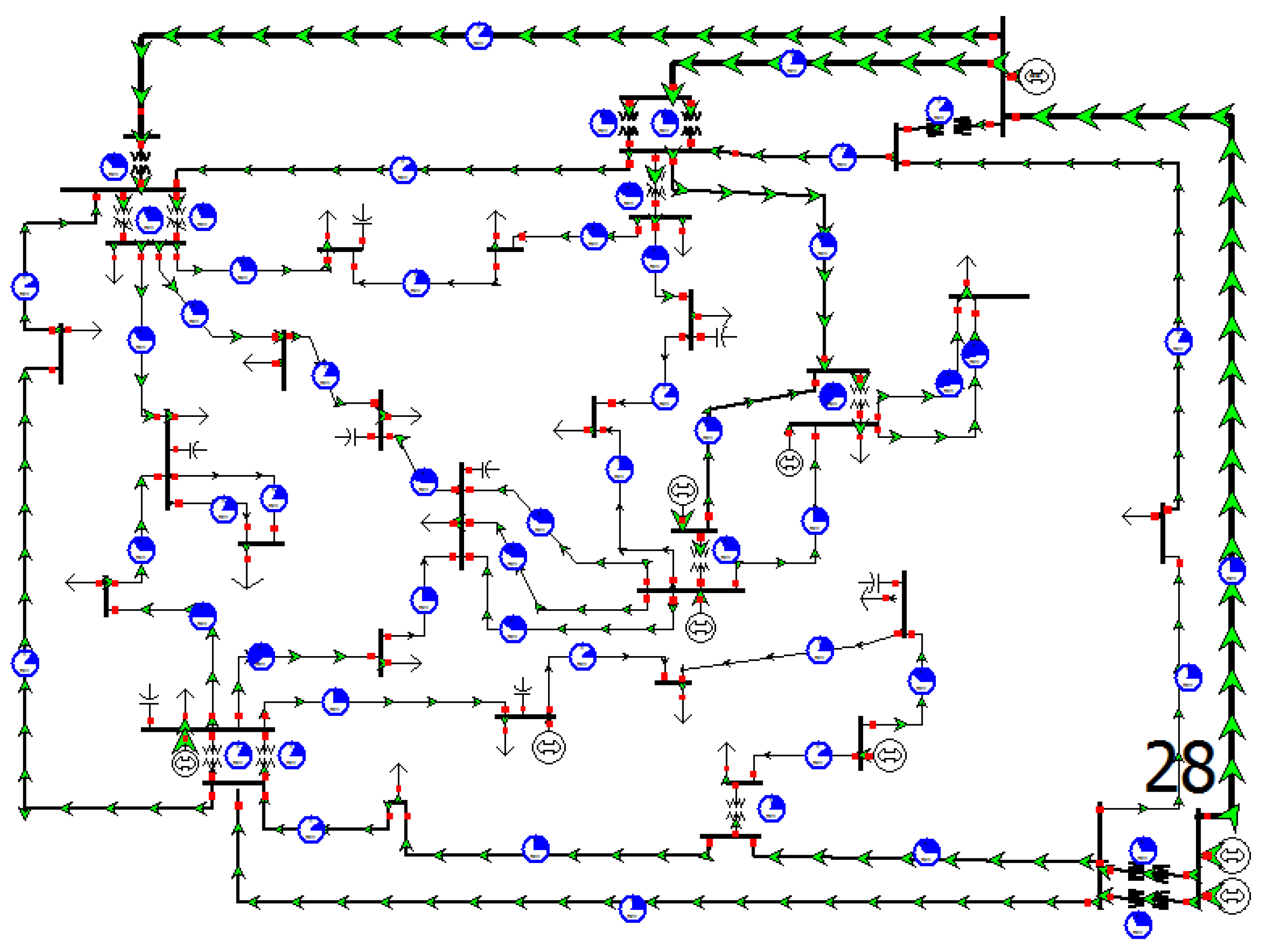
5]. The GSO 37-bus system shown in
Figure 5 is used to demonstrate the proposed method. The case has nine generators, 25 loads and 57 branches [
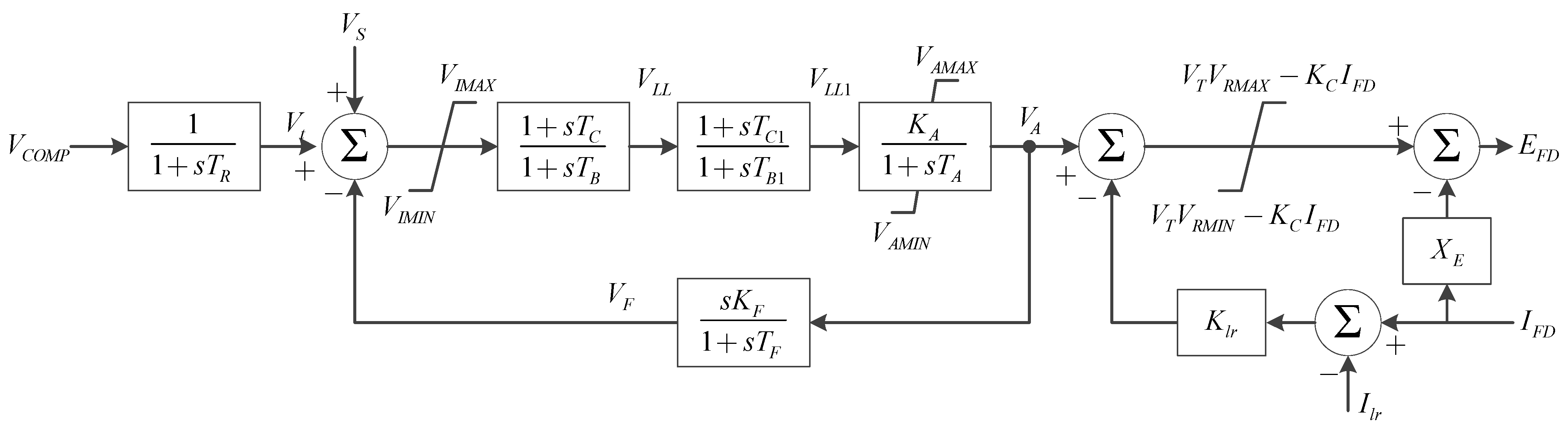
15]. One common exciter, the EXST1 (IEEE Type ST1 excitation system model) shown in
Figure 6, quite commonly introduces very fast modes to the system because fast electronic controllers are incorporated. For test purposes, parameters for each of the EXST1 exciters for the two generators at bus 28 were changed as shown in
Table 2.
Figure 5.
GSO 37-bus system.
Figure 5.
GSO 37-bus system.
Figure 6.
Block diagram of EXST1 exciter.
Figure 6.
Block diagram of EXST1 exciter.
Table 2.
EXST1 Exciter model parameters.
Table 2.
EXST1 Exciter model parameters.
| Tr = 0 | Vimax = 10 | Vimin = −10 | Tc = 1 |
| Tb = 1 | Ka = 150 | Ta = 0.01 | Vrmax = 3.6 |
| Vrmin = 0 | Kc = 0 | Kf = 0.04 | Tf = 0.4 |
| Tc1 = 1 | Tb1 = 1 | Vamax = 99 | Vamin = −99 |
| Xe = 0 | Ilr = 0 | Klr = 0 | |
4.1. SMIB Eigenvalue Analysis
With the test case considered, SMIB systems for all generators were created and modal analysis of each SMIB system was then performed. The results in
Table 3 indicate that two big negative eigenvalues (−1602) are originated from the two generators at bus 28. The participation factors in
Table 4 identify that these modes are solely contributed by exciter dynamic state V
A. Therefore, the required time step for the state V
A to avoid numerical instability can be determined with the real part of eigenvalue information, which represents how much the dynamic state varies.
Table 3.
Single machine infinite bus (SMIB) eigenvalue analysis with the GSO 37-bus case.
Table 3.
Single machine infinite bus (SMIB) eigenvalue analysis with the GSO 37-bus case.
| Bus Number | Generator ID | Max Eigenvalues | Bus Number | Generator ID | Max Eigenvalues |
|---|
| 28 | 1 | −1602 | 54 | 1 | −44 |
| 28 | 2 | −1602 | 53 | 1 | −42 |
| 31 | 1 | −49 | 44 | 1 | −42 |
| 14 | 1 | −45 | 50 | 1 | −38 |
| 48 | 1 | −44 | – | – | – |
Table 4.
Participation factor of a generator at bus 28.
Table 4.
Participation factor of a generator at bus 28.
| Real Part of Eigenvalues | Machine Angle | Machine Speed | Machine Eqp | Machine PsiDp | Machine PsiQpp | Exciter VA | Exciter VF |
|---|
| −1602 | 0 | 0 | 0.0001 | 0 | 0 | 1 | 0.0015 |
| −45 | 0.0178 | 0.0183 | 0 | 0 | 0.9997 | 0 | 0 |
| −32 | 0.0008 | 0.0007 | 0.0511 | 0.9987 | 0.0001 | 0.0001 | 0.0002 |
| −22 | 0 | 0.0017 | 0 | 0 | 0.0002 | 0 | 0 |
| −0.6 | 0.709 | 0.6983 | 0.0329 | 0.0056 | 0.0915 | 0 | 0.0007 |
4.2. Subinterval Step Size
Due to the extremely fast modes (−1602), if a single rate approach was used, the time step for the entire system would need to be just 0.05 cycles to avoid numerical instability; this can be determined with Equation (3) and
Table 1. On the other hand, the use of the multi-rate method can increase the step size by using the subinterval time step only for the dynamic states associated with the fastest modes (or as previously mentioned more commonly for all the states associated with the fast exciter model). When a quarter-cycle is selected as the step size for the entire simulation, the subinterval ratio should be greater than five based on Equation (9). The following equation shows how the ratio can be determined:
4.3. Simulation Comparisons
PowerWorld Simulator has options that allow the user to override the built-in heuristics and directly specify the desired number of subintervals (in powers of two from two up to 128) for specific models. Hence, eight subintervals were chosen here to meet the minimum. In order to validate the performance of the proposed method, simulation comparisons were made by changing the subinterval step ratio. A three-phase bus to ground fault was applied at bus 28, which has the two EXST1 exciter generators. The fault was applied at 1.0 s and cleared at 1.1 s.
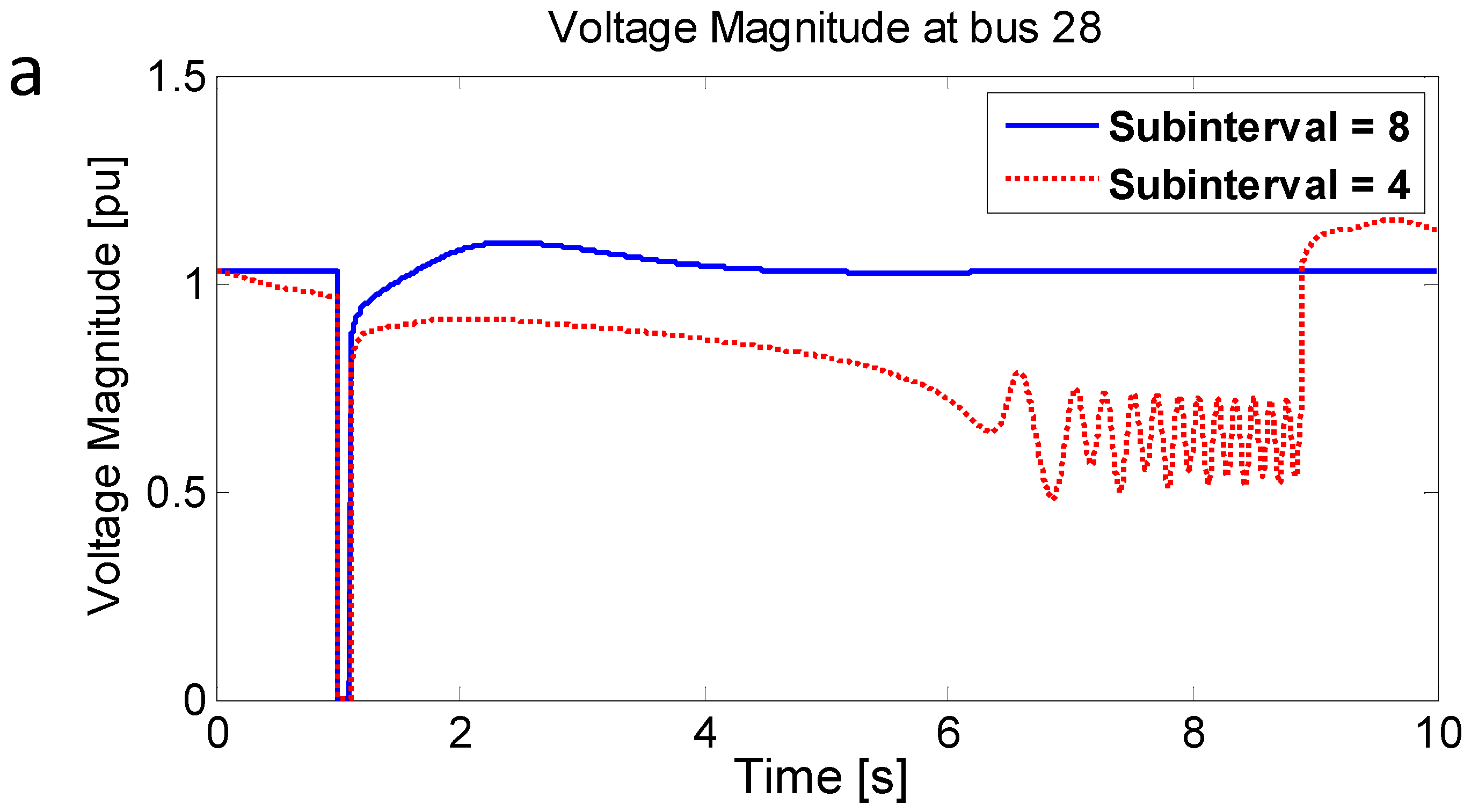
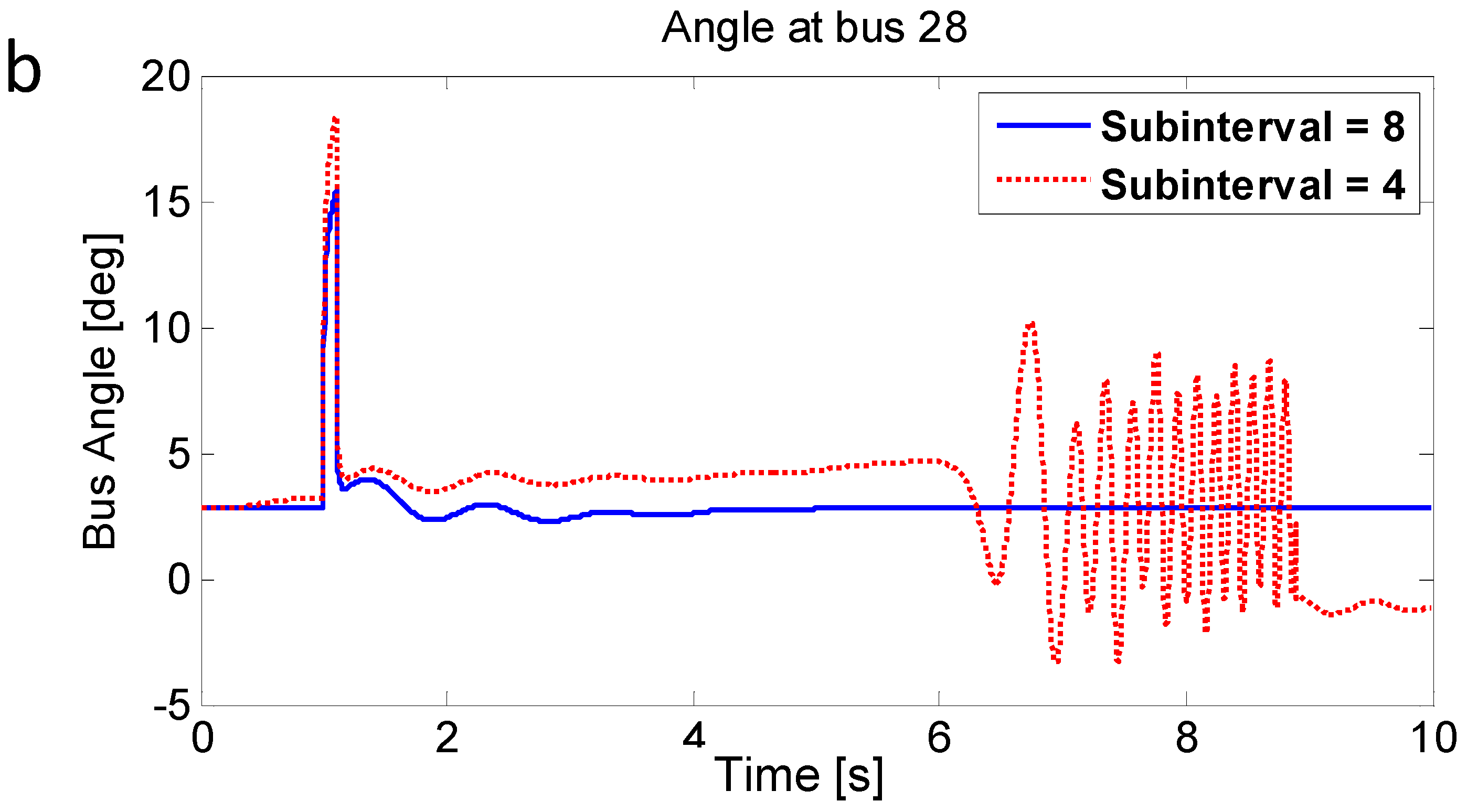
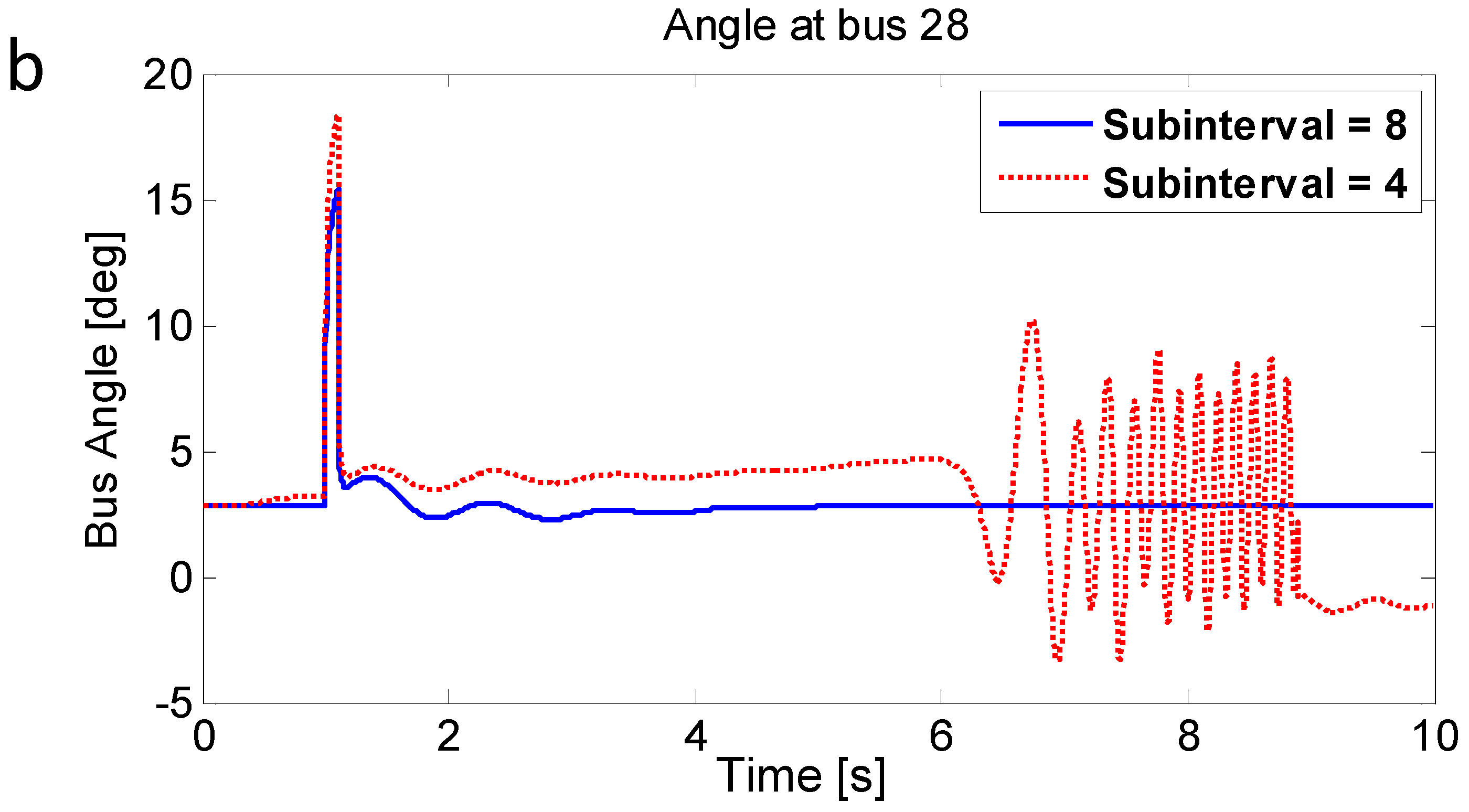
Figure 7 shows the bus voltage magnitude at bus 28 with two different subintervals (eight and four). When the subinterval was set to four, the simulation results show numerical instability even before the fault. This is because the subinterval step size for the fast variables is still bigger than the requirements. However, when the number of subinterval is increased to eight, it shows a stable simulation response. The appropriate step size for the fast ones is correctly estimated with the proposed method.
Figure 7.
Simulation comparison between four and eight subintervals: (a) Voltage magnitude; (b) Angle.
Figure 7.
Simulation comparison between four and eight subintervals: (a) Voltage magnitude; (b) Angle.
Next, a comparison was made between single rate and multi-rate methods. With the single rate method, 0.05 cycles was used for the time step, which is determined based on
Table 1 to prevent numerical instability. For the multi-rate method, a quarter-cycle (0.25 cycles) for the slow dynamics and an eight subinterval option was used, which showed a stable response in
Figure 7. As shown in
Figure 8, the two simulation results are essentially identical.
Table 5 shows the computation time with two different simulation approaches. The computation time is an average of running the simulation ten times and it does not include the required computation for SMIB eigenvalue analysis. Because the SMIBs are only associated with the local machines, they can be computed quite quickly. For example, in benchmarking, the PowerWorld simulator can perform complete SMIB eigenvalue analysis for a 3500 generator system within two seconds; for this nine generator system, the time would be less than a millisecond. The multi-rate method shows excellent computational performance by reducing the simulation time by about 80% compared to the single rate method.
Figure 8.
Simulation comparison with single-rate and multi-rate methods: (a) Voltage magnitude; (b) Angle.
Figure 8.
Simulation comparison with single-rate and multi-rate methods: (a) Voltage magnitude; (b) Angle.
Table 5.
Computational time comparison.
Table 5.
Computational time comparison.
| Method Used | Time Step (Cycle) | Subinterval for Fast States | Computation Time (s) | Ratio of the Computation Time |
|---|
| Singlerate | 0.05 | – | 51.3 | 1 |
| Multirate | 0.25 | 8 | 10.6 | 0.21 |