Analysis and Optimization Design of a Solar Water Heating System Based on Life Cycle Cost Using a Genetic Algorithm
Abstract
:1. Introduction
2. Mathematical Model of SWH System
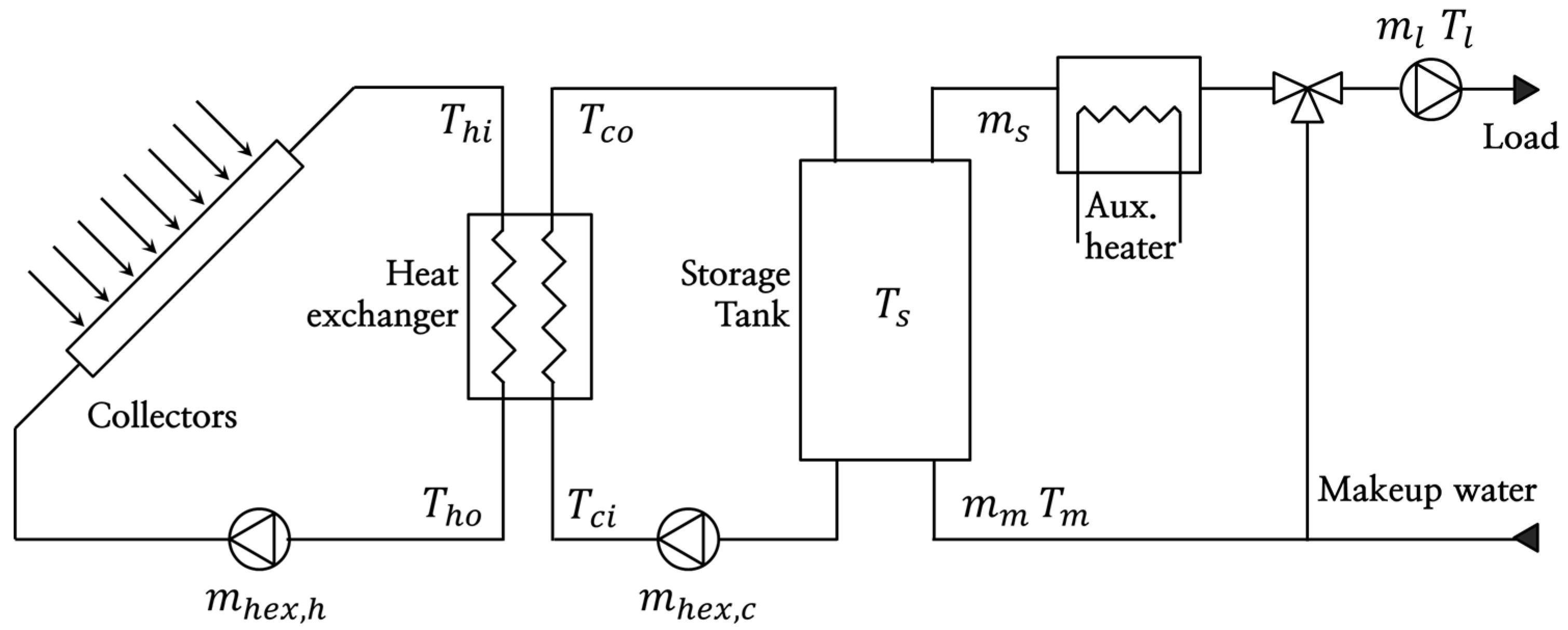
3. Optimization Method of SWH System
3.1. Decision Variable
3.2. Objective Function
3.3. Constraint Conditions
- (a)
- Energy balance:
- (b)
- Solar fraction (penetration of the solar energy):
- (c)
- Available space to install the collector array:
3.4. Optimization Algorithm
4. Simulation Results and Discussion
4.1. Simulation Parameters or Data
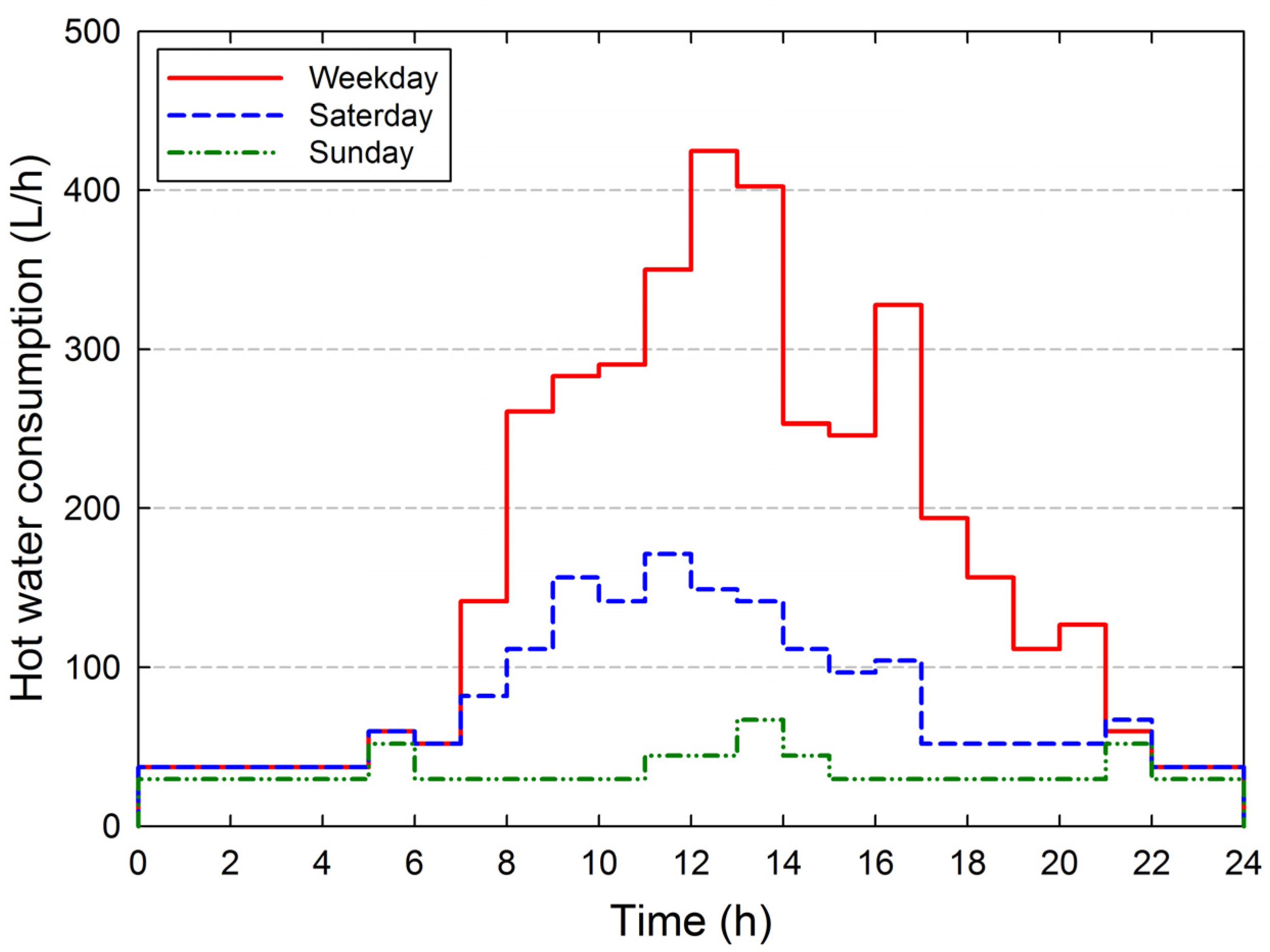
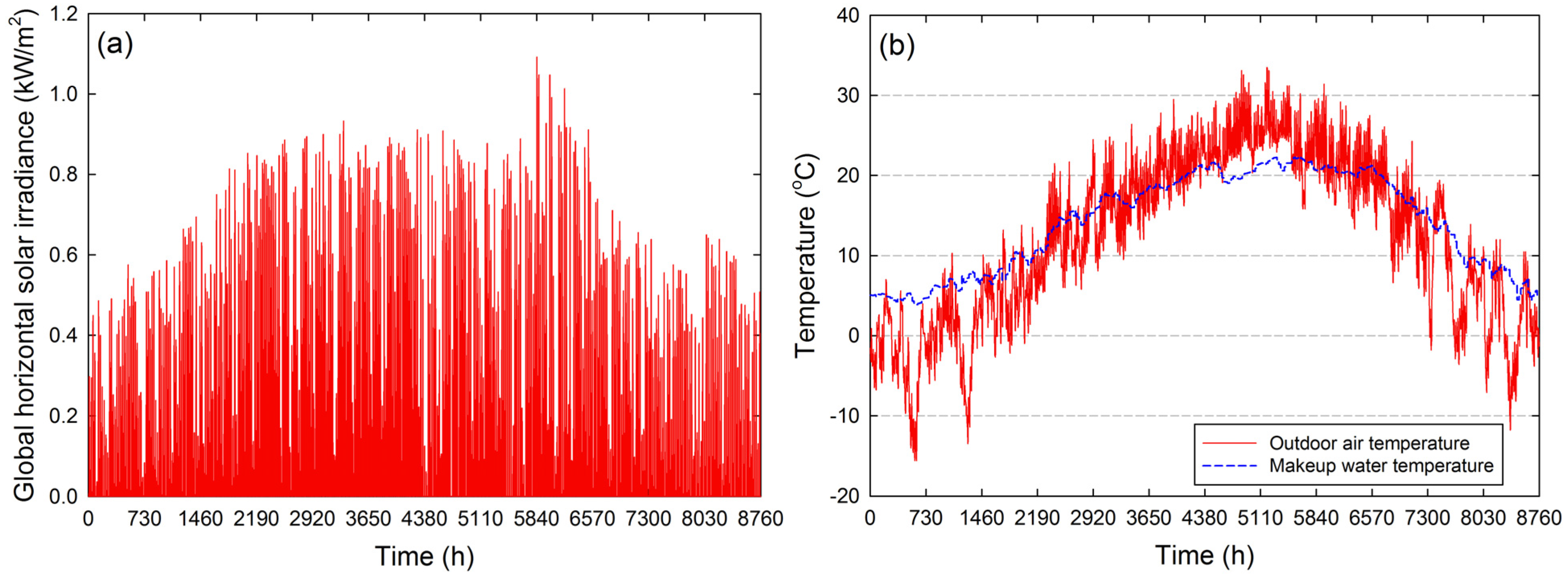
| Parameters | Types | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| Useful gain (kWh/m2 day) | 2.228 | 2.361 | 2.417 | 2.444 | 2.556 |
| Intercept of the collector efficiency (–) | 0.7200 | 0.7208 | 0.7445 | 0.7043 | 0.7203 |
| Negative of the slope of the collector efficiency (W/m2·°C) | 4.09 | 4.7999 | 4.8483 | 4.5368 | 3.9488 |
| Flow rate of the fluid at standard condition (kg/s) | 0.0400 | 0.0373 | 0.0381 | 0.0368 | 0.0533 |
| Overall height (m) | 2.00 | 2.00 | 2.00 | 2.00 | 2.40 |
| Overall width (m) | 1.00 | 1.00 | 1.00 | 0.99 | 1.18 |
| Lifetime (years) | 20 | 20 | 20 | 20 | 20 |
| Purchase cost (1,000 KRW/ea.) | 520 | 530 | 545 | 540 | 820 |
| Parameters | Types | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Tank volume (m3) | 0.44 | 0.96 | 1.72 | 2.65 | 3.76 | 4.91 | 5.54 | 6.21 | 6.92 | 9.58 |
| Heat loss coefficient (W/°C) | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Overall height (m) | 1.22 | 1.22 | 1.52 | 2.00 | 2.44 | 2.44 | 2.44 | 2.44 | 3.05 | 3.05 |
| Overall diameter (m) | 0.68 | 1.00 | 1.20 | 1.30 | 1.40 | 1.60 | 1.70 | 1.80 | 1.70 | 2.00 |
| Lifetime (years) | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Purchase cost (1,000,000 KRW/ea.) | 6.60 | 7.15 | 9.49 | 10.73 | 12.65 | 15.88 | 17.33 | 18.02 | 18.98 | 24.20 |
| Parameters | Types | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Rated heating capacity (kW) | 15.12 | 18.61 | 23.26 | 29.08 | 34.89 | 58.15 | 81.41 | 116.30 |
| Rated efficiency (%) | 83 | 84 | 85 | 86 | 86 | 82 | 83 | 83 |
| Lifetime (years) | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Purchase cost (1000 KRW/ea.) | 807 | 844 | 909 | 964 | 1,039 | 2,291 | 2,565 | 3,207 |
| Parameters | Value |
|---|---|
| Slope of collector array (°) | 35 |
| Azimuth of collector array (°) | 0 |
| Meridian altitude in winter season (°) | 29 |
| Desired hot water temperature (°C) | 60 |
| Maximum allowable storage tank temperature (°C) | 100 |
| Temperature of the environment surrounding the storage tank (°C) | 20 |
| Specific heat of collector fluid (J/kg·°C) | 3560 |
| Specific heat of water (J/kg·°C) | 4180 |
| Density of collector fluid (kg/m3) | 1043 |
| Density of water (kg/m3) | 1000 |
| Product of the overall heat transfer coefficient and area of a heat exchanger (W/°C) | 3000 |
| Maximum number of collectors in series (ea.) | 6 |
| Project lifetime (years) | 40 |
| Real discount rate (%) | 2.91 |
| Nominal interest rate (%) | 6.00 |
| Inflation rate (%) | 3.00 |
| Electricity cost escalation rate (%) | 4.00 |
| Gas cost escalation rate (%) | 4.00 |
| Maximum capacity available to receive the subsidy cost (m2) | 500 |
| Area available to install solar collectors (m2) | 600 |
| Supplementary cost ratio against the purchase cost (%) | 30 |
| Maintenance cost ratio against the initial cost (%) | 1.5 |
| Subsidy cost ratio against the initial cost (%) | 50 |
| Classification | Value | ||
|---|---|---|---|
| Electricity | Basic charge | 6160 | |
| Energy charge (KRW/kWh) | Summer (June, July and August) | 105.7 | |
| Spring/Fall (March, April, May, September, and October) | 65.2 | ||
| Winter (November, December, January and February) | 92.3 | ||
| Natural gas | Energy charge (KRW/MJ) | Summer (May, June, July, August and September) | 19.26 |
| Spring/Fall (April, October and November) | 19.28 | ||
| Winter (December, January, February and March) | 19.46 | ||
4.2. Optimization Results of the Base Case
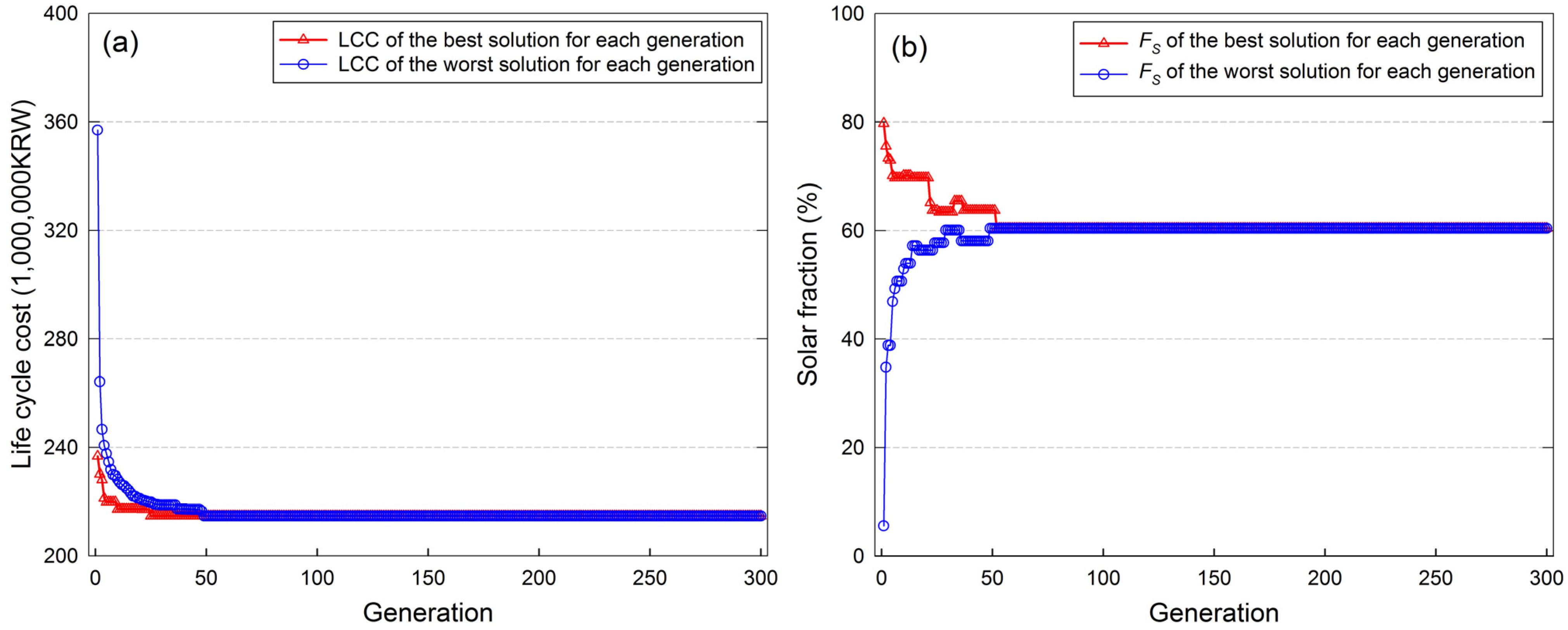
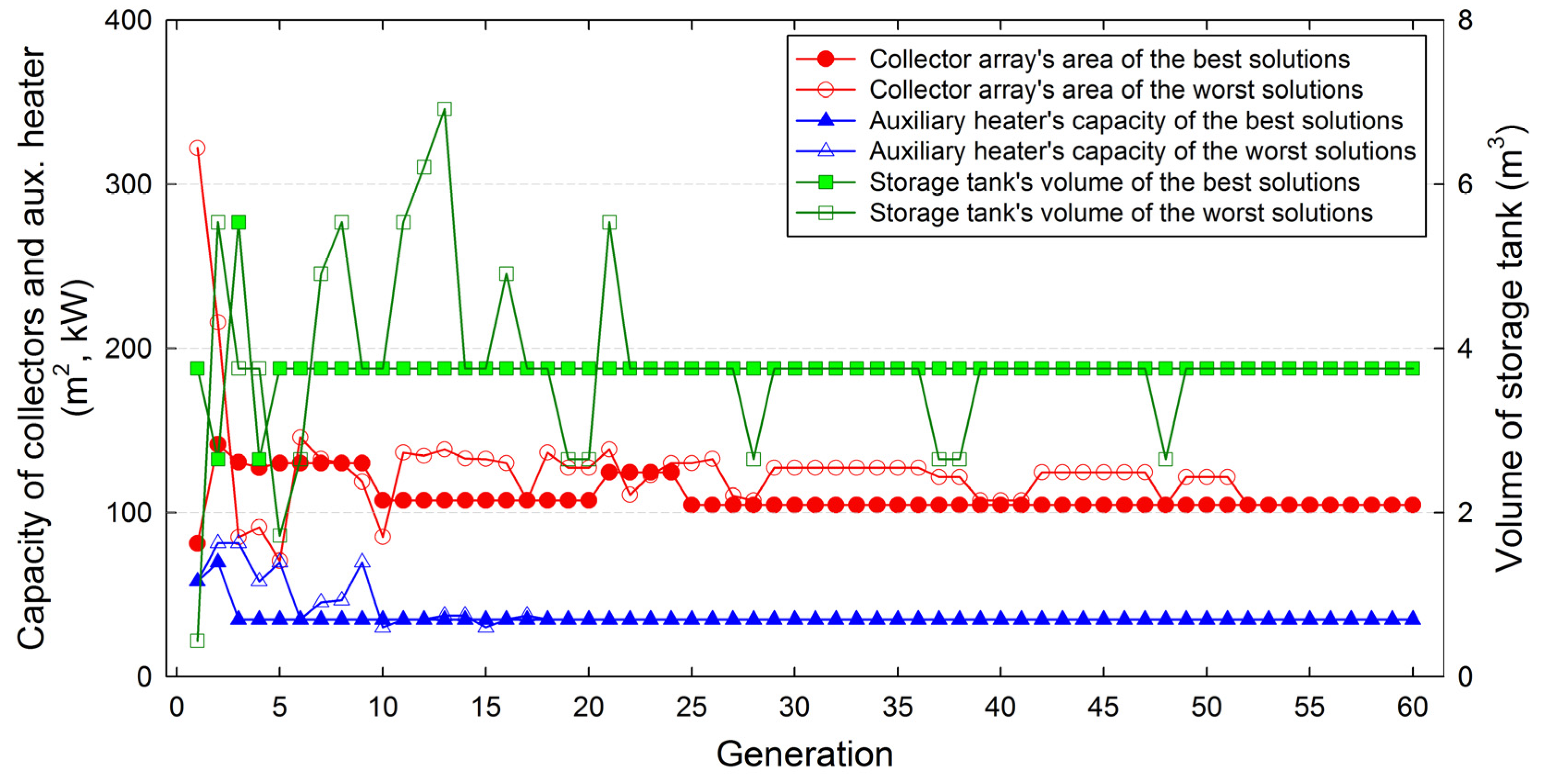
| Variable | Description | Value |
|---|---|---|
| Type of the solar collector (–) | 4 | |
| Number of the solar collectors (ea.) | 37 | |
| Type of the storage tank (–) | 4 | |
| Type of the auxiliary heater (–) | 4 | |
| Number of the auxiliary heaters (ea.) | 1 | |
| Total area of the solar collector (m2) | 104.71 | |
| Volume of the storage tank (m3) | 3.76 | |
| Capacity of the auxiliary heaters (kW) | 34.89 | |
| Installation area of the solar collectors (m2) | 194.3 | |
| Peak hot water load (kW) | 27.35 | |
| Annual hot water load (kWh/year) | 60,218 | |
| Annual solar irradiance on the collector array (kWh/year) | 137,495 | |
| Annual useful heat gain of the collector array (kWh/year) | 39,986 | |
| Annual solar energy supplied to the storage tank (kWh/year) | 37,332 | |
| Annual heat loss of the storage tank (kWh/year) | 752 | |
| Annual discharged heat from the storage tank (kWh/year) | 4 | |
| Annual solar energy supplied by the storage tank (kWh/year) | 36,386 | |
| Annual auxiliary energy supplied by the heaters (kWh/year) | 23,832 | |
| Annual LNG consumption (m3/year) | 2562 | |
| Annual electricity consumption (kWh/year) | 1413 | |
| Annual solar fraction (%) | 60.42 | |
| Initial cost (1000 KRW) | 57,238 | |
| Maintenance cost (1000 KRW) | 20,129 | |
| Replacement cost (1000 KRW) | 41,302 | |
| Energy cost (1000 KRW) | 124,616 | |
| Subsidy cost (1000 KRW) | 28,619 | |
| Life cycle cost (1000 KRW) | 214,666 |
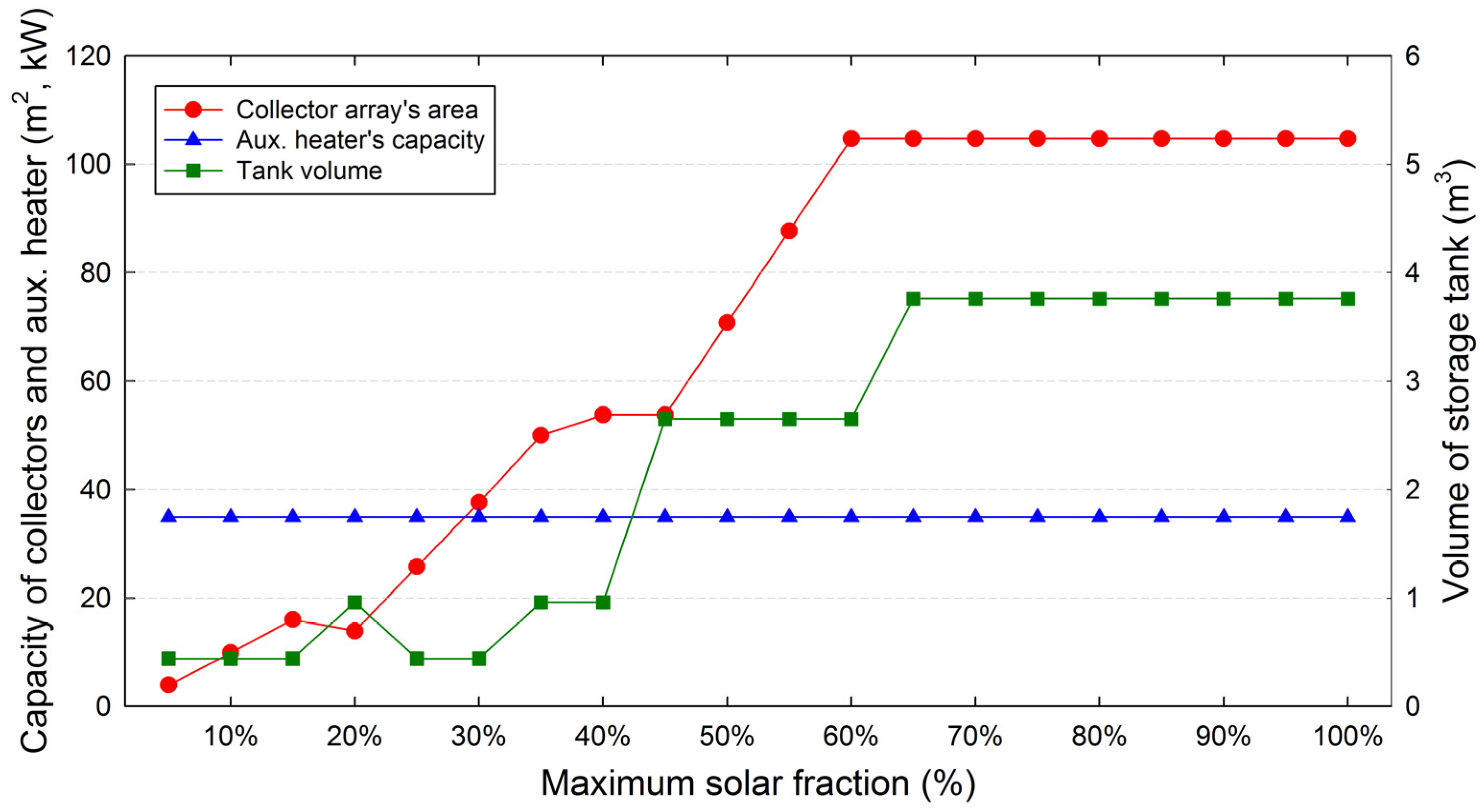
4.3. Effect According to Variation of the Maximum Solar Fraction
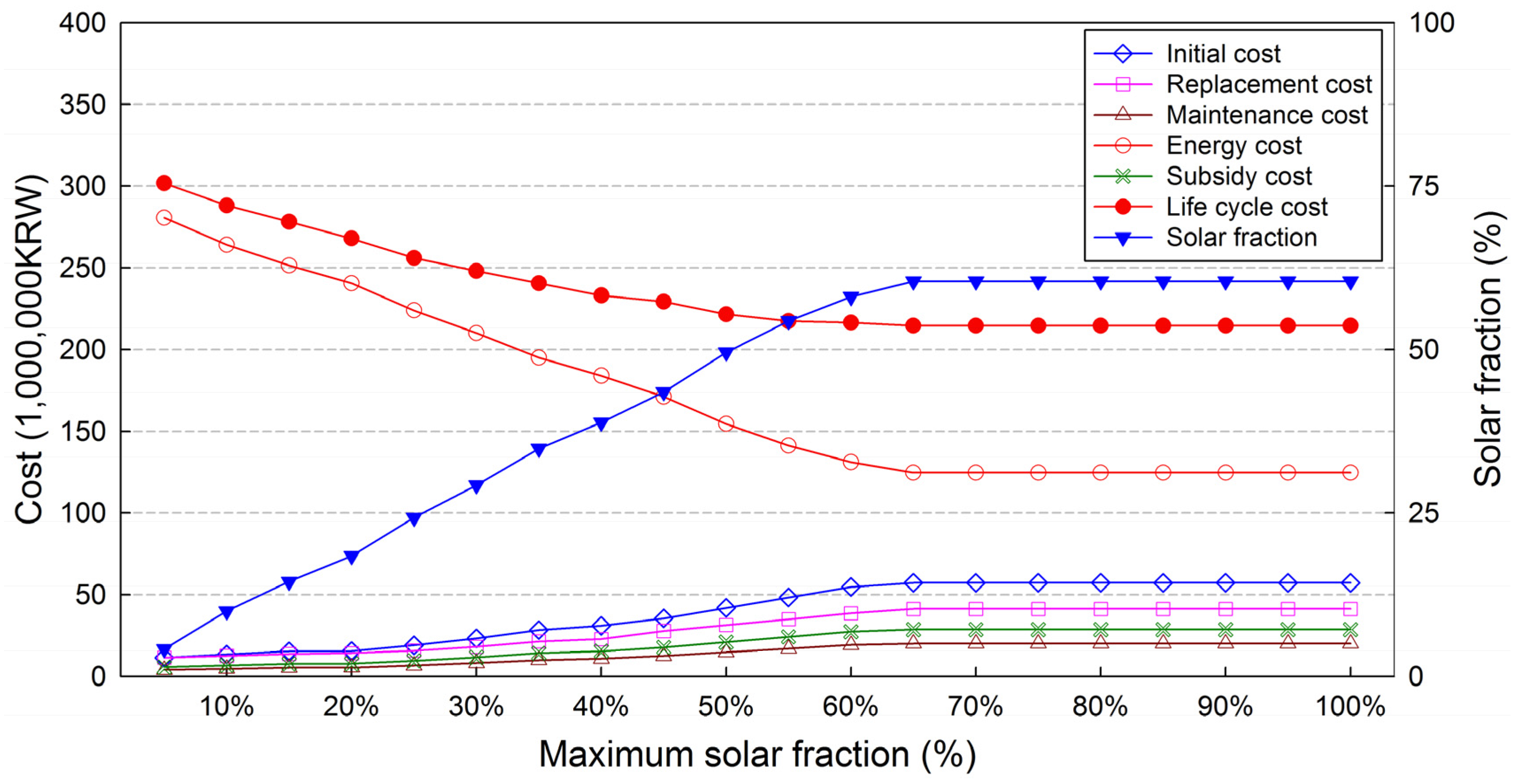
| Parameter | Maximum Solar Fraction | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | 65% | |
| (–) | 3 | 3 | 0 | 3 | 3 | 3 | 2 | 4 | 4 | 4 | 4 | 4 | 4 |
| (ea.) | 2 | 5 | 8 | 7 | 13 | 19 | 25 | 19 | 19 | 25 | 31 | 37 | 37 |
| (–) | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 3 | 3 | 3 | 3 | 4 |
| (–) | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| (ea.) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (m2) | 3.96 | 9.90 | 16.00 | 13.86 | 25.74 | 37.62 | 50 | 53.77 | 53.77 | 70.75 | 87.73 | 104.71 | 104.71 |
| (m3) | 0.44 | 0.44 | 0.44 | 0.96 | 0.44 | 0.44 | 0.96 | 0.96 | 2.65 | 2.65 | 2.65 | 2.65 | 3.76 |
| (kW) | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 |
| (m2) | 7.4 | 18.4 | 29.7 | 25.7 | 47.8 | 69.8 | 92.7 | 99.8 | 99.8 | 131.3 | 162.8 | 194.3 | 194.3 |
| (kW) | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 |
| (kWh/year) | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 |
| (kWh/year) | 2462 | 5994 | 8740 | 11,159 | 14,698 | 17,754 | 21,185 | 23,695 | 26,625 | 30,374 | 33,440 | 35,901 | 37,332 |
| (kWh/year) | −57 | −19 | 7 | 49 | 68 | 98 | 165 | 200 | 375 | 455 | 524 | 583 | 752 |
| (kWh/year) | 0 | 0 | 0 | 0 | 0 | 3 | 1 | 7 | 0 | 0 | 5 | 21 | 4 |
| (kWh/year) | 2523 | 6013 | 8731 | 11,103 | 14,624 | 17,622 | 20,986 | 23,385 | 26,195 | 29,848 | 32,744 | 34,966 | 36,386 |
| (kWh/year) | 57,695 | 54,205 | 51,487 | 49,115 | 45,594 | 42,596 | 39,232 | 36,833 | 34,023 | 30,370 | 27,474 | 25,252 | 23,832 |
| (m3/year) | 6083 | 5715 | 5428 | 5186 | 4810 | 4497 | 4154 | 3904 | 3623 | 3244 | 2940 | 2704 | 2562 |
| (kWh/year) | 142 | 186 | 335 | 354 | 516 | 632 | 799 | 909 | 892 | 1076 | 1260 | 1425 | 1413 |
| (%) | 4.19 | 9.99 | 14.50 | 18.44 | 24.28 | 29.26 | 34.85 | 38.83 | 43.50 | 49.56 | 54.37 | 58.06 | 60.42 |
| (1000 KRW) | 11,335 | 13,441 | 15,339 | 15,560 | 19,057 | 23,269 | 28,359 | 30,900 | 35,548 | 41,944 | 48,340 | 54,736 | 57,238 |
| (1000 KRW) | 3986 | 4727 | 5394 | 5472 | 6702 | 8183 | 9973 | 10,867 | 12,501 | 14,750 | 17,000 | 19,249 | 20,129 |
| (1000 KRW) | 11,444 | 12,630 | 13,699 | 14,188 | 15,793 | 18,165 | 21,395 | 22,826 | 27,812 | 31,414 | 35,016 | 38,618 | 41,302 |
| (1000 KRW) | 280,705 | 264,059 | 251,502 | 240,506 | 223,934 | 210,091 | 195,048 | 184,011 | 171,145 | 154,502 | 141,301 | 131,163 | 124,616 |
| (1000 KRW) | 5668 | 6721 | 7670 | 7780 | 9529 | 11,635 | 14,179 | 15,450 | 17,774 | 20,972 | 24,170 | 27,368 | 28,619 |
| (1000 KRW) | 301,802 | 288,136 | 278,264 | 267,946 | 255,957 | 248,073 | 240,596 | 233,154 | 229,232 | 221,638 | 217,487 | 216,398 | 214,666 |
4.4. Effect According to Variation of the Minimum Solar Fraction
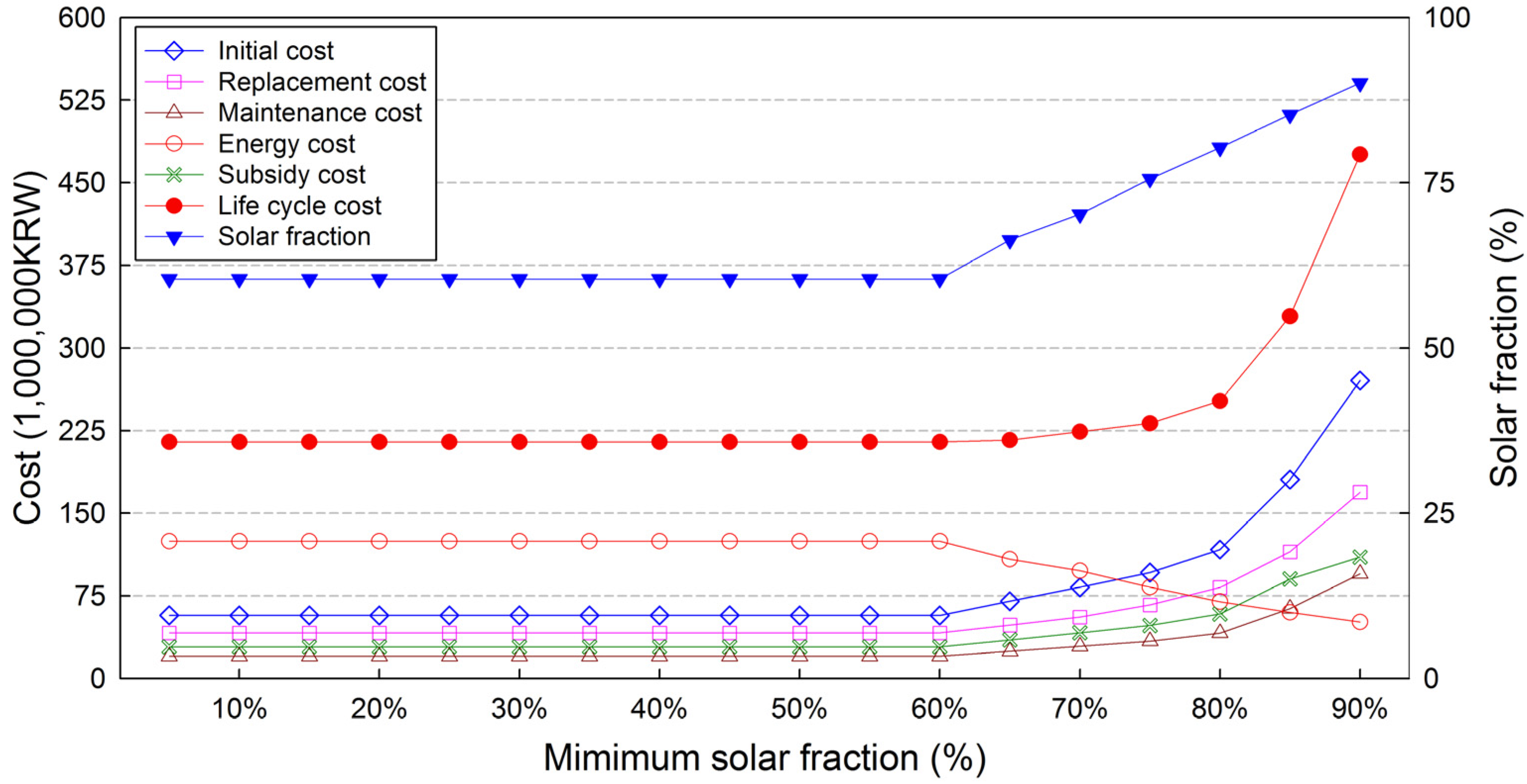
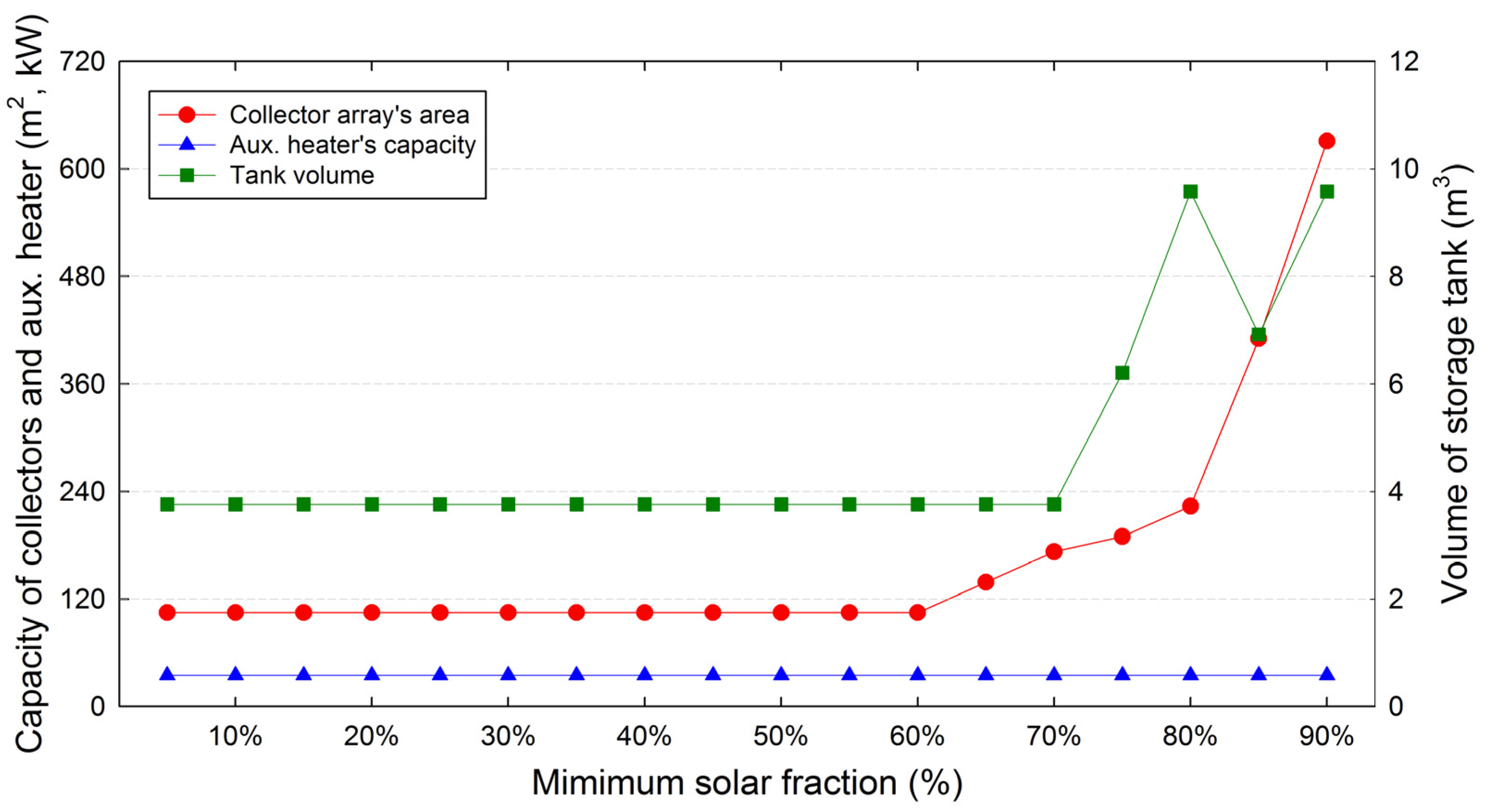
| Parameter | Minimum Soar Fraction | ||||||
|---|---|---|---|---|---|---|---|
| 60 | 65 | 70 | 75 | 80 | 85 | 90 | |
| (–) | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| (ea.) | 37 | 49 | 61 | 67 | 79 | 145 | 223 |
| (–) | 4 | 4 | 4 | 7 | 9 | 8 | 9 |
| (–) | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| (ea.) | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| (m2) | 104.71 | 138.67 | 172.63 | 189.61 | 223.57 | 410.35 | 631.09 |
| (m3) | 3.76 | 3.76 | 3.76 | 6.21 | 9.58 | 6.92 | 9.58 |
| (kW) | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 | 34.89 |
| (m2) | 194.3 | 257.3 | 320.3 | 351.8 | 414.8 | 761.3 | 1170.9 |
| (kW) | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 | 27.35 |
| (kWh/year) | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 | 60,218 |
| (kWh/year) | 37,332 | 41,410 | 44,318 | 47,618 | 51,206 | 58,867 | 65,290 |
| (kWh/year) | 752 | 886 | 994 | 1138 | 1684 | 1922 | 2221 |
| (kWh/year) | 4 | 36 | 78 | 49 | 43 | 402 | 607 |
| (kWh/year) | 36,386 | 39,949 | 42,303 | 45,517 | 48,367 | 51,372 | 54,256 |
| (kWh/year) | 23,832 | 20,269 | 17,915 | 14,701 | 11,851 | 8846 | 5962 |
| (m3/year) | 2562 | 2181 | 1928 | 1595 | 1291 | 966 | 660 |
| (kWh/year) | 1413 | 1712 | 1986 | 2064 | 2279 | 3630 | 5053 |
| (%) | 60.42 | 66.34 | 70.25 | 75.59 | 80.32 | 85.31 | 90.10 |
| (1000 KRW) | 57,238 | 70,030 | 82,822 | 96,197 | 117,025 | 180,589 | 270,529 |
| (1000 KRW) | 20,129 | 24,628 | 29,126 | 33,830 | 41,155 | 63,508 | 95,137 |
| (1000 KRW) | 41,302 | 48,506 | 55,710 | 66,797 | 82,622 | 114,957 | 169,068 |
| (1000 KRW) | 124,616 | 108,296 | 97,765 | 82,838 | 69,716 | 59,867 | 51,207 |
| (1000 KRW) | 28,619 | 35,015 | 41,411 | 48,098 | 58,513 | 90,294 | 110,214 |
| (1000 KRW) | 214,666 | 216,445 | 224,012 | 231,564 | 252,005 | 328,627 | 475,727 |
5. Conclusions
Acknowledgments
Conflicts of Interest
Nomenclature
gross area of a single collector module, m2 | |
gross area of the jth device of solar collectors, m2 | |
installation area of solar collectors, m2 | |
total area of solar collectors, m2 | |
available space to install collector array, m2 | |
maximum capacity available to receive the subsidy cost, m2 | |
surface area of a storage tank, m2 | |
capacity rate of fluid on cold side of a heat exchanger, W/°C | |
capacity rate of fluid on hot side of a heat exchanger, W/°C | |
maximum capacity rate, W/°C | |
minimum capacity rate, W/°C | |
specific heat of water, J/kg·°C | |
specific heat of collector fluid, J/kg·°C | |
purchase price of the jth auxiliary heater, KRW | |
purchase price of the jth solar collector, KRW | |
purchase price of the jth storage tank, KRW | |
energy cost, KRW | |
initial cost, KRW | |
initial cost of each component, KRW | |
maintenance cost, KRW | |
replacement cost, KRW | |
replacement cost of each component, KRW | |
subsidy cost, KRW | |
life cycle cost, KRW | |
hourly electricity cost, KRW/kWh | |
hourly liquid natural gas (LNG) cost, KRW/m3 | |
capacity rate ratio of a heat exchanger | |
fuel price escalation rate, % | |
hourly electricity consumption, kWh | |
hourly LNG consumption, m3 | |
collector heat removal factor of identical collectors in series | |
collector heat removal factor of a collector | |
solar fraction of any solar water heating system, % | |
minimum solar fraction, % | |
maximum solar fraction, % | |
height of the jth device of solar collectors, m | |
hourly total solar radiation on the tilted collector array, W/m2 | |
real discount rate, % | |
mass flow rate of the collector fluid, kg/s | |
mass flow rate of the discharged water from a storage tank, kg/s | |
mass flow rate from the storage tank to the load, kg/s | |
mass flow rate of the desired hot water load, kg/s | |
number of identical collectors in series | |
number of the jth device of solar collectors | |
number of the jth device of auxiliary heaters | |
number of exchanger heat transfer units | |
planning period, year | |
lifetime of each component, year | |
replacement times of each component | |
heating capacity of the jth device of auxiliary heaters, kW | |
total heating capacity of the auxiliary heaters, kW | |
annual auxiliary heating energy, kWh | |
peak hot water load, kW | |
annual hot water load, kWh | |
auxiliary heating energy, W | |
discharged heat to avoid overheating of a storage tank, W | |
heat loss of a storage tank, W | |
solar energy extracted from the storage tank to the load, W | |
solar energy supplied to a storage tank, W | |
solar useful heat gain of identical collectors in series, W | |
a percentage of the supplementary cost against the direct purchase cost, % | |
a percentage of the annual maintenance cost against the initial cost, % | |
a percentage of subsidy cost against the initial cost, % | |
outdoor dry-bulb temperature, °C | |
ambient temperature, °C | |
cold stream outlet temperature of a heat exchanger, °C | |
cold stream inlet temperature of a heat exchanger, °C | |
hot stream inlet temperature of a heat exchanger, °C | |
hot stream outlet temperature of a heat exchanger, °C | |
desired hot water temperature, °C | |
make-up water temperature, °C | |
storage tank temperature at the beginning of the time step, °C | |
storage tank temperature at the end of the time step, °C | |
maximum allowable storage tank temperature, °C | |
type of auxiliary heater | |
type of solar collector | |
type of storage tank | |
collector overall heat loss coefficient of identical collectors in series, W/m2·°C | |
collector overall heat loss coefficient of a collector, W/m2·°C | |
heat loss coefficient of a storage tank, W/m2·°C | |
product of the overall heat transfer coefficient and area of a heat exchanger, W/°C | |
uniform present value factor adjusted to reflect the electricity price escalation rate | |
uniform present value factor adjusted to reflect the LNG price escalation rate | |
uniform present value factor adjusted to reflect the fuel price escalation rate | |
storage tank volume, m3 | |
width of the jth device of solar collectors, m | |
meridian altitude in winter, ° | |
slope of the collector array, ° | |
effectiveness of a heat exchanger | |
density of water, kg/m3 | |
product of the transmittance and the absorptance of identical collectors in series | |
product of the transmittance and the absorptance of a collector |
References
- Wang, Z.; Yang, W.; Qiu, F.; Zhang, X.; Zhao, X. Solar water heating: From theory, application, marketing and research. Renew. Sustain. Energy Rev. 2015, 41, 68–84. [Google Scholar] [CrossRef]
- Balusamy, T.; Sadhishkumar, S. Performance improvement in solar water heating systems—A review. Renew. Sustain. Energy Rev. 2014, 37, 191–198. [Google Scholar]
- Islam, M.R.; Sumathy, K.; Khan, S.U. Solar water heating systems and their market trends. Renew. Sustain. Energy Rev. 2013, 17, 1–25. [Google Scholar] [CrossRef]
- Renewable Energy Policy Network. Renewable Energy 2010: Key Facts and Figures for Decision Makers. Global Status Report. Available online: http://www.ren21.net/gsr (accessed on 10 July 2015).
- Kulkarni, G.N.; Kedare, S.B.; Bandyopadhyay, S. Determination of design space and optimization of solar water heating systems. Sol. Energy 2007, 81, 958–968. [Google Scholar] [CrossRef]
- Hottel, H.C.; Whillier, A. Evaluation of Flat-Plate Collector Performance; University of Arizona Press: Tucson, AZ, USA, 1958. [Google Scholar]
- Klein, S.A. Calculation of flat-plate collector utilizability. Sol. Energy 1978, 21, 393–402. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A.; Duffie, J.A. A design procedure for solar heating systems. Sol. Energy 1976, 18, 113–127. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A. A general design method for closed-loop solar energy systems. Sol. Energy 1979, 22, 269–282. [Google Scholar] [CrossRef]
- Yan, C.; Wang, S.; Ma, Z.; Shi, W. A simplified method for optimal design of solar water heating systems based on life-cycle energy analysis. Renew. Energy 2015, 74, 271–278. [Google Scholar] [CrossRef]
- Klein, S.A.; Cooper, P.I.; Freeman, T.L.; Beekman, D.L.; Beckman, W.A.; Duffie, J.A. A method of simulation of solar processes and its application. Sol. Energy 1975, 17, 29–37. [Google Scholar] [CrossRef]
- Lund, P.D.; Peltola, S.S. SOLCHIPS—A fast pre-design and optimization tool for solar heating with seasonal storage. Sol. Energy 1992, 48, 291–300. [Google Scholar] [CrossRef]
- Matrawy, K.K.; Farkas, I. New technique for short term storage sizing. Renew. Energy 1997, 11, 129–141. [Google Scholar] [CrossRef]
- Loomans, M.; Visser, H. Application of the genetic algorithm for optimization of large solar hot water systems. Sol. Energy 2002, 72, 427–439. [Google Scholar] [CrossRef]
- Krause, M.; Vajen, K.; Wiese, F.; Ackermann, H. Investigation on optimizing large solar thermal systems. Sol. Energy 2002, 73, 217–225. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Optimization of solar systems using artificial neural-networks and genetic algorithms. Appl. Energy 2004, 77, 383–405. [Google Scholar] [CrossRef]
- Kulkarni, G.N.; Kedare, S.B.; Bandyopadhyay, S. Design of solar thermal systems utilizing pressurized hot water storage for industrial applications. Sol. Energy 2008, 82, 686–699. [Google Scholar] [CrossRef]
- Kim, Y.D.; Thu, K.; Bhatia, H.K.; Bhatia, C.S.; Ng, K.C. Thermal analysis and performance optimization of a solar hot water plant with economic evaluation. Sol. Energy 2012, 86, 1378–1395. [Google Scholar] [CrossRef]
- Atia, D.M.; Fahmy, F.H.; Ahmed, N.M.; Dorrah, H.T. Optimal sizing of a solar water heating system based on a genetic algorithm for an aquaculture system. Math. Comput. Model. 2012, 55, 1436–1449. [Google Scholar] [CrossRef]
- Bornatico, R.; Pfeiffer, M.; Witzig, A.; Guzzella, L. Optimal sizing of a solar thermal building installation using particle swarm optimization. Energy 2012, 41, 31–37. [Google Scholar] [CrossRef]
- Cheng Hin, J.N.; Zmeureanu, R. Optimization of a residential solar combisystem for minimum life cycle cost, energy use and exergy destroyed. Sol. Energy 2014, 100, 102–113. [Google Scholar] [CrossRef]
- Kusyy, O.; Kuethe, S.; Vajen, K. Simulation-based optimization of a solar water heating system by a hybrid genetic-binary search algorithm. In Proceedings of the 2010 Xvth International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, GA, USA, 27–30 September 2010.
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 3rd ed.; Willey: Hoboken, NJ, USA, 2006. [Google Scholar]
- Choi, D.S.; Ko, M.J. Optimization design for a solar water heating system using the genetic algorithm. Int. J. Appl. Eng. Res. 2015, 10, 27031–27042. [Google Scholar]
- Kanpur Genetic Algorithms Laboratory. Available online: http://www.iitk.ac.in/kangal/codes.shtml (accessed on 29 January 2015).
- Ko, M.J.; Kim, Y.S.; Chung, M.H.; Jeon, H.C. Multi-objective optimization design for a hybrid energy system using the genetic algorithm. Energies 2015, 8, 2924–2949. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. U.S. Department of Energy Commercial Reference Building Models of the National Building Stock. Available online: http://www.nrel.gov/docs/fy11osti/46861.pdf (accessed on 29 January 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, M.J. Analysis and Optimization Design of a Solar Water Heating System Based on Life Cycle Cost Using a Genetic Algorithm. Energies 2015, 8, 11380-11403. https://doi.org/10.3390/en81011380
Ko MJ. Analysis and Optimization Design of a Solar Water Heating System Based on Life Cycle Cost Using a Genetic Algorithm. Energies. 2015; 8(10):11380-11403. https://doi.org/10.3390/en81011380
Chicago/Turabian StyleKo, Myeong Jin. 2015. "Analysis and Optimization Design of a Solar Water Heating System Based on Life Cycle Cost Using a Genetic Algorithm" Energies 8, no. 10: 11380-11403. https://doi.org/10.3390/en81011380
APA StyleKo, M. J. (2015). Analysis and Optimization Design of a Solar Water Heating System Based on Life Cycle Cost Using a Genetic Algorithm. Energies, 8(10), 11380-11403. https://doi.org/10.3390/en81011380






