The Application of Discontinuous Galerkin Methods in Conjugate Heat Transfer Simulations of Gas Turbines
Abstract
:1. Introduction
2. Discontinuous Galerki Methods for Conjugate Heat Transfer Problems
2.1. Fluid Domain
2.2. Solid Domain
2.3. Fluid-Solid Interface
2.4. The Taylor Basis
3. Numerical treatments for turbulence and Transition models
4. Method Verification
4.1. Heat Convection along a Flat Plate
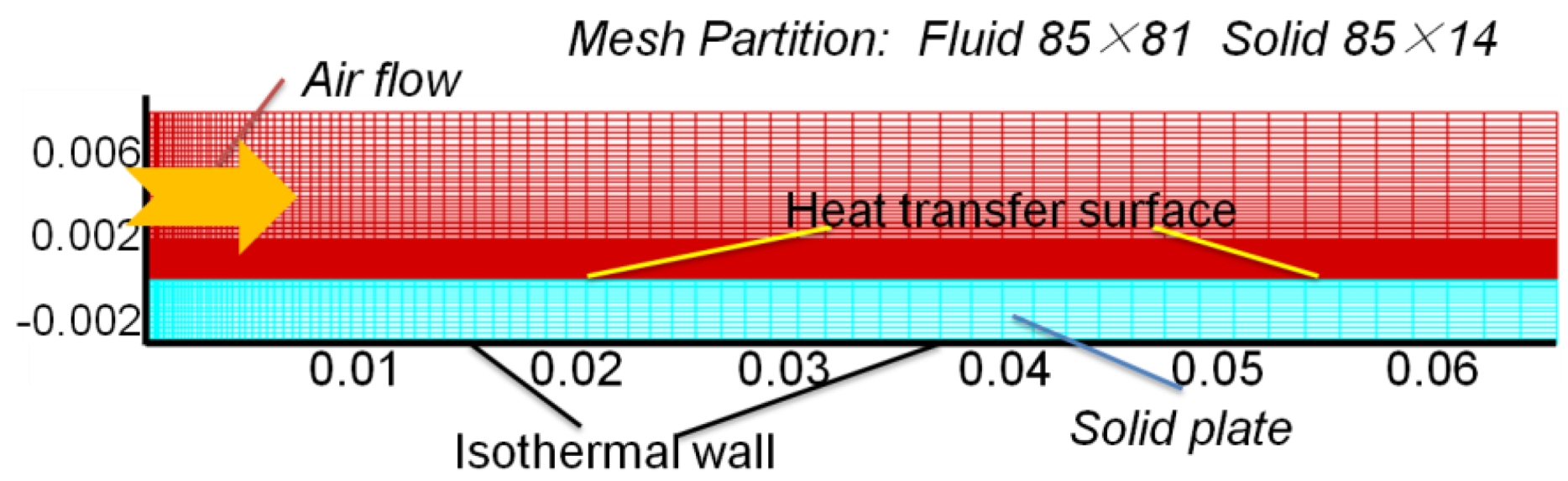


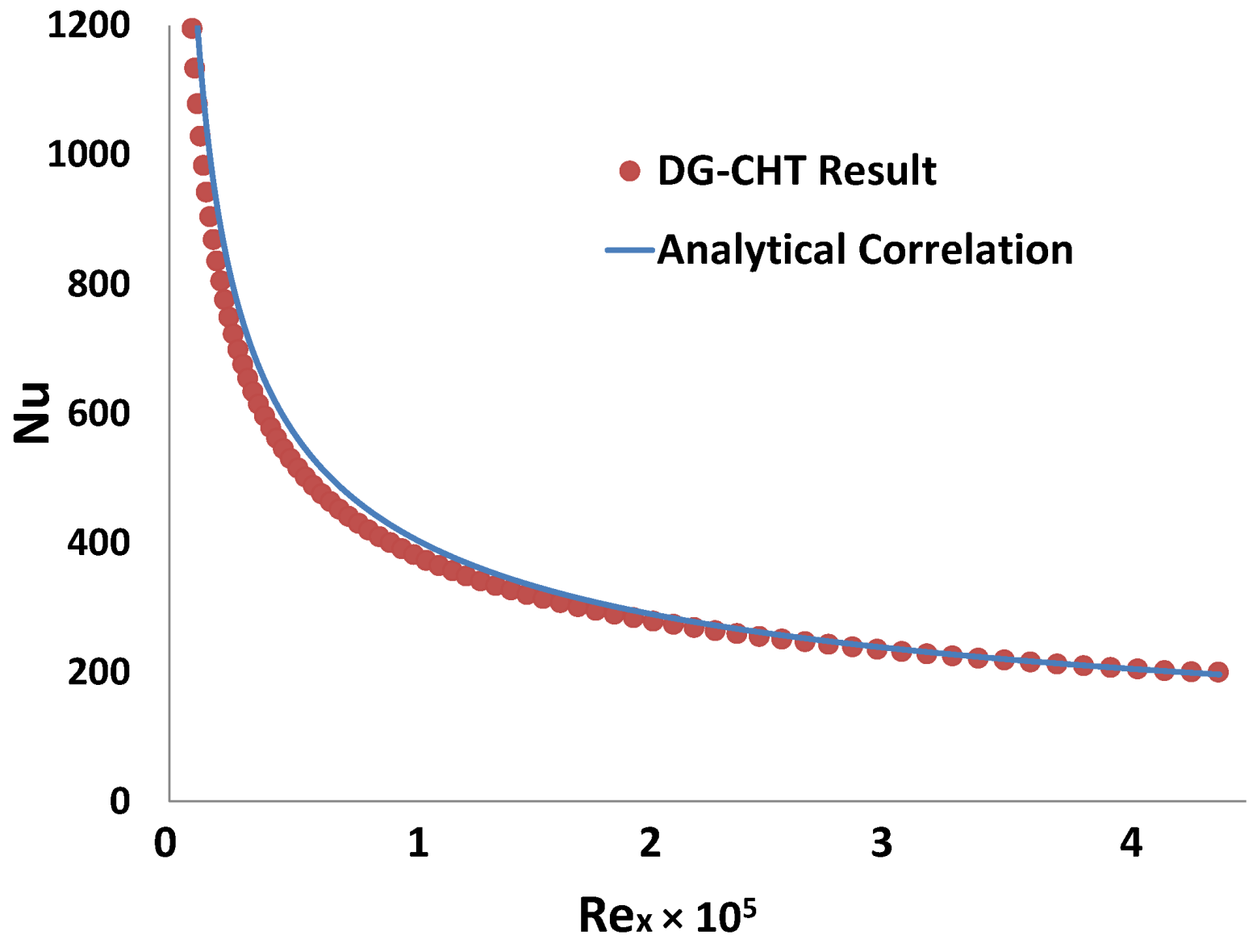
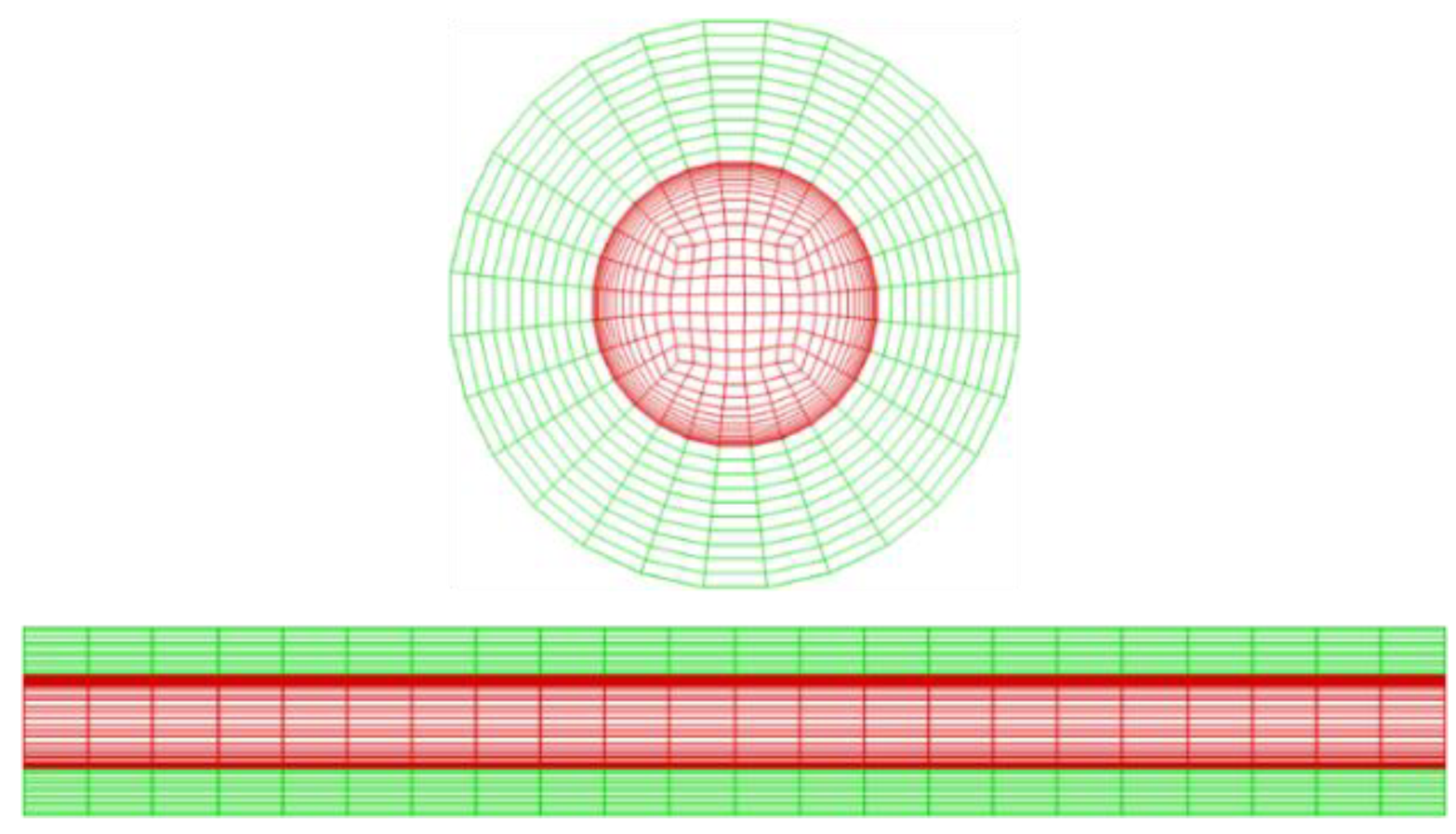
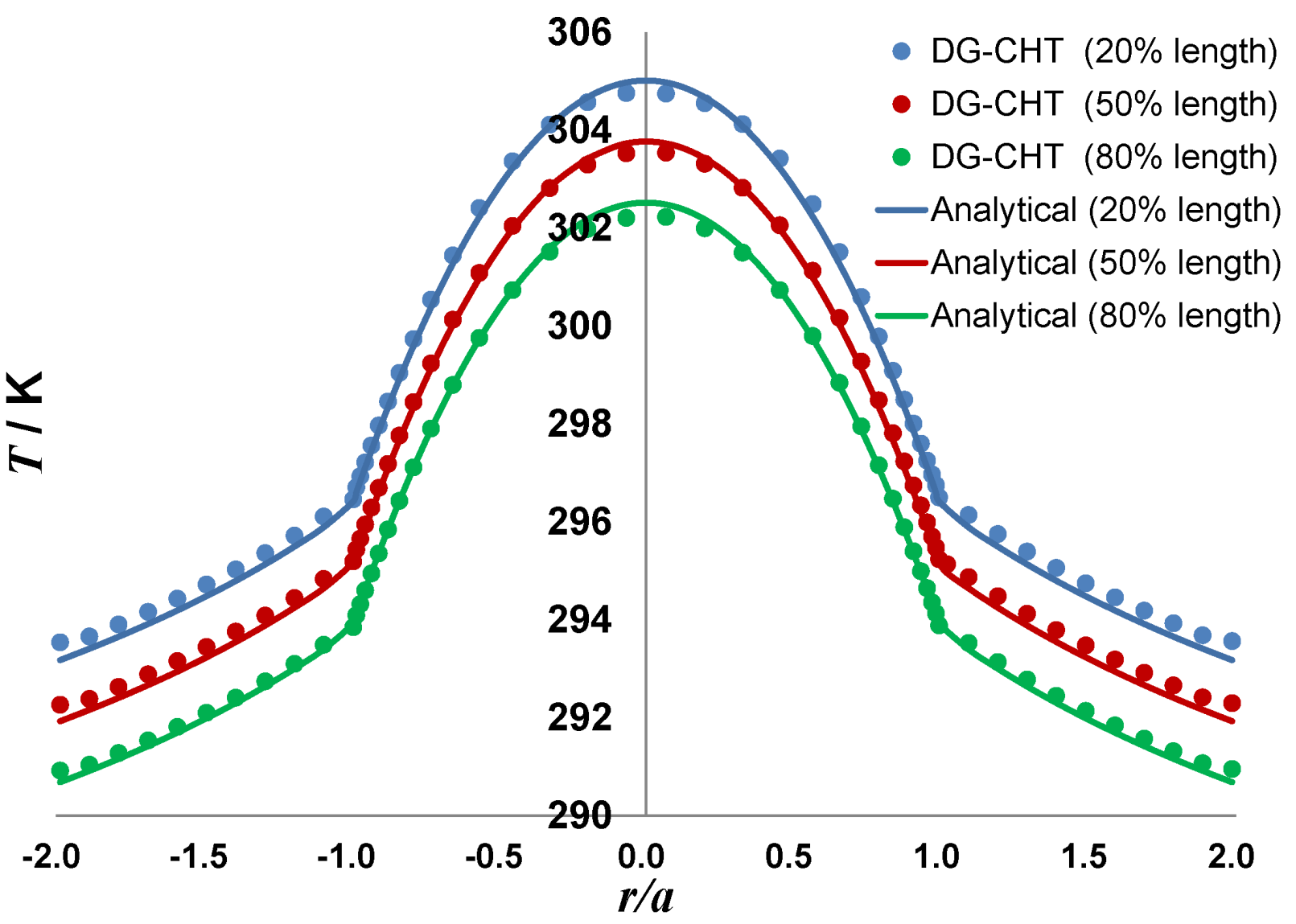
4.2. Heat Transfer of a Poiseuille Pipe Flow

4.3. Application and analysis in a turbine vane
| Quantity | ptin | Tref | Tuin | pout |
|---|---|---|---|---|
| Unit | kPa | K | % | kPa |
| Value | 337.080 | 788.0 | 6.5 | 169.849 |
| Hole index | Average temperature of cooing air (K) | Average heat transfer coefficient (W/m2·K) |
|---|---|---|
| 01 | 336.39 | 1943.67 |
| 02 | 326.27 | 1881.45 |
| 03 | 332.68 | 1893.49 |
| 04 | 338.86 | 1960.62 |
| 05 | 318.95 | 1850.77 |
| 06 | 315.58 | 1813.36 |
| 07 | 326.26 | 1871.88 |
| 08 | 359.83 | 2643.07 |
| 09 | 360.89 | 1809.89 |
| 10 | 414.85 | 3056.69 |
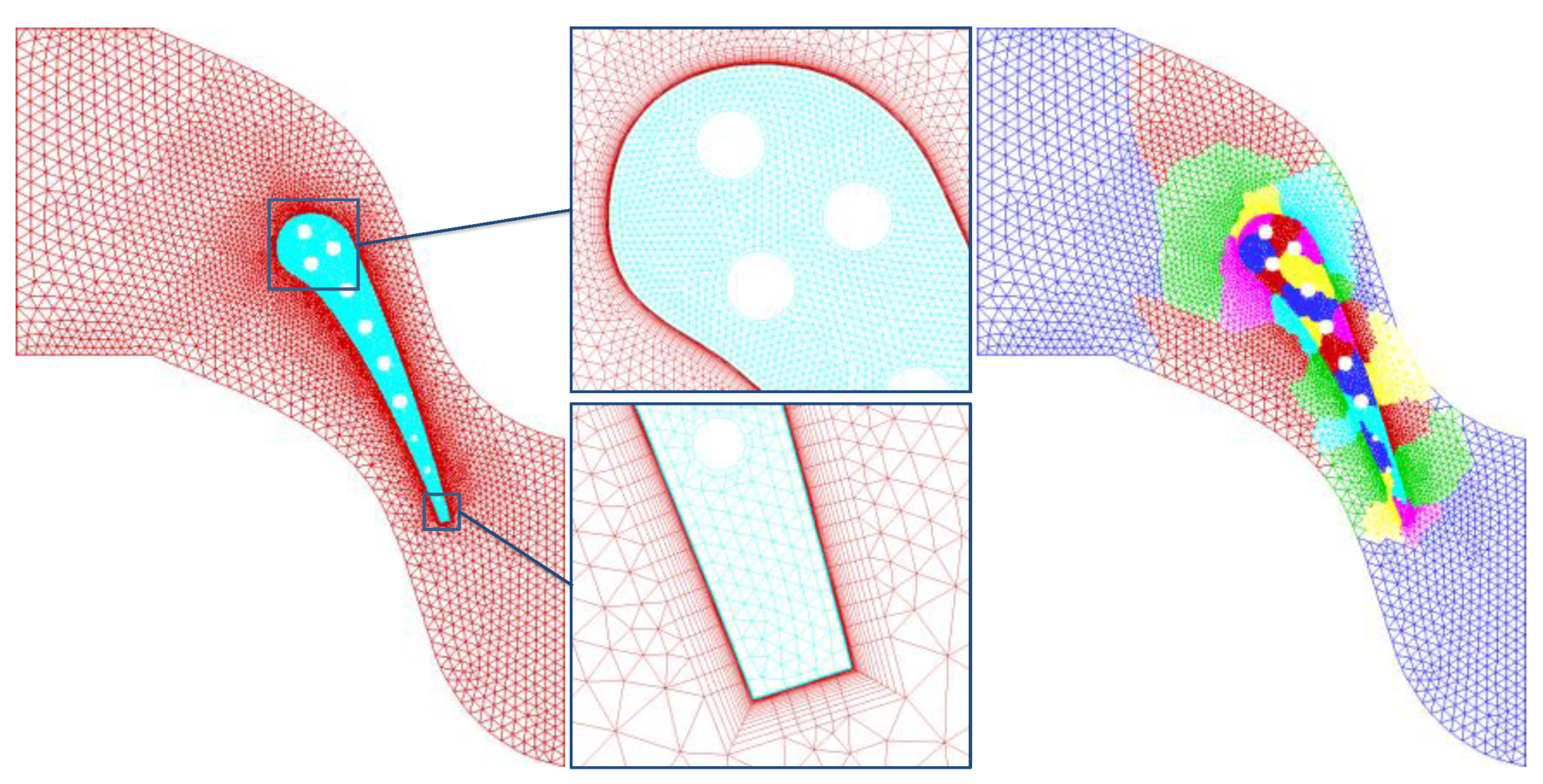
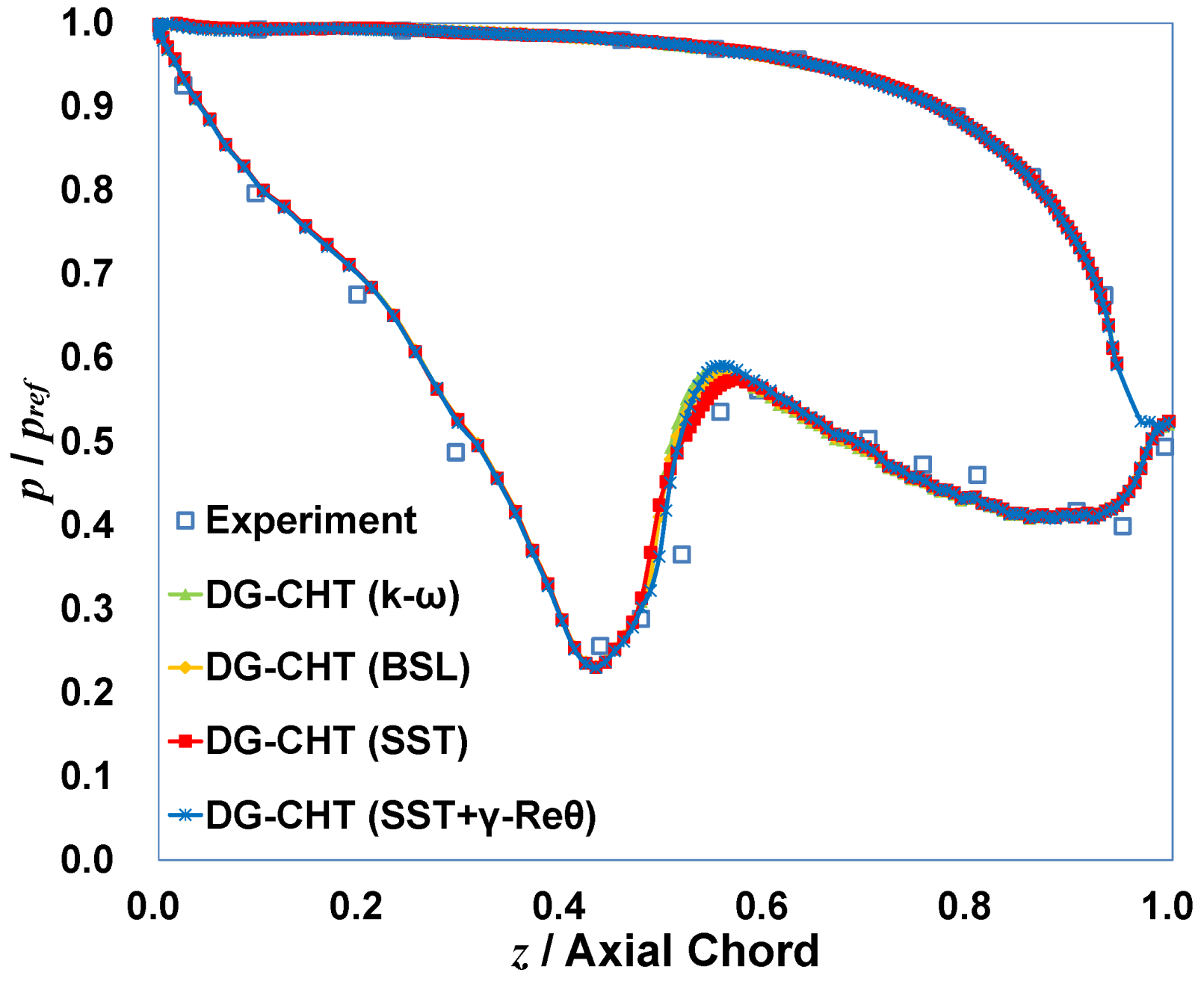
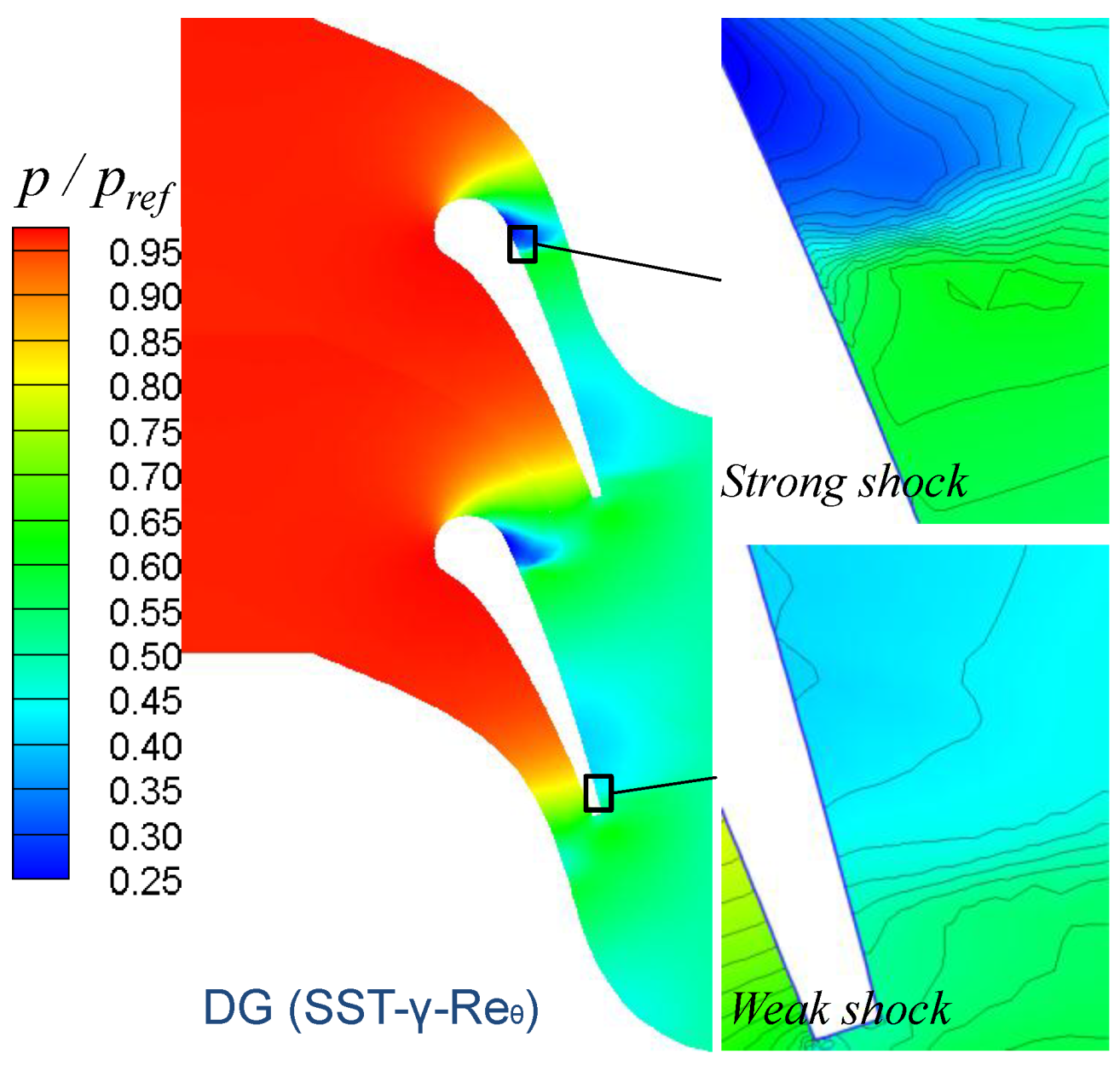
4.3.1. Aerodynamic Features
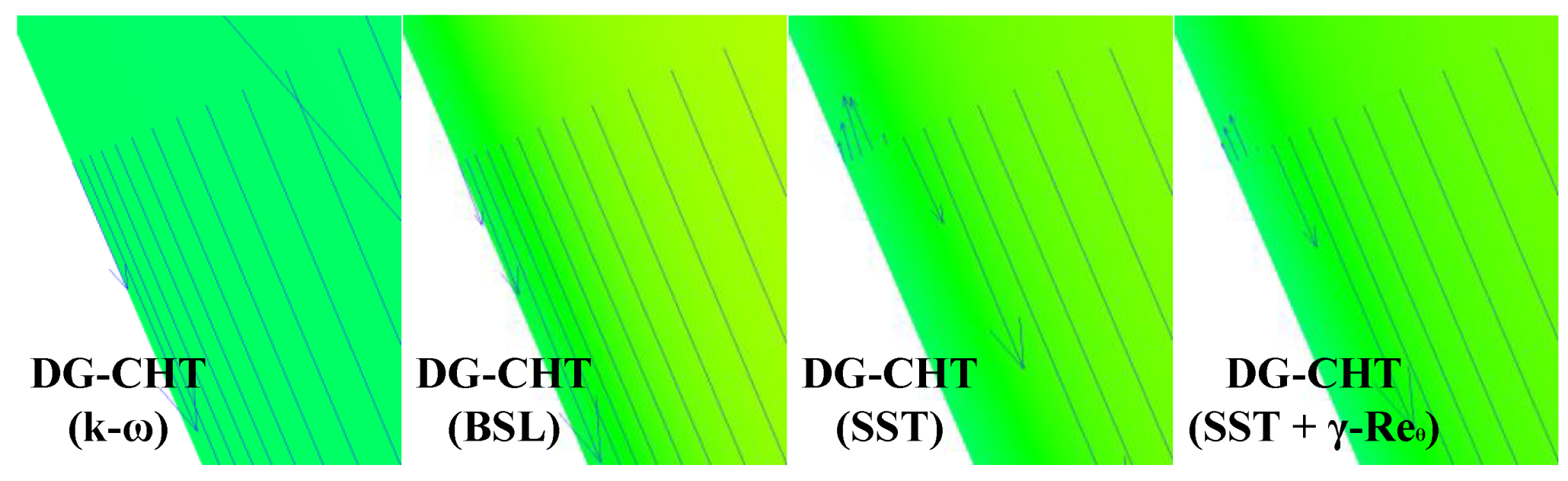
4.3.2. Heat Transfer Features

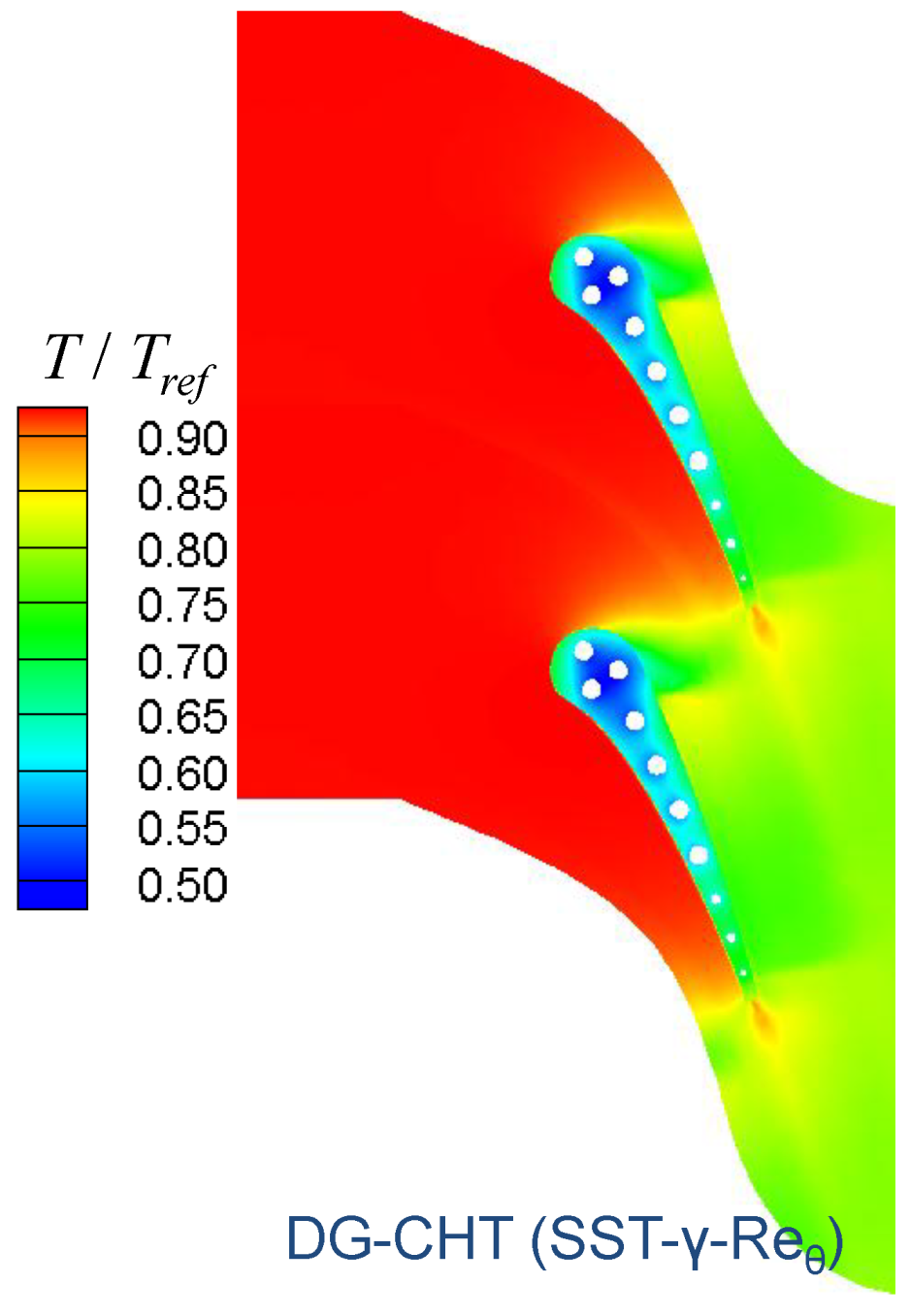
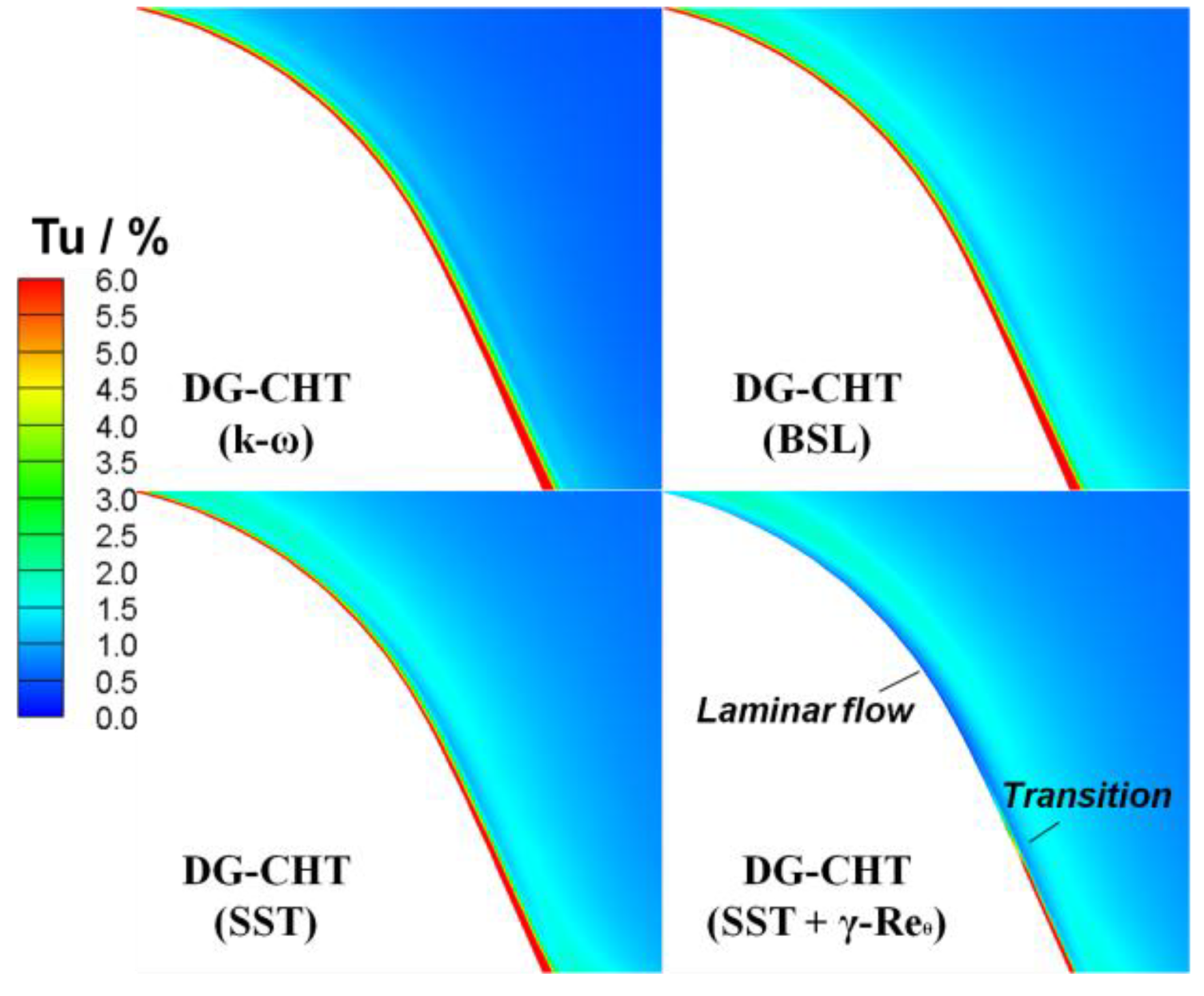
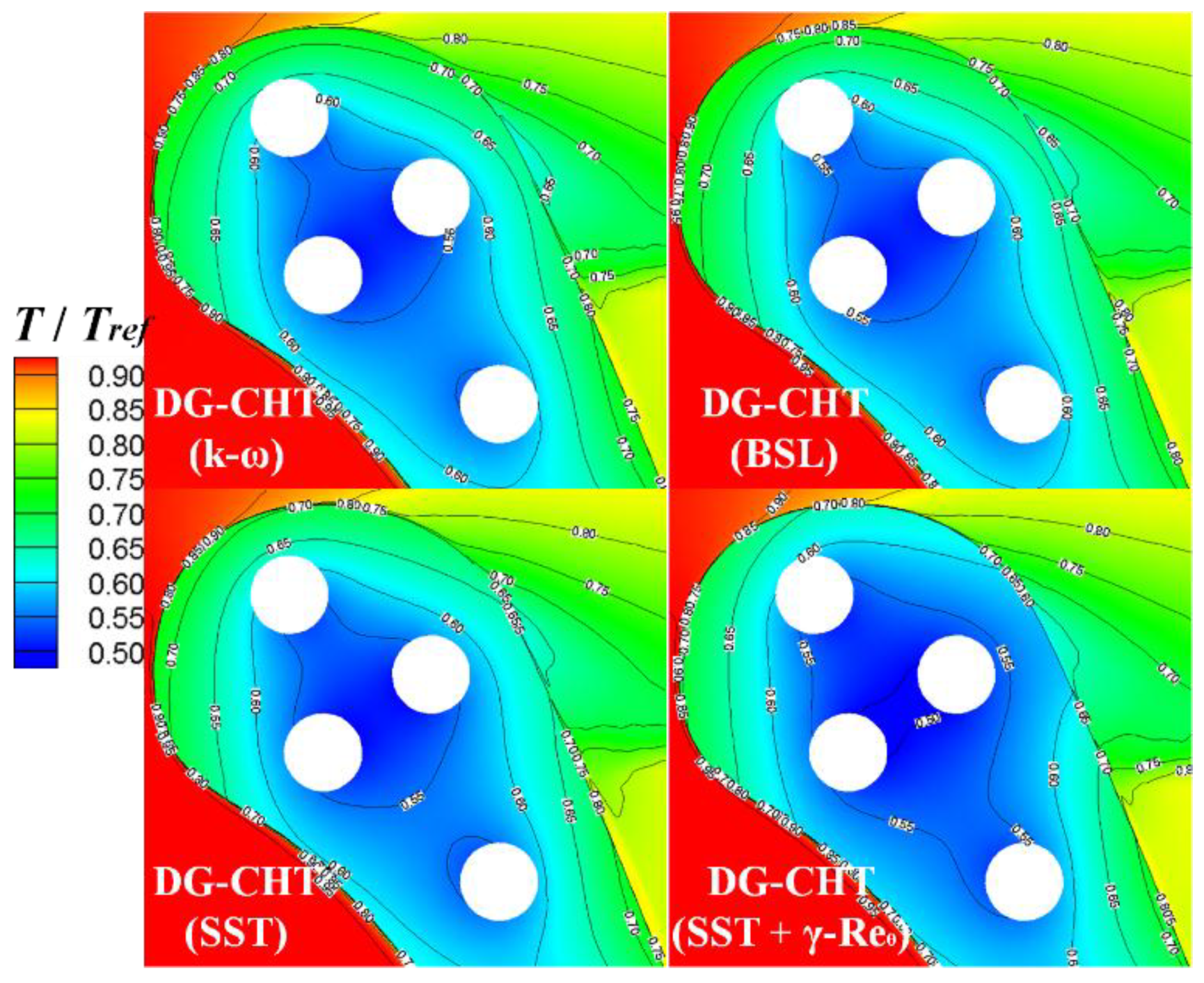
5. Conclusions
Notation
| cp | specific heat capacity at constant pressure (set to be 1004.8 J/(kg·K) for air) |
| CDω | cross diffusion term of turbulence frequency |
| CDῶ | cross diffusion term of logarithm of turbulence frequency |
| Dj | diffusive flux term |
numerical diffusive flux term | |
| Dk | dissipation term of turbulence kinetic energy |
| Dω | dissipation term of turbulence frequency |
| Dῶ | dissipation term of logarithm of turbulence frequency |
| d | thickness value |
| E | total energy per unit mass |
| Ek | the k-th element |
| ej | unit vector |
| eq | number of governing equations |
| Fj | convective flux term |
numerical convective flux term | |
| H | total enthalpy per unit mass |
| h | heat transfer coefficient (h = qw/Tf − Tw) |
| K | turbulence kinetic energy per unit mass |
| L | length value |
| L2 | space of square integrable functions |
| l | number of freedoms in each element |
| Ma | Mach number |
| Nu | Nusselt number |
| n | number of elements |
| nj | component of normal vector |
| Pj | gradient component of the conservative variable U |
| Pm | space of all the polynomials with the degree at most m |
| Pk | production term of turbulence kinetic energy |
| Pω | production term of turbulence frequency |
| Pῶ | production term of logarithm of turbulence frequency |
| Pr | Prandtl number (set to be 0.71 for air) |
| Prt | Turbulent Prandtl number (set to be 0.90 for air) |
| PS | pressure surface of vane or blade |
the s-th freedom of the numerical solution of conservative variable gradient Ph,j in the k-th element | |
| p | pressure |
| pt | total pressure |
| q | heat flux vector |
| qj | heat flux component |
numerical heat flux component | |
| ReL | Reynolds number based on the length of the flat plate |
| Rex | Reynolds number based on the distance away from the leading edge of the flat plate |
transition onset Reynolds number based on momentum thickness of boundary layer | |
| RMS | L2-norm of the residuals |
| s | source term |
| SS | suction surface of vane or blade |
total stress tensor | |
| T | temperature |
numerical flux of temperature | |
| Tt | total temperature |
| Tu | turbulence intensity () |
| t | time |
| U | conservative variable term |
numerical flux of conservative variable term | |
| uj | velocity component |
the s-th freedom of the numerical solution of conservative variable Uh in the k-th element | |
| V | velocity vector |
| v | test function |
| x | position vector |
| xj | Cartesian coordinate component |
| Yῶ | extra term coming from the logarithmetics procedure of the original transport equation of turbulence frequency |
| y+ | non-dimensional wall distance |
| Г | space of the solution |
| γ | intermittency factor of turbulent flow |
the s-th freedom of the numerical solution of heat flux component qh,j in the k-th element | |
the s-th freedom of the numerical solution of temperature Th in the k-th element | |
| λ | thermal conductivity |
| μ | dynamic molecular viscosity coefficient (calculated from
) |
| μt | dynamic turbulent viscosity coefficient |
| ρ | density |
| σ | surface of certain domain |
| σω | turbulence diffusion constant of ω in k-ω/BSL/SST models |
the s-th base function in the k-th element | |
| φrs | the Taylor base function series |
| Ω | computational domain |
| ω | turbulence frequency |
| ῶ | logarithm of turbulence frequency ω |
Superscripts
| T | transpose of a matirx |
| tran | transition variables |
| turb | turbulence variables |
Subscripts
| b | bottom surface value |
| c | cell center |
| F or Fluid | fluid value |
| h | numerical value or set |
| in | inlet value |
| out | outlet value |
| ref | reference value |
| S or Solid | solid value |
| w | wall surface value |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Martin, T.J.; Dulikravich, G.; Han, Z.-X.; Dennis, B.H. Minimization of coolant mass flow rate in internally cooled gas turbine blades. In Proceedings of the ASME Turbo Expo, Indianapolis, IN, USA, 7–10 June 1999.
- Montenay, A.; Pate, L.; Duboue, J. Conjugate heat transfer analysis of an engine internal cavity. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000.
- Sondak, D.L.; Dorney, D.J. Simulation of coupled unsteady flow and heat conduction in turbine stage. J. Propuls. Power 2000, 16, 1141–1148. [Google Scholar] [CrossRef]
- Verdicchio, J.; Chew, J.; Hills, N. Coupled fluid/solid heat transfer computation for turbine discs. In Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001; Volume 3.
- Duchaine, F.; Mendez, S.; Nicoud, F.; Corpron, A.; Moureau, V.; Poinsot, T. Coupling heat transfer solvers and large eddy simulations for combustion applications. In Proceedings of the Summer Program, Stanford, CA, USA, 6 July–1 August 2008; pp. 113–126.
- Amaral, S.; Verstraete, T.; van den Braembussche, R.; Arts, T. Design and optimization of the internal cooling channels of a HP turbine blade: Part 1—Methodology. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008.
- Pelletier, D.; Ignat, L.; Ilinca, F. Adaptive finite element method for conjugate heattransfer. Numer. Heat Trans. Part A Appl. 1997, 32, 267–287. [Google Scholar] [CrossRef]
- Kao, K.-H.; Liou, M.-S. Application of chimera/unstructured hybrid grids for conjugate heat transfer. AIAA J. 1997, 35, 1472–1478. [Google Scholar] [CrossRef]
- Han, Z.-X.; Dennis, B.H.; Dulikravich, G.S. Simultaneous prediction of external flow-field and temperature in internally cooled 3-D turbine blade material. Int. J. Turbo Jet Engines 2000, 18, 47–58. [Google Scholar]
- Agostini, F.; Arts, T. Conjugate heat transfer investigation of rib-roughened cooling channels. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005; Volume 3, pp. 239–247.
- Luo, J.; Razinsky, E.H. Conjugate heat transfer analysis of a cooled turbine vane using the V2F turbulence model. J. Turbomach. 2007, 129, 773–781. [Google Scholar] [CrossRef]
- Reed, W.; Hill, T. Triangular Mesh Methods for the Neutron Transport Equation; Technical Report LA-UR-73-479; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1973. [Google Scholar]
- Cockburn, B.; Shu, C.-W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comput. 1989, 52, 411–435. [Google Scholar]
- Cockburn, B.; Lin, S.-Y.; Shu, C.-W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: One-dimensional systems. J. Comput. Phys. 1989, 84, 90–113. [Google Scholar] [CrossRef]
- Cockburn, B.; Hou, S.; Shu, C.-W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case. Math. Comput. 1990, 54, 545–581. [Google Scholar]
- Cockburn, B.; Shu, C.-W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 1998, 141, 199–224. [Google Scholar] [CrossRef]
- Bassi, F.; Rebay, S. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-stokes equations. J. Comput. Phys. 1997, 131, 267–279. [Google Scholar] [CrossRef]
- Bassi, F.; Crivellini, A.; Rebay, S.; Savini, M. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω turbulence model equations. Comput. Fluids 2005, 34, 507–540. [Google Scholar] [CrossRef]
- Kanapady, R.; Jain, A.; Tamma, K.; Siddharth, S. Local discontinuous Galerkin formulations for heat conduction problems involving high gradients and imperfect contact surfaces. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; pp. 8447–8455.
- Menter, F.; Langtry, R.; Likki, S.; Suzen, Y.; Huang, P.; Volker, S. A correlation-based transition model using local variables—Part I: Model formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Li, X.-S.; Gu, C.-W. An all-speed roe-type scheme and its asymptotic analysis of low Mach number behaviour. J. Comput. Phys. 2008, 227, 5144–5159. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Kuzmin, D. A vertex-based hierarchical slope limiter for p-adaptive discontinuous Galerkin methods. J. Comput. Appl. Math. 2010, 233, 3077–3085. [Google Scholar] [CrossRef]
- Eckert, E.; Weise, W. Die temperatur unbeheizter Koerper in einem Gasstrom hoher Geschwindigkeit. Forsch. Geb. Ing. A. 1941, 12, 40–50. (In German) [Google Scholar] [CrossRef]
- Hylton, L.; Mihelc, M.; Turner, E.; Nealy, D.; York, R. Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes; Technical Report for the National Aeronautics and Space Administration (NASA): Indianapolis, IN, USA, 1 May 1983. [Google Scholar]
- Bradshaw, P.; Ferriss, D.; Atwell, N. Calculation of boundary layer development using the turbulent energy equation. J. Fluid Mech. 1967, 28, 593–616. [Google Scholar] [CrossRef]
- Coakley, T.; Huang, P. Turbulence modeling for high speed flows. In Proceedings of the AIAA 30th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1992.
- Bovle, R.; Simon, F. Mach number effects on turbine blade transition length prediction. J. Turbomach. 1999, 121, 694–702. [Google Scholar] [CrossRef]
- Steelant, J.; Dick, E. Modeling of laminar-turbulent transition for high freestream turbulence. J. Fluids Eng. 2001, 123, 22–30. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Z.-R.; Gu, C.-W.; Ren, X.-D. The Application of Discontinuous Galerkin Methods in Conjugate Heat Transfer Simulations of Gas Turbines. Energies 2014, 7, 7857-7877. https://doi.org/10.3390/en7127857
Hao Z-R, Gu C-W, Ren X-D. The Application of Discontinuous Galerkin Methods in Conjugate Heat Transfer Simulations of Gas Turbines. Energies. 2014; 7(12):7857-7877. https://doi.org/10.3390/en7127857
Chicago/Turabian StyleHao, Zeng-Rong, Chun-Wei Gu, and Xiao-Dong Ren. 2014. "The Application of Discontinuous Galerkin Methods in Conjugate Heat Transfer Simulations of Gas Turbines" Energies 7, no. 12: 7857-7877. https://doi.org/10.3390/en7127857
APA StyleHao, Z.-R., Gu, C.-W., & Ren, X.-D. (2014). The Application of Discontinuous Galerkin Methods in Conjugate Heat Transfer Simulations of Gas Turbines. Energies, 7(12), 7857-7877. https://doi.org/10.3390/en7127857




