Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation
Abstract
:1. Introduction
2. Game Theory Concepts
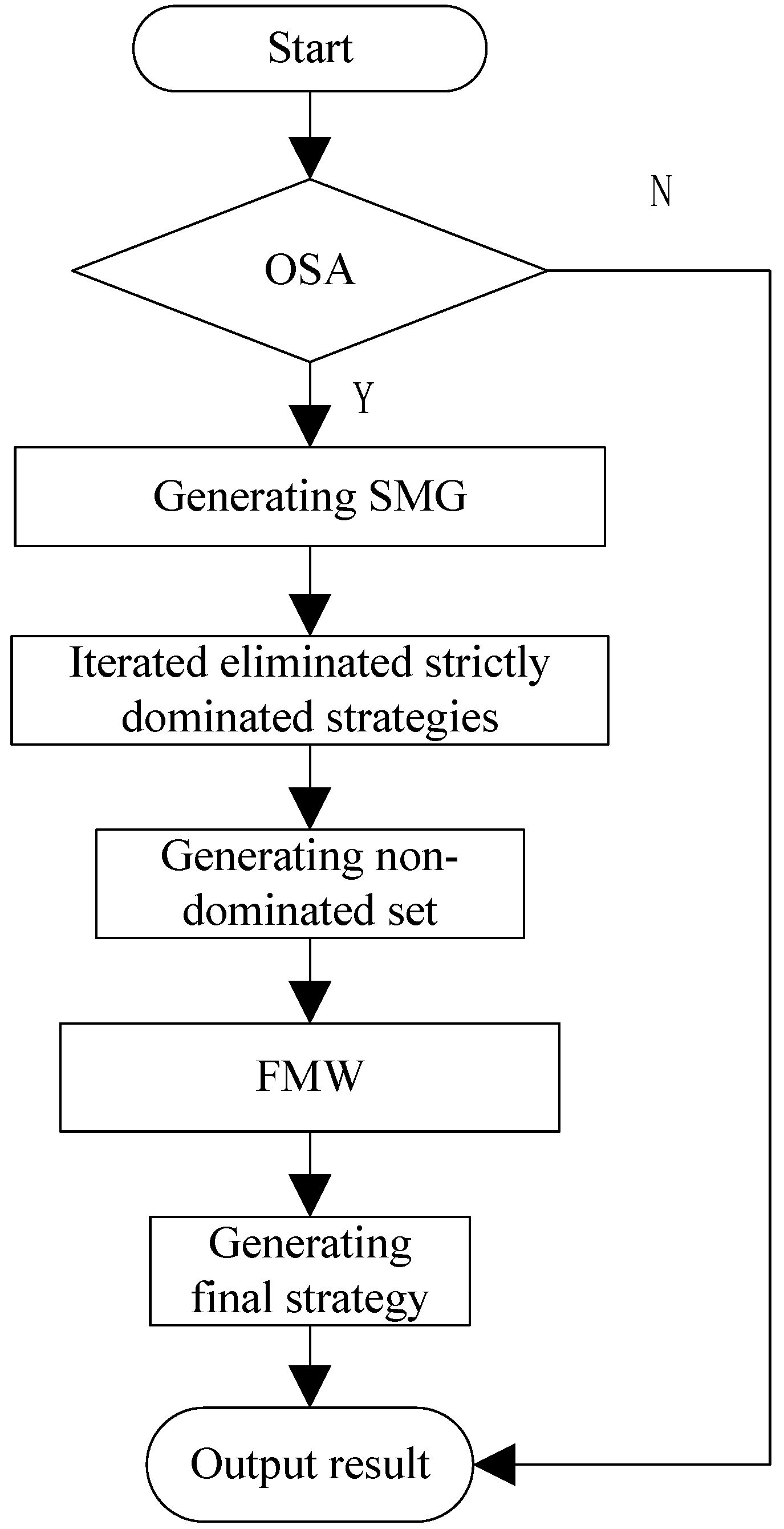
3. Game Optimization Theory
- (1)
- Optimization Stability Analysis (OSA);
- (2)
- Iterated Elimination of Strictly Dominant Strategies;
- (3)
- Generate the final strategy.
3.1. Optimization Stability Analysis
| O | M | |
| O | α11; β11 | α12; β12 |
| M | α21; β21 | α22; β22 |
| 1 − ε | ε |
| O | M | |
| O | α11; β11 | α12; β12 |
| M | α21; β21 | α22; β22 |
| ε | 1 − ε |
3.2. Iterated Elimination of Strictly Dominant Strategies
3.2.1. The Establishment of a Game
| F1 | ||||
| Low | Middle | High | ||
| F2 | Low | a1 ;b1; c1 | a1; b2; c1 | a1; b3; c1 |
| Middle | a2; b1; c1 | a2; b2; c1 | a2; b3; c1 | |
| High | a3; b1; c1 | a3; b2; c1 | a3; b3; c1 | |
3.2.2. Iterated Elimination of Strictly Dominant Strategies
| F1 | ||||
| Low | Middle | High | ||
| F2 | Low | a1 ;b1; c1 | a1; b2; c1 | a1; b3; c1 |
| Middle | a2; b1; c1 | a2; b2; c1 | a2; b3; c1 | |
| High | a3; b1; c1 | a3; b2; c1 | a3; b3; c1 | |
| F1 | ||||
| Low | Middle | High | ||
| F2 | Low | a1 ;b1; c1 | a1; b2; c1 | a1; b3; c1 |
| Middle | a2; b1; c1 | 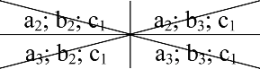 | ||
| High | a3; b1; c1 | |||
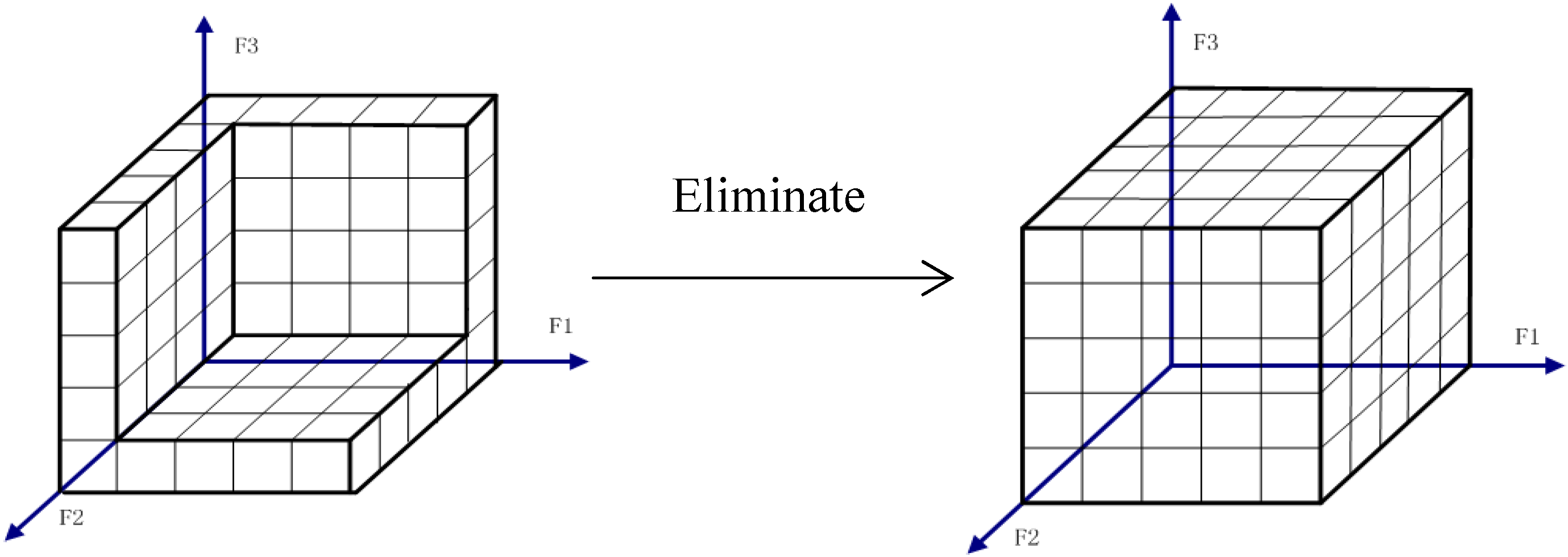



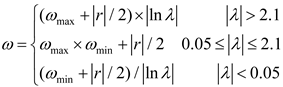

3.3. Generation of the Final Strategy
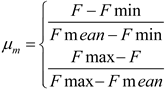
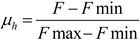
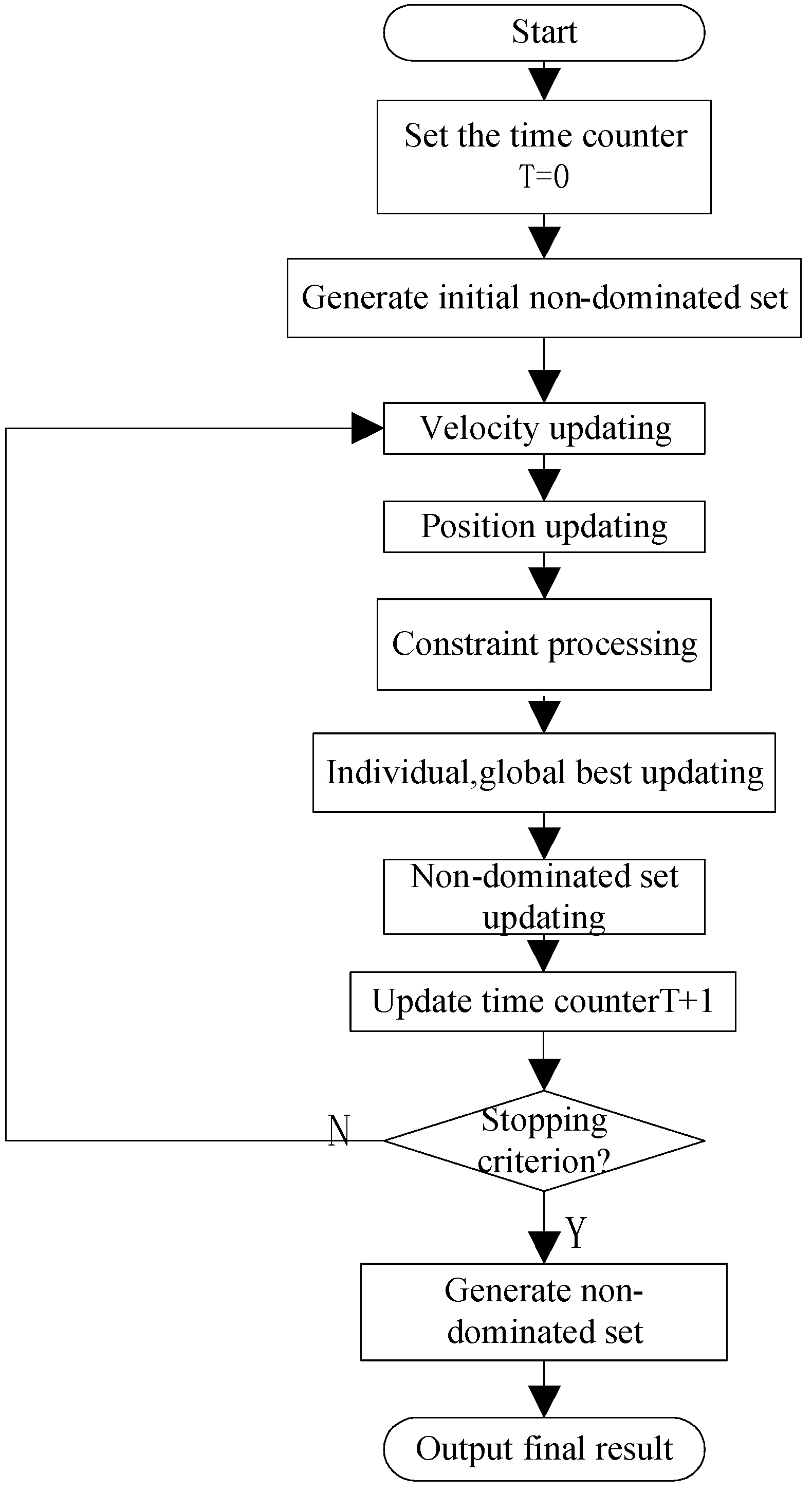
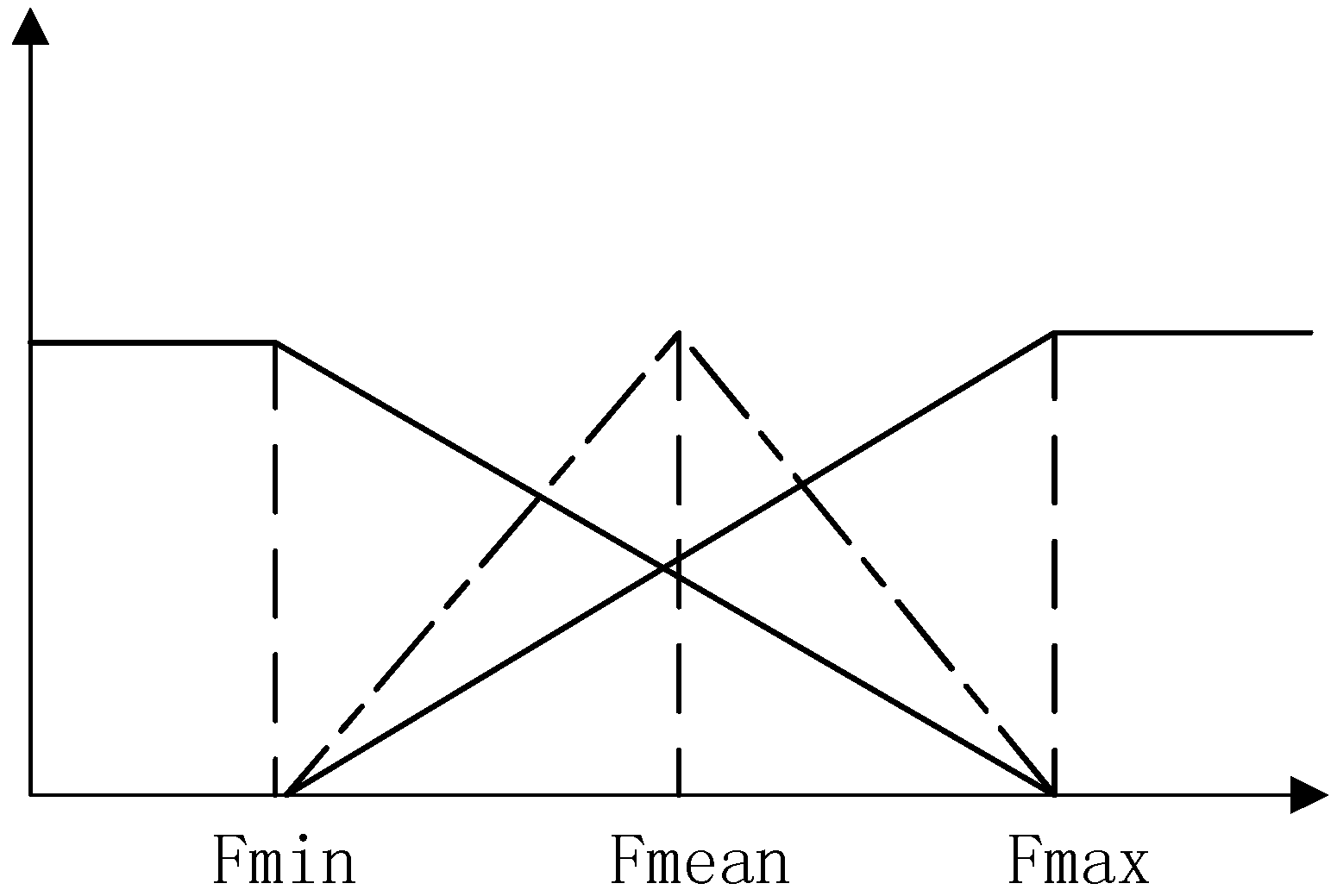
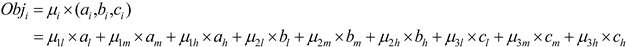
| F1 | F2 | F3 | |
|---|---|---|---|
| Low | al | bl | cl |
| Middle | am | bm | cm |
| High | ah | bh | ch |
4. Results and Discussion
4.1. Mathematical Formulation
- (1)
- To minimize the investment costs of DG;
- (2)
- To maximize the reduction in line losses;
- (3)
- To maximize the improvement in the voltage profile.
4.1.1. Investment Costs
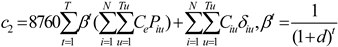
4.1.2. Line Losses

4.1.3. Voltage Profile
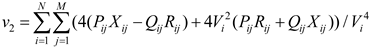
4.1.4. Constraints
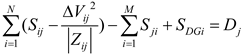
4.2. DG Optimization Similar Mixed Game
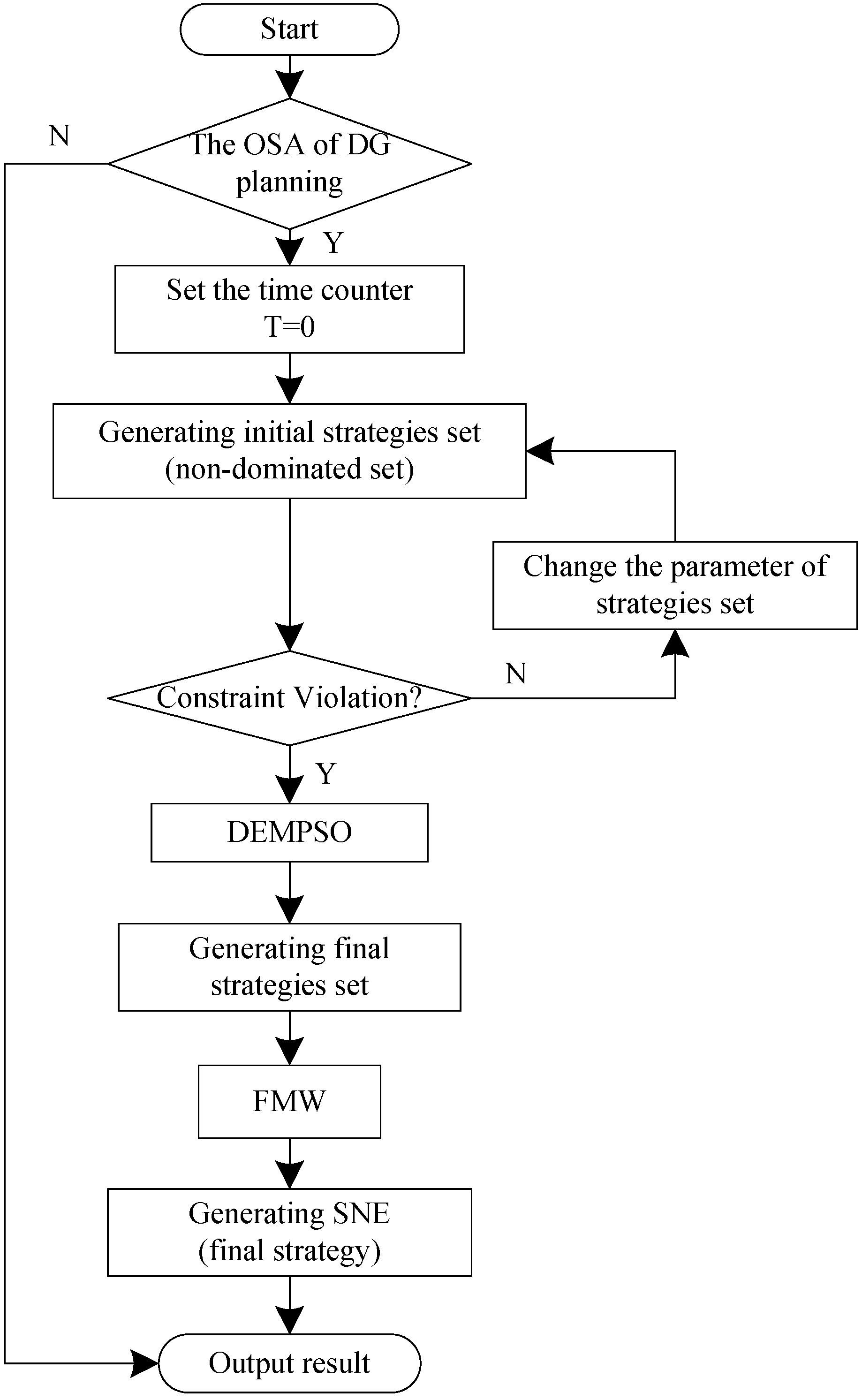

4.3. The OSA of DG Optimization Planning
| NDG | DG | |
|---|---|---|
| NDG | 3;0 | 3;1 |
| DG | 4;0 | 4;1 |
4.4. Case Study
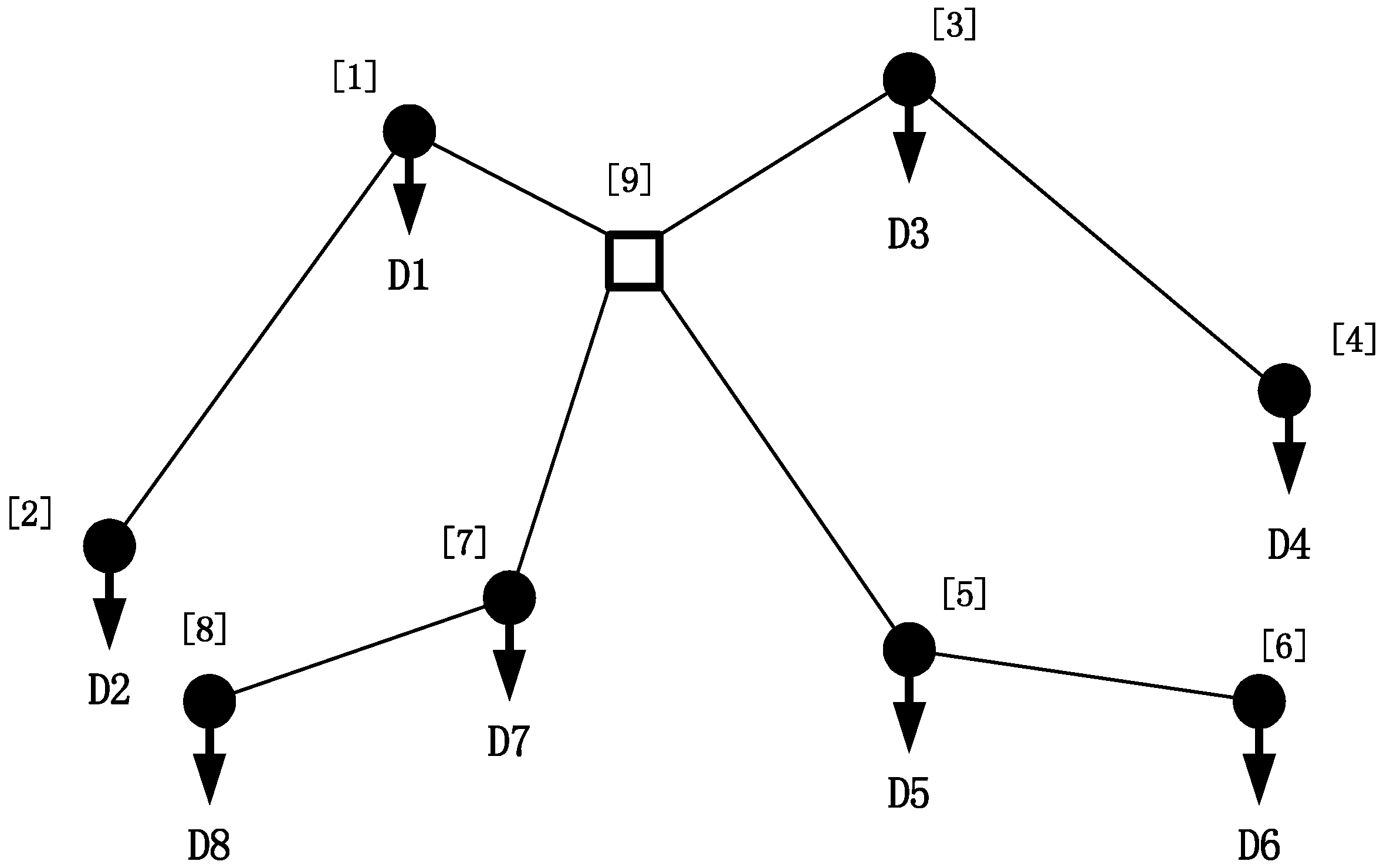
| Bus | Base Year/MVA | Horizon Year/MVA |
|---|---|---|
| 1 | 5.98 | 7.64 |
| 2 | 6.83 | 8.72 |
| 3 | 5.98 | 7.64 |
| 4 | 3.13 | 4.00 |
| 5 | 4.78 | 6.11 |
| 6 | 4.02 | 5.14 |
| 7 | 3.59 | 4.58 |
| 8 | 3.69 | 7.27 |
| From | To | Resistance/Ω | Reactance/Ω | Length/km |
|---|---|---|---|---|
| 9 | 1 | 1.390 | 2.255 | 8 |
| 9 | 3 | 2.085 | 3.383 | 12 |
| 9 | 5 | 2.259 | 3.664 | 13 |
| 9 | 7 | 1.738 | 2.819 | 10 |
| 1 | 2 | 2.780 | 4.510 | 16 |
| 3 | 4 | 2.780 | 4.510 | 16 |
| 5 | 6 | 2.433 | 3.946 | 14 |
| 7 | 8 | 2.085 | 3.383 | 12 |
4.4.1. Iterated Elimination of Strictly Dominant Strategy
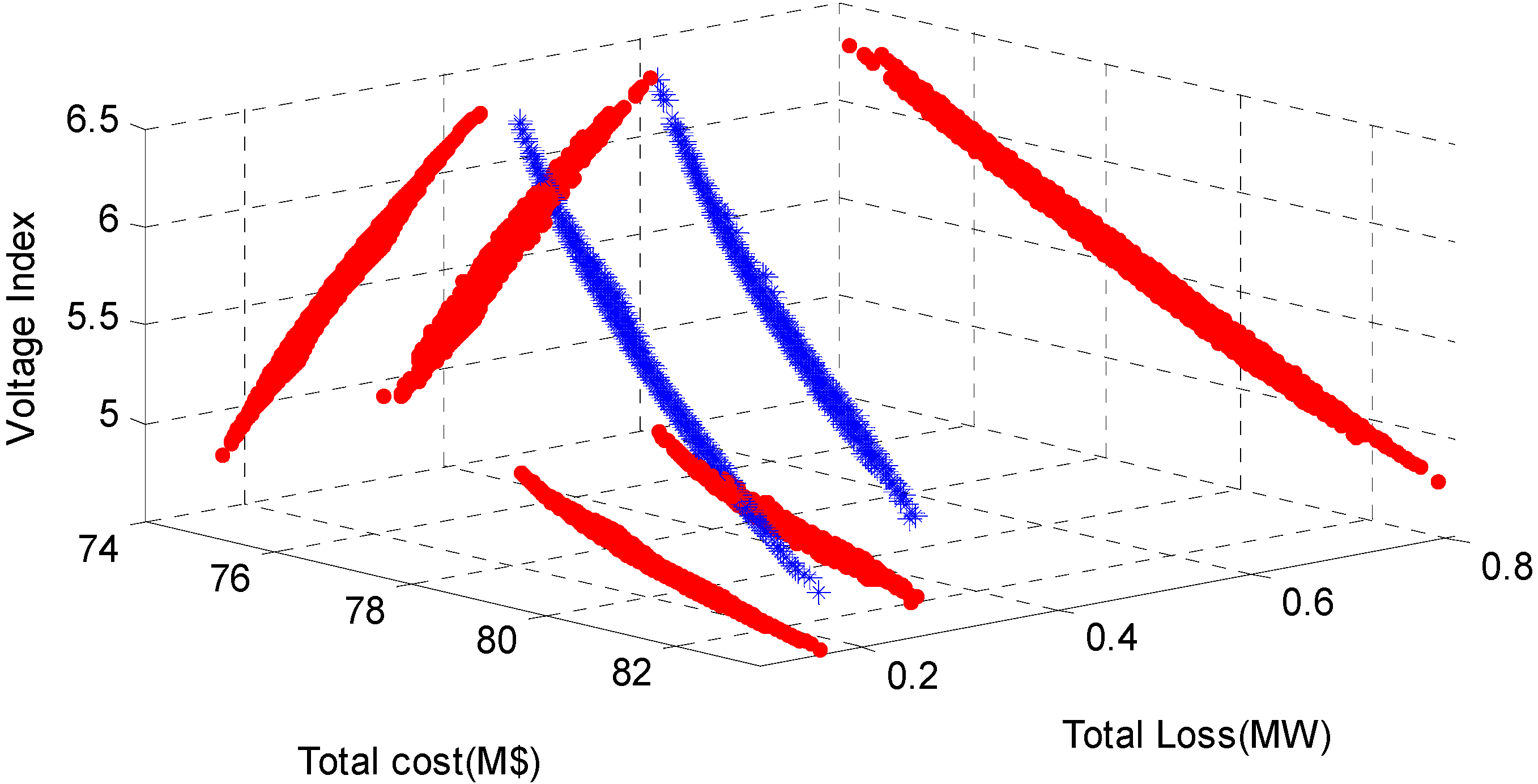
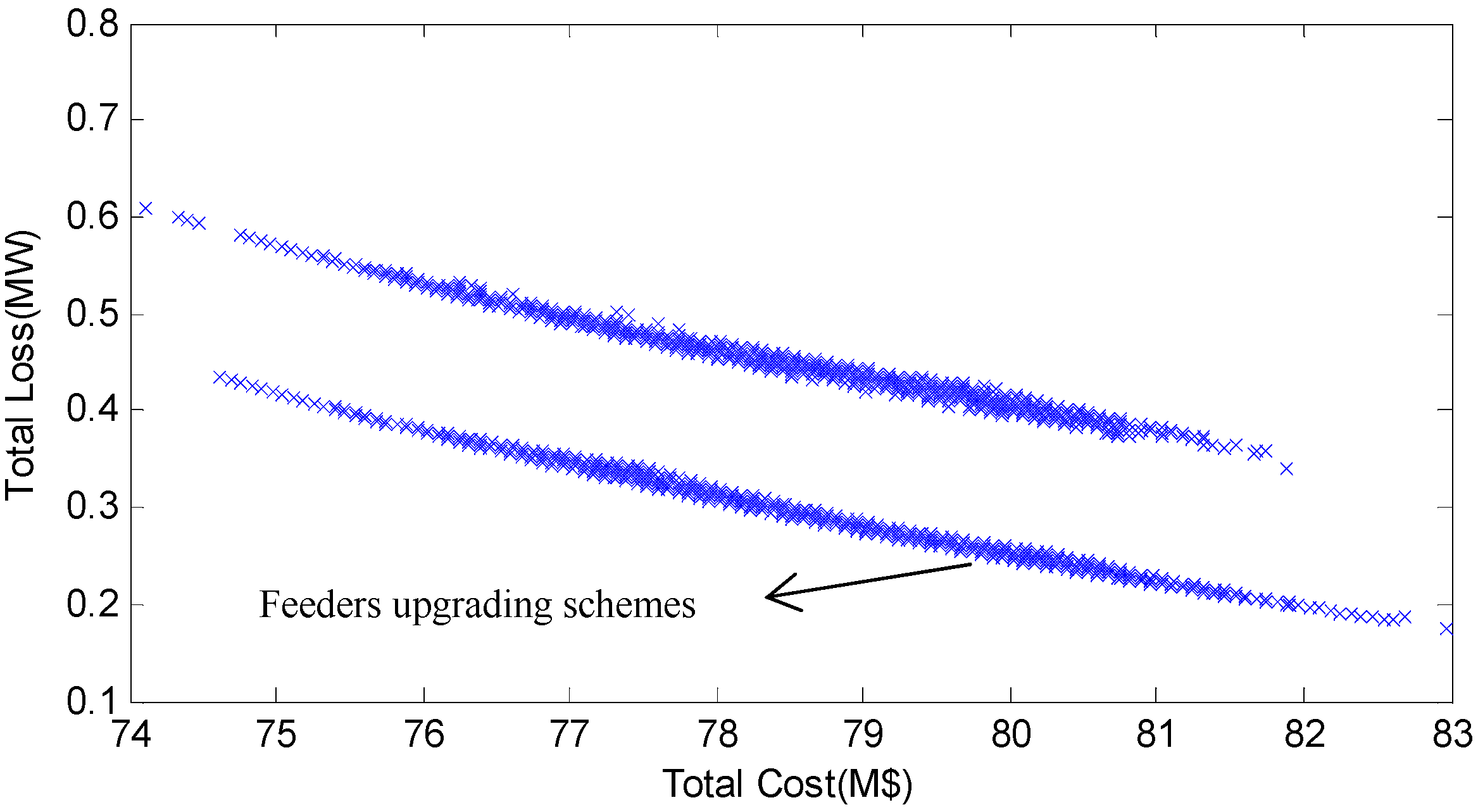
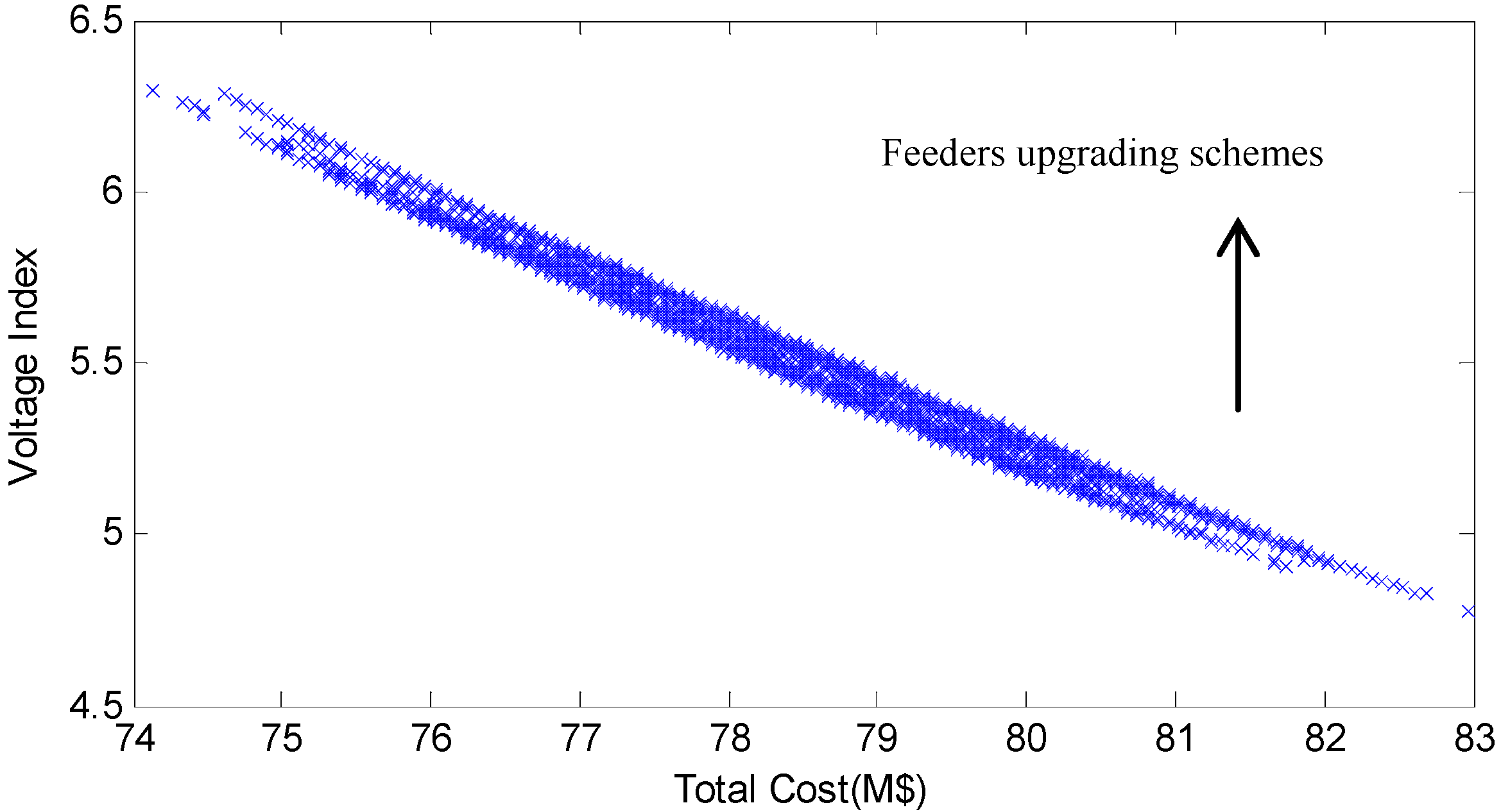
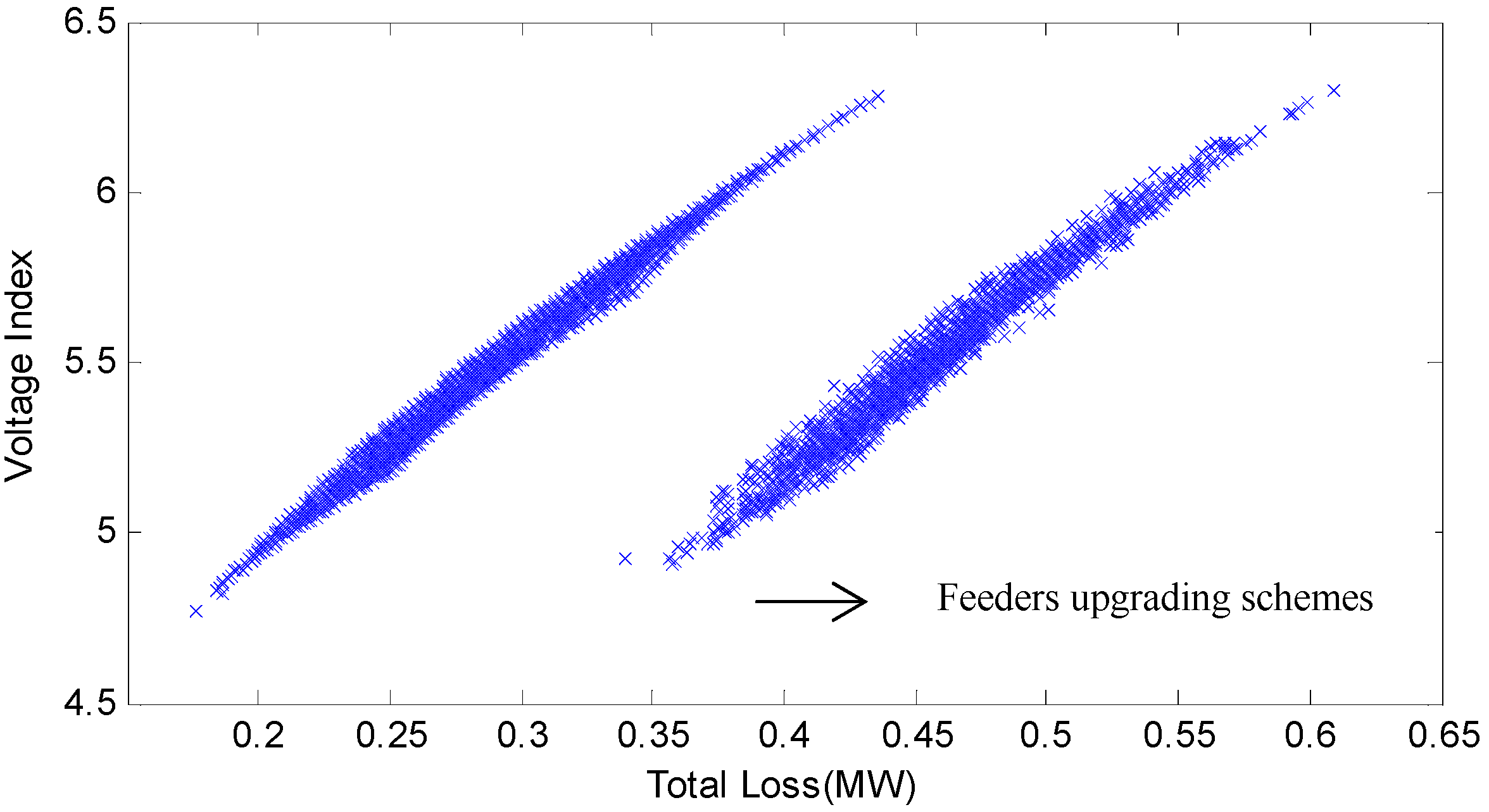
4.4.2. Generate Final Strategy
- Scheme 1: The final strategy is proposed by fuzzy method [26];
- Scheme 2: The final strategy is proposed by FMW, the subjective preference is total costs;
- Scheme 3: The final strategy is proposed by FMW, the subjective preference is total losses;
- Scheme 4: The final strategy is proposed by FMW, the subjective preference is voltage profile;
- Scheme 5: The final strategy is proposed by FMW, there is no subjective preference among the objectives.
| Economical parameter | Scheme1 | Scheme2 | Scheme3 | Scheme4 | Scheme5 |
|---|---|---|---|---|---|
| Number of Feeders Upgrades | 0 | 1 | 1 | 0 | 1 |
| Feeders Fixed Cost/M$ | 0 | 1.2 | 1.2 | 0 | 1.2 |
| Number of New Transformers | 0 | 0 | 0 | 0 | 0 |
| Substation Total Cost/M$ | 34.21 | 39.92 | 36.71 | 31.58 | 37.01 |
| DG Capacity/MVA | 32.7 | 26.6 | 29.9 | 35.4 | 29.6 |
| DG Total Cost/M$ | 45.62 | 35.34 | 40.90 | 50.16 | 40.39 |
| Total Planning Cost/M$ | 79.83 | 76.46 | 78.81 | 81.74 | 78.60 |
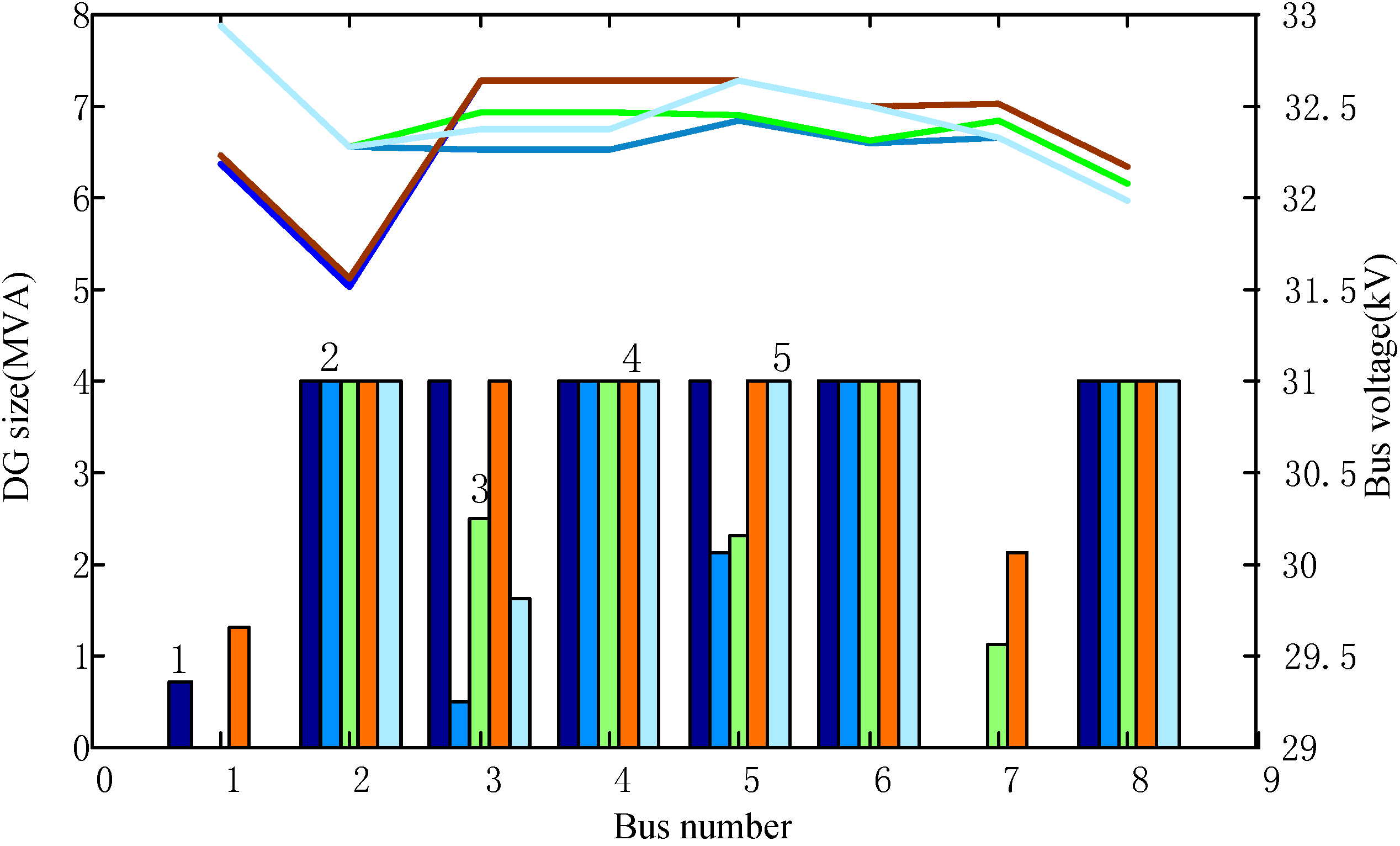
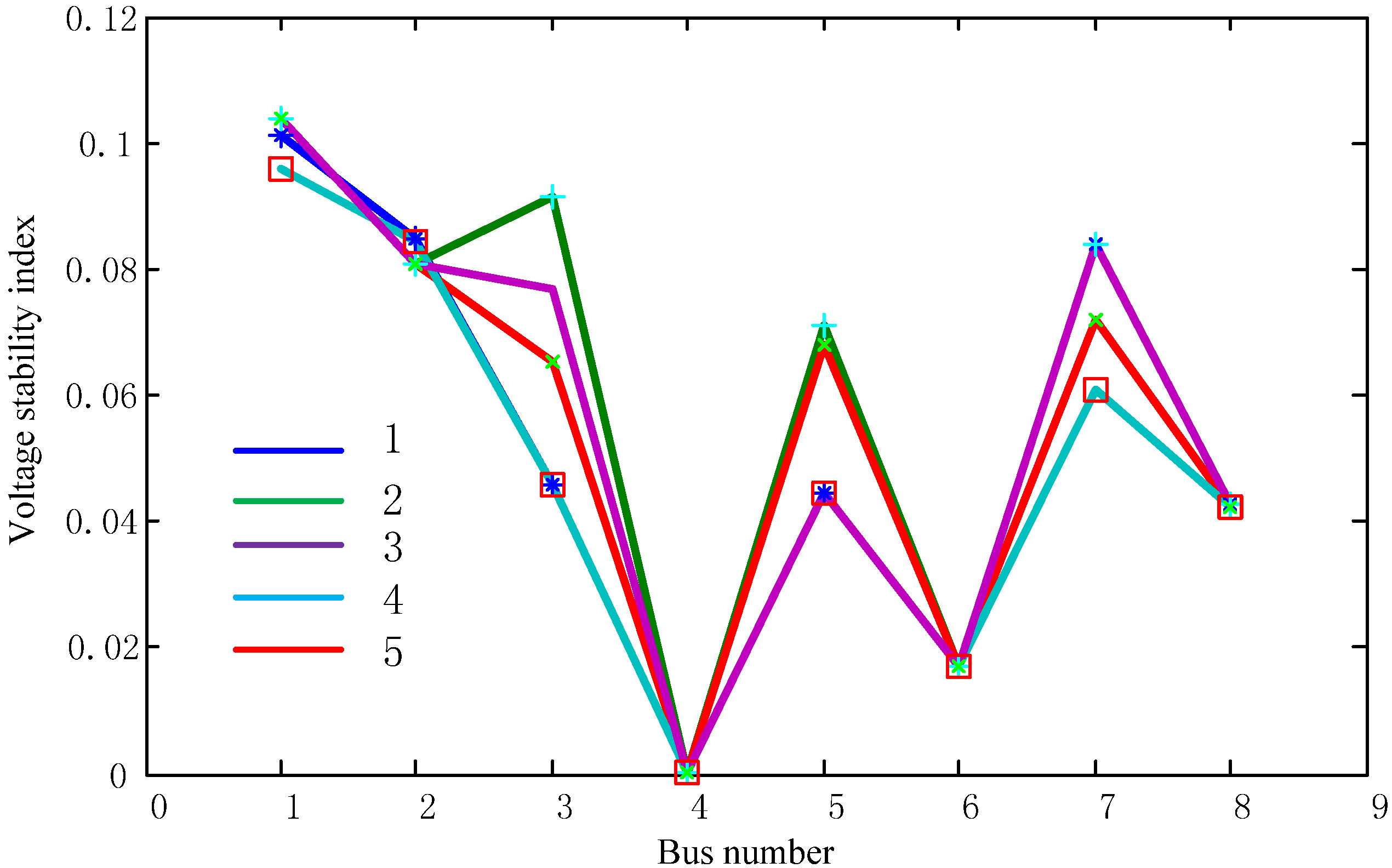
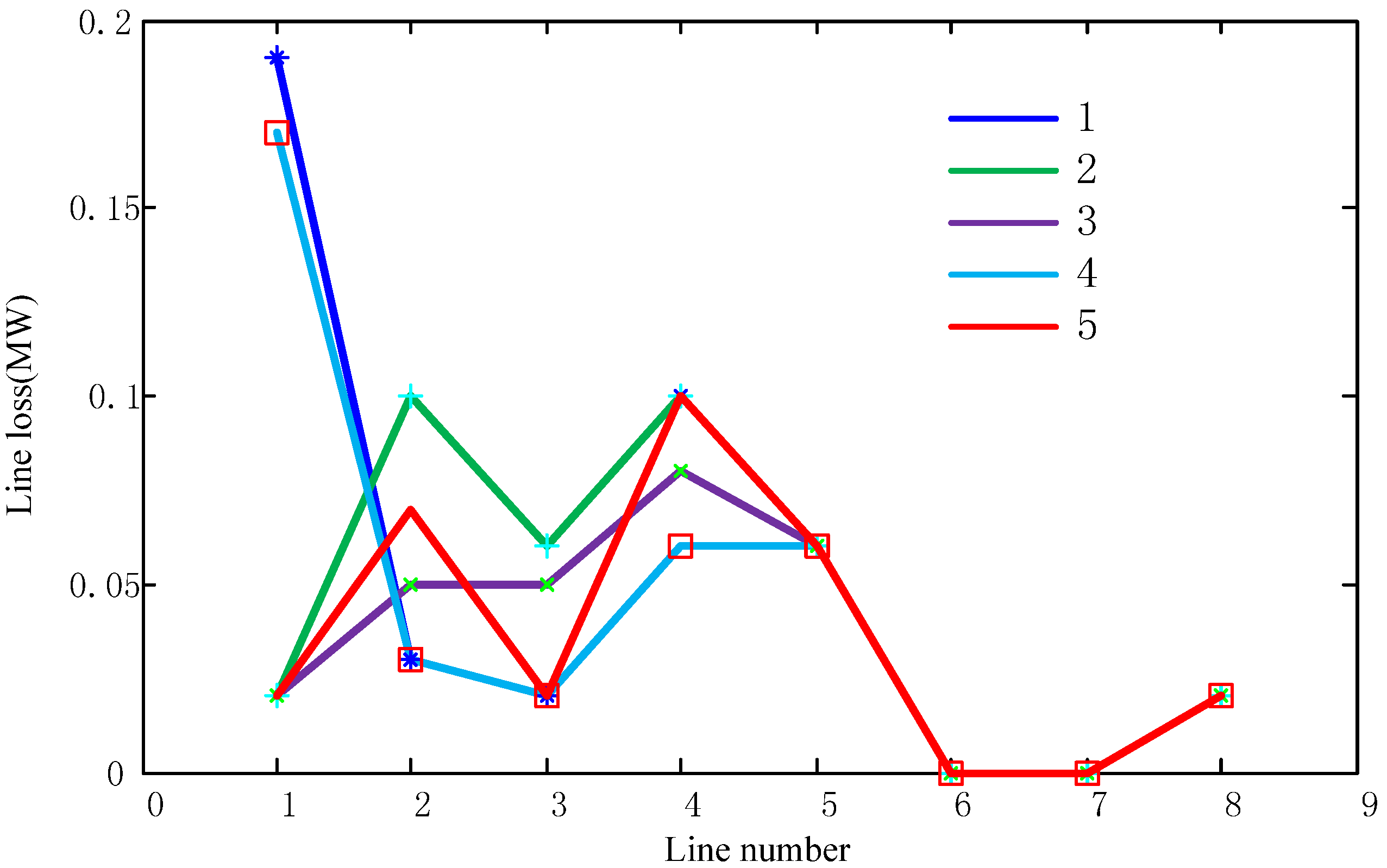
5. Conclusions
- (1)
- The establishment of GOT supplies a new method to explain MOP, and GOT is used for the first time in solving the distribution system planning problem by implementing DG. The results obtain a suitable final DSP scheme.
- (2)
- Optimization Stability Analysis offsets the disadvantage of calculating directly with an optimization algorithm after the object functions are selected for an optimal problem. The OSA process could offer an assessment of the value of the optimization and improved measures.
- (3)
- The concept of SMG constructs a new type of game to handle the MOP and enriches the concepts of Game Theory. The DEMPSO could find the Pareto front quickly and generate a non-dominant set reasonably. The FMW could weaken the influences produced by subjective preference information by taking multi-weight into consideration in the evaluation of non-dominant solutions.
- (4)
- A mathematical model consisting of costs, line losses and voltage profile, is constructed in this paper. This model could assess comprehensively the influence of implementing DG in a distribution system. The result of optimization shows that the scheme of DG embedded in distribution system could bring benefits to the operation of the power system, reduce power losses, improve the amplitude of voltage and improve the voltage stability of feeders, and this method could dominate the substation expansion scheme.
Nomenclature:
| N | total number of system buses |
| M | total number of load buses |
| Tu | total number of substation transformers |
| Cij | the total feeder costs from i to j |
| Ce | electricity market price |
| Ciu | the costs of potential transformer u in substation i |
| Cri | the operation costs for DG |
| T | horizon planning year |
| β | present worth factor |
| d | discount rate |
| Piu | transformer u in substation i dispatched power |
| SDGi | power generated from distributed generation |
| pf | system power factor |
| σij | feeder i to j binary decision variable |
| σiu | transformer u in substation i binary decision variable |
| σDGi | distributed generation binary decision variable |
| V | bus voltage |
| Y | the line admittance |
| θij | the angle of admittance connecting i to j |
| σji | the difference of phase of voltage |
| Pij | the active power flow from node i to j |
| Qij | the reactive power flow from node i to j |
| R | the line resistance |
| X | the line reactance |
| Sij | power flow in feeder connecting bus i to j |
| σij max | feeder’s thermal capacity limit |
| SDGi max | distributed generation capacity limit |
| SSmax | substation capacity limit |
References
- Nash, J.F. Equilibrium points in N-Person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.F. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Nash, J.F. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Gibbons, R. A Primer in Game Theory; The MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Koichi, N.; Hayashi, Y.; Ikeda, K.; Ashizawa, T. Application of Tabu Search to Optimal Placement of distributed Generators. In Proceedings of IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; pp. 918–923.
- Griffin, T.; Tomsovic, K.; Secrest, D.; Law, A. Placement of Dispersed Generations Systems for Reduced Losses. In Proceedings of the IEEE 33rd Hawaii International Conference on System Sciences, Hawaii, HI, USA, 7 January 2000; pp. 1–9.
- Khalesi, N.; Rezaei, N.; Haghifam, M.-R. DG allocation with application of dynamic programming for loss reduction and reliability improvement. Electr. Power Energy Syst. 2011, 33, 288–295. [Google Scholar] [CrossRef]
- Kuri, B.; Redfern, M.A.; Li, F. Optimization of Rating and Positioning of Dispersed Generation with Minimum Network Disruption. In Proceedings of IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 2074–2078.
- EI-Khattam, W; Hegazy, Y.G.; Salama, M.M.A. An integrated distributed generation optimization model for distribution system planning. IEEE Trans. Power Syst 2005, 20, 1158–1165. [Google Scholar]
- EI-Khattam, W.; Bhattacharya, K.; Hegazy, Y.; Salama, M.M.A. Optimal investment planning for distributed generation in a competitive electricity market. IEEE Trans. Power Syst. 2004, 19, 1674–1684. [Google Scholar] [CrossRef]
- Mantwy, A.H.; AL-Muhaini, M.M. Multi-Objective BPSO Algorithm for Distribution System Expansion Planning Including Distributed Generation. In Proceedings of IEEE Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–8.
- Alarcon-Rodriguez, A.; Haesen, E.; Ault, G.; Driesen, G.; Belmans, R. Multi-objective planning framework for stochastic and controllable distributed energy resources. IET Renew. Power Gener. 2009, 19, 227–238. [Google Scholar] [CrossRef]
- Maynard Smith, J.; Price, G.R. The logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Edgeworth, F.Y. Mathematical Psychics; Kessinger Publishing: Whitefish, MT, USA, 2007. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948.
- Van den Bergh, F. An Analysis of Particle Swarm Optimizers. PhD Dissertation, University of Pretoria, Pretoria, South Africa, 2001. [Google Scholar]
- Coello, C.; Pulido, G.; Lechuga, M. Handling multiple objectives with particles swarms optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Li, N.; Sun, D.; Cen, Y. Particle swarm optimization with mutation operator. Comput. Eng. Appl. 2004, 17, 12–14. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence; John Wiley & Sons Inc.: New York, NY, USA, 2007. [Google Scholar]
- Chakravotry, M; Das, D. Voltage stability analysis of radial distribution networks. Electr. Power Energy Syst. 2001, 23, 129–135. [Google Scholar] [CrossRef]
- Bayod-Rújula, A.A. Future development of the electricity systems with distributed Generation. Energy 2009, 34, 377–383. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M. A distribution network expansion planning model considering distributed generation options and techo-economical issues. Energy 2010, 35, 3364–3374. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghoshal, S.P.; Ghosh, S. Optimal sizing and placement of distributed generation in a network system. Electr. Power Syst. 2010, 32, 849–856. [Google Scholar] [CrossRef]
- Maciel, R.S.; Rosa, M.; Miranda, V.; Padilha-Feltrin, A. Multi-objective evolutionary particle swarm optimization in the assessment of the impact of distributed generation. Electr. Power Syst. Res. 2012, 89, 100–108. [Google Scholar] [CrossRef]
- Farjah, E.; Bornapour, M.; Niknam, T.; Bahmanifirouzi, B. Placement of combined heat, power and hydrogen production fuel cell power plants in a distribution network. Energies 2012, 5, 790–814. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, R.; Ma, H.; Wang, F.; Wang, Y.; Liu, Y.; Li, Z. Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation. Energies 2013, 6, 1101-1124. https://doi.org/10.3390/en6021101
Li R, Ma H, Wang F, Wang Y, Liu Y, Li Z. Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation. Energies. 2013; 6(2):1101-1124. https://doi.org/10.3390/en6021101
Chicago/Turabian StyleLi, Ran, Huizhuo Ma, Feifei Wang, Yihe Wang, Yang Liu, and Zenghui Li. 2013. "Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation" Energies 6, no. 2: 1101-1124. https://doi.org/10.3390/en6021101
APA StyleLi, R., Ma, H., Wang, F., Wang, Y., Liu, Y., & Li, Z. (2013). Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation. Energies, 6(2), 1101-1124. https://doi.org/10.3390/en6021101




