Abstract
A second-order discrete-time sliding mode observer (DSMO)-based method is proposed to estimate the state of charge (SOC) of a Li-ion battery. Unlike the first-order sliding mode approach, the proposed method eliminates the chattering phenomenon in SOC estimation. Further, a battery model with a dynamic resistance is also proposed to improve the accuracy of the battery model. Similar to actual battery behavior, the resistance parameters in this model are changed by both the magnitude of the discharge current and the SOC level. Validation of the dynamic resistance model is performed through pulse current discharge tests at two different SOC levels. Our experimental results show that the proposed estimation method not only enhances the estimation accuracy but also eliminates the chattering phenomenon. The SOC estimation performance of the second-order DSMO is compared with that of the first-order DSMO.
1. Introduction
Li-ion batteries are used in a wide range of applications, such as in portable electronic devices and electric vehicles, because of their advantages, e.g., high energy density, high electromotive force, and low cost. To improve the performance of Li-ion batteries, battery management systems (BMSs) have been studied [1,2]. In the various functions of BMSs, it is necessary to estimate the state of charge (SOC) and model the battery dynamics [3,4,5]. In the present study, we focus on enhancing the accuracy of not only the SOC estimation but also the battery model.
To accurately estimate the SOC, a variety of methods based on ampere-hour counting, a linear SOC equation, artificial neural networks, impedance spectroscopy measurements, and battery modeling have been proposed in recent papers. The ampere-hour counting method [6] is the most commonly used SOC estimation method because of its simplicity. This method measures the charge and discharge current and estimates the SOC using the integral of the current over time. However, there are several problems associated with this method. First, integration errors caused by current measurement noise or energy losses during charging/discharging, could accumulate. Moreover, determining the initial SOC is difficult unless the battery is fully charged or conditionally discharged. The linear equation method [7] calculates the variation of the SOC using the voltage output, current input, and previous SOC data. In this equation, the coefficients are determined from the reference data of a specific battery. Thus, if the battery is changed, then the coefficients must also be re-calculated. An artificial neural network used for SOC estimation is presented in [8]. Fundamentally, because the battery dynamics exhibit nonlinear behavior, this method usually produces a more accurate SOC estimate than the other methods. However, the estimation process strongly depends on the training data (similar to the case of the linear model method), and the learning process is difficult to implement on-line owing to the burdensome computations required. The impedance spectroscopy method [9] examines the electrochemical impedance of the battery to determine the SOC. However, sensors for impedance measurement are expensive, and unexpected situations can arise when a signal is injected into the battery to measure the impedance while the battery is powering electronic devices. The battery model-based SOC estimation method [10,11] consists of a state equation derived from an equivalent circuit battery model and a state observer. In this method, the SOC is considered a state variable; it is estimated using a state observer. This method has been widely used because this approach enables to apply existing observers. In [10], a Kalman filter (KF) was employed to estimate the SOC of a lead-acid battery. However, the KF suffers from a well-known drawback in that no analytical selection methods are available for either the process or measurement noise covariance matrices. Indeed, incorrectly selected covariance matrices can reduce the estimation performance. A first-order sliding mode observer (SMO) for SOC estimation was presented first in [11]. An SMO is widely used owing to its simplicity and robustness to both parameter variations and external disturbances. In spite of these attractive properties, the first-order SMO introduces a chattering phenomenon, which involves oscillations with high frequency and finite amplitude [12]. This shortcoming is a major drawback of the sliding mode approach in practical implementations. In order to reduce the chattering phenomenon, a second-order sliding mode based-observer [13,14,15] has received a lot of attention recently, because the second-order sliding mode approach can drive to zero not only the sliding variable, but also its derivative.
In the present paper, a novel SOC estimation method based on a second-order discrete-time SMO (DSMO) is proposed to eliminate the chattering phenomenon. In addition, a dynamic resistance model is proposed to more accurately describe the dynamics of the Li-ion battery. The resistance parameters are updated on the basis of both the discharge current and the SOC level. The proposed SOC estimation method and dynamic resistance model are validated by experimental results.
The remainder of this paper is organized as follows. Section 2 presents information on the equivalent circuit-based battery model and the limitations of the existing schemes. Section 3 proposes an SOC estimation method based on the second-order DSMO. Section 4 presents both our experimental results for the SOC estimation performance using the second-order DSMO described in Section 3 and the validation of the dynamic resistance model. Finally, Section 5 presents our conclusions.
2. Battery Modeling
The equivalent circuit-based battery model [10,11] is often used because it can be easily transformed into a state-space equation form. In this paper, the circuit in Figure 1 is employed in consideration of both the model accuracy and complexity. This model consists of a nonlinear voltage source, a capacitor, and three resistors.
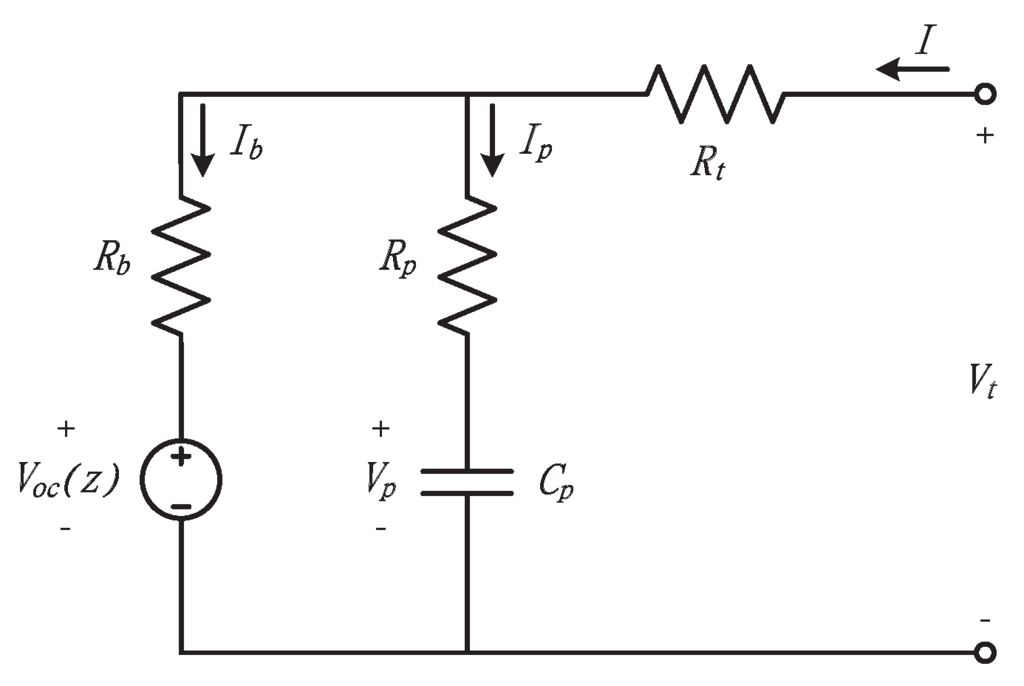
Figure 1.
Equivalent circuit-based battery model.
The voltage source Voc(Z) represents the relationship between the open circuit voltage (OCV) and the SOC, as shown in Figure 2. The OCV-SOC curve is obtained from the conditional discharge test data [16]. The nominal capacitance Cn characterizes the capacity of the battery to store charge. The polarization capacitance Cp describes the polarization effect of the battery. In addition, the terminal resistor Rt, the diffusion resistor Rp, and the propagation resistor Rb represent the resistive components in the battery.
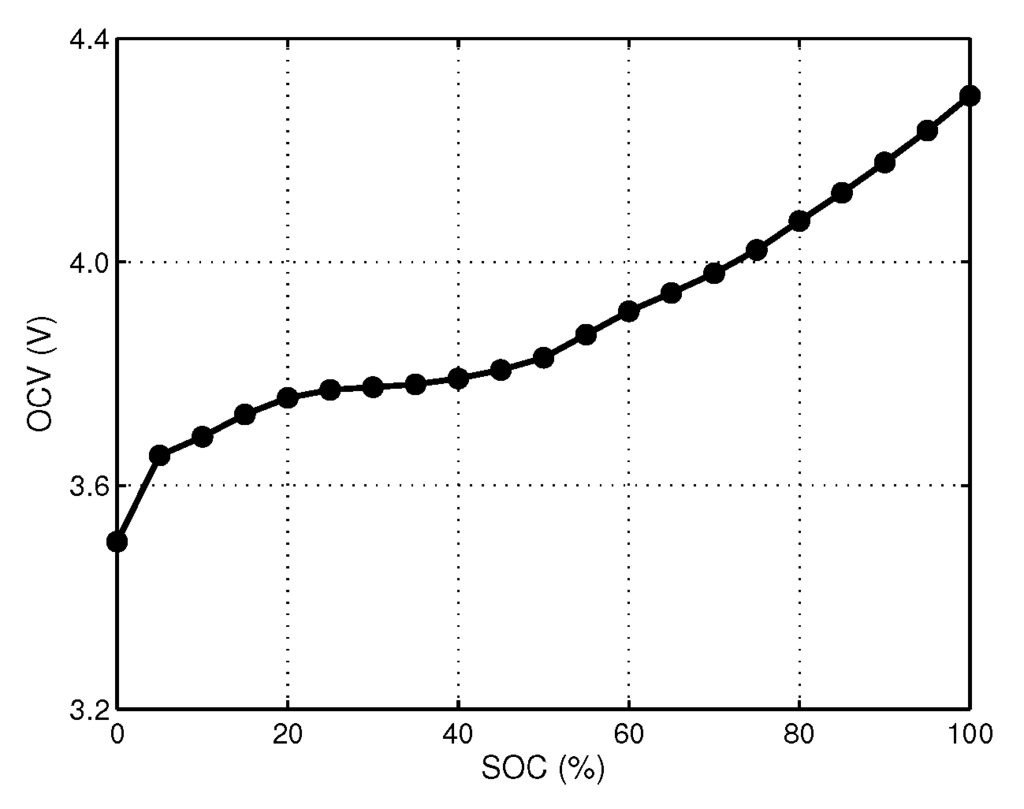
Figure 2.
Open circuit voltage (OCV)-state of charge (SOC) curve at room temperature.
In [11], the state-space representation of the battery model is given by Equation (1). These equations consist of three state variables: the output terminal voltage Vt, the SOC Z, and the polarization voltage Vp:
where:
In previous papers, the parameters of the battery were assumed to be constant during discharge [10,11]. However, the actual internal resistance changes depending on the operating conditions; this resistance variation causes modeling errors [17]. Therefore, we propose a dynamic resistance battery model to represent the battery dynamics more accurately. The proposed model employs a dynamic resistance that varies according to both the magnitude of the discharge current and the SOC level. The modeling accuracy performance of the proposed model is verified in Section 4.
3. Second-Order DSMO for SOC Estimation
In this section, the second-order DSMO [13], which is used for the estimation of the SOC and the terminal voltage, is introduced. We consider a system described by:
where x ∈ ℜn is the state variable vector; u ∈ ℜ is the input; y ∈ ℜ is the system output; and Δ represents the uncertainties caused by parameter variations and non-linearities. A, B, and H are the system nominal matrices, and (A, H) is assumed to be observable. Then, the second-order DSMO of the system [Equation (3)] has the form:
where is the estimated state vector; is the estimated output; ϕ determines the boundary layer; and L and M are the observer gain vectors (which are related to and the sign of , respectively). In general, the sign function sign(·) in the SMO is replaced by the saturation function sat(·) in practical implementations of sliding mode concepts.
On the other hand, linearization and discretization of the battery model in Equation (1) are required because the second-order DSMO is developed on the basis of a discrete-time linear system. To obtain a linear system, we assume that the value of the voltage source Voc is constant value αk over a sampling interval [k, k + 1]. This assumption is valid because the rate of change of Z over the interval is negligible, and errors caused by this assumption can be regarded as part of the uncertainty. Taking Voc(Z(t)) = αk, t ∈ [k, k + 1], Equation (1) is rewritten as follows:
where:
Then, using the Euler discretization method with a sampling period T, the discrete-time linear state equation is given by:
where Λ(k) represents modeling errors caused by parameter uncertainties, linearization, and discretization. We assume that the variation of each Λi(k), which is an element of the uncertainty vector Λ(k), is bounded by the known bound σi:
the bound σi is determined experimentally by comparing the modeling output with the actual battery output.
Remark 1: We note that the SOC at the sampling instant k + 1, i.e., Zk+1, is updated according to Equation (7), and the value of the voltage source is also reset as Voc(Z(t)) = Voc(Zk+1) = αk+1, t ∈ [k + 1, k + 2].
Finally, the proposed SOC estimation method based on the second-order DSMO is formed by:
by Theorem 1 in [13], if the observer gain vector M satisfies the inequalities:
then the estimation error converges to a finite bound when k→ ∞. A stability analysis of the second-order DSMO is presented in Appendix.
4. Experimental Results
Two types of experiments are performed to show the following:
- improvement of the battery modeling accuracy with the dynamic resistance varied with the operating conditions;
- the SOC estimation method using the second-order DSMO for the elimination of chattering.
The battery test bench is composed of an electrical load, a power supply, and an National Instruments Data Acquisition device. The electrical load and the power supply are used to discharge/charge the battery, and the output voltage is measured using LabView, a PC-based program. In the experiment, a fresh 18650-type Li-ion battery is used; it has a 3.0 A h nominal capacity and a 3.7 V nominal voltage. All experiments are carried out at room temperature.
4.1. Parameter Extraction
The parameters of the battery model are determined from the battery characterization test data. The initial value of the nominal capacitance is obtained from the energy stored in the capacitor and the OCV at 100% and 0% SOC:
where AmpSec_rated is the rated battery capacity.
The polarization capacitance is derived from high-frequency excitation tests, which apply a 1.0C discharge pulse in 0.5 s intervals. Using the results in Figure 3, we approximate the time constant using the following equation:
The time constant associated with Cp is represented by its associated resistance:
The internal resistance Rint is obtained using the direct current-internal resistance (DC-IR) method:
where Idis represents the discharge current. Generally, it is assumed that Rb and Rp are taken to be 75% of Rint and Rt is equivalent to 25% of Rint [10].
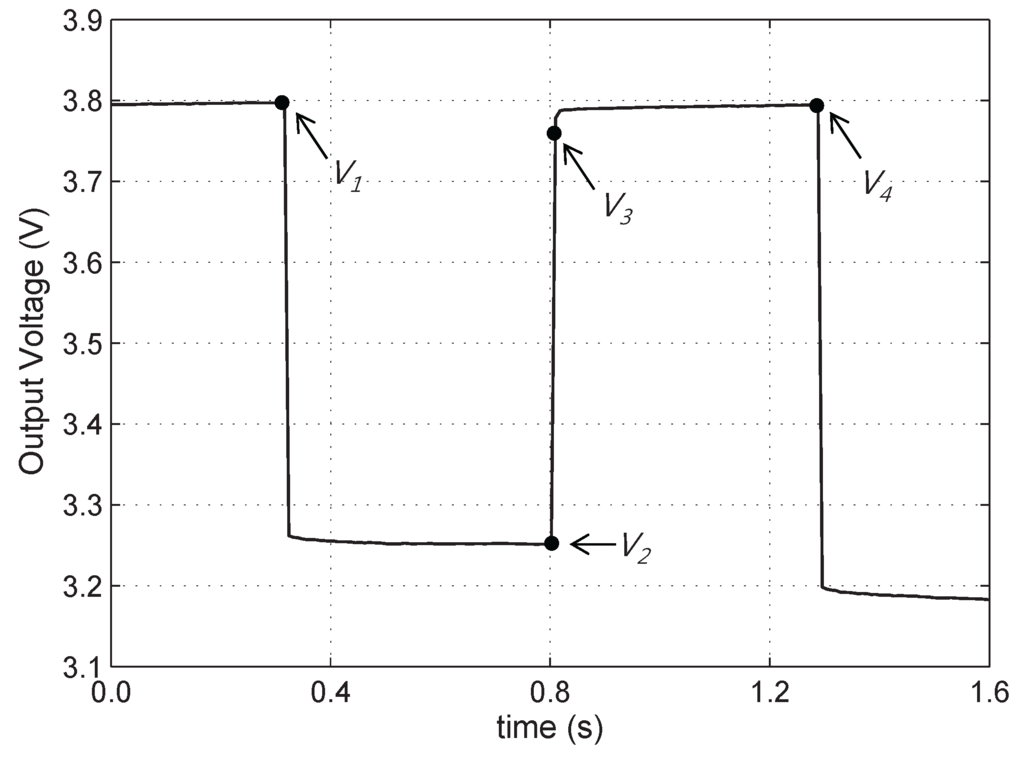
Figure 3.
Output voltage when a discharge current of 1.0C is applied in 0.5 s intervals.
4.2. Dynamic Resistance
As mentioned in Section 2, previous papers assumed that the parameters used in the battery model are constant. However, this assumption leads to large modeling errors because the internal resistance of the battery depends on the operating conditions such as the magnitude of the discharge current and the SOC level. To examine this change in the internal resistance, our first experiment is performed. The current profile used in this experiment is composed of a 3 s discharge pulse and a 3 s rest, as shown in Figure 4.
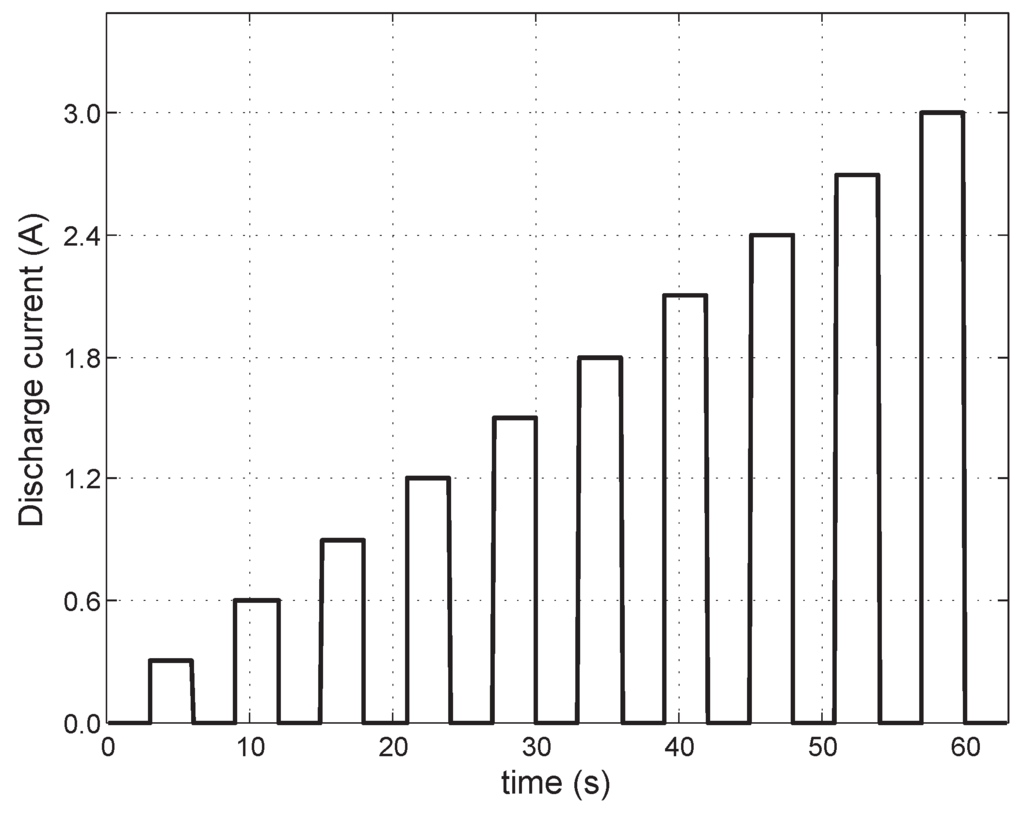
Figure 4.
Pulse discharge current used to examine the variation in the internal resistance.
To verify the effect of the discharge current and the SOC on the internal resistance, the discharge current is increased from 0.1C to 1.0C in intervals of 0.1C; this profile is repeated from 100% to 0% SOC. The experimental results in Figure 5 show the SOC versus Rint curves for each discharge current. These results are obtained from 10 independent trials. As expected, the internal resistance has a higher value at higher discharge currents and at both ends of the SOC level. Therefore, allowing the resistance to vary with the discharge current and the SOC level is a reasonable way of more accurately representing the battery dynamics.
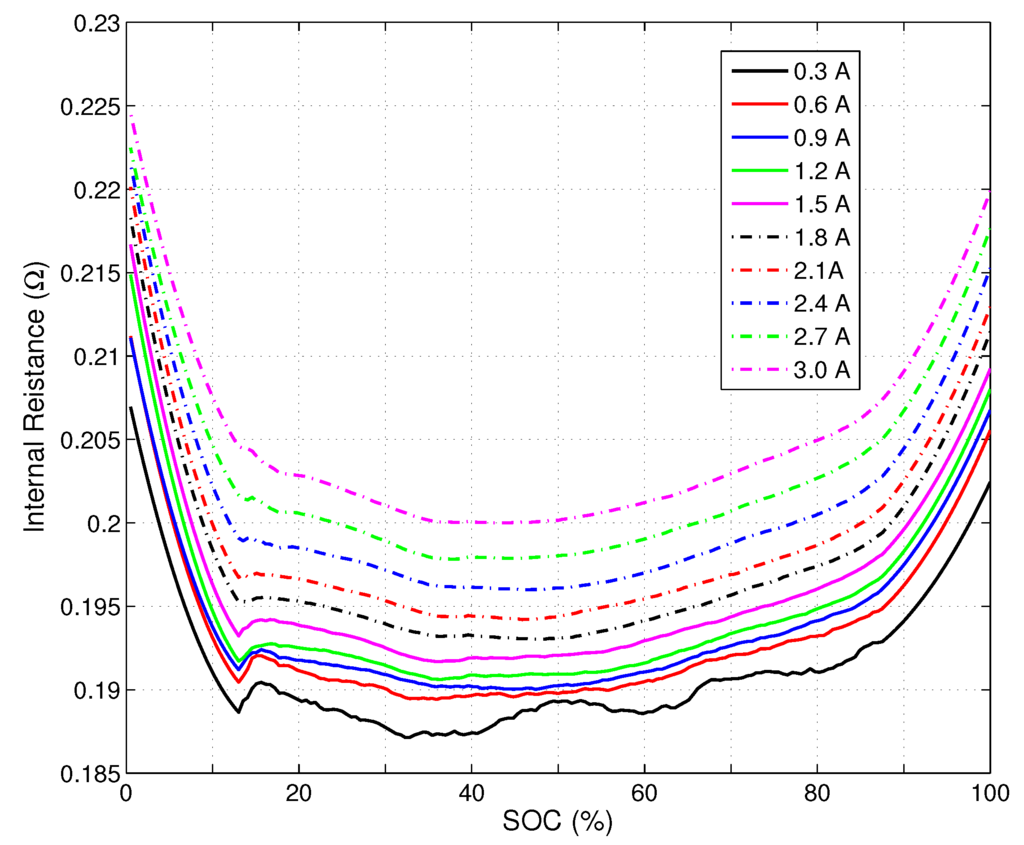
Figure 5.
Internal resistance variation for different discharge currents and different SOC levels.
To validate the dynamic resistance model, the current profile in Figure 4 is applied repeatedly over the 100%–0% SOC range. Figure 6 shows the output voltage modeling results at 100% and 50% SOC, respectively.
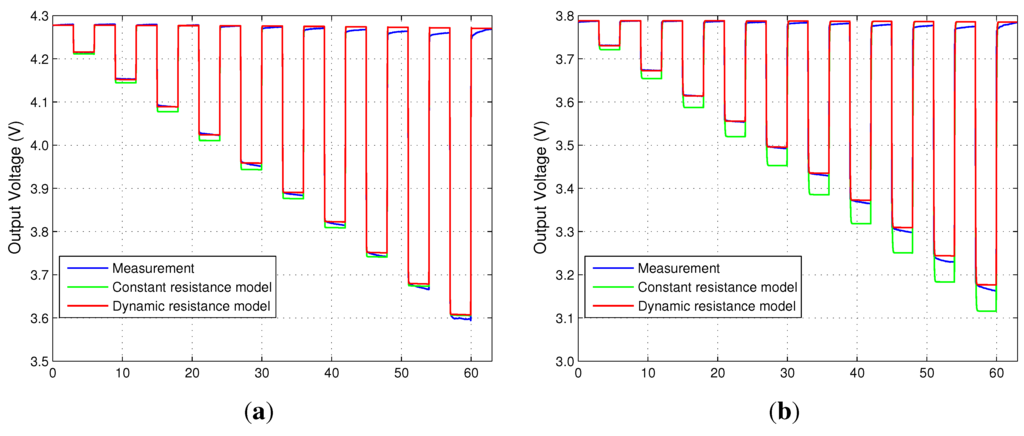
Figure 6.
Comparison of the modeling performance: at (a) 100% SOC; and (b) 50% SOC.
In the constant resistance model, the initial parameters are extracted from the battery with 100% SOC, and they are fixed as, which are independent of the SOC level, Cn = 1.491 × 104 F, Cp = 17.6735 F, Rb = 0.165 Ω, Rp = 0.165 Ω, and Rt = 0.055 Ω. On the other hand, the resistance is updated using the SOC versus Rint curves according to the operating conditions in the dynamic resistance model. Here, the capacitance is assumed to be constant, because its variation is negligibly small and the sampling period T is 0.01 s. The results show that the accuracy of both models is similar at 100% SOC. However, at 50% SOC, the dynamic resistance model shows better accuracy than the constant resistance model. Similarly, in other SOC levels, modeling errors are caused by differences between actual and constant resistance value. It represents that the proposed battery model is more suitable for the modeling of Li-ion batteries.
4.3. Random Current Discharge Test
The second experiment is designed to verify the estimation performance of the proposed SOC estimation method. In this experiment, a random discharge current (shown in Figure 7) is applied repeatedly over the 100%–0% SOC range to simulate the actual battery usage.
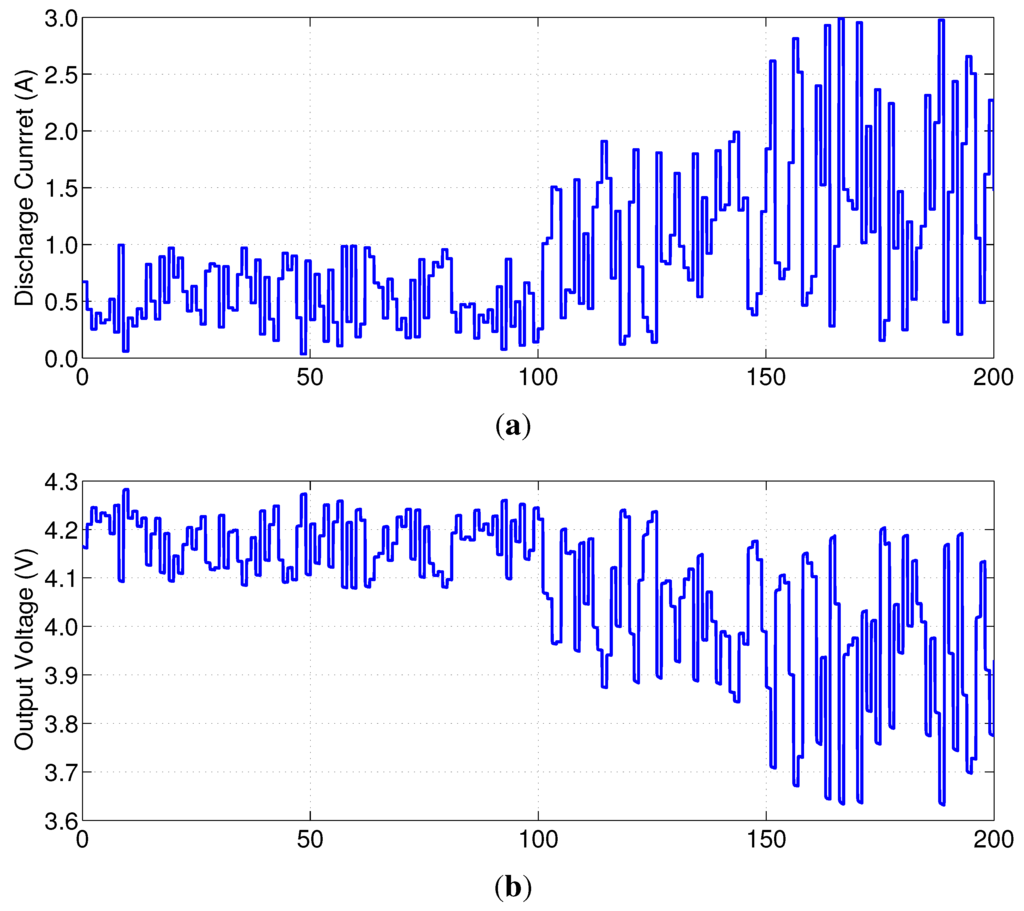
Figure 7.
(a) Random discharge current; and (b) measured output voltage.
Then, the second-order DSMO is used in the dynamic resistance model to estimate both the SOC and the output voltage of the battery. The gains of the second-order DSMO, are chosen as follows:
Remark 2: To compare the second-order DSMO with the first-order DSMO under the same conditions, the gain M is applied equally to each one and the sign function sign(·) is used for second-order DSMO [Equation (9)] instead of the saturation function sat(·).
The SOC estimation results are shown in Figure 8. For the desired SOC, the ampere-hour counting method that takes into account the Coulombic efficiency is used. Here, the battery is initially fully charged using the constant-current/constant-voltage method. The results show that the estimated SOC using the first-order DSMO exhibits the undesirable chattering phenomenon, and the SOC estimation error increases gradually to about 5%. In contrast, the proposed SOC estimation method enhances the estimation performance in terms of chattering elimination and SOC estimation precision. Additionally, for the clear view, we present the one-cycle estimation results of the SOC in Figure 8b.
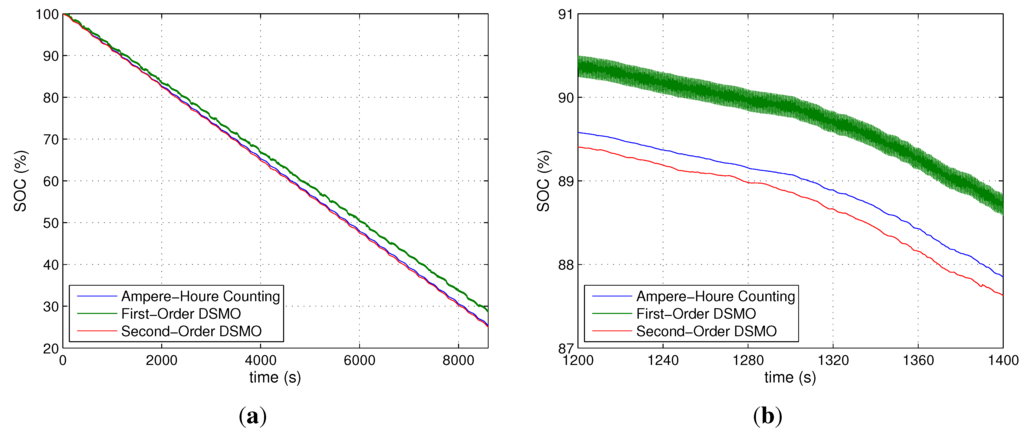
Figure 8.
SOC estimation results for the proposed method.
Figure 9 shows an improvement in the chattering elimination when the second-order DSMO is used for output voltage estimation. In contrast, the chattering phenomenon occurred in the results for output voltage estimation when the first-order DSMO is used. It is possible to verify the improvement in the accuracy by comparing the estimation errors over a single cycle, as shown in Figure 9b. It is clear that the estimation error is reduced drastically by the second-order DSMO.
To investigate the robustness of the second-order DSMO to the situation where the initial SOC is unknown, we repeat the same experiment above but the initial value of estimated SOC is set to be 90%. As shown the results in Figure 10, we can find that the both estimated SOC values converges to the actual one within 70 s. This implies that the proposed SOC estimation method based on the second-order DSMO can reduce the chattering phenomenon while maintaining the robustness properties of the sliding mode approach.
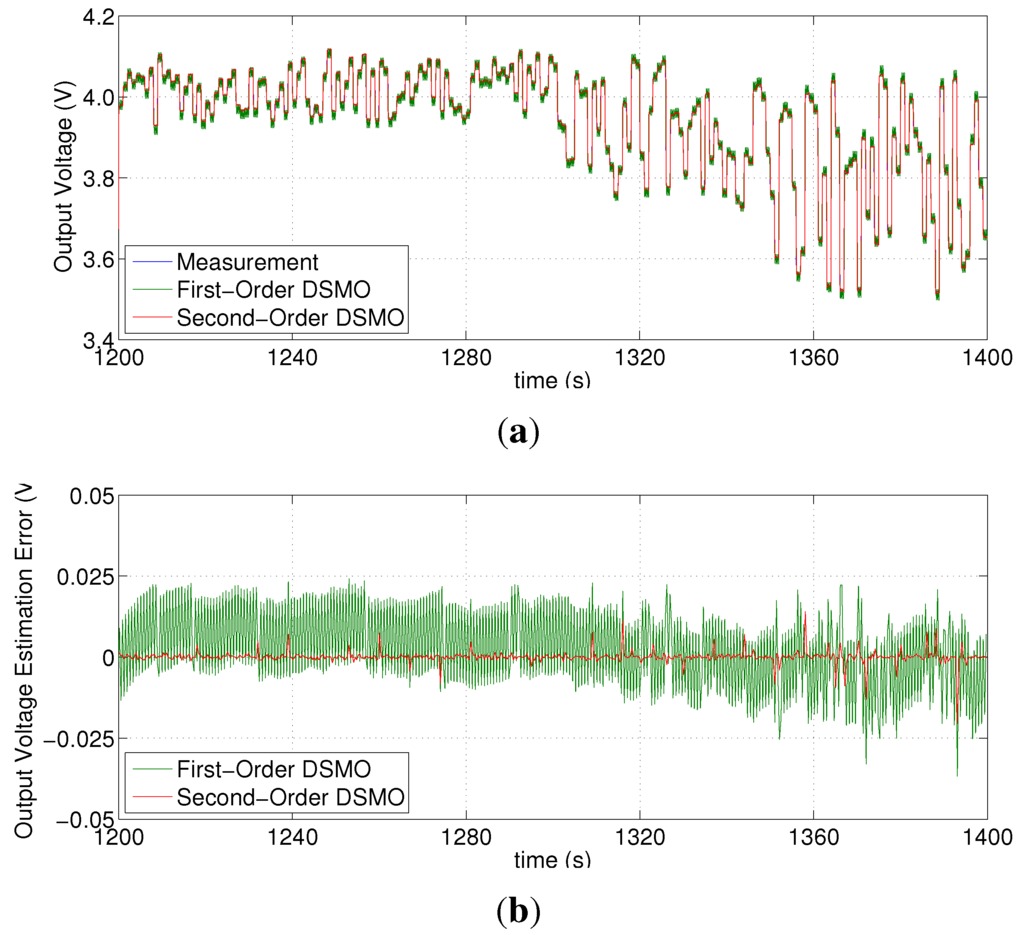
Figure 9.
One-cycle estimation results for the proposed method: (a) output voltage estimation; and (b) estimation errors.
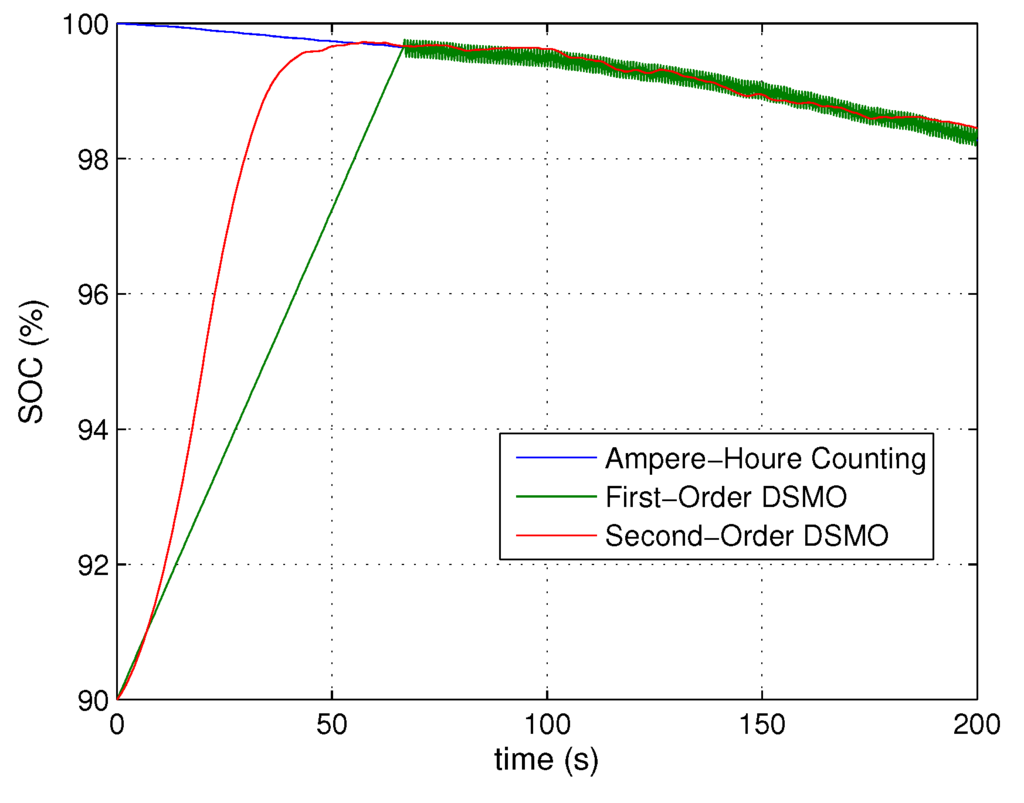
Figure 10.
SOC estimation results with unknown the initial SOC.
5. Conclusions
The chattering phenomenon in SOC estimated by a first-order SMO deteriorates estimation accuracy. To overcome this drawback and improve accuracy, a second-order DSMO-based SOC estimation method is proposed. Furthermore, a dynamic resistance battery model is also proposed to more accurately represent the dynamics of a Li-ion battery. The improvement of model accuracy is achieved with the resistance parameters which are varied with both the magnitude of the discharge current and the SOC level. This approach is suitable for on-line implementation because the SOC vs. Rint curves for each discharge current can be obtained in advance through a simple experiment. Our experimental results show that the proposed battery model has a better modeling accuracy than the constant resistance model. In addition, elimination of chattering in both the SOC and output voltage estimates is achieved using the second-order DSMO.
Appendix: Stability Analysis
The stability analysis of the second-order DSMO has been investigated by Mihoub et al. [13]. From Equations (7) and (9), the estimation error dynamics given by:
where Λ(k) and M satisfy the conditions in Equations (8) and (10), respectively.
Then we have:
which can be written as:
Consider now the following two cases:
- Case 1 : suppose that .In this case, we have:By Lemma 1 in [13], for , there exists a bounded function F(k) ≥ 0 such that:where:Thus, Equation (18) can be written as follows:From Equation (22), we obtain the state equations:where:It is easily to ensure the convergence of Z(k) when eigenvalues’ modules of matrix A are smaller than one. Therefore, the convergence of the estimation error is also guaranteed.
- Case 2: .In this case, Equation (18) can be expressed as:Then we have:where:Consequently, if the uncertainty Λ(k) satisfies the condition in Equation (8) and eigenvalues’ modules of matrix A’ are smaller than one, Z(k)′ is bound. Also, the estimation error is bounded.
Thus, the convergence of the estimation error can be guaranteed.
Acknowledgments
This research was supported by the MKE (The Ministry of Knowledge Economy), Korea, under the “IT Consilience Creative Program" support program supervised by the NIPA (National IT Industry Promotion Agency) (C1515-1121-0003).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xing, Y.; Ma, E.W.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar]
- Piao, C.; Fu, W.; Lei, G.; Cho, C. Online parameter estimation of the Ni-MH batteries based on statistical methods. Energies 2010, 3, 206–215. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive Luenberger observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Alzieu, J.; Smimite, H.; Glaize, C. Improvement of intelligent battery controller: State-of-charge indicator and associated functions. J. Power Sources 1997, 67, 157–161. [Google Scholar] [CrossRef]
- Sato, S.; Kawamura, A. A New Estimation Method of State of Charge Using Terminal Voltage and Internal Resistance for Lead Acid Battery. In Proceedings of the Power Conversion Conference (PCC), Osaka, Japan, 2–5 April 2002; Volume 2, pp. 565–570.
- Cheng, B.; Zhou, Y.; Zhang, J.; Wang, J.; Cao, B. Ni–MH batteries state-of-charge prediction based on immune evolutionary network. Energy Convers. Manag. 2009, 50, 3078–3086. [Google Scholar] [CrossRef]
- Huet, F. A review of impedance measurements for determination of the state-of-charge or state-of-health of secondary batteries. J. Power Sources 1998, 70, 59–69. [Google Scholar] [CrossRef]
- Bhangu, B.; Bentley, P.; Stone, D.; Bingham, C. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Kim, I.S. Nonlinear state of charge estimator for hybrid electric vehicle battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034. [Google Scholar]
- Utkin, V.; Lee, H. Chattering Problem in Sliding Mode Control Systems. In Proceedings of the International Workshop on Variable Structure Systems, Alghero, Italy, 5–7 June 2006; pp. 346–350.
- Mihoub, M.; Said Nouri, A.; Ben Abdennour, R. A second order discrete sliding mode observer for the variable structure control of a semi-batch reactor. Control Eng. Pract. 2011, 19, 1216–1222. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov Approach to Second-Order Sliding Mode Controllers and Observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861.
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Andrea, D. Battery Management Systems for Large Lithium-Ion Battery Packs, 1st ed.; Artech House: London, UK, 2010; pp. 1–105. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).