An Innovative Hybrid 3D Analytic-Numerical Approach for System Level Modelling of PEM Fuel Cells

Abstract

The PEM fuel cell model presented in this paper is based on modelling species transport and coupling electrochemical reactions to species transport in an innovative way. Species transport is modelled by obtaining a 2D analytic solution for species concentration distribution in the plane perpendicular to the gas-flow and coupling consecutive 2D solutions by means of a 1D numerical gas-flow model. The 2D solution is devised on a jigsaw puzzle of multiple coupled domains which enables the modelling of parallel straight channel fuel cells with realistic geometries. Electrochemical and other nonlinear phenomena are coupled to the species transport by a routine that uses derivative approximation with prediction-iteration. A hybrid 3D analytic-numerical fuel cell model of a laboratory test fuel cell is presented and evaluated against a professional 3D computational fluid dynamic (CFD) simulation tool. This comparative evaluation shows very good agreement between results of the presented model and those of the CFD simulation. Furthermore, high accuracy results are achieved at computational times short enough to be suitable for system level simulations. This computational efficiency is owed to the semi-analytic nature of its species transport modelling and to the efficient computational coupling of electrochemical kinetics and species transport.

1. Introduction

Proton exchange membrane fuel cells (PEMFC) are emerging as an advantageous power source in the alternative power sources segment due to their high power density and zero tank-to-wheel emissions. However, as analysed in [1], commercialization of fuel cell technology is lagging behind owing to several disadvantageous characteristics of the fuel cell, summarised by [2] as: cost and complexity, immaturity, and its role as replacement technology. These facts call for increased application of advanced mathematical modelling and simulation tools to efficiently address and tackle the shortcomings of today’s fuel cell technology [2]. PEMFC are characterized by fully interrelated transports of mass, charge and heat, which are governed by convection, diffusion, phase transition and electrochemical reactions. Many fuel cell models can be found in the literature or are available as packages in commercial software as systematically analysed in [3,4,5]. Among these models the most comprehensive are the ones based on 3D computational fluid dynamic (CFD) modelling with extended capabilities of solving electrochemical reactions (e.g., [6,7,8,9]). CFD-based models indeed provide insight into detailed phenomena along with high level of predictability and high accuracy; however, they are also characterized by very long computational times inherent to their comprehensive modelling framework. Long computational times are a major disadvantage whenever a large number of simulation results are required to be obtained in reasonable amount of time which is typical for tasks such as: (a) rapid testing of different design options [10,11] including the ultra large scale [9]; (b) modelling of larger systems powered by fuel cells, e.g., the entire fuel cell powered vehicle [12,13]; (c) modelling transient operation of the fuel cell powered systems [14,15] and (d) development of control functionalities [15,16]. Among these, fast computation is of most crucial importance in models for which real time capability is mandatory such as in [12,14,16] or any hardware-in-the-loop model application. Models featuring shorter computational times can be categorised as:

-

Fully empirical models such as equivalent circuits, neural-network models, support and relevance vector machines which are all highly accurate and require very short computational times. However, these, unlike the CFD models, lack any predictability since they are characteristic of a specific (i.e., non general) system part and are thus useful in simulations only as computer model representation of an existing or a non-modifiable component. Examples found in references: [17,18,19,20].

-

1D models that are usually mechanistic and 0D models that are often fully analytic. These require short computational times which, however, come at the expense of lower accuracy. Examples found in references: [21,22,23,24,25,26,27].

-

Reduced dimensionality models which are predictable mechanistic models that feature reduced computational load yet retain higher accuracy of current density predictions. These are typically 2D models (e.g., [28], the 2D model in [29]) modelling straight channel fuel cell configurations (such as depicted in Figure 1) solving governing equations in the plane that is parallel to the gas flow and perpendicular to the membrane (e.g., green plane in Figure 1). Further simplification of 2D models leads to the so called 1D + 1D (e.g., [30]) models where mathematical treatment of the dimension that runs along direction of gas flow addresses only the most dominant physical phenomena (e.g., mass transport via bulk gas flow in channel). Applying these 2D models to a fuel cell geometry such as presented in Figure 1 leads to certain systematic discrepancies since the area through which mass is exchanged between the gas diffusion layer (GDL) and the channel is considerably smaller than the area where mass is exchanged between the membrane and the GDL. To compensate for this discrepancy some models employ additional correction parameters, obtained through fitting results of full 3D CFD models or experimental data, yielding pseudo 3D models (e.g., [31,32] and Sherwood number adjusted 2D model in [29]). An alternative to this pseudo 3D modelling is the so called 2D + 1D approach (as found in [29]) where the physical phenomena are fully addressed in the plane perpendicular to the gas flow and the reduced treatment of the 1D + 1D approach is used in the direction of gas flow.

These pseudo 3D and 2D + 1D models aim to take into account all three dimensions whilst being considerably faster than 3D CFD simulations. However with the exception of [31], they are still much slower than 1D models due to their inherent numerical nature. The model found in [31] features computational times comparable to 1D models owing to its analytic nature. However the approximate analytic solution for direct liquid fuel cells in [31] is only valid when the velocity along channels can be approximated as constant.

An article by Tavčar and Katrašnik [33] proposes a hybrid 3D analytic numerical approach to modelling species transport (HAN-ST) in a PEM fuel cell as a way to achieve full 3D resolution whilst featuring short computational times. The principles of HAN-ST modelling in [32] are presented on a theoretical straight channel co-flow fuel cell of very simple geometry and its core principle can be summarized as:

Figure 1. Schematic breakdown of fuel cell geometry onto elementary units for HAN-FC computation. The blue and the spotted translucent regions represent the membrane and GDL respectively, the green surfaces represent the plane of symmetry across the middle of a rib and the yellow surfaces the plane of symmetry between two ribs. (a) A five-rib parallel channel co-flow fuel cell geometry. The two symmetry planes that apply to all ribs are shown on one half of rib defining the representative unit; (b) Representative unit with indicated slice (red); (c) Slice as a sliced-out section of the representative unit that has sufficiently small depth to be treated as a 2D object and (d) Slice domains from top to bottom: cathode channel domain, cathode GDL domains (left cathode GDL#1, right cathode GDL#2), MEA domain, anode GDL domains (left anode GDL#1, right anode GDL#2), anode channel domain.

Figure 1. Schematic breakdown of fuel cell geometry onto elementary units for HAN-FC computation. The blue and the spotted translucent regions represent the membrane and GDL respectively, the green surfaces represent the plane of symmetry across the middle of a rib and the yellow surfaces the plane of symmetry between two ribs. (a) A five-rib parallel channel co-flow fuel cell geometry. The two symmetry planes that apply to all ribs are shown on one half of rib defining the representative unit; (b) Representative unit with indicated slice (red); (c) Slice as a sliced-out section of the representative unit that has sufficiently small depth to be treated as a 2D object and (d) Slice domains from top to bottom: cathode channel domain, cathode GDL domains (left cathode GDL#1, right cathode GDL#2), MEA domain, anode GDL domains (left anode GDL#1, right anode GDL#2), anode channel domain.

A quasi 3D model constructed by taking a 1D numerical model for the gas-flow along the channel and superimposing onto it a 2D analytic solution for the plane perpendicular to the gas-flow. This proves to be computationally efficient due to the additional computational load introduced by the calculation of 2D analytic solution being of the same order of magnitude as the computational load of the base 1D calculation. It was shown in [33] that for the simple theoretical geometry of fuel cell (FC), HAN-ST enables resolving a 3D species transport with very high accuracy while preserving computational speed characteristic for 1D models owing to its partially analytic nature. Due to its high accuracy and computational efficiency the HAN-ST model offers a promising basis for an efficient standalone PEM fuel cell model suitable for system level simulations. HAN-ST as presented in article [33] is a species transport sub-model and needs to be coupled to an electrochemistry sub-model in order to yield a full standalone fuel cell model. Additionally the simple theoretical geometry of HAN-ST from [33] enables devising the 2D analytic solutions on a single domain which is practically impossible in cases of more complex realistic geometries.

As a full realistic standalone PEMFC model derived from the HAN-ST of [33], this paper presents and describes an innovative isothermal standalone hybrid 3D analytic numerical fuel cell model (HAN-FC) featuring:

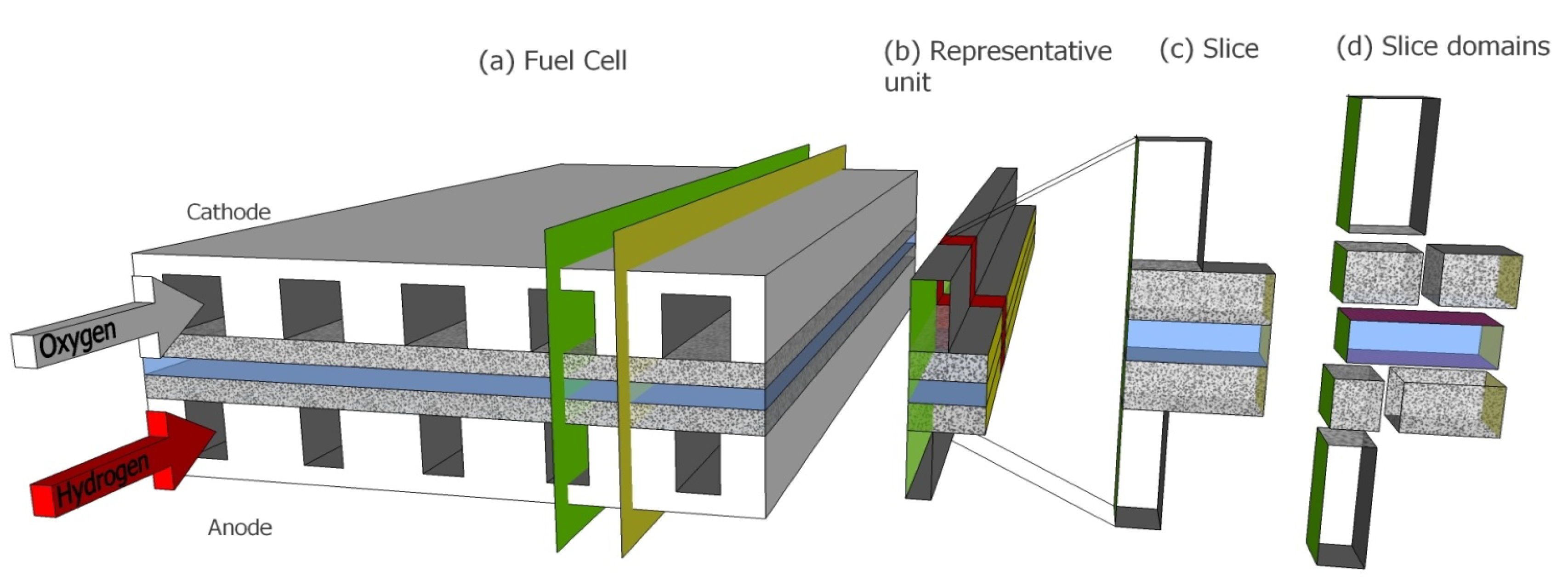
• The HAN-ST principle extended to more general realistic straight parallel channel FC geometries by devising the 2D analytic solution on a jigsaw puzzle of multiple domains and
• An electrochemistry sub-model efficiently coupled to this extended HAN-ST sub-model.

Thus, in terms of categorization introduced above, this is a 2D + 1D model resembling that found in [28], with the difference that it features analytically (instead of numerically) resolved species concentration in the 2D cross-sectional plane in both GDL and channel, making it computationally much faster. The nature of HAN-FC’s analytic solution also fundamentally differs from the one in [31] where the 2D analytic solution is obtained for the plane that is parallel to the gas flow and perpendicular to the membrane. Differences of HAN-FC from other similar models found in literature are further discussed in Section 3.

The model assumptions and geometry of HAN-FC are outlined in Section 2 and the underlying governing equations of the species transport and electrochemical reactions are given in Section 3. For validation the simulation results of the HAN-FC is benchmarked with the results obtained by a professional 3D CFD tool: the simulation setup of HAN-FC and CFD is presented in Section 4, and the comparative results and their analysis is provided in Section 5. In all instances the accuracy of HAN-FC is to be understood as the accuracy relative to the CFD results, which is typically done for the 2D and pseudo 3D models [28,29,31,33]. Section 6 summarizes the main conclusions. Detailed mathematical derivation of the model is given in Appendix.

2. Model Assumptions and Geometry

The modelled fuel cell is a straight, co-flow, hydrogen-oxygen type PEM fuel cell (FC) with its geometry taken from a laboratory test fuel cell. The fuel cell topology and geometry are illustrated in Figure 1 where the following sub-elements can be distinguished: cathode channels, cathode-side gas diffusion layer (GDL), thin catalyst layer for oxygen reduction, hydrated proton exchange membrane, thin catalyst layer for hydrogen oxidation, anode-side GDL, anode channels. Due to the symmetric geometry of the fuel cell a half of one rib, as depicted in Figure 1, is taken as the representative unit of the fuel cell. The derivation of HAN-FC is based on three sets of assumptions: (1) regarding gaseous species transport, (2) regarding species transport in membrane and (3) regarding electrochemical reactions. The gaseous species transport assumptions are summarised as follows:

• A steady state solution of the problem is sought.
• The problem is isothermal meaning a constant uniform temperature is assumed for the whole fuel cell and no energy equation is calculated.
• The gases are treated as ideal.
• There is no liquid water in GDLs and Channels.
• Pressure variations are small enough that constant pressure is assumed in gas equations and the gas flow is assumed incompressible over the whole fuel cell. This is justifiable due to very small pressure variations in the fuel cell owing to the short straight channel geometry.
• The diffusion system is always bi-componential (either oxygen and water vapour or hydrogen and water vapour) with a constant binary diffusion coefficient.
• The effective (macroscopic) diffusion constant used in GDL is the diffusion constant for empty space (which applies in the channel) divided by the tortuosity of GDL.
• Diffusion in gas in the direction of channel gas-flow is neglected due to the large aspect ratio of the relevant fuel cell dimensions.
• In GDL there is no convective transport in the direction of channel gas flow. The very small pressure drop from inlet to outlet produces only negligible convective flow in the GDL in the direction along channel length.
• The flow in channels is laminar.

HAN-FC extends the assumptions regarding membrane species transport made by HAN-ST amounting to the following:

XI.

There is no gas crossover in the membrane. Thus water is the only species transported through the membrane besides protons.

XII.

The mobility of both water molecules and protons (in form of hydronium ions) at a given point in membrane are linearly proportional to the membrane water content at that point.

XIII.

Species transport within the membrane only occurs in the direction perpendicular to the membrane sheet.

XIV.

The average number of water molecules dragged by the electro-osmotic pull of each proton is an independent constant.

XV.

The concentration of mobile protons is constant within the whole membrane. This is due to the humidification of membrane being always sufficiently high that full or close to full proton dissociation can be assumed.

XVI.

The membrane water content at the membrane/gas boundary is in equilibrium with water vapour concentration in the gas.

The assumptions regarding electrochemical reactions inherent to HAN-FC are:

XVII.

Only the electrochemical kinetics of oxygen reduction on the cathode catalyst is considered. The electrochemical kinetics of hydrogen oxidation on the anode catalyst is much faster and its contribution to the over-potential is several orders of magnitude smaller and thus neglected.

XVIII.

The catalyst layer is infinitely thin and characterised by an effective exchange current density as current per unit area [A/m²].

XIX.

The electrical resistance of the GDL is neglected and uniform constant electrical potential is assumed within the whole GDL.

All the above assumptions follow the assumptions made by other models of comparable modelling depth presented in the introduction.

3. Governing Equations

The modelled fuel cell is made of number of equal parallel symmetrical ribs where a half of one such rib is indicated between the green and the yellow plane in Figure 1a. The symmetry condition between ribs is defined in the GDL and membrane (yellow surfaces in Figure 1) requiring that there be no species flux across the symmetry plane. In the case of the two outermost ribs the wall boundary of the fuel cell also allows no species flux across that boundary. Thus, taking into account that zero velocity in the direction of channel gas flow is assumed in GDL (assumption IX), this wall boundary condition is the same as the symmetry condition allowing treating all ribs as identical. Since the two halves of one rib are mirror images and since all ribs are identical the so defined half of one rib is a representative unit of the fuel cell. This representative unit is sliced along the direction of gas flow into a number of thin slices as depicted in Figure 1b,c. Within each slice only variation of variables in the plane perpendicular to channel gas flow is addressed effectively making a slice a 2D object. The slice has three parts: the cathode gas part, the membrane electrode assembly (MEA) part and the anode gas part. The three parts are, as discernible form Figure 1d, further divided onto seven computational domains: each gas part is divided into one channel domain and two GDL domains (GDL#1, GDL#2 as depicted in Figure 2) whilst the whole MEA part is contained within its MEA domain. The so defined computational domains, depicted in Figure 2 as shallow rectangular cuboids, share the 2D nature of the slice and are thus simple rectangles. An analytic 2D solution for the distribution of species concentration in a slice is sought as a jigsaw puzzle of seven individual 2D solutions for each domain that are appropriately coupled to one another.

Figure 2. Detailed schematic of gas part comprising three computational domains. The top cuboid is the channel domain, bottom left cuboid GDL#1 domain and bottom right cuboid GDL#2 domain. The “Source” arrow represents the convective inflow of species from the channel domain of the previous upstream slice and the “Sink” arrow represents the outflow into the channel domain of the next downstream slice. Blue arrows represent the molar fluxes of water traversing the borders between domains that serve as boundary conditions for the individual solutions in domains. The ribbed purple surface represents the catalyst layer, i.e., the MEA/GDL interface. At the grey surfaces, i.e., the walls, and at the green and yellow surfaces, i.e., the two symmetry planes, the boundary condition requires zero flux through the boundary.

Figure 2. Detailed schematic of gas part comprising three computational domains. The top cuboid is the channel domain, bottom left cuboid GDL#1 domain and bottom right cuboid GDL#2 domain. The “Source” arrow represents the convective inflow of species from the channel domain of the previous upstream slice and the “Sink” arrow represents the outflow into the channel domain of the next downstream slice. Blue arrows represent the molar fluxes of water traversing the borders between domains that serve as boundary conditions for the individual solutions in domains. The ribbed purple surface represents the catalyst layer, i.e., the MEA/GDL interface. At the grey surfaces, i.e., the walls, and at the green and yellow surfaces, i.e., the two symmetry planes, the boundary condition requires zero flux through the boundary.

The analytic solutions for the consecutive slices are, due to assumptions VIII, IX and XIII, coupled only via the two bulk gas flows in channels. The cross-sectional velocity profile of the gas flow (i.e., profile in the 2D plane of a slice) is assumed to take on the dome shape of laminar flow (graphically shown in Section 5.2). This is similar to the 1D laminar velocity profile used in [34] and [28] however, unlike [28] where this profile does not change along the channel, in the HAN-FC model the profile scales with average cross-sectional gas velocity that varies along the channel. This variation of average gas velocity along the channel is calculated stepwise from slice to slice, i.e., as a numerical 1D pipe flow model. The net convective transport into and out of the 2D plane of a slice is then obtained by multiplying the 2D velocity profile by the 2D species concentration distribution profile. This 2D profile of convective transport thus differs from the uniform plug flow used in [29]. HAN-FC essentially treats the bulk gas flow as a 1D flow with a superimposed simple 2D velocity profile of laminar flow and a 2D species concentration profile which enables coupling of the 2D solutions of consecutive slices. The two 1D gas flows are calculated numerically meaning that the change in mean gas velocity is calculated stepwise from slice to slice.

Obtaining 2D analytical solutions for slices that are coupled to one another via the perpendicular numerically resolved 1D gas flow gives this approach the name “hybrid 3D analytic-numerical”. The HAN-FC model thus gives full 3D information on species concentration distribution, differing from the approach of [31] where the model is essentially 2D and the effects in the third dimension are accounted for by means of calibration parameters.

The division of the gas part onto three computational domains is inherent to HAN-FC and differs from HAN-ST of [33] where the very simple geometry allows each gas part to be contained within a single computational domain. Section 3.1 and Section 3.2 describe in detail the equations governing production, consumption and transport of species in the different types of calculation domains, Subsection 3.3 describes the coupling conditions between domains of one slice and Subsection 3.4 describes the procedure for obtaining a solution for the whole fuel cell by finding consecutive solutions for all the slices.

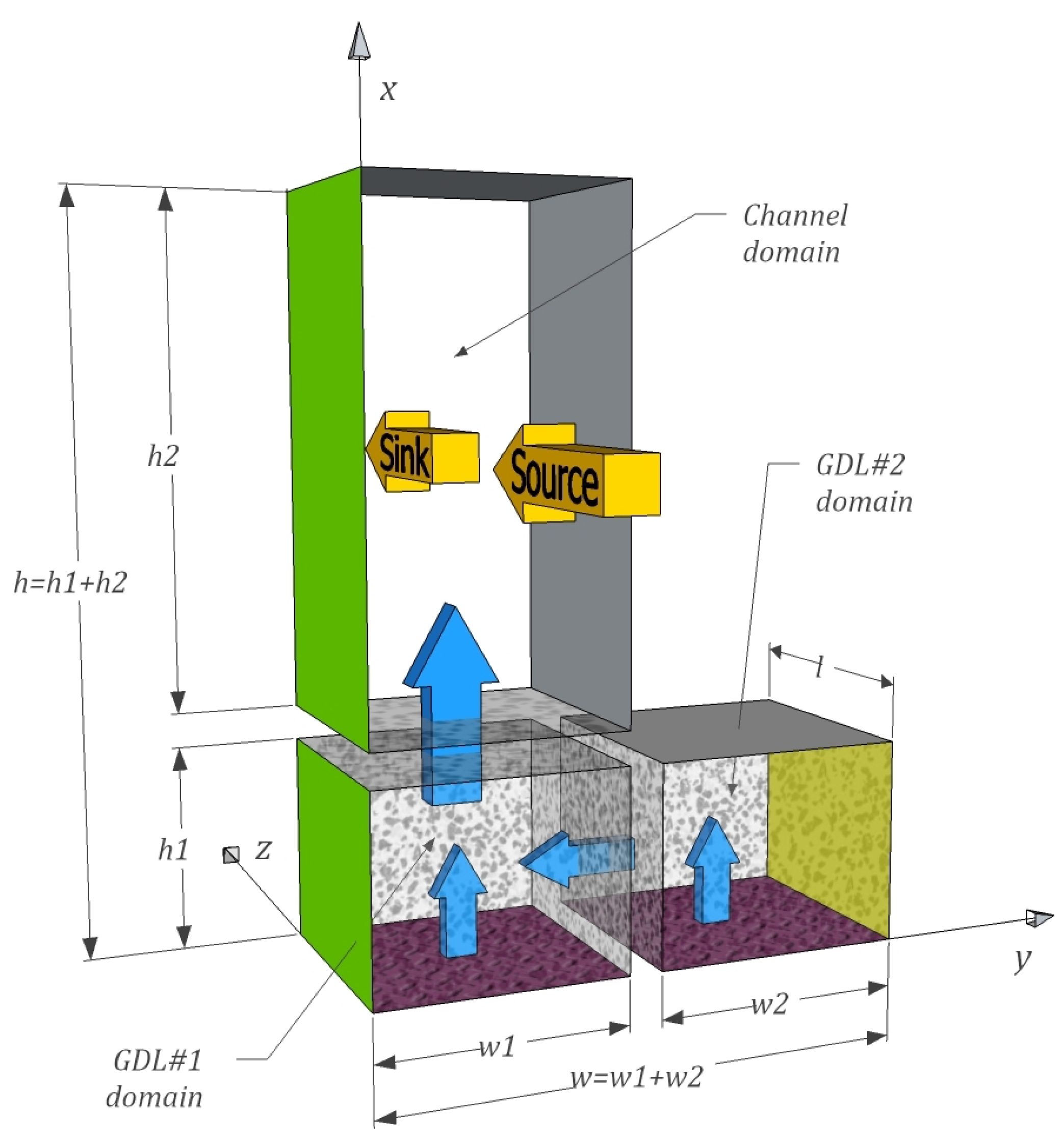
3.1. Gas Part

In the gas part only species transport takes place. The species transport in an ideal gas is modelled by Stefan–Maxwell diffusion equations which, for the case of binary gas mixtures (i.e., gas mixtures of two components) as assumed in VI, read [35]:

$$J_w=u c_w-D\nabla c_w$$

(1)

$$J_r=u c_r-D\nabla c_r$$

(2)

where vectors $J_w$ and $J_r$ are the molar fluxes of the two components: the water vapour and the reactant (either oxygen for cathode gas part or hydrogen for anode gas part) respectively, $c_w$ and $c_r$ are the corresponding molar concentrations, $u$ is the net molar velocity of the gas, $D$ is the binary diffusion coefficient for the binary solution of the two components and $\nabla ={\left({\partial }_x, {\partial }_y, {\partial }_z\right)}^{\text{T}}$ is the 3D nabla operator. Due to assumptions II and V, the temperature and pressure are constant and thus the total molar concentration $c_0=c_w+c_r=\frac{p}{RT}$ is also constant which means that $c_w$ and $c_r$ are complementary and the distribution of both concentrations can be obtained by solving only for $c_w$ and obtaining the other by:

$$c_r=c_0-c_w$$

(3)

Taking the latter into account and adding together Equations (1) and (2) the expression for net molar velocity is obtained:

$$u=\frac{J_w+J_r}{c_0}$$

(4)

All the subsequent derivation of governing equations for species transport in gas will be aimed at finding the distribution of only water vapour concentrations by means of solving Equations (1) and (4) since the reactant concentration is directly given by Equation (3) and thus the subscript $w$ shall be omitted.

The requirement for a steady state solution is expressed as:

$$\frac{\partial c}{\partial t}=-\nabla \cdot J=D{\nabla }^{2}c-\nabla \cdot \left(u c\right)=0$$

(5)

where $c$ is the water vapour molar concentration and $J$ the corresponding molar flux. The assumption of incompressible flow (V) requires that divergence of velocity be zero:

$$\text{div} u=\nabla \cdot u={\partial }_x{u}_x+{\partial }_y{u}_y+{\partial }_z{u}_z=0$$

(6)

At this point it is worth introducing a distinction that splits the general 3D notation into a 2D + 1D notation reflecting the different treatment of physical phenomena in the dimension along the channel gas-flow and in the dimensions perpendicular to the channel gas-flow. This distinction will be used in deriving the “2D + 1D type” equations in the following two subsections. Placing the gas part into the coordinate system defined in Figure 2 a 2D nabla operator$\nabla$, a 2D Laplace operator ${\nabla }^2$, a 2D velocity $\beta$ and a velocity component along the direction of channel gas flow $v$ are defined in the cross-sectional plane as:

$$\nabla =\left(\begin{array}{c}{\partial }_x\\ {\partial }_y\end{array}\right), {\nabla }^2={\partial }_x^2+{\partial }_y^2, \beta =\left(\begin{array}{c}{u}_x\\ u_y\end{array}\right) , v=u_z$$

(7)

(the 3D nabla $\nabla$ is not to be confused with its 2D version$\nabla$). The condition in Equation (6) can be thus rewritten as:

$${\partial }_x{u}_x+{\partial }_y{u}_y+{\partial }_z{u}_z=0\Rightarrow \nabla \beta =-{\partial }_{z}v$$

(8)

Rewriting Equation (5) using the 2D + 1D notation and taking into account the assumption of no diffusive transport along the $z$ coordinate (VIII), leading to neglecting the term $D\frac{{\partial }^{2}c}{\partial z^2}$, reads:

$$\frac{\partial c}{\partial t}=D{\nabla }^{2}c-\left(\nabla \cdot \left(\beta c\right)+\frac{\partial \left(v c\right)}{\partial z}\right)=\underset{2D}{\underbrace{D{\nabla }^{2}c-\nabla \cdot \left(\beta c\right)}}-\underset{1D}{\underbrace{\frac{\partial \left(v c\right)}{\partial z}}}=0$$

(9)

Equation (9) is solved for each computational domain. In favour of finding an analytic solution for species transport in the $xy$ plane within a computational domain the term $\nabla \cdot \left(\beta c\right)$ in equation (9) is approximated as:

$$\nabla \cdot \left(\beta c\right)\cong \tilde{c} \nabla \cdot \beta$$

(10)

where $\tilde{c}$ is the average concentration in the relevant computational domain. $\beta ,$ being a 2D vector field, can be represented as a sum of gradient of a scalar field $U\left(x,y\right)$ and “2D curl” of a scalar field $A\left(x,y\right)$:

$$\beta =\left(\begin{array}{c}{\partial }_{x}U\\ {\partial }_{y}U\end{array}\right)+\left(\begin{array}{c}{\partial }_{y}A\\ -{\partial }_{x}A\end{array}\right)=\nabla U+\nabla \times A$$

(11)

where the “2D curl” is defined as $\nabla \times =\left(\begin{array}{c}{\partial }_y\\ -{\partial }_x\end{array}\right)$. Since divergence of curl is zero (i.e., $\nabla \cdot \left(\nabla \times A\right)=0$), Equation (9), together with approximation (10) reads:

$$\frac{\partial c}{\partial t}=\underset{2\text{D}}{\underbrace{{\nabla }^2\left(D c-\tilde{c} U\right)}}-\underset{1D}{\underbrace{{\partial }_z\left(v c\right)}}=0$$

(12)

where the fact that $D$ and $\tilde{c}$ are constants in the relevant channel domain is taken into account. In the following manipulations of the species transport equation for the three calculation domains that constitute a gas part in a slice the following subscript notation is used to distinguish quantities in different calculation domains: subscript $c$ (as in e.g., $c_c$, ${\beta }_c$, $U_c$) pertains to the channel domain, subscript $1$ pertains to the GDL#1 domain and subscript $2$ to the GDL#2 domain.

3.1.1. GDL Domains

Assumption IX infers that the velocity of gas is in GDL has zero component along $z$ coordinate, i.e., $v=0$. Thus, Equation (12) in GDL simplifies to:

$$\frac{\partial c\left(x,y\right)}{\partial t}={\nabla }^2\left(D_{GDL} c\left(x,y\right)-\tilde{c} U\left(x,y\right)\right)=0$$

(13)

where $D_{GDL}$ is the effective binary diffusion coefficient in GDL. Furthermore, gas-flow in GDL is governed by Darcy’s law:

$$\beta =-\frac{k}{\mu }\nabla p=\nabla U$$

(14)

where $k$ is the permeability of GDL and $\mu$ viscosity of the gas. Since Equation (14) is a form of Equation (11) with $A=0$ and $U=-\frac{k}{\mu }p$ the gas flow in GDL is fully defined by scalar field $U$, in other words: gas-flow in GDL is potential. The definition region of Equation (13) is a “$w1$ by $h1$” rectangle for GDL#1 domain and a “$w2$ by $h1$” rectangle for GDL#2 domain as discernible from Figure 2. For devising analytic solutions in the GDL domains also boundary conditions at the four boundaries must be defined for each GDL domain.

The requirement that there is no total gas-flow through walls and across the symmetry planes yields the boundary conditions of zero velocity component perpendicular to these boundaries:

$${\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial U_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=0}=0$$

(15)

where $x=h1$, $y=w$ and $y=0$ denote the positions at: wall on top of GDL#1 domain, the symmetry plane on the left side of GDL#1 domain and the symmetry plane on the right side of GDL#2 domain respectively. Since there can be no species flux through these boundaries either there has to be, in addition to zero velocity component, also zero concentration gradient perpendicular to these boundaries:

$${\frac{\partial c_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial c_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial c_1\left(x,y\right)}{\partial y}|}_{y=0}=0$$

(16)

The molar flux of water vapour from MEA into GDL, schematically represented with the two narrower vertical blue arrows in Figure 2, defines two boundary conditions:

$$\kappa \left(D_{GDL} {\frac{\partial c_1\left(x,y\right)}{\partial x}|}_{x=0}-{\tilde{c}}_1{\beta }_1\left(x=0,y\right)\right)=\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)$$

(17)

$$\kappa {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)$$

(18)

where $\kappa$ is volume fraction of the gaseous phase in the GDL, $x=0$ denotes the position at GDL/MEA interface and $j_{M\to 1}$ and $j_{M\to 2}$ are the molar fluxes of water exiting MEA and entering GDL#1 and GDL#2 domains respectively.

According to Equation (4) the molar fluxes of water exchanged between MEA and GDL and the consumption of reactant at the MEA/GDL interface define the boundary condition for net molar gas flow at this interface:

$$c_0\kappa {\frac{\partial U_1\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)-j_{r1}(y)$$

(19)

$$c_0\kappa {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)-j_{r2}(y)$$

(20)

where $j_{r1}$ and $j_{r2}$ are the molar fluxes of reactant consumed at the interface between MEA and GDL#1 and GDL#2 domains respectively.

Species molar flux between GDL#1 and GDL#2, schematically represented with the blue horizontal arrow in Figure 2, defines the boundary condition at the border plane between the two GDL domains:

$$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial y}|}_{y=w1}=j_{2\to 1}\left(x\right)=\kappa {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{y=w1}$$

(21)

and similarly, the continuity condition for the net molar gas flow:

$${\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=w1}={\beta }_{2\to 1}\left(x\right)= {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{y=w1}$$

(22)

where $y=w1$ denotes the position at the border between the two GDL domains, $j_{2\to 1}$ is the molar flux of water vapour exiting GDL#2 and entering GDL#1 and ${\beta }_{2\to 1}$ the gas velocity component perpendicular to the boundary between GDL#1 and GDL#2 evaluated at that boundary. GDL#2 exchanges species also with the channel domain, defining a boundary condition:

$$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$$

(23)

where $x=h1$ denotes the position at the border between the GDL#1 and the channel domain and $j_{1\to C}$ is the molar flux of water exiting GDL#1 domain and entering the channel domain at that channel/GDL boundary. The boundary condition for the velocity potential $U$ at that channel/GDL interface is obtained by assuming uniform pressure in the channel region and thus defining the value of $U$ at that boundary according to Equation (14):

$$U_1\left(x=h1,y\right)=-\frac{k}{\mu }{p}_c$$

(24)

where $p_c=p_0$ is the pressure in the adjacent channel domain.

The 2D analytic general solution of species concentration distribution $c$ and the velocity potential distribution $U$ for every GDL domain is obtained as a linear combination of eigen functions of the $D{\nabla }^2$ operator. As defined in Subsection A.1.2 of Appendix A, there are two families of these eigen functions:

-

the first, defined by Equation (A31), deals with species transport induced by convective transport along the $z$ coordinate, and thus does not apply to GDL domains;

-

the second, defined by Equation (A41), deals with species transport induced by the boundary conditions at the boundaries of the 2D computational domains and applies also to GDL domains.

The general solution for each GDL domain (represented by Equations (A56) to (A60) in Appendix A) is obtained by treating the molar fluxes at its boundaries as input parameters. The full derivation is given in Subsection A.1 of Appendix A.

3.1.2. Channel Domain

Governing equations of gas flow in a channel are of Navier -Stokes type and thus generally the flow in channels is not potential i.e., the scalar field $A$ in Equation (11) is not zero. However, since in any case the non-potential part of the 2D velocity profile $\beta$ vanishes in Equation (12) the subsequent derivation of species transport equations in the channel domain neglects the non potential part of velocity field in the cross-sectional plane.

According to assumption VIII and IX the channel domain is the only domain type in which species transport along $z$ coordinate takes place thus the term ${\partial }_z\left(v c\right)$ in Equation (12) is nonzero only in the channel domain. The core of the numerical treatment of the gas flow in channel is the following finite-difference approximation for the derivative ${\partial }_z\left(v c_c\right)$:

$$\frac{\partial \left(v c_c\right)}{\partial z}\cong \frac{1}{l}\left(\left(v c_c\right){|}_{z=z_{exit}}-\left(v c_c\right){|}_{z=z_{enter}}\right)$$

(25)

where $l=z_{exit}-z_{enter}$ is the depth of slice with $z_{enter}$ and $z_{exit}$ denoting the value of $z$ coordinate at the points where gas-flow enters and exits the channel domain respectively as indicated in Figure 2. Using approximation (25) in (12) yields:

$$\frac{\partial c}{\partial t}=\underset{2\text{D}}{\underbrace{{\nabla }^2\left(D c-\tilde{c} U_c\right)}}-\underset{1D}{\underbrace{\frac{1}{l}\left(\left(v c\right){|}_{z=z_{exit}}-\left(v c\right){|}_{z=z_{enter}}\right)}}=0$$

(26)

Equation (26) can be interpreted as a simple species transport equation in a 2D plane with source and sink terms where the source term is $\frac{1}{l}\left(v c_c\right){|}_{z=z_{enter}}$ (i.e., the species inflow contribution) and the sink term is $-\frac{1}{l}\left(v c_c\right){|}_{z=z_{exit}}$ (i.e., the species outflow contribution). This interpretation enables the species transport along the $z$ coordinate and in the $xy$ plane to be treated within a channel domain with a single 2D differential equation:

$$\frac{\partial c_c\left(x,y\right)}{\partial t}={\nabla }^2\left(D c_c\left(x,y\right)-{\tilde{c}}_c U\left(x,y\right)\right)+s^{src}\left(x,y\right)-s^{snk}\left(x,y\right)=0$$

(27)

where the source term $s^{src}$ and the sink term $s^{snk}$, schematically represented by the yellow arrows in Figure 2, are expressed as:

$$s^{src}\left(x,y\right)=\frac{1}{l}{v}^{pr}\left(x,y\right)c_c^{pr}\left(x,y\right)$$

(28)

$$s^{snk}\left(x,y\right)=\frac{1}{l}v\left(x,y\right)c_c\left(x,y\right)$$

(29)

where $v(x,y)$ is the cross-sectional profile of the $z$-component of velocity and superscript $pr$ denotes the values from previous channel domain i.e., the channel domain in the upstream neighbour slice. The velocity profile always has, according to assumption X, the same dome-like shape of laminar flow (as found in Section 5.2) scaled by the average $z$-component velocity in the channel domain in question:

$$v\left(x,y\right)=\tilde{v} \mathsf{{\rm Y}}\left(x,y\right)$$

(30)

where $\tilde{v}$ is the average $z$-component velocity (obtained according to 1D gas-flow Equation (85) or (86)) and$\mathsf{{\rm Y}}(x,y)$ is the unit-less dome shape as given in [33].

The definition region of Equation (27) is, for the channel domain, a “$w1$ by $h2$” rectangle whose four edges represent the boundaries of channel domain with: two walls (gray surfaces in Figure 2), one symmetry plane (translucent yellow surface in Figure 2) and one channel/GDL boundary (translucent dotted surface in Figure 2). There are two types of boundary conditions on the four edges:

• The total molar gas flow and the molar flux of water vapour between the channel and the GDL, schematically represented with the wider vertical blue arrow in Figure 2, manifest as boundary conditions:

  $$D {\frac{\partial \left(D{c}_c\left(x,y\right)-{\tilde{c}}_c{U}_c\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$$

  (31)

  and:

  $${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h1}={\beta }_{1\to C}\left(y\right)$$

  (32)

  where $x=h1$ denotes the position at the GDL/channel boundary and ${\beta }_{1\to C}$ is the gas velocity component perpendicular to the boundary between GDL#1 and channel evaluated at that boundary.
• Analogous to conditions (15) and (16) there is no flux through walls and across the symmetry plane, leading to the boundary condition for the other three edges:

  $${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=0}=0$$

  (33)

  and:

  $${\frac{\partial c_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=0}=0$$

  (34)

  where $x=h$, $y=w2$ and $y=0$ denote the position at the two walls and the symmetry plane respectively.

The 2D analytic general solutions of species concentration and velocity potential distribution for a channel domain are obtained as a linear combination of both families of eigen functions of the $D{\nabla }^2$ operator since species transport in the channel domain is induced both by the convective transport along $z$ coordinate and by the boundary condition at the boundary between channel domain and GDL#1 domain.

A general solution for a channel domain (represented by Equations (A53) to (A55) in Appendix A) is obtained by treating the average $z$-component velocity of gas flow, the molar fluxes from GDL and the source term as input parameters. The full derivation is given in Subsection A.1 of Appendix A.

3.2. MEA Part

Contrary to the two gas parts that are each split onto three computational domains the whole MEA part is contained within one computational domain as discernible from Figure 1 and Figure 3.

Figure 3. Schematic representation of species production, consumption and transport in the MEA. The two ribbed purple surfaces represent the catalyst layers at the MEA/GDL interfaces. The brown arrows represent the species transport from/to cathode gas part, whilst cyan arrows indicate the species transport from/to the anode gas part and the grey arrow represents the proton flow across the membrane. Hydrogen and oxygen are consumed on the anode and cathode catalyst layer respectively. All the water is produced on the cathode catalyst layer and the molar flux of water traversing the membrane is equal to the flux entering the anode gas part.

Figure 3. Schematic representation of species production, consumption and transport in the MEA. The two ribbed purple surfaces represent the catalyst layers at the MEA/GDL interfaces. The brown arrows represent the species transport from/to cathode gas part, whilst cyan arrows indicate the species transport from/to the anode gas part and the grey arrow represents the proton flow across the membrane. Hydrogen and oxygen are consumed on the anode and cathode catalyst layer respectively. All the water is produced on the cathode catalyst layer and the molar flux of water traversing the membrane is equal to the flux entering the anode gas part.

In the MEA part, two types of physical processes are distinguished:

• species transport across the membrane (water molecules and hydronium ions represented by the cyan “H₂O” and the gray “H⁺” arrow in Figure 3);
• species production and consumption by the electrochemical reactions on the catalysts that are on the top and bottom boundary of the MEA domain as observed in Figure 3.

The following two subsections thus deal with the species transport and electrochemical reactions respectively.

3.2.1. Species Transport across Membrane

The equations for membrane species transport are derived with membranes for low temperature PEMFCs in mind; however, as indicated in Section 3.5, they are also applicable to membranes for high temperature PEMFCs.

The following equations governing species transport across the membrane are expressed with respect to the orientation of the coordinate system indicated in Figure 3 which is such that $x=0$ represents the position at the anode catalyst layer and $x=\vartheta$ the position at the cathode catalyst layer. According to assumption XIII the species transport in the membrane takes place only along $x$ coordinate, thus the dependency of variables with respect to $y$ coordinate is left out from notation in this subsection (recalling that within a slice the variables are also constant along $z$ coordinate).

Molar fluxes of water $j_w$ and protons $j_{+}$ are defined by equations taken from [34]:

$$j_w=-D_w\frac{\partial \Lambda }{\partial x}+n_{drg} j_{+}$$

(35)

$$j_{+}=-\frac{F}{RT}{D}_{+}{c}_{+}\frac{\partial V}{\partial x}-D_{+}\frac{\partial c_{+}}{\partial x}$$

(36)

$$D_w={\mathfrak{D}}_w\Lambda , D_{+}={\mathfrak{D}}_{+} \Lambda$$

(37)

where membrane water content $\Lambda$ is the concentration of water normalised with the sulphonic group concentration, $c_{+}$ is the concentration of dissociated protons, $n_{drg}$ is the electroosmotic drag coefficient, $F$ is Faraday constant, $V$ is electric potential and $D_w$ and $D_{+}$ are the diffusion coefficients of water molecules and dissociated protons (in form of hydronium ions) respectively. According to assumption XII both these two diffusion coefficients are linear functions of the membrane water content with their coefficients of proportionality ${\mathfrak{D}}_w$ and ${\mathfrak{D}}_{+}$ depending only on temperature. The explicit notation of temperature dependence has been omitted due to the isothermal nature of the model. Following the assumption XV the concentration of dissociated protons is approximately equal to the membrane sulphonic group concentration $c_{·HS{O}_3}$:

$$c_{+}\cong c_{·HS{O}_3}$$

(38)

meaning that any proton concentration gradient is negligibly small and thus the term $–D_{+}{\partial }_x{c}_{+}$ in Equation (36) is neglected and $c_{+}$ is treated as constant along the $x$ coordinate, i.e.,: $c_{+}\ne c_{+}(x)$. Following the derivation of [34] and taking into account this simplification of zero proton concentration gradient, Equations (35) and (36) can be written as:

$$j_w=-d_w\frac{\partial \left({\Lambda }^2\right)}{\partial x}+n_{drg} j_{+}$$

(39)

$$j_{+}=-d_{+}\Lambda \frac{\partial V}{\partial x}$$

(40)

where the constants $d_w$ and $d_{+}$ are defined as: $d_w=\frac{{\mathfrak{D}}_w}{2}$ and $d_{+}=\frac{F {\mathfrak{D}}_{+}{c}_{+}}{RT}$. In steady state the continuity condition requires that:

$$D_w\frac{\partial j_w}{\partial x}=-\frac{\partial \Lambda }{\partial t}=0=-\frac{\partial c_{+}}{\partial t}=D_{+}\frac{\partial j_{+}}{\partial x}$$

(41)

leading to the molar fluxes $j_w$ and $j_{+}$ being constant along the $x$ coordinate. In the previously defined coordinate system the membrane water content at the interface with the anode electrode and at the interface with the cathode electrode are expressed as ${\Lambda }_{AND}=\Lambda \left(x=0\right)$ and ${\Lambda }_{CTH}=\Lambda (x=\vartheta )$ respectively and the general solution for $j_w$ and $\Lambda$ in differential Equations (39) and (40) can be expressed as:

$$\Lambda \left(x\right)=\sqrt{\frac{x}{\vartheta }{\Lambda }_{AND}^2+\left(1-\frac{x}{\vartheta }\right){\Lambda }_{CTH}^2}$$

(42)

$$j_w=d_w\frac{\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }-n_{drg} j_{+}$$

(43)

where $d_w\frac{\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }=-d_w\frac{\partial \left({\Lambda }^2\right)}{\partial x}$, the back diffusion flux of water, is also constant with respect to $x$ coordinate. Rearranging Equation (40), integrating it over the membrane thickness and taking into account that $j_{+}$ and $d_{+}$ are independent of $x$ gives:

$$\frac{j_{+}}{d_{+}}{{\displaystyle \int }}_0^{\vartheta }\frac{dx}{\Lambda \left(x\right)}=-{{\displaystyle \int }}_0^{\vartheta }\frac{\partial V}{\partial x}dx$$

(44)

The integral on the left side of Equation (44) evaluates to:

$${{\displaystyle \int }}_0^{\vartheta }\frac{dx}{\Lambda \left(x\right)}={{\displaystyle \int }}_0^{\vartheta }{\left(\frac{x}{\vartheta }{\Lambda }_{AND}^2+\left(1-\frac{x}{\vartheta }\right){\Lambda }_{CTH}^2\right)}^{- \frac{1}{2}}dx=\frac{2\vartheta }{{\Lambda }_{AND}+{\Lambda }_{CTH}}=\frac{\vartheta }{\overline{\Lambda }}$$

(45)

where $\overline{\Lambda }$ is the arithmetic mean of water content at the anode and cathode side, and the integral on the right side of Equation (44) represents the voltage drop due to the membrane’s ohmic resistance $\Delta V_{\mathsf{\Omega }\text{m}}$:

$$-{{\displaystyle \int }}_0^{\vartheta }\frac{\partial V}{\partial x}dx=\Delta V_{\mathsf{\Omega }\text{m}}$$

(46)

Taking into account that the proton flux is proportional to the current density $i$:

$$j_{+}=\frac{i}{F}$$

(47)

Equation (44) can be formulated as the “Ohm’s law” equation for charge transport across the membrane:

$$\frac{i \vartheta }{F{d}_{+}} \frac{1}{\overline{\Lambda }}=i R\left({\Lambda }_{AND},{\Lambda }_{CTH}\right)=\Delta V_{\mathsf{\Omega }\text{m}}$$

(48)

where $R\left({\Lambda }_{AND},{\Lambda }_{CTH}\right)=\frac{2\vartheta }{F{d}_{+}\left({\Lambda }_{AND}+{\Lambda }_{CTH}\right)}$ is the membrane’s specific ohmic resistance.

3.2.2. Electrochemical Reaction Kinetics

Following assumption XIX, the fuel cell operates at an uniform operational voltage $V_{op}\ne V_{op}\left(y,z\right)$. $V_{op}$ is a sum of four contributions [36]:

$$V_{op}={\mathsf{\Phi }}_{AND}-\Delta V_{\mathsf{\Omega }m}+{\mathsf{\Phi }}_{CTH}-\Delta V_{\mathsf{\Omega }e}$$

(49)

where ${\mathsf{\Phi }}_{AND}$ and ${\mathsf{\Phi }}_{CTH}$ are anode and cathode Galvani potentials respectively and $\Delta V_{\mathsf{\Omega }m}$ and $\Delta V_{\mathsf{\Omega }e}$ are voltage losses due to ohmic resistance of proton transport in membrane and electron transport in GDL respectively. Generally all four depend on current density, however taking the definition of zero galvanic potential of a standard hydrogen electrode, following assumption XVII that neglects reaction kinetics effects on the anode and following assumption XIX that neglects electric resistance of GDL yields ${\mathsf{\Phi }}_{AND}\left(y,z\right)=\Delta V_{\mathsf{\Omega }e}=0$. This simplifies Equation (49):

$$V_{op}=\mathsf{\Phi }-\Delta V_{\mathsf{\Omega }m}$$

(50)

where $\mathsf{\Phi }={\mathsf{\Phi }}_{CTH}$ (i.e., the subscript $CTH$ in ${\mathsf{\Phi }}_{CTH}$ is from here on dropped for brevity). Current density, proportional to the rate of oxygen reduction reaction at the cathode catalyst, is given as a function of $\mathsf{\Phi }$ by the Butler-Volmer equation:

$$i=B\left(\mathsf{\Phi },c_r,c_p\right)=i_{ex}\left(\frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}-{\left(\frac{c_p}{c_{ref}}\right)}^s{e}^{- \frac{F\left(1-\alpha \right)}{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}\right)$$

(51)

where $B\left(\mathsf{\Phi },c_r,c_p\right)$ denotes a Butler-Volmer function, $i_{ex}$ is the exchange current density defined as current per unit area of catalyst layer, $c_r$ and $c_p$ are the surface concentrations of reactant and product (in this case oxygen and water) respectively, $s$ is the stoichiometry ratio, $F$ is the faraday constant, $\alpha$ is the electron transfer coefficient, $c_{ref}$ is the reference concentration and ${\mathsf{\Phi }}^0$ is the cathode open circuit Galvani potential at reference conditions (reference conditions mean that species participating in the cathode reaction assume reference concentration $c_{ref}$). The variable represented by $\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)$ is not to be confused with overvoltage which is the departure from the open circuit potential that would be exhibited at conditions equal to the actual conditions in the immediate surroundings of the electrode under operation.

Defining the current density $i$ directly by Butler-Volmer (or Tafel) Equation (51) is applicable only to very thin catalyst layers (CL). In [37] it is shown that when finite thickness of CL is considered the local current density additionally depends also on the local proton conductivity of the ionomer phase in the CL. According to Equation (40) the local proton conductivity is linearly proportional to the local ionomer water content, which means that the current density $i$ additionally depends also on ${\Lambda }_{CTH}$. In the limit of very small CL thickness this dependency vanishes and the function of current density reduces to Equation (51). The assumption of negligibly thin CL is typically made by the reduced dimensionality models, e.g., [28,31,32], it is made by the benchmarking CFD model and thus also used in the HAN-FC model. However, the function defining the current density in the HAN-FC model can easily be extended to account also for the effects of non-negligibly thick CL: instead of Equation (51) an equation for current density $i$ as a function of not only $\mathsf{\Phi }$, $c_r$ and $c_p$ but also ${\Lambda }_{CTH}$, as derived for example in [37], can be used. This can be done since the approach of derivative approximation and estimation iteration, described in Section 2.4.1., is applicable to any nonlinear function of any number of arguments.

Expressing $\Delta V_{\mathsf{\Omega }\text{m}}$ from Equation (50), substituting it into Equation (48) and assuming a given species concentration at boundaries (i.e., ${\Lambda }_{AND}$, ${\Lambda }_{CTH}$,$c_r$ and $c_p$ are treated as parameters) the two unknowns $i$ and $\mathsf{\Phi }$ are obtained by solving the set of the two transcendent equations:

$$i=B\left(\mathsf{\Phi }\right), i=\frac{\mathsf{\Phi }-V_{op}}{R}$$

(52)

Current density in turn also defines the rates of species production and consumption:

$${\dot{n}}_{O_2}=-\frac{i}{4F}$$

(53)

$${\dot{n}}_w=\frac{i}{2F}$$

(54)

$${\dot{n}}_{H_2}=-\frac{i}{2F}$$

(55)

where ${\dot{n}}_{O_2}$ and ${\dot{n}}_w$ are molar consumption/production per unit area of oxygen and water at cathode catalyst layer and ${\dot{n}}_{H_2}$ is that of hydrogen at the anode catalyst layer.

Since the species consumption/production takes place at the boundaries it is at this point worth defining boundary conditions for the MEA domain in the same fashion as was done for the gas part domains. As indicated by the cyan “H₂O” arrow in Figure 3 the molar flux of water traversing the membrane is equal to the molar flux of water crossing the interface between the MEA and the anode gas part:

$$j_{AND}=-j_w$$

(56)

where $j_{AND}$ is molar flux of water across the interface between the MEA and the anode gas part and is, with respect to the orientation of coordinate system in Figure 3, defined as positive when pointing in the negative $x$ direction. Using Equations (43) and (47) in Equation (56) leads to the boundary condition at the interface between MEA and anode GDL:

$$j_{AND}=\frac{d_w\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }-n_{drg} \frac{i}{F}$$

(57)

The steady state condition requires that all water produced at the cathode catalyst layer diffuses to the anode and the cathode gas parts thus:

$${\dot{n}}_w=j_{CTH}+j_{AND}$$

(58)

where $j_{CTH}$ is molar flux of water across the interface between the MEA and the cathode gas part. Equations (54), (57) and (58) lead to the boundary condition at the interface between the MEA and cathode the GDL:

$$j_{CTH}=\left(\frac{1}{2}+n_{drg}\right) \frac{i}{F}-\frac{d_w\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }$$

(59)

3.3. Coupling of General Solutions in Domains

Coupling of general solutions in domains is done by fulfilling the conditions of continuity of species activity, of species molar fluxes, of net molar gas flows and of pressure at those boundaries that are shared by two domains. In the gas part the continuity of species activity simply requires continuity of species concentration. The two couplings between gas part domains are thus straight forward: At the boundary between the GDL#1 and the GDL#2, domain continuity of activity requires that:

$$c_1\left(x,y=w1\right)=c_2\left(x,y=w1\right)$$

(60)

continuity of molar flux, using Equation (21), requires that:

$${\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1(x,y)\right)}{\partial y}|}_{y=w1}= {\frac{\partial (D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2(x,y))}{\partial y}|}_{y=w1}$$

(61)

and continuity of net molar gas flow, using Equation (14), requires that:

$${\frac{\partial U_1(x,y)}{\partial y}|}_{y=w1}=\kappa {\frac{\partial U_2(x,y)}{\partial y}|}_{y=w1}$$

(62)

continuity of pressure, using Equation (22), requires that:

$$U_1\left(x,y=w1\right)=U_2\left(x,y=w1\right)$$

(63)

Similarly, using Equations (23), (31) and (32), the coupling between GDL#1 and channel domain requires that:

$$c_C\left(x=h1,y\right)=c_1\left(x=h1,y\right)$$

(64)

$${\frac{\partial \left(D{c}_c\left(x,y\right)-{\tilde{c}}_c{U}_c(x,y)\right)}{\partial x}|}_{x=h1}=\kappa {\frac{\partial (D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1(x,y))}{\partial x}|}_{x=h1}$$

(65)

$${\frac{\partial U_c(x,y)}{\partial x}|}_{x=h1}=\kappa {\frac{\partial U_1(x,y)}{\partial x}|}_{x=h1}$$

(66)

where the continuity of pressure is already comprehended in the boundary condition (24).

Coupling the MEA domain to the GDL domains has to take into account the fact that water in membrane is in absorbed liquid phase while in GDL it is in gaseous phase. Activity $a$ of water vapour is simply its relative humidity:

$$a=\frac{c}{c_{sat}}$$

(67)

where $c_{sat}$ is concentration of saturated water vapor, while activity of absorbed water in membrane follows the relationship from [23]:

$$\Lambda =\Lambda \left(a\right)=0.043+17.8 a+39.85 a^2+36 a^3$$

(68)

Assumption XVI requires continuity of water activity also at the membrane/GDL interface meaning that the activity of liquid water in membrane at that interface is equal to the activity of water vapour in GDL at that interface. This equality together with Equation (67) leads to the activity continuity condition at the boundary between the MEA domain and the domains of anode and cathode GDL:

$${\Lambda }_{AND}\left(y\right)=\Lambda \left(a_{AND}\left(y\right)\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{AND}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{AND}\\ \Lambda \left(\frac{c_2^{AND}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{AND}\le y<w\end{array}$$

(69)

$${\Lambda }_{CTH}\left(y\right)=\Lambda \left(a_{CTH}\left(y\right)\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{CTH}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{CTH}\\ \Lambda \left(\frac{c_2^{CTH}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{CTH}\le y<w\end{array}$$

(70)

where $a_{AND}\left(y\right)$ and $a_{CTH}\left(y\right)$ are water activity at the anode and cathode MEA/GDL interface and $AND$ and $CTH$ in superscript or subscript denote values pertaining to the anode and the cathode side respectively. The continuity of molar fluxes of water vapour from MEA to the anode and the cathode side, defined as:

$$j_{AND}\left(y\right)=\{\begin{array}{c}{j}_{M\to 1}^{AND}\left(y\right), 0\le y<w{1}_{AND}\\ j_{M\to 2}^{AND}\left(y\right), w{1}_{AND}\le y<w\end{array}$$

(71)

$$j_{CTH}\left(y\right)=\{\begin{array}{c}{j}_{M\to 1}^{CTH}\left(y\right), 0\le y<w{1}_{CTH}\\ j_{M\to 2}^{CTH}\left(y\right), w{1}_{CTH}\le y<w\end{array}$$

(72)

and continuity of molar fluxes of reactant consumed at the anode and cathode defined as:

$${\dot{n}}_{H_2}\left(y\right)=\{\begin{array}{c}{j}_{r1}^{AND}\left(y\right), 0\le y<w{1}_{AND}\\ j_{r2}^{AND}\left(y\right), w{1}_{AND}\le y<w\end{array}$$

(73)

$${\dot{n}}_{O_2}\left(y\right)=\{\begin{array}{c}{j}_{r1}^{CTH}\left(y\right), 0\le y<w{1}_{CTH}\\ j_{r2}^{CTH}\left(y\right), w{1}_{CTH}\le y<w\end{array}$$

(74)

lead, according to Equations (57), (59), (17) and (18), to equations for water vapour molar fluxes:

$$\frac{d_w\left({\Lambda }_{AND}^2\left(y\right)-{\Lambda }_{CTH}^2\left(y\right)\right)}{\vartheta }-n_{drg} \frac{i\left(y\right)}{F}=\{\begin{array}{c}\begin{array}{cc}\kappa {\frac{\partial \left(D_{GDL}{c}_1^{AND}\left(x,y\right)-{\tilde{c}}_1^{AND}{U}_1^{AND}\left(x,y\right)\right)}{\partial x}|}_{x=0},& 0\le y<w{1}_{AND}\end{array} \\ \begin{array}{cc}\kappa {\frac{\partial \left(D_{GDL}{c}_2^{AND}\left(x,y\right)-{\tilde{c}}_2^{AND}{U}_2^{AND}\left(x,y\right)\right)}{\partial x}|}_{x=0},& w{1}_{AND}\le y<w\end{array} \end{array}$$

(75)

$$\left(\frac{1}{2}+n_{drg}\right) \frac{i\left(y\right)}{F}-\frac{d_w\left({\Lambda }_{AND}^2\left(y\right)-{\Lambda }_{CTH}^2\left(y\right)\right)}{\vartheta }=\{\begin{array}{c}\begin{array}{cc}\kappa {\frac{\partial \left(D_{GDL}{c}_1^{CTH}\left(x,y\right)-{\tilde{c}}_1^{CTH}{U}_1^{CTH}\left(x,y\right)\right)}{\partial x}|}_{x=0},& 0\le y<w{1}_{CTH}\end{array} \\ \begin{array}{cc}\kappa {\frac{\partial \left(D_{GDL}{c}_2^{CTH}\left(x,y\right)-{\tilde{c}}_2^{CTH}{U}_2^{CTH}\left(x,y\right)\right)}{\partial x}|}_{x=0},& w{1}_{CTH}\le y<w\end{array} \end{array}$$

(76)

and according to Equations (19), (20), (53), (55), (57), (59) to equations for total gas flow:

$$\frac{d_w\left({\Lambda }_{AND}^2\left(y\right)-{\Lambda }_{CTH}^2\left(y\right)\right)}{\vartheta }-\left(\frac{1}{2}+n_{drg}\right)\frac{i\left(y\right)}{F}=\{\begin{array}{c}\begin{array}{cc}{c}_0\kappa {\frac{\partial U_1^{AND}\left(x,y\right)}{\partial x}|}_{x=0},& 0\le y<w{1}_{AND}\end{array} \\ c_0\begin{array}{cc}\kappa {\frac{\partial U_2^{AND}\left(x,y\right)}{\partial x}|}_{x=0},& w{1}_{AND}\le y<w\end{array} \end{array}$$

(77)

$$\left(\frac{1}{4}+n_{drg}\right) \frac{i\left(y\right)}{F}-\frac{d_w\left({\Lambda }_{AND}^2\left(y\right)-{\Lambda }_{CTH}^2\left(y\right)\right)}{\vartheta }=\{\begin{array}{c}{c}_0\begin{array}{cc}\kappa {\frac{\partial U_1^{CTH}\left(x,y\right)}{\partial x}|}_{x=0},& 0\le y<w{1}_{CTH}\end{array} \\ c_0\begin{array}{cc}\kappa {\frac{\partial U_2^{CTH}\left(x,y\right)}{\partial x}|}_{x=0},& w{1}_{CTH}\le y<w\end{array} \end{array}$$

(78)

Equations (75) and (76) couple boundary values of water vapour concentration, membrane water content and current density. The coupling of species concentrations and current density is also required by the electrochemical Equations (48) and (51). As defined by Equation (3) the concentration of reactant $c_r$ at the cathode catalyst is an explicit function of the concentration of product i.e., $c_r=c_0-c_p$. The Butler-Volmer function can therefore be treated as a function of two variables: $B\left(\mathsf{\Phi },c_r,c_p\right)=B\left(\mathsf{\Phi },c_p\right)$. Furthermore, since $c_p$ is the water vapor concentration at the cathode catalyst surface and since according to Equation (67) it can be expressed in terms of $a_{CTH}$, i.e., $c_p=c_{sat} a_{CTH}$ the Butler-Volmer function can be expressed as a function of $\mathsf{\Phi }$and $a_{CTH}$ i.e.,: $B\left(\mathsf{\Phi },c_p\right)=B\left(\mathsf{\Phi },a_{CTH}\right)$.

The main governing equations and corresponding boundary conditions are summarised in Table 1.

Table 1. Summary of key governing equations and their boundary conditions.

GDL domains
Species transport	Governing equation	${\nabla }^2\left(D_{GDL} c_1\left(x,y\right)-{\tilde{c}}_1 U\left(x,y\right)\right)=0$
	Boundary conditions	${\frac{\partial c_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial c_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial c_1\left(x,y\right)}{\partial y}|}_{y=0}=0$
		${\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial y}|}_{y=w1}= {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{y=w1}$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$
Velocity profile	Governing equation	${\nabla }^{2}U\left(x,y\right)=0$
	Boundary conditions	${\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial U_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=0}=0$
		$c_0\kappa {\frac{\partial U_1\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)-j_{r1}\left(y\right)$
		$c_0\kappa {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)-j_{r2}\left(y\right)$
		${\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=w1}= {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{y=w1}$
		$U_1\left(x=h1,y\right)=-\frac{k}{\mu }{p}_c$
Channel domain
Species transport	Governing equation	${\nabla }^2\left(D c_c\left(x,y\right)-{\tilde{c}}_c U\left(x,y\right)\right)+s^{src}\left(x,y\right)-s^{snk}\left(x,y\right)=0$
	Boundary conditions	$s^{src}\left(x,y\right)=\frac{1}{l}{v}^{pr}\left(x,y\right)c_c^{pr}\left(x,y\right)$
		$s^{snk}\left(x,y\right)=\frac{1}{l}v\left(x,y\right)c_c\left(x,y\right)$
		${\frac{\partial c_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=0}=0$
		$D {\frac{\partial \left(D{c}_c\left(x,y\right)-{\tilde{c}}_c{U}_c\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$
Velocity profile	Governing equation	${\nabla }^{2}U\left(x,y\right)=\frac{\left(v\left(x,y,z=z_{enter}\right)-v\left(x,y,z=z_{exit}\right)\right)}{l}$
	Boundary conditions	$v\left(x,y,z\right)=\tilde{v}\left(z\right)\mathsf{{\rm Y}}\left(x,y\right),$
		${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=0}=0$
		${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h1}={\beta }_{1\to C}\left(y\right)$
MEA domain
Species transport	Governing equation	$j_w=d_w\frac{\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }-n_{drg} \frac{i}{F}$
	Boundary conditions	${\Lambda }_{AND}\left(y\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{AND}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{AND}\\ \Lambda \left(\frac{c_2^{AND}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{AND}\le y<w\end{array}$
		${\Lambda }_{CTH}\left(y\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{CTH}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{CTH}\\ \Lambda \left(\frac{c_2^{CTH}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{CTH}\le y<w\end{array}$
Electrochemical kinetics		$i=\left(\mathsf{\Phi }-V_{op}\right)\frac{F{d}_{+}\left({\Lambda }_{AND}+{\Lambda }_{CTH}\right)}{2\vartheta }=i_{ex}\left(\frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}-{\left(\frac{c_p}{c_{ref}}\right)}^s{e}^{- \frac{F\left(1-\alpha \right)}{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}\right)$

Table 1. Summary of key governing equations and their boundary conditions.

GDL domains
Species transport	Governing equation	${\nabla }^2\left(D_{GDL} c_1\left(x,y\right)-{\tilde{c}}_1 U\left(x,y\right)\right)=0$
	Boundary conditions	${\frac{\partial c_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial c_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial c_1\left(x,y\right)}{\partial y}|}_{y=0}=0$
		${\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial y}|}_{y=w1}= {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{y=w1}$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_2\left(x,y\right)-{\tilde{c}}_2{U}_2\left(x,y\right)\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)$
		$\kappa {\frac{\partial \left(D_{GDL}{c}_1\left(x,y\right)-{\tilde{c}}_1{U}_1\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$
Velocity profile	Governing equation	${\nabla }^{2}U\left(x,y\right)=0$
	Boundary conditions	${\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=h1}={\frac{\partial U_2\left(x,y\right)}{\partial y}|}_{y=w}={\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=0}=0$
		$c_0\kappa {\frac{\partial U_1\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 1}\left(y\right)-j_{r1}\left(y\right)$
		$c_0\kappa {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{x=0}=j_{M\to 2}\left(y\right)-j_{r2}\left(y\right)$
		${\frac{\partial U_1\left(x,y\right)}{\partial y}|}_{y=w1}= {\frac{\partial U_2\left(x,y\right)}{\partial x}|}_{y=w1}$
		$U_1\left(x=h1,y\right)=-\frac{k}{\mu }{p}_c$
Channel domain
Species transport	Governing equation	${\nabla }^2\left(D c_c\left(x,y\right)-{\tilde{c}}_c U\left(x,y\right)\right)+s^{src}\left(x,y\right)-s^{snk}\left(x,y\right)=0$
	Boundary conditions	$s^{src}\left(x,y\right)=\frac{1}{l}{v}^{pr}\left(x,y\right)c_c^{pr}\left(x,y\right)$
		$s^{snk}\left(x,y\right)=\frac{1}{l}v\left(x,y\right)c_c\left(x,y\right)$
		${\frac{\partial c_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial c_c\left(x,y\right)}{\partial y}|}_{y=0}=0$
		$D {\frac{\partial \left(D{c}_c\left(x,y\right)-{\tilde{c}}_c{U}_c\left(x,y\right)\right)}{\partial x}|}_{x=h1}=j_{1\to C}\left(y\right)$
Velocity profile	Governing equation	${\nabla }^{2}U\left(x,y\right)=\frac{\left(v\left(x,y,z=z_{enter}\right)-v\left(x,y,z=z_{exit}\right)\right)}{l}$
	Boundary conditions	$v\left(x,y,z\right)=\tilde{v}\left(z\right)\mathsf{{\rm Y}}\left(x,y\right),$
		${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=w1}={\frac{\partial U_c\left(x,y\right)}{\partial y}|}_{y=0}=0$
		${\frac{\partial U_c\left(x,y\right)}{\partial x}|}_{x=h1}={\beta }_{1\to C}\left(y\right)$
MEA domain
Species transport	Governing equation	$j_w=d_w\frac{\left({\Lambda }_{AND}^2-{\Lambda }_{CTH}^2\right)}{\vartheta }-n_{drg} \frac{i}{F}$
	Boundary conditions	${\Lambda }_{AND}\left(y\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{AND}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{AND}\\ \Lambda \left(\frac{c_2^{AND}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{AND}\le y<w\end{array}$
		${\Lambda }_{CTH}\left(y\right)=\{\begin{array}{c}\Lambda \left(\frac{c_1^{CTH}\left(x=0,y\right)}{c_{sat}}\right), 0\le y<w{1}_{CTH}\\ \Lambda \left(\frac{c_2^{CTH}\left(x=0,y\right)}{c_{sat}}\right), w{1}_{CTH}\le y<w\end{array}$
Electrochemical kinetics		$i=\left(\mathsf{\Phi }-V_{op}\right)\frac{F{d}_{+}\left({\Lambda }_{AND}+{\Lambda }_{CTH}\right)}{2\vartheta }=i_{ex}\left(\frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}-{\left(\frac{c_p}{c_{ref}}\right)}^s{e}^{- \frac{F\left(1-\alpha \right)}{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}\right)$

Similarly, the membrane ohmic resistance can, according to Equations (69) and (70), be expressed as a function of $a_{AND}$ and $a_{CTH}$ i.e., $R\left({\Lambda }_{AND},{\Lambda }_{CTH}\right)=R\left(\Lambda \left(a_{AND}\right),\Lambda \left(a_{CTH}\right)\right)=R\left(a_{AND},a_{CTH}\right)$. The system of Equations (52) thus reads:

$$i\left(y\right)=B\left(\mathsf{\Phi }(y),a_{CTH}\left(y\right)\right)$$

(79)

$$i\left(y\right)=\frac{\mathsf{\Phi }(y)-V_{op}}{R\left(a_{AND}\left(y\right),a_{CTH}\left(y\right)\right)}$$

(80)

Equations (75) to (80) therefore couple the species transport in membrane and electrochemical reactions on the cathode catalyst to species transport in both gas parts.

3.4. Solution for the Whole Cell

A full 3D solution for the whole representative unit is obtained as series of consecutive 2D analytic solutions for slices. Each solution for a slice is coupled to the solution for the neighbouring upstream slice by taking the anode and cathode sink terms of the upstream slice as the source terms for the slice in question. Obtaining the analytic 2D solution for a slice requires knowing the value of the mean gas velocity z component in the sink term defined in Equation (29). The mean gas velocity z component is calculated by equations of 1D gas-flow given in the Subsection 3.4.2. Description of obtaining the analytic 2D solution for a slice is given in the following Subsection 3.4.1.

3.4.1. 2D Analytic Solution for a Slice

A general solution of the 2D diffusion problem in each of the seven computational domains of a given slice (Figure 1d) is obtained by finding the domain specific eigen functions (also called harmonics) of the $D{\nabla }^2$ operator. These harmonics are 2D trigonometric functions characterised by mode numbers $n$ and $m$: $n$ numbering modes along $x$ coordinate and the $m$ modes along $y$ coordinate. (Fully detailed construction of the eigen functions is given in Appendix A). For each domain the full solution comes in the form of a specific linear combination of its eigen functions, i.e., a type of 2D Fourier series (Equations (A53) to (A60) in Appendix A). Finding the full solution for water concentration and velocity potential in a slice thus means finding all Fourier coefficients in the linear combinations of eigen functions of the seven computational domains. These Fourier coefficients are defined by the couplings between domains. Two types of coupling are distinguished: coupling between domains within a slice and coupling between channel domains in consecutive slices.

• Within a slice the coupling of two domains at their common boundary via the coupling conditions described in Section 3.3 is, on the level of eigen functions, manifested in algebraic coupling of the two sets of Fourier coefficients pertaining to the two linear combinations of harmonics in the two domains as described in Section A.3.1 of Appendix A.
• Coupling to the neighbour upstream slice via the two source terms in cathode and anode channel domain fully defines the solution for a slice (at a given operational voltage). Coupling to the downstream slice has no influence on the solution in the slice in question since sink terms are fully defined by concentration distribution in the two channel domains and are, due to assumption VIII, not influenced by the conditions in the neighbour downstream slice. Source terms, defined in Equation (28), also come in the form of a linear combination of eigen functions [Equation (A27)] thus the seven linear combinations that constitute the full solution for a slice are an algebraic function of the two linear combinations of the two source terms.

Equations (27) and (13) that govern species transport in gas parts are linear differential equations and, within a slice, the couplings between linear combinations of eigen functions of the coupled domains of gas parts are handled by linear algebra as described in Section A.4 of Appendix A. Contrary to this, the couplings between MEA and the two gas parts contain the electrochemical equations and the relationship of activity to water content dependence which are nonlinear. In order to handle also these nonlinear phenomena with linear algebra the approach of derivative approximation and estimation-iteration, described in the following paragraph, is used.

The approach of derivative approximation and estimation-iteration is applied to linearly approximating nonlinear functions such as$B\left(\mathsf{\Phi }\left(y\right),a_{CTH}\left(y\right)\right)$, $R\left(a_{AND}\left(y\right),a_{CTH}\left(y\right)\right)$, $\Lambda \left(a_{AND}\left(y\right)\right)$ and $\Lambda \left(a_{CTH}\left(y\right)\right)$. This approach assumes that within a slice each argument of these nonlinear functions (i.e., $\mathsf{\Phi }\left(y\right)$, $a_{AND}\left(y\right)$ or $a_{CTH}\left(y\right)$) has only small deviations from its average along the $y$ coordinate. Let $f_{NL}$ stand for any of the aforementioned nonlinear functions and ${\text{arg}}_1,{\text{arg}}_2,\dots$ stand for its arguments:

$$f_{NL}\left(y\right)=f_{NL}\left({\arg }_1\left(y\right),{\arg }_2\left(y\right),\dots \right)$$

(81)

Each argument is split into two parts:

$$\arg \left(y\right)=\mathsf{\Pi }+\Delta \arg \left(y\right)$$

(82)

where $\text{arg}$ stands for any of the arguments, $\mathsf{\Pi }$ is a predictor of the average of $\text{arg}$ over $y$ (not necessarily the average itself but a close enough estimate of it) and $\Delta \arg \left(y\right)$ is its deviation from the predictor $\mathsf{\Pi }$ along $y$. The assumption of small deviations means that $\Delta \arg \left(y\right)$ is sufficiently small to justify the following derivative approximation:

$$\begin{gathered} f_{NL}\left(y\right)\cong \\ {f}_{NL}\left({\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2\dots \right)+{\frac{\partial f_{NL}}{\partial {\text{arg}}_1}|}_{\begin{array}{c}{\text{arg}}_1={\mathsf{\Pi }}_1\\ {\text{arg}}_2={\mathsf{\Pi }}_2\\ \cdots \end{array}} \Delta {\arg }_1\left(y\right)+{\frac{\partial f_{NL}}{\partial {\text{arg}}_2}|}_{\begin{array}{c}{\text{arg}}_1={\mathsf{\Pi }}_1\\ {\text{arg}}_2={\mathsf{\Pi }}_2\\ \cdots \end{array}} \Delta {\arg }_2\left(y\right)+\dots = \\ {f}_L\left(\Delta {\arg }_1\left(y\right),\Delta {\arg }_2\left(y\right)\dots \right) \end{gathered}$$

(83)

where $f_L$ is a linear function of $\Delta {\arg }_1\left(y\right),\Delta {\arg }_2\left(y\right)\dots$ and due to linear Equation (82) it is thus also a linear function of ${\arg }_1\left(y\right),{\arg }_2\left(y\right),\dots$. A nonlinear function $f_{NL}$ is therefore linearised by substituting it with its corresponding $f_L$ (pink box in Figure 4). The specific linearization equations for the nonlinear functions are given in Section A.2 of Appendix A.

Having all nonlinear functions linearised in this way, all coupling equations become linear and a fully linear algebraic solution for species concentration distribution in a slice is sought (blue box in Figure 4). The obtained algebraic solution gives, among others, values of $\mathsf{\Phi }\left(y\right)$, $a_{AND}\left(y\right)$ and $a_{CTH}\left(y\right)$ i.e., the arguments ${\arg }_1\left(y\right),{\arg }_2\left(y\right),\dots$.. The derivative approximation is repeated this time taking the average over the $y$ coordinate of each of the arguments as the new value for the corresponding predictors:

$$\mathsf{\Pi }=\overline{\text{arg}}=\frac{{{\displaystyle \int }}_0^w\arg \left(y\right)dy}{w}$$

(84)

Additionally, the average species concentrations in the corresponding domains, required by Equations (13), (27) and others, are calculated in this step.

Figure 4. Calculation procedure for obtaining the solution for the whole fuel cell as a sequence of solutions for individual slices. Symbols in bold denote sets of variables of the same type i.e., $s^{snk}=\{s_{AND}^{snk},s_{CTH}^{snk}\}$, $\tilde{v}=\{{\tilde{v}}_{AND},{\tilde{v}}_{CTH}\}$, $\dot{n}=\{{\dot{n}}_{AND},{\dot{n}}_{CTH}\}$, $\overline{\text{arg}}=\{{\overline{\text{arg}}}_1,{\overline{\text{arg}}}_2\}$, $\mathsf{\Pi }=\{{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2\}$; ${\tilde{v}}^{\mathsf{\Pi }}$ is the predictor value for mean $z$-component velocity. The blue box represents solving the set of linear algebraic equations described in Subsection A.4 of Appendix A, the pink box represents the derivative approximation of all nonlinear functions according to (general) Equation (83) or (specific) Equations (A71), (A75) and (A76) in Appendix A. Purple box represents calculating the 1D gas-flow Equations (85) and (86).

Figure 4. Calculation procedure for obtaining the solution for the whole fuel cell as a sequence of solutions for individual slices. Symbols in bold denote sets of variables of the same type i.e., $s^{snk}=\{s_{AND}^{snk},s_{CTH}^{snk}\}$, $\tilde{v}=\{{\tilde{v}}_{AND},{\tilde{v}}_{CTH}\}$, $\dot{n}=\{{\dot{n}}_{AND},{\dot{n}}_{CTH}\}$, $\overline{\text{arg}}=\{{\overline{\text{arg}}}_1,{\overline{\text{arg}}}_2\}$, $\mathsf{\Pi }=\{{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2\}$; ${\tilde{v}}^{\mathsf{\Pi }}$ is the predictor value for mean $z$-component velocity. The blue box represents solving the set of linear algebraic equations described in Subsection A.4 of Appendix A, the pink box represents the derivative approximation of all nonlinear functions according to (general) Equation (83) or (specific) Equations (A71), (A75) and (A76) in Appendix A. Purple box represents calculating the 1D gas-flow Equations (85) and (86).

This procedure of linearising the problem using predictors and re-evaluating the predictors using the solution of the linearised problem is represented in the flowchart in Figure 4 as the repetition loop that follows a negative (red box) test of convergence criteria (yellow box). This loop is iterated until sufficient convergence i.e., until positive outcome (green box) of convergence criteria test. It has to be noted that the derivative approximation is done only on the level of a slice requiring that the variation of arguments of nonlinear functions is small only along the $y$ coordinate. Variation of these arguments along the length of the representative unit ($z$ direction) need not be small since the nonlinear variation from slice to slice is fully captured through the estimation-iteration procedure.

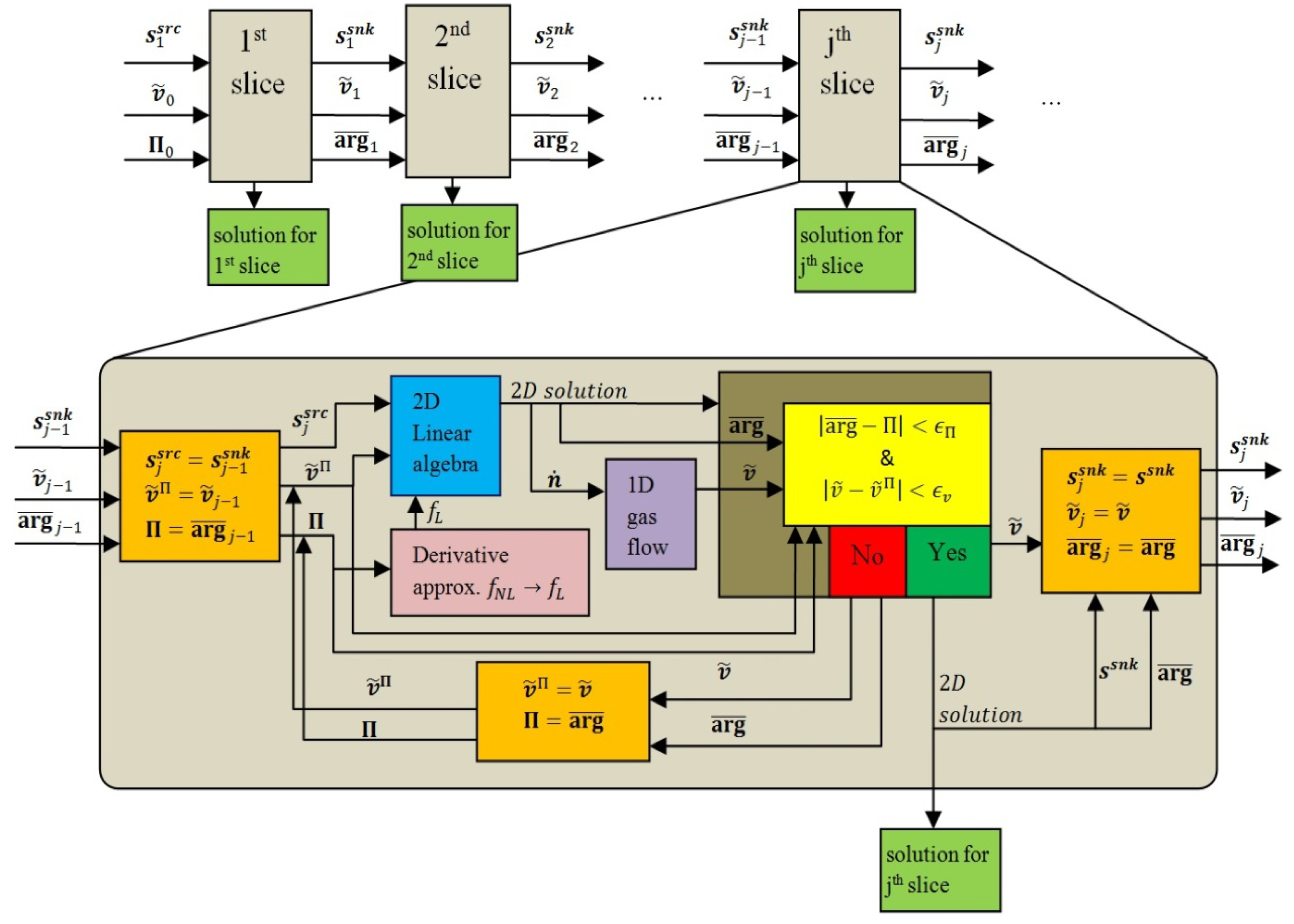
3.4.2. 1D Gas-Flow Equations

Within the iterative procedure described in previous subsection and depicted in Figure 4 the channel domain mean gas velocity $\tilde{v}$, needed in Equation (30), is also repeatedly re-evaluated (purple box) according to the following equations:

$${\tilde{v}}_{AND}={\tilde{v}}_{AND}^{pr}+\frac{RT}{p{A}_{AND}} {\dot{n}}_{AND}$$

(85)

$${\tilde{v}}_{CTH}={\tilde{v}}_{CTH}^{pr}+\frac{RT}{p{A}_{CTH}} {\dot{n}}_{CTH}$$

(86)

where ${\tilde{v}}^{pr}$ is the gas $z$-component velocity of gas in channel domain in previous upstream slice, $A=w1\times h2$, as discernible from Figure 2, is the area of channel cross-section ($A_{AND}=w{1}_{AND} \times h{2}_{AND}$ for anode channel and $A_{CTH}=w{1}_{CTH} \times h{2}_{CTH}$ for cathode) and $\dot{n}$ is the net molar flux added or taken from the gas flow within the slice depth defined as:

$${\dot{n}}_{AND}={\dot{n}}_{H_2}+l{{\displaystyle \int }}_0^w{j}_{AND}\left(y\right) dy$$

(87)

$${\dot{n}}_{CTH}={\dot{n}}_{O_2}+l{{\displaystyle \int }}_0^w{j}_{CTH}\left(y\right) dy$$

(88)

where $w=w{1}_{AND}+w{2}_{AND}=w{1}_{CTH}+w{2}_{CTH}$ is the width of a slice, $j_{AND}$ and $j_{CTH}$ are the molar fluxes of water from the membrane to the anode and cathode gas parts as defined by Equations (57) and (59) and ${\dot{n}}_{H_2}$ and ${\dot{n}}_{O_2}$ are the changes in molar flux of hydrogen and oxygen due to consumption at the catalyst as defined by Equations (53) and (55). Once a converged solution for a slice is obtained, the sink terms of the anode and cathode channel domains are passed on to the next downstream slice to serve as the two source terms.

3.5. HAN Concept Extendibility

Assuming no liquid water in the channels and GDL the model is readily applicable to high temperature PEM fuel cells (HT-PEM) that typically feature only single phase flow. This is owed to the fact that PBI membranes that are used in HT-PEMs feature linear relationship between conductivity and relative humidity [38] and no electroosmotic drag [39], making the equations for membrane species transport as given in Section 3.2 directly applicable also to the PBI membranes.

The presented framework of solving the diffusion equation on rectangular definition regions can be applied to treat also other phenomena governed by diffusion-type mechanisms such as heat transport, multi-component diffusion and Darcy-type flow of liquid water induced by gradients of capillary pressure, leading to a comprehensive treatment of also low temperature PEM fuel cells.

The principles of HAN model have been demonstrated on a simple straight channel fuel cell, however, the HAN model can be further extended to model also fuel cells with more complex geometries. In serpentine channel geometries the pressure difference between neighbor channel menders leads to a bulk gas cross-flow between the meanders, i.e., nonzero flow across the yellow plane in Figure 1 and Figure 2 (which is thus no longer a symmetry plane). Having a routine for calculating the pressure drop along the channel as given in [33] and noting that the channel pressure directly translates to the velocity potential boundary condition, as defined by Equation (24), the velocity field of this cross-flow is obtained using the formalism in Section 2.1. This leads to coupling each slice not only to its upstream neighbor but also to its two side neighbor slices.

4. Simulation Setup

To make the simulation setup of HAN-FC and CFD models as identical as possible all material and operational parameters, with the exception of exchange current density, were set to the same values in both HAN-FC and CFD model settings. The parameter defining the effective exchange current density, for which the user manual of the CFD software gives insufficient information, was obtained through calibration procedure performed on a case of higher operational voltage (low current densities) while the comparative analysis was performed for a case of lower operational voltage (high current densities). Calibration of HAN-FC for obtaining the parameter of effective exchange current density is described in Section 5.1 while other parameters used in HAN-FC and CFD models are summarised in Table 2.

Table 2. Operational, geometrical and material parameters used in CFD and HAN-FC models.

Parameter	Symbol	Value
Operational voltage	$V_{op}$	0.95 V, 0.9 V, 0.85 V, 0.8 V, 0.75 V
Temperature	$T$	343.15 K
Pressure *	$p$	1.0 × 105 Pa
Inlet gas velocity (anode and cathode)	${\tilde{v}}_0$	0.3 m/s
saturated water vapour partial pressure at 343.15 K	$c_{sat}$	3.12 × 104 Pa
Inlet gas relative humidity (anode and cathode)	$a, c/c_{sat}$	0.5
H2O(g)/O2 binary diffusion coeff. (at 343.15 K) **	$D$	3.01 × 10−5 m2/s
H2O(g)/H2 binary diffusion coeff. (at 343.15 K) **	$D$	1.12 × 10−4 m2/s
Coefficient of proportionality to water content of water diffusion coefficient in membrane (at 343.15 K)	${\mathfrak{D}}_w$	2.1 × 10−7 m2/s
Coefficient of proportionality to water content of proton diffusion coefficient in membrane (at 343.15 K)	${\mathfrak{D}}_{+}$	1.6 × 10−8 m2/s
Membrane sulphonic group concentration	$c_{·HS{O}_3}$	1900 mol/m3
GDL gaseous phase volume fraction (anode and cathode)	$\kappa$	0.78
GDL tortuosity (anode and cathode)	$D/D_{GDL}$	1.34
Cathode charge transfer coefficient	$\alpha$	0.855
Channel height (anode and cathode)	$h2$	1.5 × 10−3 m
Half of anode channel width	$w{1}_{AND}$	2.5 × 10−4 m
Half of cathode channel width	$w{1}_{CTH}$	3.75 × 10−4 m
GDL thickness (anode and cathode)	$h1$	2.85 × 10−4 m
width of representative unit	$w$	7.5 × 10−4 m
length of Representative unit	$L$	2.7 × 10−2 m
Membrane thickness	$\vartheta$	3.5 × 10−4 m

* In CFD this is the value of outlet pressure, maximal deviations from this value anywhere in the representative unit are +0.53% and −0.28% justifying assumption V of isobaric HAN-FC; ** In CFD these are the mean values since the CFD simulation takes into account the dependence of binary diffusion coefficient on the ratio of two the components. However, the relative standard deviation is below 0.09% with maximal deviations from the mean value anywhere in the representative unit being +0.45%and −0.26% justifying the assumption VI, i.e., the use of component ratio independent diffusion coefficient in HAN-FC.

Table 2. Operational, geometrical and material parameters used in CFD and HAN-FC models.

Parameter	Symbol	Value
Operational voltage	$V_{op}$	0.95 V, 0.9 V, 0.85 V, 0.8 V, 0.75 V
Temperature	$T$	343.15 K
Pressure *	$p$	1.0 × 105 Pa
Inlet gas velocity (anode and cathode)	${\tilde{v}}_0$	0.3 m/s
saturated water vapour partial pressure at 343.15 K	$c_{sat}$	3.12 × 104 Pa
Inlet gas relative humidity (anode and cathode)	$a, c/c_{sat}$	0.5
H2O(g)/O2 binary diffusion coeff. (at 343.15 K) **	$D$	3.01 × 10−5 m2/s
H2O(g)/H2 binary diffusion coeff. (at 343.15 K) **	$D$	1.12 × 10−4 m2/s
Coefficient of proportionality to water content of water diffusion coefficient in membrane (at 343.15 K)	${\mathfrak{D}}_w$	2.1 × 10−7 m2/s
Coefficient of proportionality to water content of proton diffusion coefficient in membrane (at 343.15 K)	${\mathfrak{D}}_{+}$	1.6 × 10−8 m2/s
Membrane sulphonic group concentration	$c_{·HS{O}_3}$	1900 mol/m3
GDL gaseous phase volume fraction (anode and cathode)	$\kappa$	0.78
GDL tortuosity (anode and cathode)	$D/D_{GDL}$	1.34
Cathode charge transfer coefficient	$\alpha$	0.855
Channel height (anode and cathode)	$h2$	1.5 × 10−3 m
Half of anode channel width	$w{1}_{AND}$	2.5 × 10−4 m
Half of cathode channel width	$w{1}_{CTH}$	3.75 × 10−4 m
GDL thickness (anode and cathode)	$h1$	2.85 × 10−4 m
width of representative unit	$w$	7.5 × 10−4 m
length of Representative unit	$L$	2.7 × 10−2 m
Membrane thickness	$\vartheta$	3.5 × 10−4 m

* In CFD this is the value of outlet pressure, maximal deviations from this value anywhere in the representative unit are +0.53% and −0.28% justifying assumption V of isobaric HAN-FC; ** In CFD these are the mean values since the CFD simulation takes into account the dependence of binary diffusion coefficient on the ratio of two the components. However, the relative standard deviation is below 0.09% with maximal deviations from the mean value anywhere in the representative unit being +0.45%and −0.26% justifying the assumption VI, i.e., the use of component ratio independent diffusion coefficient in HAN-FC.

The gas composition was, according to assumption VI, taken as bi-componential, i.e., H₂ with H₂O_(g) for the anode and O₂ with H₂O_(g) for the cathode. The parameters for membrane assumed no gas crossover.

CFD simulation was done using AVL FIRE® v2011 with the “Fuel cell” module (validation of which is found in references [40] and [41]). Two meshes differing in meshing density shown in Figure 5 were used for simulations. The denser mesh was used for obtaining results with high spatial resolution needed for plotting smooth 3D graphs in Section 5. The coarser mesh was used for estimating the shortest computational times of a CFD simulation that still gives accurate results on current density. Meshing of the representative unit for CFD simulation shown in Figure 5 was done as follows (numbers apply to the denser/coarser mesh): the mesh of the representative unit is made of anode and cathode side meshes containing equal number of subdivisions. Both GDLs are thus sectioned into 12/6 sections along GDL thickness $h1$, 12/6 along the width of representative unit $w$ and both channels are sectioned into 12/6 sections along channel height $h2$, 6/3 along the channel width $w1$ and the whole model is sectioned into 80/40 sections along the direction of gas flow (i.e., along the length of the representative unit $L$). Meshing of the membrane is done internally by the AVL FIRE fuel cell module as described in [42] and [33]. AVL FIRE fuel cell module treats the catalyst layers as zero-thickness surfaces. The isothermal conditions were obtained by omitting calculation of energy equation.

Figure 5. CFD simulation mesh of representative unit as presented in Figure 1. Left is the coarser mesh, right the denser. Volume elements of cathode channel are coloured blue, cathode GDL magenta, anode GDL green and the anode channel red. The same symmetry boundary conditions as presented in Figure 1 apply also to CFD simulation settings.

Figure 5. CFD simulation mesh of representative unit as presented in Figure 1. Left is the coarser mesh, right the denser. Volume elements of cathode channel are coloured blue, cathode GDL magenta, anode GDL green and the anode channel red. The same symmetry boundary conditions as presented in Figure 1 apply also to CFD simulation settings.

HAN-FC model was programmed in Wolfram Mathematica 9.0.1. In HAN-FC the representative unit was sliced into 40 sections (slices) along the direction of gas flow. To study the dependency of computational efficiency and accuracy of results on the number of harmonics taken into account in the linear combinations of analytic solutions three HAN-FC models differing in the number of harmonics taken into account were studied. The three models are labelled HAN₃, HAN₆ and HAN₉ and are defined as:

• In HAN₃ only first 3 modes per each coordinate. (i.e., 3 modes along y and 3 modes along x coordinate) are taken into account in harmonics in each gas part computational domain.
• In HAN₆ first 6 modes per each coordinate are taken into account in harmonics in each gas part computational domain.
• In HAN₉ first 9 modes per each coordinate are taken into account in harmonics in each gas part computational domain.

Taking into account a greater number of harmonics brings higher accuracy but also requires longer computational times as presented at the end of Subsection 5.2 and in Subsection 5.3.

5. Calibration and Results

HAN-FC was calibrated by finding the value of effective exchange current density that leads to the best agreement between HAN-FC and CFD results on current density at operational voltage of 0.85 V. The HAN-FC model with the so obtained exchange current density parameter was then evaluated globally by a comparative plot of the polarisation curve and locally by a detailed comparative analysis of spatial distribution of key variables at the operating point of highest current.

To aid the interpretation of the graphs in the following figures. Figure 6 shows the modelled representative unit placed in the coordinate system with respect to which all graphs of CFD and HAN-FC results are plotted. It should be noted that the choice of directions and origins of coordinates in Figure 6 is such that it enables easy interpretation of graphs in Section 5.2 and differs from the choice in Figure 2 or Figure 3 where the coordinate directions and origins are chosen in such a way to best suit expressions of governing equations in Section 3. Additionally it should be noted that the gap between anode and cathode GDL in Figure 6 does not reflect the thickness of the membrane but only the positioning of the meshes of the anode and cathode side in the CFD model as seen in Figure 5.

Figure 6. Representative unit in coordinate system. Cathode channel is coloured blue, cathode GDL magenta, anode GDL green and anode channel red. The central symmetry plane of a rib and the symmetry plane between ribs (respectively depicted as green and yellowish surfaces in Figure 1) that define representative unit are at y = 0 and at y = 0.75 mm respectively. Anode and cathode inlets are at, z = −13.5 mm outlets at z = 13.5 mm and the cross-sectional plane midway between inlet and outlet is at z = 0.

Figure 6. Representative unit in coordinate system. Cathode channel is coloured blue, cathode GDL magenta, anode GDL green and anode channel red. The central symmetry plane of a rib and the symmetry plane between ribs (respectively depicted as green and yellowish surfaces in Figure 1) that define representative unit are at y = 0 and at y = 0.75 mm respectively. Anode and cathode inlets are at, z = −13.5 mm outlets at z = 13.5 mm and the cross-sectional plane midway between inlet and outlet is at z = 0.

5.1. Calibration

At operational voltages of 0.85 V and lower the Butler-Volmer Equation (51) is well approximated by the Tafel equation:

$$i=BV\left(\mathsf{\Phi },c_r,c_p\right)=i_{ex}\left(\frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}({\mathsf{\Phi }}^0-\mathsf{\Phi })}-{\left(\frac{c_p}{c_{ref}}\right)}^s{e}^{- \frac{F\left(1-\alpha \right)}{RT}({\mathsf{\Phi }}^0-\mathsf{\Phi })}\right)\cong i_{ex}\frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^0-\mathsf{\Phi }\right)}$$

(89)

By defining:

$$i_{ex}^{*}=i_{ex} e^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^0-{\mathsf{\Phi }}^{⦵}\right)}$$

(90)

where $i_{ex}^{*}$ represents a renormalized current density and ${\mathsf{\Phi }}^{\mathsf{⦵}}=1.229\text{ V}$ is the cathode open circuit Galvani potential at standard conditions, the Tafel equation can be expressed as:

$$i=i_{ex}^{*} \frac{c_r}{c_{ref}}{e}^{\frac{F\alpha }{RT}\left({\mathsf{\Phi }}^{\mathsf{⦵}}-\mathsf{\Phi }\right)}$$

(91)

Finding the best fit of HAN-FC to CFD is done by adjusting the parameter $i_0^{*}$ in Equation (91) which avoids the need to define the exact value of ${\mathsf{\Phi }}^0$. The best fit of current density results of HAN-FC to those of CFD, graphically depicted in Figure 7, is found at $i_{ex}^{*}=0.1195 A/m^2$.

Figure 7. Best fit of results on current density distribution at 0.85 V of operational voltage. Green are CFD results and brown HAN₆ results.

Figure 7. Best fit of results on current density distribution at 0.85 V of operational voltage. Green are CFD results and brown HAN₆ results.

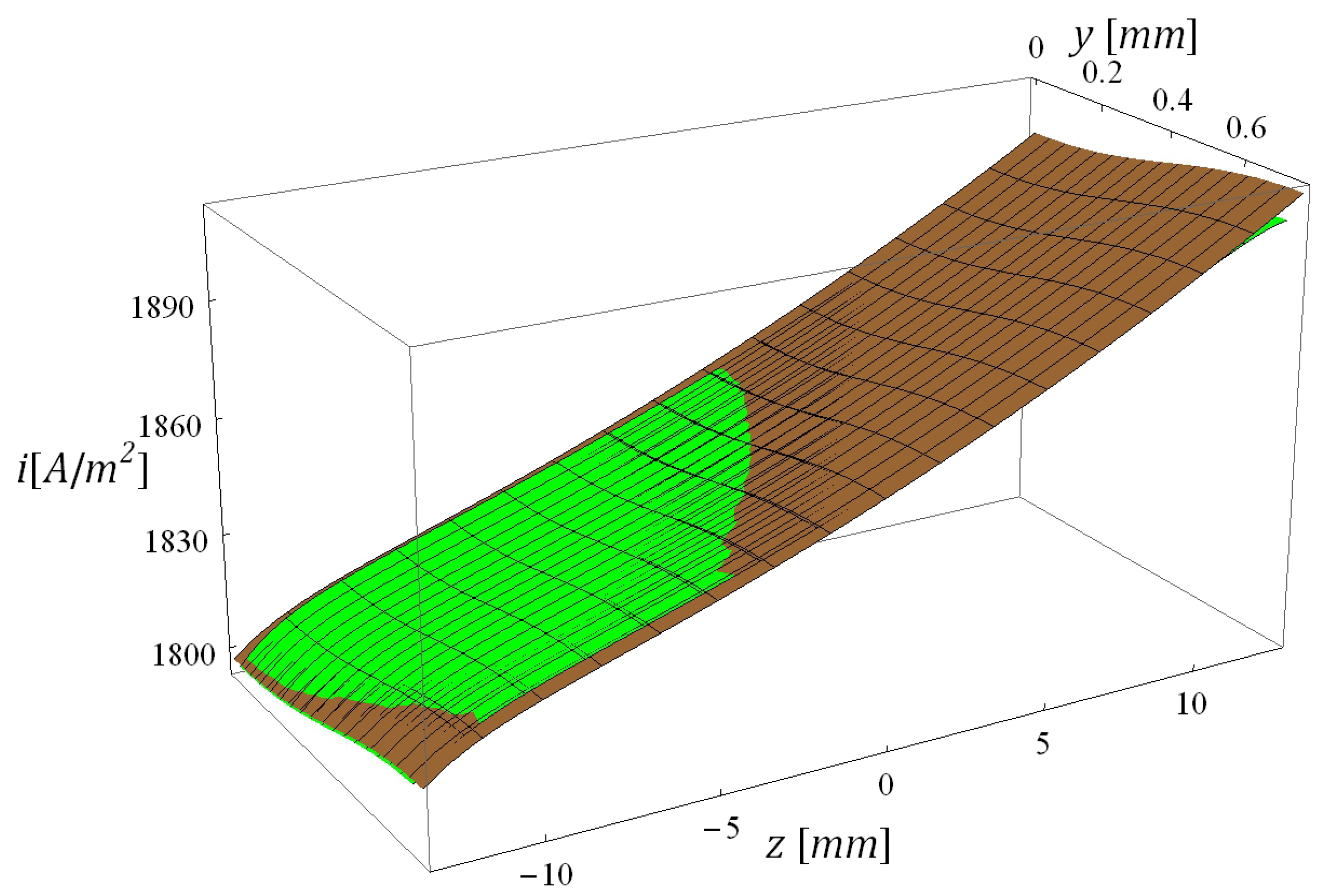
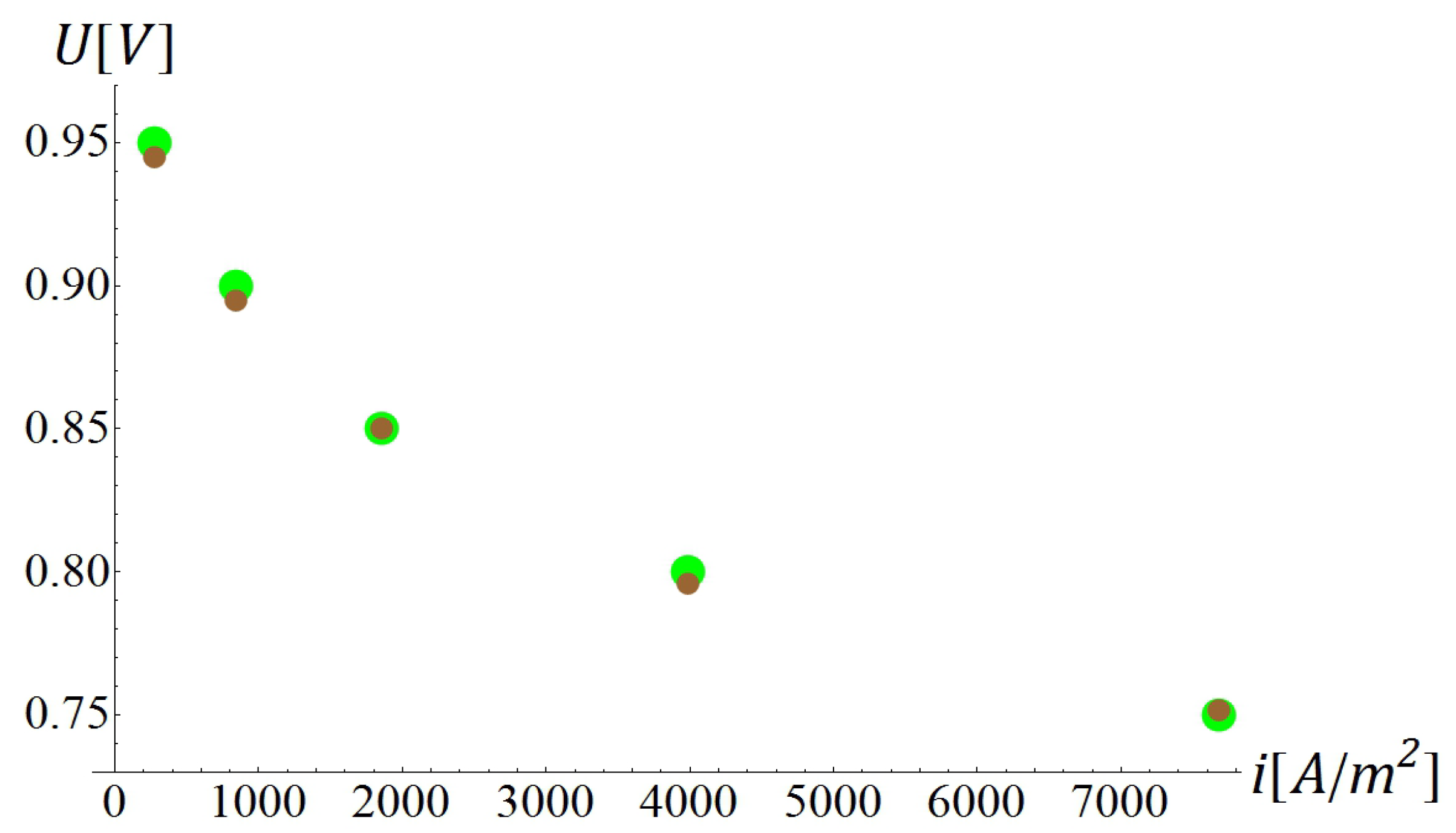
5.2. Plots of Comparative Results

In this subsection a number of comparative results are presented where in all graphs the CFD results are coloured green and are obtained using the denser mesh and HAN-FC results are coloured brown and are obtained using HAN₆ model. At the end of this subsection also a plot comparing results of HAN₃ and HAN₆ is shown.

Figure 8 shows the polarisation curve as calculated by the CFD and by the HAN-FC where the points representing the CFD results are obtained by calculating current density at five predefined operational voltages (with all other operational parameters fixed) whereas the points representing the HAN-FC results are obtained by finding the values of voltages that give the same current densities as the CFD results. The lowest operational voltage chosen for CFD simulation was 0.75 V, since at lower voltages liquid water, which cannot be comprehended by the HAN-FC model, starts occurring at the outlets.

Figure 8. Polarisation curve. Green are CFD results of current density obtained at voltages: 0.95 V, 0.9 V, 0.85 V, 0.8 V and 0.75 V. Brown are HAN₆ results of voltages that give current densities that match those of CFD.

Figure 8. Polarisation curve. Green are CFD results of current density obtained at voltages: 0.95 V, 0.9 V, 0.85 V, 0.8 V and 0.75 V. Brown are HAN₆ results of voltages that give current densities that match those of CFD.

Comparison of Figure 7 and Figure 9 shows that the operational voltage of 0.75 V, i.e., the operational point with highest current density, leads to considerably different operational conditions compared to the calibration case of 0.85 V. All following analyses are done for the operational point with the highest current density that fully exposes all governing phenomena that are comprehended in governing equations of Section 3. These analyses are thus aimed at validating the capability of HAN-FC to accurately treat these governing phenomena in a general straight parallel channel fuel cell.

As the most important simulation result Figure 9 shows graph of current density distribution. The primary objective of a fuel cell simulation is obtaining the net eclectic current at given operational conditions and in this respect the close agreement between HAN-FC and CFD results in Figure 9 speaks of high level of fidelity of the HAN-FC model. However it is instructive to analyse the underlying physical phenomena responsible for the shape of plots in Figure 9 and validate HAN-FC model under higher level of scrutiny.

The trend of current density rising with increasing values of z (i.e., from inlet to outlet), as discernible from Figure 9a,b, and rising with increasing values of y, as discernible from Figure 9b,c, can be explained by first using the Tafel equation [Equation (91)]. According to this equation the current density falls with decreasing reactant surface concentration c_r (plotted in Figure 10) and rises with decreasing cathode Galvani potential Φ (plotted in Figure 11). Since the dependence of current density on c_r is linear and dependence on Φ is exponential the influence of decrease of Galvani potential measuring a few hundredths of a volt, as observed in Figure 11, has a much larger effect than the decrease in oxygen concentration of around ten percent as observed in Figure 10. The decrease of Galvani potential is, according to Equation (50), equal to decrease of membrane overpotential. A decrease in membrane overpotential comes as a consequence of decreased membrane ohmic resistance that is inversely proportional to the mean membrane water content [Equation (48)]. Figure 12 shows that the two gas-flows get increasingly more saturated with water vapour on their way from inlet to outlet and consequentially also the membrane water content rises from inlet to outlet as discernible from Figure 13. Altogether this means that the increase in membrane hydration increases current density and indeed the plots of mean water content in Figure 12 and current density in Figure 9a are very similar. The trend of the increasing current density on the way from inlet to outlet thus reflects the influence of membrane hydration on fuel cell performance.

Figure 9. Current density distribution at the lowest operational voltage. Green are CFD results and brown HAN-FC results. (a) 3D plot of current density distribution over whole catalyst surface of the representative unit (b) 2D plot of current density distribution over the width of the representative unit at the inlet (z = −13.5 mm), midway (z = 0 mm) and outlet (z = 13.5 mm) represented by bottom, middle and top curves respectively; (c) Close-up 2D plot of current density distribution over the width of the representative unit midway between inlet and outlet.

Figure 9. Current density distribution at the lowest operational voltage. Green are CFD results and brown HAN-FC results. (a) 3D plot of current density distribution over whole catalyst surface of the representative unit (b) 2D plot of current density distribution over the width of the representative unit at the inlet (z = −13.5 mm), midway (z = 0 mm) and outlet (z = 13.5 mm) represented by bottom, middle and top curves respectively; (c) Close-up 2D plot of current density distribution over the width of the representative unit midway between inlet and outlet.

Figure 10. Cathode catalyst surface mole fraction of oxygen ∈(O₂) at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Figure 10. Cathode catalyst surface mole fraction of oxygen ∈(O₂) at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Figure 11. Cathode Galvani potential distribution at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Figure 11. Cathode Galvani potential distribution at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Figure 12. Water activity (relative humidity) on the central symmetry plane of a rib. Values in the membrane are obtained by interpolating values at the anode and cathode GDL/MEA interfaces.

Figure 12. Water activity (relative humidity) on the central symmetry plane of a rib. Values in the membrane are obtained by interpolating values at the anode and cathode GDL/MEA interfaces.

Figure 13. Mean membrane water content at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Figure 13. Mean membrane water content at 0.75 V of operational voltage. Green plot are CFD results and brown HAN-FC results.

Additionally, Figure 13 reveals that the membrane water content rises slightly also with increasing values of y. This is explained with the help of Figure 2: Water diffusing from MEA into GDL at lower y values enters GDL#1 domain (as indicated by the left narrower vertical blue arrow) and from there it diffuses into the channel domain (as indicated by the wider vertical blue arrow) where the stream of gas-flow caries it away. Water diffusing into GDL at higher y values enters GDL#2 domain (as indicated by the right narrower vertical blue arrow) and from there it first has to diffuse into GDL#1 domain (as indicated by the horizontal blue arrow) before reaching the gas stream in channel domain. This leads to a higher water vapour build-up in the GDL#2 domains compared to GDL#1 domains and consequently regions of membrane adjacent to GDL#2 domains feature higher water content than regions adjacent to GDL#1 domains. This in turn also explains the higher current densities observed at higher values of y in Figure 9c.

All comparative graphs of the MEA variables in the yz plane presented in Figure 9, Figure 10, Figure 11 and Figure 13 show close agreement between HAN-FC and CFD results and thus show important agreement of results on distribution of cathode Galvani potential and mean membrane water content, shown in Figure 11 and Figure 13, that directly reflect the nonlinear phenomena of membrane ohmic resistance, electrochemical reaction kinetics and membrane water activity [reflected for example in Equations (48), (51) and (68)]. This validates the capability of HAN-FC to accurately treat the coupled linear and nonlinear phenomena through the estimation-iteration loop described in Section 3.4.1. Furthermore Figure 9b and especially Figure 9c show that HAN-FC with its derivative approximation is also capable of accurately capturing variation of variables along the y coordinate.

It is also valuable to comparatively validate HAN-FC with results on species concentration distribution presented in Figure 12 and Figure 14. The brown plot in Figure 14 represents HAN-FC’s full 2D analytic solution for water vapour concentration distribution in the slice that is midway between inlet and outlet. Figure 15 shows the x component of net molar gas velocity (i.e., component perpendicular to membrane) at the GDL/MEA interface. The discontinuity and the notable ondulations in the HAN-FC plot in Figure 15 are inherent to the domain approach and the finite number of harmonics used in the HAN-FC model. The comparative graphs in Figure 14 and Figure 15 validate the approach of splitting diffusion problem into computational domains and finding solutions as linear combinations of eigen functions. Figure 12 shows the species concentration distribution on the rib’s central symmetry plane and thus shows the variations along the length of the representative unit. The variation of HAN-FC’s results along the length of representative unit reflects the variation of the 2D analytic solution from slice to slice. Since 2D solutions in consecutive slices depend on the coupling between slices via sink and source terms the close agreement between HAN-FC and CFD in Figure 12 validates the approach to treating the convective gas-flow with source and sink terms in conjunction with the 1D bulk gas-flow model.

Figure 14. Relative humidity in the slice that is midway between inlet and outlet i.e., z = 0. Green plot are CFD results and brown HAN-FC results.

Figure 14. Relative humidity in the slice that is midway between inlet and outlet i.e., z = 0. Green plot are CFD results and brown HAN-FC results.

Figure 15. 2D plot of distribution of the x component of net molar velocity over the width of the representative unit at the midway between inlet and outlet (z = 0 mm).

Figure 15. 2D plot of distribution of the x component of net molar velocity over the width of the representative unit at the midway between inlet and outlet (z = 0 mm).

As a CFD simulation result Figure 16 shows a profile of z-component velocity of cathode gas on the cross section that is midway between inlet and outlet. It is discernible from this plot that gas z-component velocity in GDL is negligible and that the velocity profile in the channel assumes the dome shape of laminar flow. This shape of the velocity profile is the same for any cross section meaning that only the height of the dome shape varies and that z-component velocity in GDL is always negligibly small. Since the same also holds true for anode gas, this justifies assumption IX.

Overall Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show a very good agreement between CFD and HAN-FC in terms of trends in analysed variables and in terms of their absolute values. It has been shown that by calibrating the model on a case where the resulting current density is relatively uniform (Figure 7), very good agreement with CFD results were achieved for a case where the variation of current density is substantial (Figure 9), confirming the capability of HAN-FC to model coupled 3D species transport and electrochemical phenomena with high fidelity.

Figure 16. Cross-sectional profile of absolute velocity of cathode gas at cross-section midway between inlet and outlet as obtained by CFD simulation.

Figure 16. Cross-sectional profile of absolute velocity of cathode gas at cross-section midway between inlet and outlet as obtained by CFD simulation.

Figure 17 shows a comparison between two analytic HAN-FC solutions for a slice where one takes into account three modes along each coordinate within a domain and the other six modes. The two analytic solutions are hardly distinguishable from one another with the difference in accuracy being noticeable only at the interfaces between computational domains where the analytic solutions for domains are sewed together. This means that as little as three modes per coordinate taken into account in harmonics of each computational domain already capture the essential features of the concentration distribution. Furthermore plots of HAN-FC results in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 stay practically identical when plotted using results obtained with HAN₃ instead of HAN₆ indicating that HAN-FC can give accurate results at low computational demands.

Figure 17. Comparison between HAN₆ (brown) and HAN₃ (yellow). Close-up of the concentration distribution in cathode GDL domains and part of cathode channel domain of the slice that is midway between inlet and outlet is shown.

Figure 17. Comparison between HAN₆ (brown) and HAN₃ (yellow). Close-up of the concentration distribution in cathode GDL domains and part of cathode channel domain of the slice that is midway between inlet and outlet is shown.

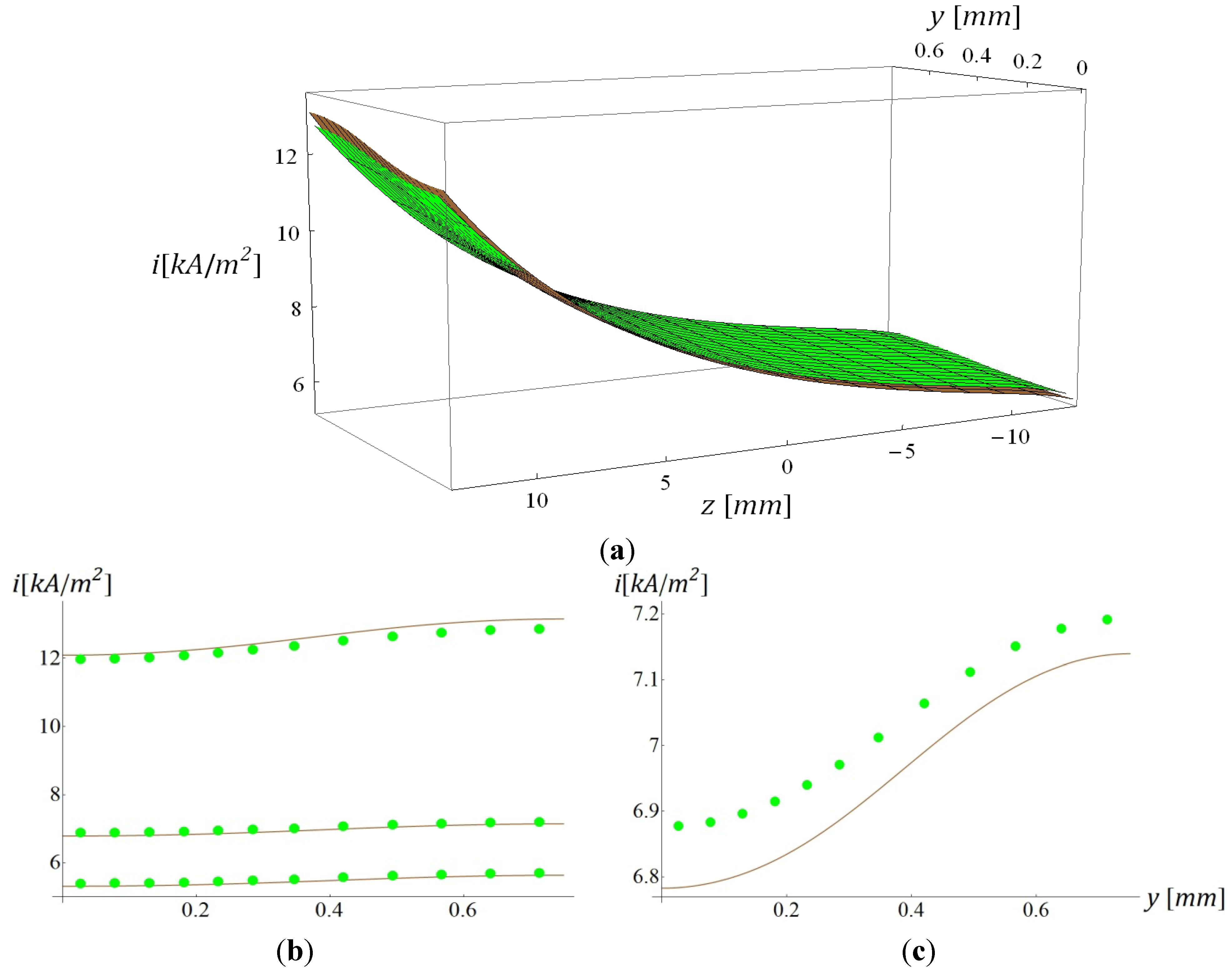
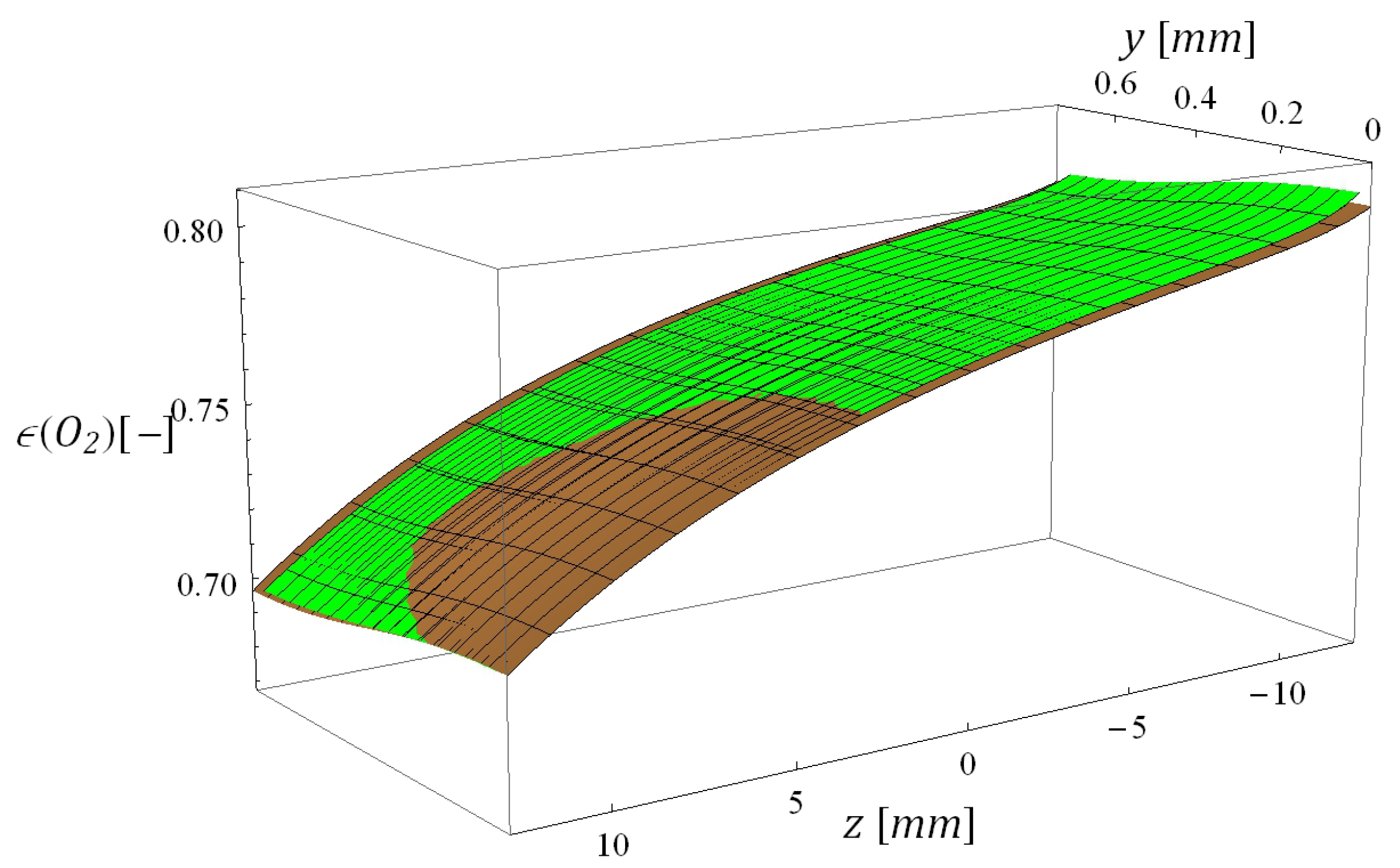
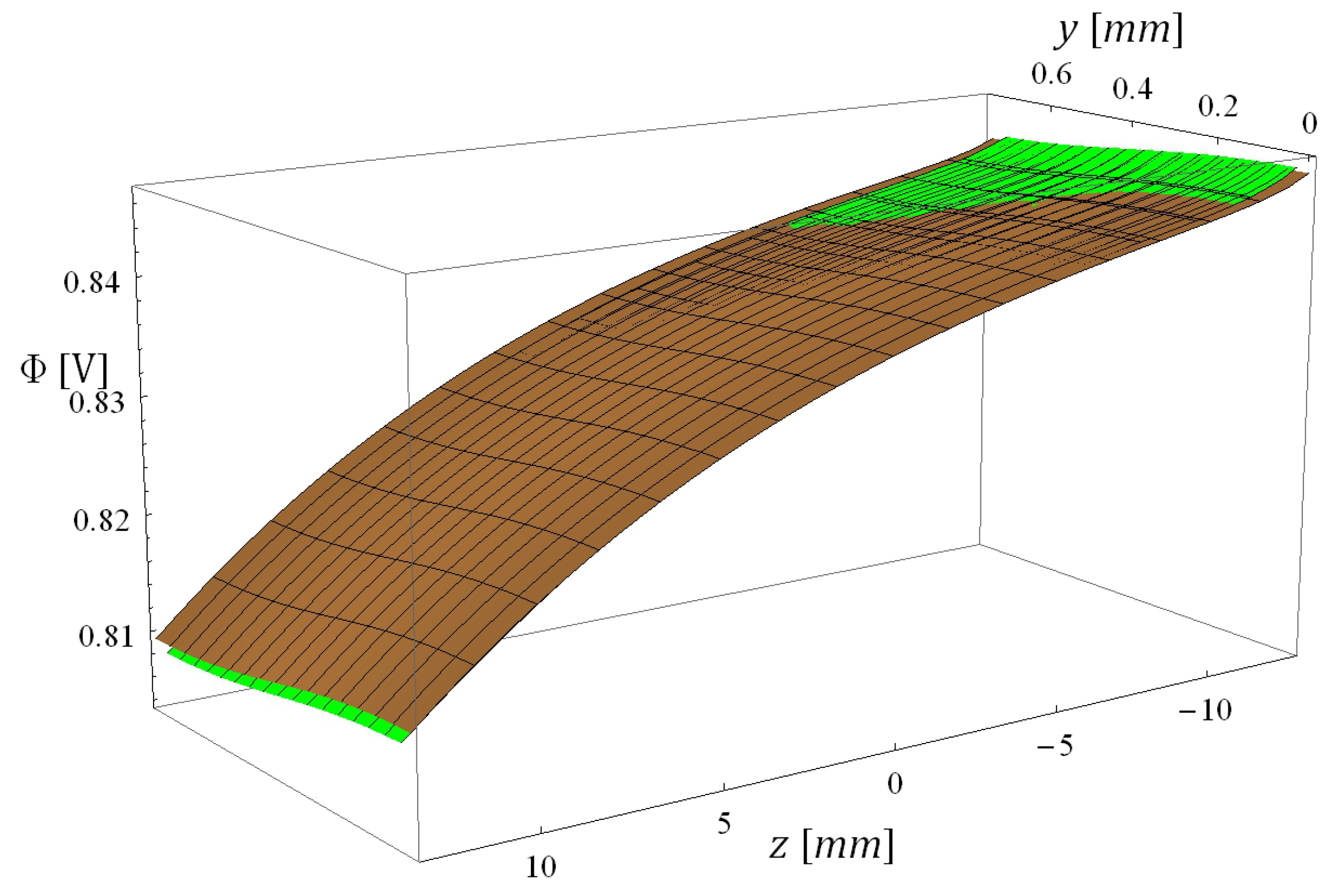
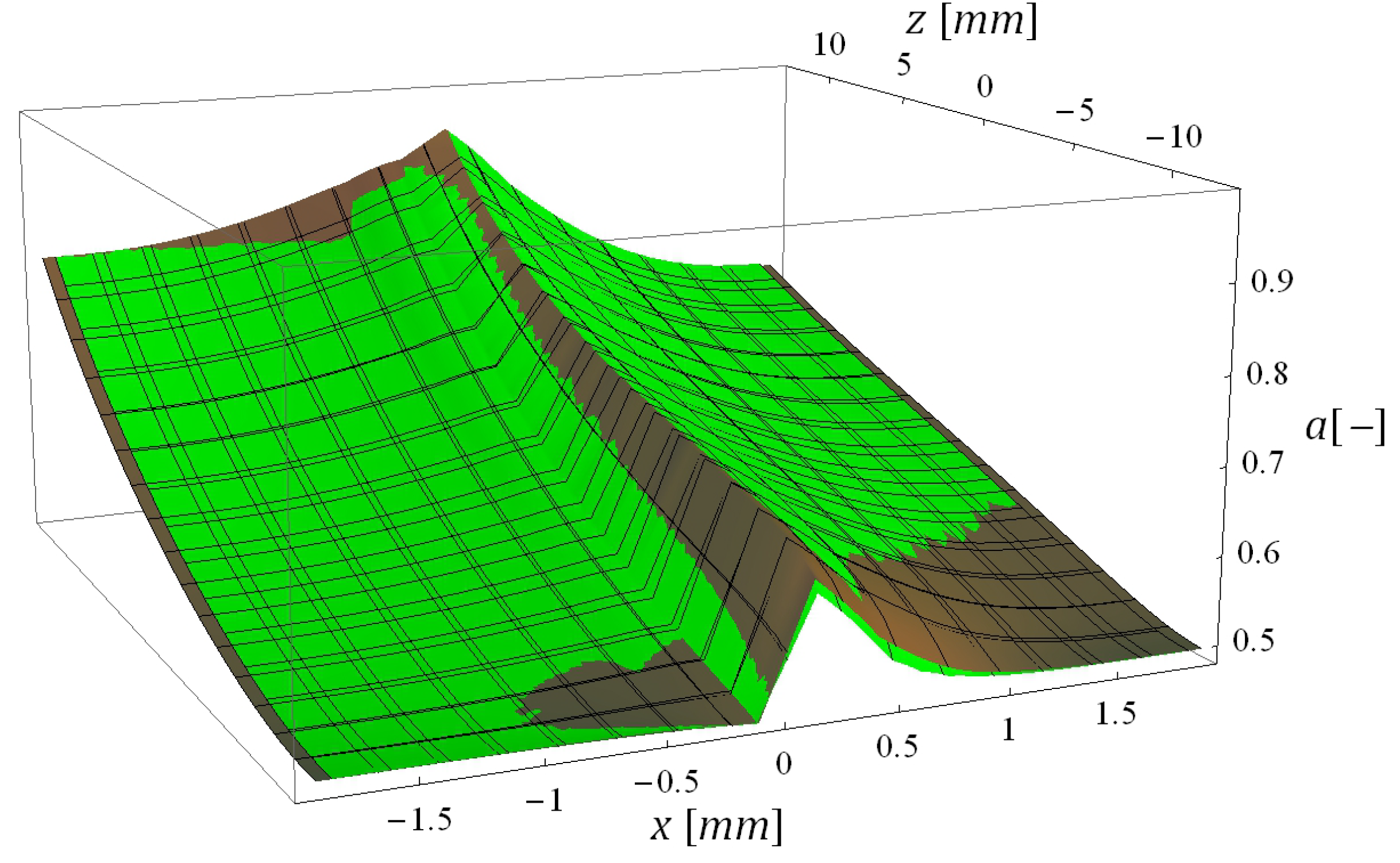
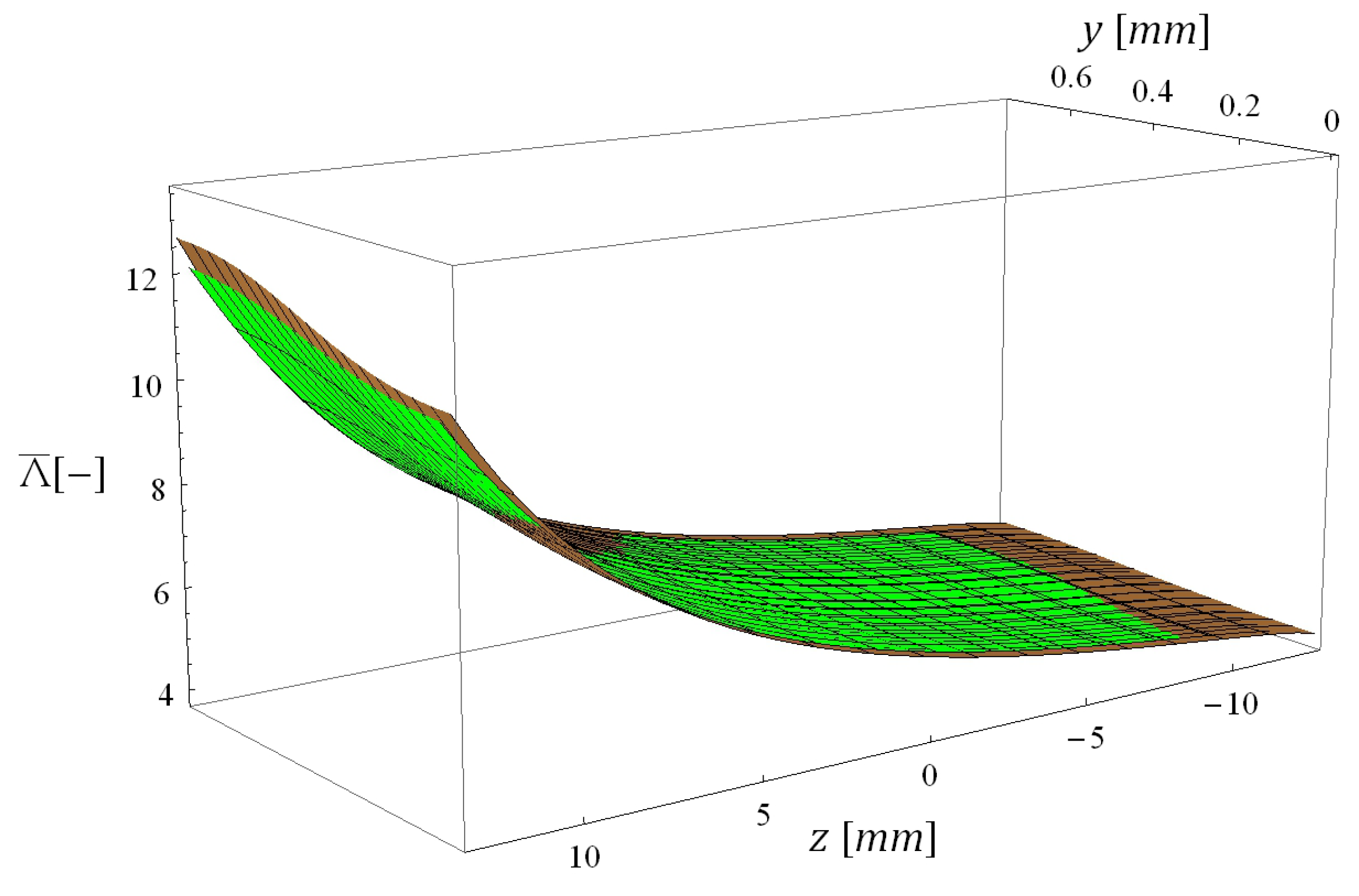
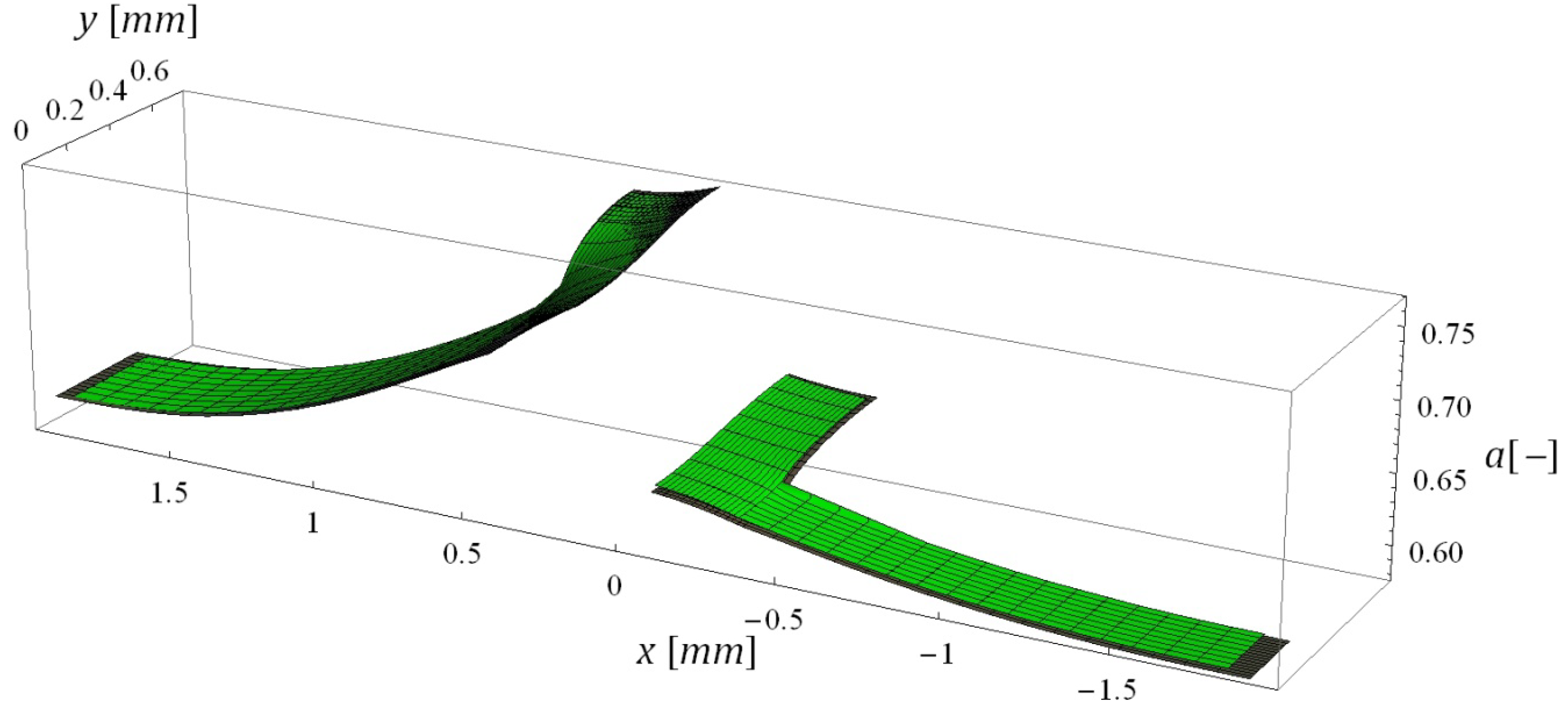
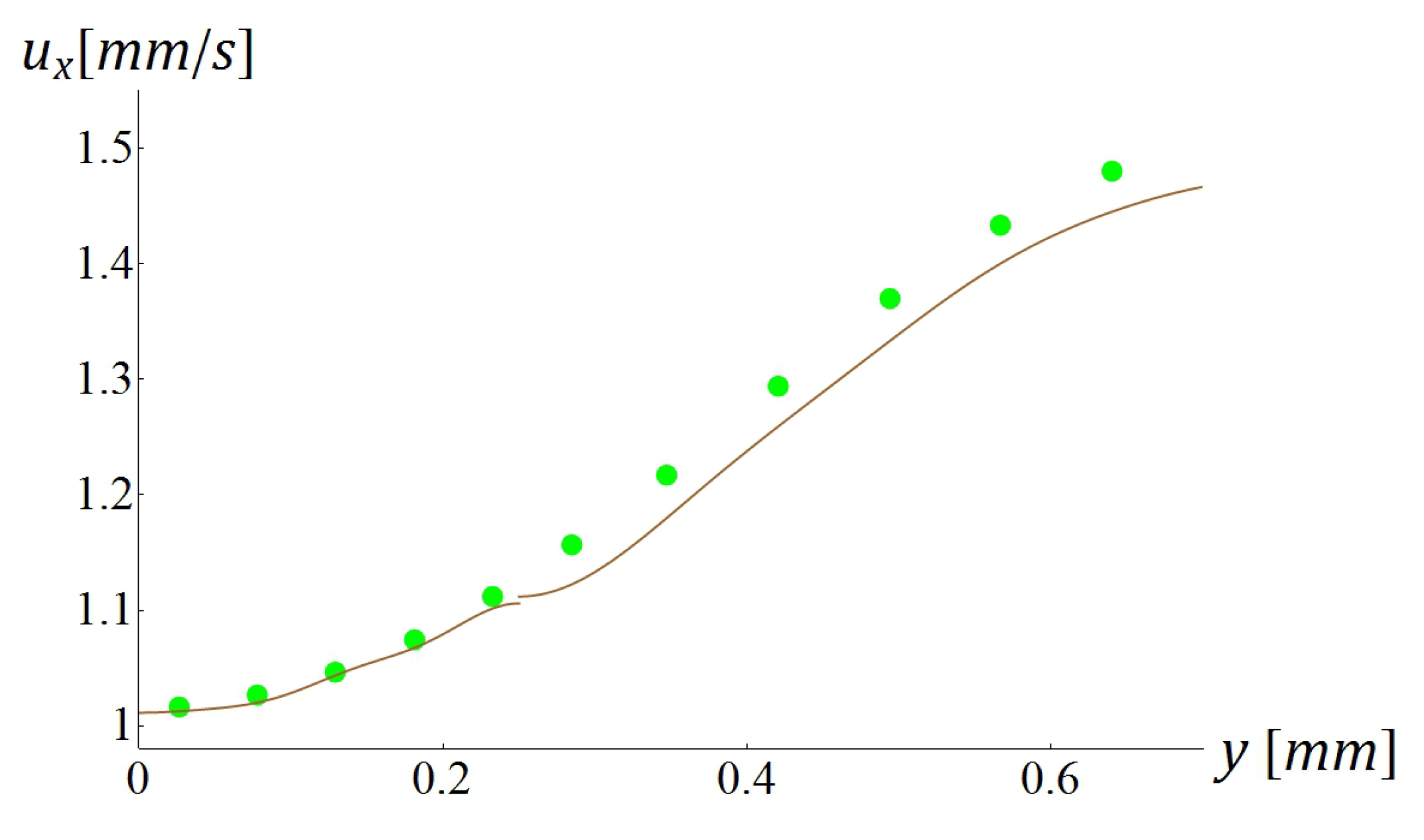
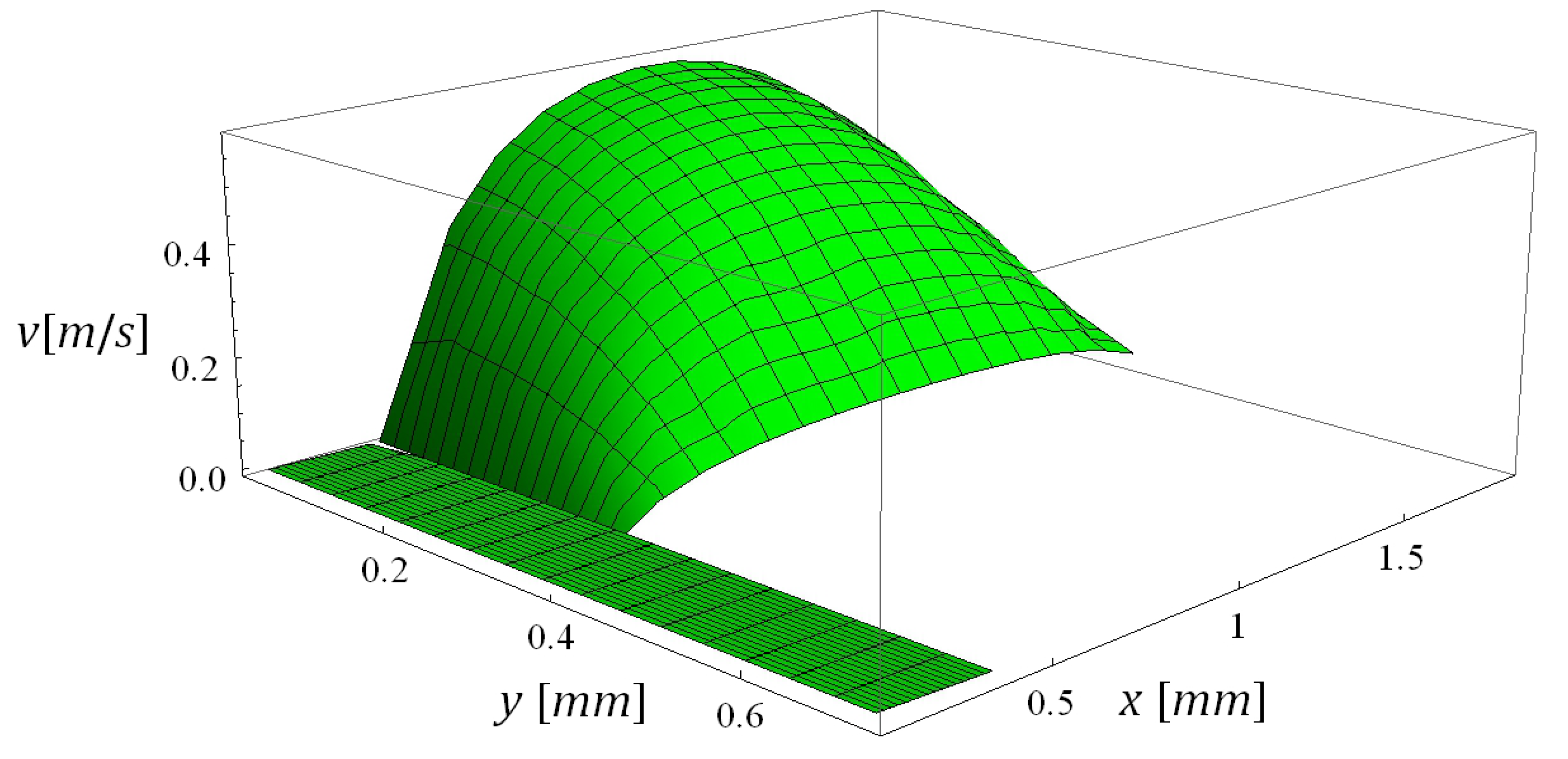
5.3. Computational Times

Table 3 shows computational times for models with different spatial resolution. The spatial resolution in case of CFD models is defined by the number of volume elements of the mesh whereas the spatial resolution of HAN-FC model is defined by the number of harmonic modes per coordinate taken into account in each computational domain.

Table 3. Calculation times (on a desktop computer).

Model	Resolution	No. of iterations *	CPU cores used	CPU time (s)	Total time (s)
CFD(denser)	34,560 vol. el.	10,000	4	38,000	13,000
CFD(coarser)	4320 vol. el.	5000	4	2400	640
HAN3	3 modes	1	1	0.85	0.85
HAN6	6 modes	1	1	3.7	3.7
HAN9	9 modes	1	1	6.0	6.0

* Iterations of obtaining solution for whole representative unit.

Table 3. Calculation times (on a desktop computer).

Model	Resolution	No. of iterations *	CPU cores used	CPU time (s)	Total time (s)
CFD(denser)	34,560 vol. el.	10,000	4	38,000	13,000
CFD(coarser)	4320 vol. el.	5000	4	2400	640
HAN3	3 modes	1	1	0.85	0.85
HAN6	6 modes	1	1	3.7	3.7
HAN9	9 modes	1	1	6.0	6.0

* Iterations of obtaining solution for whole representative unit.

The denser CFD mesh features twice as many divisions along each coordinate as coarser one thus featuring eight times more volume elements. Larger number of volume elements also requires more iterations to reach adequate convergence. The large difference between computational times of HAN-FC and those of CFD originates from the fact that CFD requires from a few hundred to a few thousand iterations of the solution for the whole mesh to reach convergent results, whereas the isothermal and isobaric HAN-FC calculates everything in one go. This single iteration of the solution for the whole representative unit is not to be confused with iterations performed within each slice that are performed by the estimation-iteration routine for treating nonlinear functions. Typically 5 to 6 of these iterations were required in each slice to reach relative accuracy of 10⁻⁴(convergence criteria in yellow box in Figure 4).

Recalling from Figure 17 the high accuracy of the lower resolution HAN-FC together with Table 3 reveals that HAN-FC gives accurate results at computational times that are two to three orders of magnitude shorter than that of CFD. The core of computational operations of HAN-FC is the linear algebraic solving for eigen function coefficients, described in Appendix A, which is in the case of simulations presented in this paper done using vector algebra as introduced in HAN-ST of [33]. Furthermore, the computational times of HAN-FC model evaluated in this paper have a considerable margin for additional improvement by programming the model in a programming language such as C or Fortran that are more suitable for numerical computation than Mathematica and by executing the simulation on multiple CPU cores.

6. Conclusions

The paper presented a Hybrid Analytic-Numerical approach to fuel cell modelling (HAN-FC) efficiently applied to modelling a realistic straight parallel channel fuel cell. The HAN-FC approach efficiently combines three main features:

• The 1D numerical treatment of gas flow;
• The analytic 2D solution for the species concentration profile in the plane perpendicular to the gas flow and
• The electrochemical sub-model.

The key to the hybrid 3D solution is constructing it as a series of consecutive 2D analytic solution that are obtained by splitting the 2D diffusion problem onto separate computational domains which on one hand enables modelling of realistic fuel cell geometries and on the other hand gives computationally efficient results with high accuracy already at very moderate number of harmonic modes taken into account. The efficiency of incorporation of the electrochemical sub-model lies in the derivative approximation and estimation-iteration approach and is reflected in the fact that electrochemical calculations do not need a separate routine but are performed alongside calculations of the nonlinear coupling of water activity in gas to the water activity in membrane. Overall, HAN-FC proves to be very accurate and computationally efficient and as such a very promising standalone fuel cell model for system level simulations. Further challenges in developing HAN-FC for system level simulations remain the treatment of liquid water in GDLs and channels.