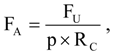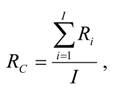3.1. Estimating Fatality Rates
Fatality search effort varied in frequency and number of turbines searched throughout the study period 1998–2003 [
4]. During fatality searches biologists searched for bird carcasses within 50 m of each wind turbine, walking parallel routes at about 8–16 m intervals along rows of turbines. From March 1998 through September 2002, groups of turbines were added to the search rotation as access was granted and ultimately a total of 1,526 wind turbines arranged in 182 rows were searched at various intervals (mean = 53 days). From November 2002 to May 2003 another 2,548 turbines arranged in 380 rows were searched twice at intervals of 90+ days. Carcasses found in 1998–2003 were used for developing predictive models. Carcasses found during another monitoring period, from March 2005 through March 2007 [
2], were used for model validation. Searches for these carcasses were performed with an average interval of 41 days at 2,650 wind turbines in stratified random plots, using comparable field methods to the earlier fatality monitoring program.
All carcasses or body parts found were examined to assign species, age, sex, and probable cause of death. Cause of death was determined by evidence of injuries, when available, such as burn marks or singed feathers typical of electrocution, and cut or twisted torsos, dismemberment and other forms of blunt force trauma typical of collisions with wind turbine blades. Unless assigned another cause of death, carcasses were assumed to have been killed by a wind turbine if found within 125 m of a wind turbine. Carcasses were used in fatality rate estimation if the estimated time since death was ≤90 days, because we did not want to include fatalities caused prior to the study period. The number of days since death was estimated after assessing carcass condition (e.g., fresh, weathered, dry, bleached bones) and decomposition level (e.g., flesh color, presence of maggots, odor).
Figure 1.
Some of the various old-generation wind turbine models in the APWRA during 1998-2007, including Nordtank 65-kW (A), KCS56 100-kW (B), Bonus 150-kW (C), Polenko 100-kW (D), Windmatic 65-kW (E), Howden 330-kW (F), Micon 65-kW (G), Enertech 40-kW (H), Flowind 150-kW (I), and KVS-33 400-kW (J). These photos are not to scale.
Figure 1.
Some of the various old-generation wind turbine models in the APWRA during 1998-2007, including Nordtank 65-kW (A), KCS56 100-kW (B), Bonus 150-kW (C), Polenko 100-kW (D), Windmatic 65-kW (E), Howden 330-kW (F), Micon 65-kW (G), Enertech 40-kW (H), Flowind 150-kW (I), and KVS-33 400-kW (J). These photos are not to scale.
Figure 2.
Vestas 660-kW turbines in Diablo Winds Energy Project, which replaced Flowind vertical axis turbines (left photo), and Mitsubishi 1-MW turbines in Buena Vista Wind Energy project that replaced Windmaster, Nordtank, and Danwin turbines (right photo).
Figure 2.
Vestas 660-kW turbines in Diablo Winds Energy Project, which replaced Flowind vertical axis turbines (left photo), and Mitsubishi 1-MW turbines in Buena Vista Wind Energy project that replaced Windmaster, Nordtank, and Danwin turbines (right photo).
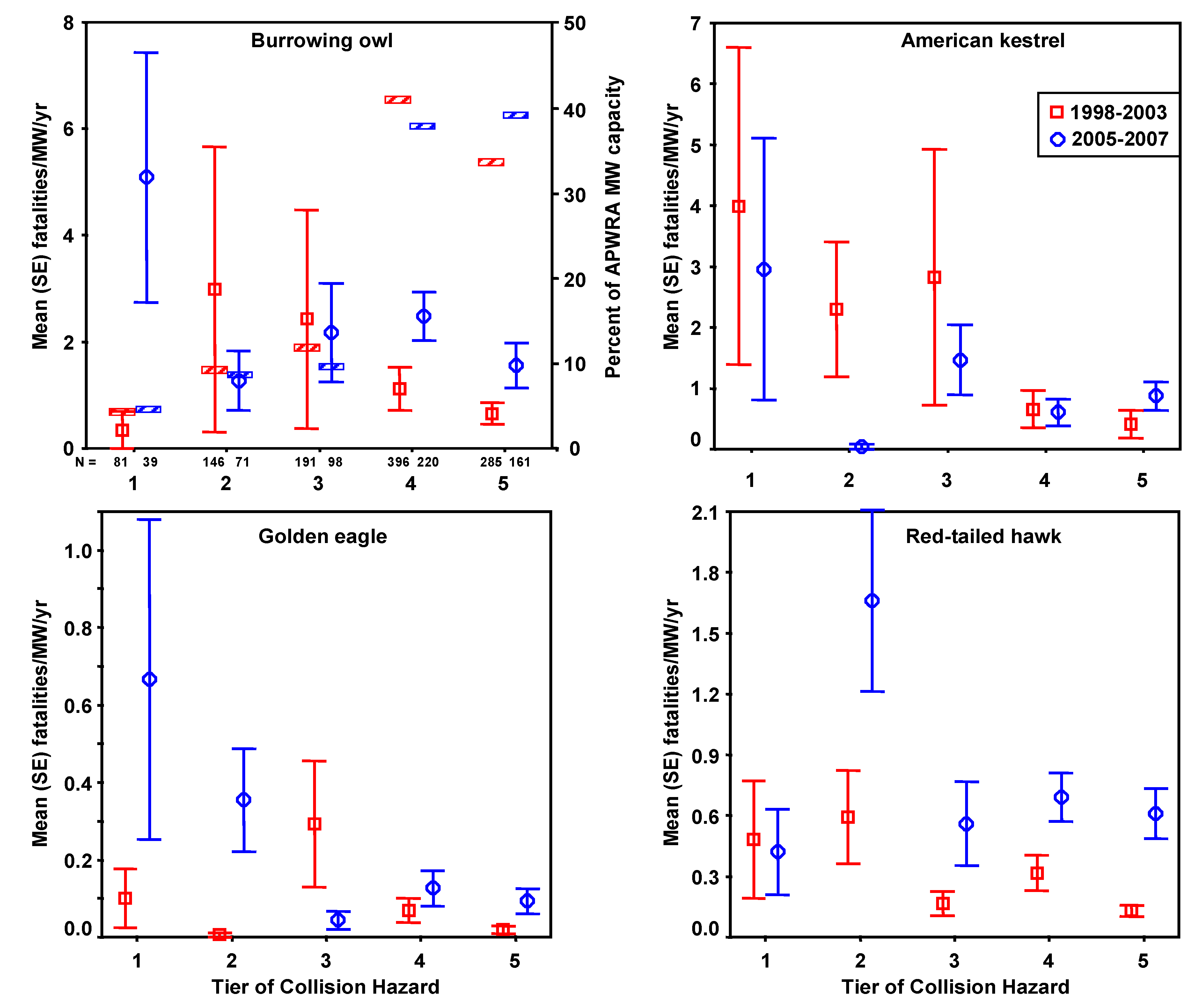
Fatality rates were expressed as the number of fatalities per MW per year, where MW was the rated power output of the wind turbines composing a row of wind turbines, and the number of years or fractions of a year were the time spans over which searches were performed at that wind turbine row. Fatality rates were based on fatalities occurring ≤90 days before discovery, and 0.25 years was added to the number of years used in each fatality rate calculation to represent the time period when fresh carcasses could have accumulated prior to the first search. We adjusted fatality rates,
FA, for carcasses not found due to searcher detection error and scavenger removal [
2]:
where
FU was unadjusted fatality rate,
p was the average proportion of fatalities found by searchers during searcher detection trials across the U.S. [
15], and
RC was the average cumulative proportion of carcasses remaining since the last fatality search, assuming wind turbines deposit carcasses steadily through the search interval. Preliminary
RC values were estimated using reports of scavenger removal trials across the U.S. [
15]:
where
Ri was the proportion of carcasses remaining by the
ith day into a scavenger removal trial and corresponding with days since the last search during fatality monitoring, and
I was the average search interval (days). We looked up
RC values in [15, App.], but we note that new approaches to scavenger removal trials have been generating faster removal rates (Smallwood
et al., manuscript in preparation). Searcher detection and scavenger removal rates varied across the U.S., but not nearly to the degree they varied by typical body size categories and by whether raptors or nonraptors [
15]; nevertheless, multiple sources of error and bias have yet to be characterized.
3.3. Spatial Models to Predict Burrowing Owl Locations
We mapped burrowing owl burrows as point features in ArcMap GIS layered onto a digital elevation model (DEM). We characterized the location of each burrowing owl burrow by slope aspect, slope grade, rate of change in slope, direction of change in slope, and elevation. These variables were also used to generate raster layers of the study area, one raster expressing the aspect of the corresponding slope (hereafter referred to as ‘slope aspect’), and the other expressing whether the landscape feature was tending toward convex versus concave orientation. These features were defined using geoprocessing.
The United States Geological Survey (USGS) 10-m DEM was used as a starting point for characterizing the terrain of the Altamont Pass. To replace poorer quality data across about 25% of the study area, geo-referenced USGS 7.5’ digital raster graphics (DRG) were used with GIS to capture the contour lines (hypsography). These contour vectors were then run through ESRI’s Topograph tool to create a 10-m DEM, which was inserted into the existing USGS 10-m DEM. Elevation was assigned to each grid cell according to its centroid.
From the final DEM of the Altamont Pass region, the statistical analyses were limited (masked) to data within the areas searched for ground squirrel and burrowing owl burrows. The resulting analytical grid was composed of 187,908 10 × 10 m2 cells. The analytical grid was used to develop and test predictive models, which were later projected across the 2,281,169 grid cells composing the APWRA. The analytical grid was not selected randomly from within the APWRA because the focus of the burrow mapping was on raptor prey species nearby the wind turbines, most of which were placed along ridge crests and ridgelines between peaks and valley bottoms. Thus, some landscape features within the analytical grid were disproportional to their occurrence within the APWRA, such as ridge crests. Model predictions will be more reliable for landscape features represented within the analytical grid than for landscape features typically farther away from wind turbines.
Figure 3.
Ridge and valley features expressed as blue and gold, respectively, and typical of convex-trending groups of DEM grid cells (ridges) and concave-trending groups of grid cells (valleys).
Figure 3.
Ridge and valley features expressed as blue and gold, respectively, and typical of convex-trending groups of DEM grid cells (ridges) and concave-trending groups of grid cells (valleys).
We used the Curvature function in the Spatial Analysis extension of ArcGIS 9.2 to calculate the curvature of a surface at each cell centroid. A positive curvature indicated the surface was upwardly convex at that cell, a negative curvature indicated the surface was upwardly concave, and a value of zero indicated the cell surface was flat. The curvature data (–51 to 38) were classified using the NaturalBreaks (Jenks) function with three classes of curvature–convex, concave and mid-range. The break values were visually adjusted to minimize the size of the mid-range class. We used a series of geoprocessing steps called ‘expand,’ ‘shrink,’ and ‘regiongroup,’ as well as ‘majority filter tools’ to enhance the primary slope curvature trend of a location. The result was a surface almost exclusively defined as either convex or concave (
Figure 3). The convex surface areas consisted primarily of ridge crests and peaks, hereafter referred to as ridges, and the concave surface areas consisted primarily of valleys, ravines, ridge saddles and basins, hereafter referred to as valleys.
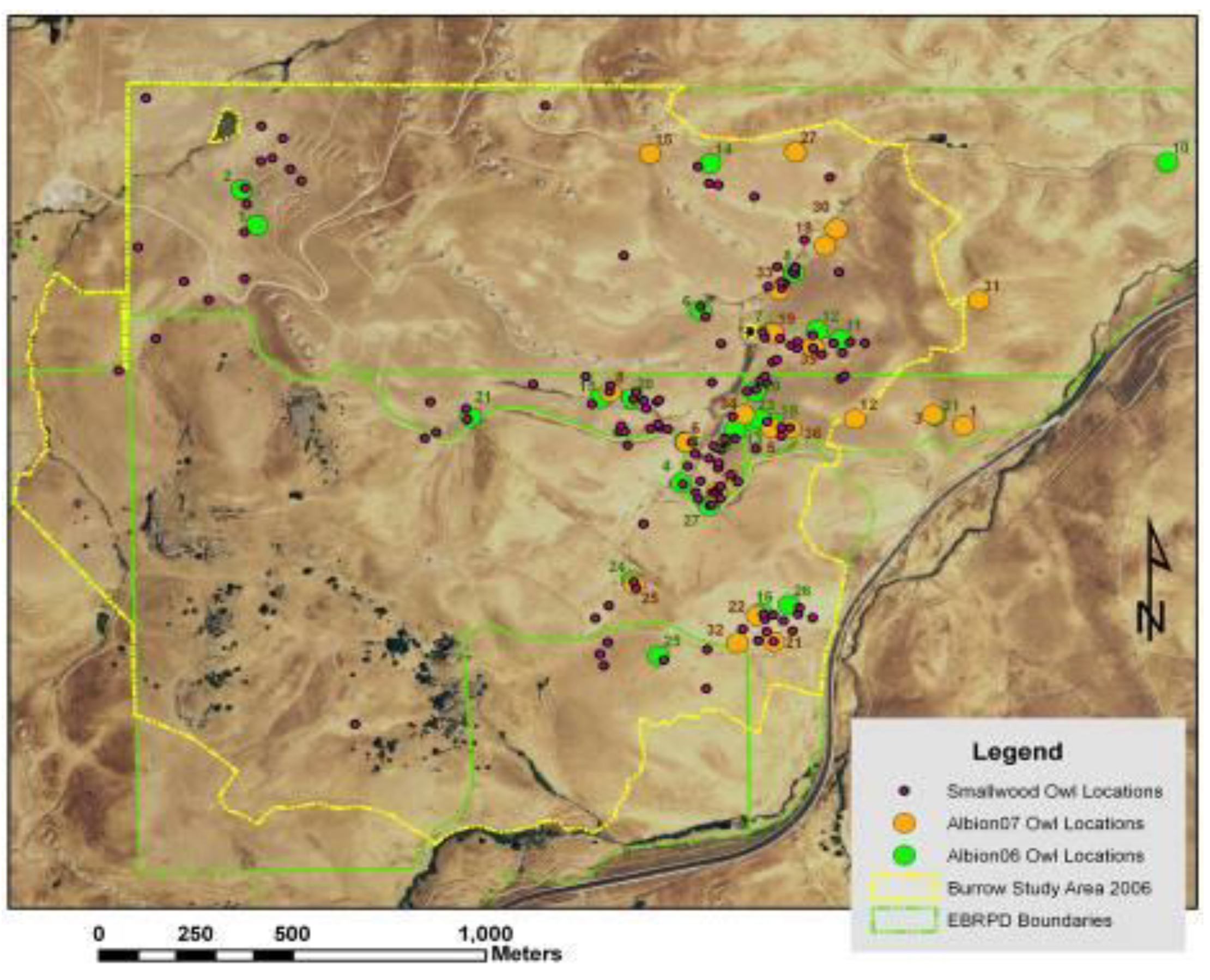
Line features representing the estimated average centers of ridge crests and valley bottoms (
Figure 4) were derived from the following steps. ESRI’s ‘Flowdirection’ function was used to create a flow direction from each cell to its steepest down-slope neighbor, and then the ‘Flowaccumulation’ function was used to create a grid of accumulated flow through each cell by accumulating the weight of all cells flowing into each down-slope cell. A valley started where 50 upslope cells had contributed to it in the Flowaccumulation function, and a ridge started where 55 cells contributed to it. The flowdirection and flowaccumulation functions were applied to the ridges by multiplying the DEM by −1 to reverse the flow. Line features that represented ridges and valley bottoms were derived from ESRI’s gridline and thin functions, which feed a line through the centers of the cells composing the valley or ridge. Thinning put the line through the centers of groups of cells ≥40 in the case of valleys.
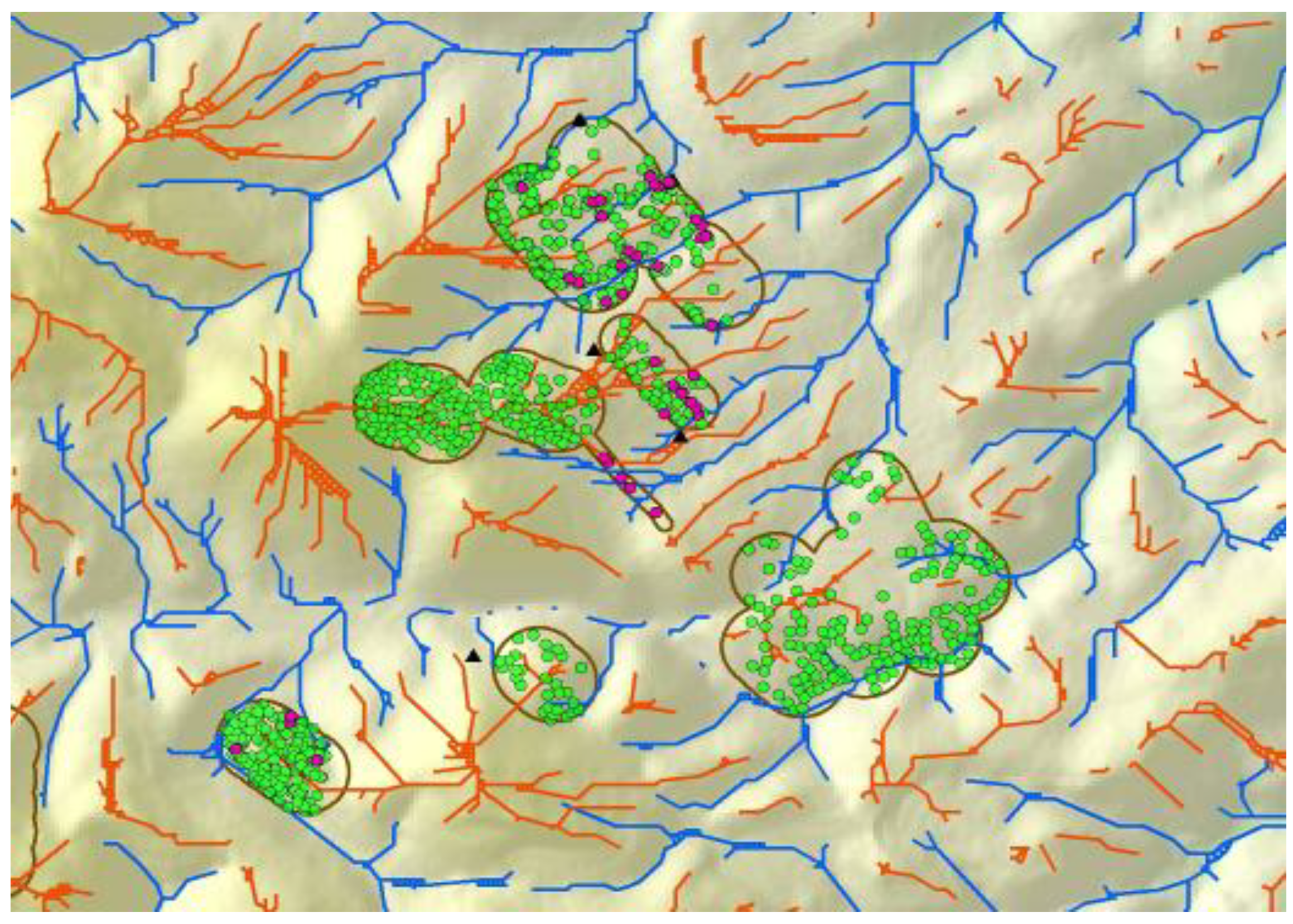
Figure 4.
Line coverages of ridge tops (orange) and valley bottoms (blue) following multiple geoprocessing steps assessing trends in neighboring DEM grid cells. Polygons enclose areas around wind turbines where burrow systems of ground squirrel (green) and burrowing owls (magenta) were mapped to develop predictive models.
Figure 4.
Line coverages of ridge tops (orange) and valley bottoms (blue) following multiple geoprocessing steps assessing trends in neighboring DEM grid cells. Polygons enclose areas around wind turbines where burrow systems of ground squirrel (green) and burrowing owls (magenta) were mapped to develop predictive models.
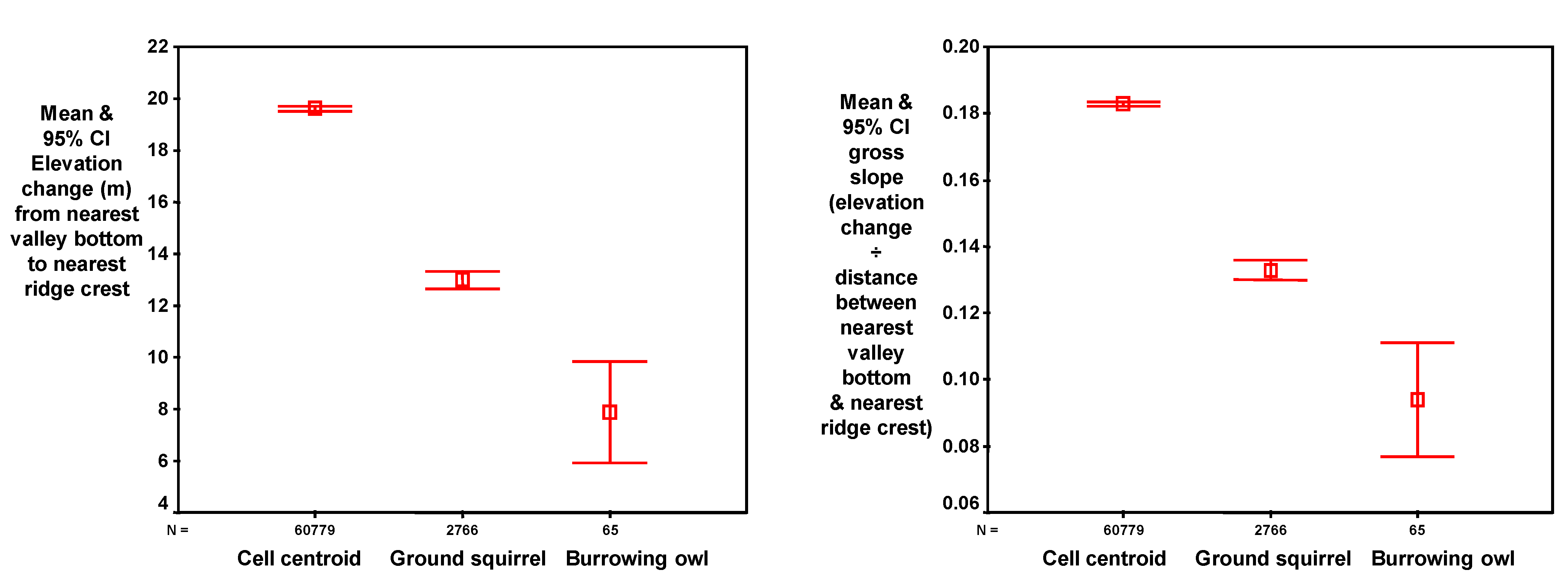
The horizontal distance (m) of each DEM grid cell was then measured from the nearest valley bottom and the nearest ridgeline, referred to as
distance to valley and
distance to ridge, respectively (
Figure 5). These distances were measured from the DEM grid cell to the closest grid cell of a valley bottom or ridgeline, respectively, not including vertical differences in position. The total distance across the underlying slope was the sum of the distance to the valley bottom and the distance to the ridgeline, and expressed the size of the slope (
total slope distance). The DEM grid cell’s position in the slope was also expressed as the ratio of the distance to the valley and the distance to the ridge, referred to as the
distance ratio. This expression of the grid cell’s position on the slope removed the size of the slope as a factor.
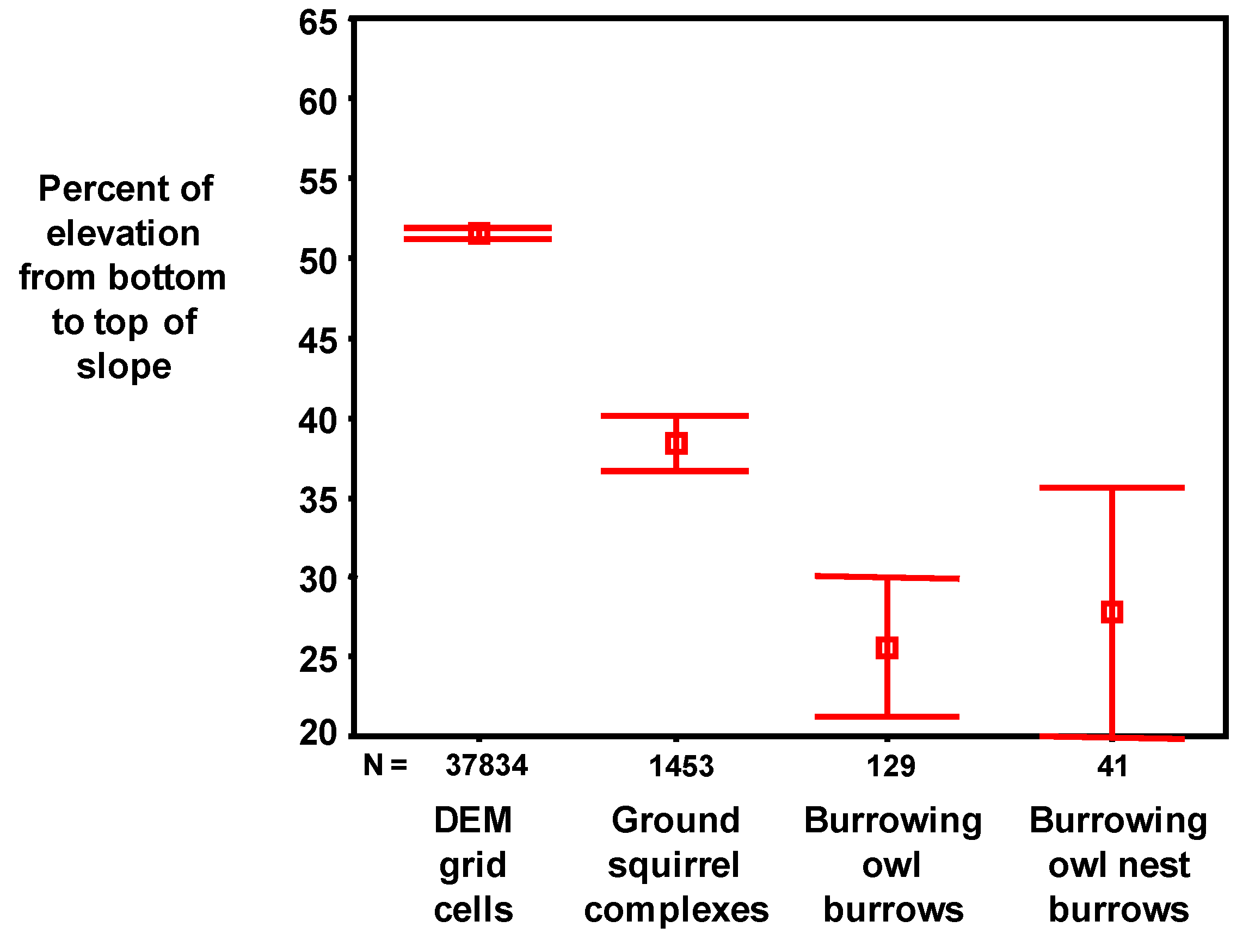
The vertical differences between each DEM grid cell and the nearest valley bottom and nearest ridgeline were referred to as
elevation difference (
Figure 5), and this measure also expressed the size of the slope. In addition to the trend in slope grade at each DEM grid cell, the
gross slope was measured as the ratio of
elevation difference and
total slope distance (
Figure 5). The DEM grid cell’s position on the slope was also expressed as the ratio of the elevation differences between the grid cell and the nearest valley and the grid cell and the nearest ridge, referred to as
elevation ratio.
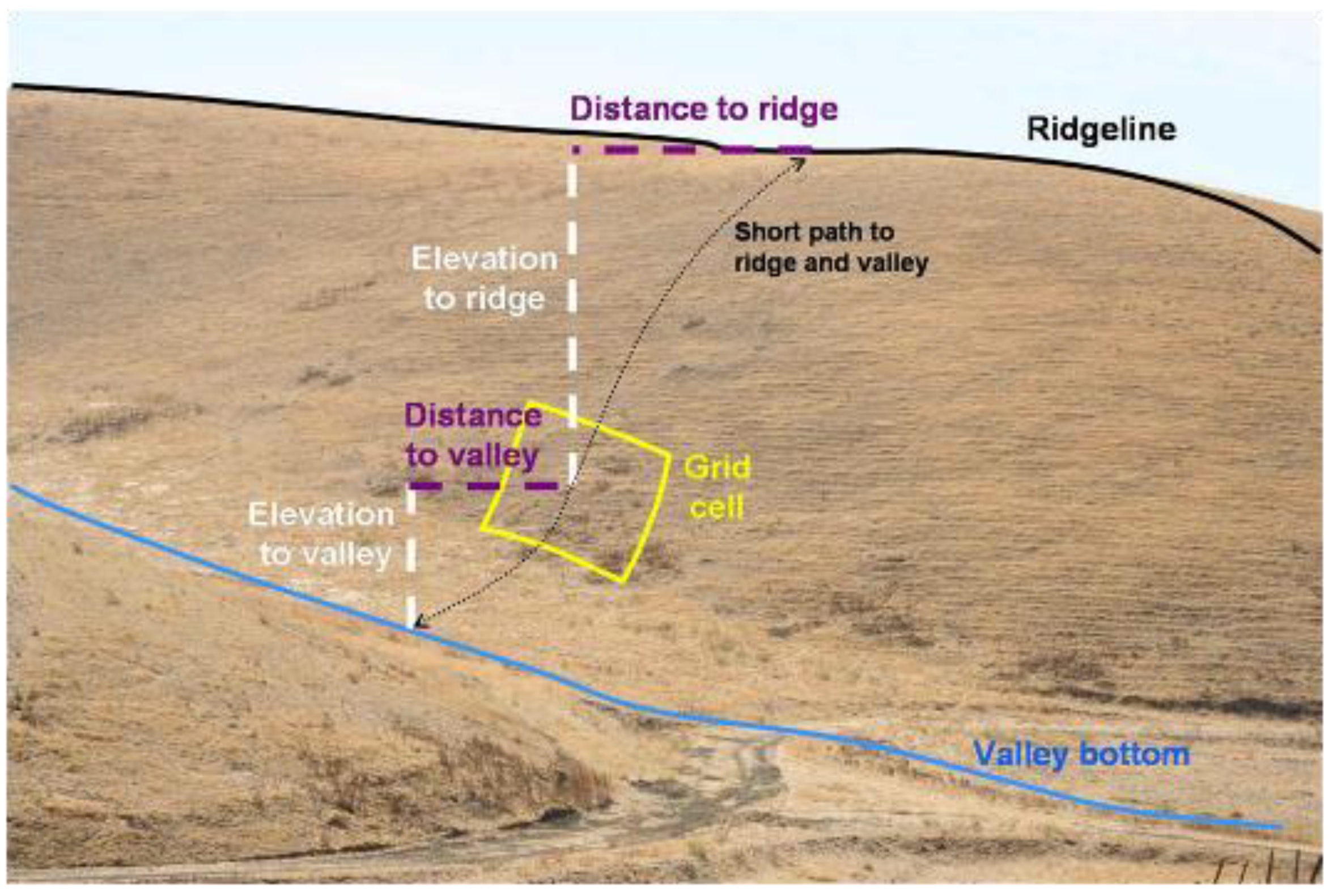
Figure 5.
Example depiction of how slope attributes were measured from 10 m2 DEM grid cells. The elevation difference was the Elevation to valley + Elevation to ridge, and elevation ratio was Elevation to valley ÷ Elevation to ridge. Total slope distance was Distance to valley + Distance to ridge, and distance ratio was Distance to valley ÷ Distance to ridge. Gross slope was elevation difference ÷ total slope distance. The hypothetical grid cell overlaps a burrowing owl burrow located on another project site in the APWRA.
Figure 5.
Example depiction of how slope attributes were measured from 10 m2 DEM grid cells. The elevation difference was the Elevation to valley + Elevation to ridge, and elevation ratio was Elevation to valley ÷ Elevation to ridge. Total slope distance was Distance to valley + Distance to ridge, and distance ratio was Distance to valley ÷ Distance to ridge. Gross slope was elevation difference ÷ total slope distance. The hypothetical grid cell overlaps a burrowing owl burrow located on another project site in the APWRA.
Each DEM grid cell was classified by
slope aspect according to whether it faced north, northeast, east, southeast, south, southwest, west, northwest, or if it was on flat terrain. For analysis slope aspect was aggregated into five categories: northeast and east, southeast and south, southwest and west, northwest and north, and no aspect (flat terrain). Each grid cell was categorized as to whether its center on the landscape was windward, leeward or perpendicular to the prevailing southwest and northwest wind directions as recorded during earlier behavior observation sessions [
9,
18].
Log
10 and natural log transformations were used to better fit normal distributions, and then chi-square tests for association and principal components analysis (PCA) were used to further understand how the variables related to burrowing owl burrow locations and to each other. To minimize the effects of confounding, no more than one predictor variable was selected from each principle component for any model developed to classify grid cells according to whether they supported burrowing owl burrows. The first modeling approach used discriminant function analysis (DFA), and the second used fuzzy logic [
19,
20]. Both produced likelihood surface areas, one referred to as the DFA surface and the other as FL surface. The performance of each model was based on the lowest number of predictor variables, the smallest portion of the study area occurring within the likelihood surface area, and the most number of mapped burrows occurring within the likelihood surface.
Log
10 distance to valley and
elevation difference were the two variables used in fuzzy logic to predict the likelihood of each grid cell containing a burrowing owl burrow (
Table 1). These two variables were selected from a pool of candidates, based on relatively larger magnitudes of differences between mean values where burrowing owls were and were not found, and based on their relatively lower level of shared variation as judged from examination of a correlation matrix and the output from principal components analysis.
Table 1.
Fuzzy logic membership functions of grid cells belonging to the set of cells with burrowing owl burrows, based on a sample of 187,908 10 × 10 m2 grid cells. For log10 distance to valley, mean = 1.27302, SE = 0.11455, and SD = 0.46176, and for elevation difference, mean = 7.5846 and SE = 0.97564.
Table 1.
Fuzzy logic membership functions of grid cells belonging to the set of cells with burrowing owl burrows, based on a sample of 187,908 10 × 10 m2 grid cells. For log10 distance to valley, mean = 1.27302, SE = 0.11455, and SD = 0.46176, and for elevation difference, mean = 7.5846 and SE = 0.97564.
| Value of variable Y for ith grid cell | Basis of membership function | Membership function of grid cell belonging to set with a burrowing owl burrow |
|---|
| Y = log10 distance to valley | | |
| 1.15847 < Y < 1.38757 | Within 1 SE of mean | 1 |
| 0.81126 ≤ Y ≤ 1.15847 | 1 SD to 1 SE < mean | 0.5 × (1 – cos(π × (Y − 0.81126) ÷ (1.15847 − 0.81126))) |
| 1.73478 ≥ Y ≥ 1.38757 | 1 SD to 1 SE > mean | 0.5 × (1 + cos(π × (Y − 1.38757) ÷ (1.73478 − 1.38757))) |
| Y < 0.81126 or Y > 1.73478 | >1 SD away from mean | 0 |
| Y = elevation difference | | |
| 5.63332 < Y < 9.53588 | Within 1 SE of mean | 1 |
| 3.68204 ≤ Y ≤ 5.63332 | Within 4 × SE; 2 × SE < mean | 0.5×(1 − cos(π × (Y − 3.68204) ÷ (5.63332 − 3.68204))) |
| 11.48716 ≥ Y ≥ 9.53588 | Within 4 × SE; 2 × SE > mean | 0.5×(1 + cos(π × (Y − 9.53588) ÷ (11.48716 − 9.53588))) |
| Y < 3.68204 or Y > 11.48716 | >4 SE; away from mean | 0 |
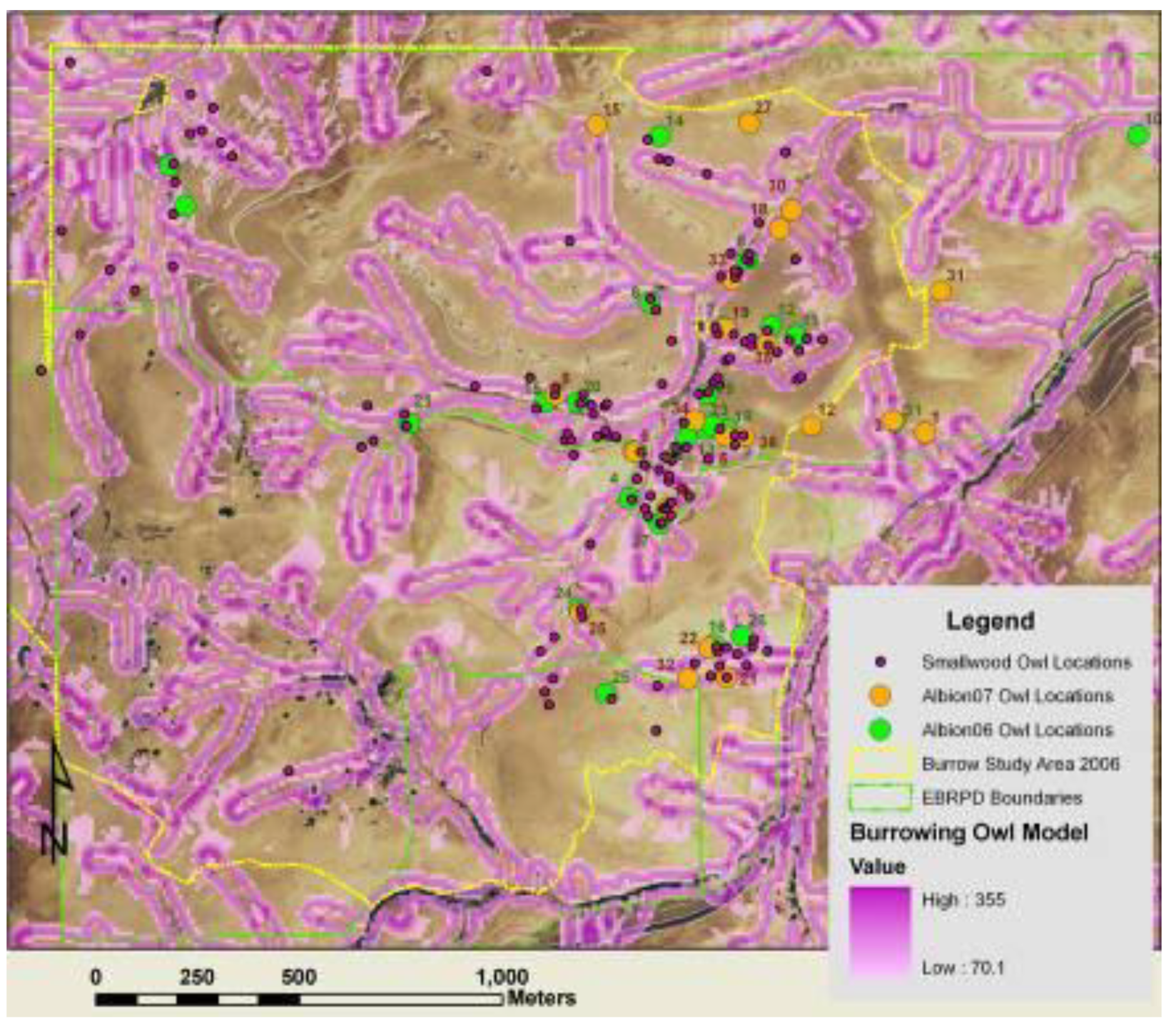
Based on log10 distance to valley, the grid cell’s membership value in the burrowing owl burrow set was multiplied by 2.55 × 100, and based on elevation difference it was multiplied by 100 in order to obtain a value range that was easier to report and interpret. These two products were added and all sum values >70 were used to obtain the fuzzy logic surface because 70 appeared to be a natural break in the frequency distribution.
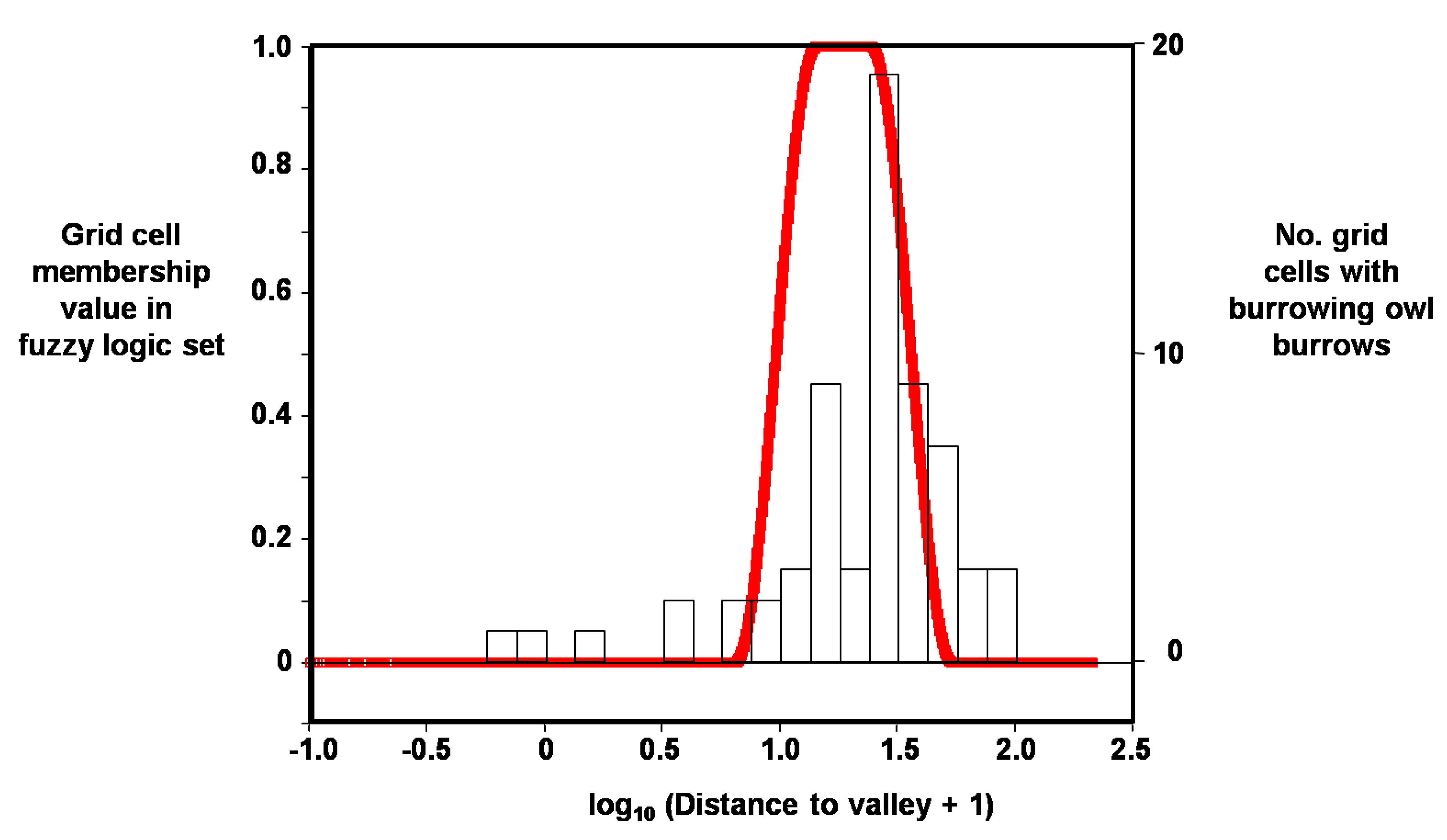
Figure 6.
Example distribution of membership values in fuzzy logic set (red line), in this case for grid cells containing burrowing owl burrows as a function of log10 distance to valley.
Figure 6.
Example distribution of membership values in fuzzy logic set (red line), in this case for grid cells containing burrowing owl burrows as a function of log10 distance to valley.