MILP-Based Pareto Optimization of Electric Bus Scheduling and Charging Management †
Abstract
1. Introduction
2. Problem Definition
2.1. Electric City Bus Scheduling Framework
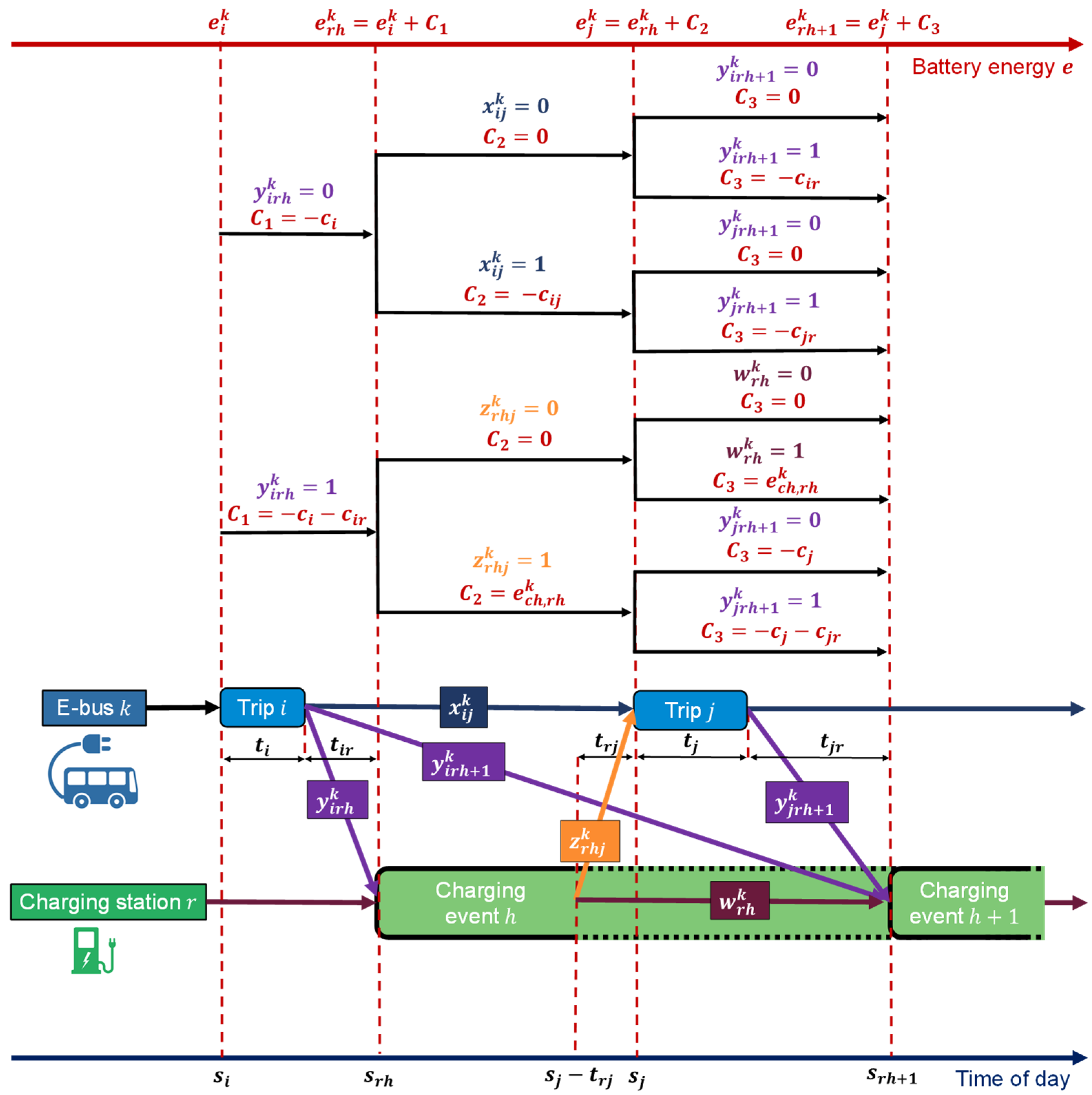
2.2. Problem Formulation
- Start time: (minutes from midnight).
- Duration: (minutes).
- Energy consumption: (kWh).
- Start location: (2D Cartesian coordinates [m, m]).
- End location: (2D Cartesian coordinates [m, m]).
- Its location: Situated either at the starting or end stations of the trips (, ), , or at the depot (, ), or at any other designated charging location (terminal) within the network.
- Charging power : Defined in kWh/min at which an EB is recharged.
- Charging spot capacity : The maximum number of EBs that can charge simultaneously (i.e., the number of chargers).
- Hourly charging price : Defined in monetary units per kWh at time , where denotes a discrete time point within the total operational timeline of the EB system.
- 1.
- Trip assignment condition where each service trip must be assigned to one, and only one, EB:where is a binary variable indicating whether th trip is assigned to th EB () or not ().
- 2.
- Feasible sequences, where each EB must follow an operationally achievable sequence of service trips:where the set comprises ordered consecutive trip pairs of th EB, ensuring that the start time of succeeding trip must not be earlier than the end time of preceding trip plus the travel time between them .
- EB scheduling is constrained by the predetermined lower and upper battery energy capacities:
- : The set of trips that can feasibly follow trip , where according to (2).
- : The set of trips that can precede trip , where .
- : The set of charging events at charging station , which can begin after trip is completed and the EB reaches the charging station, where .
- : The set of charging events at charging station , which occur before the EB starts trip , where .
- : The set of trips that can start after charging event at charging station , where .
- : The set of trips that can end before charging event at charging station , where .
- : Indicating whether EB performs service trip after service trip (implies in (1)).
- : Indicating whether EB begins charging at event on charging station after completing service trip .
- : Indicating whether EB starts service trip after completing charging event on charging station .
- : Indicating whether EB continues charging at the subsequent event on the same charging station after charging event .
- (or for trip ): The battery energy level th EB just before starting service trip .
- : The battery energy level of th EB just before it begins charging at event on charging station .
- : Amount of energy charged to th EB during charging event at charging station .
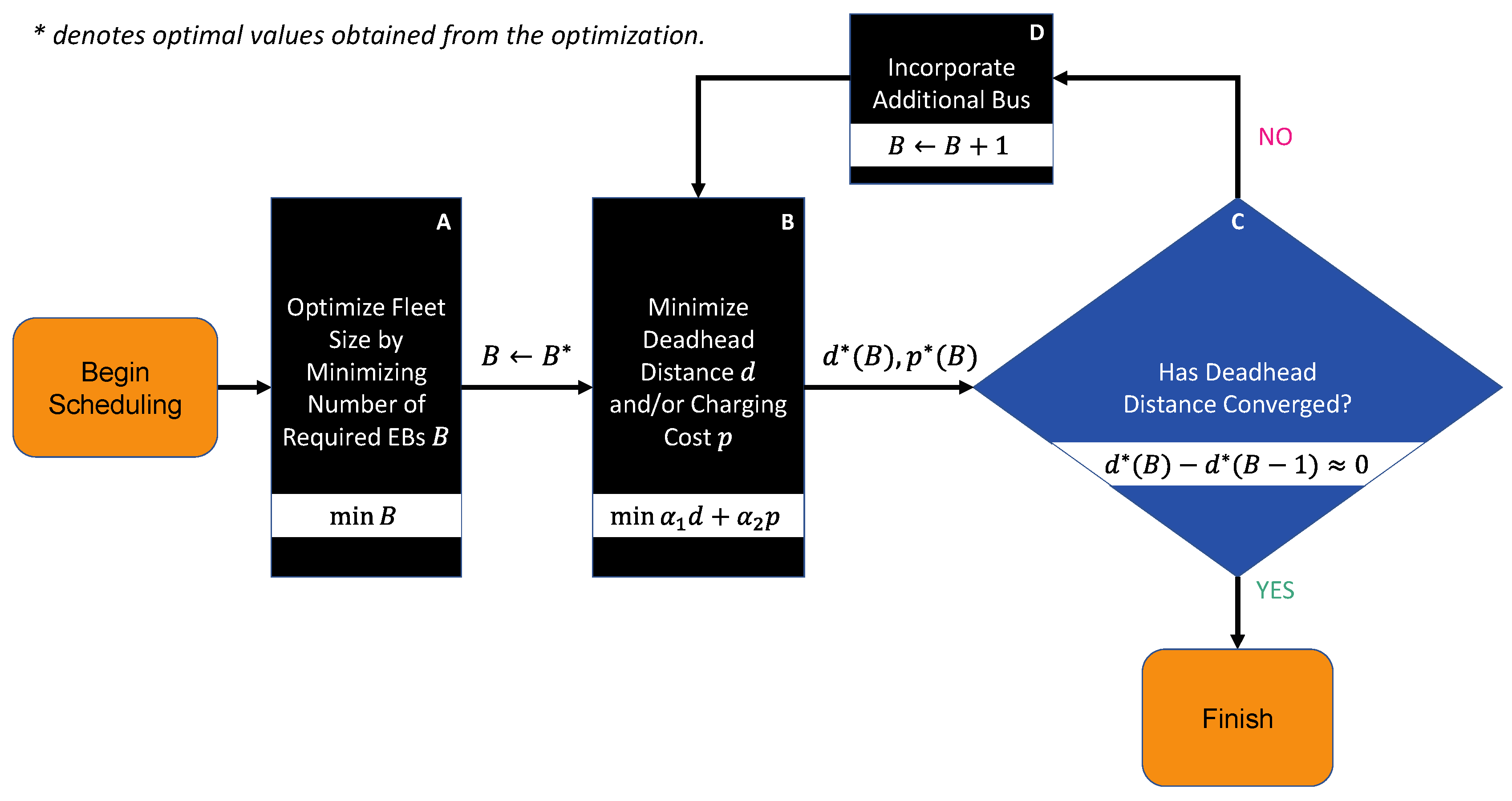
3. Solution Approaches
3.1. Insertion Heuristic (IH) Algorithm
3.2. Mixed-Integer Linear Programming (MILP) Formulation
3.2.1. General MILP Formulation
3.2.2. Objective Functions
3.2.3. Vehicle Scheduling Constraints
3.2.4. Energy Consumption Constraints
4. Case Study and Optimization Results
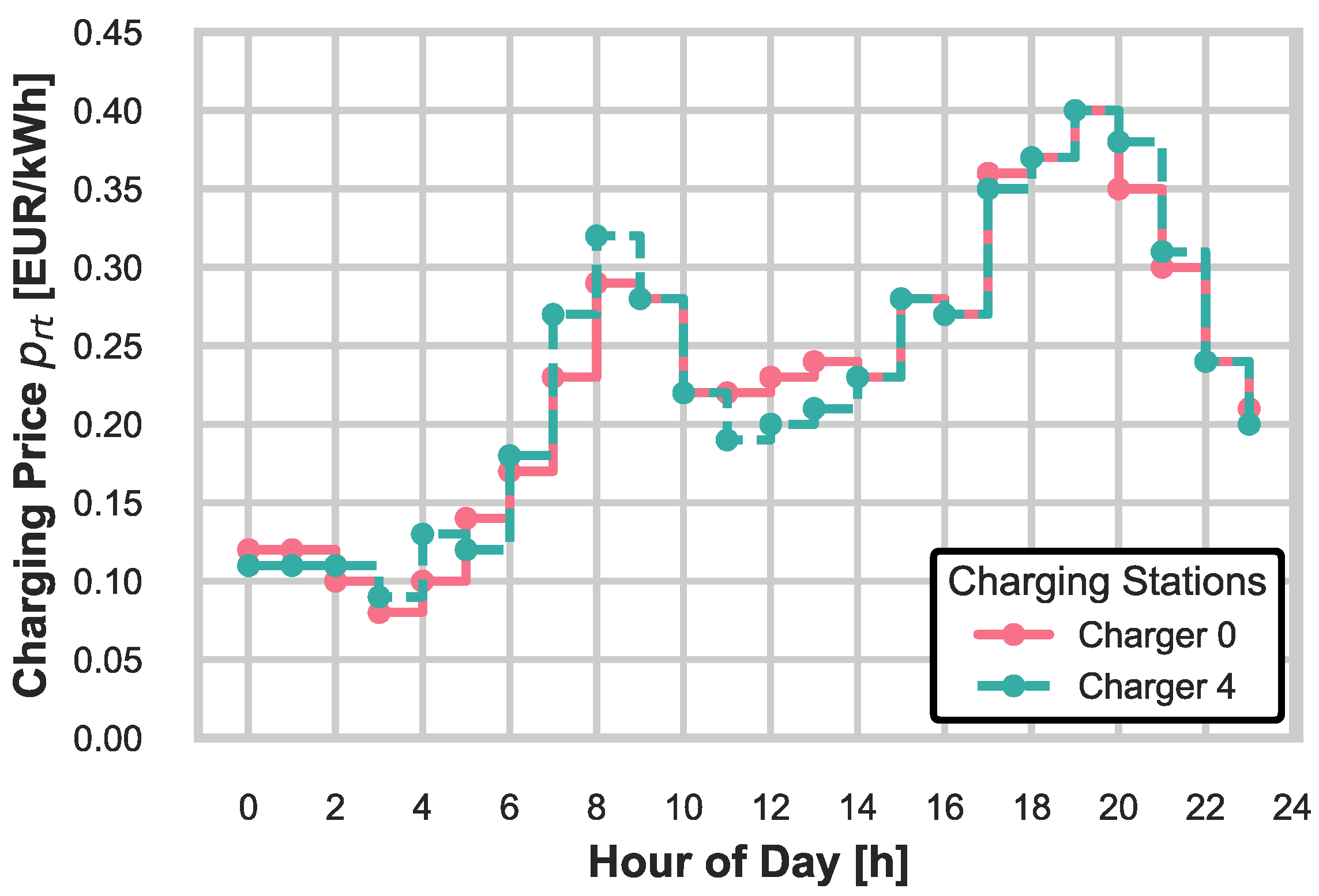
4.1. Case Study Description
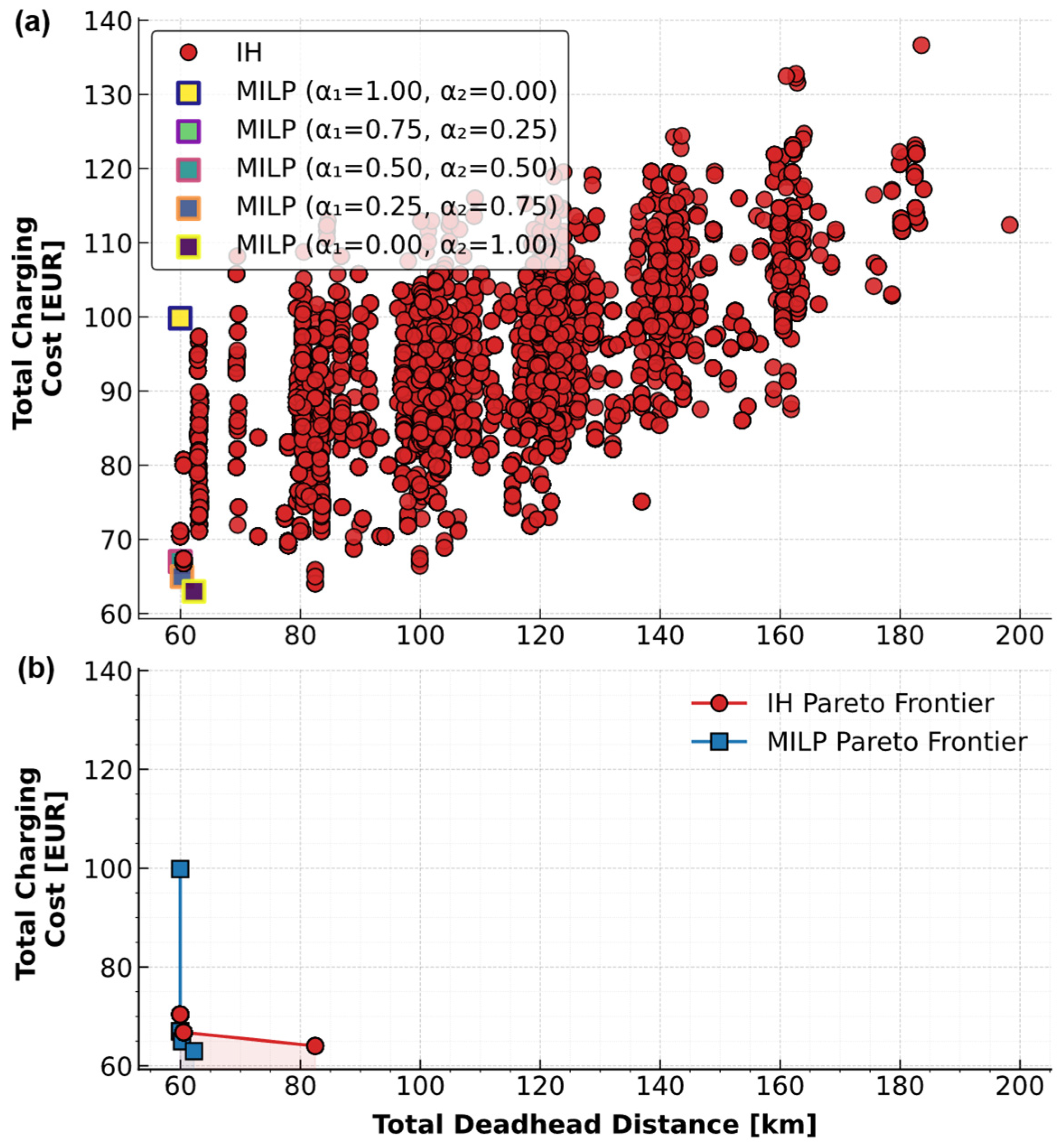
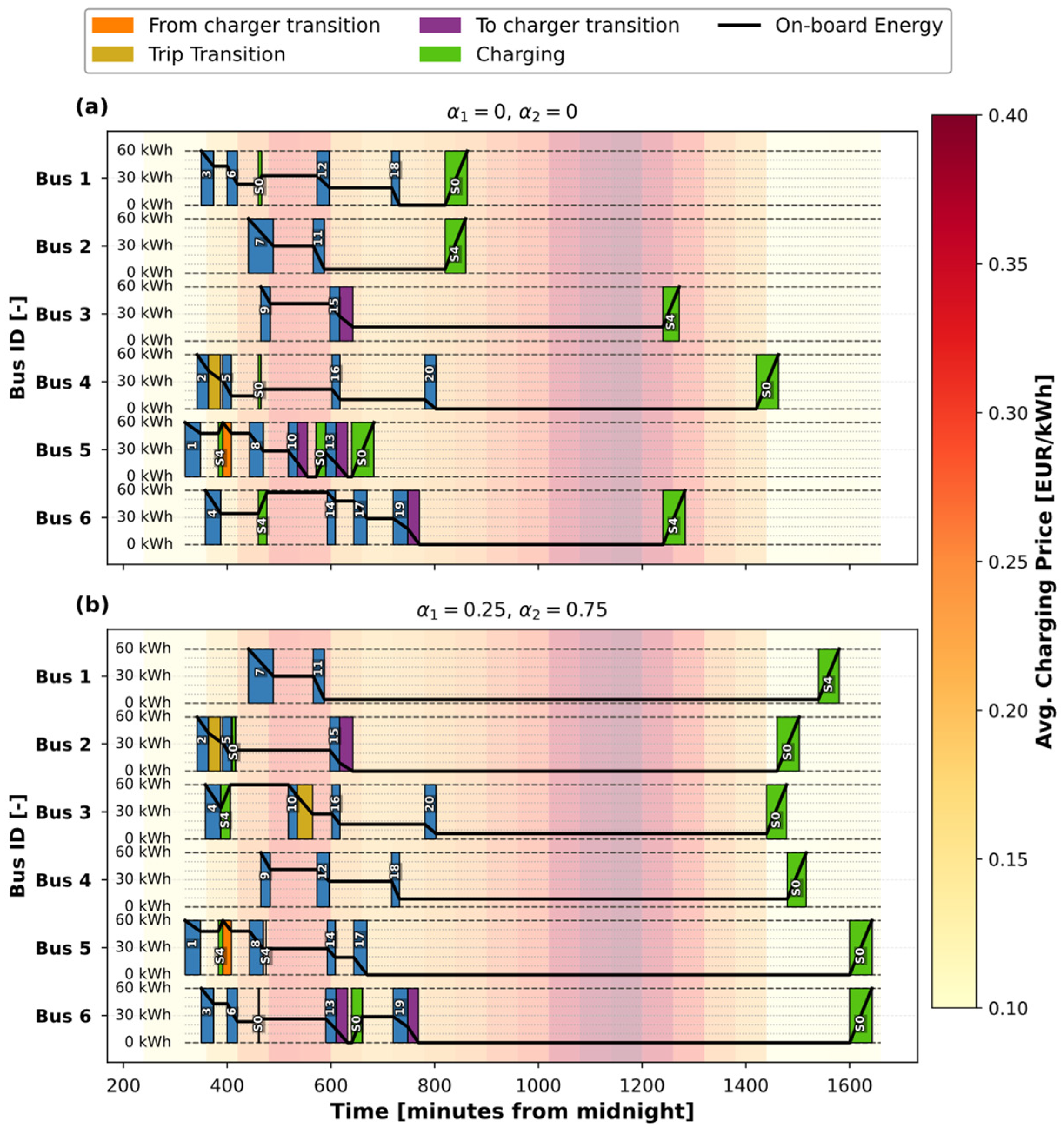
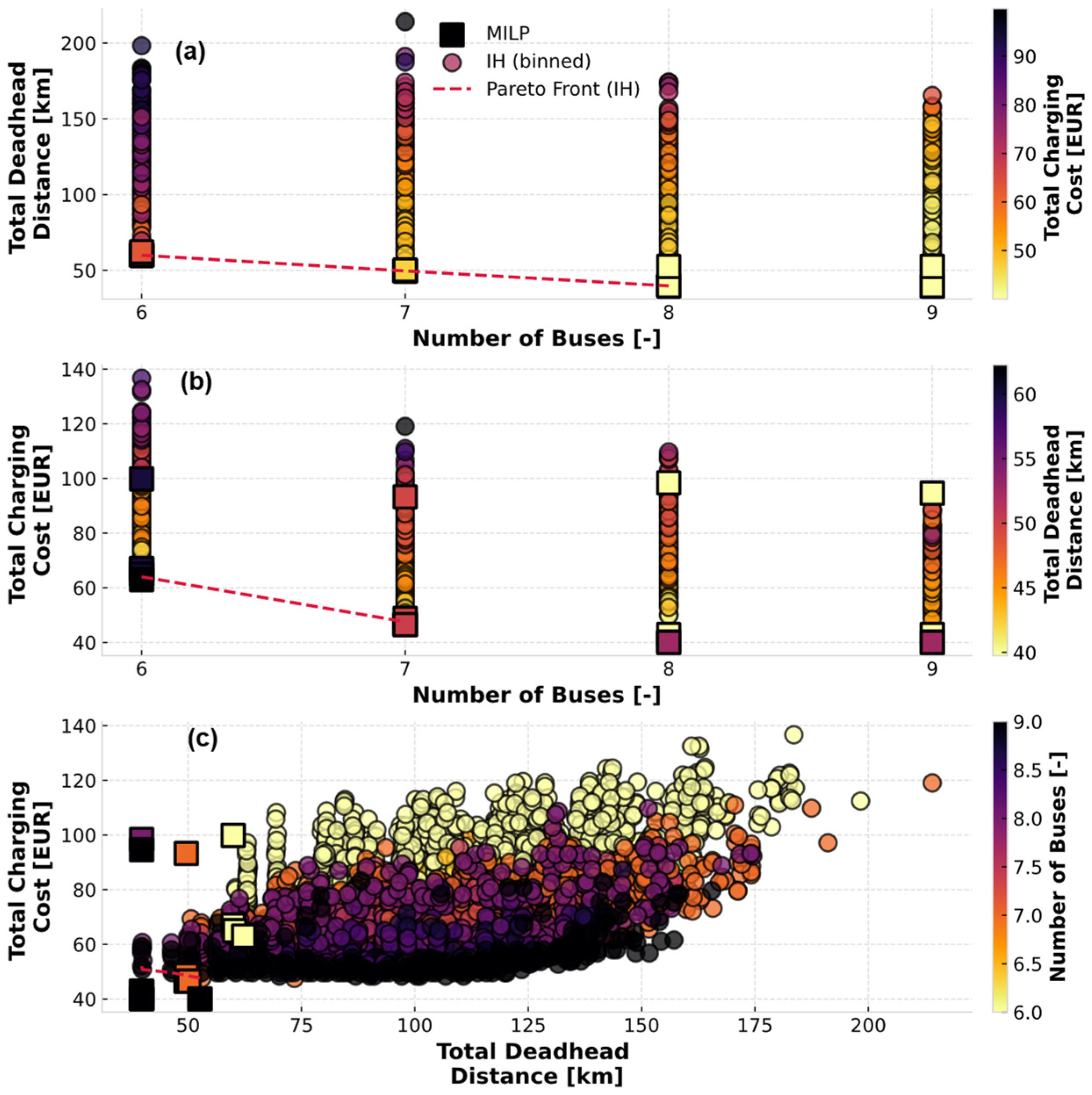
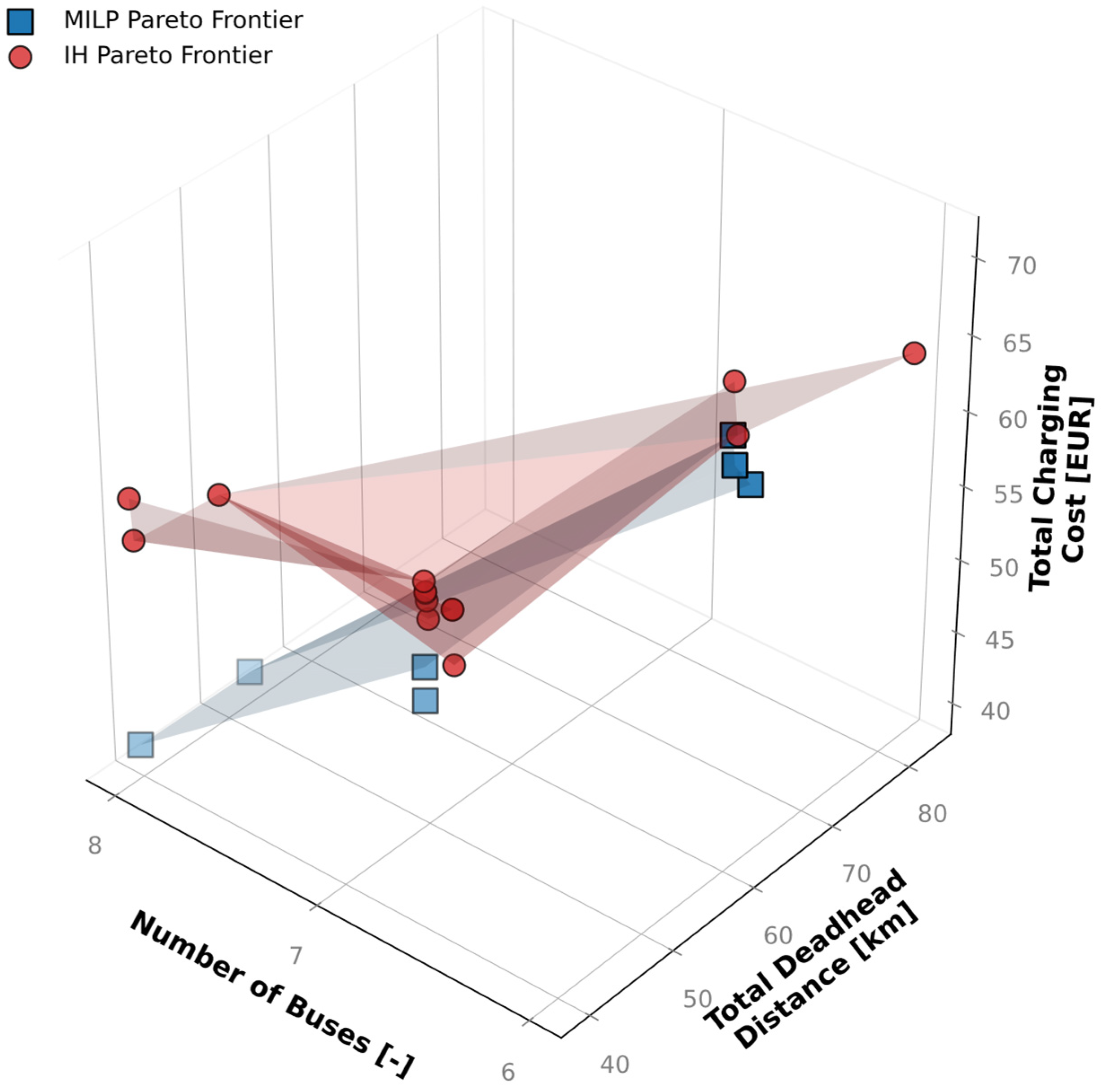
4.2. Multi-Objective Optimization Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional | |
| BEB | Battery Electric Bus | |
| EB | Electric Bus | |
| EBSP | Electric Bus Scheduling Problem | |
| EV | Electric Vehicle | |
| GA | Genetic Algorithm | |
| IH | Insertion Heuristic | |
| LNS | Large Neighborhood Search | |
| MILP | Mixed-Integer Linear Programming | |
| PHEB | Plug-in Hybrid Electric Bus | |
| SoC | State of Charge | |
| SDVSP | Single Depot Vehicle Scheduling Problem | |
| VSP | Vehicle Scheduling Problem | |
| Nomenclature | ||
| Sets | ||
| set of service trips, indexed by | ||
| set of electric buses (EBs), indexed by | ||
| set of charging stations, indexed by | ||
| set of charging events (time slots) at station , indexed by | ||
| discrete time points within operational horizon | ||
| depot source node (start of operation) | ||
| depot sink node (end of operation) | ||
| set of trips that can feasibly follow trip | ||
| set of trips that can feasibly precede trip | ||
| set of charging events at station feasible after trip | ||
| set of charging events at station feasible before trip | ||
| set of trips feasible after charging event | ||
| set of trips feasible before charging event | ||
| Parameters | ||
| start time of trip , min | ||
| duration of trip , min | ||
| energy consumption of trip , min | ||
| start and end location of trip , m | ||
| deadhead travel from trip to , min | ||
| deadhead distance from trip to , m | ||
| deadhead energy consumption from trip to , kWh | ||
| charging power at station , kWh/min | ||
| charging spot capacity (number of chargers) at station | ||
| electricity price at station at time , EUR/kWh | ||
| electricity price during charging event , EUR/kWh | ||
| start time of charging event , min | ||
| duration of a charging event (charging time discretization step), min | ||
| minimum and maximum battery energy of th EB, kWh | ||
| safety time margin used in feasibility checks, min | ||
| time required to fully charge EB, min | ||
| fixed fleet size used in multi-objective analysis | ||
| weighting coefficients for deadhead distance and charging cost objectives | ||
| deadhead distance normalization constant | ||
| charging cost normalization constant | ||
| large positive constants used for conditional constraints | ||
| Decision Variables | ||
| 1 if th EB performs trip directly after trip , 0 otherwise | ||
| 1 if th EB starts charging at charging event after trip , 0 otherwise | ||
| 1 if th EB starts trip after charging at event , 0 otherwise | ||
| 1 if th EB continues charging from event to , 0 otherwise | ||
| battery energy of th EB before starting trip , kWh | ||
| battery energy of th EB before charging at event , kWh | ||
| energy charged to th EB during charging event , kWh | ||
Appendix A
| Algorithm A1. Insertion Heuristic (IH) scheduling approach | |||
| Input | |||
| ← | set of service trips, sorted by start time | ||
| ← | set of EBs | ||
| ← | set of charging stations | ||
| ← | set of trips that can legally follow trip | ||
| ← | set of charging events available at station | ||
| ← | number of chargers per charging station | ||
| ← | lower and upper individual battery energy limits | ||
| ← | energy required for driving | ||
| ← | charging rate during event at charging station | ||
| ← | starting and final point of each EB being at depot | ||
| Output—decision variables | |||
| ← | EB starts trip immediately after trip | ||
| ← | EB starts charging in slot of charging station after trip i | ||
| ← | EB continues charging in the next slot | ||
| ← | EB starts trip immediately after charging | ||
| ← | battery energy level of EB before starting trip | ||
| ← | battery energy level of EB before starting charging at event at station | ||
| INITIALIZATION | |||
| for each EB do | |||
| ← // previous trip, starting from depot | |||
| ← | |||
| ← ∞ | |||
| ← 0, ← 0, ← 0, ← 0; | |||
| end for | |||
| for each charging station do | |||
| for each charging event at charging station do | |||
| ← 0 | |||
| end for | |||
| end for | |||
| MAIN LOOP—assign every trip j ∈ N | |||
| for each trip do | |||
| ← RandomShuffle() // working list for this trip | |||
| trip_assigned ← False | |||
| // A. Direct assignment (no intermediate charging) | |||
| for each EB while !trip_assigned do | |||
| ← | |||
| // sequence & charge sustain checks | |||
| if ≠ or or !ChargeSustain(k, j) then | |||
| ← // Excluding EB k from set | |||
| continue // To next EB candidate | |||
| ← nearest charging station after trip | |||
| if then | |||
| ← | |||
| trip_assigned ← True | |||
| ← | |||
| if == then | |||
| ← | // Define start of first trip for following day | ||
| end if | |||
| end for | |||
| // B. assignment with pre-charging (if needed) | |||
| for each EB while !trip_assigned do | |||
| ← | |||
| for each station r ∈ R (nearest-first from end of trip ) do | |||
| if then continue | |||
| ← | |||
| ← { | |||
| // contains ordered charging events | |||
| if then | |||
| ← first(); ← last() | |||
| ← 1; ← + 1; ← | |||
| for each consecutive pair (, ) in S do | |||
| if then | |||
| ← 1; ← + 1 | |||
| end if | |||
| ← min (,()) | |||
| end for | |||
| ← 1; ← + 1 | |||
| ← | |||
| trip_assigned ← True | |||
| ← | |||
| break | |||
| end if | |||
| end for | |||
| end for | |||
| if !trip_assigned then | |||
| report “Trip infeasible” and terminate algorithm | |||
| end if | |||
| end for | |||
| CHARGE SUSTAINING CONDITION | |||
| sort(K) by , in ascending order | |||
| for each EB do | |||
| for each station r ∈ R (nearest-first from end of final trip) do | |||
| if then continue | |||
| ← { | |||
| if then | |||
| ← first(S); ← last(S) | |||
| ← 1; ← + 1; | |||
| ← | |||
| for each consecutive pair (, ) in S do | |||
| if then | |||
| ← 1; ← + 1 | |||
| end if | |||
| ← min (,()) | |||
| end for | |||
| ← 1 | |||
| ← | |||
| break | |||
| end if | |||
| end for | |||
| end for | |||
| Auxiliary procedures | |||
| ChargeSustain (k, j): | |||
| for each station r ∈ R (nearest-first from end of trip ) do | |||
| ← | |||
| if return True | |||
| return False | |||
References
- Braun, A.; Rid, W. Energy consumption of an electric and an internal combustion passenger car: A comparative case study from real-world data on the Erfurt circuit in Germany. Transp. Res. Procedia 2017, 27, 468–475. [Google Scholar] [CrossRef]
- Kalghatgi, G. Is it really the end of internal combustion engines and petroleum in transport? Appl. Energy 2018, 225, 965–974. [Google Scholar] [CrossRef]
- Topić, J.; Soldo, J.; Maletić, F.; Škugor, B.; Deur, J. Virtual simulation of electric bus fleets for city bus transport electrification planning. Energies 2020, 13, 3410. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Lusby, R.M.; Larsen, J. Electric bus planning and scheduling: A review of related problems and methodologies. Eur. J. Oper. Res. 2022, 301, 395–413. [Google Scholar] [CrossRef]
- Teng, J.; Chen, T.; Fan, W. Integrated approach to vehicle scheduling and bus timetabling for an electric bus line. J. Transp. Eng. Part A Syst. 2020, 146, 04019073. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Dollevoet, T.; Huisman, D.; Lusby, R.M.; Larsen, J.; Riis, M. Solution approaches for integrated vehicle and crew scheduling with electric buses. Comput. Oper. Res. 2021, 132, 105268. [Google Scholar] [CrossRef]
- Dallmann, T.; Delgado, O.; Jin, L.; Minjares, R.; Gadepalli, R.; Cheriyan, C.A. Strategies for deploying zero-emission bus fleets: Route-level energy consumption and driving range analysis. Int. Counc. Clean Transp. 2021, Working Paper 2021–24. [Google Scholar]
- Dabčević, Z.; Škugor, B.; Cvok, I.; Deur, J. A trip-based data-driven model for predicting battery energy consumption of electric city buses. Energies 2024, 17, 911. [Google Scholar] [CrossRef]
- Dabčević, Z.; Škugor, B.; Topić, J.; Deur, J. Synthesis of Driving Cycles Based on Low-Sampling-Rate Vehicle-Tracking Data and Markov Chain Methodology. Energies 2022, 15, 4108. [Google Scholar] [CrossRef]
- Gkiotsalitis, K. Bus holding of electric buses with scheduled charging times. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6760–6771. [Google Scholar] [CrossRef]
- Tian, X.; Wan, M.; Chen, X.; Cai, Y.; Sun, X.; Zhu, Z. Driver-Oriented Adaptive Equivalent Consumption Minimization Strategy for Plug-in Hybrid Electric Buses. Energies 2025, 18, 5033. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Tang, X.; Lin, X.; He, F. Robust scheduling strategies of electric buses under stochastic traffic conditions. Transp. Res. C Emerg. Technol. 2019, 105, 163–182. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kepaptsoglou, K. Integrated transit route network design and infrastructure planning for on-line electric vehicles. Transp. Res. D Transp. Environ. 2019, 77, 178–197. [Google Scholar] [CrossRef]
- Cokyasar, T.; Verbas, O.; Davatgari, A.; Mohammadian, A.K. Solving the electric vehicle scheduling problem at large-scale. In Proceedings of the 26th IEEE International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 24–28 September 2023; pp. 1134–1139. [Google Scholar]
- Li, J.-Q. Transit bus scheduling with limited energy. Transp. Sci. 2014, 48, 521–539. [Google Scholar] [CrossRef]
- van Kooten Niekerk, M.E.; van den Akker, J.M.; Hoogeveen, J.A. Scheduling electric vehicles. Public Transp. 2017, 9, 155–176. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Iliopoulou, C.; Kepaptsoglou, K. An exact approach for the multi-depot electric bus scheduling problem with time windows. Eur. J. Oper. Res. 2023, 306, 189–206. [Google Scholar] [CrossRef]
- Janovec, M.; Koháni, M. Exact approach to the electric bus fleet scheduling. Transp. Res. Procedia 2019, 40, 1380–1387. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling High-Efficiency Economic Dispatch of Hybrid AC/DC Networked Microgrids: Steady-State Convex Bi-Directional Converter Models. IEEE Trans. Smart Grid 2025, 16, 45–61. [Google Scholar] [CrossRef]
- Dabčević, Z.; Deur, J. Interactive optimization of electric bus scheduling and overnight charging. Energies 2025, 18, 4440. [Google Scholar] [CrossRef]
- Xu, X.; Yu, Y.; Long, J. Integrated electric bus timetabling and scheduling problem. Transp. Res. C Emerg. Technol. 2023, 149, 104057. [Google Scholar] [CrossRef]
- Rinaldi, M.; Picarelli, E.; D’Ariano, A.; Viti, F. Mixed-fleet single-terminal bus scheduling problem: Modelling, solution scheme and potential applications. Omega 2020, 96, 102070. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, Y.; Zhang, Y. Multi-depot electric bus scheduling considering operational constraints and partial charging: A case study in Shenzhen, China. Sustainability 2022, 14, 255. [Google Scholar] [CrossRef]
- De Vos, M.; van Lieshout, R.N.; Dollevoet, T. Electric vehicle scheduling with capacitated charging stations and partial charging. arXiv 2022, arXiv:2207.13734. [Google Scholar] [CrossRef]
- Najafi, A.; Gao, K.; Parishwad, O.; Tsaousoglou, G.; Jin, S.; Yi, W. Integrated Optimization of Charging Infrastructure, Electric Bus Scheduling and Energy Systems. Transp. Res. Part D Transp. Environ. 2025, 141, 104664. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, M.; Zhang, R.; Peng, R. Joint Optimization of Electric Bus Infrastructure Planning, Fleet Composition, and Charging Schedule Considering Multi-Gun Charging and Compatibility. IEEE Trans. Intell. Transp. Syst. 2025, 26, 6690–6701. [Google Scholar] [CrossRef]
- Dabčević, Z.; Škugor, B.; Deur, J. Pareto optimization of electric city bus scheduling. In Proceedings of the 18th Conference on Sustainable Development of Energy, Water and Environment Systems (SDEWES), Dubrovnik, Croatia, 1–6 October 2023; pp. 1–14. [Google Scholar]
- Lu, T.; Yao, E.; Zhang, Y.; Yang, Y. Joint optimal scheduling for a mixed bus fleet under micro driving conditions. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2464–2475. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Wolsey, L.A. Integer and Combinatorial Optimization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Sobel, J. Linear Programming Notes V: Problem Transformations; University of California San Diego: La Jolla, CA, USA, 2002; Available online: https://econweb.ucsd.edu/~jsobel/ (accessed on 5 March 2025).
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Beaverton, OR, USA, 2024; Available online: https://www.gurobi.com (accessed on 5 March 2025).
- Clímaco, J.C.N.; Pascoal, M.M.B. An Approach to Determine Unsupported Non-Dominated Solutions in Bicriteria Integer Linear Programs. INFOR Inf. Syst. Oper. Res. 2016, 54, 317–343. [Google Scholar] [CrossRef]
- Williams, H.P. Model Building in Mathematical Programming, 5th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- OLGA Consortium. OLGA Project—Public Reports and Deliverables. 2024. Available online: https://www.olga-project.eu/reports (accessed on 28 January 2026).
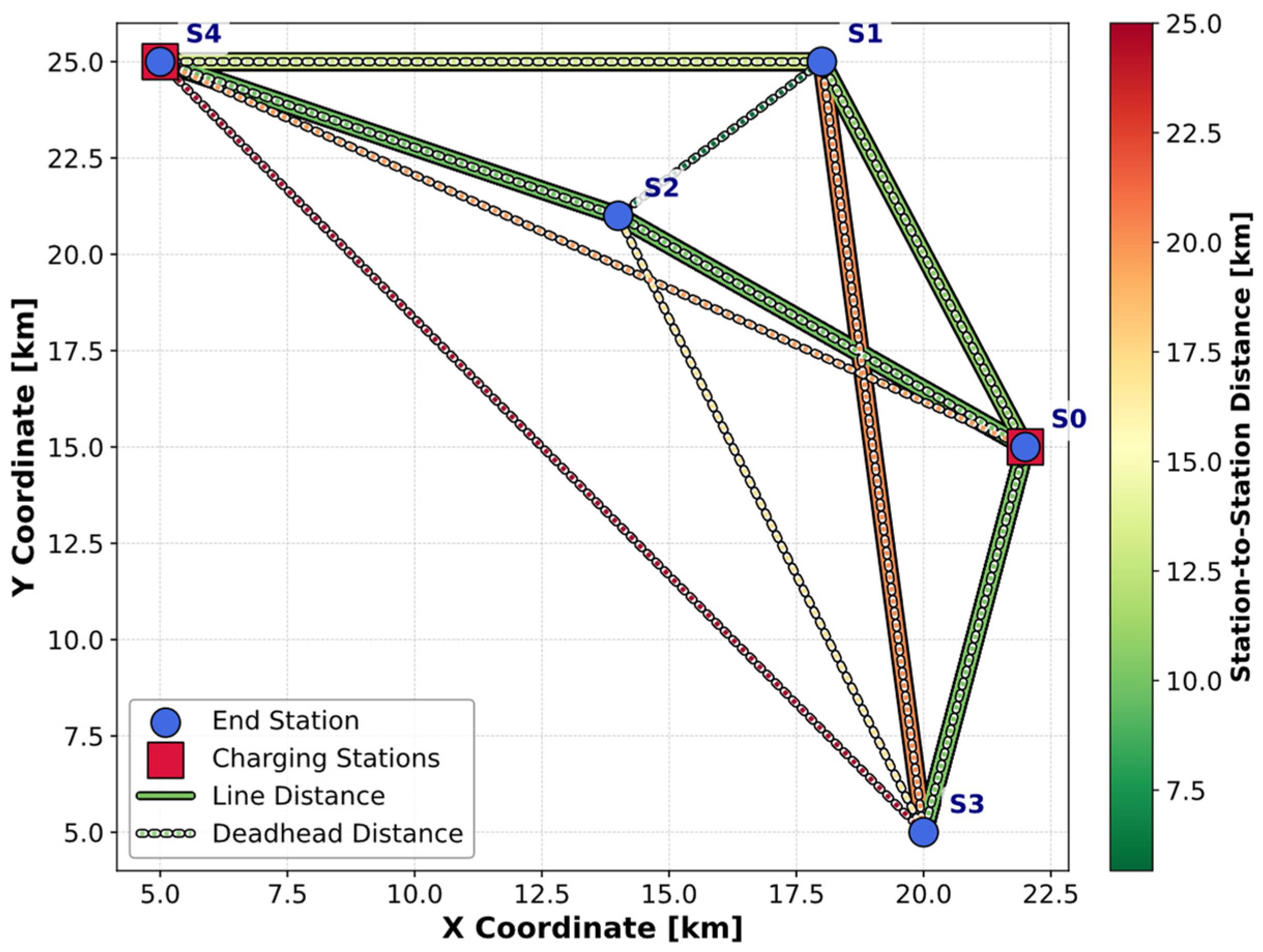
| [min] | [min] | [-] | [-] | [kWh] | |
|---|---|---|---|---|---|
| 1 | 319 | 348 | S1 | S4 | 12.03 |
| 2 | 342 | 364 | S2 | S0 | 17.91 |
| 3 | 350 | 374 | S0 | S3 | 16.89 |
| 4 | 358 | 388 | S1 | S4 | 25.62 |
| 5 | 391 | 408 | S3 | S0 | 18.21 |
| 6 | 400 | 420 | S3 | S0 | 19.83 |
| 7 | 441 | 489 | S3 | S1 | 30 |
| 8 | 443 | 470 | S2 | S4 | 19.57 |
| 9 | 465 | 483 | S1 | S0 | 18.57 |
| 10 | 518 | 535 | S4 | S2 | 12.62 |
| 11 | 566 | 587 | S1 | S4 | 25.63 |
| 12 | 573 | 597 | S0 | S2 | 13.15 |
| 13 | 590 | 610 | S0 | S3 | 11.35 |
| 14 | 593 | 608 | S4 | S2 | 9.69 |
| 15 | 598 | 617 | S0 | S2 | 14.13 |
| 16 | 602 | 618 | S0 | S3 | 11.39 |
| 17 | 644 | 670 | S2 | S0 | 19.27 |
| 18 | 717 | 732 | S2 | S0 | 19.45 |
| 19 | 720 | 748 | S0 | S2 | 11.38 |
| 20 | 781 | 803 | S3 | S0 | 10.34 |
| Number of Buses | Minimal Total Deadhead Distance (MILP) | Minimal Total Deadhead Distance (IH) | Minimal Total Charging Cost (MILP) | Minimal Total Charging Cost (IH) |
|---|---|---|---|---|
| 6 | 59.95 km | 59.95 km | 62.98 EUR | 65.03 EUR |
| 7 | 49.60 km | 49.60 km | 46.52 EUR | 47.55 EUR |
| 8 | 39.75 km | 39.75 km | 40.02 EUR | 49.80 EUR |
| 9 | 39.75 km | 39.75 km | 40.02 EUR | 48.40 EUR |
| MILP Runtime [s] | IH Runtime [s] | MILP Memory Usage [MB] | IH Memory Usage [MB] | |
|---|---|---|---|---|
| 6 | 9050 | 90 | 162 | 141 |
| 7 | 15,250 | 86 | 166 | 141 |
| 8 | 24,300 | 74 | 171 | 142 |
| 9 | 36,400 | 70 | 175 | 142 |
| Charging-Slot Discretization Step [min] | Total MILP Runtime (5 Weight Combinations) [s] | Avg. Runtime per Weight Combination | Mean MILP Memory Usage [MB] | Minimal Deadhead Distance [km] | Minimal Charging Cost [EUR] |
|---|---|---|---|---|---|
| 60 | 9050 | 1810 | 161.8 | 59.95 | 62.98 |
| 15 | 28,146 | 5629 | 174.4 | 59.95 | 62.98 |
| [-] | [-] | Number of Stations ) | Total Runtime [s] | Avg. Runtime per Solution [s] | Memory Usage [MB] | |
|---|---|---|---|---|---|---|
| 60 | 15 | 6 (2) | 3 | 378 | 0.038 | 142 |
| 100 | 20 | 10 (3) | 3 | 574 | 0.057 | 145 |
| 150 | 30 | 15 (3) | 3 | 827 | 0.083 | 152 |
| 200 | 40 | 20 (3) | 4 | 1099 | 0.110 | 156 |
| 300 | 50 | 25 (4) | 4 | 1843 | 0.184 | 177 |
| 500 | 60 | 30 (4) | 5 | 3076 | 0.308 | 217 |
| 1000 | 80 | 40 (5) | 5 | 6633 | 0.663 | 410 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Dabčević, Z.; Škugor, B.; Deur, J. MILP-Based Pareto Optimization of Electric Bus Scheduling and Charging Management. Energies 2026, 19, 867. https://doi.org/10.3390/en19030867
Dabčević Z, Škugor B, Deur J. MILP-Based Pareto Optimization of Electric Bus Scheduling and Charging Management. Energies. 2026; 19(3):867. https://doi.org/10.3390/en19030867
Chicago/Turabian StyleDabčević, Zvonimir, Branimir Škugor, and Joško Deur. 2026. "MILP-Based Pareto Optimization of Electric Bus Scheduling and Charging Management" Energies 19, no. 3: 867. https://doi.org/10.3390/en19030867
APA StyleDabčević, Z., Škugor, B., & Deur, J. (2026). MILP-Based Pareto Optimization of Electric Bus Scheduling and Charging Management. Energies, 19(3), 867. https://doi.org/10.3390/en19030867








