An Intelligent Dynamic Cluster Partitioning and Regulation Strategy for Distribution Networks

Abstract

As distributed generators (DGs) and flexible adjustable loads (FALs) further penetrate distribution networks (DNs), to reduce regulation complexity compared with traditional centralized control frameworks, DGs and FALs in DNs should be packed in several clusters to enable their dispatch to become standard in the industry. To mitigate the negative influence of DGs’ and FALs’ spatiotemporal distribution and uncertain output characteristics on dispatch, this paper proposes an intelligent dynamic cluster partitioning strategy for DNs, from which the DN’s resources and loads can be intelligently aggregated, organized, and regulated in a dynamic and optimal way with relatively high implementation efficiency. An environmental model based on the Markov decision process (MDP) technique is first developed for DN cluster partitioning, in which a continuous state space, a discrete action space, and a dispatching performance-oriented reward are designed. Then, a novel random forest Q-learning network (RF-QN) is developed to implement dynamic cluster partitioning by interacting with the proposed environmental model, from which the generalization and robust capability to estimate the Q-function can be improved by taking advantage of combining deep learning and decision trees. Finally, a modified IEEE-33-node system is adopted to verify the effectiveness of the proposed intelligent dynamic cluster partitioning and regulation strategy; the results also indicate that the proposed RF-QN is superior to the traditional deep Q-learning (DQN) model in terms of renewable energy accommodation rate, training efficiency, and portioning and regulation performance.

1. Introduction

With the global energy transition, renewable energy, energy storage systems (ESSs), and flexible adjustable loads (FALs) have further penetrated into power systems on a large scale [1]; for distribution networks (DNs), they are challenged by both the source and load uncertainty and the interaction between them [2], so the traditional DN management method (i.e., the full centralized control-based method [3,4]) demonstrates limited effectiveness in addressing the regulation of DNs with a high proportion of distributed generators (DGs), ESSs, and FALs [5]. To improve the security, the control flexibility, the renewable energy resource’s utilization rate (RERUR), and the operation efficiency of DNs, the aggregation concept [6,7,8] and the related dispatching strategy are regarded as an attractive technological path; the scattered DGs, ESSs, and FALs in DNs can be organized and controlled in the form of clusters (or groups), by which the number of the central controller’s control object can be significantly reduced to the number of the cluster, the controller of each cluster can only focus on regulating resources within the cluster, and all the cluster controllers can work in parallel; hence, more flexible, robust, and efficient operation performance can be obtained [9]. However, how to achieve this aggregation/group process, ensuring that the aggregators can intelligently respond to grid demands while optimizing resource allocation, is a new and crucial technological challenge in realizing the above concept.

For the control and allocation of the DN’s resources, conventional control algorithms [10,11,12] always provide deterministic optimal or quasi-optimal solutions for every controllable resource. However, with the expansion of the physical and mathematical scale of the focused problem, the computational complexity and the requirement of model accuracy increase significantly, which limits the adaptability of the conventional algorithm to the dynamic and uncertain objects in DNs [13]. On the other hand, compared with the traditional control methods, the heuristic algorithm shows better adaptability to modern DNs [14,15,16], but the relatively slow convergence speed still inhibits its further application.

Reinforcement learning (RL) [17], a machine learning method, provides a new perspective for the dynamic management of DNs; it can automatically discover the optimal control strategy through trial and error from the environment without pre-knowing the explicit model of the plan, which shows applicable potential in DNs with the characteristics of time—variety, complexity, and uncertainty—e.g., by adjusting the output of DGs, FALs, and ESSs to realize load balance, voltage control, and even frequency regulation in isolated networks [18]. By introducing hierarchical constrained RL and a gated recurrent unit, Ref. [19] proposes an interaction power optimization strategy among several microgrids, by which the dispatching robustness and stability are improved, and in which the decision space is also simplified. To reuse historical dispatching knowledge, Ref. [20] proposes a power system with a real-time dispatching optimization method integrated with deep transfer RL technology; by expanding the input and output channels of the deep-learning network, the transfer of knowledge of the state and action spaces in the expanded scenario is realized, and the learning efficiency of agents is also improved. Ref. [21] presents a deep RL method to analyze and solve the optimal power flow (OPF) problem in DNs, in which the historical data is extracted from the operational knowledge and then approximated by deep neural networks, and quasi-optimal decision-making performance can be realized.

In addition, for DNs with high penetration of adjustable resources (ARs), multi-agent RL is regarded as an effective technical path for optimal dispatching. By learning the coordinated control strategy through a counter-training model, Ref. [22] presents a multi-agent deep RL method (MADRL) to mitigate voltage issues in DNs. In [23], an attention mechanism is adopted to decompose the DN into several sub-DNs, and a modified MADRL is developed to execute distributed voltage-reactive control. Furthermore, to enhance agents’ interregional cooperation ability, an interregional auxiliary rewards mechanism is proposed in [24], and the evolutionary game strategy optimization method is further developed to improve the voltage regulation performance in DNs.

As discussed above, the application of RL shows its great potential in the field of DN optimal regulation, but little research discusses DNs’ dynamic cluster partitioning by use of an RL-based method, though this is normally regarded as a critical step in highly effective organization and control of modern DNs [25,26,27,28,29]. During the cluster partitioning phase, resources most conducive to achieving the DN’s control objectives can be aggregated according to their inherent characteristics and grid topology, which alleviates computational burdens in subsequent grid regulation stages and enhances control efficiency [27]. Furthermore, once the cluster partitioning model is well-trained, its execution becomes liberated from the constraints of traditional optimization models, leading to improved computational efficiency [28]. On this basis, it also strengthens the DN’s decision-making capabilities regarding cluster responses under extreme operating conditions [29]. Hence, exploring an appropriate RL strategy that can be applied for DN dynamic cluster partitioning will be valuable for smart DN management level improvement.

Based on the above discussion, this paper proposes an intelligent dynamic partitioning for DNs, and a self-consistent regulation framework is also embedded. The main contributions of this paper are as follows:

(1)

An environmental model with continuous state space, discrete action space and two dispatching performance-oriented reward functions is first developed for DN cluster partitioning.

(2)

A novel random forest Q-learning network (RF-QN) with a node-based multi-agent parallel calculating framework and weight self-adjusting mechanism is developed and trained to implement the cluster partitioning, from which the generalization and robustness of the trained model are improved by taking advantage of both deep learning and decision trees.

(3)

A dispatching framework with an intelligent dynamic cluster generating mechanism in each cluster partitioning period and a parallel cooperation mechanism between clusters in each regulating moment is proposed in this paper. It leverages the advantages of RL in handling uncertain and complex decision-making processes; while ensuring efficient utilization of the ARs within each cluster, the operation flexibility and robustness of the whole system are improved.

The remainder of this article is organized as follows. The cluster partitioning environmental model is developed in Section 2. The deep RL cluster partitioning strategy and its training method for implementing dynamic cluster partitioning are presented in Section 3. Then, the overall dynamic cluster partitioning and dispatching framework is discussed in Section 4. Section 5 gives the simulation results, and the conclusion is given in Section 6.

2. Cluster Partitioning Environmental Model

2.1. Assumptions

The term “intelligent dynamic cluster partitioning” in this paper refers to putting the nodes/buses of DNs (they are normally connected with some DGs or FALs) into groups at each time interval (e.g., one hour), which is aimed at effectively configuring the ARs according to their output characteristics. To execute this process (especially in the training stage of the proposed method (see Section 3.3, Section 3.4 and Section 3.5)), a good control for each group/cluster, normally OPF, to facilitate optimally allocating these ARs within a group is also included. In addition, to maintain the stable and efficient operation of the whole DN, the dispatching center also needs to supervise the cluster partitioning model and send power commands to each cluster in this process (note: the specific dispatching framework will be discussed in Section 4).

Hence, to realize the proposed cluster partitioning strategy, this paper makes the following assumptions:

(1)

All ARs connect the grid via converters, which enables the resources to be flexibly regulated within their output range.

(2)

The output active power of DGs is affected by weather or other natural factors, and there is a certain upper limit, while the regulation range of the DG’s reactive power should be constrained by both the setup’s normal rating and the output active power.

(3)

To maintain the safe and stable operation of the whole system, it is necessary to ensure that the power commands issued by the dispatching center to each cluster as well as to the entire DN cannot exceed the output boundary of each resource and cluster.

2.2. The Environmental Model for Cluster Partitioning and Rewards

Inspired by the memory-free characteristics of the Markov decision process (MDP) [30], dynamic cluster partitioning can be described as follows:

(1)

Each bus/node in the DN can be defined as an agent; the state of an agent represents the AR’s configuration of a node, and the action of an agent determines the cluster number selecting method of a node.

(2)

The state space of agent-$i$ at time moment $t$-${\mathbb{S}}_{t,i}$ is

$${\mathbb{S}}_{t,i}=\left\{{\mathcal{p}}_{l,t}^{\mathrm{m}\mathrm{a}\mathrm{x}},{\mathcal{p}}_{l,t}^{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathcal{s}}_{l,\mathrm{N}},\mathcal{c}\left(i\right)\right\},l\in \mathbf{L}$$

(1)

where ${\mathcal{p}}_{l,t}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\mathcal{p}}_{l,t}^{\mathrm{m}\mathrm{i}\mathrm{x}}$ denote the upper and lower limits of the output active power of AR-$l$ at time $t$, ${\mathcal{s}}_{l,\mathrm{N}}$ is the installed capacity/normal rating of AR-$l$, $\mathcal{c}\left(i\right)$ is the cluster number of node-$i$’s upstream node, and $\mathbf{L}$ is the set of ARs in the concerned DN.

(3)

The action space of agent-$i$-${\mathbb{A}}_i$ is

$${\mathbb{A}}_i=\left\{\mathfrak{a}\left(i\right)=\mathcal{c}\left(i\right),\mathfrak{a}\left(i\right)=max\left\{\mathcal{c}\right\}+1\right\},i\in \mathbf{B}$$

(2)

where $\mathfrak{a}\left(i\right)$ denotes the cluster number node-$i$ belongs to, $\mathcal{c}$ is the current cluster number of node-$i$, and $\mathbf{B}$ is the set of the nodes in the concerned DN. (Note: This paper sets $\mathfrak{a}\left(i\right)\le M$, $\forall i\in \mathbf{B}$, where $M$ denotes the preset maximum number of clusters. The value of $M$ is designed to balance clustering flexibility and computational efficiency. In this study, $M=6$ is selected based on the scale and resource distribution of the modified IEEE 33-node test system).

Thus, the cluster number of agent-$i$ at time moment $t$-$a_{i,t}$ can be expressed as

$$a_{i,t}=\mathfrak{a}\left(i\right)=\left\{\begin{array}{l}\mathrm{action1}:\mathcal{c}\left(i\right)\\ \mathrm{action2}:\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathcal{c}\right)+1\end{array}\right.,i\in \mathbf{B}$$

(3)

where whether action 1 or 2 is selected depends on the Q-value in the experience replay buffer (see Section 3.5); the larger related action should be selected.

(4)

To evaluate the quality of action in the dynamic cluster partitioning process, dispatching models—automatic generation control (AGC) and automatic voltage control (AVC)—are discussed in this paper, the reward (or comprehensive score) of which can be defined as

$$\left\{\begin{array}{c}{\mathbb{r}}^{\mathrm{A}\mathrm{G}\mathrm{C}}={\left({\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{G}\mathrm{C}}\right)}^{\mathrm{T}}\mathbf{Index}\\ {\mathbb{r}}^{\mathrm{A}\mathrm{V}\mathrm{C}}={\left({\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{V}\mathrm{C}}\right)}^{\mathrm{T}}\mathbf{Index}\end{array}\right.$$

(4)

where ${\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{G}\mathrm{C}}$ and ${\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{V}\mathrm{C}}$ are the weights of ${\mathbb{r}}^{\mathrm{A}\mathrm{G}\mathrm{C}}$ and ${\mathbb{r}}^{\mathrm{A}\mathrm{V}\mathrm{C}}$; their specifications in this paper are set as

$$\left\{\begin{array}{c}{\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{G}\mathrm{C}}=\left(31.61\mathrm{\%},0.29\mathrm{\%},31.16\mathrm{\%},12.46\mathrm{\%},21.81\mathrm{\%},3.12\mathrm{\%}\right)\\ {\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}}^{\mathrm{A}\mathrm{V}\mathrm{C}}=\left(5.30\mathrm{\%},64.49\mathrm{\%},5.30\mathrm{\%},13.24\mathrm{\%},3.76\mathrm{\%},11.92\mathrm{\%}\right) \end{array}\right.$$

(5)

and

$$\mathbf{I}\mathbf{n}\mathbf{d}\mathbf{e}\mathbf{x}=\left({\mathrm{I}\mathrm{n}\mathrm{d}}_1^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_1^{\mathrm{A}\mathrm{V}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_2^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_2^{\mathrm{A}\mathrm{V}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_3^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_3^{\mathrm{A}\mathrm{V}\mathrm{C}}\right)$$

(6)

which indicates the dispatching performance indexes relating to RERUR (i.e., ${\mathrm{I}\mathrm{n}\mathrm{d}}_1^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_1^{\mathrm{A}\mathrm{V}\mathrm{C}}$), network losses (i.e., ${\mathrm{I}\mathrm{n}\mathrm{d}}_2^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_2^{\mathrm{A}\mathrm{V}\mathrm{C}}$), and voltage deviation rate (i.e., ${\mathrm{I}\mathrm{n}\mathrm{d}}_3^{\mathrm{A}\mathrm{G}\mathrm{C}},{\mathrm{I}\mathrm{n}\mathrm{d}}_3^{\mathrm{A}\mathrm{V}\mathrm{C}}$), which are defined as

$${\mathrm{I}\mathrm{n}\mathrm{d}}_1^{\mathrm{m}\mathrm{o}\mathrm{d}}={\displaystyle \frac{1}{T}}\left[{\sum }_{t=1}^T\left({\displaystyle \frac{{\sum }_{i\in \mathit{B}}{\sum }_{l\in {\rho }_{\left(i\right)}^{\mathrm{n}\mathrm{e}\mathrm{w}}}{p}_{l,t}^{\mathrm{m}\mathrm{o}\mathrm{d}}}{{\sum }_{i\in \mathit{B}}{\sum }_{l\in {\rho }_{\left(i\right)}^{\mathrm{n}\mathrm{e}\mathrm{w}}}{\mathcal{p}}_{l,t}^{\mathrm{m}\mathrm{a}\mathrm{x}}}}\right)\right]$$

(7)

$${\mathrm{I}\mathrm{n}\mathrm{d}}_2^{\mathrm{m}\mathrm{o}\mathrm{d}}=-{\displaystyle \frac{1}{T}}\left[{\sum }_{t=1}^T\left({\sum }_{i\in \mathit{B}}{\sum }_{l\in \rho \left(i\right)}{p}_{l,t}^{\mathrm{m}\mathrm{o}\mathrm{d}}-{\sum }_{i\in \mathit{B}}{p}_{i,t}^D+p_{\mathrm{P}\mathrm{C}\mathrm{C},t}\right)\right]$$

(8)

$${\mathrm{I}\mathrm{n}\mathrm{d}}_3^{\mathrm{m}\mathrm{o}\mathrm{d}}=-{\displaystyle \frac{1}{T}}\left({\sum }_{t=1}^T{\sum }_{i\in \mathit{B}}\left|1-{\displaystyle \frac{V_{i,t}^{\mathrm{m}\mathrm{o}\mathrm{d}}}{V_{\mathrm{B}}}}\right|\right)$$

(9)

where $\mathrm{m}\mathrm{o}\mathrm{d}=\mathrm{A}\mathrm{C}\mathrm{G},\mathrm{A}\mathrm{V}\mathrm{C}$; ${\rho }_{\left(i\right)}^{\mathrm{n}\mathrm{e}\mathrm{w}}$ is the set of distributed renewable energy resources in node-$i$; $p_{l,t}^{\mathrm{m}\mathrm{o}\mathrm{d}}$ denotes the output active power of AR-$l$ at moment $t$ in operation model mod; ${\mathcal{p}}_{l,t}^{max}$ is the maximum active power of AR-$l$ at moment $t$; ρ(i) is the set of distributed ARs (including DGs, FALs, ESSs, etc.) in node-$i$; $p_{i,t}^D$ is the active power of the un-adjustable node-$i$ at moment $t$; $p_{\mathrm{P}\mathrm{C}\mathrm{C},t}$ is the active power injected into the grid at the PCC point at moment $t$; $T$ is the total number of time periods; $V_{i,t}^{\mathrm{m}\mathrm{o}\mathrm{d}}$ is node-$i$’s voltage at moment $t$ in operation model mod; and $V_{\mathrm{B}}$ is the voltage’s base value.

In fact, the physical meaning of the reward defined in (4) is not unique, and depends on the performance metrics that cluster partitioning and dispatching focus on. In this paper, the indexes shown in (6) to (9) prioritize dispatching performance, indicating that the cluster partitioning strategy proposed here is dispatch-oriented. The weight parameters in (5) are derived from a dispatch-oriented cluster evaluation framework developed in our prior research, which employs a two-stage sample screening method followed by a feedback-based weight correction mechanism tailored for distribution network static clustering. Specifically, the two-stage screening process first eliminates redundant and low-correlation operational scenarios, after which each performance indicator’s weight is adaptively adjusted according to its contribution to overall dispatch performance. This approach ensures that the reward function reflects practical operational priorities—such as maximizing renewable energy utilization, minimizing network losses, and maintaining voltage stability—and has been validated in earlier studies on cluster-based dispatching in active distribution networks. Consequently, these weights are adopted directly in this study to align the reward function with real-world dispatching objectives.

3. Deep Reinforcement Learning Cluster Partitioning Strategy

As discussed in Section 2, the environmental model for dynamic cluster partitioning is formulated as a Markov decision process with continuous state space (reflecting real-time power variations) and discrete action space (representing node-level cluster assignment choices). Within this framework, each node observes its operational state—including power limits, installed capacity, and upstream cluster affiliation—and selects an action to either join the same cluster as its upstream neighbor or initiate a new cluster. Following the partitioning decision, a dispatch-oriented reward is computed based on renewable energy utilization, network loss, and voltage deviation. Hence, dynamic cluster partitioning can be demonstrated to find a balance between the fluctuating power demand and supply in every time section concerned to create an optimal resource grouping model, which is useful in a deep reinforcement learning algorithm.

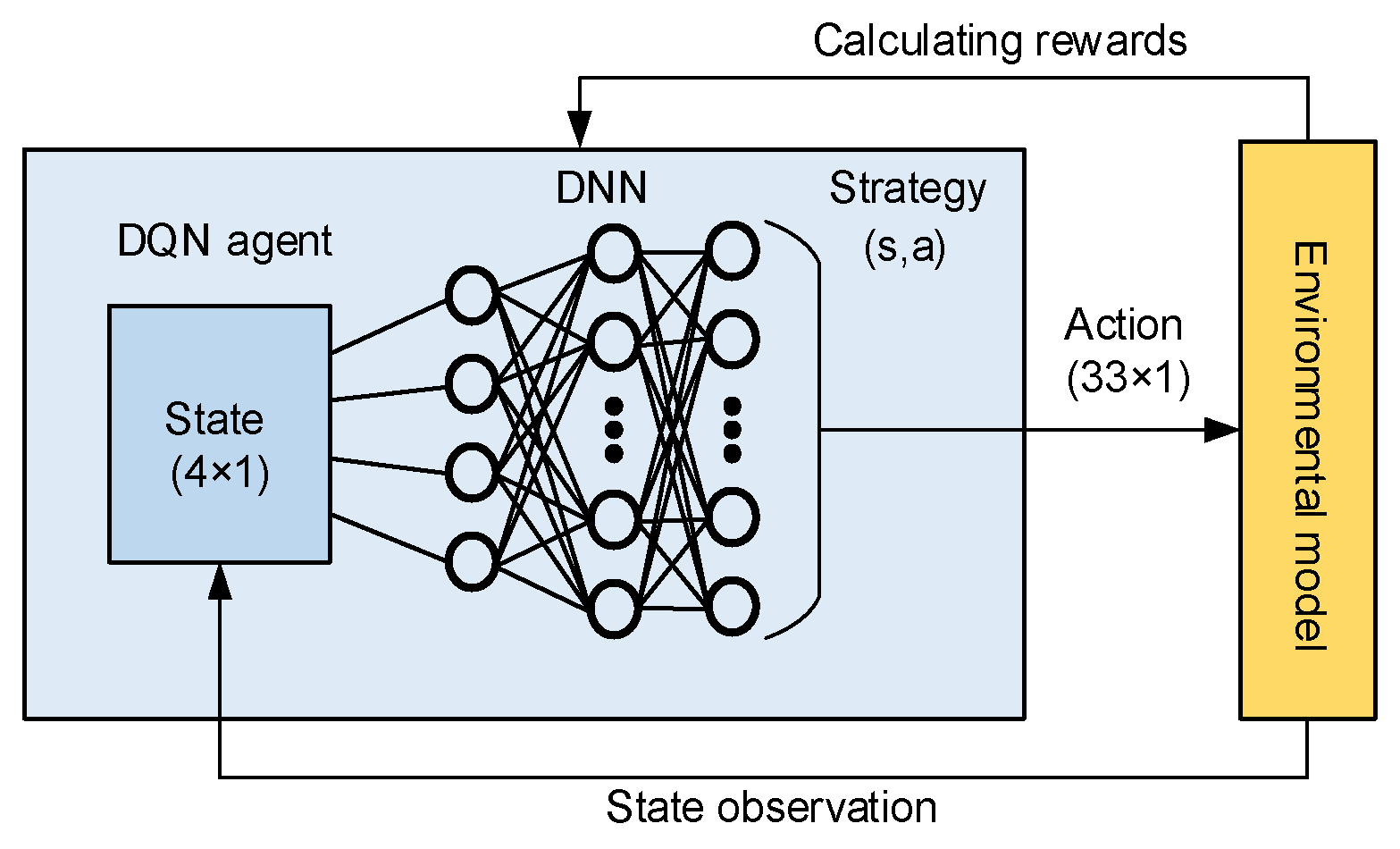
3.1. Classical Deep Q-Learning Network (DQN) Model

As can be seen from Figure 1, a deep neural network (DNN) is embedded in a deep Q-learning network (DQN) [31], which enables the DQN to fit an approximate Q-function by learning from the continuous state space (e.g., (1)) and thereby predicting the expected rewards for each possible state–action pair $(s,a)$.

By defining the Q-value of the DNN as ${\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)$, and the true Q-value as ${\mathbb{Q}}_{\mathrm{\ast }}\left(s,a\right)$, the loss function in the fitting process can be expressed as

$$J_{\mathrm{D}\mathrm{N}\mathrm{N}}={‖{\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)-{\mathbb{Q}}_{\mathrm{*}}\left(s,a\right)‖}_2^2$$

(10)

Minimizing $J_{\mathrm{D}\mathrm{N}\mathrm{N}}$ in the training process, the DNN can achieve value network regression, and find the value $(s,a)$ in every step to realize dynamic cluster partitioning.

3.2. Random Forest Q-Learning Network (RF-QN) Model

To address the limitations of classical DQNs in handling noisy grid data and high-dimensional state spaces, we propose a random forest (RF) Q-learning network (RF-QN) that synergizes ensemble learning with reinforcement learning. As shown in Figure 2, the RF-QN replaces the DNN in a traditional DQN with an RF regression system. The RF-QN leverages ensemble learning to achieve better generalization (through feature subsampling and voting) and inherent stability against noisy grid data [32]. The integration provides three distinct advantages [33]: (1) RF’s parallelizable structure enables faster training, (2) decision trees naturally handle sparse data regimes, reducing experience buffer dependency, and (3) explicit feature importance outputs make cluster partitioning decisions interpretable.

The loss function of the RF-QN is

$$J_{\mathrm{R}\mathrm{F}}={‖{\mathbb{Q}}_{\mathrm{R}\mathrm{F}}\left(s,a\right)-{\mathbb{Q}}_{\mathrm{*}}\left(s,a\right)‖}_2^2$$

(11)

where ${\mathbb{Q}}_{\mathrm{R}\mathrm{F}}\left(s,a\right)$ is the Q-function of RF.

Minimizing $J_{\mathrm{R}\mathrm{F}}$ in the training process, RF can achieve value network regression, and find a more suitable $(s,a)$ value for dynamic cluster partitioning.

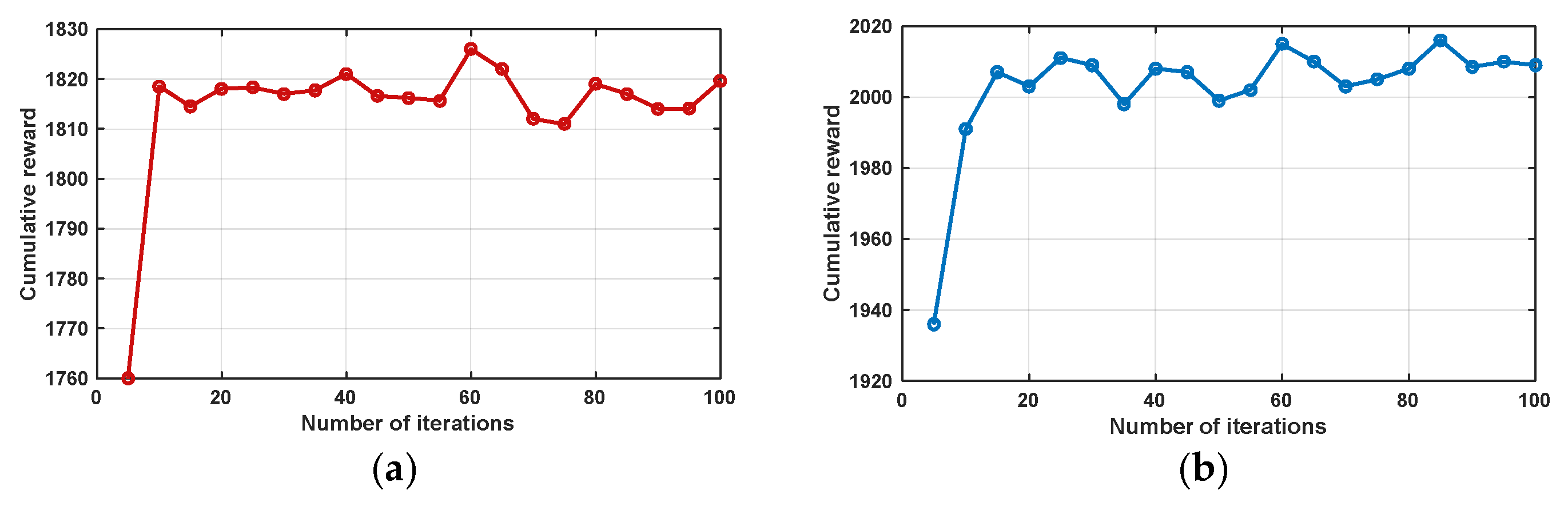
3.3. Training and Parameter Update Principles

For the DNN-integrated DQN [31], the update principle of the Q-value can be expressed as

$${\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)\leftarrow {\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)+\alpha \left[r+\gamma \underset{a^{\mathrm{\prime }}\in \mathbb{A}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)-{\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)\right)\right]$$

(12)

where $\alpha$ is the learning rate, $\gamma$ is the discount factor, $r$ indicates the current reward, $s^{\mathrm{\prime }}$ is the status of the next moment, and $a^{\mathrm{\prime }}$ is the action of the next moment.

Based on the update principle shown in (12), ${\mathbb{Q}}_{\mathrm{*}}\left(s,a\right)$ can be approximated as

$${\mathbb{Q}}_{\mathrm{*}}\left(s,a\right)=\alpha \left[r+\gamma \underset{a^{\mathrm{\prime }}\in \mathbb{A}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)-{\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)\right)\right]$$

(13)

and (10) can be rewritten as

$$J_{\mathrm{D}\mathrm{N}\mathrm{N}}={‖\begin{array}{c}{\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)\\ -\alpha \left[r+\gamma \underset{a^{\mathrm{\prime }}\in \mathbb{A}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)-{\mathbb{Q}}_{\mathrm{D}\mathrm{N}\mathrm{N}}\left(s,a\right)\right)\right]\end{array}‖}_2^2$$

(14)

By incrementally updating the Q-value network fitted by the DNN, it gradually approaches the temporal difference target until it is closer to the true Q-value network.

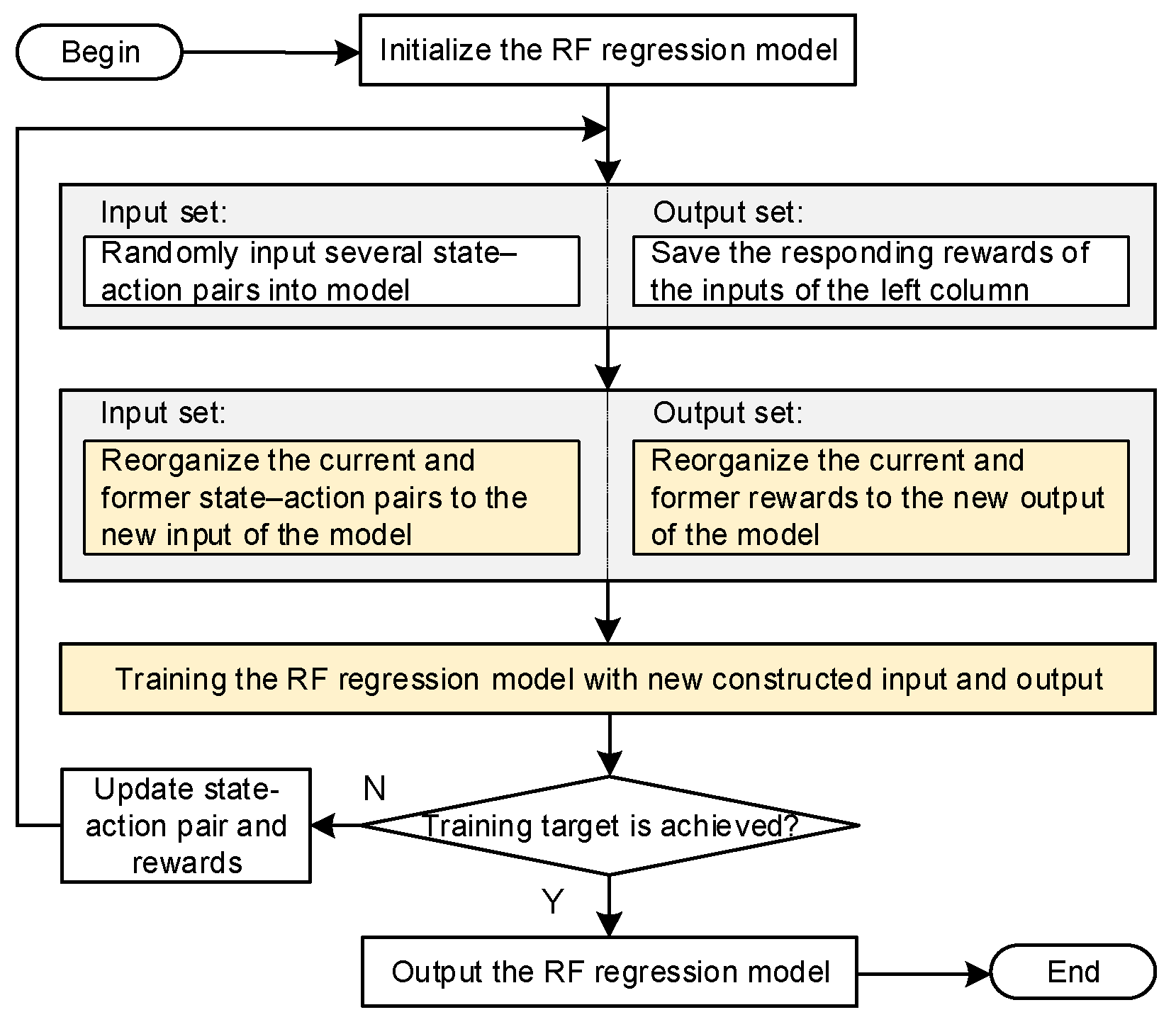
For the proposed RF-QN, different from the DNN, the RF regression model cannot update parameter weights in real time. A training result rumination update regression model is proposed in this paper to address this; the framework is shown in Figure 3.

As can be seen from Figure 3, we should first initiate an RF regression model; then, we randomly select several state–action pairs $\left(s,a\right)$ as the input set (note: they should be restricted within their operation boundary) and save the related rewards of the regressive model as the output set. Then, before training the new regression model, we combine the current state–action pair and the rewards with the input and output sets from the previous step to construct new input and output sets, and the reorganized input and output sets can be adopted to train the model. This process is repeated until the expected accuracy or the maximum training number is reached. The mechanism of reconstructing the trained results with the current input and output set facilitates the updating of the RF’s weights, and in this process the immature results will be gradually abandoned.

3.4. Specific Training Procedure

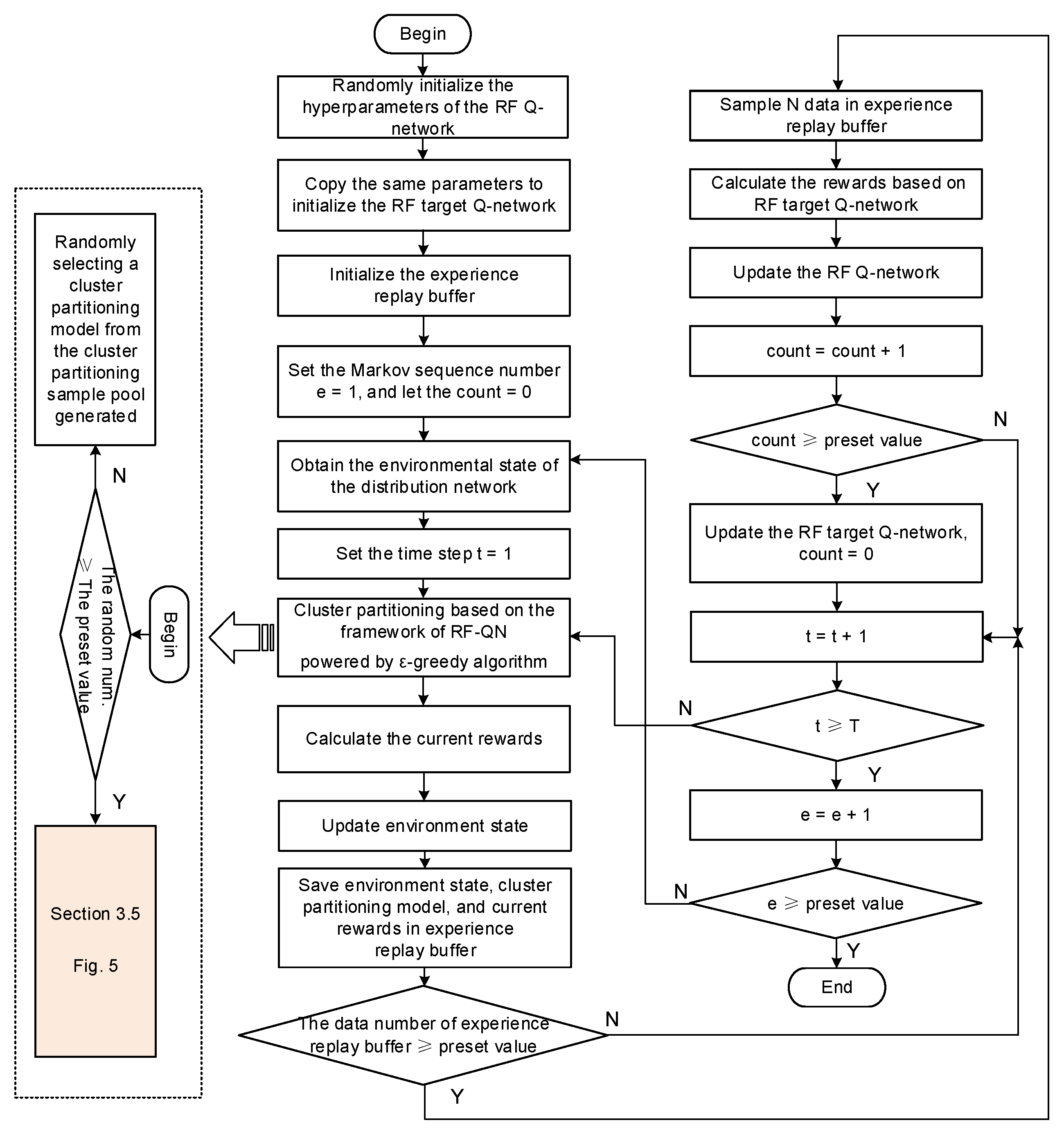
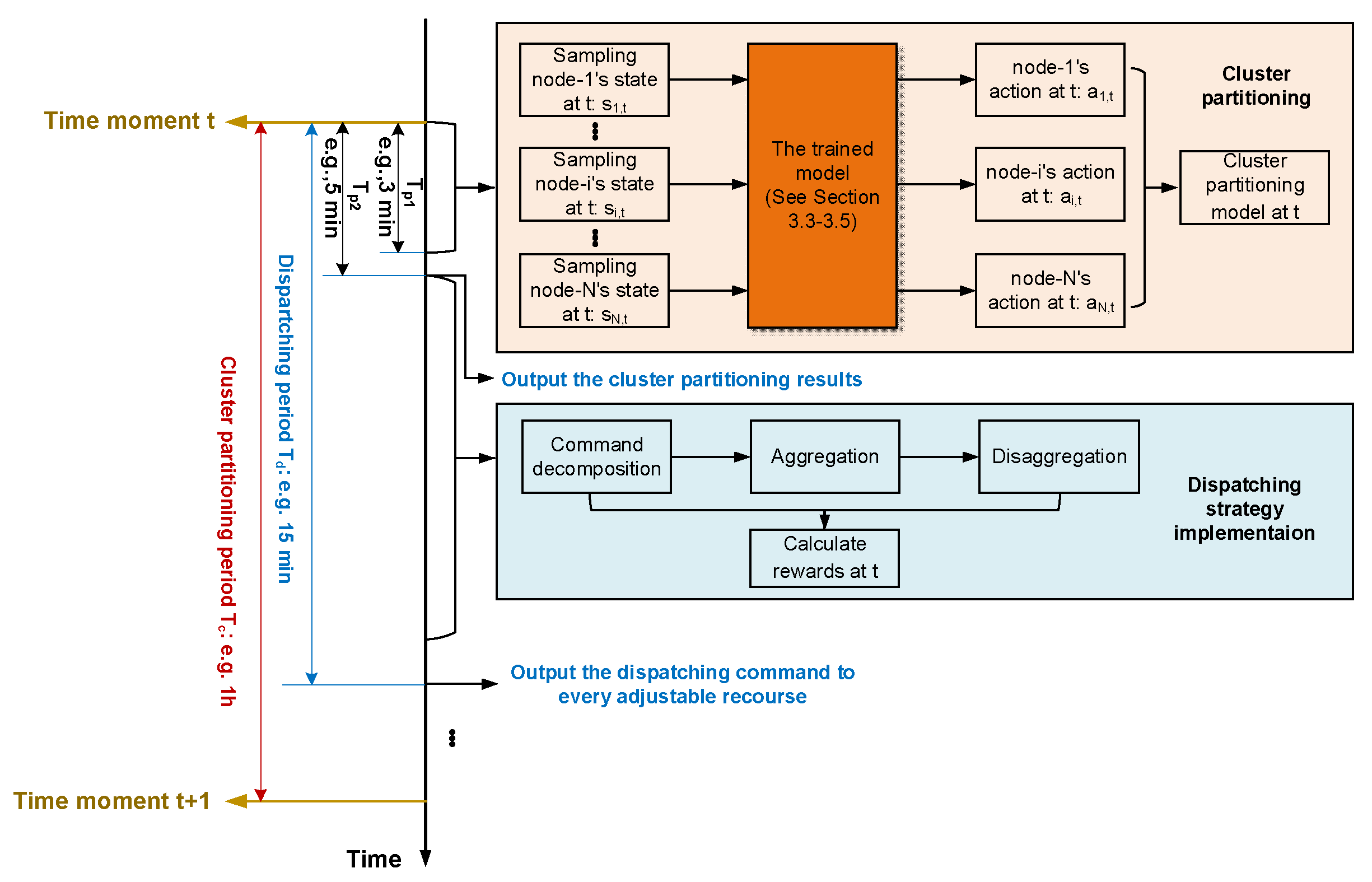
Figure 4 illustrates the detailed training procedure of the proposed RF-QN for dynamic cluster partitioning, which consists of the following steps:

Step 1: Initialize the hyperparameters of the RF Q-network and assign a cluster number from 1 to node-1.

Step 2: Compute the current and target Q-networks of the RF model.

Step 3: Initialize the experience replay buffer (note: the buffer stores and retrieves experiences for each agent independently).

Step 4: Let Markov sequence number e = 1 and the training counter count = 0.

Step 5: Obtain the environmental state of the concerned DN, including the output power and the installing capacity of ARs (for specifications, refer to Section 3.5).

Step 6: Let the time step t = 1.

Step 7: Initialize the environmental states of the concerned DN and assign each node to a cluster using the ε-greedy algorithm, and record the current states, actions (i.e., cluster partitioning modes), and rewards in the experience replay buffer.

According to the ε-greedy algorithm, when the random number is larger than the preset value, the system will randomly select a cluster partitioning model from the sample pool; otherwise, the procedure will follow the process shown in Figure 5 (see Section 3.5).

Step 8: Calculate the current reward (see (4)) and update the environmental state (i.e., the output power and the installing capacity of ARs) at time step t.

Step 9: Store the current states, actions, and rewards in the experience replay buffer. If the buffer reaches its preset capacity, randomly sample data to train the RF Q-network with the following objective:

$$min{J}_{\mathrm{R}\mathrm{F}}={‖\begin{array}{c}{\mathbb{Q}}_{\mathrm{R}\mathrm{F}}\left(s,a\right)\\ -\alpha \left[r+\gamma \underset{a^{\mathrm{\prime }}\in \mathbb{A}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\mathbb{Q}}_{\mathrm{R}\mathrm{F}\mathrm{\prime }}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)-{\mathbb{Q}}_{\mathrm{R}\mathrm{F}}\left(s,a\right)\right)\right]\end{array}‖}_2^2$$

(15)

where ${\mathbb{Q}}_{\mathrm{R}\mathrm{F}\mathrm{\prime }}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)$ is the trained target Q-network/function.

Step 10: Update the Q-network and increment $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}$ by 1.

Step 11: If count exceeds the preset threshold, update the target Q-network as ${\mathbb{Q}}_{\mathrm{R}\mathrm{F}\mathrm{\prime }}\left(s^{\mathrm{\prime }},a^{\mathrm{\prime }}\right)={\mathbb{Q}}_{\mathrm{R}\mathrm{F}}\left(s,a\right)$.

Step 12: Increment $t$ by 1 and proceed to the next training round until $t\ge T$.

Step 13: Terminate the training process once all Markov sequences are completed (i.e., $e\ge$ a preset value) and $t\ge T$.

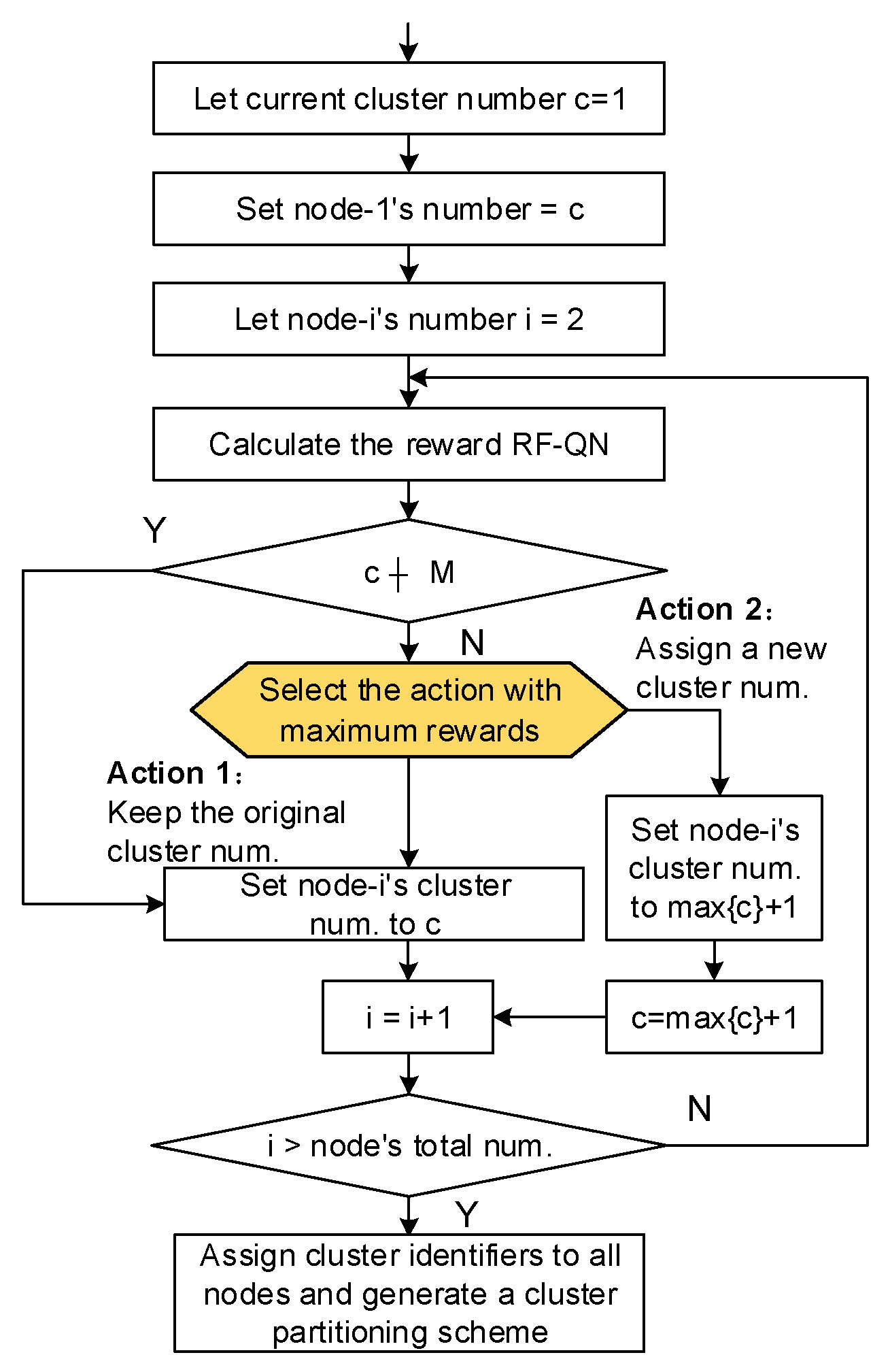
3.5. The RF-QN Model-Driven Cluster Partitioning Method

To adapt the training process given in Figure 4, the cluster partitioning method driven by the RF-QN model is shown in Figure 5. The basic idea here is assigning a cluster number to each node in DN, after which nodes with the same cluster identifier will be grouped together. It can be seen from Figure 5 that the number of the current cluster $c$ and node-1’s cluster number are first set as 1. And then, the following nodes, e.g., node-$i$, will be numbered based on the cluster number of the upstream node, and two possible cluster numbers can be assigned to node-$i$—action 1: $\mathfrak{a}\left(i\right)=\mathcal{c}\left(i\right)$; and action 2: $\mathfrak{a}\left(i\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathcal{c}\right\}+1$ (see (2) and (3) in Section 2). Furthermore, the action with the largest RF-QN reward will finally be implemented, and node-$i$’s cluster number $\mathfrak{a}\left(i\right)$ can then be determined based on (3). Finally, the cluster number $c$ and node number $i$ are updated until all nodes are assigned to the cluster number.

4. Dynamic Cluster Partitioning-Integrated Dispatching Framework

4.1. The Cluster Dispatching Model in DNs

As discussed in Section 2, Section 3.4 and Section 3.5, the cluster dispatching model/process should be used in the training process of the proposed dynamic cluster partitioning strategy.

The DN’s cluster dispatching model is given in Figure 6. After each cluster is partitioned by the strategy proposed in Section 2 and Section 3, the command power of the concerned DN (i.e., the PCC power), $p^{\mathrm{*}}$ and $q^{\mathrm{*}}$, is first issued by the dispatching center of the upstream network, and it will be appropriately decomposed into each cluster; in this paper, this is expressed as

$$\left\{\begin{array}{c}{\mathcal{P}}_m^{\mathrm{*}}=p^{\mathrm{*}}{\displaystyle \frac{{\mathcal{P}}_m^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathcal{P}}_m^{\mathrm{m}\mathrm{i}\mathrm{n}}}{\sum _{i=1}^M{\mathcal{P}}_i^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathcal{P}}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}}}+{\mathcal{P}}_m^{\mathrm{m}\mathrm{i}\mathrm{n}}\\ {\mathcal{Q}}_m^{\mathrm{*}}=q^{\mathrm{*}}{\displaystyle \frac{{\mathcal{Q}}_{\mathrm{m}}^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathcal{Q}}_{\mathrm{m}}^{\mathrm{m}\mathrm{i}\mathrm{n}}}{\sum _{i=1}^M{\mathcal{Q}}_i^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathcal{Q}}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}}}+{\mathcal{Q}}_m^{\mathrm{m}\mathrm{i}\mathrm{n}}\end{array}\right.$$

(16)

where ${\mathcal{P}}_m^{\mathrm{*}}$ and ${\mathcal{Q}}_m^{\mathrm{*}}$ are the reference active and reactive power of cluster-$m$, respectively; ${\mathcal{P}}_i^{\mathrm{m}\mathrm{a}\mathrm{x}}$, ${\mathcal{P}}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ and ${\mathcal{Q}}_i^{\mathrm{m}\mathrm{a}\mathrm{x}}$, ${\mathcal{Q}}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ are the maximum and minimum active and reactive power of cluster-$i$, $i=1,\dots ,m,\dots ,M$.

Obtaining the operation boundary of each cluster is referred to as “aggregation” in Figure 6; it can be calculated using the OPF, in which all the ARs outside the concerned cluster are “turned off”, and then $\mathrm{m}\mathrm{a}\mathrm{x}\{P,Q\}$ and $\mathrm{m}\mathrm{i}\mathrm{x}\{P,Q\}$ are taken as the objects (note: $P$, $Q$ here means the power at the node of the concerned cluster interfacing with the external grid). When the aggregation is finished, the boundary of cluster-$m$ can be obtained and is described as

$$\left\{\begin{array}{c}{\mathcal{P}}_m^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathcal{P}}_m\le {\mathcal{P}}_m^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {\mathcal{Q}}_m^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathcal{Q}}_m\le {\mathcal{Q}}_m^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ \cos {\theta }_l\ge {\mathrm{PF}}^{\min },\forall l\in \sigma \left(m\right)\end{array}\right.$$

(17)

where ${\mathcal{P}}_m$ and ${\mathcal{Q}}_m$ are the operation active and reactive power of cluster-$m$; $\sigma \left(m\right)$ is the AR set of cluster-$m$; ${\theta }_l$ is the power factor angle of AR-$l$; and ${\mathrm{PF}}^{\min }$ is the minimum power factor of all the ARs belonging to cluster-$m$.

After aggregation, an OPF is implemented for each cluster to regulate the ARs within it, which is named “disaggregation” in Figure 6. In our paper, the target of OPF is to track the reference active and reactive power of each cluster, in which the operation boundary of each AR can be generally expressed as

$$\left\{\begin{array}{c}{\mathcal{p}}_l^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathcal{p}}_l\le {\mathcal{p}}_l^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {\mathcal{p}}_l^2+{\mathcal{q}}_l^2\le {\mathcal{s}}_{l,N}^2\\ \cos {\theta }_l\ge {\mathrm{PF}}^{\min }\\ p_i=\sum _{l\in \rho \left(i\right)}{\mathcal{p}}_l\\ q_i=\sum _{l\in \rho \left(i\right)}{\mathcal{q}}_l\end{array}\right.$$

(18)

where ${\mathcal{p}}_l$ and ${\mathcal{q}}_l$ are the operation active and reactive power of AR-$l$; $\rho \left(i\right)$ is the AR set at node-$i$.

4.2. Dispatching Framework with Dynamic Cluster Partitioning

The dispatching framework with dynamic cluster partitioning is shown in Figure 7. The cluster partitioning strategy is first implemented, and the calculation time $T_{p1}$ is normally less than 3 min for a real DN branch which normally has 20–60 nodes; to ensure a certain margin, the cluster partitioning results are delivered to the dispatching subsystem at $t+T_{p2}$ (note: if $T_{p1}\le 3 \min$, $T_{p2}$ can be selected as 5 min, but it can be adjusted according to the practical situation). Then, implementing the dispatching strategy shown in Figure 7, it can be seen that it is fast and robust because the scale of each cluster is appropriate and the OPF is implemented in each cluster independently; in addition, their control target and the command decomposing method are easy to implement (see Section 4.1). The final dispatching results and the rewards at $t$ are issued to each adjustable resource at the end of the dispatching period $T_d$ (it is normally set as $15 \min$ in some practical systems). If the cluster partitioning period $T_c=T_d$, the process will be repeated in the next partitioning period beginning at $t+1$. If $T_c>T_d$, e.g., $T_c=1 \mathrm{h}$ and $T_d=15 \min$, three other dispatching periods will be implemented in $T_c$.

5. Case Study

5.1. System Configuration

A modified IEEE 33-node test system [34] is adopted here for a case study, in which 11 ARs are installed. The specific configuration of those ARs is given in

Table 1. Specifications of the installed adjustable resources.

Identification Number	Node Installed	Attributes	Installation Capacity
1	6	ESS	100 kVA
2	9	PV 1	150 kVA
3	12	DWP 1	100 kVA
4	13	PV 2	150 kVA
5	18	MH	100 kVA
6	21	PV 3	150 kVA
7	22	PV 4	150 kVA
8	23	DWP 2	100 kVA
9	25	EV-CS 1	100 kVA
10	30	EV-CS 2	100 kVA
11	33	DWP 3	100 kVA

and Figure 8, and their output characteristics are shown in Figure 9. (Note: These curves are based on the real measured data in our other practical work, and some of them are proportionally scaled to adapt to the power and voltage level of the concerned DN). The total installation capacity of the ARs is 20% of the loads (note: the loads’ installed active and reactive power are 3715 kW and 2300 kVar, respectively); the installed energy capacity and initial SoC of the ESSs are set as 1000 kWh and 50%, respectively.

The initial parameters of the neural network, the RF model, and RL, which were obtained from several turns of debugging, are listed in

Table 2. Neural network model hyperparameters.

Parameter		Parameter
Learning rate	0.1	Input dimension	34
Training episodes	1	Number of hidden layers	6
Learning rate decay factor	0.9	Output dimension	2

,

Table 3. Random forest model hyperparameters.

Parameter		Parameter
Number of decision trees	100	Input dimension	34
Maximum splits per tree	10	Output dimension	1
Minimum samples per leaf	5	Type	Regression

and

Table 4. Reinforcement learning hyperparameters.

Parameter		Parameter
Q-network update frequency	50	Discount factor	0.98
ε-greedy sampling probability	0.1	Experience replay buffer batch size	100
Number of neural network-based agents	32	Number of random forest-based agents	64

.

5.2. Cluster Partitioning Results Driven by DQN

The reward curves of the first 100 training steps in which the DN accepts AGC and AVC regulations are given in Figure 10a,b, in which the traditional DQN is adopted. The curves in Figure 10 show that the cumulative rewards of AGC and AVC (i.e., $\sum _{i=1}^{24}{\mathbb{r}}_i^{\mathrm{A}\mathrm{G}\mathrm{C}}$ and $\sum _{i=1}^{24}{\mathbb{r}}_i^{\mathrm{A}\mathrm{V}\mathrm{C}}$) increase at the beginning of the iteration and gradually tend to reach relatively high steady values with some fluctuations (especially for the curve of AGC). Actually, the fluctuation originally comes from the ϵ-greedy algorithm in the training process (see Section 3.4 and Section 3.5); the agent preferentially selects a high-reward action with probability (1—ϵ), while retaining probability ϵ to perform random action exploration. Although this mechanism results in short-term reward fluctuation, it plays a key role in ensuring the global convergence of the proposed training algorithm.

The comprehensive scores (i.e., the reward in (4)) of the static cluster partitioning strategy and the DQN-driven dynamic cluster partitioning strategy are given in Figure 11a,b (note: as shown in Figure 7, they are obtained after dispatching). It can be seen in Figure 11 that both the AGC and AVC regulation performance of the DQN-driven dynamic cluster partitioning are better than that when adopting the static cluster partitioning strategy. As the training performance of AVC is better than that of AGC (see Figure 10), the dynamic cluster partitioning performance of AVC is better than that of AGC (see Figure 11b).

5.3. Cluster Partitioning Results Driven by RF-QN

The AGC and AVC reward curves in the RF-QN-driven cluster partitioning training process are given in Figure 12a,b; though their trends are similar to that of the DQN-driven system (see Figure 10), their fluctuation amplitudes are smaller and the reward values are larger, especially for that of AGC, which means the training convergency of the proposed RF-QN-driven dynamic cluster partitioning is better than that of the DQN-driven strategy. In addition, when the dynamic cluster partitioning strategy is implemented in the dispatching process (see Section 4.2 (note: in our simulation, we set $T_c=T_d=1 \mathrm{h}$)), as can be seen in Figure 13a,b, both the AGC’s and AVC’s comprehensive scores in the dynamic cluster partitioning process driven by the proposed RF-QN are obviously higher than that when adopting static cluster partitioning and DQN-driven dynamic cluster partitioning strategies.

To further illustrate the performance of the proposed method more physically, some typical AVC cluster partitioning results under different cluster partitioning strategies at 20:00 are given in Figure 14, and the related dispatching performances are listed in

Table 5. The specific performance of each partitioning method at 20:00.

Cluster Partitioning Strategies	RERUR (%)	Network Loss (p.u.)	Voltage Deviation Rate (%)
Static cluster partitioning strategy	30.29	0.1431	5.637
DQN-driven dynamic partitioning strategy	85.96	0.0785	3.582
RF-QN-driven dynamic partitioning strategy	94.73	0.0493	2.984

.

For the all-day optimal static cluster partitioning result shown in Figure 14a, as there is almost no sunlight at 20:00, the PVs (e.g., DG-6 and 7 connect to nodes 21–22) in Clus-ter-2 have sufficient reactive power supply capability, but this kind of Q-support ability to support adjacent clusters is restricted by rigid cluster boundaries, so this sub-optimal resource configuration yields a low reward score of 25 (see Figure 13b), and the related renewable energy utilization rate (RERUR), the network losses, and the voltage deviation rate, as listed in Table 5, are 30.29%, 0.1431 p.u., and 5.637%, respectively. The DQN-driven dynamic cluster partitioning strategy addresses this by intelligently regrouping PVs into cluster-1 with proximal nodes; the PVs connected at nodes-21 and 22 in this scenario are grouped as a cluster including more adjacent nodes than Figure 14a (see cluster-1 in Figure 14b). The reactive power coordinate control ability can then be improved, which elevates the reward/score to 64 (see Figure 13b), and the concerned dispatching performances in Table 5 are also improved. Compared with Figure 14b, the proposed RF-QN-driven dynamic cluster partitioning strategy further optimizes performance by reorganizing the PVs and other ARs into four clusters based on the reactive power coordinate capability and electrical distance, as shown in Figure 14c: each cluster is equipped with sufficient ARs to ensure voltage stability (voltage deviation is reduced to 2.984%), while the electrical distance between nodes in each cluster is maintained at a relatively low level, and the transmission losses are reduced to 0.0493 p.u. correspondingly; hence, the score/reward increases to 80, surpassing both static and DQN-driven methods while achieving a RERUR of 94.73%—the highest among all concerned strategies shown in Figure 14.

Table 6. Average scores of different cluster partitioning strategies.

Method	AGC Dispatching	AVC Dispatching
Static cluster partitioning strategy	65.36	61.83
DQN-driven dynamic partitioning strategy	69.66	76.74
RF-QN-driven dynamic partitioning strategy	75.73	83.65
Exhaustive search-based dynamic cluster partitioning strategy	80.16	88.07

lists the comprehensive scores of the concerned cluster partitioning strategies. It can be seen from Table 6 that both the scores of the DQN- and RF-QN-driven dynamic partitioning strategies in the AGC and AVC models are higher than that of the static cluster partitioning strategy, but compared to the dynamic partitioning strategy driven by DQN, the score/dispatching performance of the RF-QN-driven dynamic partitioning strategy is closer to that of the exhaustive search-based dynamic cluster partitioning strategy, which is regarded as the optimal dynamic cluster partitioning strategy, though it has the lowest implementation efficiency.

The former analysis has verified that the proposed FR-QN-driven dynamic cluster partitioning strategy is better than the DQN-driven one in the aspects of training robustness, resource organization capability, and regulation performance. Next, we will discuss the execution adaptability of the proposed FR-QN-driven dynamic cluster partitioning strategy to the dispatching framework proposed in Section 4.2. The training and implementation efficiency when the proposed strategy is executed on an ordinary PC are listed in

Table 7. Training and implementation efficiency of the proposed FR-QN-driven dynamic cluster partitioning.

Items	Dynamic Partitioning Strategy Driven by RF-QN
AGC training time consumption for max. 100 iterations	26.426 h
AVC training time consumption for max. 100 iterations	28.515 h
Cluster partitioning time consumption for AGC when training is finished	47.47 s
Cluster partitioning time consumption for AVC when training is finished	59.52 s

Note: The simulation is implemented on the Matlab platform and is tested on a PC with the following hardware configuration: a 2.60 GHz Intel(R) Core(TM) i7-9750H CPU and 16.0 GB RAM.

. It can be seen from Table 7 that though the training time consumption slightly exceeds one day (it will be shorter when a high-performance dedicated server is adopted), the implementation times of the proposed strategy for both AGC and AVC applications are at the second level, which means it can be conveniently executed in the dispatching system discussed in Section 4.2.

6. Conclusions

This paper aimed to develop an intelligent dynamic cluster partitioning and regulation strategy for distribution networks with high penetration of distributed and flexible resources, with the goals of improving operational efficiency, enhancing renewable energy utilization, and maintaining voltage stability while reducing computational complexity. To achieve these objectives, we first constructed an environment model based on a Markov decision process, which formally describes the state space, action space, and dispatch-oriented reward function for cluster partitioning. We then proposed a novel RF-QN (random forest Q-learning network) with a node-based multi-agent framework, incorporating a rumination update mechanism that enables adaptive weight adjustment during training, thereby enhancing the model’s generalization and robustness. Furthermore, an integrated dispatching framework was designed to realize dynamic cluster partitioning and cooperative regulation in practical operations.

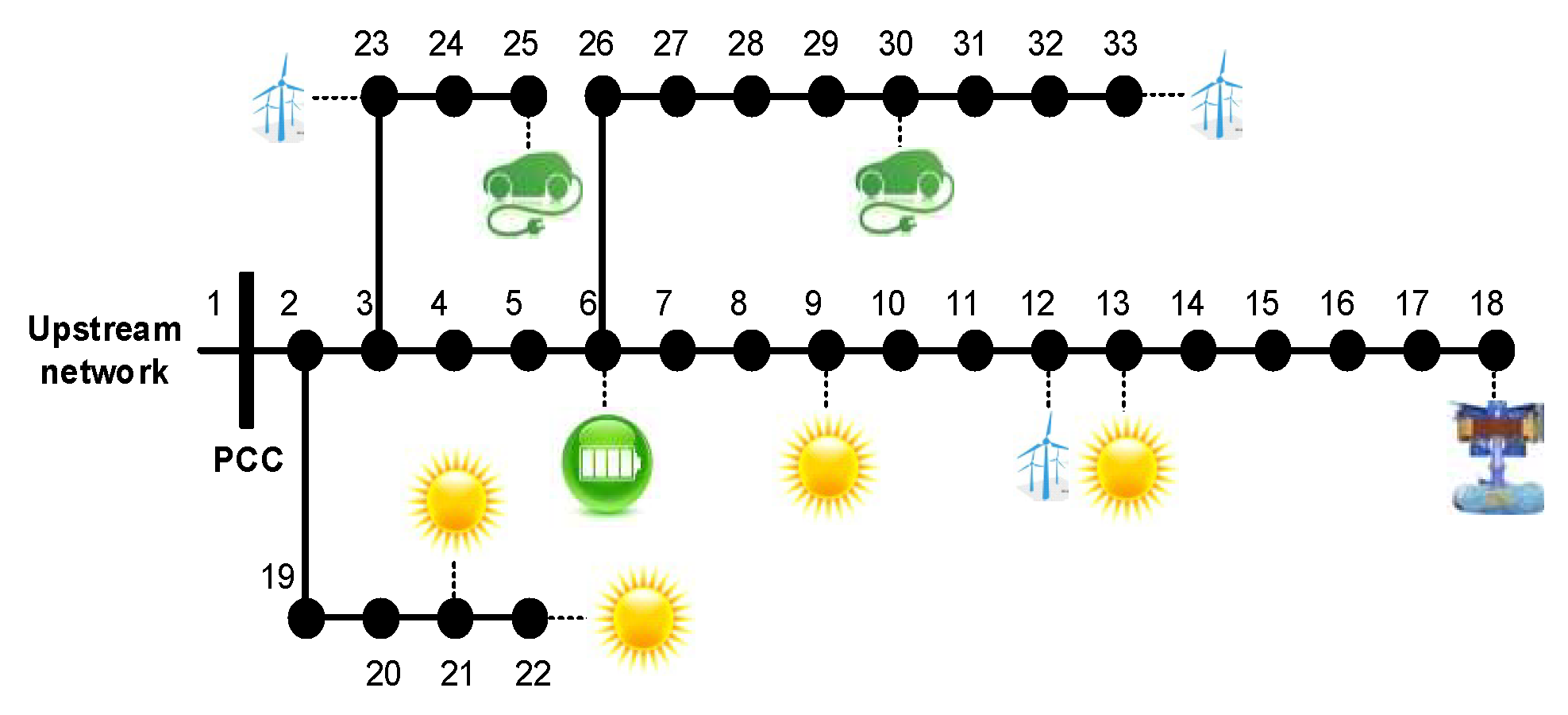
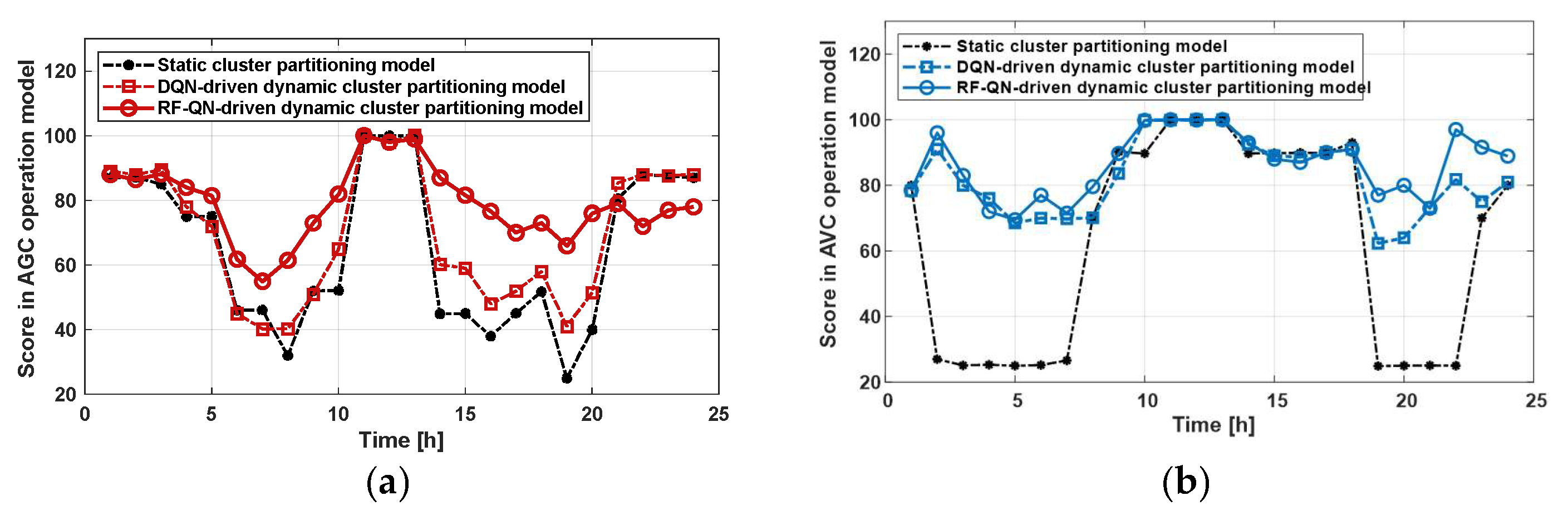
The proposed strategy was validated on a modified IEEE-33-node test system. The results demonstrate the following:

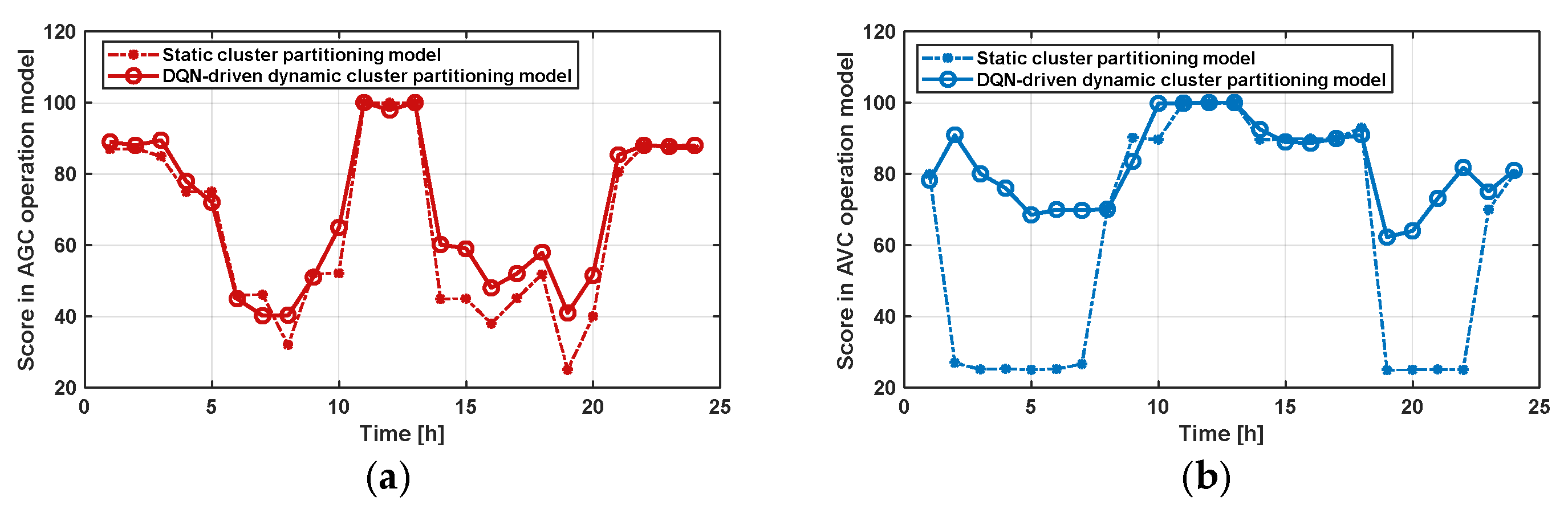
Significant Performance Improvement: Compared with static clustering and DQN-based dynamic clustering, the RF-QN approach increases the renewable energy utilization rate to 94.73%, reduces network losses to 0.0493 p.u., and lowers the voltage deviation rate to 2.984% under the AVC scenario (see Table 5).

Operational Efficiency: The cluster partitioning and dispatch execution time remains under one minute, meeting the requirements of real-time or intra-hour grid operation.

Practical Applicability: The framework is particularly suitable for modern distribution networks with high shares of photovoltaic, wind, energy storage, and electric vehicle charging loads, where traditional centralized or static control methods struggle with variability and uncertainty.

In conclusion, the objectives of this study have been successfully achieved. The proposed intelligent dynamic cluster partitioning strategy not only provides a scalable and efficient solution for resource aggregation and dispatch but also offers a novel integration of random forest and reinforcement learning that balances interpretability, robustness, and computational performance. Future work will focus on extending the method to larger-scale networks and more extreme operational scenarios to further validate its adaptability and resilience.