Constrained and Unconstrained Control Design of Electromagnetic Levitation System with Integral Robust–Optimal Sliding Mode Control for Mismatched Uncertainties

Abstract

In real life, almost all systems are nonlinear in nature. The electromagnetic levitation system (EMLS) is one such system that has a wide range of applications due to its frictionless, fast, and affordable technique. Optimal control and sliding mode control (SMC) techniques are often used controllers for EMLS. However, these techniques can achieve the required levitation but lag in having perfect set-point tracking and robustness against uncertainties. To get over these drawbacks, this article proposes the design of unconstrained mismatched uncertainties, constrained mismatched uncertainties, and integral sliding mode control with mismatched uncertainties for the current-controlled-type electromagnetic levitation system (CC-EMLS). The modeled equations of CC-EMLS are transfomed in terms of the mismatched uncertainties, and the required control action is obtained with and without constraints on the control input. The quadratic performance function is suggested for the unconstrained control scheme and is solved using the Hamilton–Jacobi–Bellman (HJB) equation. The non-quadratic cost function is designed for the constrained control method, and the HJB equation is utilized to obtain the solution. Both control schemes provide robustness to the system, but deviations in the set point are observed in tracking the position of the ball when the changes in the payload occur in the system. Therefore, integral sliding mode control with robust–optimal (IOSMC) gain is proposed for the CC-EMLS to overcome the steady-state error in the other two schemes. The stability is proven using the direct method of Lyapunov stability. The essential studies based on the simulation are carried out to showcase the performance of the proposed control schemes. The integral performance indicators are compared for all three proposed control schemes to highlight the efficacy, robustness, and efficiency of the designed controllers.

1. Introduction

The recent studies confirm that the EMLS has become one of the most widely accepted techniques in diverse domains. The frictionless operation of EMLS requires less maintenance [1]. The application of magnetic levitation systems (Maglev) is extensively used, for example, in transportation, wind turbines, space crafts, magnetic levitation trains, nuclear engineering, civil engineering, metal slabs, military weapons, and many more [2,3,4,5,6,7,8,9]. In electromagnetic suspension (EMS) schemes, the suspension of an object is recorded due to the force of attraction [10]. The system’s efficiency, responsiveness, and stability are taken into consideration when choosing a controller. The fundamental aim of designing the controllers involves certain important performance metrics such as undershoot, overshoot, rise time, settling time, and peak time.

Over the years, many linear control schemes are designed to cater the required control actions for the EMLS; such controllers are the Linear Quadratic Regulator [11], feedback linearization [12], linear matrix inequality (LMI) control [13,14], and many more. These approaches usually limit the disturbances of the system’s states around a small region of operation. The LQR and linearization techniques require knowledge of disturbance variables and an approximate process variable model for real-time implementation. The LMI approach has fixed controller gain; due to this, it cannot track the trajectories of different varieties. To stabilize the rotor suspension of the magnetic bearing system, the fractional-order proportional–integral–derivative (PID) controller is designed [15,16]. The proportional–integral–derivative regulator helps the rotor to achieve the required set point against the force of gravity. The linear quadratic Gaussian regulator based on the PID controller is used to estimate the position [17,18].

Nevertheless, the linearized model is employed in these controllers, which typically degrades system performance and efficiency. Several nonlinear control systems have been used to overcome the shortcomings of the linear approaches. Such controllers are the neural-network-based regulator [19], sliding mode control [20,21], fuzzy logic control [14,22,23], model predictive control [24,25], robust–optimal control, and many more. The complexity of optimization, time requirements, high-frequency chattering, a large number of rules, and computational burdens are some of the limitations associated with nonlinear controllers [26]. The literature reveals that the majority of research has been carried out with the voltage-controlled electromagnetic levitation system; very few literature studies are available on the CC-EMLS. The article [27] is based on the CC-EMLS, and a nonlinear controller has been designed, but the article lags in addressing the variation in the payload.

The research reviewed above offers distinct benefits for manipulating the electromagnetic levitation system and accommodating perturbations resulting from changes in parameters and external disturbances. Nevertheless, the literature under discussion continues to explicitly address the uncertainties in the parameters throughout the controller design process, and it ignores any input constraints. The fixed-time-constraint control with the neural network for generalized nonlinear systems has been covered by [28,29]. Constrained control for spacecraft has been covered by [30], although the robustness of the controller design has not been extensively explored. The goal of this work is to design the mismatched-uncertainties-based unconstrained and constrained control using a robust–optimal method along with the integral optimal sliding mode control (IOSMC) method for the CC-EMLS. The following section highlights the article’s motivation and structure.

2. Contribution and Article Structure

This article addresses the development of constrained and unconstrained control schemes for mismatched uncertainties. The robust–optimal approach, along with the robust integral sliding mode control technique, is presented. Due to the nonlinear nature and stability concern of the CC-EMLS, the proposed methods will provide the desired tracking of the object position. Moreover, the proposed control strategy directly addresses the constraints and uncertainties in the cost function, making the CC-EMLS more robust and stable to the internal and external uncertainties.

• Due to nonlinear nature of levitation system, initially a robust control scheme based on the optimal control approach with unconstrained mismatched uncertainties is introduced for CC-EMLS, utilizing a quadratic performance function solved via the HJB equation, with stability confirmed using the Lyapunov direct method.
• The designed controller is effective against uncertainties; however, it faces steady-state errors at higher uncertainties levels. Therefore, a constrained-based approach with a non-quadratic cost function is proposed to address this issue, enhancing robustness and stability while requiring less control effort.
• Nevertheless, the problem of steady-state error remains partially unsolved in the constrained-based robust–optimal control outline for CC-EMLS with mismatched uncertainties. To address this drawback, an integral sliding mode control scheme is proposed. Since the traditional sliding mode control provides the tracking at the desired set point and robustness against external disturbances, it is fundamentally susceptible to high-frequency chattering, which can affect system stability.
• To overcome the aforementioned limitations, the designed control technique incorporates an integral sliding mode control with a robust–optimal design scheme, where the integral action eliminates the steady-state error from the start and enhances the disturbance rejection capability. The robust–optimal action guarantees optimal performance under parametric variations. This combined approach results in improved transient response, reduced chattering amplitude, and enhanced steady-state accuracy.
• The stability is verified through the Lyapunov method, and the integral error metrics of all three proposed control schemes are compared to highlight their robustness.

The subsequent sections of the article are organized as follows: Section 3 presents the development of the nonlinear state equation of CC-EMLS. Section 4 focuses on the controller design. Section 5 highlights the simulation results and discussion on the performance of the EMLS. Finally, Section 6 provides a conclusion that summarizes the proposed work and its findings.

3. Model of EMLS

The levitation system has the ability to lift objects. The model of the EMLS is shown in Figure 1. Newton’s law of motion is used to obtain Equation (1). This law involves the force exerted on the object due to gravity and the force produced due to the electromagnetic induction [27].

$$m_b\ddot{x}=m_b{g}_e-F_c=m_b{g}_e-{\displaystyle \frac{G_e{i}_c^2}{{(x+A_c)}^2}}$$

(1)

where $m_b$ is the weight of the object, the force due to the electromagnetic induction is $F_c$, x is the position of the object, $G_e$ is the electromagnetic constant, the actuator constant is denoted by $A_c$, $g_e$ is the gravitational constant, and $i_c$ is the current in the coil. The coil current acts as a control input for the CC-EMLS, which is given as $\widehat{u}=i_c^2$. Therefore, Equation (1) can be modeled as

$$\left[\begin{array}{c}\dot{\widehat{x_a}}\\ \dot{\widehat{x_b}}\end{array}\right]=\left[\begin{array}{c}\widehat{x_b}\\ g_e-{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{\widehat{u}}{{(x_a+A_c)}^2}}\end{array}\right]$$

(2)

where $\widehat{x_a}=x$ is the object position, object velocity is $\widehat{x_b}=\dot{x}$, $x_0$, and $i_{c0}$ is the object position and current operating set-points. The equation that connects the object position and coil current is shown below:

$$i_{c0}=\sqrt{{\displaystyle \frac{m_b{g}_e{(x_0+A_c)}^2}{G_e}}}$$

(3)

The coordinate transformation can be defined as

$$x={\left[\begin{array}{cc}{x}_a& x_b\end{array}\right]}^T={\left[\begin{array}{cc}\widehat{x_a}-x_{a0}& \widehat{x_b}\end{array}\right]}^T,u=\widehat{u}-i_{c0}^2$$

Therefore, Equation (2) can be reframed with the coordinate transformation as

$$\left[\begin{array}{c}\dot{x_a}\\ \dot{x_b}\end{array}\right]=\left[\begin{array}{c}{x}_b\\ g_e-{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{i_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u$$

(4)

4. Statement of the Problem and Controller Design

4.1. Problem Statement

This research addresses the three prominent difficulties related to the CC-EMLS, listed as nonlinearity, open-loop instability, and parametric variations. Section 4.2 deals with designing the unconstrained mismatched/unmatched uncertainty via a robust–optimal approach to address the issues related to the CC-EMLS.

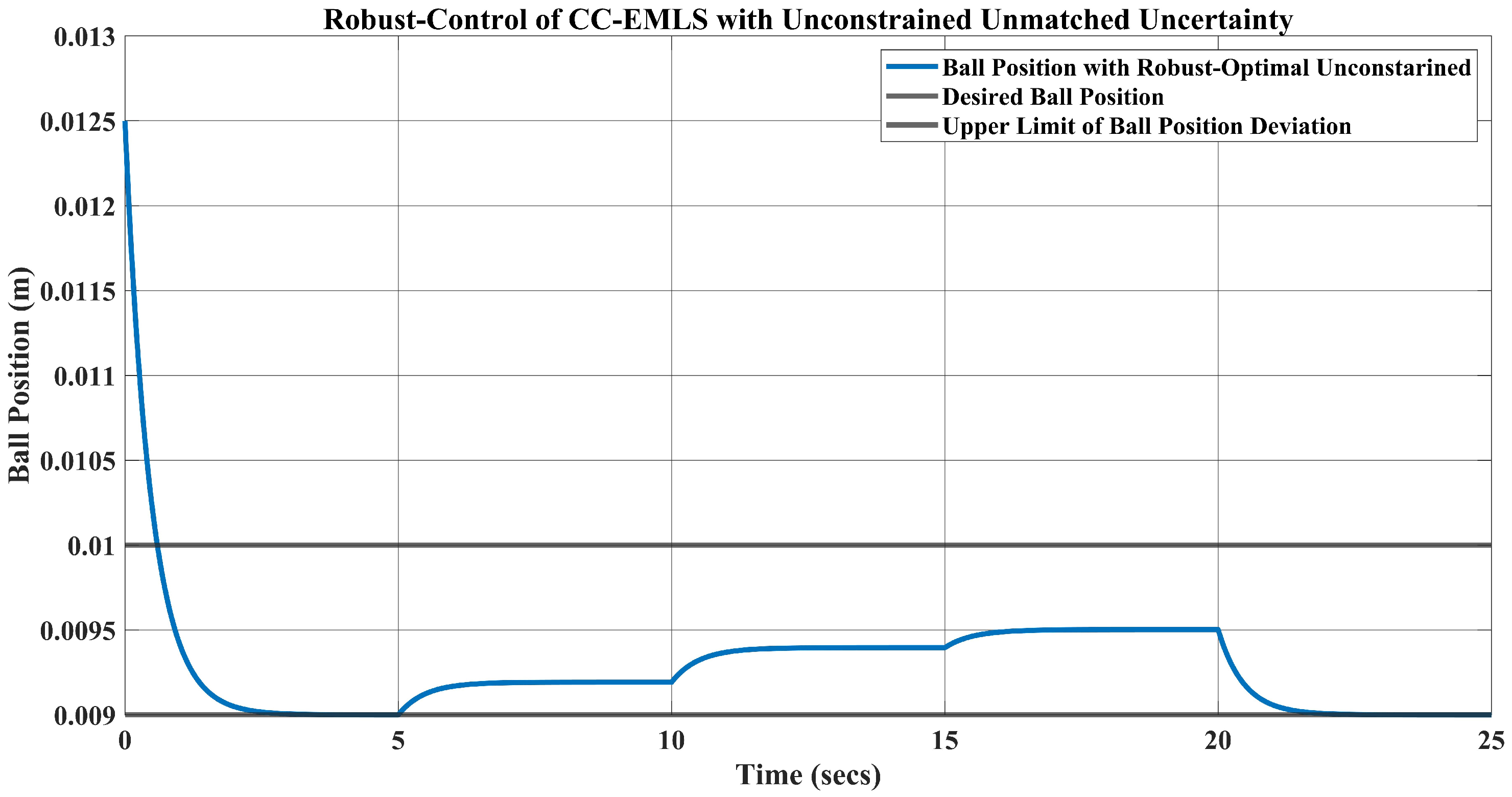
4.2. Unconstrained Mismatched Uncertainties

Consider Equation (5):

$$\dot{x}=\varphi \left(x\right)+\psi \left(x\right)u$$

(5)

where $\varphi \left(x\right)$ and $\psi \left(x\right)$ are nonlinear functions such that $x\in R^n$ is the system state and $u\in R^m$ is the control input. Using Equations (4) and (5), the $\varphi \left(x\right)$ and $\psi \left(x\right)$ can be articulated as shown in (6):

$$\varphi \left(x\right)=\left[\begin{array}{c}{x}_b\\ g_e-{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{i_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right],\psi \left(x\right)=\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]$$

(6)

Therefore, using Equation (6), Equation (5) can be rewritten as

$$\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e-{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{i_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u$$

(7)

Equation (8) shows the generalized representation of mismatched uncertainties:

$$ẋ=\varphi \left(\mathit{x}\right)+\psi \left(\mathit{x}\right)\mathit{u}+\mathit{C}\left(\mathit{x}\right)\Delta \left(\mathit{x}\right)$$

(8)

The weight of the object is assumed to be one of the external disturbances that can affect the system, such as Maglev trains. Therefore, considering the weight of the object as one of the uncertain parameters and reframing in terms of Equation (8), we obtain

$$\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]u+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]{\displaystyle \frac{1}{m_b}}$$

(9)

where $\varphi \left(x\right)=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]$, $\psi \left(x\right)=\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]$, $C\left(x\right)=\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]$, and $\Delta \left(x\right)={\displaystyle \frac{1}{m_b}}$.

4.2.1. Robust Control Challenges with Mismatched Uncertainties of CC-EMLS

The essential feedback control $u=k\left(x\right)$ has to be obtained for the open-loop CC-EMLS with the mismatched uncertainties shown in Equation (9). The objective of designing the feedback control is to make the system globally asymptotically stable under the influence of uncertainties, with the following assumptions:

Assumption 1.

A positive function ${\Delta }_{max}\left(x\right)$ is assumed such that the weight of the object remains restricted.

$$∥\psi {\left(x\right)}^{+}C\left(x\right)\Delta \left(x\right)∥\le {\Delta }_{max}\left(x\right)$$

where $\psi {\left(x\right)}^{+}$ is a pseudo-inverse of $\psi \left(x\right)$. This is used to separate the uncertainties according to matched and mismatched uncertainties.

$$C\left(x\right)\Delta \left(x\right)=\psi \left(x\right)\psi {\left(x\right)}^{+}C\left(x\right)\Delta \left(x\right)+(I-\psi \left(x\right)\psi {\left(x\right)}^{+})C\left(x\right)\Delta \left(x\right)$$

(10)

where $\psi {\left(x\right)}^{+}$ can be calculated $\psi {\left(x\right)}^{+}={\left(\psi {\left(x\right)}^T\psi \left(x\right)\right)}^{-1}\psi {\left(x\right)}^T$.

Therefore, $\psi {\left(x\right)}^{+}$ can be obtained as highlighted.

$${\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]}^{+}={\left[{\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]}^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]\right]}^{-1}{\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]}^T$$

(11)

On simplification, the above expression can be written as

$${\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+d_A)}^c}}\end{array}\right]}^{+}=\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]$$

(12)

The maximum restriction on the uncertainty ${\Delta }_{max}\left(x\right)$ can be calculated by using the equation of $\psi {\left(x\right)}^{+}$:

$$∥\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]{\displaystyle \frac{1}{m_b}}∥\le {\Delta }_{max}\left(x\right)$$

(13)

Equation (13) can be further simplified as

$$∥{\displaystyle \frac{1}{m_b}}∥\le {\Delta }_{max}\left(x\right)$$

(14)

Assumption 2.

A function $b_{max}\left(x\right)>0$ exists, which holds relation

$$∥\Delta \left(x\right)∥\le b_{nmax}\left(x\right)$$

Hence,

$$∥{\displaystyle \frac{1}{m_b}}∥\le b_{nmax}\left(x\right)$$

(15)

The above-discussed robust issue can be translated into an optimal control issue and can be solved using the same method.

4.2.2. Optimal-Control Challenges with Mismatched Uncertainties of CC-EMLS

We define an auxiliary equation with a mismatched uncertainty element of Equation (10) for the CC-EMLS as

$$\dot{x}=\varphi \left(x\right)+\psi \left(x\right)u+(I-\psi \left(x\right)\psi {\left(x\right)}^{+})C\left(x\right)v$$

(16)

where u and v are control inputs. Transforming the CC-EMLS equation aligned with the Equation (16), the subsequent equation is attained:

$$\begin{array}{c}\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[0,-{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\right]\right)\hfill \\ \hfill \left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v\end{array}$$

(17)

The feedback controller $(u,v)$ has to be calculated for Equation (17), such that it reduces the resulting performance function:

$${\int }_0^{\infty }({\Delta }_{max}{\left(x\right)}^2+{\rho }^2{b}_{max}{\left(x\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2)dt$$

(18)

where $\rho$ and $\gamma$ are greater than zero. With mismatched uncertainties, it is hard to propose a controller. The optimal control designed in this section has two control components $u\in R^m$ and $v\in R^q$. An extended control v is presented to provision the control action u, such that the extended control v will handle the part of the mismatched uncertainties as highlighted in Equation (10). However, for the actual CC-EML system shown in Equation (9), only the control u will be used. The cost function shown in Equation (19) can be articulated inline of the equation of the CC-EMLS, as highlighted below.

$${\int }_0^{\infty }\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2\right)dt$$

(19)

To prove the closed-loop asymptotic stability of a CC-EMLS with mismatched uncertainties, the extended control v has a significant impact, which is discussed in Theorem 1.

Theorem 1.

If the solution to the optimal control challenge highlighted above, denoted by u and $v,$ is calculated, with the condition described in Equation (20) being satisfied for some constant ${\gamma }^{\prime }$ such that $\left|{\gamma }^{\prime }\right|<\left|\gamma \right|$, then u constitutes the solution to the optimal control problem, simultaneously serving as the solution to the robust control problem for the CC-EMLS with unconstrained mismatched uncertainties.

$$2{\rho }^2{∥v∥}^2\le {\gamma }^{\prime 2}{∥x∥}^2\forall x\in R^n$$

(20)

Proof. 

Consider the feedback regulator $(u,v)$ as the solution to the optimal control problem highlighted in relation to the CC-EMLS. It has to be established that Equation (21) is globally asymptotically stable under all the uncertainties ${\Delta }_{max}\left(x\right)$.

$$\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]{\displaystyle \frac{1}{m_b}}$$

(21)

To prove the above statement, assume $V\left(x_0\right)$ to be the minimum performance of the optimal control defined in Equation (17) from initial condition $x_0$.

$$\begin{array}{c}\hfill V\left(x_0\right)=mi{n}_{u,v}{\int }_0^{\infty }\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2\right)dt\end{array}$$

(22)

Since $V\left(x\right)$ is a performance function, it must satisfy the HJB equation as shown below:

$$\begin{array}{c}\hfill mi{n}_{u,v}\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2\right)+mi{n}_{u,v}\left(V_x^T\right(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]\\ +\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\\ \hfill \left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v\left)\right)\end{array}$$

(23)

Furthermore, to establish a minimum for Equation (23), the outcome should also be zero. By satisfying these two conditions, Equation (23) can be further refined as

$$\begin{array}{c}{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2+V_x^T(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u\hfill \\ \hfill +\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v)=0\end{array}$$

(24)

Calculating the derivative of Equation (24) in relation u,

$$2u^T+V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=0$$

(25)

Therefore, Equation (25) can be written as

$$V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=-2u^T$$

(26)

Similarly, calculating the derivative of Equation (24) in relation to v,

$$\begin{array}{c}\hfill 2{\rho }^2{v}^T+V_x^T\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right])=0\end{array}$$

(27)

Therefore, Equation (27) can be written as

$$\begin{array}{c}\hfill 2{\rho }^2{v}^T=-V_x^T\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right])\end{array}$$

(28)

By utilizing the above-mentioned equation, it can be shown that $V\left(x\right)$ serves as a Lyapunov function for Equation (9) as $V\left(x\right)>0\forall x\ne 0$. Furthermore, it will be established that the time derivative of the Lyapunov function $\dot{V}\left(x\right)$ is less than zero $\forall x\ne 0$.

Consider the expression shown in (29):

$$\dot{V}\left(x\right)=V_x^T\dot{x}$$

(29)

Subsituting the value of $\dot{x}$ from Equation (9) in Equation (29),

$$\begin{array}{c}\hfill \dot{V}\left(x\right)=V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]{\displaystyle \frac{1}{m_b}}\right)\end{array}$$

(30)

For an easy understanding of the equations, the following assumptions are made: ${\theta }_1=\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]$, ${\theta }_2=\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]$ and ${\theta }_3=\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]$

By the addition and subtraction of term $V_x^T\left(I-{\theta }_1{\theta }_2\right)C_{1}v$ in Equation (30), Equation (30) can be reframed as;

$$\begin{array}{c}\hfill \dot{V}\left(x\right)=V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+{\theta }_{1}u+\left(I-{\theta }_1{\theta }_2\right)C_{1}v\right)-V_x^T\left(I-{\theta }_1{\theta }_2\right)C_{1}v+V_x^T{C}_1{\displaystyle \frac{1}{m_b}}\end{array}$$

(31)

By adding and subtracting the term $V_x^T{\theta }_1{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}$ in Equation (31), Equation (31) can be rewritten as;

$$\begin{array}{c}\dot{V}\left(x\right)=V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+{\theta }_{1}u+\left(I-{\theta }_1{\theta }_2\right)C_{1}v\right)-V_x^T\left(I-{\theta }_1{\theta }_2\right)C_{1}v+V_x^T{\theta }_1{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}\hfill \\ \hfill +V_x^T\left(I-{\theta }_1{\theta }_2\right)C_1{\displaystyle \frac{1}{m_b}}\end{array}$$

(32)

Rewriting Equation (24) in terms of ${\theta }_1$, ${\theta }_2$, and $C_1$, it can be reframed as

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥u∥}^2+V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+{\theta }_{1}u+\left(I-{\theta }_1{\theta }_2\right)C_{1}v\right)=0\end{array}$$

(33)

Equation (33) can be reframed as

$$\begin{array}{c}\hfill V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+{\theta }_{1}u+\left(I-{\theta }_1{\theta }_2\right)C_{1}v\right)=-{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\gamma }^2{∥x∥}^2-{\rho }^2{∥v∥}^2-{∥u∥}^2\end{array}$$

(34)

Subsituting the value of $V_x^T\left(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+{\theta }_{1}u+\left(I-{\theta }_1{\theta }_2\right)C_{1}v\right)$ from Equation (34) in Equation (32),

$$\begin{array}{c}\dot{V}\left(x\right)=-{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\gamma }^2{∥x∥}^2-{\rho }^2{∥v∥}^2-{∥u∥}^2-V_x^T\left(I-{\theta }_1{\theta }_2\right)C_{1}v\hfill \\ \hfill +V_x^T{\theta }_1{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}+V_x^T\left(I-{\theta }_1{\theta }_2\right)C_1{\displaystyle \frac{1}{m_b}}\end{array}$$

(35)

Equations (26) and (27) can be rewritten as $V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=-2u^T$ or $V_x^T{\theta }_1=-2u^T$ and

$$\begin{array}{c}\hfill 2{\rho }^2{v}^T=-V_x^T\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right])\end{array}$$

or $2{\rho }^2{v}^T=-V_x^T(I-{\theta }_1{\theta }_2)C_1$.

Using the above findings in Equation (35),

$$\begin{array}{c}\hfill \dot{V}\left(x\right)=-{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\gamma }^2{∥x∥}^2-{\rho }^2{∥v∥}^2-{∥u∥}^2+2{\rho }^2{v}^{T}v-2u^T{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}-2{\rho }^2{v}^T{\displaystyle \frac{1}{m_b}}\end{array}$$

(36)

Therefore, reducing the above equation,

$$\begin{array}{c}\hfill \dot{V}\left(x\right)=-{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2-{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2-{∥u∥}^2-2u^T{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}-2{\rho }^2{v}^T{\displaystyle \frac{1}{m_b}}\end{array}$$

(37)

However,

$$-{∥u∥}^2-2u^T{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}\le {∥{\theta }_2{C}_1{\displaystyle \frac{1}{m_b}}∥}^2\le {\left({\displaystyle \frac{1}{m_b}}\right)}^2$$

and

$$-2{\rho }^2{v}^T{\displaystyle \frac{1}{m_b}}\le {\rho }^2{∥v∥}^2+{\rho }^2{∥{\displaystyle \frac{1}{m_b}}∥}^2\le {\rho }^2{∥v∥}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2$$

Therefore, the condition stated in Theorem (1) $2{\rho }^2{∥v∥}^2\le {\gamma }^{\prime 2}{∥x∥}^2\forall x\in R^n$ is satisfied then

$$\dot{V}\left(x\right)\le -{\gamma }^2{∥x∥}^2+2{\rho }^2{∥v∥}^2$$

$$=2{\rho }^2{∥v∥}^2-{\gamma }^{\prime 2}{∥x∥}^2-({\gamma }^2-{\gamma }^{\prime 2}){∥x∥}^2$$

$$\le -({\gamma }^2-{\gamma }^{\prime 2}){∥x∥}^2$$

The aforementioned equation highlights that the time derivative of the Lyapunov function $\dot{V}\left(x\right)$ is less than or equal to zero $\forall x\ne 0$. Therefore, the proposed control scheme, which applies an unconstrained-mismatched-uncertainties-based robust–optimal approach to the current-controlled electromagnetic levitation system, shows the stability in the sense of Lyapunov. The next section will discuss the design of a constrained mismatched uncertainties control design for the CC-EMLS via a robust–optimal approach. □

4.3. Constrained Mismatched Uncertainties

The robust control problem and assumptions remains the same as discussed in Section 4.2.1. Here also the same robust control issue will be translated into the optimal control problem and will be solved using the optimal control method. The next part of this section will directly deal with the design of the optimal control for constrained unmatched uncertainty for CC-EMLS.

Optimal Control Challenges with Mismatched Uncertainties of CC-EMLS

Defining an auxiliary equation with a mismatched uncertainty element of Equation (10) for the CC-EMLS,

$$\dot{x}=\varphi \left(x\right)+\psi \left(x\right)u+(I-\psi \left(x\right)\psi {\left(x\right)}^{+})C\left(x\right)v$$

(38)

where u and v are control inputs. Translating the equation of the CC-EMLS inline of Equation (38), the below mentioned equation is obtained.

$$\begin{array}{c}\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\hfill \\ \hfill \left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v\end{array}$$

(39)

The feedback control action $(u,v)$ needs to be calculated for Equation (39), such that it reduces the subsequent performance function:

$$J={\int }_0^{\infty }({\Delta }_{max}{\left(x\right)}^2+{\rho }^2{b}_{max}{\left(x\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+H\left(u\right))dt$$

(40)

Here in this part of the controller design, the control input $u\in R^m$, which is shown in Equation (5), is restricted by a constant $\alpha$, which is greater than zero, such that $\left|u_i\right|\le \alpha$, where $\alpha \in R$; $i=1,2,\dots \dots m$.

Where

$$H\left(u\right)=2{\int }_0^u\alpha {tanh}^{-1}(v/\alpha )Rdv$$

(41)

$$H\left(u\right)=2\alpha uR{tanh}^{-1}(u/\alpha )+{\alpha }^{2}Rln\left(1-{\displaystyle \frac{u^2}{{\alpha }^2}}\right)$$

(42)

where the term $H\left(u\right)$ is the non-quadratic component that accounts for the performance associated with the constrained input. Positive-definite matrices Q and R indicate the relative weights assigned to the system states and control inputs, respectively. The cost function, as expressed in Equation (40), can be formulated in relation to the equation of the CC-EMLS, as detailed below.

$$J={\int }_0^{\infty }\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+H\left(u\right)\right)dt$$

(43)

To prove the closed-loop asymptotic stability of a CC-EMLS with constrained mismatched uncertainties, the extended control v has a significant impact, which is discussed in Theorem 2.

Theorem 2.

Consider Equation (9), which highlights the nominal CC-EMLS characterized by the performance function shown in Equation (43). Let us assume that a function $V(x,t)$ constitutes the solution to the Hamilton–Jacobi–Bellman (HJB) Equation (45), following the proper selection of $rho$ and $gamma$. If the mentioned condition is met, the global asymptotic closed-loop stability of CC-EMLS can be guaranteed with mismatched uncertainties by the bounded control law (55) provided with some constant ${\gamma }^{*}$, such that $\left|{\gamma }^{*}\right|$<$\left|\gamma \right|$, if the condition in Equation (44) is satisfied.

$$2{\rho }^2{\left|\right|v\left|\right|}^2\le {\gamma }^{*2}{\left|\right|x\left|\right|}^2\forall x\in R^n$$

(44)

Proof. 

Consider the feedback regulator $(u,v)$ as the solution to the optimal control problem highlighted in relation to the CC-EMLS. It has to be established that Equation (21) is globally asymptotically stable under all the uncertainties ${\Delta }_{max}\left(x\right)$.

$$\dot{x}=\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_{c0}^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]{\displaystyle \frac{1}{m_b}}$$

(45)

To prove the above statement, assume $V\left(x_0\right)$ to be the minimum performance of the optimal control defined in Equation (17) from initial condition $x_0$.

$$\begin{array}{c}\hfill V(x,t)=mi{n}_{u,v}{\int }_0^{\infty }\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥H\left(u\right)∥}^2\right)dt\end{array}$$

(46)

Since $V(x,t)$ is minimum cost function, it must satisfy the HJB equation as shown below:

$$\begin{array}{c}mi{n}_{u,v}\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+N\left(u\right)\right)+mi{n}_{u,v}\left(V_x^T\right(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]\hfill \\ +\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_a)}^2}{G_e}}\end{array}\right]\right)\\ \hfill \left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v\left)\right)\end{array}$$

(47)

The u can be computed by solving the following HJB equation:

$$\begin{array}{c}HJB\left(V(x,t)\right)=mi{n}_{u,v}\left({\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\rho }^2{\left({\displaystyle \frac{1}{m_b}}\right)}^2+{\gamma }^2{∥x∥}^2+{\rho }^2{∥v∥}^2+{∥H\left(u\right)∥}^2\right)+\hfill \\ mi{n}_{u,v}\left(V_x^T\right(\left[\begin{array}{c}{x}_b\\ g_e\end{array}\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]u+(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\\ \hfill \left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+d_a)}^2}{G_e}}\end{array}\right]\left)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]v\right))\end{array}$$

(48)

The HJB equation is computed as ${\displaystyle \frac{\partial HJB\left(V\right(x,t\left)\right)}{\partial u}}$$=0$ and ${\displaystyle \frac{\partial HJB\left(V\right(x,t\left)\right)}{\partial v}}$$=0$.

$${\displaystyle \frac{\partial H\left(u\right)}{\partial u}}+V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=0$$

(49)

With the help of Equation (42), Equation (49) can be reframed as

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial u}}\left[2\alpha uR{tanh}^{-1}\left({\displaystyle \frac{u}{\alpha }}\right)+{\alpha }^{2}Rln\left(1-{\displaystyle \frac{u^2}{{\alpha }^2}}\right)\right]+V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=0\end{array}$$

(50)

$$\begin{array}{c}\hfill 2\alpha R{tanh}^{-1}\left({\displaystyle \frac{u}{\alpha }}\right)+{\displaystyle \frac{2\alpha uR}{\alpha \left(1-\frac{u^2}{{\alpha }^2}\right)}}-{\displaystyle \frac{2{\alpha }^{2}uR}{{\alpha }^2\left(1-\frac{u^2}{{\alpha }^2}\right)}}+V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=0\end{array}$$

(51)

$$2\alpha R{tanh}^{-1}\left({\displaystyle \frac{u}{\alpha }}\right)+V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=0$$

(52)

but $V_x^T\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]=-2u\left(x\right)$

$$2\alpha R{tanh}^{-1}\left({\displaystyle \frac{u}{\alpha }}\right)=2u\left(x\right)$$

(53)

$$2\alpha R{tanh}^{-1}\left({\displaystyle \frac{u}{\alpha }}\right)=2k\left(x\right)$$

(54)

Therefore, on rearranging the above equation,

$$u=\alpha tanh\left({\displaystyle \frac{k\left(x\right)}{R\alpha }}\right)$$

(55)

The augmented control v can be obtained as

$$\begin{array}{c}\hfill v=-{\displaystyle \frac{1}{2{\rho }^2}}{V}_x^T\left(I-\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e}{m_b}}{\displaystyle \frac{1}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\left[\begin{array}{cc}0& -{\displaystyle \frac{m_b{(x_a+x_{a0}+A_c)}^2}{G_e}}\end{array}\right]\right)\left[\begin{array}{c}0\\ -{\displaystyle \frac{G_e{i}_0^2}{{(x_a+x_{a0}+A_c)}^2}}\end{array}\right]\end{array}$$

(56)

It is clear that $V(x,t)>0$$\forall x\ne 0$ and $t\ne 0$. The time derivative of V(x,t) is negative, definitively, and can be proved using the similar analysis as proposed in Section 4.2.2. The next section deals with designing the integral optimal sliding mode control. □

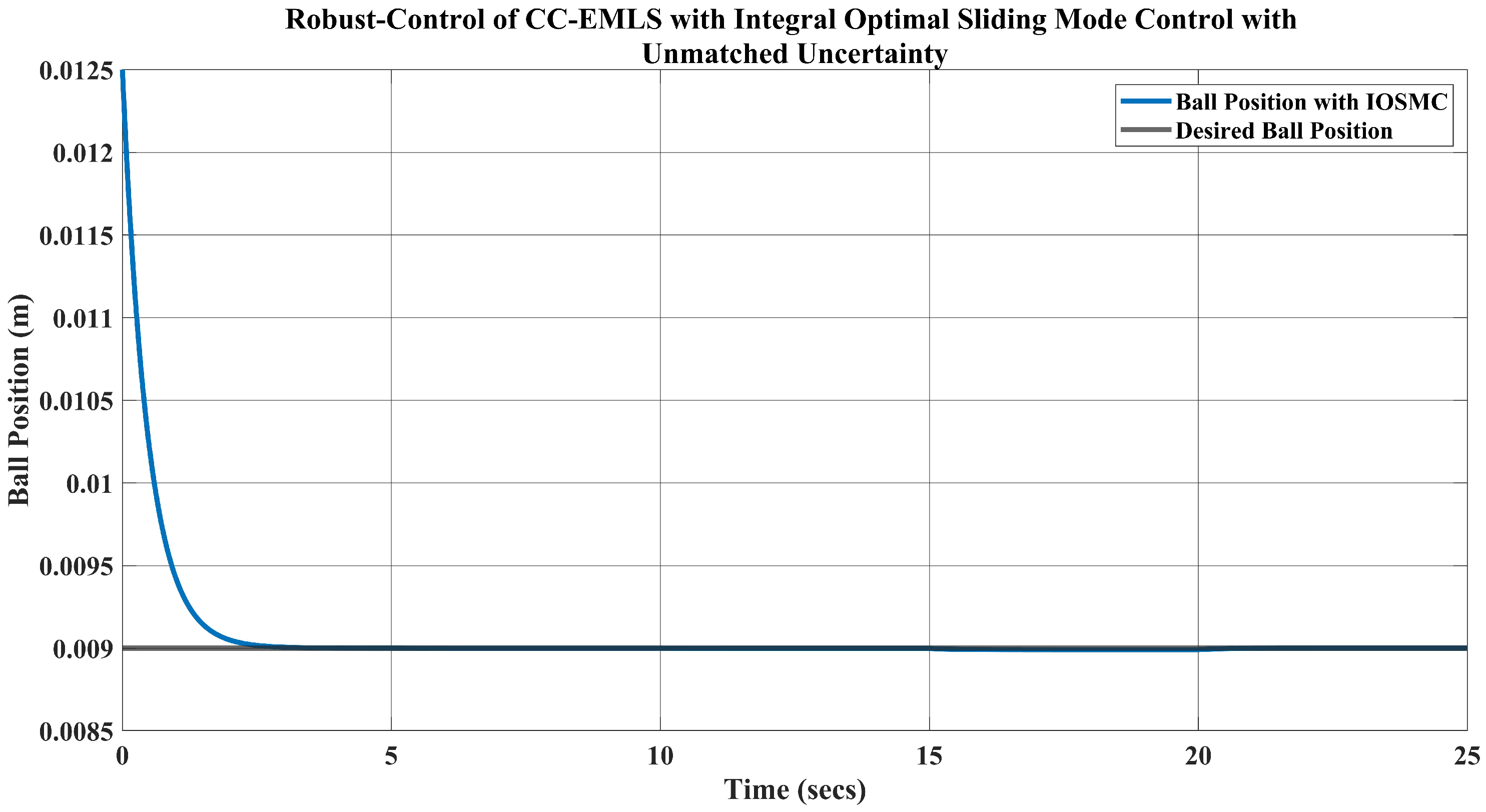
4.4. Integral Sliding Mode Control with Robust–Optimal Method

SMC is an effective method for dealing with the sudden and significant changes that occur in the system. However, high-frequency chattering is the major challenge that happens in the sliding mode control. Therefore, the integral sliding mode control with the robust–optimal approach is proposed to overcome the above-mentioned disadvantage. Consider the system shown in Equation (57)

$$\dot{x}=Ax+Bu$$

(57)

where $x\in {\mathbb{R}}^{n\times 1}$ is the state vector, A is the system matrix $A\in {\mathbb{R}}^{n\times n}$, B is the input matrix $B\in {\mathbb{R}}^{n\times m}$, and u represents the input vector $u\in {\mathbb{R}}^{m\times 1}$. The main objective lies in designing the switching surface for the SMC for which it is assumed that the system matrix A and control matrix B are controllable and in standard form. Equation (58) represents the system in the normal form.

$$\begin{array}{c}\hfill \left[\begin{array}{c}\dot{\overline{x}}\end{array}\right]=\left[\begin{array}{cc}{A}_{aa}& A_{ab}\\ A_{ba}& A_{bb}\end{array}\right]\left[\begin{array}{c}\overline{x}\end{array}\right]+\left[\begin{array}{c}0\\ B_u\end{array}\right]u\end{array}$$

(58)

where $A_{aa}\in {\mathbb{R}}^{(n-m)\times (n-m)}$, $A_{ab}\in {\mathbb{R}}^{(n-m)\times m}$, $A_{ba}\in {\mathbb{R}}^{n\times (n-m)}$, $A_{bb}\in {\mathbb{R}}^{m\times m}$, and $B_2\in {\mathbb{R}}^{m\times m}$. Equation (59) highlights the assumed switching surface $S{S}_u$:

$$S{S}_u=N\overline{x}=0$$

(59)

where $N=\left[N_{1}I\right]$ and $N_1\in {\mathbb{R}}^{m\times (n-m)}$. Hence, Equation (60) showcases the sliding phase:

$$\begin{array}{c}\hfill S_u=\left[\begin{array}{cc}{N}_1& I\end{array}\right]\left[\begin{array}{c}\overline{x_1}\\ \overline{x_2}\end{array}\right]=0\end{array}$$

(60)

where $\overline{x_1}\in {\mathbb{R}}^{(n-m)\times 1}$, and $\overline{x_2}\in {\mathbb{R}}^{m\times 1}$.

Using Equation (60), $\overline{x_2}=-N_1\overline{x_1}$. Furthermore, utilizing Equation (58) and the equation of $\overline{x_2}$, $\dot{\overline{x_1}}$ is given by Equation (61)

$$\dot{\overline{x_1}}=\left(A_{aa}-A_{ba}{N}_1\right)\overline{x_1}$$

(61)

The value of $N_1$ is so chosen such that $\dot{\overline{x_1}}$ is Hurwitz.

Assuming that $x_{1d}$, $x_{2d}$, and $x_{3d}$ are the desired values of the steel ball position, the velocity of the ball, and the coil current. The equations of the errors in the terms of the desired value of position of the ball, the velocity of the ball, and the coil current are given by Equations (62), and (63)

$$e_p=x_a-x_{ad}$$

(62)

$$e_v=x_b-x_{bd}$$

(63)

where $e_p$ is the position error of the ball, and $e_v$ is the velocity error of the ball. The fundamental concept of introducing the integral action in the sliding mode control is to initiate the sliding phase from the start of the system response. It also means that the ISMC can handle the matched uncertainties by catering for the required control action for the entire system. Assuming the nominal system model is available, the integral sliding mode control enables the design of the feedback controller for the system, which is asymptotically stable. The discontinuous control action is also desired in the integral sliding mode control to handle the external disturbances. Equation (64) describes the general form of a nonlinear system with uncertainties and disturbances.

$$\dot{x}=f\left(x\right)+g\left(x\right)u+\omega \left(x\right)$$

(64)

where the function $f\left(x\right)=A\left(x\right)+M\left(x\right)$, $\omega \left(x\right)$ is the change due to external disturbances and uncertainties, and $M\left(x\right)$ consists of the nonlinear part of the system model.

Assumption 3.

Assumption 1 states that the number of inputs is equal to the rank of the input matrix $\left(g\right)$.

This assumption ensures that the input is linearly independent, providing unique and non-redundant information.

Assumption 4.

Assumption 2 states that the unknown disturbance $\omega \left(x\right)$ is restricted by some known function.

This assumption simplifies the analysis and ensures that the system can be controlled and optimized within predictable bounds.

Therefore, the total control effort in the integral sliding mode control can be written as

$$u_{ism}=u_0+u_{idc}$$

(65)

To ensure the optimality of EMLS, the control effort $u_0$ is important; the control effort $u_0$ is a nominal controller, which is discussed in the next section of the article. Moreover, $u_{idc}$ serves as a second control effort for the integral sliding mode control, which is known as the discontinuous control input. The discontinuous control mechanism is responsible for handling the system disturbances. This control effort helps the ISMC to achieve its set point efficiently. Equation (66) represents the integral sliding surface.

$$s_{ism}=N\left[x\left(t\right)-x\left(0\right)-{\int }_0^{t}Ax\left(\tau \right)+g{u}_0(x,\tau )d\tau \right]$$

(66)

where N is selected such that the product of matrix $Ng$ must be invertible, and the term $-Nx\left(0\right)$ should ensure that the sliding surface is equal to zero, such that it will eliminate the reaching phase. Therefore, the discontinuous control effort is highlighted by Equation (67):

$$u_{idc}=-\lambda {\displaystyle \frac{{\left(Ng\right)}^T{s}_{ism}}{\parallel {\left(Ng\right)}^T{s}_{ism}\parallel }}$$

(67)

where $\lambda$ is a gain that guarantees the sliding phase motion. The uncertainty $\omega$, which is Equation (64), is separated into two parts, i.e., matched and mismatched uncertainties, given by Equation (68);

$$\omega ={\omega }_m+{\omega }_{mm}$$

(68)

where ${\omega }_m$ is the matched component of uncertainties, and ${\omega }_{mm}$ is the mismatched component of uncertainties.

The matched component ${\omega }_m=g{g}^{+}\omega$, and the mismatched component ${\omega }_{mm}=g^{-}{g}^{-+}\omega$, where $g^{+}$ is called the pseudo-inverse, which is used to decompose the uncertainties into the matched and mismatched components, which are given as $g^{+}={\left(g^{T}g\right)}^{-1}{g}^T$, and $g^{-}$ spans the null space of $g^{+}$. Taking the derivative of Equation (66), we have;

$${\dot{s}}_{ism}=N\left[\left(f+g(u_0+u_{idc})+g{g}^{+}\omega +g^{-}{g}^{-+}\omega \right)-(f+g{u}_0)\right]$$

(69)

Therefore, Equation (69) can be reframed as given in Equation (70):

$${\dot{s}}_{ism}=Ng(u_{idc}+g^{+}\omega )+N{\omega }_{mm}$$

(70)

To prove the stability of the designed controller, consider the Lyapunov function:

$$V={\displaystyle \frac{1}{2}}{s}_{ism}^2$$

(71)

Equation (72) highlights the time derivate of the Lyapunov function:

$$\dot{V}=s_{ism}^T\left(Ng\left[-\lambda {\displaystyle \frac{{\left(Ng\right)}^T{s}_{ism}}{\parallel {\left(Ng\right)}^T{s}_{ism}\parallel }}+g^{+}\omega \right]+N{\omega }_{mm}\right)$$

(72)

$$\dot{V}\le -\parallel {\left(Mg\right)}^T{s}_{ism}\parallel (\lambda -\parallel g^{+}\varphi -{\left(Mg\right)}^{-1}M{\varphi }_{mm}\parallel )$$

(73)

Therefore, Equations (72) and (73) show that the system shown in Equation (64) is stable in the sense of Lyapunov. The next section of the article gives a detailed discussion on the simulation results and its findings.

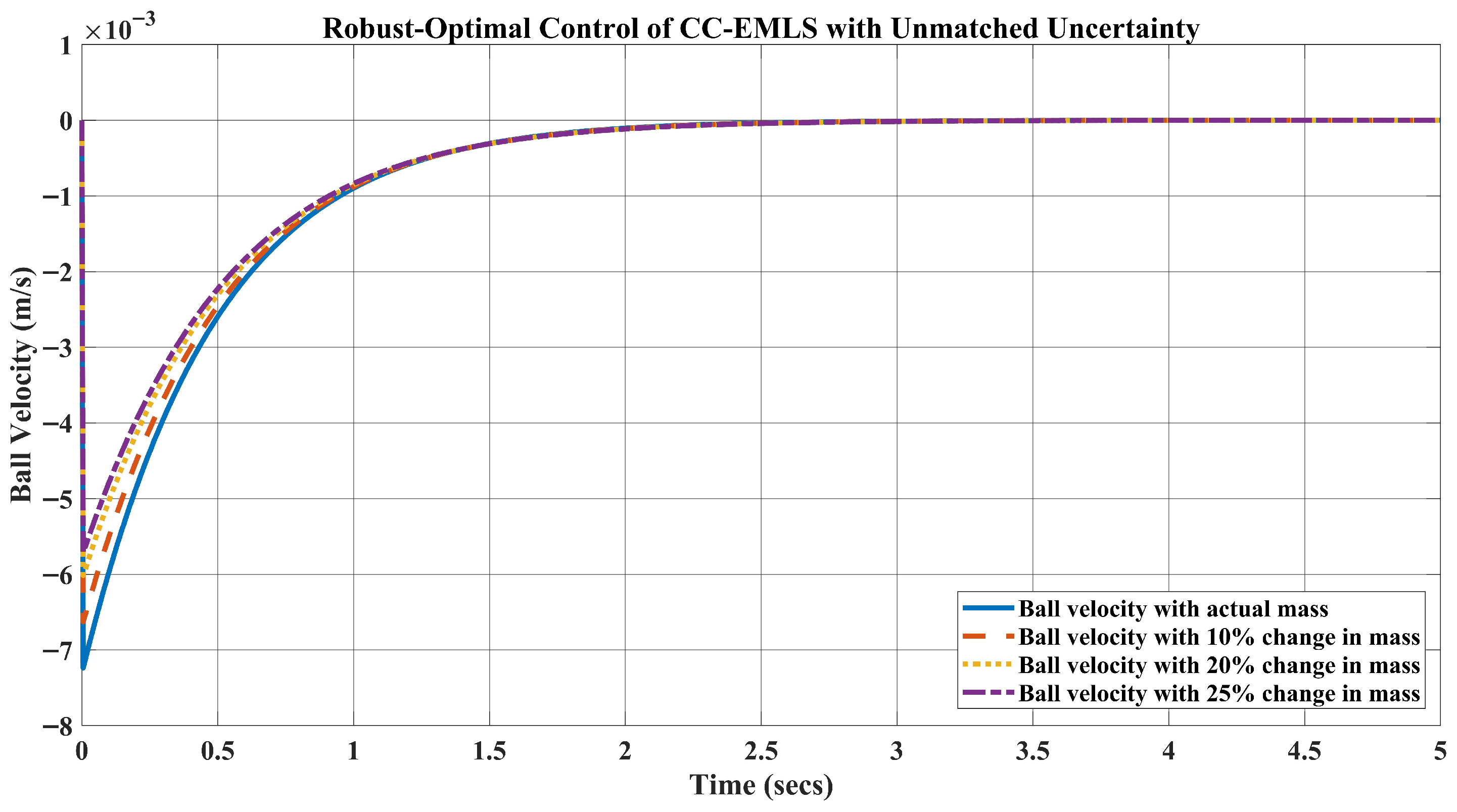
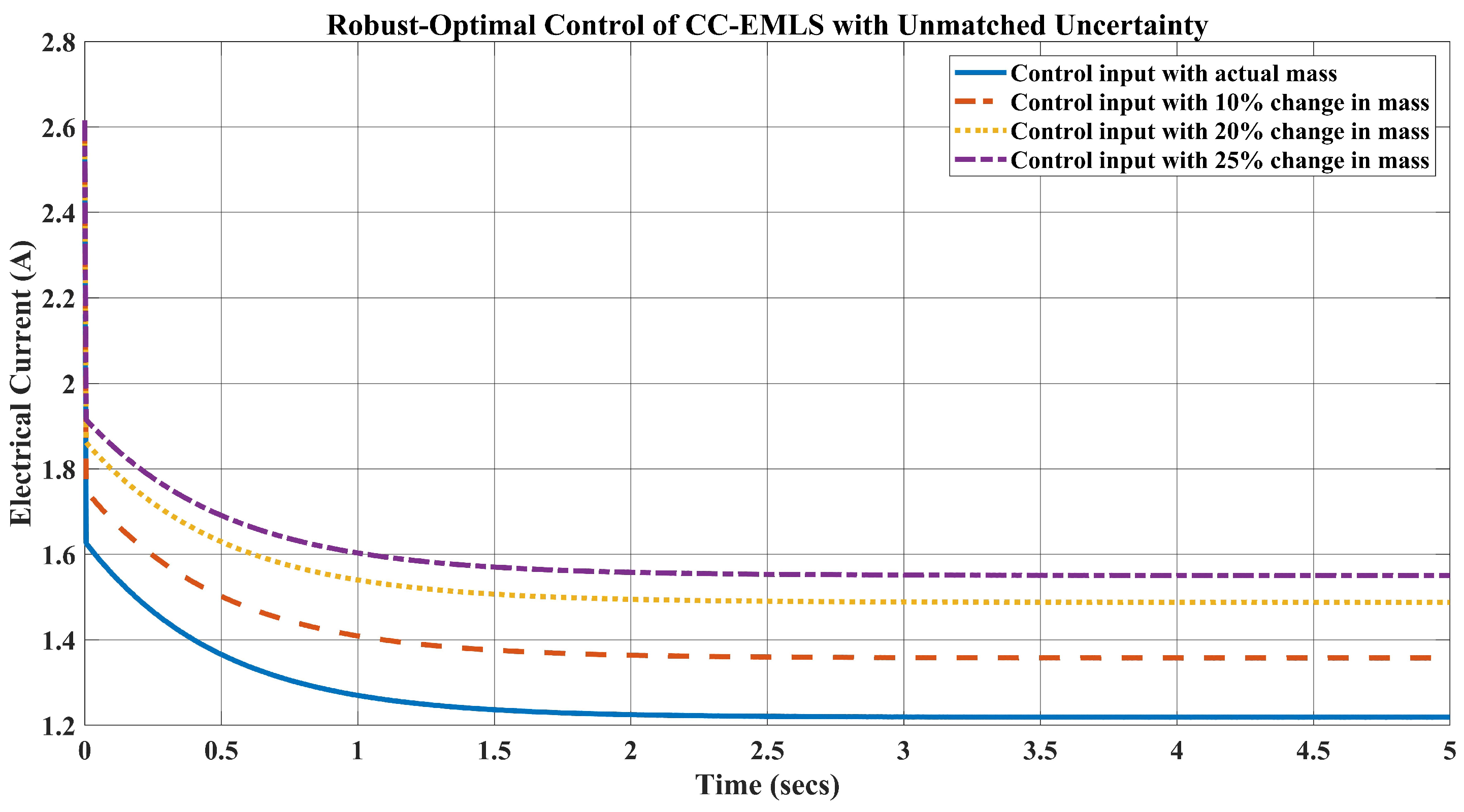
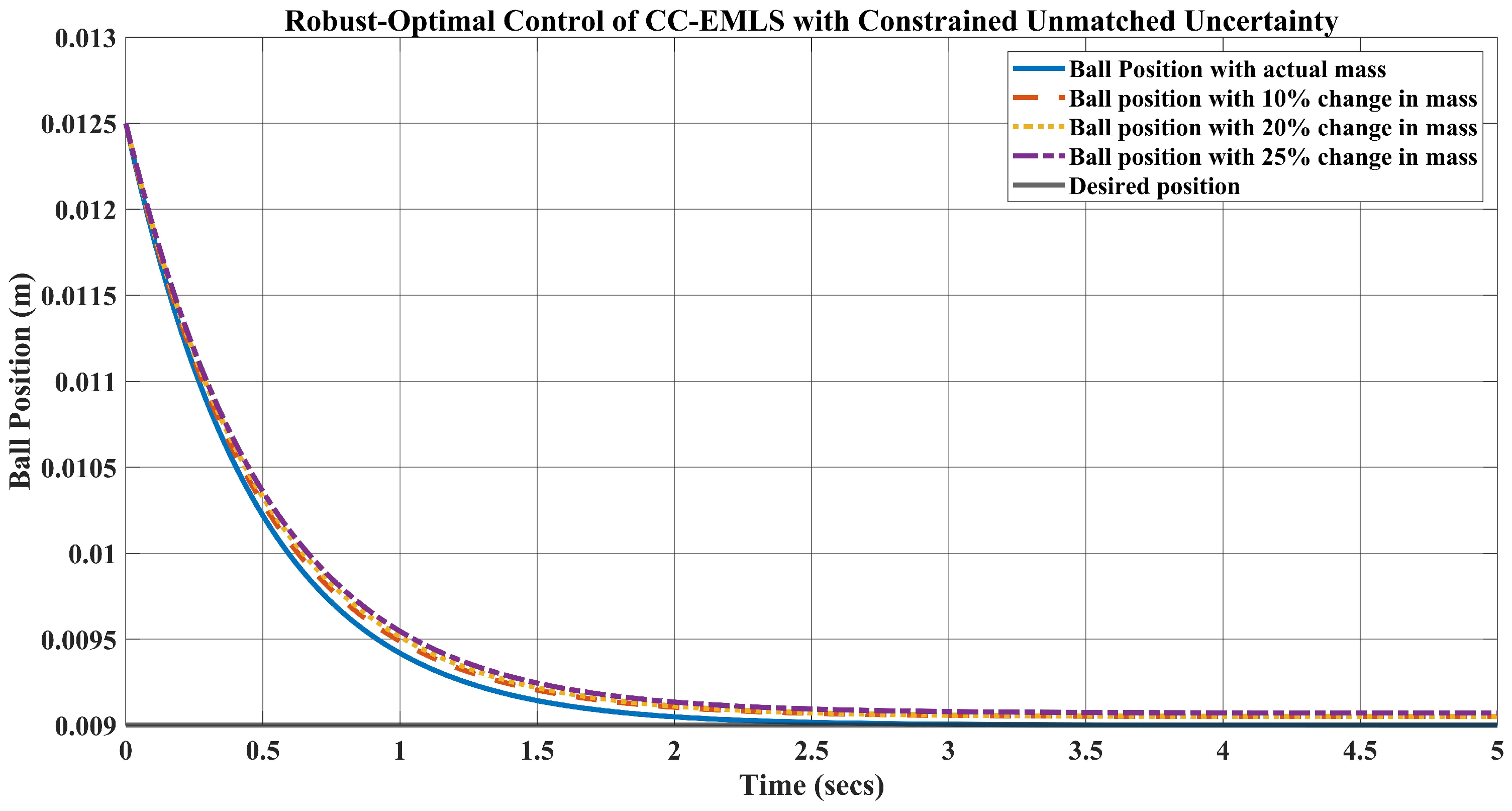
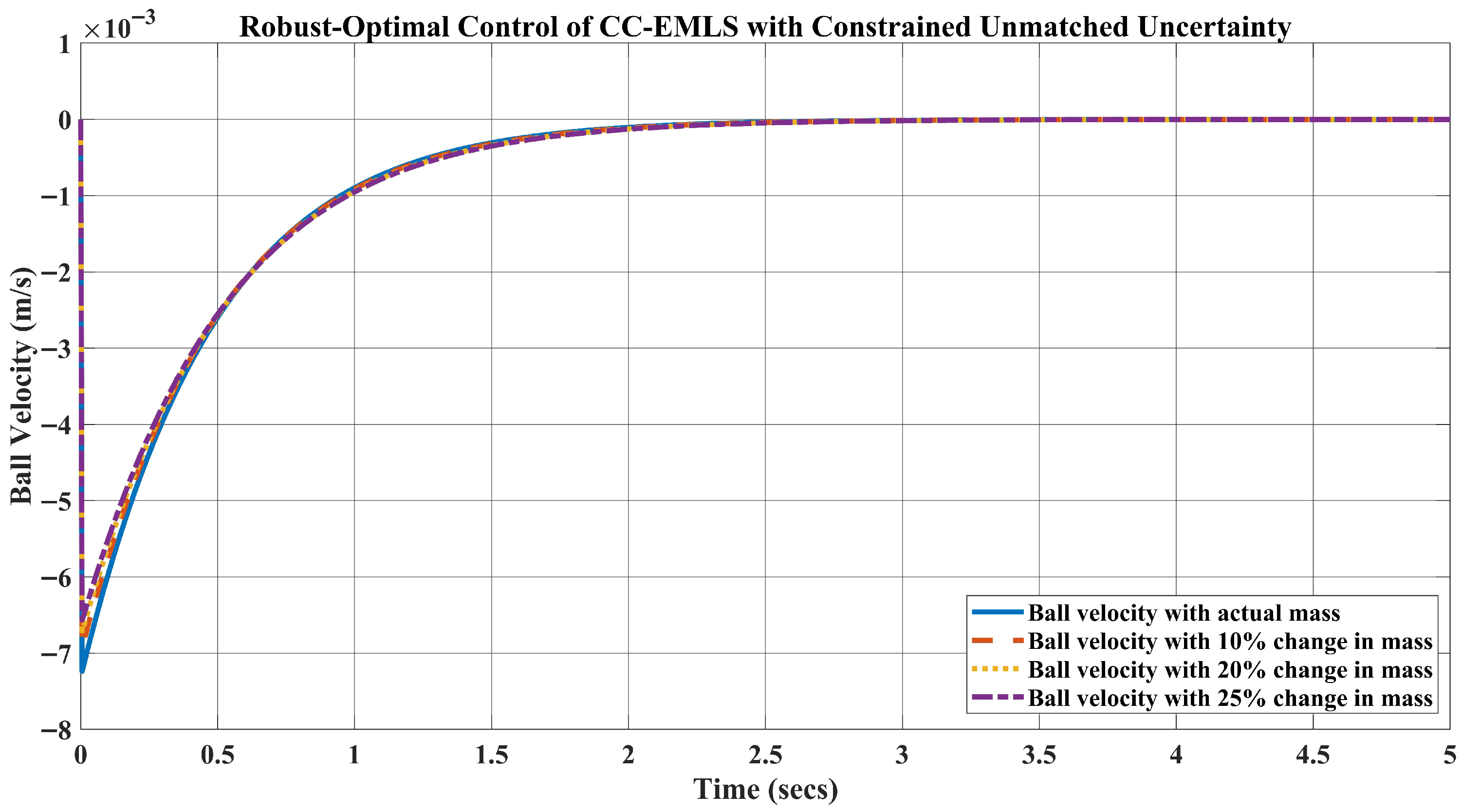
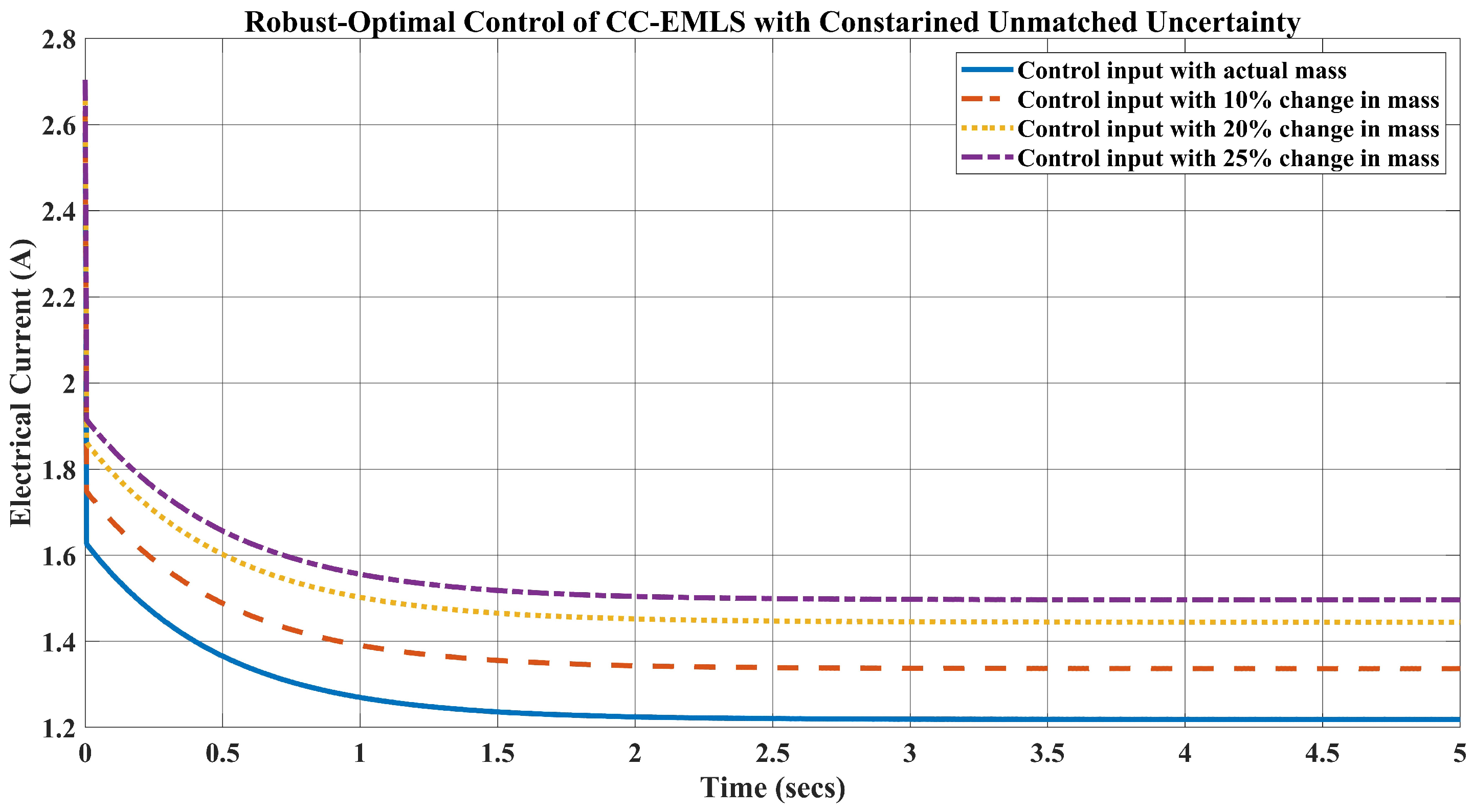
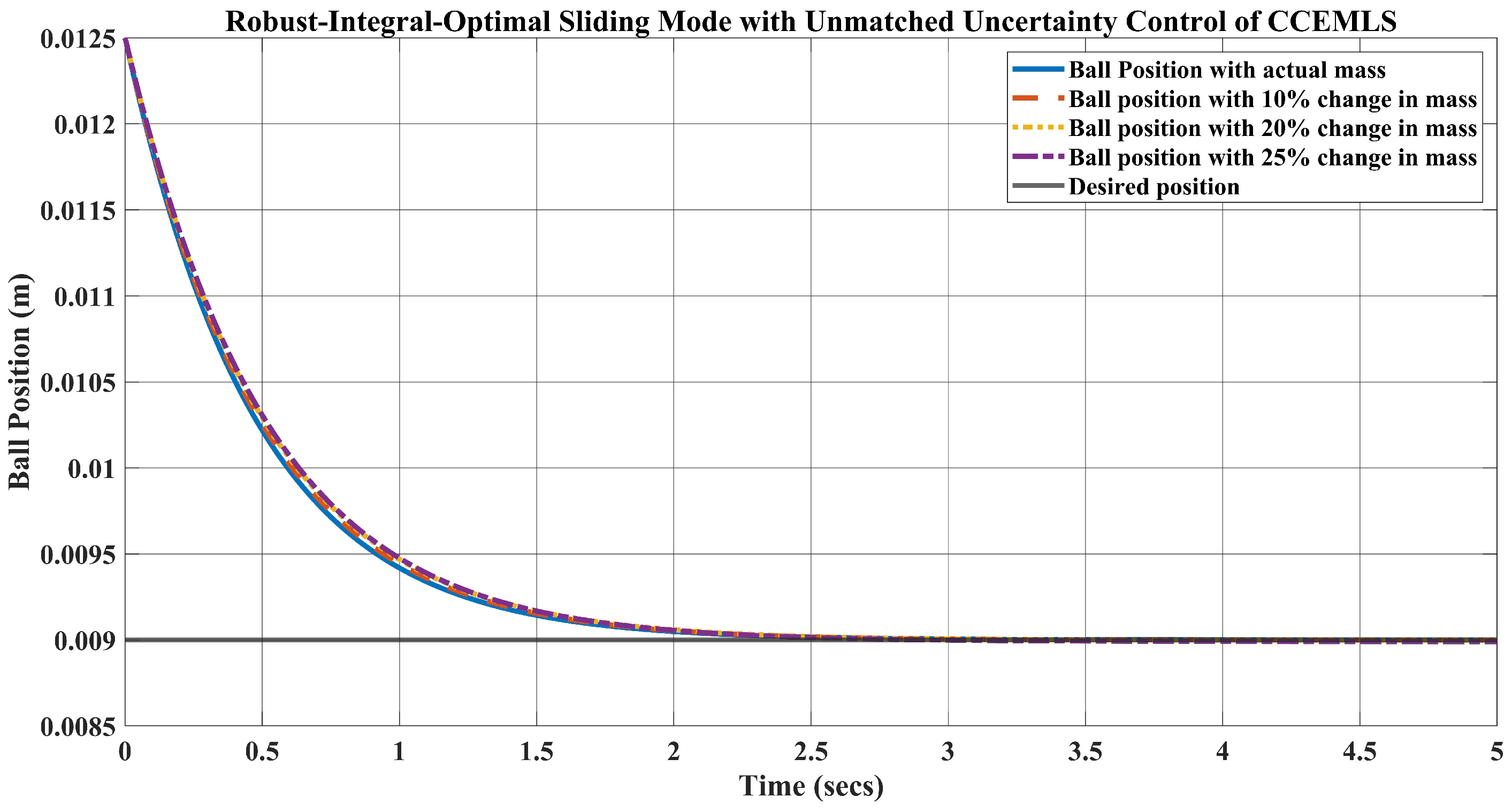
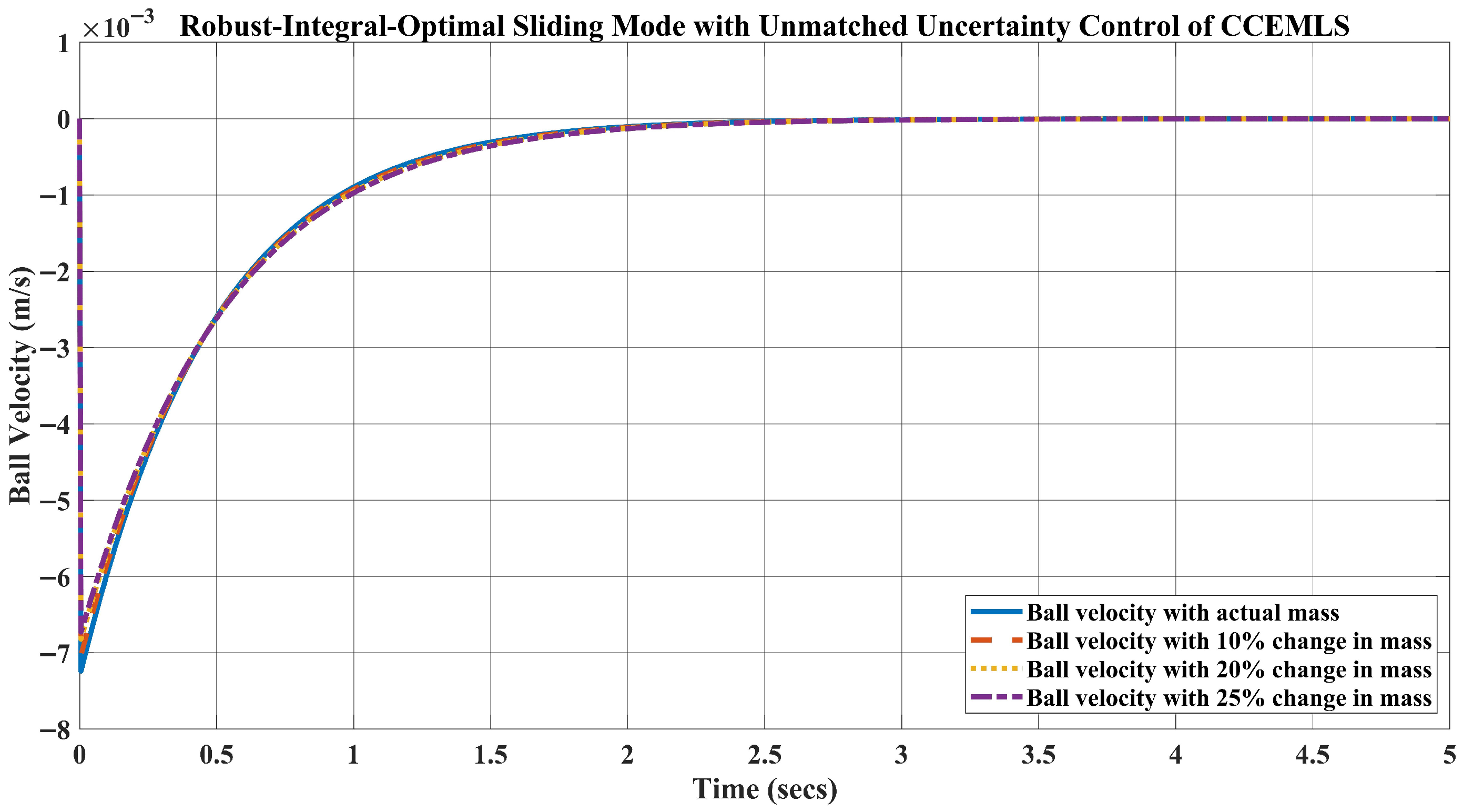
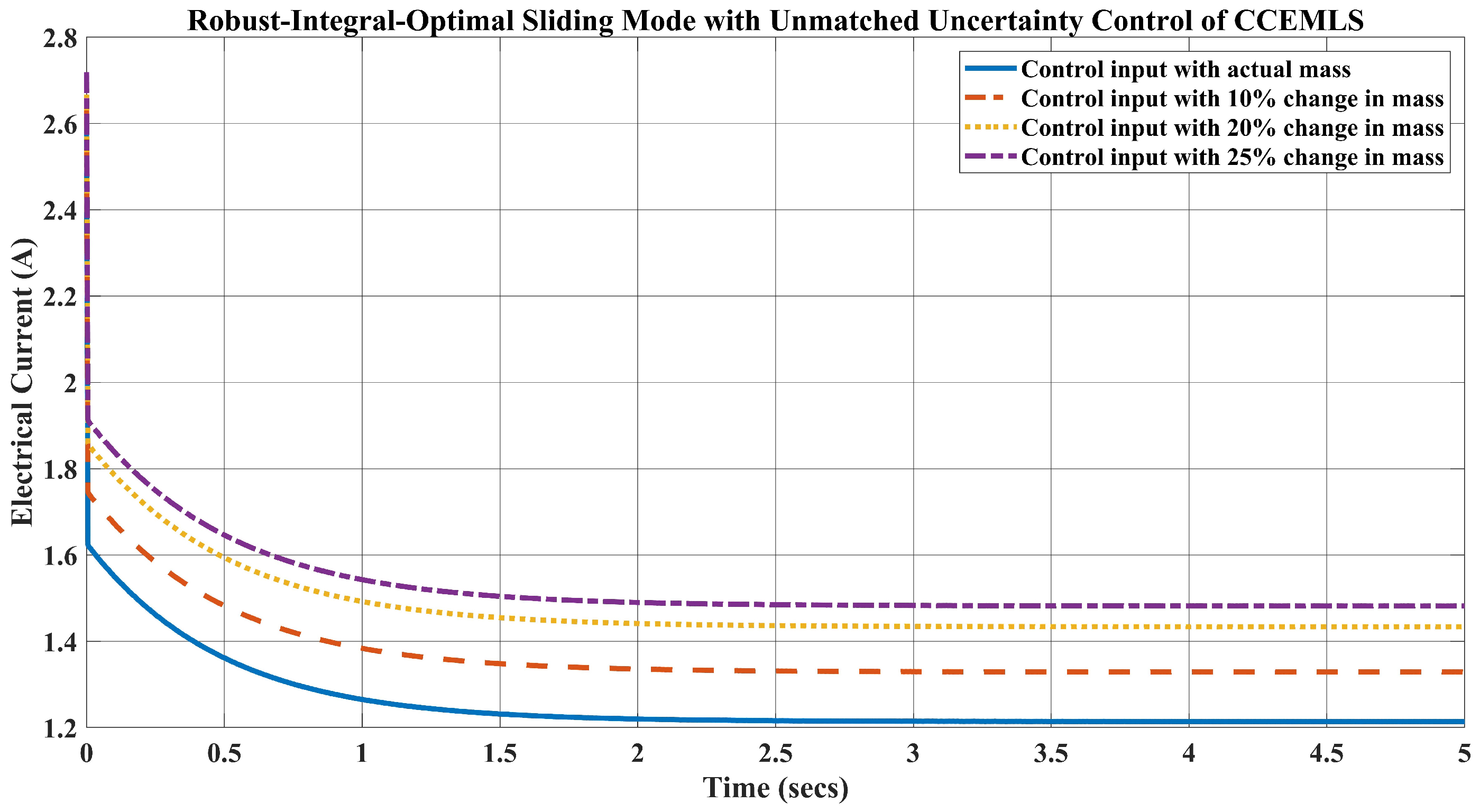
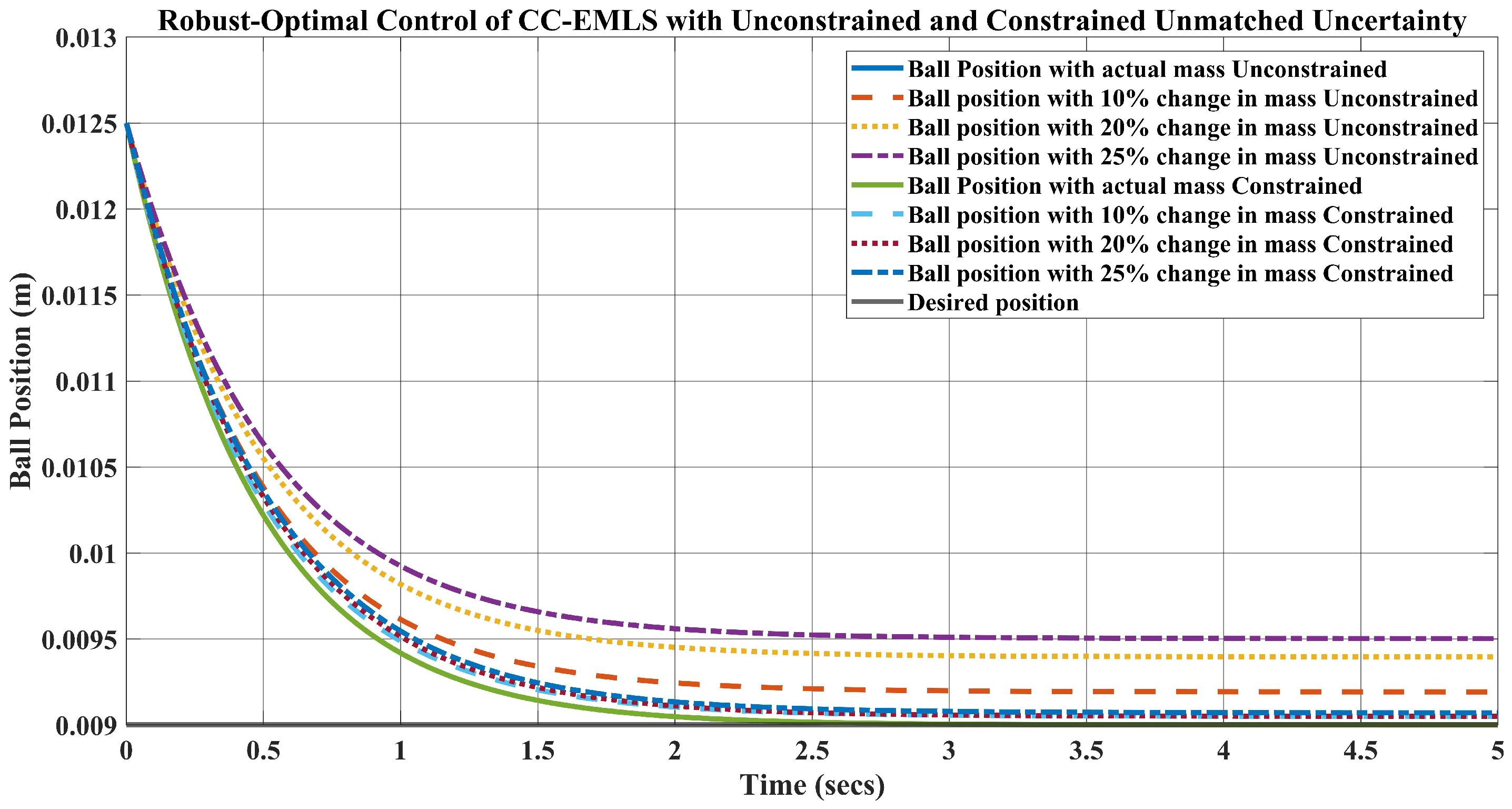
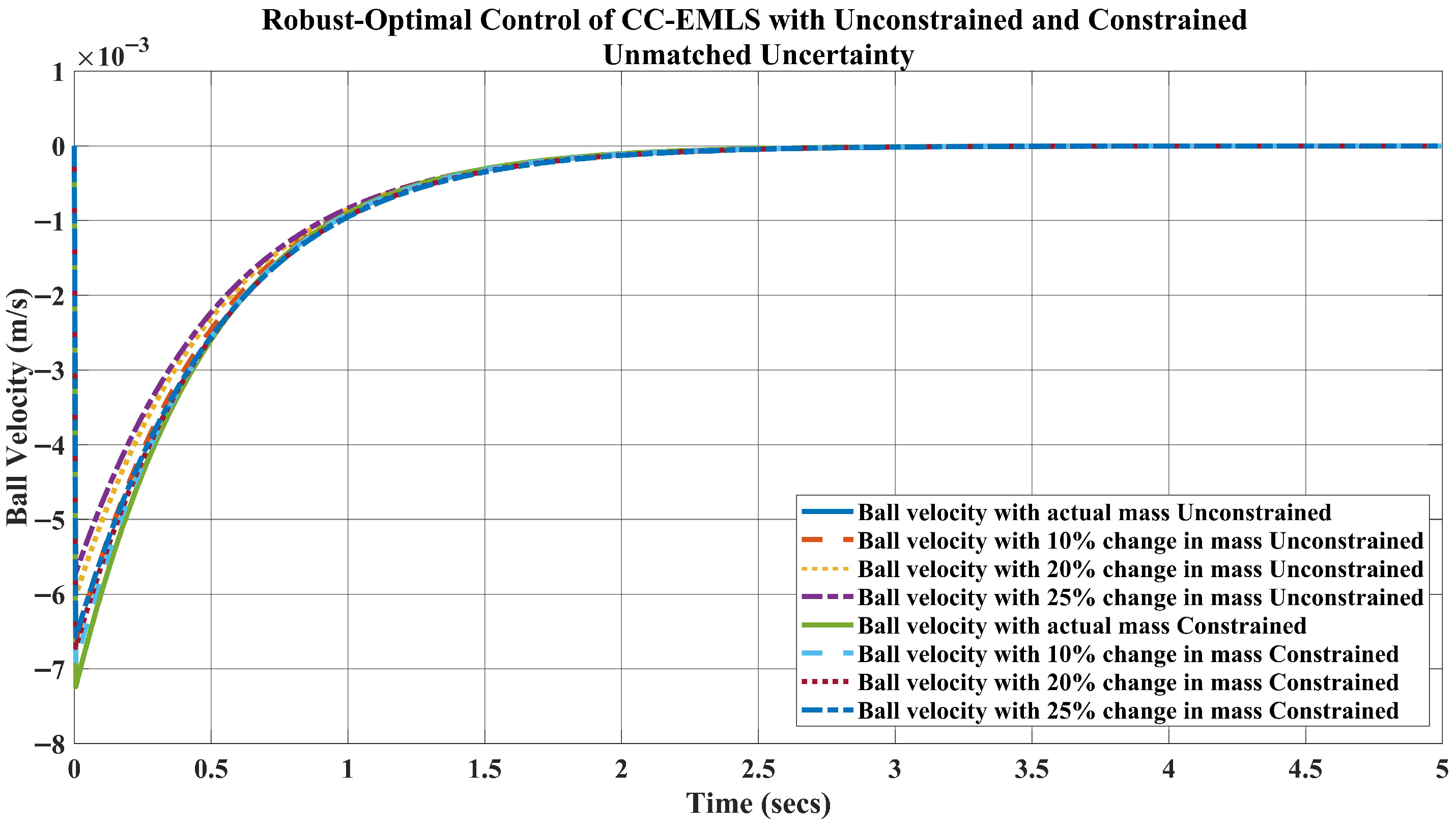
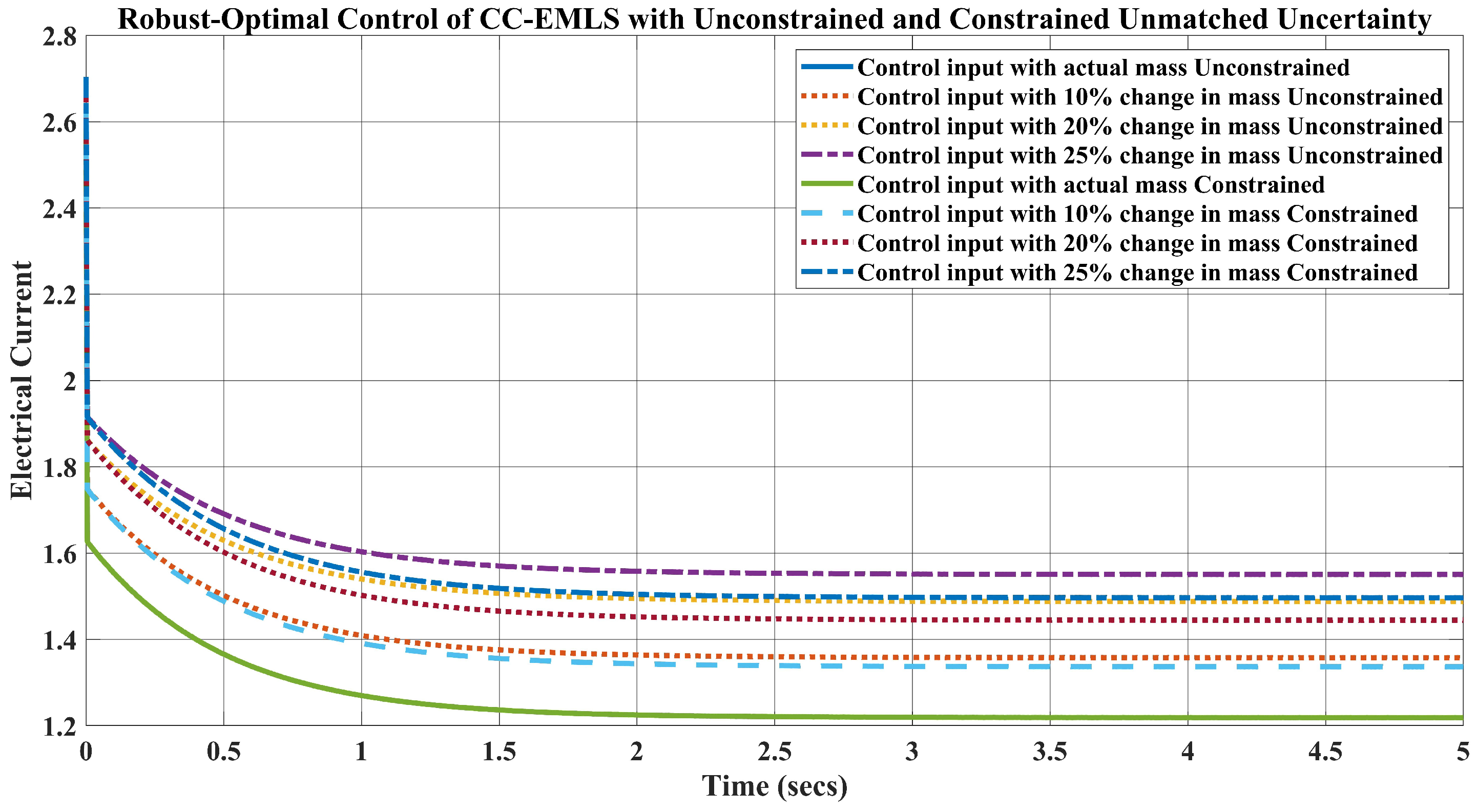
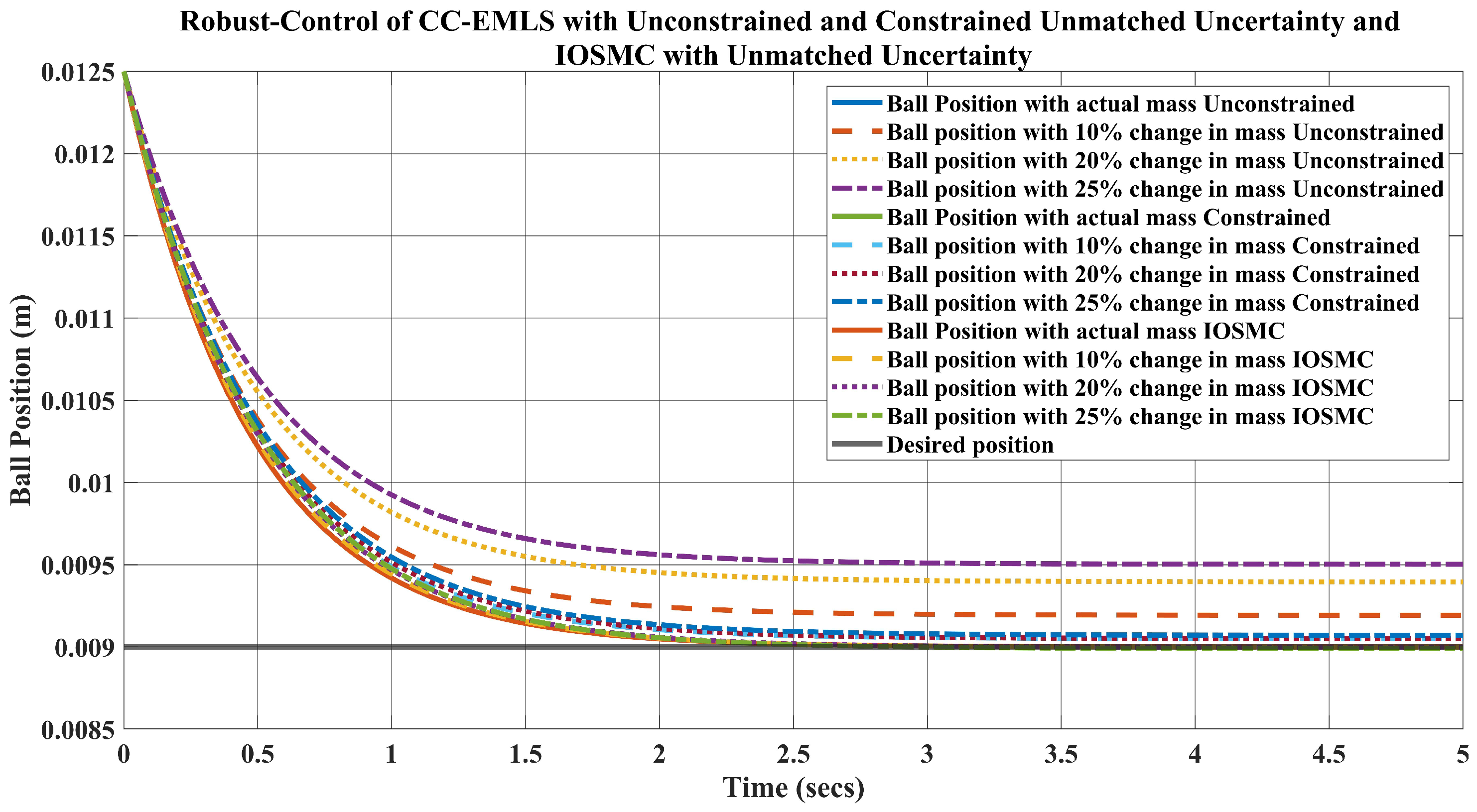
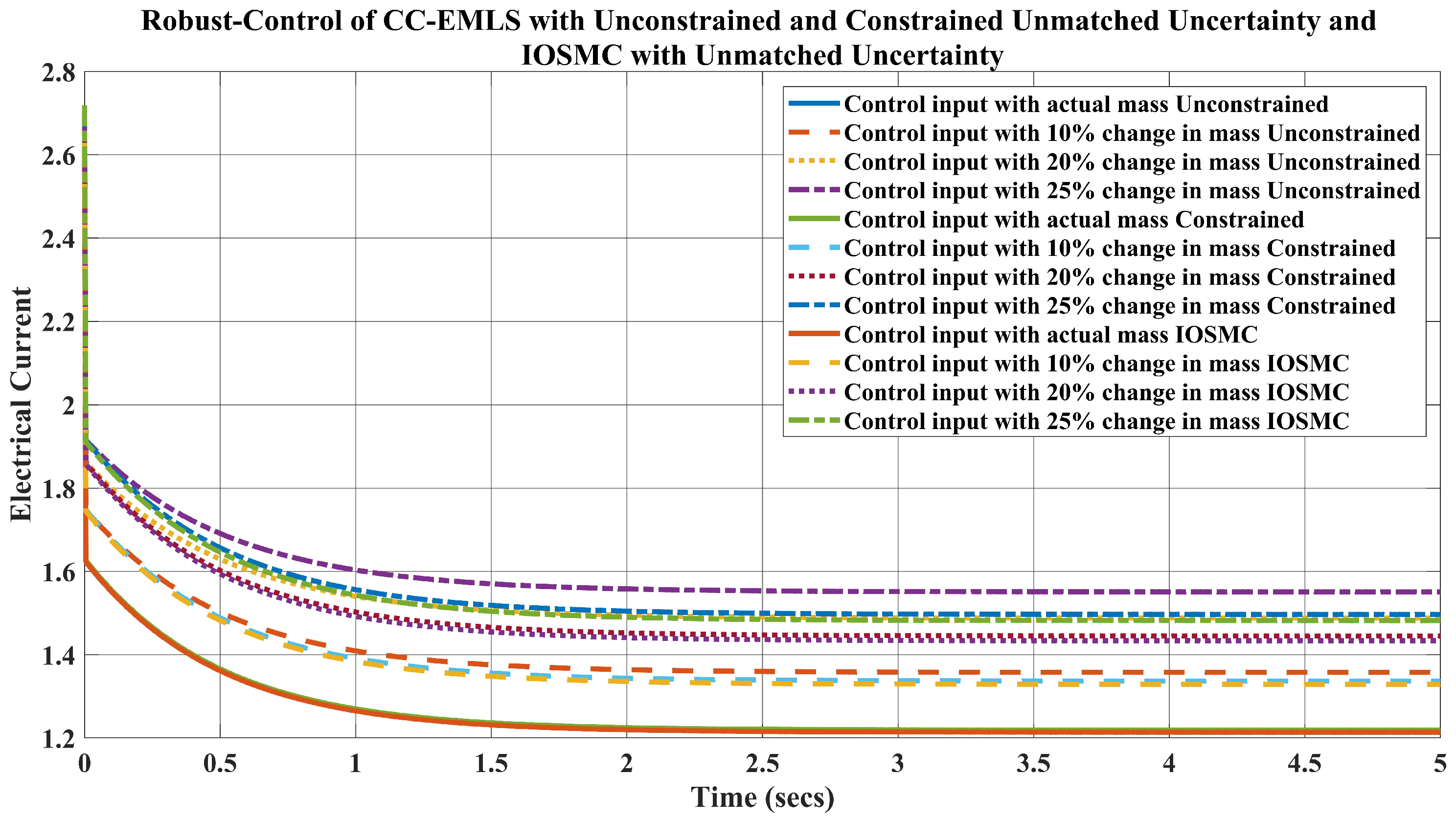
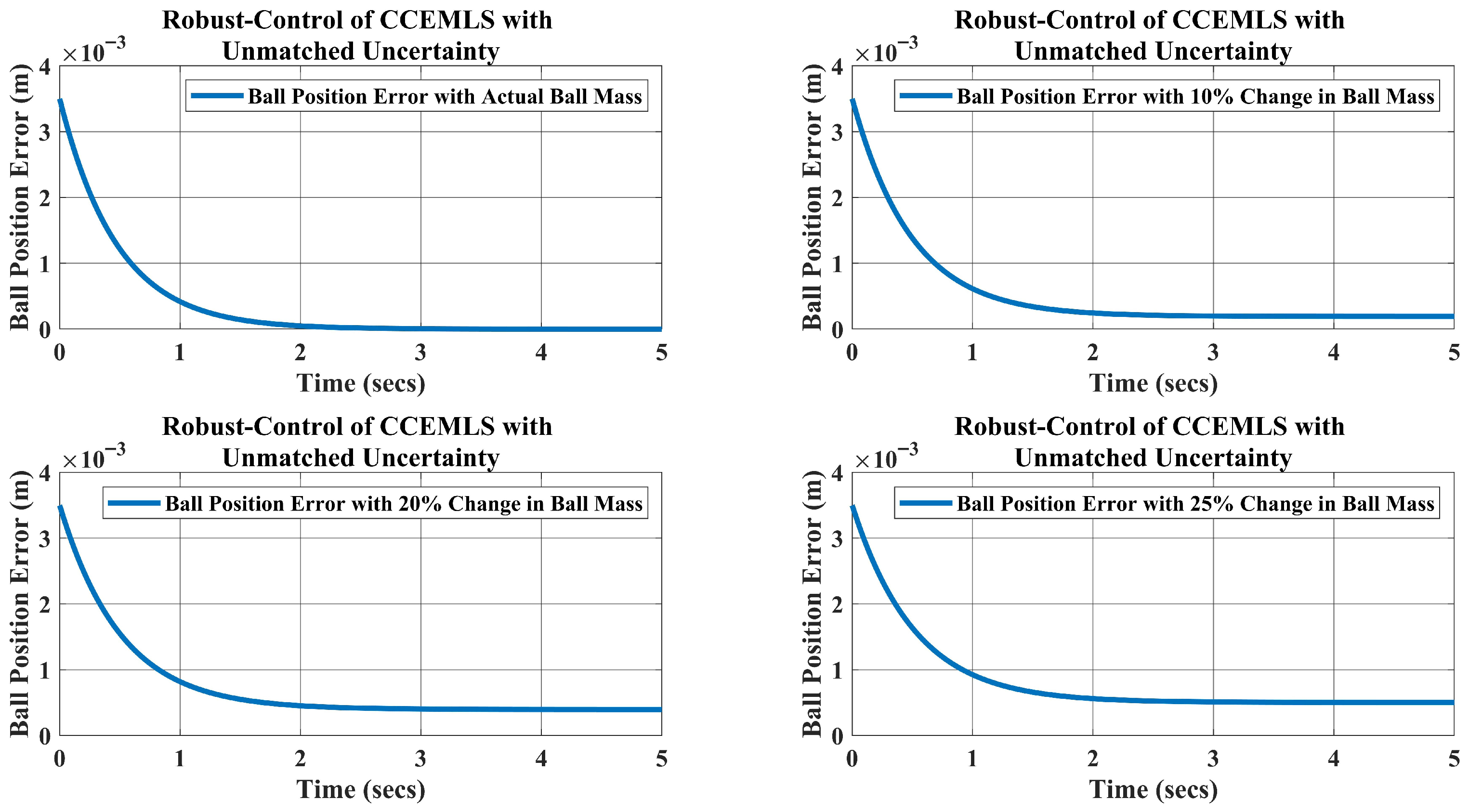
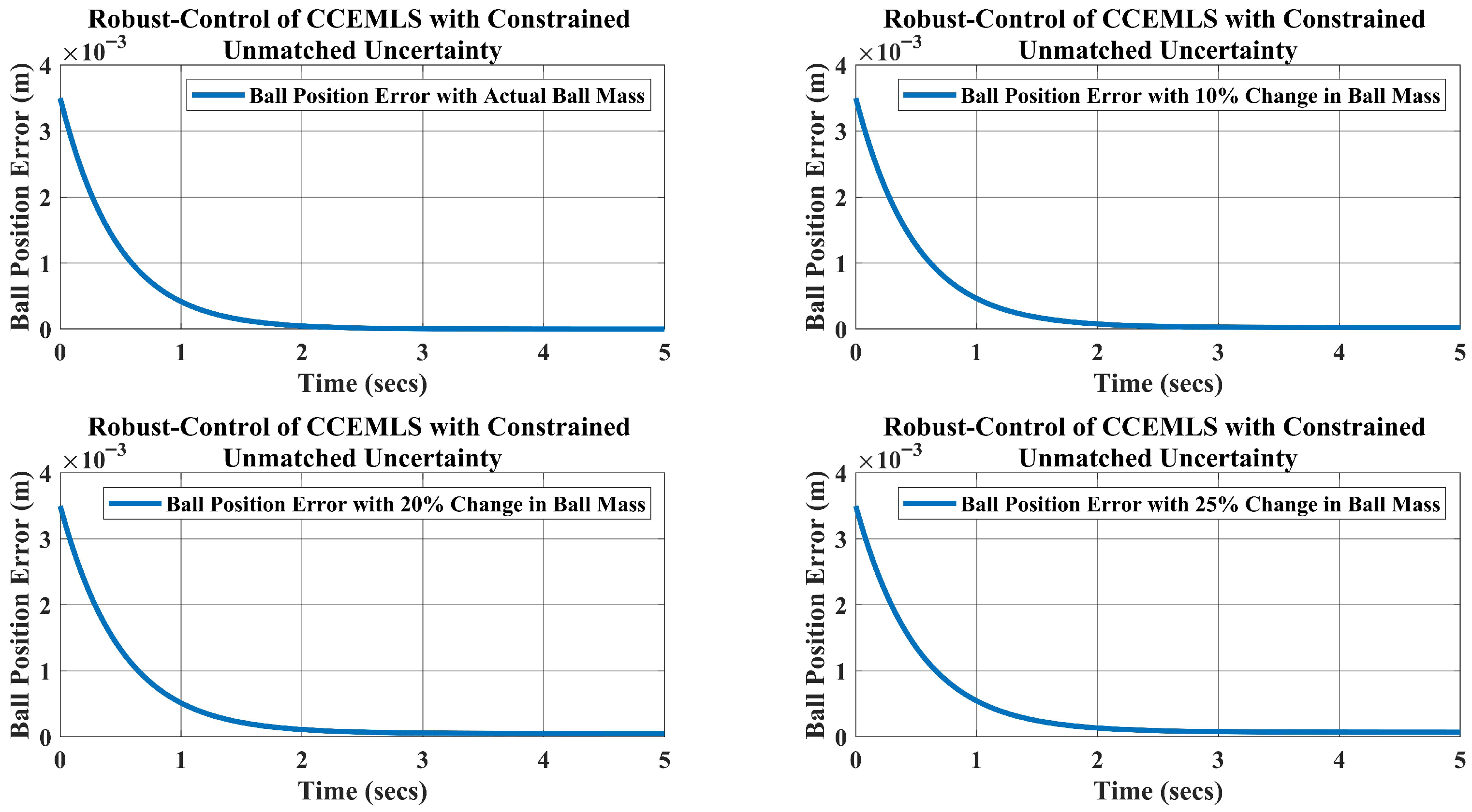
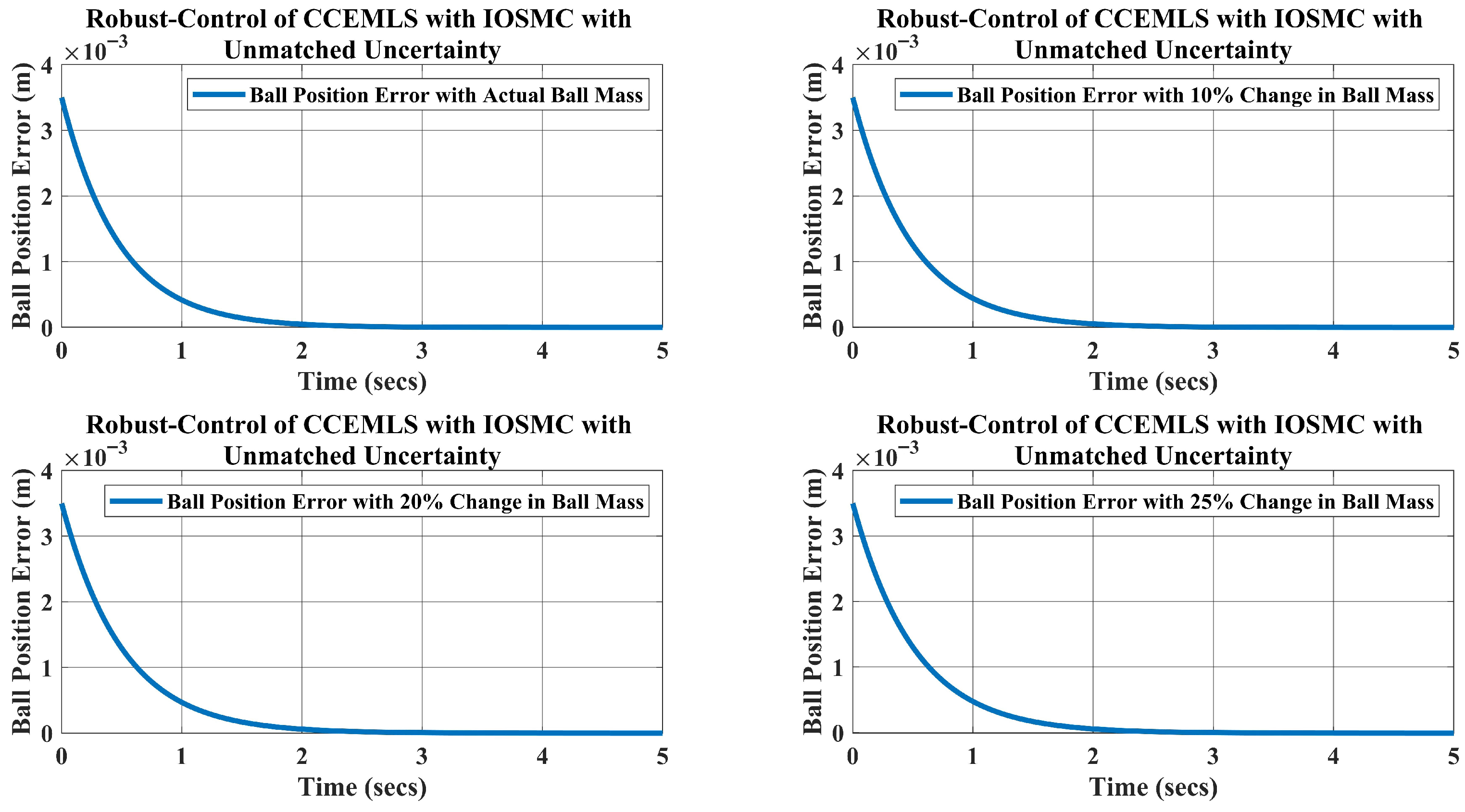
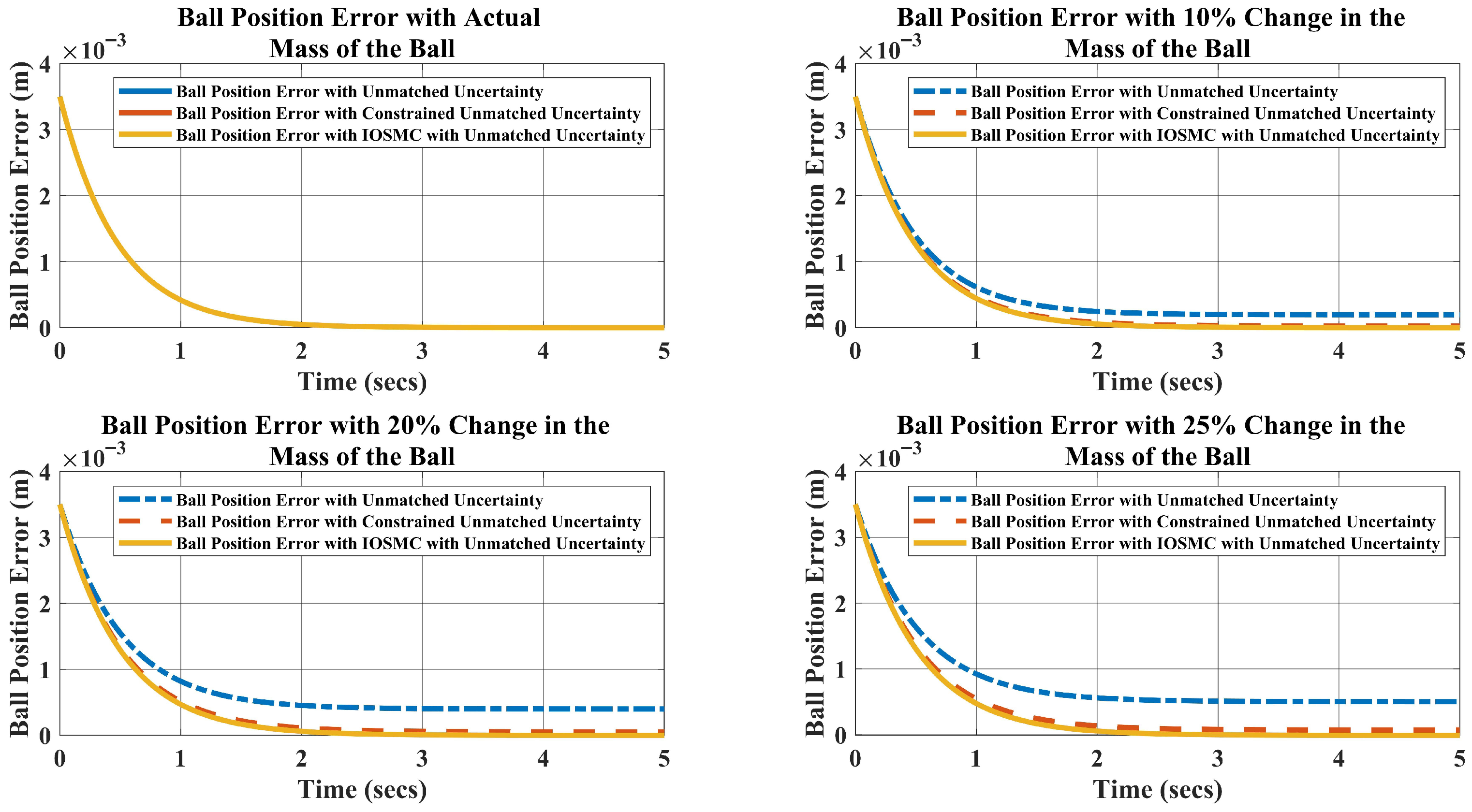
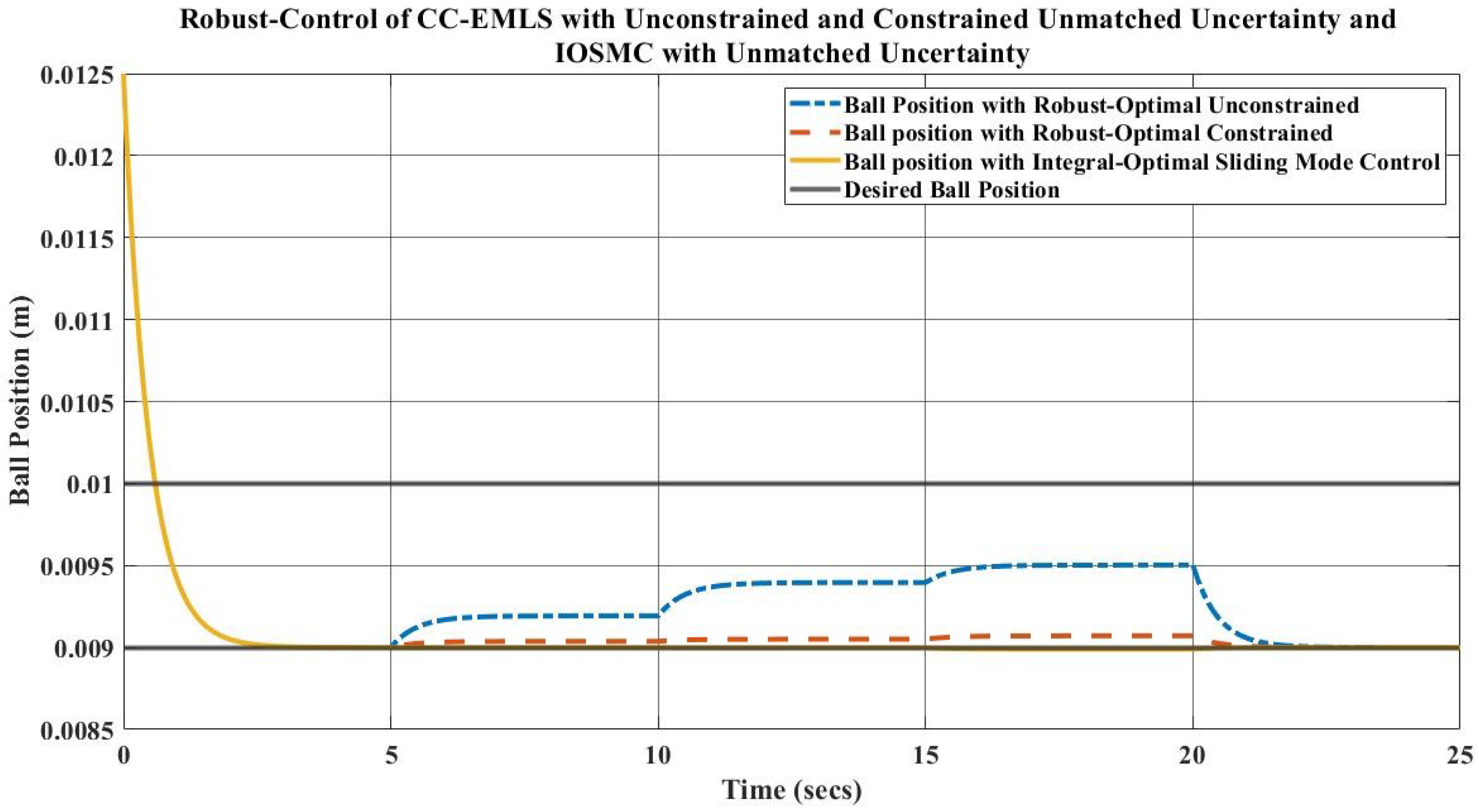
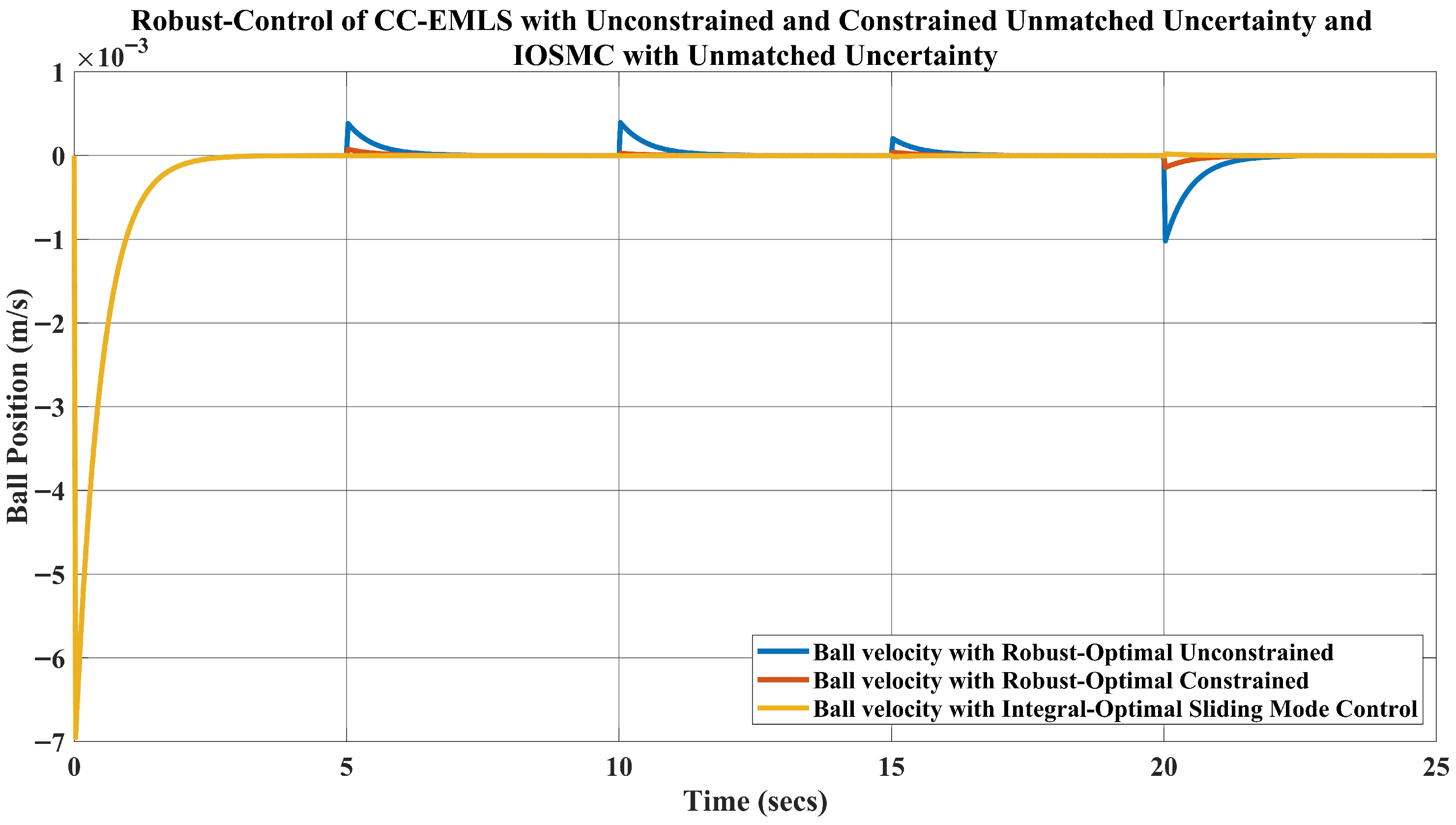
5. Simulation Results and Disscusion

This section presents the simulation results aimed at assessing the efficacy of the designed control strategies and providing insight into the design procedures for the CC-EMLS. The simulation studies are carried out using MATLAB 2024a, and the ordinary differential equation (ODE45) syntax is employed to simulate the equations of CC-EMLS, which utilizes the Runga–Kutta method to provide solutions for different values of x. The simulation is performed using the following values of the parameters: the weight of ball $m_b=0.068$ kg, electromagnetic constant $G_e=6.3508\times {10}^{-5}{\displaystyle \frac{\mathrm{N}-{\mathrm{m}}^2}{{\mathrm{A}}^2}}$, gravitational constant $g_e=9.81{\displaystyle \frac{\mathrm{m}}{{\mathrm{s}}^2}}$, actuator parameter $A_c=5.711\times {10}^{-3}$ m, set point $x_{a0}=0.009$ m, and the current required to levitate the object to the set point is given by $i_{c0}=\sqrt{{\displaystyle \frac{m_b{g}_e{(x_{a0}+d_a)}^2}{G_e}}}$ = $\sqrt{{\displaystyle \frac{0.068\times 9.81\times {(0.009+5.711\times {10}^{-3})}^2}{6.5308\times {10}^{-5}}}}$ = $1.4867$ A. The set point of the ball is kept at $x_{a0}=9$ mm, and the weight of the ball is varied from 0 to 25%. The control input to the system is the coil current, which is dependent on the weight of the ball; therefore, there will be a variation in the current value when the disturbance is applied with the different weights of the ball. The corresponding changes are as follows:

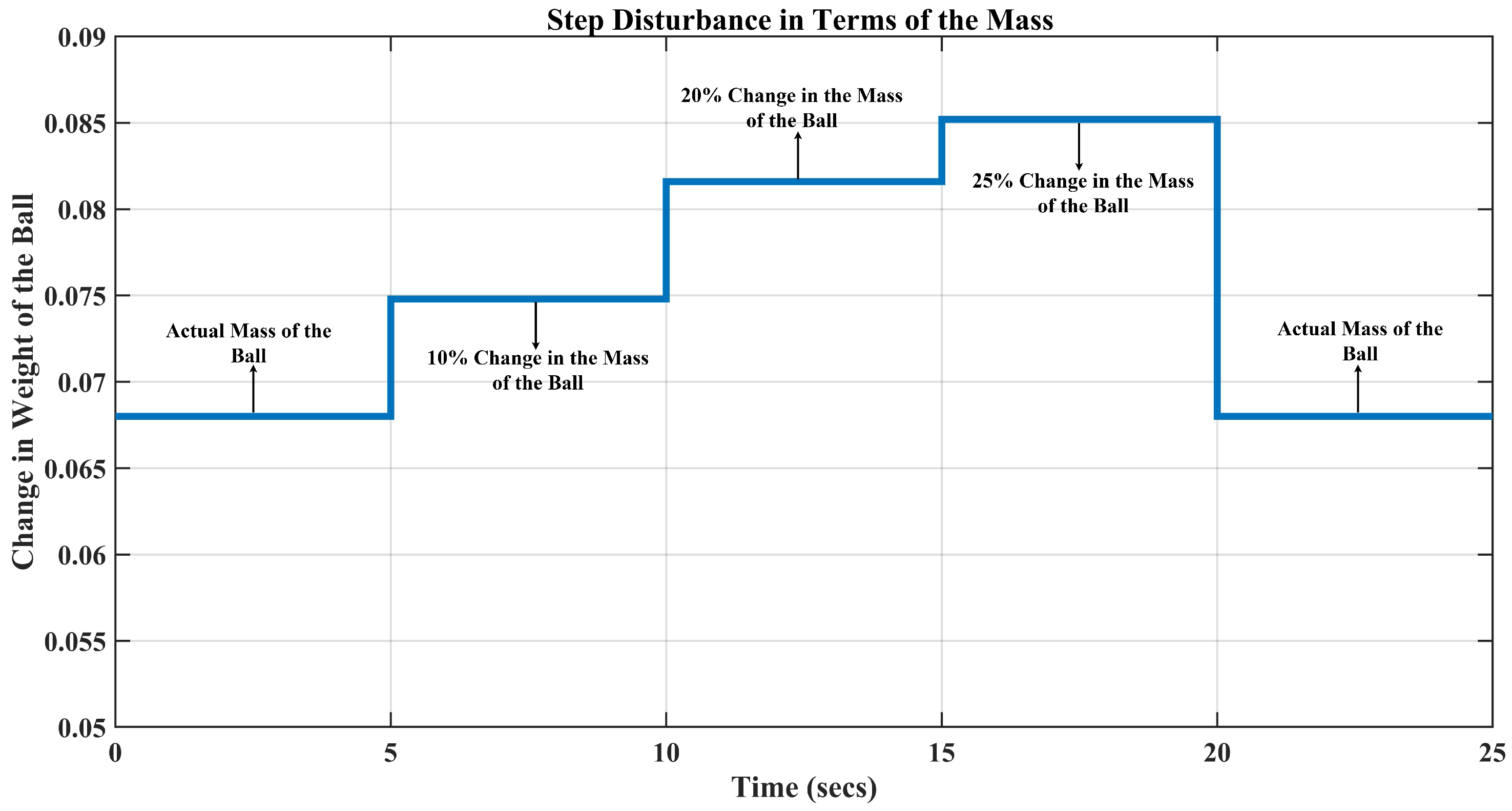
• For the weight $m_b=0.0748$ kg, which is a $10\%$ change in the mass, the requirement of the current is $i_c=1.5593$ A to keep the ball levitated at $x_a=0.009$ m.
• Likewise, when the weight of the ball is $m_b=0.0816$ kg, the requirement of the current $i_c=1.6286$ A.
• Lastly, for the ball’s mass, $m_b=0.085$ kg, which is a $25\%$ change in the mass, the current required to lift the object upward at $x_a=0.009$ m is $i_c=1.6622$ A.

As discussed in Section 4, the values of Q and R are taken as follows:

$$Q=\left[\begin{array}{cc}1000& 0\\ 0& 597.4291\end{array}\right],R=0.001$$

So, the required feedback control gain K is obtained as

$$K=\left[\begin{array}{cc}-1480.4& -548.9\end{array}\right]$$

The values of ${\Delta }_{max}$ and $b_{max}$ are used for the performance function and to calculate the matrix Q. This value of K is obtained from controller design with mismatched uncertainties. The constrained is added to the controller, which is designed using mismatched uncertainties. The value of $\alpha$ is chosen to be 10 for the constrained controller. In the IOSMC control, the optimal action is provided using the controller gain of mismatched uncertainties. Figure 2, Figure 3 and Figure 4 show the ball position, ball velocity, and control input when the simulation is carried out with mismatched uncertainties. The four different observations are simulated, such as the actual ball weight, with a $10\%$, $20\%$, and $25\%$ variations in the mass. The figures highlight that, with the actual weight, the proposed control scheme can achieve the selected set point of 9 mm without any steady-state error. However, when the disturbance is added in weight as $10\%$, $20\%$, and $25\%$, a small steady-state error is observed. The maximum deviation of error is less than 1 mm, which is considerable for such a complex system. The ball velocity is seen to be a constant of zero when the set position of the ball is attained. Figure 4 showcases the control effort required by the system to levitate the steel ball with and without disturbance. It is clear from the plot that the current requirement is 1.219 A to levitate the ball at 9 mm, with the mass $m_b$ = $0.068$ kg. Similarly, control efforts of 1.3576 A for a $10\%$, 1.4879 A for a $20\%$, and 1.5509A for a $25\%$ change in the weight of the ball are needed.

Similarly, Figure 5, Figure 6 and Figure 7 highlight the ball’s position, ball velocity, and controller efforts for the constrained mismatched uncertainties control scheme. Figure 5 gives a detailed understanding of the ball position. A simulation is carried out for four different disturbances, as mentioned above. It is seen that the position of the ball achieves a selected set point of 9 mm when the original weight of the ball is considered. A very small deviation of 0.5 mm is observed when the disturbance is applied in the range of $10\%$ to $25\%$, which shows that the designed controller is able to handle the uncertainties efficiently.

The ball velocity with constrained-based, mismatched uncertainties is shown in Figure 6. The figure shows that the ball’s velocity attains zero value when it reaches its set point. The figure highlights that with applied disturbances also, the velocity becomes zero. The control input is highlighted in Figure 7.

This figure gives the value of the control effort essential to hold the ball at the selected set point of 9 mm with and without disturbance. For the original ball mass, the control effort required by calculation is 1.4867 A. Still, the simulation result shows that with the constrained control, the requirement of electrical current is 1.219 A, which is less than what is obtained in the calculation.

The observation highlights that constrained control with mismatched uncertainties requires less control effort and has a reduced deviation from the set point, which proves that the proposed control strategy is resilient to the uncertainties in terms of the changing mass.

In Figure 8, Figure 9 and Figure 10, the position, velocity, and control input results are highlighted by using the control scheme IOSMC with mismatched uncertainties. The simulation result in Figure 8 shows that position of the ball is reaching its required set point of 9 mm with and without disturbance. No steady-state error is observed with this control scheme in the ball position. Moreover, the ball velocity also attains its required value of zero when the ball tracks the set value of 9 mm. The control effort requirement with IOSMC is shown in Figure 10. It is observed that for the original weight of the ball, the control effort needed for levitation at 9 mm is 1.214 A. Similarly, 1.329 A, 1.4336 A, and 1.4819 A are the simulation values of the control inputs for the $10\%$, $20\%$, and $25\%$ mass variation.

The comparison of unconstrained and constrained mismatched uncertainties is highlighted in Figure 11, Figure 12 and Figure 13. Figure 11 shows the ball position with both controllers, out of which it is seen that constrained-based unmatched uncertainty has less deviation as compared to unconstrained-based unmatched uncertainty. When the simulation is carried out with the ball’s mass having a $25\%$ change in its value, the unconstrained mismatched uncertainties controller attains a steady value of 9.5 mm, which is 0.5 mm more than its set value. However, when the simulation is carried out for the same case with constrained unmatched uncertainty, a deviation of just 0.07 mm is seen. The control effort required in unconstrained is greater as compared to constrained mismatched uncertainties, which is evident in Figure 13. It is seen that with a change in mass of $25\%$, the control effort for the unconstrained control is 1.5509 A, whereas with the constrained control, it is 1.4966 A, which is 0.054 A less. Hence, it can be said that the constrained control with unmatched uncertainty is more robust and efficient than the unconstrained control with unmatched uncertainty.

Another comparative analysis is shown in Figure 14, Figure 15 and Figure 16 for the position, velocity, and control effort with unconstrained and constrained mismatched uncertainties and integral sliding mode control with mismatched uncertainties. Figure 14 shows the ball position with all three controllers. It is noticed that IOSMC has no steady-state error even when a disturbance of $25\%$ is applied to the weight of the ball as compared to the constrained-based mismatched uncertainties and unconstrained-based mismatched uncertainties. The control effort required in the unconstrained control is more significant as compared to the other two controllers, as shown in Figure 16. It is seen that with a change in the mass of $25\%$, the control effort for the unconstrained control is 1.5509 A, whereas with the constrained control, it is 1.4966 A, which is 0.054 A less, and with the integral sliding mode control with unmatched uncertainty, it is 1.4819 A, which is 0.069 A less than the unconstrained control and $0.0147$ less than the constrained unmatched uncertainty. Hence, it can be said that the integral sliding mode control with the unmatched uncertainty performs better as compared to the other two controllers, and it offers more robustness to disturbances.

A detailed comparison of the ball position error is shown in Figure 17, Figure 18 and Figure 19 with unconstrained mismatched uncertainties, constrained mismatched uncertainties, and integral sliding mode control with mismatched uncertainties. It is seen that when the system has no disturbance, all the designed controllers perform well with zero ball position errors. However, when a disturbance is applied to CC-EMLS in terms of the mass of different values, a small error is observed in the case of the unconstrained and constrained-based unmatched uncertainty robust–optimal approach. In contrast, zero ball position error is observed even in the presence of disturbance when the system is designed using integral sliding mode control with unmatched uncertainty. To highlight the result more clearly, Figure 20 is drawn to compare all three designed control schemes for the ball position error. In this comparison result, it is observed that the error remains zero with IOSMC even in the presence of the disturbance.

Figure 21 shows the payload variation with different values at different time intervals. The step disturbance is added to the mass at various instances of time. For example, from 0 to 5 s, the weight is $0.068$ kg, and from 5 to 10 s, the ball mass is $0.0748$ kg, which is a $10\%$ change in the mass value. Similarly, from 10 to 15 s and 15 to 20 s, a ball mass of $0.0816$ kg and $0.085$ kg is chosen. Again, the actual ball’s mass is considered over a time interval of 20–25 s.

Figure 22 shows the ball position variation when the step disturbance shown is added to the mass of the ball with unconstrained, mismatched uncertainties. It is clear from the figure that when step disturbance is applied to the weight, there is a steady-state error, but this error is below a deviation of 1 mm, which is an acceptable limit for such a complex system. Similarly, Figure 23 is simulated for the constrained control with mismatched uncertainties with various step disturbances in the weight of the ball. It is observed that there is a steady-state that is less than $0.5$ mm as compared to the unconstrained mismatched uncertainties. Figure 24 highlights the step disturbance with the integral sliding mode control with mismatched uncertainties, which shows that no steady-state error is observed even when the maximum disturbance of a $25\%$ is applied.

Figure 25 and Figure 26 provide a detailed comparison of all three proposed controllers with the step disturbance for the ball position and ball velocity. As discussed above, the integral optimal sliding mode control with the mismatched uncertainties approach outperforms all the designed control schemes. No steady-state error is observed at the desired set point with this scheme, and no overshoot is observed in the ball velocity compared to the other two proposed controllers. However, the other two control strategies, which are unconstrained and constrained-mismatched-uncertainties-based robust–optimal approaches, have seen a steady-state error of $0.5$ mm and less than $0.1$ mm. When these controllers are compared with the previous proposed control technique [31], it is observed that the control scheme in [31] has a higher steady-state error of $0.8$ mm. Therefore, in comparison with the already existing work, it can be demonstrated that the designed control schemes are efficient and effective, providing adequate robustness against external disturbances and uncertainties.

The articles referenced as [14,23] provide an in-depth analysis of a fuzzy-based controller specifically designed for a current-controlled electromagnetic levitation system. These studies demonstrate that while the controllers developed exhibit commendable efficiency in maintaining levitation, they also reveal a significant drawback: a pronounced steady-state error arises whenever there is a variation in the payload weight. Furthermore, the analysis of integral errors—particularly the integral square error (ISE) and the integral absolute time error (ITAE)—indicates that their values are notably higher when compared to the results presented in this current article. This observation highlights the limitations of the controllers discussed in [14,23] when handling variations in payload. In contrast, the controllers introduced in this article not only mitigate the effects of these disturbances more effectively but also demonstrate a higher level of robustness. They manage to respond more adeptly to changes in the electromagnetic levitation system, ensuring enhanced implementation in terms of both dynamic response and steady-state error reduction, thus offering a significant improvement over the previously mentioned controller designs. This leads to the conclusion that the controllers developed in this work are superior in handling disruptions related to payload changes and maintaining lower integral error values, establishing their effectiveness in applications requiring precise control within electromagnetic levitation systems.

Table 1. Evaluation of integral indices for position error considering the actual weight of the ball.

Controller	IAE	ISE	ITAE	ITSE
IOSMC	$0.0016$	$2.9034\times {10}^{-6}$	$7.5326\times {10}^{-4}$	$6.6731\times {10}^{-7}$
Constrained	$0.0017$	$2.9126\times {10}^{-6}$	$6.8607\times {10}^{-4}$	$1.7159\times {10}^{-7}$
Unconstrained	$0.0017$	$2.9125\times {10}^{-6}$	$6.8606\times {10}^{-4}$	$5.4985\times {10}^{-7}$
Unconstrained Input	$0.0015$	$4.159\times {10}^{-6}$	$4.1807\times {10}^{-4}$	$5.5149\times {10}^{-7}$

,

Table 2. Evaluation of integral indices for position error considering $10\%$ variation in weight of the ball.

Controller	IAE	ISE	ITAE	ITSE
IOSMC	$0.0017$	$2.9949\times {10}^{-6}$	$8.1126\times {10}^{-4}$	$7.2419\times {10}^{-7}$
Constrained	$0.0019$	$3.0949\times {10}^{-6}$	$0.0014$	$8.1191\times {10}^{-7}$
Unconstrained	$0.0026$	$3.4884\times {10}^{-6}$	$0.0032$	$1.4136\times {10}^{-6}$
Unconstrained Input	$0.0029$	$5.179\times {10}^{-6}$	$0.0038$	$1.7159\times {10}^{-6}$

,

Table 3. Evaluation of integral indices for position error considering $20\%$ variation in weight of the ball.

Controller	IAE	ISE	ITAE	ITSE
IOSMC	$0.0017$	$3.0821\times {10}^{-6}$	$8.5532\times {10}^{-4}$	$7.6562\times {10}^{-7}$
Constrained	$0.0020$	$3.1874\times {10}^{-6}$	$0.0015$	$8.6629\times {10}^{-7}$
Unconstrained	$0.0035$	$4.4627\times {10}^{-6}$	$0.0057$	$3.1887\times {10}^{-6}$
Unconstrained Input	$0.0044$	$7.149\times {10}^{-6}$	$0.0076$	$5.1877\times {10}^{-6}$

and

Table 4. Evaluation of integral indices for position error considering $25\%$ variation in weight of the ball.

Controller	IAE	ISE	ITAE	ITSE
IOSMC	$0.0018$	$3.1158\times {10}^{-6}$	$8.9591\times {10}^{-4}$	$7.7963\times {10}^{-7}$
Constrained	$0.0021$	$3.2826\times {10}^{-6}$	$0.0018$	$9.4838\times {10}^{-7}$
Unconstrained	$0.0040$	$5.1198\times {10}^{-6}$	$0.0071$	$4.5268\times {10}^{-6}$
Unconstrained Input	$0.0052$	$8.6615\times {10}^{-6}$	$0.0098$	$8.1766\times {10}^{-6}$

provide a comparison of ball position error for various ball weights following the designed controllers. Integral errors include integral absolute error $\left(IAE\right)$, integral square error $\left(ISE\right)$, integral time absolute error $\left(ITAE\right)$, and integral time square error $\left(ITSE\right)$. From the tables, it is more evident that ISMC with mismatched uncertainties as the optimal approach caters to the best result in terms of error compensation as compared to the other two control schemes. However, the error value with unconstrained and constrained mismatched uncertainties is also negligible, which implies that the designed control schemes offer better rejection of all uncertainties and provide the required robustness against disturbances. To provide a better understanding of the robustness and efficiency of the proposed control work, the comparison of integral errors is performed with [31] to highlight the controller’s performance. It is seen that with the rising uncertainties, i.e., the $10\%$, $20\%$, and $25\%$ change in the mass of the ball, the designed control schemes that are the integral optimal sliding mode control and the unconstrained mismatched uncertainties and constrained-mismatched-uncertainties-based robust–optimal approaches outperform in terms of maintaining the negligible error, whereas in [31], the error is increasing with every change in the weight of the ball. Therefore, the designed control schemes prove to be robust against the uncertainties and efficient for disturbance rejection.

6. Conclusions

Parameter variation and external disturbances cause significant performance degradation in the Maglev system. Therefore, the article proposes three control techniques—unconstrained mismatched uncertainties, constrained mismatched uncertainties, and integral sliding mode control with mismatched uncertainties—to handle such variations and disturbances in a CC-EMLS. Initially, the unconstrained-mismatched-uncertainties-based robust–optimal control is designed using the quadratic cost function, solved with the help of the HJB equation, and the Lyapunov stability is used to provide the required stability proof. Due to steady-state error in the ball position with the unconstrained control, the constrained control is designed. The non-quadratic cost function is proposed and solved in this control scheme using the HJB equation. The Lyapunov theorem is utilized to provide a necessary stability proof. Again, due to the minor steady-state error in constrained mismatched uncertainties, the third control scheme, IOSMC, is proposed. In this, the optimal action is provided using a robust–optimal approach with mismatched uncertainties. The problem of the steady-state error is resolved in IOSMC, which performs better in the presence of uncertainties and disturbances. The outcomes of the three proposed controllers are compared based on the quantitative error metrics method. It is worth highlighting that the comparison is made using the same level of disturbance in all the proposed control methods. Forthcoming research will focus on the real-time hardware implementation of the proposed control strategies, and this work will be extended for the unbounded uncertainties.