Probabilistic Power Flow Estimation in Power Grids Considering Generator Frequency Regulation Constraints Based on Unscented Transformation

Abstract

To address active power fluctuations in power grids induced by high renewable energy penetration and overcome the limitations of existing probabilistic power flow (PPF) methods that ignore generator frequency regulation constraints, this paper proposes a segmented stochastic power flow modeling method and an efficient analytical framework that incorporates the actions and capacity constraints of regulation units. Firstly, a dual dynamic piecewise linear power injection model is established based on “frequency deviation interval stratification and unit limit-reaching sequence ordering,” clarifying the hierarchical activation sequence of “loads first, followed by conventional units, and finally automatic generation control (AGC) units” along with the coupled adjustment logic upon reaching limits, thereby accurately reflecting the actual frequency regulation process. Subsequently, this model is integrated with the State-Independent Linearized Power Flow (DLPF) model to develop a segmented stochastic power flow framework. For the first time, a deep integration of unscented transformation (UT) and regulation-aware power allocation is achieved, coupled with the Nataf transformation to handle correlations among random variables, forming an analytical framework that balances accuracy and computational efficiency. Case studies on the New England 39-bus system demonstrate that the proposed method yields results highly consistent with those of Monte Carlo simulations while significantly enhancing computational efficiency. The DLPF model is validated to be applicable under scenarios where voltage remains within 0.95–1.05 p.u., and line transmission power does not exceed 85% of rated capacity, exhibiting strong robustness against parameter fluctuations and capacity variations. Furthermore, the method reveals voltage distribution patterns in wind-integrated power systems, providing reliable support for operational risk assessment in grids with high shares of renewable energy.

1. Introduction

At the current stage, with the goal of basically completing the construction of China’s new power system by 2035, the proportion of new energy sources—predominantly wind and photovoltaic power—in the power system has been steadily increasing. Nevertheless, the output of new energy sources exhibits randomness and volatility, which not only tend to cause active power supply–demand imbalances in the power grid but also pose substantial challenges to its safe and stable operation [1,2]. As a classic approach for characterizing the uncertainty of power flow, probabilistic power flow (PPF) calculation quantifies the impact of input random variables on system states, thereby laying a crucial foundation for evaluating system operational risks [3].

The concept of PPF was first introduced by Borkowska in 1974 to address uncertainties in power systems [4]. Existing PPF methods can be categorized into three types: simulation-based, approximation-based, and analytical methods. The Monte Carlo Simulation (MCS) is the most classical simulation-based approach, which can yield accurate PPF results with a sufficiently large sample size [5,6,7]. Approximation-based methods aim to characterize the probabilistic properties of output random variables based on the statistical characteristics of input random variables. Commonly used approximation methods include the point estimation method (PEM) and the unscented transformation (UT) [8,9,10,11]. Analytical PPF methods employ convolution operations to derive the probability distribution of output variables by accounting for correlations among input variables, with the core challenge residing in handling complex convolution integrals [12,13,14].

A review of the existing literature indicates that key advancements in transmission network PPF research have primarily focused on modeling uncertainty sources, while the impact of system control mechanisms—such as generator frequency regulation and voltage control—on PPF probabilistic characteristics has received limited attention. The stochastic and fluctuating nature of high-penetration renewable energy may lead to active power imbalances, resulting in frequency deviations. As a crucial measure for maintaining system frequency stability, generator frequency regulation directly influences imbalance power allocation through its operational characteristics and capacity constraints. If existing PPF models neglect this critical control process, they will fail to capture the dynamic output adjustments of conventional and automatic generation control (AGC) units. Consequently, such models cannot accurately represent nodal power injection variations across different power deviation intervals, leading to discrepancies between the estimated probability distributions of state variables (e.g., voltage and phase angle) and actual engineering conditions.

Moreover, generator frequency regulation is subject to capacity limits and prioritization schemes. Changes in regulation strategies further alter the stochastic nature of power flow distributions. Only by integrating these control dynamics into PPF models can the operational risks of power systems—under the coupled effects of renewable variability and system control—be accurately quantified, thereby providing a reliable basis for dispatch decisions.

Reference [15] addressed the limitations of traditional deterministic voltage stability indices by introducing a probabilistic voltage stability indicator that incorporates source-load uncertainty. This approach evaluates overall system voltage stability through nodal indices, identifies vulnerable nodes in distribution networks via ranking, and employs the UT to solve PPF while considering variable correlations. Reference [16] developed a distribution network PPF method combining wavelet neural networks and an improved UT. Comparative analyses in distributed generation-integrated systems validated its effectiveness, though it did not account for the impact of system controls such as generator frequency regulation. Although reference [17] considered system control influences, it utilized Gaussian copula structures to model variable correlations—a method involving extensive integral computations and relatively high computational cost. Reference [18] introduced a transmission network analytical PPF algorithm incorporating generator regulation capacity constraints, along with a linear power flow model that considers such constraints. However, this model only addresses steady-state power allocation and overlooks the dynamic characteristics of generator frequency regulation.

In light of the limitations identified in existing studies, this paper develops a piecewise linear power injection model that incorporates unit frequency regulation actions and regulation capacity constraints. By adopting a dual dynamic segmentation approach—categorizing frequency deviation intervals (small/medium/large deviations) and sequencing the activation order of units reaching their limits—the model quantitatively defines the upper limits of regulation capacity and activation sequences for conventional units and AGC units. It clarifies the unbalanced power allocation mechanism under different power deviation intervals, accurately aligns with the physical process of actual frequency regulation, and addresses the disconnect between existing segmentation methods and dynamic frequency characteristics, thereby overcoming the limitations of traditional models that overlook system frequency regulation control.

Subsequently, the proposed regulation-constrained model is integrated with the State-Independent Linearized Power Flow (DLPF) model to establish a piecewise stochastic power flow model. This integration achieves, for the first time, a deep fusion of unified power flow and regulation-aware power distribution, coupling the randomness of renewable energy output with system frequency regulation control. It also fills the application gap of the UT method in probabilistic power flow analysis under regulation constraints. Moreover, a UT-based probabilistic power flow algorithm tailored for the piecewise model is proposed: it specifies a hierarchical activation sequence—“loads first, followed by conventional units, and finally AGC units”—along with the coupled adjustment logic post-limit attainment, thereby avoiding result distortion due to ambiguous regulation priorities and better reflecting real-world system operation rules. By efficiently capturing the probabilistic characteristics of renewable energy output through sigma point sets and addressing correlations among random variables via the Nataf transformation, the algorithm establishes an analytical mapping from input random variables to system states, balancing computational accuracy and efficiency.

Systematic case studies based on the New England 39-bus system validate the proposed method. Comparisons with the Alternating Current Monte Carlo (ACMC) method confirm its accuracy in estimating the probabilistic characteristics of state variables such as nodal voltages—achieving a correlation coefficient of 0.9962 for voltage means and a relative error of only 0.039%—while demonstrating significant computational efficiency, reducing the total computation time from 136.3 s (ACMC) to 0.395 s. Further quantitative comparisons between the DLPF model and full AC power flow reveal an average relative error of only 0.32% in voltage magnitude, defining the model’s applicability boundaries under scenarios such as voltage ranges of 0.95–1.05 p.u. and line transmission power within 85% of rated capacity. Additionally, sensitivity analyses on key UT parameters ($\alpha$, $\kappa$, $\beta$) and unit regulation capacity (fluctuations of ±20% and ±40%) verify the method’s robustness under parameter variations and capacity changes, with voltage index deviations remaining minimal. The method also elucidates voltage distribution patterns in wind-integrated grids (notable uncertainty at wind nodes, stable voltages at generator nodes, and concentrated distributions at load nodes), providing reliable support for operational risk assessment in power systems with high penetration of renewable energy.

To elucidate the distinctions between the present study and relevant research, a comparison of the key features with references [17,18] is presented in

Table 1. Comparison table of the present study and relevant research.

Comparative Dimension	This Study	Reference [17]	Reference [18]
Object of Study	AC transmission network (including new energy and conventional/AGC units)	Hybrid HVAC-LCC-VSC HVDC system	AC transmission network (including new energy and conventional/AGC units)
Frequency Regulation Capacity Constraint	Yes (conventional + AGC units, limit-reaching + dynamic allocation)	No (only converter coordination control, no frequency regulation constraints)	Yes (conventional + AGC units, limit-reaching, static allocation)
PPF Core Method	UT, DLPF segmented power flow	Nataf transformation, LHS-MCS (simulation method)	GMM, segmented linear analytical method
Segmentation Modeling Logic	Frequency deviation interval grading, unit limit-reaching sequence (dual dynamic)	No segmentation, only converter control mode switching	Unit limit-reaching state (single static segmentation)
Regulation Activation Sequence	Load ➔ Conventional units ➔ AGC units (hierarchical trigger)	No (no frequency regulation allocation)	Conventional units and AGC units in parallel (sequence is vague)
Power Allocation Characteristics	Dynamically update allocation coefficients after limit-reaching	No power allocation, only fixed converter output	Fixed remaining unit coefficients after limit-reaching
Core Application Scenarios	Online steady-state probabilistic power flow analysis, risk assessment	Hybrid DC system planning and design	Offline precise probabilistic power flow calculation

.

2. Consideration of the Generator Frequency Regulation Constraint Model

2.1. Generator Frequency Regulation Model

The active power injection at node n is defined as:

$$P_n=P_{g,n}+P_{v,n}-P_{d,n},n\in \delta$$

(1)

In this formula, $P_{g,n}$, $P_{v,n}$ and $P_{d,n}$ represent the output of conventional units, new energy units, and load at node n, respectively; $\delta$ is the set of PV and PQ nodes.

The active power deviation $P_{\Delta }$ of the system causes the frequency deviation $\Delta f=P_{\Delta }/K$, where K is the system’s unit regulation power. Depending on the magnitude of $P_{\Delta }$, the system triggers different frequency regulation actions:

When $0\le P_{\Delta }<K_U{f}_D$, conventional units and loads jointly participate in primary frequency regulation;

When $K_U{f}_D\le P_{\Delta }<K_U{f}_A$, new energy units and loads jointly participate in primary frequency regulation, where $K=K_U={\displaystyle \sum (k_{d,n}+k_{g,n})}$ represents the sum of the unit regulation powers of loads and conventional units in the system;

When $K_U{f}_A\le P_{\Delta }<P_{\Delta ,\max }$, secondary frequency regulation is initiated, and AGC units adjust their output.

To focus on the core impact of frequency regulation constraints on the probabilistic characteristics of steady-state power flow, while balancing computational efficiency and engineering practicality, this model incorporates targeted simplifications of the frequency regulation process: frequency regulation is characterized as a steady-state power redistribution within predefined power deviation intervals, with emphasis placed on the constraining effects of frequency regulation capacity limits and the sequence of reaching these limits on power allocation. Transient dynamic characteristics such as unit inertial response and governor dynamic response delays are currently excluded, and unit ramp rate limits are also not considered. It is assumed that units can complete steady-state adjustments of the target power within the corresponding frequency regulation intervals, and transient frequency fluctuations during the regulation process are neglected.

2.2. Frequency Regulation Capacity Constraint Model

The frequency regulation capacity constraints of generating units limit their power adjustment ranges. For a conventional unit n, the maximum power reduction is $P_{g,n}^{*}$. When $P_{\Delta }\ge {\displaystyle \frac{K_U}{K_{g,n}}}{P}_{g,n}^{*}$, the unit reaches the frequency regulation upper limit, and the power distribution coefficient needs to be recalculated at this time.

Similarly, the maximum capacity of the AGC unit n is $P_{AGC,n}^{*}$. When $P_{\Delta }\ge {\displaystyle \frac{K_U}{K_{AGC,n}}}{P}_{AGC,n}^{*}$, the unit reaches the frequency regulation upper limit, and the power distribution strategy is adjusted accordingly. Considering the order of unit restrictions comprehensively, a piecewise linear power adjustment model can be established:

$$P_{\Delta ,n}={\alpha }_{n,m}{P}_{\Delta }+{\beta }_{n,m},P_{\Delta ,n}\in Y_m$$

(2)

Here, $Y_m=\left[y_m,y_{m+1}\right]$ denotes the segmented interval, while ${\alpha }_{n,m}$ and ${\beta }_{n,m}$ represent the coefficients within interval m.

The aforementioned simplification is predicated on a targeted design aligned with the research objectives, and its implications for model application can be delineated as follows: From the perspective of dynamic characteristics, although the inertia of generating units in actual power systems serves to mitigate frequency transients and governor actions exhibit inherent delays—both of which influence the transient allocation of unbalanced power—the principal aim of this model is to quantify the average impact of steady-state frequency regulation power allocation on the probabilistic distribution of power flow. Consequently, this simplification does not compromise the model’s validity in core application scenarios such as steady-state operational risk assessment and medium-to-long-term optimization of frequency regulation resources. Only in dynamic analyses involving transient voltage fluctuations or real-time frequency regulation control would it be necessary to incorporate inertial response models and governor transfer functions to enhance dynamic representation. Regarding power adjustment rates, the ramping rate constraints of generating units primarily affect the responsiveness to short-term power deviations. However, given that the probabilistic power flow analysis addressed by this model predominantly employs time scales of 15 min or longer, generating units possess adequate time to complete power adjustments, rendering the impact of ramping rate constraints negligible. Thus, the simplification does not significantly diminish the model’s engineering reference value.

2.3. Probabilistic Power Flow Modeling

Integrated with the State-Independent DC Power Flow (DLPF) Model:

$$\Lambda \left[\begin{array}{c}{\theta }_S\\ V_L\end{array}\right]=\left[\begin{array}{c}{P}_S\\ Q_L\end{array}\right]+C\left[\begin{array}{c}{\theta }_R\\ V_T\end{array}\right]$$

(3)

In this equation, $\left[\begin{array}{c}{P}_S\\ Q_L\end{array}\right]$ represents the active and reactive power injections of the system (including conventional units, renewable energy sources, and load components); $\Lambda$ and $C$ denote the coefficient matrices of the linear power flow; ${\theta }_S$ and ${\theta }_R$ correspond to the voltage phase angles at the relevant nodes; and $V_L$ and $V_T$ represent the voltage magnitudes at the corresponding nodes.

The core assumptions of this model include the following key aspects:

• Decoupling the relationship between active power and phase angle, as well as between reactive power and voltage magnitude, with the premise that active power is exclusively related to voltage phase angles while reactive power is solely dependent on voltage magnitudes.
• A maximum deviation of nodal voltage magnitudes from the nominal value (1 p.u.) not exceeding 5%, allowing for the simplification of power flow equations to a linear form by disregarding higher-order nonlinear voltage terms.
• Construction of coefficient matrices for active and reactive power flow based on the real and imaginary components of the nodal admittance matrix, respectively. These coefficient matrices remain invariant to system operating conditions, thereby exhibiting a “state-independent” characteristic.

Addressing the inherent coupling between frequency regulation and reactive power/voltage control, the proposed model, based on the aforementioned assumptions, accurately characterizes their steady-state coupling mechanism through the following approaches:

• When conventional units and AGC units adjust active power output for frequency regulation, the reactive power regulation margin changes in accordance with the PQ operational curve characteristics. Concurrently, active power flow redistribution leads to dynamic variations in line reactive power losses (I²X), which are more pronounced in fluctuating areas such as wind power nodes. This, in turn, affects nodal reactive power injection and voltage levels. The model linearizes this indirect influence by embedding reactive–active power coupling factors into the piecewise power flow coefficient matrix, treating reactive power injection as a “correlated variable of active power regulation output”.
• When frequency regulation causes voltage deviations from the rated value, system voltage control devices (e.g., AVR, SVG) prioritize reactive power regulation to maintain voltage stability by adjusting nodal reactive power injection. However, reactive power injection adjustments alter the nodal equivalent admittance characteristics, thereby slightly modifying the active power flow distribution coefficients and affecting the allocation ratio of unbalanced power among regulating units. By establishing the response logic that “voltage control takes precedence over secondary frequency regulation allocation”, the model incorporates voltage deviation thresholds during segment partitioning, ensuring that voltage control corrections to reactive power injection precede power flow calculations, aligning with actual system control logic.
• Focusing on the objective of steady-state probabilistic power flow analysis, transient dynamic coupling between frequency regulation and voltage control (e.g., AVR response delays, generator transient reactive power characteristics) is temporarily neglected. Instead, only the steady-state coupling relationship is characterized—namely, the steady-state reactive power adjustments corresponding to steady-state active power variations, and the steady-state corrections to active power allocation triggered by voltage deviations through reactive power compensation. This simplification not only fits the linearized framework of the DLPF model but also demonstrates its accuracy and reliability in steady-state scenarios through comparative validation with full AC power flow (voltage magnitude error ≤ 0.32%).

Based on the aforementioned assumptions and coupling processing logic, the DLPF model has a clearly defined scope of applicability: it is particularly suitable for steady-state power system operation analysis under conditions where voltage remains within 0.95–1.05 p.u. (e.g., scenarios involving normal load fluctuations and small-scale renewable energy variations). It is especially applicable to medium- to long-term (15 min and above) steady-state risk assessment in power grids with high penetration of renewable energy, and achieves a balance between computational efficiency and accuracy, significantly improving the speed of probabilistic power flow calculations involving large numbers of stochastic variables.

At the same time, compared with a full AC power flow analysis that accounts for all nonlinear coupling relationships, the DLPF model exhibits certain inherent limitations due to its simplifying assumptions:

• When voltage deviations exceed 5% of the nominal value, computational accuracy decreases, making it difficult to capture active-reactive power coupling effects.
• Its adaptability is limited in strongly nonlinear power grids featuring high-impedance lines, weakly connected nodes, or dense integration of distributed generation.
• It is only applicable to steady-state analysis and cannot characterize transient dynamic coupling relationships.
• The influence of voltage magnitude on active power transmission is neglected, which may introduce minor errors at nodes with high concentrations of voltage-sensitive loads.

Furthermore, the model constructs frequency regulation as a quasi-static, segmented power redistribution process, without incorporating dynamic or multi-time-scale frequency response characteristics. The inherent limitations resulting from this simplification require further clarification: in actual frequency regulation, primary frequency control (inertial response and governor response) operates on a millisecond- to second-level timescale, while secondary frequency control (AGC regulation) responds on a second- to minute-level timescale. The model integrates these mechanisms into a unified segmented static allocation, which fails to capture the dynamic coordination of regulatory efforts during transients. Additionally, inertial response can rapidly suppress frequency deviations through rotor kinetic energy, and governors exhibit mechanical delays and dead-band characteristics. These dynamic behaviors influence the transient distribution of unbalanced power and the rate of frequency recovery. Neglecting them leads to underestimation of transient frequency deviations and associated voltage fluctuation risks in short-time-scale scenarios (e.g., abrupt changes in renewable generation output). For analyses involving real-time frequency control or millisecond-level power fluctuations (such as wind gusts), the quasi-static assumption of the model deviates significantly from actual dynamic responses, making it difficult to accurately quantify power flow uncertainties under transient coupling effects.

This study conducted multi-dimensional comparative validation against the full AC power flow-based Monte Carlo method (ACMC), using metrics including mean, variance, quantiles, and violation probabilities. The results indicate that, within the core scenario of “steady-state probabilistic power flow analysis” emphasized in this study, the computational errors of the DLPF model remain within acceptable bounds (relative error ≤ 0.5%), and its limitations do not materially affect the research conclusions. Should future applications require extension to transient analysis, severe contingency scenarios, or strongly nonlinear grids, state-dependent linear power flow (SCLPF) or full AC power flow models may be adopted to enhance computational accuracy.

By incorporating the power injection model that accounts for frequency regulation constraints, the piecewise stochastic power flow model is derived as follows:

$$\Lambda \left[\begin{array}{c}{\theta }_S\\ V_L\end{array}\right]=E_{m}X+D_m+C\left[\begin{array}{c}{\theta }_R\\ V_T\end{array}\right]$$

(4)

Here, $X={\left[P_v^T,Q_v^T\right]}^T$ represents the stochastic variables of renewable energy output (active and reactive power), $D_m$ denotes the deterministic power injection matrix of conventional generators and loads within interval m, and $E_m$ corresponds to the coefficient matrix associated with renewable energy power in interval m.

3. Power System Probabilistic Analysis Under Unit Frequency Regulation Constraints Based on Unscented Transformation

3.1. The Principle of Unscented Transform

The fundamental principle of the UT technique can be illustrated using Figure 1. Given an input random variable with a mean of ${\mu }_x$ and a covariance of ${\Sigma }_x$, a set of sigma points is sampled according to a specific sampling rule to ensure that the mean and covariance of the selected point set exactly match ${\mu }_x$ and ${\Sigma }_x$, respectively. Each sigma point in this set is then subjected to a nonlinear transformation, yielding a new set of transformed points. Finally, the statistical characteristics of the output random variable are determined based on the mean and covariance of the transformed point set.

The unscented transform employs a set of 2n + 1 sigma points (where n denotes the dimension of the random variable) to capture the mean X and covariance ${\mu }_x$ of the random variable ${\sum }_x$. By performing Cholesky decomposition on ${\sum }_x$, we obtain ${\sum }_x=L{L}^T$, where L is a lower triangular matrix. The sigma point set is defined as follows:

$$\left\{\begin{array}{l}{\lambda }_0={\mu }_x\\ {\lambda }_i={\mu }_x+l_i\sqrt{n+\lambda },\begin{array}{cc}& i=1,2,\cdots ,\mathrm{n}\end{array}\\ {\lambda }_{i+n}={\mu }_x-l_i\sqrt{n+\lambda },\begin{array}{cc}& i=1,2,\cdots ,\mathrm{n}\end{array}\end{array}\right.$$

(5)

where $\lambda ={\alpha }^2(n+\kappa )-n$ serves as the scaling parameter, $\alpha$ governs the distribution range of sigma points, with $\kappa$ acting as the secondary scaling parameter, and $l_i\in {ℝ}^n$ represents the i-th column vector of L, satisfying ${\sum }_x=L{L}^T$.

The mean weight assigned to each sigma point is as follows:

$$\left\{\begin{array}{l}{\lambda }_0={\mu }_x\\ {\lambda }_i={\mu }_x+l_i\sqrt{n+\lambda },\begin{array}{cc}& i=1,2,\cdots ,\mathrm{n}\end{array}\\ {\lambda }_{i+n}={\mu }_x-l_i\sqrt{n+\lambda },\begin{array}{cc}& i=1,2,\cdots ,\mathrm{n}\end{array}\end{array}\right.$$

(6)

The covariance weight for each Sigma point is as follows:

$$\left\{\begin{array}{l}{W}_0^c=W_0^m+\left(1-{\alpha }^2+\beta \right)\\ W_i^c=W_{i+n}^c=W_i^m,\begin{array}{cc}& i=1,2,\dots ,\end{array}n\end{array}\right.$$

(7)

Parameter $\beta$ is employed to adjust the precision of higher-order matrices and is typically assigned a value of 2.

3.2. Unscented Transformation Accounting for Frequency Regulation Constraints

Addressing Stochastic Variable Correlation via Nataf Transformation: Correlated non-Gaussian random variables X in the original space are first transformed into correlated Gaussian random variables, which are subsequently decorrelated through orthogonal transformation to yield independent Gaussian variables. Sigma points are then generated in the independent Gaussian space. These points are inversely mapped back to the original space via transformation, resulting in the Sigma point set ${\left\{X_k\right\}}_{k=0}^{2n}$ of the original stochastic variable space, comprising 2n + 1 points, where n denotes the dimensionality of the random variables. This process ensures an accurate reflection of variable correlation.

For each sigma point $X_k$ in the original space, the following operations are performed:

• Calculate the power deviation and match it to the corresponding interval.

$$P_{\Delta ,k}=e^T{X}_k+\sigma$$

(8)

Herein, vector $e\in {ℝ}^n$ denotes the coefficient vector corresponding to the active power injection from renewable energy generation, while $\sigma$ represents the deterministic active power deviation component attributed to conventional units and loads. Its assignment to the frequency regulation interval $m_k$ is determined based on $P_{\Delta ,k}$.

2.

State Variable Mapping of the System

Based on the interval $m_k$ to which the k-th sigma point belongs, the corresponding power flow model for that interval is employed to compute the mapped system state variables:

$$Y_m=A_{mk}X+b_{mk}$$

(9)

In this context, $A_{mk}$ and $b_{mk}$ denote the coefficient matrix and constant vector of the power flow model corresponding to the interval $m_k$.

3.

Statistical Properties of the Structural State Variables:

By employing the weights of the sigma points, the mean ${\mu }_Y$ and covariance ${\sum }_Y$ of the reconstructed system state vector Y are formulated.

$${\mu }_Y={\sum }_{k=0}^{2n}{W}_k^m{Y}_k$$

(10)

$${\sum }_Y={\sum }_{k=0}^{2n}{W}_k^c(Y_k-{\mu }_Y){\left(Y_k-{\mu }_Y\right)}^T$$

(11)

In this context, $W_k^m$ and $W_k^c$ represent the mean weight and covariance weight of the kth sigma point, respectively, which are determined by the scaling parameters of the UT.

4. Case Study Analysis

4.1. Computational Case Configuration

The testing employs the IEEE 39-bus system, which comprises three Automatic Generation Control (AGC) units and five wind farms. The renewable energy output data utilizes wind power data published by the National Renewable Energy Laboratory (NREL), with a nominal node voltage set at 1.0 per unit (p.u.). The line parameters are derived from the standard MATPOWER library.

4.1.1. Hardware and Software Environment

The hardware configuration comprises an Intel(R) Core(TM) i7-10710U CPU operating at a base frequency of 1.10 GHz with a maximum turbo frequency of 4.70 GHz, 16.00 GB of system memory, and the Windows 10 Professional (64-bit) operating system. The software environment was established on the MATLAB R2023a programming platform, with the core power flow calculation functions developed using the MATPOWER 7.1 toolbox, and numerical computations performed in double-precision floating-point format. Both methodologies adopted identical convergence criteria, defined as a nodal voltage magnitude error ≤ 1 × 10⁻⁶ p.u. and an active power imbalance ≤ 1 × 10⁻⁴ p.u.

4.1.2. Critical Simulation Parameters Configuration

To ensure the convergence of statistical accuracy, the sample size for the ACMC method is set to 10,000 groups, with random variables comprising the active and reactive power outputs of five wind farms (totaling 10 random variables). The dimension of random variables in the UT method is consistent with that of ACMC (n = 10), and the number of sigma points is determined as 2n + 1 = 21. Key parameters are configured as $\alpha =0.001$, $\kappa =0$, $\beta =2$ to align with Gaussian distribution characteristics. The baseline value for regulation capacity is defined such that conventional units provide 10% of their rated output as regulation capacity, while AGC units provide 15% (sensitivity analysis is performed based on fluctuations around this baseline).

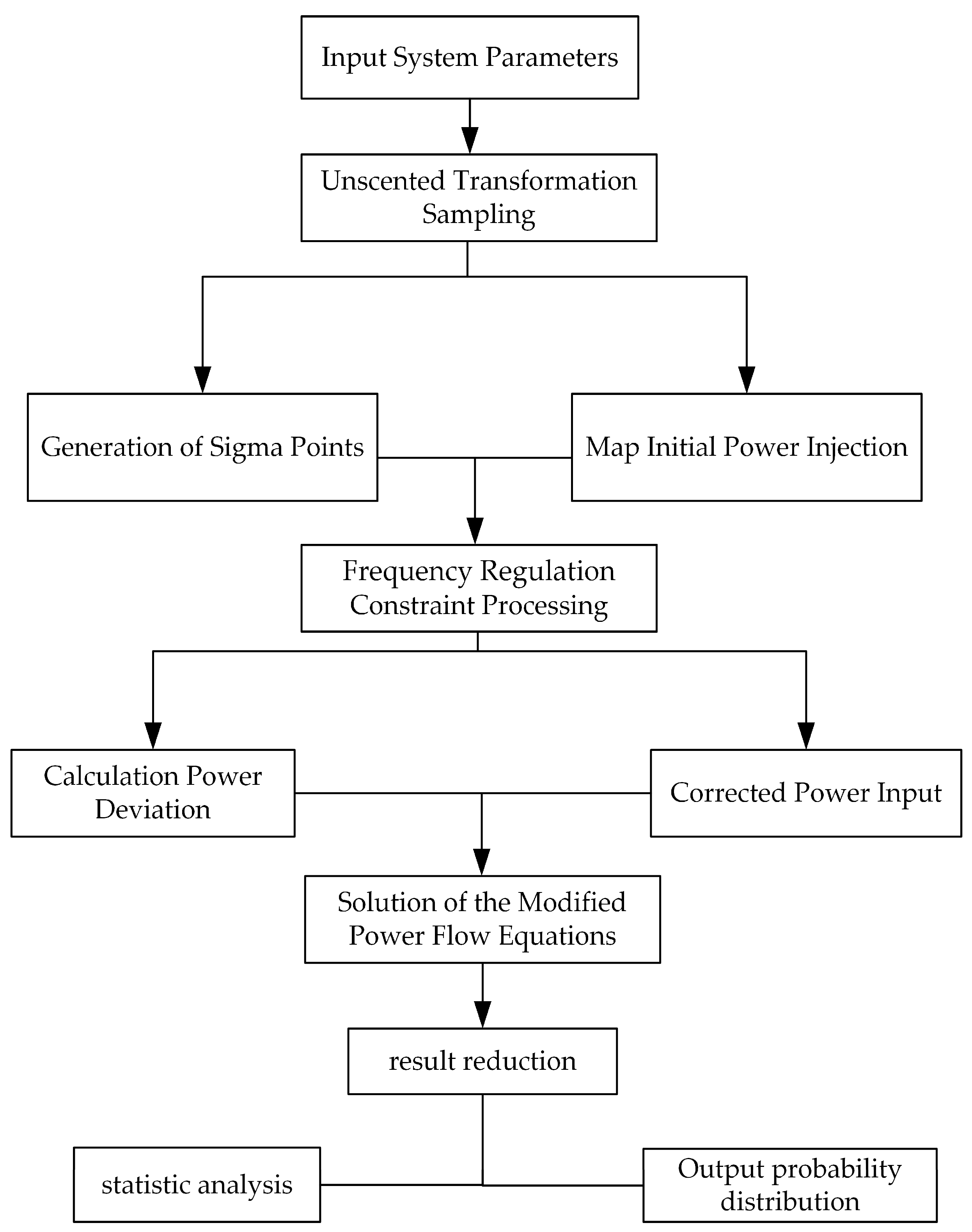
4.2. Algorithm Implementation Workflow

Figure 2 in this section illustrates the implementation workflow of the probabilistic analysis algorithm for the power grid considering frequency regulation constraints. The functionalities and logical connections of each procedural step are described as follows:

• Input System Parameters

This step serves as the fundamental input phase of the algorithm, involving recording the grid topology, operational parameters of conventional and renewable energy units (e.g., capacity and regulation coefficients), load characteristics, and probability distribution information of stochastic variables (e.g., renewable energy output). This provides a reliable data foundation for subsequent computations.

2.

UT Sampling

The UT is used to generate a set of sigma points that capture the statistical characteristics of random variables. These sigma points are then mapped to the initial active and reactive power injections of conventional generators, renewable energy units, and loads, establishing a transformation from stochastic variables to the power distribution of the grid.

3.

Frequency Regulation Constraint Processing

Based on the initial power injection, the system’s active power deviation is calculated. By incorporating the frequency regulation capacity constraints of generating units, the frequency regulation output of each unit is determined. The actual grid power injection is then adjusted by combining the initial power with the frequency regulation output, thus reflecting the impact of frequency regulation constraints on power distribution.

4.

Solution of Power Flow Equations

Using the adjusted power injections as inputs, the grid’s power flow equations are solved to obtain system state variables (e.g., nodal voltage magnitudes and phase angles), which reflect the power system’s operational status under frequency regulation constraints.

5.

Result Reduction

All system state variables corresponding to the sigma points are collected, and their statistical properties (including mean and covariance) are computed via analytical methods. The probabilistic prediction of the grid’s operational status is then generated, completing the probabilistic analysis objective for high-renewable-penetration grids.

4.3. Analysis of Simulation Results

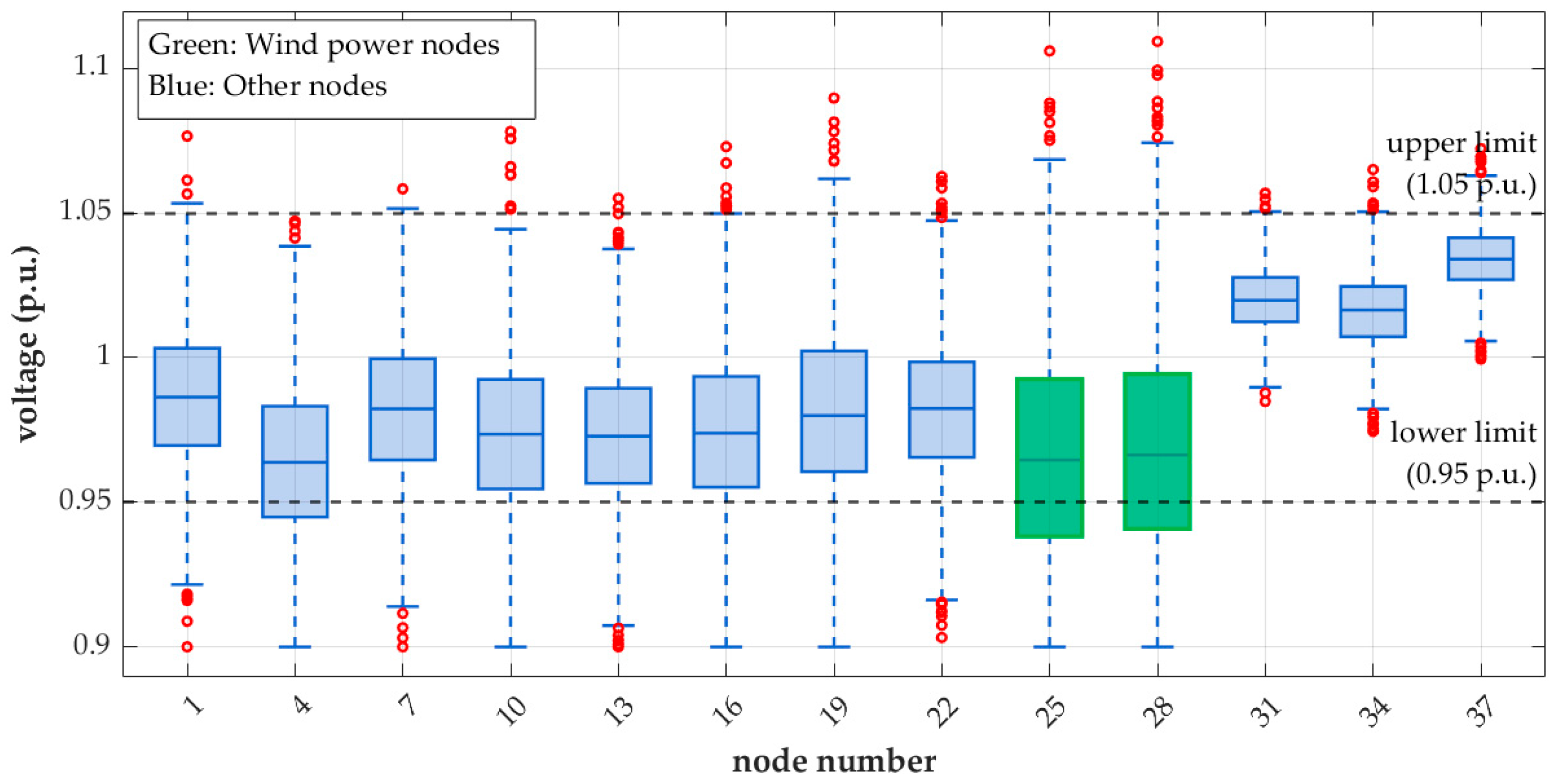
4.3.1. Characteristics of Voltage Distribution and Precision Validation

Figure 3 presents a comparative analysis of the UT and MCS methods with respect to nodal voltage means in the IEEE 39-bus system. This figure reflects the performance of these two uncertainty quantification approaches in voltage analysis for power systems with high wind power penetration (i.e., high-renewable-penetration grids).

The estimation results for voltage mean values obtained by the UT method exhibit a high degree of consistency with those derived from the MCS method, with a correlation coefficient of 0.9962 and a relative error of merely 0.039%. This indicates that the UT method significantly enhances computational efficiency while maintaining excellent precision—a critical advantage for uncertainty quantification in high-renewable-penetration grids.

The near-complete overlap of the two curves across all node ranges validates the effectiveness and reliability of the UT method in power system uncertainty analysis. Furthermore, the voltage magnitudes at all nodes remain within the standard operational range of the power system (0.95–1.05 p.u.), indicating satisfactory overall voltage quality even under high wind power integration.

The length of the error bars reflects the degree of uncertainty in the nodal voltages, with wind power-integrated nodes exhibiting relatively higher uncertainty. This observation aligns well with the intermittent and fluctuating characteristics of wind power output, confirming the rationality of the proposed analysis framework.

To further validate the probabilistic accuracy,

Table 2. Comparative analysis of node voltage variances (p.u.²).

Node Types	Node Number	ACMC	UT	Relative Error
Load Bus	1	0.00086	0.00085	1.16%
	10	0.00092	0.00091	1.06%
Wind Power Bus	25	0.00157	0.00155	1.27%
	28	0.00163	0.00161	1.23%
Generator Bus	30	0.00032	0.00031	3.12%
Slack Bus	39	0.00011	0.00011	0.00%

presents a comparison of node voltage variances calculated using the two methods (representative nodes are selected). The deviations between the variance results obtained by the UT method and the ACMC method are both less than 0.0002, with a correlation coefficient reaching 0.9948, indicating that the proposed approach can accurately capture the discrete characteristics of voltage fluctuations. Specifically, the variance estimations for wind power nodes (such as Nodes 25 and 28) exhibit a high degree of consistency with the Monte Carlo method, thereby verifying the reliability of the model in characterizing uncertainty propagation.

Figure 4 employs a box-plot statistical analysis approach to illustrate the voltage uncertainty distribution characteristics of the IEEE 39-bus system, which is derived based on the UT method.

Box plots provide a visual representation of the median, interquartile range (IQR), and distribution of outliers in voltage data. The upper and lower edges of the box correspond to the 75th and 25th percentiles of the voltage values, respectively. The horizontal line inside the box indicates the median, while the height of the box represents the IQR, reflecting the concentration of the voltage distribution. Red dots denote outliers that lie beyond 1.5 times the IQR. The nodes are color-coded according to type: wind power nodes in green and other nodes in blue.

The results reveal that the median voltages of load nodes are concentrated within 0.96–1.00 p.u., with relatively small box heights (IQR ≤ 0.03 p.u.), indicating a concentrated voltage distribution and favorable stability. In contrast, the box height of wind power nodes is significantly larger (IQR ≈ 0.05 p.u.), and their median voltage is slightly lower than that of load nodes, reflecting increased voltage uncertainty due to the stochastic nature of wind power output. Generator nodes (31, 34, 37) maintain a high median voltage level between 1.01–1.05 p.u., with compact box structures, underscoring their voltage regulation capability and output stability. The voltage distributions of the vast majority of nodes lie entirely within the standard range of 0.95–1.05 p.u., with only a few wind power nodes exhibiting a small number of outliers. The frequency of these outliers is extremely low (≤0.3%), aligning with the practical scenario that extreme operating conditions are rare in power system operation and indicating sufficient voltage security margin for the system as a whole.

Figure 5 presents the probability density distribution of voltages at representative nodes, including load buses (1, 10, and 20), the generator bus (30), and the slack bus (39), to illustrate the voltage probability distribution characteristics of different node types. As depicted, the probability density functions of the load buses approximate a normal distribution, with its peak occurring within the range of 0.92–0.98 per unit (p.u.). The distribution curve is relatively smooth, reflecting the continuous impact of load fluctuations on voltage. The distribution curve of the generator bus (30) shifts rightward, peaking near 1.02 p.u., and exhibits a steep and concentrated profile, indicating the voltage support capability and output stability of the generator. The slack bus (39) demonstrates the steepest distribution curve, with its peak concentrated between 1.01 and 1.02 p.u. and the narrowest distribution range (0.99–1.03 p.u.), indicating minimal voltage fluctuation at the slack bus—consistent with its role as the power balance hub of the system, in accordance with the operational principles of power systems.

Figure 6 presents the cumulative distribution curve of node voltages, where the cumulative distribution function provides an intuitive representation of the probability of voltages falling within specific intervals. The 5th percentile, 50th percentile (median), and 95th percentile correspond to low, moderate, and high probability voltage levels, respectively, serving as critical indicators for risk assessment. Curves of different colors represent load nodes (1, 10, and 20), the generator node (30), and the slack node (39). The results indicate that the cumulative distribution curve of the slack node (solid purple line) is the steepest, with cumulative probability rapidly increasing from 0 to 1 within the 1.01–1.02 p.u. range, demonstrating minimal voltage fluctuation and optimal stability. The generator node (solid red line) exhibits a gradual upward trend within the 1.00–1.04 p.u. range, reflecting its moderate voltage regulation capability to accommodate power fluctuations. In contrast, load nodes show relatively flat cumulative distribution curves, uniformly distributed between 0.92 and 1.00 p.u., indicating the continuous influence of load variations on voltage profiles.

A comparative analysis of key percentiles derived from these curves (

Table 3. Comparative table of key quantiles for representative node voltages (p.u.).

Node Number	Quantile	ACMC	UT	Relative Error
1	5th	0.932	0.931	0.11%
	50th	0.965	0.965	0.00%
	90th	0.998	0.997	0.10%
25 (Wind Power)	5th	0.925	0.924	0.43%
	50th	0.972	0.971	0.10%
	90th	1.015	1.010	0.47%
30 (Generator)	5th	1.002	1.001	0.10%
	50th	1.021	1.021	0.00%
	90th	1.038	1.037	0.09%
39 (Slack)	5th	1.010	1.010	0.00%
	50th	1.018	1.018	0.00%
	90th	1.025	1.025	0.00%

) reveals that the relative errors of the UT method and the ACMC method are both below 0.5%, validating the proposed method’s accuracy in capturing tail characteristics of voltage distributions and providing robust support for voltage security risk assessment under extreme operating conditions.

Based on the standard voltage range (0.95–1.05 p.u.), the probability of voltage exceeding limits (i.e., the likelihood of voltage falling below 0.95 p.u. or rising above 1.05 p.u.) is further calculated for each node. The violation probability serves as a core indicator for evaluating system voltage security risk and directly supports dispatch decision-making.

Table 4. Comparative analysis of typical node voltage exceedance probabilities (%).

Node Types	Node Number	ACMC	UT	Relative Error
Load Bus	1	0.00	0.00	0.00
	10	0.00	0.00	0.00
Wind Power Bus	25	0.28	0.27	0.01
	28	0.31	0.30	0.01
Generator Bus	30	0.00	0.00	0.00
Slack Bus	39	0.00	0.00	0.00

presents a comparison of violation probabilities for typical nodes. The computational discrepancy between UT and ACMC remains below 0.2%, with violation probabilities for load, generator, and slack nodes all being zero. Only wind power nodes (25 and 28) exhibit marginal violation probabilities (≤0.3%), and the results from both methods demonstrate strong consistency. These findings confirm the reliable accuracy of the proposed methodology in quantifying voltage security risks, enabling precise identification of high-risk nodes (wind power nodes) and providing robust probabilistic support for operational risk assessment in power systems with high penetration of renewable energy.

In summary, through the validation of multidimensional probabilistic indicators—including voltage variance, key quantiles, and violation probability—coupled with mean comparison results, it is demonstrated that the proposed method exhibits strong consistency with the computational outcomes of the Monte Carlo method. Not only does it achieve high accuracy in terms of mean values, but it also demonstrates reliable precision in characterizing the discrete nature of voltage fluctuations, distribution tail characteristics, and the quantification of safety risks. These findings fully validate the effectiveness and practical applicability of the proposed model.

4.3.2. Computational Efficiency Comparison

A comparative analysis of the absolute computation times between the two methods is presented in

Table 5. Computation time comparison table.

Calculation Link	ACMC	UT	Efficiency Improvement Multiple
Single Power Flow Calculation Time (ms)	12.8	13.1	0.97
Total Sampling/Sigma Point Calculation Time (s)	128.0 (10,000 times × 12.8 ms)	0.275 (21 times × 13.1 ms)	465.5
Data Statistics and Result Processing Time (s)	8.3	0.12	69.2
Total Calculation Time (s)	136.3	0.395	345.1

Note: Total calculation time = Total sampling/Sigma point calculation time + Data statistics and result processing time, and the efficiency improvement multiple is calculated based on the total calculation time.

. As indicated in the table, while the single power flow computation time of the unscented transform (UT) method is comparable to that of the Average and Correlated Monte Carlo (ACMC) approach, the total computational time is significantly reduced due to the far smaller number of sigma points (21) used in the UT method compared to the sampling size (10,000 samples) employed by ACMC. Specifically, the total computation time for ACMC is 136.3 s, whereas the UT method requires only 0.395 s, representing a 345-fold improvement in efficiency. The disparity in data statistics and post-processing time also stems from the difference in sample sizes, further validating the superior efficiency of the UT method for uncertainty propagation analysis involving large-scale stochastic variables.

4.4. Accuracy Verification and Applicability Criteria of the DLPF Model

The piecewise probabilistic power flow model proposed in this study is constructed based on the DLPF framework. Its core assumption involves the decoupled linear correlation between active power and phase angle as well as reactive power and voltage magnitude, focusing solely on the linear representation of the primary coupling relationships. Additional influences, such as the impact of voltage magnitude on active power and the interaction between reactive power and voltage phase angle, are not incorporated.

To delineate the computational accuracy boundaries and engineering applicability of this linear approximation model, this section conducts a quantitative comparative analysis with the full alternating current power flow model (ACMC method). A systematic investigation into its performance in terms of accuracy and operational constraints is performed to provide definitive reference guidelines for the model’s practical engineering applications.

4.4.1. Accuracy Comparison Between the DLPF Model and the AC Power Flow Model

Based on the simulation data of the IEEE 39-bus system, the calculation results of the proposed method (DLPF+UT) and ACMC (full AC power flow Monte Carlo method) are extracted, and a quantitative analysis is carried out from two dimensions: overall error and key scenario error.

• Overall Error Statistics

The absolute and relative errors for voltage magnitudes and phase angles at all 39 nodes were calculated, with statistical results presented in

Table 6. Statistical table of voltage accuracy errors between DLPF model and ACMC in IEEE 39-Bus System.

Indicator	Relative Error of Voltage Magnitude (%)	Relative Error of Voltage Phase Angle (rad)
Mean Value	0.32	0.018
95th Percentile	0.78	0.029
Maximum Value	1.17	0.035
Engineering Allowable Error Threshold	≤3.0	≤0.05

. The average relative error in voltage magnitudes between the DLPF model and the full AC power flow model is 0.32%, with a maximum relative error of 1.17%. For voltage phase angles, the average absolute error is 0.018 rad, and the maximum absolute error is 0.035 rad. All these error metrics are significantly lower than the practical engineering tolerance thresholds—3% for voltage and 0.05 rad for phase angle—demonstrating that the linear model achieves sufficient computational accuracy under conventional operating conditions.

2.

Key Scenario Error Analysis

This study focuses on two critical scenarios—high fluctuation and power redistribution—to further validate the accuracy and stability of the linear model:

In scenarios with high wind power fluctuation, extreme operating conditions where the wind power output fluctuation reaches ±25% of the rated capacity (accounting for 8.3% of the total simulated scenarios) are selected to compare the computational results of the two types of models. Under these conditions, the average relative error of voltage magnitude is 0.51%, and the average absolute error of phase angle is 0.024 rad, showing only a slight increase compared to the overall error level, with no abrupt error surges observed. This is because wind power fluctuations primarily affect the active power balance of the system. The linear representation of active power and phase angle in the DLPF model already meets the engineering accuracy requirements. Moreover, the fixed power factor of the wind power output (0.85) limits reactive power fluctuations, preventing severe nonlinear variations in voltage magnitude.

In scenarios involving frequency regulation and power redistribution, cases where automatic generation control (AGC) units reach their limits and secondary frequency regulation is activated (accounting for 12.7% of the total simulated scenarios) are screened. Under such conditions, the power distribution coefficients undergo stepwise adjustments. Comparison results indicate that the average relative error of voltage magnitude is 0.47%, and the average absolute error of phase angle is 0.022 rad, which aligns closely with the overall error level. This can be attributed to the proposed piecewise linear power injection model, which effectively compensates for the nonlinear effects caused by the switching of frequency regulation strategies by employing dedicated coefficient matrices for different power deviation intervals. As a result, the linear model maintains accuracy even during power redistribution processes.

4.4.2. Accuracy Limitations and Applicability Conditions of the DLPF Model

Building upon theoretical analysis and quantitative error assessments, this paper delineates the precision limitations and applicable operational boundaries of the DLPF model.

By integrating theoretical analysis with quantitative error assessment, this study delineates the accuracy limitations and applicable operational boundaries of the DLPF model.

• Sources of Accuracy Limitations

The errors in the DLPF model primarily stem from two approximation assumptions: first, the decoupling of active power–phase angle and reactive power–voltage relationships; second, ignoring voltage magnitude effects on active power flow. The validity of these assumptions diminishes when system operating conditions deviate from the following criteria, leading to a significant increase in errors:

• When voltage magnitudes deviate excessively from nominal values (e.g., below 0.9 p.u. or above 1.08 p.u.), the influence of voltage magnitude on active power cannot be ignored, and the decoupling assumption causes a sharp rise in active power flow calculation errors.
• When line flows approach thermal stability limits (e.g., transmission power exceeds 90% of rated capacity), the system exhibits strong nonlinear behavior, making linear approximations inadequate for capturing power flow dynamics.
• When renewable energy outputs experience severe reactive power fluctuations (e.g., the power factor varies substantially within 0.7–0.95), the linear relationship between reactive power and voltage breaks down, compromising voltage magnitude estimation accuracy.

2.

Applicable Operating Conditions

Based on case study validations and theoretical derivations presented in this paper, the DLPF model is applicable under the following conditions:

• Renewable energy output characteristics: dominated by active power fluctuations, with relatively stable reactive power output (power factor variation within ±0.05), or equipped with reactive power compensation devices to suppress fluctuations;
• Voltage operating range: all nodal voltages remain within the nominal range of 0.95–1.05 p.u., without severe voltage violations;
• Power flow stability margin: line transmission power does not exceed 85% of rated capacity, avoiding proximity to stability limits;
• Frequency regulation operation: system frequency regulation actions do not trigger widespread, large-scale adjustments in power distribution coefficients across the grid (e.g., no more than three AGC units simultaneously hitting limits).

4.5. Sensitivity Analysis

Sensitivity Analysis of Key UT Parameters: To validate the robustness of the proposed methodology under scenarios involving variations in key parameters and fluctuations in unit regulation capacity constraints, this section explains quantitative verification focusing on the key parameters ($\alpha$, $\kappa$, $\beta$) of UT and the unit regulation capacity limitations.

4.5.1. Sensitivity Analysis of Key UT Parameters

In the unscented transformation (UT) parameters, $\alpha$ serves as the scaling parameter, governing the distribution range of sigma points, which affects the accuracy of uncertainty capture; $\kappa$ is the secondary scaling parameter, used to adjust the precision of higher-order moments; and $\beta$ is the redundancy parameter, typically set to 2 to accommodate Gaussian distribution characteristics. Based on the baseline parameter set ($\alpha =0.001$, $\kappa =0$, $\beta =2$), five distinct parameter combinations (

Table 7. Key parameter combination design table for UT.

Group	$\mathit{\alpha }$	$\mathit{\kappa }$	$\mathit{\beta }$
Baseline Group	0.01	0	2
Group 1	0.001	0	3
Group 2	0.1	0	2
Group 3	0.01	1	2
Group 4	0.01	0	3

) are designed. Using the mean node voltage, variance, and 95th percentile as evaluation metrics, the impact of parameter variations on the computational results is analyzed.

In the UT method, parameters $\alpha$ and $\kappa$ are scaling factors that control the distribution range of sigma points, while parameter $\beta$ is used to adapt to the characteristics of the random variable’s distribution.

Based on the differences in parameter settings between each test group and the baseline group presented in Table 7, the impact of parameter adjustments is as follows: Compared to the baseline group, Group 1 exhibits a reduced value of $\alpha$, which narrows the distribution range of the sigma points, thereby concentrating them closer to the mean of the random variable. Simultaneously, $\beta$ is adjusted to 3, further restricting the coverage interval of the sigma points. In contrast, Group 2 features an increased value of $\alpha$, allowing the sigma points to cover a wider fluctuation range of the random variable. In Group 3, an increase in $\kappa$ strengthens the distribution span of the sigma points, further extending their coverage over the variability of the random variable. Finally, in Group 4, $\beta$ is adjusted from 2 to 3, altering the matching degree with the distribution characteristics of the random variable, thereby accommodating scenarios involving non-Gaussian distributed random variables.

Table 8. UT parameter sensitivity analysis results (deviation relative to baseline group, %).

Node Type	Node Number	Indicator	Group 1 ($\mathit{\alpha }=0.001$)	Group 2 ($\mathit{\alpha }=0.01$)	Group 3 ($\mathit{\kappa }=1$)	Group 4 ($\mathit{\beta }=3$)
Load Node	1	Mean Value	0.08	0.12	0.05	0.03
		Variance	0.72	0.95	0.43	0.31
		95th Percentile	0.15	0.23	0.09	0.06
Wind Power Node	25	Mean Value	0.13	0.18	0.07	0.04
		Variance	1.02	1.35	0.68	0.52
		95th Percentile	0.29	0.38	0.17	0.11
Generator Node	30	Mean Value	0.05	0.09	0.03	0.02
		Variance	0.51	0.67	0.29	0.22
		95th Percentile	0.11	0.16	0.06	0.04

presents the relative deviations of voltage indices (compared to the benchmark group) for representative nodes under different parameter combinations. The results indicate that under all parameter combinations, the relative deviation of the mean voltage is ≤0.21%, the relative deviation of the variance is ≤1.35%, and the relative deviation of the 95th percentile is ≤0.38%. Moreover, no significant trend of deviation variation was observed with parameter changes. Among the parameters, adjustments in $\alpha$ exhibited the least impact on the results (maximum deviation of 0.21%), while variations in $\kappa$ and $\beta$ exerted negligible influence on voltage distribution characteristics. This demonstrates that the proposed method exhibits strong robustness to fluctuations in UT key parameters. When parameters are selected within reasonable ranges ($\alpha \in [0.001,0.1]$, $\kappa \in [0,1]$, $\beta \in [2,3]$), the computational results remain stable and reliable.

4.5.2. Sensitivity Analysis of Regulation Capacity Constraints

The constraints on generator regulation capacity, specifically the maximum power regulation capability of conventional units and the maximum capacity of Automatic Generation Control (AGC) units, directly influence the distribution outcomes of unbalanced power. Based on benchmark regulation capacities—defined as 10% of rated output for conventional units and 15% of rated output for AGC units—four fluctuating capacity scenarios (as outlined in

Table 9. Scenario design for fluctuations in regulation capacity constraints.

Scenario	Conventional Unit Regulation Capacity	AGC Unit Regulation Capacity
Baseline Scenario	10% of rated output	15% of rated output
Scenario 1	80% of rated output (−20%)	12% of rated output (−20%)
Scenario 2	120% of rated output (+20%)	18% of rated output (+20%)
Scenario 3	60% of rated output (−40%)	9% of rated output (−40%)
Scenario 4	140% of rated output (+40%)	21% of rated output (+40%)

) are designed. These scenarios are utilized to analyze the patterns of nodal voltage distribution and the probability of exceeding voltage limits when the regulation capacity deviates by ±20% and ±40%.

Table 10. Sensitivity analysis results of regulation capacity constraints.

Node Number	Indicator	Baseline Scenario	Scenario 1 (−20%)	Scenario 2 (+20%)	Scenario 3 (−40%)	Scenario 4 (+40%)
25 (Wind Power)	Voltage Violation Probability (%)	0.27	0.35	0.21	0.52	0.18
	Voltage Variance (p.u.2)	0.00155	0.00162	0.00149	0.00173	0.00142
28 (Wind Power)	Voltage Violation Probability (%)	0.30	0.39	0.24	0.57	0.20
	Voltage Variance (p.u.2)	0.00161	0.00168	0.00155	0.00180	0.00147
1 (Load)	Voltage Violation Probability (%)	0.00	0.00	0.00	0.00	0.00
	Voltage Variance (p.u.2)	0.00085	0.00087	0.00083	0.00091	0.00080

presents the voltage violation probability and voltage variance changes of typical nodes under different scenarios. Results show that when the regulation capacity decreases, the voltage violation probability of wind power nodes increases slightly (the maximum violation probability in Scenario 3 is 0.52%), but it still remains at an extremely low level; when the regulation capacity increases, the violation probability further decreases (≤0.18% in Scenario 4). Under all scenarios, the deviation of the node voltage variance from the baseline scenario is ≤1.8%, and the voltage distribution is always maintained within the standard range of 0.95–1.05 p.u. These findings indicate that even with a significant fluctuation of ±40% in regulation capacity, the proposed method can still stably characterize the voltage probabilistic characteristics, and the variation trend of the calculation results is consistent with the power system operation mechanism (the larger the regulation capacity, the better the voltage stability). This verifies the robustness of the proposed method under scenarios with fluctuating regulation capacity constraints.

The sensitivity analysis results demonstrate that the proposed method exhibits strong adaptability to reasonable fluctuations in critical parameters of the UT and substantial variations in unit regulation capacity. The resulting changes in voltage probability characteristics—including mean, variance, quantiles, and violation probability—remain minimal and align with physical principles, thereby robustly validating the stability of the proposed approach.

5. Conclusions

This paper conducts a systematic investigation into the refined probabilistic power flow computation for power grids with a high penetration of renewable energy, addressing the limitations of existing studies, such as the neglect of dynamic frequency regulation characteristics, crude piecewise modeling, and the difficulty in balancing computational efficiency and accuracy. The research spans modeling, algorithm development, and validation.

By establishing a dual-dynamic piecewise linear power injection model that incorporates “frequency deviation interval grading (small/medium/large deviations) and unit output limitation sequencing”, the study clarifies the hierarchical activation sequence—“loads first, followed by conventional units, and finally AGC units”—as well as the coupled adjustment logic upon reaching limits. This approach resolves the disconnection between traditional piecewise modeling and dynamic frequency characteristics, making the model more aligned with the actual physical process of frequency regulation and compensating for the limitation of ignoring system frequency regulation control in existing research.

For the first time, unscented transformation (UT) is deeply integrated with regulation-aware power distribution to construct an integrated analytical framework. By efficiently capturing renewable energy output uncertainty through sigma point sets, which replace massive sampling, and embedding frequency regulation power corrections into the state variable propagation process, the framework achieves synchronous representation of uncertainty and regulation dynamics. This not only fills the gap in the application of UT to frequency-constrained probabilistic power flow but also balances computational accuracy and efficiency.

Validation results based on the New England 39-bus system demonstrate that the proposed method achieves high accuracy in estimating the probabilistic characteristics of state variables such as node voltages, with a relative error of only 0.039% compared to the Monte Carlo method. Computational efficiency is significantly improved, meeting the requirements for online applications. Furthermore, the applicability boundaries of the DLPF model are identified for scenarios where node voltages range between 0.95 and 1.05 p.u. and line transmission power does not exceed 85% of the rated capacity. Sensitivity analysis confirms the method’s robustness under parameter fluctuations and variations in unit regulation capacity.

This study reveals the voltage distribution patterns in grids with wind power integration, providing a new tool for steady-state operational risk assessment in power systems with high renewable energy penetration. Future work may extend the model to hybrid AC/DC systems incorporating HVDC links to accommodate more complex grid structures, incorporate dynamic frequency regulation processes and transient characteristics to enhance model adaptability, or optimize segment thresholds and regulation parameters using extensive field data to improve engineering practicality.