Flow Loss and Transient Hydrodynamic Analysis of a Multi-Way Valve for Thermal Management Systems in New Energy Vehicles

Abstract

With the rapid advancement of integrated thermal management systems (ITMS) for new energy vehicles (NEVs), flow losses and hydrodynamic characteristics within multi-way valves have become critical determinants of system performance. In this study, a three-dimensional computational fluid dynamics model is established for a multi-way valve used in a representative NEV ITMS, where PAG46 coolant is employed as the working fluid. The steady-state pressure-loss characteristics under three typical operating modes—cooling, heating, and waste heat recovery—are investigated, together with the transient hydrodynamic response during mode switching. The steady-state results indicate that pressure losses are primarily concentrated in regions with abrupt changes in flow direction and sudden variations in cross-sectional area, and that the cooling mode generally exhibits the highest overall pressure loss due to the involvement of all flow channels and stronger flow curvature. Furthermore, a parametric analysis of the valve body corner chamfers and valve spool fillets reveals a non-monotonic dependence of pressure drop on chamfer radius, highlighting a trade-off between streamline smoothness and the effective flow cross-sectional area. Transient analysis, exemplified by the transition from heating to waste heat recovery mode, demonstrates that dynamic changes in channel opening induce a significant reconstruction of the internal velocity and pressure fields. Local high-velocity zones, transient pressure peaks, and pronounced fluctuations of hydraulic torque on the valve spool emerge during the switching process, imposing higher requirements on the torque output and motion stability of the actuator mechanism. Consequently, this study provides a theoretical basis and engineering guidance for the structural optimization and actuator matching of multi-way valves in NEV thermal management systems.

1. Introduction

With the rapid advancement of electric vehicles, aerospace engineering, and high-end equipment manufacturing, requirements for thermal safety, energy efficiency, and reliability at the system level have become increasingly stringent. Consequently, thermal management systems are evolving toward highly integrated and efficient architectures [1]. By deeply integrating multiple heat sources—such as batteries, electric motors, and passenger cabins—with compressors, expanders, and heat exchangers, an ITMS can achieve synergistic utilization of cold and heat sources within stringent space and weight constraints [2,3].

In such systems, the multi-way valve serves as a pivotal component. By enabling flexible switching and precise regulation of coolant flow channels, it directly determines the flow distribution among circuits, the response speed of thermal equilibrium, and the overall operational efficiency and safety of the system [4,5]. In advanced EV thermal management platforms, a single multi-way valve can facilitate rapid switching between various operating modes, including cooling, heating, and waste heat recovery. It provides active cooling or preheating for the battery pack, manages air conditioning and heating for the passenger cabin, and coordinates the motor cooling circuit, thereby significantly enhancing energy utilization efficiency and the vehicle’s driving range.

Current investigations into valve pressure drop and internal flow characteristics have predominantly focused on conventional configurations, such as four-way valves, spool valves, and globe valves. Conversely, research concerning multi-way valves with more complex structures remains relatively limited. Previous studies have established that the working fluid undergoes a significant pressure reduction in localized regions when passing through a valve. Specifically, Edvardsen et al. [6] and Rahmatmand et al. [7] experimentally investigated single-phase flow in globe valves and thermostatic mixing valves, respectively. Their findings indicated that abrupt changes in internal geometry are the primary cause of substantial pressure drops. Using numerical methods, Tripathi et al. [8] compared two reversing valves with distinct structures, confirming that variations in the valve spool configuration result in significant differences in pressure drop characteristics. Furthermore, numerical simulations conducted by Ye et al. [9] on needle valves demonstrated that the fluid experiences a drastic pressure drop within the throttling region when the valve opening is small. Experimental results from Hemamalini et al. [10] further revealed that the maximum pressure drop in control valves can reach up to 68 times that of the pipeline, exhibiting an inversely proportional relationship with the valve opening. Synthesizing these findings, it is evident that pressure losses primarily occur in regions where the flow direction and cross-sectional area change abruptly; these losses generally decrease as the valve opening increases.

To enhance hydrodynamic performance and optimize pressure characteristics, researchers have extensively focused on the modification of key structural parameters, specifically by reconstructing flow channel topologies and wall curvatures to mitigate local losses or regulate pressure drops. Qian et al. [11] optimized the length of the throttling gap, which ameliorated the internal flow field distribution, increased the pressure differential across the valve, and improved the overall throttling efficiency. Zhang et al. [12] modified the internal valve profile from a linear to a circular arc configuration, effectively mitigating the sudden pressure surges observed under small opening conditions. Monika et al. [13] investigated multi-stage Tesla valves and achieved an optimal configuration balancing pressure drop and heat dissipation performance by varying the number of channels and valve spacing. Furthermore, Gan et al. [14] systematically analyzed the impact of geometric parameters—including stage count, inlet width, and channel depth—on labyrinth valve performance. Their findings indicated that increasing the stage count and inlet width while decreasing channel depth facilitates higher pressure drops, thereby optimizing the design of high-resistance labyrinth valves. Collectively, existing studies demonstrate that the synergistic optimization of flow channel shapes and key geometric parameters enables precise regulation of pressure drop and flow field characteristics, providing significant references for valve structural design.

In the field of valve hydrodynamics, flow forces are generally categorized into steady-state and transient forces based on flow regimes. Steady-state flow forces correspond to the force characteristics under fixed operating conditions where flow parameters remain time-invariant. Conversely, transient flow forces primarily stem from fluid inertia variations induced by spool motion and flow rate fluctuations, typically occurring during mode switching or start-stop processes. The magnitude and direction of these forces directly dictate the load characteristics of the driving motor, representing a fundamental research focus in fluid power transmission and control [15,16]. Regarding structural optimization, Simic et al. [17] demonstrated that by optimizing the structural parameters of the valve spool and body, flow forces could be reduced while improving response time by approximately 20% and reducing power consumption by 10%. The 3D CFD simulations and experimental results by Lisowski et al. [18] indicated that an increase in the internal flow rate of a directional control valve significantly amplifies the flow force, thereby disrupting the original force equilibrium of the spool. Furthermore, Gao et al. [19] revealed a dual effect of flow forces in high-flow directional valves, characterized as “initially assisting, subsequently resisting” the spool motion: the force acts as a driving force during the startup phase and transitions to a resistive force once the displacement exceeds a certain threshold. Wu et al. [20] changed the angle between the intake port in the valve sleeve and the valve spool axis to compensate for the valve’s hydrodynamic forces. Consequently, clarifying the evolution laws of steady-state and transient flow forces with respect to structural parameters and flow variations is critical for optimizing spool dynamic characteristics and the matching design of the driving motor.

In recent years, numerical modelling has become an indispensable tool for valve design and flow analysis, as it can resolve the internal hydrodynamics in complex geometries at a much lower cost than purely experimental approaches. Brazhenko et al. [21] developed a CFD model of a semi-direct acting water solenoid valve using measured diaphragm displacements from a transparent prototype, and showed that the simulated pressure drop and internal flow structure agree well with experimental data, demonstrating that properly validated CFD models can reliably support valve design and optimization. Hadebe et al. [22] further combined CFD and finite-element analysis to investigate a non-return multi-door reflux valve, using a detailed 3D model and mesh-independence testing to evaluate pressure drop, flow coefficient and backflow-prevention performance under different operating conditions, and showed that numerical simulations can capture the key flow and structural features of multi-port valves. More recently, Yu et al. [23] carried out a numerical study of a diaphragm valve and systematically compared several turbulence models and inlet boundary conditions, finding that the SST k–ω model provides the best agreement with measured head-loss data over a range of openings. These studies confirm that CFD-based numerical valve models, when combined with appropriate turbulence modelling and validation, can accurately predict valve hydraulic performance. Building on this foundation, the present work adopts the SST k–ω model and a mesh-independent grid to simulate the internal flow and pressure characteristics of the proposed coolant control valve during mode switching.

Despite significant progress in investigating the flow losses, structural optimization, and hydrodynamic characteristics of traditional valves, there remains a lack of systematic research regarding multi-way valves within integrated ITMS. These valves are characterized by highly complex topological structures and multiple flow channels. In particular, the mechanisms of steady-state pressure loss and the laws of transient hydrodynamic response require further exploration. Consequently, existing findings cannot be directly applied to guide the structural design and actuator selection for multi-way valves in the ITMS of NEVs. To address this gap, this study focuses on a multi-way valve utilized in the ITMS of a specific NEV. By employing three-dimensional numerical simulation, the flow loss mechanisms and hydrodynamic characteristics under typical operating modes are systematically investigated.

The main contributions and innovations of this paper are summarized as follows:

A three-dimensional geometric model and a multi-condition hydrodynamic model for the multi-way valve in the Integrated Thermal Management System of electric vehicles were established. High-fidelity flow field simulations were realized under three typical operating modes: cooling, heating, and waste heat recovery. The study deeply investigated the pressure loss distribution characteristics within the complex multi-channels and precisely quantified the proportions and influence mechanisms of local resistance loss versus frictional resistance loss in the total pressure drop.

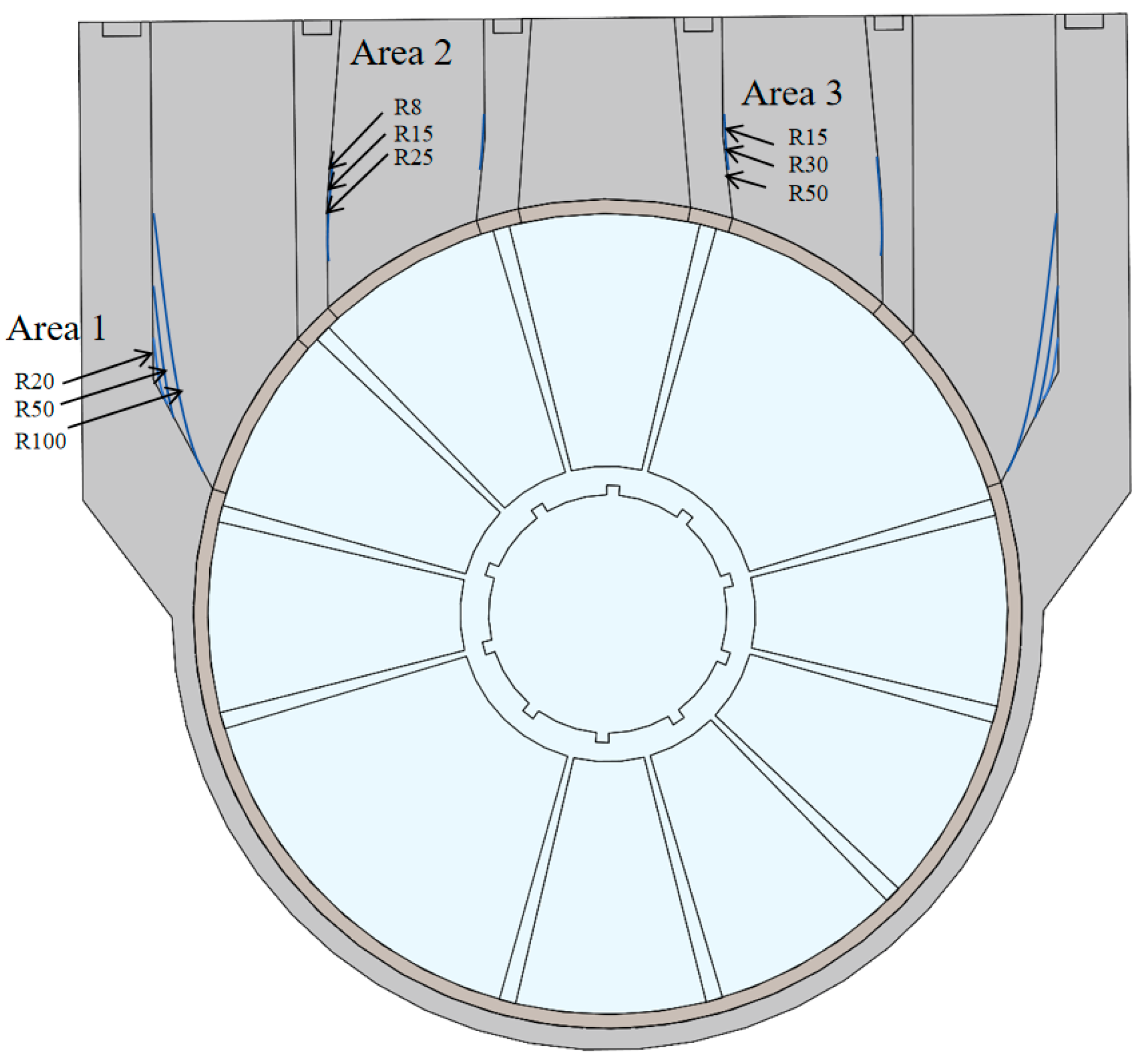
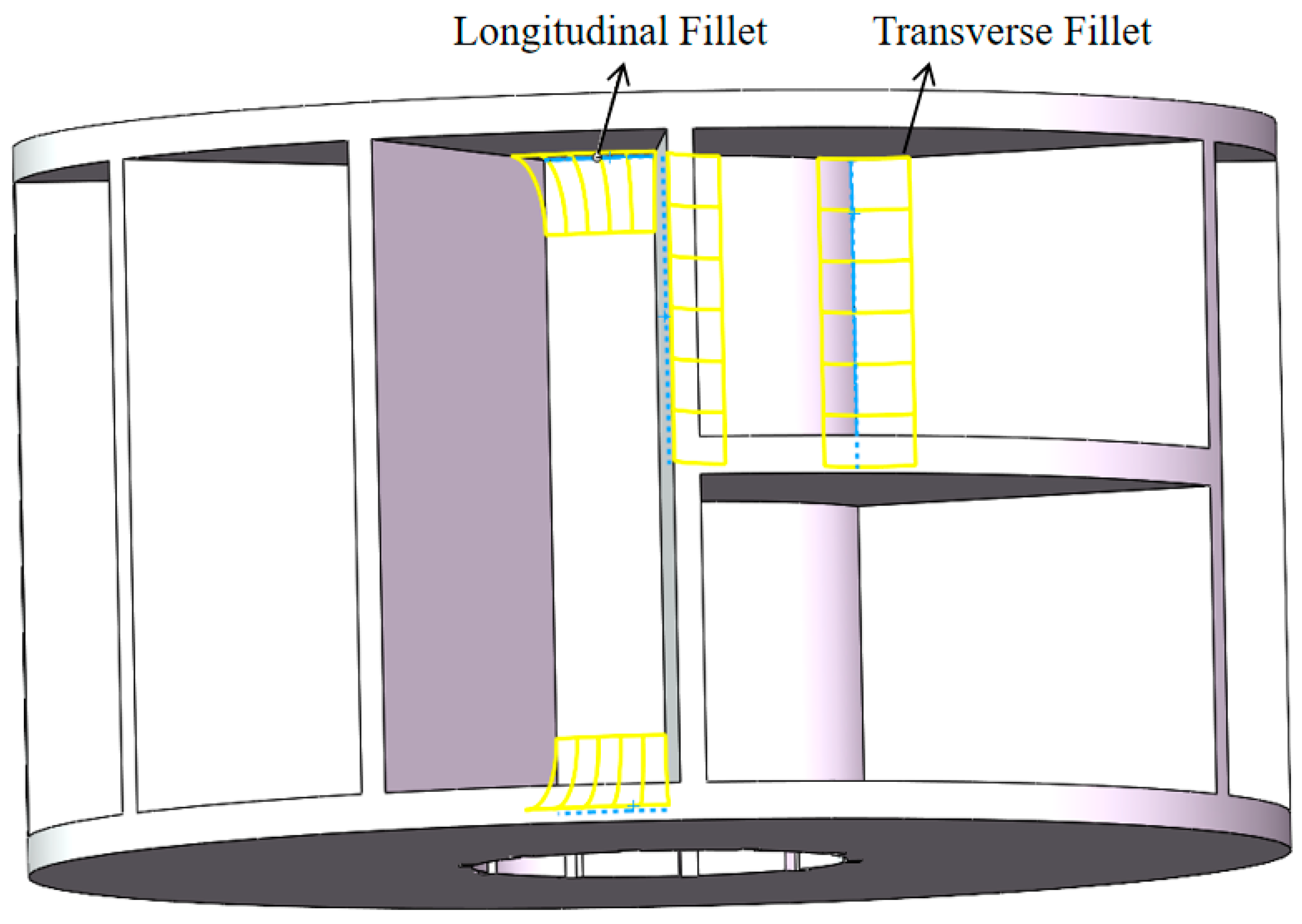
Based on the sensitivity analysis of key structural parameters, geometric optimization criteria for the flow channels were proposed. Through a parametric study on the valve body corner chamfers and the longitudinal/transverse fillets inside the valve spool, the non-monotonic evolution law of flow channel pressure drop with respect to geometric parameters was revealed. Furthermore, the competitive coupling mechanism between flow direction smoothness and effective flow cross-sectional area was elucidated, providing a clear quantitative basis for the low-flow-resistance design of multi-way valves.

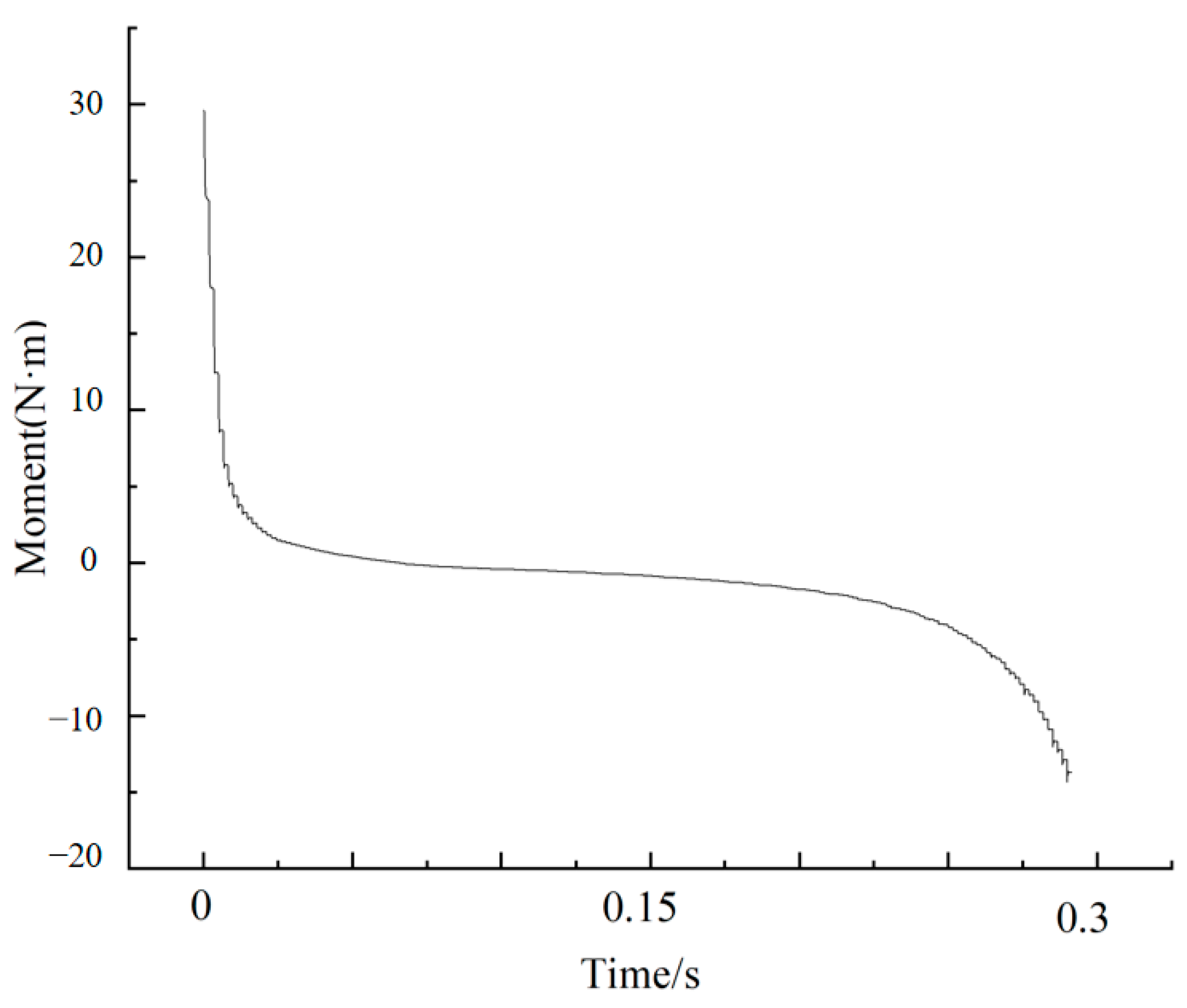
A transient computational model for the dynamic switching process of the valve spool was constructed, addressing the limitations of steady-state analysis. The dynamic process of the valve spool rotating from the heating mode to the waste heat recovery mode was simulated. The time-varying characteristics of the velocity field, pressure field, and hydraulic torque on the valve spool during the switching period were analyzed. The study captured the critical moments when local pressure peaks and hydraulic torque peaks occurred during the transient process, offering significant guidance for actuator selection and the formulation of control strategies.

2. Numerical Model and Computational Method

Thermal management technology is pivotal to the advancement of NEVs. It requires the efficient regulation of temperature fields across multiple heat sources—including batteries, motors, and passenger cabins—under complex operating conditions. Consequently, it directly influences vehicle performance, safety, and user experience. As a critical component of the integrated vehicle thermal management system, the multi-way valve plays an essential role in system performance. In this study, a geometric model is established for a multi-way valve within a specific thermal management system, and its characteristics are investigated using numerical simulation.

2.1. Structure and Operating Modes of the Multi-Way Valve

The multi-way valve investigated in this study is integrated into the integrated thermal management systems of a NEV. The ITMS employs PAG46 coolant to regulate the temperatures of key components, including the battery, motor, compressor, expander, and the indoor and outdoor heat exchangers. By coordinating the operation of these components, the ITMS enables flexible switching among cooling, heating, and waste heat recovery modes to meet thermal management requirements under different driving conditions. In the ITMS considered in this work, thermal energy is transported by a circulating liquid coolant, denoted as PAG46. Specifically, PAG46 refers to an ISO VG 46 polyalkylene glycol (PAG)-based working fluid, as defined by the ISO viscosity classification standard [24].

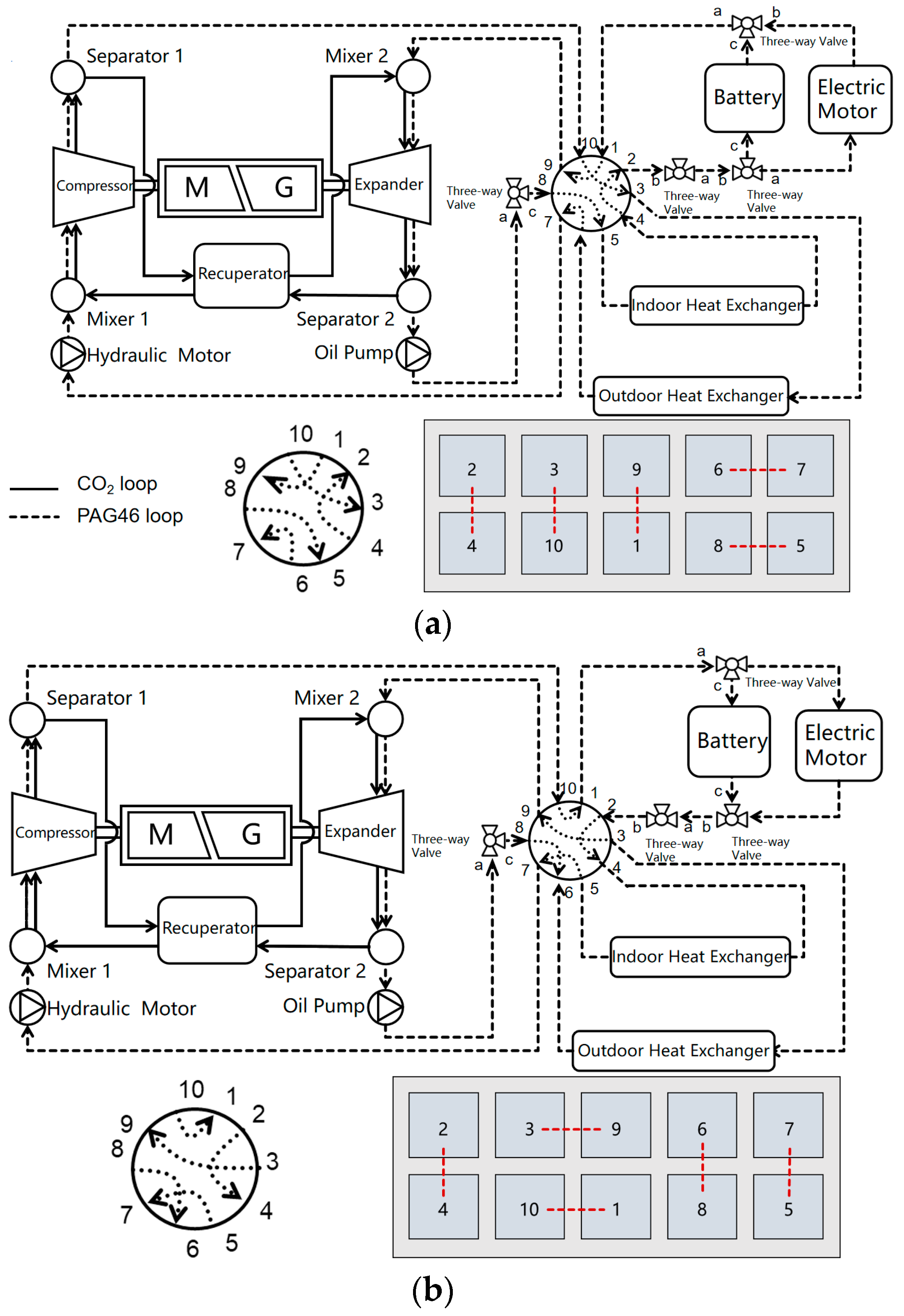
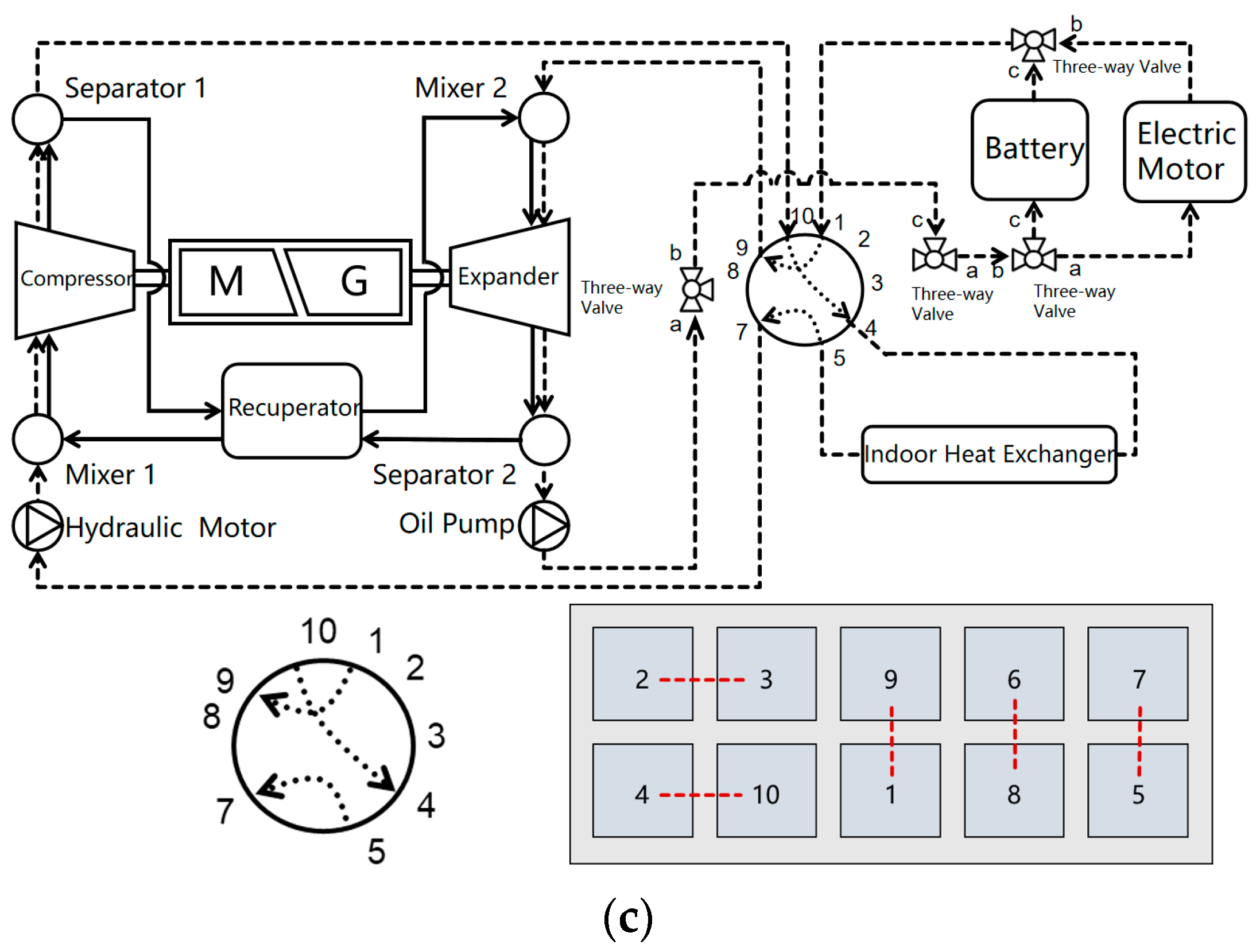
The investigated ITMS is a sensible-heat heat-exchange system; therefore, the coolant remains in the liquid state and no phase change is involved in the loop under the studied conditions. Accordingly, the internal flow in the multi-way valve is treated as single-phase liquid flow in the numerical model. Figure 1. Schematic of the investigated integrated thermal management system (ITMS) and the three operating modes of the multi-way valve: (a) cooling mode, (b) heating mode, and (c) waste-heat recovery mode. Solid lines indicate the CO₂ loop, and dashed lines indicate the PAG46 coolant loop. Arrowheads denote the bulk flow direction in each loop. The multi-way valve is a 10-port rotary valve (ports 1–10); in each mode, the spool connects ports in pairs to form the corresponding flow channels. The dotted flow paths inside the valve symbol illustrate the internal passages opened by the spool position, and the red dashed links in the inset highlight the active port-pair connections for each mode. Mixer 1/2 denote junctions where streams merge, and Separator 1/2 denote phase separators in the CO₂ loop. Oil pump circulates the PAG46 coolant, and hydraulic motor provides the driving power for the coolant circulation unit. M and G denote the motor and generator coupled to the compressor/expander shaft. In this study, PAG46 is treated as a single-phase liquid under the investigated conditions. In this context, the ‘cooling’ and ‘heating’ modes refer to specific ITMS flow-path topologies designed to prioritize cabin climate control while simultaneously managing the thermal requirements of the battery and powertrain. Typically, the cooling mode is activated under high ambient temperatures, whereas the heating mode is engaged at lower temperatures to facilitate both cabin heating and battery preheating. Furthermore, the waste-heat recovery mode is specifically utilized to harvest and repurpose excess thermal energy generated by the battery and traction components.

In the cooling mode Figure 1a, the high-temperature PAG46 coolant discharged from the compressor flows through the multi-way valve to the outdoor heat exchanger, where it releases heat to the ambient environment before returning to the compressor. Meanwhile, the low-temperature PAG46 coolant, having passed through the expander, provides cooling for the passenger cabin, battery, and motor circuits.

In the heating mode Figure 1b, the high-temperature PAG46 coolant discharged from the compressor is directed via the multi-way valve to preheat the battery and motor circuits and to supply heat to the passenger cabin. Conversely, the low-temperature PAG46 coolant discharged from the expander absorbs heat from the ambient environment, completing the heat recovery process on the source side.

In the waste heat recovery mode Figure 1c, the low-temperature PAG46 coolant first absorbs excess heat from the battery and motor circuits and then flows back to the expander. Simultaneously, PAG46 coolant in a separate circuit absorbs heat from the passenger cabin and returns to the compressor. In this way, waste heat from multiple components is effectively recovered and reutilized, thereby improving the overall energy efficiency of the ITMS.

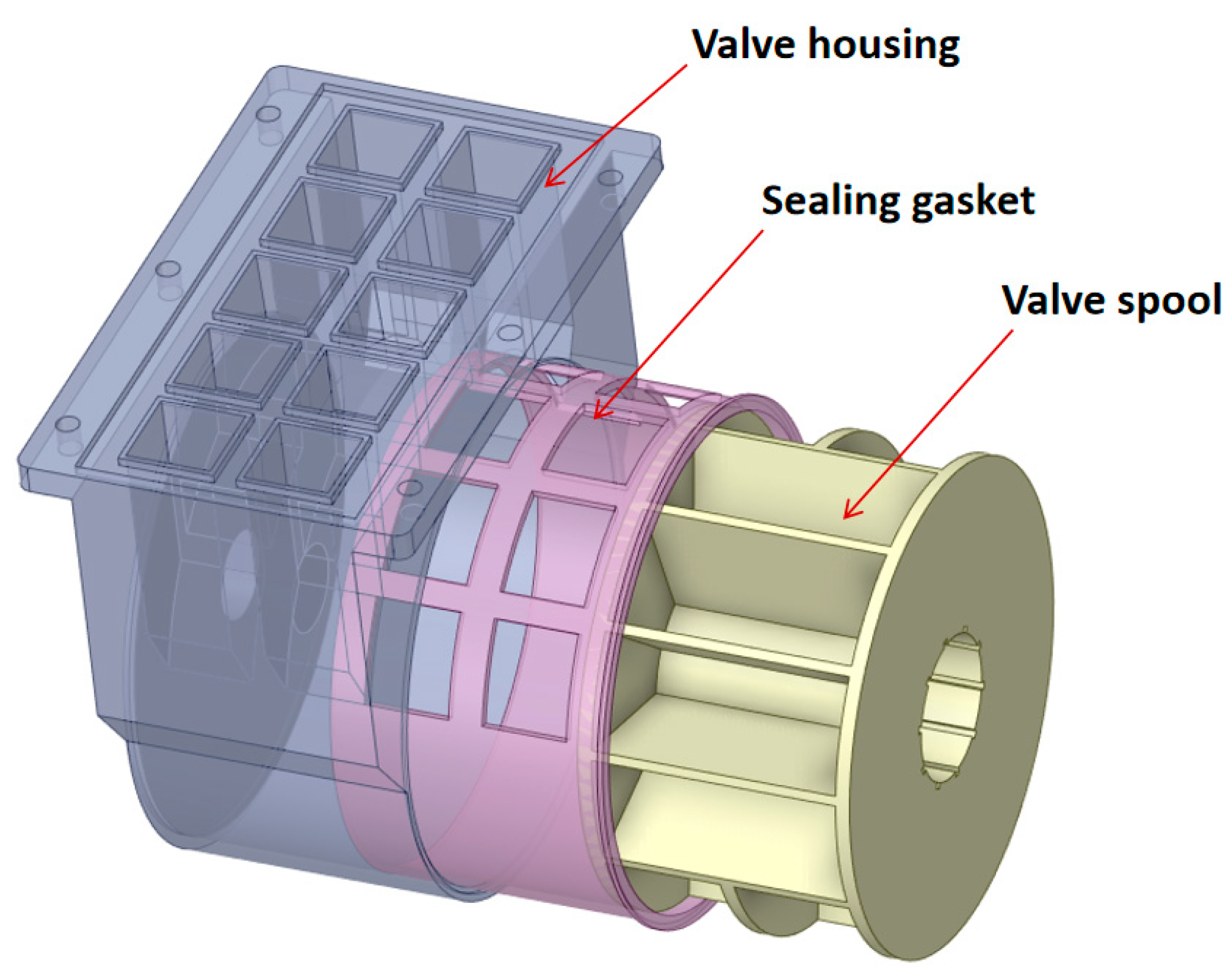
The geometric configuration of the multi-way valve primarily consists of the valve housing, sealing gaskets, and a rotary spool, as illustrated in Figure 2. The valve features ten ports connected to the inlets and outlets of key ITMS components, including the battery, motor, compressor, expander, and the indoor and outdoor heat exchangers. These ports are interconnected in pairs to form five distinct flow channels. The valve body has overall envelope dimensions of 160 mm in width and 155.5 mm in height. Specifically, the inlet and outlet ports feature a side length of 22 mm each, while the internal rotary spool has a diameter of 108 mm and the sealing gasket thickness is 3 mm. These dimensions represent the characteristic scale of the valve used in the ITMS of the investigated new energy vehicle.

Mode switching is achieved by an electric motor that actuates the rotation of the valve spool, thereby altering the connectivity among the ten ports and reconfiguring the internal flow channels. Depending on the spool position corresponding to cooling, heating, or waste heat recovery mode, different subsets of the five flow channels are activated, and the flow paths of the PAG46 coolant are rearranged accordingly.

In summary, the multi-way valve provides a total of ten distinct port connections and five primary flow channels. Structural variations in these channels govern the direction and distribution of the PAG46 coolant under different operating modes, enabling the ITMS to satisfy thermal management requirements across a wide range of operating conditions.

2.2. Governing Equations and Turbulence Model

In this study, the coolant is treated as an incompressible Newtonian fluid. The flow is governed by the continuity equation and the Reynolds-Averaged Navier–Stokes equations, which describe the mass conservation and momentum transport within the multi-way valve. The continuity equation for incompressible flow is expressed as follows:

$$\nabla \cdot u=0$$

(1)

Considering the complex flow field within the multi-way valve, characterized by multiple sharp turns, narrow channels, and significant local flow separation, the RANS momentum equations are employed for the numerical solution:

$$\rho \left({\displaystyle \frac{\partial u}{\partial t}}+u\cdot \nabla u\right)=-\nabla p+\nabla \cdot \left[\left(\mu +{\mu }_t\right)\left(\nabla u+\nabla u^T\right)\right]$$

(2)

The Shear Stress Transport SST k–ω turbulence model does not rely on wall functions in the near-wall region and is capable of directly resolving the viscous sublayer. Consequently, this model is highly suitable for capturing the flow characteristics in this study, particularly the drastic channel variations and significant local separation.

For the numerical solution, the second-order upwind scheme is adopted to discretize the convection terms, and the SIMPLE algorithm is used for pressure-velocity coupling. To satisfy the near-wall resolution requirements of the SST k–ω model, the average dimensionless wall distance (y+) of the mesh is maintained at approximately 0.83. This ensures the accurate prediction of flow structures and pressure gradients in corners, high-velocity regions, and within the valve spool.

2.3. Mesh Generation and Grid Independence Verification

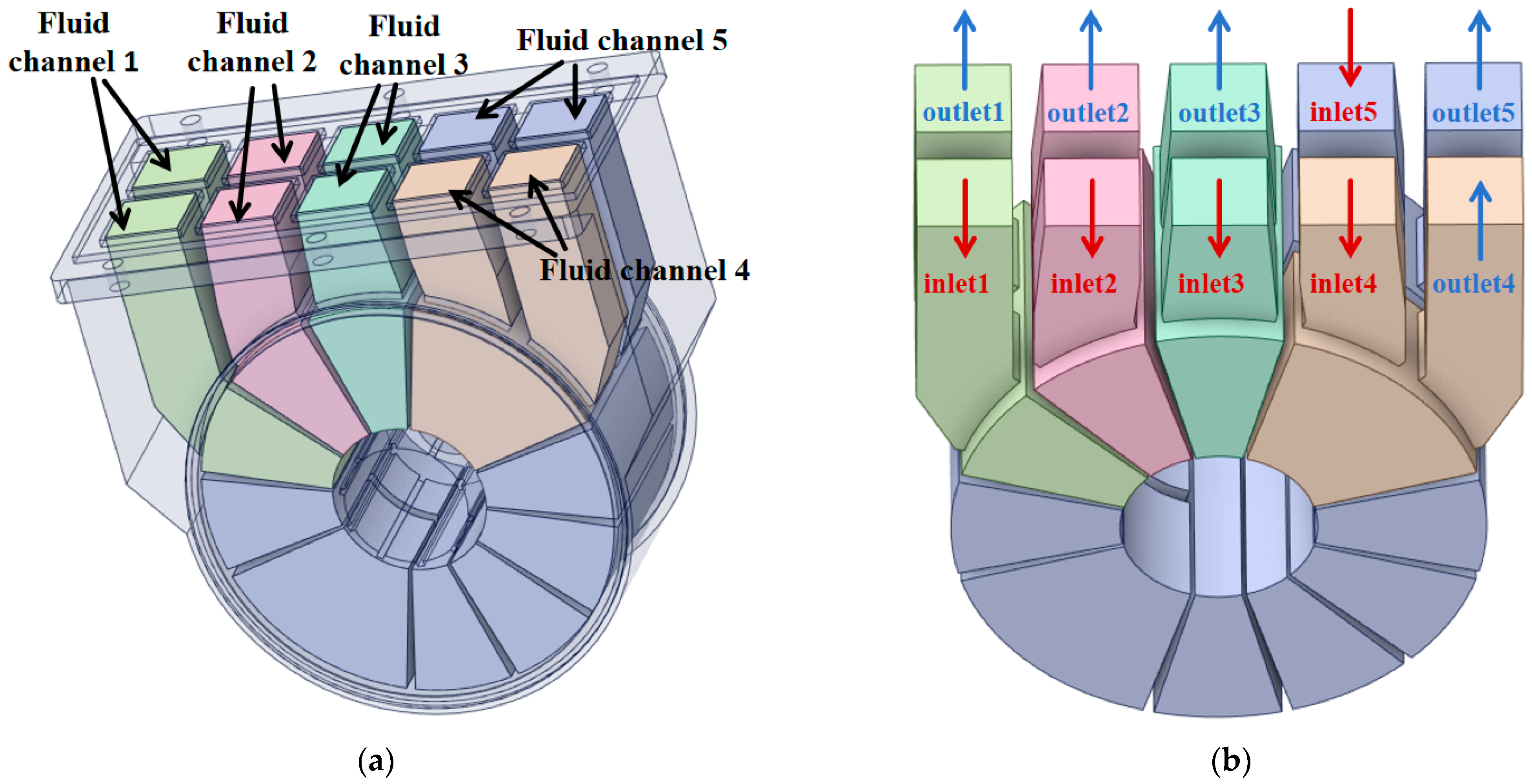
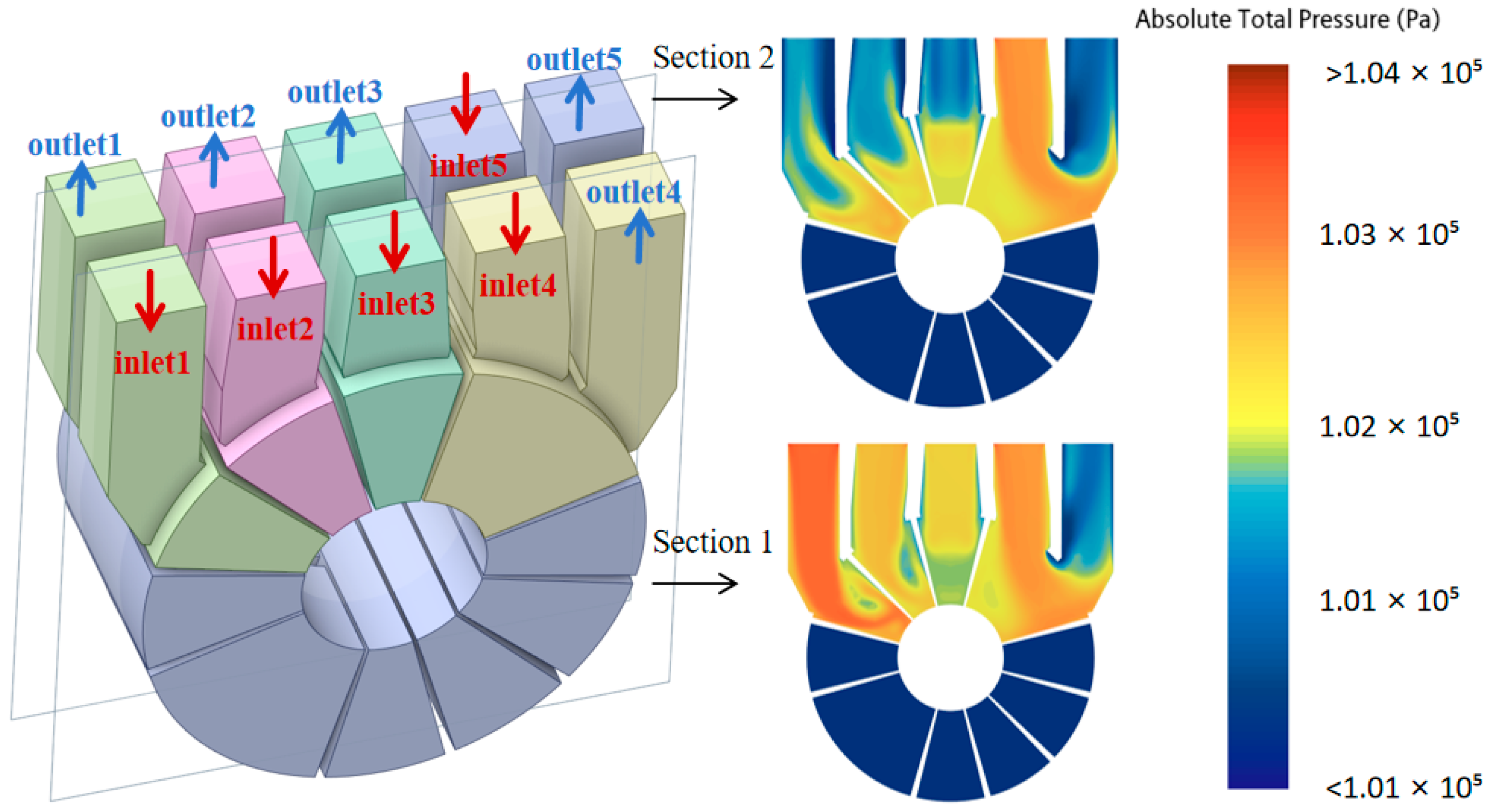
The multi-way valve investigated in this study comprises five flow channels. Following appropriate geometric simplification, the overall simulation model retains only the valve housing, sealing gasket, and valve spool as key components. In both cooling and heating modes, all internal flow channels of the valve are active with coolant flow. For the purpose of illustration, the cooling mode is selected as the representative operating condition: the extracted fluid computational domain is shown in Figure 3a, and the arrangement of the inlets and outlets is presented in Figure 3.

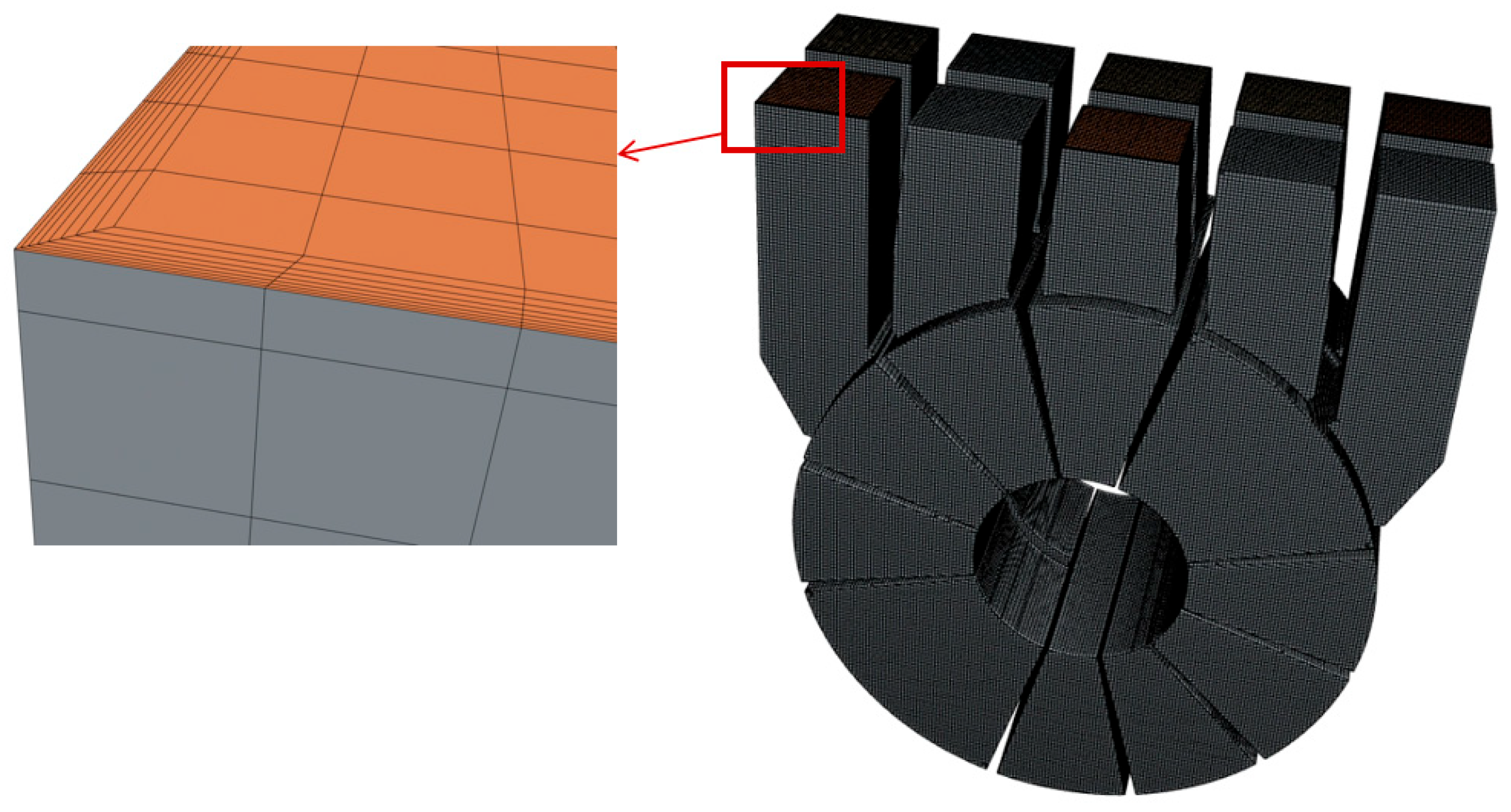
The mesh generation was performed using the automated meshing workflow in STAR-CCM+. The fluid domain was discretized using the Trimmed Cell mesher with a base size of 1 mm. To accurately capture the near-wall flow gradients, boundary layer refinement was implemented using the Prism Layer mesher. Specifically, the boundary layer consisted of 8 prism layers with a stretching ratio of 1.2 and a moderate surface growth rate. The resulting mesh topology and details of the boundary layer refinement are illustrated in Figure 4.

To ensure computational accuracy and improve efficiency, a mesh-independence study was carried out using the pressure drop as the evaluation criterion. Five meshes with total cell numbers ranging from 8.22 × 10⁵ to 3.06 × 10⁶ were generated under the same boundary conditions. The pressure drops in Channel 1 and Channel 4, which have different geometries, were calculated and the results are summarized in

Table 1. Errors under the number of different grids for channel 1.

Number of Grids	Pressure Drop (Pa)	Relative Error (%)	GCI (%)
821,805	1502.31	0.804	0.80
1,324,606	1481.11	0.634	-
1,912,555	1487.72	0.191	0.19
2,431,708	1488.93	0.112	-
3,057,956	1490.57	-	0.14

and

Table 2. Errors under the number of different grids for channel 4.

Number of Grids	Pressure Drop (Pa)	Relative Error (%)	GCI (%)
821,805	1291.48	1.18	1.18
1,324,606	1302.51	2.03	-
1,912,555	1265.90	0.86	0.84
2,431,708	1269.86	0.55	-
3,057,956	1276.63	-	1.40

. When the mesh size reaches approximately 1.9 × 10⁶ cells, the variation in pressure drop between the medium and fine meshes becomes negligible: the relative differences are 0.191% for Channel 1 and 0.86% for Channel 4. Therefore, the mesh with about 1.9 × 10⁶ elements is considered sufficiently grid-independent and is adopted for all subsequent simulations.

To rigorously quantify the discretization uncertainty, a statistical procedure based on the Grid Convergence Index (GCI) was performed following the standard method recommended by Celik et al. [25] Although five grid sets were tested for overall sensitivity, a representative triplet—comprising a fine mesh ($3.06\times {10}^6$ cells), a medium mesh $1.96\times {10}^6$ cells), and a coarse mesh ($0.82\times {10}^6$ cells)—was selected for the formal GCI analysis. The apparent order of convergence ($p$) for Channel 1 and Channel 4 was calculated to be 6.37 and 3.59, respectively. The resulting $GC{I}_{fine}$ values are 0.14% and 1.40%, both of which are significantly below the 5% threshold. This confirms that the numerical solutions are well within the asymptotic range of convergence and the discretization error is negligible.

2.4. Boundary Conditions

Since the investigated ITMS is a sensible-heat heat-exchange system and no phase change in PAG46 occurs under the studied operating conditions, the internal flow in the multi-way valve is modelled as an incompressible single-phase liquid under isothermal conditions. The temperature is fixed at 313 K, and the thermo-physical properties of PAG46 are evaluated at this reference temperature and treated as constants. Therefore, heat transfer and thermal coupling are not activated in the present simulations, and the analysis focuses exclusively on the hydrodynamic characteristics of the flow.

In all simulations, the PAG46 working fluid is modelled as an incompressible Newtonian single-phase liquid, consistent with the fact that the investigated ITMS is based on sensible heat transfer and the coolant does not undergo phase change under the studied conditions. The thermo-physical properties used in the CFD simulations are summarized in

Table 3. Thermophysical properties of PAG46 working fluid used in CFD simulations.

Property	Value	Unit
Density	985	kg·m−3
Dynamic viscosity	0.04984	Pa·s
Specific Heat	1899.0	J/(kg·K)
Thermal Conductivity	0.14	W/(m·K)

(evaluated at T = 313 K and treated as constants).

The inlet boundary condition is prescribed as a mass-flow inlet with a total mass flow rate of 0.84 kg/s. The outlet is set as a pressure outlet with a specified static pressure. All solid walls are treated as no-slip boundaries. For turbulence specification, the inlet turbulence quantities are initialized using standard turbulence intensity/length-scale settings available in STAR-CCM+. The temperature is uniformly set to 313 K for all operating conditions.

3. Results and Discussion

To elucidate the mechanisms governing the internal flow within the multi-way valve, this chapter initially presents numerical simulations conducted on the complete flow channel model. Subsequently, the effects of varying key structural parameters are analyzed to reveal the underlying internal flow evolution patterns and influence mechanisms.

3.1. Steady-State Pressure-Loss Characteristics and Main Loss Regions

The pressure loss within the multi-way valve primarily consists of frictional pressure loss and local pressure loss. Due to the high integration, complex flow channels, and directional switching functions of the multi-way valve, the internal flow field contains sections characterized by abrupt changes in flow direction or cross-sectional area, as shown in Figure 5. Specifically, the flow direction changes frequently within various channels, with the working fluid undergoing multiple turns in certain sections. Furthermore, the cross-sectional area of the flow experiences sudden expansion or contraction as the coolant flows into or out of the valve spool. From a lateral view, the coolant flow typically undergoes a near 90° change in direction when entering or exiting the valve ports. These complex flow structures induce intense vortices and flow separation, exacerbating internal fluid friction and impact. Consequently, local pressure loss becomes the dominant source of the total pressure loss in the multi-way valve.

3.1.1. Pressure, Velocity and Entropy Generation Field Distributions

Two radial cross-sections along the valve spool were selected for analysis. Figure 5 illustrates the internal pressure distribution when the PAG46 coolant inlet mass flow rate is 0.84 kg/s. As the PAG46 coolant flows through the multi-way valve, pressure loss occurs, resulting in a pressure drop at the outlet.

The pressure drops for Channels 1 through 5 are 1487.7 Pa, 976.8 Pa, 925.5 Pa, 1265.9 Pa, and 1342.9 Pa, respectively. Notably, Channels 1, 4, and 5 exhibit significantly higher pressure losses due to their longer flow channels and frequent changes in flow direction. Furthermore, the cross-sectional area of the fluid domain within the valve shell is smaller than that within the valve spool. Consequently, as the coolant flows into and out of the valve spool, it undergoes not only changes in flow direction but also abrupt changes in cross-sectional area. Both of these factors contribute to the total pressure loss.

To further distinguish the frictional losses in straight sections from the local losses induced by geometric discontinuities, Flow Channel 1—with a relatively large overall pressure drop—was selected, and eight monitoring sections were arranged along its length, as shown in Figure 6a. The corresponding pressure distribution is presented in Figure 6b. It can be seen that between Sections 1–4 and 5–8 the pressure decreases only slightly and almost linearly, indicating that frictional losses in these straight or mildly curved segments are relatively small. In contrast, a pronounced pressure drop occurs between Sections 4 and 5, where both the flow direction and the cross-sectional area change abruptly. Specifically, the PAG46 coolant begins to deviate from a straight path at Section 3 and returns to an almost straight flow near Section 6. The pressure drop in this region reaches 877 Pa, accounting for 59% of the total pressure drop. These results demonstrate that the local losses concentrated in a few regions with sharp bends and sudden expansions/contractions dominate the overall pressure drop, whereas the contribution of frictional losses along the remaining channel length is relatively limited.

To better relate the CFD pressure loss to its physical causes, we decompose the total pressure drop into frictional and local losses and compare the dominant loss segment with a simple analytical approximation. The total pressure drop can be expressed as

$$\mathsf{\Delta }p=\mathsf{\Delta }{p}_f+\mathsf{\Delta }{p}_m$$

(3)

where the frictional loss is approximated by Darcy–Weisbach

$$\mathsf{\Delta }{p}_f=f{\displaystyle \frac{L}{D_h}}{\displaystyle \frac{\rho V^2}{2}}$$

(4)

and the local loss is written using minor-loss coefficients (K-value method)

$$\mathsf{\Delta }{p}_m=\sum K_i{\displaystyle \frac{\rho V_i^2}{2}}$$

(5)

To directly compare CFD results with empirical correlations, an equivalent CFD-based loss coefficient is defined as

$$K_{CFD}={\displaystyle \frac{2\mathsf{\Delta }{p}_{CFD}}{\rho V_{ref}^2}}$$

(6)

The disturbed region is bounded by Sections 3–6 because the flow starts to deviate from an almost straight path near Section 3 and returns to a nearly straight state near Section 6, while the pronounced pressure drop occurs around the geometric discontinuity between Sections 4 and 5.

Using mass-averaged total pressures extracted at each monitoring section, the CFD pressure drops are Δp_3–4 = 13.2 Pa, Δp_4–5 = 681.9 Pa, and Δp_5–6 = 181.5 Pa, yielding Δp_3–6 = 876.6 Pa for the disturbed region. Segment 4–5 contributes 77.8% of Δp_3–6, confirming that the losses are dominated by the compound turning discontinuity rather than gradual frictional effects in quasi-linear segments.

As shown in

Table 4. CFD segment losses and equivalent loss coefficients (upstream-velocity reference).

Segment	Aup (mm2)	ΔpCFD (Pa)	Vup (m/s)	KCFD	Share of Δp3–6
3–4	924.86	13.2	0.922	0.0315	1.51%
4–5	1073.58	681.9	0.794	2.1943	77.79%
5–6	1073.58	181.5	0.794	0.5841	20.70%
3–6	924.86 (ref)	876.6	0.922 (ref)	2.0934	100%

, The compound turning in Segment 4–5 is approximated as an equivalent series combination of two 90° turning elements. Typical loss coefficients for 90° elbows reported in common K-value tabulations span roughly K ≈ 0.45 (long-radius) to K ≈ 1.3–1.5 (tighter or more resistive turns). Therefore, an effective ΣKi ≈ 2.2 is used for Segment 4–5 as a compact engineering approximation. Using ρ = 985 kg/m³, coolant mass flow rate ṁ = 0.84 kg/s, and upstream cross-sectional area A₄ = 1073.58 mm², the upstream mean velocity is: $V_4={\displaystyle \frac{\dot{m}}{\rho A_4}}=0.794{\displaystyle \frac{m}{s}},{\displaystyle \frac{\rho V_4^2}{2}}=310.76\mathrm{P}\mathrm{a},$ and the analytical estimate becomes $\Delta p_{4-5,ana}=683.7\mathrm{P}\mathrm{a},$ which is in excellent agreement with CFD (Δp_4–5,_CFD = 681.9 Pa, error ≈ 0.26%). The corresponding CFD-equivalent coefficient is $K_{4-5,CFD}=2.19.$

Figure 7a illustrates the velocity vector distribution at Cross-section 1 of the flow channel. It can be observed that due to variations in the flow cross-sectional area, local high-velocity regions emerge in both Channel 1 and Channel 4 as the coolant enters and exits the valve spool. Specifically, a vortex is generated within Channel 1 near the valve spool. Furthermore, the abrupt change in flow direction at the outlet of Channel 4 induces significant flow separation, resulting in substantial flow losses. Figure 7b shows the contours of entropy generation at the same cross-section. It is evident that the entropy generation is highly localized, with the dominant contribution arising from the near-wall boundary layer and a few pronounced local peaks occurring around the outer-wall side of the curved section, the expansion corners, and the separation zones downstream of the abrupt turning near the outlet of Channel 4. These locations coincide with jet impingement/reattachment and separation-vortex–induced shear-layer development, which significantly increase local velocity gradients, thereby intensifying irreversibility and leading to the observed entropy generation maxima. In contrast, the core flow in the relatively straight regions remains at a low level, indicating that localized wall friction and separation-induced mixing/dissipation dominate the overall entropy generation.

3.1.2. Comparison of Pressure Drops Across Multiple Channels and Operating Modes

This study primarily focuses on the cooling mode. As previously described, the multi-way valve operates in three distinct modes, toggled by rotating the valve spool by 60° and 30°, respectively. These modes involve a total of 10 flow channels with varying structural geometries. To quantify the pressure loss characteristics for each channel under different modes, the calculated pressure drop results are summarized in Figure 8.

At an inlet mass flow rate of 0.84 kg/s, the pressure drops for Channels 6 through 10 are 977.1 Pa, 1484.3 Pa, 629.1 Pa, 641.6 Pa, and 1316.9 Pa, respectively. The total pressure losses for the three operating modes were calculated to be 5998.8 Pa, 5219.9 Pa, and 3726.7 Pa, respectively. The waste heat recovery mode exhibits a lower pressure loss because only a portion of the channels are active. In contrast, the cooling mode involves full-channel flow, resulting in the maximum pressure loss. Consequently, subsequent research and analysis will focus on the cooling mode, which represents the most critical hydraulic condition.

3.2. Impact of Key Structural Parameters on Steady-State Hydrodynamic Characteristics

The preceding pressure drop analysis indicates that pressure losses are primarily concentrated in regions characterized by pipe bends, abrupt changes in flow direction, and variations in cross-sectional area. Consequently, the subsequent investigation focuses on parametric structural modifications targeting these critical regions to evaluate their influence on the flow field.

3.2.1. Impact of Pipe Shape Parameters on Pressure Loss

Given that Channel 4 and Channel 5 possess nearly identical geometric shapes, Channel 4 is selected as the representative model for the optimization analysis. Channel 3 offers limited scope for optimization due to structural constraints. Furthermore, considering the symmetrical distribution of the overall multi-way valve structure, the optimization process focuses on the three corner regions illustrated in Figure 9. The specific fillet radii used for optimization are detailed in

Table 5. Fillet radii of the three regions.

Chamfer Radius of Area 1/mm	Chamfer Radius of Area 2/mm	Chamfer Radius of Area 3/mm
20	4	12
50	8	25
80	15	38
100	20	50

.

Applying fillets to the optimization regions inherently alters the cross-sectional area. Due to the symmetry of the multi-way valve, Channel 5 exhibits properties identical to Channel 4; thus, the analysis focuses on Channel 4. Since Channels 1 and 4 encompass all optimization regions, their pressure drops are selected as the primary indicators for evaluation. As illustrated in Figure 10, at a mass flow rate of 0.84 kg/s, the flow cross-sectional area decreases continuously as the fillet radius increases, while the pressure drop exhibits a trend of initial decrease followed by an increase. Specifically, Channel 1 achieves minimal pressure loss when the fillet radii for the three regions are 50 mm, 8 mm, and 25 mm, respectively. Similarly, Channel 4 reaches its minimum pressure loss at radii of 20 mm, 4 mm, and 12 mm.

Mechanistically, introducing fillets at the pipe wall mitigates abrupt changes in flow direction but simultaneously encroaches upon the original flow channel, thereby reducing the available effective flow cross-sectional area. To quantify this trade-off, the minimum effective flow area in Channel 1 was extracted for several representative fillet-radius combinations in Areas 1–3. Taking the baseline geometry as a reference, a case with relatively small-to-moderate fillet radii (50, 8, and 25 mm) leads to a reduction in the minimum local flow area by about 4.9%, whereas a case with larger fillet radii (100, 20, and 50 mm) results in a reduction of approximately 9.7%. This progressive contraction of the local cross-section is consistent with the trend in Figure 10a: when the fillet radii are increased from the baseline to moderate values, the beneficial effect of smoother flow turning dominates and the pressure drop decreases; when the fillet radii are further increased and the cross-section reduction exceeds about 4.9%, the adverse effect of area contraction becomes dominant and the pressure drop starts to rise again. A similar tendency is observed in Channel 4 Figure 10b.

3.2.2. Influence of Variation in Flow Direction Parameters on Pressure Loss

To investigate the influence of the internal flow direction within the valve spool on the pressure drop characteristics, longitudinal and transverse fillet designs were implemented in the internal channels of the valve spool, while keeping the valve body and external piping structure unchanged, as shown in Figure 11. Specifically, fillets of varying radii were applied to the inlet corners of the valve spool to facilitate a smoother entry of the coolant into the internal channels. Four comparative models were constructed: the Baseline, 10 mm fillet, 20 mm fillet, and 30 mm fillet, as detailed in

Table 6. Fillet radii.

Chamfer Radius of Area 1/mm	Chamfer Radius of Area 2/mm
10	10
20	20
30	30

.

Figure 12 illustrates the impact of the fillet radius on the pressure drop. It can be observed that Channels 2 and 3 involve longitudinal fillets where the change in flow direction is relatively minor. The pressure drop in these channels gradually decreases as the fillet radius increases. This indicates that increasing the fillet radius mitigates the severity of the flow turn and suppresses local flow separation, thereby reducing pressure loss. In contrast, Channel 1 involves a longitudinal fillet at a sharp corner. The pressure drop exhibits a trend of initial decrease followed by an increase. Specifically, the minimum pressure drop is observed at a fillet radius of 20 mm. However, when the radius reaches 30 mm, the pressure drop rises. This suggests that an excessively large fillet radius encroaches upon the original flow channel, causing flow contraction, which leads to increased pressure loss.

Channel 4 involves a transverse fillet modification. As indicated in Figure 12, the pressure loss exhibits a trend of initial increase followed by a decrease, representing a relatively complex pattern. To analyze this, the velocity vector diagram of Channel 4 is presented in Figure 13. In the prototype structure, the cross-section after the valve spool inlet is relatively large, and the mainstream distribution is uniform. Although secondary flows and weak vortices exist at the corner, the scale of flow separation is limited, maintaining a low pressure drop level. With the introduction of 10 mm and 20 mm fillets, the fillet surface encroaches upon the flow cross-section, causing flow contraction at the valve spool inlet. The high-speed mainstream is forced towards the opposite wall, increasing the local velocity peak and shear intensity. Consequently, the separation vortex zone behind the fillet expands, and kinetic energy dissipation increases, resulting in a pressure drop higher than that of the prototype.

When the fillet radius increases to 30 mm, the transition at the valve spool inlet becomes significantly smoother. The streamlines in the mainstream region adhere better to the wall, and the separation vortex and high-shear zones shrink notably, reducing local losses. Although the effective cross-sectional area is slightly reduced, the effects of smoother flow direction and mitigated separation become dominant. This causes the total pressure drop of Channel 4 to decrease to a level approaching that of the prototype, thereby forming the observed trend of initial increase followed by a decrease.

In summary, the steady-state pressure losses of the multi-way valve are primarily concentrated at corners and regions characterized by abrupt changes in flow direction and cross-sectional area. Furthermore, the impact of key structural parameters on the pressure drop varies significantly across different channels. Increasing the corner fillet radius exerts a dual effect. On one hand, it mitigates abrupt changes in flow direction and suppresses separation, which is beneficial for reducing local pressure loss. On the other hand, the fillet encroaches upon the flow cross-section, leading to flow contraction and increased flow resistance. This results in a trend where the pressure drop initially decreases and then increases for certain channels. Specifically, regarding the longitudinal and transverse fillet modifications in the valve spool, the pressure drops of Channels 2 and 3 generally decrease as the fillet radius increases. Conversely, Channels 1 and 4 exhibit complex patterns of initial decrease followed by an increase and initial increase followed by a decrease, respectively. This indicates that structural variations have distinct impacts on different channels, necessitating tailored optimization strategies.

3.3. Analysis of Transient Hydrodynamic Characteristics

In the preceding section, the pressure loss distribution and the influence of key structural parameters under typical operating conditions were systematically analyzed based on steady-state numerical calculations. However, steady-state results only reflect the average force levels at fixed valve openings and cannot reveal the flow field reconstruction and time-varying hydrodynamic characteristics during mode switching. Given that ITMS frequently undergo mode transitions and valve spool rotations in practical operation, this section investigates the transient flow field evolution during the transition from Heating Mode to Waste Heat Recovery Mode, maintaining boundary conditions and geometric parameters consistent with the steady-state analysis.

The analysis encompasses the temporal evolution of the velocity field, pressure field, and the hydrodynamic forces and torques acting on the valve spool. As illustrated in Figure 14, the transition involves a 30° counter-clockwise rotation at a constant speed of 1.75 rad/s.

3.3.1. Transient Hydrodynamic Torque Response Characteristics of the Valve Spool

As shown in Figure 15, the hydrodynamic torque acting on the valve spool during rotation exhibits distinct unsteady characteristics over time. As the valve spool begins to rotate, influenced by the redistribution of pressure across multiple channels and the dynamic changes in channel openings, the pressure field on the two sides of the valve spool rapidly becomes imbalanced. Consequently, the hydrodynamic torque rises rapidly within a short period. In the present case, the maximum transient torque reaches 27.9 N·m, whereas the maximum steady-state torque obtained in the Heating and Waste Heat Recovery modes is only 0.65 N·m. Thus, the transient peak is approximately 42.9 times the steady-state level. The emergence of this peak indicates that the flow-field asymmetry is most pronounced at this stage, and the fluid-induced resistive effect acting on the valve spool attains its highest level.

As the valve spool approaches the Waste Heat Recovery mode, although the channel openings tend to stabilize, the flow rate and pressure drop within each channel have not yet reached equilibrium. Consequently, the hydrodynamic torque reverses direction and acts as a driving torque that assists the rotation. However, to cease rotation precisely at the end of the mode switch, the motor must provide a reverse torque of considerable magnitude. The transient analysis in this section demonstrates that the internal flow and pressure fields of the multi-way valve undergo distinct unsteady reconstruction during mode switching. The dynamic changes in channel openings induce local high-speed zones, pressure peaks, and substantial hydrodynamic torque fluctuations within a short timeframe. Compared with the maximum steady-state torque of 0.65 N·m, the peak transient torque of 27.9 N·m clearly shows that the torque demand during mode switching is dominated by transient effects rather than by the steady hydrodynamic load.

3.3.2. Evolution Characteristics of the Transient Velocity Field

As shown in Figure 16, at t = 0 s, the valve spool remains stationary, and the internal velocity distribution is consistent with the steady-state conditions described earlier. The velocity distribution within the mainstream channels is relatively stable, with only small-scale separation vortices and high-speed jets present at local corners and regions with abrupt cross-sectional changes.

As the valve spool begins to rotate, during the interval from t = 0.1 s to 0.2 s, the opening degree of channels that were originally fully open gradually decreases, while new flow channels are progressively established. During this process, the fluid exhibits significant acceleration and deflection near the valve spool. The extent of local high-speed zones expands, and the intensity of vortices and recirculation zones at certain corners intensifies.

At t = 0.2 s, the mainstream paths within the original channels undergo redistribution. A portion of the high-speed mainstream is directed towards new outlets, causing significant bending of local streamlines. Concurrently, small-scale vortex structures begin to migrate downstream and gradually decay. Although strong jets and shear layers are still observable in the flow field, the overall structure appears more ordered compared to t = 0.1 s.

By t = 0.3 s, the valve spool approaches its target position. The velocity contour plots indicate that the streamlines in the major channels have aligned with the geometric paths corresponding to the Waste Heat Recovery Mode. The positions of high-speed zones tend to stabilize, while the extent of vortices and flow separation decreases significantly, indicating that the flow field is transitioning to a new steady-state distribution.

3.3.3. Transient Pressure Distribution and Local Pressure Peaks

Figure 17 illustrates the evolution of the transient pressure field within the multi-way valve during the period from 0 to 0.3 s. At t = 0 s, the pressure distribution corresponds to the initial steady-state mode, with high-pressure zones primarily concentrated near the inlet and at a few locations with cross-sectional contraction.

As the valve spool begins to rotate, the effective flow cross-sectional area of certain channels decreases rapidly. This leads to an increase in local flow velocity and a significant rise in pressure in these regions. Simultaneously, transient low-pressure zones form at the inlets of newly opening channels, resulting in significant asymmetry in the circumferential pressure distribution of the valve spool.

At t = 0.2 s, as channels further approach their closed or fully open states, the original high-pressure zones shift towards the new main flow channels. Local pressure gradients increase significantly, and more concentrated pressure peaks emerge near certain corners and valve spool inlets. This stage represents the period of most intense local pressure fluctuations during the mode switch.

By t = 0.3 s, as the valve spool approaches the target position, the pressure distribution in each channel gradually stabilizes, and the high and low-pressure zones transition towards a new steady-state distribution. Overall, the dynamic changes in channel openings during valve rotation cause a significant reconstruction of the internal pressure field within a short timeframe. Particularly during the transition phase, local regions are prone to generating transient pressure peaks and substantial pressure drop fluctuations, which warrants close attention in engineering applications.

4. Conclusions

This study presents a comprehensive investigation into the multi-way valve within the ITMS of NEVs using three-dimensional numerical simulations. The steady-state pressure loss characteristics and transient hydrodynamic behaviours under typical operating conditions were analyzed. The main conclusions are drawn as follows:

(1)

Under a mass flow rate of 0.84 kg/s, the total pressure drops of the multi-way valve in Cooling, Heating, and Waste Heat Recovery modes are 5998.8 Pa, 5219.9 Pa, and 3726.7 Pa, respectively. The results demonstrate that local pressure losses, concentrated in limited regions with sharp bends and sudden expansions/contractions, dominate the overall pressure drop, whereas the contribution of frictional losses along the straight channel segments is relatively limited. The Cooling mode exhibits the highest pressure drop due to the extensive flow channels and numerous turns. This confirms that local geometric structure is the critical factor determining the energy consumption level of the valve.

(2)

The parametric analysis of the valve body corner fillets and the valve spool’s longitudinal/transverse fillets reveals a distinct non-monotonic influence on pressure drop. As the fillet radius increases, the pressure drop typically exhibits a trend of initially decreasing and then increasing, or vice versa. This reflects the trade-off mechanism between the flow smoothing effect and the reduction in effective flow area. Optimal matching of geometric parameters for different channels can significantly suppress flow separation and impact, reducing local pressure drop and improving the overall hydraulic performance.

(3)

Transient simulations of the transition from Heating mode to Waste Heat Recovery mode demonstrate significant reconstruction of the internal velocity and pressure fields. During the intermediate stage of switching, local high-speed zones and pressure peaks are most prominent. The hydrodynamic torque acting on the valve spool exhibits substantial unsteady fluctuations, with peaks appearing at the start and stop phases. In the present case, the maximum transient torque reaches 27.9 N·m, while the largest steady-state torque among all operating modes is only 0.65 N·m. Thus, the transient peak torque is approximately 42.9 times the steady-state torque. This quantitative difference indicates that, when checking actuator capacity and setting control parameters, the transient torque during mode switching should be taken as the controlling condition to ensure sufficient torque margin and motion stability.