Complexity of Horizontal Oil–Gas–Water Flows in Deepwater Simulation Well: Insights from Multiscale Phase Permutation Entropy Analysis

Abstract

Deepwater oil–gas–water three-phase flow is widely regarded as a multiphase system. Intense interfacial interactions cause significant nonuniform fluid distributions in the wellbore, giving rise to complex nonlinear dynamics. In this study, a distributed conductance sensor (DCS) was developed to capture local flow information from a horizontal oil–gas–water simulation well. To quantify the complexity of nonlinear time series, phase permutation entropy (PPE) was first validated using artificial data, including the Tent map, Hénon map, and Lorenz system. PPE demonstrates superior capability in detecting abnormal dynamical changes compared with permutation entropy (PE). Subsequently, PPE is combined with the multiscale approach, i.e., multiscale phase permutation entropy (MPPE), to analyze the DCS signals and uncover the complexity of horizontal oil–gas–water flows. The results show that the MPPE analysis can reveal the spatial distribution characteristics of elongated gas bubbles, gas paths, dispersed bubbles and oil droplets.

1. Introduction

Deep-water oil–gas–water three-phase flow is widely recognized as a multiphase system [1]. The strong interfacial interactions give rise to pronounced nonuniform distributions within the wellbore and lead to highly complex nonlinear dynamics. Applying nonlinear analysis methods to investigate the spatiotemporal characteristics of such flows is of great importance for optimizing well-logging sensor deployment, understanding flow pattern transitions, and thereby modeling phase volume fractions and total flow rates [2,3].

Entropy has been established as a fundamental measure of complexity in nonlinear systems, with widely used examples including approximate entropy [4], sample entropy [5], cross-entropy [6], and diffusion entropy [7], among others. Costa et al. [8,9,10] originally introduced the concept of multiscale entropy (MSE) to characterize complex physiological time series, providing insights into system dynamics from both macroscopic and microscopic perspectives. Since then, MSE has been extensively applied across various dynamical domains, including physiological processes [11,12], financial markets [13], atmospheric dynamics [14], and beyond. Given that complex systems typically comprise interacting components with intrinsic coupling relationships [15,16], multivariate time-series analysis has become a powerful tool for system-level diagnosis and interpretation.

Meanwhile, Bandt and Pompe [17] proposed a complexity metric known as permutation entropy (PE), which characterizes time series by evaluating the ordinal patterns formed through comparisons of adjacent data points. Owing to its robustness and sensitivity to underlying dynamics, permutation entropy has been widely recognized as an effective measure of complexity for chaotic signals, particularly when dynamical disturbances and measurement noise are present. On this basics, He et al. [18] developed the multivariate permutation entropy (MPE) algorithm, which demonstrated strong robustness to noise and high computational efficiency, making it suitable for real-time monitoring of multivariable complexity. Building on the univariate MSE framework, Ahmed and Mandic [19] generalized the approach to multivariate data and proposed multivariate multiscale sample entropy (MMSE), the effectiveness of which in evaluating traffic system complexity has been validated [20]. Subsequently, Morabito et al. [21] introduced multivariate multiscale permutation entropy (MMPE) for assessing the complexity of physiological signals. On this basis, Yin and Shang [22] further advanced the method by proposing multivariate weighted multiscale permutation entropy (MWMPE), which not only improves robustness but also provides a more accurate representation of the complexity inherent in multichannel time series.

Recently, by incorporating phase information into permutation entropy (PE), Kang et al. [23] proposed the phase permutation entropy (PPE) method and demonstrated that PPE enhances the sensitivity to dynamical variations compared with conventional PE, both in logistic maps and real-world signals. In this work, we further combine PPE with the multiscale approach and introduce multiscale phase permutation entropy (MPPE) to analyze distributed conductance sensor (DCS) signals obtained from horizontal oil–gas–water flows, aiming to uncover the complexity of multiphase flow systems.

The remainder of this paper is organized as follows. Section 2 presents the principles of PE, PPE and MPPE. Section 3 evaluates the performance of PPE under different conditions. Section 4 describes the experimental setup of the horizontal oil–gas–water simulation well and the acquisition of DCS data. Section 5 discusses the complexity of horizontal three-phase flows by using MPPE, and Section 6 concludes the paper.

2. PE, PPE and MPPE Algorithm

2.1. PE Algorithm [17]

Consider a time series $X(i)=\left\{x_i\right.,i=1,2,\cdots ,N\}$ of length N. It can be reconstructed in an m-dimensional state space as

$$X_j^{m,\tau }=[x_j,x_{j+\tau },\cdots ,x_{j+(m-1)\tau }],j=1,2,\cdots ,N-(m-1)\tau$$

(1)

where $m$ denotes the embedding dimension and $\tau$ represents the delay time. Each embedded vector $X_j^{m,\tau }$ is then rearranged in ascending order, expressed as $x_{j+(k_1-1)\tau }\le x_{j+(k_2-1)\tau }\le \cdots \le x_{j+(k_m-1)\tau }$. Thus, every vector $X_j^{m,\tau }$ corresponds to a specific ordinal pattern, given by

$$S_j=[k_1,k_2,\cdots ,k_m],j=1,2,\cdots ,N-(m-1)\tau$$

(2)

leading to a total of $m!$ possible patterns. The occurrence frequency of each ordinal pattern is defined as

$$P_v^{m,\tau }={\displaystyle \frac{Num(v)}{N-(m-1)\tau }},v=1,2,\cdots ,m!$$

(3)

where $Num(v)$ is the number of each possible type in all ordinal patterns and $N-(m-1)\tau$ is the total number of patterns observed. Based on Shannon entropy, the permutation entropy of order $m$ is formulated as

$$PE(m)=-{\displaystyle \sum _{V=1}^{m!}{P}_v^{m,\tau }}\ln (P_v^{m,\tau })$$

(4)

To facilitate comparison, $PE(m)$ is further normalized by dividing with $\ln (m!)$, giving

$$P{E}_N(m)=PE(m)/\ln (m!)$$

(5)

2.2. PPE Algorithm [23]

Let us take a discrete time series $X(i)=\left\{x_i\right.,i=1,2,\cdots ,N\}$. Its analytic signal $Z(i)$ is defined as a complex-valued function, given by

$$Z(i)=X(i)+j\tilde{X}(i)=A(i)e^{j\theta (i)}$$

(6)

where $\tilde{X}(i)$ denotes the Hilbert transform of $X(i)$. From this representation, the instantaneous phase sequence $\theta (i)$ can be obtained as [23]:

$$\theta (i)=\arctan {\displaystyle \frac{\tilde{X}(i)}{X(i)}},i=1,2,\cdots ,N$$

(7)

Here, $\theta (i)$ varies between $-\pi$ and $\pi$, representing the instantaneous phase, which reflects the joint contribution of the phases of all frequency components at each time point.

Subsequently, the procedure of PPE follows the same framework as the conventional PE algorithm. Specifically, $\theta (i)$ is embedded into an m-dimensional state space, expressed as

$${\mathsf{\Theta }}_j^{m,\tau }=[{\theta }_j,{\theta }_{j+\tau },\cdots ,{\theta }_{j+(m-1)\tau }],j=1,2,\cdots ,N-(m-1)\tau$$

(8)

Next, ${\mathsf{\Theta }}_j^{m,\tau }$ is ordered in ascending fashion, yielding a position vector $S_j$. The relative frequency $P_v^{m,\tau }$ of every ordinal pattern is computed accordingly. The PPE value is then defined using Shannon entropy as:

$$PPE(m)=-{\displaystyle \sum _{v=1}^{m!}{P}_v^{m,\tau }}\ln (P_v^{m,\tau })$$

(9)

Finally, normalization is performed by dividing with $\ln (m!)$, resulting in

$$PP{E}_{\mathrm{N}}(m)=PPE(m)/\ln (m!)$$

(10)

2.3. MPPE Algorithm

Given a phase series $\theta (i),i=1,2,\cdots ,N$, a set of coarse-grained time series is obtained through scale-dependent averaging [8,9,10]. For a time scale S, coarse-grained time series ${\theta }_J^S$ can be expressed as:

$${\theta }_J^S={\displaystyle \frac{1}{S}}{\displaystyle \sum _{i=(J-1)S+1}^{JS}\theta (i),1\le J\le L,L=[\frac{N}{S}]}$$

(11)

where $[{\displaystyle \frac{N}{S}}]$ denotes the greatest integer less than or equal to ${\displaystyle \frac{N}{S}}$. As for the coarse-grained time series ${\theta }_J^S$, the remaining steps of MPPE are consistent with PPE. Thus, for each time scale S, a $PPE$ can be obtained, and its normalized value can be denoted by $MPP{E}_{\mathrm{N}}$.

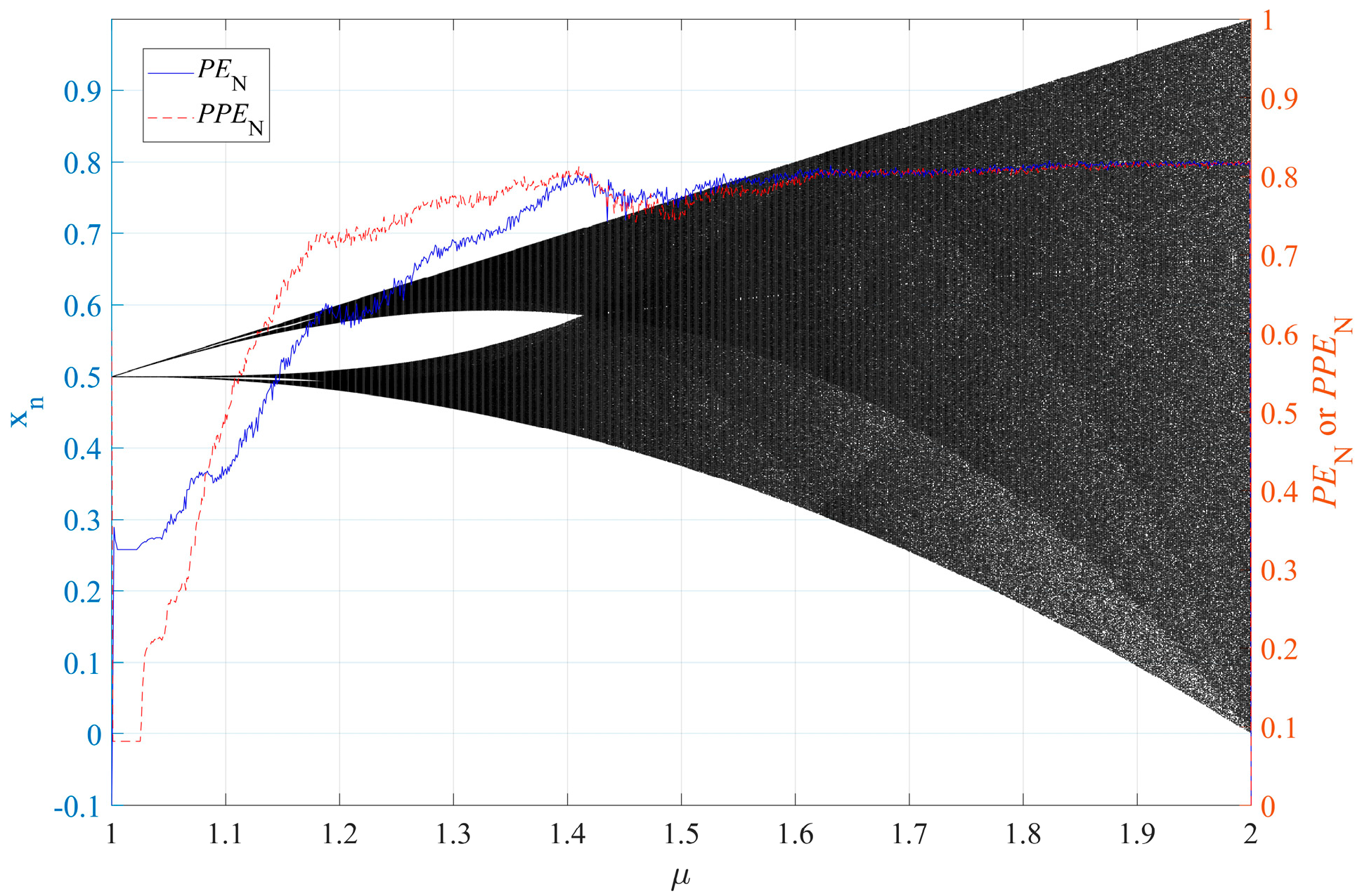
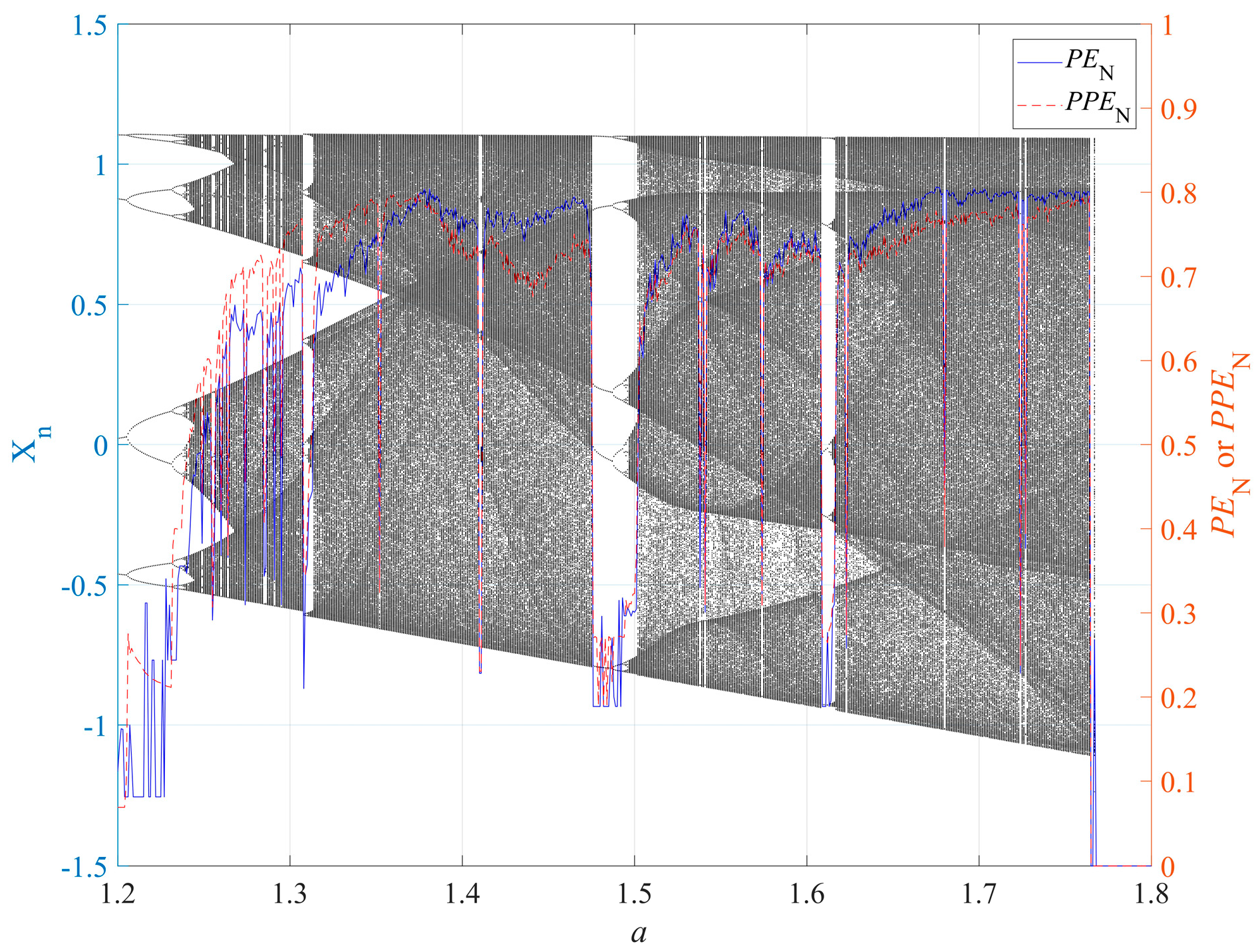
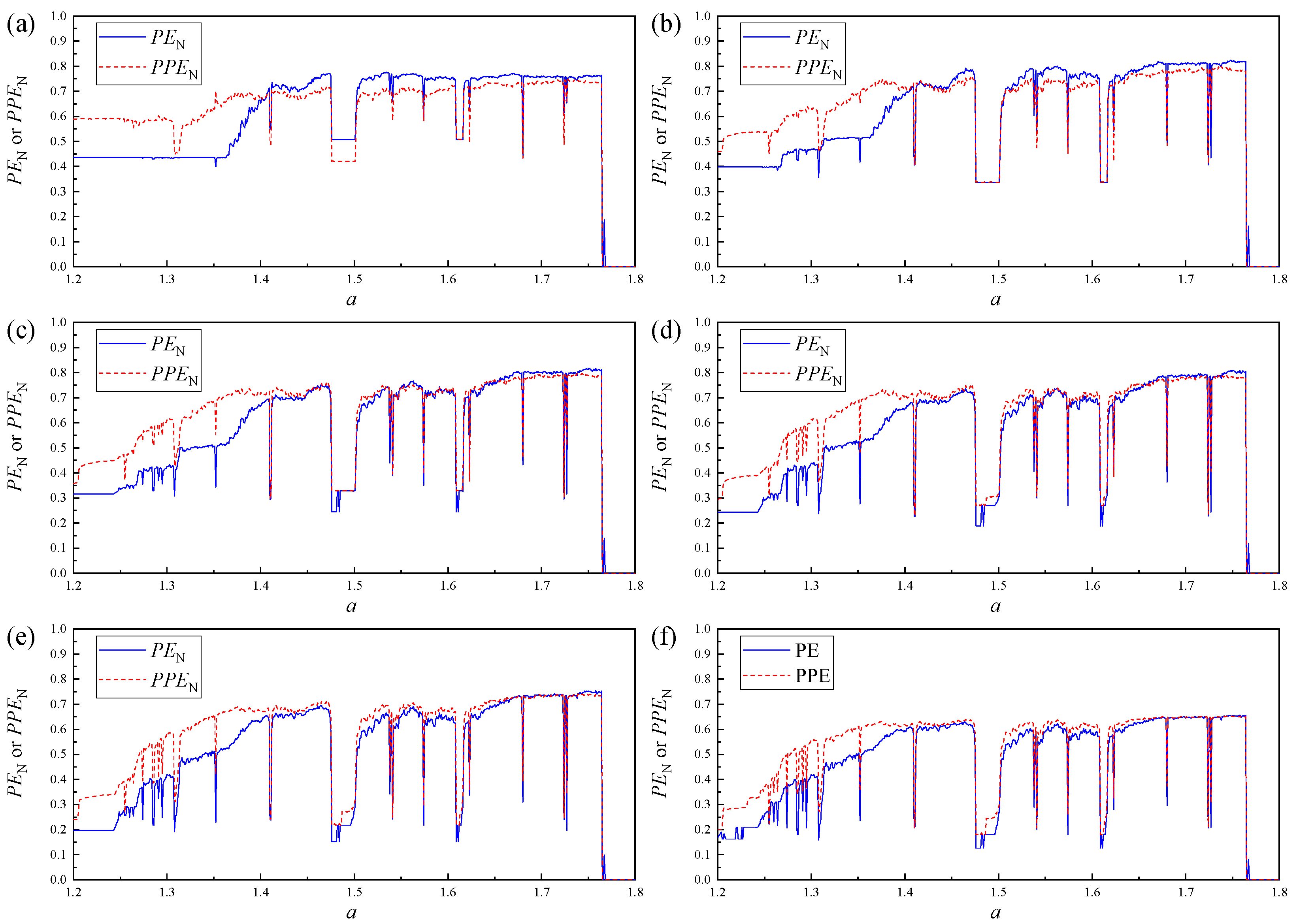
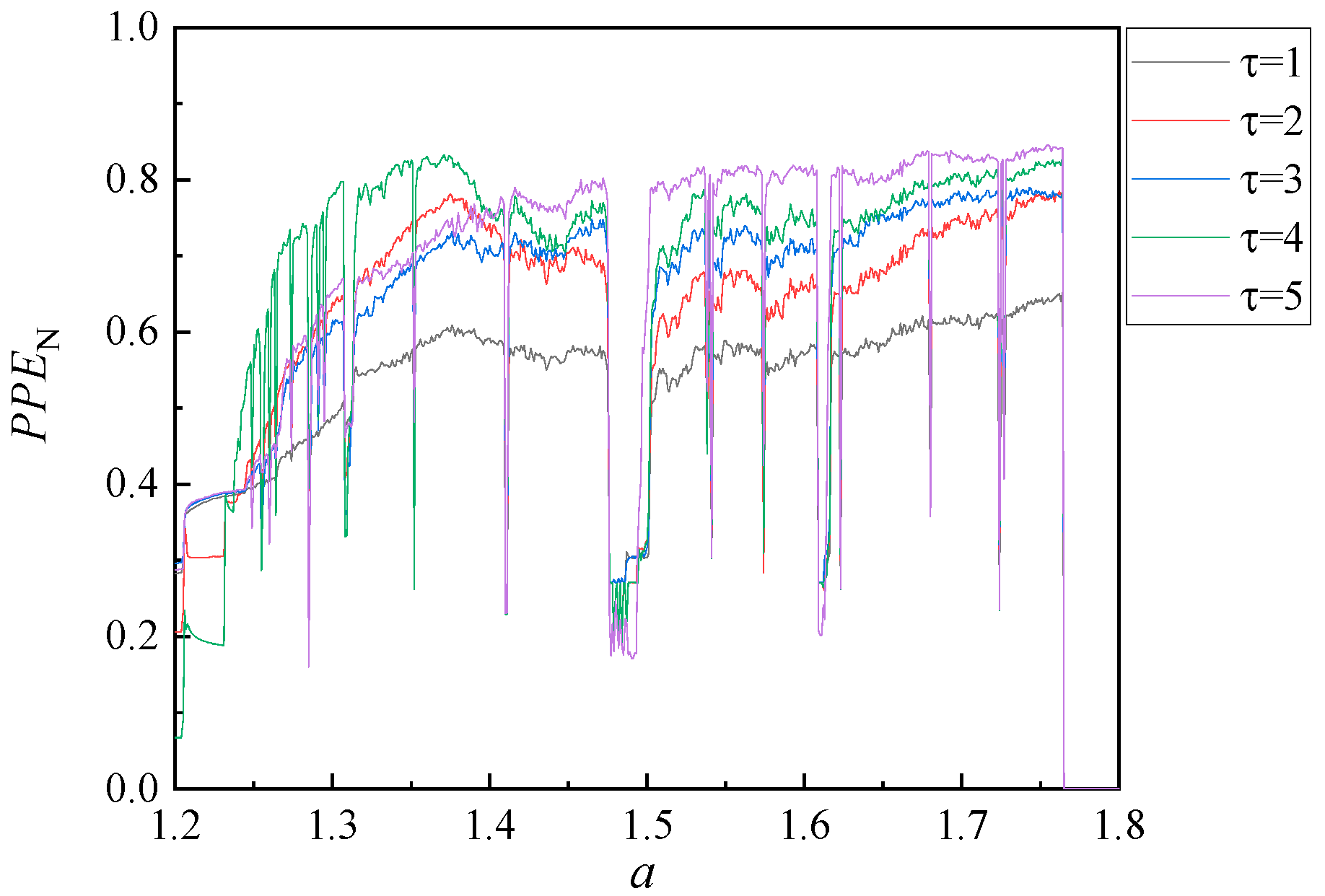
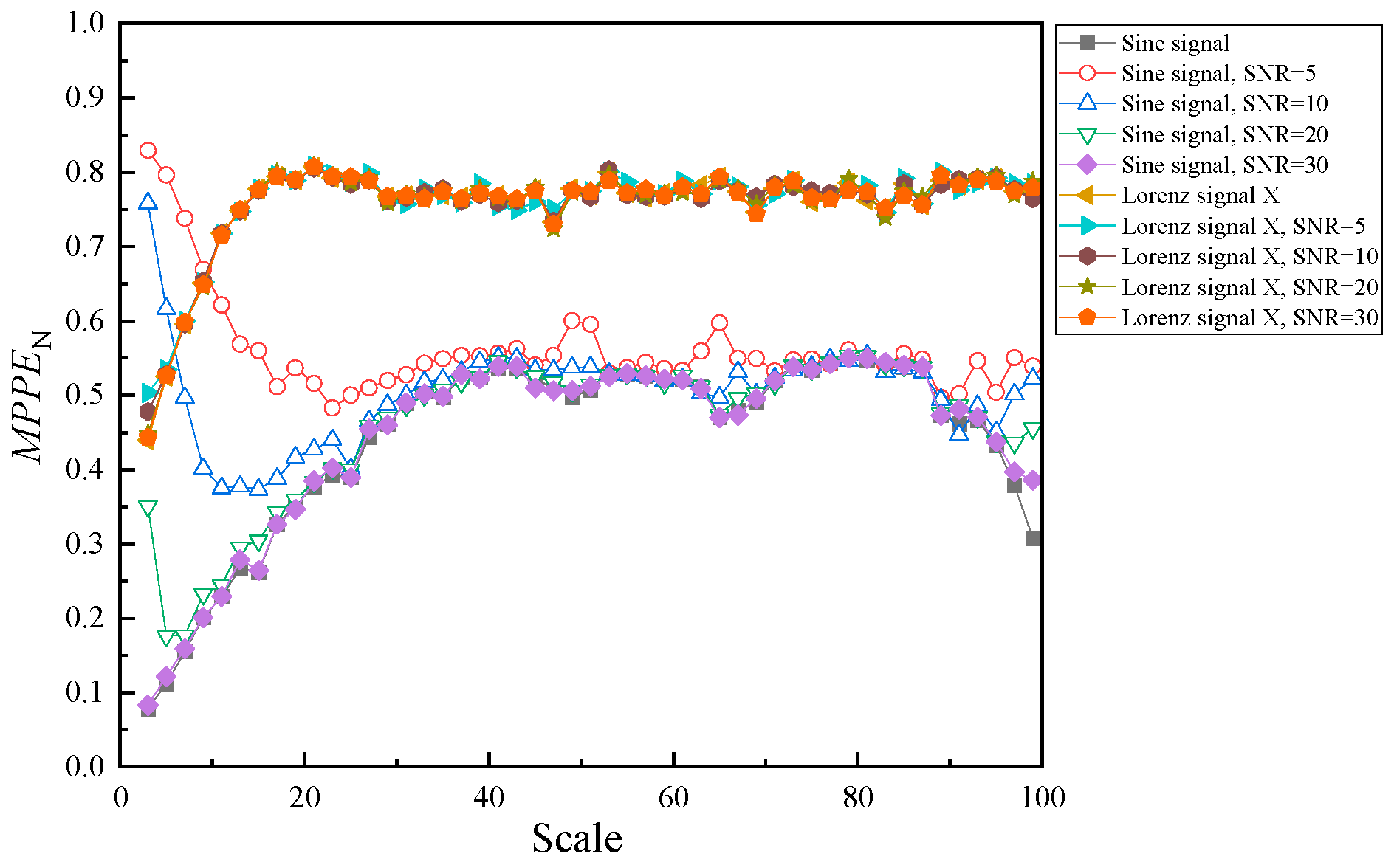
3. Algorithm Evaluation

3.1. PPE Evaluation

Tent map is a one-dimensional piecewise linear mapping, and it serves as a typical model of discrete dynamical systems. In mathematics, the Tent map with parameter $\mu$ is defined as the real-valued function $f_{\mu }$:

$$f_{\mu }(x):=\mu \min \left\{x,1-x\right\}$$

(12)

For the values of the parameter $\mu$ within the interval $0<\mu <2$, the Tent map transforms the unit interval [0, 1] into itself, thereby defining a discrete-time dynamical system. Iterating a point $x_0\in [0,1]$ generates a sequence $x_n$:

$$x_{n+1}=f_{\mu }(x_n)=\left\{\begin{array}{l}\mu x_n \mathrm{for}{x}_n<{\displaystyle \frac{1}{2}}\\ \mu (1-x_n)\mathrm{for}{\displaystyle \frac{1}{2}}<x_n\end{array}\right.$$

(13)

where $\mu$ denotes a positive real constant. Different choices of $\mu$ lead to distinct regimes, ranging from deterministic to chaotic evolution. Specifically, as the system approaches the chaotic regime, the following transitions are observed. When $\mu$ is close to 1, finite-period orbits (e.g., period-2 and period-4) appear. As $\mu$ increases, the system undergoes period-doubling bifurcations and gradually evolves into chaos. Within the chaotic regime, the iterates become extremely sensitive to initial conditions, exhibiting the hallmark features of deterministic chaos [24]. Bifurcation diagram for the Tent map is shown in Figure 1. Here, $\mu$ ranges from 1 to 2 with a step of 0.001, the data length is 10,000, and the initial value is set to 0.3. The diagram clearly illustrates the evolution of the dynamical behavior of the Tent map. Moreover, it can be observed that both PE and PPE provide effective indicators of this evolution. In particular, when the system is in a periodic state, PE and PPE remain relatively low; as the system progresses into chaos, both measures exhibit a distinct increasing trend.

Hénon map is a classical two-dimensional discrete nonlinear dynamical system, expressed as

$$\left\{\begin{array}{l}{x}_{n+1}=1-a{x}_n^2+y_n\\ y_{n+1}=b{x}_n\end{array}\right.$$

(14)

where a and b are control parameters. When b is equal to 0.12, the system’s evolution primarily depends on the value of a. As shown in Figure 2, when a varies from 1.2 to 1.8 with a step size of 0.001, the system exhibits a mixed state of weak chaos, periodic behavior, and strong chaos, with periodic windows and chaotic regimes repeatedly alternating throughout the interval (the data length is 10,000). PE and PPE can accurately detect the occurrence of period-doubling windows in the Hénon map, where both measures maintain relatively low values, indicating simpler system dynamics. In contrast, once the system enters a chaotic regime, PE and PPE rapidly increase to higher values.

Overall, PE and PPE exhibit comparable performance in characterizing behavioral variations in complex nonlinear systems. We further examine the effects of embedding dimension of state space reconstruction on PE and PPE. Taking the Hénon map as an example, as shown in Figure 3, variations in the embedding dimension $m$ influence the ability of both PE and PPE to detect dynamical transition. When the embedding dimension is relatively low, PPE can clearly capture the transition between period-doubling and chaos in the Hénon map (see Figure 3a). By definition, as the embedding dimension increases, the size of the symbolic sequence space expands substantially, leading to a higher computational burden. From this perspective, PPE demonstrates superior capability in detecting abnormal dynamical changes compared with PE in the Hénon map.

Furthermore, the effect of delay time $\tau$ on PPE is examined, as depicted in Figure 4. The results indicate that PPE values rise with increasing delay time, while the method continues to perform effectively in detecting anomalous system behavior. For state-space reconstruction of one-dimensional signals, it is generally recommended to select the embedding dimension $m$ and delay time $\tau$ using the false nearest neighbors method [25] and the average mutual information method [26], respectively.

3.2. MPPE Evaluation

Lorenz system was originally proposed as a simplified model for describing atmospheric convection [27,28]. It is a three-dimensional autonomous nonlinear system of ordinary differential equations:

$$\left\{\begin{array}{l}\dot{x}=\sigma (y-x)\\ \dot{y}=x(\rho -z)-y\\ \dot{z}=xy-\beta z\end{array}\right.$$

(15)

where x represents the convection intensity (a velocity component of fluid motion), y denotes the temperature difference (the horizontal temperature gradient), and z describes the vertical distribution of the temperature field. The parameter $\sigma$ is the Prandtl number (the ratio of momentum diffusivity to thermal diffusivity), $\rho$ is the Rayleigh number (the strength of convection driven by the temperature gradient), and $\beta$ is a geometric factor. When $\sigma$ = 10, $\beta =8/3$, $\rho =28$, the system exhibits chaotic dynamics and generates the well-known Lorenz attractor.

This section investigates the multiscale phase permutation entropy (MPPE) of the Lorenz system x-series and a sinusoidal series, as shown in Figure 5. It can be observed that the complex chaotic characteristics of the Lorenz x-series produce relatively high PPE across different scales. In addition, white noise is added to both the sinusoidal and x-series to examine the noise robustness of MPPE. The results show that, for the x-series, PPE increases progressively with scale and is only weakly affected by noise. For the sinusoidal series, when the signal-to-noise ratio is low, PPE deviates significantly at small scales; however, as the scale increases, the influence of noise on PPE gradually diminishes. In this sense, MPPE, by probing system information across multiple scales, provides a more effective means of revealing the intrinsic characteristics of the system.

4. Data Acquisition for Horizontal Oil–Gas–Water Simulation Well

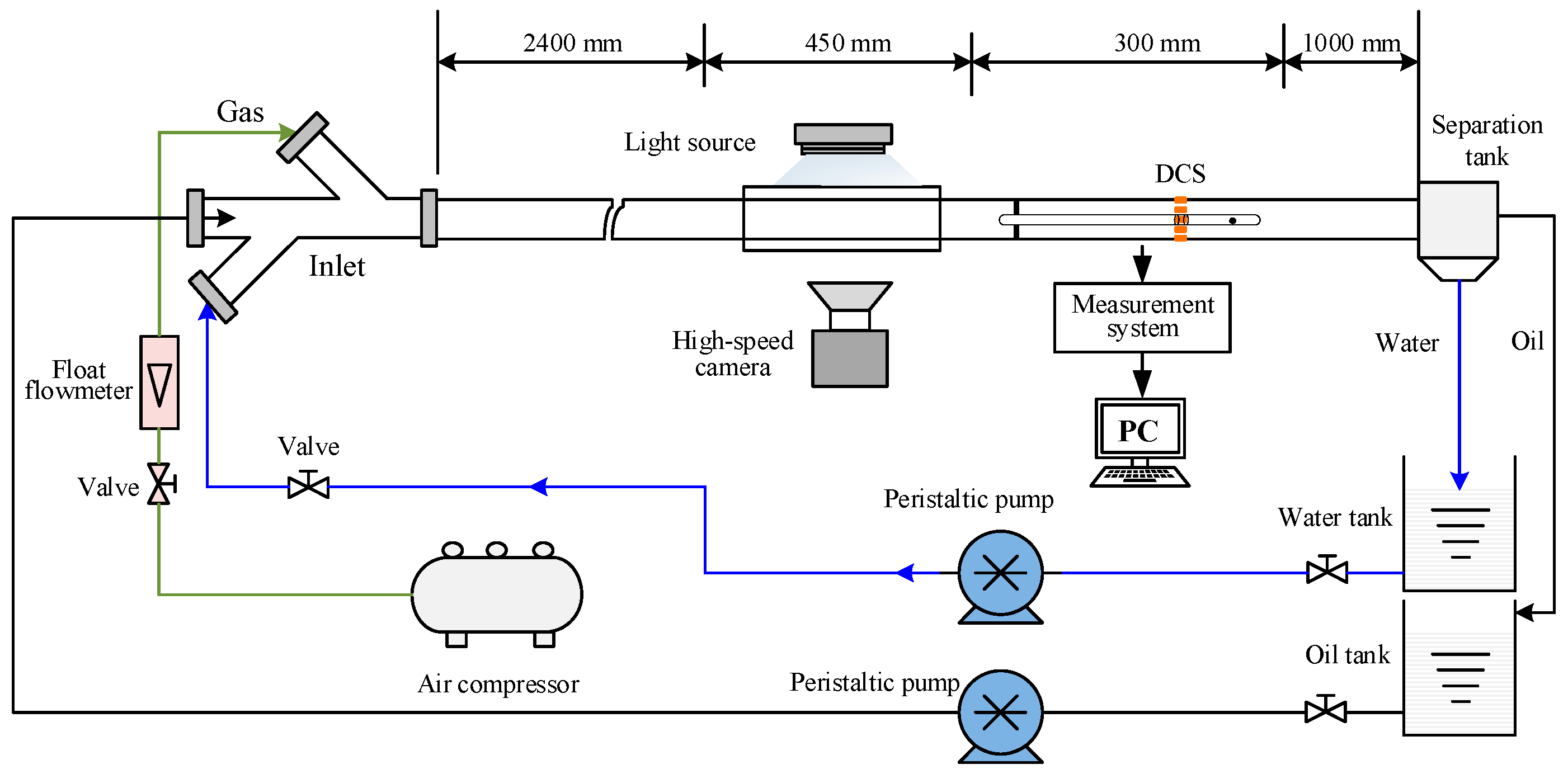
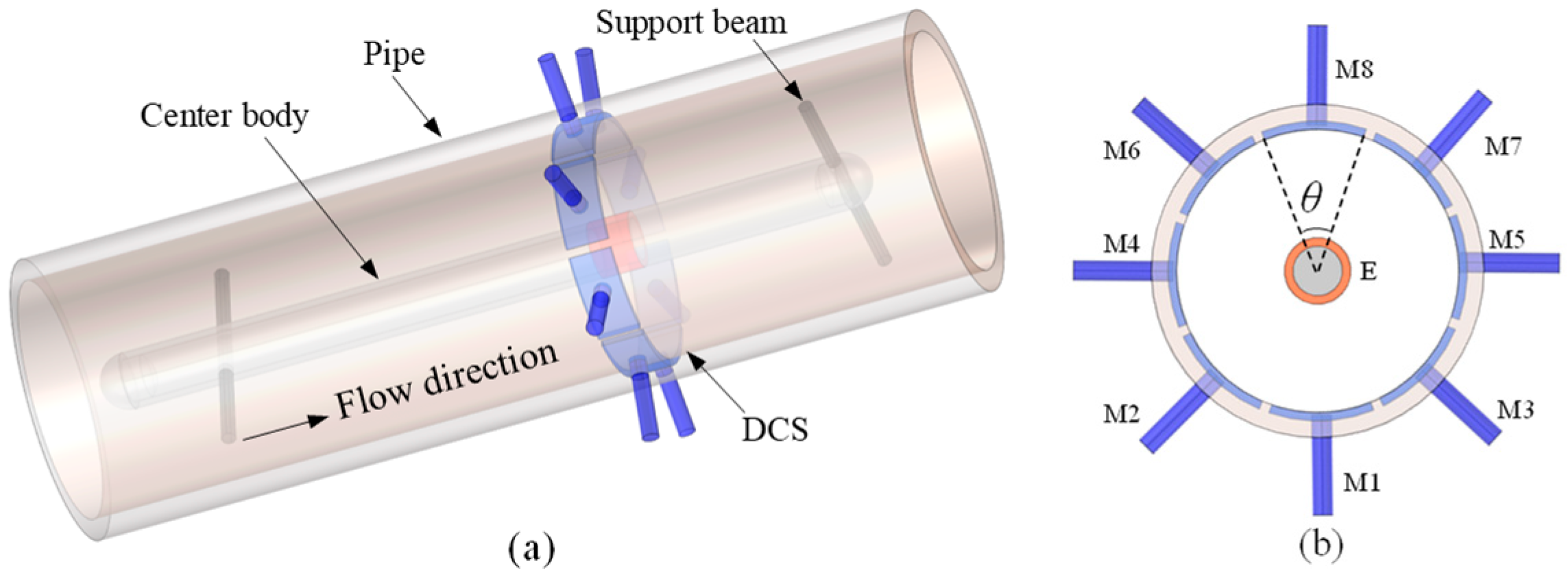
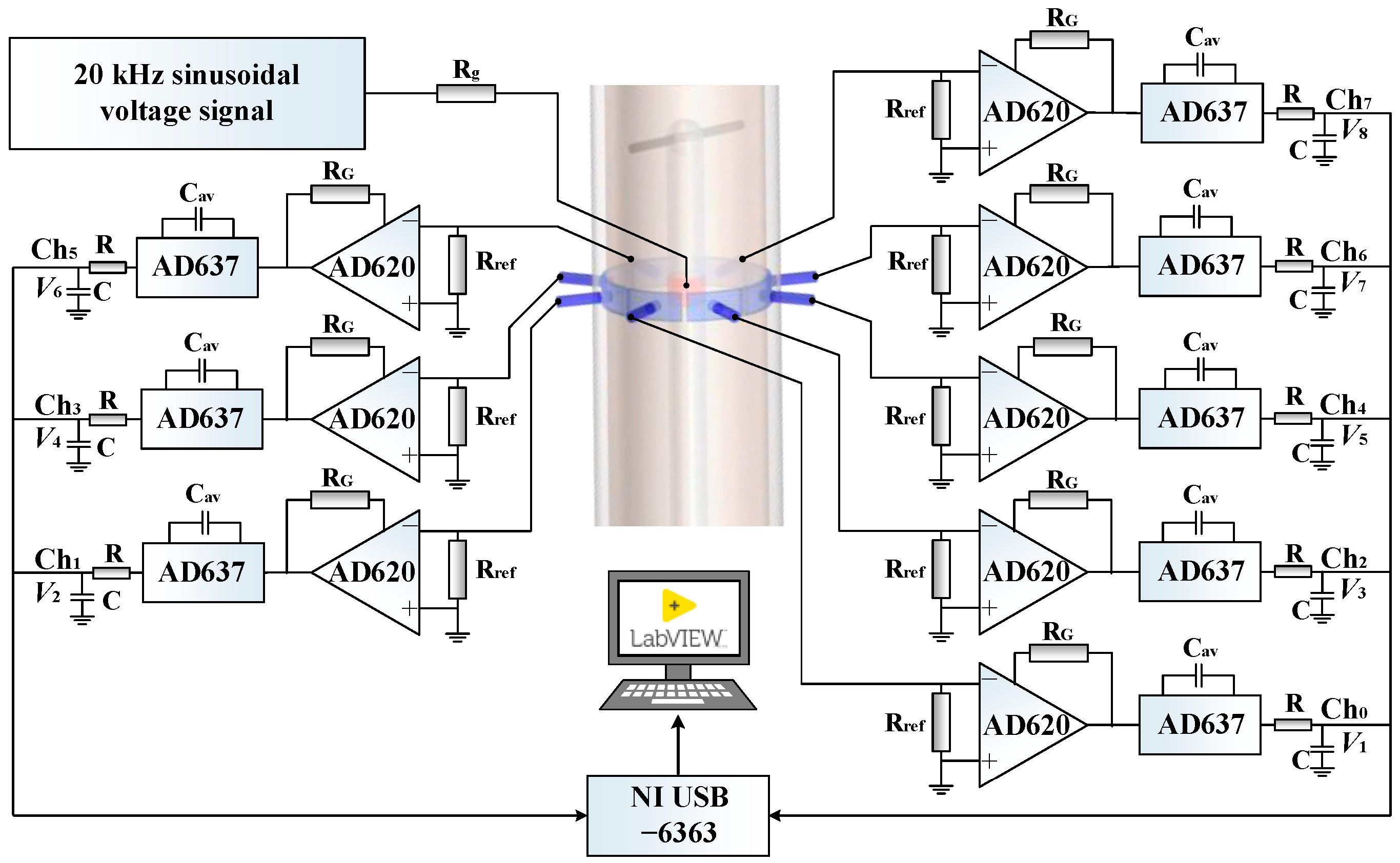
4.1. Experimental Setup

The experimental setup for horizontal oil–gas–water three-phase flow is shown in Figure 6. The working fluids used in this study were No. 3 industrial white oil, tap water, and air. The test section consisted of a transparent acrylic pipe with an inner diameter of 20 mm and an outer diameter of 30 mm. At the pipe inlet, a four-way inlet was employed to connect the water inlet, oil inlet, gas inlet, and the test section.

To facilitate visual observation, a red dye was added to the No. 3 industrial white oil, which allowed clear distinction from the aqueous phase without altering its physical or chemical properties. Tap water was supplied and metered by a dual-channel industrial peristaltic pump (Longer, WG600F, accuracy: ±0.2%, flow range per channel: 8.3–13,800 mL/min). White oil was delivered and measured by another dual-channel industrial peristaltic pump (Longer, WT600F, accuracy: ±0.5%, flow range per channel: 0.006–6000 mL/min). The gas phase was provided by an air compressor (Dailo, DA805), and the airflow rate was regulated and measured by a rotameter (Yihuan, YHFZ type, accuracy: 1.5) before entering the test section.

To ensure fully developed flow patterns, a 2400 mm development section was installed downstream of the inlet, followed by the test section. The outlet flow was then routed through a U-shaped pipe to a separation tank, in which the oil–water mixture underwent gravitational settling before the separated phases were pumped back into the corresponding storage tanks for recycling.

A high-speed camera (Photron FASTCAM Mini UX50/100) was positioned 2625 mm downstream of the inlet to record flow images for structural analysis. Image acquisition was conducted at a frame rate of 1000 fps, with a shutter speed of 1/5000 s and a total recording duration of 4 s. To reduce optical distortions arising from reflection and refraction at the curved pipe wall and multiphase interfaces, the test pipe was placed inside an acrylic visualization box filled with glycerol. By matching the refractive indices, this configuration effectively corrected optical distortions and allowed clearer observation of the intrinsic flow structures.

The structure of the distributed conductance sensor (DCS) is illustrated in Figure 7. It consists of a ring-shaped excitation electrode (E) and eight arc-shaped measuring electrodes (M1–M8). The excitation electrode was embedded on a cylindrical center body made of insulating material, which was supported by a set of orthogonal beams at the pipe center. To reduce flow disturbance caused by the center body, both ends were designed in a spherical shape, with a central body diameter of 6 mm. The eight measuring electrodes were embedded in the inner surface of the pipe wall, each having the same subtended angle $\theta$, with numbering and distribution shown in Figure 7b. Both the excitation electrode and the measuring electrodes were in direct contact with the fluid. The excitation electrode was connected through a lead wire inside the central body, routed via the supporting beams to the external circuit. The distributed conductance sensor was installed 2950 mm downstream of the inlet, enabling the capture of flow dynamics across eight distinct regions of the pipe cross-section.

The DCS measurement system is illustrated in Figure 8. It consists of the sensor, excitation module, signal conditioning module, and data acquisition module. The measurement principle is as follows: the fluid between the excitation electrode and each measuring electrode can be equivalently modeled as a resistor. When an excitation voltage is applied to the excitation electrode, the current flows through the fluid and the reference resistor (R_ref) before reaching the ground. Since oil, gas, and water exhibit significantly different electrical conductivities, variations in phase distribution within the pipe lead to changes in the equivalent resistance between the excitation electrode and the measuring electrode. Consequently, the voltage drop across R_ref provides information on the local phase distribution inside the pipe.

The excitation module generates a sinusoidal signal using an oscillator (CG-402R2), producing a 20 kHz sine wave with a peak-to-peak amplitude of 4 V. The signal conditioning module comprises a differential amplification stage and a signal demodulation stage. Differential amplification is implemented with an AD620 chip, chosen for its low cost, high precision, and adjustable gain via an external resistor R_G. In this study, the gain was set to 3.5 with R_G configured as 20 kΩ. For signal demodulation, an AD637 chip was employed, which functions as a true RMS-to-DC converter, converting the amplified AC voltage into a DC voltage. During the use of the AD637, the key parameters considered were ripple level and settling time. A smaller settling time and ripple level can be achieved by increasing the external capacitor C_av, though at the cost of higher ripple and reduced signal-to-noise ratio (SNR). To improve signal quality, a first-order RC passive low-pass filter was added after demodulation, with R = 10 kΩ and C = 3300 pF, effectively attenuating noise above 50 Hz.

The data acquisition module employs an NI USB-6363 DAQ card with a sampling frequency of 2 kHz. The output voltages (V1–V8) of the DCS measurement system are transmitted through channels Ch0–Ch7 to the host computer. Differential connection was used between the DAQ card and the circuit, which effectively suppresses ground-loop noise compared with single-ended connection, thereby improving measurement reliability.

4.2. Flow Images and DCS Responses

For horizontal oil–gas–water three-phase flow with an oil volume fraction of 0.05, the oil content in the liquid phase is sufficiently low that the flow-pattern classification can be reasonably referenced to gas–water two-phase flow. Accordingly, the flow pattern is identified based on the behavior of the gas phase and the state of the continuous liquid phase, particularly whether the oil and water phases are emulsified. Under the present experimental conditions, the horizontal three-phase flow is dominated by slug flow, which is characterized by a quasi-periodic alternation between film regions (FRs) and slug regions (SRs).

In the film region, an elongated bubble (EB) occupies the upper portion of the pipe, with a liquid film flowing beneath it. In contrast, within the slug region, water serves as the continuous phase, in which dispersed bubbles (DBs) and dispersed oil droplets (ODs) are suspended. Based on these flow characteristics, three representative types of horizontal oil–gas–water slug flow are identified.

(1)

Oil-dispersed slug flow: As illustrated in Figure 9, this flow pattern exhibits a clear quasi-periodic succession of film and slug regions. The slug region contains a limited number of dispersed bubbles and oil droplets, with the oil droplets generally exhibiting relatively large diameters. In the film region, only a small number of bubbles and droplets are observed within the liquid film beneath the elongated bubble.

(2)

Emulsified slug flow: With an increase in gas flow rate, as shown in Figure 10, both the film and slug regions display a markedly higher concentration of dispersed bubbles and oil droplets. The slug region becomes strongly aerated, characterized by a greater number and broader spatial distribution of bubbles. Simultaneously, the oil droplets in the slug region are significantly reduced in size, leading to the formation of an oil–water emulsion.

(3)

Pseudo slug flow: As the aeration of the slug region intensifies further, gas pathways develop within the slug, progressively disrupting its structure (Figure 11). The liquid phase also appears as an oil-water emulsion, while the overall fluid motion becomes increasingly irregular and chaotic.

At typical conditions with U_sl = 0.295 m/s, the response signals of the DCS are shown in Figure 12. From a macroscopic perspective, the alternation of high- and low-amplitude signals reflects the quasi-periodic switching between slug regions and film regions, while the signal fluctuations across different measurement electrodes reveal the nonuniform distribution of the oil–gas–water three-phase flow.

(1)

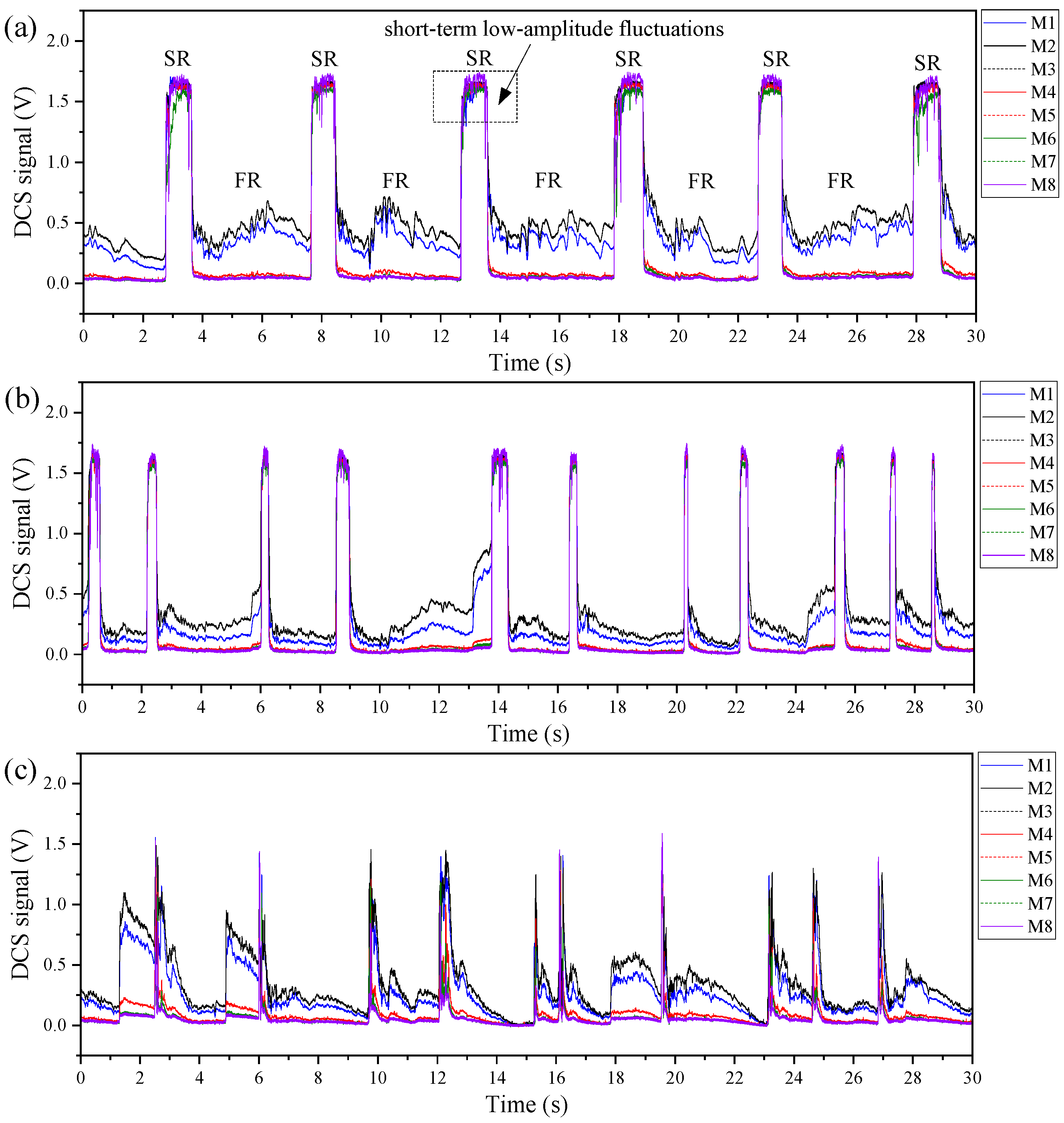
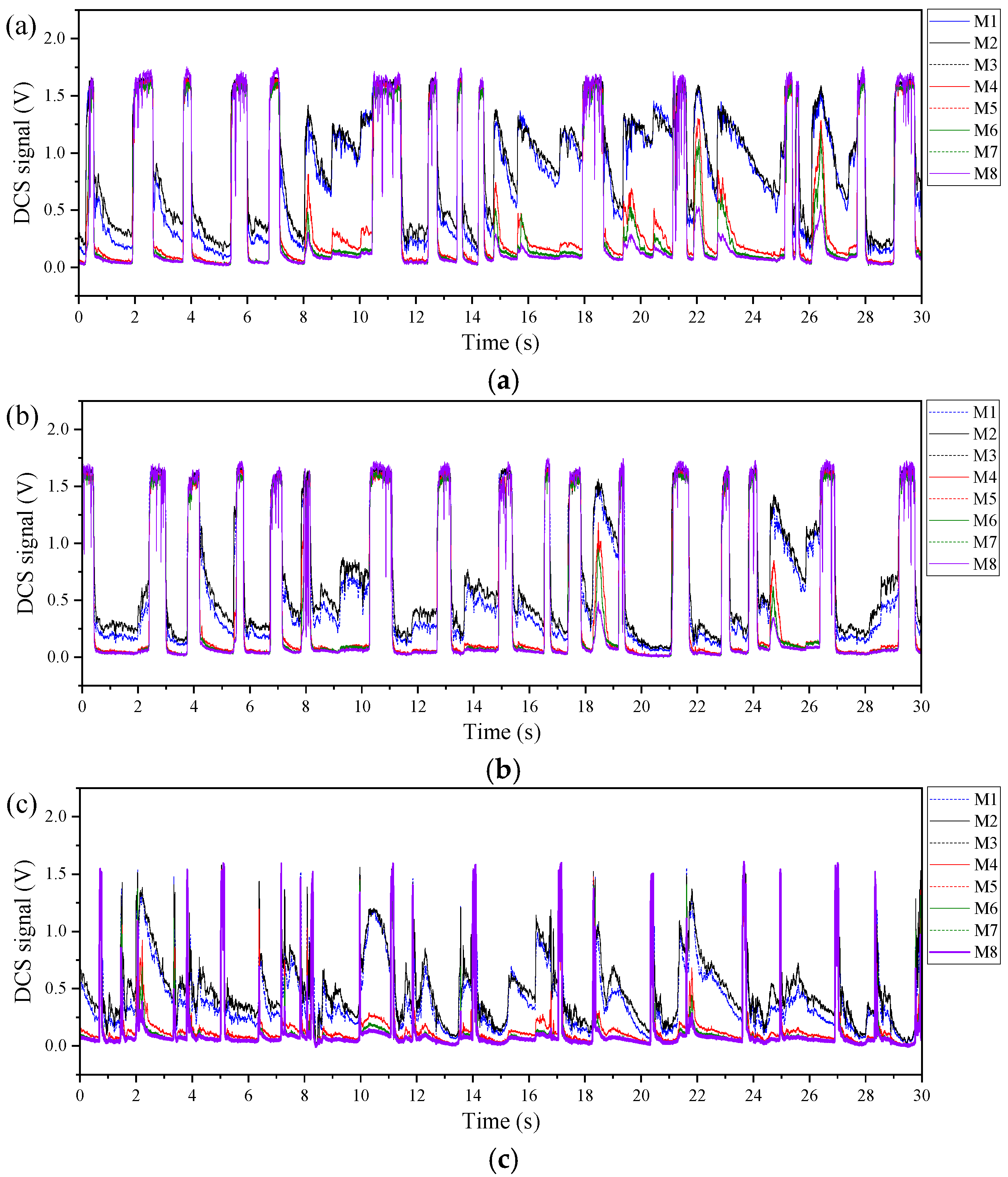
Due to the presence of dispersed bubbles and oil droplets, short-term low-amplitude fluctuations are embedded within the high-amplitude signals corresponding to slug regions, as illustrated in Figure 12a. With increasing gas flow rate, the slug length gradually decreases, and the low-amplitude fluctuations caused by dispersed bubbles and droplets become less evident, as shown in Figure 12b. When the flow transitions into pseudo slug flow, the slug-region signals exhibit sharp peaks, primarily dominated by gas pathways; in this case, the effects of dispersed bubbles and droplets almost vanish, as seen in Figure 12c.

(2)

Because of the varying liquid-film thickness beneath the elongated bubble, the signals from electrodes M1, M2, and M3 show large-amplitude oscillations. In contrast, electrodes M4 and M5 are mainly sensitive to the elongated-bubble structure and thus display stable, low-level signals, as observed in Figure 12a,b. Interestingly, when the flow shifts to pseudo slug flow, complex gas coalescence in the film region leads to noticeable fluctuations even in the signals of electrodes M4 and M5. Meanwhile, the responses of M1, M2, and M3 also effectively indicate the intensified instability of the liquid film.

At typical conditions with U_sl = 0.589 m/s, the response signals of the DCS are presented in Figure 13. Compared with Figure 12, the higher total flow rate enhances flow turbulence, resulting in more complex signal fluctuations. Specifically, almost all electrodes become sensitive to structural variations in the film region, with significantly larger fluctuation amplitudes. In addition, the low-amplitude disturbances induced by dispersed bubbles and oil droplets in the slug region appear more frequently. Once the flow transforms into pseudo slug flow, the presence of continuous gas pathways within the slug region blurs the boundary between slug and film regions, and the quasi-periodic flow behavior gradually disappears, exhibiting instead a highly irregular spatial distribution.

5. Complexity of Horizontal Oil–Gas–Water Flows

The analytic signal, $Z(i)$, of experimentally acquired DCS signal is obtained using Equation (6), and the corresponding instantaneous phase sequence $\theta (i)$ is calculated according to Equation (7). Then, the coarse-grained time series ${\theta }_J^S$ at different time scales S is constructed using Equation (11). Finally, the coarse-grained time series ${\theta }_J^S$ is processed following Equations (1)–(5), from which $PPE$ and its normalized value $MPP{E}_{\mathrm{N}}$ can be obtained for each time scale S. When the superficial liquid velocity U_sl is 0.295 m/s, the $MPP{E}_{\mathrm{N}}$ corresponding to different flow patterns is shown in Figure 14, in which The circle represents the circumference of the pipe. It can be observed that, as a complex chaotic system, the $MPP{E}_{\mathrm{N}}$ of oil–gas–water three-phase flow exhibits a gradual increase with scale S.

(1)

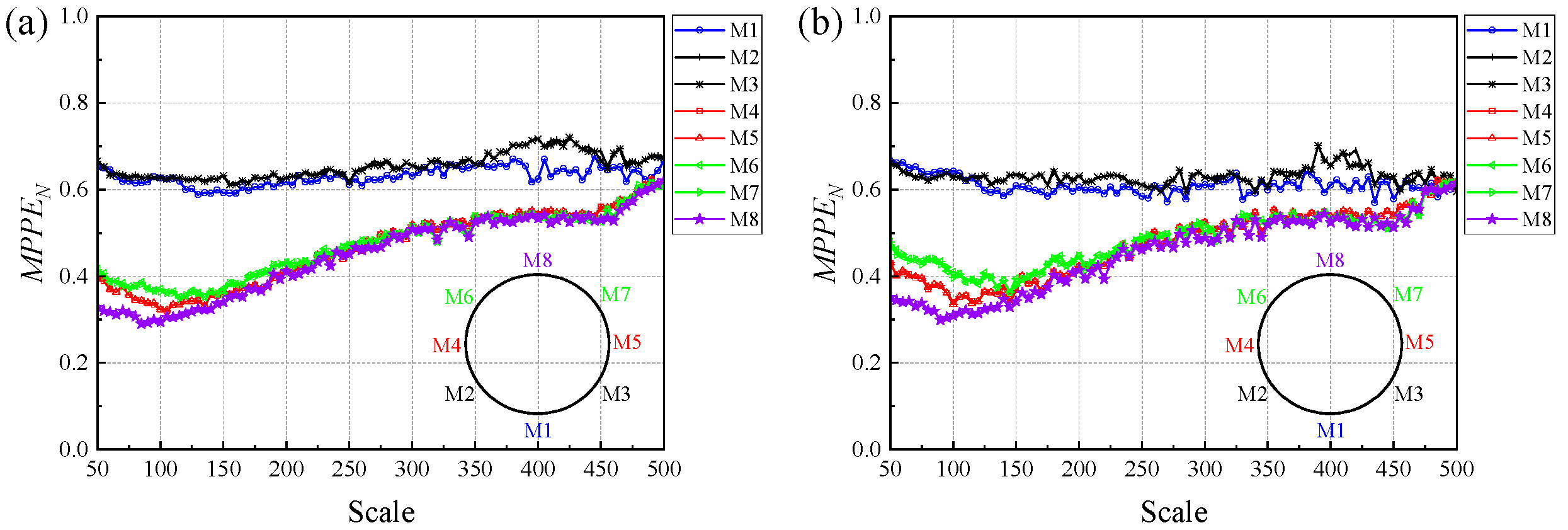
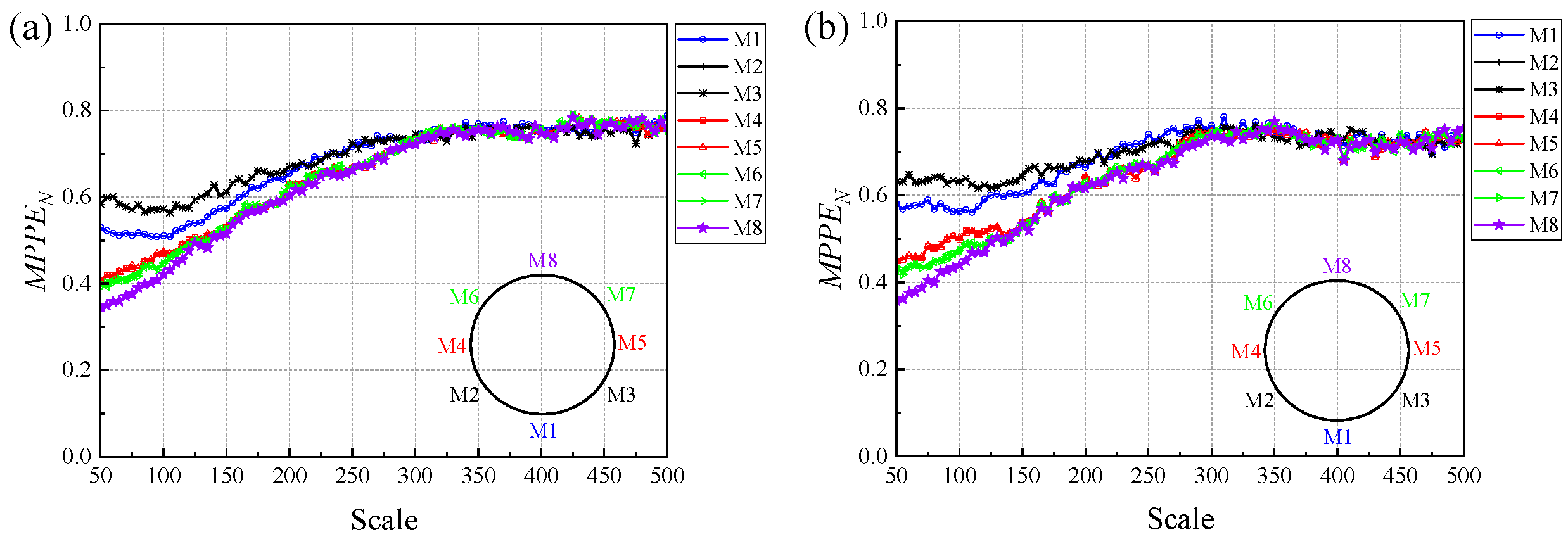
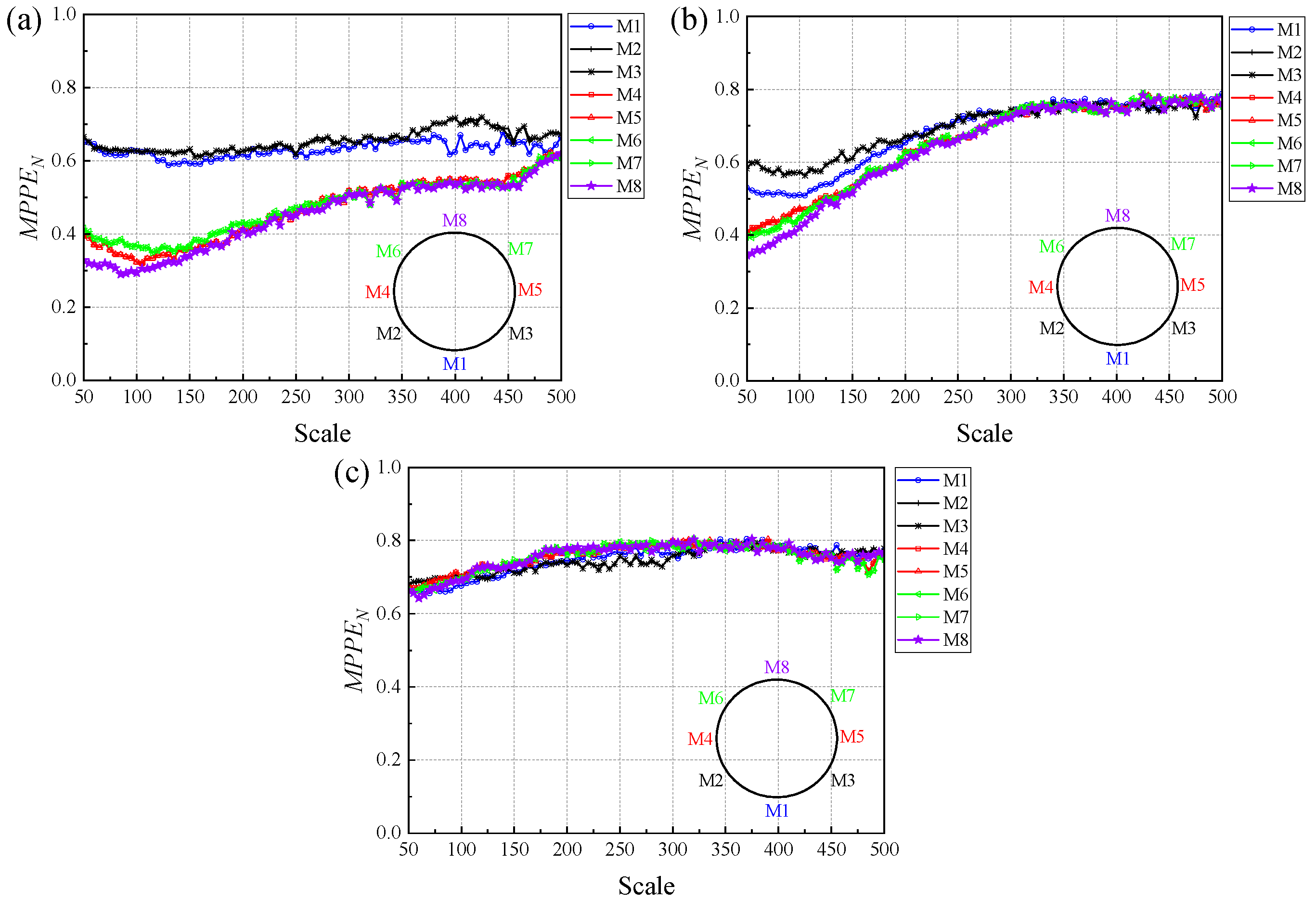
At low gas flow rates, as shown in Figure 14a, the flow pattern corresponds to oil-dispersed slug flow. Because electrodes M1, M2, and M3 are located at the bottom of the pipe, they are able to capture information on the motion of dispersed bubbles and oil droplets as well as fluctuations in liquid-film thickness. Their $MPP{E}_{\mathrm{N}}$ values are relatively high, indicating more complex hydrodynamic behavior near the pipe bottom. In comparison, electrodes M4–M8 are more sensitive to the quasi-periodic motion of elongated bubbles and liquid slugs in the upper part of the pipe, and thus show lower $MPP{E}_{\mathrm{N}}$ values within the examined scales.

(2)

With increasing gas flow rate, as illustrated in Figure 14b, the $MPP{E}_{\mathrm{N}}$ values of signals from different electrodes tend to converge at larger scales and exhibit a noticeable increasing trend. At smaller scales, however, the $MPP{E}_{\mathrm{N}}$ shows a distinct difference according to electrode height: as the electrode position rises, the $MPP{E}_{\mathrm{N}}$ gradually decreases. This indicates that the motion complexity of small-scale bubbles and oil droplets presents a spatial gradient distribution.

(3)

When pseudo slug flow occurs, as shown in Figure 14c, the overall motion complexity of the flows increases throughout the entire pipe cross-section, and the $MPP{E}_{\mathrm{N}}$ values at different spatial positions become relatively close.

Figure 15 presents the $MPP{E}_{\mathrm{N}}$ under different flow patterns at a superficial liquid velocity U_sl of 0.589 m/s. For the oil-dispersed slug flow and emulsified slug flow, as shown in Figure 15a,b, the $MPP{E}_{\mathrm{N}}$ values of different electrode signals are all relatively high, with reduced variability (in comparison with Figure 14a,b). This indicates that an increase in the total flow rate generally enhances the overall fluid complexity across both the full range of scales and the entire pipe cross-section. When the flow pattern transitions to pseudo slug flow, as shown in Figure 15c, the relatively high liquid flow rate, combined with the coexistence of large-scale gas paths, dispersed bubbles, and oil droplets, leads to a highly non-uniform spatial distribution of the flows. As a result, the flow complexity gradually decreases from the bottom to the top of the pipe over the scale range of 50–500.

In addition, we calculated the mean $MPP{E}_{\mathrm{N}}$ of different flow conditions across all scales, as shown in Figure 16. The results indicate the following:

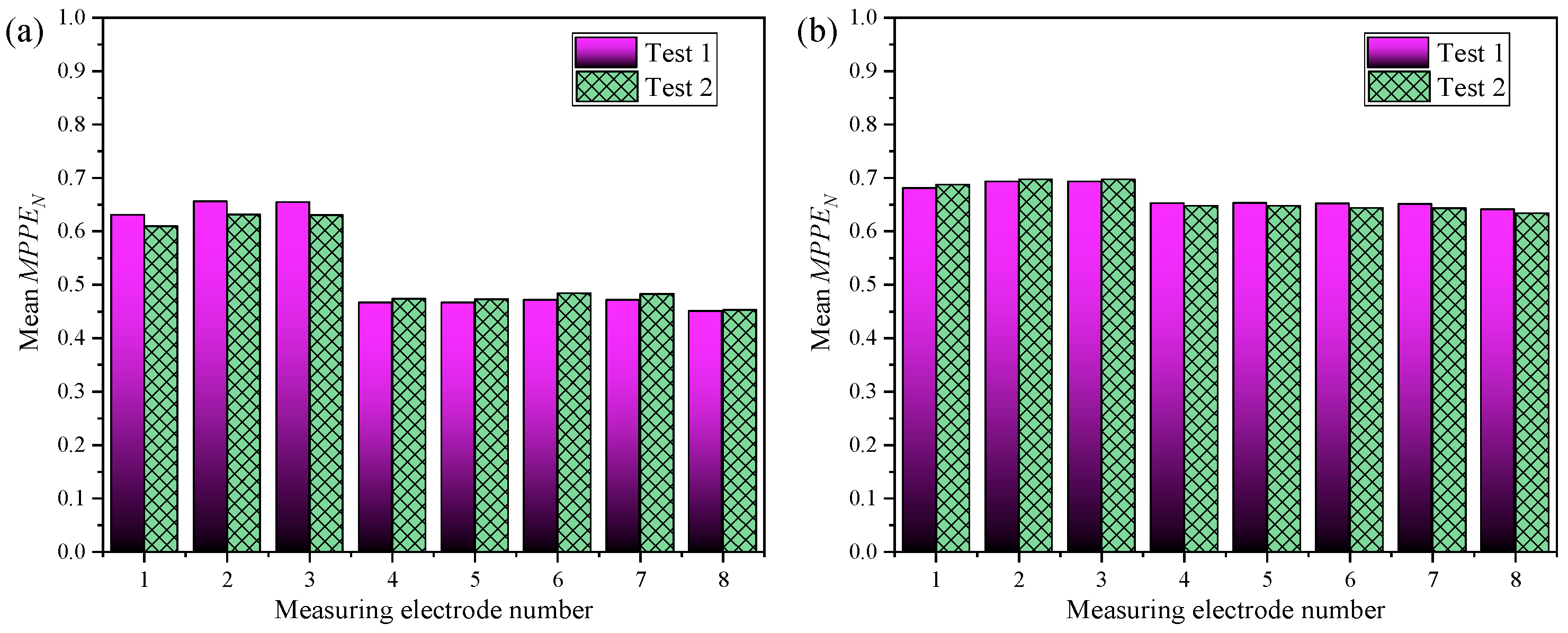
(1)

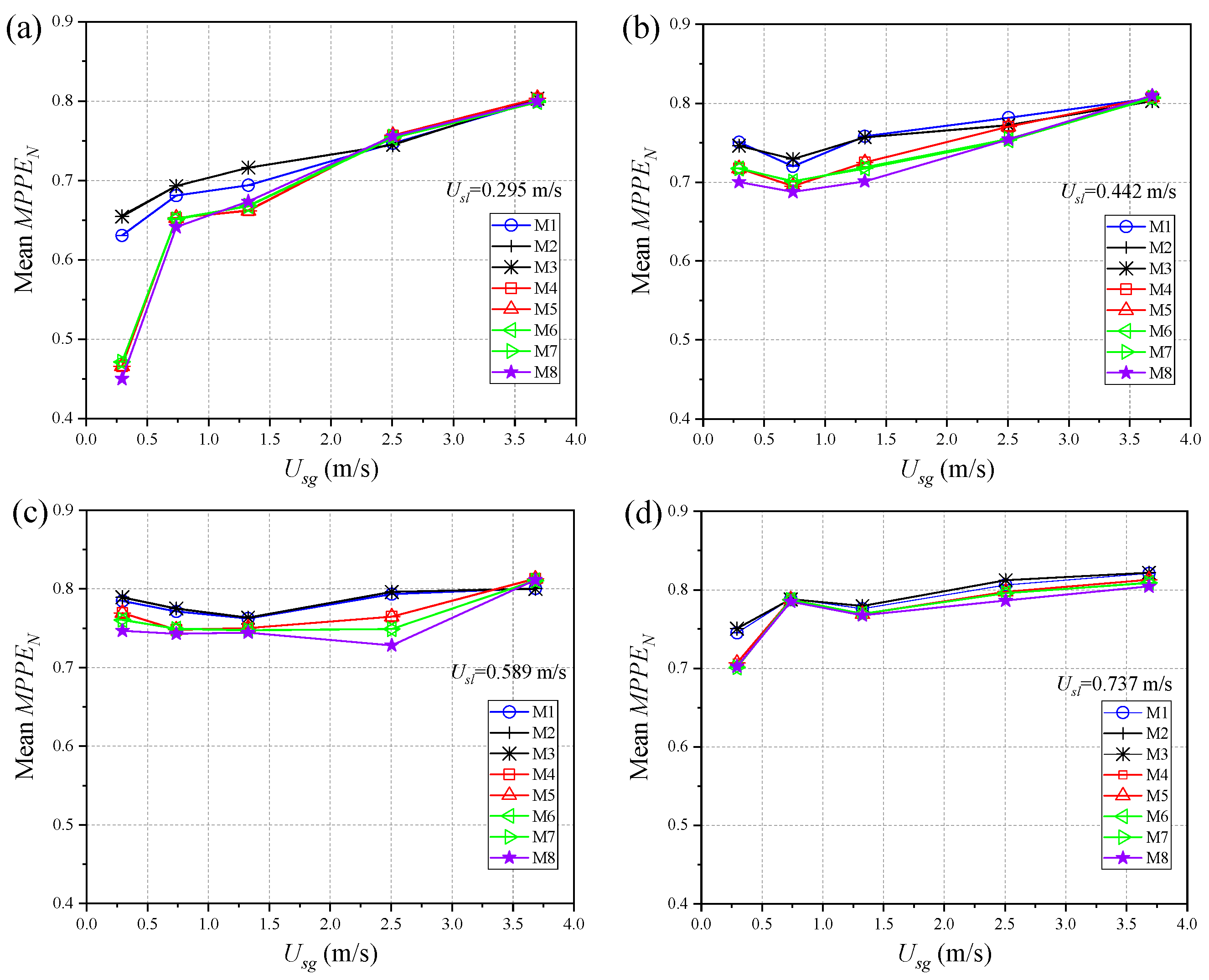
When the superficial liquid velocity is relatively low, as shown in Figure 16a, the flow complexity at the eight local positions in the pipe increases with the rise in gas flow rate. At low gas flow rates, the mean $MPP{E}_{\mathrm{N}}$ of the M1, M2, and M3 electrode signals is higher, suggesting that the flow complexity is dominated by dispersed phase motion and liquid film fluctuations near the pipe bottom. At higher gas flow rates, however, the mean $MPP{E}_{\mathrm{N}}$ values obtained from different electrode signals show better consistency, indicating that the flow complexity has expanded across the entire pipe.

(2)

When the superficial liquid velocity increases to 0.442 m/s, as shown in Figure 16b, higher gas flow rates always produce higher mean $MPP{E}_{\mathrm{N}}$ values for all electrode signals, while the mean $MPP{E}_{\mathrm{N}}$ of the M1, M2, and M3 electrode signals remains relatively high.

(3)

With a further increase in superficial liquid velocity, as shown in Figure 16c,d, all electrodes exhibit relatively high mean $MPP{E}_{\mathrm{N}}$ values under various gas flow rates, and the difference in flow complexity between the pipe bottom and top no longer follows a clear pattern.

Note that, to demonstrate that the observed differences in Figure 14, Figure 15 and Figure 16 reflect genuine changes in flow dynamics rather than random fluctuations, an additional verification experiment was conducted. Two representative flow conditions were selected, and repeated measurements were performed for each condition. Please refer to Appendix A.

6. Conclusions

To quantify the complexity of nonlinear time series, phase permutation entropy (PPE) was first validated using artificial data, including the Tent map, Hénon map, and Lorenz system. The results indicate that PPE and PE exhibit comparable performance in characterizing behavioral variations in complex nonlinear systems. Note that when the embedding dimension is relatively low, PPE can clearly capture the transition between period-doubling and chaos in the Hénon map. From this perspective, PPE demonstrates superior capability in detecting abnormal dynamical changes compared with PE.

Deep-water oil–gas–water three-phase flow is widely recognized as a chaotic system. The strong interfacial interactions give rise to pronounced nonuniform distributions within the wellbore and lead to highly complex nonlinear dynamics. A distributed conductance senso (DCS) with eight measurement electrodes is designed in this study to capture the flow information. PPE is combined with the multiscale approach to uncover the complexity of horizontal oil–gas–water flows. The results show the following:

(1)

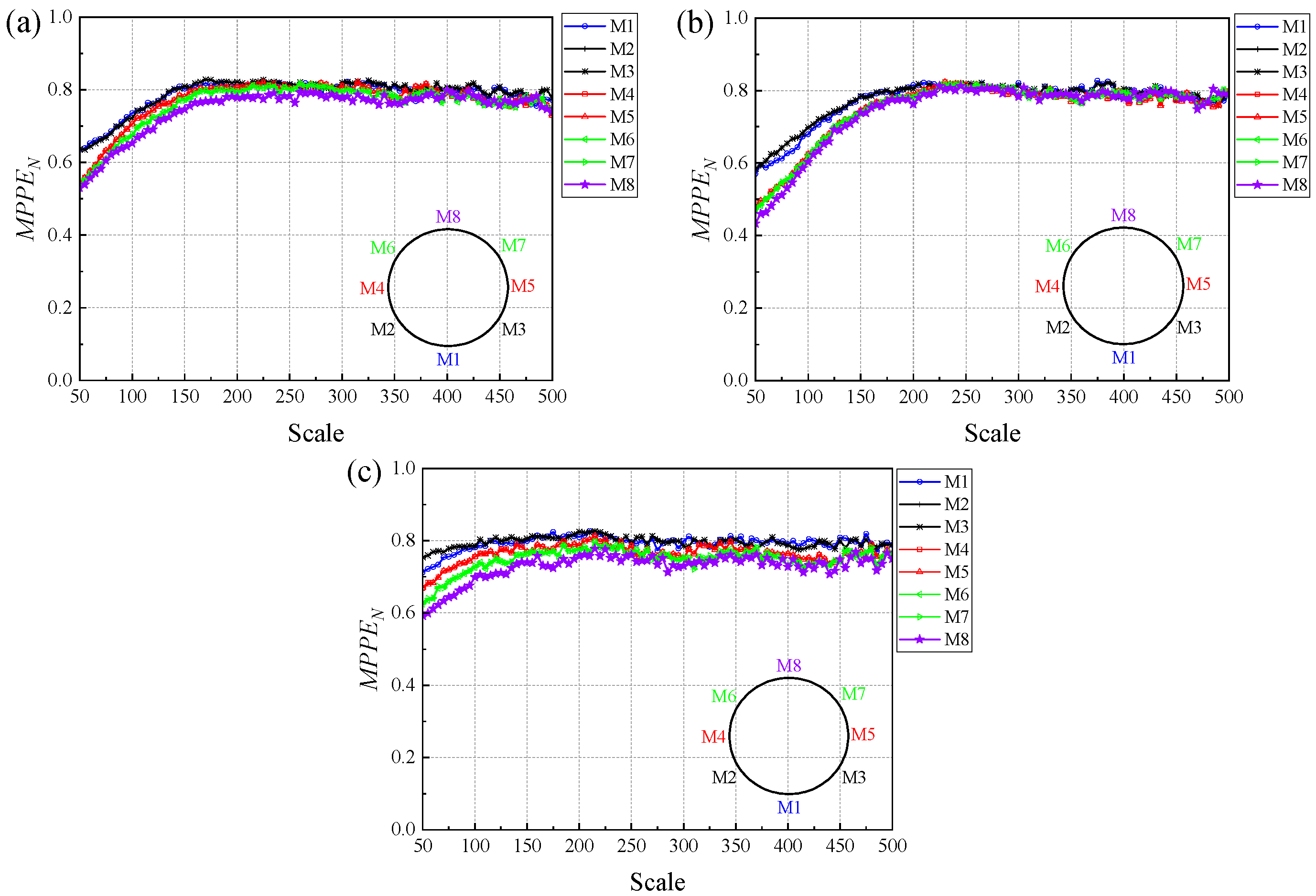
For oil-dispersed slug flow, the presence of dispersed bubbles and oil droplets can produce high flow complexity at the lower part of the pipe. In comparison, measuring electrodes at the upper part of the pipe are more sensitive to the quasi-periodic motion of elongated bubbles, and thus show lower $MPP{E}_{\mathrm{N}}$ values within the examined scales.

(2)

For emulsified slug flow, $MPP{E}_{\mathrm{N}}$ values of different electrodes tend to converge at larger scales. At smaller scales, however, the $MPP{E}_{\mathrm{N}}$ shows a distinct difference according to electrode height. As the electrode position rises, the $MPP{E}_{\mathrm{N}}$ gradually decreases, indicating that the motion complexity of small-scale bubbles and oil droplets presents a spatial gradient distribution.

(3)

For pseudo-slug flow, the overall dynamical complexity increases across the pipe cross-section. It is worth noting that when the superficial liquid velocity is relatively low, the complexity values at different electrodes remain close to each other. However, when the superficial liquid velocity becomes sufficiently high, the flow complexity gradually decreases from the bottom to the top of the pipe. This behavior is mainly attributed to the coexistence of large-scale gas pathways, dispersed bubbles, and oil droplets, which leads to a highly non-uniform spatial distribution of the flow structures.

Moreover, the $MPP{E}_{\mathrm{N}}$ curves and their multiscale evolution patterns constitute meaningful numerical features that could be incorporated into machine learning or AI-driven models for future flow pattern identification and intelligent interpretation of complex multiphase flow behavior.