Optimization Models for Distributed Energy Systems Under CO₂ Constraints: Sizing, Operating, and Regulating Power Provision

Abstract

The increasing penetration of variable renewable energy sources has intensified the need for ancillary services to maintain grid stability, and demand-side flexibility, particularly through distributed energy systems (DESs), is expected to play an important role. This study proposes a two-stage optimization framework for DESs under CO₂ constraints that enables gas engines and battery energy storage systems (BESS) to provide regulating power equivalent to Load Frequency Control (LFC). The framework consists of an Equipment Sizing Optimization Model (ESM) and an Equipment Operation Optimization Model (EOM), both formulated as mixed-integer linear programming (MILP) models. The ESM determines equipment capacities using simplified operational representations, where partial-load efficiencies are approximated through linear programming (LP)-based constraints. The EOM incorporates detailed operational characteristics, including start-up/shutdown states and partial-load efficiencies, to perform daily scheduling. Information obtained from the ESM, such as the CO₂ emissions, the equipment capacities, and the BESS state of charge, is passed to the EOM to maintain consistency. A case study shows that providing regulating power reduces total system cost and that CO₂ reduction constraints alter the equipment mix. These findings demonstrate that the proposed framework offers a practical and computationally efficient approach for designing and operating DESs under CO₂ constraints.

1. Introduction

1.1. Background

In recent years, many countries have announced CO₂ emission reduction targets aimed at achieving carbon neutrality in response to global warming [1]. In the power sector, efforts are underway to transition toward energy systems that rely primarily on renewable energy sources. However, renewable generation such as wind power and photovoltaic (PV) systems is inherently variable, making grid stability a critical issue as their penetration increases.

Traditionally, power system stability has been maintained through regulating power sources such as thermal and hydroelectric plants. As the share of variable renewable energy grows, the demand for regulating power to compensate for output fluctuations and forecast errors is expected to rise [2]. In Europe, balancing power markets have been established to efficiently procure resources for frequency control and flexibility. In Japan, a flexibility market was established in April 2021.

Against this backdrop, demand-side flexibility has attracted increasing attention. Distributed energy resources (DERs) on the consumer side are expected to play a significant role in balancing electricity supply and demand [3]. In particular, distributed energy systems (DESs), which supply electricity and heat to multiple demand groups using gas engine cogeneration and other distributed resources, are gaining traction due to their efficient energy utilization. By optimizing the operation of these resources, DESs can effectively integrate variable renewable energy sources with high uncertainty and contribute to grid stability by providing balancing services [4,5].

1.2. Related Work

A considerable number of studies have investigated optimal operation strategies for DESs. These works highlight the importance of incorporating resources with diverse characteristics, such as gas engines, BESS, and heat pumps [6,7]. For example, A. Aoun et al. reported that a mixed-integer linear programming (MILP) formulation of a DER model including PV and generators can enhance both economic and environmental benefits [8]. Similarly, L. Kanaan et al. demonstrated cost reduction effects using an MILP model that integrates PV, diesel generators, and energy storage systems [9]. However, these studies focus solely on operational optimization and do not provide an integrated optimization framework that includes equipment sizing.

In addition to operational optimization, numerous studies have also examined optimal equipment sizing for DESs. These works commonly reduce computational burden through approaches such as representative-day selection and clustering methods [10,11,12]. However, representative-day optimization is not suitable when determining the required capacity of storage systems intended to facilitate the integration of renewable energy. To realistically capture storage operation, it is necessary to model continuous operation over time while accounting for daily variations in solar irradiance and energy demand.

Furthermore, in recent years, research has expanded beyond cost reduction and CO₂ emission mitigation to also address the provision of balancing services to the power grid. BESS, as shown by K. Prakash et al., offer significant operational flexibility, enabling applications such as grid stabilization and power quality improvement [13]. For instance, J. Wang et al. demonstrated that the optimal operation of PVs and BESS in microgrids can increase revenues from participation in ancillary service markets [14]. Moreover, not only BESS but also cogeneration systems and water pumping facilities have been reported to contribute to balancing services through optimal operation strategies [15,16,17].

1.3. Research Objectives

This study aims to develop an optimization model for DESs designed to supply electricity, steam, hot water, and chilled water demands and provide flexibility services to the power grid. In this context, flexibility refers specifically to the provision of load frequency control (LFC) regulating power through gas engines and BESS. To represent regulating power provision in DESs, the framework consists of two components: (i) an equipment sizing optimization model (ESM), which determines the number of units and their approximate annual operation, and (ii) an equipment operation optimization model (EOM), which calculates detailed daily operation. Both models incorporate constraints to reflect the system’s capability to provide regulating power.

Although a multi-year optimization framework that accounts for the gradual introduction of equipment would be desirable, the associated computational burden is considerable. Therefore, the proposed model focuses on optimizing equipment deployment and operation within a one-year horizon.

Furthermore, to address future CO₂ emission constraints, the model has been extended to include hydrogen-related equipment. This enables the evaluation of optimal operation strategies under various CO₂ emission scenarios, thereby highlighting the role of hydrogen energy in enhancing system flexibility and sustainability.

2. Methods

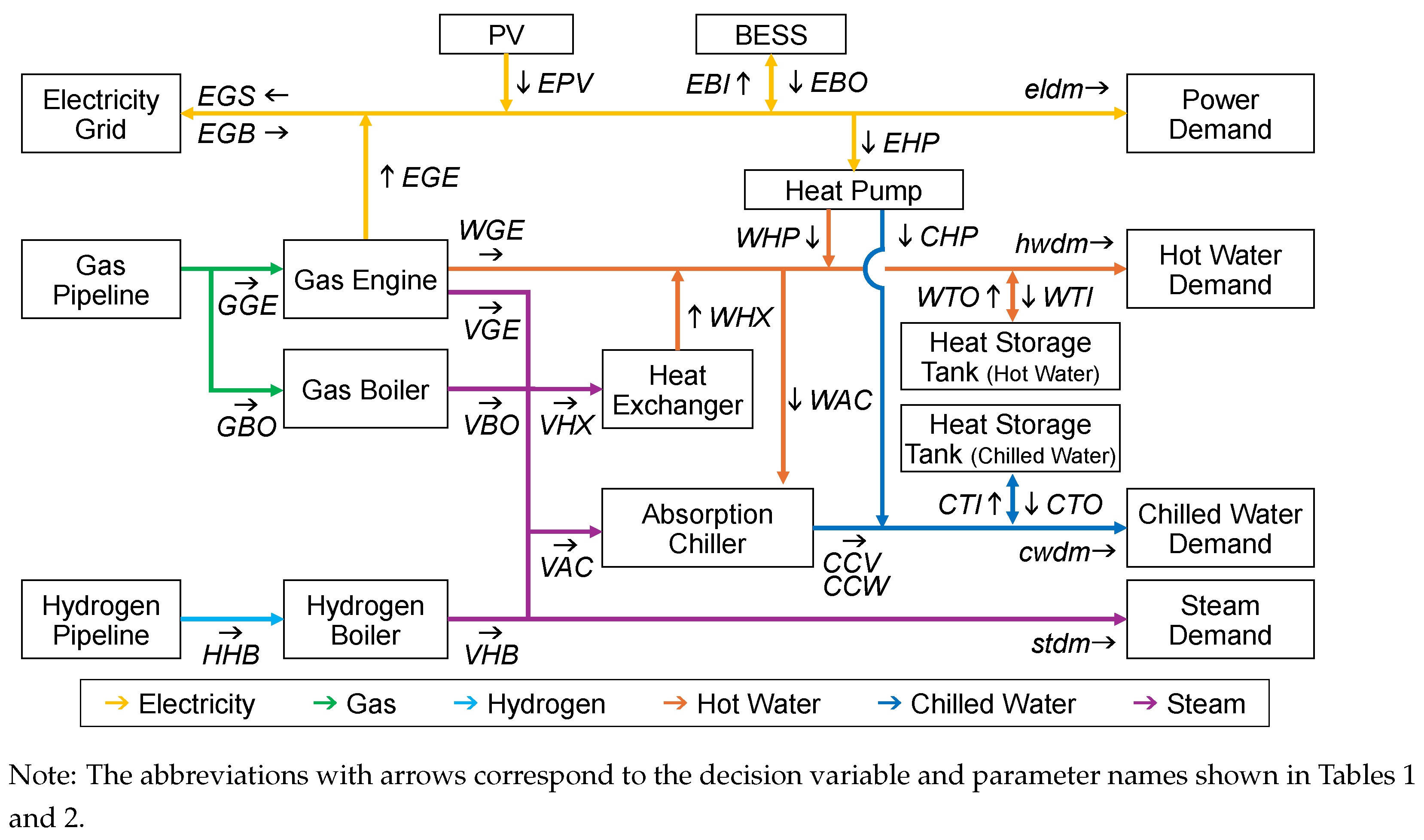
2.1. System Energy Flow and Notation

The DES considered in this study assumes a region comprising a factory with a total floor area of 10,000 m² and an office building with a total floor area of 7000 m², both requiring electricity, steam, hot water, and chilled water. Figure 1 illustrates the energy and utility flows within the system.

Electricity demand is met by PV generation, gas engines, and electricity purchased from the power grid. Surplus electricity is stored in the BESS. Steam demand is fulfilled using waste heat from gas engines, gas boilers, and hydrogen boilers. Hot water demand is supplied by waste heat from gas engines, heat pumps, and heat exchangers. Chilled water demand is met by heat pumps and absorption chillers. Excess hot and chilled water can be stored in separate hot-water and chilled-water storage tanks, respectively.

Regulating power for LFC is provided to the power grid via the gas engines and BESS, enabling the DES to contribute to grid stability.

In addition to the system configuration shown in Figure 1, the variables, parameters, and indices used throughout this study are summarized in

Table 1. List of variables and indices.

Decision Variables
$I{C}_{eq}$	Total installation cost of equipment [JPY]	$WGE$	HW output from GEs [MJ]
$N{M}_{eq}$	Number of equipment unit	$WHX$	HW output from HEX [MJ]
$C{P}_{b{t}_s}$	Installed storage capacity of the BESS [kWh]	$WHP$	HW output from HPs [MJ]
$C{P}_{b{t}_p}$	Installed power capacity of the BESS [kW]	$WTO$	HW output from TST [MJ]
$OB{J}_s$	Annual total cost of ESM [JPY]	$WTI$	HW supplied to TST [MJ]
$C_{electricity}$	Total electricity purchase cost [JPY]	$WAC$	HW supplied to ACs [MJ]
$C_{gas}$	Total gas purchase cost [JPY]	$CHP$	CW output from HPs [MJ]
$C_{equipment}$	Total equipment installation cost [JPY]	$CTO$	CW output from TST [MJ]
$R_{lfc}$	Total flexibility revenue [JPY]	$CTI$	CW supplied to TST [MJ]
$EGB$	Purchased electricity [kWh]	$CCV$	CW output from ACs (steam-driven) [MJ]
$GGE$	Gas cons. of GEs [${\mathrm{Nm}}^3$]	$CCW$	CW output from ACs (HW-driven) [MJ]
$GBO$	Gas cons. of GBs [${\mathrm{Nm}}^3$]	$STW$	Stored HW [MJ]
$LUP$	Upward regulating power of GEs [$\Delta$kW]	$STC$	Stored CW [MJ]
$BUP$	Upward regulating power of the BESS [$\Delta$kW]	$HHB$	Hydrogen cons. of HBs [${\mathrm{Nm}}^3$]
$LDW$	Downward regulating power of GEs [$\Delta$kW]	$COE$	${\mathrm{CO}}_2$ emissions [kg-${\mathrm{CO}}_2$]
$BDW$	Downward regulating power of the BESS [$\Delta$kW]	$SCOE$	Total annual ${\mathrm{CO}}_2$ emissions [kg-${\mathrm{CO}}_2$]
$EGE$	Electricity generated by GEs [kWh]	$OB{J}_o$	Daily total cost of EOM [JPY]
$EPV$	Electricity generated by PV systems [kWh]	$C_{storage}$	Net reward/penalty of remaining storage [JPY]
$EBO$	BESS discharge energy [kWh]	$PEN$	Shortage amount of storage [kWh], [MJ]
$EBI$	BESS charge energy [kWh]	$REW$	Surplus amount of storage [kWh], [MJ]
$EGS$	Electricity sold [kWh]	$UGE$	Number of operating GEs [unit]
$EHP$	Electricity cons. of HPs [kWh]	$UGEON$	Number of GEs started [unit]
$VGE$	Steam output from GEs [MJ]	$UGEOF$	Number of GEs stopped [unit]
$VBO$	Steam output from GBs [MJ]	$UCV$	Number of operating ACs [unit]
$VHB$	Steam output from HBs [MJ]	$UCVON$	Number of ACs started [unit]
$VAC$	Steam supplied to ACs [MJ]	$UCVOF$	Number of ACs stopped [unit]
$VHX$	Steam supplied to HEX [MJ]
Index
m	Month index in a year (1 $\le m\le$ 12) [month]	$hpw$	Index of HP for HW usage
d	Day index in a year ($1\le d\le 365$) [day]	$hpc$	Index of HP for CW usage
t	Hourly time step in a year (1 $\le t\le$ 8760) [hour]	$pv$	Index of PV system
h	Hourly time step ($1\le h\le 24$) [hour]	$b{t}_s$	Index of the BESS storage capacity
$eq$	Index of equipment	$b{t}_p$	Index of the BESS power capacity
$ge$	Index of GE	$hb$	Index of HB
$bo$	Index of GB	$hx$	Index of HEX
$ac$	Index of AC	$tw$	Index of TST for HW usage
$hp$	Index of HP	$tc$	Index of TST for CW usage

Note: GE, gas engine; BESS, battery energy storage system; GB, gas boiler; HP, heat pump; HB, hydrogen boiler; AC, absorption chiller; HEX, heat exchanger; TST, thermal storage tank; HW, hot water; CW, chilled water.

and

Table 2. List of parameters.

Parameters
$crf$	Capital recovery factor	–	$ol{s}_{bt}$	BESS round trip efficiency [-]	0.95
r	Discount rate	0.04	$el{s}_{bt}$	BESS time loss factor [-/day]	0.01
n	Useful life [year]	15	$ol{s}_{tw,tc}$	Thermal storage round trip efficiency [-]	0.98
$i{c}_{ge}$	Install. cost of GE [JPY/kW]	290,000	$el{s}_{tw,tc}$	Thermal storage time loss factor [-/day]	0.15
$i{c}_{bo}$	Install. cost of GB [JPY/MJ]	8100	$lf{c}_{ge}$	Regulating range coefficient (GE) [-]	0.30
$i{c}_{ac}$	Install. cost of AC [JPY/MJ]	23,300	$lf{c}_{bt}$	Regulating range coefficient (BESS) [-]	0.05
$i{c}_{hp}$	Install. cost of HP [JPY/MJ]	51,800	$pu$	Per-unit output of PV system [kW/kW]	–
$i{c}_{pv}$	Install. cost of PV system [JPY/kW]	116,666	$co{2}_g$	${\mathrm{CO}}_2$ factor of gas [kg-${\mathrm{CO}}_2/$${\mathrm{Nm}}^3$]	2.29
$i{c}_{b{t}_s}$	Install. cost of BESS storage unit [JPY/kWh]	17,640	$co{2}_e$	${\mathrm{CO}}_2$ factor of electricity [kg-${CO}_2/$kWh]	0.29
$i{c}_{b{t}_p}$	Install. cost of BESS power unit [JPY/kW]	26,888	$bcoe$	Annual CO2 emissions (reference) [t-${\mathrm{CO}}_2$]	35,657
$i{c}_{hb}$	Install. cost of HB [JPY/MJ]	13,450	p	${\mathrm{CO}}_2$ reduction rate [-]	0.2, 0.4, 0.6
$elb$	Electricity price [JPY/kWh]	–	$pbt$	Penalty cost (BESS) [JPY/kWh]	${10}^6$
$gsb$	Gas price [JPY/${\mathrm{Nm}}^3$]	–	$rbt$	Reward (BESS) [JPY/kWh]	${10}^{-6}$
$spu$	Upward flexibility price [JPY/$\Delta$kW]	–	$ptw$	Penalty cost (TST, HW) [JPY/MJ]	${10}^6$
$spd$	Downward flexibility price [JPY/$\Delta$kW]	–	$ptc$	Penalty cost (TST, CW) [JPY/MJ]	${10}^6$
$eldm$	Electricity demand [kWh]	–	$num$	Number of equipment unit in the ESM [unit]	–
$stdm$	Steam demand [MJ]	–	$ug{e}_{24}$	Operating GEs at final hour of day d-1 [unit]	–
$hwdm$	HW demand [MJ]	–	$a{g}_{ge}$	Gas cons. coefficient [(${\mathrm{Nm}}^3$/h)/kW]	0.17
$cwdm$	CW demand [MJ]	–	$b{g}_{ge}$	No-load gas cons. coefficient [${\mathrm{Nm}}^3$/h]	24.9
$cp{e}_{ge}$	Rated electricity output per GE [kW]	1250	$s{g}_{ge}$	Additional gas cons. for startup [${\mathrm{Nm}}^3$/h]	–
$cp{e}_{pv}$	Rated electricity output per PV unit [kW]	1000	$a{v}_{ge}$	Steam gen. coefficient [(MJ/h)/kW]	0.91
$cp{v}_{bo}$	Rated steam output per GB [MJ/h]	5000	$b{v}_{ge}$	No-load steam gen. coefficient [MJ/h]	614
$cp{v}_{hb}$	Rated steam output per HB [MJ/h]	5000	$a{w}_{ge}$	HW gen. coefficient [(MJ/h)/kW]	1.74
$cp{w}_{hp}$	Rated HW output per HP [MJ/h]	1000	$b{w}_{ge}$	No-load HW gen. coefficient [MJ/h]	328
$cp{c}_{hp}$	Rated CW output per HP [MJ/h]	1000	$a{v}_{ac}$	Steam gen. coefficient [(MJ/h)/(MJ/h)]	0.65
$cp{c}_{ac}$	Rated CW output per AC [MJ/h]	5000	$b{v}_{ac}$	No-load steam gen. coefficient [MJ/h]	53.3
$cp{s}_{tw}$	Rated TST capacity (HW) [MJ]	60,000	$s{v}_{ac}$	Additional heat cons. for startup [MJ/unit]	–
$cp{s}_{tc}$	Rated TST capacity (CW) [MJ]	40,000	$s{w}_{ac}$	Additional heat cons. for startup [MJ/unit]	–
$ef{v}_{ge}$	Steam efficiency of GE [(MJ/h)/kW]	1.39	$sb{t}_{d,h}^{\prime }$	SOC at hour h on day d in the ESM [kWh]	–
$ef{w}_{ge}$	HW efficiency of GE [(MJ/h)/kW]	2.01	$sb{t}_{d,h}$	SOC at hour h on day d [kWh]	–
$ef{g}_{ge}$	Gas cons. efficiency of GE [(${\mathrm{Nm}}^3/$h)/kW]	0.19	$c{p}_{b{t}_p}$	BESS power capacity in the ESM [kWh]	–
$ef{v}_{bo}$	Steam efficiency of GB [MJ/kWh]	0.95	$c{p}_{b{t}_s}$	BESS storage capacity in the ESM [kWh]	–
$ef{v}_{ac}$	Steam efficiency of AC [(MJ/h)/(MJ/h)]	0.66	$st{w}_{d,h}^{\prime }$	Stored HW at hour h on day d in the ESM [MJ]	–
$ef{w}_{ac}$	HW efficiency of AC [(MJ/h)/(MJ/h)]	1.14	$st{w}_{d,h}$	Stored HW at hour h on day d [MJ]	–
$co{p}_w$	COP of HP (HW) [-]	4.3	$sco{e}_d^{\prime }$	Daily CO2 emission limit in the ESM [kg-CO2]	–
$co{p}_c$	COP of HP (CW) [-]	4.1	$pco2$	Penalty cost (CO2 surplus)	${10}^9$
$ef{w}_{hx}$	HW efficiency of HEX [-]	0.98

Note: GE, gas engine; BESS, battery energy storage system; GB, gas boiler; HP, heat pump; HB, hydrogen boiler; AC, absorption chiller; HEX, heat exchanger; TST, thermal storage tank; HW, hot water; CW, chilled water.

. This table provides a comprehensive list of the notation employed in the formulation of the DES optimization model, including equipment capacities, operational variables, cost parameters, and efficiency coefficients.

2.2. DES Optimization Model

This study develops a two-stage equipment optimization model for DESs capable of providing regulating power via gas engines and BESS. To reduce computational complexity, the analysis is divided into two parts as shown in Figure 2: (1) an equipment sizing optimization model (ESM), which determines the optimal size and the number of equipment units to be installed on an annual basis, and (2) an equipment operation optimization model (EOM), which calculates the detailed daily operation of each unit. First, the ESM determines the optimal number of equipment units and their approximate annual operation plan based on simplified equipment assumptions. The resulting data—such as the number of units and storage capacity—are then transferred to the EOM, which performs a detailed daily optimization simulation. Unlike the ESM, which optimizes over a single one-year horizon, the EOM performs 365 sequential daily optimizations, thereby simulating detailed operation throughout the year.

Both models are formulated as mixed-integer linear programming (MILP) problems; however, their treatment of equipment operation differs. In the ESM, which adopts a relatively long optimization horizon, equipment start-up and shutdown states are omitted to reduce computational burden. The operational constraints are partially formulated using linear programming (LP)-based approximations: partial-load efficiencies are represented by piecewise linear functions, and equipment operation is modeled with linear constraints and continuous variables. Integer variables are introduced only to determine the number of installed units. In contrast, the EOM, which considers a shorter optimization horizon, is formulated as a MILP model, introducing integer variables for all operational decisions and explicitly representing the start-up/shutdown states and partial-load efficiencies of each unit.

(1)

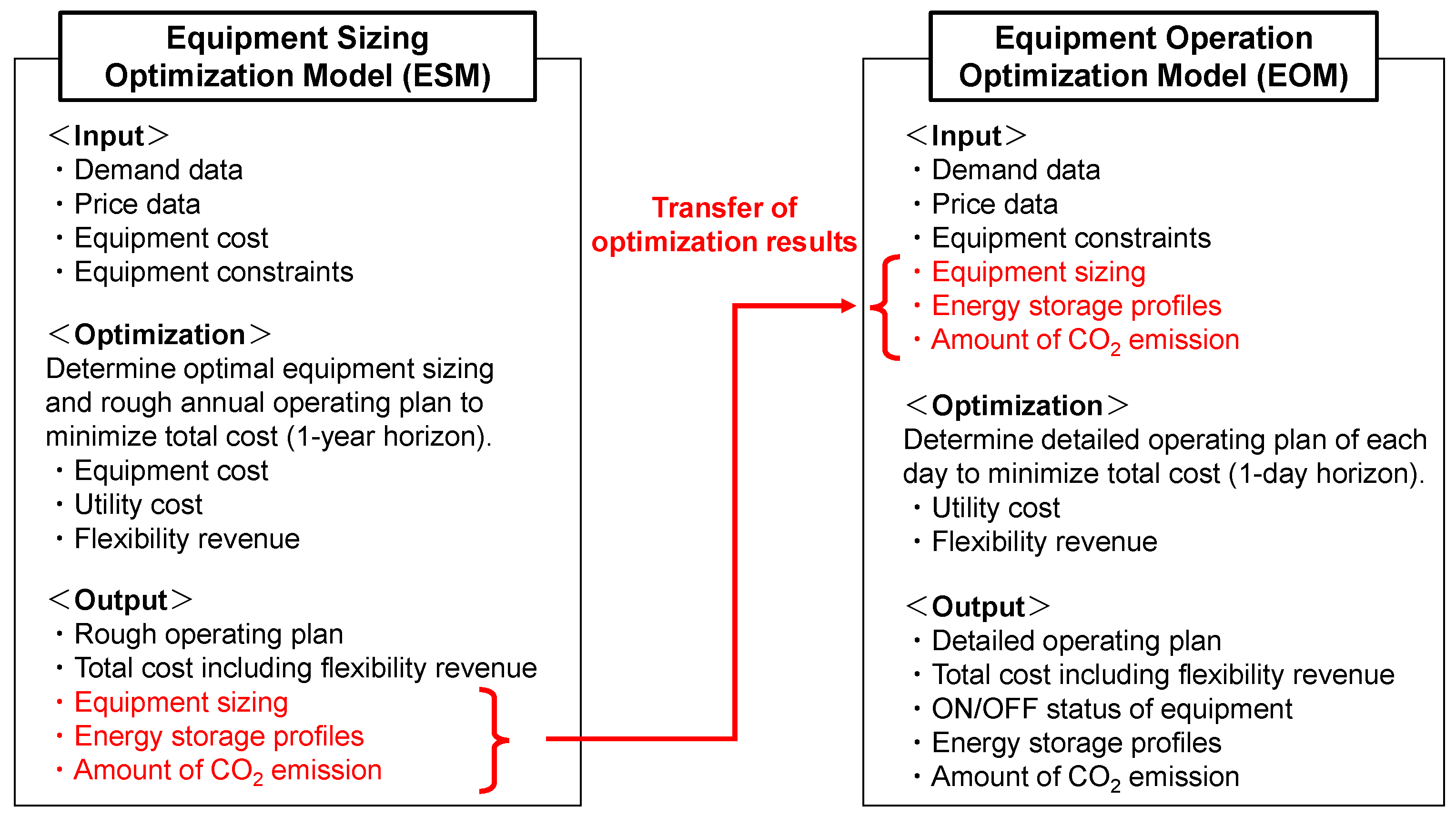
Equipment Sizing Optimization Model (ESM)

The ESM uses input data such as DES demand (electricity, steam, hot water, and chilled water), equipment installation costs, electricity tariffs, and gas prices. Its objective function minimizes the total cost over one year, comprising both installation and operational costs, while accounting for depreciation. The model outputs include the number of equipment units, hourly operational profiles (including energy storage levels), CO₂ emissions, and the total operating cost.

(2)

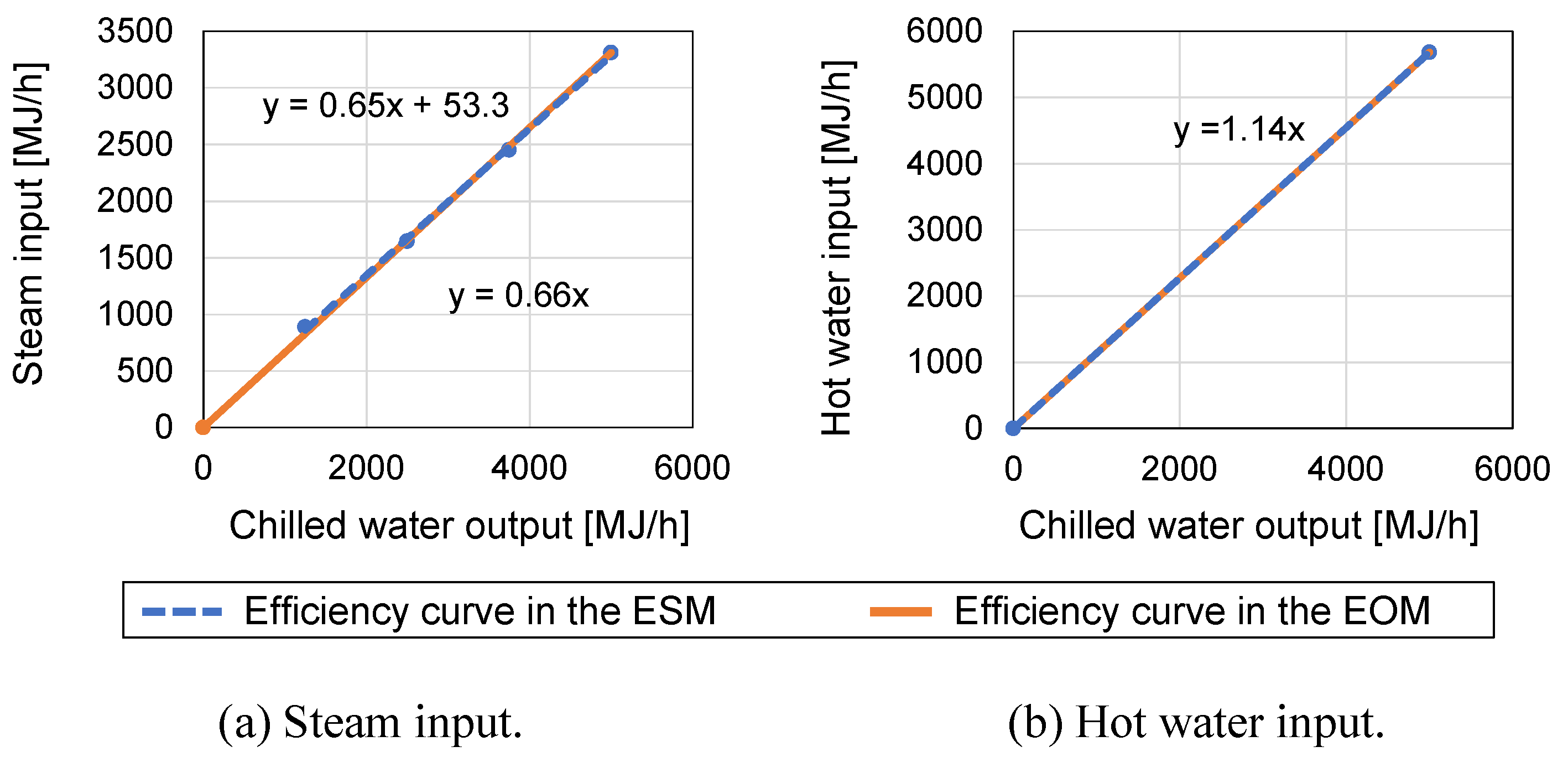
Equipment Operation Optimization Model (EOM)

The EOM uses both the input and output data from ESM—specifically, the number of units, energy storage profiles, and the daily allowable CO₂ emission level. Its objective is to minimize daily operating costs. Since stored energy is assumed to be fully discharged at the end of each optimization period, the storage capacity calculated in the ESM is used to represent continuity across days. In particular, the model incorporates constraints requiring that the storage level at the beginning of day N equals that at the end of day $N-1$, and that the end-of-day storage level is no less than the corresponding value specified in the ESM.

For equipment such as gas engine and absorption chiller with non-continuous minimum output constraints, the model explicitly accounts for start-up and shut-down states to enable more accurate operational scheduling. Regarding CO₂ emissions, the daily emission values obtained from the ESM are imposed as upper limits in the EOM, ensuring that emissions do not exceed the results determined in the sizing stage. However, because the EOM incorporates more detailed operational scheduling—such as gas engine startup fuel consumption—the resulting emissions may differ from those in the ESM. To address this discrepancy, a penalty term is introduced to ensure that the daily CO₂ emissions in the EOM do not exceed the upper limits derived from the ESM.

Similar to the ESM, the EOM also incorporates constraints related to regulating power provision. Its outputs include hourly equipment status, energy storage levels, start-up/shut-down events, CO₂ emissions, and the total operating cost.

2.3. Case Study

Two case studies were conducted to evaluate the validity of the models constructed in this study, assuming fiscal year 2040.

• The first case study examined the impact of enabling or disabling regulating power provision on equipment configuration and profitability.
• The second case study used a DES without a PV, a BESS and a hydrogen boiler as the baseline, with the baseline conditions set for fiscal year 2025, and examined changes in equipment configuration, operations, and profitability when CO₂ emissions were reduced by a specified percentage.

3. Scenario Assumptions and Input Data

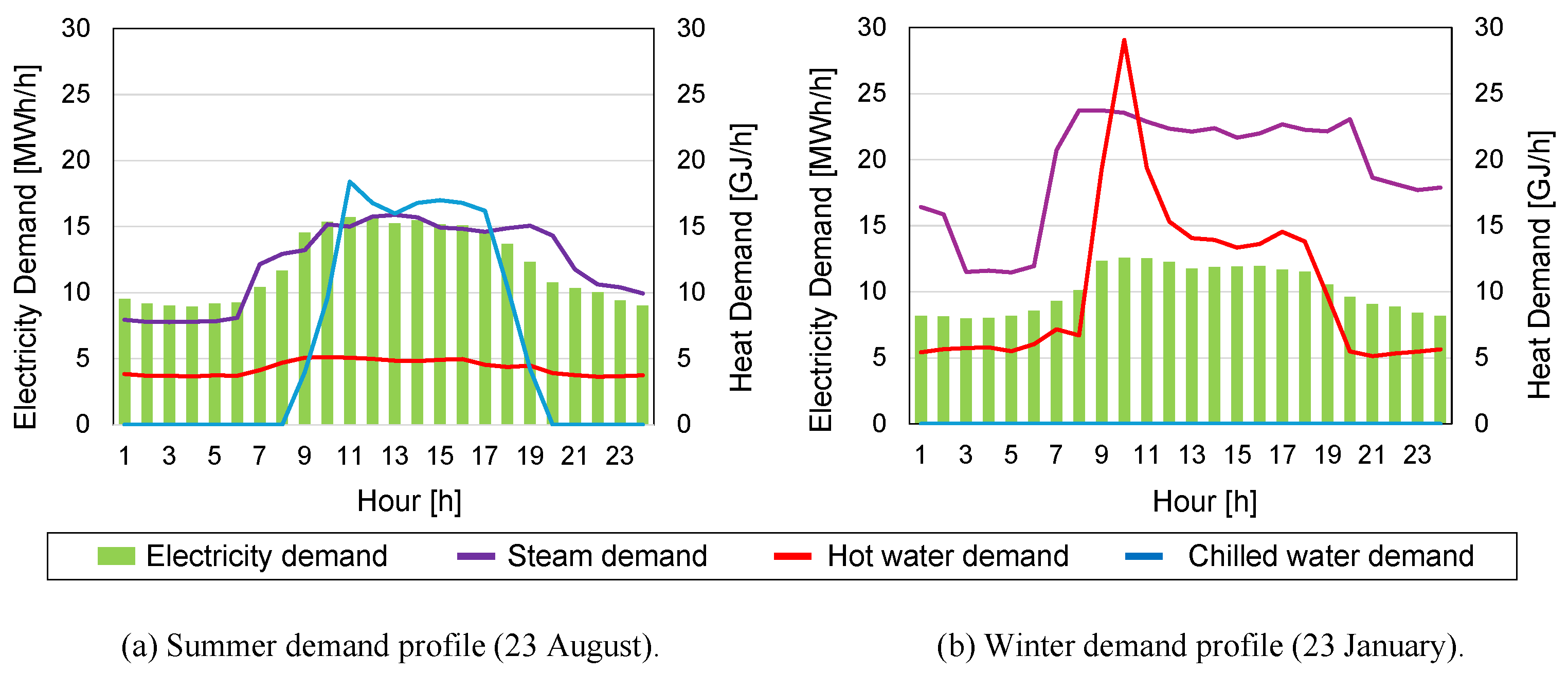
3.1. Demand Data

The demand data used in this study represent the electricity, steam, hot water, and chilled water demands of a DES composed of factories and office buildings. All datasets were prepared with an hourly resolution over a full year (8760 h), and were derived from actual measured demand data of factories and office buildings, scaled to match the total floor area assumed in this study. Figure 3 illustrates the demand profiles for a representative (a) summer day (23 August) and (b) winter day (23 January). In the figures, electricity demand is shown separately on the left axis, whereas steam, hot water, and chilled water are categorized under heat demand, consistent with the right axis labels. A comparison of these figures reveals that electricity and chilled water demands are higher in summer, while steam and hot water demands are more pronounced in winter.

3.2. PV Output Data

The PV power generation data used in this study were constructed based on the total installed capacity and actual generation records of PV systems in the Kyushu region, where solar penetration is relatively high. Specifically, the dataset was developed using the FY2016 PV generation records published by the transmission system operator in the Kyushu area [18], together with the actual installed PV capacity data for the same year in the Kyushu region [19]. The dataset covers a full year with hourly resolution, comprising 8760 data points.

3.3. Price Data

The electricity price and regulating power price used in this study were derived from a power supply-demand analysis model. This model represents a nationwide unit commitment problem formulated as a MILP problem, based on the methodology reported in the literature [12,20]. The optimization variables include thermal power output, pumped hydro output, generator start-up/shut-down states, and load frequency control (LFC) regulating power. The constraints considered in the formulation include supply-demand balance, LFC regulating power requirements, interconnection line capacity, and pumped hydro capacity.

Using this power supply-demand analysis model, optimization was performed under the high renewable energy penetration scenario in 2040. From the optimization results, the shadow prices of the supply-demand balance constraint and the LFC regulating power requirement constraint at each time step were interpreted as marginal costs, and were used to calculate the electricity price [JPY/kWh] and regulating power price [JPY/$\Delta$kW], respectively. The electricity price was defined as the shadow price of the supply-demand balance constraint plus an additional 10 JPY/kWh to account for fixed costs, transmission charges, and renewable energy surcharges. The regulating power price was directly taken from the shadow price of the LFC regulating power requirement constraint.

The selling price of electricity was set to 0 JPY/kWh, reflecting the assumption that most electricity sold to the grid originates from PV generation. Since surplus electricity during low-demand periods is expected to have low market value, this zero-price assumption was adopted to encourage the use of storage systems.

The gas price was estimated using current retail gas prices and projected increases in natural gas prices, scaled proportionally to the expected rise in 2040. Reference values for the 2040 natural gas price were obtained from materials published by the Institute of Energy Economics, Japan (IEEJ) [21]. The hydrogen cost was set at 81 JPY/Nm³, based on domestic renewable-energy-derived hydrogen reference data provided by IEEJ [22], assuming that hydrogen may also be produced on-site using surplus renewable electricity.

These datasets were independently constructed with an hourly resolution over a full year (8760 h).

3.4. Equipment Specification

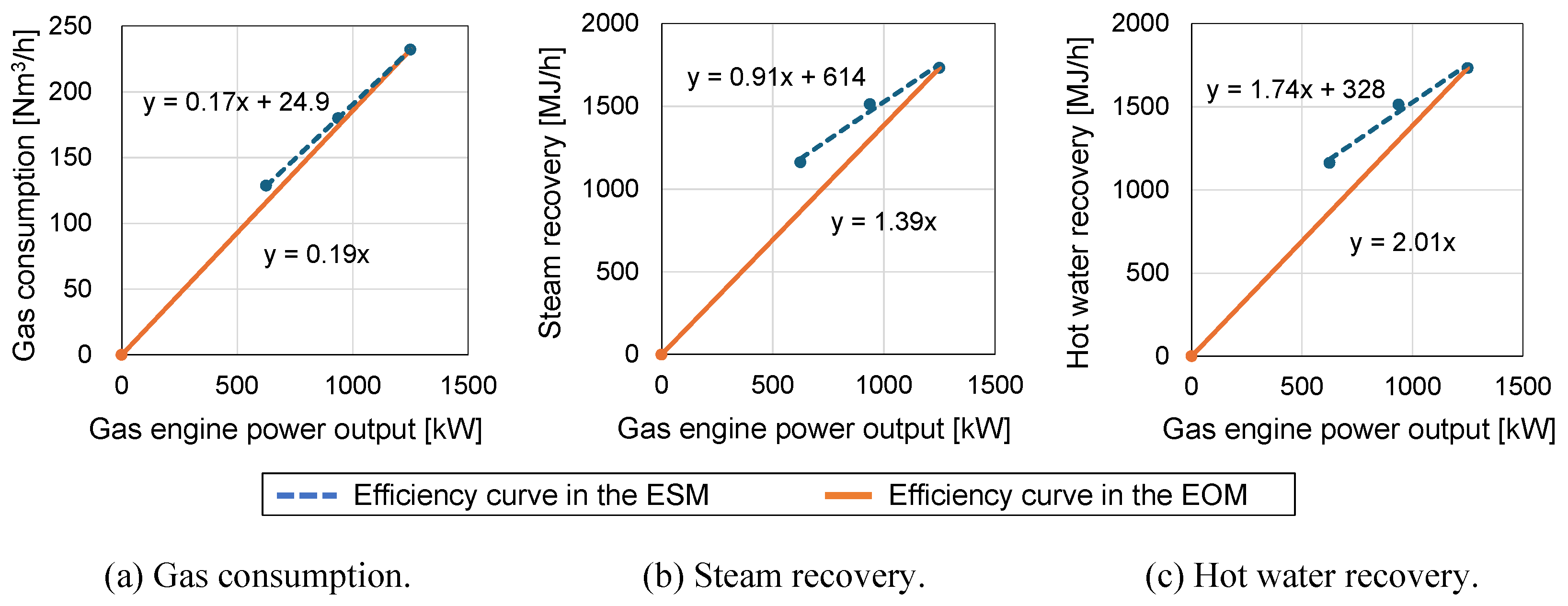
3.4.1. Gas Engine

The gas engine is a type of combined heat and power (CHP) system. In this study, a gas engine with a rated output of 1250 kW was used to supply electricity and regulating power, while also recovering exhaust heat as steam and hot water. Since efficiency varies with load factor,

Table 3. Gas engine load factor.

Load Factor	50%	75%	100%
Power generation efficiency [%]	38.9	41.7	43.1
Steam recovery efficiency [%]	20.1	18.7	16.6
Hot water recovery efficiency [%]	24.7	23.9	24.1

lists the generation output, gas consumption, steam recovery, and hot water recovery at each load level referenced from the data book [23]. The corresponding performance curves are shown in Figure 4, comparing part-load characteristics under the ESM and EOM formulations: (a) gas consumption, (b) steam recovery, and (c) hot water recovery. In each graph, the ESM curve is shown as an orange solid line, while the EOM curve is shown as a blue dash line. The slopes and intercepts used in this approximation are summarized in Table 1.

In the ESM, the part-load efficiency of the gas engine is represented using an LP formulation, where efficiency is defined as the slope between zero and rated output. The EOM was formulated as a MILP problem, in which the part-load efficiency of the gas engine is modeled using an approximation that combines continuous and integer variables. In the EOM, the minimum operating output is set to 30% of rated capacity, and the start-up cost to 20%.

3.4.2. Gas Boiler

The gas boiler uses city gas as its fuel and contributes to steam supply, hot water production via heat exchangers, and chilled water production via absorption chillers. The rated output of the gas boiler is set to 5000 MJ/h, with a thermal conversion efficiency of 95%. Partial load efficiency is not considered in this study.

3.4.3. Absorption Chiller

The absorption chiller supplies chilled water using steam or hot water as input. Its rated output is set to 5000 MJ/h. Based on the COP values under part-load operation, referenced from manufacturer speifications [24] and shown in

Table 4. Adsorption chiller load factor.

Load Factor	25%	50%	75%	100%
COP of steam consumption [-]	1.41	1.52	1.53	1.51
COP of hot water consumption [-]				0.88

, the steam and hot water consumption efficiencies are represented in Figure 5a,b, respectively. For steam input, the ESM defines efficiency as the slope of a straight line from zero to rated output, without accounting for start-up or shut-down behavior, whereas the EOM uses a proportional formulation in the same manner as the gas engine. For hot water input, both models adopt the same constant efficiency, as part-load effects are negligible. The slopes and intercepts used in this approximation are summarized in Table 1.

3.4.4. Heat Pump

The heat pump consumes electricity to produce hot and chilled water. In this study, it is assumed to supply only to meet hot and chilled water demand. The operating mode—hot water or chilled water output—is switchable on a monthly basis, and each unit operates in a single mode within a given month. The rated output is set to 1000 MJ/h for both hot and chilled water. The coefficient of performance (COP), defined as the amount of thermal energy output per 1 kWh of electricity consumed, is set to 4.3 for hot water production and 4.1 for chilled water production, referenced from manufacturer specifications [25]. Since the impact of partial load on efficiency is considered negligible, the efficiency is assumed to be constant. The minimum operating output is set to 30% of the rated capacity and the start-up cost is defined as the electricity consumption when operating at 20% of the rated output.

3.4.5. Heat Exchanger

The heat exchanger is used to convert excess steam, generated relative to steam demand, into hot water. The conversion efficiency is assumed to be 98%. In this study, the capacity of the heat exchanger is assumed to be sufficiently large, and its rated capacity is not explicitly defined.

3.4.6. Thermal Storage Tank

In this study, dedicated hot-water and chilled-water storage tanks are used, each supplying stored energy exclusively to meet the corresponding demand. The tank capacities were set to exceed the peak values observed in the demand dataset, with 60,000 MJ for hot water and 40,000 MJ for chilled water. Thermal losses are assumed to occur even without discharge, as well as during charging and discharging operations. The time-dependent loss is set at 15% per day, and the input/output loss is set at 2%.

3.4.7. PV Generation Unit

In this study, photovoltaic (PV) systems are modeled in units of 1000 kW rated output. The hourly PV generation is calculated as the product of the total installed PV capacity and the corresponding per-unit (p.u.) value for each hour. Here, the p.u. value represents the ratio of the actual generation to the installed capacity at each hour. These data from the Kyushu region are used in this study, as described in Section 3.2.

3.4.8. Battery Storage Systems

The BESS is responsible for storing surplus or deficient electricity and providing regulating power. In this study, rated output and capacity per unit are not predefined; instead, optimization is performed without fixed unit sizing. The BESS storage capacity is assumed to be at least twice the power output capacity. Charging and discharging losses are set at 5%, and time-dependent loss are assumed to be 1% per day.

3.4.9. Hydrogen Boiler

The hydrogen boiler is introduced in this study in anticipation of future CO₂ emission regulations. The rated output is set to 5000 MJ/h, with a thermal efficiency of 95%. It uses hydrogen as fuel and, similar to the gas boiler, is assumed to supply steam to meet steam demand, as well as to the heat exchanger and absorption chiller. Partial load efficiency is not considered.

3.5. Equipment Installation Cost

The $i{c}_{eq}$ on Table 1 summarizes the equipment costs assumed for 2040. The costs of the gas engine, absorption chiller, heat pump, and gas boiler are determined with reference to the study by Sumitomo et al. [26]. The cost of PV system was based on the price outlook published by the government in 2018 [27]. The BESS was divided into a storage component and an power output component, and the cost of each was set based on the report by the National Renewable Energy Laboratory (NREL) [28].

For the thermal storage tank, its installation cost is not considered in this study. Thermal storage tanks are typically constructed as part of the building infrastructure, making it difficult to define their cost on a per-unit basis, and they are generally much less expensive than other DES components. Therefore, this study assumes that sufficient thermal storage is available without explicitly modeling its installation cost.

In addition, hydrogen boiler, equipment cost data were unavailable; therefore, it was independently determined in this study, set higher than the gas boiler while considering expected reductions by 2040.

3.6. CO₂ Emission Factor

The CO₂ emission factor per unit of purchased electricity, shown in

Table 5. CO₂ emission factor for electricity.

Year	2020	2025	2030	2040
CO2 Emission Factor [kg-${\mathrm{CO}}_2/$kWh]	0.441	0.4055	0.370	0.299

, was estimated by linear interpolation between the CO₂ intensity in 2020 [29] and the target intensity for 2030 set by the government [30]. Since the case study in this research considers the years 2040 and the baseline year of 2025 for CO₂ emissions, these interpolated and fixed emission factors are applied accordingly. The CO₂ emission per unit of city gas was set to 2.29 kg-CO₂$/$Nm³ [31].

4. Equipment Sizing Optimization Model (ESM)

The ESM aims to minimize the annual total cost of the DES, defined as installation and operating costs minus revenues from regulating power, while accounting for the annual expense ratio of equipment. The model is formulated as a MILP problem and solved using Gurobi Optimizer v8.1, a integer linear programming solver. The following sections formulate the objective function and constraints of the proposed model.

4.1. Capital Costs

Since equipment in the DES is intended for long-term use, it is necessary to account for present value. The Capital Recovery Factor (CRF) is defined in Equation (1) by considering both the useful life and the discount rate. The present-value-based installation cost per unit and the total installation cost are then calculated using Equations (2)–(4).

$$\begin{array}{cc}\hfill & cr{f}_{eq}={\displaystyle \frac{r}{1-{(1+r)}^{-n_{eq}}}}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & I{C}_{eq}=cr{f}_{eq}·i{c}_{eq}·N{M}_{eq}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & I{C}_{b{t}_s}=cr{f}_{b{t}_s}·i{c}_{b{t}_s}·C{P}_{b{t}_s}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & I{C}_{b{t}_p}=cr{f}_{b{t}_p}·i{c}_{b{t}_p}·C{P}_{b{t}_p}\hfill \end{array}$$

(4)

where the CRF converts the initial investment into an equivalent annualized cost based on the discount rate and equipment lifetime. The installation cost is computed using the present value of its unit cost, and the total installation cost is determined using the number of installed units as decision variables. For the BESS, the installation amount is defined not by the number of units but separately by its storage capacity and power capacity.

4.2. Objective Function of the ESM

The ESM minimizes the total annual cost, including equipment installation costs, electricity charges, and gas expenses, net of flexibility revenue, as defined in Equation (5). Equation (6) denotes the total installation cost across all equipment types. Equations (7) and (8) calculate the annual electricity and gas costs, respectively, obtained by summing hourly consumption multiplied by the corresponding price. Equation (9) represents the revenue from upward and downward regulating power provided by gas engines and the BESS.

$$\begin{array}{cc}\hfill & OB{J}_s=C_{equipment}+C_{electricity}+C_{gas}-R_{lfc}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & C_{equipment}=I{C}_{ge}+I{C}_{bo}+I{C}_{ac}+I{C}_{hp}+I{C}_{pv}+I{C}_{b{t}_s}+I{C}_{b{t}_p}+I{C}_{hb}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & C_{electricity}=\sum _{t=1}^{8760}(EG{B}_t·el{b}_t)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & C_{gas}=\sum _{t=1}^{8760}\left((GG{E}_t+GB{O}_t)·gsb\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & R_{lfc}=\sum _{t=1}^{8760}\left((LU{P}_t+BU{P}_t)·sp{u}_t+(LD{W}_t+BD{W}_t)·sp{d}_t\right)\hfill \end{array}$$

(9)

4.3. Supply–Demand Balance Constraints of the ESM

This section presents the supply–demand balance constraints. Equations (10)–(14) ensure that the energy supply from the DES matches the corresponding demand values provided as input data.

$$\begin{array}{cc}\hfill & eld{m}_t=EG{B}_t+EG{E}_t+EP{V}_t+EB{O}_t-EG{S}_t-EH{P}_t-EB{I}_t\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & std{m}_t=VG{E}_t+VB{O}_t+VH{B}_t-VA{C}_t-VH{X}_t\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & hwd{m}_t=WG{E}_t+WH{X}_t+WH{P}_t+WT{O}_t-WA{C}_t-WT{I}_t\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & cwd{m}_t=CT{O}_t+CH{P}_t+CC{V}_t+CC{W}_t-CT{I}_t\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & WG{E}_t+WH{X}_t\ge WA{C}_t\hfill \end{array}$$

(14)

where $eld{m}_t$, $std{m}_t$, $hwd{m}_t$, and $cwd{m}_t$ denote the electricity, steam, hot-water, and chilled-water demand at time t, respectively. The terms on the right-hand side represent the corresponding supply from each DES component, including gas engines, boilers, PV, heat pumps, heat exchangers, and BESS charging/discharging. The final inequality ensures that the hot-water used for absorption chilling is supplied only from high-temperature hot water derived from steam.

4.4. Equipment Constraints of the ESM

This section describes the constraints formulated in the ESM.

4.4.1. Gas Engine Constraints

Equation (15) ensures that the electric output of the gas engines does not exceed their installed capacity. Equations (16)–(18) describe the relationships between the hourly generation of steam and hot water, and the consumption of gas, corresponding to the electric output of the gas engines. The conversion efficiencies such as $ef{v}_{ge}$, $ef{w}_{ge}$, and $ef{g}_{ge}$ used here correspond to the slopes of the linear efficiency curves developed for the LP model, as presented in Figure 4. Steam and hot water generated by the gas engines are assumed to be discarded when in excess, allowing the system to flexibly respond to varying thermal demand without requiring additional storage or redistribution.

Equations (19)–(24) define the constraints for regulating power provision. Specifically, Equations (19)–(21) describe the conditions for upward regulation, while Equations (22) and (23) describe the conditions for downward regulation. Equations (19) and (22) determine the available regulating power, with the regulating range set to 30% of the rated output for both upward and downward directions. Equation (20) ensures that the sum of the gas engine output and upward regulating power does not exceed the rated output. Equations (21) and (23) impose constraints on regulating power provision at the minimum output level of 30% of rated output.

In this study, the ESM does not consider the on/off status of gas engines in order to reduce computational burden. As a result, regulating power provision below the minimum output is restricted and approximated as shown in Equations (21) and (23). Equation (24) represents the operational constraint in the case study where regulating power is not provided.

$$\begin{array}{cc}\hfill & EG{E}_t\le cp{e}_{ge}·N{M}_{ge}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & VG{E}_t\le ef{v}_{ge}·EG{E}_t\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & WG{E}_t\le ef{w}_{ge}·EG{E}_t\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & GG{E}_t=ef{g}_{ge}·EG{E}_t\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & LU{P}_t\le cp{e}_{ge}·lf{c}_{ge}·N{M}_{ge}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & LU{P}_t\le cp{e}_{ge}·N{M}_{ge}-EG{E}_t\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & LU{P}_t\le {\displaystyle \frac{lf{c}_{ge}·cp{e}_{ge}}{0.3}}·EG{E}_t\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & LD{W}_t\le cp{e}_{ge}·lf{c}_{ge}·N{M}_{ge}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & LD{W}_t\le EG{E}_t\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & LU{P}_t+LD{W}_t=0\hfill \end{array}$$

(24)

4.4.2. BESS Constraints

Constraints related to BESS are presented in Equations (25)–(36).

$$\begin{array}{cc}\hfill & SB{T}_t=eI{s}_{bt}·SB{T}_{t-1}+ol{s}_{bt}·EB{I}_t-{\displaystyle \frac{1}{oI{s}_{bt}}}·EB{O}_t\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & SB{T}_t\le C{P}_{b{t}_s}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & SB{T}_{t-1}\ge {\displaystyle \frac{1}{oI{s}_{bt}}}·EB{O}_t\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & SB{T}_0=SB{T}_{8760}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & C{P}_{b{t}_s}\ge 2·C{P}_{b{t}_p}\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & BU{P}_t\le lf{c}_{bt}·C{P}_{b{t}_p}\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & BD{W}_t\le lf{c}_{bt}·C{P}_{b{t}_p}\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & EB{O}_t-EB{I}_t+BU{P}_t\le C{P}_{b{t}_p}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & EB{I}_t-EB{O}_t+BD{W}_t\le C{P}_{b{t}_p}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & eI{s}_{bt}·SB{T}_{t-1}+oI{s}_{bt}·EB{I}_t-{\displaystyle \frac{1}{oI{s}_{bt}}}·EB{O}_t+BD{W}_t\le C{P}_{b{t}_s}\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & eI{s}_{bt}·SB{T}_{t-1}+oI{s}_{bt}·EB{I}_t-{\displaystyle \frac{1}{oI{s}_{bt}}}·EB{O}_t-BU{P}_t\ge 0\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & BU{P}_t+BD{W}_t=0\hfill \end{array}$$

(36)

where Equation (25) defines the state of charge (SOC) at time t, considering charging/discharging losses and time-dependent degradation. Equation (26) limits the SOC to the installed storage capacity, while Equation (27) ensures that discharging power does not exceed the available SOC from the previous time step. Equation (28) enforces cycle consistency by setting the final SOC equal to the initial value. Equation (29) requires that the installed storage capacity be at least twice the installed power capacity.

Equations (30)–(36) define the constraints for regulating power provision. Equations (30) and (31) constrain upward and downward regulating power to within 5% of the power capacity. Equations (32) and (33) ensure that charging and discharging power, including regulating provision, do not exceed the power capacity. Equations (34) and (35) define the upper and lower bounds of the SOC. Equation (36) represents the operational constraint in the case study where regulating power is not provided.

4.4.3. Gas Boiler Constraints

The constraints related to the operation of the gas boiler are defined below.

$$\begin{array}{cc}\hfill & VB{O}_t\le cp{v}_{bo}·N{M}_{bo}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & VB{O}_t=45·ef{v}_{bo}·GB{O}_t\hfill \end{array}$$

(38)

where Equation (37) ensures that the hourly steam output does not exceed the installed capacity of the gas boiler. Equation (38) calculates the hourly steam output by multiplying the city gas consumption by the equipment efficiency and the standard heating value, which is set to 45 MJ/Nm³.

4.4.4. Absorption Chiller Constraints

The constraints related to the operation of the absorption chiller are defined below.

$$\begin{array}{cc}\hfill & CC{V}_t+CC{W}_t\le cp{c}_{ac}·N{M}_{ac}\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & VA{C}_t=ef{v}_{ac}·CC{V}_t\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & WA{C}_t=ef{w}_{ac}·CC{W}_t\hfill \end{array}$$

(41)

where Equation (39) ensures that the hourly chilled water output does not exceed the installed chilled water capacity of the absorption chiller. Equations (40) and (41) define the hourly consumption of steam and hot water, respectively, based on the chilled water output. As the ESM determines the number of installed units, start-up status and minimum output are not considered. Accordingly, the conversion efficiencies applied here such as $ef{v}_{ac}$ and $ef{w}_{ac}$ correspond to the slopes of the linear efficiency curves developed for the LP model, as shown in Figure 5.

4.4.5. Heat Pump Constraints

The constraints related to the output and operation of heat pumps are defined below.

$$\begin{array}{cc}\hfill & N{M}_{hp}\ge N{M}_{hp{w}_m}+N{M}_{hp{c}_m}\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & WH{P}_t\le cp{w}_{hp}·N{M}_{hp{w}_m}\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & CH{P}_t\le cp{c}_{hp}·N{M}_{hp{c}_m}\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{WH{P}_t}{co{p}_w}}+{\displaystyle \frac{CH{P}_t}{co{p}_c}}=3.6·EH{P}_t\hfill \end{array}$$

(45)

where Equation (42) ensures that hot water and chilled water use are mutually exclusive within each month m, and its does not exceed the number of installed units. Equations (43) and (44) ensure that the hourly output of hot water and chilled water, respectively, does not exceed the rated capacity. Equation (45) calculates the electricity consumption of the heat pump based on the coefficient of performance (COP) for hot water and chilled water output, as defined in Section 3.4.4. Here, 3.6 MJ/kWh is the unit conversion coefficient.

4.4.6. Heat Exchanger Constraints

The constraints related to the heat exchanger are defined below. Equation (46) calculates the hourly hot water output based on the steam input and the efficiency of the heat exchanger.

$$\begin{array}{cc}\hfill & WH{X}_t=ef{w}_{hx}·VH{X}_t\hfill \end{array}$$

(46)

4.4.7. Thermal Storage Tank Constraints

The constraints related to the output and operation of thermal storage tanks are defined below.

$$\begin{array}{cc}\hfill & WT{I}_t\le cp{s}_{tw}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & CT{I}_t\le cp{s}_{tc}\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill & ST{W}_t\le cp{s}_{tw}\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & ST{C}_t\le cp{s}_{tc}\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill & WT{O}_t\le hwd{m}_t\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & CT{O}_t\le cwd{m}_t\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & ST{W}_{t-1}\ge {\displaystyle \frac{1}{ol{s}_{tw}}}·WT{O}_t\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill & ST{C}_{t-1}\ge {\displaystyle \frac{1}{ol{s}_{tc}}}·CT{O}_t\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill & ST{W}_0=ST{W}_{8760}\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill & ST{C}_0=ST{C}_{8760}\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill & ST{W}_t=el{s}_{tw}·ST{W}_{t-1}+ol{s}_{tw}·WT{I}_t-{\displaystyle \frac{1}{ol{s}_{tw}}}·WT{O}_t\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill & ST{C}_t=el{s}_{tc}·ST{C}_{t-1}+ol{s}_{tc}·CT{I}_t-{\displaystyle \frac{1}{ol{s}_{tc}}}·CT{O}_t\hfill \end{array}$$

(58)

where Equations (47)–(50) ensure that the hourly input and storage levels of hot and chilled water do not exceed the rated capacities of the thermal storage tanks. Since the supply from the tanks is assumed to be primarily used to meet thermal demand, Equations (51) and (52) constrain the output to be no greater than the hourly demand for hot and chilled water, respectively. Equations (53) and (54) ensure that the output from the tanks does not exceed the available stored energy. Equations (55) and (56) impose a cyclic condition, requiring the initial storage level to match the final level at the end of the year. Equations (57) and (58) represent the thermal storage levels at time t, incorporating standing losses and input/output losses.

4.4.8. PV Generation Constraints

Equation (59) calculates the hourly PV generation as the product of the installed PV capacity and the p.u. value for each hour. Equation (60) ensures that the electricity sold does not exceed the generated PV output.

$$\begin{array}{cc}\hfill & EP{V}_t=cp{e}_{pv}·p{u}_t·N{M}_{pv}\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill & EG{S}_t\le EP{V}_t\hfill \end{array}$$

(60)

4.4.9. Hydrogen Boiler Constraints

Equation (61) ensures that the hourly steam output does not exceed the total installed capacity of the hydrogen boilers. As shown in Equation (62), the steam output calculated from the hydrogen consumption, the output efficiency, and the lower heating value of hydrogen that 10.8 MJ/Nm³ [32].

$$\begin{array}{cc}\hfill & VH{B}_t\le cp{v}_{hb}·N{M}_{hb}\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & VH{B}_t=10.8·ef{v}_{hb}·HH{B}_t\hfill \end{array}$$

(62)

4.5. CO₂ Emissions Constraints of the ESM

The constraints related to CO₂ emissions in this model are defined below.

$$\begin{array}{cc}\hfill & CO{E}_t=(GG{E}_t+GB{O}_t)·co{2}_g+EG{B}_t·co{2}_e\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill & SCOE=\sum _{t=1}^{8760}CO{E}_t\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill & SCOE\le p·bcoe\hfill \end{array}$$

(65)

where Equation (63) calculates the hourly CO₂ emissions by multiplying the city gas consumption of the gas engine and gas boiler, as well as purchased electricity, by their respective CO₂ emission factors. Equation (64) computes the total annual CO₂ emissions. Equation (65) imposes a constraint to ensure that the total emissions remain below the designated reduction target.

5. Equipment Operation Optimization Model (EOM)

The EOM aims to minimize the net cost of electricity and gas, after accounting for revenues from regulating power provision, by formulating the problem as a MILP model. The number of installed units for each type of equipment, as well as the installed BESS storage and power output capacity, are treated as fixed inputs based on the results obtained from the ESM. Furthermore, the daily CO₂ emissions calculated in the ESM are imposed as upper-limit constraints in the EOM, ensuring consistency with the sizing stage while enabling detailed operational scheduling.

5.1. Objective Function of the EOM

The EOM minimizes the daily total cost through optimization problems, each covering a 24-h period at hourly resolution and repeated over the one-year horizon.

$$\begin{array}{cc}\hfill & OB{J}_o=C_{electricity}+C_{gas}+C_{storage}-R_{lfc}+C_{co2}\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill & C_{electricity}=\sum _{h=1}^{24}\left(EG{B}_h·el{b}_h\right)\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill & C_{gas}=\sum _{h=1}^{24}\left((GG{E}_h+GB{O}_h)·gsb\right)\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill & C_{storage}=PE{N}_{bt}·pbt-RE{W}_{bt}·rbt+PE{N}_{tw}·ptw+PE{N}_{tc}·ptc\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill & R_{lfc}=\sum _{h=1}^{24}\left((LU{P}_h+BU{P}_h)·sp{u}_h+(LD{W}_h+BD{W}_h)·sp{d}_h\right)\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill & C_{co2}=pco2·PE{N}_{co2}\hfill \end{array}$$

(71)

where Equation (66) represents the total cost, including electricity charges after subtracting revenues from regulating power provision, gas expenses, and the net reward or penalty associated with the remaining energy storage. Equations (67) and (68) calculate the daily electricity and gas purchase costs, respectively. Equation (70) represents the revenue from upwards and downwards regulating power provided by gas engines and the BESS.

Equation (69) evaluates the reward and penalty associated with the remaining energy storage at the end of each day. In this model, the final state of energy storage at the end of each day is inherited from the ESM. However, since the ESM simplifies certain operational aspects—such as gas engine dispatch—discrepancies may arise between the two models. To address this, a small reward is assigned to surplus storage and a penalty to shortages, to encourage convergence while avoiding significant influence on dispatch decisions. Note that no reward is assigned for thermal storage surplus, as shortages in thermal storage were found to be rare.

5.2. Supply–Demand Balance Constraints of the EOM

In the EOM, the supply–demand balance constraints are the same as those in the ESM (Section 4.3), except that the calculation horizon is shortened from one year to a single day. Accordingly, the detailed explanation is omitted here, and in the following sections descriptions are likewise omitted when only the calculation horizon is modified.

5.3. Equipment Constraints of the EOM

5.3.1. Gas Engine Constraints

In the EOM, startup/shutdown status are incorporated to reflect operation closer to actual practice, with Equations (72)–(75) defining the operating units and their transitions. In this formulation, startup states are treated as a clustered system rather than as individual units to reduce computational load. In Equation (72), the number of units determined in the ESM is set as the upper limit. Equations (73) and (74) restrict startups and shutdowns so that they do not exceed the operating units, while Equation (75) ensures that any increase or decrease in operating units is explained by startups and shutdowns. Equations (76) and (77) specify the initial operating units.

Equations (78)–(81) calculate hourly gas consumption and steam and hot water production. Differ from ESM, efficiency curves factor such as $a{g}_{ge}$, $b{g}_{ge}$, $a{v}_{ge}$, $b{v}_{ge}$, $a{w}_{ge}$, and $b{w}_{ge}$ for partial loads are approximated by the slope and intercept of linear functions, as shown in Figure 4. To avoid frequent startups and shutdowns, additional gas consumption is considered, with the startup cost assumed to be 20% of the rated output. As in the ESM, excess thermal output is discarded when not required. The output constraints are formulated in Equations (82)–(85). These equations ensure that generation output, including upward and downward regulation, remains between 30% and 100% of the rated capacity, accounting for startup status.

$$\begin{array}{cc}\hfill & UG{E}_h\le nu{m}_{ge}\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill & UG{E}_h\ge UGEO{N}_h\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill & UG{E}_{h-1}\ge UGEO{F}_h\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill & UG{E}_h-UG{E}_{h-1}=UGEO{N}_h-UGEO{F}_h\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill & UG{E}_0=nu{m}_{ge}(\mathrm{in}\mathrm{case}\mathrm{day}1)\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill & UG{E}_0=ug{e}_{24}(\mathrm{from}\mathrm{day}2\mathrm{onwards})\hfill \end{array}$$

(77)

$$\begin{array}{cc}\hfill & GG{E}_h=a{g}_{ge}·EG{E}_h+b{g}_{ge}·UG{E}_h+s{g}_{ge}·UGEO{N}_h\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill & s{g}_{ge}=0.2·(a{g}_{ge}·cp{e}_{ge}+b{g}_{ge})\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill & VG{E}_h\le a{v}_{ge}·EG{E}_h+b{v}_{ge}·UG{E}_h\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill & WG{E}_h\le a{w}_{ge}·EG{E}_h+b{w}_{ge}·UG{E}_h\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & LU{P}_h\le lf{c}_{ge}·cp{e}_{ge}·UG{E}_h\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill & LD{W}_h\le lf{c}_{ge}·cp{e}_{ge}·UG{E}_h\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill & LU{P}_h\le cp{e}_{ge}·UG{E}_h-EG{E}_h\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill & LD{W}_h\le 0.3·cp{e}_{ge}·UG{E}_h+EG{E}_h\hfill \end{array}$$

(85)

5.3.2. BESS Constraints

Constraints related to the BESS are presented in Equations (86)–(93).

$$\begin{array}{cc}\hfill & SB{T}_{d,24}+PE{N}_{b{t}_{d,24}}-RE{W}_{b{t}_{d,24}}=sb{t}_{d,24}^{\prime }\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill & SB{T}_{1,0}=sb{t}_{1,0}^{\prime }(\mathrm{in}\mathrm{case}\mathrm{d}=1)\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill & SB{T}_{d,0}=sb{t}_{d-1,24}(\mathrm{from}\mathrm{day}2\mathrm{onwards})\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill & BU{P}_h\le lf{c}_{bt}·c{p}_{b{t}_p}\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill & BD{W}_h\le lf{c}_{bt}·c{p}_{b{t}_p}\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill & EB{O}_h-EB{I}_h+BU{P}_h\le c{p}_{b{t}_p}\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill & EB{I}_h-EB{O}_h+BD{W}_h\le c{p}_{b{t}_p}\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill & el{s}_{bt}·SB{T}_{h-1}+ol{s}_{bt}·EB{I}_h-{\displaystyle \frac{1}{ol{s}_{bt}}}·EB{O}_h+BD{W}_h\le c{p}_{b{t}_s}\hfill \end{array}$$

(93)

where Equation (86) ensures consistency between the SOC in the EOM and that in the ESM, accounting for any surplus or deficit due to model differences. The initial SOC is defined in Equations (87) and (88), referencing the ESM result for day 1 and the final SOC of the previous day thereafter.

Equations (89)–(92) set upper and lower bounds on charging and discharging outputs, including regulation power provision. The BESS is assumed to provide regulation power up to 5% of its total storage capacity, reflecting the rated capacity and output limits determined by the ESM. Equation (93) updates the SOC, incorporating charging/discharging losses and time-based degradation.

5.3.3. Absorption Chiller Constraints

Equations (94)–(97) define the number of operating units, restricting startups and shutdowns and ensuring consistency in unit changes. Equations (98) and (99) set the operating range between 25% and 100% of the rated capacity, accounting for startup status. For hot water usage, the same constraints apply and are omitted here. Equations (100) and (101) calculate hourly steam and hot water consumption, with partial-load efficiency curves factor such as $a{v}_{ac}$ and $b{v}_{ac}$ given in Figure 5. To avoid frequent startups and shutdowns, additional steam and hot water consumption is considered, with the startup cost assumed to be 20% of the rated output.

$$\begin{array}{cc}\hfill & UC{V}_h+UC{W}_h\le nu{m}_{ac}\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill & UC{V}_h\ge UCVO{N}_h\hfill \end{array}$$

(95)

$$\begin{array}{cc}\hfill & UC{V}_{h-1}\ge UCVO{F}_h\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill & UC{V}_h-UC{V}_{h-1}=UCVO{N}_h-UCVO{F}_h\hfill \end{array}$$

(97)

$$\begin{array}{cc}\hfill & CC{V}_h\ge cp{c}_{ac}·UC{V}_h\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill & CC{V}_h\le 0.25·cp{c}_{ac}·UC{V}_h\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill & VA{C}_h=a{v}_{ac}·CC{V}_h+b{v}_{ac}·UC{V}_h+s{v}_{ac}·UCVO{N}_h\hfill \end{array}$$

(100)

$$\begin{array}{cc}\hfill & WA{C}_h=ef{w}_{ac}·CC{W}_h+s{w}_{ac}·UCWO{N}_h\hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill & s{w}_{ac}=0.2·(a{w}_{ac}·cp{c}_{ac}+b{w}_{ac})\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill & s{v}_{ac}=0.2·(a{v}_{ac}·cp{c}_{ac}+b{v}_{ac})\hfill \end{array}$$

(103)

5.3.4. Thermal Storage Tank Constraints

Equation (104) ensures consistency between the stored hot water in the EOM and that in the ESM, accounting for any surplus or deficit due to model differences. The initial storage level is defined in Equations (105) and (106), referencing the ESM result for day 1 and the final storage level of the previous day thereafter. For chilled water output, the same constraints apply and are therefore omitted here.

$$\begin{array}{cc}\hfill & ST{W}_{d,24}+PE{N}_{t{w}_{d,24}}\ge st{w}_{d,24}^{\prime }\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill & ST{W}_{1,0}=st{w}^{\prime }1,0(\mathrm{in}\mathrm{case}\mathrm{day}1)\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill & ST{W}_{d,0}=st{w}_{d-1,24}(\mathrm{from}\mathrm{day}2\mathrm{onwards})\hfill \end{array}$$

(106)

5.4. CO₂ Emissions Constraints of the EOM

Equations (107) calculates the hourly CO₂ emissions by multiplying the gas consumption of the gas engines and gas boilers, as well as purchased electricity, by their respective CO₂ emission factors. Equation (108) computes the total daily CO₂ emissions. Equation (109) sets an upper bound on daily CO₂ emissions, using the value obtained from the ESM. Since the EOM incorporates more detailed scheduling —such as gas engine startup fuel consumption—emissions may differ from those in the ESM. Therefore, a penalty term is introduced to ensure that the daily CO₂ emissions in the EOM do not exceed the value obtained from the ESM.

$$\begin{array}{cc}\hfill & CO{E}_h=(GG{E}_h+GB{O}_h)·co{2}_g+EG{B}_h·co{2}_e\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill & SCO{E}_d=\sum _{h=1}^{24}CO{E}_h\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill & SCO{E}_d-PE{N}_{co2}\le sco{e}_d^{\prime }\hfill \end{array}$$

(109)

6. Analysis Results

As described in Section 2.2, this study conducted two case studies. Section 6.1 presents the baseline case. Section 6.2 presents the impact of regulating power provision on the equipment configuration, operation, and profitability of the DES. Section 6.2.1 discusses the effects of CO₂ emission constraints on the DES.

6.1. Baseline Case

First, an optimization calculation was conducted under the assumption that a PV, BESS, and hydrogen boiler were not installed, and that regulating power provision was not implemented. As shown in

Table 6. Installed equipment capacity in the baseline case.

Equipment Type	Unit	Installed Capacity
Gas engine	kW	10,000
Gas boiler	MJ/h	15,000
Absorption chiller	MJ/h	15,000

, the resulting equipment configuration includes only the minimum necessary systems to meet electricity, steam, hot water, and chilled water demands. Under this condition, the annual CO₂ emissions from the DES were 35,657 t-CO₂, which set as the reference value for subsequent comparisons.

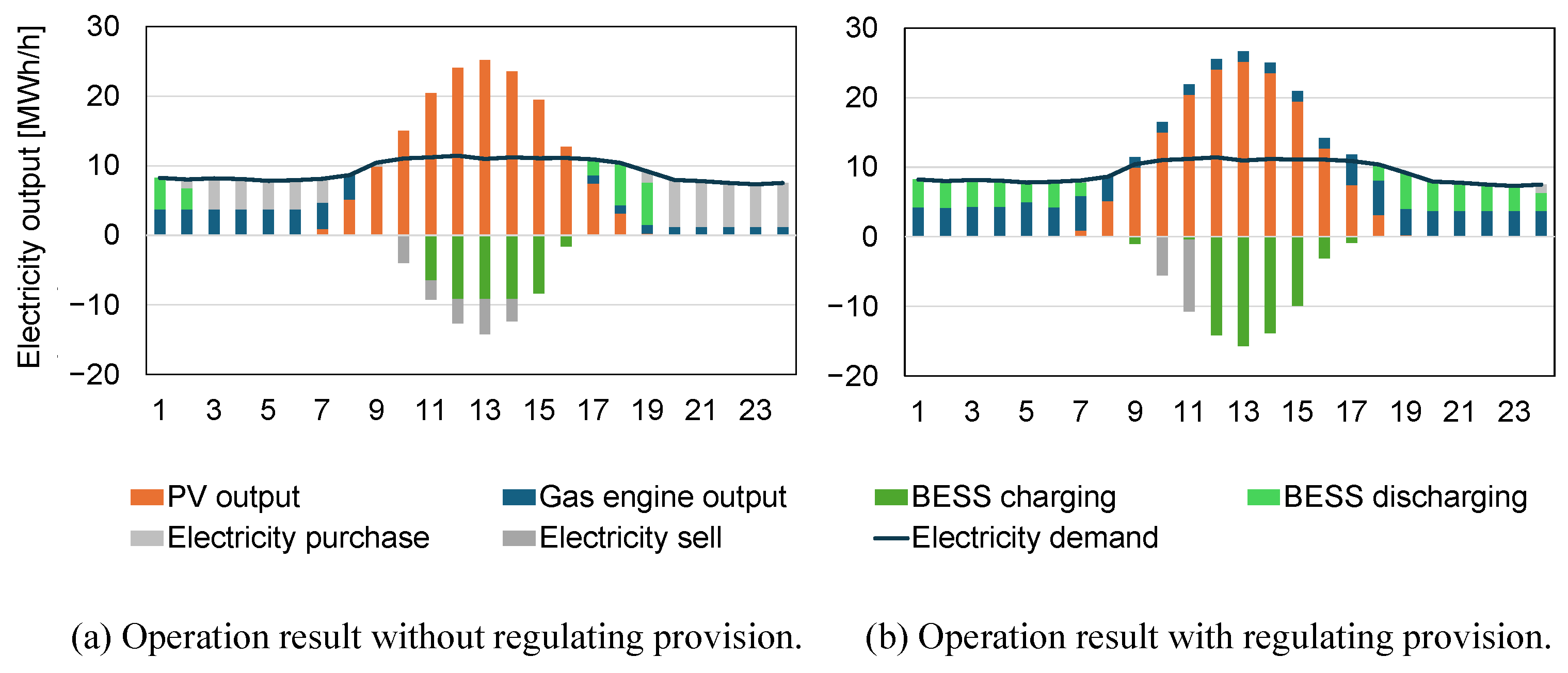
6.2. Impact of Regulating Power Provision

This section examines the differences in equipment configuration, operation, and profitability of the DES depending on whether regulating power is provided by the gas engines and BESS. The CO₂ emission constraint was set to achieve a 40% reduction relative to the baseline CO₂ emissions determined in Section 6.1.

6.2.1. Comparison of Installed Equipment Capacity

The optimized equipment capacities obtained from the model are presented in

Table 7. Comparison of installed equipment capacity.

Equipment Type	Unit	Baseline Case	Without LFC	With LFC
Gas engine	kW	10,000	5000	6250
Gas boiler	MJ/h	15,000	20,000	20,000
Absorption chiller	MJ/h	15,000	15,000	10,000
Heat pump	MJ/h	-	0	0
PV	kW	-	38,000	38,000
BESS (Storage)	kWh	-	41,554	57,758
BESS (Power)	kW	-	9117	28,879

. In the case without regulating power provision, compared to the baseline case, the introduction of gas engines decreased due to the CO₂ emission constraint, while the installation of PV systems, heat pumps, and BESS was promoted. Hydrogen boilers were not installed.

In contrast, when regulating power provision is enabled, both gas engines and BESS show increased installed capacities relative to the non-regulating case, and PV capacity also increased accordingly. This is presumably because the revenue enhancement from regulating power provision outweighs the additional equipment costs. Furthermore, the increase in PV capacity is driven by the expectation of additional revenue from regulating power services, which incentivizes further investment in gas engines and BESS within the DES.

6.2.2. Comparison of Operational Result

This section compares the operational outcomes with and without the provision of regulating power. As an illustrative example, Figure 6a,b present the optimal operation results on 31 August for the cases without and with regulating power provision, respectively. Each stacked bar graph shows the PV generation, gas engines generation, BESS charging/discharging, and electricity purchase. Reverse power flow to the grid is represented as a negative value. When regulating power provision is considered, a notable difference is observed: the gas engine operates even during periods of electricity surplus in order to provide regulating power.

Table 8. Annual cost comparison under different regulating power provision scenarios.

Item	Unit	Without LFC	With LFC
Equipment cost	million JPY	690	793
Electricity purchase cost	million JPY	252	139
Gas purchase cost	million JPY	651	713
Hydrogen purchase cost	million JPY	0	0
Revenue from regulating power provision	million JPY	0	−161
Total annual cost	million JPY	1593	1485
CO2 reduction cost	JPY/t-CO2	18,306	10,735

summarizes the total annual cost for both cases, including equipment cost, annual electricity purchase cost, annual gas purchase cost, and revenue from regulating power provision. Although the equipment cost increases, the reduction in electricity purchase cost combined with the revenue from regulating power results in a lower total annual cost when regulating power is provided, corresponding to a 6.8% reduction relative to the case without regulating power. Moreover, the CO₂ reduction cost shows that the additional cost required to achieve CO₂ emission reductions is reduced when regulating power provision is enabled.

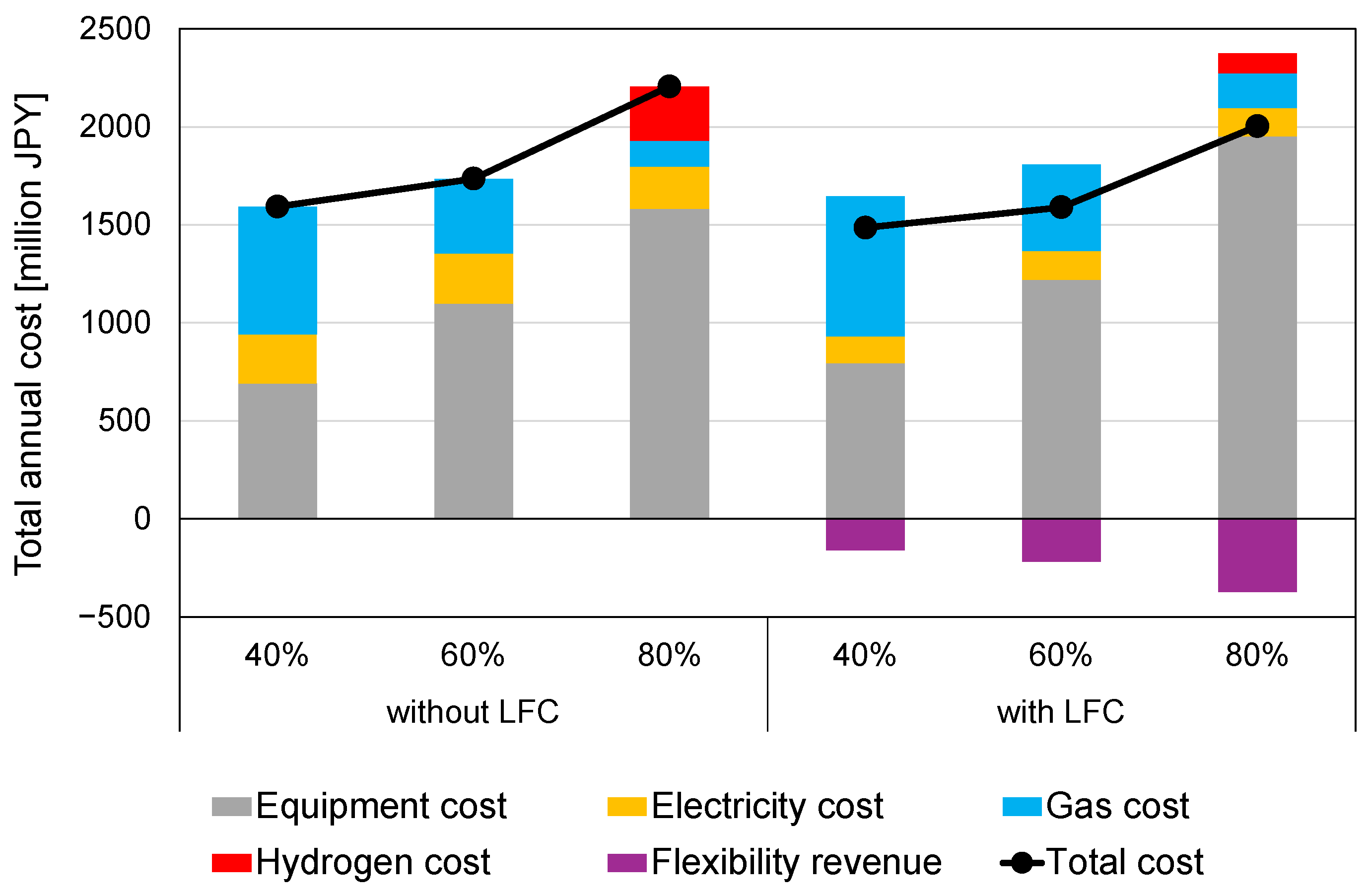
6.3. The Effect of CO₂ Emission Constraints

6.3.1. The Result of Equipment Sizing

Table 9. Comparison of equipment configuration under CO₂ emission reduction constraints.

Item	Unit	Without LFC				With LFC
		40%	60%	80%		40%	60%	80%
Gas engine	kW	5000	2500	0		6250	3750	0
Gas boiler	MJ/h	20,000	25,000	20,000		20,000	20,000	20,000
Absorption chiller	MJ/h	15,000	10,000	5000		15,000	10,000	5000
Heat pump	MJ/h	0	6000	13,000		0	6000	13,000
PV generation	kW	38,000	64,000	96,000		38,000	63,000	100,000
BESS (storage)	kWh	41,554	108,128	178,640		57,758	123,834	252,304
BESS (power)	kW	9117	21,232	32,263		28,879	61,917	126,152
Hydrogen boiler	MJ/h	0	0	5000		0	0	5000

presents the differences in equipment configuration under CO₂ emission reduction targets of 40%, 60%, and 80% based on the emission level of baseline case. The results are shown for two scenarios: without and with the provision of regulating power, referred to as “without LFC” and “with LFC,” respectively. As the reduction target becomes more stringent, the installed capacity of gas engines decreases. To meet electricity demand, the capacities of PV generation, heat pumps, and BESS increase accordingly.

In the scenario with an 80% reduction from the baseline emission level, gas engine installation is eliminated, and the introduction of hydrogen boilers to meet steam demand is observed as a result of the optimization model. Under the CO₂ emission factors and the cost assumptions for hydrogen equipment and hydrogen fuel adopted in this study, the model tends to favor the installation of hydrogen boilers in such highly stringent reduction scenarios.

6.3.2. Comparison of Total Cost Under CO₂ Emission Reduction Constraints

Figure 7 illustrates the total system cost and its breakdown under CO₂ emission reduction targets of 40%, 60%, and 80%. The total cost comprises equipment cost (gray bars), electricity purchase cost (yellow bars), gas cost (blue bars), and hydrogen cost (red bars), along with revenue from the provision of regulating power (purple bars). The overall cost is represented by the black polyline. Regarding the impact of CO₂ constraints, the equipment cost increases as the reduction target becomes more stringent. This trend reflects a shift in optimal equipment configuration under CO₂ emission restrictions, as evidenced by the observed reduction in gas-based systems and the corresponding expansion of PV generation and the BESS, as discussed in the previous section. Comparing the scenarios with and without regulating power provision, the total cost is consistently lower in the “with LFC” case across all emission reduction levels. This cost reduction is particularly pronounced in the 80% reduction scenario. Although equipment cost is higher in the “with LFC” case—likely due to increased BESS installation—the revenue from regulating power provision offsets the additional investment, resulting in a net cost benefit as observed from the optimization results.

6.3.3. Comparison of CO₂ Emissions Between the ESM and EOM

In this study, the ESM is partially formulated as a simplified LP model, whereas the EOM is formulated as a detailed MILP model. Because the EOM accounts for operational features such as startup fuel consumption, its CO₂ emissions may differ from those of the ESM even though it inherits the daily emission limits calculated by the ESM. To reconcile this difference, a penalty term is introduced to ensure that the daily CO₂ emissions in the EOM do not exceed the corresponding values obtained from the ESM. To examine the validity of the proposed two-stage modeling approach,

Table 10. Comparison of CO₂ emissions between the ESM and EOM.

Item	Unit	Baseline	Without LFC				With LFC
			40%	60%	80%		40%	60%	80%
Annual CO2 Emission in ESM	t-CO2/yr	–	21,394	14,263	7131		21,394	14,263	7131
Annual CO2 Emission in EOM	t-CO2/yr	35,657	21,387	14,272	7131		21,367	14,255	7131
CO2 Reduction Rate	%	–	40.02%	59.97%	80.00%		40.08%	60.02%	80.00%
Max. Daily CO2 Cap	%	–	5.1%	11.1%	–		–	2.4%	–
Overshoot Rate (Date)			(13 August)	(28 July)				(28 July)

presents the differences in CO₂ emissions between the ESM and EOM for each case. In terms of annual CO₂ emissions, the EOM yields lower emissions than the ESM in most cases. However, in the 60% CO₂ reduction case without regulating power provision, the EOM slightly exceeds the ESM emissions. In addition, several cases exhibit a few days in which the EOM exceeds the daily CO₂ emissions of the ESM, with the maximum overshoot observed at 11.1%.

These results confirm that the proposed model can account for CO₂ constraints while capturing detailed equipment-level operational characteristics, thereby producing realistic CO₂ emission estimates. If strict compliance with CO₂ emission targets is required, a more conservative emission target may be set in the EOM to account for potential overshoot.

7. Conclusions

In this study, we developed and validated a simulation model capable of evaluating optimal equipment sizing and operation for a distributed energy system (DES) under CO₂ emission constraints, while considering the provision of regulating power to the electricity grid. The main findings are summarized as follows:

• The proposed framework consists of two models: the Equipment Sizing Optimization Model (ESM), which determines the equipment configuration and approximate operation, and the Equipment Operation Optimization Model (EOM), which calculates detailed operation based on the ESM results. Both models are formulated as mixed-integer linear programming (MILP) models. This two-stage approach reduces computational burden. Although this study focused on the year 2040, the model is applicable to long-term scenario analysis.
• The model formulation allows gas engines and battery energy storage systems (BESS) to provide regulating power equivalent to Load Frequency Control (LFC).
• In the ESM, the partial-load efficiency characteristics of equipment such as gas engines and absorption chillers are represented using linear approximations formulated as a linear programming (LP) model without integer variables by omitting startup and shutdown states. This simplification reduces computational complexity and enables efficient equipment sizing. In contrast, the EOM incorporates these operational details through a full MILP formulation, allowing more accurate representation of equipment behavior in detailed scheduling.
• CO₂ emissions, equipment capacities, and the remaining state of charge of the BESS determined in the ESM are passed to the EOM as daily upper bounds and initial conditions. Because the CO₂ emissions calculated in the ESM and EOM do not necessarily coincide—owing to the simplified partial-load efficiency representation in the LP formulation—a penalty term is introduced in the EOM to ensure that its daily emissions do not exceed the ESM-derived limits. Similarly, for the state of charge of the BESS and the heat storage tank, penalties for deficit and rewards for surplus are incorporated to prevent inconsistencies between the two models and to maintain feasible energy balances in detailed operation.
• The BESS is modeled with separate cost parameters for power output and storage capacity, allowing the model to determine optimal sizing for both components.
• A case study was conducted to validate the proposed model. The results confirmed that equipment configurations vary depending on the presence of regulating power provision and the level of CO₂ emission reduction, and in the 40% CO₂ reduction case, the cost reduction achieved through regulating power provision was 6.8%. In addition, the analysis of total system cost under different CO₂ reduction targets showed that providing regulating power consistently lowers the overall cost across all scenarios.
• Under the 80% CO₂ reduction constraint, the optimization results indicate that hydrogen-related equipment becomes cost-effective and is incorporated into the optimal system configuration. This demonstrates that hydrogen plays an important role in maintaining system flexibility when emission limits become highly stringent. These findings highlight the potential of hydrogen technologies as a key option for future low-carbon energy systems.
• Although this study evaluated cost minimization of a DES providing LFC-type regulating power, the long-term degradation of equipment has not been considered, and impacts on the power system other than regulating power provision—such as voltage fluctuations caused by output variations—were not included in the present analysis. Furthermore, hydrogen was assumed to be supplied externally; however, future extensions of the model could incorporate on-site hydrogen production, for example by introducing a water electrolyzer into the DES to convert surplus PV electricity into hydrogen. Addressing these aspects in future work will further enhance the applicability and robustness of the proposed framework.