Fuzzy Comprehensive State Evaluation Method of Filter Circuit Breaker Based on Field Operation Data

Abstract

This study focuses on an 800 kV Filter Circuit Breaker (FCB) equipped with phase-controlled closing. The real-time health status of the circuit breaker was evaluated by analyzing the factors influencing its condition based on field-operation data. Key performance parameters, including mechanical characteristics, switching performance, and insulation properties, were employed for the assessment. Furthermore, field operation data are preprocessed to establish a comprehensive database that integrates data from C2-class margin tests, phase-controlled switching tests, and phase-controlled closing factory tests. A combined subjective–objective weighting method is applied to assign weights to health impact factors, and an improved fuzzy comprehensive evaluation method incorporating field operation data is proposed. Based on this evaluation, different operation and maintenance strategies were formulated. The results demonstrate that the proposed method enables a comprehensive and accurate assessment of the health status of FCBs, offering a reliable framework for optimizing condition-based maintenance in practical engineering applications.

1. Introduction

With the rapid development of DC transmission projects, converter stations are typically equipped with filters to compensate for the reactive power and eliminate harmonics. However, circuit breakers in the filter field undergo frequent operation, which leads to severe contact erosion. Consequently, circuit breaker failures in the filter field occur frequently, and the existing maintenance system can no longer meet the current demands [1].

The current maintenance system for circuit breakers primarily relies on post-failure repair and scheduled maintenance, both of which are relatively crude and lack a theoretical basis [2]. To enhance operational reliability, a condition-based maintenance (CBM) model tailored to the overall operational conditions has emerged [3]. The condition assessment of high-voltage circuit breakers involves integrating multiple parameters to evaluate operational performance comprehensively. In contrast to passive maintenance, Condition-Based Maintenance (CBM) is a proactive data-driven strategy. This approach utilizes historical and real-time data to schedule maintenance, which improves operational efficiency and reduces the rate of equipment failures [4].

Power system operations involve the monitoring of data from multiple sources and heterogeneous systems. The massive scale and complex interconnections of such data impose strict requirements on information-processing systems. Data-fusion technology integrates and analyzes multidimensional information. It uncovers coupling patterns among various parameters, filters out redundant data, and accurately extracts effective feature parameters [5,6].

Data fusion can be categorized into three levels: data, features, and decision level fusion [7]. Early studies primarily adopted neural network-based approaches for feature-level data fusion. For example, Ye et al. proposed a deep-learning model using multichannel sensory signals and feature fusion with deep neural networks for fault diagnosis, demonstrating effective feature integration from multiple sources [8]. Qi et al. employed wavelet analysis combined with neural networks for time–frequency feature extraction and fusion in fault diagnosis tasks [9]. However, these methods suffer from structural complexity and limited generalization capabilities. Miao et al. proposed a quantum genetic algorithm for multi-sensor data-level fusion to enhance system fault tolerance [10,11]. However, their study focused primarily on single-signal types. Given the complex and diverse fault modes of circuit breakers, single-type signals fail to accurately reflect the true equipment condition, thereby compromising the accuracy of the operating status assessment. To overcome the unreliability of single-sensor diagnostics, Zhang et al. integrated current and vibration signals. They employed a fuzzy clustering algorithm to extract optimal feature sets and used a support vector machine for fault classification [12].

The technology for assessing the condition of high-voltage circuit breakers traces its origins to research by Japanese and American researchers. Their work produced a first generation of monitoring systems. These systems were capable of extracting fundamental parameters such as opening/closing times and coil current. Some scholars have developed algorithms to assess the operating mechanism status based on coil current waveforms. However, these methods often fail to incorporate mechanical dynamic characteristics, such as contact travel time [13]. The literature used normal cloud models to establish membership functions for quantitative parameters, such as gas pressure, but failed to effectively integrate qualitative assessment elements, such as contact temperature rise [14]. Evidence theory was introduced to address uncertainties in the assessment [15], but conflicts in evidence during multisource data fusion can lead to fusion failure [16].

Domestic research has begun relatively late. Studies on signal acquisition for fault diagnosis have mainly focused on vibration and coil current signals [17,18]. Research on diagnostic methods is diverse, with significant applications of fuzzy logic owing to its advantages in handling fuzziness and uncertainty [19,20,21]. Tianjin University proposed a predictive maintenance strategy that combines data-driven and degradation models [22]. In the weight calculation for the evaluation algorithms, Henan Polytechnic University employed a method combining cooperative game theory with variable weight formulas [23].

Current research on the operational status assessment of filter-field circuit breakers is in its nascent stage. Although control systems have been installed in converter stations, data utilization and analytical depth remain inadequate. There is a pressing need to deeply integrate multi-source information from circuit breakers, extract critical parameters, and accurately evaluate equipment conditions to improve the operational reliability. Based on field operation data from 800 kV filter-field circuit breakers, this study analyzes key health-related indicators, presents an engineering-oriented fuzzy comprehensive evaluation framework, and demonstrates its applicability through a representative field case.

The main contributions of this work are summarized as follows:

(1) Construction of an Engineering-Oriented Indicator Hierarchy: While previous studies [19,20,21] established general indicator systems for circuit breakers, they often relied on idealized laboratory parameters that are unavailable in live 800 kV converter stations. This study reconstructs the indicator hierarchy specifically for the high-frequency operation characteristics of filter-field SF₆ circuit breakers, strictly filtering parameters based on field-monitoring constraints.

(2) Introduction of a Deterioration-Based Variable Weighting Strategy: Traditional fuzzy evaluation methods typically rely on constant weights [23], which suffer from the “short-board effect.” In these models, severe degradation of a critical indicator can be masked by high scores for other indicators. This study improves the evaluation method by integrating a variable weight mechanism (Equation (13)), which dynamically amplifies the weight of deteriorating indicators, ensuring that safety-critical defects are effectively captured rather than smoothed out by the average.

(3) Integration of Heterogeneous Field Test Data: Unlike previous studies that focused on single-signal analysis or vibration signals [17,18], this study integrates discrete and heterogeneous data sources, specifically combining C2-class margin tests, phase-controlled switching type tests, and factory tests. This data-fusion approach provides a robust baseline for membership functions, addressing the lack of fault samples in practical engineering.

The remainder of this paper is organized as follows. Section 2 introduces the improved fuzzy evaluation theory. Section 3 details the field data processing and indicator extraction. Section 4 presents a case study and comparative analysis. Finally, Section 5 concludes the paper.

2. Improvement of the Fuzzy Comprehensive Evaluation Method

The state quantification assessment method based on the fuzzy set theory employs membership functions to quantify and characterize parameters with uncertain boundaries. It is particularly well-suited for analyzing the condition of equipment subject to the coupled effects of multiple factors, such as high-voltage circuit breakers. The implementation of this approach requires addressing several key issues. These include feature parameter selection, weight configuration optimization, membership function construction, and comprehensive evaluation computations. The technical framework for implementation is structured as follows [21].

(1) Establishment of an evaluation indicator system: To address the hierarchical evaluation requirements for filter bank circuit breakers, a multidimensional feature screening method is adopted to establish a hierarchical evaluation parameter system. By combining mechanism analysis and data verification, core parameters sensitive to state changes were extracted, forming a multilevel indicator set denoted mathematically as $U=(u_1,u_2,\cdots ,u_n)$, where each element u_i corresponds to a key characteristic parameter during equipment operation.

(2) Status classification: A state grading standard set $V=(v_1,v_2,\cdots ,v_n)$ is established based on equipment operation and maintenance regulations. It is typically categorized into states such as Normal, Attention, Abnormal, and Fault, forming a benchmark for state determination. Each element in this set clearly defines technical parameter thresholds and operational guidance implications.

(3) Weight allocation model: A hybrid subjective–objective weighting approach is adopted by combining the Analytic Hierarchy Process (AHP) and Entropy Weight Method to construct the weight vector $W=({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)$, satisfying the normalization constraint ${\displaystyle \sum {\omega }_i=1}$. This methodology integrates expert knowledge with operational data to quantify the influence of each characteristic parameter on the overall system state, thereby forming a differentiated weighting scheme that is suitable for condition assessment.

(4) Membership degree modeling and fuzzy matrix: To address the random fuzzy dual characteristics of the equipment state parameters, a normal cloud model-based membership degree calculation method is proposed. Compared with traditional empirical approaches, this method utilizes three numerical features—expectation (Ex), entropy (En), and hyper-entropy (He)—to effectively integrate the random distribution properties of indicator data and the fuzziness of state boundaries. Consequently, the membership degree r_ij of the characteristic factor u_i to the evaluation subset v_j constructs the fuzzy relation matrix R:

$$R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{nm}\end{array}\right]$$

(1)

(5) Comprehensive evaluation calculation: The weighted averaging composition operator is adopted to combine the weight vector W and fuzzy relation matrix R, generating the comprehensive evaluation vector B. This operation is formalized as a fuzzy transformation $B=W\times R$, where the composition operator employs a weighted averaging mode for matrix computation. This process achieves a nonlinear mapping between parameters while preserving the interdependent dynamics of multidimensional indicators.

(6) Evaluation results: The fuzzy output vector is clarified using the maximum membership criterion or the weighted average method to determine the specific status level of the equipment. The assessment results can provide a quantitative basis for maintenance decisions, realizing closed-loop management, from condition monitoring to operation and maintenance strategies.

A.

Technical Framework of the Proposed Method

Standard fuzzy comprehensive evaluation methods generally employ static weighting, where the importance of each factor is fixed, regardless of the real-time state of the equipment. However, for high-voltage filter circuit breakers, a single critical defect (e.g., in insulation or pre-breakdown time) must trigger a high-risk assessment, even if other mechanical parameters are perfect. The specific improvement proposed in this study is the integration of a Variable Weighting Strategy into the Normal Cloud Model framework. Unlike the static models used in [19,20,21], the proposed method incorporates a deterioration degree-based adjustment (detailed in Section B) that dynamically modifies the weight vector W. This improvement solves the “masking effect” inherent in traditional fuzzy averaging, enabling the detection of early-stage hidden faults that standard methods would classify as “Normal”.

In this study, a flow chart of the improved fuzzy comprehensive judgment method used to assess the health status of filter-field circuit breakers based on field operation data is shown in Figure 1.

B.

Principles of Weighting Evaluation Indicators

For the condition assessment of filter field circuit breakers, health factors must be extracted from experimental and operational data, and a health assessment model must be established through indicator normalization and data fusion. Among these, determining factor weights is critical.

(1) Analytic Hierarchy Process

AHP is a typical multi-criteria decision-making method, whose core principle lies in assigning weights through hierarchical structuring and matrix operations. The main steps are as follows.

First, a three-layer structure consisting of an objective layer, a criterion layer, and an indicator layer is constructed. Decision objectives are addressed layer-by-layer to ensure that elements within the same layer are mutually independent and fully covered. Pairwise comparisons were conducted using a 1–9 proportional scale to form a positive reciprocal matrix:

$$A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right)={(a_{ij})}_{n\times n}$$

(2)

where $a_{ij}$ > 0, $a_{ij}$ = 1/$a_{ji}$, and $a_{ii}$ = 1.

Next, solve for the principal eigenvector W of the judgment matrix and then perform normalization operations on it to determine the weight coefficients.

$${\overline{W}}_i={({\displaystyle \prod _{j=1}^n{a}_{ij}})}^{{\displaystyle \frac{1}{n}}}\hspace{1em}\hspace{1em}(i=1,2,\cdot \cdot \cdot ,n)$$

(3)

$$W={\displaystyle \sum _{i=1}^n{\overline{W}}_i}\hspace{1em}\hspace{1em}{W}_i={\overline{W}}_i/W$$

(4)

The above equations calculate the weight vector. To verify the judgment rationality, the consistency index (C.I.) is defined as:

$$C.I.={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(5)

where ${\lambda }_{\max }$ is the maximum eigenvalue of judgment matrix A. This is derived from the following equation:

$${\lambda }_{\max }={\displaystyle \sum _{i=1}^n\frac{{[AW]}_i}{n{W}_i}}$$

(6)

where [AW]_i is the i-th component of vector [AW].

Define the stochastic consistency ratio CR as:

$$CR={\displaystyle \frac{C.I.}{R.I.}}$$

(7)

where R.I. is the stochastic consistency index (see the table to obtain it). In hierarchical analysis, the consistency test of the judgment matrix is based on the value of the CR: when CR < 0.1, the matrix is consistent, and the result is credible; otherwise, the scale needs to be adjusted until the condition is satisfied.

(2) Entropy Weight Method

As an objective assignment method, the entropy weight method calculates the weight value of each indicator based on the information entropy theory by analyzing the degree of dispersion of the indicator data, and then makes corrections to obtain indicator weights with strong objectivity [11]. The implementation process of this method involves the following key steps:

First, data standardization pre-processing was performed. For a positive matrix containing n evaluation objects and m evaluation indicators, data standardization is required. If negative elements are detected, the data should be converted to nonnegative intervals using the normalization method to generate a normalized matrix Z. The formula for calculating its elements is as follows:

$$X=\left(\begin{array}{ccc}{x}_{11}& \cdots & x_{1m}\\ x_{21}& \cdots & x_{2m}\\ ⋮& ⋮& ⋮\\ x_{n1}& \cdots & x_{nm}\end{array}\right)$$

(8)

The matrix for its standardization is set as Z, and each element in Z is.

$$z_{ij}=x_{ij}/\sqrt{{\displaystyle \sum _{i=1}^n{x}_{ij}^2}}$$

(9)

Next, a probability matrix was constructed. The distribution proportion of the i-th sample for the j-th evaluation index was quantified and used as the probability parameter in the information entropy model for subsequent calculations.

In the dataset containing n samples to be evaluated and m feature indicators, the normalization matrix obtained after the pre-normalization process can be expressed as:

$$Z=\left(\begin{array}{ccc}{\tilde{z}}_{11}& \cdots & {\tilde{z}}_{1m}\\ {\tilde{z}}_{21}& \cdots & {\tilde{z}}_{2m}\\ ⋮& ⋮& ⋮\\ {\tilde{z}}_{n1}& \cdots & {\tilde{z}}_{nm}\end{array}\right)$$

(10)

For the probability matrix $P$, the formula for each element $P_{ij}$ in $P$ is as follows:

$$p_{ij}={\tilde{z}}_{ij}/\sqrt{{\displaystyle \sum _{i=1}^n{\tilde{z}}_{ij}}}$$

(11)

Finally, the entropy and weights were calculated. The information entropy value is calculated for each indicator using the following formula:

$$e_j=-{\displaystyle \frac{1}{\ln n}}{\displaystyle \sum _{i=1}^n{p}_{ij}\ln }\left(p_{ij}\right)$$

(12)

The method is based on the entropy value characteristics: the greater the discrete degree of the indicator, the smaller its entropy value, the higher the information content, and the greater the corresponding weight. This method avoids the interference of subjective factors and is particularly suitable for the weight allocation of non-smooth signal characteristics.

(3) Variable Weighting Strategy

Power equipment has the “short-board effect”. If the key indexes are seriously deteriorated, the equipment should be shut down even if other indexes are normal. The traditional weighting method can be ignored because of the deterioration of low-weight indicators, leading to misjudgment. For this reason, a variable weighting strategy is adopted based on combined weighting, which is dynamically adjusted according to the degree of indicator deterioration; thus, the weights of the key indicators are adaptively improved when they deteriorate, thus supporting timely and conservative shutdown decisions when critical indicators deteriorate [23]. The specific calculation formula is as follows:

$$w_i^y={\displaystyle \frac{w_i{x}_i^{\alpha -1}}{{\displaystyle \sum _{i=1}^n{w}_i{x}_i^{\alpha -1}}}}$$

(13)

where $w_i^y$ is the dynamic variable weight and $w_i$ is the preset constant weight. To ensure reproducibility, the parameters in Equation (13) is defined as follows:

1. x_i represents the Standardized Health Status Value of indicator i. This was derived from the pre-processing step (Equations (16)–(20)). To ensure the mathematical consistency in Equation (13), all indicators are unified to a positive orientation: a value closer to 1 indicates a better health state, whereas a value closer to 0 indicates severe deterioration. For cost-type indicators (where a larger raw value implies worse health), a direction inversion (e.g., 1-normalized value) was applied prior to the calculation.

2. The α is a balancing factor ($0\le \alpha \le 1$). According to the variable weight formula mechanism, when $\alpha <1$, a smaller $x_i$ (poorer state) results in a larger weight multiplier.

3. In this study, based on engineering experience, we select $\alpha =0.5$. This setting ensures that indicators with low normalized values (indicating potential defects) are penalized with higher weights in the comprehensive evaluation.

C.

Normal cloud model

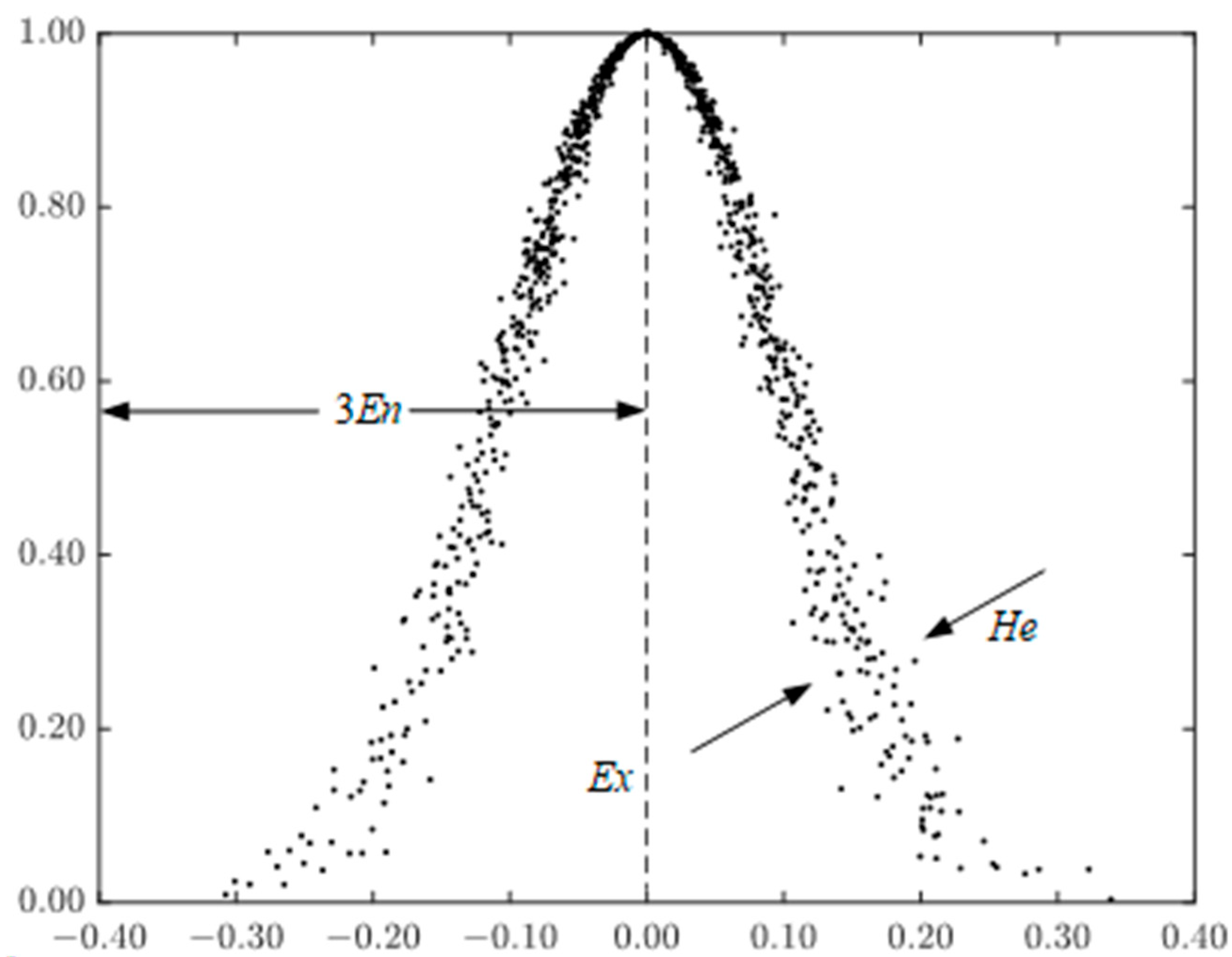
The cloud model, proposed by Deyi Li, integrates probability theory and fuzzy mathematics. It realizes a two-way mapping between qualitative concepts and quantitative data. Its core lies in the synergy of the random distribution and membership functions to portray the double uncertainty of complex systems. Compared with traditional fuzzy sets, the cloud model provides a flexible representation for handling randomness and fuzziness in the indicator data. Since SF₆ circuit breaker parameters are mostly normally or approximately normally distributed, it is practical to construct the membership function and fuzzy judgment matrix based on the normal cloud model.

The basic connotation of the cloud model is: under the premise of a known quantization domain U, if its corresponding fuzzy concept is C, and there is a specific value x, so that its affiliation to the concept C shows a randomness with a stable trend, then the distribution of x in U is called “cloud”. It is described in mathematical language as

$$\mu :U\to [0,1]\hspace{1em}\hspace{1em}\forall x\in U\hspace{1em}\hspace{1em}x\to \mu (x)$$

(14)

The normal cloud model is described by three numerical features: (1) the expected value Ex, representing the center position of the concept, corresponding to the centralized tendency of the data; (2) entropy En, reflecting the ambiguity and randomness of the concept, which determines the width of the cloud; and (3) hyper-entropy He, which measures the degree of dispersion of the cloud droplets, which affects the density of the distribution of cloud droplets in the space.

The cloud Generator (Cloud Generator) is the core algorithmic component to realize subordinate cloud modeling, which is divided into two categories according to its function: forward cloud generator and inverse cloud generator. Among them, the forward cloud generator is the basic algorithm form, and its operation mechanism can be described as follows: receive the three-dimensional characteristic parameters of the normal cloud model: the expected value Ex, the information entropy En, and the hyper-entropy He, combined with the preset number of cloud droplets N. The output is the value of the N cloud droplets and the corresponding affiliation degree. The specific steps are as follows.

(1) Based on entropy En and hyper-entropy He, generate a normal random number ${En}_i^{\prime }$ with variance He² and mean En;

(2) A cloud droplet location x_i extracted from a normal distribution is generated with expectation Ex as the mean and variance ${{En}_i^{\prime }}^2$;

(3) Calculate ${\mu }_i(x)=\exp \left(-{\left(x_i-Ex\right)}^2\right)/(2{{En}_i^{\prime }}^2)$, that is, obtain a cloud droplet $(x,\mu (x))$;

(4) This process is repeated until N cloud drops are output.

Based on the above method, only three numerical characteristic parameters (Ex, En, He) of the normal cloud model must be determined to generate a specified number of cloud droplets and realize the construction process of the normal cloud.

There are two ways to solve the three eigenvalues: when n sample data exist, the inverse cloud generator is used to invert the numerical features; when only the indicator boundaries [A_min, A_max] are known, they can be obtained by an approximation method:

$$\left\{\begin{array}{l}Ex=(A_{\min }+A_{\max })/2\\ En=(A_{\min }-A_{\max })/6\\ He=k\end{array}\right.$$

(15)

where hyper-entropy He is usually taken as an empirical constant k, and its value is determined based on the parameter fuzzy threshold. Special scenarios with single boundaries can obtain default boundary parameters by extreme-value expansion.

The cloud distribution generated by typical parameter combinations is shown in Figure 2, which shows the aggregation characteristics of cloud droplets in the core region.

3. Field Operation Data Processing and Analysis

A.

Determination of evaluation index

Breaker opening and closing time refers to the length of time from the energization of the breaker opening (closing) circuit to the completion of the separation (or contact) of all pole arc contacts. This index directly reflects the opening and closing performance of the circuit breaker; only the appropriate opening and closing speed can ensure its ability to open and close the current and reduce the electrical wear and tear and electrical abrasion of the contacts during operation. In addition, the opening and closing times can also reveal abnormal operation statuses, such as contact vibration, mechanism failure, or contact wear, which can lead to abnormalities at this time. Generally, owing to the high cost of circuit breaker operation in trip-monitoring devices, it is not possible to accurately collect the circuit breaker opening and closing times.

Therefore, by obtaining the pre-breakdown time from the closing oscillograph data and combining it with the closing time provided by the pole selection controller action report, a circuit breaker closed-time acquisition method was proposed [24]. By processing the field operation data, the key action parameters of the circuit breaker can be extracted, including the breaker closing time, opening time, auxiliary switch action time, closing action dispersion, and the number of actions and running times, which can reflect the mechanical performance of the circuit breaker. The proposed multisource fusion framework was robust. If direct opening/closing time data are unavailable, the system can rely on coupled parameters (e.g., auxiliary switch action time) or adjust the indicator set dynamically, ensuring that the evaluation continues with reduced but acceptable precision. Second, existing on-site monitoring equipment can be used to obtain the local discharge level and moisture content of the circuit breaker, which can reflect the insulation performance of the circuit breaker. Finally, the key performance parameters of the circuit breaker can be extracted by combining the on-site recorded data with the circuit breaker action report, including the closing time, auxiliary switch action time, moisture content, and pre-breakdown time. These parameters reflect the mechanical and insulation performance of the circuit breaker.

The health impact indicators of the health state of the circuit breaker are summarized in

Table 1. Status Indicator Items for Circuit Breakers.

Performance Indicator	Status Indicator
Mechanical performance	I1: Closing time
	I2: Auxiliary switch action time
	I3: Closing dispersion
	I4: Action times
	I5: Operating time
Opening and closing performance	I6: Pre-breakdown voltage
	I7: Pre-breakdown time
	I8: Closing current
Insulation performance	I9: Moisture content
	I10: partial discharge

. The indicators in Table 1 are screened based on the most frequent failure modes (mechanical jamming and insulation degradation) of the 800 kV FCBs. While other minor indicators (e.g., appearance inspection) exist, their exclusion has a negligible impact on quantitative health assessment.

It should be noted that the complete evaluation system established in Table 1 comprises ten status indicators, including mechanical, opening/closing, and insulation performance. Although the proposed method is designed to utilize all 10 indicators for a holistic assessment, for the sake of brevity and clarity in this demonstration, only four representative parameters (closing time, auxiliary switch action time, moisture content, and pre-breakdown time) were selected for detailed calculation and case study analysis. These four were chosen because they are the most sensitive indicators that reflect the three key subsystems. The calculation process for the remaining indicators follows an identical procedure.

B.

Characterization of evaluation index distribution

First, the field operation data of a group of circuit breakers in the filter field of a converter station in Northwest China were analyzed and processed. Through the processing of the field operation data, the mechanical performance parameters, including the closing time, auxiliary switch action time, and dispersion of the closing time, insulation performance parameter of the moisture content, and opening and closing performance parameters, including the pre-breakdown voltage and pre-breakdown time, can be extracted.

Based on the basis of obtaining the above database, the health range of each index is divided by combining the C2-class margin test of the circuit breaker, type test of phase-selective opening and closing, and factory test data of phase-selective closing.

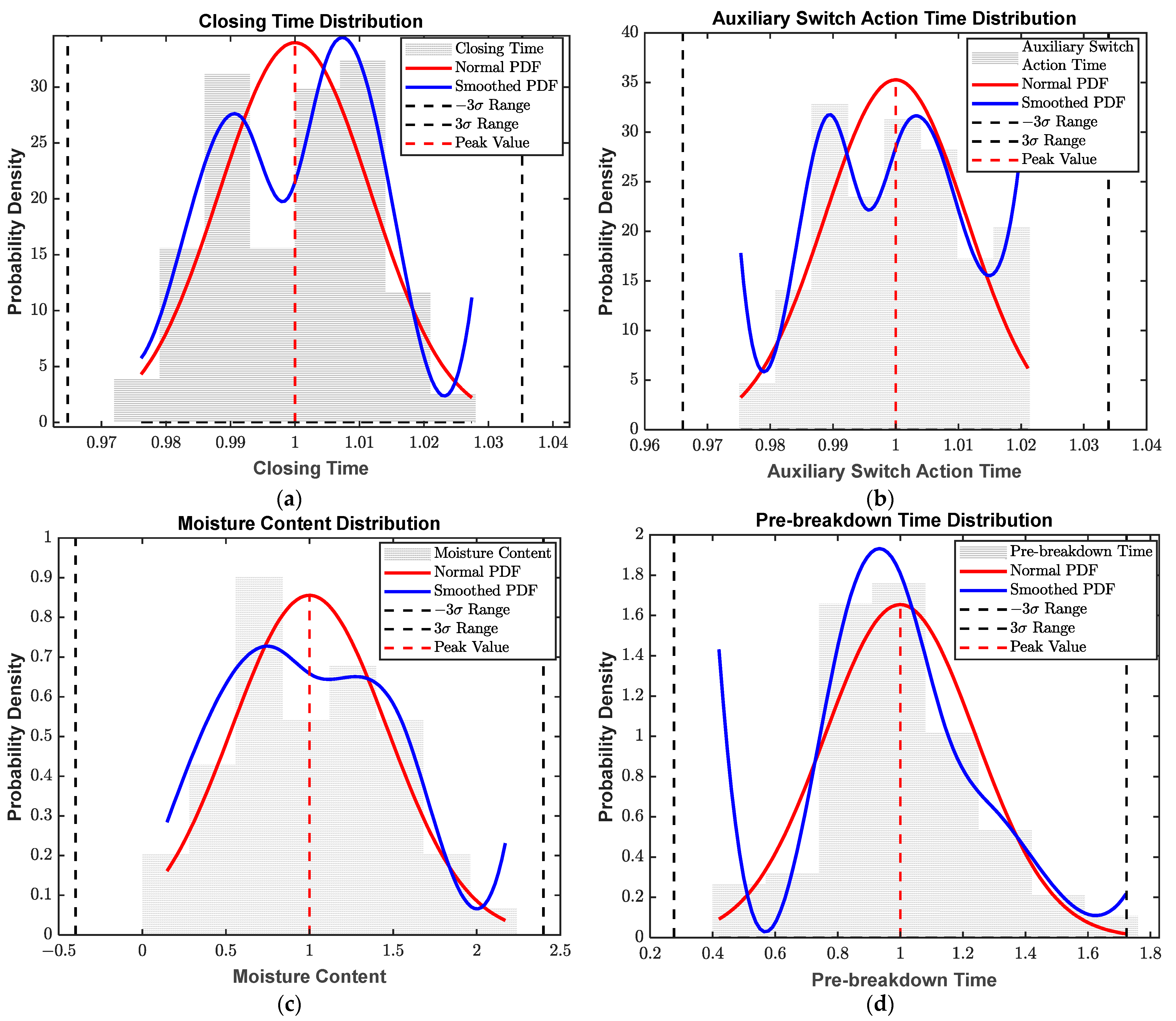
As shown in Figure 3, the fitting results of the circuit breaker parameters, such as the closing time (a), auxiliary switch action time (b), moisture content (c), and pre-breakdown voltage (d), indicate that the distribution law of the characteristic parameters of the filter field circuit breaker obeys a normal distribution. Therefore, the technical processing and condition assessment of the closing time based on the field operation analysis can be carried out according to the fitted normal distribution curve. Subsequently, the fault level can be delineated by combining the range of the fault-recording data.

Meanwhile, the p-value returned by the Jarque–Bera test for the above four types of parameters of this breaker group (usually when the p-value is greater than 0.05) is counted, and all of them satisfy the normal distribution, as shown in

Table 2. Jarque–Bera Test p-Values for Indicator Distributions.

Status Indicator Items	p-Value
I1: Closing time	0.118 08
I2: Auxiliary switch action time	0.091 528
I9: Moisture content	0.055 376
I7: Pre-breakdown time	0.149 78

.

For the circuit breaker state evaluation, the value of the indicators affecting the health state of the circuit breaker is currently in what stage that has a certain degree of ambiguity and randomness. Therefore, this study analyzes the distribution of the circuit breaker health factor data based on the use of a normal cloud model to determine the degree of affiliation of the circuit breaker health factor.

C.

Evaluation index preprocessing

In this study, for a variety of indicators, such as circuit breaker mechanical performance, opening and closing performance, and insulation performance, the current operating health state of the circuit breaker is comprehensively analyzed. Owing to the existence of unit differences, different weights, and inconsistent degradation degree of each indicator, it is necessary to carry out standardization to eliminate the influence of magnitude, and the indicators are divided into four state intervals: normal, attention, abnormality, and failure: x₁[0, a], x₂[b, c], x₃[d, e], x₄[f, g] [g, +∞] [25]. And according to Equation (15), it is possible to determine the three characteristic indicators of the affiliation function of the indicator, which is not repeated here.

(1) Mechanical performance index

At present, the mechanical performance parameters that can be extracted from the on-site operation monitoring data of the circuit breaker include the closing time of the circuit breaker and auxiliary switch action time, in which the closing time directly reflects the closing performance of the circuit breaker, and the auxiliary switch action time reflects the operation status of the circuit breaker, and both of them can reflect the healthy state of the circuit breaker’s mechanical performance.

(a) Closing time

The closing time of the filter field circuit breaker can be read by combining the field recording data with the action report, which is an intermediate indicator, and the closing time should be neither too long nor too short. Referring to, the Gaussian function was used to normalize the closing speed:

$$y=\exp [-{({\displaystyle \frac{x-m}{n}})}^2]$$

(16)

In general, the circuit breaker will give the action range of the closing time when it is shipped from the factory, and for the LW56-800 circuit breaker used in the filter place of a converter station in Northwest China, m is taken as 62, and n is taken as 3 here:

$$y_{11}=\exp [-{({\displaystyle \frac{x_{11}-62}{3}})}^2]$$

(17)

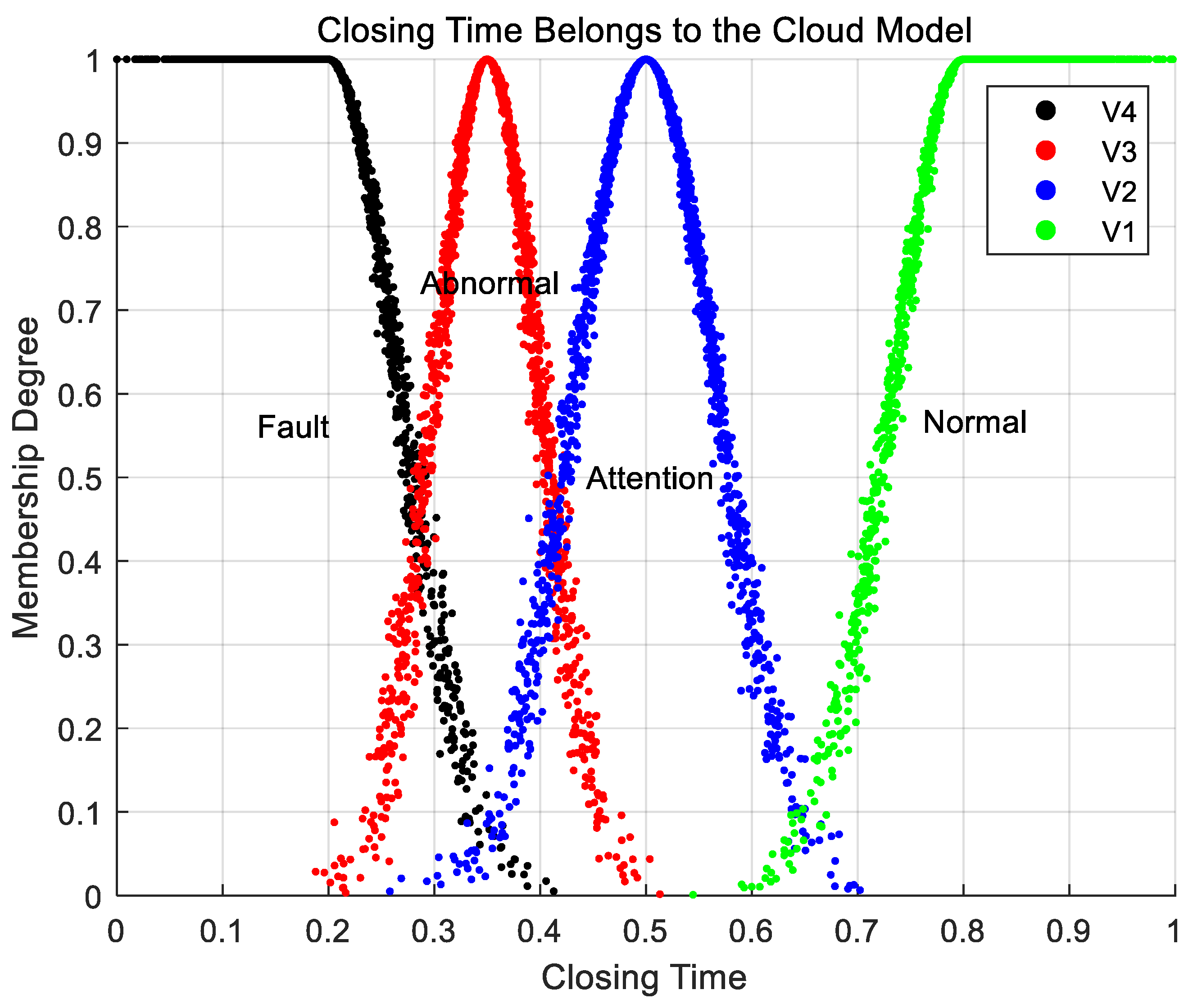
Based on the results of the circuit breaker C2-class margin test, the type test of selective phase opening and closing, and the factory test of selective phase closing, in combination with the manufacturer’s type test results and the actual maintenance strategy, according to the experience of experts and with reference to the literature and relevant regulations and guidelines, the closing time state rating interval can be divided into V4(0, 0.4], V3(0.2, 0.5], V2(0.3, 0.7], and V1(0.5, 0.8] (0.8,∞]. The three eigenvalues of the cloud model for each state evaluation level interval are D4(0.2, 0.067, 0.005), D3(0.35, 0.05, 0.005), D2(0.5, 0.067, 0.005), and D1(0.8, 0.067, 0.005), respectively. The number of cloud droplets was chosen to be 1500 to generate a cloud model of the gas pressure indicator affiliation at the closing time, as shown in Figure 4, where D1 and D4 are half-normal clouds, and D2 and D3 are normal clouds.

According to the normal cloud model of the closing time, for a given raw data point $x_{11}$, the output value $y_{11}$ is obtained after normalization transformation. Input $y_{11}$ into the four pre-constructed state-level cloud models and search for the state clouds with which there are cloud droplet intersections. If $y_{11}$ intersects with a state-level cloud, extract the cloud drops in that state-level cloud that intersect with $y_{11}$ and compute the mean value of the affiliation of these cloud drops as the affiliation of the closing time at that state level. If $y_{11}$ does not intersect with all state-level clouds, to avoid missing information, the affiliation averages of all cloud droplets within the range of $y_{11}\pm 5\%$ are used as supplements to calculate their affiliations under each state level. The remaining characteristic indicators, such as auxiliary switch action time, moisture content, and pre-breakdown voltage, can be processed according to this method and finally form a set of affiliation degrees for each indicator under the four state levels, which will provide the basis for the subsequent state assessment.

(b) Auxiliary switch action time

High-voltage circuit breakers are generally equipped with multiple auxiliary switches, which are used in the secondary circuit to reflect the opening and closing positions of circuit breakers and realize automatic control of circuit breakers [26]. The auxiliary switch action time was also obtained from the data recorded at the circuit breaker site. Because the auxiliary switch action time is generally fixed in proportion to the closing time, the Gaussian function is also taken here for normalization:

$$y_{12}=\exp [-{({\displaystyle \frac{x_{12}-28}{3}})}^2]$$

(18)

Based on expert experience, the closing time state rating interval can be divided into V4(0, 0.4], V3(0.3, 0.7], V2(0.4, 0.8], V1(0.7, 0.8] (0.8, ∞]. The three eigenvalues of each state evaluation level interval cloud model are D4(0.2, 0.067, 0.005), D3(0.5, 0.067, 0.005), D2(0.6, 0.067, 0.005), and D1(0.8, 0.067, 0.005), respectively.

The number of cloud droplets was selected as 1500 to generate the auxiliary switch action time indicator affiliation cloud model, as shown in Figure 5.

(2) Insulation performance indicators

(a) Moisture content

Moisture content is an important indicator of SF₆ gas insulation performance. Excessive water content may lead to condensation in low-temperature environments, which may reduce the insulation strength inside the circuit breaker and affect the safety of equipment operation. According to the “Regulations for Preventive Testing of Electric Power Equipment,” the moisture content of SF₆ gas in operation should be controlled below 300 μL/L, which is regarded as the normal state. When the moisture content exceeds 300 μL/L and shows a rapidly rising trend, it should attract the attention of the operation and maintenance personnel. If the value further increases to more than 500 μL/L and still shows an obvious rising trend, it can be judged as a fault state and needs to be dealt with in time. Therefore, the normalization of the moisture content is as follows:

$$y_{13}=\exp [{\displaystyle \frac{(x_{13}-500)}{500}}]$$

(19)

According to the protocol, the closing time state rating intervals can be divided into V1(0, 0.7], V2(0.4, 0.8], V3(0.6, 0.9], V4(0.8, 0.9] (0.9, ∞]. The three eigenvalues of the cloud model for each state evaluation level interval are D1(0.35, 0.117, 0.005), D2(0.6, 0.067, 0.005), D3(0.75, 0.05, 0.005), and D4(0.9, 0.05, 0.005).

The number of cloud droplets was chosen as 1500 to generate the moisture content indicator affiliation cloud model, as shown in Figure 6.

(3) Opening and closing performance indicators

(a) Pre-breakdown time

For a phase-selective closing circuit breaker, the pre-breakdown moment is the target point for selective closing, and a longer pre-breakdown time may lead to an increase in the duration of the arc when the circuit breaker closes, which affects the arc extinguishing capability of the circuit breaker. Excessively long arcs may damage the circuit breaker contacts and lead to failure of the relay. In this study, the pre-breakdown time was obtained by reading the circuit breaker operation recorded data. Let $x_{14}$ denote the actual measured pre-breakdown time, expressed in milliseconds (ms). As a typical cost-type indicator (smaller-is-better), its value ranges from zero to the maximum allowable limit $x_{\max }$(i.e., $x_{14}\in [0,x_{\max }]$). To unify the dimension with other indicators, the pre-breakdown time is pre-processed by normalization as follows:

$$y_{14}={\displaystyle \frac{x_{14}}{4}}$$

(20)

The error requirement of the phase-selective closing circuit breaker is ±2 ms, so according to expert experience, the pre-breakdown time state rating intervals can be divided into V1(0, 0.75], V2(0.5, 0.8], V3(0.7, 0.8], V4(0.75, 0.9] (0.9, ∞]. The three eigenvalues of the cloud model for each state evaluation level interval are D1(0.375, 0.125, 0.005), D2(0.65, 0.05, 0.005), D3(0.75, 0.017, 0.005), and D4(0.9, 0.05, 0.005), respectively.

The number of cloud droplets was chosen as 1500 to generate the pre-breakdown time indicator affiliation cloud model, as shown in Figure 7.

D.

Determination of evaluation index weights

In assigning weights to the above evaluation indices, this study adopts both subjective and objective methods, namely subjective hierarchical analysis and objective entropy weighting based on the degree of data dispersion, given the “short-board effect” of the circuit breaker. Accordingly, the theory of variable weights was used to address the indices.

(1) Subjective weighting

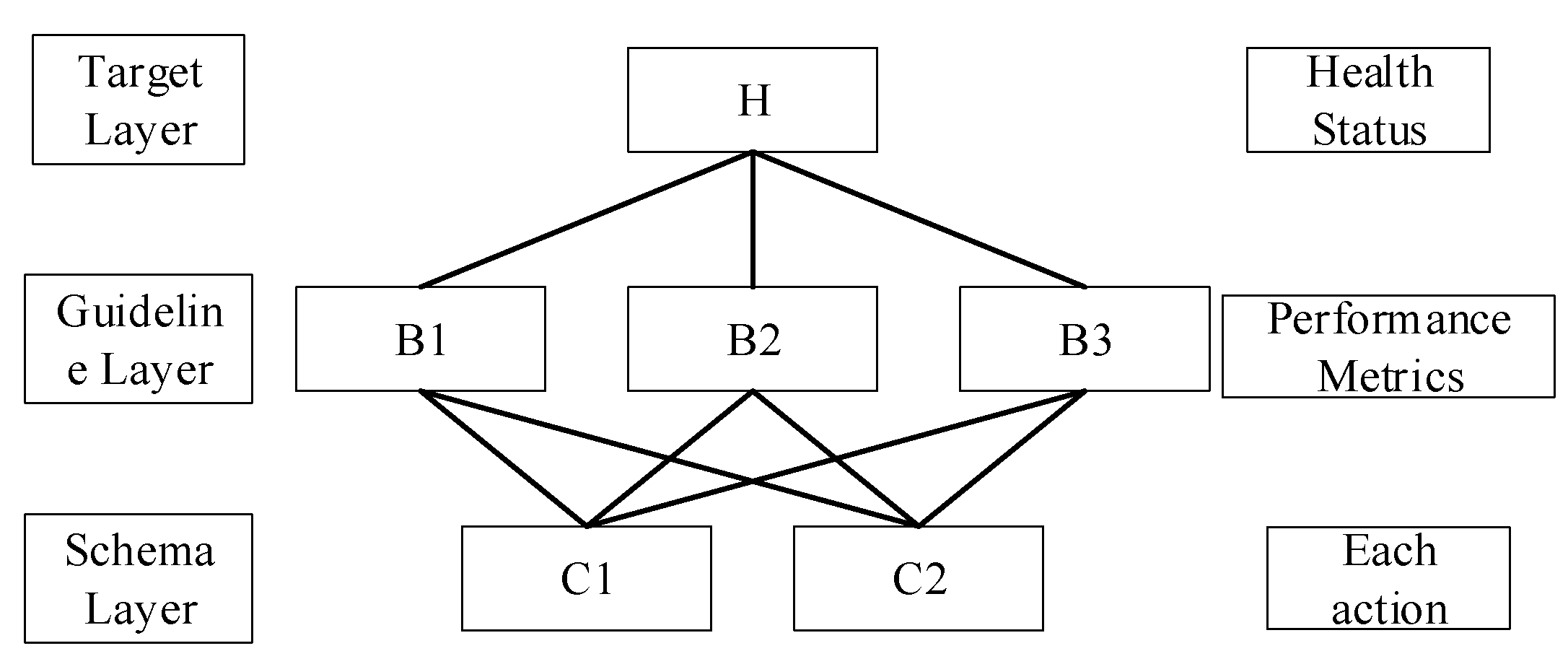
The Analytic Hierarchy Process is a multicriteria decision-making tool. The basic idea is to decompose the complex decision-making problem into levels, and through a comparison of the relative importance of each factor, gradually arrive at the final decision-making results. This study adopts the hierarchical structure shown in Figure 8, and its main purpose is to assign the evaluation indexes to their corresponding weights. The main steps are to construct the hierarchical structure, compare the elements in the hierarchy, conduct a consistency test, calculate the weight vector, and make a comprehensive assessment.

(a) Constructing a judgment matrix

In the following, the importance of the indicators is compared, and the judgment matrix is constructed to determine the weights scientifically. Based on the results of the previous normalization and the current performance parameters monitored by the circuit breaker, four types of performance parameters were selected for comparison: the closing time of the breaker, auxiliary switch action time, moisture content, and pre-breakdown time.

According to the aforementioned judgment matrix construction rules, combined with previous related studies and careful considerations, the judgment matrix for the four performance parameters of the filter field circuit breaker is proposed as follows:

$$A=\left(\begin{array}{cccc}1& 1& 5& 2\\ 1& 1& 5& 2\\ {\displaystyle \frac{1}{5}}& {\displaystyle \frac{1}{5}}& 1& 1\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1& 1\end{array}\right)$$

(b) Conducting a consistency test

The consistency index CI was 0.0021, the corresponding average random consistency index RI was 0.89, the calculated consistency ratio CR was 0.0023, and the matrix passed the consistency test because CR < 0.1.

(c) Calculate the weight vector

In this step, the weights of each performance indicator are calculated based on the judgment matrix. The weight vector is solved using the arithmetic average method, geometric average method, and eigenvalue method.

The weights of the three methods are listed in

Table 3. Subjective Hierarchy Analysis Standing Weights.

Performance Indicator	Arithmetic Average	Geometric Mean	Eigenvalue
Closing Time	0.3722	0.3725	0.3724
Auxiliary switch closing time	0.3722	0.3725	0.3724
Moisture content	0.0790	0.0788	0.0789
Pre-breakdown time	0.1765	0.1762	0.1763

.

It can be seen that the difference between the weights given by the three methods is very small, and the weight values derived from the eigenvalue method are chosen here.

(2) Objective weights

To reduce the bias caused by human factors and consider the non-stationarity of the signal, the entropy weight method was introduced to weight the feature quantity. The smaller the entropy value, the richer the information it contains; the larger the entropy value, the less information that the feature represents. The objective assignment of the following data was carried out in accordance with the calculation process of the aforementioned entropy weight method:

First, the information entropy values of the four indicators, namely, closing time, auxiliary switch action time, moisture content, and pre-breakdown time of the circuit breaker, were calculated, as shown in Figure 9.

The weights of these four indicators and the objective weights of the circuit breaker health impact factors were obtained, as listed in

Table 4. Indicator entropy weights.

Performance Indicator	Entropy Weights
Closing time	0.2977
Auxiliary switch action time	0.3219
Moisture content	0.1837
Pre-breakdown time	0.1967

.

(3) Combined weights

The arithmetic average of the constant weights obtained by the subjective hierarchical analysis method and objective entropy weight method were taken as the constant weights of the evaluation circuit breaker, as shown in

Table 5. Constant weighting of evaluation indicators.

Indicator Type	Hierarchical Analysis Method	Entropy Weighting Method	Constant Weighting Mean Value
Closing time	0.3724	0.2977	0.33505
Auxiliary switch action time	0.3724	0.3219	0.34715
Moisture content	0.0789	0.1837	0.1313
Pre-breakdown time	0.1763	0.1967	0.1865

.

With the increase in the number of circuit breaker opening and closing times, the influence weight of different influencing factors on the health status of the circuit breaker also changes; therefore, Formula (13) is used to establish the dynamic weight calculation method of the health influence factors. Figure 10 shows the main objective weight comparison diagram.

4. Calculation Example Analysis

In this study, the field operation data mainly comes from a converter station in the Northwest China State Grid, and the circuit breaker model is an 800 kV SF6 circuit breaker. The main parameters are listed in

Table 6. 800 kV SF6 circuit breaker main parameters.

Parameter Name	Parameter Name
Rated voltage	800 kV
Rated current	5000 A
Rated frequency	50 Hz
Rated short-time withstand current	63 kA
Rated peak withstand current	171 kA
Rated lightning impulse withstand voltage	2100 kV
Rated pressure of sulfur hexafluoride gas	0.7 MPa

.

The evaluation index parameters extracted from the recorded waveform data and the action report of this circuit breaker on 13 November 2024, were normalized according to the preprocessing method described above, and the results are presented in

Table 7. 7621B Circuit Breaker Field Operational Data.

Parameter Name	Data	Normalization Result
Closing time	63.1471 ms	0.8640
Auxiliary switch action time	29.1 ms	0.8742
Moisture content	21.4148 µL/L	0.3840
Pre-breakdown time	2.0904 ms	0.5226

. It is worth noting that each circuit breaker operates on average once every two and a half days, reflecting a relatively frequent operation pattern, and data collection was carried out continuously for three years. The performance of the proposed scheme relies on continuous updating of the cloud model. Frequent surgeries (approx. every two days) provides a steady stream of status samples, ensuring real-time tracking of degradation trends. In contrast, a significantly lower operation frequency would lead to “data lag,” reducing the timeliness of the health assessment.

According to the aforementioned method of determining the affiliation function, the affiliation degree of the evaluation indices on each state evaluation level can be derived separately, and the results are as follows:

$$R=\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 0& 0\\ 0.9565& 0.0104& 0& 0\\ 0.1077& 0.8565& 0& 0\end{array}\right)$$

In accordance with the aforementioned subjective–objective combination of constant weights processed by the variable weight formula, a variable weight vector W is obtained. A detailed calculation process demonstrating the transition from constant to variable weights is presented in

Table 8. Calculation process from constant weights to variable weights ($\alpha =0.5$).

Indicator	Normalization Result	Constant Weight	xi	${\mathit{x}}_{\mathit{i}}^{-0.5}$	Variable Weight
Closing time	0.8640	0.3351	0.8640	1.0758	0.295
Aux switch	0.8742	0.3472	0.8742	1.0695	0.3003
Moisture content	0.3840	0.1313	0.616	1.2741	0.1847
Pre-breakdown	0.5226	0.1865	0.4774	1.4473	0.22

.

As shown in Table 8, the moisture content and pre-breakdown time had relatively low normalized values. Consequently, their weights were effectively amplified by the variable weighting strategy, ensuring that these potential weak points significantly influenced the final evaluation. The final variable weight vector was obtained as follows:

$$W=(0.295,0.3003,0.1847,0.22)$$

Then, according to the obtained judgment matrix and weight vector, the evaluation results were calculated using the weighted average-type operator:

$$B=W\times R=(0.8069,0.1931,0,0)$$

Based on the fuzzy comprehensive evaluation vector B = (b1, b2, b3, b4), a maintenance decision-making mechanism is established. In this study, we adopted the Maximum Membership Principle combined with risk-sensitive adjustment. The mapping between the evaluation results and the recommended maintenance strategies is presented in

Table 9. Mapping of Health Status to Maintenance Strategies.

State Level	Dominant Membership	Maintenance Strategy
Normal (V1)	max(B) = b1	Routine inspection according to schedule. No immediate action required.
Attention (V2)	max(B) = b2 OR (b2 ≥ 0.2 AND b1 is dominant)	Shorten the inspection cycle. Monitor indicators with high variable weights (e.g., Moisture content, Pre-breakdown).
Abnormal (V3)	max(B) = b3	Diagnostic testing required (e.g., partial discharge location). Plan for outage maintenance.
Fault (V4)	max(B) = b4	Immediate power cut and emergency overhaul.

.

For the tested 800 kV circuit breaker, the evaluation result is B = (0.8069, 0.1931, 0, 0). Although the primary membership points to “Normal” (0.8069), the secondary membership in “Attention” (0.1931) is significant, near the critical threshold of 0.2.

Impact of variable weights on decision-making: The variable weighting strategy played a decisive role in this assessment. As shown in Table 8, the moisture content and pre-breakdown time deteriorated (normalized values dropped to 0.3840 and 0.5226, respectively), triggering the algorithm to amplify their weights to 0.1847 and 0.2200, respectively. Without this mechanism (i.e., using constant weights), the contribution of these defects would have been averaged out by the healthy mechanical parameters, likely resulting in a negligible “Attention” membership (e.g., <0.1). By verifying the field data, the signs of partial discharge were confirmed. The proposed method successfully pushed the evaluation result toward the “Attention” zone, prompting the maintenance team to intervene early. This validates that the variable weight mechanism effectively prevents “false negatives” by accelerating the transition from “Normal” to “Attention” when critical indicators degrade rapidly. Furthermore, the variable-weighting strategy facilitates fault isolation. By observing which indicator’s weight is amplified (e.g., moisture content in Table 8), maintenance personnel can directly pinpoint the specific subsystem (e.g., insulation system) responsible for degradation.

5. Discussion

5.1. Effectiveness of Variable Weighting and Cloud Model

The case study validates the superiority of the Variable Weighting Strategy over traditional constant weighting methods in handling the “short-board effect.” In the evaluation of the 800 kV FCB, mechanical parameters (e.g., Closing time) indicated a “Normal” state, which would typically mask the degradation of the Moisture content under static weighting schemes. However, the proposed mechanism successfully identified the insulation defect by dynamically amplifying the weight of the deteriorating indicator. Furthermore, the application of the Normal Cloud Model proved effective in managing the uncertainty of field operation data. By utilizing the hyperparameters (Ex, En, He), the model accommodates the inherent mechanical dispersion and data randomness better than rigid fuzzy sets, ensuring a robust assessment of the real-time health status.

5.2. Engineering Implications for Condition-Based Maintenance

The proposed framework extends beyond theoretical calculation to practical Condition-Based Maintenance (CBM). Unlike single-parameter monitoring, the integration of heterogeneous data (including C2-class margin tests and real-time waveforms) provides a holistic view of the equipment. The evaluation results directly support differentiated operation and maintenance strategies. Specifically, the ability to pinpoint the subsystem with the highest variable weight allows maintenance personnel to isolate faults (e.g., distinguishing insulation performance issues from mechanical characteristics) and implement targeted interventions, such as shortening inspection cycles, thereby improving the operational reliability of converter stations.

6. Conclusions

This study analyzes the circuit breaker health factors using field data. It also presents an engineering-oriented assessment framework for the evaluation of circuit-breaker conditions. The key conclusions are as follows:

(1) We developed a comprehensive fuzzy evaluation model for circuit breakers. It incorporates numerous monitoring parameters from the field operation data. This enhanced the practical applicability of the method under real operating conditions.

(2) A combined weighting strategy was introduced. It uses both subjective and objective weights, with variable weights. Constant weights were derived from expert experience (AHP) and data-based entropy weights. Variable weights were then applied based on the degradation level of each indicator. This allows precise and adaptive weighting.

(3) A fuzzy hierarchical evaluation framework with combined and variable weighting was established for the condition assessment of the filter-field circuit breakers. It assesses the health of the filter-field circuit breakers more reliably. This study offers a practical reference for condition-based maintenance.