Biomethane Yield Modeling Based on Neural Network Approximation: RBF Approach

Abstract

Biogas production plays a key role in the development of renewable energy systems; however, forecasting biomethane yield remains challenging due to the nonlinear nature of anaerobic digestion. The objective of this study was to develop a predictive model based on Radial Basis Function Neural Networks (RBF-NN) to approximate biomethane production using operational data from the Przybroda biogas plant in Poland. Two separate models were constructed: (1) the relationship between process temperature and daily methane production, and (2) the relationship between methane fraction and total biogas flow. Both models were trained using Gaussian activation functions, individually adjusted neuron parameters, and a zero-level correction algorithm. The developed RBF-NN models demonstrated high approximation accuracy. For the temperature-based model, root mean square error (RMSE) decreased from 531 m³ CH₄·day⁻¹ to 52 m³ CH₄·day⁻¹, while for the methane-fraction model, RMSE decreased from 244 m³ CH₄·day⁻¹ to 27 m³ CH₄·day⁻¹. The determination coefficients reached R² = 0.99 for both models. These results confirm that RBF-NN provides an effective and flexible tool for modeling complex nonlinear dependencies in anaerobic digestion, even when only limited datasets are available, and can support real-time monitoring and optimization in biogas plant operations.

1. Introduction

1.1. Biogas Production and Its Role in Renewable Energy

In the current conditions of the growing energy crisis and burden on the environment, biogas production is gaining strategic importance as one of the key areas of renewable energy development [1]. Biogas, which is formed as a result of anaerobic digestion of organic waste, is an environmentally friendly type of fuel that allows reducing greenhouse gas emissions, utilizing agricultural residues and reducing dependence on fossil fuels [2]. This area is considered in detail, in particular, by Kostetskyi and Sakhatskyi [3] and Scarlat et al. [4].

According to estimates by Palamarchuk and Riabchenko (2022) [5], the potential for biogas production in Ukraine is 7–10 billion m³ per year, which allows partially covering domestic energy needs and contributing to the decentralization of energy supply. In the European Union, biogas plays an important role in the implementation of climate policy: in particular, according to the European Biogas Association [6], more than 9500 biogas plants are operating in Germany, which provide almost 5% of electricity production.

In addition, biogas technologies ensure effective management of organic waste in the agro-industrial complex, the food industry and the municipal sector [7]. The processing of manure, poultry droppings, food waste and the organic fraction of solid household waste allows for not only producing energy, but also obtaining high-quality organic fertilizers, as noted by Holm-Nielsen et al. [8] and Stetsenko and Hlushchenko [9].

Thus, the development of the biogas industry is an important tool for the transition to a circular economy and the achievement of the Sustainable Development Goals, in particular, Goal 7 (“Clean and Affordable Energy”) and Goal 13 (“Combating Climate Change”), as stated in the UN program [10].

The choice of raw materials plays a crucial role in ensuring the stability and efficiency of the anaerobic digestion process. In today’s conditions of rapid growth in food prices, the issue of rational use of agricultural products arises, in particular, regarding their use as raw materials for energy needs. The use of food crops for biogas production is of concern due to ethical, social and economic consequences, as it reduces food availability and contributes to the deepening of the food crisis. In this context, an alternative solution is to switch to the use of agricultural waste, by-products of agro-industrial production and non-traditional raw materials, such as biomass of energy crops, food industry waste, manure, crop residues and other organic components unsuitable for consumption. According to the study by [8], urbanized agro-systems in Europe have the potential for balanced development through digitization and satellite monitoring, which allows for a rapid assessment of the available biomass of by-products and waste [11]. This approach contributes to efficient resource planning without affecting the main food supply. In addition, the results of Beila et al. show that fields intended for growing energy crops can be optimally used based on the results of remote monitoring, which allows avoiding excessive withdrawal of areas from food turnover [12]. This ensures increased land use efficiency without harming agricultural production, which is key in the context of the European Green Deal. Recent studies also demonstrate the importance of effective biomass handling and pretreatment in optimizing energy recovery from lignocellulosic materials. Witaszek et al. compared combustion and anaerobic digestion of Silphium perfoliatum L. and showed that proper mechanical and thermal pretreatment significantly improves methane yield and energy balance, supporting sustainable biogas production [13]. Similarly, Yuan et al. emphasized the advantages of integrating bioethanol and biogas production to increase the overall conversion efficiency of lignocellulosic substrates [14]. Traditionally, the main source is cattle manure, but modern research focuses on the possibilities of combining it with other organic waste to intensify methanogenesis. For example, adding fruit and vegetable waste to cow manure increases biogas yield by enriching the substrate with easily digestible sugars [15]. Similarly, the use of straw pellets with the addition of crude glycerin is effective, creating favorable conditions for methanogenic microorganisms, as noted by Polishchuk et al. [16].

Separate studies are aimed at modeling the operation of a bioreactor during manure fermentation without and with additives, which allows optimizing the technological parameters of the installation, as highlighted by Polishchuk et al. [17]. Pretreatment of wheat straw improves the accessibility of cellulose and significantly increases biogas yield, as shown for thermally pretreated wheat straw mixtures producing up to 94% more biogas compared with untreated material [18]. Considerable attention is paid to the selection and dosage of additional components—agricultural residues, molasses, fatty substances and soap waste—which serve as additional sources of energy [19,20,21]. Of particular note are studies demonstrating the potential for the influence of physical fields on the processes of biomethanogenesis of mixtures of poultry manure with lignin-containing raw materials, thus opening up new prospects in intensification technologies [20].

1.2. Feedstock Types and Challenges of Anaerobic Digestion

That is, taking into account the different nomenclature and conditions of organic raw materials, as well as various methods of influence, choosing the optimal additives and fermentation modes is a difficult task. The study by Ghazizade-Fard and Koupaie applied machine learning-based mathematical modeling to optimize anaerobic co-digestion of wastewater sludge and food waste. Their model identified the optimal mixing ratios and key parameters affecting methane yield, demonstrating that computational optimization can effectively enhance process stability and biogas productivity [22]. The developed model allows you to assess the impact of different combinations of substrates on the efficiency of anaerobic digestion and helps to choose the most promising options for stable biogas production. Thus, the use of mathematical models in anaerobic digestion processes is the basis for the development of effective control technologies that allow stabilizing the process and improving the amount and quality of produced biogas. This also contributes to the development of new methods for optimizing digestion processes, taking into account the variability of environmental conditions and the diversity of substrates used. For example, in the work of Zablodsky et al. [17], a mathematical simulation model was proposed to assess the technical and economic efficiency of using the technology of converting agricultural waste into biogas, in particular, taking into account seasonal fluctuations, which allows predicting the biogas yield and optimizing its use in energy systems. Mathematical models are an important tool for understanding and optimizing processes, such as anaerobic digestion, as they allow predicting the result based on certain parameters and external factors. However, such models often require accurate and detailed input data, which can be a difficult task in conditions of variable technological processes or changing raw material composition. In such cases, artificial neural networks (ANNs) come to the rescue, as they are able to adapt to complex and nonlinear relationships between process parameters, which allows reducing the requirements for input data accuracy and providing more flexible and effective control. ANNs allow modeling complex, nonlinear dependencies between process parameters and system outputs, which makes them a powerful tool for analyzing and controlling technological processes, in particular, in biogas production. Thus, in the work of Palaniswamy et al. [23], an ANN model was developed to predict and optimize biogas yield from mixed substrates of food waste and cow dung. The model used key process parameters such as substrate ratio, temperature, pH, and digestion time as input variables. This approach enabled accurate prediction of methane yield and rapid adjustment of process conditions, contributing to stable biogas production and improved conversion efficiency.

However, the use of ANNs in such applications is not without challenges. One of the main difficulties is the requirement for large and representative datasets to train accurate models. In biogas production, where process parameters can vary widely, collecting consistent and high-quality data is often problematic. Moreover, ANNs are prone to overfitting, where the model becomes too closely aligned with the training data and loses its ability to generalize to new situations, as reported by Hunter et al. [24]. Another limitation concerns the interpretability of neural network models, which often behave as “black boxes”, making it difficult to understand which specific factors drive individual model predictions or recommendations. Therefore, balancing model complexity and generalization remains a crucial challenge for applying ANN-based tools in anaerobic digestion.

For example, in the context of biogas production, it is important to understand how specific changes in process parameters, such as temperature, pH, and C/N ratio, affect the final biogas yield, and not just rely on model predictions, as demonstrated by Al-Zoubi et al. [25]. It is also worth noting that ANN-based models require significant computational resources, which can be an important factor when implementing such systems in real production conditions. Given the large amounts of data and complex computational processes, there may be a need for powerful hardware or significant costs for computing power, which can complicate their implementation in small and medium-sized enterprises. As noted by Alcin et al., integrating ANNs with hardware accelerators such as field programmable gate arrays (FPGAs) allows for high computational precision and real-time optimization, but also requires substantial processing capacity and technical expertise [26]. Thus, although ANNs open up great opportunities for improving biogas production management, their application requires overcoming the above-mentioned problems, which calls for further research and improvement of training, interpretability, and optimization methods, as highlighted by Ghazizade-Fard and Koupaie and Ge et al. [22,27].

1.3. Modeling Needs in Anaerobic Digestion

Forecasting biogas yield is an important step in optimizing the operation of anaerobic plants, especially under conditions of variable feedstock quality and fluctuations in technological parameters. One of the promising approaches to solving the problem of modeling such processes is the use of neural networks with radial basis functions (RBFs), which are able to effectively approximate complex nonlinear dependencies even with a limited amount of input data. The study by Karamichailidou et al. [28] demonstrated the advantages of RBF networks in combination with differential evolution for accurate modeling of biogas yield in wastewater treatment plants. The results obtained indicate the possibility of using such models as an effective decision support tool in energy systems. Another study by Gupta et al. [29] demonstrated the effectiveness of using machine learning techniques to predict methane production from microwave-pretreated anaerobic digestion of food waste, achieving an accuracy above 90%. Their model confirmed that machine learning (ML) based prediction can significantly enhance process optimization and biogas productivity. Recent studies highlight the increasing role of artificial intelligence in enhancing the accuracy and adaptability of anaerobic digestion modeling. For instance, Kowalczyk-Juśko et al. developed an RBF-based neural network model to estimate methane productivity from various silage substrates, achieving satisfactory prediction quality while significantly reducing the need for time-consuming biochemical tests [30].

1.4. Artificial Neural Networks in Biogas Research

Further progress was reported by Sakiewicz et al., who developed an ANN-based modeling framework for an integrated biogas–wastewater treatment system, including RBF-type neural architectures optimized with multi-stage training algorithms, achieving high predictive accuracy and demonstrating the suitability of such models for complex and dynamic biogas systems [31].

Finally, Karamichailidou et al. conducted a comparative analysis of different ANN structures for biogas modeling and demonstrated that RBF-based architectures provide faster convergence, better generalization, and higher prediction accuracy than traditional multilayer perceptron models. These findings are consistent with the present study, confirming that the RBF-NN approach ensures robust and computationally efficient performance under variable feedstock and process conditions [28]. Thus, neural networks employing radial basis functions represent a robust and adaptable tool for forecasting biogas yield, ensuring higher process stability and supporting decision-making in intelligent energy systems.

1.5. Objective of the Study

Therefore, the objective of this study was to develop a predictive model based on Radial Basis Function Neural Networks (RBF-NNs) to approximate biomethane production using operational data from the Przybroda biogas plant. The study focuses on two relationships: (1) process temperature vs. methane output and (2) methane fraction vs. total biogas flow.

2. Materials and Methods

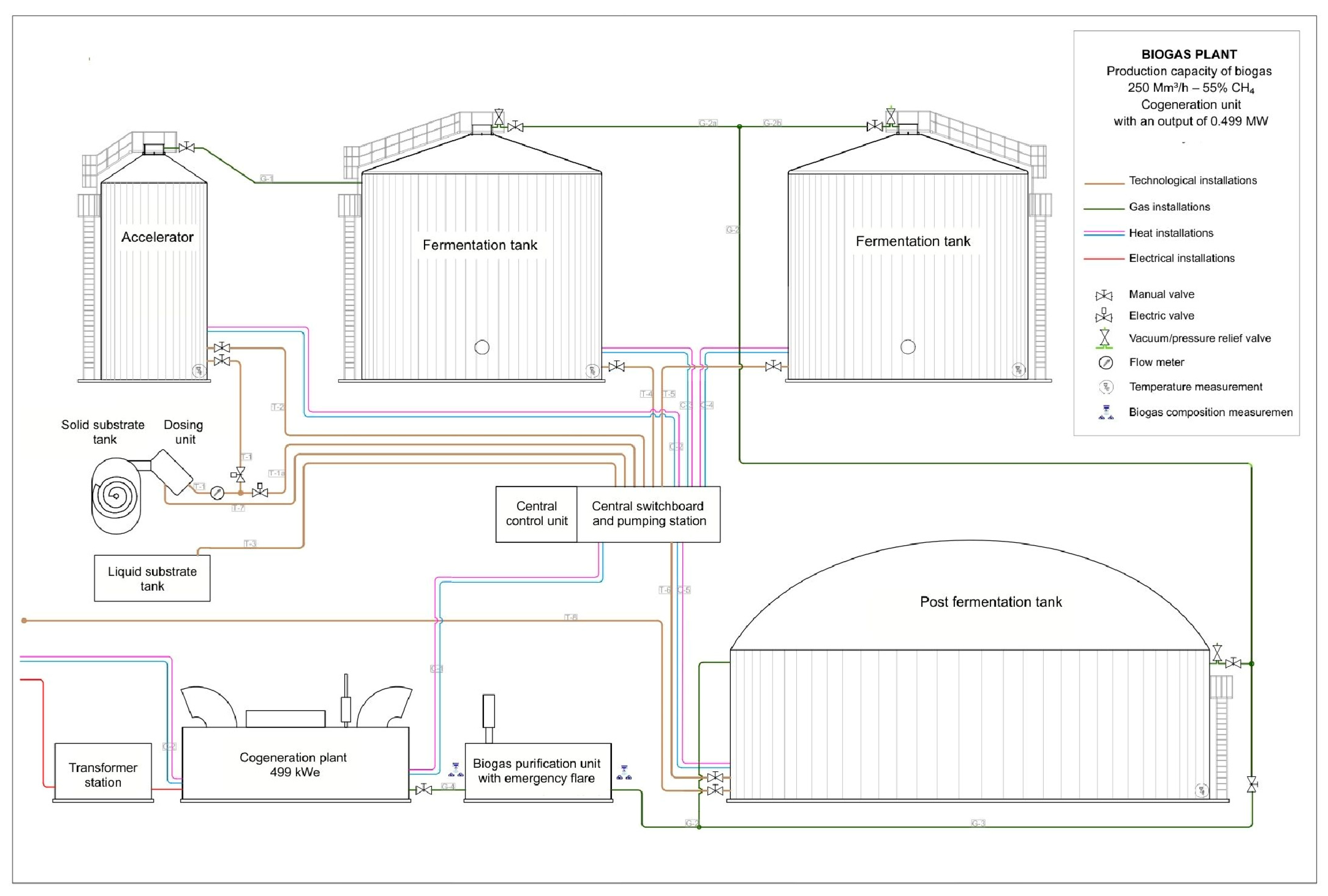
2.1. Description of the Przybroda Biogas Plant

This study used experimental data collected for 2 years (from the beginning of 2022 to the end of 2023) from the biogas plant in the village of Przybroda (Figure 1), in the Rokietnica commune, 26 km from the northwestern city of Poznań in Poland. The biogas plant was originally built with an installed capacity of 499 kWe/560 kWt, with plans to expand its capacity to 1 MWe/1.2 MWt in the coming years. The biogas plant consists of two fermentation reactors (tanks) equipped with vertical mixing systems and a post-fermentation reactor, which is integrated with a biogas storage dome. Furthermore, it includes a hydrolyzer (biotechnological accelerator), which, due to its lowered pH, is capable of accelerating the initial stages of fermentation and the degradation of substrates. The biogas produced in mesophilic conditions is combusted in a combined heat and power (CHP) engine to generate electricity and heat, covering approximately one-third of the village’s total heat demand. Electricity, after subtracting self-consumption, is sold directly to the power grid to the obligated seller. In 2022, it was 3495.349 MWh and in 2023, 2762.651 MWh.

The biogas plant in Przybroda in located on land owned by the Poznan University of Life Sciences (PULS) and primarily functions as an experimental facility. Due to application of several innovative technical and technological solutions, in particular, a maceration system, the installation allows for relatively frequent modification of the substrate composition. The types of substrates and their amounts used in the biogas plant in Przybroda during the analyzed years are presented in

Table 1. Substrates used in the Przybroda biogas plant.

Substrate	2022 [mg]	2023 [mg]
Corn silage	6397.0	3842.0
Distillers’ stillage	4362.0	2692.9
Ground corn	181.0	–
Onion husks	215.6	–
Cattle manure	13.5	–
Animal feed unfit for consumption	15.8	–
Distillery syrup	194.5	1096.0
Cattle slurry	–	133.3
Total	11,379.4	7764.2

.

The diagram presents the main technological units and process flows within the Przybroda agricultural biogas plant (Poland). The installation consists of a hydrolyzer (accelerator), two primary fermentation reactors equipped with vertical mixers, and a post-fermentation tank integrated with a biogas storage dome. Solid and liquid substrates are fed from dedicated storage tanks through the dosing unit into the hydrolyzer and fermenters. The system includes technological, gas, heat and electrical pipelines, equipped with manual and electric valves, pressure-relief valves, temperature sensors, biogas composition analyzers and flow meters. Biogas generated in the reactors is routed to the biogas purification unit with an emergency flare and subsequently to the CHP unit (499 kWe), where electricity and heat are produced. A transformer station ensures grid connection, while the central control and pumping station manages operational processes. The scheme illustrates all measurement points used in this study, including temperature sensors, methane-content analyzers and biogas-flow meters.

2.2. Data Collection and Preprocessing

The operational data used to develop the RBF-NN model were collected at the Przybroda biogas plant, where substrates included corn silage, distillers’ stillage, onion husks, cattle manure, distillery syrup, and cattle slurry (Table 1). For the purpose of model development, two datasets were extracted from the full two-year operational database (2022–2023).

The first dataset contained 10 paired measurements of process temperature and corresponding methane production, manually recorded in the BIOGAZ+ 2.0 system (Poznań University of Life Sciences, Poznań, Poland). The second dataset consisted of 10 paired measurements of the methane fraction in biogas and the total biogas flow rate. In both cases, 70% of the data points (7 samples) were used for training, and 30% (3 samples) for validation. Although the datasets were relatively small, they exhibited stable monotonic behavior, which enabled effective approximation using compact RBF-NN architectures.

Data preprocessing included verification of measurement completeness, removal of inconsistent or erroneous entries, and normalization of all variables prior to training.

The model development, training, and visualization of results were carried out in Python 3.9 (Python Software Foundation, Wilmington, DE, USA) using the PyCharm Community Edition 2021.2.2 environment (JetBrains, Prague, Czech Republic) together with the NumPy and Matplotlib libraries (NumPy Developers, Austin, TX, USA; Matplotlib Development Team, Cambridge, UK). The Radial Basis Function Neural Network (RBF-NN) model and its components were implemented manually using object-oriented programming, which enabled full control over parameter updates and detailed tracking of the training process. This approach is consistent with recent studies employing custom RBF-based neural architectures for bioprocess modeling and highlights the advantages of transparent, modular implementations [28,32].

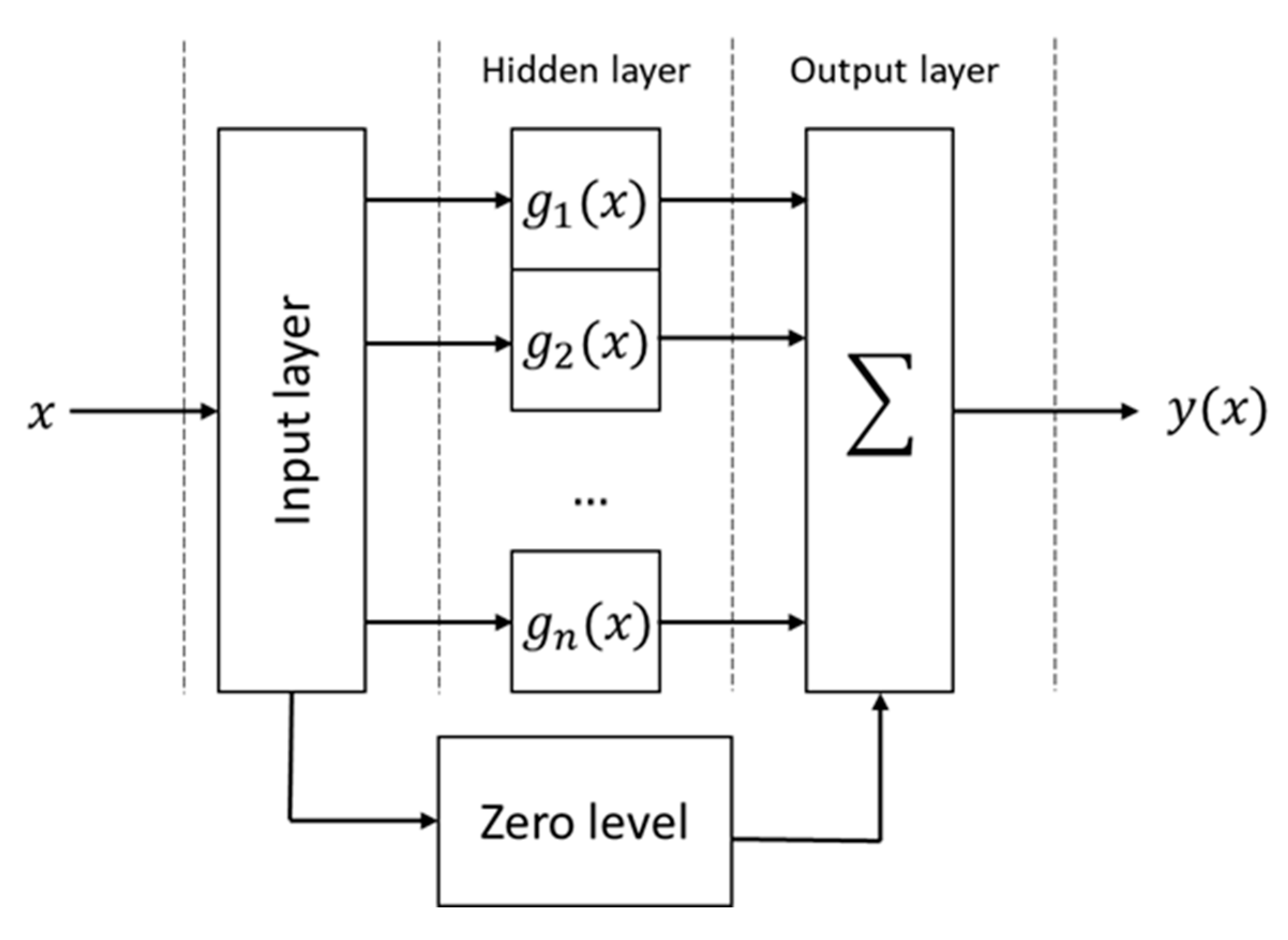
2.3. RBF-NN Model Architecture

To implement the Radial Basis Function Neural Network (RBF-NN), a modular object-oriented architecture was developed to ensure full transparency of the mathematical operations performed during training. The model consists of three key components: the Neuron class, responsible for generating individual Gaussian basis functions; the RadialBasedNN controller class, which manages neuron initialization, parameter updates and loss calculations; and the Pauline class, used to generate and adjust the zero-level baseline for improved curve fitting. This structure allows precise control over each stage of the approximation process and facilitates tracking the contribution of individual neurons to the final output.

The program also has a Pauline class. This class sets the neurons to a zero level relative to a certain curve of an arbitrary rank. This mechanism enables the neuronal curves to be aligned more closely with the experimental data while simultaneously providing an initial approximation of the target curve. As a result, the training process becomes faster, more stable, and yields a smoother and more accurate final approximation. The equation of the relative zero level curve is calculated using the least squares method.

A crucial step in designing the model was determining the appropriate number of neurons. Preliminary tests were conducted for a range of N = 3 to N = 12, evaluating each configuration using root-mean-square error (RMSE) and qualitative inspection of curve smoothness and overfitting tendencies. Networks with fewer than 6 neurons produced underfitted approximations with large residuals at inflection points, while networks with more than 7 neurons showed instability in parameter optimization, including oscillatory behavior of the neuron spreads and excessive sensitivity to local noise in the data. Therefore, the selection of 6 neurons for the temperature-based model and 7 neurons for the methane-fraction model represented an optimal balance between approximation accuracy and model stability. This choice is consistent with earlier studies reporting that small RBF architectures are sufficient for modeling monotonic or unimodal relationships in biogas production systems.

To make the architecture of the developed model clearer, the overall structure of the RBF-NN is illustrated in Figure 2, which shows a single-input radial basis network composed of N Gaussian neurons and a linear output unit combining their responses with a bias (zero-level component).

The network consists of one input variable, N Gaussian radial neurons, and a linear output neuron combining weighted neuron responses with a bias (zero-level component).

2.4. Training Procedure and Model Calibration

It was decided that the training process would select the height (gain) of the Gaussian curve and its width (sigma), separately to the left and right. The training algorithm was based on the principle of error back-propagation: at each iteration, the loss was calculated for every data point, and the corresponding update was computed for each adjustable neuron parameter, gradually bringing the curve closer to the experimental data. The gain and sigma parameters were updated using differentiated rules, where the influence of the error was weighted by Gaussian-based coefficients: deviations near the neuron center primarily affected the gain, whereas distant deviations contributed more strongly to sigma adjustments.

To prevent instability, the neuron centers were fixed during training, update magnitudes were limited to 10% of the current parameter value, and an additional correction term was applied to the zero-level component, allowing it to shift toward the direction of maximal residual and improving convergence. These measures ensured stable model behavior and prevented divergence during approximation.

The progression of the training process is summarized in

Table 2. Data table showing the change in RMSE during training (values in m³ CH₄·day⁻¹).

Epoch	0	10	50	1000	2000	5000
RMSE temperature approximation	531	291	212	138	87	52
RMSE fraction approximation	244	165	158	110	92	27

, which illustrates the systematic reduction of RMSE across successive training epochs for both developed models. All RMSE values reported in Table 2 are expressed in m³ CH₄·day⁻¹, corresponding to the units of methane production used in the approximation.

2.5. Performance Evaluation (RMSE, R²)

To quantitatively assess the quality of the approximation obtained by RBF-NN, two standard regression metrics were used: RMSE and the coefficient of determination (R²). These metrics allow evaluating both the absolute magnitude of the approximation error and the proportion of variance in the target data explained by the model.

The RMSE was computed as

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(1)

where $y_i$ are the measured values, ${\widehat{y}}_i$ are the model predictions, and n is the number of samples used for training. RMSE characterizes the average deviation between the predicted and measured outputs.

The coefficient of determination was calculated using

$${\mathrm{R}}^2=1-{\displaystyle \frac{\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(2)

where $\overline{y}$ is the mean of the measured data.

The value R² reflects the fraction of the total variance of the output variable explained by the RBF-NN. A value close to 1 indicates a strong correspondence between the model and the data.

Both metrics were applied independently to each of the two constructed models:

(1)

the model based on the temperature, and

(2)

the model based on methane fraction.

These values were used to compare the predictive performance of the RBF-NN configurations and to verify the stability of the fitting process.

3. Results and Discussion

3.1. Data Characteristics and Preprocessing Results

The experimental data used to develop the model were collected at the Przybroda biogas plant, where the feedstock composition consisted primarily of corn silage, distillers’ stillage, cattle slurry, onion husks, distillery syrup, and smaller amounts of various agro-industrial by-products (Table 1). Although the facility operates continuously and 2 years of process data were available, only periods with complete and internally consistent measurements were selected for modeling. This resulted in two compact and noise-free datasets, each consisting of 10 representative data points:

• Temperature dataset (10 points): daily mean digester temperature paired with corresponding methane production.
• Methane-fraction dataset (10 points): measured methane percentage in biogas paired with total biogas flow.

Each dataset was divided into training (70%) and validation (30%) subsets.

The reduced and curated datasets were intentionally used to evaluate the ability of the RBF-NN architecture to generalize from limited, high-quality measurements, which aligns with previous studies demonstrating that compact RBF models can perform effectively when trained on well-structured small datasets. The first dataset represented the relationship between methane output and process temperature, while the second described the share of methane in the total biogas volume. The RBF-NN models were configured with 7 and 6 neurons, respectively, and in both cases, the zero-level curve was defined as a first-rank polynomial (a straight line).

Preprocessing included verification of measurement completeness, removal of inconsistent records, and normalization of all values prior to training. Despite the relatively small size of the datasets, both exhibited clear monotonic trends, which allowed the RBF-NN to approximate the underlying functional relationships effectively. This demonstrates that even limited operational data from full-scale biogas plants can be sufficient to train compact RBF architectures, provided that the datasets are representative and preprocessing procedures are properly applied.

3.2. Model Architecture: Practical Implications

A key step in designing the RBF-NN architecture was determining the appropriate number of neurons. Preliminary experiments were conducted for network sizes ranging from N = 3 to N = 12. Each configuration was evaluated using RMSE values, curve smoothness, local fitting behavior, and the tendency toward overfitting.

Networks with fewer than 6 neurons produced underfitted approximations, characterized by large residuals around inflection regions and insufficient flexibility to capture nonlinear variability in the datasets. Conversely, configurations exceeding 7 neurons exhibited instability during parameter optimization, including oscillatory adjustments of neuron spreads and increased sensitivity to local noise in the input data. Such behavior reduced the generalization capability of the model, despite marginal improvements in training RMSE.

Therefore, selecting 6 neurons for the temperature-based model and 7 neurons for the methane-fraction model provided an optimal balance between prediction accuracy, smoothness of approximation, and training stability. This choice aligns with previous studies indicating that compact RBF architectures are sufficient for modeling monotonic or unimodal functional relationships commonly observed in biogas production systems. These architectural characteristics directly influenced the model’s predictive behavior and provide an important context for comparing the observed performance with existing ANN-based biogas modeling studies.

The results of this study align with recent advances in ANN-based biogas modeling. Kowalczyk-Juśko et al. demonstrated that a relatively simple RBF network using five input parameters of silage quality achieved satisfactory prediction accuracy, with prediction errors below 3% relative to the measured values, confirming the suitability of RBF architectures for nonlinear bioprocesses [30]. Similarly, Gupta et al. reported that non-linear ML models, particularly Support Vector Machine (SVM) and ANN, achieved R² > 0.9 when predicting methane yield from microwave-pretreated substrates. The high approximation accuracy obtained in the present work (absolute losses reduction from 3880 to 278 m³ CH₄∙day⁻¹) further supports the reliability of RBF-NN for process-level forecasting and its ability to generalize effectively from limited datasets through localized radial functions [29].

The performance of the developed RBF-NN models—characterized by substantial RMSE reduction (531 → 52 m³ CH₄∙day⁻¹ and 244 → 27 m³ CH₄∙day⁻¹) and high determination coefficients—corroborates previous studies applying RBF architectures to anaerobic digestion modeling. Gonçalves Neto et al. developed an ANN model using experimental and literature data for food and vegetable waste digestion, achieving R² = 0.99 during training, which confirmed the robustness of neural models for complex feedstocks [32]. Likewise, Karamichailidou et al. introduced a hybrid RBF–Differential Evolution algorithm that provided superior accuracy for biogas prediction in full-scale wastewater treatment plants [28]. The comparable R² and RMSE values obtained in this study demonstrate that the RBF-NN trained on data from the Przybroda biogas plant performs on par with advanced hybrid approaches while maintaining a simpler structure suitable for on-site process control and real-time forecasting.

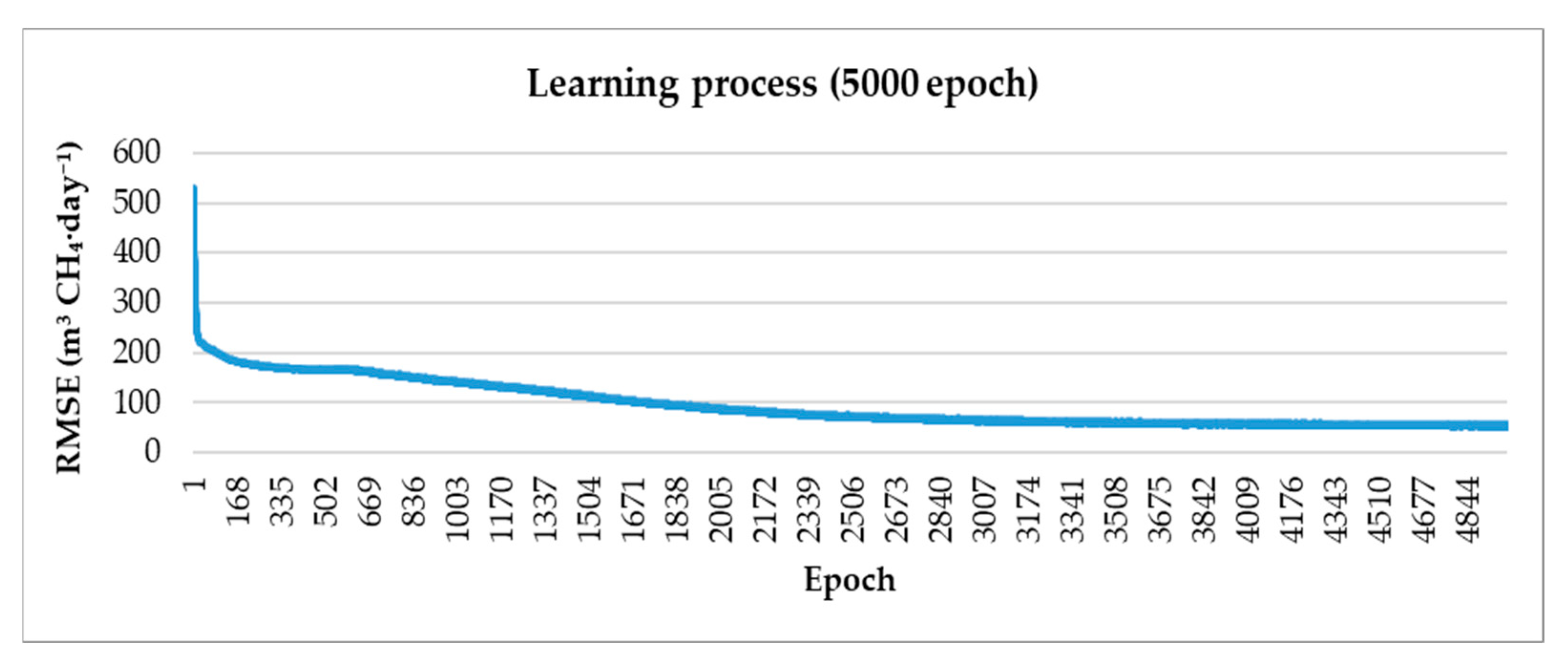
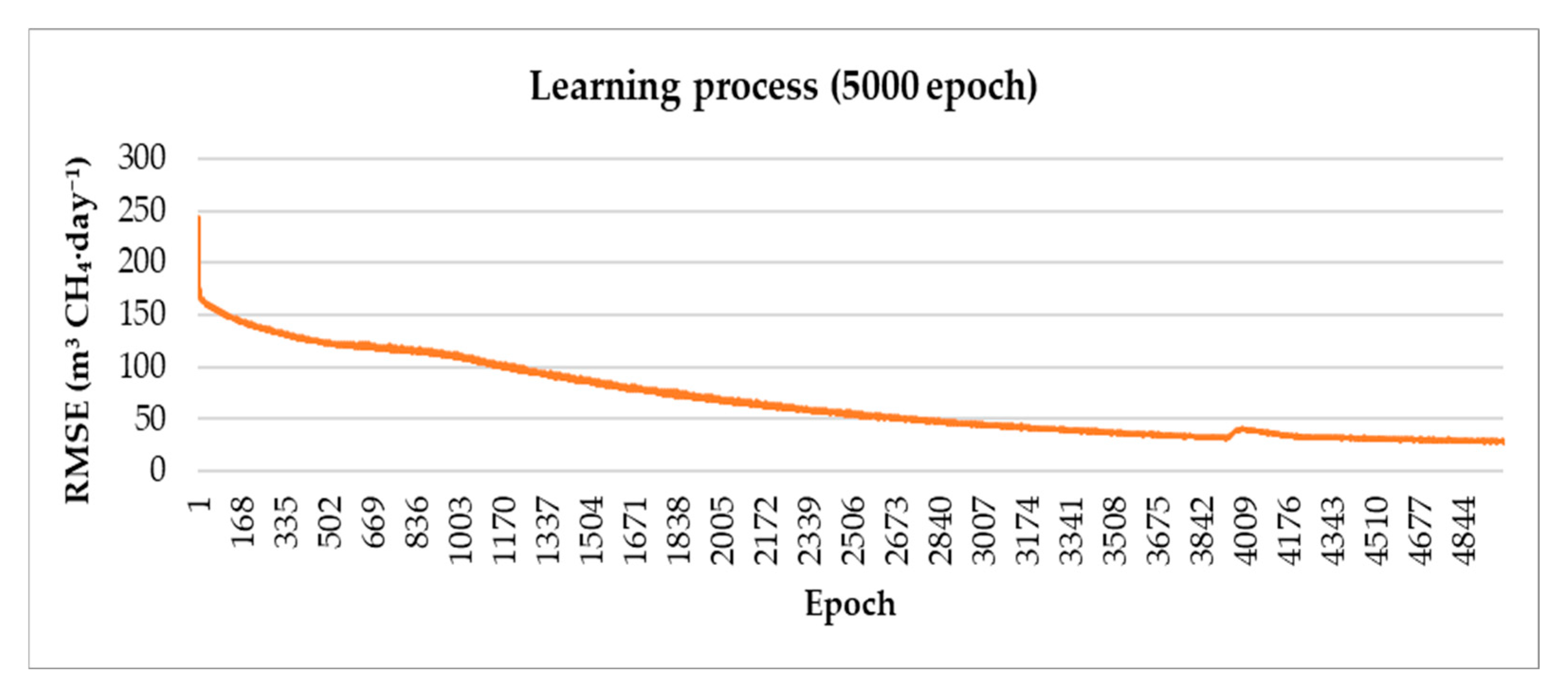
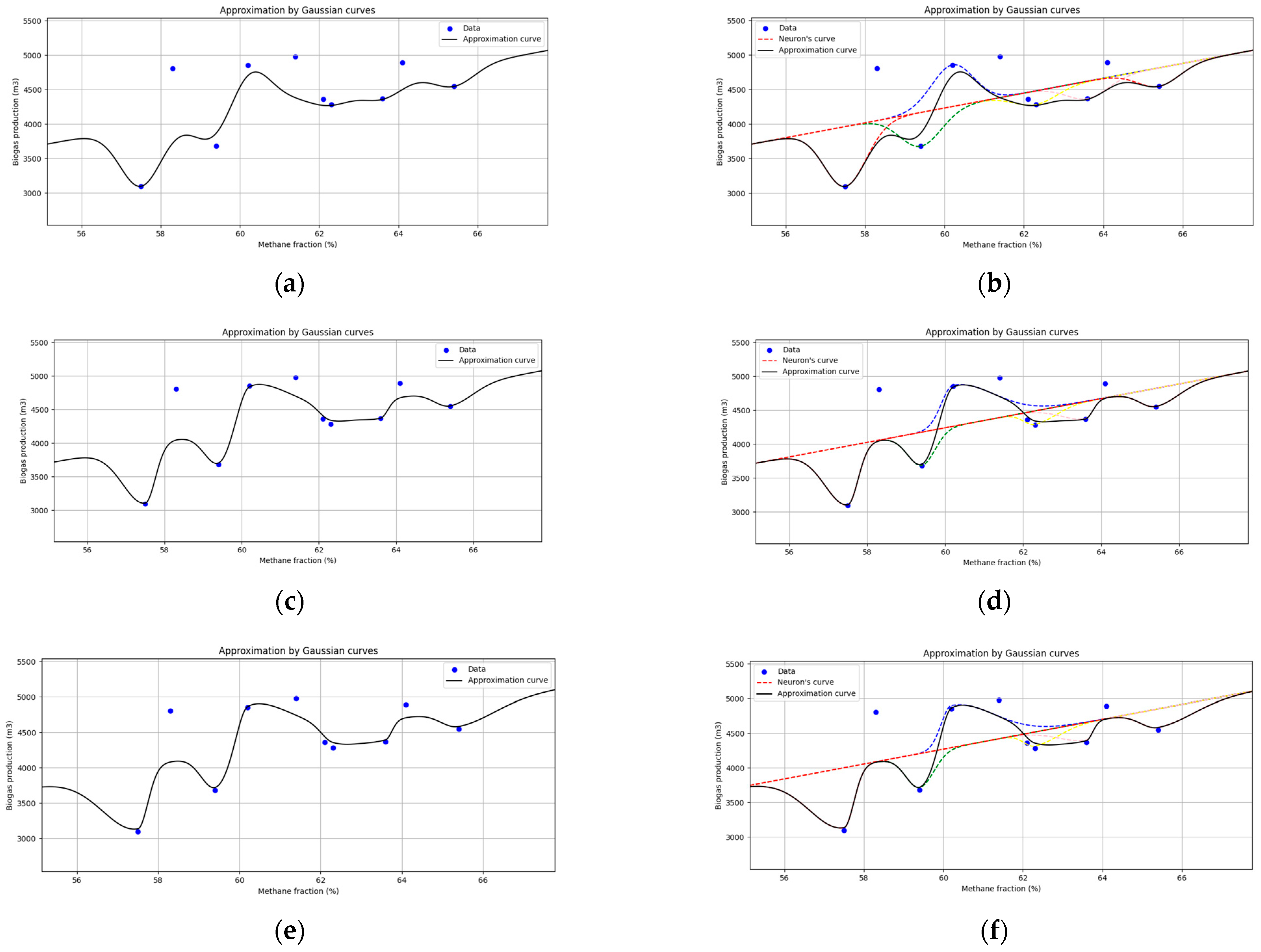
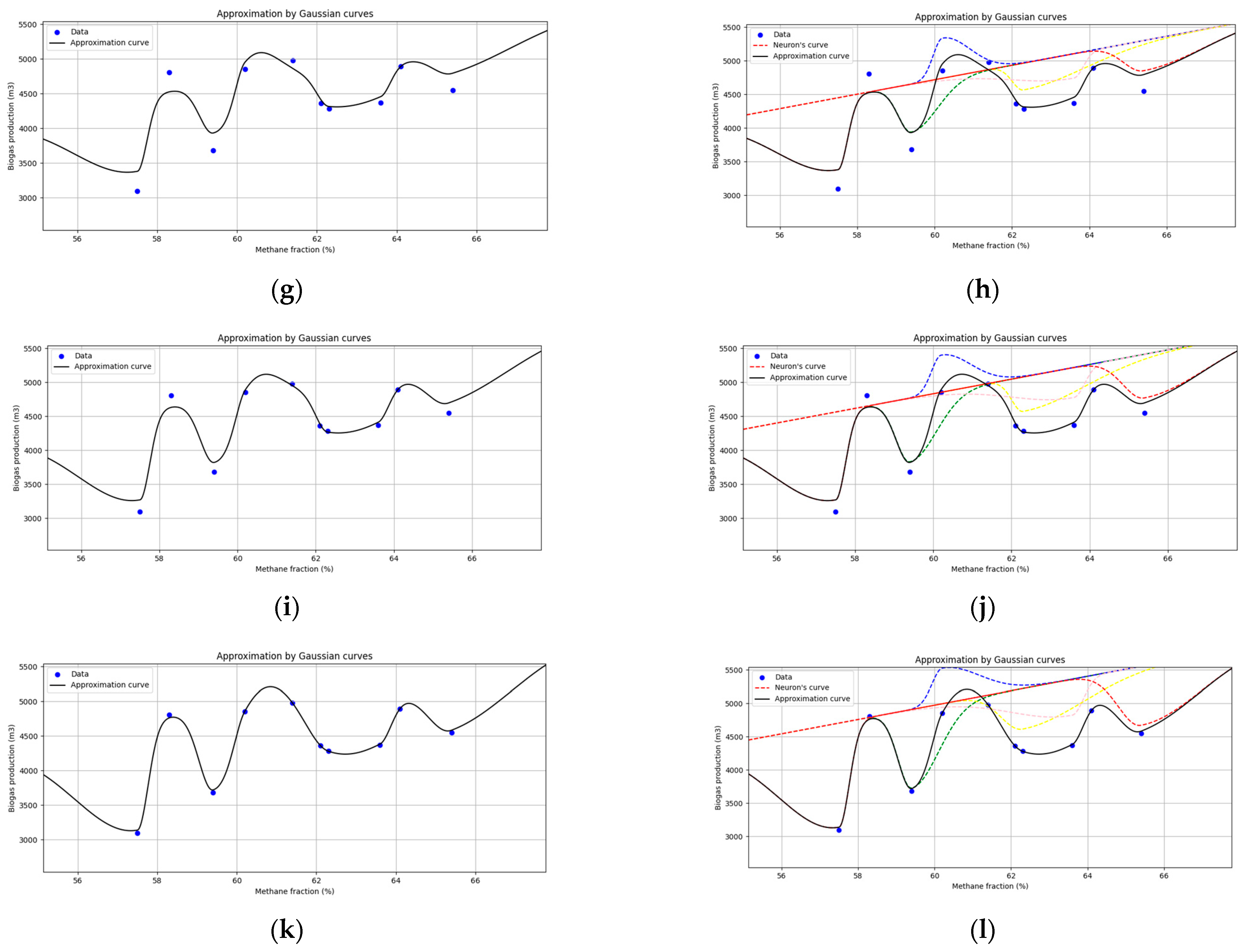
3.3. Training Dynamics and Convergence Behavior

The predictive performance of the two RBF-NN models was assessed using RMSE and R² metrics. For the temperature-based model, the loss function decreased from 531 m³ CH₄∙day⁻¹ to 52 m³ CH₄∙day⁻¹ after training, demonstrating a substantial improvement in approximation accuracy. The corresponding coefficient of determination reached R² = 0.99, indicating that the model accurately captured the monotonic temperature–methane relationship present in the dataset. The methane-fraction model achieved similarly strong performance, reducing RMSE from 244 m³ CH₄∙day⁻¹ to 27 m³ CH₄∙day⁻¹, with a determination coefficient of R² = 0.99. These results confirm that both models were able to generalize effectively despite the limited number of data points.

The observed predictive quality is consistent with previous findings in the field. Studies such as Kowalczyk-Juśko et al. and Gupta et al. reported high accuracy of ANN and SVM models in methane-yield forecasting, achieving R² > 0.9 for substrate-specific datasets [29,30]. The performance obtained in this work—particularly the reduction of error by more than an order of magnitude—confirms that compact RBF architectures are well suited for modeling monotonic or unimodal dependencies typical of biogas production processes. Additionally, the model trained on operational data from the Przybroda facility performed comparably to more complex hybrid approaches reported in the literature, including RBF–Differential Evolution and ANN–Genetic Algorithm frameworks. This highlights the practical advantage of the proposed architecture, which achieves reliable forecasting while maintaining computational simplicity appropriate for on-site integration and real-time decision support.

Figure 3 and Figure 4 show the dynamics of changes in the model’s performance at each training epoch. The most pronounced decline in the error occurs during the first 50 iterations. This was due to the relatively faster fitting of the width of the Gaussian curve, after which only the process of fitting the height took longer. Fluctuations or a sharp increase in losses are caused by a shift of the zero-level curve. Its movement is directed toward the points that are poorly approximated by the neurons due to their relatively large distance from the neuron centers. The shift of the curve allows for achieving higher possible accuracy; however, it instantly increases the losses at the current iteration, as it affects the entire data range.

3.4. Model Performance and Comparative Evaluation

Figure 5 and Figure 6 present the approximation results for the two modeled relationships. Figure 5 illustrates the fitted curves for the temperature–methane dataset, showing the dependence between process temperature and daily methane production. Figure 6 presents the corresponding results for the methane-fraction model, i.e., the relationship between methane share in biogas and total biogas flow.

Figure 5 and Figure 6 illustrate the fitted curves for both models alongside the measured data. In both cases, the RBF-NN successfully reproduced the smooth functional trends, with local deviations remaining within acceptable limits. The temperature model showed tighter alignment around inflection regions, whereas the methane-fraction model exhibited slightly higher sensitivity to point-wise variability, likely due to wider fluctuations in the measured methane share.

Next, the resulting approximation curves (Figure 5 and Figure 6) are shown for different training epochs (from top to bottom: initialization, 10, 50, 1000, 2000, 5000 epochs). The left column ((a), (c), (e), (g), (i), (k)) displays only the data and the total fitted curve, whereas the right column ((b), (d), (f), (h), (j), (l)) additionally includes the output of individual neurons, allowing visualization of how neuron interactions contribute to the final approximation. In the neuron-level plots ((b), (d), (f), (h), (j), (l)), the pink lines represent the output of individual radial basis neurons, while the yellow line corresponds to the aggregated baseline (zero-level correction) applied during training. These elements illustrate how individual neuron responses combine to form the final approximation curve.

In general, the approximation yielded quite good results: despite the uneven location of the dataset and the implicit functional relationship, the curve smoothly reproduces the change in the output parameter from the input. The absolute losses decreased from the initial 3880 m³ CH₄·day⁻¹ to 278 m³ CH₄·day⁻¹ for the temperature-based approximation, and from 2527 m³ CH₄·day⁻¹ to 183 m³ CH₄·day⁻¹ for the fraction-based approximation.

Further evidence of ANN versatility in biogas optimization is provided by Gueguim Kana et al., who applied an ANN–Genetic Algorithm hybrid to optimize co-digestion of sawdust, cow dung, and crop residues, achieving an 8.6% improvement in biogas yield. Their 5–2–1 network topology effectively captured nonlinear substrate interactions, consistent with the RBF-NN configuration adopted in the current study [32]. Similarly, Şenol et al. extended ANN applications to regional biogas forecasting in Türkiye, integrating socioeconomic indicators and GIS analysis to estimate a biogas potential of 4964 GWh by 2035 [33]. These findings, consistent with our RBF-based results, highlight the adaptability of neural modeling for both process-level optimization and large-scale energy resource prediction.

Additional advances further illustrate the applicability of ANNs in biogas-related energy systems. Mehrabian and Mahmoudimehr employed ANN modeling to optimize the steam-to-fuel ratio in a biogas-fueled solid oxide fuel cell (SOFC), revealing a strong dependence of the optimal ratio on methane content and temperature [34]. Their ANN-derived correlation simplified process design while maintaining high predictive accuracy. Complementarily, Nair et al. used a feed-forward ANN to predict methane yield from anaerobic bioreactors treating municipal solid waste, achieving 60–70% CH₄ under optimized pH and volatile fatty acid (VFA) conditions [35]. Together, these studies validate the broad applicability of ANN models—from detailed process optimization to system-level energy prediction—consistent with the robust RBF-NN performance demonstrated here.

Similarly, Sakiewicz et al. modeled biogas generation in a full-scale wastewater treatment plant using ANN structures, demonstrating that both RBF and MLP networks effectively captured nonlinear effects of operational and wastewater quality parameters on gas yield [31]. Seo et al. compared recurrent neural networks with the ADM1 process-based model for dry anaerobic digestion of food waste, confirming that data-driven black-box models can outperform mechanistic models under dynamic operating conditions [36]. These findings further substantiate the potential of RBF-NN for robust prediction and real-time control of biogas production processes.

Finally, recent research underscores the expanding role of intelligent modeling in optimizing biogas utilization across biological and thermochemical domains. Nweke et al. [37] showed that ANN and ANFIS models accurately simulated the effects of thermo-chemical pretreatment parameters (temperature, NaOH concentration, time) on biogas yield from plantain peel waste, achieving R² > 0.98 and RMSE < 0.01. In parallel, Girmay et al. combined ANN prediction with experimental testing to optimize biogas–diesel dual-fuel combustion, obtaining R² > 0.96 for brake power and efficiency [38]. Collectively, these studies confirm that hybrid ANN-based modeling enables reliable prediction and control across both anaerobic digestion and energy conversion systems, reinforcing the high adaptability and precision of the RBF-NN model developed in this work.

3.5. Broader Implications and Applications

Future research should focus on expanding the RBF-NN framework to include adaptive learning mechanisms and multi-sensor data integration. The integration of real-time measurements of O₂, CO₂, and CH₄ concentrations with RBF-based predictive control could enable autonomous adjustment of aeration and mixing in biogas plants. Furthermore, coupling RBF-NN with fuzzy inference or reinforcement learning algorithms may improve model interpretability and long-term stability under variable feedstock conditions. Experimental validation of such hybrid intelligent controllers at the Przybroda facility is planned, aiming to establish a fully data-driven system for continuous monitoring and optimization of biogas production efficiency and environmental performance.

The developed model is well suited for approximating complex dependencies with implicit functional relationships between input and output parameters. This includes the prediction of biomethane yield. The use of the Gaussian curve to generate the resulting curve allows a sufficient degree of freedom to choose the desired shape (height, width, position and zero level), it is smooth, which is typical for inertial transients, and the superposition of curves (Figure 5h–l) allows the formation of complex shapes with steeper or slower gradients. Nevertheless, a number of challenges need to be overcome to actually implement such a model:

• Optimization of the learning process. Depending on the input and output data dimensions, some controlled parameters learn more slowly than others, which can lead to slower learning due to uneven parameter changes or even overlearning. It is necessary to develop an algorithm that would allow fitting the parameters evenly to stabilize learning.
• Optimizing the number of neurons. A large number of neurons leads to an increase in computation without obtaining equivalent utility, while a lack of neurons worsens the accuracy or makes the approximation impossible, so it is necessary to develop a methodology for optimal neuron choice to strike a balance between accuracy and computation. In this case, algorithms that modify the number of neurons directly during the training process are quite popular: adding neurons to a place with a consistently high error and/or removing a ‘dead’ neuron.
• Expanding the number of dimensions. This program is designed for approximation in the 2D space. Accordingly, the code itself needs to be improved for an arbitrary number of input and output parameters for multi-criteria approximation.

The solution of the above problems is quite realistic today, thus providing opportunities for further research and improvement.

3.6. Comparison with Recent Modeling Approaches in the Literature

The novelty of this study lies in the development of a simplified RBF-NN model that accurately predicts methane production using only two single-variable operational datasets from a full-scale biogas plant, supported by a custom zero-level correction algorithm that stabilizes training under limited data conditions. Unlike existing ANN-based approaches requiring multiple inputs and extensive preprocessing, the proposed model achieves comparable accuracy with significantly lower data and computational requirements.

Recent developments in machine-learning-based modeling of biogas and biomethane systems demonstrate a rapid shift toward data-driven prediction tools, including ANN, hybrid neural systems, ensemble learning and optimization-supported models. Compared with these approaches, the RBF-NN framework developed in the present study exhibits competitive accuracy while maintaining a significantly simpler structure and lower data requirements.

Cruz et al. (2022) [39] reviewed machine-learning applications in anaerobic digestion and highlighted that many high-performance models—such as deep learning, ANFIS or ensemble neural networks—require large datasets, extensive hyperparameter tuning, and high computational resources. They also emphasized the chronic problem of process instability in AD and the need for models capable of generalizing from incomplete or noisy operational data. In contrast, the RBF-NN model proposed in this study effectively learned functional relationships from only 10 data points per dataset while achieving low RMSE values (52 and 27 m³·day⁻¹). This aligns with their observation that lightweight architectures can be advantageous in real-time AD environments, where data availability is often limited.

Other studies have applied neural networks in more complex energy-conversion contexts. Pallicheruvu and Gnanasekaran (2025) [40] used ANN and machine-learning classifiers to predict engine performance in dual-fuel systems powered by biogas and biodiesel. Their optimized ANN architectures (e.g., 3–12–8 topology) achieved R ≈ 0.97–0.98 but required high-resolution sensor data and multi-parameter training. Compared with such models, our RBF-NN approach relies on a minimal input space (single-input functional relationships), making it more practical for biogas plants with limited measurement infrastructure.

Across the reviewed literature, hybrid models—such as GA-optimized RBF networks, RBF-ANN combinations, or ANFIS systems—often achieve slightly higher predictive accuracy but at the cost of computational complexity, parameter instability, or the need for extensive experimental datasets. The current model, based on manually parameterized Gaussian neurons and zero-level correction, achieved high accuracy without hybrid optimization techniques, demonstrating that robust forecasting can be obtained through careful architectural selection and preprocessing rather than computationally intensive enhancements.

Overall, the comparison indicates that the RBF-NN model developed in this work provides a strong balance between predictive capability, interpretability, and operational feasibility. It performs on par with more complex ANN-based systems reported in the recent literature while requiring substantially less data, making it well suited for practical biogas plant monitoring and control, especially in facilities with constrained sensor availability and limited historical datasets.

4. Conclusions

This study demonstrated that Radial Basis Function Neural Networks (RBF-NN) represent an effective and computationally efficient tool for approximating key operational relationships in biogas production systems. Using real operational data from the Przybroda biogas plant, two predictive models were developed: (i) the relationship between process temperature and methane output, and (ii) the relationship between methane fraction and total biogas flow. Despite the limited size of the datasets, both RBF-NN architectures achieved high approximation accuracy, confirming their suitability for modeling monotonic or unimodal dependencies commonly observed in anaerobic digestion.

The results show that compact RBF-NN structures, when properly tuned, can replicate nonlinear process behavior with low prediction error, making them particularly attractive for full-scale facilities where datasets are often incomplete or sparse. The models developed in this work provide a methodological foundation for data-driven monitoring of anaerobic digestion and may serve as a baseline for more advanced forecasting and control strategies in biogas plants. The developed models are intended for plant-specific approximation and operational support rather than for universal prediction across heterogeneous biogas installations.

Future research should focus on extending the RBF-NN framework to multi-sensor integration and adaptive learning algorithms, enabling real-time predictive control and improved process stability under variable feedstock and operating conditions. The planned implementation of such intelligent controllers at the Przybroda facility will support the development of a fully data-driven biogas production system.