A Review of Quantitative Characterization of Phase Interface Dynamics and Optimization of Heat Transfer Modeling in Direct Contact Heat Transfer

Abstract

Direct contact heat transfer as an efficient heat recovery method. It is used in the fields of waste heat recovery, nuclear engineering, desalination, and metallurgy. This study examined two key issues of the direct contact heat transfer process: difficulty in accurately characterizing the dynamics of the flow field–phase interface; and difficulty in coupling the complex multiphysics fields involved in direct contact heat transfer. This paper systematically reviews the spatio-temporal evolution characteristics and quantitative characterization methods of bubble dynamics in direct contact heat transfer processes, with an in-depth discussion on theoretical modeling approaches and experimental validation strategies for coupled heat and mass transfer mechanisms within multiphase flow systems. An interesting phenomenon was found in this study. Many scholars have focused their research on optimizing the working conditions and structure of direct contact heat transfer in order to improve heat transfer efficiency. The non-equilibrium phenomenon between the two phases of direct contact heat transfer has not been thoroughly studied. The non-equilibrium phase transition model can deepen the understanding of the microscopic mechanism of interfacial energy exchange and phase transition dynamics in direct contact heat transfer by revealing the transient characteristics and non-equilibrium effects of heat and mass transfer at dynamic interfaces. Based on the findings above, three key directions are proposed to guide future research to inform the exploration of direct contact heat transfer mechanisms in future work: 1 dynamic analysis of multi-scale spatio-temporal coupling mechanisms, 2 accurate quantification of unsteady interfacial heat transfer processes, and 3 synergistic integration of intelligent optimization algorithms with experimental datasets.

1. Introduction

Direct contact heat transfer (DCHT) represents an efficient thermal energy transfer mechanism wherein thermal exchange is accomplished through direct interfacial contact between cold and hot fluid phases. It is distinguished by its low operational costs, simplified maintenance requirements, and exceptional heat exchange capability under limited temperature differential conditions [1,2,3,4]. DCHT is widely used in industries such as heat dissipation of microelectromechanical system equipment [5], industrial waste heat recovery [2], and nuclear safety engineering [6].

Direct contact heat transfer (DCHT) technologies are systematically classified into three different types based on different interfacial conditioning strategies: 1 spray-type DCHT [7,8], 2 film-type DCHT [9,10], and 3 bubble-type DCHT [11,12]. Figure 1 illustrates these three different types of heat exchange mechanisms. Film-type systems are based on the formation of a continuous liquid film along the pipe wall by fluid flow to achieve efficient heat exchange with counter current airflow. Film-type systems are mainly used in desalination projects [13].

Spray-type systems perform heat exchange by atomizing a liquid into a gaseous medium, where the thermal efficiency is determined by the density of the interfacial area in a multiphase flow state. Spray-type systems are mainly used in industrial cooling towers.

Bubble-type systems achieve heat and mass transfer by dispersion of the gas phase within the fluid. This model is widely used in gas–liquid reaction enhancement scenarios. In the bubble-type direct contact heat transfer process, there is an idiosyncratic mode—gas–liquid phase change heat transfer. This mode of heat transfer is illustrated schematically in Figure 1d. This heat transfer mode is divided into two phases: the latent heat phase where the dispersed phase draws heat from the continuous phase and undergoes a phase change, and the sensible phase, which is direct contact heat transfer between the gas and liquid phases.

The above discussion of the three different types of direct contact heat transfer leads to the following conclusion: the phase interface of the direct contact process between the cold and hot phases is an important research indicator for exploring the effectiveness of direct contact heat transfer. The larger the phase contact surface is, the better is the heat transfer effect [16]. The spatial distribution of bubbles and the gas content of bubbles affect the effectiveness of heat and mass transfer [17,18].

At multiphase flow interfaces, phase interfaces are deformed by turbulence and exchange heat and mass [19], unlike fluid–solid coupling using the Lagrangian–Eulerian approach to the fluid–solid interface [20]. During fluid flow, the inhomogeneous distribution between the gas–liquid mixing phases and the discrete phases shows complex patterns of variation with the change of flow properties, leading to difficulty in the accurate characterization of the phase interface parameters [21]. Phase interfaces drive the transport of heat and mass. For example, during direct contact heat transfer, the phase transformation of the dispersed phase changes the local flow velocity, which in turn changes the temperature gradient within the flow field, and the local flow field affects the shape of the phase interface. Therefore, the direct contact heat transfer process is an interaction of multiple physical processes (flow, heat transfer, phase change) in time and space, and the interactions of these processes need to be considered simultaneously. The dynamics of the phase interface in direct contact heat transfer change dramatically, such as droplet breakup and merging, and bubble formation and detachment, all of which require high-resolution interface tracking methods.

However, multiphase flow systems have complex flow field characteristics. The mechanism of heat transfer in direct contact is still unclear. Current research is focused on obtaining high heat transfer efficiency. The heat transfer process at the phase interface during phase change heat transfer has been neglected. Obtaining spatio-temporal evolution data of bubble populations in real time and accurate extraction of flow field characteristic data is a great challenge.

Direct contact heat transfer currently faces two critical problems that need to be solved: the difficulty of accurately characterizing the dynamics of the flow field–phase interface, and the difficulty in coupling complex multi-physical fields. To address these two problems, this study reviews the acquisition and quantitative assessment of the spatial distribution of bubbles, the construction of theoretical models, and the optimization path of numerical simulations of the heat transfer process. A suggestion for future research is provided to address the difficulty of coupling multi-physical fields—the use of the non-equilibrium phase transition model as a theoretical tool to study the mechanism of the direct contact heat transfer process. This study discusses the optimization and mechanism study of direct contact heat transfer processes to promote the scale application of DCHT technology in key fields such as the energy and chemical industries.

2. Measurement and Quantification of Multiphase Mixing in Direct Contact Heat Transfer Processes

In multiphase fluid systems, the heat transfer process becomes complex and highly nonlinear due to the interaction of gas and liquid phases. This section reviews the measurement methods and evaluation techniques for the uniformity of bubble distribution for direct contact heat transfer in multiphase mixing systems. Image processing and mathematical modeling-based techniques for monitoring the temperature distribution of multiphase fluids and evaluating thermal performance are highlighted. Key factors such as the interfacial area of bubbles, flow characteristics, contact time, and mixing intensity affect heat and mass transfer efficiency [22,23]. During heat transfer, bubbles with small diameters (D ≤ 1 mm) have a larger specific surface area. This will increase the gas–liquid contact area and thus improve the heat transfer efficiency. Small bubbles in the fluid are easily broken by the shear action of the flow field, resulting in a high frequency of interfacial renewal, which effectively breaks the local temperature saturation of the flow field. In terms of the spatial distribution of bubbles, bubbles can reflect the distribution of the dispersed phase in the continuous phase. Uniformly distributed bubbles can effectively avoid the phenomenon of local overheating or mass transfer saturation in the flow field. Therefore, many scholars estimate the heat transfer by studying the kinetic behavior of bubbles in the flow field.

2.1. The Role of Bubbles in the Study of Direct Contact Heat Transfer Processes

In direct contact heat transfer, convective heat transfer between multiphase flows is accompanied by the formation and bursting of bubbles. The bubbles are caused by volume changes due to temperature differences within the two fluids. Heat is transferred directly through the phase interface into the other phase. The size of the contact surface between the phases determines the efficiency of heat transfer. Therefore, the size and spatial distribution of bubbles can be used to characterize the effectiveness of direct contact heat transfer during gas–liquid phase change heat transfer in direct contact.

Liao et al. [24] numerically simulated the thermal phase transitions in condensation and evaporation by means of a unified interfacial heat transfer model. This was used to calculate the heat transfer between bubbles and droplets through detailed validation and evaluation. The results show that the model proposed by Liao is more effective in predicting the interphase heat transfer coefficients, especially under turbulent conditions involving steady bubble growth and bubble condensation, showing significant advantages. Georgoulas et al. [25] studied the process of bubble growth and detachment in saturated pool boiling by using a modified VOF (Volume of Fluid) method. The quantitative effects of different control parameters (e.g., wall superheat, gravity level, etc.) on the detachment characteristics of isolated bubbles were analyzed, and more than 100 high-resolution transient numerical simulations were performed. The authors used these simulations to reveal the changing patterns of bubble detachment diameter and time, and pointed out the order of importance of each parameter. They suggest that accurately modeling the nuclear boiling process requires a focus on measuring the liquid-phase thermal boundary layer thickness.

In addition to the simulation of the dynamical behavior of bubbles, obtaining accurate characterization of bubble surface morphology and spatial distribution has also been the research goal of many researchers. This includes the extraction of morphological features and the quantification of the spatial distribution of bubbles. The most critical problem to be solved here is the accurate splitting of overlapping bubbles.

2.2. Phase Change Bubble Cluster Capture and Segmentation

The regulation mechanism of heat transfer efficiency is closely related to bubble dynamics interactions. To accurately quantify the dynamic features of bubbles (including nucleation mechanism, growth mode, aggregation behavior, and rupture process), a reliable image segmentation method needs to be established. Currently, there are two main methodologies for bubble segmentation based on image processing: numerical analysis based on physical field modeling and neural network based on feature learning.

In traditional numerical methods, bubble segmentation is achieved by a combination of several image processing techniques, mainly including watershed algorithms, shadow detection, and color space transformation methods. Segmentation algorithms are used to segment the background from the image based on the difference in pixel values in the image. The problem of overlapping bubbles can be solved by accurately separating the bubbles from the background by different pixel values in the RGB and HSV color spaces. Figure 2 illustrates the process of implementing the mechanism of the mathematical morphological watershed algorithm in the dynamic segmentation of bubbles. The main principle is that the grayscale image is mapped as a three-dimensional topographic surface, in which the high grayscale value region corresponds to the peak ridge of the topography (morphology boundary), and the low grayscale value region characterizes the inner basin of the bubble (the main body of the phase domain). The algorithm realizes the separation of overlapping bubbles by simulating the diffusion of water flow from the local minima (bubble core) to the gradient of the neighboring domains, and constructing a watershed line with topological preservation. According to the principle of the watershed algorithm, Li et al. [26] split the overlapping bubbles into individual bubbles using the proposed watershed splitting function, and thus obtained the area and perimeter of the bubbles. Unlike Li’s work. Sun [27] used the watershed algorithm to split the bubbles in the field-of-view window of the heat exchanger when exploring the direct contact phase change heat transfer process. The uniformity of the distribution of the segmented bubbles inside the heat exchanger is quantified by segmenting the bubbles. The work of Li and Sun shows that the watershed algorithm plays an important role in the splitting of bubbles. However, the watershed algorithm is applicable for gas contents ranging from 1% to 40% in the heat exchanger. Conventional numerical methods have limitations on the diameter and distribution of bubbles or particles [28,29].

The segmentation principle of the watershed algorithm relies on the gray gradient change in the image, so in the case of too much background noise the watershed algorithm cannot effectively segment the image. Therefore, the image needs to be processed for noise reduction before processing with the watershed algorithm. The general process of image noise reduction includes bubble image background removal, image edge enhancement, and image void filling. As shown in Figure 3, Deng [31], Lau [30], and others have used the above image-filtering enhancement techniques in bubble-dense and bubble-sparse images, respectively.

Traditional numerical methods for processing images take a long time in the filtering and thresholding stage. The optimal image threshold is affected by the external environment, such as shooting environment and image background [32,33]. In the process of bubble treatment, especially the process involving gas–liquid phase change, bubbles undergo dynamic behaviors such as deformation, fragmentation, and merging during flow, with real-time changes in shape and size. The rigid assumptions of traditional image processing algorithms (fixed threshold, morphological a priori) make it difficult to cope with dynamic, low image quality, and complex flow field mixing experimental scenarios. With the continuous iteration and updating of image processing techniques, splitting bubbles using neural networks has become the first choice of researchers. Neural networks are used to identify and extract bubbles in complex flow fields through dynamic feature learning, physical constraint embedding, and multimodal fusion. The drawbacks of traditional processing are effectively avoided. Convolutional neural networks have become an important tool for bubble recognition by virtue of their short processing time for irregular bubbles [34]. In addition to the processing of bubbles, neural networks have been applied to analyze the evolution of two-phase flows [35,36,37,38,39]. Igor et al. [35] developed a new technique based on artificial neural networks for the measurement of experimental data in turbulent and bubble flows. A convolutional neural network (CNN) was used as the basic architecture. A multilayer perceptron (MLP) and an autoencoder of the CNN were selected to remove image noise [35], as shown in Figure 4.

Deep learning models are applied to state detection of heat transfer processes by separating bubbles from complex backgrounds. The advantages of neural networks in direct contact heat transfer state detection are their nonlinear modeling capability and physical constraint compatibility, such as the boiling of bubbles in a pool during the film formation process. Gustavo et al. [40] used Bayesian optimization combined with a convolutional neural network to successfully detect the transition from nucleation to film boiling during pool boiling. Experimental results show that Gustavo’s work outperforms conventional temperature measurement sensors (thermocouples) for monitoring the heat transfer state of pool boiling. Sub-second non-invasive film boiling detection can be achieved. Seyed et al. [41] developed and trained a convolutional neural network model using the public boiling dataset (DS1). The main process is shown in Figure 5. CNN and transfer learning (TL) models were used to monitor the critical heat flux. The models were validated using a new dataset (DS2). By comparing the training time and recognition accuracy of the two models, it was found that the TL model outperforms the CNN model for monitoring critical heat flux. Seyed believes that the application of the TL model will be effective in reducing the number of hazardous accidents in equipment due to reaching the critical heat flux. In 2023, Malakhov et al. [42] used a neural network to monitor the dynamic boiling properties of bubbles in the boiling state. The density of nucleation sites, bubble growth rate, lifetime and departure diameters, waiting time at the moment of bubble departure, and nucleation frequency of boiling bubbles in the range of 42–103 kPa were obtained by the trained Mask R-CNN neural network. Malakhov used the obtained data for simulation of heat transfer using different methods of heat flux distribution and gave the the scope of application.

After the above discussion, it can be seen that different image processing methods have different application scenarios. Traditional numerical methods are used as mechanism studies for heat exchange bubble cluster segmentation. Deep learning methods are used in industry to predict heat transfer action. Sun et al. [27] and Deng et al. [31] utilized image segmentation techniques to segment bubble clusters and to study the heat transfer process of phase change. From these studies, it is shown that the watershed algorithm is considered to be an effective tool for segmenting overlapping bubbles. Appropriate threshold configuration is a key factor in improving the segmentation accuracy of the watershed algorithm. Future research should focus on the optimization of the watershed algorithm using deep learning models. This intelligent fusion paradigm shifts the algorithmic kernel from empirical judgments based on grayscale thresholds to data-driven topology understanding, thereby reducing the algorithm’s dependence on traditional thresholding techniques.

2.3. Quantification and Evaluation of the Spatial Distribution of Bubbles

Direct contact heat transfer is affected by the degree of mixing uniformity of bubbles in space [43]. Uniformly distributed bubbles can effectively promote turbulent mixing of liquids and increase the heat transfer coefficient. In direct contact heat transfer processes, the distribution of bubbles is used to characterize the mixing properties. The time required for bubbles to reach a certain level of mixing in a heat exchanger [44] is considered as a measure of heat transfer performance. Mixed techniques have been investigated including colorimetry, resistive tomography (ERT) [45,46], capacitive tomography (ECT) [47], planar laser-induced fluorescence (PLIF), thermography, electrical conductivity, and pH. In quantifying the mixing process, mathematical methods from mathematical theory are used to calculate the mixing time. Methods such as the Betti number are used to quantify gas–liquid mixing efficiency [48]. The Betti numbers are characterized by the binary image of the acquired mix. The 0th Betti number is used to characterize the homogeneity of mixing, and the 1st Betti number is used to characterize the non-uniformity. However, the method does not take into account the spatial distribution of the bubbles. There are limited applications of the method. Xu et al. proposed research methods such as L2-star discrepancy (CD) and wrap-around L2-star discrepancy (WD) [49], and Moment balance [50]. A comparison of the quantitative methods is shown in

Table 1. Comparison of the advantages and disadvantages of different quantitative indicators for bubbles.

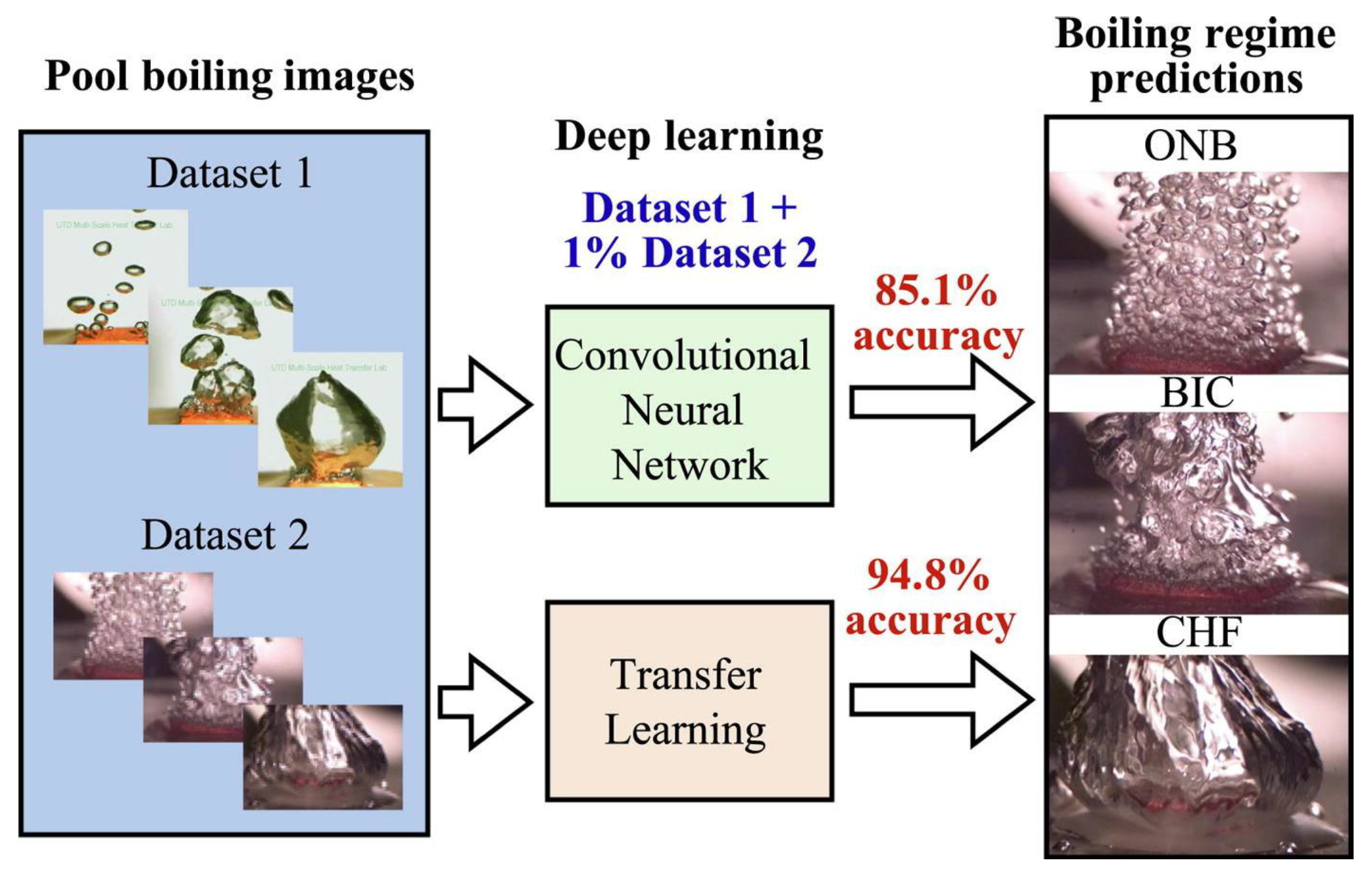
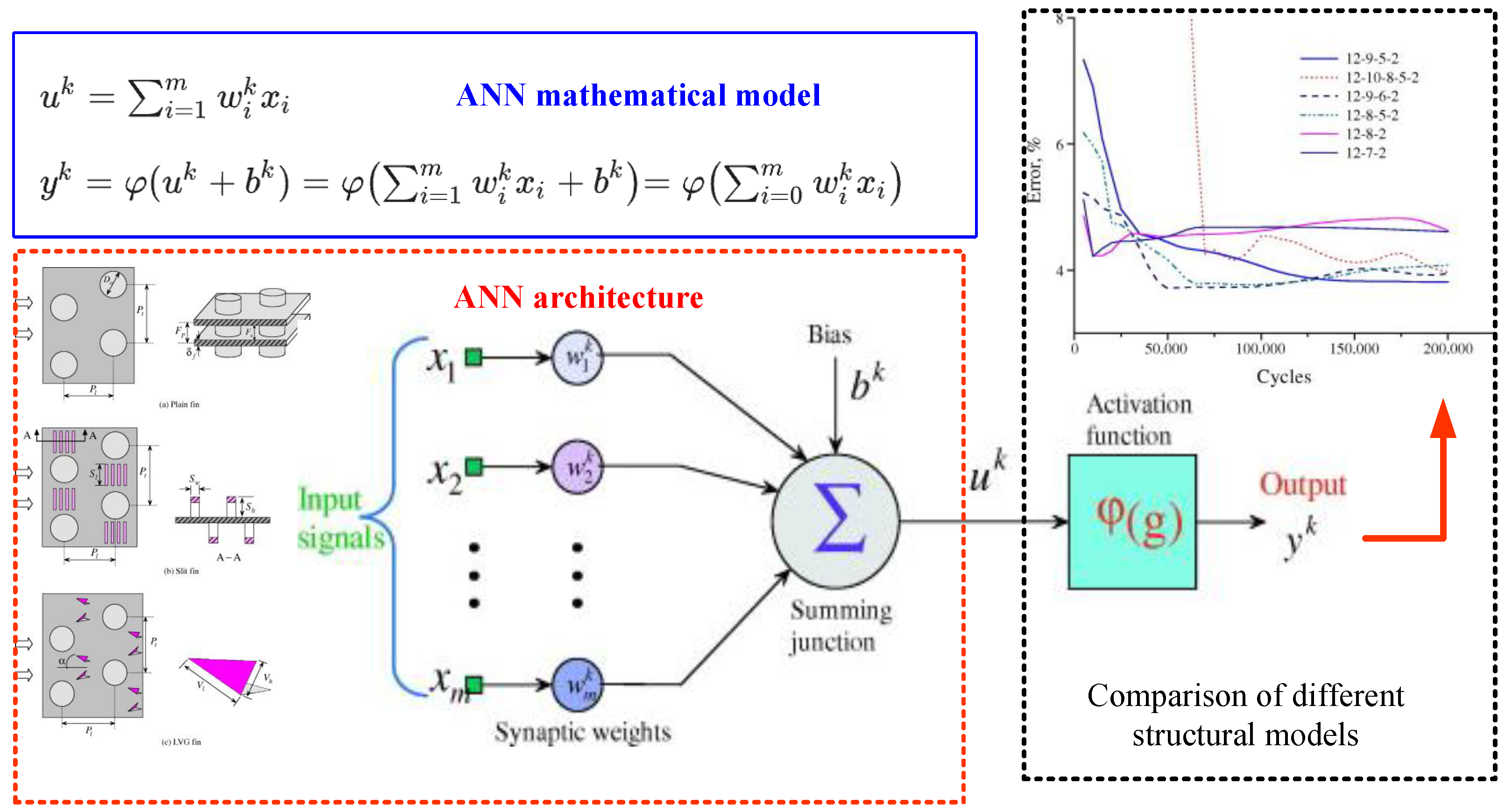
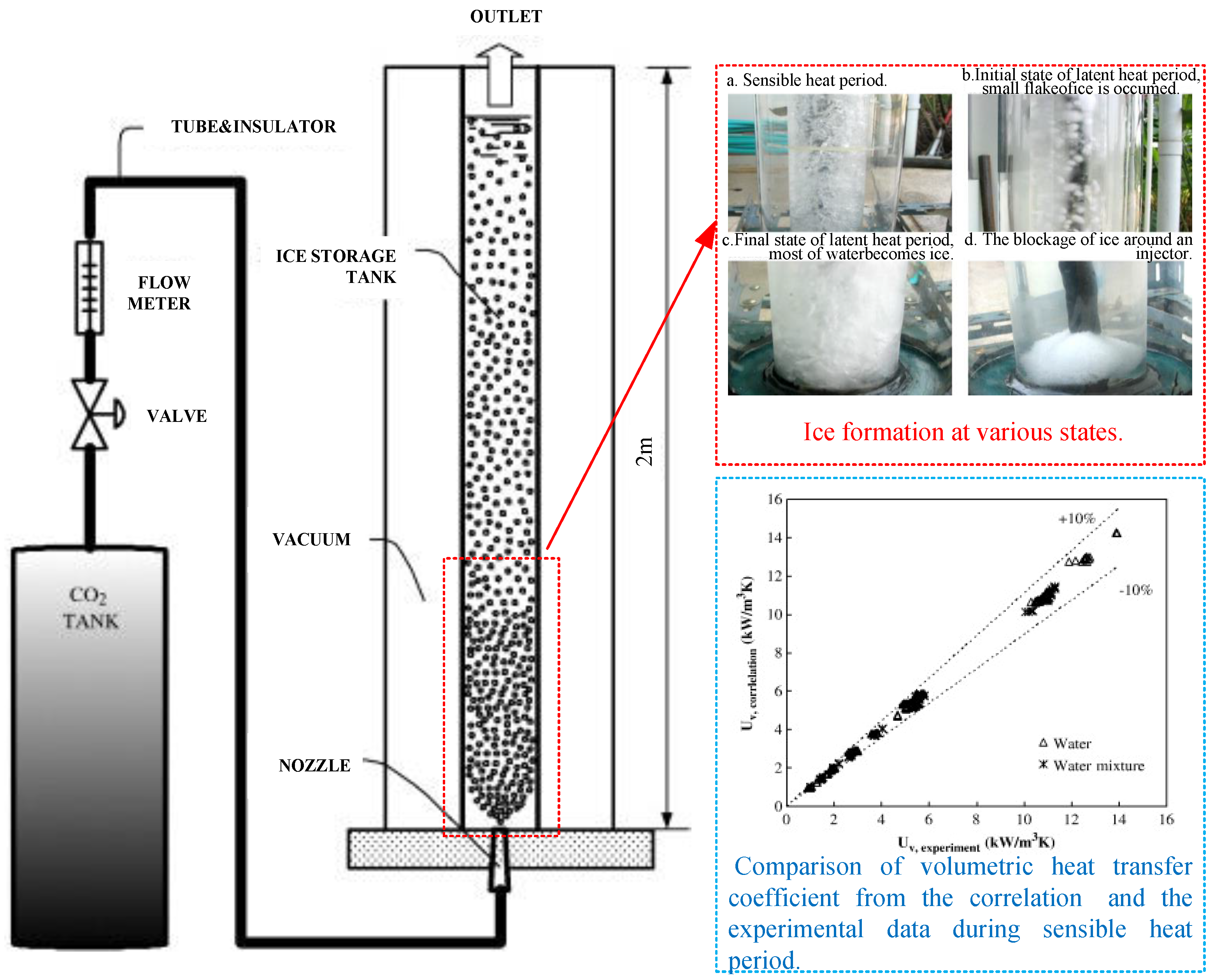
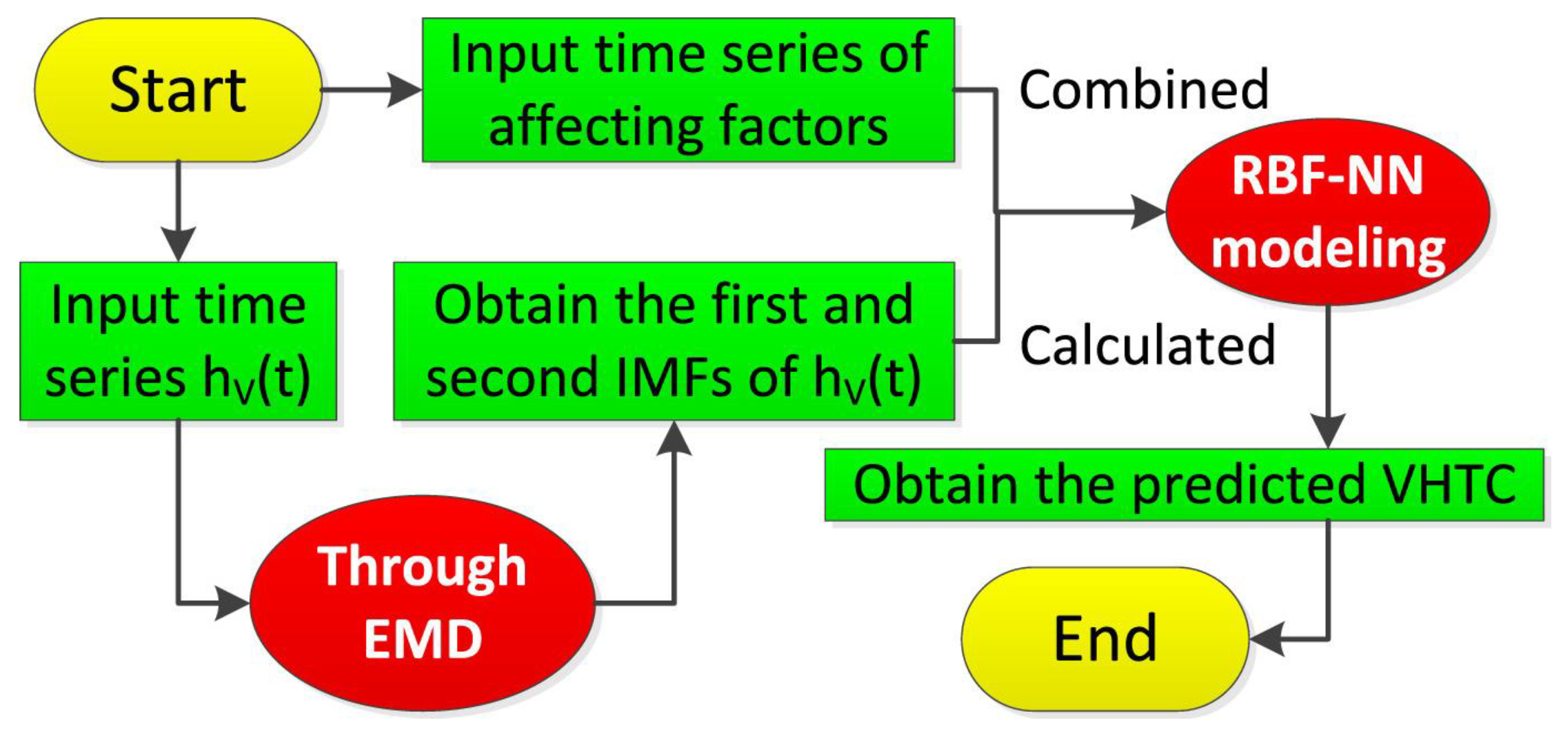
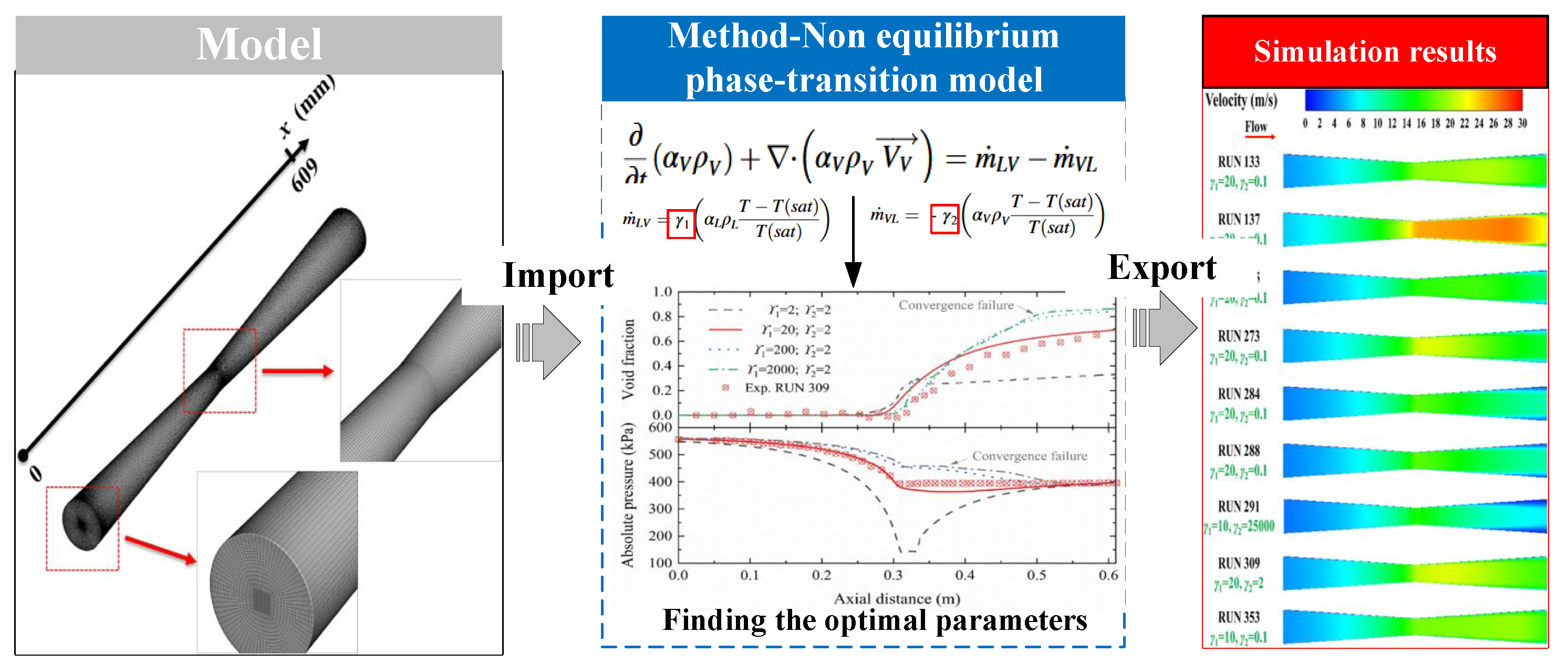
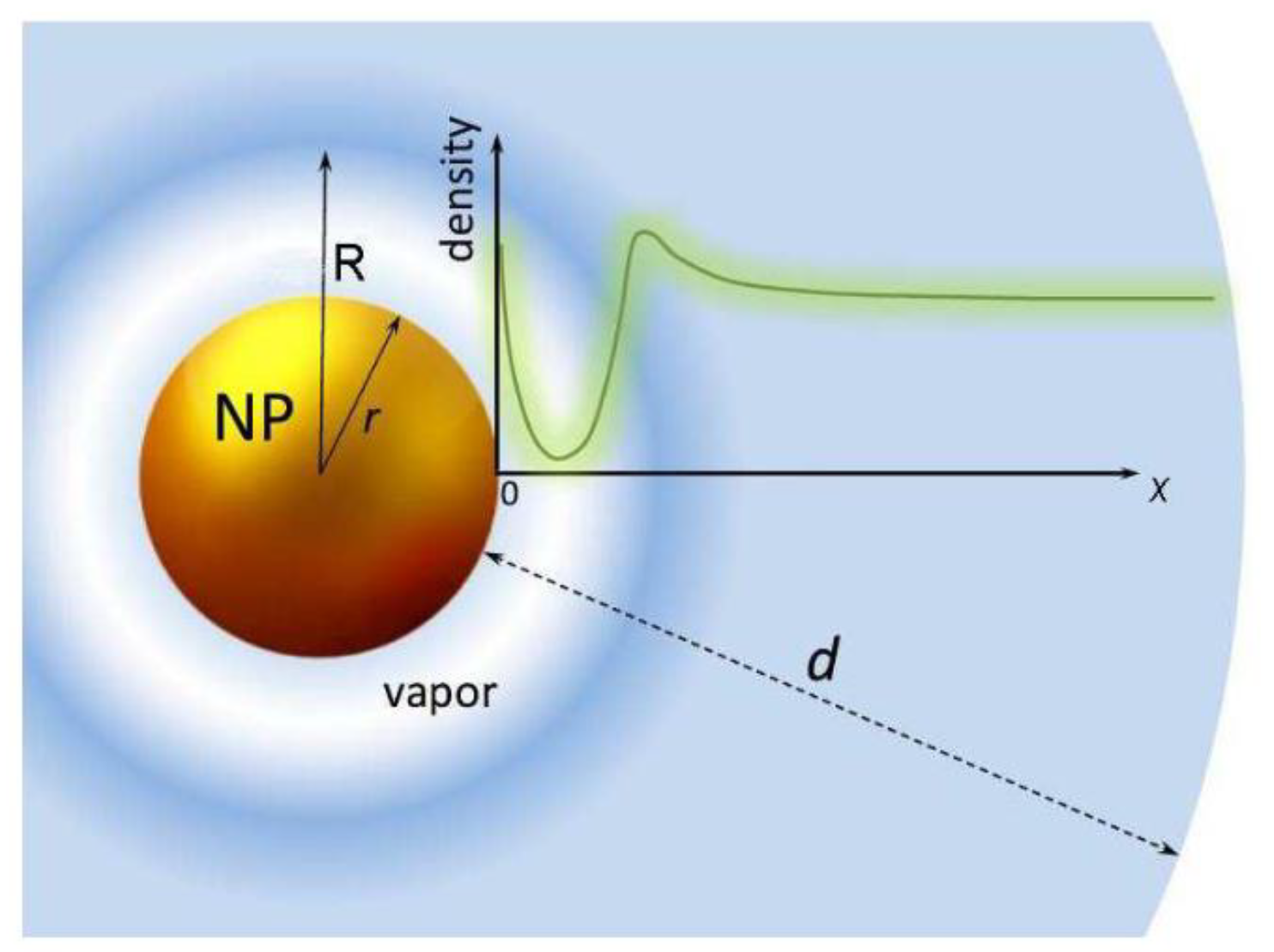
Method	Advantages	Disadvantages
Betti number method [48]	Algebraic topology is based on the flow topology and the Betti number quantitatively portrays the degree of mixing homogeneity of the metallurgical bottom-blown bubble population.	The spatial distribution of the bubbles is not taken into account and is only quantitatively described.
L2-star discrepancy (CD) and wrap-around L2-star discrepancy (WD) [49]	Both CD and WD have the advantages of alignment invariance, rotational invariance (reflection invariance), and uniformity of measurement projection.	Added time complexity for determining the bubble location.
Moment balance [50]	Tilt angles with direction are used to characterize the unbalanced structure due to heterogeneity of mass distribution.	The interplay between localized and global inhomogeneities cannot be more effectively eliminated.
Potential energy quality measure [51]	Used to measure the global distribution of a point set and can tolerate occasional close points or even overlapping points.	The relationship between particles and space is not strictly taken into account.

.

Figure 6 illustrates a novel bubble quantification method, the average distance (AD) method. Sun et al. [27] proposed a novel average distance (AD) method based on uniform distribution theory and established a comprehensive evaluation index by means of a hypercube routing method and image processing technique. In the study, the AD method was used to directly evaluate the mixing uniformity of bubbles in DCHE. The authors analyzed the relationship between transient and overall mixing efficiency on the average volumetric heat transfer coefficient with the help of the AD method in depth. Different from Xu’s study, Sun et alestablished a comprehensive index to evaluate the mixing time. And the synergistic relationship with heat transfer performance was established by the comprehensive index. However, previous studies have investigated the uniformity of bubble distribution in a square area. It is still an interesting challenge to express the uniformity of bubble distribution in a circular region.

Xiao et al. [52] discussed the difference in bubble distribution between rectangular and circular regions, and developed a statistical image processing framework to study the bubble distribution inside a circular region, and Sun et al. [53] proposed a novel method (the AD- Circle method) to characterize the bubble distribution inside a circular region using the framework [53] system. Sun et al. established a standardized reference value of 0.9054 for mixing homogeneity in a circular region. The mixing homogeneity of the bubble population in a circular region was accurately quantified by the AD- Circle method.

Bubble cluster detection techniques and the evaluation of spatial uniformity distribution mainly rely on a variety of mathematical methods and image processing techniques. For bubble segmentation, Mask R-CNN is used to segment the bubbles effectively. The segmentation accuracy can be improved by establishing its own dataset to train the neural network. The uniformity of the spatial distribution of bubbles suggests using the average distance method to calculate the average distance between bubbles. But it should not be limited to the 2D aspect. Scholars’ research focus should be on the uniformity of distribution of bubbles in three-dimensional space.

3. Modeling and Optimization of Direct Contact Heat Transfer Processes

During direct contact heat transfer experiments, the flow field presents obvious complexity and non-intuitive features that cannot be directly visualized and quantified. This limitation makes it difficult for traditional research methods based on experiments to reveal heat transfer mechanisms. In this context, the importance of numerical simulation techniques and optimization algorithms is shown. The quantitative description of the temperature field, and the velocity field and its dynamic evolution is quantitatively described by establishing an accurate mathematical model and performing numerical simulations. The coupling between the flow fields is analyzed in depth to determine the influence of the coupling on the heat transfer performance. This theoretical approach provides an important reference for experiments and shortens the development cycle. Compared with traditional experimental methods, the advantage of numerical simulation technology is that it can visualize the flow field and temperature field in the heat transfer process. It provides strong support for the study of the heat transfer mechanism and engineering optimization.

3.1. Numerical Simulation Study of Heat Transfer Characteristics and Structural Optimization of Direct Contact PCM Heat Exchangers

Numerical simulation software such as ANSYS Fluent 2021 R1 is widely used in the simulation of heat transfer, fluid dynamics, and phase change processes, which can effectively analyze the complex physical phenomena in the heat exchange process. In the process of numerical analysis, in order to save computational resources and improve computational efficiency, the 2D model, which uses relatively fewer computational resources, is selected for simulation calculation. Two-dimensional models have been used to study the melting behavior of phase change materials during direct contact heat transfer. Aina et al. [54] proposed an efficient and accurate numerical method to simulate the melting and solidification cycles of phase change materials. The research results provide a new perspective for understanding the thermophysical behavior of PCM. He et al. [55] analyzed the thermal storage properties of phase change materials in direct contact heat storage systems and their application in experiments and numerical simulations. The key features of their formation channels, and melting and final stages are revealed, and the optimization of fin design to enhance the heat transfer efficiency is proposed. Numerical simulations show that the optimized fins significantly reduce the channel formation time and effectively increase the heat storage rate (approx. 270%). Figure 7 illustrates the scenarios for which the 2D and 3D models are suitable for the study. Two-dimensional models though have the advantage of high efficiency, intuition, and low complexity in studying the heat transfer behavior of the melting process of PCMs [56,57]. However, in the study of heat exchanger structure optimization, other structures that enhance heat transfer, such as fins, cannot be accurately represented in 2D models. Therefore 3D models have been applied in the study of optimization of heat transfer structures [58]. Lewis et al. [59] successfully captured the molten PCM profile by introduced a buoyancy term in the PCM melting simulation study. The experimentally validated PCM model was applied to two Metal Hydride (MH)-PCM designs: ring-type and tube-type. Moreover, the authors optimized the design of the ring model by adjusting the PCM-MH volume-to-sandwich ratio in order to further enhance the heat transfer performance of the PCM. Jaffray et al. [60] investigated the melting process of individual 3D PCM spheres using numerical simulation methods combined with sensitivity analysis and experimental data calibrated with paste zone coefficients and thermal expansion coefficients. In the study, a method for predicting melting in encapsulated PCM-filled beds was presented. By inputting the obtained data on heat transfer versus time into a finite volume model, the melting behavior in beds of different heights was successfully predicted, and its applicability in characterizing PCM material properties, encapsulation shapes, and operating conditions was verified.

3.2. Study of Optimization Algorithms for Direct Contact Heat Transfer Systems

Optimization algorithms are important in engineering applications and have been the focus of researchers to solve complex and practical problems in design. With the continuous iterative updating of computational techniques, optimization algorithms are applied to direct contact heat transfer (DCHT) processes. The main focus is on the optimization of the heat transfer conditions to improve the efficiency of heat transfer.

Genetic algorithms are widely used in the field of heat transfer. The main reason for this is that it is a global search algorithm that is able to find the global optimal solution in complex and multi-peaked optimization problems, whereas heat transfer systems usually involve complex physical phenomena that often lead to nonlinear and multi-peaked problems. Genetic algorithms can also combine multiple algorithms for co-optimization [61,62]. Figure 8 illustrates the optimization of the parameters of Intermediate Boiling Fluid (IBF) using a multi-objective algorithm. In this study, Shahin et al. [63] optimized the direct contact heat transfer of acetone droplets on molten paraffin using a non-dominated sequential genetic (NSGA-II) algorithm. The paraffin curing region, droplet impact on paraffin maximum crater depth, and tolerance and uncertainty in the system parameters were optimized in a multi-objective manner. LINMAP and TOPSIS methods were applied to optimally solve for three parameters. This research fills the gap in the field of optimization of discharge of Intermediate Boiling Fluid (IBF).

Heat transfer efficiency is affected by the structure of the direct contact heat exchanger, in addition to the optimization of working conditions by multi-objective algorithms [64]. The introduction of artificial intelligence neural networks in heat transfer process [65,66,67] is also a very important area. Xie et al. [68] used an artificial neural network (ANN) to establish a heat transfer and flow prediction model for a large-diameter multi-row tube-fin heat exchanger (as shown in Figure 9), correlating the Nussell number and friction coefficients of the three fin structures using experimental and numerical data (Reynolds number 1000–10,000). The prediction error of the model is less than 4% in the training and extended databases (including CFD data), which verifies its ability to generalize to turbulent and laminar flow conditions. Admirably, network weights and bias parameters are provided by the authors. An efficient and accurate heat exchanger performance prediction tool is provided for engineering applications to advance the development of data-driven heat transfer analysis.

3.3. Modeling of Direct Contact Heat Transfer

The modeling of direct contact heat transfer has far-reaching implications for industrial and technological research. In industry, modeling can help to gain a more in-depth understanding of the operation of equipment [69]. It helps to optimize design and improve efficiency. Accurate heat transfer modeling is not only effective in improving the efficiency of energy use, but is also effective in preventing accidents from occurring or spreading. In gas–liquid phase change processes, modeling of the heat transfer process for direct contact membrane distillation can help researchers to better understand the behavior of gas–liquid phase change and to optimize it. Figure 10 illustrates the droplet heat transfer process studied by Park et al. Park et al. [70] investigated the heat transfer process of a single saturated droplet in direct contact during membrane gasification by measuring the heat transfer characteristics and collision kinetics of the droplet with two simultaneous cameras. A mathematical model based on fluid dynamics and heat transfer was subsequently established. The model takes into account several physical parameters including local wetting effects. The model has a high degree of accuracy compared with the work of other authors on modeling [71,72,73].

In gas–liquid direct contact heat transfer scenarios, the traditionally used Nussel number is not suitable for evaluating the heat transfer effect of direct contact because the phase transition process occurs in the non-wall-constrained free-phase interface region. VHTC avoids the dependence of the traditional Nussel number (Nu) on the feature length by defining the heat transfer capacity per unit volume, and is suitable for quantitatively characterizing the heat transfer of the dynamic evolution scenarios of free-phase interfaces. Its main expression is as follows [74]:

$$U_v={\displaystyle \frac{Q}{V\times \Delta T}}$$

(1)

where Q is the amount of heat transfer, V is the volume of the continuous phase, and $\Delta T$ is the temperature difference between the two phase flows.

$$Q={\dot{m}}_c{C}_{p,c}\left(T_{\mathrm{do}}-T_{\mathrm{di}}\right)$$

(2)

$$\Delta T=\left(T_c-T_{\mathrm{di}}\right)$$

(3)

where ${\dot{m}}_c$ is the discrete-phase mass flow rate, $T_{\mathrm{do}}$ is the discrete-phase outlet temperature, $T_{\mathrm{di}}$ is the discrete-phase inlet temperature, and $T_{\mathrm{c}}$ is the temperature of the continuous phase. In the study of mixed gas–liquid heat transfer, the above Q and $\Delta T$ can be solved by Equations (2) and (3). However, the above method of solving the volumetric heat transfer coefficient is only applicable in the case where the continuous phase is not flowing. Figure 11 illustrates the Thongwik et al. study of low-temperature carbon dioxide mixed with water direct contact heat transfer experiments [74].

In the study of direct contact heat transfer processes, both continuous and dispersed phases are flowing. The effect of heat transfer in the heat transfer process needs to be described more accurately. The logarithmic mean temperature difference [65,75,76] was proposed.

$$\Delta T_{\mathrm{lm}}={\displaystyle \frac{(T_{\mathrm{ci}}-T_{\mathrm{do}})-(T_{\mathrm{co}}-T_{\mathrm{di}})}{ln\left(\frac{T_{\mathrm{ci}}-T_{\mathrm{do}}}{T_{\mathrm{co}}-T_{\mathrm{di}}}\right)}}$$

(4)

The mentioned heat transfer coefficients for continuous phase and discrete phase flow cases are obtained by combining Equations (1), (2) and (4):

$$U_v={\displaystyle \frac{Q}{V\times \Delta T_{\mathrm{lm}}}}={\displaystyle \frac{{\dot{m}}_c{C}_{p,c}(T_{\mathrm{do}}-T_{\mathrm{di}})·ln\left(\frac{T_{\mathrm{ci}}-T_{\mathrm{do}}}{T_{\mathrm{co}}-T_{\mathrm{di}}}\right)}{V·\left[(T_{\mathrm{ci}}-T_{\mathrm{do}})-(T_{\mathrm{co}}-T_{\mathrm{di}})\right]}}$$

(5)

The volumetric heat transfer coefficient is an important design parameter in the optimization of the design of direct contact heat exchangers and responds to the effectiveness of heat transfer. The study of volumetric heat transfer coefficients using neural networks can effectively reveal the nonlinear relationships in complex flow and heat transfer processes. A high-precision prediction model is established to help optimize the design parameters and operating conditions to enhance the heat transfer efficiency and reduce energy consumption at the same time. This approach is applicable to theoretical research and also enables real-time monitoring and control of heat transfer performance in practical engineering applications. Huang et al. [77] combined the time series of VHTC with fluid parameters (flow rate) as a multivariate input to a neural network, and achieved empirical modal decomposition combined with a radial basis function neural network through the adaptive feature of EMD for noise reduction and decomposition of the original time series. A new idea is provided for modeling the fluid heat transfer coefficient. Figure 12 illustrates the establishment process of the RBF-NN model.

Similar to Huang’s modeling process, Zheng et al. [65] combined gray correlation analysis (GRA), variational modal decomposition (VMD), and a support vector machine regression algorithm (LSSVM) to establish a hybrid prediction model for the prediction of VHTC by considering different influencing factors affecting heat transfer performance. A hybrid prediction GRA-VMD-LSSVM model was proposed. The main advantages of the model are the effective distinction between primary and secondary factors and the weakening of nonlinear and unstable data series. Optimized data and extracted detailed information enable faster and better fitting of the prediction model.

Direct contact heat transfer usually involves cross-coupling of multiple physical processes such as flow, mass transfer, and heat transfer. Compared with traditional models based on physical equations (e.g., transitive or empirical relational), the use of deep learning tools can accurately describe this complexity and enable accurate predictions. Deep learning is able to automatically capture complex nonlinear features and excels when dealing with high-dimensional data. It is an important direction for future development. Moreover, in the modeling process, deep learning can combine heterogeneous data from multiple sources (e.g., experimental measurements, CFD simulation results) to construct an integrated model, overcoming the limitation of a single data source. This fusion strategy not only improves the generalization ability of the model, but also predicts the heat transfer performance at different scales.

4. Challenges and Prospects for Direct Contact Heat Transfer Processes

Mathematical modeling of direct contact heat transfer processes faces the core challenge of cross-scale multi-physics field coupling. Traditional interface tracking methods (VOF/Level Set) have large errors in the prediction of heat transfer coefficients. There is a need to explore a model that combines microscopic and macroscopic coupling to study the mechanism of direct contact heat transfer. Deep learning models provide excellent tools and methods for studying cross-scale numerical simulations. Current multi-scale analyses are mainly applied to analyze the properties of biology [78,79] and materials science [80,81]. In direct contact heat transfer, simulations are mainly focused on some macroscopic levels such as evaporation, condensation, and phase transitions. However, the heat transfer and flow problems involved in direct contact heat transfer are essentially multi-scale [82]. The core problem of direct contact heat transfer from the spatio-temporal distribution of the macroscopic gas and liquid phases to the dynamic behavior of the phase interface between the gas and liquid phases, the energy transfer mechanism, and the evolution law of the microstructure is to break through the limitations of the traditional macroscopic scale heat transfer models.

In the macroscopic view of the numerical simulation method, the fluid is considered as a continuum. The essence of numerical simulation is the macroscopic control equations based on the continuum assumption. The governing equations are determined based on the fundamental laws of physics. However, the core of microscopic numerical simulation is to abandon the continuum assumption and directly describe the molecular/particle behavior, following Newtonian trajectories [83].

Table 2. Difference between macro and micro simulation.

Dimension	Macroeconomics	Microstructure
Field descriptions	Continuous fields (velocity field, temperature field, pressure field, volume fraction)	Discrete particles (motion between molecules) [83]
Governing equation	Partial differential equations (Navier–Stokes)	Newton’s equations of motion (MD)/Euler’s equations [83]
Calculate costs	Grid-dependent and less computationally expensive.	High computational costs
Field hypothesis	The motion between molecules is neglected and relies on the intrinsic relationship of the flow field.	Direct representation of molecular collisions, non-equilibrium effects [83]

illustrates the difference between macroscopic and microscopic simulations in the study of direct contact heat transfer processes.

In the study of microscopic phase interfaces, there is no equilibrium of motion at the junction of the two phases (liquid–liquid, gas–liquid and solid–liquid) at the macroscopic and microscopic scales [84]. Niasa et al. [85] investigated the macroscopic relationship between capillary pressure, mean phase pressure, saturation, and specific interfacial area in porous media. It was demonstrated that the conventional capillary pressure–saturation relationship is not valid under kinetic conditions. The authors concluded that non-equilibrium theory is required for the study at the microscopic level. Phase transitions are mainly calculated for interfacial components by mass transfer between different phases [86]. In the study of numerical simulation of phase transitions, the Lee model is an important tool that has been used to simulate phase transition processes. In the Lee model, the governing equations for mass transfer between the gas and liquid phases is [87]:

$${\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_V{\rho }_V\right)+\nabla ·\left({\alpha }_V{\rho }_V\overrightarrow{V_V}\right)={\dot{m}}_{LV}-{\dot{m}}_{VL}$$

(6)

where ${\alpha }_V$, ${\rho }_V$, and $\overrightarrow{V_V}$ are the volume fraction, density, and velocity of the vapor phase, respectively. ${\dot{m}}_{LV}$ and ${\dot{m}}_{VL}$ are the mass transfer rate.

In the traditional Lee model, the pressure formula is a constant. Figure 13 illustrates the development of a simplified non-equilibrium phase change model applied to the prediction of gas phase fractional pressures at different spatial locations by Liu et al. [87], improving the calculation of mass and energy source terms in the conventional Lee model. This is an interesting piece of work, and effectively improves the predictive accuracy of the models developed.

Schiffbauer [88] investigated the nature of bubble nucleation on surfaces at the nanoscale level, as shown in Figure 14. A strong dependence of vapor nucleation on viscous dissipation near the heated inner surface was found. And in the context of dynamic van der Waals theory, it was shown that the Laplace pressure at the interface of a curved surface at the nanoscale level does not significantly affect phase transition and bubble nucleation. It is important to note that non-equilibrium modeling is the driving force behind cross-regime simulations. Transport coefficients such as thermal conductivity, shear viscosity, and other transport coefficients are calculated using non-equilibrium molecular dynamics (NEMD), and these are passed to macroscopic continuous medium models. Cross-scale models can solve complex system problems that cannot be described by single-scale models. Zhang et al. [89] developed a full-condition flow boiling heat transfer one-dimensional model from subcooled water to superheated steam on the water side (tube side) and its cross-scale coupled solution model with a three-dimensional refined CFD model on the sodium side (shell side). The cross-scale model effectively improves the stability and validity of the three-dimensional temperature field solution for the steam generator (OTSG). The advantage of the cross-scale model over macro- and micro-models is the ability to achieve fine numerical simulation in modeling the full-size large flow field. It also saves computational costs. However, model validation and uncertainty quantification in cross-scale simulation are still a great challenge. A number of scholars have studied this issue [90,91]. And scholars are currently focusing on combining uncertainty quantification with neural networks [92]. Future cross-scale research introduces deep learning models to be used to transfer data between models.

The above scholars have made outstanding contributions to the study of non-equilibrium phase interface contact. After the summary discussion method above, it is found that non-equilibrium phase change modeling will become a key tool for the in-depth study of direct contact heat transfer mechanisms. And there is a need to develop the integration of multi-scale modeling and data-driven methods.

5. Conclusions

This study reviews the findings and conclusions of scholars in direct contact heat transfer research, ranging from the theoretical tools for macroscopic study of direct contact heat transfer to the establishment of direct contact heat transfer models. Macroscopic direct contact heat transfer coefficients and non-equilibrium phase contact modeling of microscopic layer changes are discussed. Future research priorities and work on direct contact heat transfer processes are explained. Among the main conclusions are the following:

(1)

Phase change is an important process in the study of direct contact heat transfer. The main research of scholars has focused on studying the quantification of gas–liquid phase change and solid–liquid phase change processes, and optimization of the heat transfer process to suit industrial applications.

(2)

After discussion, we found that academics have focused on the research objective of quantifying and optimizing the direct contact heat transfer process. The in-depth mechanism of direct contact heat transfer has been neglected. The non-equilibrium phase transition model breaks through the simplified assumptions of the traditional equilibrium theory on the phase transition rate, interface behavior, and extreme conditions through dynamic interface tracking, micro-mechanism embedding, and cross-scale coupling. It has the potential to become a theoretical tool for in-depth discussion of the mechanism of direct contact heat transfer.

(3)

In future research work, it is suggested to integrate deep learning with non-equilibrium phase transition models to construct a data-physics dual-driven cross-scale heat transfer model, in order to break through the bottleneck of the traditional methods in dynamic interface capture, multi-field coupling, and extreme operating condition prediction.