Nowcasting Solar Irradiance Components Using a Vision Transformer and Multimodal Data from All-Sky Images and Meteorological Observations
Abstract
1. Introduction
1.1. Solar Irradiance Nowcasting
1.2. Related Works
1.3. The Contributions of This Study
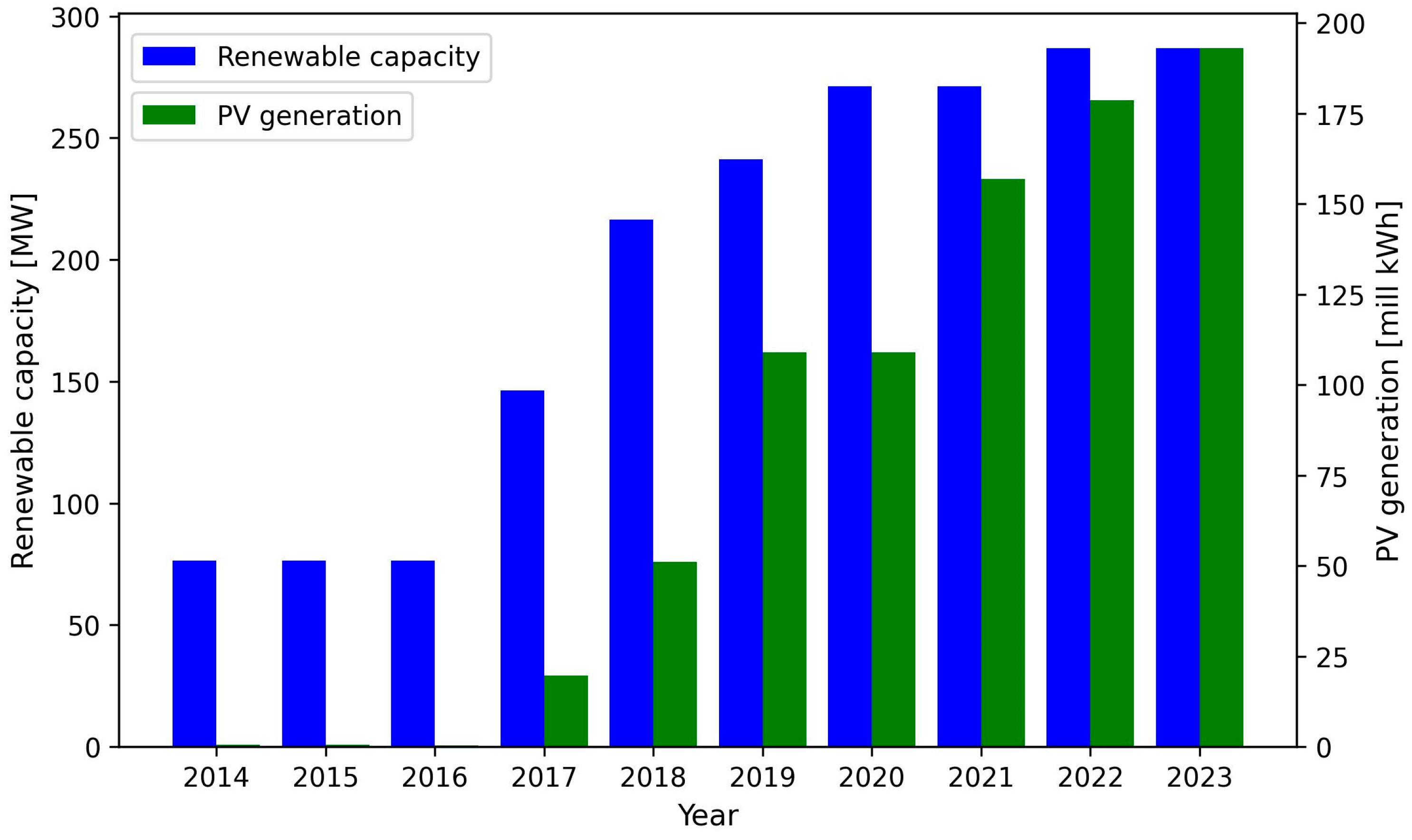
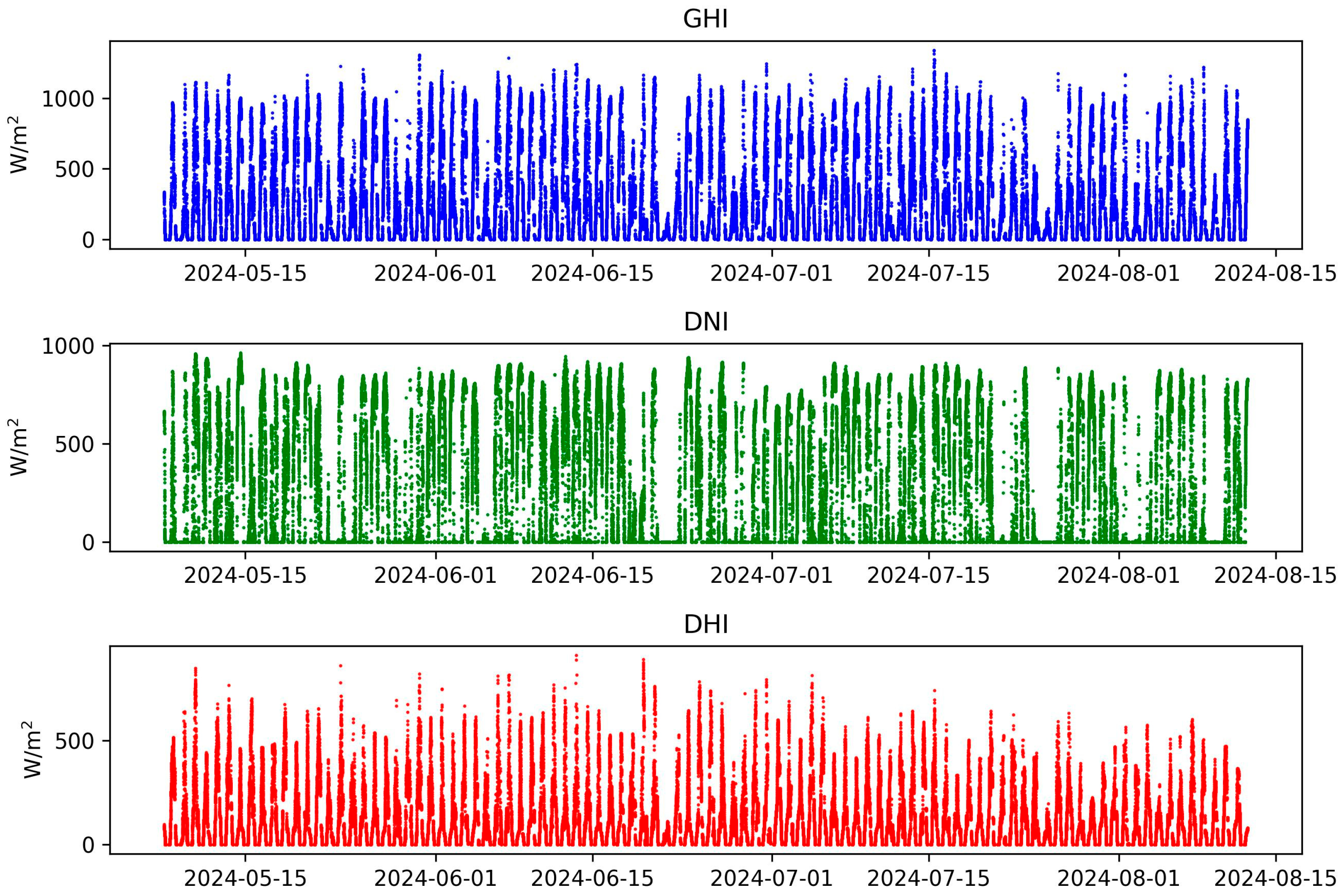
2. Dataset
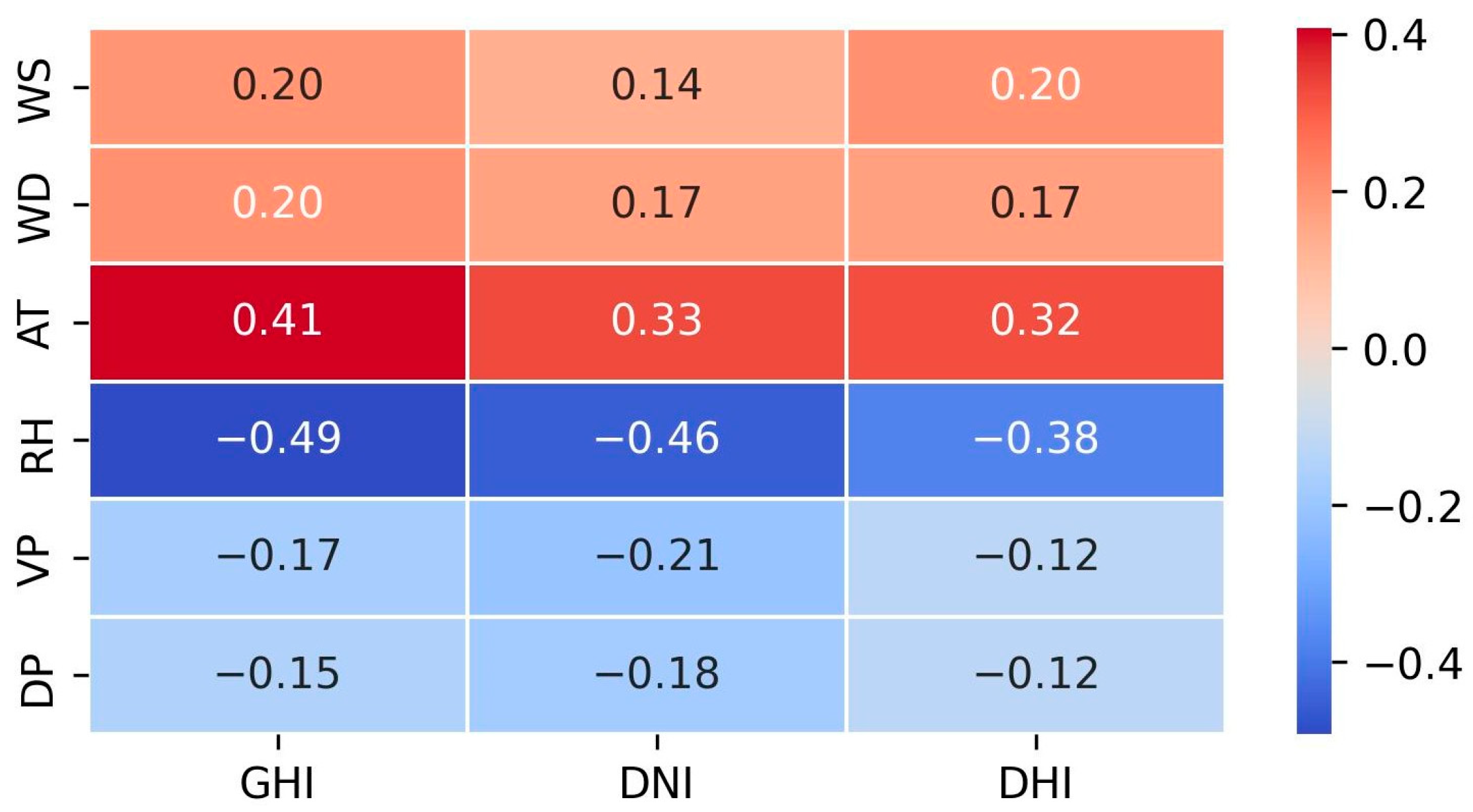
2.1. Multimodal Data
2.1.1. Meteorological Measurements
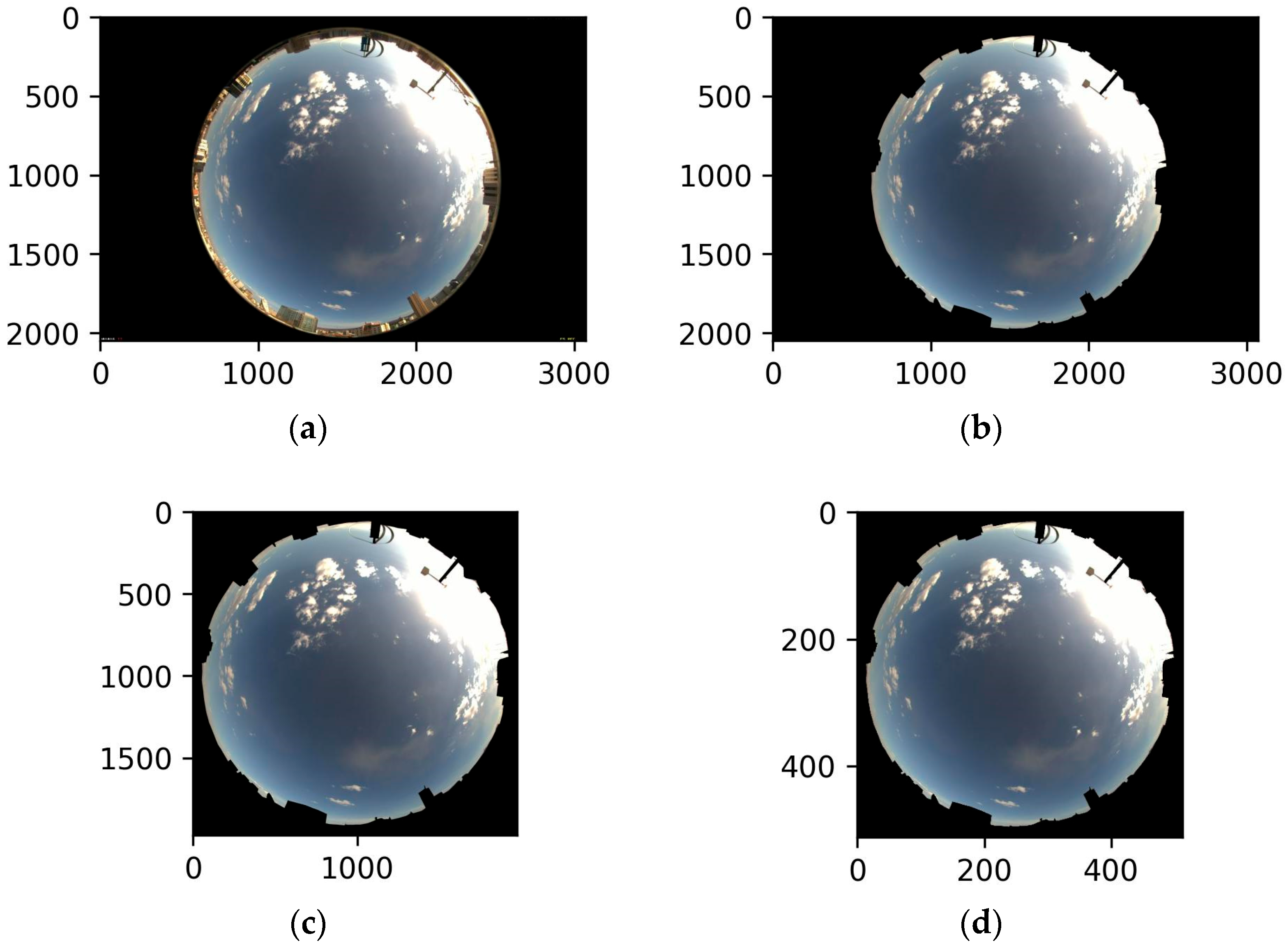
2.1.2. ASIs
2.2. Data Preprocessing
3. Methodology
3.1. Baselines
3.1.1. Clear Sky Model
3.1.2. FFNN
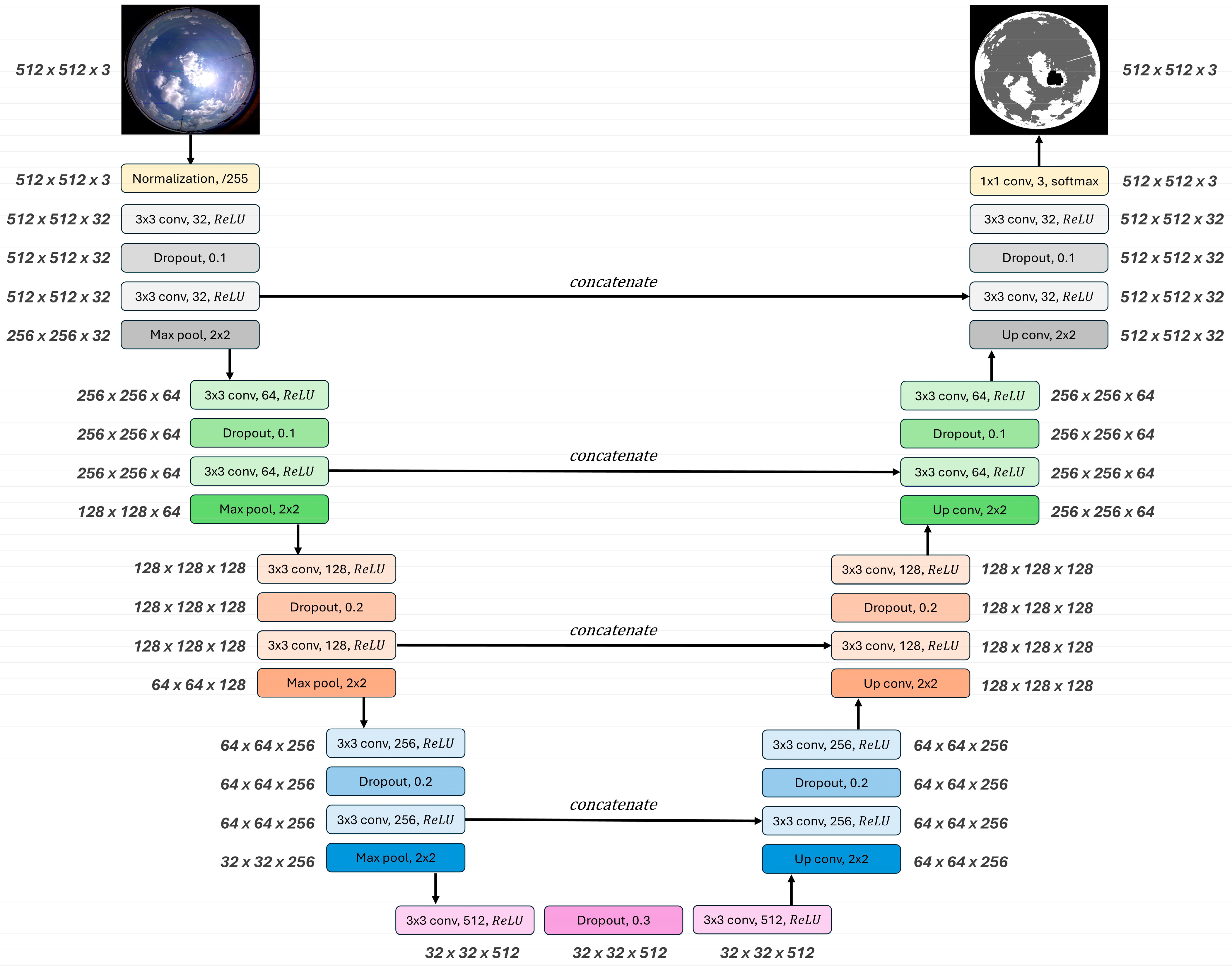
3.1.3. Hybrid of FFNN and U-Net
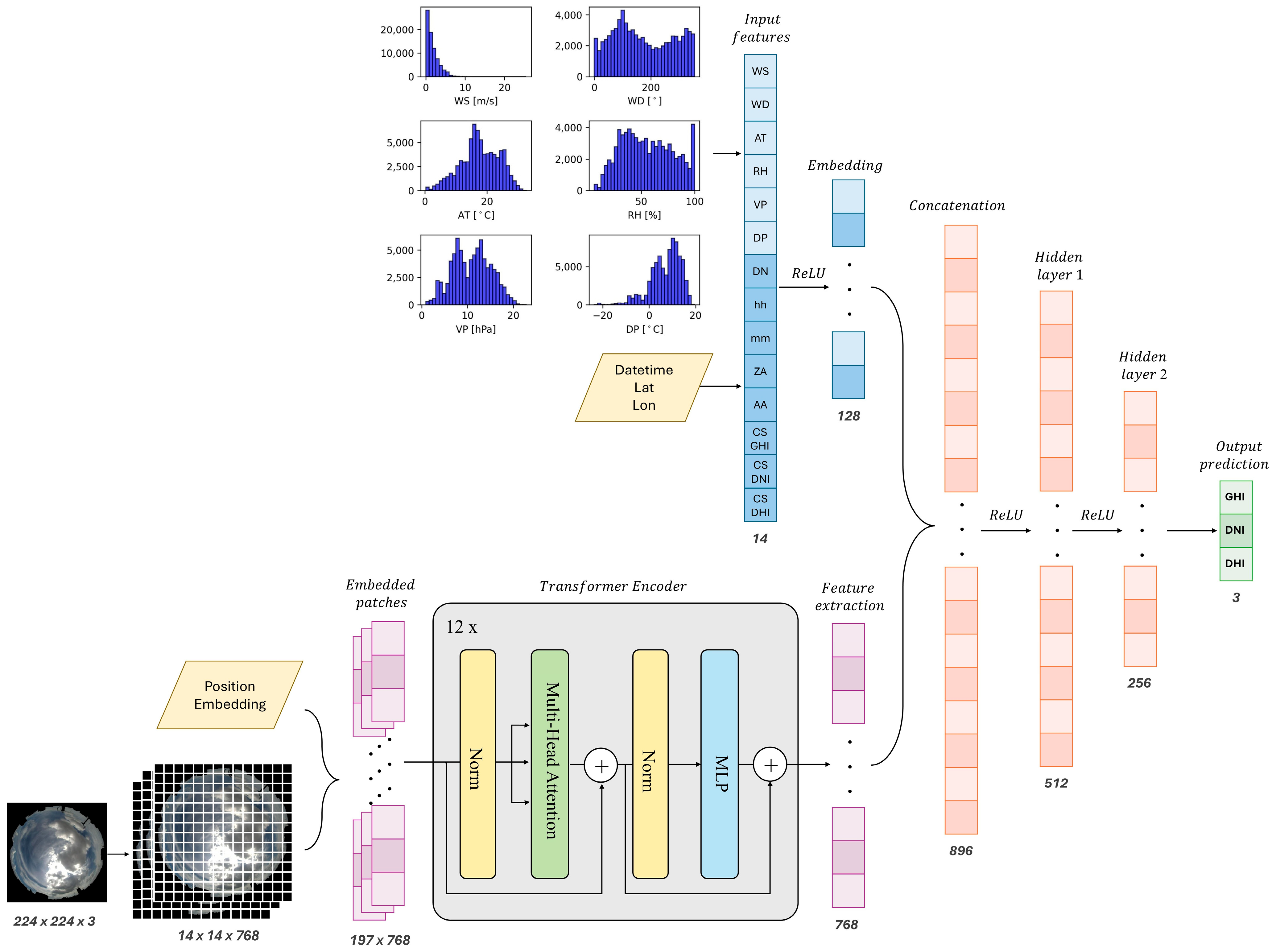
3.2. Proposed Methodology
3.3. Implementation
4. Results
4.1. Cloud Detection
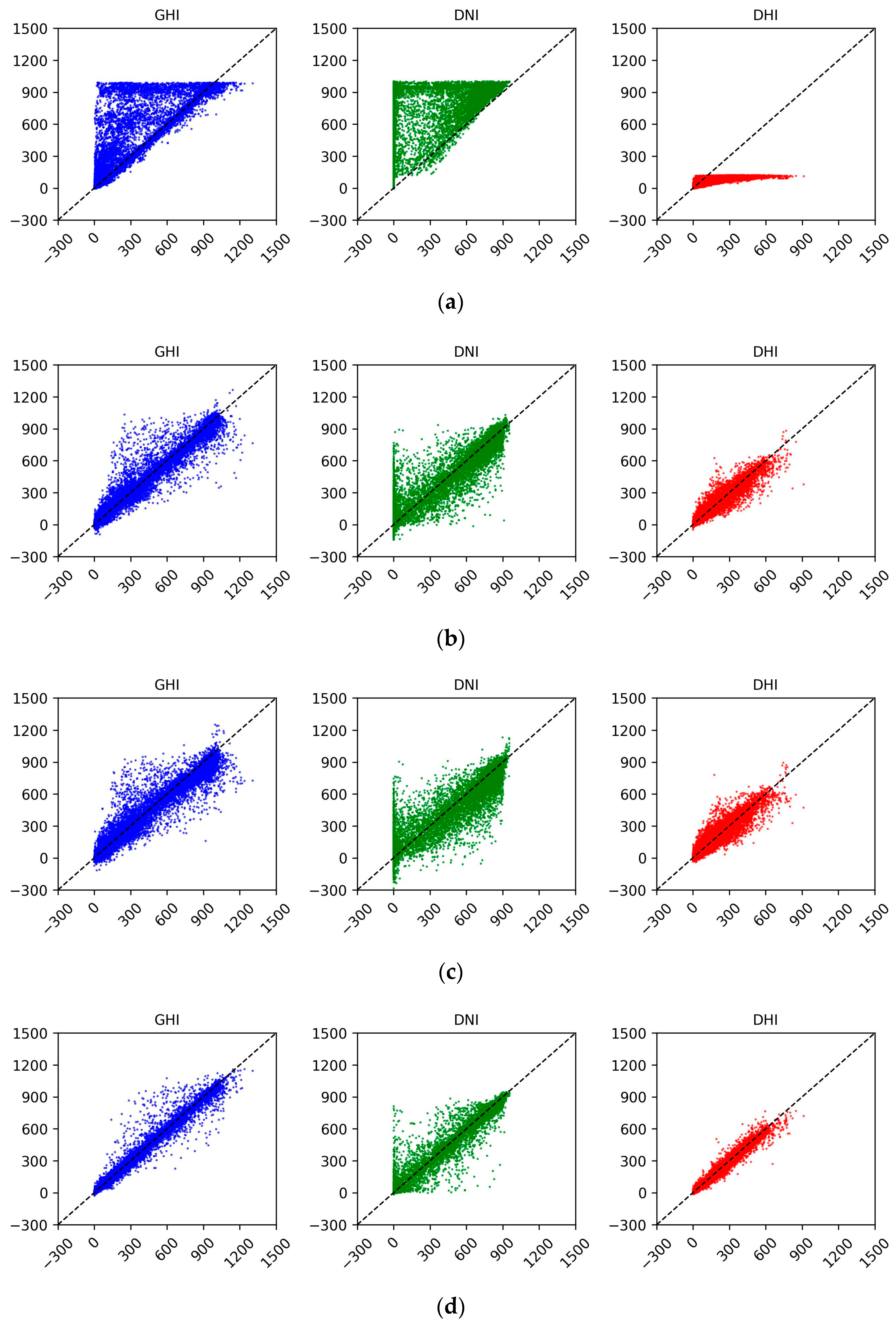
4.2. Performance Evaluation
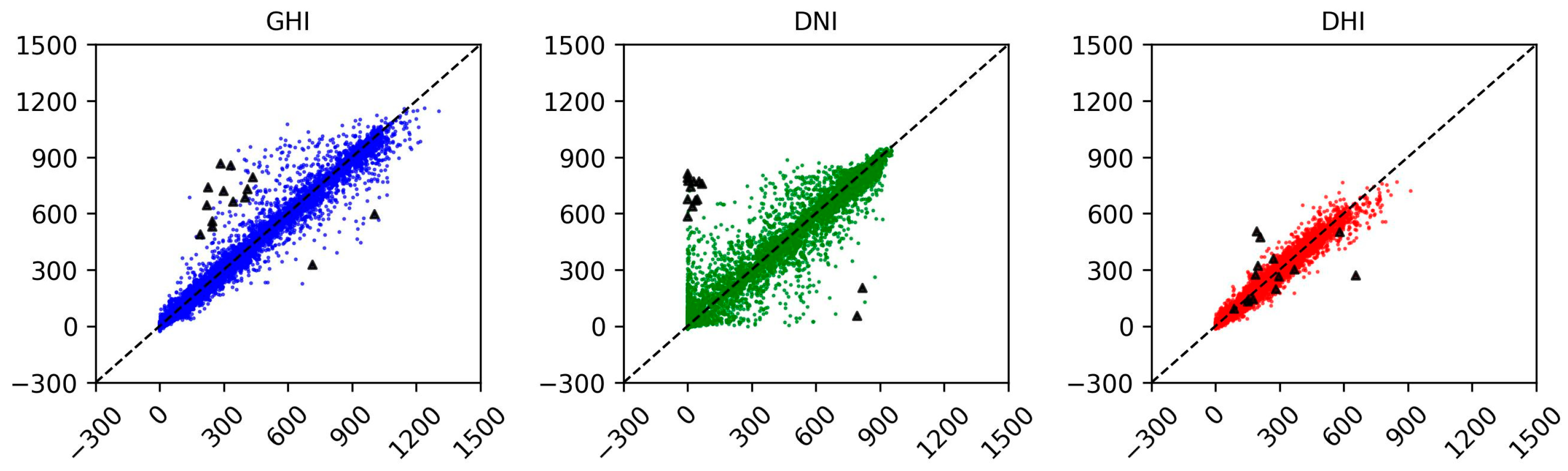
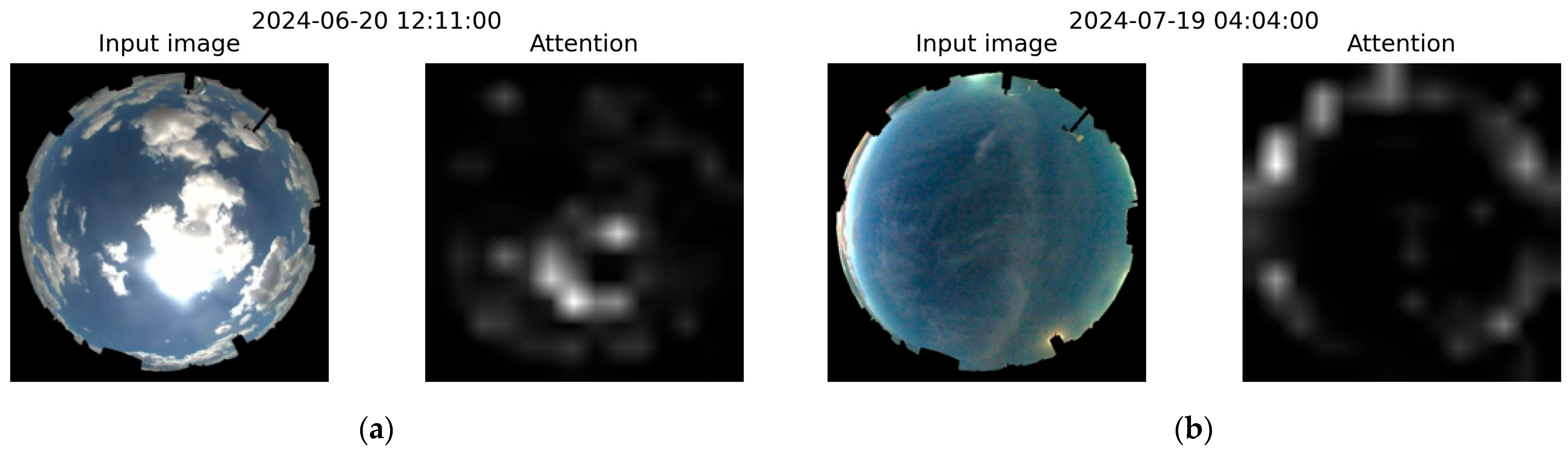
4.3. “Hard” vs. “Easy” Scenarios
4.4. Ablation Study
4.5. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AA | Solar azimuth angle [°] |
| AI | Artificial intelligence |
| ASI | All-sky image |
| AT | Ambient temperature [°C] |
| BSRN | Baseline Surface Radiation Network |
| CC | Cloud cover [%] |
| CNN | Convolutional neural network |
| COP | Conference of Parties |
| CSL | Clear sky library |
| CS DHI | Clear sky diffuse horizontal irradiance [W/m2] |
| CS DNI | Clear sky direct normal irradiance [W/m2] |
| CS GHI | Clear sky global horizontal irradiance [W/m2] |
| DHI | Diffuse horizontal irradiance [W/m2] |
| DIY | Do-it-yourself |
| DN | Day number from January 1 |
| DNI | Direct normal irradiance [W/m2] |
| DP | Dew point temperature [°C] |
| FFNN | Feedforward neural network |
| GHI | Global horizontal irradiance [W/m2] |
| hh | Hour of the day |
| Measured solar irradiance components | |
| IoU | Intersection over union |
| Predicted solar irradiance components | |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MLP | Multilayer perceptron |
| mm | Minute of the hour |
| MSE | Mean square error |
| Number of predicted and measured pairs of solar irradiance components | |
| NWP | Numerical weather prediction |
| PAR | Photosynthetically active radiation [W/m2] |
| PCA | Principal component analysis |
| PV | Photovoltaic |
| RBR | Red–blue ratio |
| ReLU | Rectified linear unit |
| RH | Relative humidity [%] |
| RMSE | Root mean square error |
| UNFCCC | United Nations Framework Convention on Climate Change |
| ViT | Vision transformer |
| VP | Vapor pressure [hpa] |
| VRE | Variable renewable energy |
| WD | Wind direction [°] |
| WMO | World Meteorological Organization |
| WS | Wind speed [m/s] |
| WSISEG | Whole-Sky Image Segmentation |
| ZA | Solar zenith angle [°] |
References
- REN21. Renewables 2024 Global Status Report—Energy Supply Module. Available online: https://www.ren21.net/gsr-2024/modules/energy_supply/01_global_trends (accessed on 28 January 2025).
- United Nations Framework Convention on Climate Change (UNFCCC). The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 28 January 2025).
- Edenhofer, O.; Madruga, R.P.; Sokona, Y. Renewable Energy Sources and Climate Change Mitigation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; p. 1076. [Google Scholar]
- Energy Regulatory Commission Mongolia. Statistics on Energy Performance. Available online: https://erranet.org/member/erc-mongolia/ (accessed on 28 January 2025).
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Deventer, W.V.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Logothetis, S.A.; Salamalikis, V.; Wilbert, S.; Remund, J.; Zarzalejo, L.F.; Xie, Y.; Nouri, B.; Ntavelis, E.; Nou, J.; Hendrikx, N.; et al. Benchmarking of solar irradiance nowcast performance derived from all-sky imagers. Renew. Energy 2022, 199, 246–261. [Google Scholar] [CrossRef]
- World Meteorological Organization. Available online: https://space.oscar.wmo.int/applicationareas/view/2_3_nowcasting_very_short_range_forecasting (accessed on 13 February 2025).
- Jain, M.; Sengar, V.S.; Gollini, I.; Bertolotto, M.; Mcardle, G.; Dev, S. LAMSkyCam: A low-cost and miniature ground-based sky camera. Hardw. X 2022, 12, e00346. [Google Scholar] [CrossRef]
- Sánchez-Segura, C.D.; Valentín-Coronado, L.; Peña-Cruz, M.I.; Díaz-Ponce, A.; Moctezuma, D.; Flores, G.; Riveros-Rosas, D. Solar irradiance components estimation based on a low-cost sky-imager. Sol. Energy 2021, 220, 269–281. [Google Scholar] [CrossRef]
- Hasenbalg, M.; Kuhn, P.; Wilbert, S.; Nouri, B.; Kazantzidis, A. Benchmarking of six cloud segmentation algorithms for ground-based all-sky imagers. Sol. Energy 2020, 201, 596–614. [Google Scholar] [CrossRef]
- Nouri, B.; Blum, N.; Wilbert, S.; Zarzalejo, L.F. A Hybrid Solar Irradiance Nowcasting Approach: Combining All Sky Imager Systems and Persistence Irradiance Models for Increased Accuracy. Sol. RRL 2022, 6, 2100442. [Google Scholar] [CrossRef]
- Fabel, Y.; Nouri, B.; Wilbert, S.; Blum, N.; Triebel, R.; Hasenbalg, M.; Kuhn, P.; Zarzalejo, L.F.; Pitz-Paal, R. Applying self- supervised learning for semantic cloud segmentation of all-sky images. Atmos. Meas. Tech. 2022, 15, 797–809. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F. Intra-hour DNI forecasting based on cloud tracking image analysis. Sol. Energy 2013, 91, 327–336. [Google Scholar] [CrossRef]
- Yamashita, M.; Yoshimura, M. Estimation of global and diffuse photosynthetic photon flux density under various sky conditions using ground-based whole-sky images. Remote Sens. 2019, 11, 932. [Google Scholar] [CrossRef]
- Scolari, E.; Sossan, F.; Haure-Touzé, M.; Paolone, M. Local estimation of the global horizontal irradiance using an all-sky camera. Sol. Energy 2018, 173, 1225–1235. [Google Scholar] [CrossRef]
- Xie, W.; Liu, D.; Yang, M.; Chen, S.; Wang, B.; Wang, Z.; Xia, Y.; Liu, Y.; Wang, Y.; Zhang, C. SegCloud: A novel cloud image segmentation model using a deep convolutional neural network for ground-based all-sky-view camera observation. Atmos. Meas. Tech. 2020, 13, 1953–1961. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, MICCAI 2015, Munich, Germany, 5–9 October 2015. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Kreuter, A.; Zangerl, M.; Schwarzmann, M.; Blumthaler, M. All-sky imaging: A simple, versatile system for atmospheric research. Appl. Opt. 2009, 48, 1091–1097. [Google Scholar] [CrossRef]
- Kuhn, P.; Nouri, B.; Wilbert, S.; Prahl, C.; Kozonek, N.; Schmidt, T.; Yasser, Z.; Ramirez, L.; Zarzalejo, L.; Meyer, A.; et al. Validation of an all-sky imager–based nowcasting system for industrial PV plants. Prog. Photovolt. Res. Appl. 2018, 26, 608–621. [Google Scholar] [CrossRef]
- Song, J.; Yan, Z.; Niu, Y.; Zou, L.; Lin, X. Cloud detection method based on clear sky background under multiple weather conditions. Sol. Energy 2023, 255, 1–11. [Google Scholar] [CrossRef]
- Niu, Y.; Song, J.; Zou, L.; Yan, Z.; Lin, X. Cloud detection method using ground-based sky images based on clear sky library and superpixel local threshold. Renew. Energy 2024, 226, 120452. [Google Scholar] [CrossRef]
- Hou, X.; Ju, C.; Wang, B. Prediction of solar irradiance using convolutional neural network and attention mechanism-based long short-term memory network based on similar day analysis and an attention mechanism. Heliyon 2023, 9, e21484. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.C.; Huh, J.H.; Hong, S.H.; Park, C.Y.; Kim, J.C. Solar Power Forecasting Using CNN-LSTM Hybrid Model. Energies 2022, 15, 8233. [Google Scholar] [CrossRef]
- Sun, Y.; Szucs, G.; Brandt, A.R. Solar PV output prediction from video streams using convolutional neural networks. Energy Environ. Sci. 2018, 11, 1811–1818. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Nie, Y.; Li, X.; Scott, A.; Sun, Y.; Venugopal, V.; Brandt, A. SKIPP’D: A SKy Images and Photovoltaic Power Generation Dataset for short-term solar forecasting. Sol. Energy 2023, 255, 171–179. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Liu, J.; Zang, H.; Cheng, L.; Ding, T.; Wei, Z.; Sun, G. A Transformer-based multimodal-learning framework using sky images for ultra-short-term solar irradiance forecasting. Appl. Energy 2023, 342, 121160. [Google Scholar] [CrossRef]
- Mercier, T.M.; Rahman, T.; Sabet, A. Solar Irradiance Anticipative Transformer. arXiv 2023, arXiv:2305.18487. [Google Scholar] [CrossRef]
- Climatec. CHF-SR11/12 Instruction Manual; Climatec: Tokyo, Japan, 2012. [Google Scholar]
- EKO Instruments. Products Catalogue. Available online: https://eko-instruments.com/products/ (accessed on 11 February 2025).
- Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J.; Lorenz, E.; van Sark, W.; Jensen, A. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications, 4th ed.; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024. [Google Scholar] [CrossRef]
- Mobotix. Camera Manual Q26 Hemispheric. Available online: https://www.mobotix.com/en/products/outdoor-cameras/q26-hemispheric (accessed on 11 February 2025).
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- PyTorch. Available online: https://pytorch.org/vision/main/models/generated/torchvision.models.vit_b_16.html (accessed on 25 February 2025).





| Models | Parameters | GHI MAE | GHI RMSE | DNI MAE | DNI RMSE | DHI MAE | DHI RMSE |
|---|---|---|---|---|---|---|---|
| Clear sky model | N/A | 129.19 | 238.20 | 340.84 | 475.14 | 86.65 | 150.64 |
| FFNN | 11,011 | 49.41 | 87.50 | 65.94 | 115.30 | 30.04 | 48.84 |
| U-Net + FFNN | 7,760,163 + 11,011 | 58.75 | 97.25 | 80.24 | 126.93 | 34.45 | 55.13 |
| Proposed model | 86,392,195 | 24.90 | 51.64 | 32.86 | 71.67 | 14.96 | 25.98 |
| Meteorological data only | 200,323 | 86.17 | 137.21 | 163.15 | 221.72 | 51.20 | 78.50 |
| Sky image only | 86,324,483 | 28.26 | 54.72 | 32.92 | 72.43 | 17.56 | 29.93 |
| Embedding Dimension | Fully Connected Layers | Parameter | Loss |
|---|---|---|---|
| 32 | 86,341,411 | 0.003448 | |
| 64 | [512, 256] | 86,358,339 | 0.003576 |
| 128 | 86,392,195 | 0.003402 | |
| 256 | 86,459,907 | 0.003613 | |
| [256] | 86,031,235 | 0.003496 | |
| [512] | 86,261,635 | 0.003583 | |
| [1024] | 86,722,435 | 0.003665 | |
| 128 | [1024, 1024] | 87,772,035 | 0.003587 |
| [1024, 512] | 87,245,699 | 0.003503 | |
| [512, 512] | 86,524,291 | 0.003551 | |
| [256, 256] | 86,097,027 | 0.003442 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayasgalan, O.; Akisawa, A. Nowcasting Solar Irradiance Components Using a Vision Transformer and Multimodal Data from All-Sky Images and Meteorological Observations. Energies 2025, 18, 2300. https://doi.org/10.3390/en18092300
Bayasgalan O, Akisawa A. Nowcasting Solar Irradiance Components Using a Vision Transformer and Multimodal Data from All-Sky Images and Meteorological Observations. Energies. 2025; 18(9):2300. https://doi.org/10.3390/en18092300
Chicago/Turabian StyleBayasgalan, Onon, and Atsushi Akisawa. 2025. "Nowcasting Solar Irradiance Components Using a Vision Transformer and Multimodal Data from All-Sky Images and Meteorological Observations" Energies 18, no. 9: 2300. https://doi.org/10.3390/en18092300
APA StyleBayasgalan, O., & Akisawa, A. (2025). Nowcasting Solar Irradiance Components Using a Vision Transformer and Multimodal Data from All-Sky Images and Meteorological Observations. Energies, 18(9), 2300. https://doi.org/10.3390/en18092300







