Transformers and Long Short-Term Memory Transfer Learning for GenIV Reactor Temperature Time Series Forecasting
Abstract
1. Introduction
2. Machine Learning Models
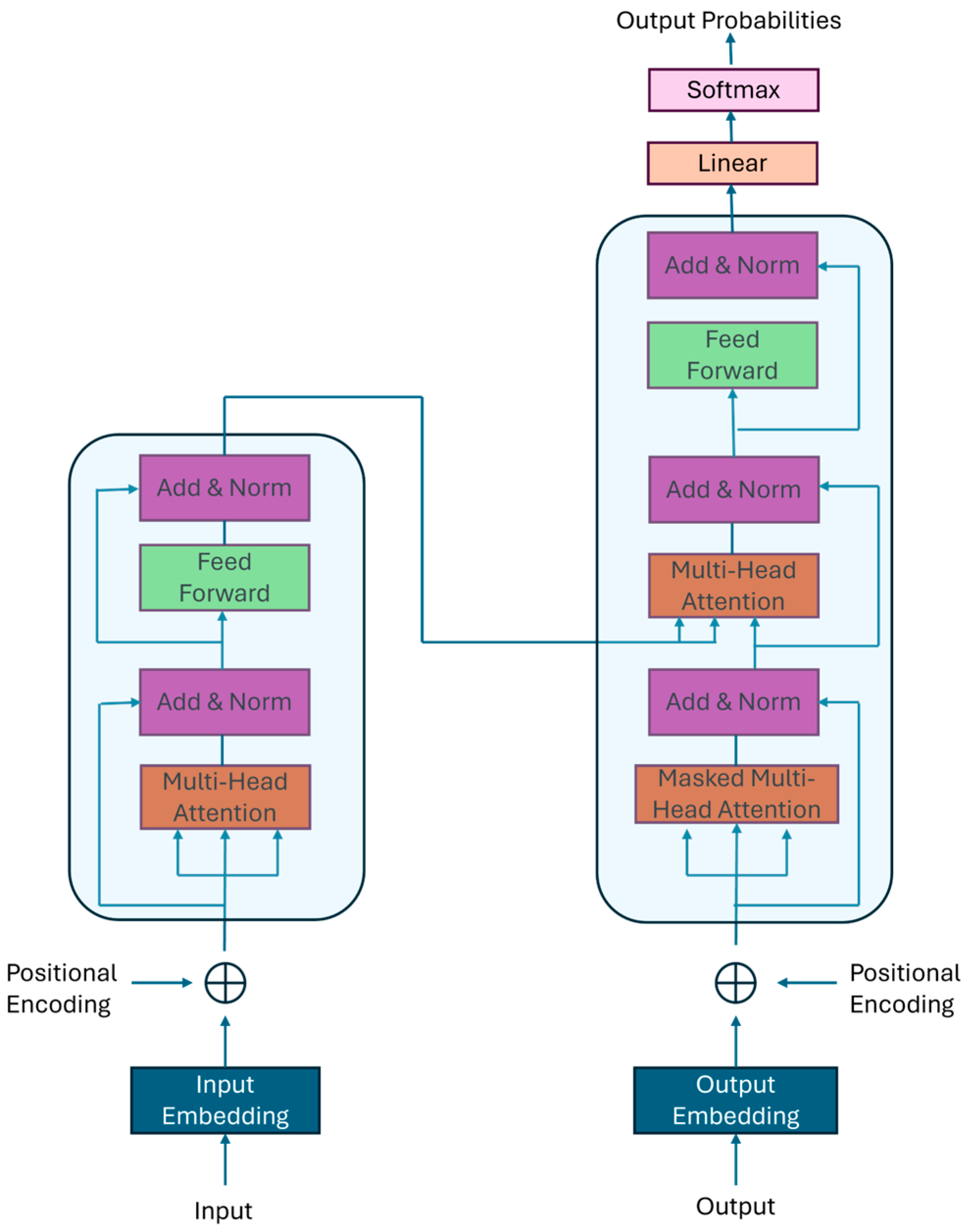
2.1. Transformers
2.2. Long Short-Term Memory (LSTM) Networks
2.3. Transfer Learning (TL)
3. Temperature Data Acquisition and Conditioning
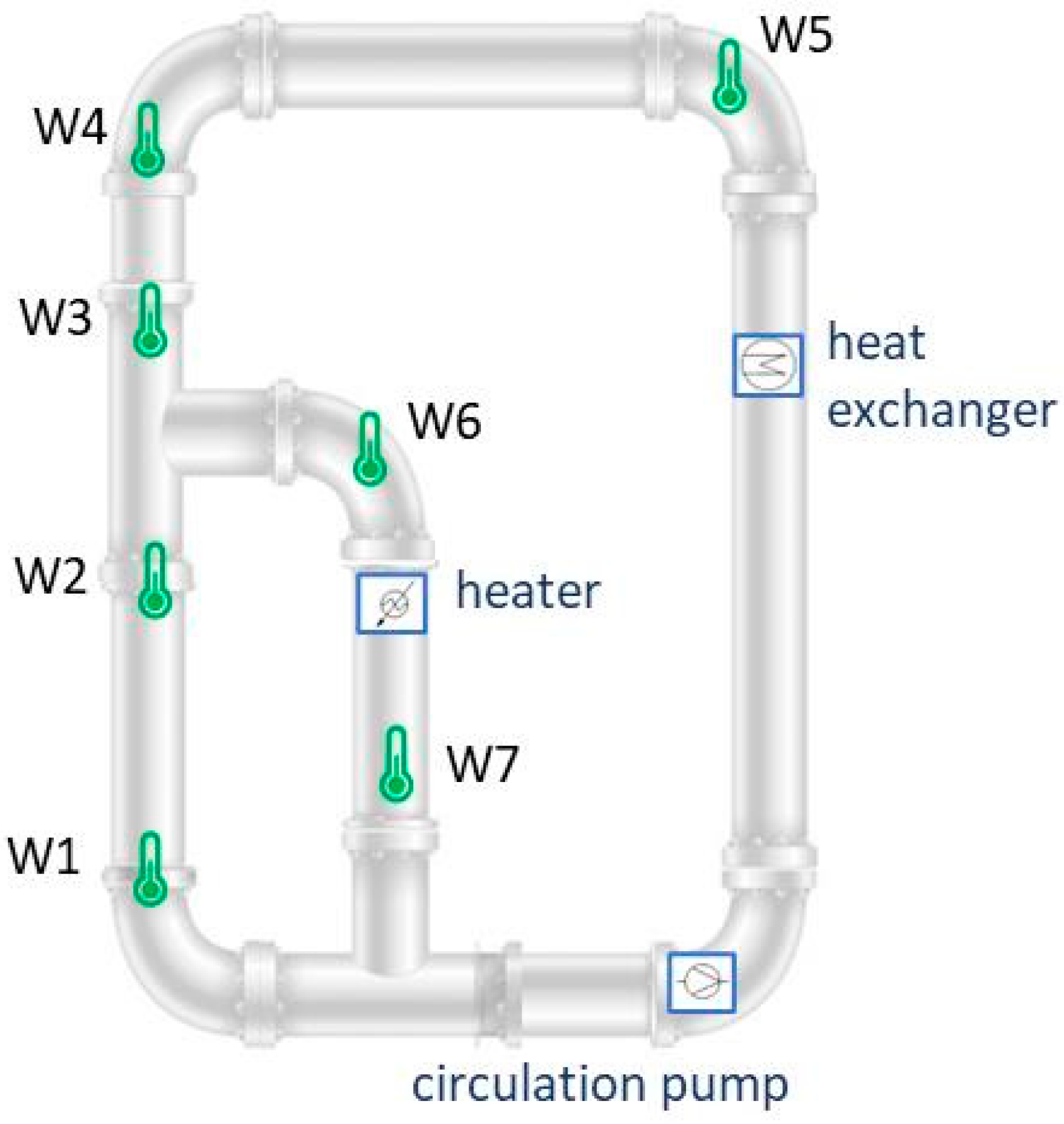
3.1. Measurements in Room Temperature Flow Loops
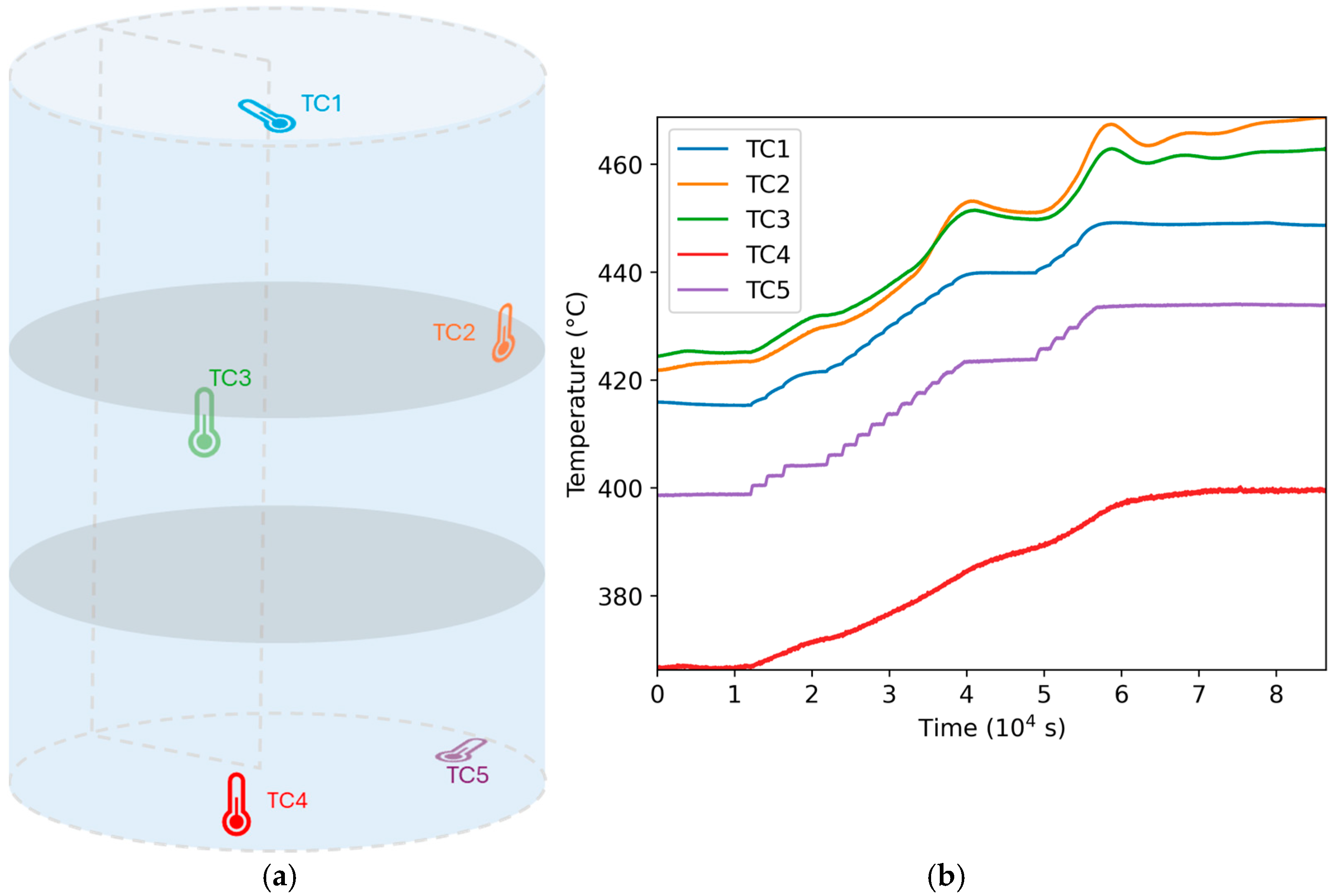
3.2. Measurements in High Temperature Vessel
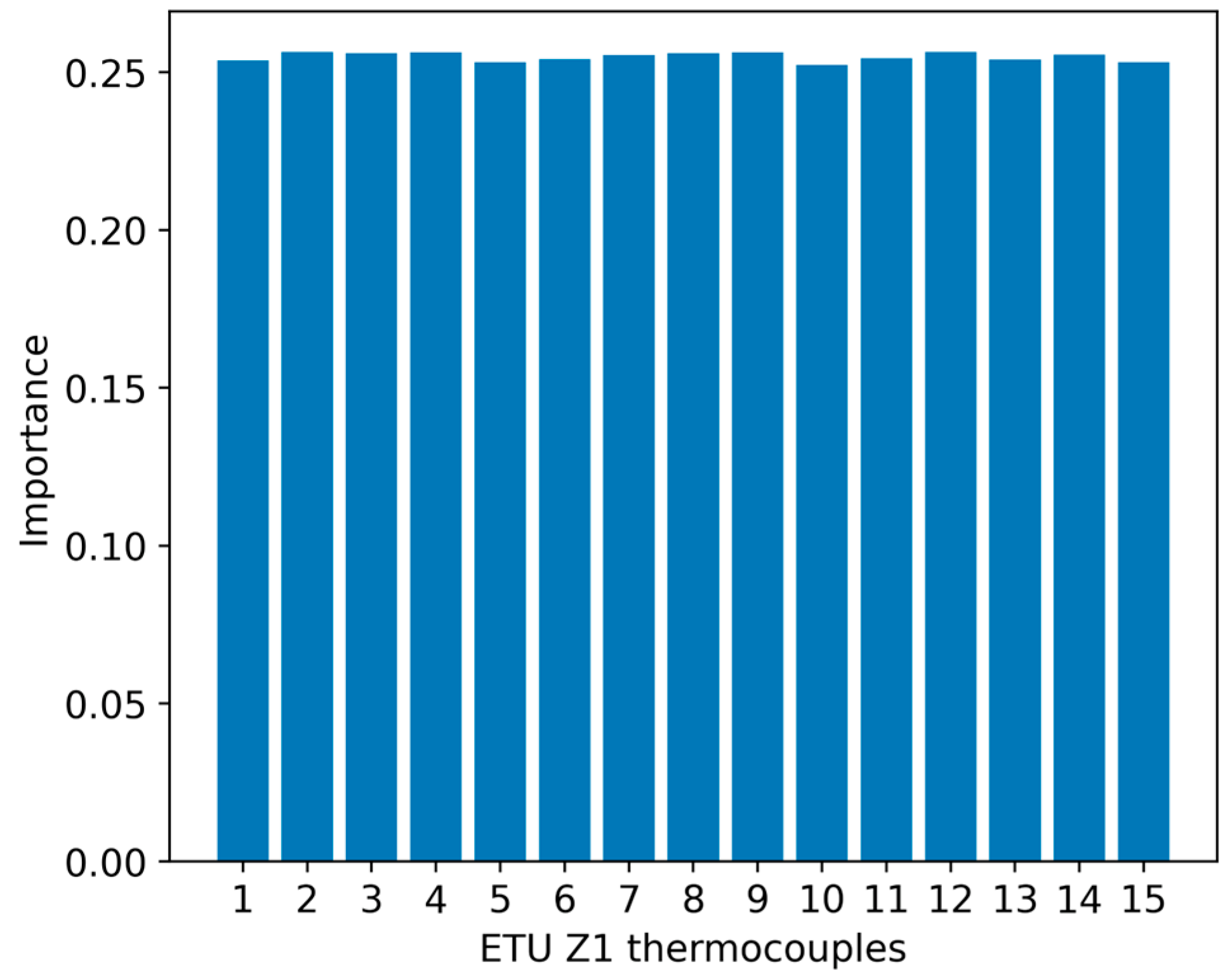
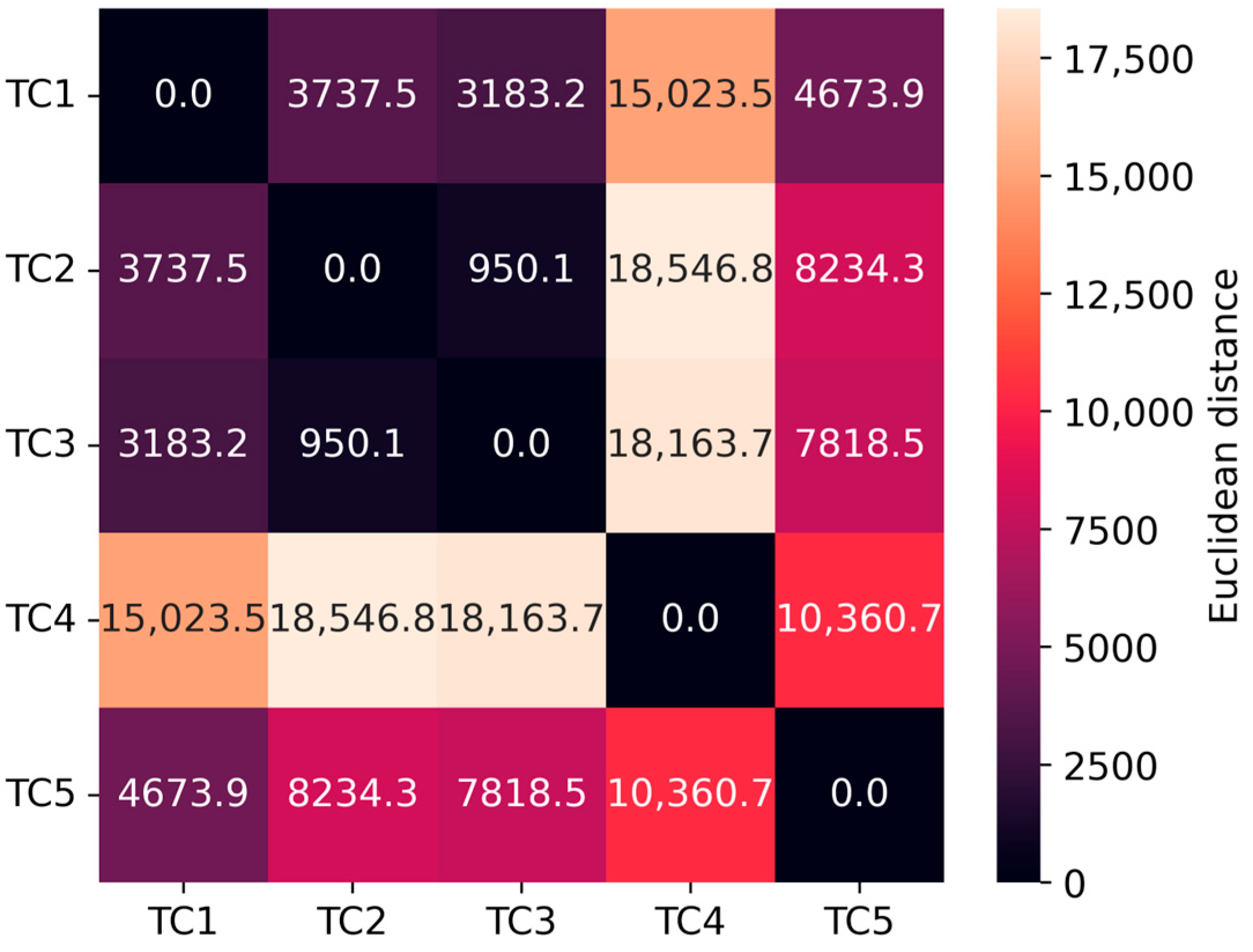
3.3. Selection of Thermocouples from Each Zone in the ETU Vessel
3.4. Augmentation of Training Data
4. Machine Learning Models Implementation
4.1. Training of Forecasting Models
4.2. Fine-Tuning of Forecasting Models
5. Results of Temperature Time Series Forecasting
5.1. Dependence of Forecasting Errors on Lookback Window Size
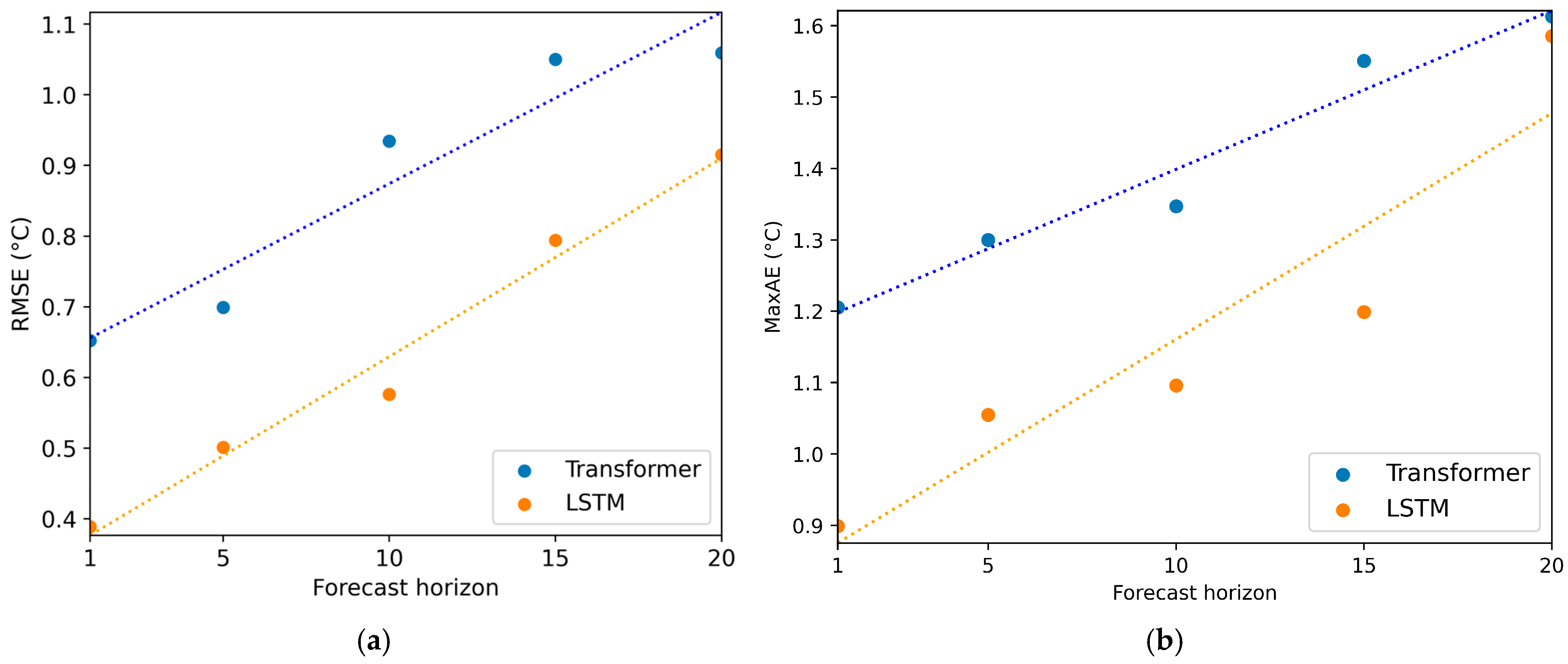
5.2. Dependence of Forecasting Errors on Forecast Horizon
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Locatelli, G.; Mancini, M.; Todeschini, N. Generation IV nuclear reactors: Current status and future prospects. Energy Policy 2013, 61, 1503–1520. [Google Scholar] [CrossRef]
- Forsberg, C. The advanced high-temperature reactor: High-temperature fuel, liquid salt coolant, liquid-metal-reactor plant. Prog. Nucl. Energy 2005, 47, 32–43. [Google Scholar] [CrossRef]
- Ayo-Imoru, R.M.; Cilliers, A.C. A survey of the state of condition-based maintenance (CBM) in the nuclear power industry. Ann. Nucl. Energy 2018, 112, 177–188. [Google Scholar] [CrossRef]
- Ayo-Imoru, R.M.; Cilliers, A.C. Continuous machine learning for abnormality identification to aid condition-based maintenance in nuclear power plant. Ann. Nucl. Energy 2018, 118, 61–70. [Google Scholar] [CrossRef]
- Rivas, A.; Delipei, G.K.; Davis, I.; Bhongale, S.; Hou, J. A system diagnostic and prognostic framework based on deep learning for advanced reactors. Prog. Nucl. Energy 2024, 170, 105114. [Google Scholar] [CrossRef]
- Schultz, R. Role of thermal-hydraulics in nuclear power plants: Design and safety. In Thermal-Hydraulics of Water Cooled Nuclear Reactors; Woodhead Publishing: Sawston, UK, 2017; pp. 143–166. [Google Scholar]
- Hashemian, H.; Riggsbee, E. I&C system sensors for advanced nuclear reactors. Nucl. Plant J. 2018, 36, 48–51. [Google Scholar]
- Kumar, V.D.; Bhattacharyya, A.; Behera, R.P.; Kasinathan, M.; Prabakar, K. Degradation and residual life assessment of thermocouples with damaged sheaths in corrosive environments. J. Instrum. 2025, 20, P01002. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, S.; Zhang, Y.; Zhang, C.; Wu, J. A Review of Statistical-Based Fault Detection and Diagnosis with Probabilistic Models. Symmetry 2024, 16, 455. [Google Scholar] [CrossRef]
- Mandal, S.; Santhi, B.; Vinolia, K.; Swaminathan, P. Sensor fault detection in Nuclear Power Plant using statistical methods. Nucl. Eng. Des. 2017, 324, 103–110. [Google Scholar] [CrossRef]
- Mandal, S.; Santhi, B.; Sridhar, S.; Vinola, K.; Swaminathan, P. A novel approach for fault detection and classification of the thermocouple sensor in nuclear power plant using singular value decomposition and symbolic dynamic filter. Ann. Nucl. Energy 2021, 103, 440–453. [Google Scholar] [CrossRef]
- Mandal, S.; Santhi, B.; Sridhar, S.; Vinolia, K.; Swaminathan, P. Minor fault detection of thermocouple sensor in nuclear power plants using time series analysis. Ann. Nucl. Energy 2019, 134, 383–389. [Google Scholar] [CrossRef]
- Pantopoulou, S.; Weathered, M.; Lisowski, D.; Tsoukalas, L.; Heifetz, A. Temporal Forecasting of Distributed Temperature Sensing in a Thermal Hydraulic System with Machine Learning and Statistical Models. IEEE Access 2025, 13, 10252–10264. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Wapachi, F.I.; Diab, A. Time-series forecasting of a typical PWR system response under Control Element Assembly withdrawal at full power. Nucl. Eng. Des. 2023, 413, 112472. [Google Scholar] [CrossRef]
- Pantopoulou, S.; Ankel, V.; Weathered, M.T.; Lisowski, D.D.; Cilliers, A.; Tsoukalas, L.H.; Heifetz, A. Monitoring of Temperature Measurements for Different Flow Regimes in Water and Galinstan with Long Short-Term Memory Networks and Transfer Learning of Sensors. Computation 2022, 10, 108. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, D.; Xiao, Y.; Wang, Z.; Zhou, H. An Interpretable Time Series Data Prediction Framework for Severe Accidents in Nuclear Power Plants. Entropy 2023, 25, 1160. [Google Scholar] [CrossRef]
- Mandal, S.; Santhi, B.; Sridhar, S.; Vinola, K.; Swaminathan, P. Nuclear power plant thermocouple sensor-fault detection and classification using deep learning and generalized likelihood ratio test. IEEE Trans. Nucl. Sci. 2017, 64, 1526–1534. [Google Scholar] [CrossRef]
- Wang, W.; Yu, J.; Xu, T.; Zhao, C.; Zhou, X. On-line abnormal detection of nuclear power plant sensors based on Kullback-Leibler divergence and ConvLSTM. Nucl. Eng. Des. 2024, 428, 113489. [Google Scholar] [CrossRef]
- Dong, F.; Chen, S.; Demachi, K.; Yoshikawa, M.; Seki, A.; Takaya, S. Attention-based time series analysis for data-driven anomaly detection in nuclear power plants. Nucl. Eng. Des. 2023, 404, 112161. [Google Scholar] [CrossRef]
- Yi, S.; Zheng, S.; Yang, S.; Zhou, G.; Cai, J. Anomaly Detection for Asynchronous Multivariate Time Series of Nuclear Power Plants Using a Temporal-Spatial Transformer. Sensors 2024, 24, 2845. [Google Scholar] [CrossRef]
- Zhou, G.; Zheng, S.; Yang, S.; Yi, S. A Novel Transformer-Based Anomaly Detection Model for the Reactor Coolant Pump in Nuclear Power Plants. Sci. Technol. Nucl. Install. 2024, 2024, 9455897. [Google Scholar] [CrossRef]
- Li, C.; Li, M.; Qiu, Z. A long-term dependable and reliable method for reactor accident prognosis using temporal fusion transformer. Front. Nucl. Eng. 2024, 3, 1339457. [Google Scholar] [CrossRef]
- Shi, J.; Wang, S.; Qu, P. Time series prediction model using LSTM-Transformer neural network for mine water inflow. Sci. Rep. 2024, 14, 18284. [Google Scholar] [CrossRef]
- Noyunsan, C.; Katanyukul, T.; Saikaew, K. Performance evaluation of supervised learning algorithms with various training data sizes and missing attributes. Eng. Appl. Sci. Res. 2018, 45, 221–229. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Cinar, E. A Sensor Fusion Method Using Transfer Learning Models for Equipment Condition Monitoring. Sensors 2022, 22, 6791. [Google Scholar] [CrossRef]
- Li, J.; Lin, M.; Li, Y.; Wang, X. Transfer learning with limited labeled data for fault diagnosis in nuclear power plants. Nucl. Eng. Des. 2022, 390, 111690. [Google Scholar] [CrossRef]
- Tanaka, N.; Moriya, S.; Ushijima, S.; Koga, T.; Eguchi, Y. Prediction method for thermal stratification in a reactor vessel. Nucl. Eng. Des. 1990, 120, 395–402. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A survey of transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Cabral, A.; Bakhtiari, S.; Elmer, T.W.; Heifetz, A.; Lisowski, D.D.; Carasik, L.B. Measurement of flow in a mixing Tee using ultrasound Doppler velocimetry for opaque fluids. Trans. Am. Nucl. Soc. 2019, 121, 1643–1645. [Google Scholar]
- Blandford, E.; Brumback, K.; Fick, L.; Gerardi, C.; Haugh, B.; Hillstrom, E.; Zweibaum, N. Kairos power thermal hydraulics research and development. Nucl. Eng. Des. 2020, 364, 110636. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Oh, C.; Han, S.; Jeong, J. Time-series data augmentation based on interpolation. Procedia Comput. Sci. 2020, 175, 64–71. [Google Scholar] [CrossRef]
- Koparanov, K.A.; Georgiev, K.K.; Shterev, V.A. Lookback Period, Epochs and Hidden States Effect on Time Series Prediction Using a LSTM based Neural Network. In Proceedings of the 28th National Conference with International Participation “Telecom 2020”, Sofia, Bulgaria, 29–30 October 2020. [Google Scholar]
- Kahraman, A.; Hou, P.; Yang, G.; Yang, Z. Comparison of the Effect of Regularization Techniques and Lookback Window Length on Deep Learning Models in Short Term Load Forecasting. In Proceedings of the 2021 International Top-Level Forum on Engineering Science and Technology Development Strategy, Nanjing, China, 14–22 August 2021; Lecture Notes in Electrical Engineering. Springer: Singapore, 2022; Volume 816. [Google Scholar]


| Water Loop | Galinstan Loop | ||
|---|---|---|---|
| Thermocouple Label | Average Temperature (°C) | Thermocouple Label | Average Temperature (°C) |
| W1 | 30 | G1 | 24 |
| W2 | 30 | G2 | 24 |
| W3 | 32 | G3 | 26 |
| W4 | 32 | G4 | 26 |
| W5 | 32 | G5 | 26 |
| W6 | 37 | G6 | 39 |
| W7 | 52 | G7 | 33 |
| ETU Vessel Thermocouple | Average Temperature (°C) |
|---|---|
| TC1 | 435 |
| TC2 | 447 |
| TC3 | 446 |
| TC4 | 384 |
| TC5 | 419 |
| ETU Vessel Zone | Explained Variance (%) |
|---|---|
| Z1 | 98.72 |
| Z2 | 99.04 |
| Z3 | 97.98 |
| Z4 | 99.65 |
| Z5 | 99.69 |
| Lookback Window Size | Training Loss (°C) | Validation Loss (°C) |
|---|---|---|
| 1 | 0.0125 | 0.0335 |
| 5 | 0.0125 | 0.0336 |
| 10 | 0.0123 | 0.0335 |
| 15 | 0.0120 | 0.0335 |
| 20 | 0.0113 | 0.0335 |
| 40 | 0.0113 | 0.0333 |
| 60 | 0.0120 | 0.0336 |
| 80 | 0.0092 | 0.0332 |
| 100 | 0.0083 | 0.0332 |
| Forecast Horizon | Transformers | LSTM | ||||
|---|---|---|---|---|---|---|
| Training Loss (°C) | Validation Loss (°C) | Epochs | Training Loss (°C) | Validation Loss (°C) | Epochs | |
| 1 | 0.0099 | 0.0333 | 20 | 0.0002 | 0.0085 | 13 |
| 5 | 0.0107 | 0.0336 | 20 | 0.0002 | 0.0086 | 13 |
| 10 | 0.0113 | 0.0335 | 20 | 0.0004 | 0.0083 | 18 |
| 15 | 0.0119 | 0.0334 | 20 | 0.0004 | 0.0086 | 20 |
| 20 | 0.0107 | 0.0338 | 20 | 0.0004 | 0.0086 | 20 |
| Lookback Window Size | LSTM | Transformers | ||
|---|---|---|---|---|
| Training Loss (°C) | Validation Loss (°C) | Training Loss (°C) | Validation Loss (°C) | |
| 1 | 0.0036 | 0.009 | 0.0089 | 0.0191 |
| 5 | 0.0035 | 0.0086 | 0.009 | 0.0191 |
| 10 | 0.0035 | 0.0085 | 0.0091 | 0.0191 |
| 15 | 0.0036 | 0.0085 | 0.0089 | 0.0171 |
| 20 | 0.0031 | 0.0085 | 0.0089 | 0.0175 |
| 40 | 0.0035 | 0.0094 | 0.0095 | 0.0176 |
| 60 | 0.0036 | 0.0095 | 0.0113 | 0.0192 |
| 80 | 0.0036 | 0.0095 | 0.0097 | 0.0176 |
| 100 | 0.0036 | 0.0096 | 0.0111 | 0.0175 |
| Forecast Horizon | Transformers | LSTM | ||||
|---|---|---|---|---|---|---|
| Training loss (°C) | Validation loss (°C) | Epochs | Training loss (°C) | Validation loss (°C) | Epochs | |
| 1 | 0.0077 | 0.0149 | 10 | 0.0014 | 0.0096 | 20 |
| 5 | 0.0085 | 0.0158 | 3 | 0.0025 | 0.0096 | 20 |
| 10 | 0.0089 | 0.0167 | 20 | 0.0041 | 0.009 | 20 |
| 15 | 0.0096 | 0.0169 | 19 | 0.0041 | 0.0097 | 20 |
| 20 | 0.01 | 0.0175 | 20 | 0.0042 | 0.0097 | 20 |
| ETU Thermocouple | Transformers | LSTM | ||
|---|---|---|---|---|
| RMSE | MaxAE | RMSE | MaxAE | |
| TC1 | 19 | 17 | 20 | 24 |
| TC2 | 21 | 20 | 17 | 22 |
| TC3 | 15 | 20 | 20 | 13 |
| TC4 | 14 | 16 | 22 | 16 |
| TC5 | 21 | 17 | 20 | 15 |
| ETU Thermocouple | Transformers R2 | LSTM R2 | ||
|---|---|---|---|---|
| RMSE | MaxAE | RMSE | MaxAE | |
| TC1 | 0.9139 | 0.961 | 0.9797 | 0.8735 |
| TC2 | 0.8948 | 0.8008 | 0.8191 | 0.9425 |
| TC3 | 0.869 | 0.9793 | 0.9142 | 0.8981 |
| TC4 | 0.874 | 0.9169 | 0.9416 | 0.9912 |
| TC5 | 0.9612 | 0.9562 | 0.8854 | 0.9434 |
| ETU Thermocouple | Transformers MaxAE | LSTM MaxAE | ||
|---|---|---|---|---|
| Correlation | Maxfh | Correlation | Maxfh | |
| TC1 | 0.0223 × fh + 1.1763 | 81 | 0.0317 × fh + 0.8437 | 68 |
| TC2 | 0.0167 × fh + 1.6429 | 81 | 0.0357 × fh + 1.0071 | 55 |
| TC3 | 0.0266 × fh + 1.4172 | 59 | 0.0341 × fh + 0.9345 | 60 |
| TC4 | 0.0233 × fh + 1.6674 | 57 | 0.0359 × fh + 1.1207 | 52 |
| TC5 | 0.0265 × fh + 0.8969 | 79 | 0.0291 × fh + 0.6986 | 79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantopoulou, S.; Cilliers, A.; Tsoukalas, L.H.; Heifetz, A. Transformers and Long Short-Term Memory Transfer Learning for GenIV Reactor Temperature Time Series Forecasting. Energies 2025, 18, 2286. https://doi.org/10.3390/en18092286
Pantopoulou S, Cilliers A, Tsoukalas LH, Heifetz A. Transformers and Long Short-Term Memory Transfer Learning for GenIV Reactor Temperature Time Series Forecasting. Energies. 2025; 18(9):2286. https://doi.org/10.3390/en18092286
Chicago/Turabian StylePantopoulou, Stella, Anthonie Cilliers, Lefteri H. Tsoukalas, and Alexander Heifetz. 2025. "Transformers and Long Short-Term Memory Transfer Learning for GenIV Reactor Temperature Time Series Forecasting" Energies 18, no. 9: 2286. https://doi.org/10.3390/en18092286
APA StylePantopoulou, S., Cilliers, A., Tsoukalas, L. H., & Heifetz, A. (2025). Transformers and Long Short-Term Memory Transfer Learning for GenIV Reactor Temperature Time Series Forecasting. Energies, 18(9), 2286. https://doi.org/10.3390/en18092286










