Comparative Sensitivity Analyses of Energy Consumption in Response to Average Speed Between Electric Vehicles and Conventional Vehicles: Case Study in Beijing, China
Abstract
1. Introduction
- (1)
- How does EV energy consumption vary with average speed, and how is the sensitivity of EV energy use different from that of CVs?
- (2)
- What is the impact of the sensitivity differences (if there are any) on energy use modeling and policy-making?
- (3)
- How do vehicle activity and energy use rates contribute to the sensitivity discrepancies, and what do the contributions tell us?
Literature Review
2. Methods
2.1. Energy Consumption Model for EVs
2.1.1. Facility- and Speed-Specific VSP Distribution
- (1)
- Data Preparation
- (2)
- Spatiotemporal Trajectory–Road Network Integration
- (3)
- Trajectory segmentation
- (4)
- Definition and Clustering Analysis of VSP
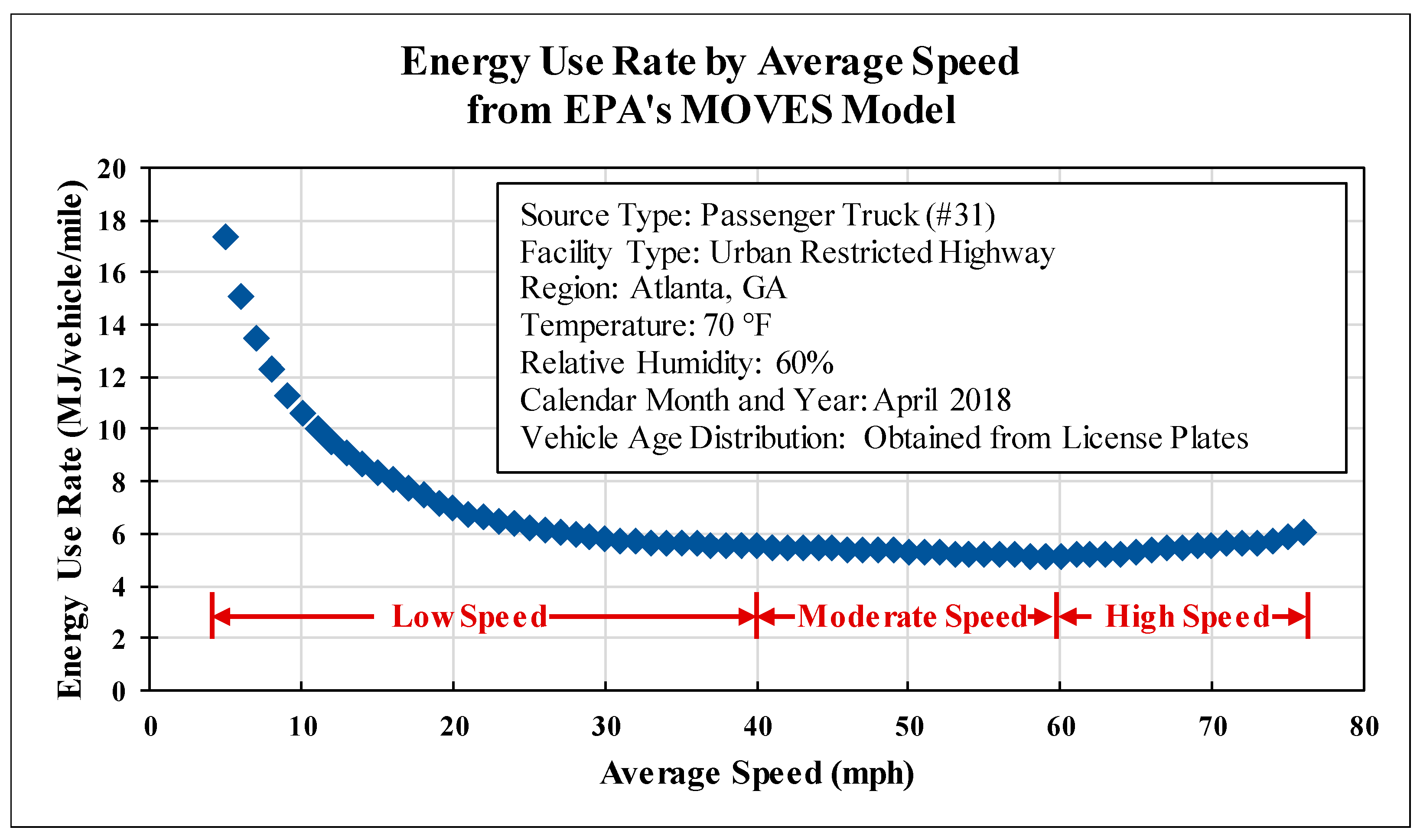
2.1.2. Facility- and Speed-Specific Energy Factor
- (1)
- Data Preparation
- (2)
- Definition of Energy Factor
2.2. Definition and Influence Factors of Energy Consumption Sensitivity Against Speed
2.2.1. Definition of Energy Consumption Sensitivity Against Speed
2.2.2. Influence Factors of Energy Consumption Sensitivity Against Speed
3. Results
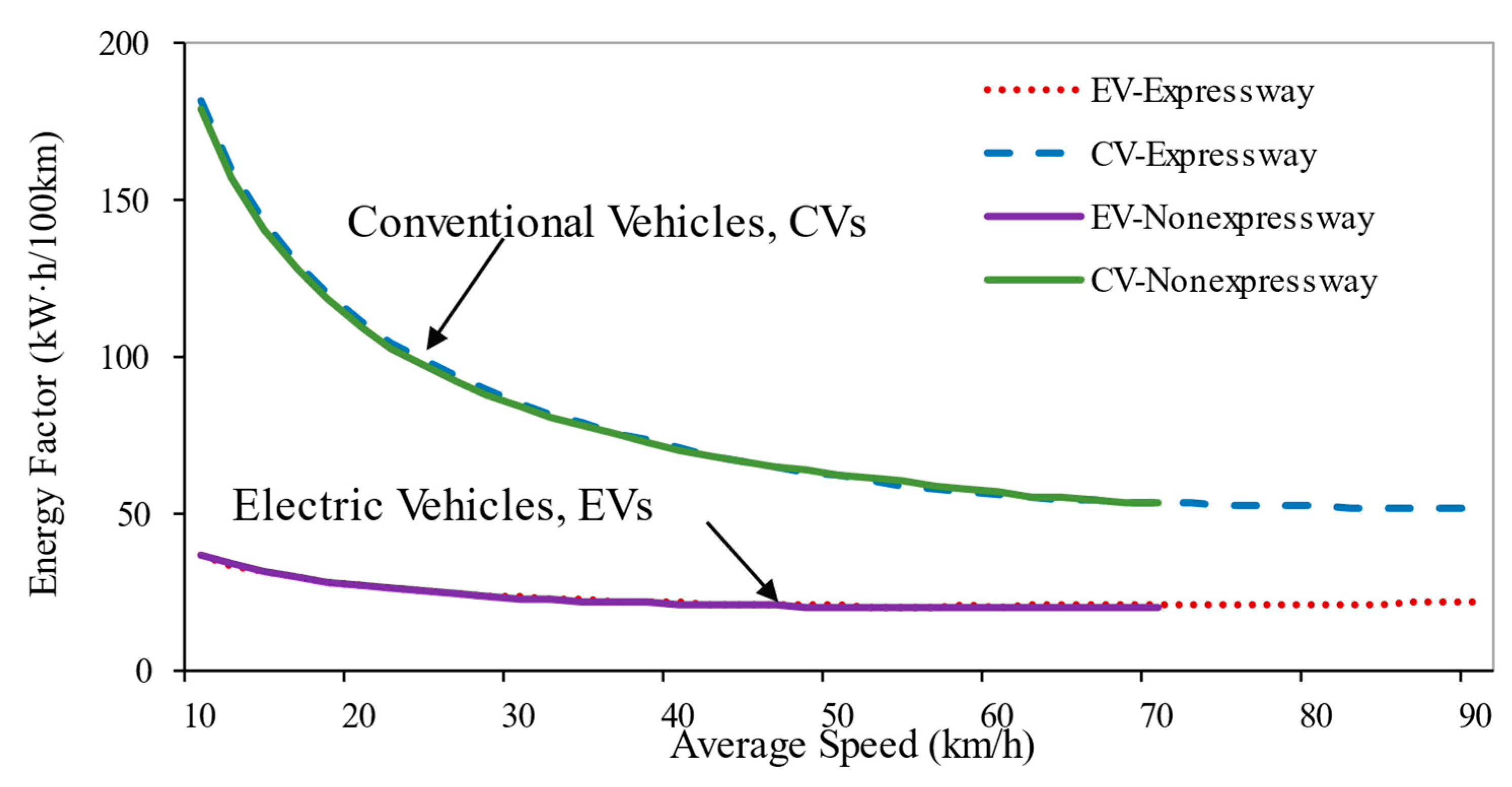
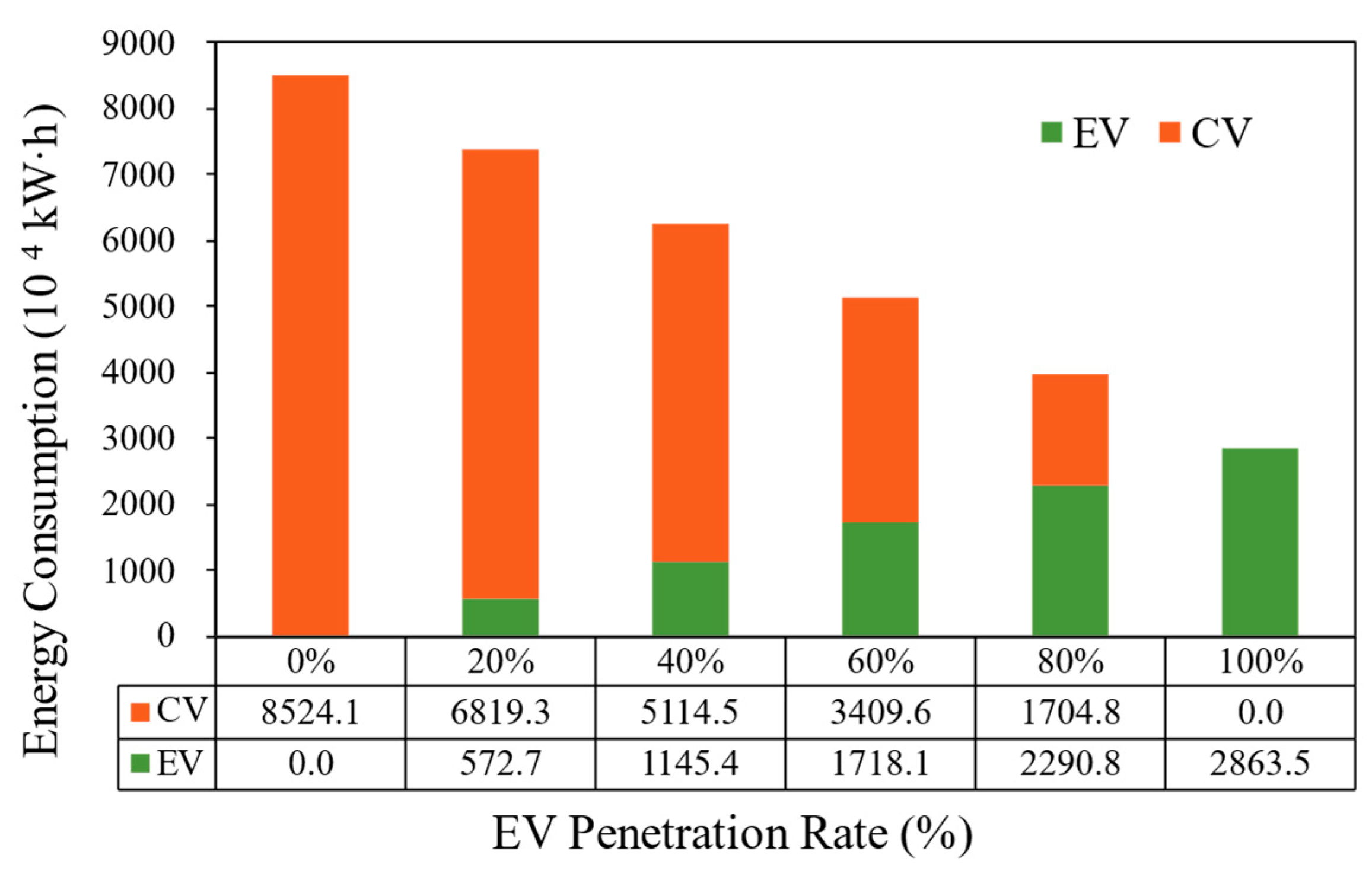
3.1. Comparison of Energy Consumption Between EVs and CVs
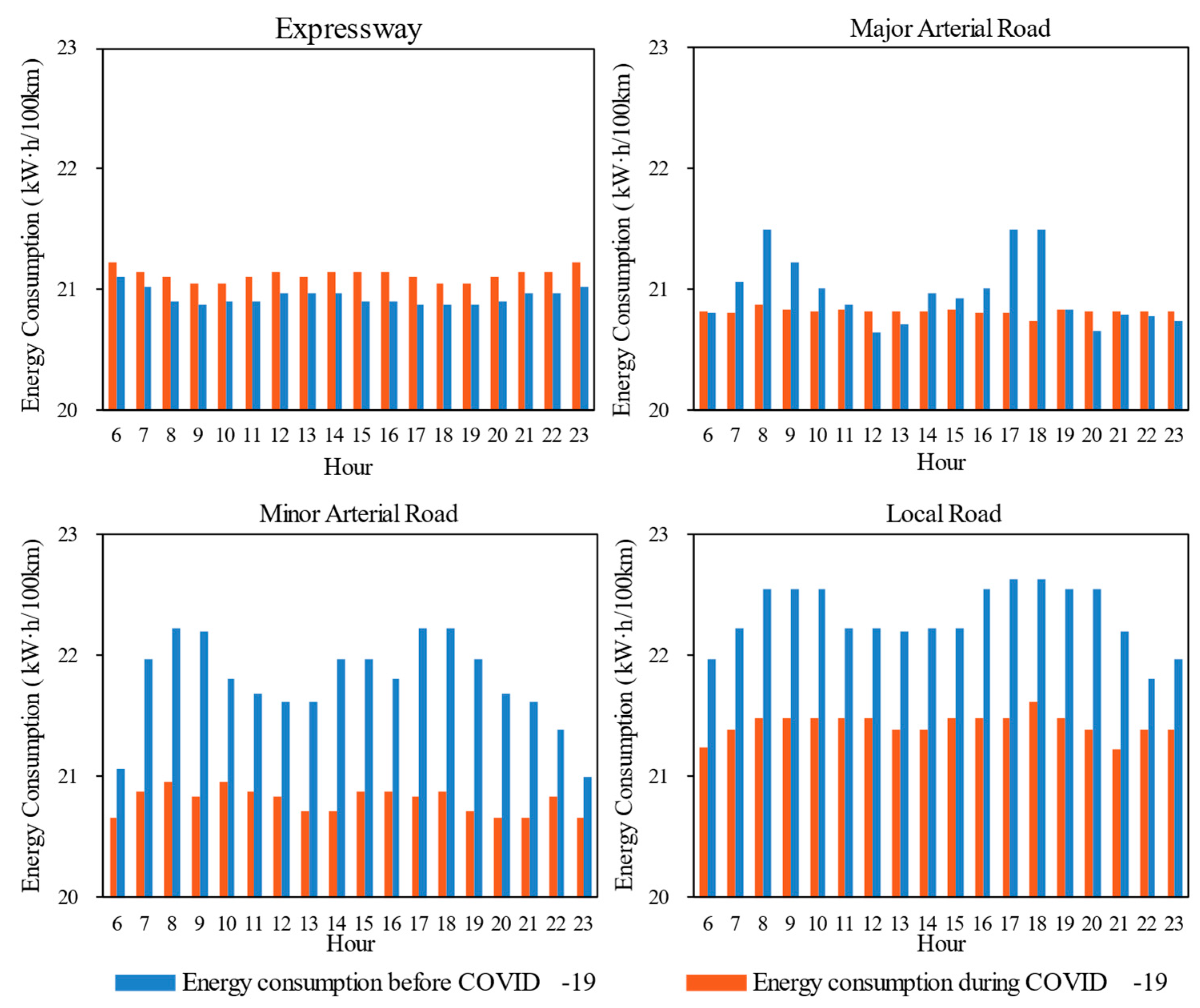
3.1.1. Absolute Energy Consumption
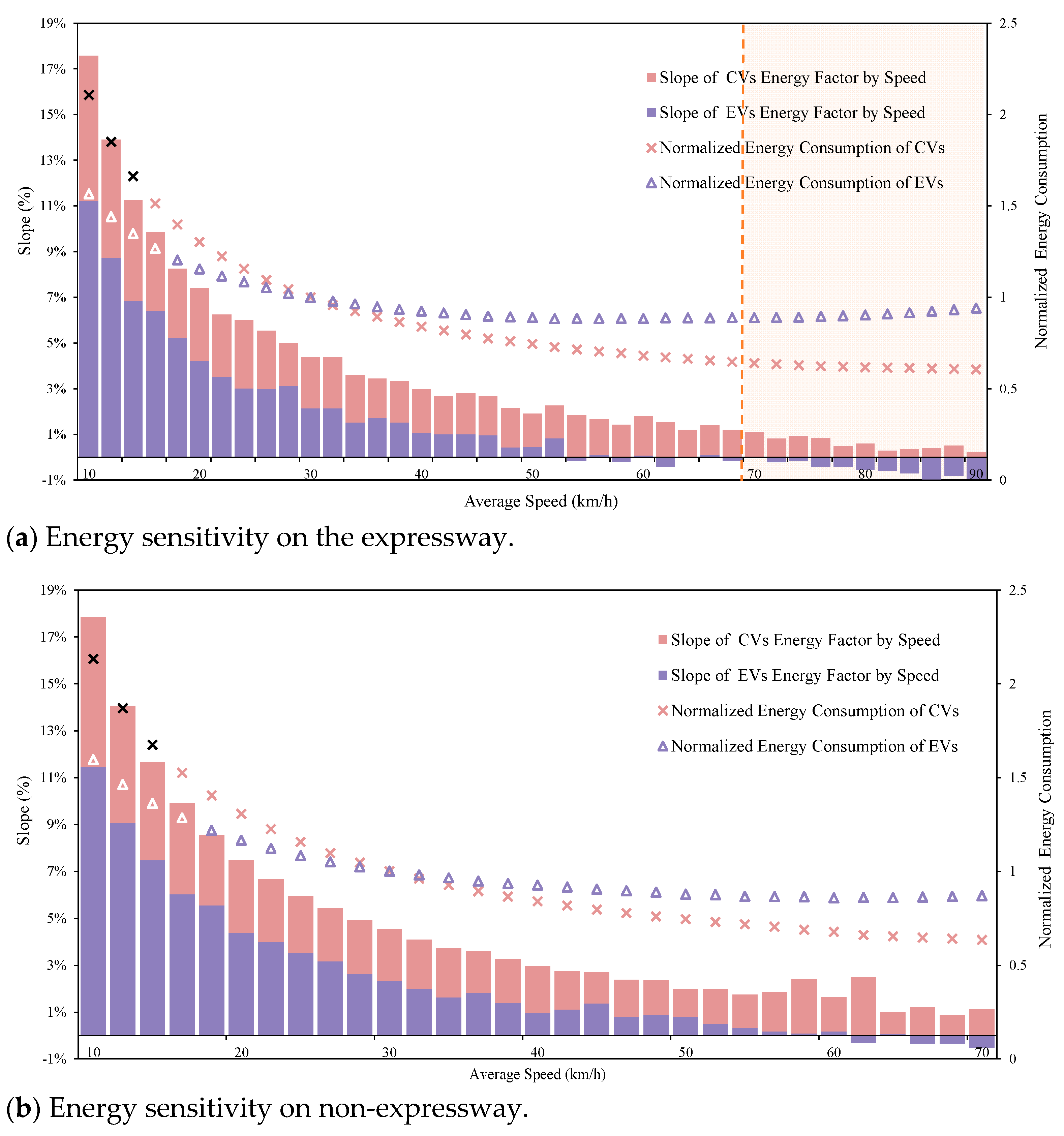
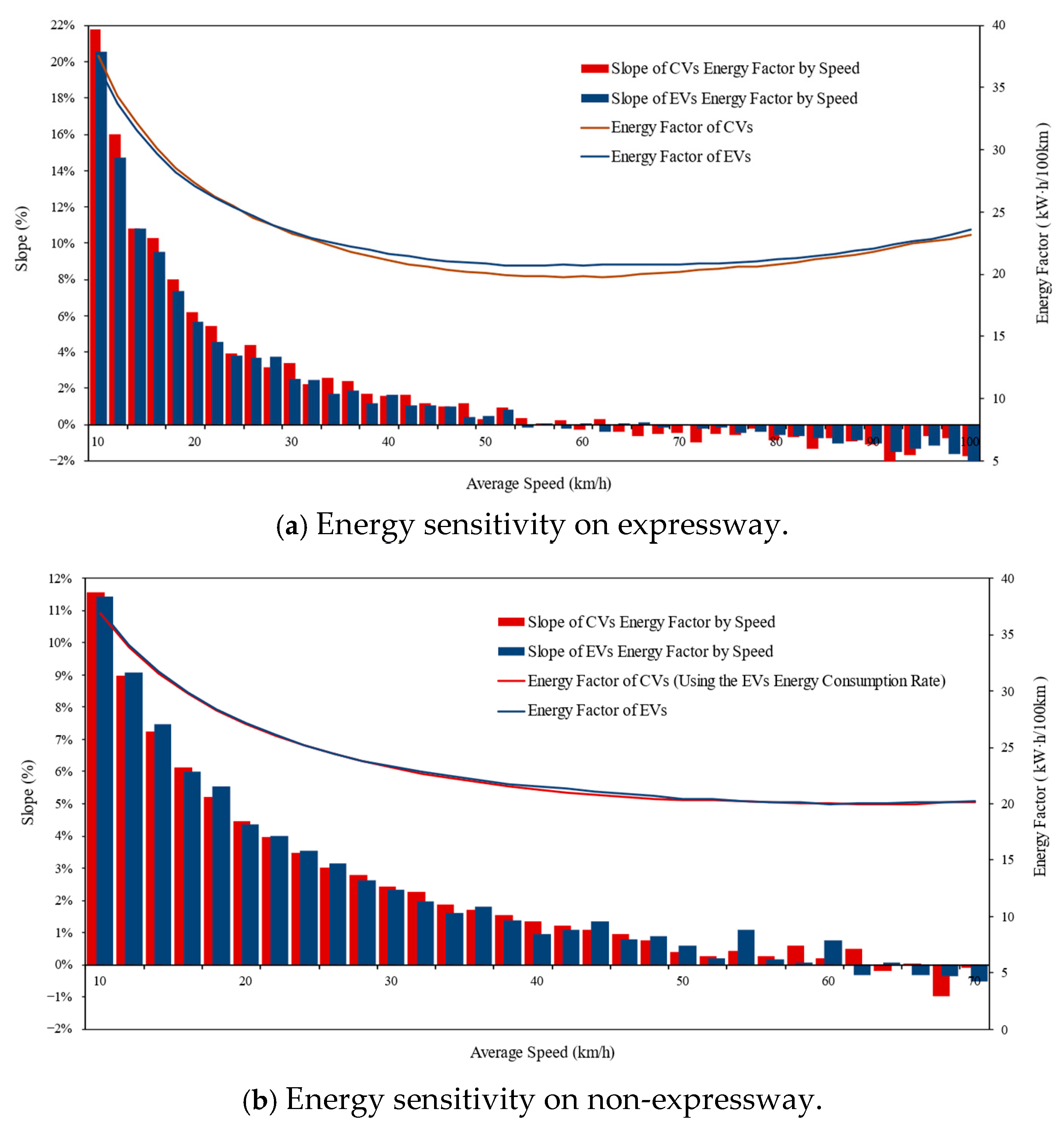
3.1.2. Energy Consumption Sensitivity Against Speed
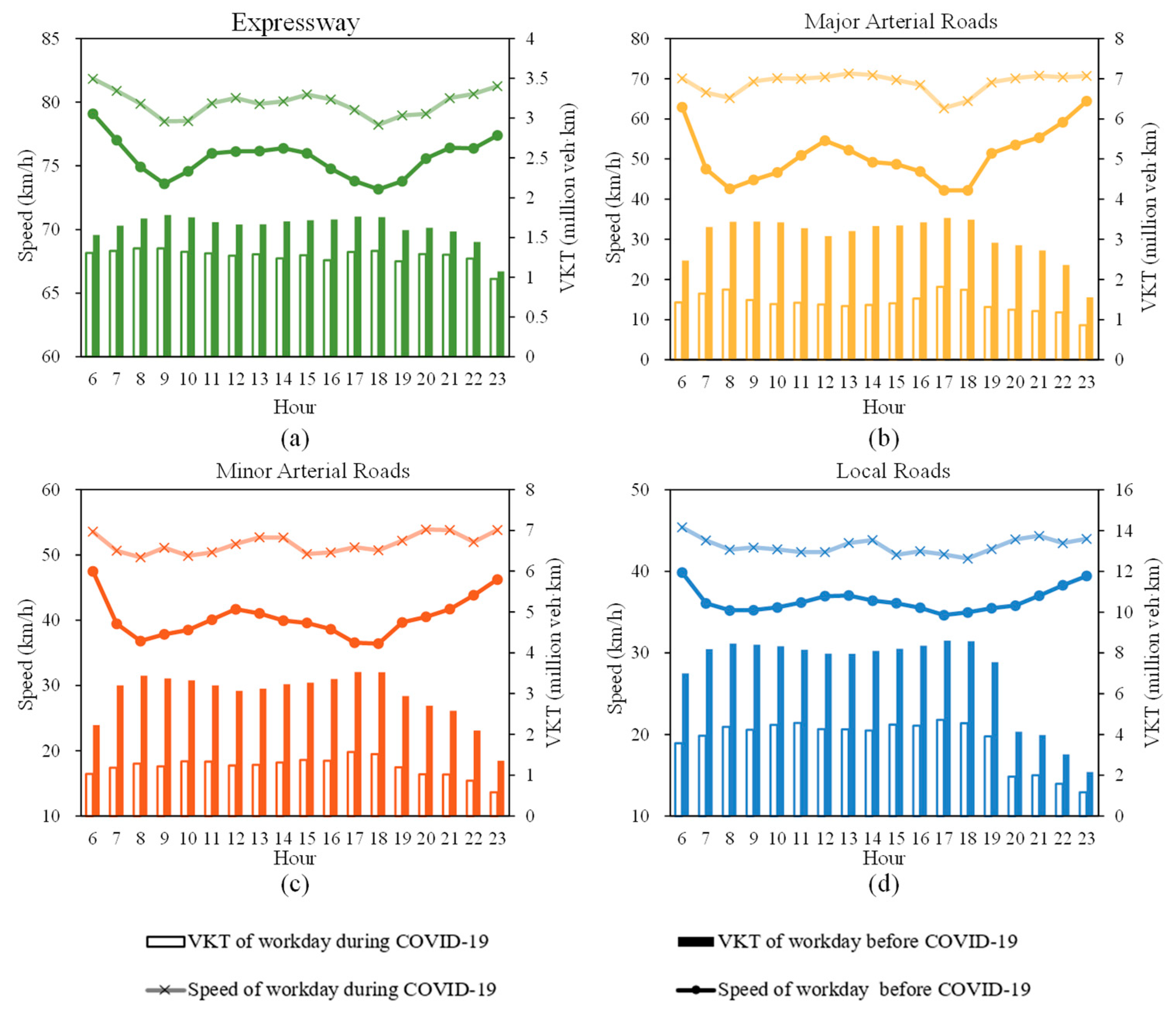
3.2. Impact of Vehicle Activities Based on VSP Distribution
3.2.1. VSP Distribution Comparison Between EVs and CVs
3.2.2. Energy Sensitivity Discrepancy Caused by VSP Distribution
- (1)
- For CVs, by applying CV-specific VSP distributions with EV energy consumption rates.
- (2)
- For EVs, by applying EV-specific VSP distributions with corresponding EV energy consumption rates
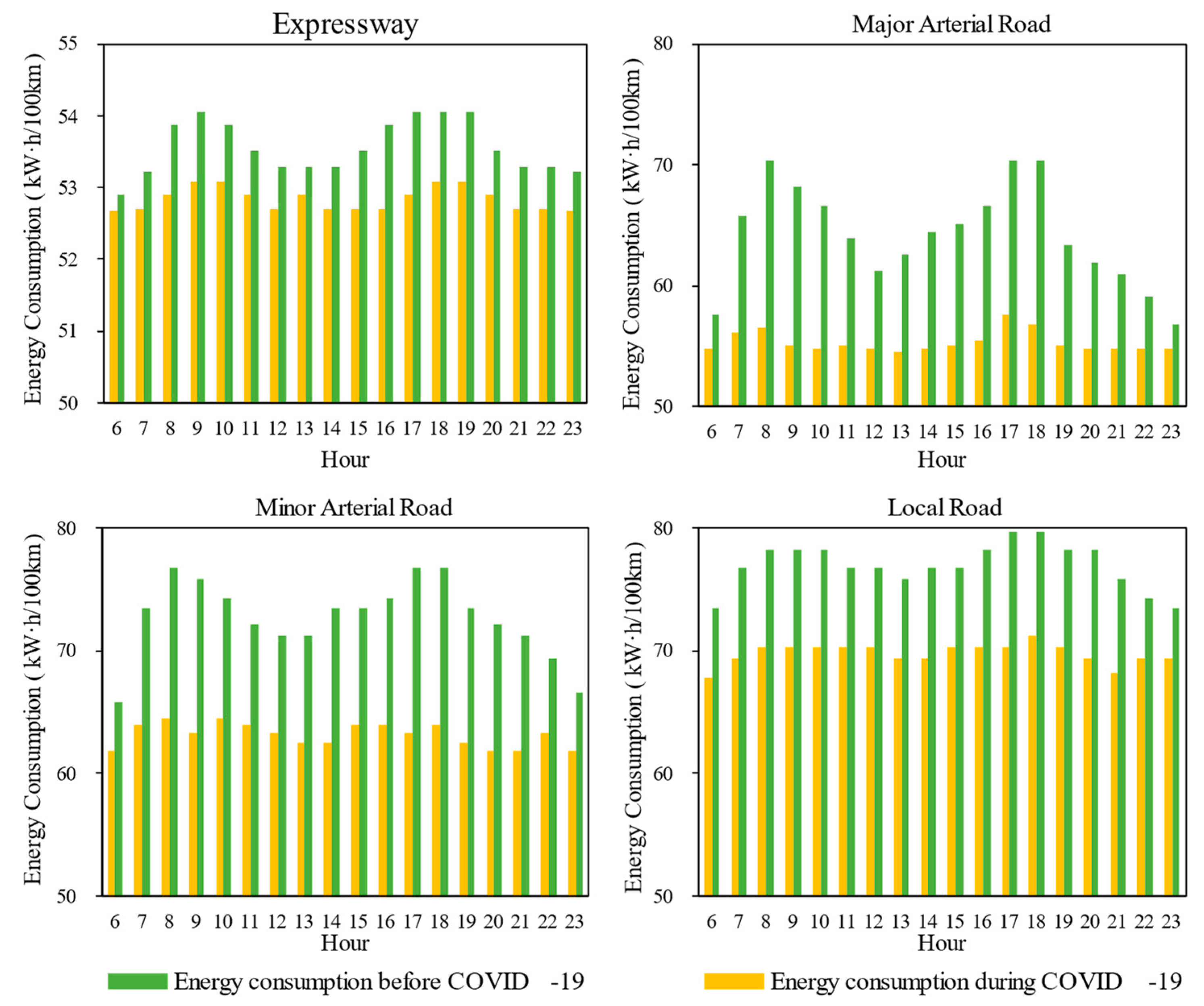
3.3. Impact of Energy Characteristics Based on Energy Consumption Rate
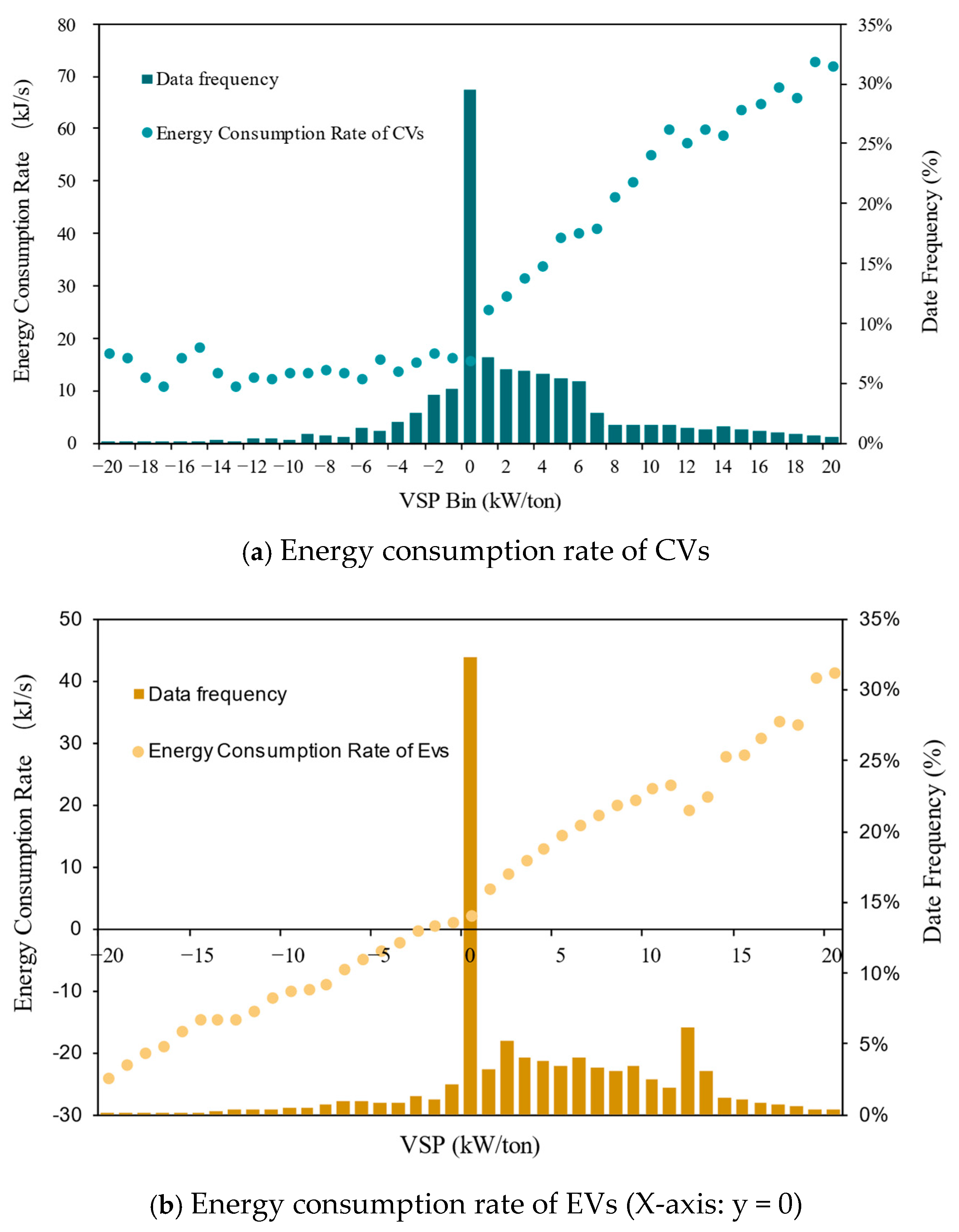
3.3.1. Energy Consumption Rate Comparison Between EVs and CVs
3.3.2. Energy Sensitivity Discrepancy Caused by Energy Consumption Rate
- (1)
- Motor efficiency dominance (59%, in VSP > 0). The majority of EV energy advantage stems from electric motors’ inherently higher energy conversion efficiency during acceleration and steady-speed operation, a phenomenon robustly observed across all three driving cycles (WLTC, CLTC, and Beijing Driving Cycle).
- (2)
- Idle loss elimination (24%, in VSP = 0). The absence of fuel consumption during stops—a well-documented CV inefficiency—is concretely quantified here through our VSP-bin analysis framework.
- (3)
- Regenerative braking contribution (17%, in VSP < 0). While modest relative to motor efficiency, this negative energy rate regime uniquely characterizes EV energy recovery potential. Though its magnitude is expected to vary with braking algorithms and battery SOC management in newer models.
- (1)
- For CVs: Applying EV-specific VSP distributions with CV energy consumption rates
- (2)
- For EVs: Applying EV-specific VSP distributions with corresponding EV energy consumption rates. The scatter plots of the normalized energy factor by speed are shown in Figure 14 for EVs and CVs, respectively. Additionally, the slope of the energy factor-speed curve, which can be used to describe the energy consumption sensitivity caused by ECR, is presented with a histogram in Figure 14. The average energy factor slopes in the three phases (4.3%, 0.3%, −0.5%) are approximately equal to those in Figure 6. The results demonstrate significant divergence between the energy consumption factor–speed curves of CVs and EVs under these conditions, consistent with the patterns observed in Figure 6. This confirms that the sensitivity differences shown in Figure 6 are primarily determined by vehicle-type-specific energy consumption rates.
4. Discussion
- (1)
- Eco-routing planning: EV energy-optimal routes should avoid road segments with excessively high average speeds (e.g., urban expressways), as high-speed conditions significantly increase power consumption. EVs demonstrate superior energy economy primarily in urban low-to-medium speed driving scenarios (average speed <50 km/h), with limited benefits in highway conditions.
- (2)
- Policy effectiveness variation. Unlike CVs, speed-increase strategies (e.g., >50 km/h) may yield diminishing energy-saving returns for EVs.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boriboonsomsin, K.; Vu, A. Real-World Activity Patterns of Heavy-Duty Battery Electric Trucks from Regional Distribution Fleets in Southern California. In Proceedings of the 2024 Forum for Innovative Sustainable Transportation Systems (FISTS), Riverside, CA, USA, 26–28 February 2024; pp. 1–6. [Google Scholar]
- Liu, H.; Hao, P.; Liao, Y.; Tanvir, S.; Boriboonsomsin, K.; Barth, M.J. Eco-Friendly Crowdsourced Meal Delivery: A Dynamic On-Demand Meal Delivery System with a Mixed Fleet of Electric and Gasoline Vehicles. IEEE Trans. Intell. Transport. Syst. 2024, 25, 11397–11410. [Google Scholar] [CrossRef]
- Le Hong, Z.; Zimmerman, N. Air Quality and Greenhouse Gas Implications of Autonomous Vehicles in Vancouver, Canada. Transp. Res. Part D Transp. Environ. 2021, 90, 102676. [Google Scholar] [CrossRef]
- Liu, H.; Guensler, R.; Lu, H.; Xu, Y.; Xu, X.; Rodgers, M.O. MOVES-Matrix for High-Performance on-Road Energy and Running Emission Rate Modeling Applications. J. Air Waste Manag. Assoc. 2019, 69, 1415–1428. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Aviquzzaman, M.; Lin, Z. Analysis of Plug-in Hybrid Electric Vehicles’ Utility Factors Using GPS-Based Longitudinal Travel Data. Transp. Res. Part C Emerg. Technol. 2015, 57, 1–12. [Google Scholar] [CrossRef]
- Hamza, K.; Laberteaux, K.P. Utility Factor Curves for Plug-in Hybrid Electric Vehicles: Beyond the Standard Assumptions. World Electr. Veh. J. 2023, 14, 301. [Google Scholar] [CrossRef]
- Goebel, D.; Plötz, P. Machine Learning Estimates of Plug-in Hybrid Electric Vehicle Utility Factors. Transp. Res. Part D Transp. Environ. 2019, 72, 36–46. [Google Scholar] [CrossRef]
- Zheng, J.; Yu, R.; Liu, Y.; Zou, Y.; Zhao, D. The Technological Progress of the Fuel Consumption Rate for Passenger Vehicles in China: 2009–2016. Energies 2019, 12, 2384. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, G.; Zhang, L.; Zhai, Z.; He, W.; Yin, H.; Yu, L. Impact of Lockdown Policies on Urban Traffic Conditions and Carbon Dioxide Emissions Based on an Emission Model on the Link Level in Hour Granularity. J. Clean. Prod. 2024, 437, 140426. [Google Scholar] [CrossRef]
- Kapustin, N.O.; Grushevenko, D.A. Long-Term Electric Vehicles Outlook and Their Potential Impact on Electric Grid. Energy Policy 2020, 137, 111103. [Google Scholar] [CrossRef]
- Ahn, K.; Bichiou, Y.; Farag, M.; Rakha, H.A. Multi-Objective Eco-Routing Model Development and Evaluation for Battery Electric Vehicles. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 867–879. [Google Scholar] [CrossRef]
- Ahn, K.; Rakha, H.A.; Park, S. Eco Look-Ahead Control of Battery Electric Vehicles and Roadway Grade Effects. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 429–437. [Google Scholar] [CrossRef]
- Chen, H.; Rakha, H.A. Battery Electric Vehicle Eco-Cooperative Adaptive Cruise Control in the Vicinity of Signalized Intersections. Energies 2020, 13, 2433. [Google Scholar] [CrossRef]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation—A Case Study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Fiori, C.; Marzano, V. Modelling Energy Consumption of Electric Freight Vehicles in Urban Pickup/Delivery Operations: Analysis and Estimation on a Real-World Dataset. Transp. Res. Part D Transp. Environ. 2018, 65, 658–673. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-Based Electric Vehicle Energy Consumption Model: Model Development and Validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Rakha, H.A.; Ahn, K.; Moran, K.; Saerens, B.; Bulck, E.V.D. Virginia Tech Comprehensive Power-Based Fuel Consumption Model: Model Development and Testing. Transp. Res. Part D Transp. Environ. 2011, 16, 492–503. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, X.; Yu, Q.; Ye, Y.; Yu, M. Development of a Representative Urban Driving Cycle Construction Methodology for Electric Vehicles: A Case Study in Xi’an. Transp. Res. Part D Transp. Environ. 2020, 81, 102279. [Google Scholar] [CrossRef]
- Achour, H.; Olabi, A.G. Driving Cycle Developments and Their Impacts on Energy Consumption of Transportation. J. Clean. Prod. 2016, 112, 1778–1788. [Google Scholar] [CrossRef]
- Rezaei, H.; Ghomsheh, M.J.; Kowsary, F.; Ahmadi, P. Performance Assessment of a Range-Extended Electric Vehicle under Real Driving Conditions Using Novel PCM-Based HVAC System. Sustain. Energy Technol. Assess. 2021, 47, 101527. [Google Scholar] [CrossRef]
- Al-Wreikat, Y.; Serrano, C.; Sodré, J.R. Driving Behaviour and Trip Condition Effects on the Energy Consumption of an Electric Vehicle under Real-World Driving. Appl. Energy 2021, 297, 117096. [Google Scholar] [CrossRef]
- Shen, Y.; Xie, J.; He, T.; Yao, L.; Xiao, Y. CEEMD-Fuzzy Control Energy Management of Hybrid Energy Storage Systems in Electric Vehicles. IEEE Trans. Energy Convers. 2024, 39, 555–566. [Google Scholar] [CrossRef]
- Fan, P.; Song, G.; Zhu, Z.; Wu, Y.; Zhai, Z.; Yu, L. Road Grade Estimation Based on Large-Scale Fuel Consumption Data of Connected Vehicles. Transp. Res. Part D Transp. Environ. 2022, 106, 103262. [Google Scholar] [CrossRef]
- Song, G.; Yu, L.; Tu, Z. Distribution Characteristics of Vehicle-Specific Power on Urban Restricted-Access Roadways. J. Transp. Eng. 2012, 138, 202–209. [Google Scholar] [CrossRef]
- Jiménez-Palacios, J.L. Understanding and Quantifying Motor Vehicle Emissions with Vehicle Specific Power and TILDAS Remote Sensing. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- US EPA Overview of EPA’s MOtor Vehicle Emission Simulator (MOVES4). Available online: https://nepis.epa.gov/Exe/ZyPDF.cgi?Dockey=P10186IV.pdf (accessed on 24 October 2023).
- Hayes, J.G.; Davis, K. Simplified Electric Vehicle Powertrain Model for Range and Energy Consumption Based on EPA Coast-down Parameters and Test Validation by Argonne National Lab Data on the Nissan Leaf. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–6. [Google Scholar]
- SAE J1634_202104; Battery Electric Vehicle Energy Consumption and Range Test Procedure. SAE International: Warrendale, PA, USA, 2021.
- ISO 6469-3:2021; Electrically propelled road vehicles—Safety specifications. International Organization for Standardization: Geneva, Switzerland, 2021.
- Hamby, D.M. A Review of Techniques for Parameter Sensitivity Analysis of Environmental Models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, J.; Brooker, A.; Wood, E. Sensitivity of Battery Electric Vehicle Economics to Drive Patterns, Vehicle Range, and Charge Strategies. J. Power Sources 2012, 209, 269–277. [Google Scholar] [CrossRef]
- Fan, P.; Yin, H.; Lu, H.; Wu, Y.; Zhai, Z.; Yu, L.; Song, G. Which Factor Contributes More to the Fuel Consumption Gap between In-Laboratory vs. Real-World Driving Conditions? An Independent Component Analysis. Energy Policy 2023, 182, 113739. [Google Scholar] [CrossRef]
- Tutuianu, M.; Bonnel, P.; Ciuffo, B.; Haniu, T.; Ichikawa, N.; Marotta, A.; Pavlovic, J.; Steven, H. Development of the World-Wide Harmonized Light Duty Test Cycle (WLTC) and a Possible Pathway for Its Introduction in the European Legislation. Transp. Res. Part D Transp. Environ. 2015, 40, 61–75. [Google Scholar] [CrossRef]
- Fan, P.; Song, G.; Lu, H.; Yin, H.; Zhai, Z.; Wu, Y.; Yu, L. Impact of Ambient Temperature on Light-Duty Gasoline Vehicle Fuel Consumption under Real-World Driving Conditions. Int. J. Sustain. Transp. 2024, 18, 589–604. [Google Scholar] [CrossRef]
- Xu, X.; Aziz, H.M.A.; Guensler, R. A Modal-Based Approach for Estimating Electric Vehicle Energy Consumption in Transportation Networks. Transp. Res. Part D Transp. Environ. 2019, 75, 249–264. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, P.; Lu, H.; Song, G. Fuel Consumption of Hybrid Electric Vehicles under Real-World Road and Temperature Conditions. Transp. Res. Part D Transp. Environ. 2025, 142, 104691. [Google Scholar] [CrossRef]
- Boggio-Marzet, A.; Monzon, A.; Rodriguez-Alloza, A.M.; Wang, Y. Combined Influence of Traffic Conditions, Driving Behavior, and Type of Road on Fuel Consumption. Real Driving Data from Madrid Area. Int. J. Sustain. Transp. 2021, 16, 301–313. [Google Scholar] [CrossRef]
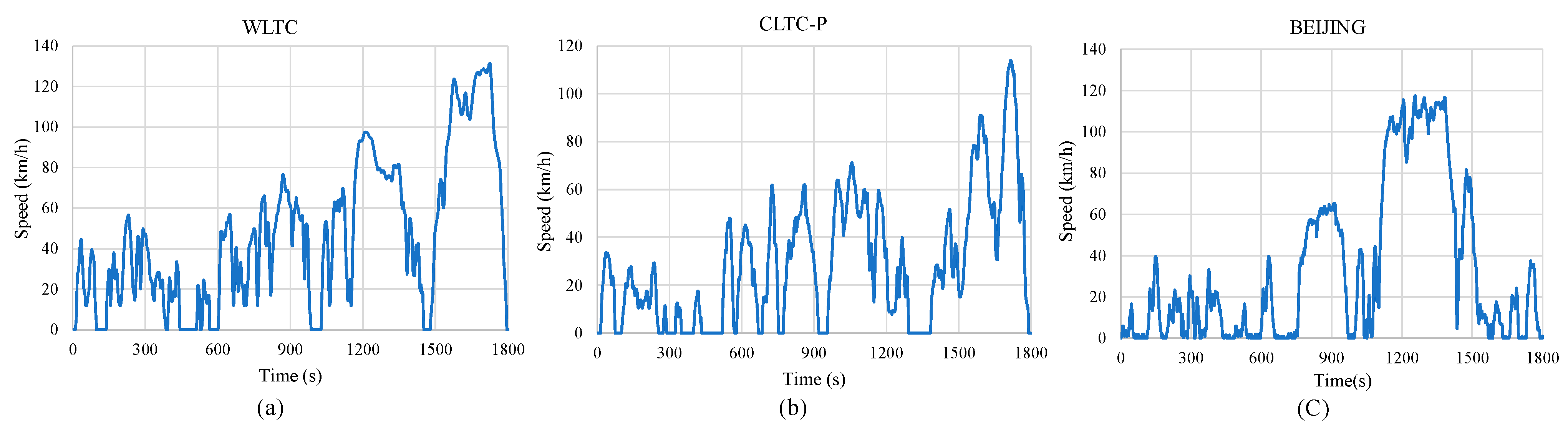





| Test Time /s | Test Distance /km | Maximum Speed /(km/h) | Average Speed /(km/h) | Energy Consumption of EVs /(kWh/100 km) | Energy Consumption of CVs /(kWh/100 km) | |
|---|---|---|---|---|---|---|
| WLTC | 1800 | 23.3 | 131.3 | 46.5 | 24.9 | 68.7 |
| CLTC-P | 1800 | 14.5 | 114.0 | 29.0 | 20.2 | 88.3 |
| BEIJING | 1800 | 16.5 | 117.5 | 32.9 | 19.3 | 81.2 |
| Energy Consumption of WLTC /(kW·h per Trip) | Energy Consumption of CLTC-P /(kW·h per Trip) | Energy Consumption of Beijing Trip Segment /(kW·h per Trip) | ||||
|---|---|---|---|---|---|---|
| EVs | CVs | EVs | CVs | EVs | CVs | |
| Positive VSP Bins | 5.9 | 12.9 | 3.5 | 8.6 | 4.2 | 8.9 |
| 0th VSP bin | 0.2 | 1.6 | 0.4 | 2.7 | 0.4 | 3.2 |
| Negative VSP Bins | −0.3 | 1.5 | −0.2 | 1.4 | −0.1 | 1.4 |
| SUM | 5.8 | 16.0 | 3.7 | 12.8 | 4.5 | 13.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Lu, H.; Fan, P.; Liu, R.; Li, S.; Wu, Y.; Song, G. Comparative Sensitivity Analyses of Energy Consumption in Response to Average Speed Between Electric Vehicles and Conventional Vehicles: Case Study in Beijing, China. Energies 2025, 18, 2268. https://doi.org/10.3390/en18092268
Lei X, Lu H, Fan P, Liu R, Li S, Wu Y, Song G. Comparative Sensitivity Analyses of Energy Consumption in Response to Average Speed Between Electric Vehicles and Conventional Vehicles: Case Study in Beijing, China. Energies. 2025; 18(9):2268. https://doi.org/10.3390/en18092268
Chicago/Turabian StyleLei, Xue, Hongyu Lu, Pengfei Fan, Rui Liu, Songsong Li, Yizheng Wu, and Guohua Song. 2025. "Comparative Sensitivity Analyses of Energy Consumption in Response to Average Speed Between Electric Vehicles and Conventional Vehicles: Case Study in Beijing, China" Energies 18, no. 9: 2268. https://doi.org/10.3390/en18092268
APA StyleLei, X., Lu, H., Fan, P., Liu, R., Li, S., Wu, Y., & Song, G. (2025). Comparative Sensitivity Analyses of Energy Consumption in Response to Average Speed Between Electric Vehicles and Conventional Vehicles: Case Study in Beijing, China. Energies, 18(9), 2268. https://doi.org/10.3390/en18092268







