An Artificial-Neural-Network-Based Direct Power Control Approach for Doubly Fed Induction Generators in Wind Power Systems

Abstract

The inherent complexity of wind energy systems has necessitated the development of sophisticated control methodologies to optimize operational efficiency. Artificial neural networks (ANN) have emerged as a powerful tool in wind turbine applications, offering sophisticated control capabilities for addressing the intricate challenges of energy conversion. This study focuses on the critical generator control block, where precise power management is essential to maintaining system stability and preventing operational disruptions. This research introduces an innovative ANN-based Direct Power Control (DPC) approach for a Doubly fed induction generator (DFIG) integrated into a wind power system, introducing a dual-MLP approach for precise power regulation. The proposed DPC-ANN controller proved effective in mitigating current ripples and achieving a near-unity power factor, indicating substantial improvement in power quality. Moreover, the spectrum harmonic analysis revealed that the controller yielded the lowest stator current total harmonic distortion of 1.29%, significantly outperforming traditional DPC-PI (2.76%) and DPC-Classic (2.24%) approaches. The proposed technique was rigorously implemented and validated using a real-time simulator (OPAL-RT) and MATLAB/Simulink (2020–2022) environment, specifically tested under a step wind profile. The real-time experimental validation highlights the practical applicability of this approach, bridging the gap between theoretical ANN-based control and real-world wind energy system implementation. These findings reinforce the potential of intelligent control strategies for optimizing renewable energy technologies, paving the way for more efficient and adaptive wind turbine control solutions.

1. Introduction

1.1. Overview

Presently, the importance of producing electricity through renewable energy systems is on the rise, driven by the growing scarcity of traditional energy sources and the urgent concern of global warming. Over the past few years, wind energy technology has garnered significant attention from both research groups and industry, as evidenced by the substantial number of published research papers. According to the International Energy Agency (IEA), the share of renewables in the electricity sector is expected to rise from 30% in 2023 to 46% by 2030, with most of this growth driven by wind and solar energy [1]. Similarly, the Global Wind Energy Council (GWEC) highlights the continued expansion of wind energy as a key contributor to global electricity generation by 2030 [2]. Currently, a prevalent system found in onshore wind farms is the variable-speed wind turbine system (WTS), incorporating a doubly fed induction generator. In this configuration, the stator is typically connected directly to the grid, while the rotor is linked through a frequency-controlled power converter [3]. Generally, the rotor-side converter manages active and reactive power, while the grid-side converter maintains the DC-link voltage to ensure unity power factor operation [4]. An outstanding feature that characterizes the DFIG involves its rotor-side converter (RSC), which requires dimensioning to just 30% of the generator capacity. This stands in stark contrast to other power generation units in variable-speed wind applications, representing a substantial reduction in size and cost [5,6].

1.2. Literature

Incorporating wind energy systems into the power grid poses challenges because of the unpredictable fluctuations in wind speeds. These variations result in issues like power fluctuations and irregularities in energy production, which, subsequently, have negative impacts on the electromagnetic torque generated by the generator, causing ripple effects. [7]. The literature to date highlights researchers’ substantial apprehension regarding the improvement in this conversion process. Conversely, there is a myriad of control strategies suggested to improve the functionality of wind turbine systems utilizing doubly fed induction generators under regular operating conditions [8]. Significantly, among these approaches, direct power control (DPC) emerges as a prominent technique for controlling DFIG due to its simplified control structure, rapid dynamic response, and reduced computational complexity [9]. The method offers direct and precise regulation of active and reactive power output, providing inherent decoupling between power components. By enabling independent and efficient management of power generation, DPC addresses critical challenges in wind turbine systems, making it a preferred control strategy for optimizing generator performance under varying wind conditions and grid requirements. Two main applications of the direct power control method are used for controlling doubly fed induction generators, each differing in their approach and implementation. Classical direct power control (DPC-Classic) directly regulates a DFIG’s stator active and reactive powers through the application of a control vector determined via a lookup table. This selection is based on the errors in active and reactive power and the angular position of the estimated voltage source vector [10]. The method employs dual comparator blocks with hysteresis bands: one dedicated to active power regulation and another for reactive power control to manage power errors. Additionally, a switching table is utilized to select the appropriate switching states for the rotor side converter (RSC), enabling efficient and responsive power control [11]. This method offers several significant advantages in wind energy systems, such as rapid transient performance, insensitivity to parameter uncertainties, reduced computational demands, and straightforward practical implementation [12]. These benefits make DPC an attractive option for controlling DFIGs in wind turbines, particularly in optimizing power extraction and grid integration. However, the approach is not without drawbacks. DPC-Classic often results in considerable power oscillations stemming from the wide bandwidth of their hysteresis controllers, which can compromise the power quality at the point of grid connection. Additionally, they result in variable switching frequencies in converters, potentially causing operational inconsistencies and increased stress on power electronic components [13].

In contrast, direct power control with PI controllers (DPC-PI) substitutes the hysteresis controllers of the classic DPC with PI controllers and replaces the switching table with Pulse Width Modulation (PWM). The PI controllers regulate the power components (active and reactive) by generating reference voltage signals, which are then utilized for the PWM-based converter control [14]. While PI controllers perform well in managing power exchange between the generator and the grid network, they have certain limitations. They may struggle with rapid wind speed variations, potentially resulting in a slower dynamic response compared to some more advanced control techniques [15]. Additionally, PI controllers can be sensitive to parameter variations in the DFIG system, which may necessitate periodic returning [16].

The DPC approach was selected for this study due to its superior dynamic response characteristics compared to conventional vector control methods, which are particularly valuable during grid fault conditions [17]. Recent studies have shown that while model predictive control offers competitive performance, DPC implementation requires significantly fewer computational resources while maintaining comparable efficiency [18]. Furthermore, research confirmed that DPC provides more robust operation under parameter variations commonly encountered in practical wind energy installations [19,20,21,22]. Despite alternative approaches, like sliding mode control, offering theoretical advantages in stability, the practical implementation complexity and chattering issues make them less suitable for commercial deployment as comprehensively analyzed [23].

The classical control tools used to implement the techniques previously discussed have limitations in their performance. In certain scenarios, these traditional approaches can even completely lose their effectiveness. The inherent complexity and nonlinearities of the systems being controlled can exceed the capabilities of standard regulators. To overcome the limitations inherent in traditional control methods for wind energy systems, artificial intelligence methods, including expert systems [24], genetic algorithms [25], artificial neural networks [26], and fuzzy logic [27], have found widespread application in the fields of power electronics and electrical machine control.

Artificial neural networks (ANNs) have emerged as a powerful alternative, offering innovative solutions for the complex, nonlinear dynamics of doubly fed induction generators. ANNs excel in processing large datasets, adapting to nonlinear relationships, and enabling rapid, multitasking computations [28], making them particularly suitable for the variable and unpredictable nature of wind power generation. In DFIG applications, ANN-based controllers have demonstrated remarkable improvements over conventional techniques. Recent research [29] showcased an ANN-enhanced super-twisting sliding mode control that significantly reduced tracking errors and improved convergence in DFIGs. Another study [16] further illustrated the versatility of neural networks in achieving stable control of nonlinear DFIGs under challenging grid conditions. The implementation of ANN controllers in DFIG systems offers remarkable performance enhancements, characterized by significantly reduced peak amplitudes during transient events, dramatically faster system response times, and substantially shortened settling periods [30]. Moreover, ANNs exhibit superior adaptability to fluctuating wind speeds and grid disturbances, thus optimizing system performance and efficiency [31].

Direct power control implementation using artificial neural networks represents an advanced approach to controlling wind-based DFIG systems, where the neural network replaces the traditional switching table and hysteresis controllers [26]. The ANN is trained to predict optimal switching states for the power converter based on the errors in active and reactive power and the position of the stator flux vector [32]. This approach offers several advantages over classical DPC, including reduced power ripples, improved dynamic performance, and enhanced robustness against parameter variations [33]. The ANN’s ability to learn and adapt to changing operating conditions makes it particularly effective in handling the variable nature of wind speed and grid disturbances [34].

Consequently, ANNs have not only established themselves as a robust technique for data processing but have also revolutionized control strategies in wind energy systems, offering a more sophisticated, adaptive, and efficient approach to DFIG management.

1.3. Contribution and Organization of This Manuscript

This study presents several key contributions to wind energy system control:

-

Development of an innovative artificial-neural-network-based direct power control (DPC-ANN) strategy for DFIGs that overcomes the limitations of conventional control techniques.

-

Demonstration of significant performance improvements, including the following:

• Enhanced power control accuracy;
• Improved dynamic response under varying wind conditions;
• Reduced harmonic distortion;
• Maintenance of the near-unity power factor.

-

Comprehensive validation through simulation and real-time implementation, providing empirical evidence of the approach’s effectiveness in practical wind energy applications.

These contributions advance the understanding of neural-network-based control strategies in renewable energy technologies.

The structure of this manuscript is as follows: Section 2 provides a comprehensive system modeling approach, establishing the theoretical foundation for this study. This includes detailed equations for the DFIG and turbine aerodynamic characteristics. Section 3 introduces the proposed DPC-ANN technique, offering an in-depth description of its architecture, training methodology, and implementation. Section 4 presents a comprehensive performance evaluation of the proposed DPC-ANN control strategy through extensive simulation studies and real-time implementation. Using the MATLAB/Simulink platform, an extensive detailed performance evaluation is performed to assess the capabilities of the proposed approach against conventional approaches, specifically classical DPC and DPC-PI control schemes. The proposed DPC-ANN strategy is then validated through real-time implementation using the OPAL-RT simulator, providing practical insights into the controller’s behavior under realistic operating conditions. The section concludes with an in-depth discussion of the obtained results, highlighting the key performance metrics and advantages of the developed strategy. Section 5 synthesizes this paper by presenting the main contributions, analyzing the implications of this research, and suggesting potential directions for subsequent research.

2. Wind Power Generation System Modeling

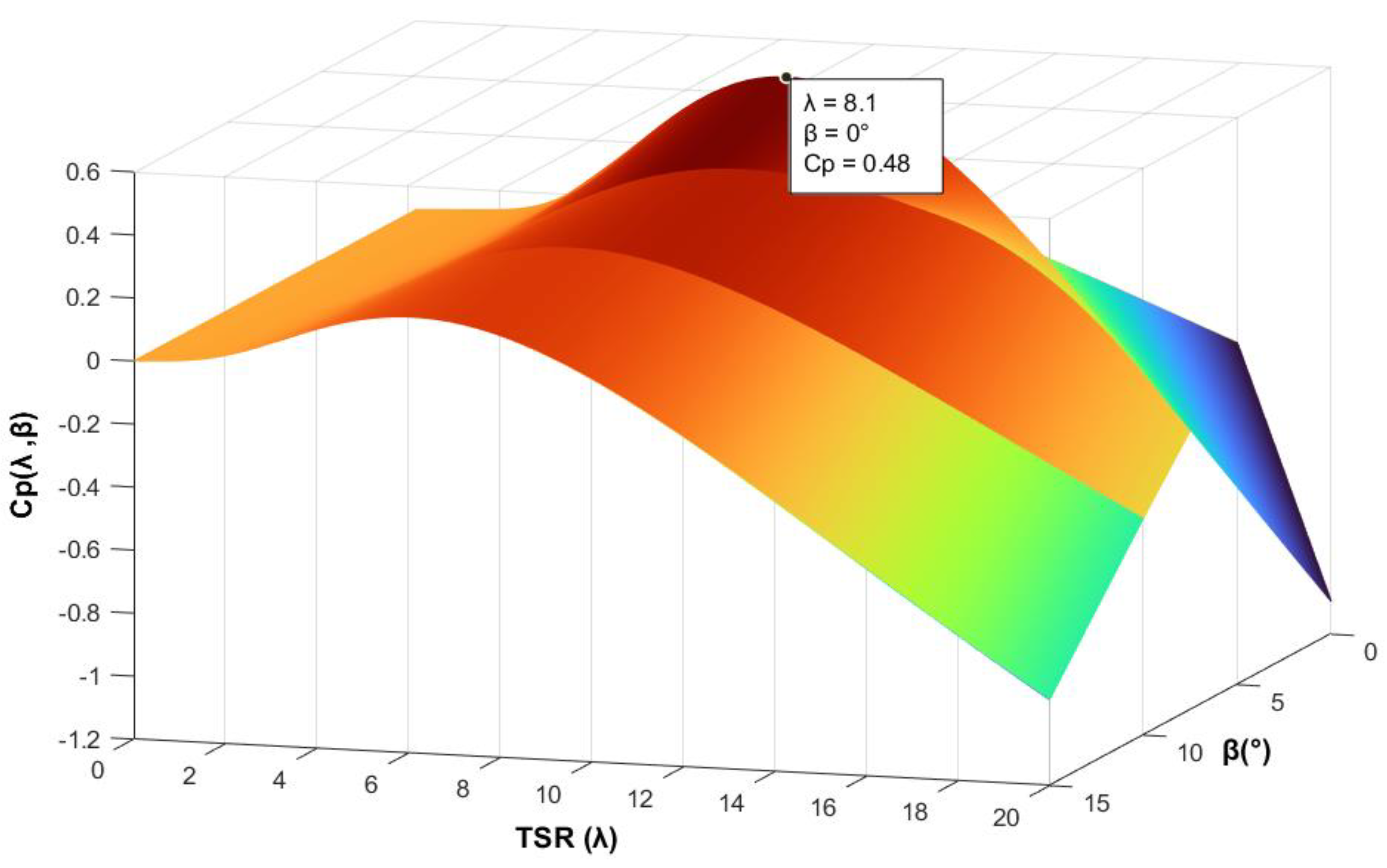
2.1. Turbine Modeling

The wind turbine model is defined by key parameters characterizing wind energy conversion: aerodynamic power $P_{aero}$, extracted from wind through a relationship involving aerodynamic torque $T_{aero}$, the tip speed ratio λ, and turbine speed ${\Omega }_t$, each described by specific mathematical equations [26]:

$$P_{aero}={\displaystyle \frac{1}{2}}{C}_p(\lambda ,\beta )\rho \pi R^2{V}_{wind}^3$$

(1)

$$T_{aero}={\displaystyle \frac{P_{aero}}{{\Omega }_t}}$$

(2)

$$\lambda ={\displaystyle \frac{{\Omega }_t R}{V_{wind}}}$$

(3)

The power coefficient $C_p(\lambda ,\beta )$ characterizes the wind turbine’s effectiveness in converting aerodynamic turbine power to mechanical power. Understanding the relationship between $C_p,\lambda ,$ and $\beta$ is pivotal for system optimization of wind energy systems.

For wind turbines with variable speeds, the power coefficient can be approximated using the following formula [26]:

$$C_p\left(\lambda ,\beta \right)=0.5176\left({\displaystyle \frac{116}{{\lambda }_i}}-0.4\beta -5\right)·e^{\left({\displaystyle \frac{-21}{{\lambda }_i}}\right)}+0.0068\lambda$$

(4)

where

$${\displaystyle \frac{1}{{\lambda }_i}}={\displaystyle \frac{1}{\lambda +0.08\beta }}-{\displaystyle \frac{0.035}{{\beta }^3+1}}$$

(5)

Engineers analyze the power coefficient’s variation with λ and pitch angle to optimize wind turbine performance. Figure 1 depicts the power coefficient variation with respect to the constant pitch angle and tip speed ratio. Maximizing generator efficiency requires implementing the Maximum Power Point Tracking (MPPT) strategy, which maintains the coefficient C_p at its optimal value by precisely adjusting the blade pitch and tip speed ratio.

2.2. DFIG Modeling

The mathematical model of a DFIG machine in the d-q frame can be formulated using the following equations [26]:

-

Electrical equation.

$$\left\{\begin{array}{c}{v}_{ds}=R_s{i}_{ds}+{\displaystyle \frac{d}{dt}}{\Phi }_{ds}-{\omega }_s{\Phi }_{qs}\\ v_{qs}=R_s{i}_{qs}+{\displaystyle \frac{d}{dt}}{\Phi }_{qs}+{\omega }_s{\Phi }_{ds}\end{array}\right.$$

(6)

$$\left\{\begin{array}{c}{v}_{dr}=R_r{i}_{dr}+{\displaystyle \frac{d}{dt}}{\Phi }_{dr}-{\omega }_r{\Phi }_{qr}\\ v_{qr}=R_r{i}_{qr}+{\displaystyle \frac{d}{dt}}{\Phi }_{qr}+{\omega }_r{\Phi }_{dr}\end{array}\right.$$

(7)

-

Magnetic equation

$$\left\{\begin{array}{c}{\Phi }_{ds}=L_{ss}{i}_{ds}+L_m{i}_{dr}\\ {\Phi }_{qs}=L_{ss}{i}_{qs}+L_m{i}_{qr}\end{array}\right.$$

(8)

$$\left\{\begin{array}{c}{\Phi }_{dr}=L_{rr}{i}_{dr}+L_m{i}_{ds}\\ {\Phi }_{qr}=L_{rr}{i}_{qr}+L_m{i}_{qs}\end{array}\right.$$

(9)

-

The equations describing the electromagnetic torque, active power, and reactive power generated by the DFIG are as follows [33]:

$$\left\{\begin{array}{c}{T}_{em}={\displaystyle \frac{3}{2}}p{\displaystyle \frac{L_m}{L_{ss}}}({\Phi }_{qs}{i}_{dr}-{\Phi }_{ds}{i}_{qr})\\ P_s={\displaystyle \frac{3}{2}}{(v}_{ds}{i}_{ds}+v_{qs}{i}_{qs})\\ Q_s={\displaystyle \frac{3}{2}}{(v}_{qs}{i}_{ds}-v_{ds}{i}_{qs})\end{array}\right.$$

(10)

Utilizing the field-oriented control methodology and disregarding stator resistance, we derive:

$$\left\{\begin{array}{c}{\Phi }_{ds}={\Phi }_s=cte\\ {\Phi }_{qs}=0\\ {\dot{\Phi }}_{ds}=0\\ v_{ds}=0\\ v_{qs}=v_s={\omega }_s{\Phi }_s\end{array}\right.$$

(11)

$$\left\{\begin{array}{c}{i}_{ds}={\displaystyle \frac{{\Phi }_s}{L_{ss}}}-{\displaystyle \frac{L_m}{L_{rr}}}{i}_{dr}\\ i_{qs}=-{\displaystyle \frac{L_m}{L_{ss}}}{i}_{qr}\end{array}\right.$$

(12)

Subsequently, the active and reactive powers can be formulated as expressions:

$$\left\{\begin{array}{c}{P}_s=-{\displaystyle \frac{3}{2}}{\displaystyle \frac{L_m}{L_{ss}}}{v}_s{i}_{qr}\\ Q_s={\displaystyle \frac{3}{2}}{v}_s({\displaystyle \frac{{\Phi }_s}{L_{ss}}}-{\displaystyle \frac{L_m}{L_{ss}}}{i}_{dr})\end{array}\right.$$

(13)

The formulation for the electromagnetic torque can be represented as follows:

$$T_{em}=K_e{i}_{qr}$$

(14)

where $K_e=-{\displaystyle \frac{3}{2}}p{\displaystyle \frac{L_m}{L_{ss}}}{\Phi }_s$.

The rotor voltages can be formulated as [23]:

$$\left\{\begin{array}{c}{v}_{dr}=R_r{i}_{dr}+\sigma L_r{\displaystyle \frac{d{i}_{dr}}{dt}}+e_{qr}\\ v_{qr}=R_r{i}_{qr}+\sigma L_r {\displaystyle \frac{d{i}_{qr}}{dt}}+e_{dr}+e_{\Phi } \end{array} \right.\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \left\{\begin{array}{c}{ e}_{qr}=-{\omega }_r\sigma L_r{i}_{qr}\\ { e}_{dr}={\omega }_r\sigma L_r{i}_{dr}\\ e_{\Phi }={\omega }_r{\displaystyle \frac{L_m}{L_s}}{\Phi }_s\\ \sigma =1-{\displaystyle \frac{L_m^2}{L_{ss}{L}_{rr}}}\end{array}\right.$$

(15)

-

Powers estimation.

The estimation of the active and reactive powers of the stator is performed using Equation (16):

$$\left\{\begin{array}{c}{P}_s=-{\displaystyle \frac{3}{2}}{\displaystyle \frac{L_m}{\sigma L_{rr}{L}_{ss}}}{v}_s{\Phi }_{\beta r}\\ Q_s={\displaystyle \frac{3}{2}}{v}_s({\displaystyle \frac{{\Phi }_s}{\sigma L_{ss}}}-{\displaystyle \frac{L_m}{\sigma L_{rr}{L}_{ss}}}{\Phi }_{\alpha r})\end{array}\right.\mathrm{with} \left\{\begin{array}{c}{\Phi }_{\alpha r}=\sigma L_{rr}{i}_{\alpha r}+{\displaystyle \frac{L_m}{L_{ss}}}{\Phi }_s\\ {\Phi }_{\beta r}=\sigma L_{rr}{i}_{\beta r}\\ \left|{\Phi }_s\right|={\displaystyle \frac{\left|\overline{v_s}\right|}{{\omega }_s}}\end{array}\right.$$

(16)

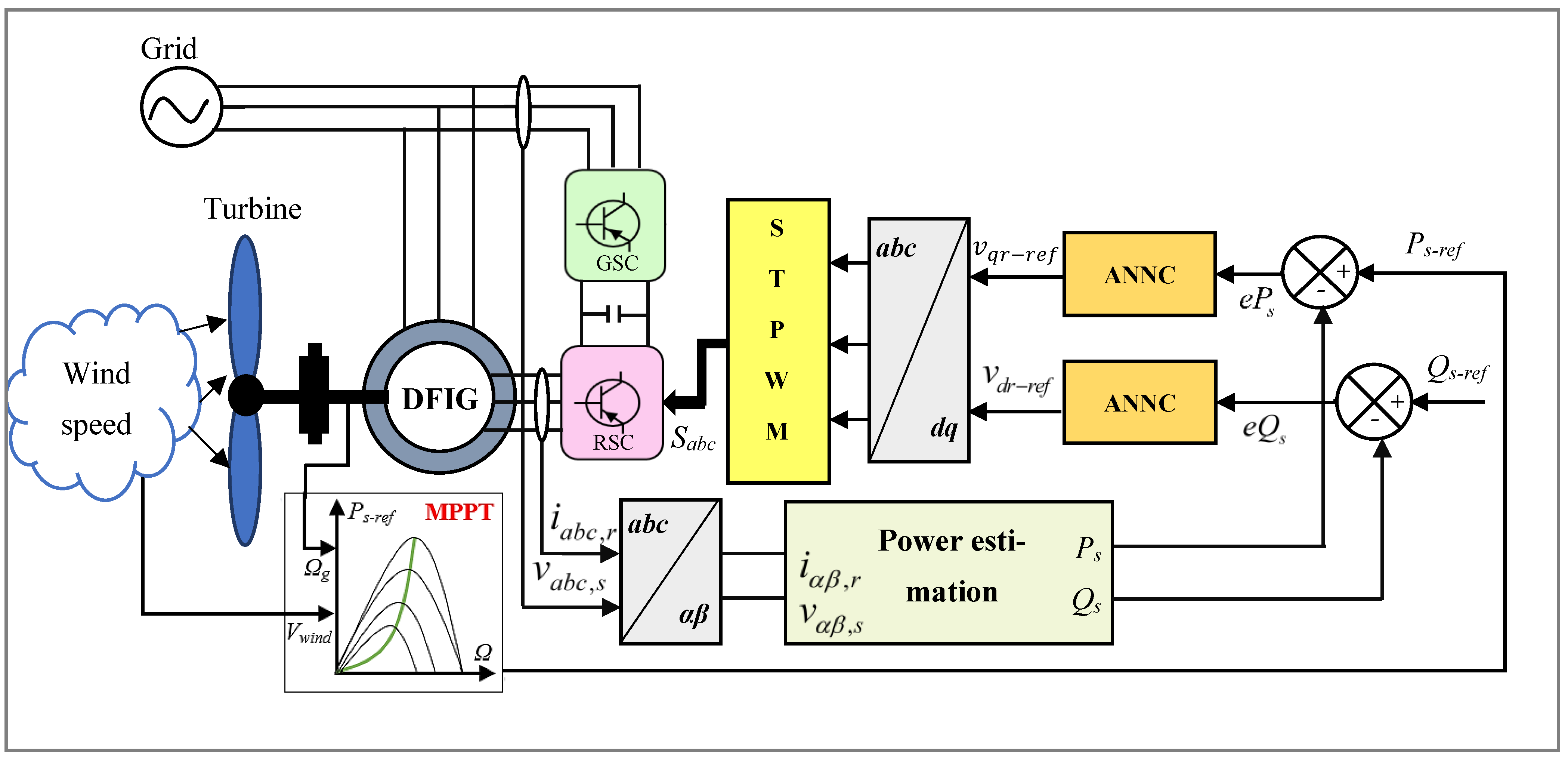
3. The Proposed DPC-ANN Technique

Artificial neural networks (ANNs) draw their fundamental concepts from the complex biological neuronal structures found in human cognition [35]. Typically, an ANN architecture comprises three primary layers: input nodes, intermediate processing layers, and output nodes. These layers contain computational units with adjustable weights that facilitate information processing and adaptation. The network’s performance critically depends on its structure and training process. Optimizing an ANN requires carefully selecting key architectural elements, neuron distribution across layers, and an appropriate adaptive learning algorithm. This optimization often involves systematic trial-and-error approaches to achieve optimal computational performance.

The implementation of a neural network follows a two-phase methodology [36], as illustrated in Figure 2. The initial phase involves network training using a pre-prepared dataset, where the network learns to recognize patterns by iteratively adjusting connection weights to reduce the error between predicted and desired outputs. Once the network achieves satisfactory performance, the second phase begins, involving network validation using new, previously unseen input data to assess its generalization capability and prediction accuracy.

The mathematical model of a neuron consists of two main computational steps represented by Equations (17) and (18) [37]. Equation (17) computes the first layer output y_i using a transfer function $f_1\left(s\right)$ operating on the weighted combination of inputs, while Equation (18) calculates the final neuron output A_i using the activation function $f_2\left(s\right)$.

$$y_i=f_1\left(s\right)·\left\{{\sum }_{i=1}^N\left(x_i·w_i+b\right)\right\}$$

(17)

$${ A}_i=f_2\left(s\right)·\left\{{\sum }_{i=1}^N\left(y_i·w_i+b\right)\right\}$$

(18)

where $x_i$, $w_i$, $b,$ and $y_i$ represent the input signals, the corresponding synaptic weights of the neural inputs, the bias parameter typically assigned values +1 or −1, and the neuron output signals, respectively. The results of the weighted sum are called the neuron’s activation level. $f_1\left(s\right)$ denotes the nonlinear hyperbolic tangent activation function, and $f_2\left(s\right)$ represents the linear transfer function are expressed by equations.

$$f_1\left(s\right)={\displaystyle \frac{e^{\alpha s}-e^{-\alpha s}}{e^{\alpha s}+e^{-\alpha s}}}$$

(19)

$$f_2\left(s\right)=\beta s$$

(20)

where $\alpha$ and $\beta$ are the gains.

The neural network learning process employs a feedforward backpropagation algorithm that continues until the Mean Square Error (MSE) between the target and actual responses reaches a minimal value.

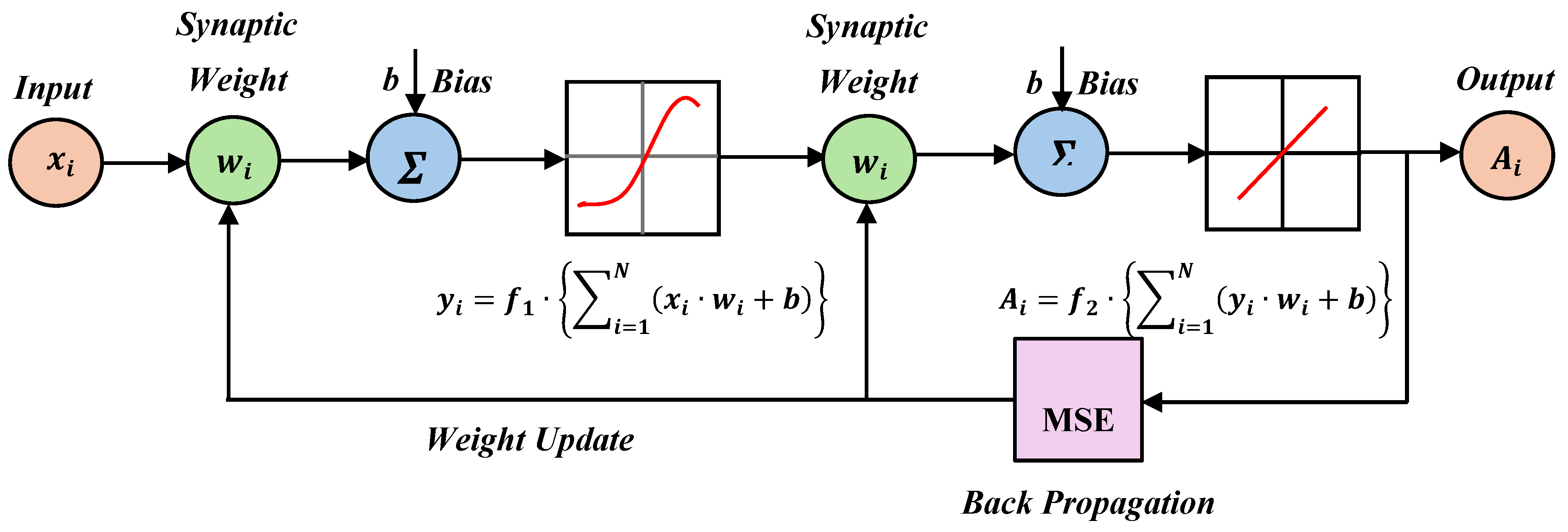
3.1. ANN Structure

For this implementation, the neural architecture is designed to regulate both active and reactive power in the DFIG system. The approach employs two independent multilayer perceptron (MLP) neural networks, each dedicated to controlling a specific power component. Each MLP follows a three-layer structure: an input layer with a single neuron, a hidden layer comprising eight neurons utilizing the hyperbolic tangent sigmoid (tansig) activation function, and an output layer with a single neuron.

During the training process, the first MLP receives the active power error as input and generates the quadrature rotor voltage reference as output. Similarly, the second MLP processes the reactive power error and produces the direct rotor voltage reference, as illustrated in Figure 3. The selection of the MLP topology (1-8-1) was driven by a balance between model complexity and generalization capability. The single input neuron corresponds to the reference power signal, while the hidden layer configuration determined through empirical testing offers an optimal trade-off between accuracy and computational efficiency. The output layer provides the predicted control signal for effective power regulation.

The tansig activation function was chosen for its ability to accommodate both positive and negative values while ensuring smooth gradient transitions during backpropagation. This enhances the network’s learning dynamics, leading to faster convergence compared to linear or purely sigmoid-based functions.

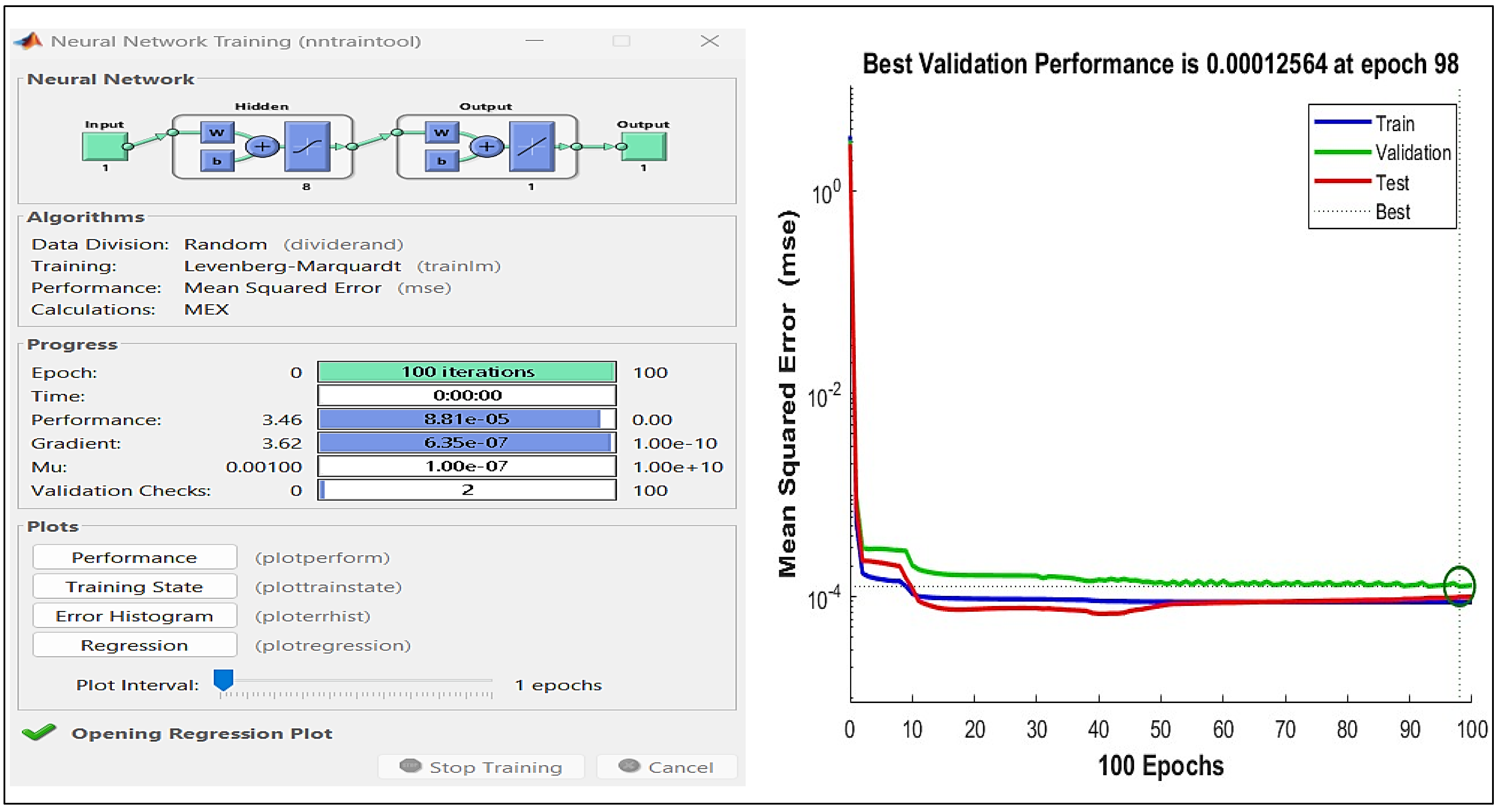
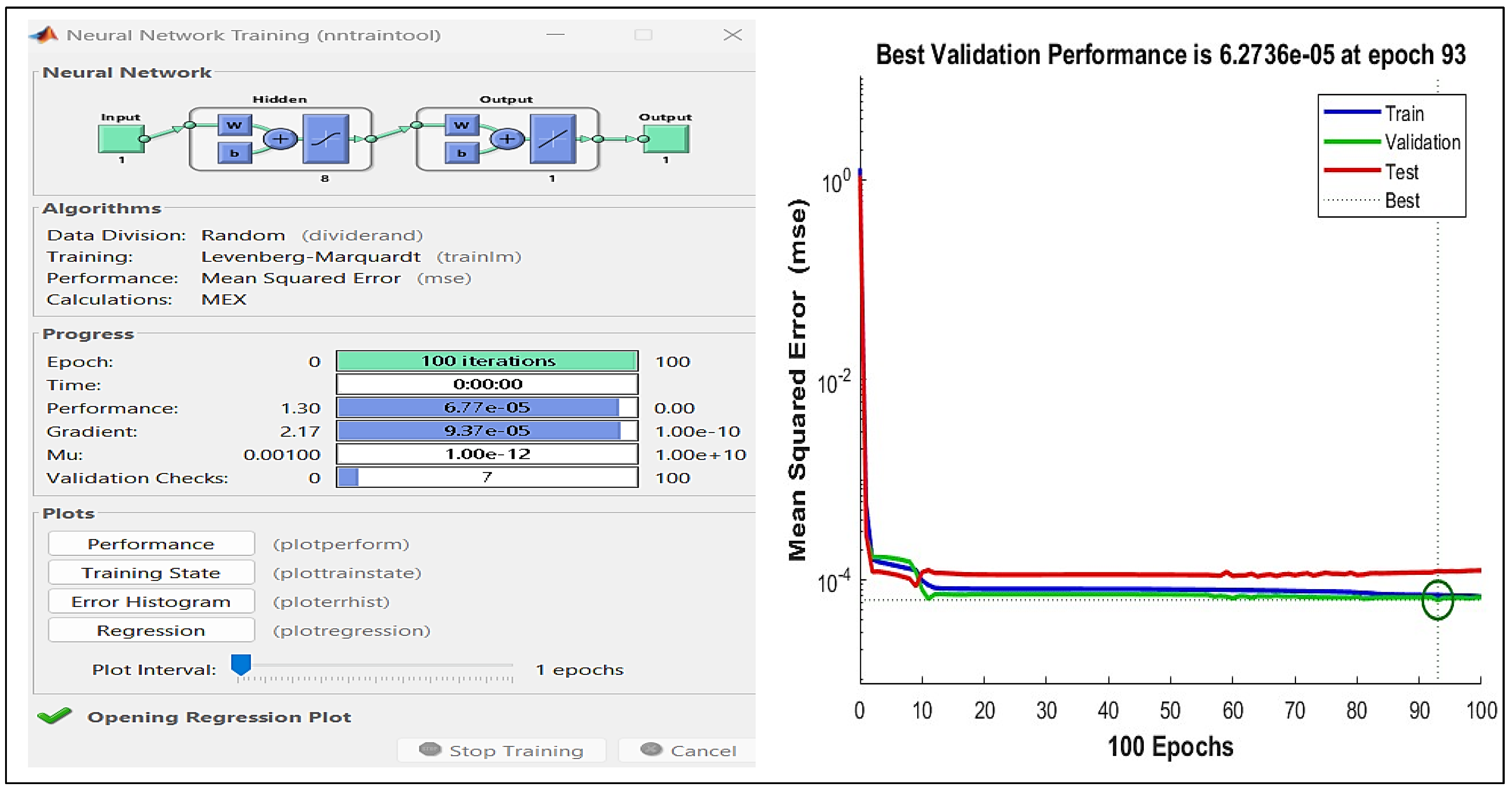
3.2. Training Process

The multilayer perceptron (MLP) controllers were trained using the Levenberg–Marquardt (LM) backpropagation technique, renowned for its rapid convergence in neural network training. By iteratively adjusting network weights and biases, the LM method enables consistent output generation for similar input values. This output approximation capability makes neural networks particularly effective in intelligent control applications.

The Mean Square Error (MSE) was selected as the evaluation metric during the training process, defined as [38]:

$$MSE={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(D_i\left(k\right)-A_i\left(k\right)\right)}^2$$

(21)

where $A_i$ represents the actual network response, $D_i$ denotes the target output, N represents the training dataset size, and k indicates the number of iterations.

The collected dataset was divided into three subsets: 70% for training, 15% for testing, and 15% for validation. A multilayer perceptron with eight hidden neurons was employed, utilizing the tansig and purelin activation functions. The ANN was trained for 100 epochs using the Levenberg–Marquardt backpropagation algorithm. The selection of 100 epochs was based on the observed convergence behavior of the neural network. The Mean Squared Error (MSE) rapidly decreased during the initial training phases and stabilized before reaching 100 epochs, ensuring both efficiency and accuracy. The best validation performance was achieved at epoch 98 for the active power (Ps) and epoch 93 for the reactive power (Qs), indicating that further training beyond this point does not provide significant improvements. Figure 4 and Figure 5 illustrate the training performance, showcasing the best validation performance achieved at epoch 98, with an MSE of $1.2564\times {10}^{-4},$ for the first controller and at epoch 93, with an MSE of $6.2736\times {10}^{-5}$.

Figure 6 illustrates the ANN-based control scheme for a DFIG wind energy system, integrating MPPT and STPWM to optimize power extraction and quality. The wind turbine converts wind energy into mechanical energy, with MPPT ensuring operation at the optimal power point. The DFIG’s rotor and stator generate electrical power, regulated through a back-to-back converter consisting of a rotor-side converter (RSC) and a grid-side converter (GSC). The RSC controls active and reactive power, while the GSC ensures power quality. STPWM generates switching signals to reduce harmonics, and a reference frame transformation simplifies control. A power estimation block calculates active and reactive power from rotor currents and stator voltages. There are two ANN controllers: one regulates quadrature rotor voltage for active power and the other adjusts direct rotor voltage for reactive power.

4. Simulation Results and Discussion

To assess the effectiveness, stability, and efficiency of the developed DPC-ANN controller, we conducted simulations using two platforms: a MATLAB/Simulink model and an OPAL-RT real-time simulator. Both simulations were developed using a 1.5 kW DFIG model, with detailed parameters provided in the Appendix A. This dual-platform approach enabled comprehensive validation of the neural-network-based control strategy through both offline simulation and real-time implementation.

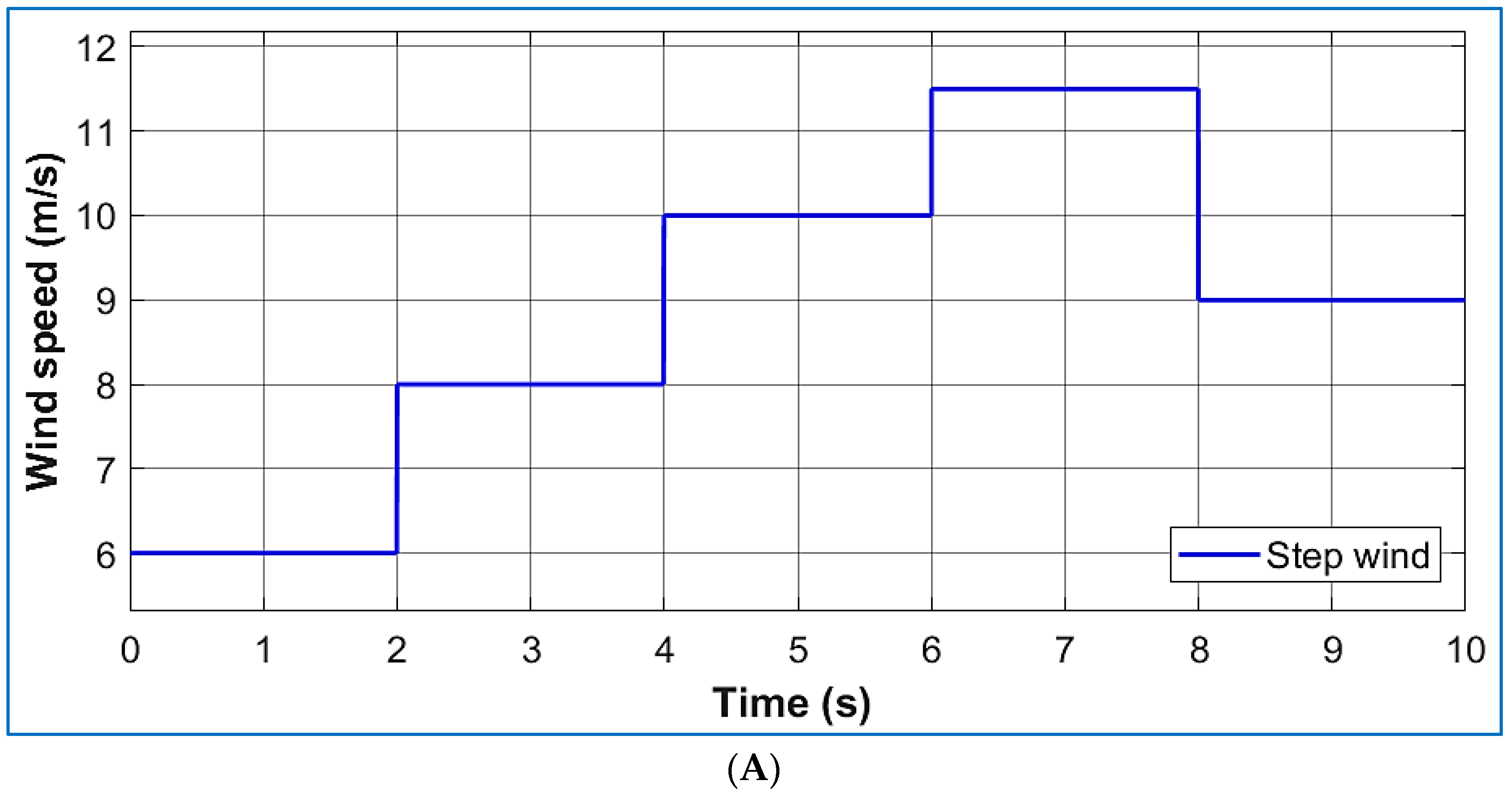
4.1. Aerodynamic Performance Analysis

Wind Speed Profile and Dynamic Response

As shown in Figure 7A, the step wind profile serves as a critical input for evaluating the wind turbine’s dynamic behavior using MATLAB/Simulink simulation. The simulation reveals the system’s response characteristics under varying wind conditions through a comprehensive analysis of key performance indicators.

Figure 7B illustrates the power coefficient behavior, which oscillates around 0.5. This value represents the turbine’s efficiency in converting wind energy to mechanical energy. The oscillations around this optimal point suggest that the control system attempts to maintain the turbine’s operation near its peak aerodynamic performance across different wind speed conditions.

The tip speed ratio analysis in Figure 7C provides further insight into the system’s performance. Ranging between 5.2 and 9.5, this parameter indicates the turbine operates within its optimal aerodynamic operating range. The consistent variation in the tip speed ratio demonstrates the system’s ability to adapt to changing wind conditions while maintaining efficient energy conversion.

As depicted in Figure 7D, the mechanical rotor speed variations validate the controller’s dynamic response. The observed speed range from 84 rpm to 171 rpm aligns with the expected operational parameters of the DFIG configuration. These speed transitions reflect the turbine’s mechanical system response to the applied step wind speed profile, showing how the rotor adjusts its speed to maintain optimal performance under varying wind conditions.

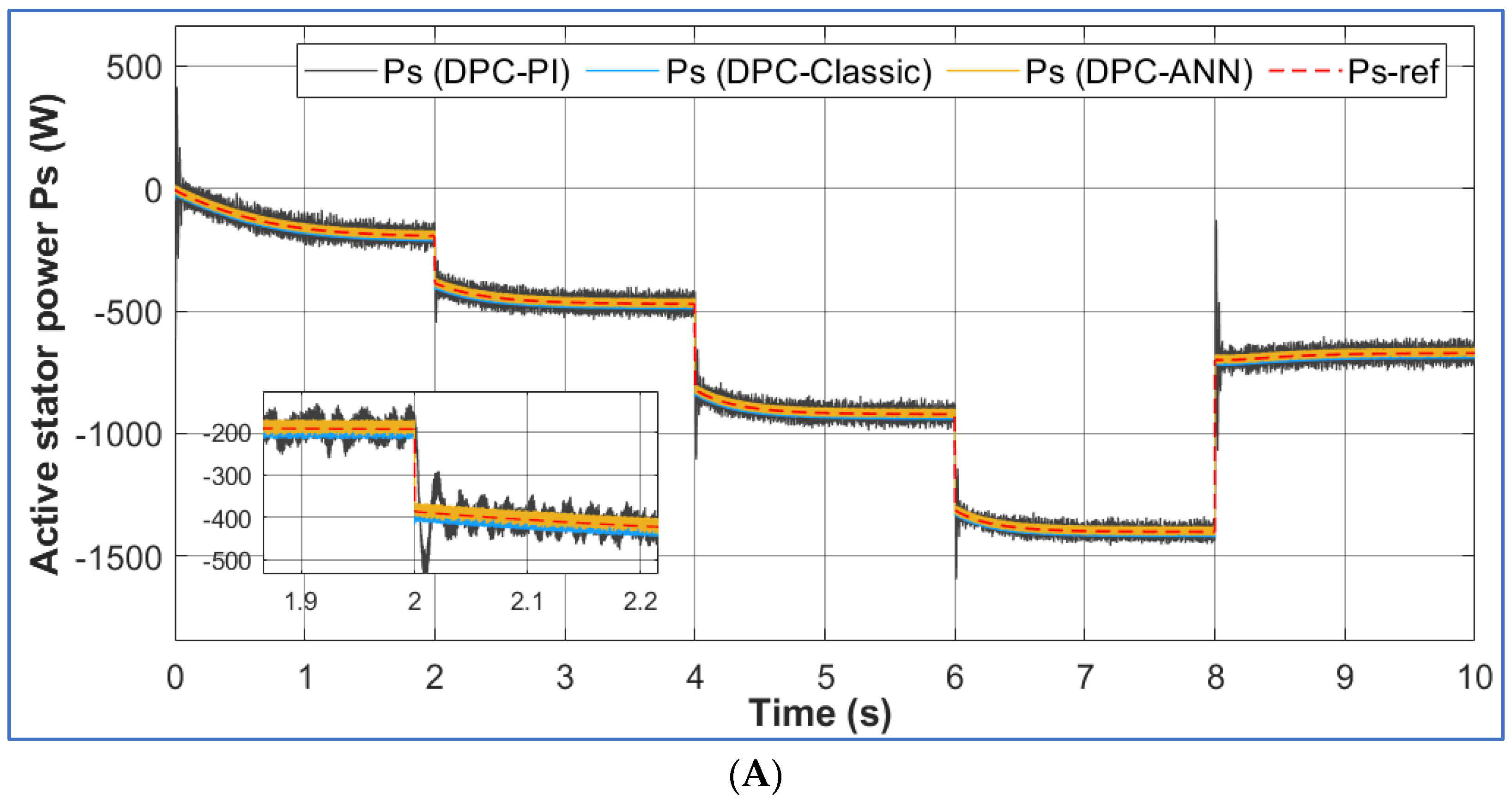
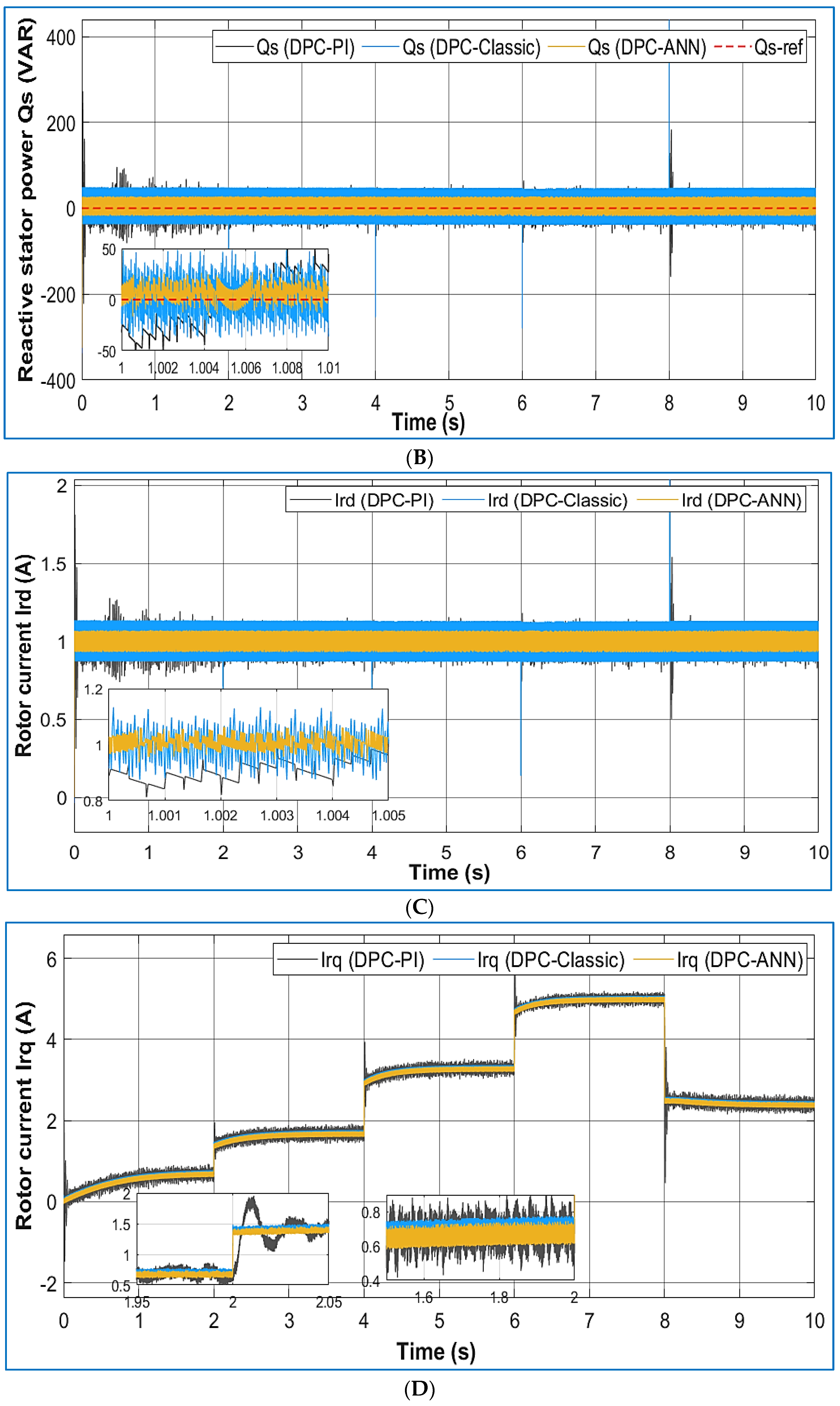
4.2. Real-Time Simulation Performance

Subsequently, real-time simulation was implemented on the OPAL-RT platform to validate the DPC-ANN controller’s performance under realistic operating conditions.

Power Flow and Electrical Parameter Control

The active power control (Figure 8A) demonstrates exceptional tracking capabilities under the proposed DPC-ANN controller. Power variations ranging from 0 W to −1400 W showcase the system’s responsiveness to different wind speed conditions. The control strategy exhibits minimal overshoots during power level transitions, rapid settling times, and smooth power tracking across step changes, ultimately validating the robustness of the proposed control methodology.

Reactive power management (Figure 8B) represents another critical aspect of the simulation results. The controller maintains precise control, consistently keeping the reactive power at the zero reference value. This performance enables unity power factor operation and maintains grid integration and power quality management.

The current waveform analysis reveals the controller’s exceptional performance. Stator currents (Figure 8C) exhibit balanced sinusoidal waveforms with carefully controlled magnitude variations from 2.5 A to 5 A peak to peak and minimal distortion. Rotor currents (Figure 8D) demonstrate synchronized three-phase behavior with amplitude modulation corresponding directly to operating conditions, reaching peak values of approximately 5A during maximum power extraction.

The power factor performance further underscores the controller’s effectiveness. After a brief initial transient period, the system rapidly stabilizes at a near-unity power factor between 0.98 and 0.99 (Figure 8E). This consistent performance is achieved through precise reactive power control and indicates high-quality grid-side power management.

4.3. Comparative Control Strategy Analysis

The comparative analysis of different control strategies using MATLAB/Simulink provides compelling evidence of the DPC-ANN controller’s superiority. Active and reactive power regulation (Figure 9A,B) shows superior convergence characteristics, with minimal oscillations during reference changes and significantly reduced power ripples compared to the DPC-PI and Classical DPC methods.

The rotor current component analysis reveals nuanced performance differences. The quadrature current (Figure 9D) exhibits expected variations corresponding to active power changes, while the direct current (Figure 9C) remains stable around 1 A. Most notably, the DPC-ANN controller achieves lower current ripples, indicating enhanced control stability of the doubly fed induction generator system. The Total Harmonic Distortion (THD) analysis presents perhaps the most striking comparative advantage (Figure 9E). The proposed DPC-ANN strategy demonstrates significantly reduced harmonic distortion, achieving 1.29% THD compared to 2.76% for DPC-PI and 2.24% for Classical DPC. This reduction in harmonic distortion directly translates to improved power quality and potential extension of system longevity.

Significant improvements achieved by the intelligent DPC strategy (DPC-ANN), including a reduction in the harmonics of the stator current signals and a lower standard deviation, can be observed in the comparison shown in

Table 1. Comparison of the three controllers.

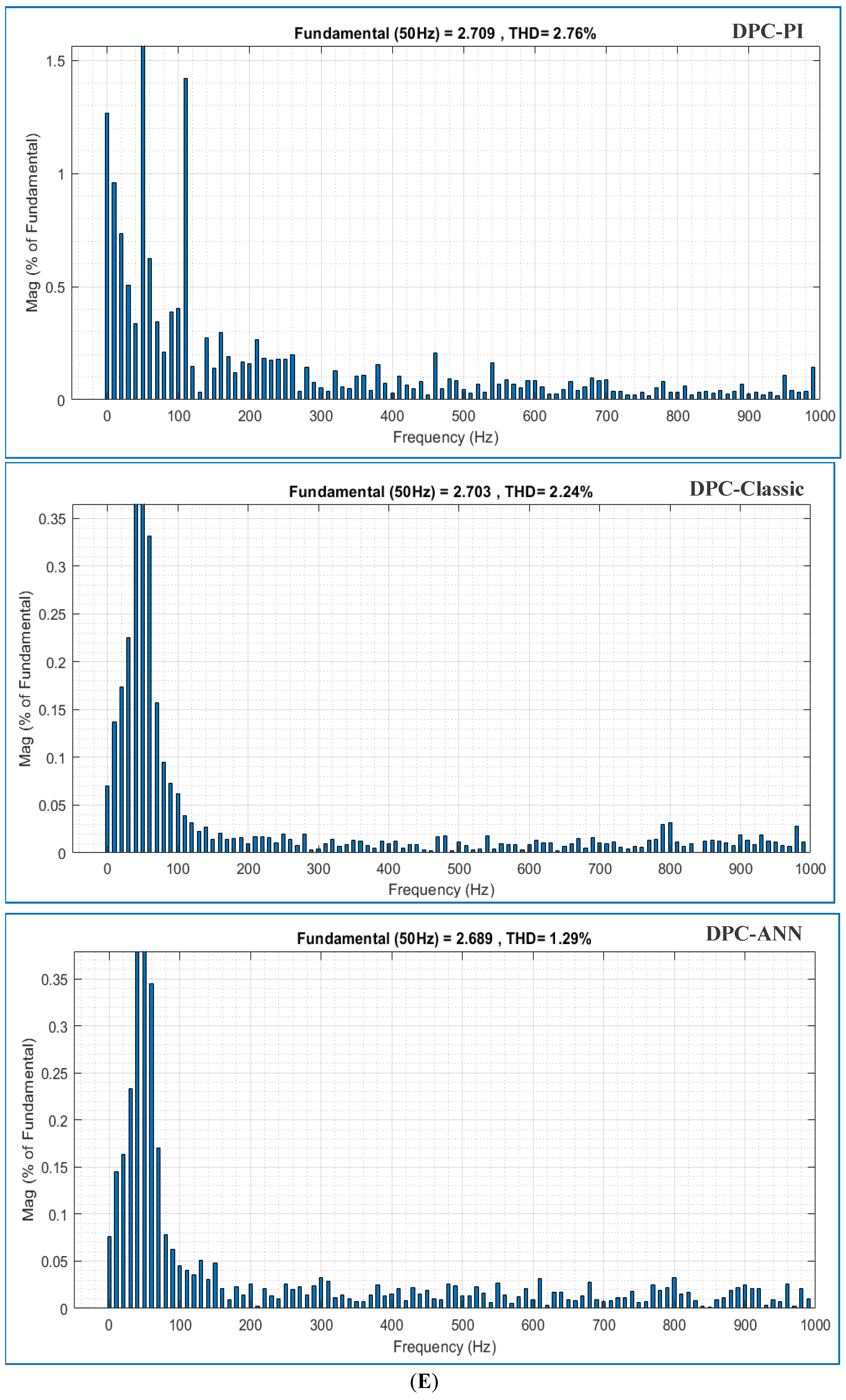
Performance		DPC-PI	DPC-Classic	DPC-ANN	Improvement
					vs. DPC-PI	vs. DPC-Classic
THD (%) of the current isa		2.76%	2.24%	1.29%	53.26%	42.41%
Standard deviation (σ)	σPs	35.97	11.64	7.66	78.70%	34.19%
	σQs	18.07	19.66	9.29	48.61%	52.75%
Set-point tracking		Good	Very good	Very good	-----
Precision		Medium	High	Very high	-----
Oscillation current		High	Medium	Low	-----

A low standard deviation (σ) indicates that the values are highly concentrated around the meaning, reflecting precise and stable regulation. Conversely, a high standard deviation reveals significant oscillations and a certain level of system instability.

A comparative analysis was conducted to evaluate the Total Harmonic Distortion of the stator current in comparison to previous studies, as depicted in

Table 2. Comparative analysis with control strategies referenced in the literature.

References	Strategies	THD (%)
[39]	DPC	2.62%
	Backstepping control	2.45%
	DPC with neural algorithm	2.22%
[40]	DPC with an L-filter	10.79%
	DPC with an LCL filter	4.05%
[37]	DTC	7.83%
	DTC with neural algorithm	3.26%
[41]	FOC	3.7%
[42]	SMC	3.05%
	FSMC	2.85%
[43]	Classic-DTC	6.7%
	Fuzzy-DTC	2.04%
Proposed strategy	DPC-ANN	1.29%

. The outcomes underscore the superior performance of the developed strategy, which yields a lower THD value compared to several other proposed control methods.

4.4. Implications and Recommendations

The comprehensive analysis definitively demonstrates the effectiveness of the DPC-ANN controller in optimizing wind turbine performance. The proposed approach exhibits superior capabilities in aerodynamic performance optimization, precise power flow control, and maintenance of high-quality electrical parameters.

Future research should focus on experimental validation under more diverse wind conditions, long-term performance assessment, and scalability testing across different wind turbine configurations to further validate and extend the findings of this study.

5. Conclusions

In conclusion, this comprehensive study has provided valuable insights into the performance and dynamic behavior of a wind turbine system equipped with a doubly fed induction generator (DFIG) under intelligent direct power control based on an artificial neuron network (DPC-ANN). Unlike conventional DPC approaches, this work introduces a dual-MLP control scheme, enabling more precise regulation of both active and reactive power components. Furthermore, the integration of real-time testing using OPAL-RT strengthens the practical relevance of this methodology.

The key findings of this research are as follows:

-

The DPC-ANN controller demonstrated superior active and reactive power control, maintaining effective tracking of reference values despite wind speed variations.

-

The DPC-ANN strategy proved effective in mitigating current ripples and achieving a near-unity power factor, indicating improved power quality.

-

Spectrum harmonic analysis showed the DPC-ANN controller yielded the lowest stator current THD of 1.29%, outperforming DPC-PI (2.76% THD) and DPC-Classic (2.24% THD).

-

The performance evaluation was conducted through both MATLAB/Simulink offline simulations and OPAL-RT real-time implementation, validating robust behavior under realistic operating conditions.

By emphasizing both real-time implementation and the novel dual-MLP structure, this study demonstrates the feasibility of ANN-based control strategies for wind energy systems. These results pave the way for more intelligent and adaptive renewable energy technologies, ensuring enhanced efficiency and stability in wind power generation.