Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review
Abstract
1. Introduction
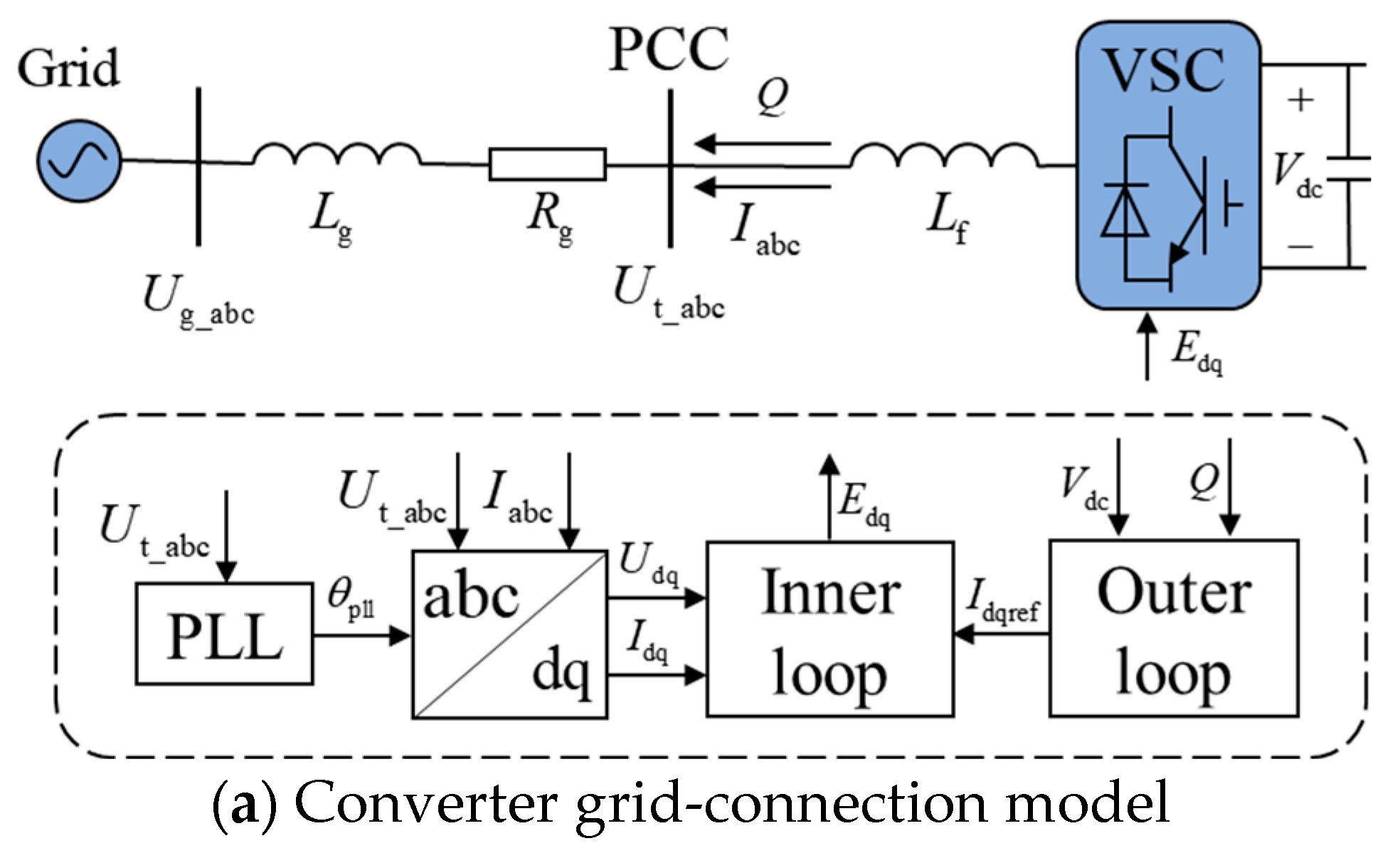
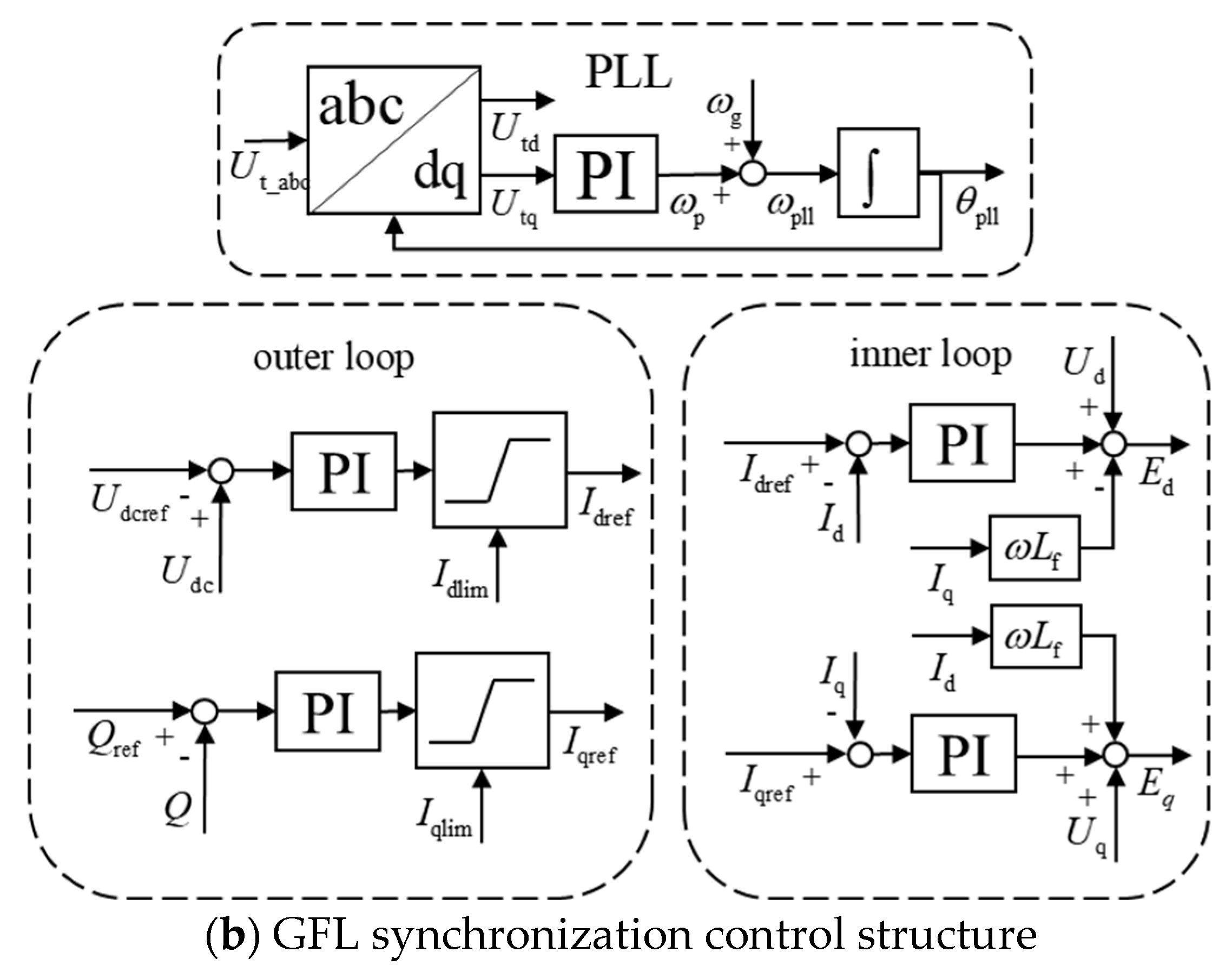
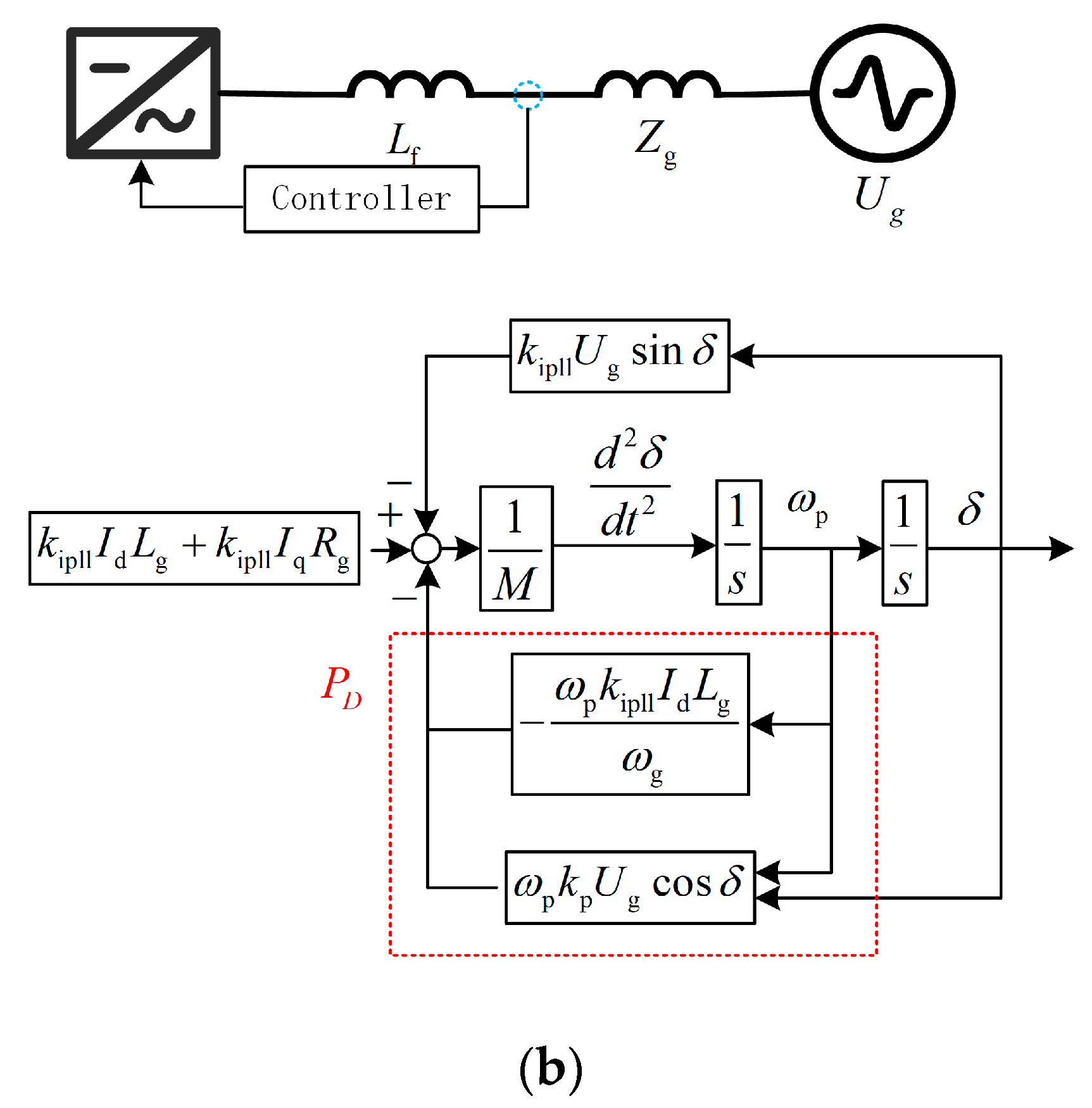
2. Model of GFL for Transient Analysis
- (1)
- Coupling terms between the PLL and other control loops (e.g., product terms of reference currents and PLL parameters) exist in the equations.
- (2)
- Nonlinear components (e.g., voltage outer loop saturation, current limiting) induce complex transient variations in system variables.
3. Understanding Transient Synchronization Stability in GFL Converters
3.1. Analysis Methods for Transient Synchronization Stability of GFL
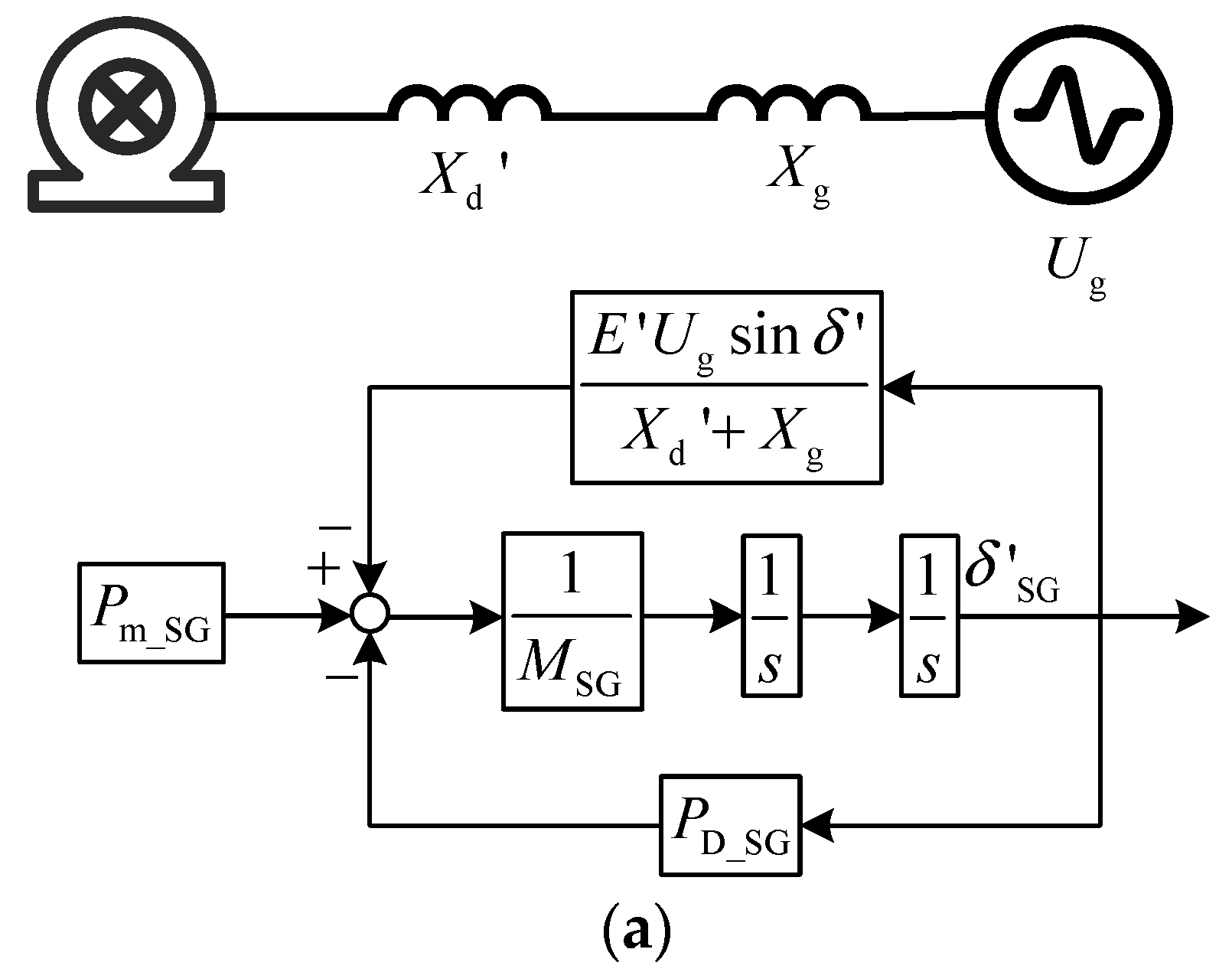
3.2. Synchronization Mechanism of GFL
3.3. Impact of Control Loop Interactions on GFL Synchronization Stability
- (1)
- The Outer Loop
- (2)
- The Inner Loop
- (3)
- Other Control Loops
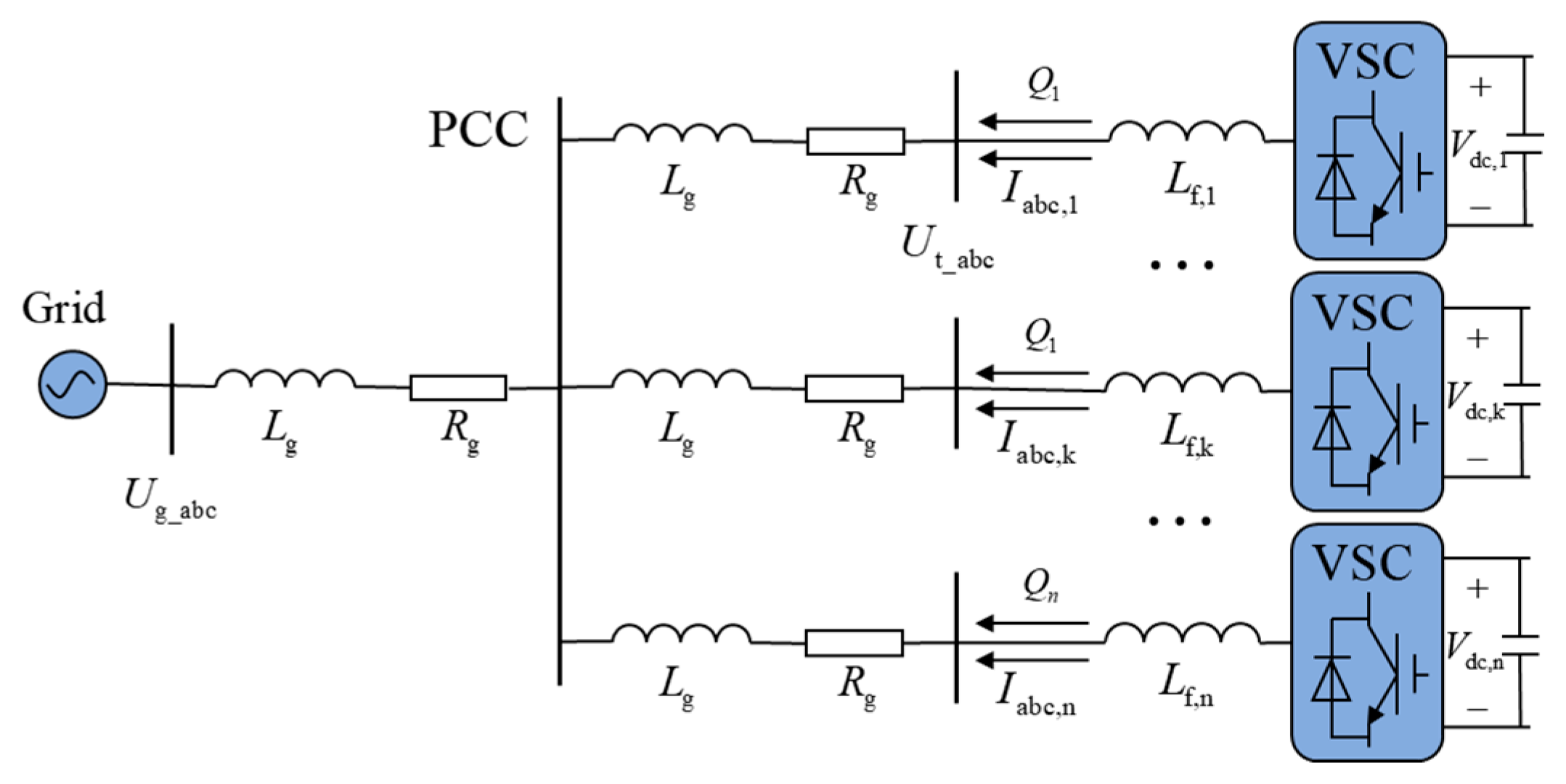
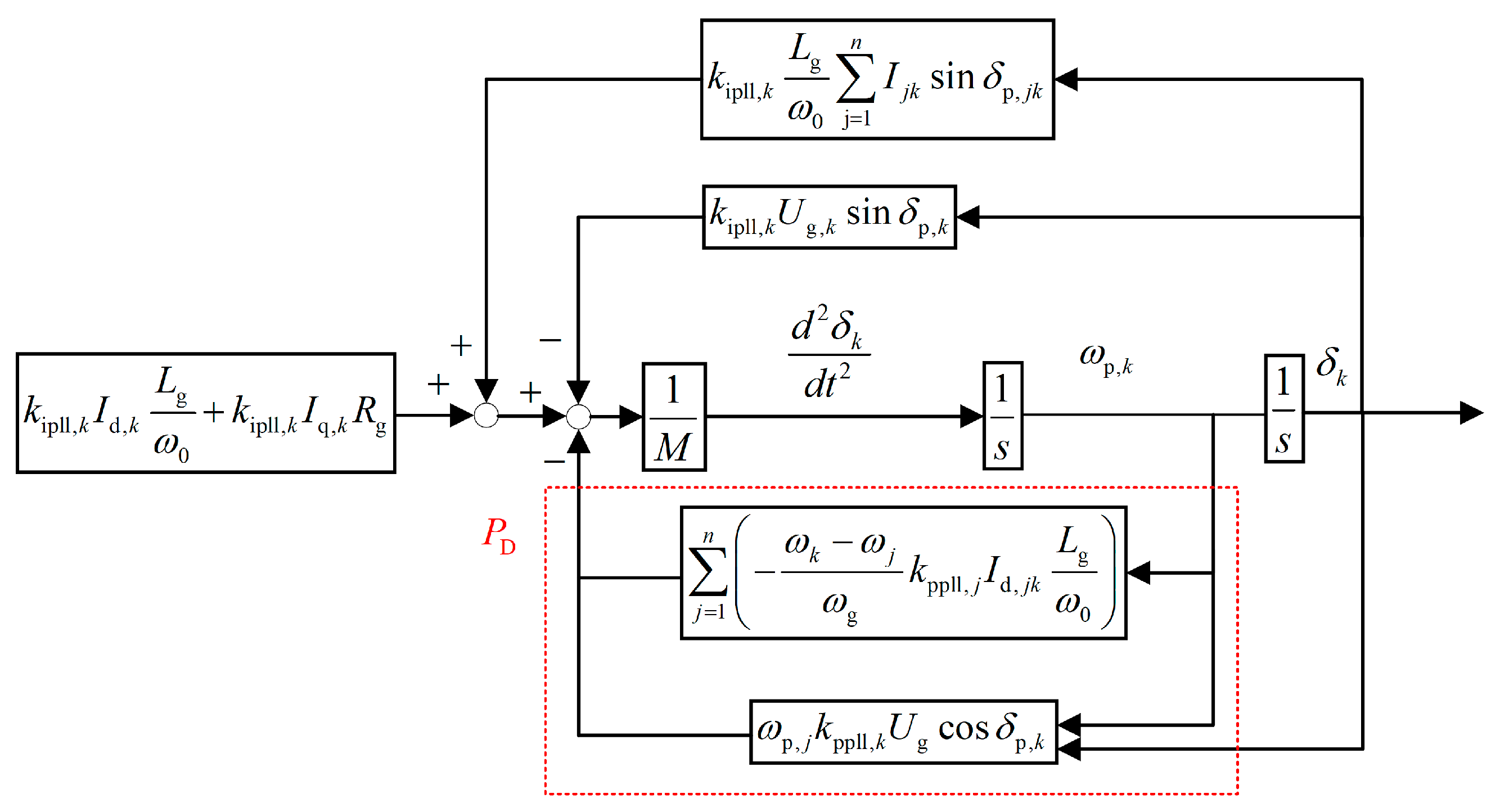
3.4. Synchronization Stability of Multi-Converter Systems
4. AI in Transient Synchronization Stability Analysis: Concepts, Applications and Future Prospects
5. Conclusions
- (1)
- The second-order motion model based on PLL dynamic equations provides an important theoretical framework for analyzing the transient synchronization stability of GFL. Its similarity to rotor motion equations of synchronous generators allows partial applicability of traditional methods. However, existing models often neglect coupling effects between outer-loop controls, current limiters, and PLL, leading to deviations in mechanistic understanding. Interactions among multiple control loops (e.g., voltage outer loop, current inner loop, and nonlinear limiting) significantly influence transient synchronization stability. Studies reveal that current loop bandwidth, DC voltage control strategies, and limiting modes alter the equivalent damping characteristics of the system, thereby affecting stability margins.
- (2)
- Traditional methods (e.g., equal-area criterion, Lyapunov functions) offer intuitiveness and computational efficiency advantages in low-order single-converter systems but struggle to extend directly to multi-converter interaction scenarios. While time-domain simulations can handle complex systems, they demand high computational resources and fail to reveal intrinsic patterns of stability boundaries. In multi-converter parallel systems, coupled power and damping terms between converters cause dynamically varying equivalent inertia. Current research has yet to fully clarify quantitative laws governing multi-converter interactions, necessitating the development of aggregated models that balance accuracy and complexity.
- (3)
- Data-driven methods (e.g., deep Bayesian learning, imbalanced sample optimization) demonstrate potential for rapid transient stability assessment but face challenges such as strong dependence on data quality and insufficient model interpretability. Physics-data fusion modeling (e.g., physics-informed neural networks), which embeds grid dynamic equations, enhances model generalization capabilities and credibility, offering new insights for stability prediction in complex scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GFL | Grid-following |
| PLL | Phase-locked loop |
| AI | Artificial intelligence |
| IBR | Inverter-based resource |
| VSC | Voltage source converter |
| PMSG | Permanent magnet synchronous generator |
| PV | Photovoltaic |
| GFM | Grid-forming |
| PCC | Point of common coupling |
| IGBT | Insulate-gate bipolar transistor |
| PWM | Pulse width modulation |
| GSI | Grid-supporting inverter |
| SISO | Single-input single-output |
| HIL | Hardware-in-the-loop |
| LVRT | Low-voltage ride-through |
| DBAL | Deep Bayesian active learning |
| BNNs | Bayesian neural networks |
| DAE | Denoising autoencoder |
| ADASYN | Adaptive synthetic sampling approach |
| MRMR | Minimum redundancy maximum relevance |
| WTA | Winner-takes-all |
| WAMS | Wide-area measurement systems |
| SVM | Support vector machine |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| GNN | Graph neural network |
| PINN | Physics-informed neural network |
References
- Gonzalez-Cajigas, A.; Bueno, E.J.; Roldan-Perez, J. Compliance of Grid-Forming Requirements of Grid Codes with a Type III Wind Turbine Controlled as a Virtual Synchronous Machine. IEEE Trans. Energy Convers. 2024, 39, 2244–2257. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Mohammed, N.; Ravanji, M.H.; Bahrani, B. Output Impedance Derivation and Small-Signal Stability Analysis of a Power-Synchronized Grid Following Inverter. IEEE Trans. Energy Convers. 2022, 37, 2696–2707. [Google Scholar] [CrossRef]
- Vahabzadeh, T.; Safavizadeh, A.; Ebrahimi, S.; Jatskevich, J. Admittance-Based Modeling for Electromagnetic Transient and Stability Analysis of Power-Electronic-Based Energy Conversion Systems. IEEE Trans. Energy Convers. 2024, 39, 1879–1890. [Google Scholar] [CrossRef]
- He, X.; Häberle, V.; Subotić, I.; Dörfler, F. Nonlinear Stability of Complex Droop Control in Converter-Based Power Systems. IEEE Contr. Syst. Lett. 2023, 7, 1327–1332. [Google Scholar] [CrossRef]
- Shi, K.; Ye, H.; Song, W.; Zhou, G. Virtual Inertia Control Strategy in Microgrid Based on Virtual Synchronous Generator Technology. IEEE Access 2018, 6, 27949–27957. [Google Scholar] [CrossRef]
- Cheema, K.M. A comprehensive review of virtual synchronous generator. Int. J. Electr. Power 2020, 120, 106006. [Google Scholar] [CrossRef]
- He, X.; Huang, L.; Subotić, I.; Häberle, V.; Dörfler, F. Quantitative Stability Conditions for Grid-Forming Converters with Complex Droop Control. IEEE Trans. Power Electr. 2024, 39, 10834–10852. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Me, S.P.; Hadavi, S.; Badrzadeh, B.; Karimi, A.; Bahrani, B. Nonlinear Transient Stability Analysis of Phased-Locked Loop-Based Grid-Following Voltage-Source Converters Using Lyapunov′s Direct Method. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2699–2709. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of PLL-Synchronized Voltage-Source Converters. IEEE Trans. Power Electron. 2020, 35, 3573–3589. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Tian, Z.; Huang, M.; Sun, P.; Zha, X.; Hu, P. A Conservatism Improved Transient Stability Analysis of Grid-Following Converters Based on the Proposed Elliptic-Equal Area Criterion. IEEE Trans. Power Deliv. 2024, 39, 1110–1123. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Cai, X. Large-Signal Grid-Synchronization Stability Analysis of PLL-Based VSCs Using Lyapunov’s Direct Method. IEEE Trans. Power Syst. 2022, 37, 788–791. [Google Scholar] [CrossRef]
- Zhang, Z.; Schuerhuber, R.; Fickert, L.; Friedl, K.; Chen, G.; Zhang, Y. Domain of Attraction′s Estimation for Grid Con-nected Converters with Phase-Locked Loop. IEEE Trans. Power Syst 2022, 37, 1351–1362. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-hill: New York, NY, USA, 1994. [Google Scholar]
- Ma, Y.; Zhu, D.; Hu, J.; Liu, D.; Ji, X.; Zou, X.; Kang, Y. Reduced-Order Modeling and Transient Stability Analysis of Grid-Connected VSC in DC-Link Voltage Control Timescale. IEEE J. Em. Sel. Top. Power Electron. 2024, 12, 2981–2993. [Google Scholar] [CrossRef]
- Kim, K.; Cui, S.; Jung, J. Current-Oriented Phase-Locked Loop Method for Robust Control of Grid-Connected Converter in Extremely Weak Grid. IEEE Trans. Power Electron. 2024, 39, 11963–11968. [Google Scholar] [CrossRef]
- Huang, S.; Yao, J.; Luo, Y.; Lin, Y.; Gong, S. Coupling characteristic analysis and synchronization stability control for Multi-Paralleled VSCs system under symmetric faults. Int. J. Electr. Power 2023, 151, 109134. [Google Scholar] [CrossRef]
- Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strat. Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, Y.; Yang, Z.; Kurths, J.; Zhan, M.; Lin, C. Synchronization stability of power-grid-tied converters. Chaos 2023, 33, 032102. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Enhanced Transient Angle Stability Control of Grid-Forming Converter Based on Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2022, 69, 9133–9144. [Google Scholar] [CrossRef]
- Yu, C.; Xu, H.; Liu, C.; Chen, C.; Sun, M.; Zhang, X. Research on Modeling, Stability and Dynamic Characteristics of Voltage-controlled Grid-connected Energy Storage Inverters Under High Penetration. Int. J. Electr. Power 2022, 143, 108397. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, Z.; Xu, Z. Proportion of Grid-forming Wind Turbines in Hybrid GFM-GFL Offshore Wind Farms Integrated with Diode Rectifier Unit Based HVDC System. J. Mod. Power Syst. Clean 2025, 13, 87–101. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; O’Donnell, T.; Milano, F. Impact of Current Transients on the Synchronization Stability Assessment of Grid-Feeding Converters. IEEE Trans. Power Syst. 2020, 35, 4131–4134. [Google Scholar] [CrossRef]
- Li, Y.; Lin, C.; Hu, J.; Guo, J. PLL Synchronization Stability of Grid-Connected VSCs Under Asymmetric AC Faults. IEEE Trans. Energy Convers. 2022, 37, 2438–2448. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Li, Z.; Ju, P.; Yuan, H.; Lan, Z.; Wang, Z. Grid-Synchronization Stability Analysis and Loop Shaping for PLL-Based Power Converters with Different Reactive Power Control. IEEE Trans. Smart Grid 2020, 11, 501–516. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, M.; Fan, L.; Miao, Z. Small-Signal Stability Analysis of Type-4 Wind in Series-Compensated Networks. IEEE Trans. Energy Convers. 2020, 35, 529–538. [Google Scholar] [CrossRef]
- Wu, C.; Lyu, Y.; Wang, Y.; Blaabjerg, F. Transient Synchronization Stability Analysis of Grid-Following Converter Con-sidering the Coupling Effect of Current Loop and Phase Locked Loop. IEEE Trans. Energy Convers. 2024, 39, 544–554. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, L.; Liu, Y.; Ye, N.; Hu, Y.; Guan, L. Transient Synchronous Stability Analysis of Grid-Following Converter Considering Outer-Loop Control with Current Limiting. Electronics 2024, 13, 3337. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, Y.; Wu, W.; Gong, W.; Guerrero, J.M. Stability Enhancing Voltage Feed-Forward Inverter Control Method to Reduce the Effects of Phase-Locked Loop and Grid Impedance. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3000–3009. [Google Scholar] [CrossRef]
- Liu, Y.; Geng, H.; He, C.; Ding, W.; Shen, C.; Yang, G. Equivalent Aggregated Modeling of Multi-VSC System for Transient Synchronization Stability Analysis. IEEE Trans. Power Syst. 2024, 39, 4296–4310. [Google Scholar] [CrossRef]
- De Caro, F.; Collin, A.J.; Giannuzzi, G.M.; Pisani, C.; Vaccaro, A. Review of Data-Driven Techniques for On-Line Static and Dynamic Security Assessment of Modern Power Systems. IEEE Access 2023, 11, 130644–130673. [Google Scholar] [CrossRef]
- Tian, Z.; Li, X.; Zha, X.; Tang, Y.; Sun, P.; Huang, M.; Yu, P. Transient Synchronization Stability of an Islanded AC Mi-crogrid Considering Interactions Between Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4463–4476. [Google Scholar] [CrossRef]
- Tang, Y.; Tian, Z.; Zha, X.; Li, X.; Huang, M.; Sun, J. An Improved Equal Area Criterion for Transient Stability Analysis of Converter-Based Microgrid Considering Nonlinear Damping Effect. IEEE Trans. Power Electron. 2022, 37, 11272–11284. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S.; Xu, S.; Bi, J.; Wang, Y. Synchronization Stability Analysis of PLL-based Grid-connected VSC System by Voltage Space Vectors. CSEE J. Power Energy Syst. 2024, 10, 2055–2064. [Google Scholar]
- Pei, J.; Yao, J.; Liu, Y.; Chen, S.; Sun, P.; Huang, S. Modeling and Transient Synchronization Stability Analysis for PLL-Based Renewa-ble Energy Generator Considering Sequential Switching Schemes. IEEE Trans. Power Electron. 2022, 37, 2165–2179. [Google Scholar]
- Fu, X.; Huang, M.; Chi, K.T.; Yang, J.; Ling, Y.; Zha, X. Synchronization Stability of Grid-Following VSC Considering Interactions of Inner Current Loop and Parallel-Connected Converters. IEEE Trans. Smart Grid 2023, 14, 4230–4241. [Google Scholar] [CrossRef]
- Wang, T.; Ji, T.; Jiao, D.; Li, Y.; Wang, Z. Transient synchronization stability analysis of PLL-based VSC using Lyapunov′s direct method. Int. J. Electr. Power 2022, 141, 13. [Google Scholar] [CrossRef]
- Li, C.; Wang, S.; Liang, J. Tuning Method of a Grid-Following Converter for the Extremely-Weak-Grid Connection. IEEE Trans. Power Syst. 2022, 37, 3169–3172. [Google Scholar] [CrossRef]
- Yang, Z.; Zhan, M.; Liu, D.; Ye, C.; Cao, K.; Cheng, S. Small-Signal Synchronous Stability of a New-Generation Power System With 100% Renewable Energy. IEEE Trans. Power Syst. 2023, 38, 4269–4280. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, H.; Duan, Z.; Jia, F.; Du, Z.; Wang, X. Small-signal Stability Analysis and Improvement with Phase-shift Phase-locked Loop Based on Back Electromotive Force Observer for VSC-HVDC in Weak Grids. J. Mod. Power Syst. Clean 2023, 11, 980–989. [Google Scholar] [CrossRef]
- Ding, Y.; Gao, F.; Khan, M.M. Transient Stability Analysis of Microgrid Considering Impact of Grid-Following Converter’s Current Controller. IEEE Trans. Power Electron. 2024, 39, 9100–9105. [Google Scholar] [CrossRef]
- Njoka, G.M.; Mogaka, L.; Wangai, A. Impact of variable renewable energy sources on the power system frequency stability and system inertia. Energy Rep. 2024, 12, 4983–4997. [Google Scholar] [CrossRef]
- Abdoli, O.; Gholipour, M.; Hooshmand, R. A novel method for synchronization stability enhancement of grid connected converters based on equal area criterion. Int. J. Electr. Power 2022, 139, 108062. [Google Scholar] [CrossRef]
- Fu, X.; Huang, M.; Pan, S.; Zha, X. Cascading Synchronization Instability in Multi-VSC Grid-Connected System. IEEE Trans. Power Electron. 2022, 37, 7572–7576. [Google Scholar] [CrossRef]
- Li, X.; Tian, Z.; Zha, X.; Sun, P.; Hu, Y.; Huang, M.; Sun, J. Nonlinear Modeling and Stability Analysis of Grid-Tied Paral-leled-Converters Systems Based on the Proposed Dual-Iterative Equal Area Criterion. IEEE Trans. Power Electron. 2023, 38, 7746–7759. [Google Scholar] [CrossRef]
- Ma, R.; Li, J.; Kurths, J.; Cheng, S.; Zhan, M. Generalized Swing Equation and Transient Synchronous Stability with PLL-Based VSC. IEEE Trans. Energy Convers. 2022, 37, 1428–1441. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, L.; Li, X.; Wang, Z.; Zang, X.; Zhu, J.; Zhou, X.; Wang, C. Transient Synchronization Stability of Grid-Tied Multi-VSCs System Considering Nonlinear Damping and Transient Interactions. IEEE Trans. Power Electron. 2024, 39, 16775–16791. [Google Scholar] [CrossRef]
- Dereje, T.; Zhan, L.; Hu, B.; Nian, H. Transient Synchronization Stability Modeling and Analysis of Grid-Following Converter Considering Current Dynamics. IEEE Access 2024, 12, 171066–171075. [Google Scholar] [CrossRef]
- Guo, J.; Zhai, D.; Li, X.; Wang, Z. Nonlinear Modeling and Transient Stability Analysis of Grid-Connected Voltage Source Converters during Asymmetric Faults Considering Multiple Control Loop Coupling. Appl. Sci. 2024, 14, 7834. [Google Scholar] [CrossRef]
- Wu, C.; Xiong, X.; Taul, M.G.; Blaabjerg, F. Enhancing Transient Stability of PLL-Synchronized Converters by Introducing Voltage Normalization Control. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 69–78. [Google Scholar] [CrossRef]
- Xing, G.; Chen, L.; Min, Y.; Tang, Y.; Li, Y.; Xu, S. Effects of PLL Frequency Limiters on Synchronization Stability of Grid Connected VSC and Strategy to Realize Global Stability. IEEE Trans. Energy Convers. 2023, 38, 2096–2107. [Google Scholar] [CrossRef]
- Yi, X.; Peng, Y.; Zhou, Q.; Huang, W.; Xu, L.; Shen, Z.J.; Shuai, Z. Transient Synchronization Stability Analysis and Enhancement of Paralleled Converters Considering Different Current Injection Strategies. IEEE Trans. Sustain. Energy 2022, 13, 1957–1968. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, G. Stability Analysis of a Weak-Grid-Connected Voltage-Sourced Rectifier Considering the Phase-Locked Loop Dynamics. IEEE Trans. Power Syst. 2023, 38, 436–446. [Google Scholar] [CrossRef]
- Li, Y.; Lu, Y.; Du, Z. Direct method of Lyapunov applied to synchronization stability of VSC with phase-locked loop. Electr. Power Syst. Res. 2023, 220, 109376. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, L.; Li, X.; Pang, X.; Li, X.; Zhou, X.; Wang, C. PLL Synchronization Transient Stability Analysis of a Weak-Grid Connected VSC During Asymmetric Faults. IEEE Trans. Power Electron. 2024, 39, 2140–2154. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhai, Z.; Sun, S.; Liu, X.; Qian, J.; Liu, S.; Fang, W. Fuzzy Optimization for Improving Transient Synchronization Stability of VSCs in Series-Compensated System. IEEE Trans. Ind. Appl. 2024, 60, 3578–3587. [Google Scholar] [CrossRef]
- Liu, A.; Cao, H.; Liu, J. Enhancing stability control of Phase-Locked loop in weak power grids. Int. J. Electr. Power 2024, 161, 110145. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, M.; Yan, H.; Tse, C.K.; Zha, X. Nonlinear and Transient Stability Analysis of Phase-Locked Loops in Grid-Connected Converters. IEEE Trans. Power Electron. 2021, 36, 1018–1029. [Google Scholar] [CrossRef]
- Han, M.; Ma, R.; Zhan, M. Transient Synchronous Stability Analysis and Assessment of PLL-Based VSC Systems by Bifurca-tion Theory. IEEE Trans. Energy Convers. 2024, 141, 108135. [Google Scholar] [CrossRef]
- Huang, S.; Yao, J.; Pei, J.; Chen, S.; Luo, Y.; Chen, Z. Transient Synchronization Stability Improvement Control Strategy for Grid-Connected VSC Under Symmetrical Grid Fault. IEEE Trans. Power Electron. 2022, 37, 4957–4961. [Google Scholar] [CrossRef]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F. Large Signal Synchronizing Instability of PLL-Based VSC Connected to Weak AC Grid. IEEE Trans. Power Syst. 2019, 34, 3220–3229. [Google Scholar] [CrossRef]
- Goksu, O.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjaer, P.C. Instability of Wind Turbine Converters During Current Injection to Low Voltage Grid Faults and PLL Frequency Based Stability Solution. IEEE Trans. Power Syst. 2014, 29, 1683–1691. [Google Scholar] [CrossRef]
- Wu, J.; Han, M.; Zhan, M. Transient synchronization stability of photovoltaics integration by singular perturbation analysis. Front. Energy Res. 2024, 12, 1332272. [Google Scholar] [CrossRef]
- Pal, D.; Panigrahi, B.K. Impact of DC-Bus Voltage Control on Synchronization Stability of Grid-Tied Inverters. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2782–2786. [Google Scholar] [CrossRef]
- Ma, M.; Wu, G.; Liu, K.; Meng, Q. Analysis of the non-minimum phase characteristics of the VSC system in a weak grid. In Proceedings of the 12th International Conference on Renewable Power Generation (RPG 2023), Shanghai, China, 14–15 October 2023; pp. 519–526. [Google Scholar]
- Wu, T.; Jiang, Q.; Huang, M.; Xie, X. Synchronization Stability of Grid-Following Converters Governed by Saturation Nonlinearities. IEEE Trans. Power Syst. 2022, 37, 4102–4105. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters with Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- He, C.; He, X.; Geng, H.; Sun, H.; Xu, S. Transient Stability of Low-Inertia Power Systems with Inverter-Based Generation. IEEE Trans. Energy Convers. 2022, 37, 2903–2912. [Google Scholar] [CrossRef]
- Liu, C.C.; Yang, J.; Chi, K.T.; Huang, M. Transient Synchronization Stability of Grid-Following Converters Considering Nonideal Current Loop. IEEE Trans. Power Electron. 2023, 38, 13757–13769. [Google Scholar] [CrossRef]
- Cheng, C.; Xie, S.; Qian, Q.; Xu, J.; Zhang, X. Nonlinear Modeling and Global Stability Condition of Single-Phase Grid-Tied Inverter Considering SRF-PLL and Duty-Cycle Saturation. IEEE Trans. Ind. Electron. 2022, 69, 6973–6983. [Google Scholar] [CrossRef]
- Cheng, C.; Xie, S.; Qian, Q.; Xu, J.; Zeng, B.; Lv, J. On Stability of Time-Invariant Current Controlled Weak-Grid-Tied Inverters Con-sidering Sinusoidal Pulsewidth Modulation Saturation and Parameter Uncertainties. IEEE Trans. Ind. Electron. 2022, 69, 11359–11369. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; He, J.; Xu, T.; Yu, Z.; Wang, C.; Zhang, C. Subsynchronous Interaction Between Direct-Drive PMSG Based Wind Farms and Weak AC Networks. IEEE Trans. Power Syst. 2017, 32, 4708–4720. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, X.; Li, F.; Fu, X.; Han, F.; Wang, J. A double-machine equivalent method for evaluating the plant-and unit-level stability of hybrid grid-connected renewable power plants. CSEE J. Power Energy Syst. 2023, 1–13. [Google Scholar] [CrossRef]
- Zheng, F.; Wu, G.; Lin, X.; Zheng, S.; Wu, X.; Lin, Y.; Deng, C. Research on control strategy for improving stability of multi-inverter parallel system under weak grid condition. Int. J. Electr. Power 2023, 153, 109121. [Google Scholar] [CrossRef]
- He, X.; Geng, H. PLL Synchronization Stability of Grid-Connected Multiconverter Systems. IEEE Trans. Ind. Appl. 2022, 58, 830–842. [Google Scholar] [CrossRef]
- Dragicevic, T.; Vazquez, S.; Wheeler, P. Advanced Control Methods for Power Converters in DG Systems and Microgrids. IEEE Trans. Ind. Electron. 2021, 68, 5847–5862. [Google Scholar] [CrossRef]
- Li, N.; Zhang, M.; Xu, X.; Qiu, S.; Li, J.; Ma, K. Transient Stability Analysis and Enhancement Strategy of Hybrid-converter System of Grid-Following and Grid-Forming. In Proceedings of the 2024 China International Conference on Electricity Distribution (CICED), Hangzhou, China, 12–13 September 2024; pp. 313–317. [Google Scholar]
- Wang, K.; Chen, Z.; Wei, W.; Sun, X.; Mei, S.; Xu, Y.; Zhu, T.; Liu, J. Power System Transient Stability Assessment Based on Deep Bayesian Active Learning. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 1692–1696. [Google Scholar]
- Tan, B.; Yang, J.; Tang, Y.; Jiang, S.; Xie, P.; Yuan, W. A Deep Imbalanced Learning Framework for Transient Stability Assessment of Power System. IEEE Access 2019, 7, 81759–81769. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, Q.; Sun, H.; Yu, Z.; Wu, J.; Hao, L. A novel data-driven approach for transient stability prediction of power systems considering the operational variability. Int. J. Electr. Power 2019, 107, 379–394. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, J.; Xu, P.; Gao, T.; Gao, D.W. Explainable AI in Deep Reinforcement Learning Models for Power System Emergency Control. IEEE Trans. Comput. Soc. Syst. 2022, 9, 419–427. [Google Scholar] [CrossRef]
- Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568. [Google Scholar] [CrossRef]
- Liu, J.; Sun, H.; Li, Y.; Fang, W.; Niu, S. An Improved Power System Transient Stability Prediction Model Based on mRMR Feature Selection and WTA Ensemble Learning. Appl. Sci. 2020, 10, 2255. [Google Scholar] [CrossRef]
- Mishra, P.; Zhang, P. Physics-informed transient stability assessment of microgrids. iEnergy 2023, 2, 231–239. [Google Scholar] [CrossRef]
- Li, B.; Xu, S.; Sun, H.; Li, Z.; Yu, L. System Strength Assessment Based on Multi-task Learning. CSEE J. Power Energy Syst. 2024, 10, 41–50. [Google Scholar]
- Du, Y.; Li, F.; Li, J.; Zheng, T. Achieving 100x Acceleration for N-1 Contingency Screening with Uncertain Scenarios Using Deep Convolutional Neural Network. IEEE Trans. Power Syst. 2019, 34, 3303–3305. [Google Scholar] [CrossRef]
| Method | Principle and Characteristic | |
|---|---|---|
| Equal area criterion | Principle | Determination of system stability by comparison of acceleration area and deceleration area based on second-order equations of motion |
| Applicable Scenarios | Single machine infinite bus system | |
| Computational Complexity | Low | |
| Adaptability to Multi-Converter Systems | Poor | |
| Data Dependency | No simulation data required | |
| Interpretability | High | |
| Advantages | It is capable of portraying the system stability boundary; it can reveal the mechanism of converter instability more clearly, which is easy to understand. It is capable of portraying the system stability boundary; it can reveal the mechanism of converter instability more clearly, which is easy to understand; it requires fewer computational resources and is faster. | |
| Disadvantages | Lack of effective treatment of the equivalent damping term, uncertainty about the conservatism and optimism of the results; difficulty in considering Lack of effective treatment of the equivalent damping term, uncertainty about the conservatism and optimism of the results; difficulty in considering more stability influences and expanding to higher order systems. | |
| Reference | Refs. [17,27,33,43,44,45,46,47,48] | |
| Phase portrait | Principle | Inscribing power system trajectory images based on numerical scoring methods. |
| Applicable Scenarios | Single machine infinite bus system | |
| Computational Complexity | Moderate | |
| Adaptability to Multi-Converter Systems | Poor | |
| Data Dependency | Dependent on initial conditions | |
| Interpretability | Moderate | |
| Advantages | The description of the stabilization mechanism is intuitive and easy to understand; the computation requires fewer resources and is faster. | |
| Disadvantages | Stabilizing the domain of attraction is difficult to determine when the system order is high. | |
| Reference | Refs. [24,49,50,51,52] | |
| Time domain simulation | Principle | Based on the numerical integration method, the system state motion process is simulated to determine the stability of the system under a given operation mode. The system state motion process is simulated to determine the stability of the system under a given operation. |
| Applicable Scenarios | Any system with detailed modeling | |
| Computational Complexity | Very High | |
| Adaptability to Multi-Converter Systems | Good | |
| Data Dependency | Full model parameters needed | |
| Interpretability | Low | |
| Advantages | Suitable for complex systems, it provides detailed system dynamic processes and allows direct observation of system stabilization or destabilization processes. It provides detailed system dynamic processes and allows direct observation of system stabilization or destabilization processes. | |
| Disadvantages | It can only obtain the stability of the system under a given operating condition, and cannot portray the stability domain of the system; and the simulation requires more resources and is slow in computation. | |
| Reference | Refs. [28,48,53] | |
| Lyapunov energy function | Principle | The stabilization problem is transformed into a problem of comparing function values with critical values by constructing a Lyapunov function and determining the critical values of the function. |
| Applicable Scenarios | Systems with analytical models | |
| Computational Complexity | High | |
| Adaptability to Multi-Converter Systems | Moderate | |
| Data Dependency | Model-based | |
| Interpretability | High | |
| Advantages | Accurate results of attraction domain calculations; applicable to higher-order system stability judgments; capable of assessing transient. Accurate results of attraction domain calculations; applicable to higher-order system stability judgments; capable of assessing transient stability margins. | |
| Disadvantages | There is no general construction method for Lyapunov functions, and proper Lyapunov functions are difficult to obtain. | |
| Reference | Refs. [36,54,55,56] | |
| Method | Principle and Characteristic | |
|---|---|---|
| DBAL Framework | Input Data | Simulation data |
| Key Findings | Uses BNNs to adaptively evaluate prediction confidence via posterior probability, reducing computational costs through uncertainty-based active learning | |
| Advantages | High accuracy with minimal data requirements; reduces simulation costs | |
| Disadvantages | Relies on simulated data; real-time performance limited by active learning iterations | |
| Deep Imbalanced Learning Framework | Input Data | High-dimensional operational data |
| Key Findings | Combines modified DAE for dimensionality reduction and ADASYN-synthesized unstable samples to enhance recognition | |
| Advantages | Improves unstable scenario detection; data compression enhances efficiency | |
| Disadvantages | Complex data balancing; synthetic samples may introduce noise | |
| ANN Hybrid Model | Input Data | Multi-scenario operational data |
| Key Findings | Integrates diverse architectures to boost classification performance with fewer training instances | |
| Advantages | High classification accuracy; reduced training data dependency | |
| Disadvantages | Black-box nature limits interpretability; requires substantial training data | |
| Hybrid Methods | Input Data | Real-time WAMS data |
| Key Findings | Combines physics-based stability equations with AI for real-time online prediction | |
| Advantages | Merges physical principles with data-driven insights; real-time reliability | |
| Disadvantages | High integration complexity; requires interdisciplinary collaboration | |
| Physics-Data Integrated Modeling | Input Data | Physical equations |
| Key Findings | Embeds PINNs to enforce physical constraints, improving credibility and interpretability | |
| Advantages | Enhances trustworthiness via physics compliance; semi-interpretable “grey-box” solutions | |
| Disadvantages | Requires domain expertise for constraint definition; higher computational costs | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhu, L.; Xu, X.; Li, D.; Liang, Z.; Ye, N. Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review. Energies 2025, 18, 1975. https://doi.org/10.3390/en18081975
Liu Y, Zhu L, Xu X, Li D, Liang Z, Ye N. Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review. Energies. 2025; 18(8):1975. https://doi.org/10.3390/en18081975
Chicago/Turabian StyleLiu, Yang, Lin Zhu, Xinya Xu, Dongrui Li, Zhiwei Liang, and Nan Ye. 2025. "Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review" Energies 18, no. 8: 1975. https://doi.org/10.3390/en18081975
APA StyleLiu, Y., Zhu, L., Xu, X., Li, D., Liang, Z., & Ye, N. (2025). Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review. Energies, 18(8), 1975. https://doi.org/10.3390/en18081975







